Open Access Article
Open Access ArticleAnticancer potential of β-sitosterol and oleanolic acid as through inhibition of human estrogenic 17beta-hydroxysteroid dehydrogenase type-1 based on an in silico approach†
Alfinda Novi Kristanti *ab,
Nanik Siti Aminah
*ab,
Nanik Siti Aminah ab,
Imam Siswantoac,
Yosephine Sri Wulan Manuharabd,
Muhammad Ikhlas Abdjanae,
Andika Pramudya Wardanaae,
Ei Ei Aungaf and
Yoshiaki Takayag
ab,
Imam Siswantoac,
Yosephine Sri Wulan Manuharabd,
Muhammad Ikhlas Abdjanae,
Andika Pramudya Wardanaae,
Ei Ei Aungaf and
Yoshiaki Takayag
aDepartement of Chemistry, Faculty of Science and Technology, Universitas Airlangga, Surabaya 60115, Indonesia. E-mail: alfinda-n-k@fst.unair.ac.id; nanik-s-a@fst.unair.ac.id
bBiotechnology of Tropical Medicinal Plants Research Group, Universitas Airlangga, Indonesia
cBioinformatic Laboratory, UCoE Research Center for Bio-Molecule Engineering, Universitas Airlangga, Surabaya, Indonesia
dDepartment of Biology, Faculty of Science and Technology, Universitas Airlangga, Surabaya 60115, Indonesia
ePhD Student of Mathematics and Natural Sciences, Faculty of Science and Technology, Universitas Airlangga, Komplek Kampus C UNAIR, Jl. Mulyorejo, Surabaya, 60115, Indonesia
fDepartement of Chemistry, Yadanarbon University, Amarapura Township, Mandalay, Myanmar
gFaculty of Pharmacy, Meijo University, 150 Yagotoyama, Tempaku, Nagoya, 468-8503 Japan
First published on 13th July 2022
Abstract
The human estrogenic enzyme 17beta-hydroxysteroid dehydrogenase type-1 (HSD17B1) provides biosynthesis regulation of active estrogen in stimulating the development of breast cancer through cell proliferation. The β-sitosterol is classified as a steroid compound and is actually a type of triterpenoid compound that has a similar structure to a steroid. This similarity provides a great opportunity for the inhibitor candidate to bind to the HDS17B1 enzyme because of the template similarity on the active site. Several in silico approaches have been applied in this study to examine the potential of these two inhibitor candidates. Pharmacokinetic studies showed positive results by meeting several drug candidate criteria, such as drug-likeness, bioavailability, and ADMET properties. A combination of molecular docking and MD simulation showed good conformational interaction of the inhibitors and HSD17B1. Prediction of binding free energy (ΔGbind) using the Molecular Mechanics-Generalized Born Surface Area (MM-GBSA) approach shows ΔGbind (kcal mol−1) of C1–HSD17B1: −49.31 ± 0.23 and C2–HSD17B1: −33.54 ± 0.34. Meanwhile, decomposition energy analysis (ΔGresiduebind) suggested several key residues that were also responsible for the interaction with inhibitors, such as C1–HSD17B1 (six residues: Leu96, Leu149, Pro187, Met193, Val225, and Phe226) and C2–HSD17B1 (four residues: Ile14, Gly94, Pro187, and Val188). Hopefully, the obtained results from this research could be considered for the mechanistic inhibition of the HSDS17B1 enzyme at molecular and atomistic levels.
Introduction
Steroids are involved in various biological processes, such as reproduction, aging, metabolism, and cancer.1–4 The estrogen-mediated effects of steroids are responsible for the genetic formation of breast tissue in women. One of the enzymes that plays a role in steroid regulation is human estrogenic 17beta-hydroxysteroid dehydrogenase type-1 (HSD17B1). The HSD17B1 enzyme is the first member of the HSD17B enzyme family that mediates the conversion of 17beta-hydroxysteroids, such as androgens and estrogens.5 This enzyme provides regulation in the final stages of active estrogen (estradiol) biosynthesis.6 It has been reported that the activity of this enzyme increases the level of estrogen. It stimulates the development of breast cancer cells through cell proliferation.7,8 Additionally, it has been reported that inhibition of HSD17B1 enzyme activity prevents proliferation in breast cancer cells in vitro and reduces tumor volume in human breast cancer lines grown (mice and rat models) in vivo.5,9 Therefore, this enzyme is a potential target in inhibiting the regulation of cancer cell development.6–9Several research projects are looking for candidate inhibitors that can block the process of estrogen biosynthesis through enzyme HSD17B1 inhibition.4,9,10 There are several inhibitors with known activity (Km) as HSD17B1 inhibitors, such as dihydrotestosterone (DHT): 32 ± 9 μM, and androstandione: 26 ± 9 μM.4 It should be noted that both inhibitors have a similar structure, which is often known as a “mimic structure”. The structural similarity is expected to have a better chance of binding to the targeted protein because of the template similarity on the active site.11 Thus, it is necessary to select a candidate inhibitor based on these considerations. Several natural product compounds can offer this feature, including triterpenoid and steroid groups as secondary metabolic compounds.12,13
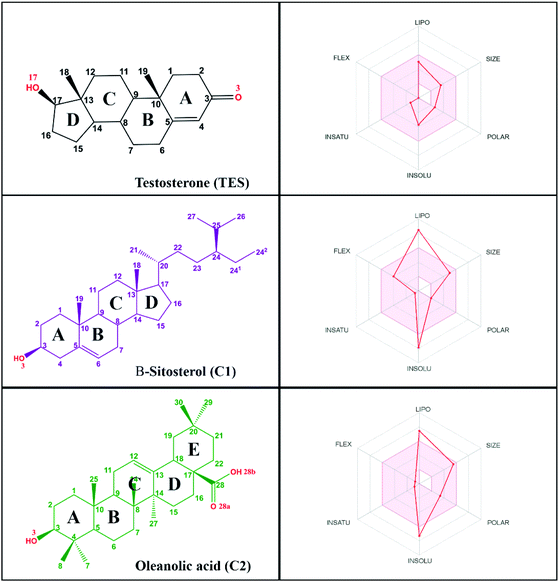
Research on natural products as inhibitor candidates shows promising prospects in finding a potential inhibitor of the HSD17B1 enzyme.14 Additionally, natural products have provided good activity in inhibiting breast cancer cells.14,15 Some of them are β-sitosterol and oleanolic acid compounds, which were isolated and characterized from the stem bark of Syzygium aqueum in a previous study.15 The structural similarity of these compounds to dihydrotestosterone (a known HSD17B1 inhibitor) is expected to mean they will interact on the active site of the HSD17B1 enzyme. Structurally, it has –OH and –COOH groups at positions C3 (β-sitosterol) and C3, C28 (oleanolic acid) (Fig. 1). These groups increase the possibility of interacting with water molecules on the enzyme active site.
Additionally, the presence of these groups can allow the formation of hydrogen bond interactions (donor or acceptor) with key residues on the enzyme active site at the molecular level.
Theoretical studies using an in silico approach provide an alternative way of finding candidate compounds that have potential as HSD17B1 inhibitors at the molecular level.16,17 A combination of molecular docking and molecular dynamics (MD) simulation provides a comprehensive structure-based approach to studying the interaction of the inhibitor with the HSD17B1 enzyme.16–18 Structure-based studies can provide a more detailed description of the inhibition mechanism through interactions with amino acid residues on the active site of the targeted protein. Molecular docking provides good calculation efficiency for inhibitor coordination on the enzyme active site.19,20 Meanwhile, the MD simulation offers a comprehensive analysis of the interaction between an inhibitor and the targeted protein during the simulation time.17,21 The evaluation proceeds by several considerations, such as grid-score20 and binding free energy,22 aiming to see the binding affinity of inhibitor to HSD17B1. In addition, an evaluation of toxicity and drug-likeness provides an initial description of the pharmacokinetic properties of each inhibitor.23–25 Several considerations of the in silico approach offered in this research are expected to explain the inhibition mechanism of the HDS17B1 enzyme by β-sitosterol and oleanolic acid at the molecular level.
Methodology
Pharmacokinetic prediction
The drug-likeness and bioavailability calculations were performed by the SwissADME web service.24 The criteria for drug-likeness and bioavailability were calculated based on several rules, namely those of Lipinski and Veber. Meanwhile, prediction of ADMET (absorption, distribution, metabolism, excretion, and toxicity) of inhibitors as drug candidates used the web service pkCSM.25 This prediction aims to study the activity of inhibitors as drug candidates when they enter the body.Data set: ligand and receptor preparation
The selection of a target protein used the HSD17B1 co-crystal from the protein databank (PDB ID: 1JTV). The crystal complex contains a native ligand on the active site of the HSD17B1 enzyme as an inhibitor (testosterone, PDB ID: TES). The TES ligand was used as a reference or control in this study by considering it as an alternative binding mode to the HSD17B1 enzyme, which had been described in previous studies.4 The TES coordinates extracted from the co-crystals were used as initial coordinates for docking purposes. Meanwhile, the standard residues (amino acid residues) from co-crystals were used as receptors. Moreover, the key residues from the HSD17B1 active site, such as (Val143, Met147, Leu149, Pro187, Tyr218, His221, Val225, Phe226, Phe259, Leu262, Met279, and Val283) were used as the main targets for analysis purposes. β-Sitosterol (C1) and oleanolic acid (C2) were the candidate inhibitors used in this research. Those compounds were isolated (from Syzygium aqueum stem bark) and characterized in previous studies.15 The electrostatic potential (ESP) for candidate charge inhibitors was calculated using the Semiempirical Quantum Parametric Method-7 (SQM-PM7) contained in the Gaussian 16 package. Meanwhile, the AMBER FF14SB force field and the Austin Model 1-Bond Charge Correction (AM1-BCC) were applied to parameterize the receptors.Molecular docking
Molecular docking was performed using the Dock6 package.20 The inhibitor–HSD17B1 energy calculation was based on functional grid scoring (grid spacing: 0.30 Å, center XYZ: 11.08, 8.46, −11.24, and dimensions XYZ: 27.21, 28.28, 23.61). A flexible conformation with a functional grid scoring approach was mainly used to evaluate the redocking process. The successful redocking process gave the best superposition with an RMSD ≤ 2.0 Å. The functional grid-based scoring process was analyzed in the gas state (eqn (1)) by considering parameters such as the van der Waals energy (EvdW) and electrostatic energy (Eele). The coordinates of each ligand obtained from the docking process were calculated in-depth using molecular dynamics simulations.| Grid-score = EvdW + Eele | (1) |
Topology preparation
The coordinates of each ligand that had been obtained from the docking process were integrated into the MD simulation using the General AMBER Force Field (GAFF).26 The topology preparation on each system used the tleap tools in the AMBER18 package. The topology preparation of each system took the form of ligand, receptor, complex, and complex-solvation. The solvent model used was TIP3P water solvent with a counter ion (Na+) as a neutralizing system. The system minimization process was carried out in three stages: water molecule minimization, complex minimization, and entire system minimization. All the minimization processes used 500 steps of steepest descent and 1500 steps of the conjugated gradient. All minimized systems were ready for use in the simulation process.Molecular dynamics simulation
The MD simulation was performed using the AMBER18 package in several stages, such as heating, equilibrium, and trajectory production. The heating process was carried out gradually (10 K to 310 K) for 200 ps with a harmonic restraint of 30 kcal mol−1 Å−2. The periodic system equilibrium stages continued with harmonic restraints of 30, 20, 10, and 5 kcal mol−1 Å−2 for 1300 ps. The entire system was simulated to 100 ns (ensemble NPT: 310 K and 1 atm). The production stage during the simulation time (0–100 ns) aimed to produce trajectories for further analysis and evaluation purposes, such as conformational dynamics, binding affinity, hydrogen bonding, and solvent accessibility.22,27Binding free energy analysis
Calculation of binding free energy (ΔGbind) and decomposition energy (ΔGresiduebind) was performed in the last 20 ns (80–100 ns) of the trajectories. This consideration was made based on calculation efficiency with the result that system stability was achieved in its trajectory range. The ΔGbind and ΔGresiduebind calculations were made using the MMPBSA.py tools available in the AMBER18 package.22 MMPBSA.py is an efficient program with the flexibility to accommodate the needs of users performing end-state free energy calculations. In detail, the analysis of ΔGbind and ΔGresiduebind was undertaken using the Molecular Mechanics-Generalized Born Surface Area (MM-GBSA) approach. In summary, ΔGbind can be described through eqn (2) by considering the energy complex (ΔGligand–HSD17B1), receptor (ΔGHSD17B1), and ligand (ΔGligand). Mathematically, ΔGbind is described through eqn (3) by considering several parameters: the gas term (ΔGgas), solvation term (ΔGsol), and entropy change (−TΔS). However, −TΔS is neglected because of the high computational cost. Additionally, each ligand shows a similar structure, so the possibility of the resulting entropy change is not significant.28 Based on some of these considerations −TΔS can be ignored in the ΔGbind calculation. In detail, the energy component in ΔGbind consists of bonded energy (ΔEbonded), van der Waals energy (ΔEvdW), and electrostatic energy (ΔEele). In particular, ΔEbonded consists of bond, angle, and torsion energies with a conformational energy equal to zero. Meanwhile, the energy component in ΔGsol is the total of the generalized Born models (ΔGelesol) and solvent-accessible surface area energy (ΔGnonpolarsol). In detail, free energy binding can be calculated by considering some of these energy components (eqn (4)).| ΔGbind = ΔGligand–HSD17B1 − (ΔGHSD17B1 + ΔGligand) | (2) |
| ΔGbind = ΔGgas + ΔGsol − TΔS | (3) |
| ΔGbind = ΔEbonded + ΔEvdW + ΔEele + ΔGnonpolarsol + ΔGelesol | (4) |
Results and discussion
Pharmacokinetic study: drug-likeness, bioavailability, and ADMET
Prediction of pharmacokinetic properties, such as drug-likeness, bioavailability, and ADMET, aims to see the potential of a compound as a drug candidate. In this section, we try to describe some of the parameters responsible for the drug-likeness and bioavailability of candidate compounds. The results showed that each compound has quite promising drug-likeness and bioavailability criteria. Several drug-likeness criteria showed that there was only one violation of the Lipinski29 and Veber30 rules on M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Log
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P (Table S1†). Notably, a good drug candidate shows fewer than a total of two violations of Lipinski's and Veber's rules. Compounds that meet the criteria of MW ≤ 500 (g mol−1), M
P (Table S1†). Notably, a good drug candidate shows fewer than a total of two violations of Lipinski's and Veber's rules. Compounds that meet the criteria of MW ≤ 500 (g mol−1), M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Log
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ≤ 4.15, ∑HBA ≤ 10, and ∑HBD ≤ 5 (ref. 29) are highly appreciated as drug candidates. Moreover, compounds that have criteria of ∑rotatable bonds ≤ 10 and TPSA ≤ 140 Å2 (ref. 30) are expected to increase the ability of drug candidates to penetrate cell membranes. Additionally, bioavailability shows that there are two violations in the range of oral bioavailability criteria for each candidate compound (Fig. 1). In general, the criteria for oral bioavailability meet the following requirements: lipophilicity (−0.7 < X
P ≤ 4.15, ∑HBA ≤ 10, and ∑HBD ≤ 5 (ref. 29) are highly appreciated as drug candidates. Moreover, compounds that have criteria of ∑rotatable bonds ≤ 10 and TPSA ≤ 140 Å2 (ref. 30) are expected to increase the ability of drug candidates to penetrate cell membranes. Additionally, bioavailability shows that there are two violations in the range of oral bioavailability criteria for each candidate compound (Fig. 1). In general, the criteria for oral bioavailability meet the following requirements: lipophilicity (−0.7 < X![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Log
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P3 < 5.0), size (150 D < MW < 500 D), polarity (20 Å2 < TPSA < 130 Å2), insolubility (0 < ESOL < 6), unsaturation (0.25 < Csp3 < 1), and flexibility (0 < number of rotatable bonds <9).24 Meanwhile, drug-likeness and bioavailability evaluations were also carried out on the TES ligand as a comparison (Table S1†). In summary, there was no violation of Lipinski's and Veber's rules. This data is supported by oral bioavailability that meets the overall criteria in a promising way (Fig. 1).
P3 < 5.0), size (150 D < MW < 500 D), polarity (20 Å2 < TPSA < 130 Å2), insolubility (0 < ESOL < 6), unsaturation (0.25 < Csp3 < 1), and flexibility (0 < number of rotatable bonds <9).24 Meanwhile, drug-likeness and bioavailability evaluations were also carried out on the TES ligand as a comparison (Table S1†). In summary, there was no violation of Lipinski's and Veber's rules. This data is supported by oral bioavailability that meets the overall criteria in a promising way (Fig. 1).
The ADMET study provides a clear image of a drug candidate's effects on the body. This parameter plays an important role in drug discovery.23–25 Prediction of ADMET properties shows that each compound shows promising potential (Table S2†). This is indicated by the value of Caco-2 permeability > 0.90 and intestinal absorption-human > 30% (+HIA).23 These results showed that the compounds were absorbed into the body very well. The distribution of C1 compound showed that it was able to penetrate the blood–brain barrier (logBB > 0.3) and CNS permeability > −2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) logPS. It identified that this compound could affect the work of the central nervous system (brain). On the other hand, compounds TES and C2 do not have the potential to penetrate the blood–brain barrier. However, they have the opportunity to penetrate the central nervous system (CNS). On the other hand, the metabolic parameters showed that each compound did not have any effect on the activity of metabolic enzymes (cytochrome isoenzymes), such as CYP1A2, CYP2C19, CYP2C9, CYP2D6, or CYP3A4. Hopefully, the compounds will not interfere with the activity of metabolic enzymes when consumed by the body. Crucial parameters such as toxicity are key parameters in the study of ADMET properties. Interestingly, all compounds belong to the non-toxic category (non-AMES toxicity and non-skin sensitization). However, compound C2 shows a category of hepatotoxicity that can cause damage to liver cells. Therefore, it is necessary to develop and modify C2 compounds for medicinal purposes. The ADMET results indicated that initial data on pharmacokinetic predictions show the compounds have potential worth considering.
logPS. It identified that this compound could affect the work of the central nervous system (brain). On the other hand, compounds TES and C2 do not have the potential to penetrate the blood–brain barrier. However, they have the opportunity to penetrate the central nervous system (CNS). On the other hand, the metabolic parameters showed that each compound did not have any effect on the activity of metabolic enzymes (cytochrome isoenzymes), such as CYP1A2, CYP2C19, CYP2C9, CYP2D6, or CYP3A4. Hopefully, the compounds will not interfere with the activity of metabolic enzymes when consumed by the body. Crucial parameters such as toxicity are key parameters in the study of ADMET properties. Interestingly, all compounds belong to the non-toxic category (non-AMES toxicity and non-skin sensitization). However, compound C2 shows a category of hepatotoxicity that can cause damage to liver cells. Therefore, it is necessary to develop and modify C2 compounds for medicinal purposes. The ADMET results indicated that initial data on pharmacokinetic predictions show the compounds have potential worth considering.
Molecular docking: superposition and inhibitor–HSD17B1 conformation
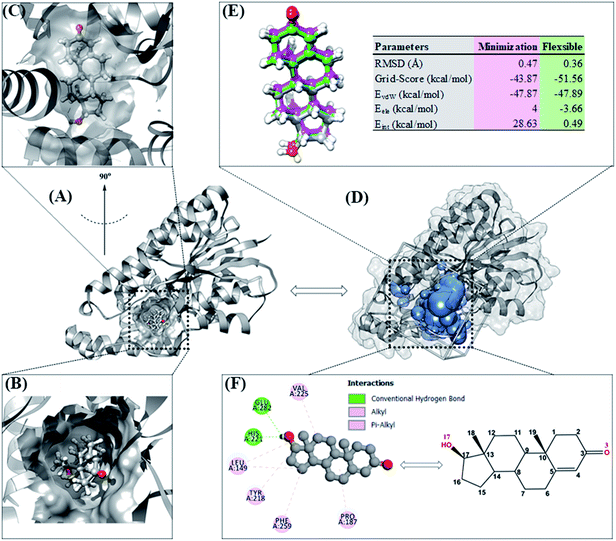
Molecular docking can provide a clear initial picture of the coordinates of the active site on the targeted protein.31 However, it is necessary to pay attention to several parameters for the required process of coordinate selection and native ligand superposition. The redocking stage is one of the validation stages of the docking process for determining the active site of the targeted protein based on the coordinates of the native ligand. The redocking step has been widely implemented for efficient molecular docking calculations.19,20 The analysis was carried out on the TES coordinates as a reference for the co-crystals. The coordinates showed that the position of TES is in the pocket of the HSD17B1 enzyme (Fig. 2A). Additionally, the TES structural conformation indicated that the position of the –OH (O17) group is deep in the pocket. On the other hand, the position of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (O3) group is in the outermost pocket (Fig. 2B and C). This is due to steric clashes between the 19-methyl group and Leu149. The conformational stability of TES in the pocket is due to hydrophobic interactions and hydrogen bonding.4 The initial coordinate selection used a cluster sphere (radius 10.0 Å) selected from the TES coordinates (Fig. 2D). The results showed that the redocking process met the criteria with an RMSD value of 0.36 Å and a grid-score of −51.56 kcal mol−1 (Fig. 2E). These results identify that the TES superposition has coordinates close to the co-crystal coordinates. It is intended that the docking inhibitor candidate process takes place at the coordinates of the HSD17B1 active site. Furthermore, the TES superposition shows hydrogen bonding (H-bond) interactions with His221 and Glu282 residues (Fig. 2F). The types of H-bond interactions are HBA (O17⋯H–N(His221)) and HBD ((Glu282)O⋯H–O17). Several parameters that have been described in the redocking stage were used for the candidate inhibitor docking process.
O (O3) group is in the outermost pocket (Fig. 2B and C). This is due to steric clashes between the 19-methyl group and Leu149. The conformational stability of TES in the pocket is due to hydrophobic interactions and hydrogen bonding.4 The initial coordinate selection used a cluster sphere (radius 10.0 Å) selected from the TES coordinates (Fig. 2D). The results showed that the redocking process met the criteria with an RMSD value of 0.36 Å and a grid-score of −51.56 kcal mol−1 (Fig. 2E). These results identify that the TES superposition has coordinates close to the co-crystal coordinates. It is intended that the docking inhibitor candidate process takes place at the coordinates of the HSD17B1 active site. Furthermore, the TES superposition shows hydrogen bonding (H-bond) interactions with His221 and Glu282 residues (Fig. 2F). The types of H-bond interactions are HBA (O17⋯H–N(His221)) and HBD ((Glu282)O⋯H–O17). Several parameters that have been described in the redocking stage were used for the candidate inhibitor docking process.
The optimized geometry of the candidate inhibitor was docked into the HSD17B1 active site. The results show that each candidate has a grid-score < grid-score reference, i.e., C1: −69.90 kcal mol−1 and C2: −61.46 kcal mol−1 (Fig. 3). This indicates that the inhibitor candidate has good interaction in the gas term.32 In detail, the results of the energy contribution (EvdW + Eele) in kcal mol−1 for each inhibitor were C1: EvdW = −70.25 and Eele = 0.35 and C2: EvdW = −55.99 and Eele = −5.47. A similar energy contribution was also shown by TES–HSD17B1 (Fig. 2E). The interaction energy based on the functional grid scoring (gas term) for each inhibitor showed good binding stability with the targeted protein. This can be identified through a grid score that has a negative value. The grid score (higher negative value) indicated more thermodynamically stable interaction between the inhibitor and the targeted protein. Overall, the contribution of van der Waals energy (EvdW) shows the largest contribution to the interaction between the inhibitor and HSD17B1 compared to electrostatic energy (Eele). Meanwhile, several residues are responsible for the inhibitor–HSD17B1 interaction (Fig. 2F and S1†), such as TES (7 residues: Leu149, Pro187, Tyr218, His221, Val225, Phe259, and Glu282), C1 (11 residues: Val143, Met147, Leu149, Tyr155, Cys185, Pro187, Val188, Tyr218, His221, Phe259, and Val283), and C2 (4 residues: Ser142, Leu149, Tyr155, and Gly186). Details of the overall interactions for each complex are provided in Table S3.† It should be noted that some of the parameters measured in the molecular docking are the initial conformations at the gas term. Therefore, the process of evaluating these results needs to be studied using MD simulation to get more comprehensive results. However, molecular docking is quite helpful in efficiently determining the initial coordinates for each complex.
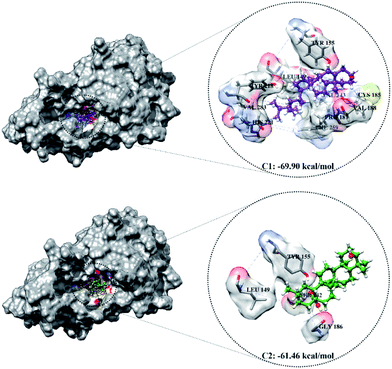 | ||
| Fig. 3 The molecular docking result of candidate–HSD17B1: the conformation of each candidate on the enzyme pocket area. | ||
Conformational dynamics analysis
The topology of each system was prepared based on the coordinates of inhibitor–HSD17B1 obtained from molecular docking.16,17 The system that formed was evaluated more comprehensively to see its conformational dynamics. Several parameters were calculated to see the conformational dynamics quality of each system for 100 ns, including the total energy (Etot), potential energy (Epot), kinetic energy (Ekin), the root-mean-square displacement (RMSD), radius of gyration (RoG), and the root-mean-square fluctuation (RMSF).Energy analysis in each system in the form of Etot, Epot, and Ekin aimed to see the convergence achieved during the simulation time. Notably, the contribution of the Etot parameter shows the contribution of Epot + Ekin.33 The results showed that each system had achieved good convergence. This can be identified by the absence of significant fluctuating changes in each system (Fig. S2†). The average value of the contribution of each energy is shown in Table S4.† A system with convergence can be used to continue the process of analyzing the compactness and stability.
System stability analysis is indicated by the complex RMSD value.21,34 The fact the simulation process reached 100 ns identified that each system has good stability. It is characterized by fairly good fluctuating stability from 15 ns to 100 ns (Fig. 4). Significant fluctuations occurred at the beginning of the simulation (0–200 ps) due to the heating process and increased gradually from 200 ps to 15 ns to reach an equilibrium process. Overall, each system has a stability difference that is not too significant. This is indicated by the average complex RMSD (nm) of TES–HSD17B1: 0.26 ± 0.03, C1–HSD17B1: 0.26 ± 0.03, and C2–HSD17B1: 0.27 ± 0.03. Based on our assumptions, the stability that occurs in the candidate inhibitor system is caused by having a similar structure to the reference ligand. Thus, the positions of the C1 and C2 structures were able to occupy the HSD17B1 enzyme pocket well. However, this assumption will be explained further in the next section by considering the binding affinity for each system.
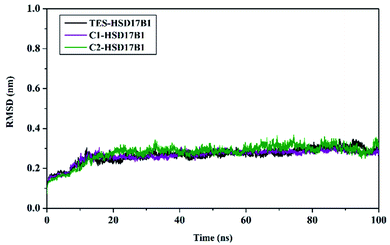 | ||
| Fig. 4 Trajectory analysis: the root-mean-square displacement of each complex plotted during the 100 ns of MD simulation. | ||
The structural compactness is based on the RoG parameter.35 The RoG analysis aims to see whether the structure is stably folded or not.
The calculation was carried out for 100 ns to see the RoG fluctuations shown in Fig. S3.† Changes in RoG fluctuations in each system did not show a significant difference. This is supported by the average values of RoG (nm), TES–HSD17B1: 19.73 ± 0.14, C1–HSD17B1: 19.79 ± 0.09, and C2–HSD17B1: 19.89 ± 0.11. Changes in the values of these fluctuations indicate that the structure of each system is well folded. This is corroborated by the average structure taken per unit time of 20 ns for each system during the simulation time of 100 ns (Fig. S4†). Overall, there was no significant change in structural conformation during the simulation time (0–100 ns) in each system.
The RMSF was calculated to identify the flexibility of the protein over the simulation time (Fig. S5†). The TES–HSD17B1 system showed higher fluctuation compared to the other systems. In summary, the flexibility trend for each system was TES–HSD17B1 > C2–HSD17B1 > C1–HSD17B1 (Table S4†). Higher fluctuation (∼2.00 nm) was shown by residues 130–133, 174–177, 199–201, 204–205, 208–210, 281, and 284–285 (alpha-helix and loop regions). Moreover, twelve key residues (Val143, Met147, Leu149, Pro187, Tyr218, His221, Val225, Phe226, Phe259, Leu262, Met279, and Val283) that affect the main thermodynamic force for binding were also analyzed. The fluctuation changes from the key residues on the active site showed that His221, Met279, and Val283 residues had higher fluctuations compared to other residues (Fig. S6†).
The description of several parameters shows that the dynamic conformation formed during the simulation time had reached a fairly good convergence and stability. Therefore, further analysis was considered in the form of binding affinity, hydrogen bonding, and water accessibility using the last 20 ns (80–100 ns) of the trajectories. This consideration was made based on the efficiency of calculations that are often used for simulation analysis.21,34 It should be noted that this consideration is useful if the complex RMSD has achieved good enough stabilization.
Binding affinity prediction: binding free energy and key binding residues
The binding affinity was calculated for each complex using the MM-GBSA method available in the AMBER18 package.22 Determination of binding affinity was calculated based on 100 snapshots extracted from the last 20 ns of the trajectories. Additionally, the calculation was carried out by considering the energy contribution in the gas and solution terms described in Table 1. The calculation process for each energy component was the main focus for looking at the energy contribution to binding free energy (ΔGbind).| Energy (kcal mol−1) | TES–HSD17B1 | C1–HSD17B1 | C2–HSD17B1 |
|---|---|---|---|
| ΔEvdW | −40.99 ± 0.27 | −57.84 ± 0.24 | −45.93 ± 0.34 |
| ΔEele | −9.36 ± 0.29 | −4.66 ± 0.33 | −15.03 ± 0.41 |
| ΔGgas | −50.35 ± 0.33 | −62.51 ± 0.36 | −60.97 ± 0.43 |
| ΔGelesol | 23.12 ± 0.24 | 20.52 ± 0.30 | 32.84 ± 0.28 |
| ΔGnonpolarsol | −5.05 ± 0.01 | −7.33 ± 0.02 | −5.41 ± 0.02 |
| ΔGsol | 18.07 ± 0.24 | 13.19 ± 0.29 | 27.42 ± 0.28 |
| ΔGbind | −32.28 ± 0.25 | −49.31 ± 0.23 | −33.54 ± 0.34 |
The energy contributions at C1 and C2 show that ΔGbind is promising as an inhibitor of the HSD17B1 enzyme. It is taken into consideration that the candidate ΔGbind (C1 and C2) is stronger than that of the native ligand ΔGbind as a reference (a higher negative value). Thus, the candidate inhibitors show promising potential to inhibit the HSD17B1 enzyme. It is hoped that candidates with good binding affinity will be able to bind strongly to the active site of the targeted protein.36 The goal is to block the active site of the HSD17B1 enzyme, which is responsible for regulating the supply of active estrogen as fuel for breast cancer cell development.7,8
Analysis of binding free energy (ΔGbind) showed the energy trend (kcal mol−1) of C1–HSD17B1 (−49.31 ± 0.23) < C2–HSD17B1 (−33.54 ± 0.34) < TES–HSD17B1 (−32.28 ± 0.25) based on the MM-GBSA approach. The binding free energy cannot be separated from the effect of the energy contribution in gas (ΔGgas) and solution (ΔGsol) terms. In general, the energy contribution in the gas term (ΔEvdW + ΔEelec) has advantages compared to the solution term (ΔGnonpolarsol + ΔGelesol). This is due to the unfavorable contribution of the polar solvation free energy (ΔGelesol) of the Generalized Born (GB) solvent model of each complex. In previous reports, the dielectric constant strongly influenced the calculation of ΔGelesol and the variable dielectric model showed potential power.28,37 However, the energy contribution of ΔGgas + ΔGsol showed quite promising results for each inhibitor.
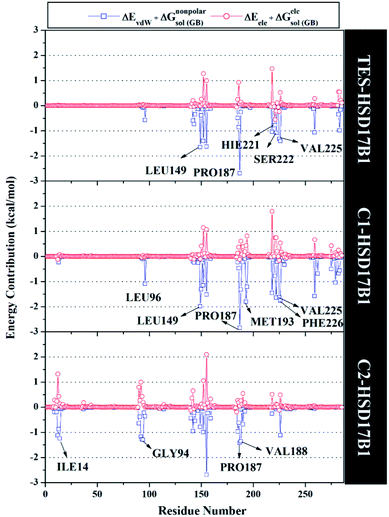
Specifically, free energy key residues play a crucial role in observing the inhibitory mechanism of the HSD17B1 enzyme in calculating energy decomposition (ΔGresiduebind). The key residues with a promising free energy contribution were evaluated based on ΔGresiduebind ≤ −1.00 kcal mol−1 criteria.38 Calculation of ΔGresiduebind was performed using 100 snapshots on the last 20 ns of the trajectories via dcomp tools. The results (Fig. 5) showed that there are key residues that have stronger free energy in each complex, including TES–HSD17B1 (five residues: Leu149, Pro187, His221, Ser222, and Val225), C1–HSD17B1 (six residues: Leu96, Leu149, Pro187, Met193, Val225, and Phe226), and C2–HSD17B1 (four residues: Ile14, Gly94, Pro187, and Val188). These results identify that these key residues interact with inhibitors on the HSD17B1 pocket. The key residues Leu149 and Pro187 were highlighted in the inhibition mechanism of the HSD17B1 enzyme. Previous research reported that the Leu149 residue plays a role in steroid discrimination and modulates DHT levels in breast tissue.4 Additionally, the residue of Pro187 is a hydrophobic and aromatic residue that contributes to the main thermodynamic force for the binding mode. Therefore, the interaction evaluation of the inhibitors with key residues plays a crucial role in understanding the inhibition mechanism. Specifically, the energy contribution ΔGresiduebind is affected by the energy contribution in the gas and solution terms, ΔEvdW + ΔGnonpolarsol(GB) and ΔEele + ΔGelesol(GB) provided by Fig. 6. We can see that the energy contribution ΔEvdW + ΔGnonpolarsol(GB) is able to stabilize the free energy of each residue. It is inseparable from the contribution of ΔEvdW energy in binding mode key residues39
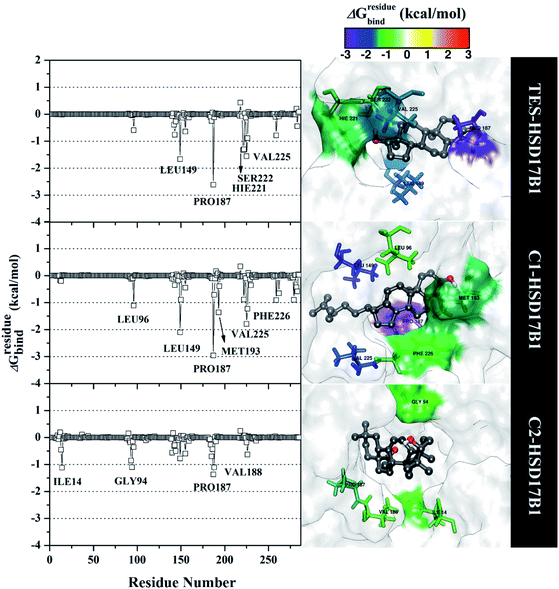 | ||
| Fig. 5 The residual energy decomposition was plotted along with the simulation over the last 20 ns of each complex. | ||
Hydrogen bonding analysis
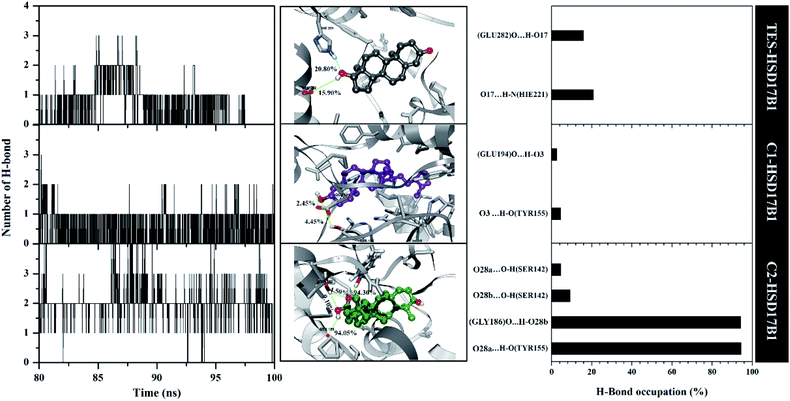
The previous section described the interaction of amino acids with inhibitors at the molecular level. In this section, we try to present the interaction of amino acids with inhibitors at the atomistic level. Hydrogen bonding (H-bond) analysis is the main ligand–protein interaction.40,41 Analyses were performed using 2000 snapshots extracted from the last 20 ns of the trajectories. The evaluation process was carried out on number, type (HBD and HBA), distance, and % occupation of H-bond (Fig. 7).The H-bond number parameter shows the number of H-bond interactions between ligand and protein. The results of the analysis during the last 20 ns of simulation time showed TES–HSD17B1 had three H-bonds, C1–HSD17B1 had three H-bonds, and C2–HSD17B1 had four H-bonds. The obtained number of H-bonds was used to look at occupation levels. This procedure aimed to see how long the bond was recorded during the simulation time. Surprisingly, the C1-HSD17B1 complex has only two H-bonds with a percentage occupation <10.0%. Meanwhile, the C2-HSD17B1 complex has four H-bonds, with two H-bonds having occupancy percentages >90.0%. Several reports state that the criterion for a strong category of H-bonding is H-bond ≥70%.42,43 This explains that the H-bond interaction which has the highest percentage occupation deserves to be considered in the ligand–protein interaction. In detail, the TES–HSD17B1 interaction involves two H-bonds: (i) O17⋯HN(His221) with 20.8%, 2.97 Å, HBA and (ii) O17–H⋯O(Glu282) with 15.9%, 2.76 Å, HBD. The interaction of the H-bond with these two residues (His221 and Glu282) showed good correlation with the molecular docking results (Fig. 2F) and the results of previous studies.4 Meanwhile, the interactions of the H-bond in C1–HSD17B1 were (i) O3⋯H–O(Tyr155) with 4.45%, 3.08 Å, HBA, and (ii) O3–H⋯O(Glu194) with 2.45%, 2.78 Å, HBD. Additionally, the interactions of the H-bonds in C2–HSD17B1 were (i) O28a⋯HO(Tyr155) with 94.30%, 2.85 Å, HBA, (ii) O28b-H⋯O(Gly186) with 94.05%, 2.93 Å, HBD, (iii) O28b⋯HO(Ser142) with 9.10%, 3.17 Å, HBA, and (iv) O28a⋯HO(Ser142) with 4.50%, 3.12 Å, HBA. In particular, the C2–HSD17B1 complex has two strong H-bond categories with the % occupation of H-bonds ≥70%. As explained, the presence of the –OH and –COOH groups contributes to the H-bond interaction. This further strengthens the existence of this group playing an important role in ligand–protein interactions at the atomistic level.
Solvent accessibility in the HSD17B1 active site
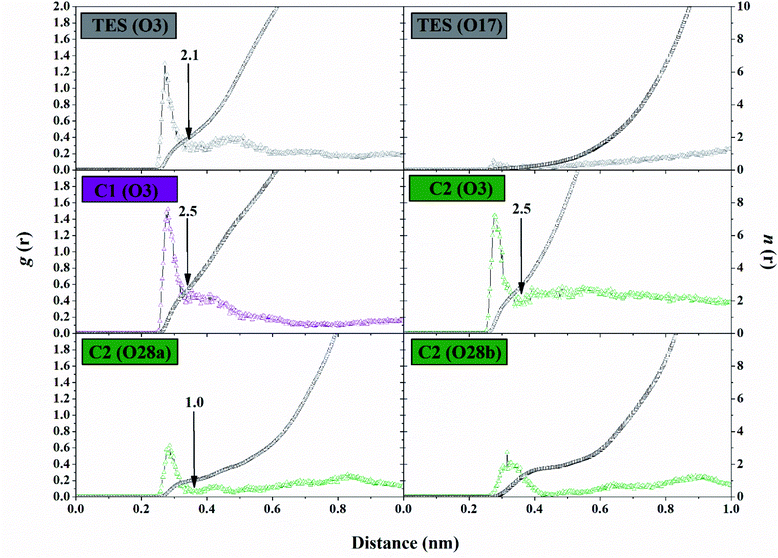
The solvent accessibility surface area (SASA) aims to see the ability of water molecules as solvents to access the surface of the active side area (pocket) during the simulation time. The role of water molecules on the active site surface plays an important role in mediating the interaction between the ligand and the targeted protein.44 It shows the solvent could access the surface of the active site up to ∼9.30 nm2. The C1–HSD17B1 system showed greater solvent access than the other systems. In detail, the SASA parameters (nm2) showed TES–HSD17B1: 7.91 ± 1.01, C1–HSD17B1: 9.30 ± 0.87, and C2–HSD17B1: 8.83 ± 0.85. However, no system showed a significant difference in this parameter (Fig. S7†). As previously mentioned, the presence of water molecules on the surface of the active site of the targeted protein affects the stability of the protein structure. Moreover, its stability can be achieved through the interaction of hydrophobic contacts, hydrogen bonds, π-stacking, salt bridges, amide stacking, or cation–π interaction.45The water molecule contained in the HSD17B1 active site needs to be studied for its distribution process during the simulation time. This aims to see the opportunities for water molecules to approach the ligand interface. In the previous section, the presence of the –OH and –COOH functional groups played an important role in the interaction with water molecules, in particular, the analysis of the oxygen (O) atoms in each ligand. Therefore, the possibility of water molecules approaching the oxygen atom can be analyzed through the radial distribution function (RDF).38 Analysis of this parameter was undertaken through the integration number on the first minimum value of the oxygen atom in each ligand.43 The TES–HSD17B1 complex showed that O3 atoms were more exposed to water molecules than O17 atoms. This can be seen in the atomic distance of O3 (n(r): 2.15 and g(r): 0.22) at the first peak, which is 0.35 nm. On the other hand, the O17 atom shows almost no hydration peak at all. Meanwhile, complexes C1–HSD17B1 and C2–HSD17B1 showed that water molecules were well distributed around the oxygen atom interface of each inhibitor. Except that O28b on the C2 inhibitor shows rather low access of water molecules at the interface. Meanwhile, the remaining atoms in each inhibitor C1 (O3) and C2 (O3 and O28a) showed promising access to water molecules (Fig. 8). In detail, the parameters measured for each atom are C1 (O3): distance = 0.33 nm, n(r) = 2.54, and g(r) = 0.37; C2 (O3): distance = 0.34 nm, n(r) = 2.51 and g(r) = 0.32; and C2 (O28a): distance = 0.36 nm, n(r) = 1.03 and g(r) = 0.04. The RDF analysis provides information about how the water molecules approach the oxygen atom in each ligand. The nonzero value at the first minimum peak indicates a high level of water transfer in the first solvation shell. These values are observed at TES (O3), C1 (O3), and C2 (O3 and O28a). This statement is supported by the value of n(r) being within ∼2.1–2.5 at TES (O3), C1 (O3), and C2 (O3). In particular, C2 (O28a) has a consistent value, being stably solvated by one molecule of water. This can be seen through the first minimum distance at ∼0.4 nm. As mentioned earlier, the oxygen atoms at TES (O17) and C2 (28b) have low hydration peaks. It can be seen that the first minimum of the two oxygen atoms is zero. This explains that there is no water transfer in the first solvation shell. Additionally, this condition also states that no water molecules are exposed at the interface of both oxygen atoms. Taking together all the findings discussed above, this explains that the presence of –OH and –COOH groups in each ligand can provide greater opportunities for interaction with water molecules. Based on the consideration of several parameters (SASA and RDF) above, the water accessibility of each system shows that the distribution of solvent molecules is quite well exposed.
Conclusions
In this work, we have presented an in silico approach including a pharmacokinetic study, molecular docking, and MD simulation to study β-sitosterol (C1) and oleanolic acid (C2) compounds as potential anticancer agents through the inhibition of human estrogenic 17beta-hydroxysteroid dehydrogenase type-1 (HSD17B1). Pharmacokinetic studies suggest that each candidate had non-toxic criteria worthy of consideration. A study of the interaction between the inhibitor and the HSD17B1 enzyme at the molecular level showed good correlation through a combination of molecular docking and MD simulation. The correlation is shown through the grid-score and binding free energy (MM-GBSA) with the energy trend C1–HSD17B1 < C2–HSD17B1 < TES–HSD17B1. Meanwhile, key residues Leu149 and Pro187 were highlighted in the HSD17B1 enzyme inhibition mechanism showing ΔGresiduebind ≤ −1.00 kcal mol−1. More specifically, the atomistic level was studied to see the interaction of ligands and amino acids through the hydrogen bond in the pocket area of the targeted protein. The results showed that the presence of –OH and –COOH groups in each inhibitor had a crucial influence in stabilizing the inhibitor–HSD17B1 interaction. In conclusion, all the calculation results suggest that candidate inhibitors C1 and C2 have worthy potential to inhibit the HSD17B1 enzyme.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
The authors would like to thank to Universitas Airlangga for funding through “Skema Hibah Penelitian Riset Group” No. 343/UN3.14/PT/2020. The authors would like also to thank The Bioinformatic Laboratory, UCoE Research Center for Bio-Molecule Engineering Universitas Airlangga, Surabaya, Indonesia for providing research and administrative facilities.References
- D. Africander and K. H. Storbeck, Mol. Cell. Endocrinol., 2018, 466, 86–97 CrossRef CAS PubMed.
- M. M. Pérez-Jiménez, J. M. Monje-Moreno, A. M. Brokate-Llanos, M. Venegas-Calerón, A. Sánchez-García, P. Sansigre, A. Valladares, S. Esteban-García, I. Suárez-Pereira, J. Vitorica, J. J. Ríos, M. Artal-Sanz, Á. M. Carrión and M. J. Muñoz, Nat. Commun., 2021, 12, 1–12 CrossRef PubMed.
- S. Hägg and J. Jylhävä, Elife, 2021, 10, 1–27 CrossRef PubMed.
- A. Gangloff, R. Shi, V. Nahoum and S. X. Lin, FASEB J., 2003, 17, 274–276 CrossRef CAS PubMed.
- E. Hilborn, O. Stål and A. Jansson, Oncotarget, 2017, 8, 30552–30562 CrossRef PubMed.
- P. Järvensivu, T. Heinosalo, J. Hakkarainen, P. Kronqvist, N. Saarinen and M. Poutanen, Endocr.-Relat. Cancer, 2018, 25, 393–406 Search PubMed.
- C. Gunnarsson, M. Ahnström, K. Kirschner, B. Olsson, B. Nordenskjöld, L. E. Rutqvist, L. Skoog and O. Stål, Oncogene, 2003, 22, 34–40 CrossRef CAS PubMed.
- J. A. Aka, M. Zerradi, F. Houle, J. Huot and S. X. Lin, Breast Cancer Res., 2012, 14, 1–14 CrossRef PubMed.
- J. M. Day, P. A. Foster, H. J. Tutill, M. F. C. Parsons, S. P. Newman, S. K. Chander, G. M. Allan, H. R. Lawrence, N. Vicker, B. V. L. Potter, M. J. Reed and A. Purohit, Int. J. Cancer, 2008, 122, 1931–1940 CrossRef CAS PubMed.
- G. Möller, B. Husen, D. Kowalik, L. Hirvelä, D. Plewczynski, L. Rychlewski, J. Messinger, H. Thole and J. Adamski, PLoS One, 2010, 5, 1–10 CrossRef PubMed.
- Y. Li, J. Pei and L. Lai, Chem. Sci., 2021, 12, 13664–13675 RSC.
- E. E. Aung, A. N. Kristanti, N. S. Aminah, Y. Takaya and R. Ramadhan, Open Chem., 2020, 18, 1256–1281 CAS.
- R. Kiyama, Eur. J. Pharmacol., 2017, 815, 405–415 CrossRef CAS PubMed.
- A. Vuorinen, R. T. Engeli, S. Leugger, F. Bachmann, M. Akram, A. G. Atanasov, B. Waltenberger, V. Temml, H. Stuppner, L. Krenn, S. B. Ateba, D. Njamen, R. A. Davis, A. Odermatt and D. Schuster, J. Nat. Prod., 2017, 80, 965–974 CrossRef CAS PubMed.
- E. E. Aung, A. N. Kristanti, N. S. Aminah, Y. Takaya, R. Ramadhan and H. T. Aung, Rasayan J. Chem., 2021, 14, 312–318 CrossRef CAS.
- J. Ding, S. You, J. Zhang, H. Zhang, H. Wang, W. Zhang, W. Qi, R. Su and Z. He, Bioresour. Technol., 2021, 341, 125833 CrossRef CAS PubMed.
- T. Klein, C. Henn, M. Negri and M. Frotscher, PLoS One, 2011, 6, 1–13 Search PubMed.
- W. Qiu, M. Zhou, M. Mazumdar, A. Azzi, D. Ghanmi, V. Luu-The, F. Labrie and S. X. Lin, J. Biol. Chem., 2007, 282, 8368–8379 CrossRef CAS PubMed.
- S. Zafar, M. I. Choudhary, K. Dalvandi, U. Mahmood and Z. Ul-Haq, Chem. Cent. J., 2013, 7, 1–12 CrossRef PubMed.
- W. J. Allen, T. E. Balius, S. Mukherjee, S. R. Brozell, D. T. Moustakas, P. T. Lang, D. A. Case, I. D. Kuntz and R. C. Rizzo, J. Comput. Chem., 2015, 36, 1132–1156 CrossRef CAS PubMed.
- M. Negri, M. Recanatini and R. W. Hartmann, PLoS One, 2010, 5, 1–12 CrossRef PubMed.
- B. R. Miller, T. D. Mcgee, J. M. Swails, N. Homeyer, H. Gohlke and A. E. Roitberg, J. Chem. Theory Comput., 2012, 8, 3314–3321 CrossRef CAS PubMed.
- Y. Han, J. Zhang, C. Q. Hu, X. Zhang, B. Ma and P. Zhang, Front. Pharmacol., 2019, 10, 1–12 CrossRef PubMed.
- A. Daina, O. Michielin and V. Zoete, Sci. Rep., 2017, 7, 1–13 CrossRef PubMed.
- D. E. V. Pires, T. L. Blundell and D. B. Ascher, J. Med. Chem., 2015, 58, 4066–4072 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- D. R. Roe and T. E. Cheatham, J. Chem. Theory Comput., 2013, 9, 3084–3095 CrossRef CAS PubMed.
- E. Wang, H. Sun, J. Wang, Z. Wang, H. Liu, J. Z. H. Zhang and T. Hou, Chem. Rev., 2019, 119, 9478–9508 CrossRef CAS PubMed.
- C. A. Lipinski, F. Lombardo, B. W. Dominy and P. J. Feeney, Adv. Drug Delivery Rev., 2012, 64, 4–17 CrossRef.
- D. F. Veber, S. R. Johnson, H. Y. Cheng, B. R. Smith, K. W. Ward and K. D. Kopple, J. Med. Chem., 2002, 45, 2615–2623 CrossRef CAS PubMed.
- B. J. Bender, S. Gahbauer, A. Luttens, J. Lyu, C. M. Webb, R. M. Stein, E. A. Fink, T. E. Balius, J. Carlsson, J. J. Irwin and B. K. Shoichet, Nat. Protoc., 2021, 16, 4799–4832 CrossRef CAS PubMed.
- S. R. Brozell, S. Mukherjee, T. E. Balius, D. R. Roe, D. A. Case and R. C. Rizzo, J. Comput.-Aided Mol. Des., 2012, 26, 749–773 CrossRef CAS PubMed.
- S. Toxvaerd, O. J. Heilmann and J. C. Dyre, J. Chem. Phys., 2012, 136, 1–8 CrossRef PubMed.
- M. Negri, M. Recanatini and R. W. Hartmann, J. Comput.-Aided Mol. Des., 2011, 25, 795–811 CrossRef CAS PubMed.
- M. Y. Lobanov, N. S. Bogatyreva and O. V. Galzitskaya, Mol. Biol., 2008, 42, 623–628 CrossRef CAS.
- A. L. Hopkins, Nat. Chem. Biol., 2008, 4, 682–690 CrossRef CAS PubMed.
- K. Ravindranathan, J. Tirado-Rives, W. L. Jorgensen and C. R. W. Guimarães, J. Chem. Theory Comput., 2011, 7, 3859–3865 CrossRef CAS PubMed.
- B. Nutho, P. Mahalapbutr, K. Hengphasatporn, N. C. Pattaranggoon, N. Simanon, Y. Shigeta, S. Hannongbua and T. Rungrotmongkol, Biochemistry, 2020, 59, 1769–1779 CrossRef CAS PubMed.
- C. J. Woods, M. Malaisree, J. Michel, B. Long, S. McIntosh-Smith and A. J. Mulholland, Faraday Discuss., 2014, 169, 477–499 RSC.
- D. Chen, N. Oezguen, P. Urvil, C. Ferguson, S. M. Dann and T. C. Savidge, Sci. Adv., 2016, 2, 1–16 Search PubMed.
- S. Salentin, V. J. Haupt, S. Daminelli and M. Schroeder, Prog. Biophys. Mol. Biol., 2014, 116, 174–186 CrossRef CAS PubMed.
- S. Kongkaew, P. Yotmanee, T. Rungrotmongkol, N. Kaiyawet, A. Meeprasert, T. Kaburaki, H. Noguchi, F. Takeuchi, N. Kungwan and S. Hannongbua, PLoS One, 2015, 10, 1–14 CrossRef PubMed.
- B. Nutho, S. Pengthaisong, A. Tankrathok, V. S. Lee, J. R. K. Cairns, T. Rungrotmongkol and S. Hannongbua, Biomolecules, 2020, 10, 1–19 CrossRef PubMed.
- M. A. Lie, R. Thomsen, C. N. S. Pedersen, B. Schiøtt and M. H. Christensen, J. Chem. Inf. Model., 2011, 51, 909–917 CrossRef CAS PubMed.
- R. Ferreira De Freitas and M. Schapira, Medchemcomm, 2017, 8, 1970–1981 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra03092f |
| This journal is © The Royal Society of Chemistry 2022 |