Open Access Article
Open Access ArticleCross-sectional structure evolution of phase-separated spin-coated ethylcellulose/hydroxypropylcellulose films during solvent quenching†
Pierre Carmona *ab,
Christian von Corswantc,
Magnus Röding
*ab,
Christian von Corswantc,
Magnus Röding ad,
Aila Särkkä
ad,
Aila Särkkä d,
Eva Olsson
d,
Eva Olsson b and
Niklas Lorén
b and
Niklas Lorén *ab
*ab
aUnit Product Design, Department Agriculture and Food, Division Bioeconomy and Health, RISE Research Institute of Sweden, Gothenburg, Sweden. E-mail: pierre.carmona@ri.se; niklas.loren@ri.se
bDivision Nano-and BioPhysics, Department of Physics, Chalmers University of Technology, Gothenburg, Sweden
cOral Product Development, Pharmaceutical Technology & Development, Operations, AstraZeneca, Gothenburg, Sweden
dDepartment of Mathematical Sciences, Chalmers University of Technology, Gothenburg University, Gothenburg, Sweden
First published on 15th September 2022
Abstract
Porous phase-separated ethylcellulose/hydroxypropylcellulose (EC/HPC) films are used to control drug transport out of pharmaceutical pellets. The films are applied on the pellets using fluidized bed spraying. The drug transport rate is determined by the structure of the porous films that are formed as the water-soluble HPC leaches out. However, a detailed understanding of the evolution of the phase-separated structure during production is lacking. Here, we have investigated EC/HPC films produced by spin-coating, which mimics the industrial manufacturing process. This work aimed to understand the structure formation and film shrinkage during solvent evaporation. The cross-sectional structure evolution was characterized using confocal laser scanning microscopy (CLSM), profilometry and image analysis. The effect of the EC/HPC ratio on the cross-sectional structure evolution was investigated. During shrinkage of the film, the phase-separated structure undergoes a transition from 3D to nearly 2D structure evolution along the surface. This transition appears when the typical length scale of the phase-separated structure is on the order of the thickness of the film. This was particularly pronounced for the bicontinuous systems. The shrinkage rate was found to be independent of the EC/HPC ratio, while the initial and final film thickness increased with increasing HPC fraction. A new method to estimate part of the binodal curve in the ternary phase diagram for EC/HPC in ethanol has been developed. The findings of this work provide a good understanding of the mechanisms responsible for the morphology development and allow tailoring of thin EC/HPC films structure for controlled drug release.
1 Introduction
Controlled drug release formulations are used to deliver drugs at predetermined rates and periods of time in the body to minimize side effects and to optimize the therapeutic effect of the drug. One means of drug administration is to use a pellet that contains a drug reservoir coated with a thin, phase-separated polymer film. When in contact with body liquids, the water-soluble phase of the film is leached out and a porous network structure is formed. The porous microstructure of the pellet coating determines the mass transport of the drug from the core to the surrounding liquids in the body. By controlling the manufacturing and the formulation, and consequently the coating structure, the drug release rate can be tailored.1 Porous polymer phase-separated films have shown good efficiency in controlling the drug transport.2 In this work, the two cellulose derivatives, water-insoluble ethylcellulose (EC) and water-soluble hydroxypropylcellulose (HPC), are used to make thin phase-separated films. EC and HPC are well-established in the pharmaceutical industry for controlled release applications.3In industry, coating of drug-containing pellets with thin phase-separated films is often performed batch-wise using fluidized bed spraying. One challenge is to relate the properties of the obtained polymer coating to the production process of the pellets. During spraying, small droplets containing EC, HPC, and ethanol hit the pellet and form a coating during multiple passages in the fluidized bed. Many mechanisms are involved in the formation of the phase-separated films on the pellets, and they interact in a complex and time-dependent manner. Examples of involved mechanisms are phase separation, kinetic trapping by viscosity increase, re-dissolution, remixing, and solvent evaporation. Since the solvent evaporation is fast there is not enough time for equilibrium structures to develop. This phenomenon is called solvent quenching.4,5 The film structure is directly related to the kinetics of phase separation. By determining the phase separation and coarsening kinetics during solvent quenching it is possible to understand the different mechanisms that influence the final structure. However, a fluidized bed is a challenging environment for observing the structure formation and phase separation during solvent evaporation in a thin film. Spin-coating is a technique where phase separation during solvent evaporation in a thin film is much easier to follow and understand than in the industrial process. Therefore, spin-coating was used in this work to mimic the structure formation occurring during fluidized bed spraying.
Spin-coating is a widely used technique for making uniform polymer films with high reproducibility of the obtained film structure. In previous work,6 spin-coating was utilized to form thin EC/HPC films, and the influence of the spin-coating parameters on the final dried structure was studied. It was found that the final characteristic length scale decreases with increasing spin speed. In addition, the film thickness decreases with increasing spin speed and strong correlation between thickness and spin speed was found for 22 wt% HPC, 30 wt% HPC and 45 wt% HPC.
In further work,7 the effect of the EC/HPC ratio (15 to 85 wt% HPC) on the in-plane structure evolution was determined. Bicontinuous structures were found for 30 to 40 wt% HPC and discontinuous structures were found for the fractions 15 to 22 and 45 to 85 wt% HPC. The growth of the characteristic length scale followed a power law, L(t) ∼ tn, with n ∼ 1 for bicontinuous structures, and n ∼ 0.45–0.75 for discontinuous structures. The characteristic length scale after kinetic trapping ranged between 3.0 and 6.0 μm for bicontinuous and between 0.6 and 1.6 μm for discontinuous structures. Two main coarsening mechanisms could be identified: interfacial tension-driven hydrodynamic growth for bicontinuous structures and diffusion-driven coalescence for discontinuous structures. However, only the in-plane view of the films during structure evolution was revealed. In this paper, we have investigated the effect of the EC/HPC ratio (15 to 85 wt% HPC) on the cross-sectional film structure evolution. Since the object of study is a thin film, boundary effects at substrate and air interfaces and confinement effects8 are likely to be non-negligible. Therefore, we cannot expect the structure formation to be isotropic, and determining cross-sectional evolution is of large interest.
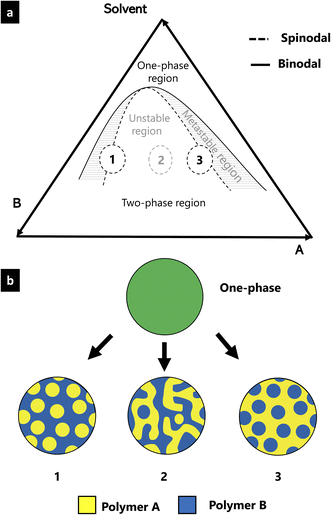
EC, HPC and ethanol is a ternary system consisting of two polymers and one solvent. The phase behavior of such a system is described by its ternary phase diagram which depends on the constituents as well as on temperature9 and pressure.10 Fig. 1 shows a typical ternary phase diagram, used to describe a ternary system consisting of two polymers (polymer A and B) and a solvent.11,12 In the diagram, two regions are described: the one-phase region where the mixture is one homogeneous phase and the two-phase region where the mixture is separated into two distinct phases. The binodal curve represents the transition from the one-phase to the two-phase region. Within the two-phase region, there are an unstable and a metastable region. The boundary between the unstable and the metastable regions is described by the spinodal curve. Compositions inside the metastable region separate according to the nucleation and growth phase separation mechanism, whereas those within the unstable region separate through the spinodal decomposition phase separation mechanism.13,14 Morphologies 1 and 3 in Fig. 1 are droplet-like structures initiated either by nucleation and growth or by spinodal decomposition followed by a percolation-to-cluster transition.7 Morphology 2 is a typical self-similar pattern caused by spinodal decomposition phase separation. By determining the position of the solution mixture in the phase diagram, it is possible to relate the phase separation mechanisms to the structure and ethanol content. In this paper, we propose a new method to estimate the binodal curve of the phase diagram using microscopy and image analysis. The method involves monitoring the in situ structure evolution during solvent evaporation and profilometry to measure the final film thickness.
Polymer phase separation can be initialized by fast solvent evaporation, also called solvent quenching. Phase separation during solvent evaporation has been studied previously.15–18 The evaporation leads to a huge increase in the viscosity of the polymer mixture, retarding and eventually halting the coarsening by kinetically trapping the structure in a non-equilibrium state.19 Phase separation induced by solvent evaporation is not fully understood,17 the difficulty arising from the fact that the solvent evaporation continuously changes the ethanol concentration in the mixture (in comparison to temperature-induced phase separation, where the concentrations of the components in the mixture do not change). The characteristic length scale of the phase-separated structure depends on the coarsening time but also on the depth of the solvent quench.19,20 Faster evaporation leads to a deeper solvent quench, and the characteristic length scale is expected to become smaller.17
The system considered in this work is a film that is shrinking over time. During the film formation, many phenomena are competing. Since the film is on a substrate, surface interactions become more and more important as the surface to volume ratio increases. At the air interface, the evaporation process might give rise to a concentration gradient. With regard to solvent-induced phase separation, for example, Cummings et al. modelled solvent evaporation during thin film formation in phase-separating polymer mixtures.18 It was demonstrated that kinetic trapping resulting from solvent-induced phase separation can lead to films with a rougher surface. De Gennes studied the instabilities that may occur at the surface of the film when the film is too thin15 or during the formation of a crust.21 Buxton et al. have simulated the evolution of a polymer–polymer–solvent mixture undergoing solvent evaporation and phase separation22 and focused their work on the lateral morphology of the film. It is also of importance to study the cross-section of the film, to understand the structure evolution. This type of information is lacking. In this paper, we focus on the cross-section to monitor in situ the phase separation and coarsening during solvent evaporation.
Theories and simulations were developed for bulk 3D systems. When studying phase separation in thin films, confinement effects need to be considered. During shrinkage of the film, the evolution of the phase-separated structure undergoes a transition from 3D to nearly 2D structure development, and the cross-over occurs when the characteristic length scale is in the order of the film thickness.23 Phase separation in confinement has been studied before.8,24–30 Wassén et al. studied the effects of confinement on the phase separation kinetics and compared the effect of wetting in bulk and in a confined environment.8 They showed that confinement influences the kinetics of phase separation. For the same biopolymer mixture, they found bicontinuous structures in bulk and columnar structures in confinement. They emphasized the importance of quantifying the impact of confinement on phase separation to control the final microstructure.
Surface effects can also play a role in the structure evolution. Zoumpouli and Yiantsios31 investigated the effects of parameters characterizing the evaporation rate and the preferential wetting of the solutes at the air interface. For example, for systems exhibiting preferential wetting, they showed that diffusion alone favors lamellar configurations for the separated phases in the dried film. There are two possible types of wetting behavior in a capillary (2D confinement) at equilibrium: the complete wetting is a layered structure; and the partial wetting is a droplet-like structure. Tanaka et al.32 discussed the hypothesis of having different types of coarsening depending on wettability strength. In the case of weak wettability, the structure coarsens in 3D, while for strong wettability the structure coarsens in 2D, due to confinement.
The overall purpose of this work was to understand the film formation and the cross-sectional structure evolution during solvent quenching. Here, spin-coating has been used to mimic the industrial process. The total time of phase separation before kinetic trapping was increased by reducing the solvent evaporation rate, to facilitate the imaging of the structure evolution in situ. In this work, we have characterized the effect of the EC/HPC ratio on the film formation process by monitoring the cross-sectional structure evolution in situ using CLSM and image analysis.
This paper is structured as follows: (i) the structure evolution during phase separation, solvent evaporation and film shrinkage is explored, and (ii) estimation of part of the binodal curve of the ternary phase diagram EC/HPC/EtOH is presented.
2 Material and methods
2.1 Solution preparation
Solutions of HPC (Klucel Pharm HPC, grade LF, Ashland Inc, Covington, Kentucky, USA) with a mean molecular weight of 95 kDa33 and EC (Ethocel Standard Premium, viscosity 10 cps, Dow Cellulosics, Dow Chemical Company, Midland, Michigan, USA) with a mean molecular weight of 30 kDa34 were prepared. 6 wt% of polymer blends were mixed in a solution of 2 mM Na-fluorescein (CAS 518-47-8, Sigma Aldrich, St. Louis, Missouri, USA) and ethanol (CAS 64-17-5 AnalaR NORMAPUR® 96%, VWR Chemical, Radnor, Pennsylvania, USA) and stirred overnight. The EC/HPC polymer ratios studied were 15, 20, 22, 25, 30, 35, 37, 40, 45, 50, 55, 60 and 85 wt% of HPC in the polymer blend.2.2 Sample preparation by spin-coating
A spin-coater (WS-650MZ-23NPP, Laurell Technologies, North Wales, Pennsylvania, USA) was used to spin-coat the EC/HPC solutions. The volume of the solution was optimized and fixed at 200 μL. The polymer solution was deposited on the surface of a round glass bottom Petri dish with diameter 22 mm (HBST-3522, Willco Wells, Amsterdam, Netherlands). The spin-coater bowl was equipped with nitrogen flow which ensures a humidity and oxygen free environment. The spin speed was fixed at 2000 rpm and the acceleration ratio, i.e. the ratio between the acceleration speed and the spin speed, was 2000 rpm s−1. Prior to spin-coating, the solutions were kept in a 25 °C water bath and the temperature of the spin-coated bowl was 25 ± 1 °C. Films were spin-coated for only 3 s so that the film was not totally dried when the microscope observation started. Directly after spinning, the Petri dish was closed with a lid to retard ethanol evaporation and placed on the CLSM microscope stage (see also Section 2.4).2.3 Slowing down the evaporation process
The objective of this work was to follow the phase separation by monitoring the phase separation process in situ using CLSM. The EC/HPC phase separation is governed by the solvent evaporation process. The evaporation of ethanol in the EC/HPC thin film is relatively fast (in the order of minutes) and the imaging of the structure evolution in situ is time-limited due to practical reasons: the sample needs to be moved from the spin coater to the CLSM, the imaging parameters must be adjusted, and the interval between each frame cannot be reduced without reducing the signal-to-noise ratio. Therefore, the total time of phase separation before kinetic trapping had to be increased by reducing the solvent evaporation rate. Indeed, the system phase separates when enough ethanol has evaporated to enter the two-phase region in the phase diagram. During the evaporation, the structure becomes kinetically trapped before reaching equilibrium. The rate of the evaporation and the distance from the binodal line to the final blend composition when all solvent has evaporated (also called the solvent quench depth) are important for the full understanding of the EC/HPC phase separation process and to modify the solvent evaporation process. In the following section we characterize the evaporation rate and the effect of the EC/HPC ratio in open/closed system.The evaporation was studied by gravimetry with a scale (Analytical Balance; AT261, Mettler Toledo, Greifensee, Switzerland). A drop of 200 μL was deposed in a Petri dish and spin-coated as described above in Section 2.2. The weight of the Petri dish was set to zero at time zero before adding the drop. The solution's weight was followed over time. We compare the weight loss after spinning in two cases: in an open Petri dish and in a Petri dish closed with a lid. The evaporation was in open air and the temperature was 21 °C. The study was performed in triplicate for the two EC/HPC ratios 30 wt% and 45 wt% of HPC.
Fig. 2 shows the result of the gravimetric evaporation study. The mean spin-coated solution weight as a function of time is displayed. Thus, it is possible to estimate the decrease in evaporation rate when closing the Petri dish. It should be noted that the solution's weight at the start is lower than if all material remains in the Petri dish. We could expect approximately 200 μL × 0.8 mg μL−1 (density of ethanol) = 160 mg at the beginning minus the ethanol that has evaporated during the first 3 s of spinning and 5 s to put the Petri dish on the scale. However, some of the polymer solution is also leaving the Petri dish during spin coating and the starting solution weight is therefore about 30 mg. The plot of mean weight loss versus time shows that the weight loss is linear down to a certain level, which is in accordance with results found in the literature.35,36 For the open Petri dish and both ratios HPC 30 wt% and HPC 45 wt%, the weight reaches a plateau, corresponding approximately to the remaining solid fraction (a small fraction of ethanol remains). The results show no significant difference in evaporation rate for HPC 30 wt% and HPC 45 wt% for both closed and open lid. This indicates that the evaporation rate is independent of the polymer blend ratio. After linear regression of HPC 30 wt% data, slopes ± sd (standard deviation) of −0.2580 ± 0.0005 and −2.10 ± 0.05 mg min−1 were obtained for the closed and open Petri dish, respectively. Hence, the evaporation is slowed down approximately 8 times at room temperature by closing the lid, which can be used to delay the onset of phase separation and to expand the observation window for CLSM analysis of the film structure evolution. Our experimental set-up using a lid, gives us good control over the parameters influencing the evaporation, which results in good reproducibility of replicates.
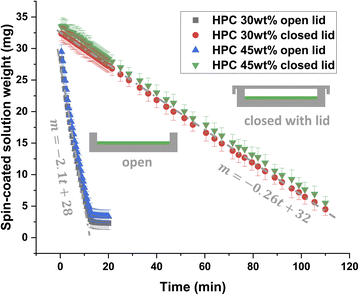 | ||
| Fig. 2 Estimation of the evaporation rate by gravimetry. Comparison of the weight (m ± sd) in an open (black and blue points) and a closed (green and red points) Petri dish with two EC/HPC ratios. | ||
2.4 Confocal laser scanning microscopy
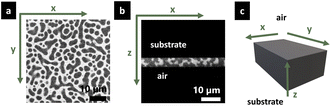
The structure evolution of the spin-coated thin film was determined using a confocal laser scanning microscope (CLSM; Leica TCS SP5, Leica, Wetzlar, Germany) with a Leica 100×/1.4 PL APO oil objective. A 488 nm argon laser was used for excitation of the Na-fluorescein used to stain the HPC phase. The signal emitted in the interval 500–600 nm was recorded (the fluorescein emission peak is expected at 515 nm). The theoretical lateral resolution was Δx ∼ 130 nm and the axial resolution was Δz ∼ 330 nm (practically, the axial resolution is in the order of Δz ∼ 500 nm). Fig. 3 shows the two observation planes used to characterize the film structure. For in-plane measurements (Fig. 3a) zooms 3× and 8× (FOV 52 and 19 μm respectively) were used, depending on the size of the structure observed. The images were acquired with 1024 × 1024 pixels resolution, a scanning rate of 400 Hz, which results in a time interval of 2.58 s between frames. For cross-sectional measurements (Fig. 3b) a zoom of 3.44× (FOV is 45 μm) and a time interval of 2.77 s between each frame were used. The latter measurements were performed with a galvanometric stage that moves rapidly up and down in the z-direction (16 μm s−1) with high precision, permitting to image a slice in the xz-plane with high quality.The stage and objective were kept at 25 °C, using an incubation stage and controller system for microscopes (Tokai Hit, Fujinomiya-shi, Japan).
2.5 Shrinkage rate estimation by image analysis
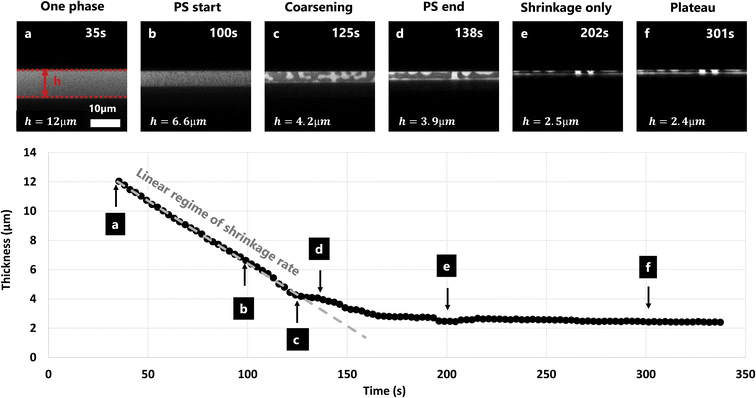
The film shrinkage rate was estimated using image analysis on the cross-section CLSM micrograph series. Fig. 4 shows the shrinkage over time of a film with EC/HPC ratio 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 wt%. It displays CLSM micrographs of the cross-section of the film. By localizing the upper and lower surface of the film it was possible to estimate the film thickness at each time point. On the lower part of Fig. 4 the corresponding calculated thickness is plotted versus time. To compare the different parameters from the experimental design (mainly EC/HPC ratio), we decided to extract 4 values at different points in time for each experiment: at 35 s (t = 0 s indicating the start of the spinning) (Fig. 4a), at the start of phase separation (Fig. 4b), at the end of the linear regime which corresponds to the time when the structure is kinetically trapped (Fig. 4d), and at the plateau which corresponds to the plateauing of the shrinkage process (Fig. 4f). During phase separation, coarsening is observed (Fig. 4c). Between the kinetic trapping of the structure and the end, only shrinkage is taking place (Fig. 4e). Since the decrease in thickness between points a and d is linear, the slope can be interpreted as a shrinkage rate in μm min−1. The slope was estimated by least-squares fitting of a straight line.
40 wt%. It displays CLSM micrographs of the cross-section of the film. By localizing the upper and lower surface of the film it was possible to estimate the film thickness at each time point. On the lower part of Fig. 4 the corresponding calculated thickness is plotted versus time. To compare the different parameters from the experimental design (mainly EC/HPC ratio), we decided to extract 4 values at different points in time for each experiment: at 35 s (t = 0 s indicating the start of the spinning) (Fig. 4a), at the start of phase separation (Fig. 4b), at the end of the linear regime which corresponds to the time when the structure is kinetically trapped (Fig. 4d), and at the plateau which corresponds to the plateauing of the shrinkage process (Fig. 4f). During phase separation, coarsening is observed (Fig. 4c). Between the kinetic trapping of the structure and the end, only shrinkage is taking place (Fig. 4e). Since the decrease in thickness between points a and d is linear, the slope can be interpreted as a shrinkage rate in μm min−1. The slope was estimated by least-squares fitting of a straight line.
2.6 Thickness measurement by profilometry
The axial resolution of the CSLM measuring the thickness is Δz ∼ 500 nm while the profilometer precision is about 1 nm. Since profilometry offers more accurate measurement it was used to determine the dried films thickness (1 week after spinning), while the film thickness during the dynamic in situ experiment, was measured with CLSM and image analysis. A stylus profilometer (Alpha-Step D-100 KLA Tencor, Milpitas, CA, USA) was utilized. Stylus profilometers use a contact probe to detect the surface. The diamond stylus is physically moving along the surface to measure the surface height. Prior to the measurement, the film surface was scratched with a razor blade. The stylus slides across the film and uses the difference in height from the film surface to the glass surface (inside of a scratch) to determine the film thickness. For each experiment, measurements on 6 scratches of 1.5 mm of each microscope slide were performed in triplicate. The measurements were performed with stylus speed 0.03 mm s−1 and stylus force 2.0 mg.2.7 Determination of the ternary EC/HPC/ethanol phase diagram
In a ternary phase diagram, the binodal curve represents the boundary between the one-phase and the two-phase region (see Fig. 1). The binodal curve was estimated by determining the EC/HPC/EtOH composition when the phase separation starts. The film thickness at the start of the phase separation was extracted from the micrographs (Fig. 4b). The onset of phase separation was determined from the CLSM micrographs using visual inspection. Recent results that we performed (not shown) revealed that after one week both the length scale of the phase-separated structure and thickness of the film were constant. Hence, at that time all ethanol has evaporated. Thus, during the dynamic experiment the mean volume fraction of solid material at time t, φS(t) is given by the final thickness measured by profilometry hdry divided by the current thickness h(t) measured with CLSM and image analysis: φS(t) = hdry/h(t).37 The estimated position of each point of the binodal in the phase diagram corresponding to the coordinate EC/HPC/EtOH is given by φEC(t)/φHPC(t)/φEtOH(t) with φEtOH(t) = 1 − φS(t), φHPC(t) = φS(t) × % HPC, φEC(t) = φS(t) × % EC, and % HPC and % EC correspond to the weight percentage of EC and HPC in the polymer blend. Since EC and HPC have approximately similar density, here, we assume that the volume fraction of each polymer corresponds to the weight fraction in the polymer blend. We assume that only ethanol is evaporating and the ratio EC/HPC stays constant throughout the whole experiment. In order to map the experimental points in the phase diagram we used a spreadsheet that plots ternary diagrams developed by Graham and Midgley,38 where, after entering the composition φEC(t)/φHPC(t)/φEtOH(t), the corresponding coordinates are calculated, and the points are plotted.3 Results and discussion
3.1 Phase separation during film shrinkage
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 wt%. Fig. 5a shows CLSM micrographs displaying the in-plane structure evolution. Fig. 5b shows the cross-sectional structure evolution. The same type of morphology development is observed in both planes. At the initiation and the early stages of the phase separation, (at 116 s in Fig. 5) typical mottled spinodal decomposition patterns are visible. Simultaneously with the shrinkage of the film, phase separation occurs, and the phase-separated structures coarsen, illustrated by the length scale increase from 2.1 μm at 116 s to 6.6 μm at 158 s (Fig. 5a). The coarsening was quantified by estimating the length scale using a Fourier transform based image analysis method, described in detail in previous work for in-plane structure evolution.7 In the cross-sectional micrographs, we were able to get access to only a few repetitions of the phase-separated pattern, while the larger imaging area in the in-plane provides the possibility for a larger number of repetitions of the structure making the estimation of the characteristic length scale more robust and accurate. Furthermore, the in-plane structure is more isotropic than the cross-sectional structure that is influenced by surfaces and confinement. Therefore, it is more robust to perform the Fourier image analysis in the in-plane than in the cross-sectional micrographs. Since the cross-sections studied in this work are replicates of the in-plane films studied in previous work from this group, we performed the quantitative image analysis in-plane (xy-plane) and extracted the film thickness from the cross-sections (xz-plane) and performed a qualitative analysis of the structure. From the micrographs series in both planes, it appears likely that hydrodynamic coarsening is taking place, as described in Carmona et al.7 From the micrograph at 158 s and particularly for the in-plane micrographs, a secondary phase separation can be observed39 where small dark EC domains appear in already phase-separated bright HPC domains. During solvent evaporation, the thickness of the film is decreasing as a function of time going from 7.5 μm at 116 s to 2.3 μm at 263 s, see Fig. 5b.
30 wt%. Fig. 5a shows CLSM micrographs displaying the in-plane structure evolution. Fig. 5b shows the cross-sectional structure evolution. The same type of morphology development is observed in both planes. At the initiation and the early stages of the phase separation, (at 116 s in Fig. 5) typical mottled spinodal decomposition patterns are visible. Simultaneously with the shrinkage of the film, phase separation occurs, and the phase-separated structures coarsen, illustrated by the length scale increase from 2.1 μm at 116 s to 6.6 μm at 158 s (Fig. 5a). The coarsening was quantified by estimating the length scale using a Fourier transform based image analysis method, described in detail in previous work for in-plane structure evolution.7 In the cross-sectional micrographs, we were able to get access to only a few repetitions of the phase-separated pattern, while the larger imaging area in the in-plane provides the possibility for a larger number of repetitions of the structure making the estimation of the characteristic length scale more robust and accurate. Furthermore, the in-plane structure is more isotropic than the cross-sectional structure that is influenced by surfaces and confinement. Therefore, it is more robust to perform the Fourier image analysis in the in-plane than in the cross-sectional micrographs. Since the cross-sections studied in this work are replicates of the in-plane films studied in previous work from this group, we performed the quantitative image analysis in-plane (xy-plane) and extracted the film thickness from the cross-sections (xz-plane) and performed a qualitative analysis of the structure. From the micrographs series in both planes, it appears likely that hydrodynamic coarsening is taking place, as described in Carmona et al.7 From the micrograph at 158 s and particularly for the in-plane micrographs, a secondary phase separation can be observed39 where small dark EC domains appear in already phase-separated bright HPC domains. During solvent evaporation, the thickness of the film is decreasing as a function of time going from 7.5 μm at 116 s to 2.3 μm at 263 s, see Fig. 5b.
In the 3rd column at 158 s, it can be noticed that the length scale of the phase-separated structure is bigger than the film thickness i.e. L = 6.6 μm and h = 4.7 μm. In addition, while the in-plane structure seems isotropic (similar structure in x- and y-directions), the cross-sectional structure seems anisotropic. On the cross-section, we observe that the structure evolution is influenced by the upper and lower surfaces resulting in more elongated structures close to the surfaces than in the middle of the film. From a structure evolution perspective, the cross-sectional structure indicates that the phase separation has transitioned from coarsening in all three directions x, y, and z (3D) to only in x and y directions (2D). This type of transition was also observed by Sung et al.23 It is also likely that the interplay with the surrounding surfaces starts to play an important role for the structure evolution. For example, it seems that the HPC phase is close to the interfaces while the EC phase is in the center of the film (center of the cross-section). Thus, the phase separation undergoes spinodal decomposition, nucleation and growth, coarsening solvent evaporation, solvent quenching, kinetical trapping, and confinement. While spinodal decomposition has been widely studied in the literature, the theory and simulations need to be modified to be able to be applied to solvent quenching and kinetical trapping. Spinodal decomposition as well as nucleation and growth are important mostly in the beginning, and kinetic trapping and confinement in the end of the phase separation.
The theory developed for bulk (3D) phase separation40–43 is certainly relevant for the early stages. However, in the later stages of the film structure evolution, confinement effects and 2D phase separation are likely more relevant since the structure cannot evolve in the z-direction anymore, only in the x- and y-directions.8,24,25 In comparison with a bulk coarsening, the confinement forces the coarsening to develop in two dimensions instead of three (transition from 3D to 2D coarsening). It results in much larger domains in the xy-plane. Thus, we observe in Fig. 5 that the length scale at plateau (at 263 s) is being 3 times greater than the film thickness. In the end, between 158 s and 263 s in Fig. 5, the structure is only shrinking when most of the ethanol evaporates.
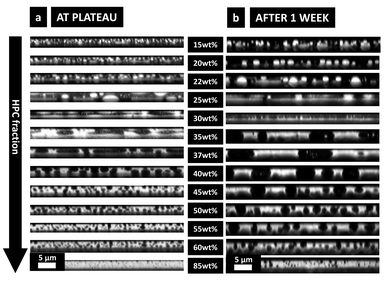
The type of morphology of the phase-separated structures in cross-sectional view are in accordance with previous in-plane observations:7 HPC 22 wt% exhibits a discontinuous structure with bright HPC inclusions in EC matrix (Fig. 6a); HPC 37 wt% exhibits a bicontinuous structure (Fig. 6b); and HPC 60 wt% exhibits a discontinuous structure with dark EC inclusions in HPC matrix (Fig. 6c). During the coarsening step, hydrodynamic coarsening can be observed for HPC 37 wt% (between 152 and 166 s in particular) and coalescence for the discontinuous structures HPC 22 wt% (between 132 and 163 s) and HPC 60 wt% (between 188 and 210 s). Additionally, the length scale of the structures at the plateau in Fig. 6 is significantly larger for the bicontinuous structure (HPC 37 wt% Fig. 6b) compared to the discontinuous structures (Fig. 6a and c) in accordance with previous results.7 However, especially for the bicontinuous structure, the domains are elongated in the xy plane and shrunk in the z plane, similar to the results shown in Fig. 5. As observed previously the structure seems isotropic for the discontinuous structure but anisotropic for the bicontinuous structure showing that there is a transition from 3D to 2D structure evolution (see also Fig. 5) for HPC 37 wt%.
Each EC/HPC phase separation displayed in Fig. 6 occurs through spinodal decomposition.14 In the case of 37 wt% HPC (Fig. 6b), the pattern at 141 s corresponds to a typical spinodal decomposition pattern and the coarsening observed at 152 s and 166 s corresponds to the self-similar growth step of spinodal decomposition.44 The micrographs corresponding to 22 wt% and 60 wt% HPC in Fig. 6a and c, respectively, show discontinuous structures that are likely formed through spinodal decomposition followed by percolation-to-cluster-transition. The relatively slow kinetics of the structure formation allows the structure to go through a percolation-to-cluster-transition and to form a discontinuous droplet-like structure.7
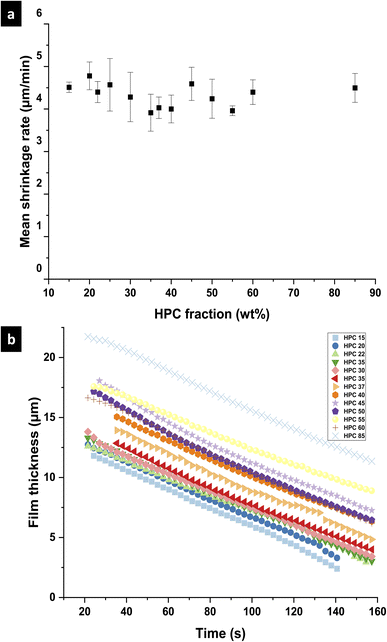
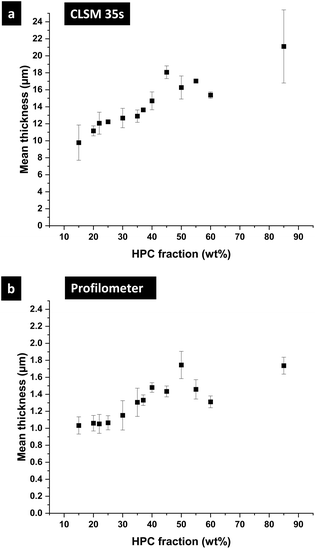
To investigate the differences between the structures for the different EC/HPC ratios, the shrinkage rate was investigated (see Fig. 4 for an explanation of the determination of the shrinkage rate). Fig. 7 shows the mean shrinkage rate in the linear regime for all 13 EC/HPC ratios (note the standard deviation was calculated on few observations, ranging from 3 to 5 per ratio). Fig. 7a shows the mean value obtained by averaging the replicates while Fig. 7b displays one replicate per EC/HPC ratio. A multiple comparison test using Tukey's honestly significant difference (HSD) criterion was used to test the pairwise differences in mean shrinkage rate between the HPC fractions. None of the differences was significant (all p-values for the pairwise comparisons were >0.05; the lowest value was p ≅ 0.3). This is in accordance with Fig. 7b where the slope of the shrinkage in the linear regime for all the ratios are parallel. Our hypothesis is that the shrinkage rate is independent of the HPC fraction and mainly depends on the evaporation process. This is also supported by the results of the gravimetric evaporation study, where no significant difference in shrinkage rate between HPC 30 wt% and HPC 45 wt% was observed.
In Fig. 9b after one week of storage, it can be seen that, even though the morphology of the phase-separated structures looks the same, they are significantly larger than in Fig. 9a. On the micrographs the change of film thickness is not obvious but the growing of the structure is. It confirms that after plateauing of the shrinkage of the film and the structure evolution,7 a very slow coarsening is taking place during the following week. The enriched atmosphere inside the Petri dish favors a very slow evaporation. Thus, the small amount of ethanol, still present in the film, allows the polymer chains to keep their mobility, which even though very low, has a pronounced effect on the domain's length scale. This could not be observed in situ in the CLSM since the evolution is very slow and takes many hours. The differences between Fig. 9a and b confirms that not all the ethanol has evaporated at plateau. In a recent study (not shown), the same experiment was performed after two weeks, and no changes were observed in structure size or film thickness between after one week and after two weeks. Therefore, the thickness used to estimate the binodal curve of the phase diagram is measured by profilometry on the films one week after the spin coating.
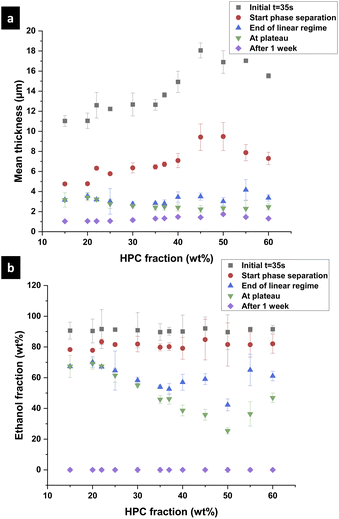
3.2 Estimation of the binodal curve in the EC/HPC/EtOH phase diagram
In the following part, we use the information from the cross-sectional micrographs (xz-plane) and the profilometry to assess the ethanol content at each time of the phase separation and to estimate the position of the binodal curve in the EC/HPC/EtOH ternary phase diagram. We assume that the evaporation process is complete after one week of drying. Hence the thickness over time is providing information about the ethanol fraction for each micrograph: the mean volume fraction of solid material is given by the final thickness divided by the current thickness: φS(t) = hdry/h(t) and the fraction of ethanol is φEtOH(t) = 1 − φS(t).37Fig. 10 shows the film thickness and the ethanol fraction versus the HPC fraction for different key times of the phase separation (note the standard deviation was calculated on few observations, ranging from 3 to 5 per ratio). In Fig. 10a, the thickness during shrinkage of the film follows the same trend as observed in Fig. 8, where the mean thickness is increasing with the HPC fraction. From the thickness estimation, the ethanol fraction is estimated and plotted in Fig. 10b. In the graph, the end of the linear regime corresponds to the kinetical trapping, however, the results are scattered and there is not a particular trend with respect to the HPC fraction. For the ethanol fraction at plateau in Fig. 10b, a minimum at 50 wt% HPC can be noted. From the information in Fig. 10, we can estimate the position of the binodal curve in the ternary phase diagram EC/HPC/EtOH. It is also possible to estimate the solvent quench for each EC/HPC ratio since the solvent quench corresponds to the final distance in the phase diagram from the binodal line to the final blend composition when all solvent has evaporated, i.e. the distance between the start of the phase separation (red circles) to the total evaporation after one week (purple diamond) in Fig. 10b.
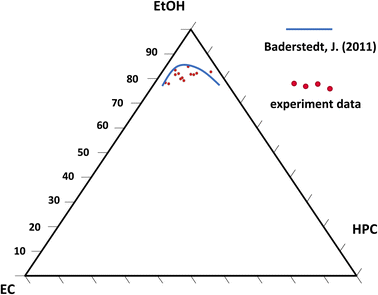
Fig. 11 is showing the estimated phase diagram. The blue curve corresponds to the binodal curve determined experimentally in previous work by Baderstedt et al.45 They studied the phase separation in EC/HPC solutions by letting EC/HPC mixtures of different compositions rest in closed vials for at least one month. By visual inspection of the meniscus, they could determine at which composition the mixture would phase separate and hence estimate the binodal curve.
The red dots are the estimated positions of the binodal curve according to our work. We note that the location of the binodal is in accordance with the one found by Baderstedt et al., which supports our method to estimate the location of the binodal curve of EC/HPC/EtOH at room temperature. However, it is difficult to comment on the shape of the curve since the experimental points scatter. In this method the EC and HPC content are determined with accuracy since the composition of the polymer blend in the polymer mixture is known. However, the start of the phase separation is determined by visual inspection of the CLSM micrographs and is hence known with less accuracy. This influences the ethanol content at the start of phase separation and thus the position of the estimated binodal curve. Since an image is taken every 2.8 s and the thickness changes of about 0.2 μm between each pair of consecutive images the variability ranges from 0.5 to 1 wt% EtOH (depending on the EC/HPC ratio) per image (if we consider that the start can be set at the image before or after the chosen one). In addition, there is also an error of about 500 nm in the thickness estimation coming from the CLSM axial resolution, which gives rise to variability ranging from 1 to 3 wt% EtOH (depending on the EC/HPC ratio). All these factors influence the estimation of the binodal curve. However, with further research it will be possible to increase the precision for instance using higher scanning rate, or CLSM with higher axial resolution, or a STED.46 The method shown in this work has the potential to become a rapid method to estimate the binodal curve in ternary mixtures.
4 Conclusion
An experimental setup was developed and optimized to observe the cross-sectional structure evolution of phase separating EC/HPC/EtOH systems in situ using CLSM. The gravimetric study of the evaporation rate showed that the evaporation was independent of the EC/HPC ratio and that it was possible to slow down the process of solvent evaporation by closing the lid of the Petri dish containing the film. The time-dependent cross-sectional micrograph series made it possible to follow the decrease of the film thickness and the structure evolution of the phase separation in the z-direction (through the film). Analysis of the time-dependent thickness observed via CLSM showed that the evaporation was independent of the EC/HPC ratio in accordance with the gravimetric investigation. It was found that the film thickness first decreases linearly with time during the first minutes after spin coating, and then slowly with a lower slope for several hours. The influence of the EC/HPC ratio on the final structure, structure evolution, shrinkage rate, evaporation and film thickness were determined. The structure evolution evolved through different stages: first the phase separation started and phase-separated domains appeared; then the structure coarsened with coalescence in discontinuous structures and hydrodynamic coarsening in bicontinuous structures; then, the phase separation became kinetically trapped and only shrinkage could be observed. However, the length scale of the structure continued to grow very slowly until about a week, until all ethanol had evaporated. Two types of structures were identified: bicontinuous structures for 30, 35, 37, and 40 wt% HPC and discontinuous structures for 15, 20, 22, 45, 50, 55, 60, and 85 wt% HPC. As observed in the in-plane, the bicontinuous systems exhibit larger structures than the discontinuous systems. It was observed that the 3D phase separation develops into a thin 2D-like phase separation system when the characteristic length scale of the in-plane structure becomes larger than the film thickness. This was particularly pronounced for the bicontinuous systems. Preferential wetting was observed for films with 25 to 40 wt% HPC. In addition, the shrinkage rate was shown to be independent of the EC/HPC ratio. The initial thickness and the final thickness of the film increases with increasing HPC fraction. Finally, a new method to rapidly estimate the binodal curve of the EC/HPC/EtOH ternary phase diagram from the CLSM cross-sections and profilometry was developed.This study of the kinetics provides valuable insights into the structure formation kinetics and the influence of the EC/HPC ratio on a single layer. However, to further explore the structure formation in the industrial process, it would be of interest to investigate multilayer films by coating successive EC/HPC layers.
Conflicts of interest
There are no conflicts of interest to declare.Nomenclature
| 2D | Two dimensions |
| 3D | Three dimensions |
| CLSM | Confocal laser scanning microscope |
| EC | Ethyl cellulose |
| h(t) | Film thickness at time t |
| HPC | Hydroxypropyl cellulose |
| L(t) | Characteristic length scale at time t |
| (m ± sd) | Mean plus/minus standard deviation |
| NG | Nucleation and growth |
| PCT | Percolation to cluster transition |
| SD | Spinodal decomposition |
| φi | Volume fraction of component i |
| wt% | Weight percentage |
Formula
| L(t) ∼ tn | Time (t) dependency of the length scale L during the coarsening stage of the phase separation. n is the exponent of the power law |
| φS(t) = hdry/h(t) | Mean volume fraction of solid material as a function of thickness at time t |
| φEtOH(t) = 1 − φS(t) | Ethanol fraction at time t |
| φHPC(t) = φS(t) × % HPC | HPC fraction at time t |
| φEC(t) = φS(t) × % EC | EC fraction at time t |
Acknowledgements
The Swedish Foundation for Strategic Research (SSF grant FID16-0013), the Swedish Research Council (VR grant 2018-03986), and the Swedish Research Council for Sustainable Development (grant 2019-01295) are gratefully acknowledged for the funding. AstraZeneca is acknowledged for the financial support and materials.References
- G. Tiwari, R. Tiwari, B. Sriwastawa, L. Bhati, S. Pandey, P. Pandey and S. K. Bannerjee, Int. J. Pharm. Invest., 2012, 2, 2–11 CrossRef.
- M. Marucci, G. Ragnarsson, C. von Corswant, A. Welinder, A. Jarke, F. Iselau and A. Axelsson, Int. J. Pharm., 2011, 411, 43–48 CrossRef CAS PubMed.
- P. Sakellariou and R. C. Rowe, Prog. Polym. Sci., 1995, 20, 889–942 CrossRef CAS.
- S. Nilsson, A. Bernasik, A. Budkowski and E. Moons, Macromolecules, 2007, 40, 8291–8301 CrossRef CAS.
- J. J. Michels, ChemPhysChem, 2011, 12, 342–348 CrossRef CAS PubMed.
- P. Carmona, M. Röding, A. Särkkä, C. Von Corswant, E. Olsson and N. Lorén, Soft Matter, 2021, 17, 3913–3922 RSC.
- P. Carmona, M. Roding, A. Sarkka, C. von Corswant, E. Olsson and N. Loren, Soft Matter, 2022, 18, 3206–3217 RSC.
- S. Wassén, N. Lorén, K. van Bemmel, E. Schuster, E. Rondeau and A.-M. Hermansson, Soft Matter, 2013, 9, 2738–2749 RSC.
- N. C. Das, J. Microsc., 2014, 253, 198–203 CrossRef CAS PubMed.
- R. Koningsveld, R. Koningsveld, W. H. Stockmayer and E. Nies, Polymer Phase Diagrams: A Textbook, Oxford University Press, 2001 Search PubMed.
- V. Tolstoguzov, Carbohydr. Polym., 2003, 51, 99–111 CrossRef CAS.
- V. Tolstoguzov, Food Hydrocolloids, 2003, 17, 1–23 CrossRef CAS.
- Supercritical Fluids, ed. P. G. Debenedetti, K. A. Publishers, 2000, pp. 123–166 Search PubMed.
- J. W. Cahn, J. Chem. Phys., 1965, 42, 93–99 CrossRef CAS.
- P. G. De Gennes, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 6, 421–424 CrossRef CAS.
- N. Bassou and Y. Rharbi, Langmuir, 2009, 25, 624–632 CrossRef CAS PubMed.
- C. Schaefer, P. Van Der Schoot and J. J. Michels, Phys. Rev. E, 2015, 91(2), 022602-1–022602-6 CrossRef.
- J. Cummings, J. S. Lowengrub, B. G. Sumpter, S. M. Wise and R. Kumar, Soft Matter, 2018, 14, 1833–1846 RSC.
- C. Schaefer, J. J. Michels and P. Van Der Schoot, Macromolecules, 2016, 49, 6858–6870 CrossRef CAS.
- C. Schaefer, P. van der Schoot and J. J. Michels, Phys. Rev. E, 2015, 91, 022602 CrossRef CAS PubMed.
- P. G. De Gennes, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 7, 31–34 CAS.
- G. A. Buxton and N. Clarke, Europhys. Lett., 2007, 78, 56006 CrossRef.
- L. Sung, A. Karim, J. F. Douglas and C. C. Han, Phys. Rev. Lett., 1996, 76, 4368–4371 CrossRef CAS.
- H. Jinnai, H. Kitagishi, K. Hamano, Y. Nishikawa and M. Takahashi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 021801 CrossRef PubMed.
- S. Fransson, N. Loren, A. Altskar and A.-M. Hermansson, Biomacromolecules, 2009, 10, 1446–1453 CrossRef CAS.
- A. M. Zolali and B. D. Favis, Soft Matter, 2017, 13, 2844–2856 RSC.
- H. Tanaka, Phys. Rev. Lett., 1994, 72, 3690–3693 CrossRef CAS PubMed.
- K. Binder, S. Puri, S. K. Das and J. Horbach, J. Stat. Phys., 2010, 138, 51–84 CrossRef CAS.
- E. A. G. Jamie, R. P. A. Dullens and D. G. A. L. Aarts, J. Chem. Phys., 2012, 137, 204902 CrossRef CAS.
- M. B. Wise and P. C. Millett, Phys. Rev. E, 2018, 98, 022601 CrossRef CAS PubMed.
- G. A. Zoumpouli and S. G. Yiantsios, Phys. Fluids, 2016, 28, 082108 CrossRef.
- H. Tanaka, J. Phys.: Condens. Matter, 2001, 13, 4637–4674 CrossRef CAS.
- Klucel Ashland hydroxypropylcellulose, Physical and chemical properties, 2017 Search PubMed.
- ETHOCEL Dow, Cellulosics, Ethylcellulose Polymers Technical Handbook, 2005 Search PubMed.
- P. Innocenzi, L. Malfatti, S. Costacurta, T. Kidchob, M. Piccinini and A. Marcelli, J. Phys. Chem. A, 2008, 112, 6512–6516 CrossRef CAS PubMed.
- P. Mokarian-Tabari, M. Geoghegan, J. R. Howse, S. Y. Heriot, R. L. Thompson and R. A. Jones, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 33, 283–289 CrossRef CAS PubMed.
- J. J. van Franeker, D. Westhoff, M. Turbiez, M. M. Wienk, V. Schmidt and R. A. J. Janssen, Adv. Funct. Mater., 2015, 25, 855–863 CrossRef CAS.
- D. J. Graham and N. G. Midgley, Earth Surf. Processes Landforms, 2000, 25, 1473–1477 CrossRef.
- H. Tanaka and T. Araki, Phys. Rev. Lett., 1998, 81, 389–392 CrossRef CAS.
- A. J. Bray, Adv. Phys., 2002, 51, 481–587 CrossRef.
- A. J. Bray, Philos. Trans. R. Soc., A, 2003, 361, 781–792 CrossRef CAS PubMed.
- A. J. Bray, Adv. Phys., 2010, 51, 481–587 CrossRef.
- E. D. Siggia, Phys. Rev. A, 1979, 20, 595–605 CrossRef CAS.
- T. Hashimoto, Phase Transitions, 1988, 12, 47–119 CrossRef CAS.
- J. Baderstedt, Master of Science thesis, Chalmers University of Technology, 2011.
- G. Vicidomini, P. Bianchini and A. Diaspro, Nat. Methods, 2018, 15, 173–182 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Figure containing micrographs of replicates of Fig. 9b. See https://doi.org/10.1039/d2ra04178b |
| This journal is © The Royal Society of Chemistry 2022 |