 Open Access Article
Open Access ArticleMeasurement and the improvement of effective thermal conductivity for a metal hydride bed – a review
Jianhua Ye acd,
Zhinian Li*abd,
Liyu Zhangabd,
Shumao Wangabd and
Lijun Jiangacd
acd,
Zhinian Li*abd,
Liyu Zhangabd,
Shumao Wangabd and
Lijun Jiangacd
aGRINM Group Co., Ltd., National Engineering Research Center of Nonferrous Metals Materials and Products for New Energy, 100088, China. E-mail: lzngrinm@163.com; Fax: +86-10-60662619; Tel: +86-10-60662633
bGRIMAT Engineering Institute Co., Ltd., 101407, China
cGRINM (Guangdong) Institute for Advanced Materials and Technology, 528000, China
dGeneral Research Institute for Nonferrous Metals, Beijing 100088, China
First published on 12th September 2022
Abstract
Solid-state hydrogen storage based on metal hydrides is considered a promising method for hydrogen storage. However, the low inherent thermal conductivity of metal hydride powder significantly limits the hydrogenation/dehydrogenation process in the metal hydride bed. Accurate measurement and improvement of the effective thermal conductivity of a hydride bed is of great significance for design of solid-state hydrogen storage devices. This article analyzes the factors that influence the effective thermal conductivity of a metal hydride bed, and also introduces different measurement methods and improvement ways for the effective thermal conductivity of a metal hydride bed. It is an effective way to improve the thermal conductivity of metal hydride beds by hydride powder mixed with a high thermal conductivity material and compaction. Accurately measuring the influence of hydrogen pressure, temperature and hydrogen storage capacity and other factors on the effective thermal conductivity of a metal hydride bed and obtaining the numerical equation of effective thermal conductivity play an important role in guiding the optimization design of heat and mass transfer structure of metal hydride hydrogen storage devices. The transient plane source method seems to be a better measurement choice because of short test time and easy to establish a pressure-tight and temperature control test system. However, there is still a lack of testing standards for the thermal conductivity of the hydride bed, as well as suggestions for the selection of test methods, improvement ways and design of in situ test room.
1. Introduction
After entering the industrial era, the global energy consumption increased by almost 1.5 times over the past three decades. It is worth noting that fossil energy consumption accounts for nearly 80% of the total.1 The lack of non-renewable energy forces people to seek renewable and clean energy as the future energy option to meet the requirements of sustainable development. Hydrogen is considered the most promising secondary energy carrier with an energy density of up to 120 MJ kg−1, and its reserve in nature is extremely rich.2 It is stored without space-time limitation unlike conventional clean energy. At the same time, the environmental friendliness of the product makes people pay more attention to the development and utilization of hydrogen.3Pressurizing and storing hydrogen in cylinders with the pressure resistance of up to 70 MPa or cryogenically hydrogenating the hydrogen to a temperature below 21 K are not economical and safe.4,5 Solid-state hydrogen storage, such as in metal hydrides, offers an attractive alternative and seems to be a preferred solution for future hydrogen storage technologies. This method relies on the reversible combination of metal atoms and hydrogen under different pressures. It has the advantages of high capacity, low cost, convenience, and can reversibly absorb and release hydrogen at the appropriate temperature and pressure.2,6 They perform these functions through the following reversible reaction equation eqn (1):
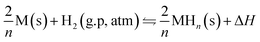 | (1) |
The combination of the host metal and hydrogen to form metal hydride is an exothermic reaction. When the metal hydride releases hydrogen, it needs to absorb heat. Different hydrogen storage alloys have different reaction heat. For example, the reaction enthalpy of magnesium-based hydrogen storage material is as high as 74 kJ mol−1.8
On-board hydrogen storage systems require high hydrogen storage density, fast hydrogen charging and discharging speed and long service life. The poor heat transfer performance of the hydride bed limits the absorption and desorption rate of hydrogen in the reaction process. If the heat of hydrogen storage material cannot be released or obtained in time, the bed temperature will change rapidly, which affects the equilibrium pressure of the hydride bed. If the plateau pressure is higher or lower than the working pressure, the absorption or desorption rate of hydrogen will decrease or even proceed in the opposite direction. This is detrimental to the practical application of solid-state hydrogen storage.
The heat transfer in the hydrogen storage tank includes the heat conduction process inside the hydride bed and the heat exchange process between the hydride bed and the environment. The latter is mainly dependent on the system structure design of the solid-state hydrogen storage device. For example, optimization design of the hydrogen storage tank size and heat exchange structure, the application of heat exchange structures, such as adding cold water jackets and fins.9–15 In which, the heat conduction in the hydride bed is the most important limiting factor, which can be characterized by the effective thermal conductivity (ETC). The effective thermal conductivity of hydride bed includes the heat conduction between hydrogen storage material particles, thermal convection between hydrogen storage material and hydrogen, and thermal radiation.
At present, different types of hydrogen storage materials have developed rapidly.16 At present, the hydrogen storage materials with practical value mainly include metal hydrides and complex hydrides. Fig. 1 shows the volumetric and gravimetric hydrogen density of some hydrogen storage materials. MgH2 exhibits high gravimetric hydrogen density of 7.6 mass %, magnesium resources are abundant and the cost is low, so MgH2 is a very promising hydrogen storage material. However, its high hydrogen absorption and desorption temperature affects its actual use, especially as a hydrogen source for fuel cells. Metal hydrides are promising candidate for solid-state hydrogen storage, with low absorption/desorption temperature, high volumetric hydrogen density, good reversibility and cyclic ability, fast kinetics and low-cost. The properties of some of the most common metal hydrides are summarized in Table 1.
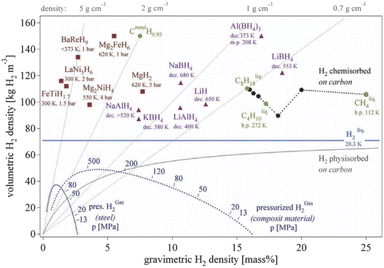 | ||
| Fig. 1 Volumetric and gravimetric hydrogen density of some selected hydrides.6 | ||
| Type | Metal | Hydride | Structure | Mass % | Peq, T |
|---|---|---|---|---|---|
| Elemental | Pd | PdH0.6 | Fm3m | 0.56 | 0.02 bar, 298 K |
| Ab5 | LaNi5 | LaNi5H6 | P6/mmm | 1.37 | 2 bar, 298 K |
| AB2 | ZrV2 | ZrV2H5.5 | Fd3m | 3.01 | 10–8 bar, 323 K |
| AB | FeTi | FeTiH2 | Pm3m | 1.89 | 5 bar, 303 K |
| A2B | Mg2Ni | Mg2NiH4 | P6222 | 3.59 | 1 bar, 555 K |
| Body-centred cubic | TiV2 | TiV2H4 | b.c.c | 2.6 | 10 bar, 313 K |
Their hydrogen storage properties are different under different temperatures and pressures. However, when the hydrogen storage materials are integrated into hydrogen storage tanks, accurate thermophysical date such as effective thermal conductivity required for heat transfer structure optimization are lacking. The heat transfer analysis and structure optimization design of the hydrogen storage tank are mainly concentrated on two parts: experimental analysis and numerical analysis. Numerical simulation analysis can greatly reduce the research cost and time. The premise is to establish an effective model verified by experiments. Otherwise, there is no guiding significance. The effective thermal conductivity of the hydride bed under working conditions is not static but dynamically changed by the synergistic influence of multiple factors. Using the varying effective thermal conductivity to modify the model can significantly improve the accuracy of the model prediction, which is the trend of numerical analysis of heat and mass transfer in hydride bed.17,18 Therefore, the heat transfer analysis of the hydrogen storage tank, especially the analysis and accurate determination of the effective thermal conductivity of the hydride bed, will provide the basis for the heat transfer analysis of the hydrogen storage tank, and guide the development and optimization of solid-state hydrogen storage tanks.
Researchers have used a variety of methods to improve the effective thermal conductivity of the hydride bed, in order to improve the hydrogen storage characteristics of the solid-state hydrogen storage devices, such as preparation of high thermal conductivity hydride bed by mixing high thermal conductivity materials and pressing molding. Different methods have different effects on the final performance of solid-state hydrogen storage devices.
Researchers used different test methods to measure and study the variation of effective thermal conductivity of various hydride beds under actual working conditions. However, each method has its uniqueness and shortcomings. Therefore, choosing a suitable test method to meet the requirements and accurately obtaining the dynamic change data of the effective thermal conductivity under working conditions will be the key to optimizing the design of the metal hydride hydrogen storage tank.
This article mainly introduces the influencing factors of the effective thermal conductivity of metal hydride bed, improvement technology, and conventional measurement methods.
2. Influence factors of metal hydride bed effective thermal conductivity
Numerous studies have shown that the effective thermal conductivity of the metal hydride bed in the process of hydrogen absorption/desorption changes dynamically with the change of working conditions. Influence factors for the hydrogen absorption and desorption performances of hydrogen storage materials include hydrogen pressure, temperature, and cycle number. Thermodynamic properties of metal hydride reflected by PCT curves, which show the strong dependence of the equilibrium pressure on the temperature and the hydrogen concentration. These external operating conditions often have a significant dynamic effect on the effective thermal conductivity of the hydride bed. In the process of hydrogenation/dehydrogenation, because the effect of expansion/contraction stress, metal hydride particles are further pulverized, thus affecting the change of contact between particles and further deteriorates the effective thermal conductivity of the metal hydride power bed. Moreover, the metal hydride hydrogen storage materials have different intrinsic thermal conductivity under hydrogenation and dehydrogenation state, and the effects of hydrogen pressure and temperature are also different. At the same time, some materials will undergo the phase change and thermal conductivity changes due to the influence of temperature and pressure. In short, under working conditions, the effective thermal conductivity of the hydride bed has very complex influencing factors. Next, the parameters and general laws that have been studied so far with the corresponding explanations of the researchers will be analyzed and summarized.2.1 Hydrogen pressure
People have generally measured the effective thermal conductivity of the powder-packed bed and the hydride compact with the hydrogen pressure. Suda et al.19 measured the effective thermal conductivity of the TiMn1.5 hydride bed with a maximum hydrogen pressure of 5 MPa by a steady state method. The results show that the effective thermal conductivity of TiMn1.5 hydride bed increases with the increase of pressure. At the temperature of 21 °C, the effective thermal conductivity increases from 0.25 W (m−1 K−1) to 1.29 W (m−1 K−1) with the increase of pressure from 0.1 MPa to 5 MPa. Suissa et al.20 measured the effective thermal conductivity of Mg2NiH2 and MmNi4FeH5.2, and the effective thermal conductivity values of the two hydrides were found to be 0.83 W (m−1 K−1) and at 375 K and 1.05 W (m−1 K−1) at 273 K under a hydrogen pressure of 4 MPa. Nagel et al.21 measured the effective thermal conductivity of a copper wire matrix improved metal hydride bed of MmNi4.46Al0.54 (Mm: misch metal) power using a steady state method. With the pressure increases, typical S-shaped curves were observed for both hydrogen and helium atmospheres, and the copper wire matrix will improve the effective thermal conductivity by about 0.4 W (m−1 K−1). Sun et al.22 measured the effective thermal conductivity of MlNi4.5Mn0.5 (Ml: lanthanum-rich misch metal) hydride bed by means of steady state method. According to the test results, it is also observed that the effective thermal conductivity also presents a typical S-shaped curve with the increase of pressure. Kumar et al.23 measure and analysed the effective thermal conductivity of a MmNi4.5Al0.5 hydride powder bed using an one-dimensional steady-state axial heat transfer comparative method, the result of this experiments showed that the effective thermal conductivity lies between 0.1 and 1.2 W (m−1 K−1) in the pressure and the temperature ranges of 0–50 bar and 0–100 °C, respectively. While hydrogen pressure and concentration showed strong influence on the effective thermal conductivity over the complete range, and it increases with increasing pressure in the form of the S-shaped curve, which is shown in Fig. 2. Kapischke et al.24 measured the effective thermal conductivity of magnesium hydride bed, it is found that the effective thermal conductivity decreases for constant pressure and temperature with increasing reacted fraction.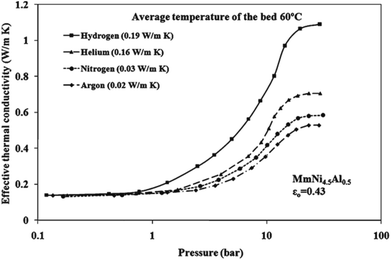 | ||
| Fig. 2 S-shaped curve of the effective thermal conductivity of the hydride bed with respect to the hydrogen pressure determined by Kumar et al.23 | ||
In this form, the pressure is generally displayed on the logarithmic scale. Hydrogen pressure has little effect on the effective thermal conductivity under near vacuum and low-pressure conditions. As the hydrogen pressure increases, the effective thermal conductivity of hydride bed increases significantly. After the pressure exceeds a certain interval, the effective thermal conductivity is almost unchanged. Saturation of the contribution of higher pressures to the effective thermal conductivity is more easily observed when using ordinary linear coordinates are used.25–27 Researchers use the dimensionless number of Knudsen number (Kn) in the gas dynamics theory to distinguish and explain this change,28 which can be expressed by the eqn (2):
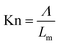 | (2) |
In 1981, Suda et al.19 gave the expression of the mean free path as shown in eqn (3):
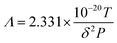 | (3) |
For the same hydrogen storage system, the change in hydrogen pressure is mainly manifested in the mean free path of the molecule. In low pressure section (Kn ≥ 10), due to the hydrogen concentration is very low, the molecules collide randomly in the pores, and the average freedom of the molecules is very large. At this time, the gas appears as the molecular flow that hardly contributes to the effective thermal conductivity of the hydride bed, which is not affected by the type of gas. Heat is almost exclusively conducted through a solid particle interface. In medium pressure section (0.01 < Kn < 10), as the concentration of hydrogen increases, the collision between hydrogen molecules intensifies, and the molecular free path begins to decrease. The contribution of hydrogen pressure to the effective thermal conductivity of the hydride bed is mainly related to the energy exchange between particles and the molecular weight of the gas. In high pressure section (Kn ≤ 0.01), the mean free path of hydrogen molecules is much lower than the characteristic pore size, the hydrogen is regarded as a viscous/continuous fluid whose thermal conductivity is independent of pressure. The contribution of hydrogen pressure to the effective thermal conductivity of the hydride bed reaches to the maximum, and the effective thermal conductivity of the hydride bed almost no longer increases with the hydrogen pressure.22,28
When people study the influence of hydrogen pressure on the effective thermal conductivity, to avoid the influence of hydride bed hydrogenation/dehydrogenation, some inert gases such as nitrogen, helium, and argon, are often used as working gases for comparison.21,23 The effective thermal conductivity in the low-pressure section of the characteristic S-shaped curve is hardly affected by the gas type. Since hydrogen is the gas with the highest thermal conductivity, as the pressure increases, the effective thermal conductivity measured under a hydrogen atmosphere is the highest. It is worth pointing out that helium gas has a similar molecular size and thermal conductivity compared to hydrogen gas, thus it is particularly widely used as a comparative gas for the effective thermal conductivity measurement.28–30
In 1980, Suda et al.31 discovered that the effective thermal conductivity of the TiMn1.5 powder bed changed with hydrogen pressure, and pointed out that it was the result of a strict relationship with the mean free path of the gas. In 1986 and 1990, Nagel21 and Sun22 divided the influence of pressure into three sections and explained the properties of fluids. And in 1994, Kapischke et al.24 quantitatively analyzed the contribution of hydrogen pressure to the effective thermal conductivity of the Mg/2 wt% Ni hydride bed using parameters such as mean free path and effective length. Although there is a relatively complete explanation for the influence of hydrogen pressure, the effective thermal conductivity changing threshold of different hydride beds is slightly different. However, according to recent researches, the effect of hydrogen pressure on the effective thermal conductivity of hydride bed reaches the maximum when it reaches about 1.5 MPa.
2.2 Temperature
The effect of temperature on the effective thermal conductivity does not as characteristic change trend as pressure. With the changes of the temperature, the effective thermal conductivity may increase, decrease, or even unchanged. It may be due to combined effect of the temperature response for the thermal conductivity of hydride powder and hydrogen. Therefore, it is necessary to specifically measure the effective thermal conductivity of hydride beds prepared by different methods.In 1981, Suda et al.19 measured the effective thermal conductivity of TiMn1.5 powder bed at different temperatures, and it has a higher measured value at 21 °C than at 38 °C. Klein et al.32 also proved that the effective thermal conductivity of LmNi4.85Sn0.15/ENG compacts decreased with increasing temperature. However, Ishido et al.7 found that the effective thermal conductivity of Mg and Mg/10 wt% Ni hydride powder increased with increasing temperature. Madaria et al.33 found that the effective thermal conductivity of La0.8Ce0.2Ni5 powder and the compact with graphite flakes were hardly affected by temperature at 5 MPa hydrogen pressure, but when the hydrogen pressure was reduced to 1 MPa, the effective thermal conductivity decreased slightly with increasing temperature. Popilevsky et al.34 determined that the effective thermal conductivity of MgH2 containing 8–9.5 vol% Mg decreased from 23 to 13 W (m−1 K−1) when the temperature increased from 300 to 525 K. Wang et al.35 measured that the effective thermal conductivity of YbH1.88 decreased from 6.2 to 3.9 W (m−1 K−1) when the temperature increased from 298 K to 413 K. They believed that it might due to the increase of dislocation density in the specimen after hydrogen absorption. The experimental values of the effective thermal conductivity of metal hydrides from some literature are summarized in Table 2.
| Material | Pressure (MPa) | Temperature (K) | ETC (W (m−1 K−1)) | Ref. |
|---|---|---|---|---|
| TiMn1.5 hydride | 0.1–5 | 294, 311 | 0.2–1.3 | 19 and 31 |
| Mg2Ni hydride | 0.2–4.5 | 373 | 0.66–0.83 | 20 |
| MmNi4Fe hydride | 0.2–4.5 | 273 | 0.8–1.05 | 20 |
| MmNi4.46Al0.54 hydride + Cu wire matrix | 0–5 | 283, 293, 313 | 0.4–2.76 | 21 |
| LaNi4.7Al0.3 hydride | 0–6 | 193–413 | 0.02–1.2 | 28 |
| Ti0.98Zr0.02V0.43Fe0.09Cr0.05Mn1.5 hydride | 0–6 | 193–413 | 0.05–1.2 | 28 |
| MlNi4.5Mn0.5 hydride | 0.1–3 | 313, 323, 333 | 0.7–1.3 | 22 |
| MmNi4.5Al0.5 hydride | 0–5 MPa | 0–373 | 0.1–1.2 | 23 |
| Mg hydride + 2 wt% Ni | 0.1–5 | 573–673 | 4–9 | 24 |
| Mg hydride | 0.1–3.5 | 313–473 | 0.8–1.4 | 7 |
| Mg hydride + 10 wt% Ni | 0.1–4 | 303–473 | 0.7–1.3 | 7 |
| Mg2Ni hydride | 0.1–4 | 308–473 | 0.35–0.75 | 7 |
| Mg hydride | 0.1–2.5 | 300–573 | 0.64–1.24 | 27 |
2.3 Desorption/absorption state and hydrogen content
The crystalline structure of metal hydride have a significant volume increase and decrease (about 10–35%) upon hydrogenation and dehydrogenation respectively, which will tread to further pulverized of the metal hydride particles during hydrogenation and dehydrogenation cycles. The particle size of hydrogen storage material tends to change during the process of hydrogen absorption and desorption, which changes the contact area and affects the heat transfer between particles.36 At the same time, the particles have different thermal conductivities in the hydrogenation and dehydrogenation state. For pure metals/alloys, the thermal conductivity is reduced because the insertion of hydrogen atoms hinders the thermal conduction of free electrons. At constant temperature, the change in the hydrogen content of the material is affected by the hydrogen pressure, so the results for the influence of a single factor of hydrogen content are often not directly available. Therefore, the influence of temperature and hydrogen pressure can usually be integrated, and the cumulative effect of these factors on the final effective thermal conductivity can be analyzed to determine the influence of the hydrogen content.Qin et al.37 determined that the effective thermal conductivity of the powder bed of LaNi4.61Mn0.26Al0.13Hx (x = 0, 1.25, 2.5, 5) with increasing hydrogen capacity. When the hydrogen capacity was from 0 to saturation, the effective thermal conductivity increased from 0.61 to 1.56 W (m−1 K−1). Matsushita et al.38 determined that the effective thermal conductivity of the nano-FeTi packed bed after 25–26 cycles of hydrogen absorption and desorption increased from 0.4 to 1.1 W (m−1 K−1) with the increasing hydrogen capacity. Bird et al.39 measured the effective thermal conductivity of Mg2FeH6 + 10 wt% Fe pellet at room temperature, which was 1.72 W (m−1 K−1), but the effective thermal conductivity of its fully dehydrogenated state of 2Mg + Fe increased to 2.20 W (m−1 K−1). Wang et al.35 measured the thermal conductivity of YHx with different hydrogen capacities at room temperature, and the results showed that the thermal conductivity of YH1.88 with higher hydrogen capacity was 3.8 W (m−1 K−1) lower than that of YH1.85. Dedrick et al.40 measured the thermal conductivity of NaAlH4 in the state of complete hydrogenation and dehydrogenation, and the results showed that the thermal conductivity increased with increasing free aluminum content formed by dehydrogenation. The thermal conductivity of the fully dehydrogenated state was about 0.2 W (m−1 K−1) higher than that of the full hydrogenation state. Pohlmann et al.41 measured the effective thermal conductivity of Mg90Ni10 pellet after 8 cycles of hydrogen absorption and desorption. Compared with the as-compacted pellet, with the porosity decreases from 38 vol% to 22 vol%, the effective thermal conductivity of the hydrogenated state increased from 6 to 11 W (m−1 K−1). Although the porosity of the hydride bed with dehydrogenated state reaches to 41 vol%, the effective thermal conductivity was 28 W (m−1 K−1), which is the largest in the comparison sample. This is due to the higher thermal conductivity of the dehydrogenated metal.
2.4 Hydrogenation/dehydrogenation cycles
At present, the research on the influence of the cycle numbers on the effective thermal conductivity is mainly based on the powder-packed bed. With the increase of the amount of hydrogen absorption and desorption, the particles may be further pulverized, resulting in the changes in particle size and particle contact. In the previous studies on the cyclic pulverization of hydrogen storage alloys, it is found that the alloy particle size will rapidly decay during the hydrogenation and dehydrogenation cycles, which often leads to a decrease in the effective thermal conductivity.28 At the same time, the powder particles may agglomerate and form a denser structure during the hydrogenation and dehydrogenation.42 For hydrogen storage materials which work under high temperature, the particles will sinter due to the continuous hydrogenation/dehydrogenation cycle, which leads to the effective thermal conductivity increase. However, for the above situation, the effective thermal conductivity of the hydride bed may not change further because the powder particles will be stable after a certain number of cycles.Suissa et al.20 studied the effective thermal conductivity of MmNi4Fe powder bed under vacuum after different hydrogenation/dehydrogenation cycles. The results showed that the effective thermal conductivity decreased from 1.6 to 1.4 W (m−1 K−1) as the number of cycles increased. And the effective thermal conductivity had not significantly change after 3 cycles. Dedrick et al.40 noticed that the ball-milled, uncycled sodium alanate had a very low thermal conductivity (<0.01 W (m−1 K−1)) under vacuum, but with the addition of hydrogen, the effective thermal conductivity increased by 5000%. The effective thermal conductivity of the absorbed state with 1 atm of hydrogen did not significantly change with cycles, however, the effective thermal conductivity of fully desorbed state increased at vacuum. The reason for the increase in the effective thermal conductivity is believed to be the result of particle sintering and geometrical arrangement during the cycling. Albert et al.27 measured the effective thermal conductivity of the MgH2 powder bed at 39 °C and 410 °C after 10 to 28 and 11 to 27 desorption/absorption cycles, respectively. The result showed that effective thermal conductivity under ambient hydrogen pressure increased from 0.8 to 1.2 W (m−1 K−1) and 0.9 to 1.3 W (m−1 K−1), respectively. The increase of thermal conductivity is considered possible due to the rearrangement and densification of powder materials. Albert et al.43 doped MgH2 powder with 4 wt% Ni and subjected it to hydrogenation and dehydrogenation cycles at 400 °C, and measured the effective thermal conductivity under dehydrogenation state at 15 bar. After 201 cycles, the thermal conductivity increased from 1.17 to 8.05 W (m−1 K−1). It may be that the formation of sintering and permeation network of dehydrogenated particles promotes heat conduction. It is worth noting that the effective thermal conductivity decreased to 7.23 W (m−1 K−1) after 451 cycles.
2.5 Particle size
As mentioned in the previous section, the metal hydride particles are further pulverized during the hydrogenation and dehydrogenation cycles. The further refinement of the hydride powder may fill the pores, but the increase of the contact area between the particles will increase the thermal contact resistance between the solid particles. At the same time, it should be noted that the distribution of different particle sizes may lead to changes in porosity and affect the effective thermal conductivity.29,30Solovey et al.44 studied the effective thermal conductivity of LaNi4.6Al0.4 compacts with the particle size of 70 μm and 70–200 μm, and the results show that the effective thermal conductivity were 9.6 and 17.6 W (m−1 K−1) under the hydrogen pressure of 0.11 MPa, respectively. The MmNi4.15Fe0.85 compact prepared in the same form also has the same trend that the effective thermal conductivity increases with the increasing particle size. However, in the researches of Chaise45 and Flueckiger,46 they found the particle size and effective thermal conductivity decreased because of the ball milling and hydrogenation activation.
2.6 Porosity and apparent density
The porosity of the powder bed or compacted bed is directly related to its apparent density.47 Through vibration or compaction can increase apparent density and decrease the porosity of hydride bed,7,48 which often increases the effective thermal conductivity of the hydride bed.49–51 Because general gas has lower thermal conductivity than solid, when porosity reduce, the solid-phase heat conduction has a higher contribution than the gas-phase heat conduction in the powder pores.52Chaise et al.45 studied the effective thermal conductivity of raw and ball-milled MgH2 under different hydrogen pressures. The results show that ball-milled MgH2 has a smaller particle size and has lower porosity during filling. The effective thermal conductivity of the ball mill powder bed starts to increase at higher pressures because of the Knudsen effect.
2.7 Material state
For some coordination hydrides, phase/state transitions may occur due to temperature and pressure changes within the operating conditions, which leads to abrupt changes in thermal conductivity. This is due to the different intrinsic thermal conductivity between different phases.53,54 And the phase change that affects the hydrogenation and dehydrogenation process needs attention.Bird et al.39 confirmed the thermal conductivity of NaH was 5 W (m−1 K−1) through experiment. However, the thermal conductivity of NaBH4 and NaAlH4 were 0.97 W (m−1 K−1) and 1.90 W (m−1 K−1), respectively, which were lower than of NaH. This is due to the phonon interaction in the compound and the high symmetry of the heteronuclear diatomic NaH molecule in the cubic crystallographic space group. Similarly, the thermal conductivity of NaF was 9.4 W (m−1 K−1), which was higher than that of NaH. This is because NaF has stronger ionic properties. In addition, the thermal conductivity of inactivated and activated alloys and powders after ball milling and heat treatment will also be different. The amorphous state caused by ball milling will change to a crystalline state after high temperature heat treatment. Therefore, the ball-milled powder after high-temperature heat treatment tends to have higher thermal conductivity than the initial state.46,55
3. Measurement methods for the effective thermal conductivity of metal hydride bed
Since the Fourier law of heat conduction was proposed, variety of thermal conductivity measurement methods have been developed for more than one hundred years. These thermal conductivity measurement methods are divided into the steady-state methods (radial heat flow method, guarded longitudinal heat flow method, guarded hot plat method, heat flow meter method) and the transient methods (hot-wire method, thermal probe method, transient plane source method, laser flash method) according to the different measuring principles. The Fourier law of steady-state heat conduction represents the heat passing through a given cross section per unit time which is proportional to the cross section area and the temperature gradient in the direction perpendicular to the cross section, and the direction of heat transfer opposite to the direction of temperature increase as shown in eqn (4):
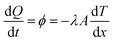 | (4) |
In the steady-state measurement methods, the specimen is heated by a given constant temperature heat source. When the internal temperature field of the specimen is stable, the thermal conductivity can be calculated by the heat flux through the specimen and the temperature gradient at a given distance. At the same time, according to the method of obtaining heat flux, the thermal conductivity test can be divided into the comparative method and the absolute method. The former usually uses reference materials whose thermal conductivity is known or whose thermal conductivity is only a function of temperature is placed on the heat flow path concentrically with the specimen, and the required heat flux can be calculated by the specified temperature gradient on the unit area of the reference material, and then the thermal conductivity of the specimen is further calculated. The latter heat flux is obtained directly from a constant heating source. The steady-state methods used to measure the effective thermal conductivity of hydride bed mainly include radial heat flow method, axial heat flow method, guarded hot plate method, and heat flow meter method.
The transient test method is to apply a given thermal pulse or periodic heat flow in the initial thermal equilibrium of the specimen, according to recording the change of the specimen temperature with time and using the non-steady-state thermal differential equation, the thermophysical parameters of a specimen like thermal conductivity and thermal diffusivity can be obtained. Thermal conductivity is used to characterize the rate of heat transfer within the specimen, and thermal diffusivity is used to characterize the rate of temperature transfer within the specimen. They are related to the volume specific heat capacity of the material, which is as eqn (5):
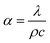 | (5) |
The transient test method is realized due to the relation of the intrinsic properties of the materials. Sometimes the thermal conductivity of the specimen cannot be obtained directly, but calculated by determining the specific heat capacity and thermal diffusivity. Because there is no need to wait until the temperature field is stable, so the test time is often short and does not require too much additional test equipment and samples. At present, the transient methods used to measure the effective thermal conductivity of hydride bed mainly include hot-wire method, thermal probe method, transient plane source method, and laser flash method.
3.1 Steady-state method
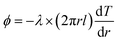 | (6) |
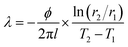 | (7) |
The radial heat flow method can be divided into the radial heat flow comparative method and the absolute method according to the way of heat flow. The corresponding operating apparatus and details are shown in ISO 8497:1994.56
In the absolute radial heat flow method, a heater with known power is coaxial with the cylindrical test cell, and thermocouples are placed in different radial positions. At the same time, a thermostatic fluid device is installed outside the device to maintain a one-dimensional radial steady-state heat flow.
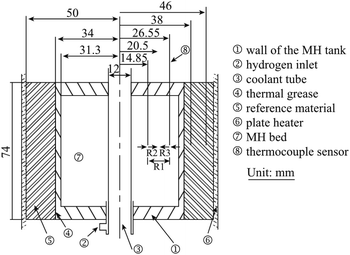
In 1994, Kapischke et al.24 designed an effective thermal conductivity test device based on the radial absolute method, which could measure the effective thermal conductivity of Mg/2 wt% Ni powder bed under different hydrogen absorption reaction fraction. As shown in Fig. 3, the outer wall was made of hydrogen-resistant steel and connected with the programmed electric heater, and wrapped with a thin steel foil to provide constant and uniform heat source. The thermocouples were fixed in a prescribed position by a ceramic plate to prevent movement.
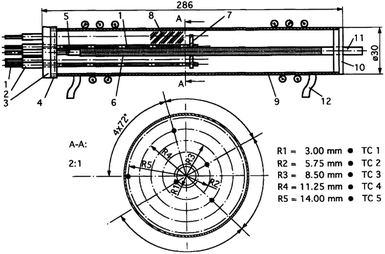 | ||
| Fig. 3 Schematic diagram of ETC measurement equipment (metal hydride reactor) designed by Kapischke et al.24 (1–5) NiCr–Ni thermocouples; (6) metallic filter tube; (7) ceramic fixing plate; (8) hydrogen storage metal; (9) seamless tube; (10) bottom plate; (11) hydrogen; (12) reactor. | ||
In 2014, Shim et al.26 measured the effective thermal conductivity of MgH2–ENG compact through radial absolute method. The heat source was provided by a miniature sheath heater in the center of the chamber, indium was coated on the heater and thermocouples to reduce the contact thermal resistance. In 2017, Madaria et al.33 designed a thermal conductivity test cell using the radial absolute method to measure the effective thermal conductivity of different forms of La0.8Ce0.2Ni5 beds, as shown in Fig. 4. The reactor was designed with length-to-diameter ratio of 4.33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to achieve unidirectional radial heat transfer. Using a similar device, in 2020, Anil et al.57 also measured the effective thermal conductivity of different forms of Mg + 50 wt% LaNi4.6Al0.4 composite pellets, and a capsule heater was used to provide heat in the center of the cell.
1 to achieve unidirectional radial heat transfer. Using a similar device, in 2020, Anil et al.57 also measured the effective thermal conductivity of different forms of Mg + 50 wt% LaNi4.6Al0.4 composite pellets, and a capsule heater was used to provide heat in the center of the cell.
 | ||
| Fig. 4 Schematic diagram of ETC cell used by Madaria et al.33 | ||
In the radial heat flow comparative method, the reference material and specimen are placed in the concentric stainless steel annular containers separately. A circulating hot water or electric heater is used to provide a constant heat source, and circulating cooling water is used as a cold source to form a temperature gradient in the radial direction. Reducing heat loss by improving thermal insulation performance. Setting multiple thermocouples at different positions along the radial direction of the reference material and specimen, and measure the temperature of the corresponding positions. Since the radial heat flux is equal, the thermal conductivity of the material can be calculated by the following eqn (8):
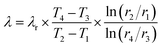 | (8) |
Generally, due to the low effective thermal conductivity of metal hydride powder bed (<1 W (m−1 K−1)), it is necessary to improve the temperature gradient to ensure the measurement accuracy. Therefore, the thermal conductivity of the reference material as small as possible.
In 1980, Suda et al.31 measured the effective thermal conductivity of TiMn1.5 powder bed by the radial comparison method. Difron blocks were used at the top and bottom test chamber to ensure thermal insulation performance, and the mixture of lead pellets and ethanol was used as the reference material. In 1986, Nagel et al.21 also used the same reference material to measure the effective thermal conductivity of MmNi4.46A10.5 powder bed which mixed with copper wire. Due to the use of ethanol and lead pellets, the convection caused by temperature change leads to the inaccurate results. Therefore, in 1984, Suissa et al.20 used stainless steel and Teflon as reference material to determine the effective thermal conductivity of MmNi4FeH5.2 powder bed. In 1990, Sun et al.22 measured the effective thermal conductivity of the MiNi4.5Mn0.5 powder bed using annual polytetrafluoroethylene block as reference material.
In 2011, Wang et al.58 determined the effective thermal conductivity of LaNi5 powder bed by establishing a radial comparison test system as shown in Fig. 5. Nylon-803 was used as reference material and the outermost layer was covered with insulation material to reduce heat loss. At the same time, errors were reduced by applying thermal grease on the contact surface. They pointed out that in order to make the hydrogen storage material powder bed reach a greater temperature gradient, the thermal conductivity of the reference material should be as small as possible.
 | ||
| Fig. 5 Schematic diagram of an effective thermal conductivity test device used by Wang based on radial heat flow comparative method.58 | ||
Radial heat flow methods often require large equipment and many additional components to minimize heat loss and maintain one-dimensional steady-state radial heat flow. The specimen usually requires a larger size and takes a long time to reach steady-state. Generally, the calculated average value obtained from multiple measured points is used to reduce the error. In the absolute method, the main error comes from the difference between the heating power of the heat source and the actual heat flow provided by the heater, and the contact thermal resistance between the heater and the specimen. In general, a thermal conductive agent with no chemical reaction and high thermal conductivity is filled between the heater/thermocouple and the specimen to reduce the error. In the comparison method, the error is mainly caused by the heat loss through natural convection, and the contact thermal resistance between the specimen and the wall of heater. Therefore, reference materials can be solid materials with known thermal conductivity, such as Teflon or nylon.
 | ||
| Fig. 6 Schematic diagram of guarded longitudinal heat flow method.59 | ||
The thermal conductivity of the specimen can be calculated by the eqn (9):
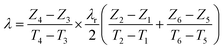 | (9) |
In 1998, Lloyd et al.63 determined the effective thermal conductivity of compact prepared by Sn and LaNi5 coated with copper. In the test device, Cu was used as the heat sink, and the silicon heat sink compound was used to reduce the contact thermal resistance. In 2001, Kim et al.64 used an experimental apparatus similar the Lloyd's to measure the effective thermal conductivity of compact with LaNi5 and recompressed expanded graphite. However, no guard heater was used, and only one meter bar made of SS304 was used between the specimen and the heater. No special protection measure was taken, but appropriate pressure and vacuum environments were used to reduce the contact thermal resistance and heat loss. In 2004, Klein32 determined the effective thermal conductivity of LmNi4.85Sn0.15/ENG compact, the effective thermal conductivity is 30.72 W (m−1 K−1) with adding 14.5 wt% ENG. In 2009, Lee et al.65 measured the effective thermal conductivity of copper-coated hydride powders (LaNi5, Ca0.6Mm0.4Ni5, and LaNi4.75Al0.25). The device used a copper meter bar which Park et al.66 also used in 2020 and an embedded cartridge heater as the heat source. Omegatherm 201 thermal compound was used to reduce the thermal resistance of the thermocouple and Cu meter bar, and the instrument was surrounded by PTFE to achieve the thermal insulation.
In 2011, Kumar et al.23 determined the effective thermal conductivity of the MmNi4.5Al0.5 hydride powder bed with the device shown in Fig. 7. The hydride bed was placed in series with the reference material using PTFE, and a guarded heater was used to eliminate radial heat loss of hydride bed.
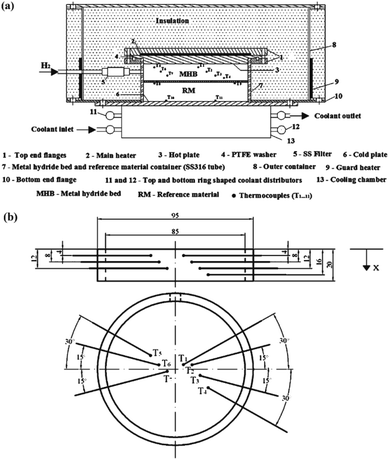 | ||
| Fig. 7 (a) The ETC test device used by Kumar; (b) the thermocouple distribution in hydride bed.23 | ||
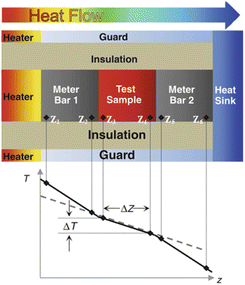
The guarded longitudinal heat flow method is a steady-state technique for measuring the axial thermal conductivity of the specimen. The meter bar as reference material and specimen are cylinders with the same cross-sectional area, also known as the cut-bar method. The application of this technology is based on the ideal assumption that the entire device is in an axial one-dimensional steady-state heat flow state. However, this method requires a long measurement time and a stringent test environment, and the error mainly come from uneven heat transfer at the interface, contact thermal resistance, and radial heat flow loss.60,67,68 In order to ensure the one-dimensional axial steady-state heat flow, it is necessary to use suitable insulating materials or shield heaters to reduce the radial heat flow loss or compensate heat loss. An appropriate clamping pressure to make the specimen and the meter bar in good contact to ensure uniform heat transfer at the interface. However, for powder specimens and specimens with poor mechanical stability, the clamping pressure will affect the porosity and thickness of the specimen, which changes the original state of the specimen and leads to measurement distortion. Therefore, how to control the clamping pressure to make the experiment comparable needs to be considered. Besides, the interface contact thermal resistance also needs to take into account. The use of a suitable thermal conductive medium can reduce contact thermal resistance and test error. Also, it takes a long time to reach a stable temperature gradient during the test, which is time consuming.
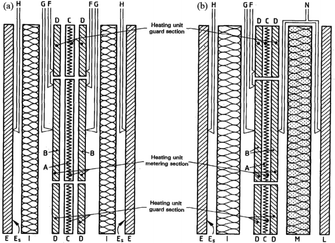 | ||
| Fig. 8 Schematic diagram of GHP (a) two-specimen apparatus; (b) single-specimen apparatus69 (A) metering section heater; (B) metering section surface plates; (C) guard section heater; (D) guard-section surface plates; (E) cooling unit; (ES) cooling unit surface plate; (F) differential thermocouples; (G) heating unit surface thermocouples; (H) cooling unit surface thermocouples; (I) test specimen; (L) guard plate; (M) guard plate insulation; (N) guard. Plate differential thermocouples. | ||
The former uses two identical specimens of similar thickness and the latter replaces the specimen and cooling unit on one side with a guard insulation plate (M) and guard heater (L). The measurement apparatus includes an inner heating unit and an outer cooling unit (E), with specimen (I) sandwiched in the middle. The required test temperature can be achieved by adjusting the heating unit and cooling unit. The heating unit consists of a central metering section heater and two guard section heaters on both sides. The former includes a metering heater (A) and metering surface plate (B), the latter includes guard heater (C) and guard surface plate (D), and there is a gap between the metering section and the guard section. The plate is made of material with high thermal conductivity, such as copper, aluminum, nickel, aluminum oxide, aluminum, and nitride, which can reduce the lateral temperature difference between the metering section and the guard section to adapt for different operating temperatures and environmental conditions.70 The apparatus adopts isothermal adiabatic method to ensure that the temperature of the guard section is consistent with the temperature of the metering section to reduce the heat loss on the metering section. In single-specimen apparatus, by adjusting the guard heater, the same heat output as the inner heating unit is achieved, the temperatures on the two sides of the guard insulation plate are the same, so that all the axial heat passes through the cooling unit on the other side. More details about this method can be found in ISO 8302:1991 (ref. 69) and ASTM C177-19.71
The thermal conductivity of the specimen can be calculated by the eqn (10):
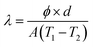 | (10) |
In 1912, Poensgen72 first introduced a ring-shaped copper guard around the heating unit and controlled their temperature to be consistent to prevent radial heat loss. At the same time, the low thermal conductivity material was filled around the specimen between the guard plate and the cooling plate to limit the lateral heat loss. At present, GHP used for the measurement of the effective thermal conductivity of hydride powder bed was only found in 2021, that Kim et al.30 used a designed miniaturized GHP apparatus to measure the effective thermal conductivity of LaNi5 packed bed. The measurement results showed that under vacuum condition, the effective thermal conductivity of LaNi5 packed bed with particle size less than 50 μm was only 0.0128 W (m−1 K−1).
The guarded hot plate method can obtain the thermal resistance of the specimen during the measurement. And it can only calculate the thermal conductivity of the thermally homogeneous specimen. According to the description of ISO 8302-1991, the accuracy of the results in the entire test range was better than 5%, and the repeatability was 1%. However, the size of the specimen is required to be large, and reasonable surface flatness is needed to avoid contact thermal resistance, and a long test time is required. Moreover, strict conditions are required to control the temperature difference between the guard section and metering section to avoid lateral heat loss to maintain one-dimensional steady-state uniform heat flow. Therefore, it can only test specimens with lower thermal conductivity and is not suitable for high temperatures (>700 °C) measurement due to its poor accuracy.
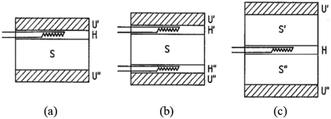 | ||
| Fig. 9 Schematic diagram of HFM typical configuration of specimen and heat flow meter: (a) single-specimen asymmetrical; (b) single-specimen symmetrical; (c) two-specimen symmetrical73 where S, S′, S′′—specimen; U′, U′′—heating unit and cooling unit; H, H′, H′′—heat flow unit. | ||
The calculation of the thermal conductivity of the specimen corresponding to the single-specimen asymmetrical, single-specimen symmetrical, and two-specimen symmetrical configuration is as follows: eqn (11)–(13).
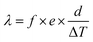 | (11) |
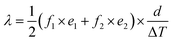 | (12) |
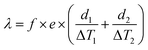 | (13) |
At present, the application of the heat flow meter method to determine the thermal conductivity of hydride materials is still lack. In 2008, Pourpoint et al.76 used this device to measure the thermal conductivity of Ti–Cr–Mn hydrogen storage alloy, which was approximately 0.18 W (m−1 K−1) at room temperature. The test device also wound glass fiber on the side of the heat flow meter to reduce the radial heat loss caused by convection. In 2013, Yasuda et al.77 prepared a metal hydride sheet from TiFe0.9Ni0.1 powder, aramid pulp, and carbon fiber. The results of thermal conductivity measurement at 323 K showed that the thermal conductivity of the MH sheet increased to 3.2 W (m−1 K−1) in the plane direction and remained low about 0.1 W (m−1 K−1) in the thickness direction when the carbon fiber ratio increased to 30 wt%.
3.2 Transient state method
The components distribution of the parallel hot-wire method and the cross hot-wire method test system are shown in Fig. 10.
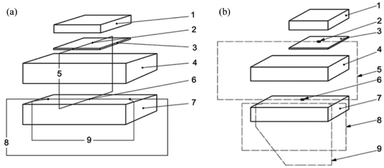 | ||
| Fig. 10 Schematic diagram of (a) cross hot-wire method; (b) parallel hot-wire method79,80 (1) cover; (2) reference thermocouple; (3) insulation layer; (4 & 7) specimen; (5) differential measurement circuit; (6) measurement thermocouple; (8) current heating circuit; (9) voltage measurement circuit. | ||
For the parallel hot-wire method, the thermal conductivity λ of the specimen is calculated by eqn (14) and (15).
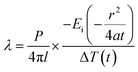 | (14) |
| P = V × I | (15) |
The value of the function −Ei(−r2/4at) can be obtained by calculating the results of ΔT(2t)/ΔT(t) and then looking up the integral list of the exponential function.
For the cross hot-wire method, the thermal conductivity can be calculated by eqn (16):
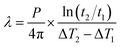 | (16) |
Since the heat storage and thermal interference exist at the hot-wire and thermocouple welding points at the beginning of heating, the minimum start time t1 cannot be too small. And the size of specimen limit t2 cannot be too large. When DC is used, it is only suitable for the test with thermal conductivity less than 1.5 W (m−1 K−1). Due to eliminating the asymmetry of the solder joints during AC usage, the thermal conductivity test range is broadened to 5 W (m−1 K−1). Because the hot-wire is buried in the material, there is often a contact thermal resistance between the hot-wire and the material, which reduces the accuracy of the test.82 In order to reduce the thermal resistance as much as possible, a large temperature rise of 10 to 20 K and a large time scale are usually used, resulting in the decrease of temperature gradient. This means that large solid must be used, so that the heat flow will not reach the boundary of the specimen during the test.83
In 1888, Schleiermacher84 firstly proposed the principle for the hot-wire method. In 1949, Held et al.85 developed the apparatus for measuring the thermal conductivity of liquid using manganine as hot-wire material, and its calculation form was consistent with that of the cross hot-wire method. To avoid corrosion of the metal wire by liquid, the enameled wire and T-type thermocouple are placed in a narrow glass capillary tube. Using the formula, the influence of the size of the heating wire, the diameter of the test container, and the test time on test results were derived and analyzed. Under the given conditions, the test error within 2% can be achieved. In 1976, Healy et al.86 introduced the expression for the correction of the hot-wire method to determine the thermal conductivity of liquids. It had strong reference significance for the further development of this method to determine the thermal conductivity of solids. The correction expression was mainly for the condition at the hot-wire, the outer cell circumference, and the variable test atmosphere properties, and nine sub-items were obtained and the specific correction formulas were given. Ishido,7 Hahne,28 and Sundqvist54 measured the effective thermal conductivity of Mg2Ni packed beds, HTW5800, and LiBH4 powder bed, respectively. Sundqvist pointed out that due to the distance between the specimen and the hot-wire was only about 3 mm to 5 mm, the temperature pulse could be reflected back, which disturbed the temperature field at the hot-wire and reduced the measurement accuracy.
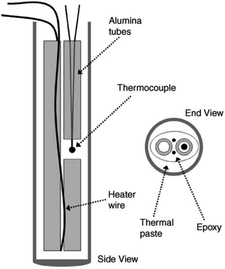 | ||
| Fig. 11 Simplified illustration of thermal probe used by Dedrick et al.40 | ||
In 1950, Hooper et al.89 first used the thermal probe method to measure the thermal conductivity of materials. However, the thermal probe method is rarely used in the measurement of the hydride bed. In 2005, Dedrick et al.40 used the thermal probe method to determine the thermal conductivity of sodium aluminum hydride. The results showed that the thermal conductivity of sodium aluminum hydride in the fully decomposed state was about 0.4 W (m−1 K−1) under the hydrogen pressure of 0.1 MPa.
The main error of the thermal probe method is caused by the finite size of the specimen and the thermal contact resistance between the probe and the specimen. Because the probe has a certain diameter and heat capacity, it is easy to form axial heat conduction leading to heat loss, so the assumption of one-dimensional radial heat conduction cannot be satisfied. Therefore, it is necessary to increase the length-to-diameter ratio of the probe and reduce the heat capacity to improve the accuracy of the results. The probe is usually filled with low heat capacity materials to reduce the influence of air convection inside the probe.
 | ||
| Fig. 12 Schematic diagram of TPS (a) polyimide insulated probe; (b) mica insulated probe.91 | ||
For different types of test specimen modules, the method has different models and formulas to fit and analyze thermal conductivity, such as bulk specimens, powder specimens, thin film specimens, and anisotropic materials.92 In the theoretical analysis, the probe is simplified into multiple concentric rings. For bulk materials, when the hot plate is heated, the variation of probe resistance with temperature is described as eqn (17) and (18):
| R(t) = R0{1 + β[ΔTi + ΔTs(τ)]} | (17) |
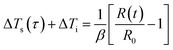 | (18) |
The temperature rise of insulation layer ΔTi will be remain constant after a very little time, which is described as eqn (19):
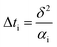 | (19) |
The solution of the thermal conductivity equation is expressed as eqn (20) and (21):
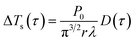 | (20) |
| P0 = I2R | (21) |
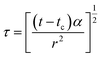 | (22) |
The dimensionless specific time function is described as eqn (23):
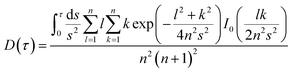 | (23) |
Taking α and tc as the iterative optimization variables, and fitting the linear relationship between ΔTs and D(τ) with the least square method to obtain the slope value. Then the thermal conductivity of the specimen can be calculated.
At the same time, it should be noted that in order to maintain the assumption that the probe is in a one-dimensional infinite medium during the test, the heat flow cannot reach the specimen boundary.93 The detection depth and characteristic time are proposed, as shown by eqn (24) and (25), that is, the minimum distance between any point of the probe and the edge of the specimen and the maximum test time in the test process, respectively.
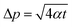 | (24) |
 | (25) |
For the thermal conductivity test of cylinder specimens, the diameter must be at least twice the diameter of the probe, and the thickness should be at least the same as the radius of the probe. The test time should be from 1/3 of the characteristic time to the entire characteristic time, and the time interval between repeated experiments should be at least 36 times the test time of the previous experiment according to the manufacturer's regulations.
The TPS method has been widely used to measure the effective thermal conductivity of hydride bed since it was proposed. From 2008 to 2010, Flueckiger et al. successively measured the effective thermal conductivity of inactivated metal hydride pellets,93 including the oxidized Ti1.1CrMn powder-packed bed94 and the activated Ti1.1CrMn powder-packed bed.46 In 2012, Yang et al.95 measured the thermal conductivity of NH3BH3. Its partial thermal decomposition product polyiminoborane under environmental conditions. In 2013, Jepsen et al.96 tested the thermal conductivity of LiH + MgB2 composite at room temperature in argon atmosphere. In 2018, Jepsen et al.53 measured the effective thermal conductivity of the hydrogen absorption state (LiBH4/MgH2) and the dehydrogenation state (LiH/MgB2) at 180 °C under 0.1 MPa Ar atmosphere, which were 0.12 and 0.09 W (m−1 K−1), respectively. In 2019, Thiangviriya et al.97 measured the thermal conductivity of 2LiBH4–MgH2 doped 30 wt% activated carbon nanofiber compact. In 2019 and 2020, Albert et al.27,43 measured the thermal conductivity of MgH2 and Ni-activated MgH2 powders, respectively. In 2020, Bird39 and Humphries98 measured the thermal conductivity of compact which prepared by Mg2FeH6 mixing with different content of Fe and ENG and the Mg(HxF1−x)2 solid solutions.
TCi thermal conductivity analyzer can also be used, which is a modified transient plane source method. The thermal conductivity test range is 0 to 100 W (m−1 K−1) for the temperature range of −50 to 200 °C, and the measurement accuracy is better than 5%.99,100 The testing setup and sensor are shown in Fig. 13.
 | ||
| Fig. 13 Schematic diagram of MTPS (a) testing set-up; (b) sensor.99,100 | ||
In 2010, Pentimalli et al.99 measured the thermal conductivity of compact prepared by MmNi4.5Al0.5/SiO2 as 1.3 W (m−1 K−1), and a non-absorbent contact agent (glycerin) was used to reduce the contact thermal resistance during the test. In 2014, Bennett et al.36 measured the thermal conductivity of commercially available ball-milling MgH2 under different operating conditions. In 2017, EI-Eskandarany et al.101 measured the effective thermal conductivity of ball-milled LaNi5 metal hydride powder at room temperature, which was about 2.0 W (m−1 K−1).
 | (26) |
 | ||
| Fig. 14 Schematic diagram of (a) laser flash method test device; (b) infrared detector recording signal.103 | ||
In 1961, Parker et al. First proposed the LFM test principle. In 2010, Pohlmann et al.48 used LFM to measure the axial and radial thermal conductivity of pellets made of Mg90Ni10 and MgH2 mixed with expanded natural graphite, respectively. In 2012, Pohlmann et al.106 measured the thermal conductivity of NaAlH4–4CeCl3 and 2LiNH2–MgH2 compacted pellets which mixed with different contents of ENG. The axial thermal conductivity of the pellets added with 25 wt% ENG and pressed at 300 MPa were as high as 34 and 30 W (m−1 K−1), respectively. In 2017, Popilevsky et al.34 measured the thermal conductivity of Mg and Mg + 2 wt% MWCNTs pellets. The results showed the thermal conductivity of pellet prepared by 84–90% hydrogenated particle was less than 10 W (m−1 K−1) at 525 K when the metal volume fraction was 11–17 vol% and porosity was 14–17%. In 2020, Wang et al.35 measured the thermal conductivity of YHx (x = 1.85, 1.88), and the thermal conductivity of YH1.85 was 10 and 6.9 W (m−1 K−1) at 298 K and 413 K, respectively.
The laser flash method is mainly used to measure the thermophysical parameters of uniform and isotropic solid materials, which has incomparable advantages such as simple specimen geometry, small size requirement, fast measurement speed and convenient operation. Since the test is based on a theoretical model, the error of the test mainly comes from the unevenness of the laser source, the performance of the detector, the data acquisition system, and the finite pulse time of heat transfer under the assumed temperature distribution used in the derivation of the calculation formula. Systematic errors can be compensated by continuous updates, moreover, the specimen radiant heat loss, which will cause problems with the temperature response time curve, which is inevitable. It was shown in Fig. 14(b). To avoid the radiant heat loss, it is often necessary to design a reasonable specimen holder and correct it for different factors.
The comparison of application range and result reliability of some available thermal conductivity measurement methods of hydride bed are summarized in Table 3.
| Measurement method | Reference standard | Temperature range (K) | Thermal conductivity range (W (m−1 K−1)) | Accuracy | Repeatability |
|---|---|---|---|---|---|
| Radial heat flow method | ISO 8497:1994 | RM–2600 K | 0.01–200 | ±3–±15% | ±2% |
| Guarded longitudinal heat flow method | ASTM E1225-20 | 90–1300 K | 0.2–200 | ±5–±8% | ±2% |
| Guarded hot plate method | ASTM C177-19 | <700 °C | <16 | ±5% | ±1% |
| ISO 8302:1991 | |||||
| Heat flow meter method | ASTM E1530-19 | 150–600 K | 0.5–30 | ±3% | ±1% |
| ASTM C518-17 | |||||
| ISO 8301:1991 | |||||
| Hot wire method | ASTM C1113/C1113M-09 | <1250 °C | Parallel array: <25 | ±5% | — |
| ISO 8894-1:2010 | Cross array: <1.5 | ||||
| ISO 8894-2:2007 | Thermal resistance: <15 | ||||
| Thermal probe method | ASTM D5334-14 | <400 °C | 0.1–5 | 7–10% | ±5% |
| Transient plane source method | ISO 22007-2:2015 | −240–1000 °C | 0.005–1800 | ±3% | ±1% |
| Laser flash method | ASTM E1461-13 | 75–2800 K | 0.1–1000 mm2 s−1 | ±5–±7% | ±3% |
4. Improvement ways for the effective thermal conductivity of metal hydride bed
The metal hydride beds have low thermal conductivity (the typical loose powder bed is about 0.1 W (m−1 K−1)64), and the particles will be further pulverized during hydrogenation and dehydrogenation cycles. Therefore, the effective thermal conductivity of the metal hydride bed will be further reduced, and the poor heat transfer of the hydride bed will lead to heat congregation, which greatly limits the reaction rate of the hydride bed and even stops hydrogenation or dehydrogenation. The hydrogenation and dehydrogenation time of hydride bed extends while heat cannot be transferred well.93,107 Improving the effective thermal conductivity of metal hydride bed is the important means to improve the heat transfer performance.108 In order to improve the effective thermal conductivity of hydride bed, various internal heat transfer enhancement measures have been proposed. The main methods include adding high thermal conductivity materials, compaction, coating with copper,65,109,110 and creating internal thermal structure, which will be introduced in detail.4.1 Compaction
Low effective thermal conductivity of metal hydride powder bed due to its high porosity. Mechanical compaction of the powder can effectively reduce the internal porosity and increase the apparent density of the bed,101 and improve the thermal conductivity and volume hydrogen storage capacity. The safety of the powder in contact with air and water will be improved after compaction.111 This is a simple method widely used in densification of loose hydride powder bed.Dehouche et al.47 compacted LaNi4.8Sn0.2, LmNi4.9Sn0.1 and MmNi4.7Al0.3 powder beds under maximum pressure of 1.5 metric tons, respectively. The apparent density could be increased from 3 g cm−3 to about 6 g cm−3. Compared with the uncompacted powder bed, the effective thermal conductivity could be increased from 0.1 to 1.7 W (m−1 K−1). Through simulation calculation, Yang et al.112 found that compared with the hydride powder, the hydrogenation completion time of LaNi5 could be significantly reduced by pressing, from 421 s to 272 s. Yang et al.95 increased the thermal conductivity of NH3BH3 from 0.19 W (m−1 K−1) to 0.44 W (m−1 K−1) by compacting, and the bulk density increased from 0.37 g cm−3 to 0.58 g cm−3 (the porosity decreased from 50% to 22%). Jepsen et al.96 improved the apparent density to 1.35 g cm−3 and reduced the porosity to 20% by compacting the desorbed state of LiH + MgB2 under the pressure of 300 MPa, the axial and radial thermal conductivity increased to about 0.3 and 0.6 W (m−1 K−1) respectively. Humphries et al.98 compacted MgH2 powder under 370 MPa pressure at room temperature in argon atmosphere, and the thermal conductivity was increased to 2.08 W (m−1 K−1).
4.2 Addition of high thermal conductivity material
Some materials with high thermal conductivity and non-reactivity with hydrides are used as thermal conductivity reinforcement materials for hydride bed, mainly including two types of materials, one is carbon materials, such as graphite powder,76,113 carbon nanotubes,114–116 carbon fibers,25,77,117 and expanded graphite,26,45,66,118 the other is metal-based materials, including powder and foam,119,120 such as copper powder,42 aluminum foam,112,121–123 and copper foam.124,125 Due to the similar density, the metal-based high thermal conductivity materials are usually added into the AB5 alloy powder bed. The metal-based reinforcement materials in the mixed addition and hydride bed hydrogenation/dehydrogenation process, due to the small difference with the metal hydride density will not cause uneven distribution. So metal-based reinforcement materials are widely used in enhanced heat transfer of metal hydride beds. Carbonaceous materials and metal foam materials also have lower bulk density and larger porosity, which will not have a great impact on the mass hydrogen storage density of the hydrogen storage material bed. Due to the different thermal conductivity and density of different metal foams, the selection of foam metal is related to the required parameters, such as the improvement of heat transfer and the mass hydrogen storage density. At the same time, the additive particles will fill the interstitial space of the bed and create a conduction channel for heat flow.Pourpoint et al.76 added different mass fractions of CNTs and graphite into TixCr2−yMny. The results showed that when the CNTs content increased from 1 wt% to 5 wt%, the thermal conductivity almost did not increase significantly, still only about 0.18 W (m−1 K−1). This might be due to the large apparent characteristic size of CNTs, and porosity and bonding strength of the composites increased during delivery. Adding 1 and 10 wt% graphite could increase the effective thermal conductivity of the composite material to the same value of about 0.3 W (m−1 K−1), which might be the result of the combined effect of the additional content and the powder density. Inoue et al.115 demonstrated that directly synthesizing SWCNT on metal hydride particles and controlling the filling ratio could increase the effective thermal conductivity of the packed bed to about 10 W (m−1 K−1). Park et al.66 added 3 wt% ENG to the un-milled and milled La0.9Ce0.1Ni5 powders. The thermal conductivity increased from 2.02 W (m−1 K−1) to 2.67 W (m−1 K−1). Through simulation, Wang et al.122 found that adding 10 wt% Al foam in a large LaNi5 hydride tank (5 kg) could improve the effective thermal conductivity of the hydride bed, and the time to reach 90% hydrogenation saturation is shortened by nearly 5 times.
4.3 Addition of high thermal conductivity material and compaction
Compaction or addition of high thermal conductivity materials can improve the volumetric hydrogen storage density and the effective thermal conductivity of hydride bed respectively. In view of the in-depth research of hydrogen storage systems and the urgent needs of mobile applications, researchers have combined the addition of high thermal conductivity materials with compaction to study the hydrogen storage systems with high heat transfer and high hydrogen storage density. In this method, thermal conductive fillers mainly include graphite flakes,106 graphite powder99, carbon fiber97 and expanded graphite(EG or ENG),32,41,48,55,64,107,126,127 among which expanded graphite is the most commonly used due to the formation of high porosity under high temperature treatment.126 When hydride powder is mixed with ENG, the graphite can be quickly filled into the void between particles through uniaxial cold pressed, and it is easy to demold, that is self-lubricating. At the same time, it can effectively avoid compact breakage during compression and demolding, and it has high mechanical stability during the hydrogen absorption/desorption cycles.99 Through this method, the expected thermal conductivity can be well controlled compared with powder-packed bed.48However, it should be noted that excessive pressure and excessive addition of thermal conductivity materials will reduce the hydrogen transfer performance in the compacted hydride bed. At the same time, excessive addition of thermal conductive agent will reduce the hydrogen storage density of the compacted hydride bed, which is very unfavorable for portable and mobile hydrogen storage applications.128,129
In 2001, Kim et al.64 proposed a recompressed expanded graphite technique, which was considered as the first to use ENG as addition and compaction of hydride bed. When 2.1 wt% ENG was added to the LaNi5 powder bed and compacted, the effective thermal conductivity of the LaNi5 powder bed increased from 0.1 W (m−1 K−1) to more than 3 W (m−1 K−1), but further increase in the amount of ENG did not bring adding too much ENG, the effective conductivity of the LaNi5 powder bed did not increase significantly. Pohlmann et al.48 measured the effective thermal conductivity of the MgH2/ENG bed formed by pressing at 600 MPa with different amounts of ENG (maximum 25.5 wt%). The results showed that with increasing ENG content and pressing pressure, the porosity of MgH2/ENG composites decreased from 35% to 16%. The axial and radial thermal conductivity increased to 5 and 43 W (m−1 K−1), respectively. Rango et al.107 mixed nano-magnesium hydride with 10 wt% ENG and pressed it into a disk. The results showed that the thermal conductivity of the compact disk was anisotropic with that of the loose powder without ENG. The radial thermal conductivity increased by nearly 30 times, while the axial thermal conductivity only slightly increased, and the bulk hydrogen storage density increased by 3 times. Anil et al.57 mixed Mg + 50 wt% LaNi4.6Al0.4 powder with graphite flakes and pressed into pellets at 200 MPa. Compared with pure loose powder, the effective thermal conductivity increased from 1 W (m−1 K−1) to 3.5 W (m−1 K−1) under 1 MPa hydrogen pressure. The bed temperature was more uniform when it was loaded into the reactor for hydrogen absorption/desorption, and the hydrogen absorption saturation could be quickly achieved. Park et al.66 prepared metal hydride composites by adding ENT to La0.9Ce0.1Ni5. The effective thermal conductivity of the powder increased from 2.02 W (m−1 K−1) to 2.37 W (m−1 K−1) after mixed with 3 wt% ENG, and further increased to 8.01 W (m−1 K−1) after pressing at 300 bar.
There are also studies using non-ENG as additives. In 1998, Lloyd et al.63 used LaNi5 coated copper and mixed it with different contents (5, 10, 15 wt%) of Sn (binder) under different compaction pressures (27, 36, 45 kpsi) to prepare pellets with a diameter of 0.953 cm. The results showed that the thermal conductivity of the pellets increased with the increasing pressure. After adding 10 wt% Sn, the thermal conductivity of the pellet was the highest, reaching 6.4 W (m−1 K−1). Lee et al.109 coated LaNi5, Ca0.6Mm0.4Ni5, and LaNi4.75Al0.25 with thin copper and pressed at 3000 psig pressure, the thermal conductivity was higher than that of powder. At the same time, they also pointed out that pelletization could reduce the permeability of the compact, thereby reducing the transfer of hydrogen. Pentimalli et al.99 prepared pellets by embedding MmNi4.5Al0.5 in silica matrix and ball milling with graphite. The results showed that embedded the SiO2 matrix could stabilize the compact size. At the same time, with the increasing carbon content from 0 to 40%, thermal conductivity of the composites increased from 1.3 to 3.2 W (m−1 K−1). It has good dimensional stability in the cycle process.
4.4 Build high thermal conductivity structure
The realization of the high thermal conductivity structure depends on the heat transfer structure design inside the metal hydride bed. The current research mainly focuses on the use of copper mesh with high porosity (about 91%), large specific surface area (6882 m2 m−3), and high thermal conductivity (389 W (m−1 K−1)).21 Copper mesh does not react with the hydride powder, and when the addition amount is limited, the weight hydrogen storage density of the metal hydride hydrogen tank will not be greatly affected.57 A great deal of pores in the powder bed are used as filling matrix, which can effectively improve the contact between the powder, and change the powder–powder contact into powder–copper wire–powder contact. There are also cases that the powder is packed into a copper mesh structure and compacted.In 1986, Nagel et al.21 measured the thermal conductivity of the MmNi4.46Al0.54 powder bed with copper wire matrix under the vacuum of 0.3–0.4 W (m−1 K−1). The effective thermal conductivity of hydride bed was improved compared with the pure hydride powder bed due to the existence of the copper wire matrix. Laurencelle et al.130 proved that after filling LaNi5 with high thermal conductivity Al foam, the difference in hydrogen content at different positions in the hydride bed was significantly reduced in the hydrogen absorption process, and the hydride bed could be expand form less than 8 mm to 6 cm, and the hydrogen charging could be completed quickly (<15 min). Romanov et al.124 added La0.9Ce0.1Ni5 into the copper foam matrix and heated the specimen from room temperature to 333 K, the time for the highest temperature of the hydride bed was shortened from 90 min to 60 min. Kim et al.131 prepared a packed bed of La(Ce)Ni5 powder by manufacturing a copper mesh structure, which sacrificing 4.3% of the volume in the container. The hydrogen charging experiment proved that the hydrogen charging time of hydride bed with copper mesh structure was shortened by 73.5%.
5. Assessment
This article systematically reviews the measurement, improvement and influence factors of the thermal conductivity of hydride bed. The current research on the effective thermal conductivity of hydride bed is mainly used to clarify the heat transfer characteristics of the system filled with hydrogen storage materials, and by couple the material thermodynamics and kinetic parameters to optimized design of solid state hydrogen system with large capacity and fast response.Although there are many methods for measuring thermal conductivity, but there is no separate test standard for the powder bed of bed hydride materials. The steady-state method is applied earlier and the test accuracy is relatively high, but it requires large test specimens and time-consuming. In order to maintain one-dimensional steady-state heat flow, large test instruments and auxiliary equipment are used to minimize heat loss, and achieve a long time to thermal steady state. The application of transient method in the measurement of thermal conductivity of hydride bed is relatively late. Based on the assumption of infinite medium, the transient test method of thermal conductivity is established by establishing model and equation derivation. The lower requirements for specimen preparation and the small quantity (certain flatness and guaranteed boundary assumption) can save a lot of cost, and the transient heat flow during testing has little effect on the specimen, which can realize fast dynamic test, thus it is widely used.
From Fig. 15 it is observed that the radial heat flow method and the guarded longitudinal heat flow method seem to be frequently used by researchers due to their simple principle and easy to build experimental apparatus. Compared with the guarded hot plate method and heat flow meter method, the transient method has fewer restrictions and have wider cope of application. The transient plane source method is adopted by many researchers because of its claimed convenient test method and acceptable accuracy of result. Although the thermal conductivity test equipment of laser flash method is expensive, it has also been widely used in the past decade. The laser flash method only measures the thermal diffusivity of the hydride bed, and then calculates the effective thermal conductivity of the hydride bed according to the density and heat capacity, which increases the error of the final calculation of the effective thermal conductivity.
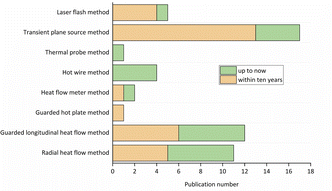 | ||
| Fig. 15 The amount of thermal conductivity measurement methods applied to the hydride bed found in the literature. | ||
Based on the corresponding standards and performance parameters provided by manufacturers, the relevant parameters of different thermal conductivity test methods are summarized, as shown in Table 3. It should be noted that near the upper limit of test temperature, the test accuracy is often reduced due to radiant heat loss.
At present, there is no specific uniform standard for the thermal conductivity measurement of the hydride bed. Researchers prefer to use the transient method to measure the effective thermal conductivity of hydride bed, which is more convenient. However, the calculation model needs to be optimized to improve the accuracy of the results. Although these methods can be used to measure the effective thermal conductivity of hydride material powder bed at room temperature and pressure (the material can be processed into inactive state). However, some methods for determining the change of effective thermal conductivity of hydride bed during hydrogen absorption/desorption have problems in their application in situ measurement. How to establish a closed test environment to simulate the actual working conditions and realize the effective thermal conductivity test of the hydride bed in the process of hydrogen absorption and desorption poses a great challenge to the design and improvement of the test vessel and device. For example, the heat source and thermocouple placement and sealing design, how to minimize the impact on the test. And there is no unified design standard and reliability judgment currently. As mentioned above, the radial heat flow method and the protected longitudinal heat flow method need to establish one-dimensional heat flow, hydride bed is easy to meet the test requirements of radial or longitudinal one-dimensional heat flow, but it takes a long time and the test is inconvenient. Equipment manufacturers only provide the probes of the transient plane source method, and researchers need to design a temperature and pressure resistant test platform for the thermal conductivity test of hydride bed. The laser flash method has not been able to measure the thermal conductivity in a closed chamber, therefore, it has not been applied to the study of the effective thermal conductivity of the hydride bed.
Due to the extremely low thermal conductivity of the hydrogen storage material powder, many methods have been proposed and adopted to improve the thermal conductivity of the hydride bed, such as adding high thermal conductivity materials and compaction, so that the bed can form composite materials or close to continuous medium. Fig. 16 shows the percentage of studies on improving the effective thermal conductivity of hydride bed by different methods in the literature.
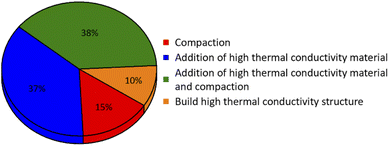 | ||
| Fig. 16 Comparison of improvement ways of thermal conductivity applied to hydride beds found in the literature. | ||
Researchers seem more inclined to add high thermal conductivity materials or further compaction. The latter can improve the thermal conductivity and hydrogen storage density of the bed more effectively to meet mobile and stationary applications, and it is easy to control the expected thermal conductivity, but the mass transfer problem needs to be concerned.97,109,132 The former is more suitable for application in AB5 and AB hydrogen storage alloy powder-packed beds with higher density and easier pulverization. High thermal conductivity materials such as Cu, Al, which are close to the density of hydrogen storage alloys, are usually selected to obtain relatively uniform thermal conductivity. However, it should be noted that some high thermal conductivity materials may react with hydrides or release impurity gases at a certain temperature during the process of hydrogen absorption/desorption. Compaction can improve safety of hydride bed, and it may be not conducive to the preparation of compact bed without adding high thermal conductivity materials.133
In order to maximize the hydrogen storage capacity and ensure the safe use of the system, it is necessary to optimize the thermal design and structural design of the hydrogen storage system to avoid the rapid decrease or useless increase of thermal conductivity under working conditions. Researchers carried out numerical analysis on various hydride reactors, and took the thermal conductivity of the bed as a fixed value to simplify the calculation.10,12,14,134 However, researchers noticed that the effective thermal conductivity of hydride beds varied with the operating conditions. With the development of numerical research and technology of hydride reactors, the accuracy of simulation results will be greatly improved by using the varying thermal conductivity at this stage. This may be the necessary means to simulate the hydrogen storage beds in the future.17 Fig. 17 shows the percentage of research covering different influence factors for the thermal conductivity of the hydride bed found in the literature so far.
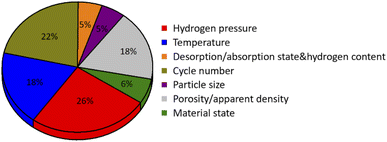 | ||
| Fig. 17 Comparison of influence factors on the thermal conductivity of hydride beds found in the literature. | ||
It can be noticed that hydrogen pressure, temperature, apparent density/porosity, and hydrogen content are main influencing factors, which are not only because of the simple operation, but also because of the importance of these factors in the process of hydrogen absorption and desorption. And they are very critical conditions in design and simulation. Researchers usually calculate the effective thermal conductivity based on the intrinsic thermal conductivity of the solid (ks), gas (kg), and porosity (ε), as shown in eqn (27):
| ke = (1 − ε)ks + εkg | (27) |
At present, the influence of hydrogen pressure on the effective thermal conductivity of the hydride bed has been determined. However, for different hydrogen storage materials, the influence trends of temperature and hydrogen content on the effective thermal conductivity may be different when the influence of particle size and material state is ignored. In engineering applications, it is necessary to obtain the fitting empirical formula by accurately measuring the effective thermal conductivity of hydride bed under working conditions,19,21,22,31 which is finally used for numerical simulation and optimization design of metal hydride hydrogen storage tanks.
The following is a summary of the shortcomings and improvement suggestions in current research on the effective thermal conductivity of metal hydride bed.
5.1 Problems
• Lack of separate standards and test parameter descriptions for thermal conductivity of hydride powder bed.• Selection of test methods to meet test needs and design of in situ test device.
• Selection of reasonable and harmless thermal conductivity improvement method.
• Accurate measurement and effective fitting of effective thermal conductivity of different hydrogen storage material powder bed under working conditions.
• Lack of in situ testing of effective thermal conductivity variation with hydrogenation and dehydrogenation.
5.2 Suggestions
Due to the shortcomings in the researches of effective thermal conductivity of metal hydride beds up to now, we believe that it is necessary to formulate the test method and reliability standard of the effective thermal conductivity of metal hydride beds. The test results of the steady-state method with higher accuracy can provide reference for the reliability of the transient method, but steady-state methods still need to minimize the complexity and time-consuming of the test as much as possible. For transient method, it is necessary to optimize the internal calculation model as much as possible to improve the accuracy under the premise of ensuring the boundary assumption. The industry should specify the suitable selection of the improvement ways and design scheme of the working condition test platform to meet the needs of accurate measurement.The transient plane heat source method seems to be the most popular test method because of its fast test speed and satisfactory accuracy. However, the design of temperature and pressure resistance test chamber suitable for the measurement of different hydrogen storage materials needs to be improved. Adding high thermal conductivity materials and compaction can simultaneously improve the apparent density, hydrogen storage density and the effective thermal conductivity of the hydride bed, but the actual hydrogen storage performance index must be considered to avoid excessive influence on hydrogen storage capacity and hydrogen permeability. Accurate measurement of the thermal conductivity of the hydride bed under different temperatures, pressures, and hydrogenation/dehydrogenation conditions and fitting the multi-factor equation will be the trend of the numerical simulation optimization design of the hydrogen storage system in the future.
6. Conclusions and outlook
Hydrogen is an ideal energy carrier and has unparalleled advantages compared with traditional fossil fuels. Hydrogen storage technology is one of the important links to realize hydrogen energy economy. Solid-state hydrogen storage, such as metal hydrides, offers an attractive alternative and seems to be a preferred solution for future hydrogen storage technologies. Due to the inherent reaction enthalpy of metal hydride and the poor heat transfer of metal hydride bed, the amplified thermal effects during hydrogen absorption and desorption poses a great challenge to the hydrogen storage performance of hydride bed. There fore, it is very important to accurately determine the effective thermal conductivity of metal hydride bed before designing a metal hydride hydrogen storage device. By accurately measuring and analyzing the influence of hydrogen pressure, temperature, hydrogen storage capacity and other factors on the effective thermal conductivity of metal hydride bed, the optimization design efficiency of heat structure of metal hydride hydrogen device can be greatly improved. This paper reviews the current researches on the measurement, improvement, and the influence of working conditions on the effective thermal conductivity of metal hydride beds based on analysis of the existing literature. The measurement methods of metal hydride bed are divide into the steady-state methods (such as the radial heat flow method, guarded longitudinal heat flow method, guarded hot plat method, heat flow meter method) and the transient methods (such as the hot-wire method, thermal probe method, transient plane source method and laser flash method). There is no clear standard between different test methods for the determination of thermal conductivity of metal hydride beds, and researchers prefer to adopt transient methods because the transient methods require less sample size and short measurement time, and is easy to establish a pressure seal and temperature control test system. Based on the literature survey of various measurement methods, it is found that the transient plane source method is the most commonly used method for measuring the effective thermal conductivity of metal hydride bed. Based on the above analysis, the authors also recommend using the transient plane source method to study the heat transfer characteristics of metal hydride bed.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the financial supports for this research from the National Key Research and Development Program of China (2019YFB1505100), and the Project of High Level Innovation Research Institute of Guangdong Province of China (2021B0909050001).References
- IEA, World energy balances, 2019, https://www.iea.org/data-and-statistics?country=WORLD%26fuel=Energyconsumption%26indicator=Totalfinalconsumption(TFC)bysource, accessed 3 2020 Search PubMed.
- L. Schlapbach and A. Züttel, Nature, 2001, 414, 353–358 CrossRef CAS PubMed.
- S. Niaz, T. Manzoor and A. H. Pandith, Renewable Sustainable Energy Rev., 2015, 50, 457–469 CrossRef CAS.
- J. Zheng, X. Liu, P. Xu, P. Liu, Y. Zhao and J. Yang, Int. J. Hydrogen Energy, 2012, 37, 1048–1057 CrossRef CAS.
- A. Demirbas, Energy Sources, Part B, 2007, 2, 287–295 CrossRef CAS.
- A. Züttel, Mater. Today, 2003, 6, 24–33 CrossRef.
- Y. Ishido, M. Kawamura and S. Ono, Int. J. Hydrogen Energy, 1982, 7, 173–182 CrossRef CAS.
- Q. Luo, J. Li, B. Li, B. Liu, H. Shao and Q. Li, J. Magnesium Alloys, 2019, 7, 58–71 CrossRef CAS.
- M. Afzal, R. Mane and P. Sharma, Int. J. Hydrogen Energy, 2017, 42, 30661–30682 CrossRef CAS.
- F. S. Yang, X. Y. Meng, J. Q. Deng, Y. Q. Wang and Z. X. Zhang, Int. J. Hydrogen Energy, 2008, 33, 1014–1022 CAS.
- S. Mellouli, F. Askri, H. Dhaou, A. Jemni and S. Ben Nasrallah, Int. J. Hydrogen Energy, 2010, 35, 1693–1705 CrossRef CAS.
- Y. Cui, X. Zeng, H. Kou, J. Ding and F. Wang, Results Phys., 2018, 9, 640–647 CrossRef.
- E. I. Gkanas, T. Statheros and M. Khzouz, Int. J. Hydrogen Energy, 2019, 44, 19267–19274 CrossRef CAS.
- J. Nam, J. Ko and H. Ju, Appl. Energy, 2012, 89, 164–175 CrossRef CAS.
- F. A. M. Elhamshri and M. Kayfeci, Int. J. Hydrogen Energy, 2019, 44, 18927–18938 CrossRef CAS.
- N. A. A. Rusman and M. Dahari, Int. J. Hydrogen Energy, 2016, 41, 12108–12126 CrossRef CAS.
- C. Bennett, C. Eastwick and G. Walker, Int. J. Hydrogen Energy, 2013, 38, 1692–1701 CrossRef CAS.
- T. Oi, K. Maki and Y. Sakaki, J. Power Sources, 2004, 125, 52–61 CrossRef CAS.
- S. Suda, N. Kobayashi and K. Yoshida, Int. J. Hydrogen Energy, 1981, 6, 521–528 CrossRef CAS.
- E. Suissa, I. Jacob and Z. Hadari, J. Less-Common Met., 1984, 104, 287–295 CrossRef CAS.
- M. Nagel, Y. Komazaki and S. Suda, J. Less-Common Met., 1986, 120, 35–43 CrossRef CAS.
- D. W. Sun and S. J. Deng, J. Less-Common Met., 1990, 160, 387–395 CrossRef CAS.
- E. A. Kumar, M. P. Maiya and S. S. Murthy, Ind. Eng. Chem. Res., 2011, 50, 12990–12999 CrossRef CAS.
- J. Kapischke and J. Hapke, Exp. Therm. Fluid Sci., 1994, 9, 337–344 CrossRef CAS.
- S.-C. Bae, T. Tanae, M. Monde and M. Katsuta, J. Therm. Sci. Technol., 2008, 3, 2–10 CrossRef CAS.
- J. H. Shim, M. Park, Y. H. Lee, S. Kim, Y. H. Im, J.-Y. Suh and Y. W. Cho, Int. J. Hydrogen Energy, 2014, 39, 349–355 CrossRef CAS.
- R. Albert, R. Urbanczyk and M. Felderhoff, Int. J. Hydrogen Energy, 2019, 44, 29273–29281 CrossRef CAS.
- E. Hahne and J. Kallweit, Int. J. Hydrogen Energy, 1998, 23, 107–114 CrossRef CAS.
- M. Shapiro, V. Dudko, V. Royzen, Y. Krichevets, S. Lekhtmakher, V. Grozubinsky, M. Shapira and M. Brill, Part. Part. Syst. Charact., 2004, 21, 268–275 CrossRef CAS.
- D.-m. Kim, J. B. Kim, J. Lee and B. J. Lee, Int. J. Heat Mass Transfer, 2021, 165, 120735 CrossRef CAS.
- S. Suda, N. Kobayashi, K. Yoshida, Y. Ishido and S. Ono, J. Less-Common Met., 1980, 74, 127–136 CrossRef CAS.
- H. Klein, Int. J. Hydrogen Energy, 2004, 29, 1503–1511 CrossRef CAS.
- Y. Madaria and E. A. Kumar, J. Alloys Compd., 2017, 691, 442–451 CrossRef CAS.
- L. Popilevsky, V. M. Skripnyuk, Y. Amouyal and E. Rabkin, Int. J. Hydrogen Energy, 2017, 42, 22395–22405 CrossRef CAS.
- Y. Wang, Y. Ohishi, K. Kurosaki and H. Muta, J. Alloys Compd., 2020, 821, 153496 CrossRef CAS.
- C. M. J. Bennett, A. J. Patman, C. Milanese, C. N. Eastwick and G. S. Walker, Int. J. Hydrogen Energy, 2014, 39, 19646–19655 CrossRef CAS.
- F. Qin, J. P. Chen, W. F. Zhang and Z. J. Chen, J. Zhejiang Univ., Sci., A, 2007, 8, 197–204 CrossRef CAS.
- M. Matsushita, I. Tajima, M. Abe and H. Tokuyama, Int. J. Hydrogen Energy, 2019, 44, 23239–23248 CrossRef CAS.
- J. E. Bird, T. D. Humphries, M. Paskevicius, L. M. Poupin and C. E. Buckley, Phys. Chem. Chem. Phys., 2020, 22, 1–9 RSC.
- D. E. Dedrick, M. P. Kanouff, B. C. Replogle and K. J. Gross, J. Alloys Compd., 2005, 389, 299–305 CrossRef CAS.
- C. Pohlmann, L. Röntzsch, T. Weißgärber and B. Kieback, Int. J. Hydrogen Energy, 2013, 38, 1685–1691 CrossRef CAS.
- I. A. Romanov, V. I. Borzenko and A. N. Kazakov, J. Phys.: Conf. Ser., 2018, 1128, 012105 CrossRef.
- R. Albert, C. Wagner, R. Urbanczyk and M. Felderhoff, Energy Technol., 2020, 200356, 1–7 Search PubMed.
- A. I. Solovey and Y. I. Shanin, Nato Sci Peace Secur, 2008, pp. 831–836, DOI:10.1007/978-1-4020-8898-8_104.
- A. Chaise, P. de Rango, P. Marty, D. Fruchart, S. Miraglia, R. Olivès and S. Garrier, Int. J. Hydrogen Energy, 2009, 34, 8589–8596 CrossRef CAS.
- S. Flueckiger, T. Voskuilen, T. Pourpoint, T. S. Fisher and Y. Zheng, Int. J. Hydrogen Energy, 2010, 35, 614–621 CrossRef CAS.
- Z. Dehouche, N. Grimard, F. Laurencelle, J. Goyette and T. K. Bose, J. Alloys Compd., 2005, 399, 224–236 CrossRef CAS.
- C. Pohlmann, L. Röntzsch, S. Kalinichenka, T. Hutsch and B. Kieback, Int. J. Hydrogen Energy, 2010, 35, 12829–12836 CrossRef CAS.
- W. C. Zhang, G. Wang, J. F. Ma, Z. Y. Wang and E. D. Wang, Int. J. Mod. Phys. B, 2009, 23, 940–946 CrossRef CAS.
- A. N. Kazakov, I. A. Romanov, V. N. Kuleshov and D. O. Dunikov, J. Phys.: Conf. Ser., 2017, 891, 012115 CrossRef.
- L. H. Ortega, B. Blamer, K. M. Stern, J. Vollmer and S. M. McDeavitt, J. Nucl. Mater., 2020, 531, 151982 CrossRef CAS.
- G. J. Cheng, J. Q. Gan, D. L. Xu and A. B. Yu, Powder Technol., 2020, 361, 326–336 CrossRef CAS.
- J. Jepsen, C. Milanese, J. Puszkiel, A. Girella, B. Schiavo, G. Lozano, G. Capurso, J. Bellosta von Colbe, A. Marini, S. Kabelac, M. Dornheim and T. Klassen, Energies, 2018, 11, 1081–1103 CrossRef.
- B. Sundqvist and O. Andersson, Int. J. Thermophys., 2009, 30, 1118–1129 CrossRef CAS.
- C. Pohlmann, B. Kieback and L. Rontzsch, Int. J. Hydrogen Energy, 2014, 39, 8331–8339 CrossRef CAS.
- ISO 8497: 1994, Thermal Insulation—Determination of Steady-State Thermal Transmission Properties of Thermal Insulation for Circular Pipes, International Organization for Standardization, Geneva, 1994 Search PubMed.
- E. A. Kumar, Y. Madaria, K. S. Babu and S. S. Murthy, Therm. Sci. Eng. Prog., 2020, 19, 100653 CrossRef.
- C. Y. Wang, H. C. Tien, S. D. Chyou, N. N. Huang and S. H. Wang, J. Mar. Sci. Technol., 2011, 19, 168–175 Search PubMed.
- C. Jensen, C. Xing, C. Folsom, H. Ban and J. Phillips, Int. J. Thermophys., 2012, 33, 311–329 CrossRef CAS.
- C. Xing, C. Jensen, C. Folsom, H. Ban and D. W. Marshall, Appl. Therm. Eng., 2014, 62, 850–857 CrossRef CAS.
- ASTM E1225-20, Standard Test Method for Thermal Conductivity of Solids Using the Guarded-Comparative-Longitudinal Heat Flow Technique, ASTM International, West Conshohocken, PA, 2020 Search PubMed.
- ASTM D5470-17, Standard Test Method for Thermal Transmission Properties of Thermally Conductive Electrical Insulation Materials, ASTM International, West Conshohocken, PA, 2017 Search PubMed.
- G. Lloyd, K. J. Kim, A. Razani and K. T. Feldman, J. Thermophys. Heat Transfer, 1998, 12, 132–137 CrossRef CAS.
- K. J. Kim, B. Montoya, A. Razani and K.-H. Lee, Int. J. Hydrogen Energy, 2001, 26, 609–613 CrossRef CAS.
- M. Lee, K. J. Kim, R. R. Hopkins and K. Gawlik, Int. J. Hydrogen Energy, 2009, 34, 3185–3190 CrossRef CAS.
- C. S. Park, K. Jung, S. U. Jeong, K. S. Kang, Y. H. Lee, Y.-S. Park and B. H. Park, Int. J. Hydrogen Energy, 2020, 45, 27434–27442 CrossRef CAS.
- C. Xing, C. Jensen, C. Folsom, H. Ban and D. W. Marshall, Appl. Therm. Eng., 2013, 59, 504–514 CrossRef.
- S. Chen, J. Marx and A. Rabiei, Int. J. Therm. Sci., 2016, 106, 70–79 CrossRef CAS.
- ISO 8302: 1991, Thermal insulation— Determination of steady-state thermal resistance and related properties— Guarded hot plate apparatus, International Organization for Standardization, Geneva, 1991 Search PubMed.
- D. Salmon, Meas. Sci. Technol., 2001, 12, 89–98 CrossRef.
- ASTM C177-19, Standard Test Method for Steady-State Heat Flux Measurement and Thermal Transmission Properties by Means of the Guarded-Hot-Plate Apparatus, ASTM International, West Conshohocken, PA, 2019 Search PubMed.
- R. Poensgen, Z. Ver. Dtsch. Ing., 1912, 41, 1653–1658 Search PubMed.
- ISO 8301: 1991, Thermal insulation—Determination of steady-state thermal resistance and related properties — Heat flow meter apparatus, International Organization for Standardization, Geneva, 1991 Search PubMed.
- ASTM C518-17, Standard Test Method for Steady-State Thermal Transmission Properties by Means of the Heat Flow Meter Apparatus, ASTM International, West Conshohocken, PA, 2017 Search PubMed.
- ASTM E1530-19, Standard Test Method for Evaluating the Resistance to Thermal Transmission by the Guarded Heat Flow Meter Technique, ASTM International, West Conshohocken, PA, 2019 Search PubMed.
- T. L. Pourpoint, A. Sisto, K. C. Smith, T. G. Voskuilen, M. K. Visaria, Y. Zheng and T. S. Fisher, ASME 2008 Heat Transfer Summer Conference, Jacksonville, Florida, USA, 2008 Search PubMed.
- N. Yasuda, T. Tsuchiya, N. Okinaka and T. Akiyama, Int. J. Hydrogen Energy, 2013, 38, 1657–1661 CrossRef CAS.
- S. G. S. Beirao, M. L. V. Ramires, M. Dix and C. A. N. D. Castro, Int. J. Thermophys., 2006, 27, 1018–1041 CrossRef CAS.
- ISO 8894-1: 2010, Refractory Materials—Determination of Thermal Conductivity—Part 1: Hot-Wire Methods (Cross-Array and Resistance Thermometer), International Organization for Standardization, Geneva, 2010 Search PubMed.
- ISO 8894-2: 2007, Refractory Materials—Determination of Thermal Conductivity—Part 2: Hot-Wire Method (Parallel), International Organization for Standardization, Geneva, 2007 Search PubMed.
- ASTM C1113/1113M-09, Standard Test Method for Thermal Conductivity of Refractories by Hot Wire (Platinum Resistance Thermometer Technique), ASTM International, West Conshohocken, PA, 2009 Search PubMed.
- K. D. Antoniadis, A. Tyrou, M. J. Assael, X. Li, J. Wu and H.-P. Ebert, Int. J. Thermophys., 2020, 41, 1–35 CrossRef.
- M. J. Assael, M. Dix, K. Gialou, L. Vozar and W. A. Wakeham, Int. J. Thermophys., 2002, 23, 615–633 CrossRef CAS.
- V. A. Schleiermacher, Ann. Phys., 1888, 270, 623–646 CrossRef.
- E. Held and F. Drunen, Physica, 1949, 15, 865–881 CrossRef.
- J. J. Healy, J. J. D. Groot and J. Kestin, Physica B+C, 1976, 82, 392–408 CrossRef.
- A. E. Wechsler, Compendium of Thermophysical Property Measurement Methods, 1992, pp. 161–185, DOI:10.1007/978-1-4615-3286-6_6.
- ASTM D5334-14, Standard Test Method for Determination of Thermal Conductivity of Soil and Soft Rock by Thermal Needle Probe Procedure, ASTM International, West Conshohocken, PA, 2014 Search PubMed.
- F. C. Hooper and F. R. Lepper, Heating Piping & Air Conditioning, 1950, vol. 56, pp. 309–324 Search PubMed.
- S. E. Gustafsson, Rev. Sci. Instrum., 1991, 62, 797–804 CrossRef CAS.
- ISO 22007-2: 2015, Plastics—Determination of Thermal Conductivity and Thermal Diffusivity—Part 2: Transient Plane Heat Source (hot disc) Method, International Organization for Standardization, Geneva, 2015 Search PubMed.
- Y. He, Thermochim. Acta, 2005, 436, 122–129 CrossRef CAS.
- S. Flueckiger, Y. Zheng and T. Pourpoint, 2008 ASME Summer Heat Transfer Conference, Jacksonville, Florida, USA, 2008 Search PubMed.
- S. Flueckiger, T. Voskuilen, Y. Zheng and T. Pourpoint, ASME 2009 Heat Transfer Summer Conference, San Francisco, California, USA, 2009 Search PubMed.
- Y. Yang, T. G. Voskuilen, T. L. Pourpoint, D. R. Guildenbecher and J. P. Gore, Int. J. Hydrogen Energy, 2012, 37, 5128–5136 CrossRef CAS.
- J. Jepsen, C. Milanese, A. Girella, G. A. Lozano, C. Pistidda, J. M. Bellosta von Colbe, A. Marini, T. Klassen and M. Dornheim, Int. J. Hydrogen Energy, 2013, 38, 8357–8366 CrossRef CAS.
- S. Thiangviriya, C. Sitthiwet, P. Plerdsranoy, G. Capurso, C. Pistidda, O. Utke, M. Dornheim, T. Klassen and R. Utke, Int. J. Hydrogen Energy, 2019, 44, 15218–15227 CrossRef CAS.
- T. D. Humphries, J. Yang, R. A. Mole, M. Paskevicius, J. E. Bird, M. R. Rowles, M. S. Tortoza, M. V. Sofianou, D. Yu and C. E. Buckley, J. Phys. Chem. C, 2020, 124, 9109–9117 CrossRef CAS.
- M. Pentimalli, A. Frazzica, A. Freni, E. Imperi and F. Padella, Adv. Sci. Technol., 2010, 72, 170–175 CAS.
- A. Harris, S. Kazachenko, R. Bateman, J. Nickerson and M. Emanuel, J. Therm. Anal. Calorim., 2014, 116, 1309–1314 CrossRef CAS.
- M. S. El-Eskandarany, E. Al-Nasrallah, M. Banyan and F. Al-Ajmi, Int. J. Hydrogen Energy, 2018, 43, 23382–23396 CrossRef CAS.
- Y. Lee, D. Y. Ku, Y.-H. Park, M.-Y. Ahn and S. Cho, Fusion Eng. Des., 2017, 124, 995–998 CrossRef CAS.
- F. Streb, D. Schweitzer, M. Mengel and T. Lampke, IEEE Trans. Compon., Packag., Manuf. Technol., 2018, 8, 1024–1031 CAS.
- M. Li and M. Akoshima, Int. J. Heat Mass Transfer, 2020, 148, 119017 CrossRef CAS.
- ASTM E1461-13, Standard Test Method for Thermal Diffusivity by the Flash Method, ASTM International, West Conshohocken, PA, 2013 Search PubMed.
- C. Pohlmann, L. Rontzsch, J. J. Hu, T. Weissgarber, B. Kieback and M. Fichtner, J. Power Sources, 2012, 205, 173–179 CrossRef CAS.
- P. D. Rango, A. Chaise, D. Fruchart, S. Miraglia and P. Marty, World Scientific Proceedings of International Conference Nanomeeting, Minsk, Belarus, 2013 Search PubMed.
- J. Yao, P. Zhu, L. Guo, F. Yang, Z. Zhang, J. Ren and Z. Wu, Int. J. Hydrogen Energy, 2021, 46, 29332–29347 CrossRef CAS.
- M. Lee, I. S. Park, S. Kim and K. J. Kim, ASME 2009 3rd International Conference on Energy Sustainability, San Francisco, California, USA, 2009 Search PubMed.
- I. S. Park, J. K. Kim, K. J. Kim, J. X. Zhang, C. Park and K. Gawlik, Int. J. Hydrogen Energy, 2009, 34, 5770–5777 CrossRef CAS.
- G. A. Lozano, J. M. Bellosta von Colbe, R. Bormann, T. Klassen and M. Dornheim, J. Power Sources, 2011, 196, 9254–9259 CrossRef CAS.
- F. S. Yang, G. X. Wang, Z. X. Zhang and V. Rudolph, Int. J. Hydrogen Energy, 2010, 35, 9725–9735 CrossRef CAS.
- G. A. Lozano, N. Eigen, C. Keller, M. Dornheim and R. Bormann, Int. J. Hydrogen Energy, 2009, 34, 1896–1903 CrossRef CAS.
- S. Meethom, D. Kaewsuwan, N. Chanlek, O. Utke and R. Utke, J. Phys. Chem. Solids, 2020, 136, 109202 CrossRef CAS.
- S. Inoue, Y. Iba and Y. Matsumura, Int. J. Hydrogen Energy, 2012, 37, 1836–1841 CrossRef CAS.
- S. Gao, X. Wang, H. Liu, T. He, Y. Wang, S. Li and M. Yan, J. Power Sources, 2019, 438, 227006 CrossRef CAS.
- K. Fujioka, K. Hatanaka and Y. Hirata, Appl. Therm. Eng., 2008, 28, 304–310 CrossRef CAS.
- M. Zamengo, J. Ryu and Y. Kato, Appl. Therm. Eng., 2013, 61, 853–858 CrossRef CAS.
- A. A. R. Darzi, H. H. Afrouzi, A. Moshfegh and M. Farhadi, Int. J. Hydrogen Energy, 2016, 41, 9595–9610 CrossRef.
- H. El Mghari, J. Huot, L. Tong and J. Xiao, Int. J. Hydrogen Energy, 2020, 45, 14922–14939 CrossRef CAS.
- H. Wang, A. K. Prasad and S. G. Advani, Int. J. Hydrogen Energy, 2012, 37, 290–298 CrossRef CAS.
- H. Wang, A. K. Prasad and S. G. Advani, Int. J. Hydrogen Energy, 2014, 39, 11035–11046 CrossRef CAS.
- M. Afzal and P. Sharma, Int. J. Hydrogen Energy, 2018, 43, 13356–13372 CrossRef CAS.
- I. A. Romanov, V. I. Borzenko and A. N. Kazakov, J. Phys.: Conf. Ser., 2019, 1359, 012103 CrossRef CAS.
- S. D. Lewis and P. Chippar, J. Energy Storage, 2021, 33, 102108 CrossRef.
- A. R. Sanchez, H.-P. Klein and M. Groll, Int. J. Hydrogen Energy, 2003, 28, 515–527 CrossRef.
- K. Herbrig, L. Rontzsch, C. Pohlmann, T. Weissgarber and B. Kieback, Int. J. Hydrogen Energy, 2013, 38, 7026–7036 CrossRef CAS.
- S. S. Murthy, J. Heat Transfer, 2012, 134, 031020 CrossRef.
- J. Bellosta von Colbe, J.-R. Ares, J. Barale, M. Baricco, C. Buckley, G. Capurso, N. Gallandat, D. M. Grant, M. N. Guzik, I. Jacob, E. H. Jensen, T. Jensen, J. Jepsen, T. Klassen, M. V. Lototskyy, K. Manickam, A. Montone, J. Puszkiel, S. Sartori, D. A. Sheppard, A. Stuart, G. Walker, C. J. Webb, H. Yang, V. Yartys, A. Züttel and M. Dornheim, Int. J. Hydrogen Energy, 2019, 44, 7780–7808 CrossRef CAS.
- F. Laurencelle and J. Goyette, Int. J. Hydrogen Energy, 2007, 32, 2957–2964 CrossRef CAS.
- J. B. Kim, G. Han, Y. Kwon, J. Bae, E. Cho, S. Cho and B. J. Lee, Int. J. Hydrogen Energy, 2020, 45, 8742–8749 CrossRef CAS.
- E. Bershadsky, Y. Josephy and M. Ron, J. Less-Common Met., 1989, 153, 65–78 CrossRef CAS.
- M. Y. Yan, F. Sun, X. P. Liu and J. H. Ye, Int. J. Hydrogen Energy, 2014, 39, 19656–19661 CrossRef CAS.
- A. Karmakar, A. Mallik, N. Gupta and P. Sharma, Int. J. Hydrogen Energy, 2021, 46, 5495–5506 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2022 |
