Polymorphism of the Co–Te nanophases in mechanochemical synthesis

Abstract

The mechanochemical synthesis of all cobalt tellurides' phases is demonstrated in this work. The samples had their structural, microstructural, and magnetic characterizations performed by X-ray powder diffraction, transmission electron microscopy, and magnetometry techniques. The initial atomic stoichiometries tested of Co₃₂Te₆₈ and Co₄₀Te₆₀ resulted in the synthesis of the γ-CoTe₂ Pnnm (marcasite), α-CoTe₂ Pa3̄ (pyrite), α-CoTe₂ P3̄m1 (CdI₂-like), and β-CoTe P6₃/mmc phases with different weight proportions in the sample. Modeling of the X-ray diffractograms employed conventional double-Voigt and crystallite shape-anisotropy DV approaches to show that the volumetric diameter average and true crystallite size of the diffraction domains are in the range of tens of nanometers. Transmission electron microscopy measurements also allowed distribution counting of the crystallite sizes via maximum caliper diameter. Electron diffraction experiments presented comparable structural parameters with Rietveld via the analysis of the Debye rings. A model using the Langevin approaches showed the phases to present both ferromagnetic and superparamagnetic contributions attributed to weakly-interacting metallic Co grains with magnetic domain sizes ranging between 2.3 and 4.0 nm. The phases' evolution with storage time was analyzed over two years and revealed to be stable regarding their structural and microstructural properties.

---

1 Introduction

Mechanochemistry is a widely explored technique for quick and simple fabrication of transition metal chalcogenides (TMC). This method relies upon the use of mechanical energy to produce physical and chemical transformations of the reagents, which can be promoted by the rubbing, collision, or grinding of the precursor materials.¹ The use of mechanochemistry techniques goes back to the stone age when it was employed especially in food-stuff preparation and to lit fires out of stones.² The first theoretical description of the phenomena was given by Theophrastus (322 B.C.) when the reduction of cinnabar to mercury was reported.³ Modern understanding of its alloying procedure of synthesis is viewed on the bases of the transfer of electrons and ion exchanges in a highly entropic environment created by the milling,⁴ which can promote the formation of unique metastable phases. The most employed types of equipment in this field are the high-energy ball mills, where the vibratory or planetary setups are of most common use.^5–15 The advantage of these milling processes is the simplicity of the single-step production of TMCs, primarily because of its capabilities of alloying materials with way different melting points. A recent review of the synthesis of TMCs showed that the binary sulfides^4–6 are most explored with this technique due to their applications as catalytic materials,¹⁶ in lithium-ion batteries,^17,18 and in solution-processed solar cells,¹⁹ where the binary selenides and tellurides still are to be better exploited.

Regarding cobalt tellurides, four polymorphs were reported to form in the literature: γ-CoTe₂ marcasite (Pnnm), α-CoTe₂ pyrite (Pa3̄), CoTe₂ trigonal (P3̄m1), and the β-CoTe niqueline (P6₃/mmc). The γ-CoTe₂ marcasite phase²⁰ synthesized by a solvothermal route was used as a catalyst material for Oxygen Evolution Reduction (OER).²¹ The good macro layer strength and high endurance of this phase in alkaline media can be compared to state-of-art RuO₂, which offered a non-noble alternative to the production of clean energy. On the other side, a less stable and layered structured phase of CoTe₂ with a P3̄m1 structure, produced by solid-state techniques, was applied for Hydrogen Evolution Reaction (HER).²² The low overpotentials and small Taffel slopes proved to be essential features to improve its electrocatalytic properties. For the β-CoTe phase, applications for the detection of uric acid and adenine,²³ and the photo-reduction process for the conversion of carbon dioxide into methane were made possible.²⁴ The synthesis of these materials was made by solvothermal routes, where the special feature of this phase relies on its band gap (2 eV) and good electrical conductivity. The only polymorph for the Co–Te system that did not present any application so far is the α-CoTe₂.²⁵ Its synthesis could only be achieved by high-pressure methods in sealed environments, a robust technique that demands a high cost of energy.²⁵ Some properties are still to be exploited for this phase, especially its low electrical resistivity if compared to other TMCs.

The mechanochemical synthesis of the β-CoTe²⁶ and γ-CoTe₂ (ref. 27) phases was already produced by this research group, where the latter already proved its efficacy in the detection of ferulic acid in real cosmetic samples. To further understand this new route of synthesis for Co–Te binary alloys, a high-energy vibratory ball mill was used to explore the Co₃₂Te₆₈ and Co₄₀Te₆₀ initial stoichiometries in this work. These initial reagent proportions were chosen as the center of the two homogeneity ranges for the Co–Te phase diagram.²⁸ The X-ray Powder Diffraction (XRPD) measurements employed both Debye–Scherrer and Bragg–Brentano geometries, using the Rietveld technique implemented in the Total Pattern Analysis Software (TOPAS)²⁹ to obtain the structural and microstructural information of the diffraction data. The weighted phase percentages were obtained using the quantitative phase analysis employed in the same software. Two different approaches of the fundamental parameter analysis (FPA) were used for the XRPD line profile analysis: standard double-Voigt (DV)³⁰ and shape-anisotropy DV³¹ using a triaxial ellipsoid for the effective shape of the crystallites. These results on the microstructure of the samples were compared with the transmission electron microscopy (TEM) direct observation of the microstructure, which allowed the direct crystallite size counting. Also, electron diffraction was used to further complement the structural information obtained via XRPD by fitting its Debye rings. Magnetometry techniques were employed to understand the paramagnetic properties of these materials. Investigation of long storage time is also analyzed for these samples.

2 Materials and methods

2.1 Synthesis

The synthesis equipment used was a high-energy ball miller SPEX 8000, employing nine stainless steel spheres inside a steel vial; where micrometer grains of Co (Sigma Aldrich 99.9%+ original purity) and tellurium (Sigma Aldrich, 99.99% original purity) were placed in and shaken at 875 cycles per minute, using the aimed atomic proportion of Co₃₂Te₆₈ and Co₄₀Te₆₀ in two separate batches. The balls inside the recipient provided the mechanical energy to the chemical reaction, with a Ball-to-Powder Ratio (BPR) selected of 10 : 1 to produce 3.1 g of material. At each 3 h, about 100 mg of the sample was fished out for characterization inside an argon atmosphere to avoid oxidation. The 6 h milled sample was reported elsewhere²⁷ with a more extensive analysis of its properties and application. The limit of 15 h for the milling was established so to avoid any contamination from the stainless steel of the milling media. The parameters selected here are set as a standard to investigate Co–Te for the other works. The resulting powder was stored in microtubes subject to room temperature and moisture for two years.

2.2 Characterization

2.2.1 X-ray powder diffraction. A Panalytical X'pert Pro X-ray Diffraction System performed the XRPD measurements using copper as the target in a Bragg–Brentano geometry in the Laboratório de Difração de Raios X (LDRX) of the Federal University of Santa Catarina. The optics in the incident beam used Soller slits of 0.04 rad, a mask of 10 mm, a fixed divergent slit of 1/2°, and an anti-scatter slit of 1°. To reduce the background contribution, K_β, and fluorescent radiation at the position-sensitive detector (X′ Celerator, RTMS, 2.122° active window), a graphite monochromator (Lorentz-polarization factor of 26.4) was positioned conveniently in the diffracted beam path. A zero-background silicon sample holder with 16 mm in diameter and 0.2 mm of depth accommodated the sample for diffraction, with scans taking around 200 s for each 2θ step of 0.05°, ranging from 10 to 150° without a knife, and were limited to 90° when using it. The knife is conveniently placed a few millimeters above the sample and contributed to reducing the air scattering, providing a better diffractogram baseline for phase analysis.

For the analysis of the diffraction data, Total Pattern Analysis Software (TOPAS) version 5 (ref. 30) was employed. The phase identification used the High-Score Software,³² with an initial crystal information file (.cif) retrieved in the Inorganic Crystal Structure Database (ICSD)³³ for all phases. This file was the input for the Rietveld refinement at TOPAS, employing two different approaches for the line profile: the standard DV approach and the crystallite shape anisotropy DV model.³⁰ Both methods use the FPA in a direct convolution approach, separating the instrumental from the sample contributions. The macro used was implemented in TOPAS by Ectors et al.,³¹ using background coefficients of the 8th order of Chebyshev polynomial, with atomic coordinates and thermal dislocation parameters refined. Comments on the effective modeling of size anisotropic are given elsewhere.²⁶ Hamilton statistical tests were also employed³⁴ to reduce the number of parameters to be refined.

2.2.2 Synchrotron measurements. The XRD 1 beamline of the UVX source at the Laboratório Nacional de Luz Síncrotron (LNLS)³⁵ was used with a beam energy of 14 keV in Debye–Scherrer transmission geometry. The detector used was a single photon counting silicon microstrip MYTHEN 24K Dectris. The sample was stacked inside a glass capillary with 0.3 mm in diameter, with data collection ranging from 2θ from 5° to 90°. Also, beforehand measurements of a silicon standard pattern 640d³⁶ were used to distinguish the instrumental contributions for FPA, like the cylindrical correction and the zero of the experiment. In the Rietveld procedure, the sample's absorption correction was considered due to the high absorption of cobalt and tellurium in this range of energy.

2.2.3 TEM and SAED. Each sample was diluted in ethanol inside a microtube and agitated for 15 min in a sonicator. Then, a small portion of it was placed in a carbon–copper grid. The TEM micrographs were retrieved in a JEOL JEM-1011 microscope with an electron acceleration voltage of 100 kV. The maximum magnification used was about 4 × 10⁵ times, a range that allowed the crystallite diameter measurement. This equipment also allowed the Selected Area Electron Diffraction (SAED) measurements, obtaining the Debye rings and diffracted spots. The JEMS software³⁷ was employed for the analysis of the diffraction data.

2.2.4 Magnetic measurements. Magnetization (M) versus magnetic field (H) major hysteresis and recoil loop measurements were carried out using a MicroSense EV9 Vibration Sample Magnetometer (VSM). The H-range used was from −20 kOe to +20 kOe for hysteresis measurements, while the recoil varied from the coercive field to +20 kOe. The magnetization signal was normalized by the total volume of the sample to further magnetic analysis.

3 Results and discussion

3.1 Structural and microstructural characterization

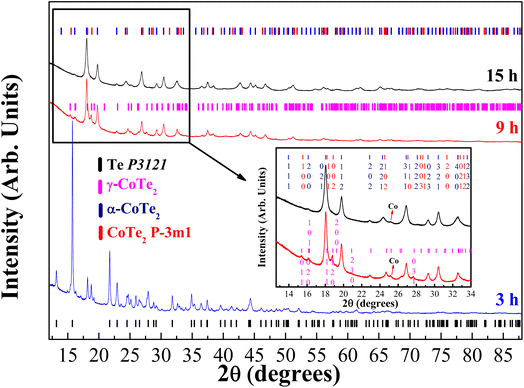
The diffractograms of the synthesized samples obtained at XRD1-LNLS for three different milling times of the Co₃₂Te₆₈ system are shown in Fig. 1, with their structural and microstructural information presented in Table 1 in parallel with the laboratory results. Within 3 h of milling, the γ-CoTe₂ starts to form, although in a small proportion if compared to the non-reacted Te and Co phases there present. Already at 9 h, the α-CoTe₂ phase occupies almost half the weight of the material, with the γ-CoTe₂ corresponding to the other half. At 15 h, however, one can notice a transition from the γ-CoTe₂ phase to the CoTe₂ P3̄m1, which remains in half-weight proportion with α-CoTe₂ for this processing time. Indication of the presence of this latter phase can be seen in the inset of Fig. 1, where one can notice that the (120) and (031) plane reflections of the Pnnm structure are not present anymore. Also, laboratory measurements corroborated to ensure the phase transition already occurred at 12 h of milling, which is depicted in Fig. S1 of the ESI.† In the Fig. S2 of the ESI,† a comparison between the modeling of both γ-CoTe₂ and the P3̄m1 structures is displayed for the Co₃₂Te₆₈ 15 h-milled sample. When a knife is used to eliminate the air scattering contribution near the sample, one can clearly distinguish a peak near 10° of 2θ that can only be modeled by the P3̄m1 structure. This ensures that a real phase transition had occurred from 9 to 12 h, but it seems to not have affected the α-CoTe₂ polymorph. The justification for the formation of a less stable phase with the P3̄m1 structure relies on the higher entropy induced by the milling for longer hours.

Fig. 1 Diffractograms obtained at the XRD1-LNLS for three different milling times of the Co₃₂Te₆₈ system: 3, 9, and 15 h. The black tick markers correspond to Te P3₁21 phase, magenta to the γ-CoTe₂, blue to the α-CoTe₂, and red to the CoTe₂ P3̄m1 phase. The inset shows the presence of a small peak of Co Fm3̄m.

Table 1 Structural and microstructural values obtained by XRPD analysis with the DV and anisotropic DV approaches. CS symbolizes the crystallite size

Measurement	9 h LNLS	9 h LDRX	12 h LDRX	15 h LNLS	15 h LDRX
Rwp/GoF			3.14/1.78	2.66/0.53	3.55/1.82
CoTe2 P3̄m1
Phase weight%	—	—	31.3(3)	40.3(1)	50.7(2)
a (Å)	—	—	3.814(1)	3.8326(3)	3.8319(6)
c (Å)	—	—	5.402(3)	5.4197(7)	5.419(1)
True CS (nm)	—	—	2.28(4)	4.60(5)	3.30(3)
DV CS (nm)	—	—	6.0(2)	8.90(5)	8.37(9)
α-CoTe2 Pa3̄
Phase weight%	51.7(2)	53.4(2)	65.9(3)	54.8(1)	46.7(2)
a (Å)	6.3186(7)	6.3207(2)	6.3204(2)	6.32054(6)	6.3202(2)
True CS (nm)	7.72(4)	7.62(9)	7.70(7)	7.62(6)	9.1(2)
DV CS (nm)	17.61(11)	18.91(19)	17.84(19)	19.51(10)	18.9(3)
MS (%)	0.510(6)	0.45(1)	0.713(8)	0.668(4)	0.84(1)
γ-CoTe2 Pnnm
Phase weight%	45.9(2)	43.9(2)	—	—	—
a (Å)	3.8879(6)	3.8848(5)	—	—	—
b (Å)	5.3209(9)	5.3220(8)	—	—	—
c (Å)	6.328(1)	6.3229(8)	—	—	—
True CS (nm)	5.08(4)	4.75(6)	—	—	—
DV CS (nm)	12.04(10)	11.83(15)	—	—	—

---

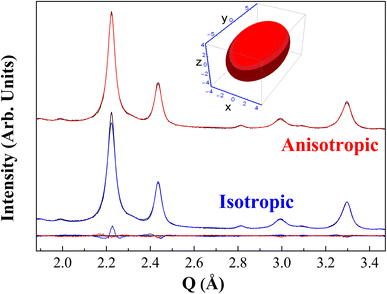
In Fig. 2 one can also observe that the isotropic DV shape description for the diffractogram cannot fit very well the main peak. Indeed, this peak presents a combination of P3̄m1 and Pa3̄ structures in this diffractogram, although the Pa3̄ contribution is the most important, so the DV-anisotropy model was only applied to this phase. A reduction of the R_wp from 3.75% to 3.38% was noticed after the crystallite shape anisotropy was employed, improving the fit by 10% by adding just one parameter in the Rietveld refinement. The ellipsoid radii found are r_x = r_z = 4.65(7) nm and r_y = 8.42(2) nm, with x-direction parallel to the [100]'s (represented in Fig. 2 inset). The same test was performed with the synchrotron data, as shown in Fig. S3 of the ESI,† where again the misfitting of the main peak was fixed by the anisotropic DV modeling. Hence, the misfit proves not to be prevenient from the instrumental contribution to the line profile but from the sample microstructure itself. It is worth mentioning that the considered anisotropy in size is accounted as an effective modeling since the crystallites themselves are of non-uniform shape. This means that some preferred directions of the crystallite structure (called column heights) tend to grow more than others. Similar observations were attained in the previous studies for the γ-CoTe₂ phase.²⁷

Fig. 2 Comparison between the conventional isotropic DV approach (blue) and the anisotropic one (red) using the Bragg–Brentano geometry. The inset represents the effective shape for the α-CoTe₂ Pa3̄ crystallites used for the correction of the main peak.

To infer statistically that two axes of this ellipsoid must be refined with the same values, the Hamilton test was used. The results of this approach are available in Table S1,† where the calculations were based on ref. 34. The probability of the less restrictive model being wrong achieved 66% – higher than the cut-off probability of 5% – if compared to the restriction of two radii, meaning that just one axis of the ellipsoid needs to be refined given the precision of the measurement available.

One can also observe some differences between the microstructural values obtained through the different experiments. The synchrotron data show important air and capillary scattering contributions for smaller angles, which difficulted the visualization of the sample's peaks in that region. The analyzed material also has a considerable X-ray absorption coefficient for the 14 keV region, meaning that the diffracted intensity is less bright than optimal, decreasing the signal-to-noise ratio. These complications mean that the values obtained there will not be the same as those obtained in the laboratory; however, they permit us to analyze more reflections with the increased energy, inferring more precise structural values.

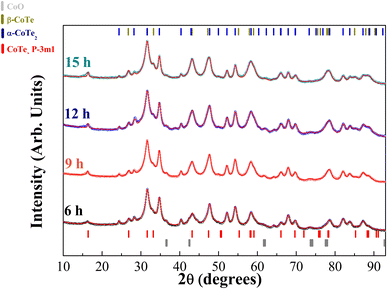
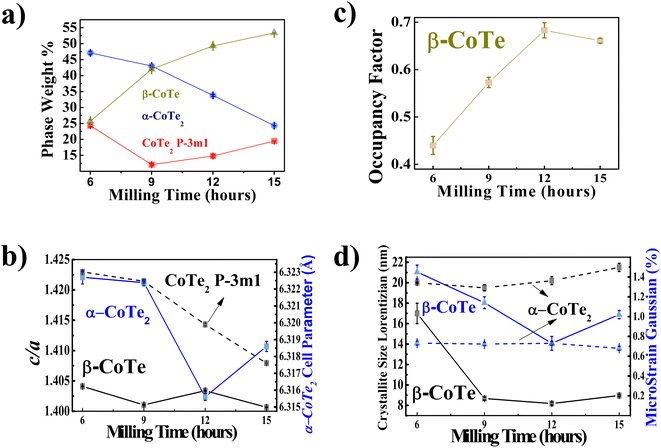
The XRPD diffractograms for the Co₄₀Te₆₀ system are displayed in Fig. 3, with Fig. 4 showing the structural and microstructural values obtained with their analyses. In the Fig. S4 of the ESI,† the fitting of the XRPD data shows that the combinations of two CoTe phases never fully describe some peaks or fit non-existent peaks without the addition of a third phase. So, it can be concluded that almost all the polymorphs of Co–Te are formed simultaneously for the Co₄₀Te₆₀ system, namely: β-CoTe P6₃/mmc, α-CoTe₂ Pa3̄, CoTe₂ P3̄m1, with some small CoO C12m1 contamination, with no creation of newer phases observed from 6 to 15 h of milling. The phase percentages in Fig. 4a show that the content of the α-CoTe₂ constantly reduced with the milling time while the opposite happened for the β-CoTe phase. The Close-Packing-Ratios (CPR) in Fig. 4b reached values close to what is reported β-CoTe phase in the literature (1.38). The CoTe₂ P3̄m1 phase presented similar values for the lattice parameters if compared to theoretical calculations in the literature.²⁰ This is also valid for the α-CoTe₂ phase lattice parameters.²⁵ The β-CoTe presented a Co occupancy factor ranging from 0.43 to 0.7, common for its vacancy defect mechanism, as displayed in Fig. 4c. In Fig. 4d, one can observe that no significant changes in the microstructure happened for the α-CoTe₂ Pa3̄ phase, but the β-CoTe phase presented a reduction of the volumetric averaged crystallite diameter and microstrain starting already within 6 h. All analyses used the standard DV approach to infer the microstructural properties.

Fig. 3 Diffractograms of the Co₄₀Te₆₀ initial stoichiometry in a Bragg–Brentano reflection geometry in logarithmic scale for the intensity. The numbers on the left side represent the milling time, blue ticks represent the α-CoTe₂ Pa3̄, red P3̄m1, dark yellow β-CoTe P6₃/mmc, and gray the CoO C12m1. The red lines are their profile fitting using the standard DV approach.

Fig. 4 Structural and microstructural information of the multiple phases present in the Co₄₀Te₆₀ samples. (a) Phase weight percentage varying with milling time, the blue color represents the α-CoTe₂ Pa3̄, red P3̄m1, dark yellow β-CoTe P6₃/mmc. (b) Occupancy factor of the cobalt atom in the β-CoTe phase. (c) c/a ratios of the CoTe₂ P3̄m1 (dashed) and β-CoTe (solid) phases in black and the α-CoTe₂ lattice parameter in blue. (d) Crystallite sizes (dark) and microstrain (blue) values of the α-CoTe₂ (dashed) and β-CoTe (solid) phases using the DV approach.

Regarding the stabilization of the samples with storage time, in general, the structural and microstructural parameters for the Co₃₂Te₆₈ samples showed no variation in two years, as can be visualized in Fig. S5 of the ESI.† The only exception is for the CoTe₂ P3̄m1 phase, where a small reduction in the microstructural parameters is observed. This can be attributed to the instability of the Rietveld refinement or the instability attributed to the unconventional layer structure of this phase pointed out by Chia X. et al.²² Some differences may be noticed between the synchrotron and laboratory XRPD measurements that were already justified in this section. A comparison between the Co₄₀Te₆₀ samples stored for 10 months and 24 months is also displayed in Fig. S6 of the ESI.† No significant changes are observed as well.

3.2 Transmission electron microscopy

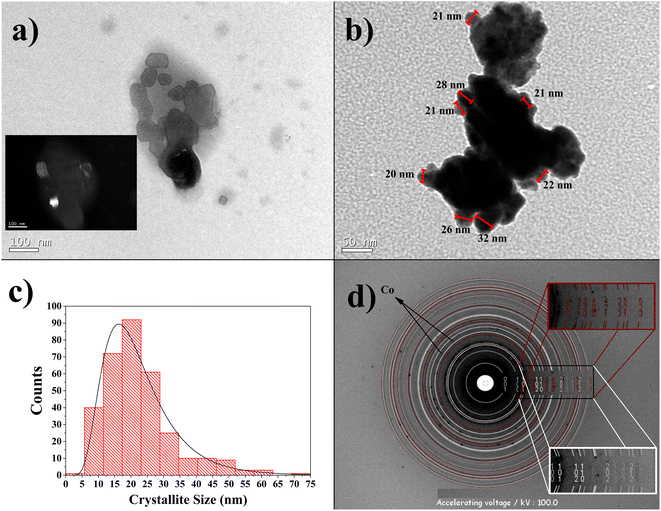
The TEM micrography of the Co₃₂Te₆₈ 15 h-milled sample is displayed in Fig. 5a. The crystallites show nanometric size with no clear indication of shape form, although they present some tendency towards anisotropy (not completely irregular shape). This characteristic can be the reason for the anisotropic model to fit better using the XRPD technique. The inset of this figure also demonstrates the single domain character of some crystallites by dark-field imaging aimed for the (2 1 0) plane of the α-CoTe₂ phase. In Fig. 5b, aggregation of the crystallites can be observed to be formed, and despite that, it is possible to identify some crystallite sizes on the edge of the particle, added to the distribution curve of Fig. 5c. This distribution retrieved an average of around 20 nm, approximately the diameter average of the α-CoTe₂ phase obtained with the XRPD analysis. The comparison between the two different techniques will never be precise, although it was expected that TEM values should be lower since the volumetric averages obtained via DV have a fourth-order dependence in size and the arithmetic mean obtained by TEM is not (more details in ref. 32). In this case, the problem with using the TEM micrographs is that crystallites sometimes present very irregular shapes and can be composed of more than one domain, which turns the definition of size itself not too precise and thus different from XRPD.³² Despite that, the order of magnitude of both experiments is the same and confirms the nanometric range of the crystallites.

Fig. 5 Images obtained by TEM for the Co₃₂Te₆₈ 15 h-milled sample. (a) Crystallites in the order of nanometers, with inset of the dark-field image using the CoTe₂ Pa3̄, (2 1 0) reflection. (b) Picture showing the crystallites agglomeration, although some are distinct enough to calculate their size, as shown by the red strait lines. (c) Histogram of the CS counting and its log-normal distribution fit. The average obtained is 22.5 nm, with a standard-deviation of 11 nm, involving 327 supposed crystallites. The boxes are ∼6 nm wide and chosen to represent a better log-normal distribution. (d) Electron diffraction pattern for this sample and its modeling by JEMS. Wine red rings represent the CoTe₂ Pa3̄ phase and white the CoTe₂ P3̄m1 phase. The inset shows Miller indices corresponded to their colors obtained by the program. No preferred orientation was selected.

Fig. 5d shows the SAED pattern for the Co₃₂Te₆₈ 15 h-milled sample. The Debye rings matched with structural values retrieved via XRPD, revealing good agreement between the two characterization techniques. The presence of cobalt is guessed to the spots not calculated from JEMS for its d-spacing being close to XRPD analysis.

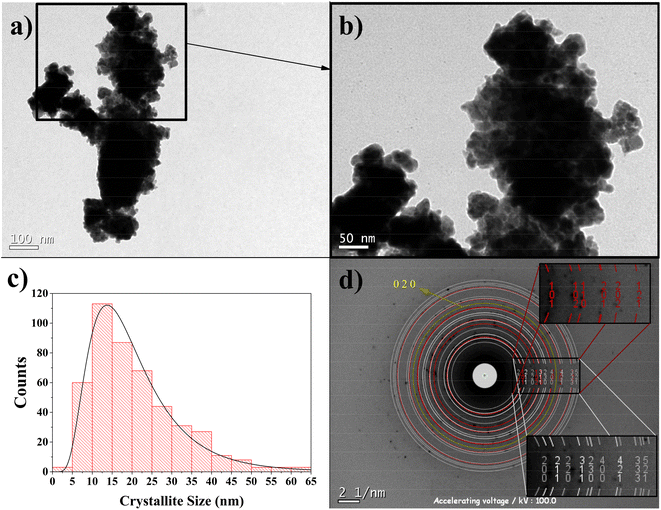
Fig. 6a shows the TEM micrography for the Co₄₀Te₆₀ sample with Fig. 6b zooming the black square region. The distinction of the crystallites in the particle's border could be counted the same way as before, using hundreds of supposed crystallites in different micrographs. The distribution results can be visualized in the histogram of Fig. 6c, presenting a log-normal fit that averages ∼20 nm with a standard deviation of 11 nm. Again, this number is close to the α-CoTe₂ diameter average. Fig. 6d shows the fit obtained using the JEMS software with Rietveld retrieved values for the SAED. Here, two phases of CoTe₂ were used since the distinction between CoTe₂ P3̄m1 and β-CoTe cannot be noticed in the experiment, being the latter preferred to be displayed. The insets of the figure show their Miller indices, which are like those obtained in the XRPD. The cobalt peak was manually set for the yellow ring since it presents a d-spacing equivalent to XRPD, and no other phase could fit it. Both phases agreed with the structural and microstructural values if compared to XRPD.

Fig. 6 TEM analysis of the Co₄₀Te₆₀ sample 15 h-milled. (a) Image showing the aggregated particle. (b) Zoom of the item a showing the crystallites that they are compounded. (c) SAED pattern with the fitted Debye rings with JEMS. The red corresponds to the β-CoTe phase, the white to α-CoTe₂, and the yellow to the (0 2 0) reflection of the CoO phase. The insets help the visualization of the corresponded reflections of the Debye rings. This fit used the cif file obtained via Rietveld. (d) Column size distribution was obtained by counting the crystallite dimensions in the TEM images. It used 461 supposed crystallites in different pictures, with bins separated over 5 nm.

3.3 Magnetic measurements and simulation results

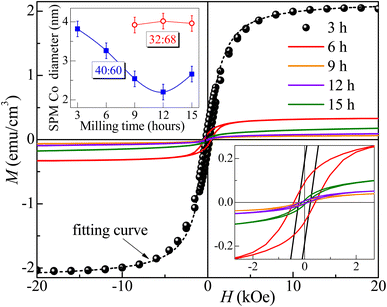
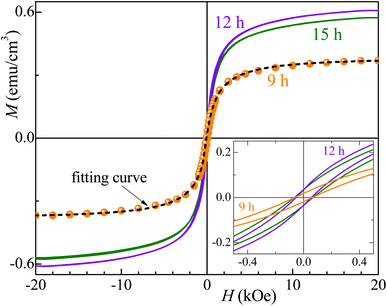
Fig. 7 and 8 show the changes in the magnetic behavior with milling time for the initial stoichiometries of Co₃₂Te₆₈ and Co₄₀Te₆₀, respectively. Tables 2 and 3 display their magnetic characteristics. Note that the amplitude of H of 20 kOe used is sufficiently high to avoid any minor-loop effects.^30,31 The M(H) curves display nonzero remnant magnetization and coercivity, H_C, characteristics of systems consisting of predominantly superparamagnetic (SPM) grains. The average SPM size, 〈d〉, and the sample's saturation magnetization, M_S, were estimated by fitting the major magnetization hysteresis loops. Representative fitting curves are displayed in Fig. 7 and 8, where both ferromagnetic, FM, and SPM contributions were taken into account.^{32,33,38–41} For the Co₃₂Te₆₈ stoichiometry, the value of M_S bumps from 9 to 12 h when the CoTe₂ P3̄m1 is synthesized. While H_C remains practically constant, a twofold increase of the remanent magnetization is observed when CoTe₂ P3̄m1 is synthesized. For the Co₄₀Te₆₀ initial stoichiometry, a clear distinction for the 6 h-milled samples is noticed. From 3 to 6 h of milling, where the CoTe₂ Pa3̄ is the predominant phase with 48% of phase percentage, the M(H) loops have rather great values of H_C. With the CoTe P6₃/mmc presence increasing, both H_C and M_S decrease drastically from 6 to 9 h of milling, with M_S slowly increasing and H_C decreasing with the hexagonal phase take-over for greater milling time.

Fig. 7 Major magnetization hysteresis loops were measured for the Co₃₂Te₆₈ samples. The inset shows the low-field region. The dashed line gives the fitting curve obtained for the 9 h milled sample.

Fig. 8 Major magnetization hysteresis loops measured for the Co₄₀Te₆₀ samples. The inset in the left top corner gives the variations with the milling time of the mean diameter of the SPM grains for both stoichiometries yield from the M(H) fittings. The lower inset shows a zoom of the low-field region. The dashed line represents the fitting curve obtained for the 3 h milled sample.

Table 2 Values obtained in the VSM experiment for the Co₃₂Te₆₈ samples

Milling time (hours)	Remnant magnetization (emu cm^−3)	Coercive field (Oe)	Saturation magnetization^a (emu cm^−3)
a Yielded from the numerical fittings to the experimental major M(H) hysteresis loops.
9	0.02	63	0.39
12	0.03	54	0.64
15	0.04	66	0.61

---

Table 3 Values obtained in the VSM experiment for the Co₄₀Te₆₀ samples

Milling time (hours)	Remnant magnetization (emu cm^−3)	Coercive field (Oe)	Saturation magnetization^a (emu cm^−3)
a Yield from the numerical fitting to the experimental major M(H) hysteresis loops.
3	0.19	229	2.12
6	0.09	414	0.34
9	0.01	167	0.08
12	0.07	129	0.12
15	0.01	82	0.21

---

Given that CoTe_x with x > 1.2 is weakly paramagnetic,⁴² the source of the small ferromagnetic signal of our samples should be solely attributed to the presence of metallic Co. Thus, using the bulk Co saturation magnetization of 1400 emu cm⁻³ and the samples' M_S − values from Tables 2 and 3, one estimates that less than 0.05% and 0.15% of the volume of the Co₃₂Te₆₈ and Co₄₀Te₆₀ systems, respectively, is due to the metallic Co. Studies on Co nanorods showed that the saturation magnetization is only 92% that of the bulk, hence bulk values are useable even for the nanometric size of the crystallites of this work. The variations of the estimated values of 〈d〉 of the SPM Co grains with the milling time are shown in the inset of Fig. 8 for both stoichiometries. While 〈d〉 remains practically the same (∼3 nm) for the stoichiometry Co₃₂Te₆₈, it shows a nearly steady decrease (from ∼4 to ∼2.3 nm) for the other series. No metallic Co is observed for the Co₄₀Te₆₀ in the X-ray diffractograms, because of its small quantity in the sample and the superposition of the Bragg peaks in the pattern.

A good agreement between the model and experiment was obtained (see Fig. 7 and 8), which also indicates that the magnetic coupling between FM grains is rather weak or absent (since it was not considered in the model). The δM_R interaction plots technique was used to evaluate these interactions,⁴³ based on measuring a recoil loop for H cycled between the saturating magnetic field and a smaller field (recoil field, H_R). Here the recoil loops with H_R ≅ H_C were employed and traced at 300 K for all samples. Magnetization loops and the respective δM_R plots are shown for two representative Co₃₂Te₆₈ and Co₄₀Te₆₀ samples in Fig. 9. Only negative deviations from the non-interaction zero magnetization line were obtained in all δM_R(H). In uniaxial-anisotropy systems, such deviations are attributed to a dipolar-like, stabilizing the demagnetized state magnetic coupling. The δM_R amplitude values are very small when compared to M_S (theoretically, an δM_R plot may reach a value twice as higher as the M_S, see ref. 43). This result − of virtually negligible coupling between FM grains − reveals that their aggregation is insignificant.

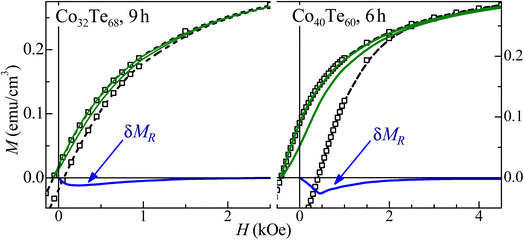Fig. 9 Major magnetization hysteresis loops (symbols), recoil loops (solid lines), and the respective δM_R plots for representative Co₃₂Te₆₈ (left panel) and Co₄₀Te₆₀ (right panel) samples.

3.4 Discussion

To point out the possible physical–chemical mechanisms involved in the phases' nucleation and transitions here reported, a discussion on our group's past work about the mechanochemical synthesis of selenides and tellurides binary alloys is needed. With this, it will highlight the importance of the current work in detail and even reinforce the need for further experimental and theoretical efforts in this field of chemistry.

Beyond the mechanochemical synthesis of the β-CoTe²⁶ and γ-CoTe₂ (ref. 27) phases, this group also developed studies on cobalt and nickel selenides, employing the same milling parameters, starting from M_xSe_100−x powder mixtures (where M = Fe, Co, and Ni, with x = 25 and 75).^44–49 Similar nucleation/transitions observed for the Co₄₀Te₆₀ sample were reported for both Fe₂₅Se₇₅ and Co₂₅Se₇₅ alloys. There, the nucleation of the cubic/orthorhombic MSe₂ phases was followed by the transition to a hexagonal P6₃/mmc β-MSe phase with higher milling times. Experiments of DSC, Raman, and Mössbauer evidenced that the remaining Se was initially in an amorphous form, and the longer milling times made it lose its long-range order. This allowed Se to migrate to the interfacial component of the hexagonal phase or to link to the major contaminants, forming a non-crystalline metal selenite phase, which was not detected by XRPD measurements.

Extended X-ray absorption analyses were performed to understand the structural behavior of FeSe₂ and β-FeSe/Fe₇Se₈ nanocrystalline phases (Fe₂₅Se₇₅ initial stoichiometry). The milled samples were then exposed to high-pressure conditions, but the FeSe₂–β-FeSe/Fe₇Se₈ phase transition previously reported for the high-energy ball milling synthesis was not reproduced when pressures up to 19 GPa were applied.⁵⁰ Further structural and vibrational studies via Raman analysis were performed for the Ni_xSe_100−x samples (with x = 25 and 75) under high-pressure conditions. There, Se-chains and Se₈ ring modes were observed to form, suggesting that the Se-balance keeps its molecular ordering, which could be in nanocrystalline form and well dispersed in the interfacial region, and/or might have been formed by photo- and/or pressure-induced nucleation/agglomeration of Se molecular units.^51,52

This group has also used the same mechanochemical synthesis setup to produce nickel tellurides starting from Ni_xTe_100−x stoichiometries, with x = 25, 34, 50, and 75.^53–56 These studies demonstrated how mechanochemistry can be used to obtain the trigonal NiTe₂ (P3̄m1), the hexagonal NiTe (P6₃/mmc), tetragonal Ni_3±xTe₂ (P4/nmm), and the monoclinic Ni₃Te₂ (P2₁/m) phases by just tuning the stoichiometry and milling time. In addition to that, the mechanochemical synthesis of the In–Te,^57,58 Zn–Te,^59,60 and Cd–Te⁶¹ systems was accomplished. Recently, a novel Fe₅Te₄ phase was produced, starting from Fe_xTe_100−x stoichiometries, with x = 50, 56, and 60.⁶² This proves the huge potential of the mechanochemical route to bypass the barriers imposed by conventional synthesis methods, especially when reactants with very different melting points are involved. Concerning the mechanochemical synthesis of other metal-chalcogenides, the following sulfide and selenide systems were also explored: Ni–S,⁶³ Zn–Se,^64–66 Ga–Se,^67–70 Cu–Se.⁷¹

In an attempt to explain the capability of mechanochemistry as a tool for the production of a plethora of different stable and meta-stable phases, L. Takacs⁷² showed in his review that the Mechanically-induced Self-propagating Reactions (MSR) are present for highly exothermic powder mixtures. This MSR process is of extreme complexity, involving several scales on lengths and time for the modeling. The author claims that the phase formation starts with an activation period, where the size reduction, mixing, and defect formation happen, followed by the ignition of the MSR process when a critical and well-defined thermodynamic state is reached by the powder sample. After its initiation, the reaction is propagated as a self-propagating high-temperature synthesis (SHS) that happens as a powder charge, similar to a combustion process. Takacs combined models with systematic empirical studies to understand ignition and the changes during the activation process that lead to this ignition. Several studies for the reaction modeling were performed, e.g., the combination reaction in transition metal-metalloid and metal-chalcogen systems. The conclusion was that the activation is adequately characterized through the mechanical dose received from the powder charge. This ignition usually occurs when the powder receives a certain amount of the total dose from this ignition process. However, this description also presents many exceptions, where the ignition time is longer than expected or a gradual reaction happens if a lower milling intensity is employed. Adding to this, if the amount of powder is too small compared to the total volume of the milling jar, no MSR is observed due to heat loss to the equipment used. A gradual reaction in some metal chalcogen systems is observed for the blending of binary powder mixtures, also presenting the effect of MSR when processed separately. In the end, Takacs concluded that further systematic experimental investigations have to be performed as a function of powder composition and milling conditions, including the effects of inert additives.

Based on this, the main scientists in the field have established a possible relationship between milling conditions, ignition time, and diffusion mechanisms in such reactions. Besides the gradual and self-propagating mechanochemical synthesis have been used to explain the mechanochemical syntheses of sulfides and selenides in the previous decade, evidence of a third type of mechanochemical synthesis (a melt-driven mechanochemical reaction) was proposed for tellurides and experimentally confirmed for Bi₂Te₃.⁷³ In this mechanistic picture it is suggested that if one or more of the powder reactants has a low melting point and low thermal effusivity, it is possible that local melting can occur from deformation-induced heating. The presence of hot liquid then triggers chemical mixing locally. The molten events are constrained to individual particles, making them distinct from self-propagating reactions, and occur much faster than conventional gradual reactions. The authors proposed a very instructive plot of thermal effusivity versus (T − T_m), where T is the temperature and T_m is the melting temperature. This plot was performed for a range of metals and semimetals where the tendency of an element to melt during impact is represented by the criterion given by the equation Ø = e(T − T_m), including SPEX mill used in this work. In the analysis, the authors suggest that a factor-of-three hardness of Te compared to Bi means that the latter deforms preferentially over Te, and thus governs the overall reactivity. The sulfides, selenides, and tellurides of Sn, Cd, Pb, and In are known to react in a self-sustaining manner under low-energy milling. However, their placement in the thermal diffusivity-melting diagram suggests these elements could undergo a melting transition if processed under sufficiently aggressive conditions. The author's identification of a threshold of milling intensity to form these compounds rapidly by melt-assisted mechanochemical synthesis offers new insight into process design for such compounds and other metal-chalcogen compounds that have functional properties with important optical, thermoelectric and photovoltaic applications.

All the selenides, tellurides, and sulfides produced by this research group can be interpreted by melt-assisted mechanochemical synthesis once we have processed them under sufficiently aggressive conditions. However, only two systems (Ga–Se and In–Te) can be interpreted as Humphry-Baker et al.⁷³ have done for the Bi–Te system. Although Te and Se have low melting points and low thermal diffusivities, suggesting they can melt, we cannot assume that Fe, Co, Ni, Zn, or Cu can deform preferentially over Te or Se, since they have considerably greater hardness (factor-of-ten for Co) than Te, in this sense, it is more reasonable to assume that Te deforms first, melts and thus governs the overall reactivity.

Regarding the polymorphism of Co–Te systems here investigated, another piece of evidence that points out that melt-assisted mechanochemical synthesis happens is the observation of the Co₃₄Te₆₆ (ref. 26) and Co₃₂Te₆₈ milling process. There, the non-reacted Te reagent does not diffuse completely into the Co ductile matrix, where a surplus of Te in the sample is present in the sample at 6 h of milling time. This exceeding Te reagent starts as a seed for the formation of the other iso-stoichiometry α-CoTe₂ phase with milling time, which was proven to form only by high-pressure synthesis.⁷⁴ This way, one can deduce that the introduction of stress (by mechanical action) is somewhat similar to what was reported by,⁷⁴ thus favoring the growth in the sample proportion for the α-CoTe₂ instead of the γ-CoTe₂. Since the formation energy of the trigonal P3̄m1 (−0.488 eV per atom) and the orthorhombic γ-CoTe₂ (−0.468 eV per atom) phases are similar (data from the materials project website⁷⁵), the guess one can have for the formation of the latter resides on the higher entropic environment of the milling, favoring the less symmetric phase. For the Co₄₀Te₆₀, since this initial stoichiometry is in the center of the β-CoTe homogeneity range, the growth in the sample's proportion for the hexagonal phase is expected with more energy introduced by the milling. It presents half the formation energy per atom (−0.276 eV per atom (ref. 75)) compared to the other polymorphs and with the energy provided by the milling its formation is then favored. Since this phase shows a defect mechanism for the Co sites,⁷⁶ this also justifies the presence of metallic Co in the magnetometry analysis. Although an explanation of why three phases had formed at 6 h of milling for the Co₄₀Te₆₀ is not yet clear, we believe that many unknown effects on the milling processes can take place at the same time for this system, and are yet to be investigated.

4 Conclusion

Exploring both initial stoichiometries of Co₃₂Te₆₈ and Co₄₀Te₆₀, all four different phases of CoTe had proven possible to be synthesized via mechanochemistry. XRPD results inferred their structural and microstructural values using two different approaches of the FPA analysis: DV and anisotropic DV, where the latter proved to be crucial in the modeling of the Co₃₂Te₆₈ samples. The Co₃₂Te₆₈ initial stoichiometry presented a phase transition within 12 h of milling from the most stable CoTe₂ Pnnm to CoTe₂ P3̄m1 structure. For the Co₄₀Te₆₀ samples, the three polymorphs present after 6 h of milling were the same until 15 h, where only mass proportions varied with time. The crystallite sizes ranged from ∼8 to ∼20 nm with volume normalized diameter average and reached ∼2 to ∼9 nm of surface-based true crystallite size. The milling procedure inflicted strain in the crystallites that ranged from ∼0.4 to ∼1.5% in some samples. TEM analysis corroborated the XRPD obtained values, with both crystallite size average counting and SAED pattern simulation for structural comparison. Magnetic simulations using the data provided by VSM showed the distinction between the phases and identified that less than 0.15% of the volume of the samples is due to the metallic Co grains with sizes between 2.3 and 4 nm, responsible for the magnetic signal. Storage time did not change the parameters within 2 years of exposure to room temperature and moisture, except for the CoTe₂ P3̄m1 phase which showed a small change in the microstructure. Further studies are necessary to obtain the CoTe₂ Pa3̄ and P3̄m1 phases in a pure form, although the difficulty of the Co–Te huge polymorphism is still a barrier to this achievement.

Author contributions

MAM was responsible for writing the article, synthesizing the samples, and performing all the characterization measurements and discussion. VZCP and JG were responsible for the magnetometry analysis. CEMC was responsible for the funding and supervision of the work. All authors contributed to the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the Brazilian agencies CNPq (grants 421747/2016-1 and 304756/2019-9) and CAPES (M. A. M. Master) for supporting us financially. The XRD1 beamline of UVX source at the Brazilian Síncrotron (LNLS) was accessed under the approval of the proposal 20190070. We are grateful for the beamline staff by their technical support during experiments. The Laboratório de Difração de Raios-X (LDRX), Laboratório Multiusuário de Caracterização Magnética de Materiais (LabCAM) and Laboratório Central de Microscopia Eletrônica (LCME) multiuser facilities at UFSC, whose allowed the XRPD, VSM, and microscopy measurements, respectively.

References

1. C. Suryanarayana, Mechanical alloying and milling, J. Powder Mater., 2004, 46, 1–472,  DOI:10.4150/kpmi.2006.13.5.371.
2. L. Takacs, The historical development of mechanochemistry, Chem. Soc. Rev., 2013, 42(18), 7649–7659,  10.1039/c2cs35442j.
3. L. Takacs, Quicksilver from Cinnabar: The First Documented Mechanochemical Reaction?, J. Met., 2000, 52(January), 12–13.
4. B. G. Fiss, A. J. Richard, G. Douglas, M. Kojic, T. Friščić and A. Moores, Mechanochemical methods for the transfer of electrons and exchange of ions: Inorganic reactivity from nanoparticles to organometallics, Chem. Soc. Rev., 2021, 50(14), 8279–8318,  10.1039/d0cs00918k.
5. J. S. Benjamin, Mechanical Alloying, Sci. Am., 1976, 234(5), 40–49.
6. A. A. L. Michalchuk, E. V. Boldyreva, A. M. Belenguer, F. Emmerling and V. V. Boldyrev, Tribochemistry, Mechanical Alloying, Mechanochemistry: What is in a Name?, Front. Chem., 2021, 9, 685789,  DOI:10.3389/fchem.2021.685789.
7. C. Suryanarayana, A. A. Al-Joubori and Z. Wang, Nanostructured Materials and Nanocomposites by Mechanical Alloying: An Overview, Met. Mater. Int., 2021, 28(1), 41–53,  DOI:10.1007/s12540-021-00998-5.
8. J. L. Do and T. Friščić, Mechanochemistry: A Force of Synthesis, ACS Cent. Sci., 2017, 3(1), 13–19,  DOI:10.1021/acscentsci.6b00277.
9. P. Baláž, M. Baláž, M. Achimovičová, Z. Bujňáková and E. Dutková, Chalcogenide mechanochemistry in materials science: insight into synthesis and applications (a review), J. Mater. Sci., 2017, 52(20), 11851,  DOI:10.1007/s10853-017-1174-7.
10. K. Lohani, et al., Experimental and Ab Initio Study of Cu2SnS3(CTS) Polymorphs for Thermoelectric Applications, J. Phys. Chem. C, 2021, 125(1), 178–188,  DOI:10.1021/acs.jpcc.0c09139.
11. E. Isotta, et al., Origin of a Simultaneous Suppression of Thermal Conductivity and Increase of Electrical Conductivity and Seebeck Coefficient in Disordered Cubic Cu2ZnSnS4, Phys. Rev. Appl., 2020, 14(6), 1,  DOI:10.1103/PhysRevApplied.14.064073.
12. K. Lohani, H. Nautiyal, N. Ataollahi, K. Maji, E. Guilmeau and P. Scardi, Effects of Grain Size on the Thermoelectric Properties of Cu2SnS3: An Experimental and First-Principles Study, ACS Appl. Energy Mater., 2021, 4(11), 12604–12612,  DOI:10.1021/acsaem.1c02377.
13. Z. Wu, D. Wang and A. Sun, Preparation of MoS2 by a novel mechanochemical method, J. Alloys Compd., 2010, 492(1–2) DOI:10.1016/j.jallcom.2009.11.070.
14. Z. Wu, D. Wang, X. Zan and A. Sun, Synthesis of WS2 nanosheets by a novel mechanical activation method, Mater. Lett., 2010, 64(7), 856–858,  DOI:10.1016/j.matlet.2010.01.040.
15. E. Dutková, et al., Properties of mechanochemically synthesized nanocrystalline Bi 2S3 particles, Mater. Sci. Semicond. Process., 2014, 27(1), 267–272,  DOI:10.1016/j.mssp.2014.05.057.
16. R. R. Chianelli, et al., Catalytic properties of single layers of transition metal sulfide catalytic materials, Catal. Rev. Sci. Eng., 2006, 48(1), 1–41,  DOI:10.1080/01614940500439776.
17. H. Yuan, L. Kong, T. Li and Q. Zhang, A review of transition metal chalcogenide/graphene nanocomposites for energy storage and conversion, Chinese Chem. Lett., 2017, 28(12), 2180–2194,  DOI:10.1016/j.cclet.2017.11.038.
18. B. Wang, Z. Wang, X. Wang, B. Zheng, W. Zhang and Y. Chen, Scalable synthesis of porous hollow CoSe2-MoSe2/carbon microspheres for highly efficient hydrogen evolution reaction in acidic and alkaline media, J. Mater. Chem. A, 2018, 6(26), 12701–12707,  10.1039/c8ta03523g.
19. N. Balis, E. Stratakis and E. Kymakis, Graphene and transition metal dichalcogenide nanosheets as charge transport layers for solution processed solar cells, Mater. Today, 2016, 19(10), 580–594,  DOI:10.1016/j.mattod.2016.03.018.
20. M. Muhler, W. Bensch and M. Schur, Preparation, crystal structures, experimental and theoretical electronic band structures of cobalt tellurides in the composition range CoTe1.3-CoTe2, J. Phys. Condens. Matter, 1998, 10(13), 2947–2962,  DOI:10.1088/0953-8984/10/13/012.
21. Q. Gao, et al., Phase-Selective Syntheses of Cobalt Telluride Nanofleeces for Efficient Oxygen Evolution Catalysts, Angew. Chem., Int. Ed., 2017, 56(27), 7769–7773,  DOI:10.1002/anie.201701998.
22. X. Chia, Z. Sofer, J. Luxa and M. Pumera, Unconventionally Layered CoTe2 and NiTe2 as Electrocatalysts for Hydrogen Evolution, Chem.–Eur. J., 2017, 23(48), 11719–11726,  DOI:10.1002/chem.201702753.
23. S. Pradhan, et al., Chemical synthesis of nanoparticles of nickel telluride and cobalt telluride and its electrochemical applications for determination of uric acid and adenine, Electrochim. Acta, 2017, 238, 185–193,  DOI:10.1016/j.electacta.2017.04.023.
24. M. S. Khan, M. N. Ashiq, M. F. Ehsan, T. He and S. Ijaz, Controlled synthesis of cobalt telluride superstructures for the visible light photo-conversion of carbon dioxide into methane, Appl. Catal. Gen., 2014, 487, 202–209,  DOI:10.1016/j.apcata.2014.09.016.
25. T. A. Bither, R. J. Bouchard, W. H. Cloud, P. C. Donohue and W. J. Siemons, Transition Metal Pyrite Dichalcogenides. High-Pressure Synthesis and Correlation of Properties, Inorg. Chem., 1968, 7(11), 2208–2220,  DOI:10.1021/ic50069a008.
26. M. A. Malagutti, K. De Fátima Ulbrich, V. Z. C. Paes, J. Geshev and C. E. Maduro De Campos, Structural, microstructural and magnetic characterization of the β-CoTe nanophase synthesized by a novel mechanochemical method, RSC Adv., 2021, 11(9), 5027–5034,  10.1039/d0ra10716f.
27. M. A. Malagutti, et al., Mechanochemical synthesis of γ-CoTe2 nanocrystals and their application for determination of ferulic acid, Mater. Today Commun., 2022, 31, 103481,  DOI:10.1016/j.mtcomm.2022.103481.
28. K. Ishida and T. Nishizawa, Co-Te (Cobalt-Telluride), in Binary Allow Phase Diagrams, ed. T. B. Massalski, ASM international, Materials Park, Ohio, 2nd edn, 1990, pp. 1247–1248.
29. Bruker AXS, “TOPAS”, Karlsruhe, Germany, 2009.
30. A. A. Coelho, TOPAS and TOPAS-Academic: an optimization program integrating computer algebra and crystallographic objects written in C++, J. Appl. Crystallogr., 2018, 51(1), 210–218,  DOI:10.1107/S1600576718000183.
31. D. Ectors, F. Goetz-Neunhoeffer and J. Neubauer, Domain size anisotropy in the double-Voigt approach: an extended model, J. Appl. Crystallogr., 2015, 48, 1998–2001,  DOI:10.1107/S1600576715018488.
32. T. Degen and J. van den Oever, D-16 A Major Update of X’pert Highscore Plus, Powder Diffr., 2009, 24(2), 163,  DOI:10.1154/1.3175894.
33. N. I. of S. and Technology, Inorganic Crystal Structure Database, Gaithersburg, MD,  DOI:10.18434/M32147.
34. W. C. Hamilton, Significance tests on the crystallographic R factor, Acta Crystallogr., 1965, 18(3), 502–510,  DOI:10.1107/s0365110x65001081.
35. A. M. G. Carvalho, et al., X-ray powder diffraction at the XRD1 beamline at LNLS, J. Synchrotron Radiat., 2016, 23(6), 1501–1506,  DOI:10.1107/S1600577516012686.
36. R. L. Watters and D. L. Kaiser, Standard Reference Material 640d, ed. D. L. Keiser and R. L. Watters, 2010, pp. 1–5,  DOI:10.1002/9783527809080.cataz11352.
37. P. Stadelmann, JEMS-SWISS, JEMS-SWISS, Jongny, 2019.
38. A. Harres, M. Mikhov, V. Skumryev, A. M. H. De Andrade, J. E. Schmidt and J. Geshev, Criteria for saturated magnetization loop, J. Magn. Magn. Mater., 2016, 402, 76–82,  DOI:10.1016/j.jmmm.2015.11.046.
39. J. Geshev, Comment on “exchange bias in the layered cobaltite Sr 1.5Pr0.5CoO4”, J. Appl. Phys., 2008, 104, 023914, J. Appl. Phys., 2009, 105(6) DOI:10.1063/1.3098262.
40. A. D. C. Viegas, J. Geshev, L. S. Dorneles, J. E. Schmidt and M. Knobel, Correlation between magnetic interactions and giant magnetoresistance in melt-spun Co10Cu90 granular alloys, 1997.
41. V. Masheva, et al., On the magnetic properties of nanosized CoFe2O4, J. Magn. Magn. Mater., 1999, 196, 128–130,  DOI:10.1016/S0304-8853(98)00688-X.
42. E. Uchida, Magnetic properties of cobalt telluride, J. Phys. Soc. Japan, 1955, 10, 517–522,  DOI:10.1143/JPSJ.10.517.
43. J. Geshev, Interaction plots obtained from in-field magnetization instead of remanence measurements, J. Magn. Magn. Mater., 2018, 467, 135–138,  DOI:10.1016/j.jmmm.2018.07.009.
44. C. E. M. Campos, J. C. de Lima, T. A. Grandi, K. D. Machado and P. S. Pizani, Structural studies of iron selenides prepared by mechanical alloying, Solid State Commun., 2002, 123(3–4), 179–184,  DOI:10.1016/S0038-1098(02)00232-6.
45. C. E. M. Campos, J. C. De Lima, T. A. Grandi, K. D. Machado, V. Drago and P. S. Pizani, XRD, DSC, MS and RS studies of Fe75Se25 iron selenide prepared by mechano-synthesis, J. Magn. Magn. Mater., 2004, 270(1–2), 89–98,  DOI:10.1016/j.jmmm.2003.08.003.
46. C. E. M. Campos, J. C. De Lima, T. A. Grandi, K. D. Machado and P. S. Pizani, Structural studies of cobalt selenides prepared by mechanical alloying, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 324, 409–418.
47. C. E. M. Campos, J. C. De Lima, T. A. Grandi, K. D. Machado, V. Drago and P. S. Pizani, Hexagonal CoSe formation in mechanical alloyed Co75Se 25 mixture, Solid State Commun., 2004, 131(3–4), 265–270,  DOI:10.1016/j.ssc.2004.03.044.
48. C. E. M. Campos, J. C. De Lima, T. A. Grandi, K. D. Machado, P. S. Pizani and R. Hinrichs, Nucleation and growth of nanocrystalline pyrite nickel diselenide by mechanical alloying, Solid State Commun., 2003, 128(6–7), 229–234,  DOI:10.1016/j.ssc.2003.08.014.
49. C. E. M. Campos, J. C. De Lima, T. A. Grandi, K. D. Machado, P. S. Pizani and R. Hinrichs, Structural, thermal and optical studies of Ni3Se2 compound produced by mechanical alloying, Solid State Ionics, 2004, 168(1–2), 205–210,  DOI:10.1016/j.ssi.2004.02.001.
50. C. E. M. Campos, J. C. De Lima, T. A. Grandi, K. D. Machado, J. P. Itié and A. Polian, Pressure-induced effects on the structural properties of iron selenides produced by mechano-synthesis, J. Phys. Condens. Matter, 2004, 16(47), 8485–8490,  DOI:10.1088/0953-8984/16/47/003.
51. C. E. M. Campos, J. C. De Lima, T. A. Grandi, J. P. Itié and A. Polian, High-pressure studies of mechanical alloyed Ni75Se25 powder mixture, Solid State Ionics, 2005, 176(35–36), 2639–2644,  DOI:10.1016/j.ssi.2005.07.003.
52. C. E. M. Campos, J. C. De Lima, T. A. Grandi, K. D. Machado, J. P. Itié and A. Polian, EXAFS and Raman studies of mechanical alloyed Ni25Se75 mixture under high-pressure conditions, J. Solid State Chem., 2005, 178(1), 93–99,  DOI:10.1016/j.jssc.2004.10.006.
53. C. E. M. Campos, Solid state synthesis and characterization of NiTe nanocrystals, J. Nano Res., 2014, 29, 35–39,  DOI:10.4028/www.scientific.net/JNanoR.29.35.
54. K. de Fatima Ulbrich, J. P. Winiarski, C. L. Jost and C. E. Maduro de Campos, Mechanochemical synthesis of a Ni3-xTe2 nanocrystalline composite and its application for simultaneous electrochemical detection of dopamine and adrenaline, Compos. B Eng., 2019, 183, 2020,  DOI:10.1016/j.compositesb.2019.107649.
55. K. F. Ulbrich and C. E. M. Campos, Mechanochemical synthesis and characterization of Ni25Te75 nanocrystalline alloy, J. Mater. Sci., 2018, 53(19), 13442–13450,  DOI:10.1007/s10853-018-2470-6.
56. K. de Fatima Ulbrich, J. P. Winiarski, C. L. Jost and C. E. M. de Campos, Green and facile solvent-free synthesis of NiTe2 nanocrystalline material applied to voltammetric determination of antioxidant morin, Mater. Today Commun., 2020, 25, 101251,  DOI:10.1016/j.mtcomm.2020.101251.
57. F. L. Faita, C. E. M. Campos, K. Ersching and P. S. Pizani, Structural, thermal and vibrational characterization of mechanical alloyed In50Te50, Mater. Chem. Phys., 2011, 125(1–2), 257–262,  DOI:10.1016/j.matchemphys.2010.09.020.
58. F. L. Faita, K. Ersching, J. J. S. Acuña, C. E. M. Campos and P. S. Pizani, Structure and microstructure of In4Te3 nanopowders prepared by solid state reaction, Mater. Chem. Phys., 2011, 130(3), 1361–1365,  DOI:10.1016/j.matchemphys.2011.09.039.
59. K. Ersching, F. L. Faita, C. E. M. Campos, T. A. Grandi and P. S. Pizani, Ageing effect on mechanically alloyed ZnTe nanocrystals, J. Alloys Compd., 2010, 493(1–2), 294–298,  DOI:10.1016/j.jallcom.2009.12.083.
60. C. E. M. Campos, J. C. de Lima, T. A. Grandi and H. Höhn, Synthesis of nanocrystalline zinc blende ZnTe by mechanical alloying, J. Non-Cryst. Solids, 2008, 354(29), 3503–3506,  DOI:10.1016/j.jnoncrysol.2008.03.040.
61. C. E. M. Campos, K. Ersching, J. C. de Lima, T. A. Grandi, H. Höhn and P. S. Pizani, Influence of minor oxidation of the precursor powders to form nanocrystalline CdTe by mechanical alloying, J. Alloys Compd., 2008, 466(1–2), 80–86,  DOI:10.1016/j.jallcom.2007.11.016.
62. K. F. Ulbrich, F. Bertolotti, N. Masciocchi, A. Cervellino, A. Guagliardi and C. E. M. Campos, A comprehensive structural and microstructural investigation of a new iron-telluride nano phase, J. Mater. Chem. C, 2018, 6(12), 3047–3057,  10.1039/c7tc05456d.
63. K. F. Ulbrich, B. S. Souza and C. E. M. Campos, Synthesis ofn-hydrated nickel sulfates from mechanically alloyed nanocrystalline nickel sulfides, Green Chem., 2021, 23(12), 4580–4593,  10.1039/d1gc01213d.
64. J. Baltazar-Rodrigues, J. C. de Lima, C. E. M. Campos and T. A. Grandi, Temperature effects on mechanically alloyed nanometric ZnSe powder, Powder Technol., 2009, 189(1), 70–73,  DOI:10.1016/j.powtec.2008.06.005.
65. J. Baltazar-Rodrigues, J. C. De Lima, C. E. M. Campos and T. A. Grandi, Effects of photoacoustic measurements on a nanostructured ZnSe mechanically alloyed, J. Phys. Condens. Matter, 2008, 20(46), 465205,  DOI:10.1088/0953-8984/20/46/465205.
66. C. E. M. Campos, J. C. De Lima, T. A. Grandi, J. P. Itié, A. Polian and A. Michalowicz, Pressure-induced phase transition of nanocrystalline ZnSe, J. Phys. Condens. Matter, 2005, 17(34), 5187–5200,  DOI:10.1088/0953-8984/17/34/003.
67. C. E. M. Campos, J. C. De Lima, T. A. Grandi, K. D. Machado and P. S. Pizani, GaSe formation by mechanical alloying Ga50Se50 mixture, Solid State Commun., 2003, 126(11), 611–615,  DOI:10.1016/S0038-1098(03)00304-1.
68. C. E. M. Campos, J. C. de Lima, T. A. Grandi, S. M. Souza and P. S. Pizani, Age-induced phase transitions on mechanically alloyed amorphous GaSe, Solid State Commun., 2007, 142(5), 270–275,  DOI:10.1016/j.ssc.2007.02.029.
69. J. C. De Lima, et al., Structural and photoacoustic studies of mechanically alloyed Ga 40Sb38Se22 powder, J. Phys. Condens. Matter, 2007, 19(18), 10,  DOI:10.1088/0953-8984/19/18/186216.
70. S. M. De Souza, J. C. De Lima, C. E. M. Campos, T. A. Grandi and D. M. Trichês, Ageing-induced structural evolution of mechanically alloyed Ga 40Se60, J. Phys. Condens. Matter, 2008, 20(34), 20–23,  DOI:10.1088/0953-8984/20/34/345226.
71. K. D. Machado, et al., Structural study of Cu2-xSe alloys produced by mechanical alloying, Acta Crystallogr., Sect. B: Struct. Sci., 2004, 60(3), 282–286,  DOI:10.1107/S0108768104007475.
72. L. Takacs, Self-sustaining reactions induced by ball milling, Prog. Mater. Sci., 2002, 47(4), 355–414,  DOI:10.1016/S0079-6425(01)00002-0.
73. S. A. Humphry-Baker, S. Garroni, F. Delogu and C. A. Schuh, Melt-driven mechanochemical phase transformations in moderately exothermic powder mixtures, Nat. Mater., 2016, 15(12), 1280–1286,  DOI:10.1038/nmat4732.
74. T. A. Bither, R. J. Bouchard, W. H. Cloud, P. C. Donohue and W. J. Siemons, Transition Metal Pyrite Dichalcoĝenides. High-Pressure Synthesis and Correlation of Properties, Inorg. Chem., 1968, 7(11), 2208–2220,  DOI:10.1021/ic50069a008.
75. A. Jain, et al., Commentary: The materials project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1(1) DOI:10.1063/1.4812323.
76. R. M. Geffken, K. L. Komarek and E. M. Miller, Thermodynamic properties of cobalt-tellurium alloys, J. Solid State Chem., 1972, 4(1), 153–162,  DOI:10.1016/0022-4596(72)90143-0.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra05757c

‡ Current address: Department of Civil, Environmental and Mechanical Engineering, University of Trento, via Mesiano 77, 38123 Trento, Italy.

---