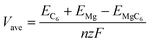Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Two dimensional twin T-graphene: monolayer for visible-light photocatalytic water splitting and bulk for anode material of magnesium batteries
Jiahe Lin†
 *ab,
Xiaowei Chen†
*ab,
Xiaowei Chen† a,
Bofeng Zhangc,
Chunrong Tana,
Qiubao Lin*ab and
Xiulin Wanga
a,
Bofeng Zhangc,
Chunrong Tana,
Qiubao Lin*ab and
Xiulin Wanga
aSchool of Science, University, Xiamen, 361021, China. E-mail: linjiahe@jmu.edu.cn; lqb@jmu.edu.cn
bSemiconductor Industry and Technology Research Institute, Jimei University, Xiamen, 361021, China
cDepartment of Chemistry, College of Chemistry and Chemical Engineering, Xiamen University, Xiamen, 361005, China
First published on 24th October 2022
Abstract
Two-dimensional (2D) carbon allotropes with all-sp2-hybridization have demonstrated great potential in nano-photoelectric devices, but the application of semiconductor photocatalysts for water splitting and anodes in magnesium batteries remains unoptimistic. Motivated by this, we theoretically study a highly stable all-sp2-hybridized 2D carbon allotrope twin T-graphene (TTG) via first-principles simulations. And through the calculations of the HSE06 functional, we find that TTG has a wide bandgap (2.70 eV) and suitable band edge positions satisfying the criteria of photocatalysts for overall water splitting. Additionally, TTG exhibits excellent photocatalytic properties for overall water splitting reflecting a high STH efficiency (12.34%), strong absorption coefficient in the visible-light region and the carrier mobility being high for electrons but low for holes. By investigating the strain effects, we get that, with biaxial compressive strain, the ability of overall photocatalytic water splitting can be effectively improved including STH up to ∼30%. Moreover, the bulk TTG also exhibits great potential as an anode material of magnesium batteries with a theoretical capacity of 556 mA h g−1, average voltage of 0.74 V and diffusion energy barrier of ∼0.96 eV. Our results would broaden the application of all-sp2-hybridized 2D carbon allotropes in the semiconductor photocatalytic and magnesium batteries field.
1. Introduction
Since the great success of monolayer graphene,1,2 2D carbon allotropes have been one of the hot research topics in both the theoretical and experimental field due to their diverse layer structures, unique properties and great potential applications in the nano-device field.3–13 Among the discovered 2D carbon allotropes, a considerable amount of systems are planar or nearly planar with their carbon atoms bonding with each other by all-sp2-hybridized chemical bonds or sp + sp2-hybridized chemical bonds. And because the π electrons in these types of 2D carbon allotropes can flow across their surface freely but bond with difficulty with Mg atoms, almost All-sp2-hybridized and sp+sp2-hybridized 2D carbon allotropes have poor performance in the applications of semiconductor photocatalysts and magnesium batteries. For instance, graphene, T-graphene, phagraphene and α-graphyne are semi-metallic owning Dirac cones in their band structures,14–21 and both graphdiyne and THD-graphene are narrow-bandgap semiconductors with ∼0.48 eV intrinsic direct bandgaps,22,23 which can not satisfy band structure conditions for photocatalysts used in water splitting. In addition, Mg intercalation into monolayer graphene even its bulk structure are very difficult, which is also a frequent phenomenon for most All-sp2-hybridized and sp + sp2-hybridized 2D carbon allotropes.24–26Recently, two types of the P6/mmm-phase All-sp2-hybridized 2D carbon allotropes, named twin graphene and hP-C18, respectively, have been theoretically proposed.27,28 The twin graphene can be viewed as AA-stacked carbon hexagons being connected together by horizontal carbon dimers, while the hP-C18 carbon can be viewed as AA-stacked carbon hexagons being connected together by vertical carbon dimers. Interestingly, unlike most other metallic or narrow-bandgap the All-sp2-hybridized and sp + sp2-hybridized 2D carbon allotropes, the twin graphene is a direct-bandgap semiconductor with a 0.981 eV bandgap, and the hP-C18 is a wide-bandgap semiconductor with a 2.93 bandgap (>2.0 eV). The significant semiconductivity of these two systems is mainly due to the carbon dimers being not coplanar with the AA-stacked carbon hexagons, which makes π electrons hard to flow across their surface unless they overcome the spatial barrier. However, the band structures of twin graphene and hP-C18 make them unsuitable for photocatalytic water splitting. Besides, twin graphene and hP-C18 also can not stably absorb Mg atoms on their surfaces. Interestingly, based on the principle of structural design, twin T-graphene (TTG) has also been proposed, which exhibited a underestimated bandgap 1.79 eV by GGA + PBE functional.29 Moreover, with the unsufficient evidences, its discoverers assumed that it was a potential photocatalyst for water splitting, which needed further study to clarify. Besides, the abilities of TTG in magnesium batteries also remain to be explored. Therefore, it is necessary to further study the performance of TTG on photocatalytic water splitting and magnesium batteries.
In this paper, we theoretically study TTG (shown in Fig. 1) based on first principles density functional theory. Through the calculations of cohesive energy, phonon spectrum and ab inito MD simulation, we confirm that TTG own high stability. The band structure, work function and optical absorption spectrum of TTG are studied by using HSE06 functional, which is well known that can get more accurate band structures than that by GGA + PBE functional for semiconductors. Our results indicates that TTG is an indirect wide-bandgap semiconductor and satisfies the band structure conditions of photocatalysts for visible-light overall water splitting. In addition, we also study the mechanical biaxial strain response of TTG. The strain response of electronic, optical and photocatalytic properties shows that biaxial strain can effectively tune the performance of TTG in the application on photoelectric devices and photocatalysts. Finally, we study the ability of TTG and its bulk structure for absorbing Mg atoms and relative properties as the anode of magnesium batteries. Then it reveals that bulk TTG structure has potential on the anode materials of magnesium batteries.
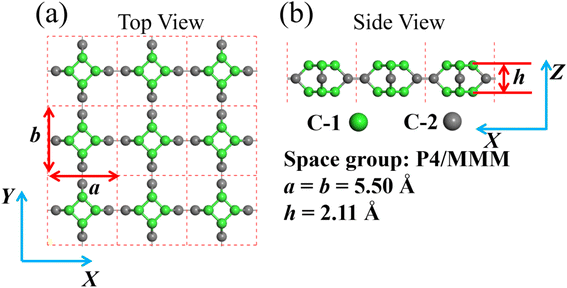 | ||
| Fig. 1 (a) and (b) are the structure model of TTG. The illustration for the lattice constants, layer height and space group of TTG is shown at the bottom right. | ||
2. Computational details
All our calculations were performed by using first principle density functional theory (DFT). The CASTEP code was adopted to calculate the phonon spectrum, band structures, work function and optical absorption spectrum, while norm-conserving pseudopotential and planewave cutoff energy of 750 eV were employed.30 For the geometry optimization and phonon spectrum, the GGA + PBE functional (the GGA is the generalized gradient approximation, and the PBE is Perdew–Burke–Ernzerhof) was used.31 Our models were fully relaxed until reaching that the forces in the systems were lower than 0.01 eV Å−1 and the energy convergence tolerances were smaller than 1 × 10−6 eV per atom. 30 Å vacuum layer for monolayer TTG were adopted. The k-point sampling for the Brillouin zone by using Monkhorst–Pack scheme was set as 4 × 4 × 1.32 The phonon spectrum was carried out by the linear response method.33 The electronic band structures and optical absorption spectrum were got through the GGA + PBE and HSE06 (the HSE is Heyd–Scuseria–Ernzerhof) functional.34 Although the initial designers of TTG have performed ab inito MD simulation (AIMD) for TTG at 300 K by using a primitive cell, it is not so accurate to reveal the thermal stability of TTG. To order to further carry out its thermal stability at 300 K, we also performed AIMD calculation for TTG at 300 K with a 4 × 4 × 1 supercell, which contains 192 atoms. The AIMD simulation is performed by the Vienna ab initio simulation package (VASP) code.35 The simulating time is 4 ps, which is executed into 4000 steps. The 1 × 1 × 1 k-point setting was adopt and energy convergence tolerance was lower than 1 × 10−4 eV per atom. Finally, the Mg diffusion barriers were calculated by the climbing image nudged elastic band (CI-NEB) method.363. Results and discussion
3.1. Structural stability of TTG
After the full geometry optimization, the structure model of monolayer TTG is exhibited in Fig. 1(a) and (b), and the lattice constants are marked in Fig. 1(a) and (b). As shown in Fig. 1, there are two types of inequivalent carbon atoms in the unit cell, denoted as C-1 (green) and C-2 (gray), respectively. In the TTG, each carbon atom connects with two C-1 atoms and one C-2 atom to form a monolayer all-All-sp2-hybridized carbon allotrope. In order to confirm the stability of TTG, the cohesive energy (Ecoh), phonon spectrum and AIMD simulation at 300 K have been carried out. Firstly, for calculating its Ecoh, we adopt the following standard expression:
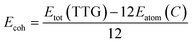 | (1) |
Additionally, we have obtained the phonon spectrum of TTG shown in Fig. 2(a). Fortunately, we get that there is no imaginary frequency through the whole Brillouin zone with its minimum of the acoustic branch being linear around the Gamma point, which demonstrates that TTG is dynamically stable. Moreover, we also have performed AIMD simulation at 300 K to further study the thermal stability of TTG at room temperature. The results are shown in Fig. 2(b). We get that the time evolution curve of free energy for TTG fluctuates around the equilibrium position, and its structure, shown in the inset of Fig. 2(b), still shows no significant structural differences as compared with its initial structure. Thus, it indicates that TTG is thermally stable at room temperature.
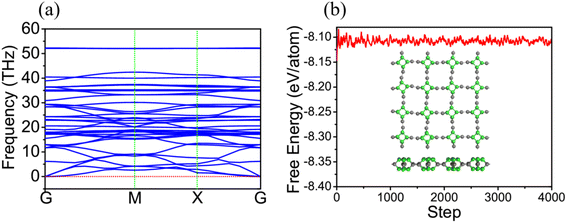 | ||
| Fig. 2 (a) is the phonon spectrum of TTG. (b) is the time evolution curve of free energy for TTG simulated by ab inito MD at 300 K, and the insets in (b) is the structure of TTG at 300 K. | ||
3.2. Electronic properties of TTG
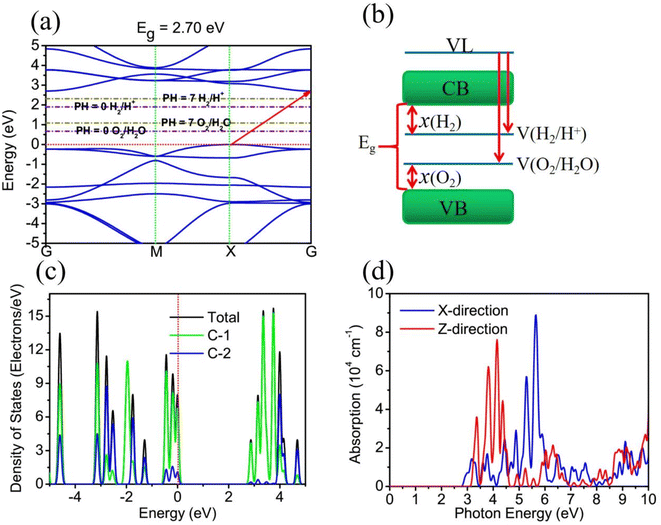
To study the electronic structure properties of TTG, we have carried out its band structure calculated by HSE06 functional, as shown in Fig. 3(a) and (b), respectively. The Fig. 3(a) shows that TTG is indirect-wide-bandgap (Eg = 2.70 eV) semiconductor with its valence band maximum (VBM) lying at X point and conduction band minimum (CBM). This decent bandgap means that TTG have potential applications on high frequency and high power electronic devices, UV-LEDs and even photocatalysts for water splitting. However, for a 2D semiconductor that can be used for overall water splitting, its CBM energy levels relative to the vacuum level must be lower than the oxidation potential [V(O2/H2O)] for H2O to O2 and its VBM energy levels relative to the vacuum level must be higher than the reduction potential [V(H2/H+)] for H+ to H2 (the schematic diagram is shown in Fig. 3(b)). And the redox potential of water splitting depended on the pH values can be calculated by V(O2/H2O) = −5.67 eV + pH × 0.059 eV and V(H2/H+) = −4.44 eV + pH × 0.059 eV. Therefore, the V(H2/H+) and V(O2/H2O) are −4.44 and −5.67 eV at pH = 0, respectively, and the V(H2/H+) and V(O2/H2O) are −4.027 and −5.257 eV at pH = 7, respectively. Unfortunately, this criteria of photocatalysts for water splitting is always hard to satisfy for most monolayer materials, such as black phosphorene, monolayer SnSe and monolayer C3N. Encouragingly, comparing the CBM and VBM of TTG with the redox potentials in water splitting at pH = 0 (pink dashed lines) and pH = 7 (wathet blue dashed lines) shown in Fig. 3(a), we obtain that the band edge positions of TTG satisfy the basic band structure conditions of photocatalytic water splitting at pH = 0 and pH = 7. This reveals that TTG can be regarded as a promising candidate 2D semiconductor for overall photocatalytic water splitting.For studying the different contribution of two types carbon atoms for the electronic occupancy states, the calculations of the total density of states (TDOS) and partial density of states (PDOS) for TTG have been performed, and the results are shown in Fig. 3(c). Learning from the TDOS of TTG, we get that the occupancy state peaks near the VBM and CBM are considerably high and the energy difference between these two peaks is ∼2.80 eV, which means that TTG would have strong optical absorption at violet-light region caused by avoiding carrier blocking effect. The PDOS of TTG indicates that both the occupied state near the VBM and CBM are mainly contributed by C-1 atoms, while the contributions from C-2 atoms are very low. Additionally, it is clear that both the occupied state of the VBM and CBM are contributed by surface C-1 atoms, which means that photogenerated charge can easier involve in photocatalytic reaction. Based on the analysis of PDOS, we find that the active π electrons have been limited in C-1 atoms and further make TTG being semiconductive.
3.3. Photocatalytic behaviour of TTG for overall water splitting
For an excellent photocatalyst, the ability of harvesting sunlight, particularly visible and ultraviolet light, to give rise to electron–hole pairs is crucial to water splitting.37–40 To determine the optical absorption coefficient of the TTG, we have calculated its optical absorption spectrums that are polarized in X-direction and Z-direction of TTG, as shown in Fig. 3(d). The frequency-dependent dielectric function that is obtained and expresses as ε(ω) = ε1(ω) + iε2(ω), which can be used to carry out the absorption coefficient as follow:
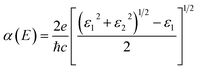 | (2) |
The Fig. 3(d) shows that, when the incident light is polarized in X-direction, TTG has strong optical absorption at the range of photon energy about 2.80–4.00 eV, and when the incident light is polarized in Z-direction, TTG has strong optical absorption at the range of photon energy about 3.10–4.00 eV. This result reveals that TTG have outstanding ability on harvesting visible and ultraviolet light whether along the polarization in in-plane or out-plane direction, which is superior to most of other monolayer materials.
Although the situation of its band edge positions and optical absorption indicates that TTG would be a good potential candidate for water splitting, its carrier mobility also should be concerned, which has important impact on photogenerated carrier transferring to the surface of photocatalysts and precipitating the redox reactions of water. Additionally, the obvious difference between the mobility of electrons and holes would be favourable for enhancing photocatalytic activity through improving the separation rate of photo-induced electron and hole. Thus, the carrier mobility of TTG in X-direction has been carried out through the deformation potential (DP) theory41 at 300 K:
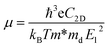 | (3) |
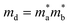 . The effective elastic modulus C2D is calculated by C2D = 2[∂2E/∂(Δa/a0)2]/S0, in which the a0 is the initial lattice constant, the Δa stands for the deformation of a0, the S0 represents the initial total area, and the E is the total energy of systems with external strain along X-direction. The T is set as 300 K. The deformation potential constant is calculated by El = ∂Eedge/∂(Δa/a0), where Eedge is the change of the band edge levels under the external strain along X-direction. The relevant evaluation parameters are listed in Table 1. We get that the electron mobility of TTG is ∼1208.32 cm2 V−1 s−1, which is higher that of monolayer MoS2 and GeTe. And interestingly, its hole mobility is only ∼18.69 cm2 V−1 s−1 mainly due to the high value of El for holes. The situation of carrier mobility reveals that TTG possesses favorable transport conditions of photo-induced carriers for water splitting.
. The effective elastic modulus C2D is calculated by C2D = 2[∂2E/∂(Δa/a0)2]/S0, in which the a0 is the initial lattice constant, the Δa stands for the deformation of a0, the S0 represents the initial total area, and the E is the total energy of systems with external strain along X-direction. The T is set as 300 K. The deformation potential constant is calculated by El = ∂Eedge/∂(Δa/a0), where Eedge is the change of the band edge levels under the external strain along X-direction. The relevant evaluation parameters are listed in Table 1. We get that the electron mobility of TTG is ∼1208.32 cm2 V−1 s−1, which is higher that of monolayer MoS2 and GeTe. And interestingly, its hole mobility is only ∼18.69 cm2 V−1 s−1 mainly due to the high value of El for holes. The situation of carrier mobility reveals that TTG possesses favorable transport conditions of photo-induced carriers for water splitting.
| TTG | m* (m0) | Md (m0) | El (eV) | C2D (eV Å−2) | μ (cm2 V−1 s−1) |
|---|---|---|---|---|---|
| h | 1.82 | 1.82 | 7.81 | 11.02 | 18.69 |
| e | 1.77 | 1.77 | 1.00 | 11.02 | 1208.32 |
For photocatalytic water splitting, the solar-to-hydrogen (STH) efficiency is important target to measure the efficiency of generating hydrogen. In the case of TTG, its optical gap basically agrees with the bandgap. Therefore, the outstanding ability of harvesting light for TTG will facilitate the high STH efficiency. Firstly, we obtain the optical absorption efficiency (ηabs) as follow:42
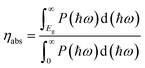 | (4) |
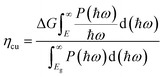 | (5) |
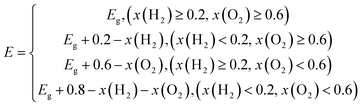 | (6) |
| ηsth = ηabs × ηcu | (7) |
We obtain that the ηsth of TTG at pH = 0 is 12.34% (>10%). And although the ηsth at v = 7 is 8.11%, it also can be tolerable. Our calculations reveals that TTG has desirable STH efficiency for overall water splitting.
3.4. Strain response of TTG on electronic and photocatalytic properties
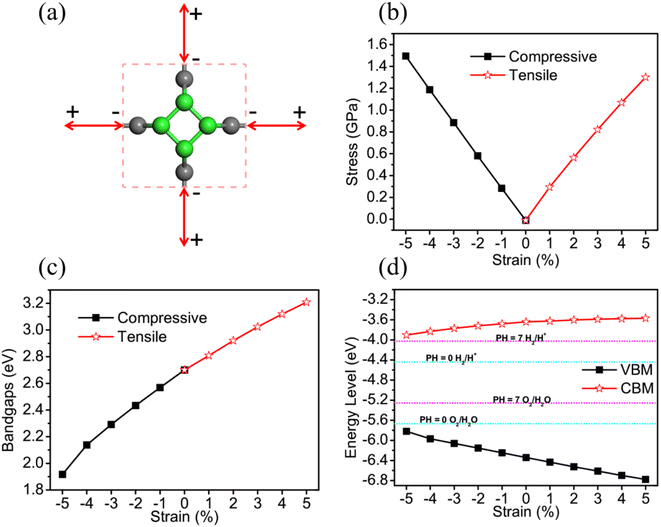
Due to predecessor's researches having proved that applying strain to 2D materials is a effective way to tune the electronic and optical properties, we have applied biaxial strain to TTG for further improving its photocatalytic properties, vas shown in Fig. 4(a). The application of biaxial strain that ranges from −5% to 5% is simulated by simultaneously freezing both lattice constant a and b at same specific values and fully relaxing carbon atoms. The biaxial strain can be defined as η = (a − a0)/a0, where a0 is the initial lattice constants, and a is the lattice constants with artificial strain. The Fig. 4(b) exhibits that both the tensile and compressive biaxial strain applied to TTG are experimentally feasible caused by their relatively low demand of applied stress (<1.60 GPa).To investigate the strain response of the electronic properties of TTG, we have obtained its bandgaps and band edge positions relative to vacuum level changing with η. We find that, with −5% ≤ η ≤ 5%, the bandgap of TTG can be tuned from 1.92 eV (η = −5%) to 3.21 eV (η = 5%) and increases at a near-liner trend with the lattice constants becoming larger, as shown in Fig. 4(c). We have compared the VBM and CBM, tuned by η, with the redox potential of water splitting at pH = 0 and pH = 7, as shown in Fig. 4(d). The result shows that, under the biaxial strain ranging from −5% to 5%, TTG still meets the conditions of photocatalysts for water splitting at pH = 0 and pH = 7. What's more, we obtain that the energy level of VBM increases with the decrease of η, while it is diametrical for CBM. This phenomenon means that, with biaxial compressive strain, the optical absorption spectrum of TTG will red shift but the driving force for the redox reaction of water splitting will abate. And for the case of that with biaxial tensile strain, the relevant situation will be opposite. Furthermore, the Fig. 4(d) also exhibits that the variation of CBM with η is gently while it is sharp for that of VBM.
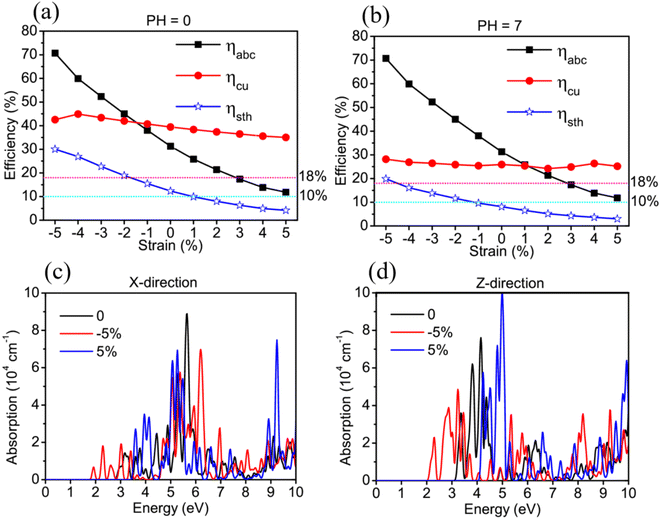
For further studying the strain effects on the photocatalytic properties of TTG, we have performed the calculations of its STH efficiency and optical absorption changing with biaxial strain. The Fig. 5(a) and (b) are the ηabc, ηcu and ηsth of TTG changing with biaxial strain at pH = 0 and pH = 7, respectively. It is clear that the values of the ηabc, ηcu and ηsth of TTG at pH = 0 and pH = 7 increase with the decrease of lattice constants. Moreover, as shown in Fig. 5(a), when 0 ≤ η ≤ 5%, the ηsth of TTG are larger than 10% at pH = 0, and when −2% ≤ η ≤ 5%, the ηsth of TTG are larger than 18% at pH = 0, which is the conventional theoretical limit ∼18%. Additionally, learning from Fig. 5(a), when −1% ≤ η ≤ 5%, the ηsth of TTG are larger than 10% at pH = 7, and when η = 5%, the ηsth of TTG (∼30%) is larger than 18% at pH = 7. This indicates that biaxial compressive strain is effective way improve the STH efficiency of TTG.
We investigate the strain effect on optical properties for TTG by calculating its optical absorption spectrum under biaxial strain η = −5%, 0 and 5%, which can present the variation trend of its optical absorption with −5%≤ η ≤ 5% well. The Fig. 5(c) and (d) are the optical absorption spectrums of TTG with incident light polarized in X-direction and Z-direction, respectively. We get that the optical absorption spectrum of TTG under biaxial compressive strain will be red-shift, while the situation is opposite under biaxial tensile strain. And with η = −5%, due to bandgap becoming smaller, the absorption spectrum of TTG is expanding to the ∼1.92 eV and have strong absorption at the range from 1.92 eV to 3.10 eV, which is conducive to solar energy conversion and visible-light photocatalytic water splitting. For the Fig. 5(d), the optical absorption spectrums of TTG with incident light polarized in Z-direction share same strain response feature with that with incident light polarized in X-direction. Furthermore, we obtain that, with η = −5%, the optical absorption spectrum of TTG with incident light polarized in Z-direction still has strong absorption at the range from 2.00 eV to 3.10 eV even surpass that with incident light polarized in X-direction.
3.5. Potential on the anode of magnesium battery
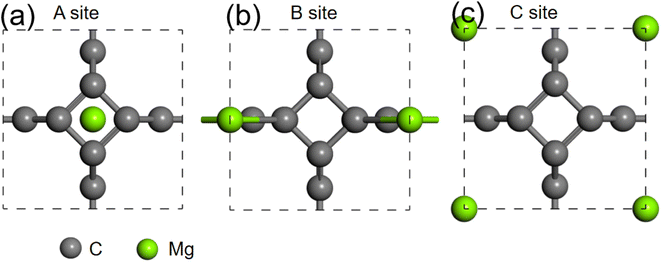
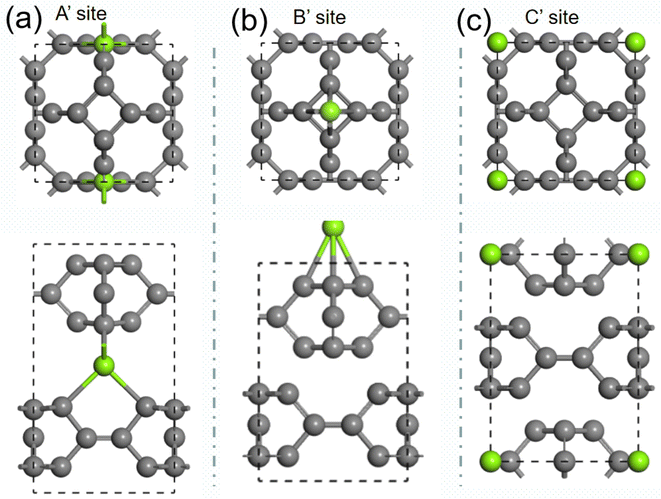
We further studied the use of monolayer TTG as a potential anode material for magnesium battery. The absorption energies of Mg atom on three different positions of monolayer TTG were calculated and presented in Fig. 6. The absorption energy is calculated by the following equation| Eab = EC+Mg − EC − EMg |
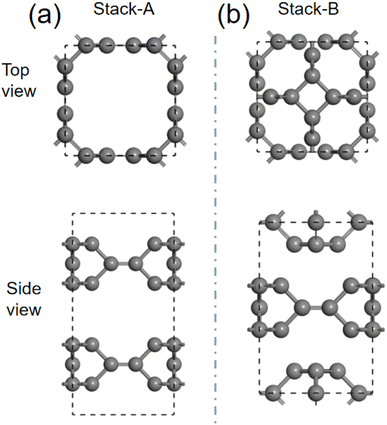
We then investigate the intercalation of Mg atoms into the bulk TTG. There are two stack styles of bulk TTG, as shown in Fig. 7. To identify which bulk structure is more stable, we have calculated their formation energy, and we get that the formation energy of stack-B (−0.86 eV) is much lower than that of stack-A (−0.35 eV). Therefore, the bulk TTG with stack-B structure is adopt to study the intercalation of Mg atoms. As shown in Fig. 8, three different absorption sites in bulk TTG were examined. The absorption energy is −1.15 eV for the A site, 0.41 eV for B site and 0.36 eV for C site. The negative adsorption energy of Mg atom on the A site means that intercalation of a Mg atom into the bulk TTG is thermodynamic favorable. Then, the number of Mg atoms intercalation into bulk TTG was gradually increased and the calculated adsorption energies were −1.71 eV for absorbing two Mg atoms, −1.92 eV for absorbing two Mg atoms and −1.67 for absorbing two Mg atoms, respectively. Such adsorption energies are strong enough to maintain the stability of the Mg intercalation configure without cluster. The above calculation indicates that bulk TTG can at most store Mg atoms with a stoichiometry of MgC6, corresponding to a theoretical capacity of 556 mA h g−1, which is higher than that of C3N and g-C3N4 sheet.46
To further characterizing the performance of bulk TTG as anode material of magnesium battery, we have firstly carried out the average voltage calculation using the following equation
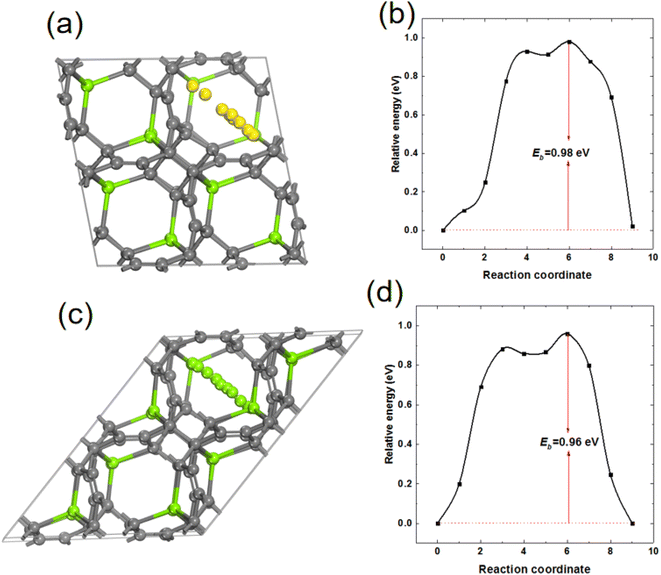
In order to study the mobility of Mg in MgC6, 2 × 2 × 2 supercell of MgC6 was used and a Mg vacancy was created from supercell MgC6. The energy barrier for the diffusion of a nearby Mg atom towards the Mg vacancy was calculated. As shown in Fig. 9(a) and (b), the energy barrier of Mg atom diffuses on the surface of TTG sublayer is 0.98 eV. Interestingly, as shown in Fig. 9(c) and (d), the diffusion energy barrier of Mg between nearby TTG sublayer is 0.96 eV, comparable to that of Mg on the surface of TTG sublayer. Previous computational screening of layered materials for Mg ion battery indicates the diffusion energy barrier of Mg in the layer boron carbide is 2.36 eV.47 The bulk TTG shows significantly low Mg diffusion energy barrier compare to that of layer boron carbide. We acknowledge that the Mg diffusion energy barrier is still too high for fast Mg ion mobility. However, our study provides a preliminary view of designed novel graphite allotropes layer materials for Mg ion battery.
4. Conclusion
In summary, we have studied all-sp2-hybridized 2D carbon allotrope TTG via first-principles calculations. Our calculations indicate that TTG is highly stable in energy, dynamic and thermodynamic. Through the calculations of electronic properties, we get that TTG has a wide bandgap (2.70 eV) and meets the criteria of photocatalysts for overall water splitting. The semiconductivity of TTG indicates that making π electrons localized is a key point for building all-sp2-hybridized 2D carbon allotrope semiconductors with considerable bandgaps. Moreover, the excellent photocatalytic behaviors, including outstanding ability of harvesting light, unique carrier mobility and desirable STH efficiency, reveal that TTG is a potential candidate for visible-light photocatalysis overall water splitting. By studying the biaxial strain response of TTG, we find that biaxial strain can effectively tune its electronic, optical and photocatalytic properties. What's more, it also reveals that biaxial compressive strain is good for improving the photocatalytic activity of TTG for overall water splitting. Finally, we have predicted that bulk TTG has potential on the application of magnesium battery as anode reflecting on suitable absorption energy, relatively lower average voltage and diffusion energy barrier. Our work provides that TTG has great potential on energy field.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the national natural science foundation of China (Grant No. 52071156, 51601068 and 12004269), the key scientific and technological program of Xiamen (China) (Grant No. 3502Z20191016), the Fujian province department of science and technology (China) (Grant No. 2019L3008, 2020J05147 and 2020J01705), and the scientific research starting foundation of Jimei University (China) (Grant No. ZQ2019015).References
- K. Novoselov, A. Geim, S. Morozov, D. Jiang, Y. Zhang, S. Dubonos, I. Grigorieva and A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- K. Novoselov, D. Jiang, F. Schedin, T. Booth, V. Khotkevich, S. Morozov and A. Geim, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10451 CrossRef CAS PubMed.
- W. Zhang, C. Chai, Q. Fan, Y. Song and Y. Yang, Appl. Surf. Sci., 2021, 537, 147885 CrossRef CAS.
- Y. Xue, Y. Li, J. Zhang, Z. Liu and Y. Zhao, Sci. China Chem., 2018, 61, 765–786 CrossRef CAS.
- Z. Wang, F. Dong, B. Shen, R. Zhang, Y. Zheng, L. Chen, S. Wang, C. Wang, K. Ho and Y. Fan, Carbon, 2016, 101, 77–85 CrossRef CAS.
- X. Gao, H. Liu, D. Wang and J. Zhang, Chem. Soc. Rev., 2019, 48, 908–936 RSC.
- V. Singh, D. Joung, L. Zhai, S. Das, S. I. Khondaker and S. Seal, Science, 2011, 56, 1178–1271 CAS.
- C. Huang, Y. Li, N. Wang, Y. Xue, Z. Zuo, H. Liu and Y. Li, Chem. Rev., 2018, 118, 7744–7803 CrossRef CAS PubMed.
- O. Erol, I. Uyan, M. Hatip, C. Yilmaz, A. Tekinay and M. Guler, Nanomedicine, 2018, 14, 2433–2454 CrossRef CAS PubMed.
- Y. Liu, G. Wang, Q. Huang, L. Guo and X. Chen, Phys. Rev. Lett., 2012, 108, 225505 CrossRef PubMed.
- A. Neto, F. Guinea, N. Peres, K. Novoselov and A. Geim, Rev. Mod. Phys., 2009, 81, 109–162 CrossRef.
- A. Balandin, Nat. Mater., 2011, 10, 569–581 CrossRef CAS PubMed.
- W. Zhang, C. Chai, Q. Fan, Y. Song and Y. Yang, Appl. Surf. Sci., 2021, 537, 147885 CrossRef CAS.
- D. Malko, C. Neiss, F. Viñes and A. Görling, Phys. Rev. Lett., 2012, 108, 086804 CrossRef PubMed.
- A. Puigdollers, G. Alonso and P. Gamallo, Carbon, 2016, 96, 879–887 CrossRef CAS.
- B. Kim and H. Choi, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 115435 CrossRef.
- H. Sun, S. Mukherjee and C. Singh, Phys. Chem. Chem. Phys., 2016, 18, 26736–26742 RSC.
- O. Oriekhov, P. Gusynin and V. Loktev, Phys. Rev. B, 2021, 103, 195104 CrossRef.
- Z. Wang, X. Zhou, X. Zhang, Q. Zhu, H. Dong, M. Zhao and R. A. Oganov, Nano Lett., 2015, 15, 6182–6186 CrossRef CAS PubMed.
- T. Oka and H. Aoki, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 081406 CrossRef.
- M. Batzill, Surf. Sci. Rep., 2012, 67, 83–115 CrossRef CAS.
- M. Long, L. Tang, D. Wang, Y. Li and Z. Shuai, ACS Nano, 2011, 5, 2593–2600 CrossRef CAS PubMed.
- X. Xu, B. Jiang, Y. Guo and Y. Cai, Mater. Chem. Phys., 2017, 200, 50–56 CrossRef CAS.
- E. Dequan, D. Eric, H. Kumar and B. Shenoy, ACS Energy Lett., 2016, 1, 638–645 CrossRef.
- K. Hansu, J. Goojin, Y. Kim, J. Kim, C. Park and H. Sohn, Chem. Soc. Rev., 2013, 42, 9011–9034 RSC.
- C. Zeng, K. Wang, L. Pan, B. Lin and H. Pan, Mater. Today Nano, 2021, 16, 100134 CrossRef CAS.
- S. Wang, J. Li, X. Zhu and M. Wang, Carbon, 2019, 143, 517–522 CrossRef CAS.
- J. Jiang, J. Leng, J. Li, Z. Guo, T. Chang, X. Guo and T. Zhang, Carbon, 2017, 118, 370–375 CrossRef CAS.
- D. Bhattacharya and D. Jana, Phys. Chem. Chem. Phys., 2020, 22, 10286–10294 RSC.
- M. Segall, P. Lindan, M. Probert, C. Pickard, P. Hasnip, S. Clark and M. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744 CrossRef CAS.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. Monkhorst and J. Pack, Phys. Rev. B: Solid State, 1977, 16(4), 1748–1749 CrossRef.
- S. Baroni, S. Gironcoli, A. Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515–562 CrossRef CAS.
- G. Kresse and J. Furthmisüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. Heyd, G. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- D. Sheppard, R. Terrell and G. Henkelman, J. Chem. Phys., 2008, 128, 134106 CrossRef PubMed.
- H. Li, F. Guo, Z. Feng and J. Li, Phys. Chem. Chem. Phys., 2022 10.1039/d2cp02779h.
- H. Li, H. Hu, C. Bao, J. Hua, H. Zhou, X. Liu, X. Liu and M. Zhao, Phys. Chem. Chem. Phys., 2015, 17, 6028–6035 RSC.
- H. Li, H. Hu, C. Bao, F. Guo, X. Zhang, X. Liu, J. Hua, J. Tan, A. Wang and H. Zhou, Sci. Rep., 2016, 6, 1–10 CrossRef PubMed.
- D. Kong, X. Hu, J. Geng, Y. Zhao, D. Fan, Y. Lu, W. Geng, D. Zhang, J. Liu and H. Li, Appl. Surf. Sci., 2022, 591, 153256 CrossRef CAS.
- J. Bardeen and W. Shockley, Phys. Rev. B: Solid State, 1950, 80, 72C80 Search PubMed.
- Z. Chen, T. Jaramillo, T. Deutsch, A. Kleiman-Shwarsctein, A. Forman, N. Gaillard, R. Garland, K. Takanabe, C. Heske, M. Sunkara, E. McFarland, K. Domen, E. Miller, J. Turner and H. Dinh, J. Mater. Res., 2010, 25(1), 3–16 CrossRef CAS.
- C. Fu, J. Sun, Q. Luo, X. Li, W. Hu and J. Yang, Nano Lett., 2018, 18(10), 6312–6317 CrossRef CAS PubMed.
- M. Sun and U. Schwingenschlögl, Chem. Mater., 2020, 32(11), 4795–4800 CrossRef CAS.
- X. Chen, F. Yuan, Q. Gu and X. Yu, J. Mater. Chem. A, 2013, 1(38), 11705–11710 RSC.
- J. Zhang, G. Liu, H. Hu, L. Wu, Q. Wang, X. Xin, S. Li and P. Lu, Appl. Surf. Sci., 2019, 487, 1026–1032 CrossRef CAS.
- Z. Zhang, X. Zhang, X. Zhao, S. Yao, A. Chen and Z. Zhou, ACS Omega, 2019, 4, 7822–7828 CrossRef CAS PubMed.
Footnote |
| † Jiahe Lin and Xiaowei Chen contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |