Open Access Article
Open Access ArticleExponential amplification by redox cross-catalysis and unmasking of doubly protected molecular probes†
Justine
Pallu
,
Charlie
Rabin
,
Pan
Hui
,
Thamires S.
Moreira
,
Geordie
Creste‡
,
Corentin
Calvet
,
Benoît
Limoges
 *,
François
Mavré
*,
François
Mavré
 * and
Mathieu
Branca
* and
Mathieu
Branca
 *
*
Université de Paris, Laboratoire d'Electrochimie Moléculaire, UMR 7591, CNRS, F-75013 Paris, France. E-mail: limoges@u-paris.fr; francois.mavre@u-paris.fr; mathieu.branca@u-paris.fr
First published on 11th February 2022
Abstract
The strength of autocatalytic reactions lies in their ability to provide a powerful means of molecular amplification, which can be very useful for improving the analytical performances of a multitude of analytical and bioanalytical methods. However, one of the major difficulties in designing an efficient autocatalytic amplification system is the requirement for reactants that are both highly reactive and chemically stable in order to avoid limitations imposed by undesirable background amplifications. In the present work, we devised a reaction network based on a redox cross-catalysis principle, in which two catalytic loops activate each other. The first loop, catalyzed by H2O2, involves the oxidative deprotection of a naphthylboronate ester probe into a redox-active naphthohydroquinone, which in turn catalyzes the production of H2O2 by redox cycling in the presence of a reducing enzyme/substrate couple. We present here a set of new molecular probes with improved reactivity and stability, resulting in particularly steep sigmoidal kinetic traces and enhanced discrimination between specific and nonspecific responses. This translates into the sensitive detection of H2O2 down to a few nM in less than 10 minutes or a redox cycling compound such as the 2-amino-3-chloro-1,4-naphthoquinone down to 50 pM in less than 30 minutes. The critical reason leading to these remarkably good performances is the extended stability stemming from the double masking of the naphthohydroquinone core by two boronate groups, a counterintuitive strategy if we consider the need for two equivalents of H2O2 for full deprotection. An in-depth study of the mechanism and dynamics of this complex reaction network is conducted in order to better understand, predict and optimize its functioning. From this investigation, the time response as well as detection limit are found to be highly dependent on pH, nature of the buffer, and concentration of the reducing enzyme.
Introduction
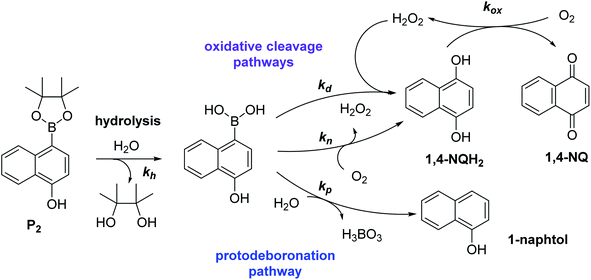
In the context of chemical or biochemical analysis, it is common to rely on molecular or biomolecular amplifications to improve the analytical performances of a detection method (i.e., sensitivity, limit of detection (LoD), analysis time, dynamic range of concentration, …).1,2 This is even more important when the targeted molecules or biomolecules are present at low concentrations. In most cases, molecular amplifications result from catalytic reactions wherein a molecule (either the analyte acting as a catalyst or a label catalyst revealing indirectly the presence of the analyte) triggers the catalysis of a reaction capable to generate a detectable signal (which can be optical, electrochemical, thermal, gravimetric, etc.). Under these conditions, the product linearly accumulates with time and the amplification factor depends only on the catalytic rate and reaction time.3 A popular example is the signal amplification resulting from the enzyme label involved in enzyme-linked immunosorbent assays.4,5 However, greater molecular amplifications can be achieved by adequately combining the reactivity of different catalysts. One possibility is to cascade the reactivity of two catalysts, wherein a first one catalyses the production of a second one. In such situation, the product of the secondary catalytic reaction accumulates quadratically with time.6–11 An even more powerful approach is to produce an exponential signal gain from an autocatalytic reaction, for which one of the products catalyses its own formation.12–14 A well-known example is the polymerase chain reaction, which through self-replication of a targeted DNA sequence allows the ultimate detection of a few molecules of nucleic acids in a few tens of microliters.15 While autocatalytic replication is well suited to nucleic acids,16–19 it is more challenging to design for other molecules.13 Among the few examples of molecular self-replication strategies developed to date for the detection of small molecules is the dendritic chain reaction (DCR) first described in 2009 by Shabat and his collaborators.20,21 In this concept, the analyte triggers its self-replication through the decomposition of a dendritic molecular probe containing at least two masked equivalents of the analyte. This methodology was applied to the autocatalytic detection of H2O2 (ref. 20, 22 and 23) and fluoride ions.24–27 More recently, alternative strategies based on self-propagating thiolate–disulfide exchange,28,29 methionase chain reaction,30 or photoinduced autocatalysis31,32 were also reported. However, all these methods suffer from undesirable background reactions, which prevent the achievement of very low analyte concentrations. The main reason of these background reactions is the intrinsic lack of stability of the starting coreactants, leading to self-initiation of the amplification cycle in the absence of analyte. Therefore, a critical issue is to design systems involving coreactants with high chemical stability and, at the same time, high reactivity and selectivity towards the trigger of the reaction. This is certainly the major challenge facing the exponential signal amplification strategies.33 An additional drawback is the slowness of the approaches proposed to date, sometimes requiring waiting several hours for an analytical response.21,23To address these drawbacks and contribute to the development of alternative solutions, we recently proposed a new versatile molecular-based autocatalytic system34,35 in which the exponential gain is generated from cross-activation of two catalytic loops, as depicted in Scheme 1A. The first loop (loop 1) is based on a H2O2-mediated deprotection of a boronate ester probe (P) to a hydroquinone derivative (QH2), which, in the presence of O2 in solution, spontaneously autoxidizes to a quinone (Q) with the concomitant regeneration of H2O2 (the latter acting thus as a catalyst in loop 1). The autocatalysis is then engendered from the back conversion of Q into its reduced QH2 form in the presence of a reducing substrate S (or alternatively an enzyme/reducing substrate couple E/S), thus forming the second catalytic loop (loop 2, which is also a redox cycle wherein Q/QH2 serves as a redox catalyst). Analytical derivations as well as numerical simulations of the kinetics of this redox cross-catalytic system allowed us to demonstrate the overstoichiometric production of H2O2 coupled with the exponential decrease of probe and substrate concentrations with time.34,36 This autocatalytic set is conceptually different from the previously reported branched-chain or self-propagating amplification reactions in that it does not require the design of a dendritic probe capable of releasing two or more equivalents of the trigger by self-immolation. Another advantage is that it offers the possibility to trigger the reaction either by H2O2 or any redox cycling compound, thus providing an extended degree of freedom to couple this molecular amplification not only to the detection of H2O2 (directly or indirectly produced), but also to the detection of molecules exhibiting redox cycling properties (also either directly or indirectly generated).
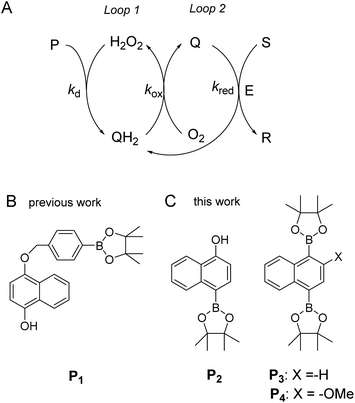 | ||
| Scheme 1 (A) General principle of the autocatalytic reaction scheme based on cross-activation of two catalytic loops. (B) Boronate-based probe previously used in ref. 34. This probe is converted by H2O2 in an intermediate phenolic compound that self-immolates into a quinone methide and a 1,4-naphthohydroquinone. (C) The new probes used in the present study. | ||
Using the boronate ester probe P1 shown in Scheme 1B, detection of submicromolar or subnanomolar concentrations of H2O2 or a naphthoquinone, respectively, within 1 h was demonstrated.34 Although these analytical performances are significantly better than those previously achieved by DCR,20,22,23,37,38 they are still limited by the lack of chemical stability of P1, which in the absence of the trigger tends to slowly self-deprotect into a naphthohydroquinone. This lack of stability turns out to be intrinsic to the self-immolating spacer installed on the probe,34 a recurrent issue of probes based on self-immolation and which is at the origin of the unsatisfactory analytical performances encountered so far. To access more robust and stable probes, it is thus important to design probes that no longer rely on self-immolation. This is what we address here with the new boronate-based probes shown in Scheme 1C. Instead of introducing the masking boronate ester function via a remote self-immolating spacer, we have chosen to place it directly on the naphthyl ring, leading either to the single-protected naphthol monoboronate ester probe P2 or the doubly protected naphthyl diboronate ester probes P3 and P4. By reaction with H2O2, these probes are expected to release a 1,4-naphthohydroquinone (1,4-NQH2), which in the presence of O2 spontaneously autoxidizes into 1,4-naphthoquinone (1,4-NQ) with concomitant regeneration of H2O2, as previously shown with P1.34 Another important feature we have considered here is to design boronate probes with an improved reactivity towards H2O2 as well as an optimized redox cycling capability, with the underlying idea to outcompete the background reactions.36
As it will be shown, the single-protected probe P2 generates a remarkably efficient autocatalytic reaction (LoD of 0.1 µM H2O2 in less than 10 min at pH 8.5) thanks to a fast H2O2-mediated deprotection rate (kd) (faster than P1). However, the lack of chemical stability of P2 pushed us to opt for a double masking strategy, as exemplified with probes P3 and P4, which finally enable us to obtain much more stable boronate probes while keeping a good reactivity towards H2O2. With these doubly protected probes, detection of nanomolar concentrations of H2O2 in less than 10 min was achieved using a simple UV-visible absorbance readout, which in terms of analytical performance is competitive with the best fluorescent-based molecular probes currently available on the market for quantitative analysis of H2O2 by fluorescence.39–41 Finally, we will show that these excellent analytical performances could be obtained thanks to a comprehensive kinetic analysis of the complex cross-catalytic reaction network, thus providing an access to its quantitative prediction and rationalization. In particular, we were able to explain why the autocatalysis is still possible for doubly protected probes, even in the absence of instability of the monoprotected intermediate.
Results and discussion
Characterization of the single-protected probe P2
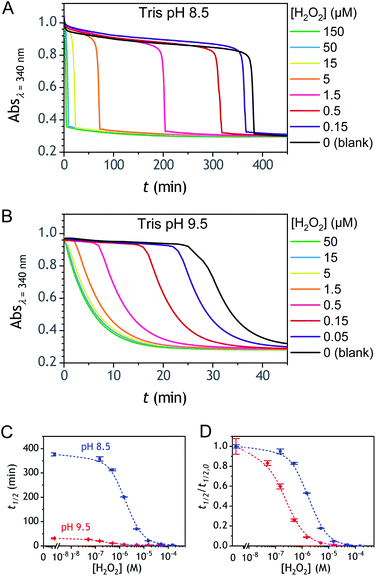
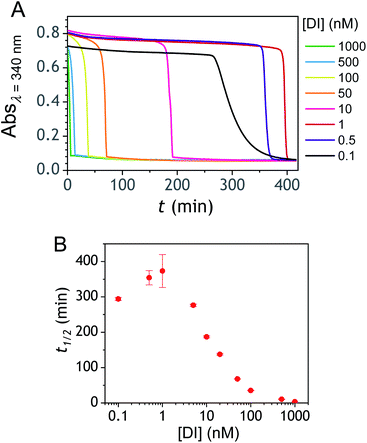
The ability to induce an autocatalytic reaction by mixing P2, H2O2 and a reducing agent has been investigated in a Tris buffer at pH 8.5. As a reductant, we used the same enzyme/reducing substrate as previously, i.e. the diaphorase/NADH couple.34 The diaphorase (DI) from Bacillus stearothermophilus (EC 1.6.99.-) is a thermostable flavin mononucleotide-dependent oxidoreductase that efficiently catalyses the obligatory two-electron reduction of naphthoquinones into naphthohydroquinones in the pH range 7 to 10.42 It is also insensitive to O2 and its NADH substrate is quite stable in slightly basic aerated buffers43 (showing almost no cross-reactivity with dissolved dioxygen unless either O2 or NADH is activated44). The time course of the autocatalytic reaction was monitored by UV-visible spectrophotometry at λ = 340 nm, a wavelength characteristic of the transformation of NADH into NAD+. A spectrophotometric microplate reader for high-throughput kinetic analysis was used to simultaneously monitor a set of different reaction mixtures (200 µL working solution per microwell). During the whole reaction, the microplate was left open to the atmosphere so as to operate under an approximately constant O2 concentration.Kinetic traces recorded at different H2O2 concentrations are shown in Fig. 1A. Their particularly steep sigmoidal shape is characteristic of an efficient autocatalytic process, for which the lag phase that precedes the exponential decrease of absorbance is a function of the triggering H2O2 concentration. Indeed, it is observed that the lower the starting H2O2 concentration, the longer the lag phase. It is also important to note the S-shaped kinetic curve obtained in the absence of H2O2 (blank) attests to a nonspecific autocatalysis triggered by undesirable reactions (the latter initiating the production of either H2O2 or Q/QH2 to eventually lead to the exponential and full consumption of NADH). The time-to-threshold values (i.e., t1/2 defined here as the time required to reach 50% of the maximal absorbance change) extracted from these kinetic traces were used to plot, on a semi-logarithmic scale, the H2O2 calibration curve reported in Fig. 1B. The fact that this calibration plot shows a quasilinear relationship between t1/2 and log[H2O2] over nearly two order of magnitude (i.e., from 0.5 to 20 µM H2O2) confirms the autocatalytic nature of the reaction. The deviation from linearity observed at the lowest concentrations (with a tendency to merge progressively with the t1/2 value determined in the absence of H2O2) illustrates the limitation imposed by the nonspecific response on the analytical performances,36 leading here to a LoD of only 0.2 µM H2O2, a value which is finally not much different from that we had previously obtained with the self-immolating probe P1 under similar experimental conditions.34 Nevertheless, the kinetics with P2 are much faster than previously (by a factor 6), which is clearly an advantage to shorten the analysis time. The influence of pH was investigated by repeating the same experiments at two slightly less basic pHs (i.e., pH 8 and pH 7.5). The resulting plots in Fig. S1† show a shift in the kinetic traces to longer times along with a reduction in the slope of the sigmoid as the pH decreases, a behaviour consistent with slower autoxidation and deprotection rates at lower pHs.34 Unfortunately, no gain in LoD was obtained, suggesting a relatively similar pH dependence of both probe reactivity and stability.36
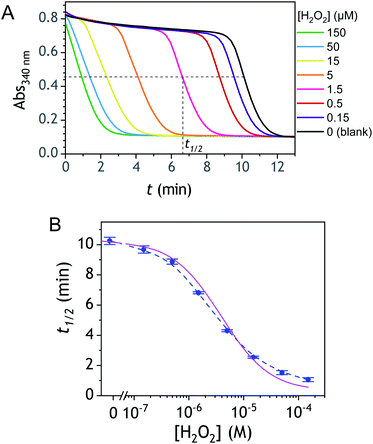 | ||
| Fig. 1 (A) UV-vis kinetic traces monitored at 340 nm in a 96-wells microtiter plate during the reaction generated from the mixing of different concentrations of H2O2 (see the caption on the graph) to solutions containing 50 µM P2, 10 nM DI and 250 µM NADH. All experiments were conducted in an air-saturated Tris buffer (0.1 M, pH 8.5) containing 10 µM EDTA. Each curve is the average of triplicate experiments. (B) Semi-logarithmic calibration curve obtained from the threshold times (t1/2) recovered from the crossing of the horizontal dashed line in A to the kinetic traces (t1/2 is defined here as the time for which the absorbance is decreased approximatively half to the maximal absorbance change). Errors bars are standard deviations from triplicates. The magenta solid line is the theoretical plot obtained by simulation (see text and ESI† for details). | ||
To understand why this new probe results in such a fast autocatalysis and also in this unexpectedly large nonspecific response, we have examined the fate of the probe alone in a Tris buffer (pH 8.5) and its reactivity towards H2O2. The rather fast evolution of the UV-vis spectrum of a dilute solution of P2 (50 µM) over 20 minutes (graph A in Fig. S2†) indicates the relatively poor stability of P2 in the aqueous buffer. Moreover, the lack of isobestic point reveals the probe degradation into several byproducts. Their structural identity was determined from analyses by HPLC and comparison of the UV-visible spectra of degraded probe with reference spectra of different byproduct candidates (see Fig. S2–S4 and ESI† for details). Independently of the naphthol boronic acid derivative generated from fast hydrolysis of the pinacol group, two byproducts were found, i.e. the 1-naphthol and 1,4-NQ (according to HPLC analysis, in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
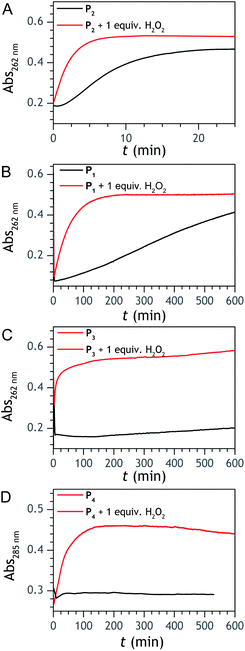
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio in the fully degraded probe solution). The formation of 1-naphthol is the consequence of the slow first-order protodeboronation of P2, a well-established reaction for aromatic boronates in aqueous media,45,46 while the formation of 1,4-NQ was attributed to the slow oxidation of C–B bond by dissolved O2 (indeed, under argon, we observed that P2 and its hydrolysed homologue only degrade into 1-naphthol – see Fig. S3†). Since the mechanism of this slow probe autoxidation is unknown, we have at first assumed it can be assimilated to a bimolecular reaction between P2 and O2, leading to H2O2 and 1,4-NQH2. Even if slow, this probe autoxidation is clearly a major issue because, unlike protodeboronation which leads to a dead-end product, it triggers the catalytic degradation of P2via the production of 1,4-NQH2 and regeneration of H2O2, which in turns further deprotects P2 until the latter is fully converted (Scheme 2). This undesirable reaction finally ends up in an important nonspecific response in the absence of H2O2, which is of course detrimental to the analytical performances. Owing to the pinacol hydrolysis occurring together with the other two nonspecific competitive reactions, it was tricky to access the individual kinetics of these reactions. For the sake of simplicity, we have assumed that the 3 rate constants characterizing the probe protodeboronation (kp), autoxidation (kn), and H2O2 deprotection (kd) are almost the same either P2 is with or without its pinacol group. To determine these rates constants, we relied on a UV-vis absorbance measurement at 262 nm, a wavelength selective of the 1,4-NQ.34 The kinetic traces in Fig. 2A and S5† were obtained either in the absence or presence of different H2O2 concentrations. Without H2O2, the change in absorbance is characterized by a small induction period followed by a nonlinear increase until it asymptotically reaches a constant value after more than 20 min. This increase in absorbance indirectly measures the autoxidation rate of P2 through the nonspecific catalytic formation of 1,4-NQ, from which we can estimate kn. In the presence of H2O2, the increase in absorbance starts sooner (and without delay) and faster as the H2O2 concentration is higher (Fig. S5†). Furthermore, with the increase of [H2O2], the maximum absorbance converges progressively towards a same maximal value, indicating complete probe transformation into 1,4-NQ. For the lowest and intermediate concentrations, the fact that the absorbance levels off at lower values suggests that a non-negligible fraction of the probe converts into another compound, not detectable at this wavelength, which we attributed to 1-naphthol. The fast kinetics recorded in the presence of H2O2 demonstrate the fast H2O2-mediated deprotection of P2, clearly much faster than previously reported for the self-immolative probe P1 (the kinetic traces of which are reminded in Fig. 2B for comparison). The trade-off is that the nonspecific self-deprotection of P2 is also faster than P1, therefore explaining the unsatisfactory detection limit of H2O2.
3 ratio in the fully degraded probe solution). The formation of 1-naphthol is the consequence of the slow first-order protodeboronation of P2, a well-established reaction for aromatic boronates in aqueous media,45,46 while the formation of 1,4-NQ was attributed to the slow oxidation of C–B bond by dissolved O2 (indeed, under argon, we observed that P2 and its hydrolysed homologue only degrade into 1-naphthol – see Fig. S3†). Since the mechanism of this slow probe autoxidation is unknown, we have at first assumed it can be assimilated to a bimolecular reaction between P2 and O2, leading to H2O2 and 1,4-NQH2. Even if slow, this probe autoxidation is clearly a major issue because, unlike protodeboronation which leads to a dead-end product, it triggers the catalytic degradation of P2via the production of 1,4-NQH2 and regeneration of H2O2, which in turns further deprotects P2 until the latter is fully converted (Scheme 2). This undesirable reaction finally ends up in an important nonspecific response in the absence of H2O2, which is of course detrimental to the analytical performances. Owing to the pinacol hydrolysis occurring together with the other two nonspecific competitive reactions, it was tricky to access the individual kinetics of these reactions. For the sake of simplicity, we have assumed that the 3 rate constants characterizing the probe protodeboronation (kp), autoxidation (kn), and H2O2 deprotection (kd) are almost the same either P2 is with or without its pinacol group. To determine these rates constants, we relied on a UV-vis absorbance measurement at 262 nm, a wavelength selective of the 1,4-NQ.34 The kinetic traces in Fig. 2A and S5† were obtained either in the absence or presence of different H2O2 concentrations. Without H2O2, the change in absorbance is characterized by a small induction period followed by a nonlinear increase until it asymptotically reaches a constant value after more than 20 min. This increase in absorbance indirectly measures the autoxidation rate of P2 through the nonspecific catalytic formation of 1,4-NQ, from which we can estimate kn. In the presence of H2O2, the increase in absorbance starts sooner (and without delay) and faster as the H2O2 concentration is higher (Fig. S5†). Furthermore, with the increase of [H2O2], the maximum absorbance converges progressively towards a same maximal value, indicating complete probe transformation into 1,4-NQ. For the lowest and intermediate concentrations, the fact that the absorbance levels off at lower values suggests that a non-negligible fraction of the probe converts into another compound, not detectable at this wavelength, which we attributed to 1-naphthol. The fast kinetics recorded in the presence of H2O2 demonstrate the fast H2O2-mediated deprotection of P2, clearly much faster than previously reported for the self-immolative probe P1 (the kinetic traces of which are reminded in Fig. 2B for comparison). The trade-off is that the nonspecific self-deprotection of P2 is also faster than P1, therefore explaining the unsatisfactory detection limit of H2O2.
Assuming that the probe has similar reactivity, whether it is hydrolysed or not, and the set of reaction in Scheme 2 is adequate to account for the different pathways of P2 transformation, one can expect to reproduce by simulation the experimental curves in Fig. 2A and S5.† For such purpose, we have considered for the 1,4-NQ autoxidation the same global apparent bimolecular rate constant (kox) than the one we had previously electrochemically determined (i.e., 3300 M−1 s−1),34 a value high enough for the autoxidation of 1,4-NQH2 to not be rate limiting. From iterative adjustment of the three other rate constants, i.e. kd, kn and kp, and assuming [O2] constant, it was possible to reproduce quite well the experimental kinetic traces in Fig. S5† using the following set of values: kd = 300 M−1 s−1, kn = 1.2 M−1 s−1, and kp = 4 × 10−4 s−1. The extracted kd indicates a rather fast H2O2 deprotection, much faster than that previously determined for the arylboronate P1 probe in a same Tris buffer (∼5 M−1 s−1).34 To our knowledge this is even the highest rate constant so far reported for an aromatic boronate compound (at neutral or slightly basic pHs, H2O2-mediated deprotection rate constants of arylboronates generally range from 0.07 to 4 M−1 s−1 (ref. 45 and 47–51)). We attribute this to the presence of the hydroxy group in para position of the naphthylboronate, whose effect is to destabilize the C–B bond by inductive and/or mesomeric effects. This is supported by the much lower kd value we separately determined for the 1-naphtylboronate in the same Tris buffer (i.e., 7.5 M−1 s−1). The protodeboronation rate is also significantly higher (by ca. one order of magnitude) than previously reported for arylboronic acids,45 a behaviour we also attribute to the same electronic effects.
Investigation of the double-protected probe P3
To address the instability issue of the single-protected probe P2, we hypothesized that double substitution of the –OH groups of 1,4-NQH2 by boronates could make the probe more stable. Therefore, the probe P3 was synthesized and then tested for its long-term stability in the Tris buffer. The data in Fig. 2C show the absorbance of a dilute P3 solution (recorded at 262 nm, for an overview of the full spectrum see Fig. S6†), which after a rapid decrease during the first few minutes (ensuing from the hydrolysis of pinacols), stabilizes at ∼0.17 over several hours. This result clearly demonstrates the high chemical stability of P3, which once hydrolysed into diboronic acid does no longer decomposes into 1,4-NQ, therefore validating our initial hypothesis. This much higher chemical stability also correlates with a slower protodeboronation rate since the kinetic trace recorded at 290 nm (specific to the probe absorbance) is also very stable over several hours (see Fig. S7†). Adding one equivalent of H2O2 to the solution results in a fast absorbance increase at 262 nm, rising to a maximal value in less than 5 min (red plot in Fig. 2C). It thus attests to an efficient H2O2-mediated deprotection of P3 into 1,4-NQ and so to a high responsiveness of the doubly protected probe to H2O2. In order to determine the deprotection rate of P3, we repeated the experiment at different H2O2 concentrations (Fig. S8†). As expected, the kinetics show a faster increase in absorbance as the H2O2 concentration is higher. However, unlike P2 the maximal absorbance change scales with the stoichiometry of H2O2 (see ESI and Fig. S8† for details), which means that for each substoichiometric H2O2 concentration added to the solution of P3, only the corresponding substoichiometric equivalent in [1,4-NQ] can be recovered. This distinct behaviour of P3 can be explained from the need to provide two equivalents of H2O2 for full deprotection of one equivalent, but also from the ability to regenerate an additional equivalent of H2O2 from each released molecule of 1,4-NQH2. This also points out that the autoxidation of 1,4-NQH2 is an efficient process for producing H2O2 at a yield close to 100% (a result which agrees with what was previously reported for the autoxidation of 1,4-NQ52). The experimental kinetics reported in Fig. S8† should therefore fulfil the mechanism presented by reactions (S5) to (S9) in ESI,† wherein P3 is first converted into the monoprotected intermediate P2 and then into 1,4-NQ according to the same H2O2-mediated catalytic transformation described above for P2. This reaction scheme is therefore characterized by two deprotection rate constants, namely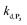 and
and 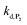 . The value of
. The value of 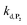 can be considered the same than the one determined above from P2, a consideration which remains also valid for all the other rate constants, the only new rate being
can be considered the same than the one determined above from P2, a consideration which remains also valid for all the other rate constants, the only new rate being 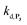 . We have thus numerically simulated the set of reactions (S5) to (S9)† using the value
. We have thus numerically simulated the set of reactions (S5) to (S9)† using the value 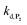 , kox, kn and kp previously recovered from P2 and iteratively adjusted the rate constant
, kox, kn and kp previously recovered from P2 and iteratively adjusted the rate constant 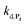 . The best fits of the simulated curves to the experimental data are shown in Fig. S8† (dashed plots in graph D) using
. The best fits of the simulated curves to the experimental data are shown in Fig. S8† (dashed plots in graph D) using 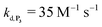 . Despite all of our attempts, it was not possible to perfectly fit the data, the simulated plots showing a systematic slower increase of 1,4-NQ with time whatever
. Despite all of our attempts, it was not possible to perfectly fit the data, the simulated plots showing a systematic slower increase of 1,4-NQ with time whatever 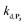 . In fact, much better fits were obtained by artificially considering the second deprotection rate fast enough
. In fact, much better fits were obtained by artificially considering the second deprotection rate fast enough 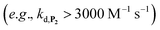 to no longer interfere on the kinetics (solid plots in graph D of Fig. S8†). This apparent inconsistency suggests that in parallel to the H2O2 deprotection of the intermediate P2, additional fast reactions contribute to an accelerated deprotection of P2. We emitted the hypothesis that it could be due to the autoxidation of P2 (reaction (S8)†), which instead of a two-electron transfer reaction, as we have at first assumed, occurs through a one-electron transfer between O2 and P2 with the concomitant production of radical species (notably
to no longer interfere on the kinetics (solid plots in graph D of Fig. S8†). This apparent inconsistency suggests that in parallel to the H2O2 deprotection of the intermediate P2, additional fast reactions contribute to an accelerated deprotection of P2. We emitted the hypothesis that it could be due to the autoxidation of P2 (reaction (S8)†), which instead of a two-electron transfer reaction, as we have at first assumed, occurs through a one-electron transfer between O2 and P2 with the concomitant production of radical species (notably 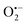 , which by dismutation can produce H2O2 for additional deprotection of both P3 and intermediate P2). One can then conceive that these radical species can either directly or indirectly further contribute to the accelerated deprotection of the intermediate P2. We will come back later on this specific point. It is to note that the value of
, which by dismutation can produce H2O2 for additional deprotection of both P3 and intermediate P2). One can then conceive that these radical species can either directly or indirectly further contribute to the accelerated deprotection of the intermediate P2. We will come back later on this specific point. It is to note that the value of 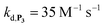 recovered from the best fits, even if lower than
recovered from the best fits, even if lower than 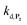 , remains high and attractive for an efficient autocatalysis.
, remains high and attractive for an efficient autocatalysis.
Autocatalysis with P3
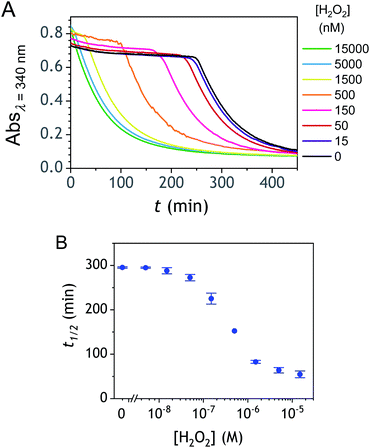
The autocatalysis with P3 was performed under the same conditions than P2. The resulting kinetics curves (see Fig. 3A) characterizing the NADH consumption as a function of time, show, similarly to P2, well-defined S-shaped kinetics traces with longer lags as the triggering H2O2 concentration is lower. However, a main difference with P2 is the much slower kinetics, requiring for the lowest concentrations more than 5 h to reach t1/2, while it takes less than 10 min with P2. Such a huge difference can be understood from the slower deprotection rate of P3 with respect to P2, as well as from the need of two equivalents of H2O2 to fully deprotect each P3 molecule. The analytical performances grasped from the semi-logarithmic calibration plot in Fig. 3C indicate a dynamic concentration range over more than two decades (i.e., from 0.1 to 20 µM H2O2) and a LoD of 0.2 µM H2O2. These analytical performances are not as good as expected, leading to a LoD similar to that of P2, which is surprising if we consider the much higher chemical stability of P3. In order to improve the reaction rate and at the same time the analytical performances, we reproduced the autocatalysis at a slightly more basic pH (pH 9.5). The resulting autocatalytic responses in Fig. 3B show a clear kinetic gain, reducing the t1/2 values to a time window < 40 min. Compared to the results obtained at pH 8.5, this corresponds to an analysis time improvement by a factor 10. Moreover, the extracted H2O2 calibration curve (Fig. 3C) demonstrates a better LoD of ∼20 nM, which is again a 10-fold improvement compared to pH 8.5 (Fig. 3D). Clearly, the pH has a strong impact on the analytical performances of the system, since by changing the pH of one unit, both LoD and analysis time are improved 10-fold. All these results led us to investigate what could lead to such a drastic pH effect, but also how to interpret the large rate difference between P3 and P2. To this end, we examined the possibility to simulate the autocatalytic kinetic traces on the basis of a reasonable set of reactions for describing the cross coupling between the H2O2-mediated catalytic deprotection of P3 (loop 1) and the enzyme-assisted redox cycling (loop 2) (see thereafter).Mechanistic and kinetics analysis of the autocatalytic process
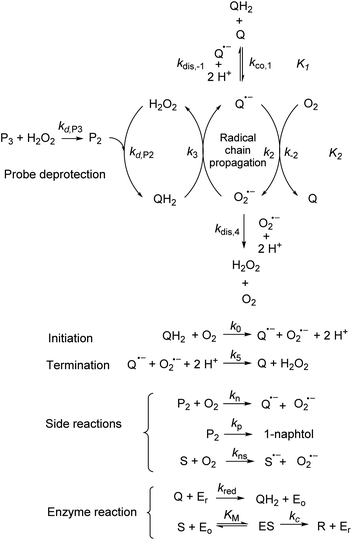
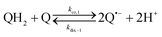
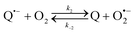
The catalysed reduction of quinones by DI is a well-established “ping-pong” mechanism,42 which under turnover conditions can be defined by two half enzyme reactions (and three rate constants), i.e. (i) a two-step Michaelis–Menten type reaction between NADH and the oxidized form of the enzyme (characterized thus by a Michaelis–Menten constant KM and a catalytic turnover rate constant kc) and (ii) a bimolecular reaction characterizing the obligatory two-electron transfer reduction of quinones (here the 1,4-NQ) by the reduced form of the enzyme (governed thus by a second-order rate constant kred). The coupling of this enzymatic “ping-pong” mechanism to the H2O2-mediated deprotection of P3 leads to the autocatalytic set of reactions (S10) to (S16) in ESI.† To simulate this mechanism, we first used for loop 2 the values of KM, kc and kred (i.e., 60 µM, 1200 s−1, 1.5 × 109 M−1 s−1, respectively) previously determined by us for an analogue of the 1,4-NQ, i.e. the menadione,42 while the other rate constants associated to loop 1 were the same as those above determined (for clarity, the list of rate constants are gathered in the entry 1 of Table 1). The simulated time course of NADH consumption at different H2O2 concentrations are shown in Fig. S9.† Their sigmoidal shapes are, as expected, in agreement with an autocatalytic reaction and also similar with those obtained experimentally (Fig. 3A). However, a main issue is that their t1/2 do not match those obtained experimentally, differing by a factor as high as 28. This result indicates that something is missing in the proposed mechanism. We figured out that it might be due to our oversimplified description of the autoxidation of 1,4-NQ. It is well established that the autoxidation mechanism of hydroquinones is more complex than a simple bimolecular reaction. It is indeed an autoinductive radical chain mechanism, in which the semiquinone (Q˙−) and anion superoxide are involved as chain propagating species as follows:52–54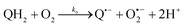 | (1) |
 | (2) |
 | (3) |
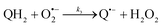 | (4) |
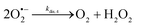 | (5) |
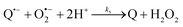 | (6) |
| Simulation entrya | |||||||
|---|---|---|---|---|---|---|---|
| Rate constant | 1 | 2 | 3 | 4 | 5 | 6 | |
| a Are highlighted in bold the change made when going step-by-step from the first simulation entry to the last one. | |||||||
| Probe deprotection reactions |
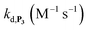
|
35 | 35 | 35 | 35 | 35 | — |
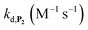
|
300 | 300 | 300 | 300 | 300 | 300 | |
| Side reactions | k n (M−1 s−1) | 1.2 | 1.2 | 0.0 | 0.0 | 0.0 | 0.25 |
| k p (s−1) | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.0004 | |
| k ns (M−1 s−1) | — | 10 −4 | 2.75 × 10 −3 | 4.1 × 10 −3 | 4.1 × 10−3 | 4.1 × 10−3 | |
| Enzyme reactions | K M (µM) | 60 | 60 | 60 | 60 | 60 | 60 |
| k c (s−1) | 1200 | 1200 | 1200 | 1200 | 1200 | 1200 | |
| k red (M−1 s−1) | 1.5 × 109 | 1.5 × 109 | 1.5 × 109 | 10 8 | 108 | 108 | |
| 1,4-NQH2 autoxidation reactions | k ox (M−1 s−1) | 3300 | — | — | — | — | — |
| k 0 (M−1 s−1) | — | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | |
| k co,1, kdis,−1 (M−1 s−1) | — |
66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 000; 10
8 000; 10
8
|
66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000; 108 000; 108 |
66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000; 108 000; 108 |
6.6 × 10 6 ; 108 | 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000; 108 000; 108 |
|
| k 2, k−2 (M−1 s−1) | — | 4.4 × 10 7 ; 2 × 10 8 | 4.4 × 107; 2 × 108 | 4.4 × 107; 2 × 108 | 4.4 × 107; 2 × 108 | 4.4 × 107; 2 × 108 | |
| k 3 (M−1 s−1) | — | 8 × 10 4 | 8 × 104 | 5 × 10 4 | 4.7 × 10 6 | 5 × 104 | |
| k 4 (M−1 s−1) | — | 2 × 10 4 | 2 × 104 | 2 × 104 | 2 × 104 | 2 × 104 | |
| k 5 (M−1 s−1) | — | 2 × 10 9 | 2 × 109 | 2 × 109 | 2 × 109 | 2 × 109 | |
This chain reaction is initiated by reaction (1), which is however considered to be very slow under near neutral conditions due to its spin-forbidden nature.55 However, once a small amount of Q˙− is produced, it is able to trigger a cascade of faster reactions, notably reactions (2), (3) and (6) (forming a set of propagation reactions), which results in an autoinductive acceleration of the oxidation of 1,4-NQ by O2. Through this reaction network, QH2 and O2 are consumed by reactions (2), (4) and (3), respectively, while Q is produced in oxidation reactions (3) and (6). This reaction scheme predicts a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry for the autoxidation of QH2, leading thus to a 1
1 stoichiometry for the autoxidation of QH2, leading thus to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 production of Q and H2O2. The rate acceleration of this mechanism originates from the product Q, which is the catalyst of its own formation through the comproportionation reaction (2). The majority of these reactions are pH-dependent but, for sake of simplicity, the rate constants used in this work are those at an effective pH (here pH 8.5). The rate constant values we have used are gathered in Table 1. Most of them were retrieved from the literature. A few were corrected for pH, while others were adjusted to fit the experimental data (see ESI† for a detailed description of the rate constant selection).
1 production of Q and H2O2. The rate acceleration of this mechanism originates from the product Q, which is the catalyst of its own formation through the comproportionation reaction (2). The majority of these reactions are pH-dependent but, for sake of simplicity, the rate constants used in this work are those at an effective pH (here pH 8.5). The rate constant values we have used are gathered in Table 1. Most of them were retrieved from the literature. A few were corrected for pH, while others were adjusted to fit the experimental data (see ESI† for a detailed description of the rate constant selection).
Incorporating the above autoxidation mechanism of 1,4-NQH2 to the coupled enzymatic reduction of 1,4-NQ and H2O2-mediated deprotection of P3 leads to the autocatalytic set depicted in Scheme 3. Furthermore, since P3 is very stable and therefore unlikely to be the source of the nonspecific triggering of autocatalysis, the alternative is to consider it originates from the slow autoxidation of NADH (characterized by the rate kns). In our model, this nonspecific reaction was assumed to be a one-electron transfer process, leading to the release of 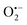 and NAD˙ (defined as S˙− in Scheme 3). Moreover, as we will see later, this reaction is apparently catalysed by DI (NADPH oxidase-like activity), which leads to a dependence of the nonspecific response on the enzyme concentration. Since there is no available information on the autoxidation kinetics of NADH in the literature (either it is catalysed or not by DI), the value of kns in our simulations was simply adjusted so that the simulated nonspecific autocatalytic response aligns with the experimental one. In this model, we also substituted the two-electron autoxidation of the intermediate P2 by a one-electron transfer reaction so as to better reflect the radical chain reaction we suspect coupled to this reaction. The S-shaped kinetic curves numerically calculated using the model in Scheme 3 and the associated rate constants gathered in entry 2 of Table 1 are shown in Fig. S9,† while the theoretical H2O2 calibration curve derived from these plots is given in Fig. 4 (green line). Compared to the previous simulations involving just a simple second order reaction between 1,4-NQH2 and O2, the new computed kinetics traces are now much closer to the experimental ones, a results which highlights the importance to consider the overall complexity of 1,4-NQH2 autoxidation. Interestingly, the discrepancy we observe between simulations and experiments is clearly on the side of the lowest H2O2 concentrations (Fig. 4), since at the highest concentrations the theoretical plot fits the experimental data almost perfectly. We suspected that this could be related to an inhibition of the autoxidation of P2 intermediate induced by the presence of the reducing enzyme/NADH substrate. As we have already mentioned, the autoxidation reaction mechanism of P2 could well be of a radical nature accompanied by a chain process. If we assume that this is the case, then one can consider that such a radical chain reaction is promoted under oxidizing conditions and inhibited under reducing conditions. To evaluate such an effect on the autocatalysis via simulation, we disabled in our model the autoxidation reaction of the monoboronic intermediate by setting its kn value to zero. Thanks to this, we were able to obtain the magenta simulated plot in Fig. 4, which now predicts the experimental data much more closely. This finding tends to support the hypothesis that the slow self-deprotection of P2 by O2 occurs through a one-electron transfer reaction with concomitant formation of radical species (possibly
and NAD˙ (defined as S˙− in Scheme 3). Moreover, as we will see later, this reaction is apparently catalysed by DI (NADPH oxidase-like activity), which leads to a dependence of the nonspecific response on the enzyme concentration. Since there is no available information on the autoxidation kinetics of NADH in the literature (either it is catalysed or not by DI), the value of kns in our simulations was simply adjusted so that the simulated nonspecific autocatalytic response aligns with the experimental one. In this model, we also substituted the two-electron autoxidation of the intermediate P2 by a one-electron transfer reaction so as to better reflect the radical chain reaction we suspect coupled to this reaction. The S-shaped kinetic curves numerically calculated using the model in Scheme 3 and the associated rate constants gathered in entry 2 of Table 1 are shown in Fig. S9,† while the theoretical H2O2 calibration curve derived from these plots is given in Fig. 4 (green line). Compared to the previous simulations involving just a simple second order reaction between 1,4-NQH2 and O2, the new computed kinetics traces are now much closer to the experimental ones, a results which highlights the importance to consider the overall complexity of 1,4-NQH2 autoxidation. Interestingly, the discrepancy we observe between simulations and experiments is clearly on the side of the lowest H2O2 concentrations (Fig. 4), since at the highest concentrations the theoretical plot fits the experimental data almost perfectly. We suspected that this could be related to an inhibition of the autoxidation of P2 intermediate induced by the presence of the reducing enzyme/NADH substrate. As we have already mentioned, the autoxidation reaction mechanism of P2 could well be of a radical nature accompanied by a chain process. If we assume that this is the case, then one can consider that such a radical chain reaction is promoted under oxidizing conditions and inhibited under reducing conditions. To evaluate such an effect on the autocatalysis via simulation, we disabled in our model the autoxidation reaction of the monoboronic intermediate by setting its kn value to zero. Thanks to this, we were able to obtain the magenta simulated plot in Fig. 4, which now predicts the experimental data much more closely. This finding tends to support the hypothesis that the slow self-deprotection of P2 by O2 occurs through a one-electron transfer reaction with concomitant formation of radical species (possibly 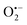 and a naphthoxyl radical), which are then inhibited or scavenged under the reducing conditions (NADH has been shown to efficiently scavenge either
and a naphthoxyl radical), which are then inhibited or scavenged under the reducing conditions (NADH has been shown to efficiently scavenge either 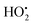 ,56 or phenoxyl radicals57 by one-electron reduction). This also demonstrates that the double masking does not prevent the autocatalytic reaction from working, even when the instability of the monoprotected intermediate is switched-off (i.e. when kn = 0). Indeed, when kn = 0, the autocatalysis still occurs with a reasonable efficiency (magenta curves in Fig. 4) because, statistically, the probability of having a double-deprotection of the probe is not null, even under the substoichiometric H2O2 conditions used here. In fact, this probability depends directly on the ratio between the first and the second deprotection rate constants
,56 or phenoxyl radicals57 by one-electron reduction). This also demonstrates that the double masking does not prevent the autocatalytic reaction from working, even when the instability of the monoprotected intermediate is switched-off (i.e. when kn = 0). Indeed, when kn = 0, the autocatalysis still occurs with a reasonable efficiency (magenta curves in Fig. 4) because, statistically, the probability of having a double-deprotection of the probe is not null, even under the substoichiometric H2O2 conditions used here. In fact, this probability depends directly on the ratio between the first and the second deprotection rate constants 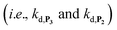 , which is more favourable when the first one is slower than the second, as it is the case here (i.e., 35 vs. 300 M−1 s−1, respectively).
, which is more favourable when the first one is slower than the second, as it is the case here (i.e., 35 vs. 300 M−1 s−1, respectively).
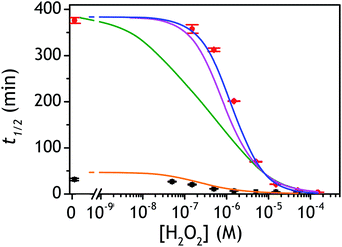 | ||
| Fig. 4 Plots of the experimental and theoretical semi-logarithmic H2O2 calibration curves. The red and black dots are the experimental data recovered for P3 at pH 8.5 and 9.5 respectively (same data than in Fig. 3C and D), while the solid lines are the theoretical plots predicted from numerical simulations of the autocatalytic set presented in Scheme 3. The parameters used for each simulated plots are those reported in Table 1 according to the following code color: (green) entry 2, (magenta) entry 3, (blue) entry 4, and (orange) entry 5. | ||
As the magenta simulated plot in Fig. 4 still does not completely superimpose to the data, we considered that it could be due to the uncertainty in the selected values of k3 and kred (the latter being moreover recovered from a previous enzymatic study performed with menadione but not with the 1,4-NQ). To experimentally access the value of these two rate constants, we have performed redox cycling experiments (loop 2) by mixing a fixed concentration of DI (10 nM) and NADH (250 µM) with different concentrations of 1,4-NQ and then monitoring the NADH absorbance decay (see graph A in Fig. S10†). From the results reported in Fig. S10 and analysed in details in ESI,† we were able to estimate the values of k3 = (5–8) × 104 M−1 s−1 and kred = (1.5–0.8) × 108 M−1 s−1 with a reasonably good degree of confidence. We thus considered these new values in our simulations and we succeeded to obtain an almost perfect agreement between the simulated calibration plot and the experimental data using kred = 108 M−1 s−1 and k3 = 5 × 104 M−1 s−1 (blue curve in Fig. 4). This latter result definitely validates the model in Scheme 3 as well as the selected set of rate constants.
With this tool in hand, it was next interesting to go back to the data with P2 in order to see to what extent the autocatalytic kinetic traces in Fig. 1 can be predicted by the model in Scheme 3 and the associated rate constants (excluding of course from the model the first deprotection, i.e.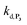 , which does not take place with P2). The best-simulated curves are reported in Fig. S12† using the rate constants gathered in the entry 6 of Table 1. To obtain such a good fit, it was necessary to adjust the rate constant kn to a non-null value, which is not surprising as for simulating the nonspecific autocatalytic response of P2, it is now necessary to consider the probe autoxidation as the main source of nonspecificity (thus controlled by kn) and no longer the NADH autoxidation (kns). A kn of 0.25 M−1 s−1 was thus set from the alignment of the simulated nonspecific response to the experimental one. This value is significantly lower than the value of 1.2 M−1 s−1 previously derived from the H2O2-mediated deprotection of P2, therefore confirming that there is an inhibition of the autoxidation of P2 under the reducing conditions of autocatalysis. The theoretical H2O2 calibration plot that was finally extracted from the simulated kinetic traces fits nicely to the experimental calibration plot in Fig. 1B. This is a strong plea for the validity of the proposed model. It also demonstrates the excellent self-consistency of our results. Armed with this knowledge, it was next interesting to identify the key rate constants controlling the rate of autocatalysis but also to determine what limits the analytical performances of the method.
, which does not take place with P2). The best-simulated curves are reported in Fig. S12† using the rate constants gathered in the entry 6 of Table 1. To obtain such a good fit, it was necessary to adjust the rate constant kn to a non-null value, which is not surprising as for simulating the nonspecific autocatalytic response of P2, it is now necessary to consider the probe autoxidation as the main source of nonspecificity (thus controlled by kn) and no longer the NADH autoxidation (kns). A kn of 0.25 M−1 s−1 was thus set from the alignment of the simulated nonspecific response to the experimental one. This value is significantly lower than the value of 1.2 M−1 s−1 previously derived from the H2O2-mediated deprotection of P2, therefore confirming that there is an inhibition of the autoxidation of P2 under the reducing conditions of autocatalysis. The theoretical H2O2 calibration plot that was finally extracted from the simulated kinetic traces fits nicely to the experimental calibration plot in Fig. 1B. This is a strong plea for the validity of the proposed model. It also demonstrates the excellent self-consistency of our results. Armed with this knowledge, it was next interesting to identify the key rate constants controlling the rate of autocatalysis but also to determine what limits the analytical performances of the method.
Rationalization of the effect of pH on the kinetics and LoD
To understand the influence of the pH on the rate of autocatalysis (as illustrated in Fig. 3), one has to start by identifying the rate constants that a priori are the most strongly pH dependent. On account of the two pKas of the 1,4-NQH2 (pKa,1 = 9.48 and pKa,2 = 11.02, see ESI†), the rate constants k0, kco,1 and k3 are clearly much pH sensitive than the other rate constants of the model (since HO2− is the reactive species involved in the oxidative cleavage of boronates,58 the constants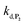 or
or 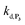 are also pH dependent but to a lesser extent than k0, kco,1 and k3). Therefore, if we consider kco,1 and k3 (k0 is not taken into account for the same reason as previously) are mainly responsible for the pH dependency of the autocatalysis rate, this should be verifiable through the simulation of the H2O2 calibration curve. From the two pKas of the 1,4-NQH2, we can calculate the values of kco,1 and k3 at pH 9.5, which are 6.6 × 106 M−1 s−1 and 4.7 × 106 M−1 s−1, respectively (see ESI†). The theoretical H2O2 calibration curve (orange line in Fig. 4) determined using these new values of kco,1 and k3 (while keeping the other rate constants the same as previously at pH 8.5) finally agrees quite well with the experimental plot at pH 9.5 (black squares in Fig. 4). This result confirms the key role played by both kco,1 and k3 in the pH-rate dependence of the autocatalysis. A better fit to the data would certainly be obtained by increasing slightly the two deprotection rate constants
are also pH dependent but to a lesser extent than k0, kco,1 and k3). Therefore, if we consider kco,1 and k3 (k0 is not taken into account for the same reason as previously) are mainly responsible for the pH dependency of the autocatalysis rate, this should be verifiable through the simulation of the H2O2 calibration curve. From the two pKas of the 1,4-NQH2, we can calculate the values of kco,1 and k3 at pH 9.5, which are 6.6 × 106 M−1 s−1 and 4.7 × 106 M−1 s−1, respectively (see ESI†). The theoretical H2O2 calibration curve (orange line in Fig. 4) determined using these new values of kco,1 and k3 (while keeping the other rate constants the same as previously at pH 8.5) finally agrees quite well with the experimental plot at pH 9.5 (black squares in Fig. 4). This result confirms the key role played by both kco,1 and k3 in the pH-rate dependence of the autocatalysis. A better fit to the data would certainly be obtained by increasing slightly the two deprotection rate constants 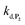 and
and 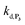 , which, as mentioned above, are also expected to rise with the pH. This kinetic analysis also explains the better detection limit obtained by increasing the pH (Fig. 3D). Indeed, if we admit that the NADH autoxidation (kns) (which determines the nonspecific response of the system and thus the LoD) varies less rapidly with the pH than the overall rate of autocatalysis (varying predominantly with the pH through kco,1 and k3), then we can understand why the LoD is 10-fold improved when the pH is increased from 8.5 to 9.5.
, which, as mentioned above, are also expected to rise with the pH. This kinetic analysis also explains the better detection limit obtained by increasing the pH (Fig. 3D). Indeed, if we admit that the NADH autoxidation (kns) (which determines the nonspecific response of the system and thus the LoD) varies less rapidly with the pH than the overall rate of autocatalysis (varying predominantly with the pH through kco,1 and k3), then we can understand why the LoD is 10-fold improved when the pH is increased from 8.5 to 9.5.
Further improving the analytical performances
To determine whether the analytical performance could be further improved and/or optimized, we performed the autocatalytic reaction in buffers of different nature adjusted at different pHs (it is to note that DI from the Bacillus stearothermophilus has a bell-shaped activity in the pH range 6.5 to 10.5, with an optimum at pH 8.0 (ref. 59)). Among the different organic and inorganic buffers investigated (see ESI and Fig. S13 to S20†), the glycine buffer at pH 10 was found superior. The analytical performances obtained with this buffer were indeed clearly improved (Fig. S18†), leading to a dynamic concentration range over nearly 3 decades (i.e., from ca. 0.01 to 10 µM H2O2) and a LoD as low as 5 nM H2O2 in less than 10 min reaction time. This is a very appealing performance since in terms of LoD, it is competitive with the best H2O2 detection kits currently commercially available (a LoD of 10 nM H2O2 within 30 min incubation time is reported for the popular fluorescent-based Amplex red® hydrogen peroxide/peroxidase assay41). Another buffer particularly attractive is the CAPS buffer at pH 9.5 (Fig. S20†). In spite of a slightly longer reaction time, the data indicates the possibility to reach the nanomolar H2O2 concentration range in less than 50 min. It is to note that with some buffers the autocatalysis was found to be inefficient in producing well-defined or discernible autocatalytic responses. This was especially true with the borate buffer (Fig. S17†). It was also observed in some buffers an anomalous shift of the nonspecific blank response to shorter times compared to the responses recorded at the lowest H2O2 concentrations. All these behaviours suggest that the buffer plays an active role in the autocatalysis that we have not yet been able to elucidate.Another parameter we examined to improve the analytical performances was the concentration of DI. As shown in Fig. 5, the concentration of the reducing enzyme was found to have a considerable impact on the nonspecific autocatalytic response, dramatically accelerating the nonspecific t1/2 value with the rise of DI concentration, an effect which suggests that the enzyme slowly catalyses the reaction between NADH and O2 to produce 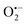 or H2O2. These results echo the residual NADH oxidase activity (<0.01%) reported by the enzyme supplier and which would be related to the presence of traces of NADH oxidase in the purified diaphorase samples. However, another possibility that cannot be ruled out is that DI has an intrinsic residual NADH oxidase activity. Indeed, one can assume that the reaction with O2 is not necessarily inexistent even though this flavoenzyme is known to not accept O2 as an electron acceptor. By gradually decreasing the concentration of DI, we can see in Fig. 5 that the value of t1/2 increases until it reaches a maximum before slightly decreasing at the lowest concentration (graph B in Fig. 5). This indicates that by lowering the concentration of DI, the nonspecific contribution associated to the residual NADH oxidase activity is reduced. This can therefore be exploited to improve the specific vs. nonspecific response, especially if the enzyme reduction rate of the naphthoquinone in loop 2 continues to be not rate limiting. This latter attribute can be easily verified from the S-shape of the autocatalytic response. Indeed, if the kinetic profiles are similar regardless of the enzyme concentration, it suggests that the naphthoquinone reduction is not rate limiting. On the other hand, when the rate of the naphthoquinone reduction becomes too slow, as illustrated for the lowest enzyme concentration (i.e. 0.1 nM in Fig. 5), the kinetic trace presents a more spread-out autocatalytic response, signing thus the slowing down of loop 2. The kinetic gain also observed at the lowest enzyme concentrations can be explained from the redox cycling (loop 2) in Scheme 3, which tends to be inhibited at high DI concentration by forcing the naphthoquinone to be rapidly doubly reduced, thus bypassing the formation of semi-naphthoquinone indispensable to sustain the free radical chain reaction. This inhibitory effect is relaxed when the enzyme concentration becomes sufficiently low, which finally leads to a slightly faster autocatalytic reaction. Considering the importance of the enzyme concentration on the nonspecific response, we reproduced the autocatalysis experiments at pH 8.5 with a DI concentration 100 times lower, i.e. 0.1 nM. The results in Fig. 6 show a significant gain in the H2O2 detection limit, allowing now to detect as low as 15 nM H2O2. Compared to the previous experiments performed at a higher enzyme concentration, this corresponds to a 10-fold gain in LoD (compare Fig. 3 and 6).
or H2O2. These results echo the residual NADH oxidase activity (<0.01%) reported by the enzyme supplier and which would be related to the presence of traces of NADH oxidase in the purified diaphorase samples. However, another possibility that cannot be ruled out is that DI has an intrinsic residual NADH oxidase activity. Indeed, one can assume that the reaction with O2 is not necessarily inexistent even though this flavoenzyme is known to not accept O2 as an electron acceptor. By gradually decreasing the concentration of DI, we can see in Fig. 5 that the value of t1/2 increases until it reaches a maximum before slightly decreasing at the lowest concentration (graph B in Fig. 5). This indicates that by lowering the concentration of DI, the nonspecific contribution associated to the residual NADH oxidase activity is reduced. This can therefore be exploited to improve the specific vs. nonspecific response, especially if the enzyme reduction rate of the naphthoquinone in loop 2 continues to be not rate limiting. This latter attribute can be easily verified from the S-shape of the autocatalytic response. Indeed, if the kinetic profiles are similar regardless of the enzyme concentration, it suggests that the naphthoquinone reduction is not rate limiting. On the other hand, when the rate of the naphthoquinone reduction becomes too slow, as illustrated for the lowest enzyme concentration (i.e. 0.1 nM in Fig. 5), the kinetic trace presents a more spread-out autocatalytic response, signing thus the slowing down of loop 2. The kinetic gain also observed at the lowest enzyme concentrations can be explained from the redox cycling (loop 2) in Scheme 3, which tends to be inhibited at high DI concentration by forcing the naphthoquinone to be rapidly doubly reduced, thus bypassing the formation of semi-naphthoquinone indispensable to sustain the free radical chain reaction. This inhibitory effect is relaxed when the enzyme concentration becomes sufficiently low, which finally leads to a slightly faster autocatalytic reaction. Considering the importance of the enzyme concentration on the nonspecific response, we reproduced the autocatalysis experiments at pH 8.5 with a DI concentration 100 times lower, i.e. 0.1 nM. The results in Fig. 6 show a significant gain in the H2O2 detection limit, allowing now to detect as low as 15 nM H2O2. Compared to the previous experiments performed at a higher enzyme concentration, this corresponds to a 10-fold gain in LoD (compare Fig. 3 and 6).
To illustrate the potential of the method to indirectly detect the activity of an oxidase through its H2O2 production, we performed the quantitative detection of glucose oxidase (GOD) under the experimental conditions used above. Indeed, in the presence of glucose, GOD catalyses the oxidation of glucose into gluconolactone with concomitant production of H2O2 from catalytic reduction of dissolved O2. The results gathered in Fig. S23† demonstrate the feasibility of the approach, allowing indirect quantification of GOD by autocatalytic molecular amplification down to subpicomolar concentrations.
Triggering the autocatalysis with a naphthoquinone
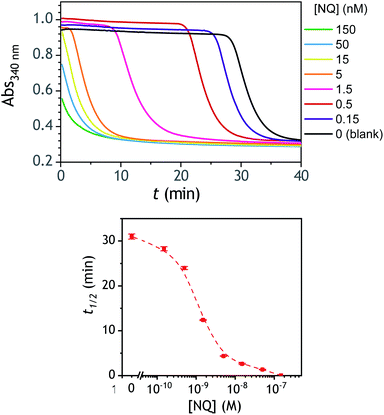
A compelling property of the present cross-catalytic reaction scheme lies in its ability to be triggered not only by H2O2 but also any redox cycling compound (i.e., by definition a redox-active compound able in the presence of O2 and a reducing species to cycle and to generate reactive oxygen species). This makes this approach potentially attractive for the design of new sensitive bioassays.60,61 This can be for instance through the upstream production of a redox cycling compound via an enzyme or an enzymatic label, which can then trigger via one of the above boronic probes an exponential molecular amplification. With the aim to evaluate the ability of P3 to be triggered by low concentrations of a given redox cycling compound, we have investigated the autocatalysis in the presence of different concentrations of 2-amino-3-chloro-1,4-naphthoquinone (from 0.15 nM to 0.15 µM), a compound we had previously identified as an efficient redox cycling compound.34 The results gathered in Fig. 7 demonstrates particularly good analytical performances, allowing to easily detect as low as 150 pM of 2-amino-3-chloro-1,4-NQ in less than 30 min, with a LoD estimated close to 50 pM. As for H2O2, the dynamic range of concentrations is also wide, extending over nearly 3 orders of magnitude. These analytical performances are definitely much better than those obtained with H2O2. This asymmetry in the analytical performances was shown to be an intrinsic property of a cross-catalytic reaction scheme.36 Indeed, if the two catalytic loops have similar rates, the detection efficiency of the catalyst of loop 1 or loop 2 is theoretically the same, thus leading to an identical LoD of each trigger. On the other hand, if the rates of each loop are different, the trigger of the fastest loop becomes the most easily detectable and therefore the one that theoretically leads to the lowest LoD. This is exactly what we observe here with the trigger naphthoquinone, which, due to its involvement in a faster catalytic loop (loop 2) is detected more sensitively than H2O2.Towards an improvement with the design of a diboronate probe able to release a better redox cycler
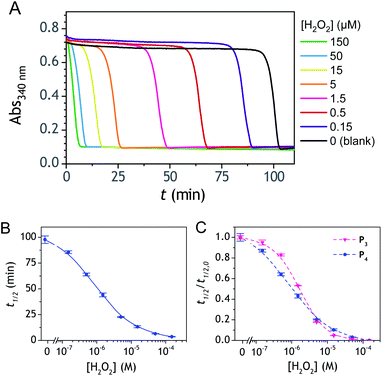
Improvement of the rates associated to each loop of the cross-catalysis reaction is a strategy to shorten the analysis time and to potentially enhance the detection limit by better discriminating the specific from nonspecific responses.36 In the present case, the background amplification stems from the instability associated to loop 2 (i.e., from NADH autoxidation or NADH-oxidase like activity of diaphorase) since the double masking of the probe makes it so stable that no nonspecific response can arise from loop 1. It is therefore particularly relevant to find a strategy that aims at improving the global rate of loop 2. To do so, a relatively straightforward method is to substitute the masked 1,4-NQH2 in P3 by an alternative faster redox cycling naphthohydroquinone. A series of different naphthoquinones were thus screened for their redox cycling properties and then compared to the 1,4-NQ (see ESI and Fig. S21† for details). From this screening, three naphthoquinones were identified as a better redox cycler than the 1,4-NQ, i.e. the 2-amino-3-chloro-1,4-NQ, 1,2-NQ and 2-methoxy-1,4-NQ. The chemical stability of these three naphthoquinones in an aqueous buffered solution was also examined and the most stable was the 2-methoxy-1,4-NQ, showing almost no change in the absorbance spectra after several hours in a Tris buffer (graph C in Fig. S22†). The chemical synthesis of the corresponding diboronic probe P4 was thus planned and successfully achieved (Scheme 1C). The long-term stability of a diluted solution of P4 was shown to be quite good (Fig. S22† and 2D), demonstrating a chemical stability of P4 at least as good as P3. Concerning the H2O2-mediated deprotection of P4 (Fig. 2D), it was found a little slower than P3 (by a factor ∼6). We attribute this slower rate to the methoxy group in ortho position, which by steric effect can slow-down the nucleophilic attack of HO2−.The autocatalytic kinetic traces collected with P4 over ∼90 min at pH 8.5 attest of a rather fast autocatalytic reaction (Fig. 8A), approximately 4-fold faster than P3 at the same pH. This gain in analysis time is clearly the result of the better redox cycling properties of 2-MeO-1,4-NQ as compared to 1,4-NQ, compensating thus for the slower H2O2 deprotection rate. This gain in time also almost completely translates into a gain in LoD since the detection limits for P3 and P4 are 0.2 and 0.06 µM H2O2, respectively (Fig. 8C). The fact that the faster kinetics with P4 results in a better LoD is not surprising because, as we had previously demonstrated from theoretical analysis of a cross-catalytic system,36 reaction time and detection limit are both inversely proportional to the geometric mean of each loop's rate (this corresponds to the limiting case where detection of H2O2 is mainly restricted by the nonspecific response resulting from NADH autoxidation).
Conclusions
Thanks to the simple strategy consisting in the double masking of a naphthohydroquinone with boronate groups, we demonstrated the feasibility to design an efficient and versatile exponential molecular amplification system, well-suited for the sensitive detection of H2O2 down to a few nM in less than 10 minutes or a redox cycling compound such as the 2-amino-3-chloro-1,4-NQ down to 50 pM in less than 30 minutes. These remarkable analytical performances are the best so far reported for an autocatalytic molecular amplification strategy, amounting to a ∼300-fold improvement in LoD compared to H2O2 detection by dendritic chain reaction.21 Such performances are the result of the high chemical stability of the diboronate ester probes (a high stability resulting from the double protection of the probe and a non-utilization of a self-immolating protective group) as well as a particularly good reactivity towards H2O2. Another important result of this work is that it demonstrates the usefulness of deciphering the mechanism and kinetics of complex reaction networks in order to better understand, predict and optimize their functioning. Through this mechanistic study we were able to explain how the pH can play an important role and how, by adjusting it, it is possible to improve significantly the analytical performances thanks to a better discrimination of the specific vs. nonspecific response. It also allowed us to demonstrate that the double masking does not prevent autocatalysis from working despite the fact that two equivalents of H2O2 are needed to completely deprotect the probe. Furthermore, as illustrated with the selection of a better redox cycler for the design of probe P4, it is clear that there is room to further improve the analytical performances of the system.Due to its numerous implications in the field of systems chemistry, the study of complex reaction networks with highly nonlinear dynamics is expected to expand rapidly in the future. Further developments and exploitations in a variety of analytical or bioanalytical applications are also expected, especially considering the versatility and generic character of the present molecular amplification strategy. Finally, we believe that the approach proposed here has also potential for applications in cellular imaging or drug delivery, notably by taking advantage of probes or pro-drugs capable of selectively and autocatalytically delivering the active molecule in vivo.
Data availability
For the numerical simulations of kinetics reported in the manuscript, we have used the software Copasi 4.34 (a freeware simulator for biochemical networks) for which we can provide the Copasi file of parameters.Author contributions
J. P. and C. R. contributed equally to this work.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Agence Nationale de la Recherche (ANR ECOSENS project – ANR-19-CE29-0022-0).References
- S. Goggins and C. G. Frost, Approaches towards molecular amplification for sensing, Analyst, 2016, 141, 3157–3218 RSC.
- P. Scrimin and L. J. Prins, Sensing through signal amplification, Chem. Soc. Rev., 2011, 40, 4488–4505 RSC.
- B. Limoges, D. Marchal, F. Mavré, J.-M. Savéant and B. Schöllhorn, Theory and Practice of Enzyme Bioaffinity Electrodes. Direct Electrochemical Product Detection, J. Am. Chem. Soc., 2008, 130, 7259–7275 CrossRef CAS PubMed.
- E. Engvall, The ELISA, enzyme-linked immunosorbent assay, Clin. Chem., 2010, 56, 319–320 CrossRef CAS PubMed.
- G. N. Konstantinou, Enzyme-Linked Immunosorbent Assay (ELISA), Methods Mol. Biol., 2017, 1592, 79–94 CrossRef CAS PubMed.
- R. Duan, X. Zuo, S. Wang, X. Quan, D. Chen, Z. Chen, L. Jiang, C. Fan and F. Xia, Lab in a Tube: Ultrasensitive Detection of MicroRNAs at the Single-Cell Level and in Breast Cancer Patients Using Quadratic Isothermal Amplification, J. Am. Chem. Soc., 2013, 135, 4604–4607 CrossRef CAS PubMed.
- S. Goggins, B. J. Marsh, A. T. Lubben and C. G. Frost, Signal transduction and amplification through enzyme-triggered ligand release and accelerated catalysis, Chem. Sci., 2015, 6, 4978–4985 RSC.
- Z. Gao, L. Hou, M. Xu and D. Tang, Enhanced colorimetric immunoassay accompanying with enzyme cascade amplification strategy for ultrasensitive detection of low-abundance protein, Sci. Rep., 2014, 4, 3966 CrossRef PubMed.
- T. Zauner, R. Berger-Hoffmann, K. Muller, R. Hoffmann and T. Zuchner, Highly adaptable and sensitive protease assay based on fluorescence resonance energy transfer, Anal. Chem., 2011, 83, 7356–7363 CrossRef CAS PubMed.
- B. Limoges, F. Mavré, D. Marchal and J.-M. Savéant, High Amplification Rates from the Association of Two Enzymes Confined within a Nanometric Layer Immobilized on an Electrode. Modeling and Illustrating Example, J. Am. Chem. Soc., 2006, 128, 6014–6015 CrossRef CAS PubMed.
- E. Valero, R. Varón and F. García-Carmona, Kinetic Analysis of a Model for Double Substrate Cycling: Highly Amplified ADP (and/or ATP) Quantification, Biophys. J., 2004, 86, 3598–3606 CrossRef CAS PubMed.
- A. J. Bisnette and S. P. Fletcher, Mechanisms of Autocatalysis, Angew. Chem., Int. Ed., 2013, 52, 12800–12826 CrossRef PubMed.
- A. I. Hanopolskyi, V. A. Smaliak, A. I. Novichkov and S. N. Semenov, Autocatalysis: Kinetics, Mechanisms and Design, ChemSystemsChem, 2020, 2, e2000026 Search PubMed.
- R. Plasson, A. Brandenburg, L. Jullien and H. Bersini, Autocatalyses, J. Phys. Chem. A, 2011, 115, 8073–8085 CrossRef CAS PubMed.
- J. Wilhelm and A. Pingoud, Real‐Time Polymerase Chain Reaction, ChemBioChem, 2003, 4, 1120–1128 CrossRef CAS PubMed.
- J. V. Ness, L. K. V. Ness and D. J. Galas, Isothermal reactions for the amplification of oligonucleotides, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 4504–4509 CrossRef PubMed.
- G. Urtel, M. Van Der Hofstadt, J.-C. Galas and A. Estevez-Torres, rEXPAR: An Isothermal Amplification Scheme That Is Robust to Autocatalytic Parasites, Biochemistry, 2019, 58, 2675–2681 CrossRef CAS PubMed.
- K. Shi, S. Xie, R. Tian, S. Wang, Q. Lu, D. Gao, C. Lei, H. Zhu and Z. Nie, A CRISPR-Cas autocatalysis-driven feedback amplification network for supersensitive DNA diagnostics, Sci. Adv., 2021, 7, eabc7802 CrossRef CAS PubMed.
- G. Gines, R. Menezes, K. Nara, A.-S. Kirstetter, V. Taly and Y. Rondelez, Isothermal digital detection of microRNAs using background-free molecular circuit, Sci. Adv., 2020, 6, eaay5952 CrossRef CAS PubMed.
- E. Sella and D. Shabat, Dendritic Chain Reaction, J. Am. Chem. Soc., 2009, 131, 9934–9936 CrossRef CAS PubMed.
- M. E. Roth, O. Green, S. Gnaim and D. Shabat, Dendritic, Oligomeric, and Polymeric Self-Immolative Molecular Amplification, Chem. Rev., 2016, 116, 1309–1352 CrossRef CAS PubMed.
- N. Karton-Lifshin and D. Shabat, Exponential diagnostic signal amplification via dendritic chain reaction: the dendritic effect of a self-immolative amplifier component, New J. Chem., 2012, 36, 386–393 RSC.
- E. Sella, A. Lubelski, J. Klafter and D. Shabat, Two-Component Dendritic Chain Reactions: Experiment and Theory, J. Am. Chem. Soc., 2010, 132, 3945–3952 CrossRef CAS PubMed.
- M. S. Baker and S. T. Phillips, A small molecule sensor for fluoride based on an autoinductive, colorimetric signal amplification reaction, Org. Biomol. Chem., 2012, 10, 3595–3599 RSC.
- X. Sun, S. D. Dahlhauser and E. V. Anslyn, New Autoinductive Cascade for the Optical Sensing of Fluoride: Application in the Detection of Phosphoryl Fluoride Nerve Agents, J. Am. Chem. Soc., 2017, 139, 4635–4638 CrossRef CAS PubMed.
- J.-A. Gu, V. Mani and S.-T. Huang, Design and synthesis of ultrasensitive off–on fluoride detecting fluorescence probe via autoinductive signal amplification, Analyst, 2015, 140, 346–352 RSC.
- S. Hisamatsu, S. Suzuki, S. Kohmoto, K. Kishikawa, Y. Yamamoto, R. Motokawa and T. Yaita, A chemiluminescence sensor with signal amplification based on a self-immolative reaction for the detection of fluoride ion at low concentrations, Tetrahedron, 2017, 73, 3993–3998 CrossRef CAS.
- S. N. Semenov, L. J. Kraft, A. Ainla, M. Zhao, M. Baghbanzadeh, V. E. Campbell, K. Kang, J. M. Fox and G. M. Whitesides, Autocatalytic, bistable, oscillatory networks of biologically relevant organic reactions, Nature, 2016, 537, 656–660 CrossRef CAS PubMed.
- X. Sun and E. V. Anslyn, An Auto-Inductive Cascade for the Optical Sensing of Thiols in Aqueous Media: Application in the Detection of a VX Nerve Agent Mimic, Angew. Chem., Int. Ed., 2017, 56, 9522–9526 CrossRef CAS PubMed.
- J. D. Adams, J. J. Røise, D. S. Lee and N. Murthy, The Methionase Chain Reaction: An enzyme-based autocatalytic amplification system for the detection of thiols, Chem. Commun., 2020, 56, 3175–3178 RSC.
- J. P. Goertz and I. M. White, Peroxidyme-Amplified Radical Chain Reaction (PARCR): Visible Detection of a Catalytic Reporter, Angew. Chem., Int. Ed., 2017, 56, 13411–13415 CrossRef CAS PubMed.
- S. Kim, A. M. Dibildox, A. Aguirre-Soto and H. D. Sikes, Exponential Amplification Using Photoredox Autocatalysis, J. Am. Chem. Soc., 2021, 143, 11544–11553 CrossRef CAS PubMed.
- X. Sun, D. Shabat, S. T. Phillips and E. V. Anslyn, Self propagating amplification reactions for molecular detection and signal amplification: Advantages, pitfalls, and challenges, J. Phys. Org. Chem., 2018, e3827 Search PubMed.
- J. Pallu, C. Rabin, G. Creste, M. Branca, F. Mavré and B. Limoges, Exponential molecular amplification by H2O2-mediated autocatalytic deprotection of boronic ester probes to redox cyclers, Chem.–Eur. J., 2019, 25, 7534–7546 CrossRef CAS PubMed.
- P. Hui, M. Branca, B. Limoges and F. Mavré, An autocatalytic organic reaction network based on cross-catalysis, Chem. Commun., 2021, 57, 11374–11377 RSC.
- M. Branca, C. Calvet, B. Limoges and F. Mavré, Specific versus non-specific response in exponential molecular amplification from cross-catalysis: modeling the influence of background amplifications on the analytical performances, ChemPhysChem, 2021, 22, 1–12 CrossRef PubMed.
- K. Yeung, K. M. Schmid and S. T. Phillips, A thermally-stable enzyme detection assay that amplifies signal autonomously in water without assistance from biological reagents, Chem. Commun., 2013, 49, 394–396 RSC.
- T. Yoshii, S. Onogi, H. Shigemitsu and I. Hamachi, Chemically reactive supramolecular hydrogel coupled with a signal amplification system for enhanced analyte sensitivity, J. Am. Chem. Soc., 2015, 137, 3360–3365 CrossRef CAS PubMed.
- F. Rezende, R. P. Brandes and K. Schröder, Detection of Hydrogen Peroxide with Fluorescent Dyes, Antioxid. Redox Signaling, 2018, 29, 585–602 CrossRef CAS PubMed.
- M. Moßhammer, M. Kühl and K. Koren, Possibilities and Challenges for Quantitative Optical Sensing of Hydrogen Peroxide, Chemosensors, 2017, 5, 28 CrossRef.
- Invitrogen, Amplex® Red Hydrogen Peroxide/Peroxidase Assay Kit, in MyQubit_Amplex_Red_Peroxide_Assay UG.pdf, 2009 Search PubMed.
- B. Limoges, D. Marchal, F. Mavré and J.-M. Savéant, Electrochemistry of immobilized redox enzymes: kinetic characteristics of NADH oxidation catalysis at diaphorase monolayers affinity immobilized on electrodes, J. Am. Chem. Soc., 2006, 128, 2084–2092 CrossRef CAS PubMed.
- J. T. Wu, L. H. Wu and J. A. Knight, Stability of NADPH: effect of various factors on the kinetics of degradation, Clin. Chem., 1986, 32, 314–319 ( Clin. Chem. , 1987 , 33 , 724 ) CrossRef CAS.
- S. Fukuzumi, M. Ishikawa and T. Tanaka, Mechanisms of photo-oxidation of NADH model compounds by oxygen, J. Chem. Soc., Perkin Trans. 2, 1989, 1037–1045 RSC.
- H. G. Kuivila, J. F. Reuwer Jr and J. A. Mangravite, Electrophilic displacement reactions: XV. Kinetics and mechanism of the base-catalyzed protodeboronation of areneboronic acids, Can. J. Chem., 1963, 41, 3081–3090 CrossRef CAS.
- P. A. Cox, M. Reid, A. G. Leach, A. D. Campbell, E. J. King and G. C. Lloyd-Jones, Base-catalyzed aryl-B(OH)2 protodeboronation revisited: from concerted proton transfer to liberation of a transient aryl anion, J. Am. Chem. Soc., 2017, 139, 13156–13165 CrossRef CAS PubMed.
- H. G. Kuivila, Electrophilic Displacement Reactions. III. Kinetics of the Reaction between Hydrogen Peroxide and Benzeneboronic Acid, J. Am. Chem. Soc., 1954, 76, 870–874 CrossRef CAS.
- A. Sikora, J. Zielonka, M. Lopez, J. Joseph and B. Kalyanaraman, Direct oxidation of boronates by peroxynitrite: Mechanism and implications in fluorescence imaging of peroxynitrite, Free Radical Biol. Med., 2009, 47, 1401–1407 CrossRef CAS PubMed.
- E. W. Miller, A. E. Albers, A. Pralle, E. Y. Isacoff and C. J. Chang, Boronate-Based Fluorescent Probes for Imaging Cellular Hydrogen Peroxide, J. Am. Chem. Soc., 2005, 127, 16652–16659 CrossRef CAS PubMed.
- L. Challier, R. Miranda-Castro, D. Marchal, V. Noël, F. Mavré and B. Limoges, Kinetic Rotating Droplet Electrochemistry: A Simple and Versatile Method for Reaction Progress Kinetic Analysis in Microliter Volumes, J. Am. Chem. Soc., 2013, 135, 14215–14228 CrossRef CAS PubMed.
- C. P. Lu, C. T. Lin, C. M. Chang, S. H. Wu and L. C. Lo, Nitrophenylboronic Acids as Highly Chemoselective Probes To Detect Hydrogen Peroxide in Foods and Agricultural Products, J. Agric. Food Chem., 2011, 59, 11403–11406 CrossRef CAS PubMed.
- X. Yuan, C. J. Miller, A. N. Pham and T. D. Waite, Kinetics and mechanism of auto- and copper-catalyzed oxidation of 1,4-naphthohydroquinone, Free Radical Biol. Med., 2014, 71, 291–302 CrossRef CAS PubMed.
- V. Roginsky and T. Barsukova, Kinetics of oxidation of hydroquinones by molecular oxygen. Effect of superoxide dismutase, J. Chem. Soc., Perkin Trans. 2, 2000, 2, 1575–1582 RSC.
- Y. Song and G. R. Buettner, Thermodynamic and kinetic considerations for the reaction of semiquinone radicals to form superoxide and hydrogen peroxide, Free Radical Biol. Med., 2010, 49, 919–962 CrossRef CAS PubMed.
- D. M. Miller, G. R. Buettner and S. D. Aust, Transition metals as catalysts of “autoxidation” reactions, Free Radical Biol. Med., 1990, 8, 95–108 CrossRef CAS PubMed.
- A. Nadezhidin and H. B. Dunford, The oxidation of ascorbic acid and hydroquinone by perhydroxyl radicals. A flash photolysis study, J. Phys. Chem., 1979, 83, 1957–1961 CrossRef.
- L. G. Forni and R. L. Willson, Thiyl and phenoxyl free radicals and NADH. Direct observation of one-electron oxidation, Biochem. J., 1986, 240, 897–903 CrossRef CAS PubMed.
- H. G. Kuivila and A. G. Armour, Electrophilic displacement reactions. 9. Effects of substituents on rates of reactions between hydrogen peroxide and benzeneboronic acid, J. Am. Chem. Soc., 1957, 79, 5659–5662 CrossRef CAS.
- https://www.nipro.co.jp/en/business/other/enzymes.html#.
- K. M. Soares, N. Blackmon, T. Y. Shun, S. N. Shinde, H. K. Takyi, P. Wipf, J. S. Lazo and P. A. Johnston, Profiling the NIH Small Molecule Repository for compounds that generate H2O2 by redox cycling in reducing environments, Assay Drug Dev. Technol., 2010, 8, 152–174 CrossRef CAS PubMed.
- K. Yeung, K. M. Schmid and S. T. Phillips, A thermally-stable enzyme detection assay that amplifies signal autonomously in water without assistance from biological reagents, Chem. Commun., 2013, 49, 394–396 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental Section and complementary figures (from S1 to S23) on the (i) influence of pH on the autocatalysis with P2, (ii) UV-vis spectrophometry and HPLC characterization of probes, (iii) kinetic analysis of the H2O2-mediated deprotection of probes, (iv) numerical simulations of the autocatalytic reactions, (v) justification of the rate constants used for the 1,4-NQ autoxidation, (vi) redox cycling experiments with the 1,4-NQ, (vii) influence of the buffer composition and pH on the autocatalysis with P3, (viii) screening of naphthoquinones for their redox cycling properties, and (ix) indirect detection of glucose oxidase. See DOI: 10.1039/d1sc06086d |
| ‡ Present address: Université de Strasbourg – LSAMM, Institut Le Bel, 4, rue Blaise Pascal, 67070 Strasbourg Cedex, France. |
| This journal is © The Royal Society of Chemistry 2022 |