Kinetics and mechanistic details of bulk ZnO dissolution using a thiol–imidazole system

Abstract

Oxide dissolution is important for metal extraction from ores and has become an attractive route for the preparation of inks for thin film solution deposition; however, oxide dissolution is often kinetically challenging. While binary “alkahest” systems comprised of thiols and N-donor species, such as amines, are known to dissolve a wide range of oxides, the mechanism of dissolution and identity of the resulting solute(s) remain unstudied. Here, we demonstrate facile dissolution of both bulk synthetic and natural mineral ZnO samples using an “alkahest” that operates via reaction with thiophenol and 1-methylimidazole (MeIm) to give a single, pseudotetrahedral Zn(SPh)₂(MeIm)₂ molecular solute identified by X-ray crystallography. The kinetics of ZnO dissolution were measured using solution ¹H NMR, and the reaction was found to be zero-order in the presence of excess ligands, with more electron withdrawing para-substituted thiophenols resulting in faster dissolution. A negative entropy of activation was measured by Eyring analysis, indicating associative ligand binding in, or prior to, the rate determining step. Combined experimental and computational surface binding studies on ZnO reveal stronger, irreversible thiophenol binding compared to MeIm, leading to a proposed dissolution mechanism initiated by thiol binding to the ZnO surface with the liberation of water, followed by alternating MeIm and thiolate ligand additions, and ultimately cleavage of the ligated zinc complex from the ZnO surface. Design rules garnered from the mechanistic insight provided by this study should inform the dissolution of other bulk oxides into inks for solution processed thin films.

---

Introduction

Macroelectronics represent a growing industry with a market value of $16.1 billion (USD) in 2020 that is estimated to reach $39.1 billion by 2027.¹ Chemical vapor deposition (CVD) and physical vapor deposition (PVD) are the two most common methods for depositing large area thin films for macroelectronics applications. These methods are capable of depositing very high-quality films but are hampered by relatively expensive processing equipment and intensive energy usage due to the combination of ultra-low vacuum pressures and high temperatures needed for deposition. Solution processing using semiconductor inks, on the other hand, has the potential to reduce module costs with its relatively low energy usage.^2,3 Solution processing also opens up avenues for new device architectures, such as easier deposition on non-planar and irregular substrates for wearable and mobile power generating devices.⁴ An attractive route for producing semiconductor inks for solution processing is through the dissolution of inexpensive, bulk metal oxides.⁵ More generally, oxide dissolution is important for the extraction of metals from ores, but many oxides dissolve so slowly that they are effectively insoluble even under thermodynamically favorable conditions.^6,7 In turn, the use of extremely hazardous conditions and reagents that generate large amounts of ensuing waste have posed problems for commercial metallurgic processes.⁸

In 2013, we developed a versatile binary solvent system consisting of a short chain thiol (e.g., 1,2-ethanedithiol) and an amine (e.g., 1,2-ethylenediamine) that is capable of dissolving and recovering nine different V₂VI₃ chalcogenides.⁹ Owing to its high reactivity, we termed this solvent system an “alkahest”; the alkahest has been subsequently shown to dissolve over 100 bulk materials, ranging from metals to metal chalcogenides to metal oxides.¹⁰ Indeed, the alkahest is known to dissolve a wide range of bulk metal oxides, including, but not limited to, Ag₂O, As₂O₃, Bi₂O₃, CdO, Cu₂O, CuO, In₂O₃, GeO₂, MnO, PbO, Sb₂O₃, SeO₂, SnO, and ZnO.^5,11–16 Through a mild dissolve and recover approach, the alkahest solvent system returns phase-pure binary metal chalcogenide thin films from dissolved oxide precursors; for example, semiconductor inks for metal sulfide thin films can be derived from dissolved metal oxides, where the sulfur source is the thiol component of the alkahest. Moreover, phase-pure, complex multinary semiconductors can also be solution processed by simply dissolving multiple bulk precursors in the proper stoichiometric ratios with the alkahest solvent system.¹³ In the same way, compositionally controlled alloyed semiconductors can be solution processed by tuning the ink formulation.^5,11 The alkahest solvent system returns functional thin films that have proven useful in a multitude of applications, including solar cells,^17,18 photodetectors,¹⁹ thermoelectrics,²⁰ neuromorphic devices,²¹ electrocatalysts,²² and it has also been used to engineer the surfaces of colloidal nanocrystals.^23–25 This approach has the potential to be translated to large-scale solution processing.¹⁴

While the alkahest has been widely adopted for device fabrication because of the simplicity of the approach, the fundamental mechanism of oxide dissolution using this solvent couple has yet to be explored. In a conceptually related, but fundamentally different, system, Rauchfuss et al. reported on the dissolution of bulk metal powders through oxidative corrosion. In that work, an N-donor solvent assisted the dissolution of Cu powder in the presence of sulfur.²⁶ This chemistry was expanded to include the dissolution of other zero-valent bulk transition metals including Fe, Mg, Mn, Ni and Zn,^27–29 and has been recently revisited for the oxidative dissolution of metallic Pb and Sn using molecular dichalcogenides.^30,31 In the particular case of metallic Zn powder, dissolution occurs via addition of N-donor solvents and elemental sulfur to yield a defined molecular solute, which is a pseudo-tetrahedral ZnS₆(L)₂ complex (where L = 1/2 tetramethylethylenediamine, 4-(dimethylamino)pyridine). These complexes can be thermally annealed under nitrogen to yield ZnS.²⁹ Based on this precedent, we sought to determine whether bulk ZnO dissolution in an alkahest solvent system might give a similarly well-defined molecular solute through a non-oxidative dissolution process. Thus, we present the dissolution of bulk ZnO via reaction with 1-methylimidazole (MeIm) and thiophenol. Whilst previous attempts to identify the products of alkahest dissolution have relied on indirect methods,^23,32,33 we unambiguously identify the molecular solute resulting from ZnO dissolution using direct crystallographic methods, which then enabled us to use ¹H NMR to measure the dissolution kinetics. The kinetic analysis of ZnO dissolution in this thiol–imidazole solution allows us to propose, for the first time, a plausible mechanism for alkahest dissolution.

Experimental

General considerations

All materials were used as received. Zinc(II) oxide (ZnO, 99.99%) was purchased from Alfa Aesar; zinc(II) sulfide (ZnS, 99.99%, 10 μm particle size), zinc metal (99.8%, 20–30 mesh size), 1-methylimidazole (or N-methylimidazole, MeIm, 99.9%), thiophenol (99%), 4-bromothiophenol (99%), 4-methylthiophenol (99%), 4-methoxythiophenol (99%), 5-chloro-1-methylimidazole (98%), diphenyl disulfide (99%), and deuterated acetonitrile (acetonitrile-d₃, 99.8%) were purchased from Sigma-Aldrich. A natural sample of the mineral zincite (mined from Poland) was obtained from a private seller. Standard air-free Schlenk techniques were used. Powders were used as received.

Preparation and crystallization of Zn(SPh)₂(MeIm)₂ (4)

For the isolation of crystals of 4, 36.3 mg (0.446 mmol, 1 eq.) of ZnO and 72.9 μL (0.914 mmol, 2.05 eq.) of MeIm were added to 4.5 mL of acetonitrile. The reaction was degassed by subjecting it to three freeze-pump-thawed cycles. After the reaction was degassed, it was brought to 75 °C in a sand bath with an in situ thermocouple under flowing nitrogen at atmospheric pressure. Once at temperature, 93.4 μL of thiophenol (0.914 mmol, 2.05 eq.) was added to the reaction via syringe. The reaction was stirred at 75 °C until the solution was optically clear and free flowing. Once fully dissolved, the solution was transferred to a 2-dram vial and the cap was left loose to allow the solution to slowly evaporate. Over the course of 1–2 d, optically transparent, yellow prismatic crystals of 4 were isolated from the bottom of the vial. For further crystallization of 4, seed crystals can be used to induce instant crystallization from the mother liquor without the need for solvent evaporation. Anal. calcd. for C₂₀H₂₂N₄S₂Zn (%): C 53.39, H 5.38, N 12.45, S 14.25. Found C 53.55, H 5.01 N 12.17, S 14.91. ¹H NMR (acetonitrile-d₃, 25 °C, 599.80 MHz): δ 7.61 (s, 1H, MeIm), 7.36 (d, 2H, Zn(SPh)), 7.05 (s, 1H, MeIm), 6.95 (t, 2H, Zn(SPh)), 6.94 (s, 1H, MeIm), 6.86 (t, 1H, Zn(SPh)), 3.65 (s, 3H, MeIm). ¹³C{¹H} NMR (acetonitrile-d₃, 25 °C, 150.84 MHz): δ 144.14, 138.71, 132.89, 127.60, 126.86, 121.85, 121.67, 33.76. Crystal data: C₂₀H₂₂N₄S₂Zn, M = 447.90 g mol⁻¹, monoclinic, a = 38.805(5), b = 6.6795(9), c = 16.442(2) Å, α = 90, β = 91.833(2), γ = 90°, V = 4259.6(10) ų, T = 100(2) K, space group C121 (no. 5), Z = 8, 51 009 reflections measured, 12 827 unique (R^int = 0.0535), which were used in all calculations. The final wR2 = 0.1104 (all data).

Aliquot studies of ZnO dissolution

For aliquot studies, 36.3 mg (0.446 mmol) of ZnO and 106.8 μL (1.339 mmol, 3 eq.) of MeIm were added to 4.5 mL of acetonitrile-d₃ in a Schenk flask. The reaction was degassed by subjecting it to three freeze-pump-thawed cycles. After the reaction was degassed, it was brought to elevated temperatures (from 30–75 °C) in a sand bath with an in situ thermocouple under flowing nitrogen at atmospheric pressure. Once at the designated temperature, 109.4 μL of thiophenol (1.07 mmol, 2.4 eq.) was added via syringe and reactions were stirred at a constant rate. Aliquots (0.05 mL) were taken via syringe and thermally quenched by mixing with 0.5 mL of acetonitrile-d₃. The aliquots were then filtered through a cotton plug into an NMR tube and the ¹H NMR spectra were immediately taken in a Varian 600 MHz VNMRS spectrometer with 64 scans, a relaxation delay of 1 s, and a pulse angle of 45°. The 2-position proton resonance for MeIm at δ = 7.4–7.5 ppm is used as an internal standard set at an integration of 1 and the bound ortho-thiophenolate proton resonances of 4 at δ = 7.36 ppm were integrated against this peak. Direct-detect ¹H NMR spectra were analyzed using MestReNova version 14.0.0 software.

Characterization

Powder X-ray diffraction (XRD) patterns were collected using a Rigaku Miniflex600 operated at 40 mA and 35 kV, in the 2θ range of 10–70° using Cu Kα radiation (λ = 1.5406 Å). Thermal gravimetric analysis (TGA) was performed on a TA Instruments TGA Q50 instrument and samples were run in an alumina crucible under a flowing nitrogen atmosphere with a heating rate of 5 °C min⁻¹. Fourier transform infrared (FT-IR) spectra were measured on a Bruker Vertex 80 spectrometer. Liquid FT-IR samples were taken between NaCl salt plates and solid samples were crushed and pressed into a pellet with KBr. Scanning electron microscopy (SEM) was performed on a Thermo Scientific Helios G4 PFIB UXe equipped with an Oxford UltimMax 170 silicon drift detector X-ray energy dispersive spectroscopy (EDS) system. Brunauer–Emmett–Teller (BET) measurements were performed on a Nova 2200e surface area and pore size analyzer (Quantachrome Instruments, Inc.). Samples were degassed overnight at 180 °C under vacuum prior to measurements. Solution NMR spectra were taken on a Varian VNMRS 600 spectrometer with 10 000 scans for ¹³C NMR spectra. The change in room-temperature electrical conductivity on adding thiophenol to MeIm in acetonitrile was qualitatively assessed by measuring the resistance between two Pt wires submerged in a nitrogen-purged cuvette of liquid using a G.W. Instec LCR-816 meter (1.275 V, 2 kHz AC output).

Density functional theory

Calculations were carried out in the gas phase using the Q-Chem ab initio quantum chemistry software³⁴ with the B3LYP^35,36 density functional approximation, def2-SVP basis set, and corresponding def2-ECP effective core potential.³⁷ To determine the role of dispersion, single point energy calculations using the D3 correction with Becke–Johnson damping³⁸ are carried out for structures optimized at the B3LYP level of theory.

A cluster model approximation for ZnO is created using the 24-atom (ZnO)₁₂ geometry identified by Chen and coworkers.³⁹ Minimum energy structures are calculated and verified via vibrational analysis for possible intermediates that must be traversed to remove a zinc atom from (ZnO)₁₂ and generate Zn(SPh)₂(MeIm)₂, H₂O, and (ZnO)₁₁. As the energetics emerging from cluster model approximations are sensitive to cluster deformations, only the zinc atom coordinating to ligands and its nearest oxygen neighbors are allowed to relax in these steps. The energy of the Zn(SPh)₂(MeIm)₂ complex is calculated using the (ZnO)₁₂ reference by removing one zinc and one oxygen atom instead of (ZnO)₁₁. This is because (ZnO)₁₂ and (ZnO)₁₁ have very different minimum energy geometries and using the former as reference enables us to minimize energy changes arising from cluster deformations. Gibbs free energies (ΔG), calculated at both 35 and 75 °C, are used to identify the most viable steps for ZnO dissolution. For free energy calculations, it is assumed that, upon binding to the (ZnO)₁₂ cluster, ligands lose all translational and rotational degrees of freedom.

Results and discussion

Identification of molecular solute

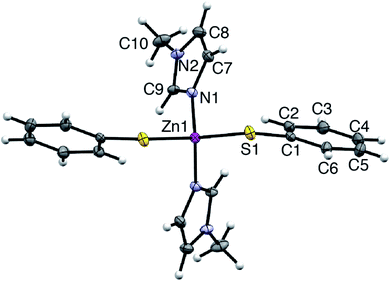
Synthetic, polycrystalline wurtzite ZnO powder (BET surface area 8 m² g⁻¹) was reacted with stoichiometric amounts of MeIm and thiophenol in acetonitrile (75 °C, 1 atm). After stirring for 8 h, the ZnO dissolution was complete, giving a colorless, optically clear solution that is free of scattering (ESI†). Importantly, the bulk ZnO powder does not dissolve in acetonitrile solutions of MeIm or thiophenol alone; that is, the combination of the two alkahest components is needed for dissolution. Slow evaporation of the fully dissolved reaction solution yielded analytically pure, yellow crystals of a neutral Zn(SPh)₂(MeIm)₂ complex (4). The air-stable crystals of 4 were isolated and characterized by single crystal X-ray diffraction and NMR spectroscopy (ESI†). Compound 4 crystallizes in the monoclinic space group C121, where zinc is in a pseudotetrahedral coordination environment bound to nitrogen atoms of two MeIm ligands and sulfur atoms of two thiophenolate ligands (Fig. 1). The solution ¹H NMR spectrum of isolated crystals of 4 in acetonitrile-d₃ matches that of the fully dissolved reaction mixture. We can therefore conclude that the molecular solute in the crude reaction mixture is a single species that unambiguously matches that of isolated complex 4; this allows us to track the temporal evolution of the molecular solute during ZnO dissolution by solution ¹H NMR spectroscopy (vide infra). Upon dissolution, the solution remains stable over the course of at least one week when exposed to air (i.e., 21 °C, 20–90% RH) with no precipitation or significant color change observed. The solution ¹H NMR spectrum of 4 in the dissolved reaction mixture also remains unchanged over this time (ESI†).

Fig. 1 ORTEP plot of the X-ray crystal structure of Zn(SPh)₂(MeIm)₂ (4).

Dissolution kinetics

The ZnO dissolution kinetics were probed by performing the reaction in acetonitrile-d₃ and removing aliquots, filtering away unreacted ZnO, and monitoring the aliquots by solution ¹H NMR as both a function of reaction time and temperature. The amounts of MeIm (3 eq.) and thiophenol (2.4 eq.) were chosen relative to ZnO to observe the reaction kinetics when the reagents are present in excess. In practice, oxide dissolution with thiols and N-donor solvents is always performed with the two reagents in stoichiometric excess.⁵ Here, non-labile binding of thiolate to the zinc center of 4 is observed by ¹H NMR, with clear chemical shift differences between the bound and unbound aromatic thiophenolate and thiophenol resonances, respectively (Fig. 2). For example, the peak intensity for the doublet corresponding to bound ortho-thiophenolate protons (δ = 7.36 ppm) increases with time as the concentration of 4 builds, while a concomitant decrease of free thiophenol is observed (i.e., multiplets at δ = 7.31, 7.26, and 7.17 ppm). Labile MeIm binding to zinc is observed by a gradual downfield shift of the peaks as the concentration of 4 increases with time (e.g., the downfield shift of the proton in the 2-position of MeIm between 7.41–7.51 ppm). Along with the disappearance of free thiophenol and the appearance of 4, we were also able to observe the release of a stoichiometric amount of H₂O derived from liberated ZnO lattice oxygen during the dissolution reaction (Fig. 2).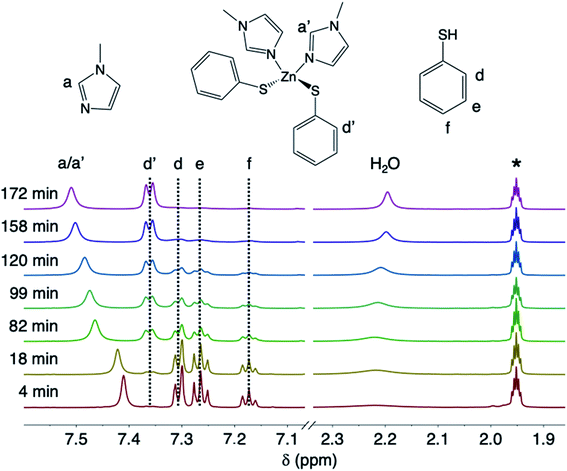

Fig. 2 Stacked room-temperature solution ¹H NMR spectra in acetonitrile-d₃ of the aromatic region and H₂O peak for aliquots taken as a function of time from the dissolution of ZnO with MeIm and thiophenol at 75 °C. Acetonitrile-d₂ is labeled as *. Full spectra are provided in the ESI.†

In order to determine the thermodynamic parameters of ZnO dissolution, the reaction was performed at a series of temperatures between 30–75 °C. At all temperatures, we observe a linear decrease in the concentration of thiophenol (and a linear increase in the concentration of 4) with time by ¹H NMR, indicative of a zero-order reaction with the rate constant increasing with increasing dissolution temperature, respectively confirmed by log–log and Eyring analyses (ESI†). Thus, thiophenol loading on the ZnO surface appears kinetically invisible. This can be explained by rapid saturation of thiol ligation to the ZnO surface under the high thiophenol concentrations used for dissolution. When thiophenol and MeIm were made stoichiometric relative to ZnO, under otherwise identical dissolution conditions, the reaction remains zero order (ESI†). When the concentrations of MeIm (2.4–4.0 eq.) and thiophenol (2.4–4.8 eq.) were independently varied into excess with all other reaction conditions being held constant, we see that ZnO dissolution also remains zero order, displaying no rate dependence on MeIm or thiophenol concentration (see ESI† for analysis). However, in a dilution experiment where both ligand concentrations are made scarce, we observe an overall reaction order of about two, as illustrated in a log–log plot with slope of 1.8 (ESI†), which we hypothesize to correspond to the binding of two ligands to each zinc center released from the ZnO surface in or prior to the rate determining step (vide infra). A rate law can be derived from a steady-state treatment of reactive sites on the ZnO surface that is first order in thiophenol with positive kinetic dependence on MeIm (ESI†), which is consistent with the experimentally observed overall reaction order between 1–2 when the surface is not saturated. To obtain the thermodynamic activation energy parameters for ZnO dissolution, we constructed an Eyring plot using the rate data recorded from 30–75 °C. We find a ΔH^‡ of 27.4(5) kJ mol⁻¹ and a ΔS^‡ of −259.8(3) J (mol K)⁻¹ (Fig. 3 and ESI†).⁴⁰ A statistically significant, negative ΔS^‡ suggests associative binding to the ZnO surface by one or more ligands in, or prior to, the rate determining step.

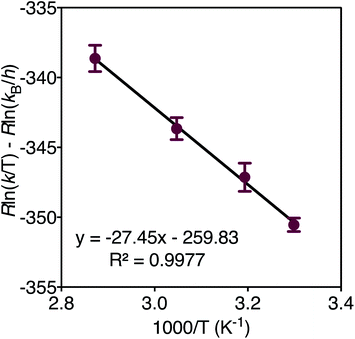Fig. 3 Eyring plot derived from the dissolution of ZnO with MeIm (3 eq.) and thiophenol (2.4 eq.) in acetonitrile-d₃ from 30–75 °C.

Next, a series of para-substituted thiophenols (i.e., 4-bromo-, 4-methyl-, and 4-methoxythiophenol) was investigated to probe how the electron donating or withdrawing substituents would affect the ZnO dissolution rate. We observe that electron donating groups (i.e., 4-methyl- and 4-methoxythiophenol) slow down the reaction, whereas the electron withdrawing group (4-bromothiophenol) speeds up the reaction (ESI†). In competition experiments where a free para-substituted thiophenol was titrated into a fully dissolved ZnO reaction mixture, a less electron-rich thiol displaces a more electron-rich thiolate off the zinc center (ESI†). These data are consistent with a polarized Zn–S bond, which is strengthened by increased polarization of the covalent bond. Replacing MeIm with 5-chloro-1-methylimidazole also allows for complete ZnO dissolution with thiophenol that is qualitatively faster than with the unsubstituted analogue; however, the dissolution kinetics are complex and are no longer zero order as with MeIm.

Proposed mechanism of dissolution

To propose a mechanism of dissolution, several additional experiments were conducted to probe reactions at the surface and in solution. We first conducted FT-IR and conductivity experiments of thiophenol and MeIm in the absence of ZnO to probe the extent of thiophenol deprotonation and determined that MeIm does not cause significant deprotonation of thiophenol in acetonitrile. When thiophenol and MeIm are mixed, the resulting FT-IR spectrum clearly shows the weak sulfhydryl ν(S–H) stretching band at 2560 cm⁻¹ is still present, with no significant change in the ν(S–C) stretching frequencies at 680–700 cm⁻¹ when compared to the FT-IR spectrum of neat thiophenol (ESI†). We also observe no significant increase in electrolytic conductivity upon addition of thiophenol to a solution of MeIm in acetonitrile (ESI†), unlike what was previously reported for other thiol–amine combinations.⁹ Taken together, this suggests that thiophenol is not deprotonated by MeIm in this system. This is consistent with pK_a values in water, where thiophenol (pK_a = 8.2) would not be expected to be completely deprotonated by MeIm (pK_a = 7.3–7.8).^41,42 As such, we expect thiophenol to be the reagent that approaches and binds to the ZnO surface, rather than an anionic thiophenolate.

An FT-IR spectrum collected on a sample of ZnO that had been stirred with thiophenol (without MeIm) at 75 °C, rinsed, and dried clearly shows the presence of aromatic ν(C–H) bands from thiophenol at 2560 cm⁻¹, the absence of the sulfhydryl ν(S–H) band, and the presence of ν(S–C) stretching frequencies at 680–700 cm⁻¹ (ESI†). An analogous experiment with MeIm (without thiophenol) does not return any diagnostic FT-IR bands from MeIm on the ZnO surface after rinsing and drying (ESI†). We conclude from these FT-IR experiments that thiophenol binds irreversibly to the virgin ZnO surface and MeIm does not.

Typically, in heterogenous dissolution chemistry, cleavage of the pre-coordinated complex is the rate determining step for metal oxide dissolution.^43–45 Computational analysis using density functional theory was performed to develop a semi-quantitative description of possible intermediates in the mechanism of ZnO dissolution with thiophenol and MeIm. Fig. 4 depicts the intermediate structures and results of this analysis by considering each of the different combinations of ligand binding events that could lead to the liberation of 4 from the ZnO surface, and Table 1 provides a description of the surface-bound ligands in intermediate states and key bond distances. Based on calculated ligand binding energies in Fig. 4, the following sequence of steps is proposed: The first ligand binding event to the zinc center is thermodynamically favorable, with thiophenol binding (and concomitant Zn–OH formation) to give structure 1 favored by 29.6 (29.1) kJ mol⁻¹ over MeIm binding at 30 °C (75 °C). For the second ligand binding event, there is a strong preference for MeIm coordination to give structure 2, which is thermodynamically downhill from structure 1 by 105.8 (97.9) kJ mol⁻¹, whereas the alternative binding by a second thiophenol is more energetically neutral. The third ligand binding event is thermodynamically uphill by 102.8 (102.0) kJ mol⁻¹, with the binding of a second thiophenol (to give structure 3) being strongly preferred over the binding of a second MeIm. We propose based on kinetics data that this conversion of 2 to 3 is rate-limiting. The final ligand binding event is thermodynamically downhill by 604.0 (595.1) kJ mol⁻¹ to give the experimentally verified solute 4.

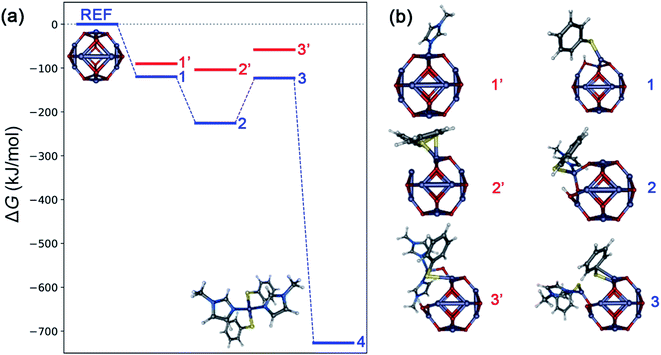Fig. 4 (a) Calculated Gibbs free energies (ΔG) at 30 °C associated with formation of possible intermediate steps constituting dissolution of bulk ZnO with thiophenol and MeIm, calculated using a reference (ZnO)₁₂ cluster model (B3LYP functional, def2-SVP basis with def2-ECP on zinc). The most favorable pathway is depicted in blue and unfavorable intermediates are shown in red. (b) Intermediate geometries: 1 and 1′ represent binding of thiophenol (with concomitant Zn–OH formation) and MeIm to (ZnO)₁₂, respectively. Structures 2 and 2′ represent binding of MeIm and thiophenol (with H₂O removal) to 1, respectively. Structures 3 and 3′ represent binding of thiophenol (with H₂O removal) and MeIm to 2, respectively. Structure 4 refers to the molecular solute state corresponding to formation of the experimentally verified Zn(SPh)₂(MeIm)₂ complex. Model visualizations are created using the Envision package.⁴⁶ The potential energy representation is created using the ‘Energy Leveller’ program developed by Furness.⁴⁷

Table 1 Description of intermediate geometries. For 2′, 3, and 3′ the sulfur atom of the bound thiophenolate ligand coordinates to more than one zinc center on the surface. The bond distance to the second zinc atom is provided in parentheses. Apart from structure 3, all ligands are bound to the same Zn atom in intermediate states. In 3, the only converged optimization calculation yields a structure in which one of the two thiophenol ligands is bound to a second, neighboring Zn atom

Label	Ligands	ΔG (kJ mol^−1) at 30 °C, 75 °C	Zn–S (Å)	Zn–N (Å)	Zn–O (Å)
1	PhSH	−119.9, −112.9	2.280	—	1.900, 1.961
1′	MeIm	−90.2, −83.8	—	2.075	1.923, 2.004
2	PhSH, MeIm	−225.7, −210.8	2.372	2.124	1.924, 2.004
2′	PhSH, PhSH	−104.0, −96.4	2.281, 2.610 (2.357)	—	1.984, 1.996
3	2 PhSH, MeIm	−122.9, −108.8	2.301, 2.793 (2.347)	2.044	1.926
3′	PhSH, 2 MeIm	−58.3, −37.3	2.440 (2.660)	2.100, 2.064	1.855
4	2 PhSH, 2 MeIm	−726.9, −703.9	2.338, 2.312	2.114, 2.116	—

---

Taken in concert with the kinetic analysis and ligand binding studies, these data suggest that the first thiophenol binding is rapid, irreversible, and kinetically invisible. This gives rise to a thiolate-coated oxide surface that has reversible MeIm binding. The equilibrium of MeIm-bound and -unbound zinc monothiolates behave like a resting state of the system, and both appear in the kinetics (vide supra), as in the case of a pre-equilibrium system. Reversible imidazole coordination is then followed by the rate determining step involving the addition of a second equivalent of thiophenol; the transition state has high covalent character as indicated by the low ΔH^‡ of 27 kJ mol⁻¹ relative to the associated bond strengths. A measured ΔG^‡ of 118 kJ mol⁻¹ at 75 °C is fit to a late rate-determining transition state for the formation of 3, according to its energy relative to 2 and 3. Following reaction of the second thiolate ligand, binding of the second MeIm and dissociation of 4 from the surface ensue rapidly to return a zinc oxide surface. These steps do not appear in the kinetics.

Analogous dissolution reactions with polycrystalline sphalerite ZnS powder (BET surface area 15 m² g⁻¹) do not readily proceed under otherwise identical conditions (ESI†). The formation of strong HO–H bonds of water (BDE = 497 kJ mol⁻¹) from the liberation of ZnO lattice oxygen appears to be a thermodynamic driver for the dissolution reaction (ZnO lattice energy = 4142 kJ mol⁻¹; melting point = 1975 °C).⁴⁸ For the analogous dissolution of ZnS, the liberation of lattice sulfur would lead to the formation of weaker HS–H bonds (BDE = 381 kJ mol⁻¹) that are too energetically neutral to drive the reaction (with a lower ZnS lattice energy = 3619 kJ mol⁻¹; melting point = 1185 °C).⁴⁸ Given the lower lattice energy of sphalerite ZnS as compared to wurtzite ZnO, this suggests that the more facile ZnO dissolution is thermodynamically driven by water formation. Moreover, even though various zero-valent bulk metals have previously been dissolved in alkahest solvent systems,^32,49 metallic Zn powder does not dissolve in freshly distilled and air-free thiophenol and MeIm. This is not surprising given the lack of an oxidizing agent in the system, and this result reveals that previous reports of metal dissolution are likely enabled by adventitious disulfide from oxidized thiols. For the analogous dissolution of bulk Zn powder, diphenyl disulfide can be employed for oxidative dissolution instead of thiophenol; in this case, 4 is also the single product of dissolution by ¹H NMR (ESI†).

Zincite mineral dissolution

To further assess the utility of the alkahest solvent system for oxide dissolution, we acquired a natural zincite (ZnO) mineral sample to see if it would also dissolve and yield the same molecular solute 4 (ESI†). The orange-colored mineral sample was ground in a mortar and pestle and analyzed by powder XRD where it was indexed to phase-pure wurtzite ZnO (ESI†). An analogous dissolution among zincite, thiophenol, and MeIm readily proceeds under identical conditions as the synthetic ZnO powder, also yielding an optically clear, colorless, free flowing ink after 24 h of dissolution at 75 °C that is qualitatively identical to the synthetic ZnO ink (ESI†). The equivalent formation of 4 as the sole molecular solute from zincite mineral dissolution was confirmed by ¹H NMR (ESI†). The dissolution of zincite further demonstrates the versatility of the alkahest to dissolve naturally occurring oxide ores.

Thermal decomposition

Alkahests are generally useful for the deposition of metal chalcogenides from the dissolution of metal oxides. In the absence of added chalcogen, the product is the analogous metal sulfide. In the case of ZnO dissolution with thiophenol and MeIm, the resulting ink is therefore expected to yield ZnS. Along these lines, we tracked the thermal decomposition of the molecular solute 4 by thermogravimetric analysis (TGA). The TGA trace of isolated crystals of 4 shows an onset of decomposition at ca. 125 °C that is complete by 600 °C (ESI†). The ceramic yield (22.5%) from TGA for the thermal decomposition of 4 to give ZnS closely matches the expected value (21.7%). Isolated crystals of 4 were then thermally decomposed and annealed at 600 °C for 30 h, and the resulting material was analyzed by powder X-ray diffraction (ESI†). The resulting diffraction pattern indexes well to cubic sphalerite ZnS, and an integrated energy dispersive X-ray spectrum of the annealed material demonstrates the presence of nearly stoichiometric amounts of zinc and sulfur (Zn/S = 1 : 0.82).

Conclusions

In summary, we probed bulk ZnO (in both synthetic and natural mineral form) dissolution using an alkahest solvent system with thiophenol and MeIm in acetonitrile. A discrete molecular solute was isolated and unambiguously identified using direct methods as a neutral pseudotetrahedral Zn(SPh)₂(MeIm)₂ complex. Concomitant with the formation of the molecular solute, we obtained the first experimental evidence of stoichiometric water formation by ¹H NMR from the liberation of ZnO lattice oxygen. A negative entropy of activation was measured by Eyring analysis, indicating associative ligand binding in, or prior to, the rate determining step, which is supported by DFT. The high ZnO lattice energy does not appear to dominate the dissolution mechanism, but rather dissolution appears to be thermodynamically driven by the strong HO–H bond formation for water. Based on this model study, it seems that metal oxides are more appropriate for kinetically facile dissolution to generate a semiconductor ink than the analogous metal sulfides, and this matches what has been empirically observed in previously reported alkahest dissolutions. Generally, metal oxides are more easily dissolved than the analogous metal sulfides in alkahest systems, where most reported sulfides have lower maximum solubility than the corresponding oxides.^5,9 We also observe that in alkahest systems, most oxides dissolve almost instantaneously whereas sulfides may take elevated temperatures and extended times for full dissolution.^5,9,11,12,32 A second design rule gleaned from this study to aid in the formulation of semiconductor inks is that the rate of dissolution increased by using a more electron-withdrawing thiol. This may help in cases where oxide dissolution appears to be kinetically inert. The mechanistic understanding of oxide dissolution, such as the one garnered here in a model ZnO system, will inform future studies for solution processing metal chalcogenide thin films with alkahest ink formulations.

Data availability

Crystallographic data for 4 has been deposited at the Cambridge Crystallographic Data Centre under CCDC 2115109. DFT geometries and photographs of inks, XRD patterns of starting oxides and resulting ZnS, SEM images of starting oxides and resulting ZnS, NMR spectra, FT-IR spectra, kinetic data and Eyring analysis, conductivity data, and TGA trace are available in the ESI.†

Author contributions

R. L. B., T. J. W., and S. M. S. conceived and designed the project. K. M. K. performed the experimental work while S. J. Q. and S. M. S. performed the computational work. K. M. K, S. M. S, T. J. W., and R. L. B. drafted the manuscript. All authors have discussed the results and given approval to the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

R. L. B. and T. J. W. acknowledge support from the National Science Foundation under DMR-1904719 and CHE-1856395, respectively. We thank the NSF (DBI-0821671, CHE-0840366, CHE-2018740) and NIH (S10 RR25434) for analytical instrumentation. S. J. Q. is grateful for support from the Provost's Undergraduate Research Fellowship at USC. S. M. S. acknowledges support from startup funds at USC. The authors are grateful to USC's Center for Advanced Research Computing for computational infrastructure and support.

References

1. Global Thin-film Semiconductor Deposition Industry 2020–2027, Reportlinker, 2020.
2. A. R. Uhl, A. Rajagopal, J. A. Clark, A. Murray, T. Feurer, S. Buecheler, A. K.-Y. Jen and H. W. Hillhouse, Adv. Energy Mater., 2018, 8, 1801254.
3. M. Cha, P. Da, J. Wang, W. Wang, Z. Chen, F. Xiu, G. Zheng and Z.-S. Wang, J. Am. Chem. Soc., 2016, 138, 8581–8587.
4. M. J. Yun, S. I. Cha, S. H. Seo and D. Y. Lee, Sci. Rep., 2014, 4, 5322.
5. C. L. McCarthy, D. H. Webber, E. C. Schueller and R. L. Brutchey, Angew. Chem., Int. Ed., 2015, 54, 8378–8381.
6. D. G. Wickham, J. Mark and K. Knox, Inorg. Synth., 1967, 9, 152–156.
7. C. F. Jones, R. L. Segall, R. S. C. Smart and P. S. Turner, J. Chem. Soc., Faraday Trans. 1, 1977, 73, 1710–1720.
8. J. Richter and M. Ruck, Molecules, 2020, 25, 78.
9. D. H. Webber and R. L. Brutchey, J. Am. Chem. Soc., 2013, 135, 15722–15725.
10. K. M. Koskela, M. J. Strumolo and R. L. Brutchey, Trends Chem., 2021, 3, 1061–1073.
11. C. L. McCarthy and R. L. Brutchey, Chem. Mater., 2018, 30, 304–308.
12. K. M. Koskela, A. C. Tadle, K. Chen and R. L. Brutchey, ACS Appl. Energy Mater., 2021, 4, 11026–11031.
13. K. M. Koskela, B. C. Melot and R. L. Brutchey, J. Am. Chem. Soc., 2020, 142, 6173–6179.
14. C. L. McCarthy and R. L. Brutchey, Chem. Commun., 2017, 53, 4888–4902.
15. T. Zhang, L. Zhang, Y. Yin, C. Jiang, S. Li, C. Zhu and T. Chen, Sci. China Mater., 2019, 62, 899–906.
16. W.-Y. Wu, Y. Xu, X. Ong, S. Bhatnagar and Y. Chan, Adv. Mater., 2019, 31, 1806164.
17. Y. Zhao, S. Yuan, Q. Chang, Z. Zhou, D. Kou, W. Zhou, Y. Qi and S. Wu, Adv. Funct. Mater., 2021, 31, 2007928.
18. Y. Zhao, X. Zhao, D. Kou, W. Zhou, Z. Zhou, S. Yuan, Y. Qi, Z. Zheng and S. Wu, ACS Appl. Mater. Interfaces, 2021, 13, 795–805.
19. M. R. Hasan, E. S. Arinze, A. K. Singh, V. P. Oleshko, S. Guo, A. Rani, Y. Cheng, I. Kalish, M. E. Zaghloul, M. V. Rao, N. V. Nguyen, A. Motayed, A. V. Davydov, S. M. Thon and R. Debnath, Adv. Electron. Mater., 2016, 2, 1600182.
20. Y. Ma, P. B. Vartak, P. Nagaraj and R. Y. Wang, RSC Adv., 2016, 6, 99905–99913.
21. P. C. Harikesh, A. Surendran, B. Ghosh, R. A. John, A. Moorthy, N. Yantara, T. Salim, K. Thirumal, W. L. Leong, S. Mhaisalkar and N. Mathews, Adv. Mater., 2020, 32, 1906976.
22. C. L. McCarthy, C. A. Downes, E. C. Schueller, K. Abuyen and R. L. Brutchey, ACS Energy Lett., 2016, 1, 607–611.
23. J. J. Buckley, M. J. Greaney and R. L. Brutchey, Chem. Mater., 2014, 26(21), 6311–6317.
24. M. Ibáñez, R. Hasler, A. Genç, Y. Liu, B. Kuster, M. Schuster, O. Dobrozhan, D. Cadavid, J. Arbiol, A. Cabot and M. Kovalenko, J. Am. Chem. Soc., 2019, 141, 8025–8029.
25. Y. Liu, M. Calcabrini, Y. Yu, S. Lee, C. Chang, J. David, T. Ghosh, M. C. Spadaro, C. Xie, O. Cojocaru-Mirédin, J. Arbiol and M. Ibáñez, ACS Nano, 2022, 16, 78–88.
26. E. Ramli, T. B. Rauchfuss and C. L. Stern, J. Am. Chem. Soc., 1990, 112, 4043–4044.
27. S. Dev, E. Ramli, T. B. Rauchfuss and C. L. Stern, J. Am. Chem. Soc., 1990, 112, 6385–6386.
28. S. Dev, E. Ramli, T. B. Rauchfuss and S. R. Wilson, Inorg. Chem., 1991, 30, 2514–2519.
29. A. K. Verma, T. B. Rauchfuss and S. R. Wilson, Inorg. Chem., 1995, 34, 3072–3078.
30. Z. Wang, Y. Ma, P. B. Vartak and R. Y. Wang, Chem. Commun., 2018, 54, 9055–9058.
31. P. B. Vartak, Z. Wang, T. L. Groy, R. J. Trovitch and R. Y. Wang, ACS Omega, 2020, 5, 1949–1955.
32. J. J. Buckley, C. L. McCarthy, J. Del Pilar-Albaladejo, G. Rasul and R. L. Brutchey, Inorg. Chem., 2016, 55, 3175–3180.
33. J. C. Lowe, L. D. Wright, D. B. Eremin, J. V. Burykina, J. Martens, F. Plasser, V. P. Ananikov, J. W. Bowers and A. V. Malkov, J. Mater. Chem. C, 2020, 8, 10309–10318.
34. E. Epifanovsky, A. T. B. Gilbert and X. Feng, et al. , J. Chem. Phys., 2021, 155, 084801.
35. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
36. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
37. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
38. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
39. M. Chen, T. P. Straatsma, Z. Fang and D. A. Dixon, J. Phys. Chem. C, 2016, 120, 20400–20418.
40. T. J. Williams, A. D. Kershaw, V. Li and X. Wu, J. Chem. Educ., 2011, 88, 665–669.
41. I. Pascal and D. S. Tarbell, J. Am. Chem. Soc., 1957, 79, 6015–6020.
42. T. Y. Chae, S. W. Row, K. S. Yoo, S. D. Lee and D. W. Lee, Bull. Korean Chem. Soc., 2006, 27, 361–362.
43. W. H. Casey and C. Ludwig, Nature, 1996, 381, 506–509.
44. M. A. Blesa, A. D. Weisz, P. J. Morando, J. A. Salfity, G. E. Magaz and A. E. Regazzoni, Coord. Chem. Rev., 2000, 196, 31–63.
45. D. Suter, S. Banwart and W. Stumm, Langmuir, 1991, 7, 809–813.
46. F. R. Manby, T. F. Miller III, P. J. Bygrave, F. Ding, T. Dresselhaus, F. A. Batista-Romero, A. Buccheri, C. Bungey, S. J. R. Lee, R. Meli, K. Miyamoto, C. Steinmann, T. Tsuchiya, M. Welborn, T. Wiles and Z. Williams, 2019,  DOI:10.26434/chemrXiv:7762646.v2.
47. W. Furness, 2017, https://github.com/JFurness1/EnergyLeveller/, accessed October 2021.
48. Y. R. Luo, Comprehensive Handbook of Chemical Bond Energies, CRC Press, Boca Raton, FL, 2007.
49. D. Zhao, Q. Tian, Z. Zhou, G. Wang, Y. Meng, D. Kou, W. Zhou, D. Pan and S. Wu, J. Mater. Chem. A, 2015, 3, 19263–19267.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2115109. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1sc06667f

---