Open Access Article
Open Access ArticleComparing interfacial cation hydration at catalytic active sites and spectator sites on gold electrodes: understanding structure sensitive CO2 reduction kinetics†
Jaclyn A.
Rebstock
 ,
Quansong
Zhu
and
L. Robert
Baker
,
Quansong
Zhu
and
L. Robert
Baker
 *
*
Department of Chemistry and Biochemistry, The Ohio State University, Columbus, Ohio 43210, USA. E-mail: baker.2364@osu.edu
First published on 15th June 2022
Abstract
Hydrated cations present in the electrochemical double layer (EDL) are known to play a crucial role in electrocatalytic CO2 reduction (CO2R), and numerous studies have attempted to explain how the cation effect contributes to the complex CO2R mechanism. CO2R is a structure sensitive reaction, indicating that a small fraction of total surface sites may account for the majority of catalytic turnover. Despite intense interest in specific cation effects, probing site-specific, cation-dependent solvation structures remains a significant challenge. In this work, CO adsorbed on Au is used as a vibrational Stark reporter to indirectly probe solvation structure using vibrational sum frequency generation (VSFG) spectroscopy. Two modes corresponding to atop adsorption of CO are observed with unique frequency shifts and potential-dependent intensity profiles, corresponding to direct adsorption of CO to inactive surface sites, and in situ generated CO produced at catalytic active sites. Analysis of the cation-dependent Stark tuning slopes for each of these species provides estimates of the hydrated cation radius upon adsorption to active and inactive sites on the Au electrode. While cations are found to retain their bulk hydration shell upon adsorption at inactive sites, catalytic active sites are characterized by a single layer of water between the Au surface and the electrolyte cation. We propose that the drastic increase in catalytic performance at active sites stems from this unique solvation structure at the Au/electrolyte interface. Building on this evidence of a site-specific EDL structure will be critical to understand the connection between cation-dependent interfacial solvation and CO2R performance.
1 Introduction
Electrochemical CO2 reduction (CO2R) is one of the most promising techniques in converting excess atmospheric CO2 to renewable feedstocks.1–4 The major challenge for large-scale CO2R is engineering an efficient catalyst that can perform CO2R with high product selectivity, low overpotentials, and long-term stability. Among the various products that can be formed from CO2R, the two-electron/two-proton reduction of CO2 to carbon monoxide (CO) has been a large research focus, owing to the practical applications of CO.4,5 Nanostructured Au is reported to have high catalytic efficiency and selectivity in converting CO2 to CO, garnering a large interest in the study of CO2R on Au catalysts.4,6,7 Although the mechanisms of the intricate CO2R reaction have been extensively studied at the Au/electrolyte interface, additional understanding of the interfacial properties that ultimately control the efficiency of CO2R is needed to enable practical applications of electrochemical CO2R.Among the many factors that mediate CO2R on metal surfaces, hydrated cations within the electrochemical double layer (EDL) strongly influence both activity and selectivity,8–11 although the exact mechanism remains a topic of significant interest. Although specific cation effects on electrocatalytic CO2R were reported as early as 1969,12 this subject has recently become a topic of renewed interest owing to its importance for efficient CO2 conversion.8,13–16 A number of mechanisms have been proposed to explain this observation, which include the cation-dependent potential drop across the OHP (i.e. Frumkin potential),14,15,17 buffering of the interfacial pH via cation hydrolysis reactions,8 and interfacial electric field effects on the electron transfer rate.10,15,18 Specifically, Singh et al. showed cation-dependent CO2R activity to follow the trend of Cs+ > Rb+ > K+ > Na+ > Li+ on Ag and Cu surfaces,8 and attributed this effect to the fact that cations with larger atomic radii, such as Cs+ and Rb+, have lower pKa values, suggesting that cation hydrolysis reactions buffer the interfacial pH during CO2R. Because the size of the hydrated cation determines the position of the outer Helmholtz plane (OHP), electric field effects may also contribute to cation-dependent CO2R activity.15,17 Ignoring effects of explicit solvation, the electric field generated between the electrode surface and the OHP is inversely proportional to the radius of the hydrated cation. Strong electric fields favor a bent CO2 configuration due to field-dipole coupling.10,19 Although a significant barrier exists for electron transfer from a metal electrode to linear CO2, electron transfer to bent CO2 is facile.19 A growing number of studies have concluded that specific cation effects are a result of the interfacial electric field that varies with the effective hydration radius of the electrolyte cation.11,20 In each of these studies, it is assumed that cation hydration at the interface follow bulk trends, where Li+ > Na+ > K+ > Rb+ > Cs+. Although CO2R on metal electrodes is a highly structure sensitive reaction, indicating that a small fraction of total surface sites may account for a majority of the observed catalytic turnover, few studies to date account for the possibility of a unique electrochemical double layer (EDL) structure at sparse catalytically active surface sites under applied potential. Our recent work has highlighted the importance of studying the interfacial solvation structure within the EDL by showing that CO2R activity is closely correlated with effects of specific cations on the solvation-induced Onsager reaction field during CO2R.13
Liu et al. previously investigated the role of structure sensitivity and found that nanostructured surfaces possessing high curvature lead to intense local electric fields that increase the presence of interfacial cations, and consequently, CO2 concentrations at the surface.21 We note that strong local electric fields at nanostructured surfaces may also influence local solvation structures of the hydrated cations. In addition to effects of nanoscale surface structure, atomic-scale structure (i.e. facet dependence) also has a significant influence on CO2R kinetics. Back et al. showed computationally that exact structure sensitivity differs for different metals.22 Comparing low index terraces with edge sites and corner sites, it was found that edge sites are most active for CO2R on Ag electrodes, while corner sites are most active on Au electrodes, with terraces being the least active on either metal. This prediction is consistent with single crystal studies using Au(111), Au(110), and Au(221) electrodes, where Mezavilla et al. showed that low coordination sites are 20-fold more active than planar terraces sites, and site selective underpotential deposition of Pb confirmed that low coordination sites on these single crystal surfaces account for nearly the entire observed CO current during CO2R.23 Marcandalli et al. also showed that both CO2R rate and CO adsorption on Au is surface facet dependent.24 Although the current work focuses on Au electrodes, additional studies have shown that CO2R on Cu is also strongly structure sensitive.25–27 DFT calculations of surface kinetics in the absence of explicit solvent often fail to reproduce these order of magnitude changes in site-specific CO2R activity,28,29 suggesting that in addition to molecule–surface interactions, local solvation structure plays a significant role in determining site-specific CO2R activity.
Surface adsorbed CO has been widely used as a vibrational Stark reporter to probe the interfacial solvation structure and electric field inside the EDL.11,13,14,30–32 Unlike other metals such as Cu and Pt, in situ generated CO on Au produces low spectroscopic signals due to both a low density of surface active sites as well as weak CO adsorption resulting in a low steady state coverage.22,23 For this reason, many studies opt to increase the CO surface concentration by directly purging CO into the electrolyte. Direct adsorption of CO on Au is also potential dependent with adsorption favored at −0.1 V vs. SCE, significantly above the onset for CO2R.33,34 Consequently, CO on Au can also be detected by a potential jump from negative to positive bias following accumulation of CO in the electrolyte by prolonged CO2R. Both of these approaches lead to sampling primarily inactive spectator sites, which occupy most of the Au surface. Owing to the strong structure sensitivity of CO2R, Stark tuning measurements of CO adsorbed indiscriminately on Au may not provide reliable information on the site dependent solvation structure at catalytic active sites. In this study using plasmon-enhanced vibrational sum frequency generation (VSFG), we demonstrate the capability of detecting two distinct binding sites for CO on Au measured at the Au/MHCO3 (M = Li+, Na+, K+, Rb+, or Cs+) electrolyte interface during active CO2R electrocatalysis. Selective poisoning of catalytic active sites reveals that one of these species is the result of in situ CO2R at catalytic active sites, while the other species correlates to spectator CO. This ability to use in situ generated CO as a Stark reporter of catalytic active sites reveals a unique cation-dependent EDL structure, which must be explicitly considered in order to obtain a molecular understanding of the strong structure sensitivity of CO2R electrocatalysis on Au.
2 Results
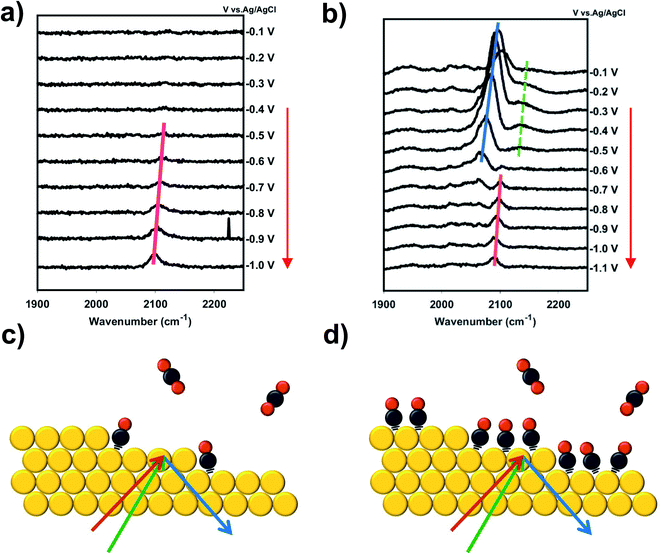
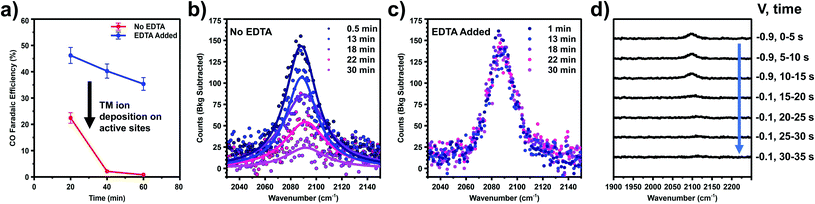
Fig. 1 shows VSFG measurements of CO adsorbed on a Au electrode as a function of potential during a scan from more positive potential (top) to negative potential (bottom). All potentials are reported relative to Ag/AgCl reference electrode. 0.1 M RbHCO3 electrolyte was prepared from high purity salts and purged with either CO2 or CO (see ESI† Section 2). During direct CO2 purging a single peak is observed, which appears near the onset of CO2R around −0.6 V and increases in intensity at more negative potentials (Fig. 1a). In contrast, two main peaks are observed under direct CO purging, which are differentiated by their slightly different frequency shifts, and more noticeably by their distinct potential-dependent adsorption profiles (Fig. 1b). At less negative potential, a prominent feature around 2090 cm−1 is observed, consistent with previous reports of CO adsorbing to Au in the atop geometry.35,36 The intensity of this peak grows from −0.1 V to −0.2 V and then begins to decrease at −0.3 V, disappearing completely by −0.8 V. This intensity profile closely matches the previously reported potential-dependent adsorption behavior of CO on Au.33,36 This same peak has been observed in a number of previous studies,14,31,37 and we assign this feature to the direct adsorption of CO at spectator sites (COSS). A second feature is also present under CO purging but this peak is relatively weak and is only observed near or below the onset of CO2R. The frequency and potential dependent intensity profile of this feature closely matches the single feature observed under CO2 purging conditions. This peak, which is present under both CO2 and CO purging conditions, matches previous reports of in situ generation of CO during active CO2R.13,30 The early detection of the CO intermediate feature has been reported previously in other spectroscopic measurements.38,39 The frequency of this feature is consistent with atop adsorption.36,40 However, we observe a shift to slightly higher frequency compared to COSS. If it is considered that Au sites on terraces are highly coordinated, the high local electron density around these sites can back donate to the π* orbital of the adsorbed CO. In contrast, the shift to higher frequency suggests that this CO is bound to under-coordinated Au atoms having lower electron density and less propensity for π back donation. This is consistent with previous observations that low coordinate sites on Au are more active for CO2R.22–24 We assign this feature to in situ generated CO at active sites (COAS), as discussed further below. However, we cannot eliminate the possibility that some spectator CO adsorption to active sites or re-adsorption of CO produced from initial step cycling contributes to this feature. These assignments for COAS and COSS are schematically depicted in Fig. 1c and d. In the case of direct CO purging, a small third peak appears as a shoulder on the high frequency side of the COSS feature. This peak can be differentiated from COAS by its potential-dependent adsorption profile and Stark tuning slope, both of which closely follow the main COSS feature. We attribute this to multiple binding sites for spectator CO on these polycrystalline electrodes. However, because Stark tuning slopes for this weak shoulder are difficult to accurately fit, the analysis below focuses only on the primary COSS and COAS features. Below we describe how COAS and COSS represent local probes of site-specific solvation structure, which is found to differ significantly between catalytic active sites and surface spectator sites. However, first we briefly discuss the role of catalyst deactivation by trace metal ion deposition.Two experiments have been performed to confirm that the peak observed near the onset of CO2R (COAS) represents the in situ generation of CO from CO2, produced at catalytically active sites on the Au electrode. The first experiment is based on selective poisoning of active sites by trace metal ion deposition. Fig. 2a shows the faradaic efficiency for CO generation from the Au electrode as a function of time. A comparison is made between two scenarios: one in which no pre-purification of the electrolyte is employed showing the effects of Au deactivation due to the deposition of trace metal ion impurities, and another in which disodium ethylenediaminetetraacetate (EDTA) has been added to the electrolyte to prevent trace metal ion deposition.41 It can be seen that while the initial CO faradaic efficiency is similar in the two cases, in the absence of EDTA the Au catalyst deactivates to near-zero faradaic efficiency within 1 h. This is consistent with previous reports by our group and others showing rapid deactivation of an unprotected Au electrode.41–44 In contrast, less than 10% of this deactivation is observed in the presence of EDTA, indicating that deactivation is primarily the result of deposition of trace amounts of contaminant ions on the Au surface. Below we show that these ions can be detected post reaction and quantified using X-ray photoelectron spectroscopy (XPS) to obtain an upper-limit estimate of the active site density responsible for CO production from CO2.
Fig. 2b and c compare the intensity vs. time at fixed potential (−1.1 V vs. Ag/AgCl) for the peak assigned as COAS in the absence (Fig. 2b) and presence (Fig. 2c) of EDTA. As shown, in the absence of EDTA the peak intensity decays almost to zero over the time scale of catalyst deactivation, indicating that the observed CO is being produced in situ via the electrocatalytic reduction of CO2. In the presence of EDTA, we observe that this peak intensity remains nearly constant over this same time period. Although this species is correlated with in situ CO generation, it is still possible that CO produced at active sites can migrate in solution and re-adsorb on Au, which would yield this species an inaccurate Stark reporter of EDL structure at catalytic active sites. To rule out this possibility, Fig. 2d shows the results of a potential step experiment where the peak assigned as COAS is monitored as a function of time during a sudden change in potential. To monitor the time-dependent intensity across this potential step, each spectrum in Fig. 2d has been averaged for only 5 s, compared to 120 s for other spectra reported. Initially, the Au electrode is held at a fixed potential of −0.9 V vs. Ag/AgCl resulting in the observation of in situ generated CO. After 15 s, the potential is suddenly increased to −0.1 V vs. Ag/AgCl where CO2R is no longer active, but at this potential any CO present in the solution will readily adsorb to the Au electrode.33,36 Due to active purging of the electrolyte with CO2 to facilitate mass transfer, we observe that the COAS intensity decays to zero in less than 10 s. This decay period is much shorter than a normal integration, indicating that the signal observed here represents the active turnover of CO2 to CO at active sites and does not contain a significant contribution from re-adsorption of solution phase CO at spectator sites. Consequently, we treat this species as a Stark probe capable of uniquely reporting on the cation-dependent EDL structure at active sites on Au.
Based on quantification of the ion deposition onto a fully deactivated Au electrode, it is possible to estimate the upper limit for active site density on these catalysts. XPS spectra in Fig. 3 reveal ion deposition onto the Au electrode. High-resolution XPS measurements of the Au 4f, Cu 2p, and Zn 2p binding energy regions were taken following exposure to various experimental conditions. While Cu, Zn, Fe, and Pb have all been detected as trace metal impurities in (bi)carbonate electrolyte salts,4,41,42 previous work has shown that only Cu and Zn deposit on Au under CO2R potentials.41 As expected, the bare Au electrode (pre-electrolysis) shows no Cu or Zn deposition on the surface. After 60 min of electrolysis under −1.2 V vs. Ag/AgCl, taken in conjunction with simultaneous kinetics measurements that confirm complete Au deactivation, post-reaction XPS shows that Cu is present on the catalytic surface with a bulk atomic ratio of 0.7% compared to Au (XPS fitting details are included in ESI† Section 4). The XPS measurements were repeated multiple times giving a range of Cu atomic fractions, and this result is representative of the Cu and Zn detected across multiple observations. Zn was not detected after 60 min of electrolysis. However, it is possible that Zn deposits on the surface below the XPS detection limit. To account for the possibility of rapid cation stripping following the removal of bias from the electrode, additional XPS samples were prepared by removing the Au electrode from the system under bias. We found negligible differences in Cu and Zn deposition when compared to removing the electrode without polarization. A 16 h electrolysis control shows that under long electrolysis times, metal deposition saturates the active sites and the concentration of Cu and Zn increase on the surface over time (see ESI† Section 4). Even in these extended electrolysis experiments, we did not observe any detectable Pb or Fe, consistent with previous observation that only Cu and Zn deposit on Au under the specified conditions.41 Despite additional metal ion deposition during extended electrolysis, complete deactivation of CO production is observed after only 60 min indicating that the surface concentration of metal deposited during this period represents an upper limit to the active site density. This control also shows that both Cu and Zn are capable of deposition under these electrolysis conditions. We have also carefully considered the possibility of Pt leaching and show that the observed CO signal is not the result of CO binding to Pt sites based on XPS and VSFG control measurements (ESI† Section 4). First, no Pt 4f signal was present post-electrolysis. Although a Au feature can be seen in this binding energy region, we have previously shown that the signal is due to the Au 5p energy overlap, and not Pt deposition on the Au electrode.13 Second, as shown in Fig. 2b, CO spectra obtained without the presence of EDTA shows that the intensity decreases with time. This observation cannot be attributed to Pt deposition on the Au electrode, which would rather show an increasing intensity as a function of time. Consequently, we exclude the possibility of Pt contamination interference in these spectral assignments. Even still, all experiments employed a Nafion membrane to separate the Au working electrode from the counter electrode.
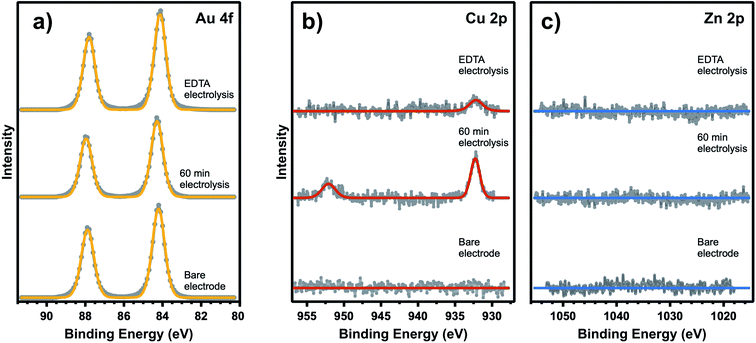 | ||
| Fig. 3 XPS measurements of (a) Au 4f, (b) Cu 2p, and (c) Zn 2p of a Au electrode as-deposited and following 60 min electrolysis in 0.1 M NaHCO3 electrolyte with and without addition of 3.4 μM EDTA. | ||
We now consider the upper limit to active site density on Au based on these XPS measurements. Due to an XPS probe depth of ∼6 nm into the Au electrode (ESI† Section 4), the surface signal of the Au 4f XPS peak must be elucidated from the bulk signal in order to accurately describe the atomic ratio of metal ions deposited on top of the Au surface. Accounting for the surface-to-bulk signal ratio (ESI† Section 4), the upper limit to the measured Cu atomic fraction of 0.7% actually represents 3.6% of the Au surface. XPS limit of detection (LOD) calculations (ESI† Section 4) also provide a LOD for Zn on the Au surface as 0.5%, which should factor into quantifying the trace metal deposition on the Au surface. From these calculations, we can see that metal deposition on 4% of the surface causes 100% loss of CO2R activity. While it is known that trace metals will preferentially deposit on the Au active sites, it is possible to have some degree of deposition at inactive spectator sites during the measurements and also in the short time between the actual surface deactivation and the end of electrolysis. Therefore, this quantity only provides an upper limit to active site density, and the majority of CO2R activity is expected to occur at less than 4% of the surface. This approximate active site density is consistent with the findings based on selective poisoning of single crystal electrodes, which showed that low coordination sites are 20-fold more active than planar terraces sites for CO2R on Au.23 Additionally, in agreement with the results shown in Fig. 2a, the addition of EDTA to the electrolyte solution shows no observable Cu or Zn deposition after 60 min of electrolysis.
Taking 4% as the upper limit to active site density, turnover frequency (TOF) values for CO2R were estimated. First, the average TOF is first calculated by taking into account the partial CO current density over the total Au surface. The total number of Au surface sites on the electrode was estimated from the known single site area based on a 0.238 nm Au lattice spacing, assuming a (111) surface for simplicity, over the entire electrochemical surface area, which was previously determined to be 1.2 cm2.43 This calculation estimates the total number of Au sites on the electrode to be 2.2 × 1015. Using the total number of Au sites, the partial CO current represents an average TOF of 0.45 s−1. However, considering that at most only 4% of the total surface sites are active for CO production, the TOF at active sites is at least 25-fold higher, or 11.20 s−1, indicating that significantly higher local activity is present at select sites on the catalyst surface. To gain insight into the mechanism of enhanced CO2R at specific actives sites, we investigate the cation-dependent Stark tuning slopes. Using Gouy–Chapman–Stern (GCS) theory, we use the measured Stark tuning slope to estimate the distance from the Au electrode to the OHP in an attempt to better understand the site-specific solvation structure. Comparing results for COAS and COSS reveals the presence of a unique EDL structure at sites that are highly active for CO2R compared to less active, spectator sites as described below.
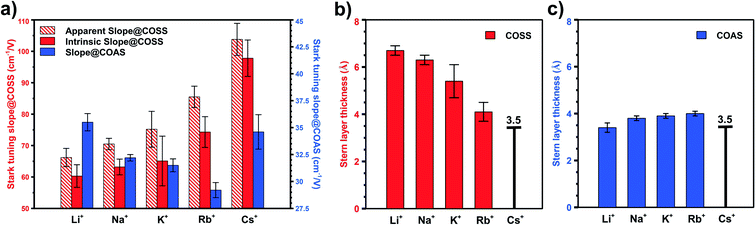
As these two types of CO serve as local probes for different sites, it enables the study of site-specific interfacial structure by looking into their potential-dependent Stark tuning behavior, i.e. how fast the frequency shifts with applied potential.13,17 For example, in the case of Rb+ (Fig. 1b), the Stark tuning slope for COAS and COSS are 31 cm−1/V and 81 cm−1/V, respectively. We repeated the direct CO purging experiment for all alkali cations (ESI† Section 5) and the averaged Stark tuning slopes of a couple of trials for both COSS and COAS are shown in Fig. 4a. Interestingly, the Stark tuning slopes exhibit opposite trends for the two CO reporters as a function of cation. The Stark tuning slope increases for COSS from Li+ to Cs+, but decreases for COAS from Li+ to Rb+, with Cs+ as an anomaly. In fact, the trend in the Stark tuning slope observed for COAS is also opposite to that previously reported for spectator CO.14 This observation must be carefully considered when seeking to provide an accurate understanding of specific cation effects and the role of the EDL in CO2R.
While Fig. 4a reveals a nearly opposite trend for alkali cation effects on the Stark tuning slope of COAS compared to the more widely studied COSS, we now seek a quantitative estimate of the distance from the electrode surface to OHP, which influences both the electric field and interfacial solvation structure during CO2R. We note here that multiple factors can influence the absolute measured CO frequency. These effects include chemical shifts due to site-specific bonding and dipolar coupling, in addition to the actual vibrational Stark effect.45–48 Chemical shifts refer to changes in adsorbate bonding with the substrate, which influences the absolute frequency and the rate of change with applied field.47 As discussed above, CO binding is sensitive to the degrees of π back donation, which varies for different sites on a metal surface.49 Thus, the absolute frequency and the observed Stark tuning rate is sensitive to the site-specific adsorption of the CO Stark reporter.50,51 In addition to chemical effects, dipolar coupling results in frequency shifts due to interactions between adsorbed dipoles, such that potential-dependent changes in the surface coverage of CO must also be considered. However, as described in the ESI† Section 6, it is possible to separate the effect of potential-dependent dipolar coupling from the vibrational Stark effect as demonstrated previously.52,53 Properly accounting for dipolar coupling enables more accurate calculation of the true vibrational Stark effect.45 Within the framework of GCS theory, the Stark tuning slope can then be related to the distance from electrode surface to the OHP (see ESI† Section 8), thereby providing information on the site-specific solvation structure during CO2R on Au.
We begin by excluding the dipolar coupling effect on the observed (apparent) Stark tuning slope by performing the potential-jump experiment, as described in previous studies.52,53 Details of this procedure are provided in Section 6 of the ESI.† Frequency shifts caused by dipolar coupling will be most prominent with high adsorbate coverage, and therefore, must be considered in the case of COSS. For COSS, the dipolar coupling effect is shown to only account for about 10% of the apparent Stark tuning slope, and the intrinsic Stark tuning slope after excluding dipolar coupling effects still follows the same trend as a function of cation, as shown in Fig. 4a. Regarding COAS, since the population of active sites is very low (<4%, as discussed above), we expect that the coverage of in situ generated CO is below the threshold surface coverage for dipolar coupling.30,54,55 However, it has recently been shown that even low pressures of CO can induce surface reconstruction of metal electrodes forming under-coordinated nanostructures on the surface that are stabilized by clusters of adsorbed CO.65,66 Consequently, we cannot exclude the possibility that some dipolar coupling influences the observed Stark tuning slope even for COAS, and this would depend on the actual dispersion of active sties on the electrode. Fig. 4a shows three different Stark tuning slopes as a function of alkali cation: (1) the apparent Stark tuning slope for COSS, including effects of dipolar coupling (red stripes), (2) the intrinsic, or actual, Stark tuning slope for COSS (red solid), with effects of dipolar coupling removed, and (3) the intrinsic Stark tuning slope for COAS (blue solid). We note that the magnitudes of the COAS Stark tuning slopes during CO purging are slightly larger than what has been previously reported during CO2 purging,13 which may be due to dipolar coupling effects resulting from CO-induced surface reconstruction.
Estimates for the OHP at both active and spectator sites can be derived from the intrinsic Stark tuning slopes in the context of GCS theory, but this calculation requires knowledge of the site-dependent Stark tuning rate 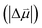 shown in eqn (1).
shown in eqn (1).
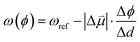 | (1) |
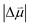 is known, it is possible to obtain Δd from the experimentally determined Stark tuning slope following removal of dipolar coupling effects as reported in Fig. 4a.
is known, it is possible to obtain Δd from the experimentally determined Stark tuning slope following removal of dipolar coupling effects as reported in Fig. 4a.
In fact, the value of 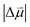 will be sensitive to the specific site of CO adsorption50,51 because varying degrees of π back donation will influence the rate at which CO frequency shifts under the influence of an interfacial electric field. Consequently, any attempt to quantify the OHP will be subject to uncertainty in the site-dependent value assumed for
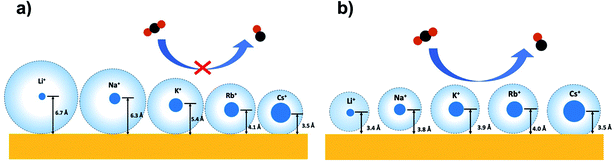
will be sensitive to the specific site of CO adsorption50,51 because varying degrees of π back donation will influence the rate at which CO frequency shifts under the influence of an interfacial electric field. Consequently, any attempt to quantify the OHP will be subject to uncertainty in the site-dependent value assumed for 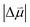 . To estimate the OHP and observe how this distance varies as a function of cation, we consider the following: it has been previously observed that Cs+ can partially desolvate upon adsorption to a metal electrode due to its low hydration free energy. We also observe evidence of Cs+ partial desolvation in the present VSFG measurements, which show that at CO2R active sites the Stark tuning slope increases from Li+ to Rb+ with increasing cation size but decreases for Cs+, suggesting a partial loss of the cation's hydration shell. This has further been observed using X-ray scattering measurements on a Pt electrode where it was shown that the OHP of a Cs+ electrolyte is 3.5 Å, which is smaller than the single layer hydrated radius for Cs+.56 Importantly, these X-ray scattering measurements were not specific to any particular active site, indicating that due to its low hydration free energy, the OHP for Cs+ is approximately 3.5 Å even at planar terrace sites. We note that partial desolvation of Cs+ can decrease the distance to the OHP even in the absence of significant charge transfer between Au and Cs+, and here we refer only to partial desolvation rather than specific cation adsorption, which would denote chemical bonding to the surface.
. To estimate the OHP and observe how this distance varies as a function of cation, we consider the following: it has been previously observed that Cs+ can partially desolvate upon adsorption to a metal electrode due to its low hydration free energy. We also observe evidence of Cs+ partial desolvation in the present VSFG measurements, which show that at CO2R active sites the Stark tuning slope increases from Li+ to Rb+ with increasing cation size but decreases for Cs+, suggesting a partial loss of the cation's hydration shell. This has further been observed using X-ray scattering measurements on a Pt electrode where it was shown that the OHP of a Cs+ electrolyte is 3.5 Å, which is smaller than the single layer hydrated radius for Cs+.56 Importantly, these X-ray scattering measurements were not specific to any particular active site, indicating that due to its low hydration free energy, the OHP for Cs+ is approximately 3.5 Å even at planar terrace sites. We note that partial desolvation of Cs+ can decrease the distance to the OHP even in the absence of significant charge transfer between Au and Cs+, and here we refer only to partial desolvation rather than specific cation adsorption, which would denote chemical bonding to the surface.
Based on these observations, we take the value of 3.5 Å obtained by X-ray scattering to represent a reasonable estimate for the OHP in a Cs+ electrolyte. Assuming this value for the OHP distance, we calibrate the Stark tuning rate for COAS and COSS (ESI† Section 8). Although this approximation introduces some uncertainty in the absolute OHP values, the trend as a function of cation is unaffected. Below we show that the cation-dependent OHP values calculated by this method actually agree quite well with previously predicted solvation radii for the alkali cations. Most importantly these results indicate that at inactive, spectator sites cations in the EDL retain nearly their entire bulk hydration shells, while at catalytically active sites, the EDL consists of only a single water layer between the Au electrode and the alkali cation.
To illustrate this, Fig. 4b shows the calculated distance from the Au electrode to the OHP at inactive spectator sites as a function of cation from Li+ to Rb+, and Fig. 4c shows the analogous results for catalytic active sites. In both cases, the assumed OHP for Cs+ is used as a calibration point. Fig. 5 illustrates how these two sets of results compare to the bulk hydration radius and the single layer hydration radius, respectively. Fig. 5a shows the estimated OHP for each cation observed at inactive spectator sites, where the smaller dark blue circles represent the crystal radius for each alkali cation, and the large light blue circles represent the corresponding bulk hydration radius reported by Ringe et al.11 As shown, there is close agreement between the measured OHP and the bulk hydration radius, which decreases from Li+ to Cs+, consistent with previous Stark tuning measurements of CO at spectator sites.14 In contrast, Fig. 5b shows the results for catalytic active sites, where the inner blue circles represent the cation crystal radius, and the outer blue circles represent the thickness of a single layer of water (i.e. the first hydration layer, calculated from the reported cation-oxygen distance57 plus 0.99 Å O–H bond length58). Here we also observe almost exact agreement between the measured OHP and the first hydration layer. This indicates that in contrast to the majority of Au surface sites, only a single layer of water exists between catalytic active sites and the electrolyte cation.
3 Discussion
In summary, the results of this work are consistent with previous reports showing that specific active sites on a Au electrode have a much higher turnover frequency than the majority of surface atoms for the structure sensitive CO2R reaction. Selective poisoning experiments indicate that these active sites occupy approximately 4% or less of the total surface, yet are responsible for nearly all of the CO2R selectivity on polycrystalline Au electrodes, with other sites primarily producing H2. Based on previous characterization of CO2R kinetics on single crystal electrodes, we attribute these highly active surface sites to under-coordinated Au atoms, such as step edges, kinks, adatoms, or grain boundaries. Despite numerous reports using CO as a vibrational Stark reporter on Au, prior studies have focused on direct adsorption of CO, which indiscriminately samples surface atoms on the Au electrode. Although useful for understanding interfacial electric fields and EDL structure at the Au/electrolyte interface, these previous measurements are insensitive to the possibility of unique interfacial solvation at catalytic active sites, which are present only at very low densities on the Au surface. Using in situ VSFG measurements with a detection limit less than 1% of a surface monolayer,30 two types of CO (COAS and COSS) are identified in the present study. In situ VSFG measurements during selective poisoning as well as potential jump experiments confirm that the peak assigned as COAS represents a Stark reporter of cation-dependent solvation structure at catalytic active sites, providing a unique window into the interfacial solvation structure at surface sites showing anomalously high activity for CO2R.The importance of selectively probing solvation structures at catalytic active sites is illustrated in Fig. 4a, which shows that Stark tuning slopes show nearly opposite trends as a function of alkali cation at active sites compared to inactive, spectator sites. These measurements also provide a basis for estimating the distance from the electrode surface to the OHP in the presence of the various alkali cations. Results indicate that while cations retain nearly their entire bulk hydration shell upon adsorption to inactive terrace sites, active sites appear to have only a single aligned water molecule between the Au surface and the adsorbed cation. The different solvation structures at the two types of surface sites may result from enhanced electric fields at active sites, which could lead to partial or full cation desolvation.21,59,60
The experimental evidence provided in this work introduces a site-dependent solvation structure that is strongly correlated with catalytic performance. Here we provide some possible explanations for this correlation based on theories from literature. First, the suppressed hydration shell at active sites could contribute to the enhanced catalytic performance compared with the bulk-like cation hydration present at spectator sites. Loss of bulk solvation could enhance the coordination between cations and surface adsorbates and stabilize the reaction intermediates.9,61 Alternatively, it could strengthen the electric field present between the Au surface and the OHP because of the compressed Stern layer.10,13,21 A single hydration layer around active sites also suggests strong alignment of interfacial water molecules, which could explain the strong Onsager reaction fields, which were previously reported to correlate with cation-dependent solvation structure.13 Last but not least, the larger solvation shell at spectator sites can also undermine the proton transfer process as a result of more disordered H-bonding network.13,62,63 This is consistent with the finding that the proton is involved in the rate determining step of CO2R at high overpotentials.10,21
A number of studies have indicated that specific cation effects are a result of electric field activation of electron transfer due to coupling with the dipole of bent CO2, facilitating the formation of CO2−.10,19,64 However, these studies typically assume that the cation-dependent interfacial electric field follows a trend where heavier cations such as Rb+ and Cs+ display an enhanced field due to their smaller solvated radii at the interface. This assumption is inconsistent with the present findings showing that this only applies to inactive spectator sites, while active sites show an opposite trend. Electric field effects may still contribute significantly to CO2 activation, but inclusion of the Onsager or solvation-induced reaction field resulting from alignment of interfacial water molecules at catalytic active sites appears to play a significant role in determining the net cation-dependent interfacial field.13
4 Conclusion
Although additional studies are required to fully explore the complex CO2R mechanism, this work elucidates the distinct solvation structure at highly active sites compared to inactive spectator sites. To reach this conclusion, we investigated the vibrational Stark tuning effect of CO adsorbed to inactive spectator sites and active sites on a Au electrode where we observed site-specific Stark behavior. Through Stark tuning analysis, we conclude that hydrated cations at the interface retain their bulk hydration shells over the majority of the surface's inactive terrace sites, which is consistent with studies that have previously probed interfacial solvation structure at these sites. However, cations adsorbed at under-coordinated active sites show an opposing cation-dependent solvation trend and indicates an overall smaller hydration shell consisting of a single hydration layer. These results affirm that solvation structure is critical to CO2R activity, where the anomalous EDL structure at a small fraction of the total surface is correlated with a ≥25-fold enhancement of catalytic activity. Based on these findings, proposed mechanisms for specific cation effects in CO2R should be re-evaluated in light of the surface site-dependent solvation structures, which indicate that improved control over CO2R kinetics will require explicit understanding of cation-dependent interfacial solvation.Author contributions
Jaclyn A. Rebstock performed VSFG, kinetics, and XPS measurements, analyzed and interpreted results, and was involved in writing the manuscript. Quansong Zhu helped perform VSFG measurements and analyzed the results. L. Robert Baker conceptualized the project, planned experiments, supervised the research, acquired funding, and was involved in writing the manuscript.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported by Chemical Sciences, Geosciences and Biosciences Division, Office of Basic Energy Sciences, Office of Science, U.S. Department of Energy under DOE Grant No. DE-SC0020977. Film deposition was performed at the OSU Nanotech West laboratory. XPS was performed at the Ohio State University Surface Analysis Laboratory.Notes and references
- S. Chu and A. Majumdar, Nature, 2012, 488, 294–303 CrossRef CAS PubMed.
- D. T. Whipple and P. J. Kenis, J. Phys. Chem. Lett., 2010, 1, 3451–3458 CrossRef CAS.
- E. V. Kondratenko, G. Mul, J. Baltrusaitis, G. O. Larrazábal and J. Pérez-Ramírez, Energy Environ. Sci., 2013, 6, 3112–3135 RSC.
- Y. Hori, in Modern Aspects of Electrochemistry, Springer, 2008, pp. 89–189 Search PubMed.
- A. A. Peterson, F. Abild-Pedersen, F. Studt, J. Rossmeisl and J. K. Nørskov, Energy Environ. Sci., 2010, 3, 1311–1315 RSC.
- W. Zhu, R. Michalsky, O. Metin, H. Lv, S. Guo, C. J. Wright, X. Sun, A. A. Peterson and S. Sun, J. Am. Chem. Soc., 2013, 135, 16833–16836 CrossRef CAS PubMed.
- H. Mistry, R. Reske, Z. Zeng, Z.-J. Zhao, J. Greeley, P. Strasser and B. R. Cuenya, J. Am. Chem. Soc., 2014, 136, 16473–16476 CrossRef CAS PubMed.
- M. R. Singh, Y. Kwon, Y. Lum, J. W. Ager III and A. T. Bell, J. Am. Chem. Soc., 2016, 138, 13006–13012 CrossRef CAS PubMed.
- M. C. Monteiro, F. Dattila, B. Hagedoorn, R. García-Muelas, N. López and M. Koper, Nat. Catal., 2021, 4, 654–662 CrossRef CAS.
- L. D. Chen, M. Urushihara, K. Chan and J. K. Nørskov, ACS Catal., 2016, 6, 7133–7139 CrossRef CAS.
- S. Ringe, E. L. Clark, J. Resasco, A. Walton, B. Seger, A. T. Bell and K. Chan, Energy Environ. Sci., 2019, 12, 3001–3014 RSC.
- W. Paik, T. Andersen and H. Eyring, Electrochim. Acta, 1969, 14, 1217–1232 CrossRef CAS.
- Q. Zhu, S. K. Wallentine, G.-H. Deng, J. A. Rebstock and L. R. Baker, JACS Au, 2022, 2, 472–482 CrossRef CAS PubMed.
- G. Hussain, L. Pérez-Martínez, J.-B. Le, M. Papasizza, G. Cabello, J. Cheng and A. Cuesta, Electrochim. Acta, 2019, 327, 135055 CrossRef CAS.
- M. M. Waegele, C. M. Gunathunge, J. Li and X. Li, J. Chem. Phys., 2019, 151, 160902 CrossRef PubMed.
- A. S. Malkani, J. Anibal and B. Xu, ACS Catal., 2020, 10, 14871–14876 CrossRef CAS.
- J. Li, X. Li, C. M. Gunathunge and M. M. Waegele, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 9220–9229 CrossRef CAS.
- S. A. Akhade, I. T. McCrum and M. J. Janik, J. Electrochem. Soc., 2016, 163, F477 CrossRef CAS.
- J. A. Gauthier, M. Fields, M. Bajdich, L. D. Chen, R. B. Sandberg, K. Chan and J. K. Nørskov, J. Phys. Chem. C, 2019, 123, 29278–29283 CrossRef CAS.
- S. Ringe, C. G. Morales-Guio, L. D. Chen, M. Fields, T. F. Jaramillo, C. Hahn and K. Chan, Nat. Commun., 2020, 11, 1–11 CrossRef.
- M. Liu, Y. Pang, B. Zhang, P. De Luna, O. Voznyy, J. Xu, X. Zheng, C. T. Dinh, F. Fan and C. Cao, et al. , Nature, 2016, 537, 382–386 CrossRef CAS PubMed.
- S. Back, M. S. Yeom and Y. Jung, ACS Catal., 2015, 5, 5089–5096 CrossRef CAS.
- S. Mezzavilla, S. Horch, I. E. Stephens, B. Seger and I. Chorkendorff, Angew. Chem., Int. Ed., 2019, 58, 3774–3778 CrossRef CAS PubMed.
- G. Marcandalli, M. Villalba and M. T. Koper, Langmuir, 2021, 37, 5707–5716 CrossRef CAS PubMed.
- Y. Hori, I. Takahashi, O. Koga and N. Hoshi, J. Phys. Chem. B, 2002, 106, 15–17 CrossRef CAS.
- W. J. Durand, A. A. Peterson, F. Studt, F. Abild-Pedersen and J. K. Nørskov, Surf. Sci., 2011, 605, 1354–1359 CrossRef CAS.
- K. J. P. Schouten, E. Perez Gallent and M. T. Koper, ACS Catal., 2013, 3, 1292–1295 CrossRef CAS.
- H. H. Heenen, J. A. Gauthier, H. H. Kristoffersen, T. Ludwig and K. Chan, J. Chem. Phys., 2020, 152, 144703 CrossRef CAS PubMed.
- H. Shang, D. Kim, S. K. Wallentine, M. Kim, D. M. Hofmann, R. Dasgupta, C. J. Murphy, A. Asthagiri and L. R. Baker, Chem. Sci., 2021, 12, 9146–9152 RSC.
- S. Wallentine, S. Bandaranayake, S. Biswas and L. R. Baker, J. Phys. Chem. C, 2020, 11, 8307–8313 CAS.
- C. M. Gunathunge, V. J. Ovalle and M. M. Waegele, Phys. Chem. Chem. Phys., 2017, 19, 30166–30172 RSC.
- C. M. Gunathunge, J. Li, X. Li and M. M. Waegele, ACS Catal., 2020, 10, 11700–11711 CrossRef CAS.
- S.-G. Sun, W.-B. Cai, L.-J. Wan and M. Osawa, J. Phys. Chem. B, 1999, 103, 2460–2466 CrossRef CAS.
- E. R. Cave, J. H. Montoya, K. P. Kuhl, D. N. Abram, T. Hatsukade, C. Shi, C. Hahn, J. K. Nørskov and T. F. Jaramillo, Phys. Chem. Chem. Phys., 2017, 19, 15856–15863 RSC.
- M. Gajdoš, A. Eichler and J. Hafner, J. Phys.: Condens. Matter, 2004, 16, 1141 CrossRef.
- A. Wuttig, M. Yaguchi, K. Motobayashi, M. Osawa and Y. Surendranath, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E4585–E4593 CrossRef CAS PubMed.
- M. Dunwell, J. Wang, Y. Yan and B. Xu, Phys. Chem. Chem. Phys., 2017, 19, 971–975 RSC.
- M. Dunwell, Q. Lu, J. M. Heyes, J. Rosen, J. G. Chen, Y. Yan, F. Jiao and B. Xu, J. Am. Chem. Soc., 2017, 139, 3774–3783 CrossRef CAS PubMed.
- Z.-C. Huang-Fu, Q.-T. Song, Y.-H. He, J.-J. Wang, J.-Y. Ye, Z.-Y. Zhou, S.-G. Sun and Z.-H. Wang, Phys. Chem. Chem. Phys., 2019, 21, 25047–25053 RSC.
- A. Wuttig, J. Ryu and Y. Surendranath, J. Phys. Chem. C, 2021, 125, 17042–17050 CrossRef CAS.
- A. Wuttig and Y. Surendranath, ACS Catal., 2015, 5, 4479–4484 CrossRef CAS.
- Y. Hori, H. Konishi, T. Futamura, A. Murata, O. Koga, H. Sakurai and K. Oguma, Electrochim. Acta, 2005, 50, 5354–5369 CrossRef CAS.
- H. Shang, S. K. Wallentine, D. M. Hofmann, Q. Zhu, C. J. Murphy and L. R. Baker, Chem. Sci., 2020, 11, 12298–12306 RSC.
- C. H. Bartholomew, Appl. Catal., A, 2001, 212, 17–60 CrossRef CAS.
- S. D. Fried and S. G. Boxer, Acc. Chem. Res., 2015, 48, 998–1006 CrossRef CAS PubMed.
- P. Dumas, R. Tobin and P. Richards, Surf. Sci., 1986, 171, 579–599 CrossRef CAS.
- J. France and P. Hollins, J. Electron Spectrosc. Relat. Phenom., 1993, 64, 251–258 CrossRef.
- K. P. Lawley, Molecule Surface Interactions, John Wiley & Sons, 2009, vol. 76 Search PubMed.
- H.-Y. Su, M.-M. Yang, X.-H. Bao and W.-X. Li, J. Phys. Chem. C, 2008, 112, 17303–17310 CrossRef CAS.
- D. C. Ferré and J. H. Niemantsverdriet, Electrochim. Acta, 2008, 53, 2897–2906 CrossRef.
- M. J. Weaver, Appl. Surf. Sci., 1993, 67, 147–159 CrossRef CAS.
- X. Chang, H. Xiong, Y. Xu, Y. Zhao, Q. Lu and B. Xu, Catal. Sci. Technol., 2021, 11, 6825–6831 RSC.
- J. H. Pfisterer, U. E. Zhumaev, W. Cheuquepan, J. M. Feliu and K. F. Domke, J. Chem. Phys., 2019, 150, 041709 CrossRef PubMed.
- W.-L. Yim, T. Nowitzki, M. Necke, H. Schnars, P. Nickut, J. Biener, M. M. Biener, V. Zielasek, K. Al-Shamery and T. Klüner, et al. , J. Phys. Chem. C, 2007, 111, 445–451 CrossRef CAS.
- B. A. Zhang, T. Ozel, J. S. Elias, C. Costentin and D. G. Nocera, ACS Cent. Sci., 2019, 5, 1097–1105 CrossRef CAS PubMed.
- Y. Liu, T. Kawaguchi, M. S. Pierce, V. Komanicky and H. You, J. Phys. Chem. Lett., 2018, 9, 1265–1271 CrossRef CAS PubMed.
- Y. Marcus, Chem. Rev., 1988, 88, 1475–1498 CrossRef CAS.
- A. Soper and C. Benmore, Phys. Rev. Lett., 2008, 101, 065502 CrossRef CAS PubMed.
- D. Ghoshal, A. Yoshimura, T. Gupta, A. House, S. Basu, Y. Chen, T. Wang, Y. Yang, W. Shou, J. A. Hachtel, C. J. Idrobo, T.-M. Lu, S. Basuray, V. Meunier, S.-F. Shi and N. Koratkar, Adv. Funct. Mater., 2018, 28, 1801286 CrossRef.
- S. Groh, H. Saßnick, V. G. Ruiz and J. Dzubiella, Phys. Chem. Chem. Phys., 2021, 23, 14770–14782 RSC.
- M. C. Monteiro, F. Dattila, N. López and M. T. Koper, J. Am. Chem. Soc., 2021, 144, 1589–1602 CrossRef PubMed.
- B. Huang, R. R. Rao, S. You, K. Hpone Myint, Y. Song, Y. Wang, W. Ding, L. Giordano, Y. Zhang and T. Wang, et al. , JACS Au, 2021, 1, 1674–1687 CrossRef CAS PubMed.
- A. Hassanali, F. Giberti, J. Cuny, T. D. Kühne and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 13723–13728 CrossRef CAS PubMed.
- K. Chan, Nat. Commun., 2020, 11, 1–4 CrossRef PubMed.
- B. Eren, D. Zherebetskyy, L.L. Patera, C.H. Wu, H. Bluhm, C. Africh, L.W. Wang, G.A. Samorjai and M. Salmeron, Activation of Cu(111) surface by decomposition into nanoclusters driven by CO adsorption, Science, 2016, 351(6272), 475–478 CrossRef CAS PubMed.
- B. Eren, D. Zherebetskyy, Y. Hao, L.L. Patera, L.W. Wang, G.A. Samorjai and M. Salmeron, One-dimensional nanoclustering of the Cu(100) surface under CO gas in the mbar pressure range, Surf. Sci., 2016, 651, 210–214 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: (1) sum frequency generation setup. (2) CO spectra measurement. (3) Kinetics measurement. (4) XPS trace metal deposition and LODs. (5) CO spectra and Stark tuning slopes. (6) Disentangling dipolar-coupling effects. (7) Potential of zero charge measurement. (8) Stark tuning slopes and Stern layer thickness. See https://doi.org/10.1039/d2sc01878k |
| This journal is © The Royal Society of Chemistry 2022 |