Strong non-Arrhenius behavior at low temperatures in the OH + HCl → H₂O + Cl reaction due to resonance induced quantum tunneling

Abstract

The OH + HCl → H₂O + Cl reaction releases Cl atoms, which can catalyze the ozone destruction reaction in the stratosphere. The measured rate coefficients for the reaction deviate substantially from the Arrhenius limit at low temperatures and become essentially independent of temperature when T < 250 K, apparently due to quantum tunneling; however, the nature of the quantum tunneling is unknown. Here, we report a time-dependent wave packet study of the reactions on two newly constructed potential energy surfaces. It is found that the OH + HCl reaction possesses many Feshbach resonances trapped in a bending/torsion excited vibrational adiabatic potential well in the entrance channel due to hydrogen bond interaction. These resonance states greatly induce quantum tunneling of a hydrogen atom through the reaction barrier, causing the reaction rates to deviate substantially from Arrhenius behavior at low temperature, as observed experimentally.

---

In the classical picture, a chemical reaction with an energetic barrier can only occur at collision energies higher than the barrier, which leads to the well-known Arrhenius formula for chemical reaction rates. However, chemical reactions can happen at energies below the reaction barrier through quantum tunneling,^1–3 resulting in the deviation of the reaction rates from the Arrhenius behavior at low temperatures. The effect of quantum tunneling on the reaction rates increases with decreasing reaction temperature, and hence becomes especially important in low-temperature environments such as the interstellar medium and atmospheric processes.^4,5 Reaction resonances are quasi-trapped quantum states in the transition state region with some lifetime, and can substantially promote quantum tunneling through the reaction barrier. Over the past decades, great efforts have been devoted to detecting resonances in chemical reactions and to studying their structures and dynamics.^6–14 Theoretical studies on the O(³P) + HCl → OH + H reaction using the accurate ³A′′ potential energy surface revealed that the tunneling induced by the resonances trapped in the van der Waals well in the reactant channel can substantially enhance the thermal rate constants at low temperatures.^15–17 A combined experimental and theoretical investigation discovered that resonance-induced quantum tunneling dramatically enhances the reactivity of the F + p-H₂ → HF + H reaction,¹⁴ and is fully responsible for the unusually high chemical reactivity of the reaction in the low temperature interstellar medium. Recently, a quantum dynamics calculation showed that the presence of two resonance peaks strongly influence the rotational quenching of HF (j = 1, 2) with H, leading to an up to two-fold increase in the thermal rate coefficients at the low temperatures characteristic of the interstellar medium.¹⁸ Thus, understanding quantum tunneling, and in particular, resonance-induced quantum tunneling, in chemical reactions is of general interest and fundamental importance to low-temperature chemistry.

The OH + HCl → H₂O + Cl reaction is of great importance in atmospheric chemistry because it releases Cl atoms from one of the principal chlorine-containing species in the stratosphere, HCl. The Cl atoms generated from the reaction can catalyze the ozone destruction reaction in the stratosphere, which was responsible for the formation of the ozone hole over Antarctica.¹⁹ Since the chlorine-catalyzed ozone destruction is proportional to the steady-state Cl atom concentration, which is directly controlled by the rate of the reaction, extensive studies have been carried out to measure the rate coefficient for the reaction with high accuracy over a wide range of temperatures.^20–29 The measured rate coefficients exhibit a small activation energy of a few hundred K, deviate substantially from the Arrhenius limit at low temperatures and become essentially independent of temperature when T < 250 K.^25,28,29 In addition, a large H/D kinetic isotope effect has also been found.^21,22,26,28 All these observations suggest the presence of an important quantum tunneling effect in the reaction.

The dynamics of this reaction and its reverse have also attracted great attention in the past decades. In particular, the endothermic Cl + H₂O → HCl + OH reaction with a late barrier has been extensively investigated as a benchmark system for mode specificity and bond selectivity chemistry.^30–35 Recently, the construction of two high-quality potential energy surfaces (PESs) in its ground electronic state using the PIP-NN method have substantially advanced the theoretical study of the dynamics and kinetics of the system. The first PES was based on a large number of ab initio data points calculated at the multi-reference configuration interaction (MRCI) level of theory by Li, Dawes, and Guo (LDG),³³ and the second one was fitted to ab initio energy points obtained using an explicitly correlated unrestricted coupled-cluster method with single, double, and perturbative triple excitations (UCCSD(T)-F12b) and the augmented correlation-consistent polarized valence triple-zeta (aug-cc-pVTZ, or AVTZ) basis set by Zuo, Zhao, Guo, and Xie (ZZGX) with a fitting error of 6.9 meV.³⁶ The static barrier height is 2.86 and 2.23 kcal mol⁻¹, respectively, for these two PESs. On both PESs, there exists a well of about 3.5 kcal mol⁻¹ in the OH + HCl entrance channel due to the hydrogen bond (HB) interaction between OH and HCl. Extensive quantum dynamics studies on the PESs have revealed many interesting features of the reaction in both directions. In particular, time-dependent wave packet calculations for the title reaction with OH in the ground and vibrational excited states found one or two broad peaks in the total reaction probabilities, which are presumed to be the signature of the resonances supported by the reactant complex well.^36,37 However, the impact of these peaks on the reaction rates has not been investigated. Ring-polymer molecular dynamics (RPMD) calculations^38,39 were also carried out on both PESs to compute the thermal rate coefficients for the reaction.^40–42 It was found that the RPMD rates on the LDG PES underestimate the experimental data, while the RPMD rates on the latest ZZGX PES agree with the experimental results much better, and do not decrease further when the temperature falls below 300 K, apparently due to quantum tunneling. Unfortunately, RPMD calculations cannot provide any clue regarding the nature of the quantum tunneling.

Therefore, despite the significant progress that has been made in theoretical studies of the system, some key issues still remain to be addressed: Are the broad peaks in the total reaction probabilities obtained from the time-dependent wave packet calculations indeed the signature of the resonances in the reaction? If not, do there exist resonances in the reaction? How do resonances affect the reaction rates at low temperature? Here, we report a quantum dynamics study of the reaction on two new and more accurate PESs. Good agreement is achieved between the rate coefficients calculated on these two PESs and the experimental data. Our calculations reveal that the HB well in the entrance channel of OH + HCl supports many low energy resonance states. These resonance states substantially enhance the quantum tunneling effect and have an important impact on the reaction rates at low temperatures.

In order to improve the fitting accuracy of the ZZGX PES, we constructed two new PESs using the fundamental invariant neural network (FI-NN) method, fitted to ∼70 000 ab initio energy points calculated at the UCCSD(T)-F12a and UCCSD(T)-F12b levels of theory, respectively, both with the AVTZ basis set. The fitting RMSE is 3.07 and 3.12 meV, respectively, for the F12a and F12b PES, which is about half that for the ZZGX PES.³⁶ The spin–orbit coupling of the channels of both the reagent OH and the product Cl have been included using FI-NN fitting to about 38 000 points calculated at the MRCI/aug-cc-pVTZ level of theory with a fitting error of 0.19 meV. The CASSCF wave-function with an active space of (5e, 3o) was used as a reference for MRCI. Details of the new PESs are provided in the ESI†. The static barrier height for PESa is 0.088 eV (0.095 eV with SO correction included), and that for PESb is 0.097 eV (0.104 eV). As can be seen from Tables S1 and S2,† the geometries and energies of all the stationary points for the F12b PES without SO correction are in good agreement with the ZZGX PES. Table S2† also shows the corresponding complete basis set (CBS) energies for these stationary points based on AVTZ, AVQZ and AV5Z calculations. Because the F12b energies are slightly closer to the CBS results, we will present the dynamical results obtained on the F12b PES in the main text and provide those for the F12a PES in the SI.

On the new PESs, we carried out potential-averaged five-dimensional (PA5D) time-dependent wave packet^43,44 calculations to obtain the total reaction probabilities for the reaction by freezing the non-reacting OH bond in its ground vibrational state. Tests revealed that the PA5D treatment is capable of providing reaction probabilities for the ground rovibrational initial state that are essentially identical to those obtained using the full six-dimensional approach, as shown in Fig. S2.†Fig. 1(A) shows the total reaction probabilities for the HCl + OH reaction as a function of collision energy calculated on the F12b PES with both reagents in the ground rovibrational state at propagation times of 60 000, 120 000, 360 000, and 2 400 000 a.u. At high collision energies, the reaction probabilities converge quickly with respect to the propagation time, and one can barely see any difference among the four reaction probability curves, which exhibit smooth increases with collision energy. However, in the low collision energy region, large differences appear for different propagation times. At t = 60 000 a.u., the reaction probability presents a smooth curve with some small and broad oscillations, as was observed in the wave packet calculations of Guo and coworkers.³⁶

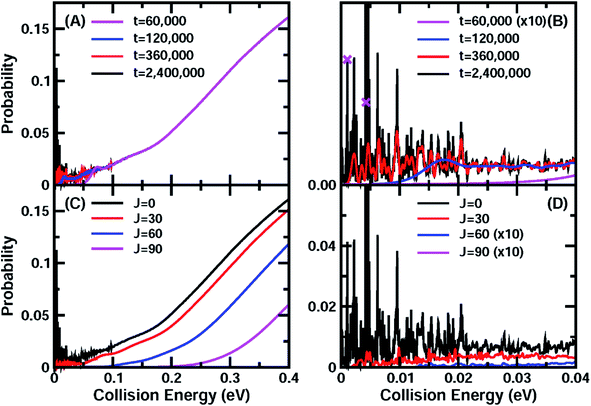Fig. 1 (A) Total reaction probabilities for the ground initial state of the OH + HCl → Cl + H₂O reaction on the F12b PES at wave packet propagation times of T = 60 000, 120 000, 360 000, and 2 400 000 a.u. (B) Same as (A), except showing the collision energy between 0.0 and 0.04 eV. The crosses mark the points for which the wavefunctions are shown in Fig. 2. (C) Total reaction probabilities for some partial waves J = 0, 30, 60, and 90 as a function of the collision energy. (D) Same as (C) except showing the collision energy between 0.0 and 0.04 eV.

When the propagation time is increased to t = 120 000, the reaction probabilities at collision energies below 0.05 eV increase substantially. With further increasing the propagation time to 360 000 a.u., many oscillatory structures emerge at collision energies below the barrier height of 0.104 eV, in particular in the very low collision energy region as shown in Fig. 1(B). These sharp structures become fully converged after around 2 400 000 a. u. of wave packet propagation (∼58 ps). The reaction probability even at a collision energy close to zero reaches 3–4%. The convergence of the total reaction probabilities on the F12a PES is very similar to that on the F12b PES (Fig. S3†), except that the final converged reaction probabilities for these two PESs exhibit a small shift, apparently due to slightly different barrier heights. Therefore, it is clear that reaction resonances exist in the title reaction in the very low collision energy region, and that these resonance states substantially induce quantum tunneling and enhance the reactivity. The lifetimes for these resonance states are quite long, with many being longer than 6.5 ps and having corresponding widths smaller than 0.1 meV.

Fig. 1(C) presents converged (t = 2 400 000 a.u. ≈ 58 ps) total reaction probabilities for the total angular momentum J = 0, 30, 60, and 90. With increasing J, the reaction probability curve shifts to higher energy. In the low collision energy region (<0.05 eV), the total reaction probabilities for J = 30 exhibit rich oscillatory structures as in the J = 0 case (Fig. 1(D)), which are expected to have a great influence on the rate constant at low temperature. With further increase of the total angular momentum, the influence of these resonances on the total reaction fades due to the centrifugal barrier, which prevents the low-energy wave function from entering the well. They only leave a small trace in the total reaction probabilities at low energies for J = 60, and do not have any effect for J = 90.

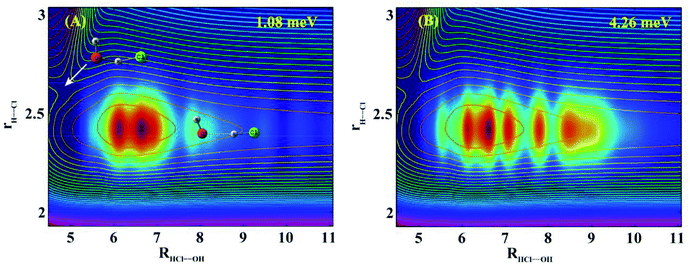
To understand the nature of these resonances, we calculated scattering wave functions at two collision energies (1.08 and 4.26 meV) with the peak reaction probabilities indicated by x in Fig. 1(B). Fig. 2(A) shows the two dimensional (2D) contour at the collision energy of 1.08 meV in the Jacobi coordinates HCl bond length (r_H–Cl) and center of mass distance between OH and HCl (R_HCl–OH), with the other coordinates integrated. As can be seen, the wave function is localized in the HB well region in the entrance channel with a few nodes in the R coordinate and no node in the r_H–Cl coordinate. Inspection of the scattering wave function for the bending and torsion coordinates reveals nodes exist in these coordinates (Fig. S4 and S5†). The 2D contour in the coordinates of R_HCl–OH and r_H–Cl at the collision energy of 4.26 meV shown in Fig. 2(B) looks similar to that shown in Fig. 2(A), except with more nodes in the R direction. Therefore, the observed resonance states in the reaction are Feshbach resonances trapped in a bending/torsion excited vibrationally adiabatic potential (VAP) well in the reactant complex region due to the HB interaction.

Fig. 2 Reactive scattering wave functions for the OH + HCl → Cl + H₂O reaction on the F12b PES in the two Jacobi coordinates R(HCl–OH) and r(H–Cl) with other coordinates integrated at the collision energies of 1.08 (A) and 4.26 meV (B). The contour lines are the corresponding 2D PESs along the two reactive bonds R(HCl–OH) and r(H–Cl) with other coordinates optimized. The geometries for the saddle point and the HB minimum are displayed in (A). The coordinate units in the figures are a₀.

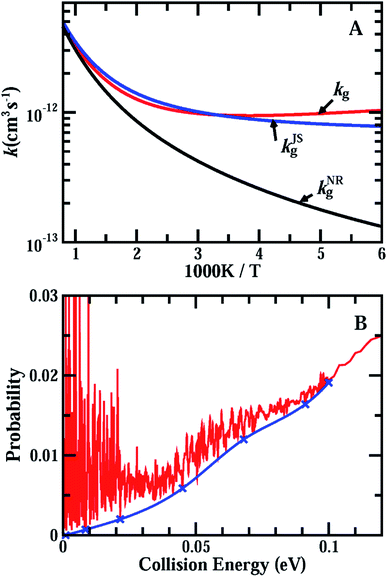
Fig. 3(A) shows the accurate rate constants for the initial ground rovibrational state, k_g, based on the probabilities for J = 0, 30, 60, 90 using the uniform J-shifting approach with a temperature-dependent shifting constant.^45–47 A test shows that the J-shifting scheme based on these four individual J values only introduces a few percent error to the rate constants in the temperature region considered here (Fig. S6†). As can be seen from the figure, with decreasing temperature, k_g first decreases rapidly from 1000 K to 700 K, then decreases slowly. It reaches a minimum at T ≈ 260 K, and increases slowly with further decrease of the temperature. At temperatures lower than 300 K, the rate constants for the ground rovibrational initial state are larger than the measured thermal rate coefficients, with k_g being larger than k_exp by ∼70% at T = 200 K.

Also shown in Fig. 3(A) are the rate constants for the ground rovibrational initial state, k^JS_g, obtained from the J = 0 reaction probabilities using the J-shifting approximation (see ESI† for details). As can be seen, the J-shifting approximation works very well at high temperatures around 1000 K, but begins to overestimate the rates with decreasing temperature. At T = 500 K, k^JS_g is about 10% higher than the true rate. At temperatures below 300 K, the J-shifting approximation underestimates the reaction rate, with k^JS_g being smaller than k_g by about 16% at T = 200 K. Overall, the J-shifting approximation works fairly well for the ground rovibrational initial state, although there are numerous resonance peaks in the reaction probabilities in the low collision energy region.

Fig. 3 (A) Accurate rate constants, k_g, for the initial ground rovibrational state of the HCl + OH → H₂O + Cl reaction calculated on the F12b PES, in comparison with k^JS_g (obtained using the J-shifting approximation) and k^NR_g (based on the background reaction probabilities for J = 0 with the resonance contribution removed shown below); (B) the background reaction probabilities up to E = 0.1 eV by connecting some valleys of the reaction probabilities marked by x.

Now we consider the issue of the effect of the resonance structures found in the reaction on the rate constant. For a reaction system with isolated resonances, it is rather straightforward to remove the resonance contributions from the reaction probabilities by fitting the resonance peaks to some Lorentzian functions and to obtain smooth background scattering probabilities, as demonstrated in the F + HD reaction and recently in the inelastic scattering of H + HF (ref. 6 and 18). However, the OH + HCl reaction possesses numerous highly overlapped resonances in the low energy region, as shown in Fig. 1(A), and it is impractical to fit these resonance peaks as accurately as the isolated resonances. Instead, we obtained an approximate background reaction probability curve, which is shown in Fig. 3(B), by smoothly connecting some resonance valleys as shown in the figure. The rate constants k^NR_g calculated using the background curve shown in Fig. 3(B) with the J-shifting approximation were compared with the original k_g in Fig. 3(A). Given the fact that the J-shifting approximation works fairly well for k^JS_g, as shown in Fig. 3(A), it is very reasonable to expect that will work even better for the k^NR_g values obtained from the background reaction probabilities with the resonance contribution removed. As can be seen, k^NR_g exhibits rate behavior typical for systems with a low barrier with some quantum tunneling effects. At T = 1000 K, k^NR_g is essentially identical to k_g, but decreases much faster than k_g as the temperature drops. At T = 200 K, k_g is larger than k^NR_g by a factor of about 5.6 (9.8 × 10⁻¹³vs. 1.74 × 10⁻¹³ cm³ s⁻¹), indicating that the reaction probabilities in the low collision energy region due to resonances substantially enhance the rate constants for the reaction at low temperatures. It is worthwhile to note that for systems with overlapped resonances like that shown in Fig. 3(B), the reaction probabilities at the valleys must be considerably higher than the true background reaction probabilities; therefore, the background curve shown in Fig. 3(B) is the upper limit of the background reaction probabilities and the rate based on the curve shown in Fig. 3(A) is also the upper limit of the rate for the ground rovibrational initial state without the resonance contributions. Therefore, the true enhancement due to the resonances must be larger than that shown in Fig. 3(A).

For reliable comparison with the measured thermal rate coefficients, we must take into account the contributions from all the thermally populated initial states of the reagents. Due to the very large number of thermally populated rotational states for this reaction even at 200 K, we opted to calculate the cumulative reaction probabilities, NE(E), (the sum of the reaction probabilities for all the initial states with a fixed total energy) for the reaction from which the thermal rate constants can be reliably evaluated.^48–52 The transition state wave packet calculations were carried out to obtain NE(E) using the details given in the ESI†. Due to huge computational efforts required to obtain the cumulative reaction probabilities for J > 0, we only calculated NE(E) for J = 0 and employed the J–K-shifting approximation^45,49,53 to obtain the thermal rate constant. NE(J = 0, E) as a function of total energy measured with respect to the ground rovibrational energy of OH and HCl is presented in Fig. S7.†

In Fig. 4, we present thermal rate constants for the reaction calculated on both the F12a and F12b PES, together with the rate constants for the ground rovibrational state (k_g) and the previous experimental measurements.^{21,22,24–29} As can be seen, the thermal rate coefficients are smaller than k_g over the entire temperature region, indicating that reagent rotation excitations diminish the reaction rates. Overall, the thermal rate coefficients calculated on both PESs agree with the experimental results rather well, with the F12a PES slightly overestimating and the other PES slightly underestimating compared to the experimental measurements. As observed in the experiments, the thermal rate coefficients decrease quickly with decreasing temperature in the high-temperature region, but decrease much more slowly at low temperatures, in particular at T < 300 K, substantially deviating from Arrhenius behavior.

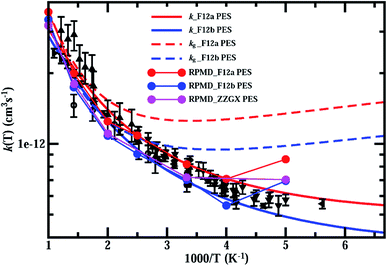Fig. 4 Thermal rate constants of the HCl + OH → H₂O + Cl reaction calculated on both the F12a and F12b PES, compared with rate constants for the ground rovibrational state, the RPMD rates on ZZGX PES and the previous experimental measurements.^{21,22,24–29} Experimental data are taken from Husain et al. (in circles),^21,22 Molina et al. (in diamonds),²⁴ Ravishankara et al. (in upward-pointing triangles),²⁵ Smith et al. (in squares),²⁶ Sharkey et al. (in triangle left),²⁷ Battin-Leclerc et al. (in downward-pointing triangles),²⁸ and Bryukov et al. (in leftward-pointing triangles).²⁹

Also shown in Fig. 4 are the RPMD rates calculated (see ESI† for details) on the F12a, F12b and ZZGX PESs.⁴² As shown, the RPMD rates on the F12b PES agree with those on the ZZGX PES extremely well, although the barrier heights for the F12b PES are higher by 9 meV. The present RPMD rates agree with the J–K-shifting quantum rates rather well, except at 200 K, at which the RPMD rates are overestimated by about 40%. As a result, the RPMD rate is higher than the experimental value at T = 200 K, in particular for the F12a PES. Previous studies have shown that RPMD tends to underestimate reaction rates in the strong quantum tunneling region, even for systems with resonances such as the O(³P) + HCl → OH + H reaction;⁵⁴ however, it overestimates the rates for the F + H₂ reaction with pronounced post-barrier Feshbach resonances⁵⁵ and some insertion reactions.⁵⁶ The discrepancy between the RPMD and J–K-shifting quantum rate at T = 200 K could be caused by a possible underestimation of the rate by the J–K-shifting approximation, as in the J-shifting approximation of the ground rovibrational initial state shown in Fig. 3(A). On the other hand, the rapid increase in the rate with decreasing temperature (from 250 K to 200 K) could also be a feature of bimolecular reaction rates in the high-pressure limit for reactions with a pre-reactive minimum.⁵⁷ RPMD rate theory in its original form employs a free energy calculation,^38,39 which allows thermalization in the pre-reactive minimum, sampling tunneling pathways with energies not accessible in the low-pressure limit. Therefore, RPMD models a rate process that resembles rates in the high-pressure limit, which could lead to an overestimation of the rate at low temperature. A recent study also reported a similar issue with RPMD.⁵⁸ The authors attributed it to spurious resonances in RPMD favoring energy transfer in the pre-reactive minimum, which is similar to our argument. Certainly, more quantum dynamics calculations to provide rigorous quantum rates at low temperatures to assess the accuracy of the J–K-shifting approximation and the RPMD method on this reaction system with strong HB interaction in the entrance channel would be highly desirable.

Therefore, the OH + HCl reaction possesses many long-lifetime Feshbach resonances trapped in a bending excited VAP well in the entrance channel due to HB interaction. These resonance states substantially induce quantum tunneling of the hydrogen atom through the reaction barrier and enhance the reactivity in the low-collision region. Consequently, the reaction rate for the reaction becomes essentially independent of temperature in the low-temperature region and deviates substantially from Arrhenius behavior, as observed experimentally. The resonance states in the reaction are very different in location from those in the F + H₂/H₂O reactions,^{8,11,12,14,59–63} which are trapped in the VAP well in the product channel. Furthermore, they are trapped in the bending/torsion excited VAP well with HCl in the ground vibrational state, unlike those in the F + H₂/H₂O reactions with HF in vibrationally excited states.^8,63,64 In nature, these resonance states in the reaction arise from HB interaction as in the F + H₂O (v = 0) reaction,^11,62,63 but are different from those in the F + H₂/HD/HOD (v = 1) reactions^{8,10,12,14,64–66} due to chemical bond softening. Because the resonance states are trapped in the bending/torsion excited VAP well, their lifetimes are much longer than those observed in the F + H₂/H₂O reactions. As a result, they should have an important impact on the differential cross sections. More efforts, and in particular more joint efforts involving theory and experiment, should be devoted to studying these Feshbach resonances in this reaction of great atmospheric importance in detail.

Data availability

Details of the PESs and time-dependent wave packet calculations are included in the ESI.†

Author contributions

D. H. Z. conceived and supervised the research, and wrote the manuscript. X. X. and J. C. developed the PES. X. X. and S. L. performed the quantum dynamical calculation. X. L. and W. F. performed the RPMD calculation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 22288201, 22022306, 21903083), and the Chinese Academy of Sciences.

References

1. R. P. Bell, The tunnel effect in chemistry, 1980.
2. P. S. Zuev, R. S. Sheridan, T. V. Albu, D. G. Truhlar, D. A. Hrovat and W. T. Borden, Science, 2003, 299, 867–870.
3. G. R. Fleming, G. D. Scholes and Y. C. Cheng, 22^nd Solvay Conference on Chemistry – Quantum Effects in Chemistry and Biology, Brussels, Belgium, Oct, 2010.
4. J. Jankunas and A. Osterwalder, Annu. Rev. Phys. Chem., 2015, 66, 241–262.
5. R. I. Kaiser, D. S. N. Parker and A. M. Mebel, Annu. Rev. Phys. Chem., 2015, 66, 43–67.
6. R. T. Skodje, D. Skouteris, D. E. Manolopoulos, S.-H. Lee, F. Dong and K. Liu, J. Chem. Phys., 2000, 112, 4536–4552.
7. G. C. Schatz, Science, 2000, 288, 1599–1600.
8. M. H. Qiu, Z. F. Ren, L. Che, D. X. Dai, S. A. Harich, X. Y. Wang, X. M. Yang, C. X. Xu, D. Q. Xie, M. Gustafsson, R. T. Skodje, Z. G. Sun and D. H. Zhang, Science, 2006, 311, 1440–1443.
9. W. Dong, C. Xiao, T. Wang, D. Dai, X. Yang and D. H. Zhang, Science, 2010, 327, 1501–1502.
10. T. Wang, J. Chen, T. Yang, C. Xiao, Z. Sun, L. Huang, D. Dai, X. Yang and D. H. Zhang, Science, 2013, 342, 1499–1502.
11. R. Otto, J. Ma, A. W. Ray, J. S. Daluz, J. Li, H. Guo and R. E. Continetti, Science, 2014, 343, 396–399.
12. J. B. Kim, M. L. Weichman, T. F. Sjolander, D. M. Neumark, J. Klos, M. H. Alexander and D. E. Manolopoulos, Science, 2015, 349, 510–513.
13. T. Yang, J. Chen, L. Huang, T. Wang, C. Xiao, Z. Sun, D. Dai, X. Yang and D. H. Zhang, Science, 2015, 347, 60–63.
14. T. G. Yang, L. Huang, C. L. Xiao, J. Chen, T. Wang, D. X. Dai, F. Lique, M. H. Alexander, Z. G. Sun, D. H. Zhang, X. M. Yang and D. M. Neumark, Nat. Chem., 2019, 11, 744–749.
15. T. Xie, D. Wang, J. M. Bowman and D. E. Manolopoulos, J. Chem. Phys., 2002, 116, 7461–7467.
16. T. Xie, J. M. Bowman, K. A. Peterson and B. Ramachandran, J. Chem. Phys., 2003, 119, 9601–9608.
17. J. M. Bowman, Chem. Phys., 2005, 308, 255–257.
18. P. G. Jambrina, L. González-Sánchez, M. Lara, M. Menéndez and F. J. Aoiz, Phys. Chem. Chem. Phys., 2020, 22, 24943–24950.
19. M. J. Molina, T. L. Tso, L. T. Molina and F. C. Y. Wang, Science, 1987, 238, 1253–1257.
20. I. W. M. Smith and R. Zellner, J. Chem. Soc., Faraday Trans. 2, 1974, 8, 1045–1056.
21. D. Husain, J. M. C. Plane and N. K. H. Slater, J. Chem. Soc., Faraday Trans. 2, 1981, 77, 1949–1962.
22. D. Husain, J. M. C. Plane and C. X. Chen, J. Chem. Soc., Faraday Trans. 2, 1984, 80, 713–728.
23. L. F. Keyser, J. Phys. Chem., 1984, 88, 4750–4758.
24. M. J. Molina, L. T. Molina and C. A. Smith, Int. J. Chem. Kinet., 1984, 16, 1151–1160.
25. A. R. Ravishankara, P. H. Wine, J. R. Wells and R. L. Thompson, Int. J. Chem. Kinet., 1985, 17, 1281–1297.
26. I. W. M. Smith and M. D. Williams, J. Chem. Soc., Faraday Trans. 2, 1986, 82, 1043–1055.
27. P. Sharkey and I. W. M. Smith, J. Chem. Soc., Faraday Trans., 1993, 89, 631–638.
28. F. Battin-Leclerc, I. K. Kim, R. K. Talukdar, R. W. Portmann and A. R. Ravishankara, J. Phys. Chem. A, 1999, 103, 3237–3244.
29. M. G. Bryukov, B. Dellinger and V. D. Knyazev, J. Phys. Chem. A, 2006, 110, 936–943.
30. A. Sinha, M. C. Hsiao and F. F. Crim, J. Chem. Phys., 1991, 94, 4928–4935.
31. J. D. Thoemke, J. M. Pfeiffer, R. B. Metz and F. F. Crim, J. Phys. Chem., 1995, 99, 13748–13754.
32. B. Jiang and H. Guo, J. Am. Chem. Soc., 2013, 135, 15251–15256.
33. J. Li, H. W. Song and H. Guo, Phys. Chem. Chem. Phys., 2015, 17, 4259–4267.
34. J. Li, B. Jiang, H. Song, J. Ma, B. Zhao, R. Dawes and H. Guo, J. Phys. Chem. A, 2015, 119, 4667–4687.
35. H. W. Song and H. Guo, J. Phys. Chem. A, 2015, 119, 6188–6194.
36. J. X. Zuo, B. Zhao, H. Guo and D. Q. Xie, Phys. Chem. Chem. Phys., 2017, 19, 9770–9777.
37. H. W. Song and H. Guo, J. Phys. Chem. A, 2015, 119, 826–831.
38. I. R. Craig and D. E. Manolopoulos, J. Chem. Phys., 2005, 123, 034102.
39. Y. V. Suleimanov, J. W. Allen and W. H. Green, Comput. Phys. Commun., 2013, 184, 833–840.
40. J. X. Zuo, Y. L. Li, H. Guo and D. Q. Xie, J. Phys. Chem. A, 2016, 120, 3433–3440.
41. J. X. Zuo, Y. L. Li, H. Guo and D. Q. Xie, J. Phys. Chem. A, 2017, 121, 5067.
42. J. Zuo, C. Xie, H. Guo and D. Xie, J. Phys. Chem. Lett., 2017, 8, 3392–3397.
43. D. H. Zhang and J. Z. H. Zhang, J. Chem. Phys., 1994, 101, 1146–1156.
44. D. H. Zhang, J. Z. H. Zhang, Y. C. Zhang, D. Y. Wang and Q. G. Zhang, J. Chem. Phys., 1995, 102, 7400–7408.
45. J. M. Bowman, J. Phys. Chem., 1991, 95, 4960–4968.
46. D. H. Zhang and J. Z. H. Zhang, J. Chem. Phys., 1994, 100, 2697–2706.
47. D. H. Zhang and J. Z. H. Zhang, J. Chem. Phys., 1999, 110, 7622–7626.
48. W. H. Miller, S. D. Schwartz and J. W. Tromp, J. Chem. Phys., 1983, 79, 4889–4898.
49. Q. Sun, J. M. Bowman, G. C. Schatz, J. R. Sharp and J. N. L. Connor, J. Chem. Phys., 1990, 92, 1677–1686.
50. D. H. Zhang and J. C. Light, J. Chem. Phys., 1996, 104, 6184–6191.
51. P. Sun, Z. J. Zhang, J. Chen, S. Liu and D. H. Zhang, J. Chem. Phys., 2018, 149, 064303.
52. D. H. Zhang and J. C. Light, J. Chem. Phys., 1997, 106, 551–563.
53. D. C. Clary, J. Phys. Chem., 1994, 98, 10678–10688.
54. M. Menéndez, P. G. Jambrina, A. Zanchet, E. Verdasco, Y. V. Suleimanov and F. J. Aoiz, J. Phys. Chem. A, 2019, 123, 7920–7931.
55. R. Collepardo-Guevara, Y. V. Suleimanov and D. E. Manolopoulos, J. Chem. Phys., 2009, 130, 174713.
56. Y. Li, Y. V. Suleimanov and H. Guo, J. Phys. Chem. Lett., 2014, 5, 700–705.
57. L. G. Gao, J. Zheng, A. Fernández-Ramos, D. G. Truhlar and X. Xu, J. Am. Chem. Soc., 2018, 140, 2906–2918.
58. P. d. Mazo-Sevillano, A. Aguado and O. Roncero, J. Chem. Phys., 2021, 154, 094305.
59. G. C. Schatz, J. M. Bowman and A. Kuppermann, J. Chem. Phys., 1973, 58, 4023–4025.
60. S. F. Wu, B. R. Johnson and R. D. Levine, Mol. Phys., 1973, 25, 839–856.
61. D. M. Neumark, A. M. Wodtke, G. N. Robinson, C. C. Hayden and Y. T. Lee, Phys. Rev. Lett., 1984, 53, 226–229.
62. J. Ma and H. Guo, J. Phys. Chem. Lett., 2015, 6, 4822–4826.
63. X. R. Zhang, L. L. Li, J. Chen, S. Liu and D. H. Zhang, Nat. Commun., 2020, 11, 223.
64. Z. F. Ren, L. Che, M. H. Qiu, X. A. Wang, W. R. Dong, D. X. Dai, X. Y. Wang, X. M. Yang, Z. G. Sun, B. Fu, S. Y. Lee, X. Xu and D. H. Zhang, Proc. Natl. Acad. Sci. U.S.A., 2008, 105, 12662–12666.
65. D. Yu, J. Chen, S. Cong and Z. Sun, J. Phys. Chem. A, 2015, 119, 12193–12208.
66. S. Liu, X. Zhang, J. Chen and D. H. Zhang, J. Phys. Chem. Lett., 2021, 12, 6090–6094.

---

Footnotes

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc01958b

‡ These authors contributed equally to this work.

---