Coacervation of poly-electrolytes in the presence of lipid bilayers: mutual alteration of structure and morphology

Abstract

Many intrinsically disordered peptides have been shown to undergo liquid–liquid phase separation and form complex coacervates, which play various regulatory roles in the cell. Recent experimental studies found that such phase separation processes may also occur at the lipid membrane surface and help organize biomolecules during signaling events; in some cases, phase separation of proteins at the membrane surface was also observed to lead to significant remodeling of the membrane morphology. The molecular mechanisms that govern the interactions between complex coacervates and lipid membranes and the impacts of such interactions on their structure and morphology, however, remain unclear. Here we study the coacervation of poly-glutamate (E₃₀) and poly-lysine (K₃₀) in the presence of lipid bilayers of different compositions. We carry out explicit-solvent coarse-grained molecular dynamics simulations by using the MARTINI (v3.0) force-field. We find that more than 20% anionic lipids are required for the coacervate to form stable contact with the bilayer. Upon wetting, the coacervate induces negative curvature to the bilayer and facilitates local lipid demixing, without any peptide insertion. The magnitude of negative curvature, extent of lipid demixing, and asphericity of the coacervate increase with the concentration of anionic lipids. Overall, we observe a decrease in the number of contacts among the polyelectrolytes as the droplet spreads over the bilayer. Therefore, unlike previous suggestions, interactions among polyelectrolytes do not constitute a driving force for the membrane bending upon wetting by the coacervate. Rather, analysis of interaction energy components suggests that bending of the membrane is favored by enhanced interactions between polyelectrolytes with lipids as well as with counterions. Kinetic studies reveal that, at the studied polyelectrolyte concentrations, the coacervate formation precedes bilayer wetting.

---

1 Introduction

Intrinsically disordered proteins (IDPs) and nucleic acids can undergo liquid–liquid phase separation (LLPS) to form bio-molecular condensates.^1–4 These exhibit properties similar to liquid droplets and play a crucial role in various cellular processes.^5–7 The formation of membraneless organelles, which facilitate intracellular compartmentalization, occurs through LLPS.^8–10 For the past few decades, substantial progress has been made in understanding the structure and dynamics of such macromolecular condensates, both theoretically and experimentally. It has also been shown that the phase behavior of IDPs is encoded in their sequence and single-chain properties.^11–14

In addition to LLPS in the bulk, it has been increasingly realized that protein phase separation at lipid membrane surface is also of biological significance.^15–17 Specific interactions between membrane and proteins help control the location and timing of LLPS for specific cellular functions (e.g., signaling).¹⁸ On the other hand, LLPS helps concentrate specific protein components for regulating the efficiency and sensitivity of signaling events.^19,20 Moreover, recent experimental studies^21–24 also observed that phase separation of proteins at the membrane surface can lead to significant membrane bending and tubulation, suggesting that LLPS near the membrane surface can serve as a novel mechanism for membrane remodeling in cells. Nevertheless, how LLPS at the membrane surface differs from that in the bulk remains to be systematically explored.^17,25 For example, if the conformational ensembles of the relevant protein(s) at the membrane surface are substantially different from those in the bulk, changes in the protein phase behaviors in the presence of the membrane are more complex to predict than merely considering the enhanced local protein concentration due to binding to the membrane.¹⁵ In addition, there can be coupling between phase behaviors of the peripheral proteins and the lipid membrane.^26,27 In a lattice model-based study, Machta et al. showed that phase separating membranes can enhance prewetting-like transitions in IDPs.²⁸ The membrane, modeled with Ising spins, was shown to promote protein phase separation on its surface, even if LLPS is unfavorable in the bulk. Due to the simplicity of the model, the impact of protein phase separation on the membrane morphology, however, was not analyzed. Continuum mechanics models have been used to rationalize membrane bending and tubulation upon adsorption of a dense protein layer,^21,24 although molecular details for the underlying driving force were difficult to establish using such models alone.

Motivated by these considerations, we study the interactions between a pair of polyelectrolytes (poly-glutamate(E) and poly-lysine(K)) and simple lipid membranes as a model system. This choice is made because several naturally occurring IDPs contain long stretches of positively or negatively charged amino acids.²⁹ These charged IDPs are present in animal cells that undergo LLPS and interact with the cell membrane. Nevertheless, the nature of the interaction of such highly charged phase-separated peptide droplets with the cell membrane and its subsequent effects were not studied before. As understood from the length- and time-scale of these processes, the use of coarse-grained (CG) models becomes inevitable for computational studies. However, the development of CG models and testing against experimental results (often unavailable) for IDPs becomes formidable. On the other hand, poly-Glutamate(E) and poly-Lysine(K) mixtures serve as suitable model candidates that readily undergo LLPS even in (very) low concentrations that are often referred to as coacervates.^30–32 Moreover, the CG parameters were already tested against the phase behavior of this particular system.³³ In addition to this, poly-E and poly-K, in some form or the other, are used in the fields of food processing, agriculture, and biomedicine.^34–37 These coacervates also find a wide range of applications from coatings and adhesives to pharmaceutical technologies and foster multiple biological processes. Several disordered synthetic polyelectrolytes, for example, an equimolecular mixture of poly-E and poly-K, find biomedical applications such as encapsulation and extraction of drug molecules.^38,39 This biodegradable polyelectrolyte pair can be produced during microbial fermentation and are also non-toxic to the human body.³⁶ Recently, coacervate formed due to the LLPS of polymers with long poly-E/K tails has been shown to work as nanocarriers for drug molecules.³⁷ They are also found to work as biological adhesives.^40,41 Given a diverse range of industrial and bio-medicinal applications of polyelectrolyte coacervates,^30,42 It is evident that they interact with living cells and could in principle remodel cell membranes to some degree. Therefore, understanding their effects on cells draws avid attention. There exist a number of studies on the phase behavior of poly-E/K in the bulk solution phase.^3,33,43,44 However, the interaction of such complex coacervates with other cellular components, such as the cell membrane, has not been studied yet, especially from a theoretical and microscopic perspective.

The physics behind phase separation of charged polymers can be comprehended with the help of a mean-field theory prescribed by Overbeek and Vroon,⁴⁵ which is an extension of the Flory-Huggins (FH) formalism^46,47 for charged systems. For a mixture of polycations and polyanions of the same length (N) and equal (but opposite) charges, the mean-field free energy per lattice cite (F) is given by eqn (1),

βF = (ϕ/N)ln(ϕ/2) + (1−ϕ)ln(1−ϕ) − α(σϕ)^3/2, (1)

where ϕ is the total volume fraction of the polymers, the parameter α is determined by charge per site, σ is the linear charge density, and β=(k_BT)⁻¹. When σ³N exceeds a value of 0.5 (critical point), the polyelectrolyte solution phase separates into polymer-rich and polymer-deficient regions that is known as complex coacervation. More recently, a combination of the FH theory with a random phase approximation (RPA) was used to study binodal and spinodal phase behaviors of neutral polyampholytes.⁴⁸ Nevertheless, minimalistic mean-field models cannot capture sequence dependence or even multivalent interactions, which are shown to be important factors in understanding LLPS of IDPs.⁴⁹ Hence, molecular simulations and more sophisticated models are needed to investigate the molecular details associated with complex coacervation.

Owing to the vast conformational space of IDPs, atomistic molecular dynamics (MD) simulations become computationally expensive. Different levels of coarse-grained (CG) approaches have been applied to study LLPS, for example, with multiple beads per residue,^50–52 single-bead per residue,^12,53,54 and even multiple-residues per bead.^55,56 However, the transferability of these force fields remains a critical issue. Hummer and co-workers used MARTINI v2.2 to model LLPS of FUS low-complexity domain (LCD) and observed good agreement with experiments by re-balancing the protein–protein non-bonded interaction parameters.⁵⁷ Recently CG simulations, with scaled-MARTINI and HPS model force-fields, have been applied to recognize the key modulators in the LLPS of DNA-binding protein TDP-43.⁵⁸

Specifically for peptides consisting of E/K residues, Das and Pappu investigated the sequence-ensemble relationship of several (E/K)₂₅ polyampholytes with atomistic simulations.²⁹ They showed that a segregated sequence (e.g., E₂₅K₂₅) is more prone to form hairpin-like conformations compared to a well-mixed sequence (e.g., (EK)₂₅). The latter explores conformations that are similar to Flory random coils. The conformational preferences of single chains indeed are reflected in the phase diagram of these polyelectrolytes, as studied by Shea and co-workers.³ Their field-theoretic simulations and RPA based phase diagrams predict that polyelectrolytes with block-charged sequences have a larger coacervation window than sequences with a random patterning of charges. De Pablo and co-workers, again with the help of RPA based calculations, demonstrated that the presence of charge blocks within a random sequence facilitates the formation of denser and more salt-resistant coacervates.⁵⁹ Their study also supports the increased width of the two-phase region as observed by Shea and co-workers. More recently, Marrink and co-workers used MARTINI v3.0 ⁵⁰ based CG simulations to study the phase behaviors of E₃₀ and K₃₀ at several salt concentrations.³³ Encouragingly, the simulations captured the key trend observed in the experimental studies of Priftis and Tirrell, who analyzed the sensitivity of ionic strength on complex coacervation of E_N and K_N mixtures.⁴³ They found that for N = 30, the mixtures did not form coacervates beyond 0.4 M NaCl, which was also observed in the MARTINI v3.0 based simulations.

Considering the favorable MARTINI results for poly-E/K coacervates³³ and the general success of the model for describing lipid membranes,⁶⁰ we have chosen to use MARTINI v3.0 to study the interaction of poly-E/K with a series of few-component lipid membranes as simple but representative examples of biomolecular condensate/membrane interactions.¹⁷ In particular, we ask the following questions: (i) How does the poly-E/K complex coacervate modulate the membrane structure and morphology? (ii) How does the membrane adsorption (or wetting) modify the structure of the coacervate? (iii) What are the driving factors for membrane adsorption and remodeling? In the subsequent sections, we aim to answer these questions with MD simulations, from structural, energetic and kinetic viewpoints. These simulations provide the first microscopic analysis of coacervate/membrane interactions and their mutual alteration of structure and morphology. The study shall lay the groundwork for future investigation of physical factors that govern protein LLPS at the membrane surface involving more complex proteins and lipid membranes.^16,18,27

2 System and simulation details

We have modeled the relevant systems with the recently developed version of the explicit-solvent CG MARTINI (v3.0) force-field.⁵⁰ The atomistic versions of the polyelectrolytes are created in pymol⁶¹ followed by a conversion into the CG model with martinize2. The parameters are kept the same as those in Marrink et al., who could reproduce the ion concentration dependence of coacervation for poly-E/poly-K mixtures using the same parameters.³³ However, in the absence of prior experimental data regarding the conformations of these IDPs on membranes, we have not used any elastic bonds between 1–3 and 1–4 backbone beads so that the polyelectrolytes can explore the preferred conformational space in the presence of different bilayers and salt concentrations in an unbiased fashion. In this description, each E and K residue is modeled by two and three CG beads, respectively (one backbone and one/two side-chain beads). The side-chain bead of each E contains −1e charge and the second side-chain bead of each K contains +1e charge. In addition to this, the N- and C-termini, respectively, contain +1e and −1e charges. To model the lipid bilayer, we have used two CG lipid molecules namely, palmitoyl oleoyl phosphatidylcholine (POPC, zwitterionic) and palmitoyl oleoyl phosphatidylglycerol (POPG, anionic). We have used the insane.py code⁶² to prepare seven different initial bilayer patches of dimensions 30 nm × 30 nm, namely, pure POPC, PC : PG = 80 : 20, PC : PG = 75 : 25, PC : PG = 70 : 30, PC : PG = 60 : 40, PC : PG = 50 : 50, and pure POPG. The system contains CG water beads (equivalent to four atomistic water molecules) and ions to maintain electrostatic neutrality. Additionally, to understand the influence of excess ions, we simulate two systems (PC : PG = 60 : 40 and PC : PG = 50 : 50) with 0.15 M NaCl.

Equal numbers (50 of each) of E₃₀ and K₃₀ polymers are simulated in a cubic box of dimension (30 nm)³ without the presence of bilayers to study the unperturbed structure of the coacervate. This approximately represents 2.5%(w/w) polymer concentration. With the different bilayers, we have performed two kinds of simulations: (i) with a preformed E₃₀–K₃₀ droplet initially placed close to the bilayer, and (ii) randomly distributed polyelectrolyte chains inside the box and around the bilayer. The first set of simulations helps to reach the equilibrium quickly and avoids scattered adsorption, whereas the second set of simulations allows us to study the kinetics and sequence of events. The simulations with the bilayers are carried out with an elongated box of dimensions 30 nm(X) × 30 nm(Y) × 40 nm(Z). We have additionally carried out simulations with 1%(w/w) and 5%(w/w) poly-E/K mixtures to understand the effect of polymer concentration. Nevertheless, for 5%(w/w) systems, the coacervate phase percolates through the periodic boundaries and extends along the XY directions. On the contrary, for 1%(w/w) systems, the size of the droplet becomes too small to observe reasonable membrane remodeling.

The bilayers are first relaxed through a series of energy minimization and equilibration steps. Then the systems (containing polyelectrolytes and a relaxed bilayer) are energy minimized by using the steepest-descent algorithm followed by equilibration in the isothermal-isobaric (NPT) ensemble for 2 μs which allows the coacervate to form stable contacts with the bilayer. After that, 5 μs production runs are carried out in an NPT ensemble with 200 ps trajectory dumping rate. All the equilibration simulations are propagated with a time step of 10 fs and production simulations are propagated with a time step of 20 fs, using the leap-frog algorithm. We have used the V-rescale thermostat⁶³ (τ_T = 1 ps⁻¹) at 298 K and Parrinello–Rahman barostat⁶⁴ with semi-isotropic pressure coupling (τ_P = 12 ps⁻¹) at 1 bar to make the bilayer tensionless. For initial equilibration purpose, we have used Berendsen barostat⁶⁵ with τ_P = 6 ps⁻¹. The electrostatic interactions are screened with a reaction-field (ε_r) of 15 within a cut-off of 1.1 nm and vdW interactions are also terminated at 1.1 nm with the Verlet cut-off scheme. For the kinetic simulations with dispersed polyelectrolytes, we have used a data dumping rate of 100 ps. The simulations are carried out with the GROMACS 2018.3 simulation package⁶⁶ and analyses are performed with a combination of Fortran codes, gmx tools, and plumed 2.5.3.⁶⁷ For visualization purposes, we have used VMD 1.9.3.⁶⁸

3 Results and discussion

3.1 Criteria of wetting

We first aim to find out the condition for a successful and persistent wetting of the bilayer by the complex polyelectrolyte coacervate. We calculate the total number of time-averaged contacts between different components, after reaching equilibrium, according to eqn (2),

q_ij(t) = (1 − Y)/(1 − Y²), (2)

where q_ij(t) is a measure of contact between i^th and j^th beads at a given time t; Y is equal to (r_ij(t)/r₀)⁶ with r₀ = 5 Å where r_ij(t) is the distance between i^th and j^th beads at time t. The particular choice of the contact order parameter (eqn (2)) has been made in order to make it smoothly vary from 1 to 0, rather than the usual Heaviside function form and also to comply with several earlier studies that used such a description.^69–71 Changing the exponents of r_ij would indeed modify the numerical value of the total number of contact, but the general trend shall remain preserved.

For a given pair, q_ij varies smoothly from 1 to 0 with increasing r_ij. Therefore, the time averaged total number of contacts (Q) is described by eqn (3), where τ is the number of timesteps over which the average is taken

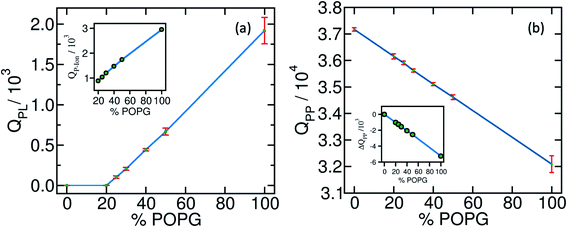
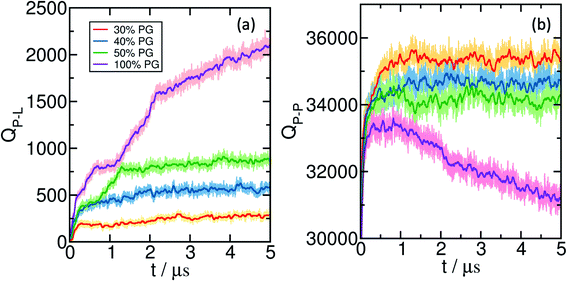
In Fig. 1(a) and (b), we plot Q between polyelectrolyte-lipid (Q_PL) and polyelectrolyte–polyelectrolyte (Q_PP) pairs in the presence of lipid bilayers. Q_PL remains zero for both pure POPC and with 20% POPG systems. It linearly increases beyond 20% POPG concentration which determines the minimum concentration of anionic lipids required for adsorption and wetting.

Fig. 1 Time-averaged total number of contacts between different components in the system plotted against POPG concentration: (a) between polyelectrolyte backbone beads and lipid head groups, and (b) self-contacts among polyelectrolyte backbone beads. Inset (a): number of contacts between polyelectrolyte backbone beads and ions. Inset (b): relative decrease in polyelectrolyte–polyelectrolyte contacts compared to the bulk phase (bilayer free) coacervate. The trends in the increase and decrease are found to be linear (the average values and error bars are calculated from block averages where each block of data consists of 500 ns trajectory).

As the extent of bilayer wetting increases, Q_PP decreases linearly. This indicates the spread of the coacervate over the bilayer surface. Interestingly, even in the absence of wetting, for the 20% POPG bilayer, we observe a decrease in Q_PP. This can be attributed to the presence of counterions in the system. Ions are known to decrease polyelectrolyte–polyelectrolyte interactions and can penetrate inside the coacervate network. As a result, Q_PP decreases without the coacervate getting adsorbed to the bilayer. The spread of the coacervate upon wetting exposes the polyelectrolytes to the ion and solvent environment. Hence, one observes an increase in the polyelectrolyte-ion contacts (Q_P-Ion) with increasing %POPG [Fig. 1(a), inset].

Further decompositions of Q_PP, Q_PL, and Q_P-Ion reveal that the bilayer wetting primarily happens through the K₃₀-POPG contact formation at the cost of E₃₀–K₃₀ and K₃₀–K₃₀ contacts. On the contrary, E₃₀–E₃₀ contacts are found to increase slightly with the increasing wetting, except for the pure POPG bilayer. This happens due to the shape of the adsorbed droplet. The K₃₀ polymers form most of the adsorbing base and E₃₀ polymers come close to each other to sustain the near-globular shape and minimize surface tension. The other pairs, namely, K₃₀-POPC, E₃₀-POPG, and E₃₀-POPC are also found to increase with increasing POPG concentrations. These are manifested in the energetics of the system as detailed below. We provide the detailed component-wise number of contacts in the ESI (Fig. S1)†.

3.2 Local demixing of lipids

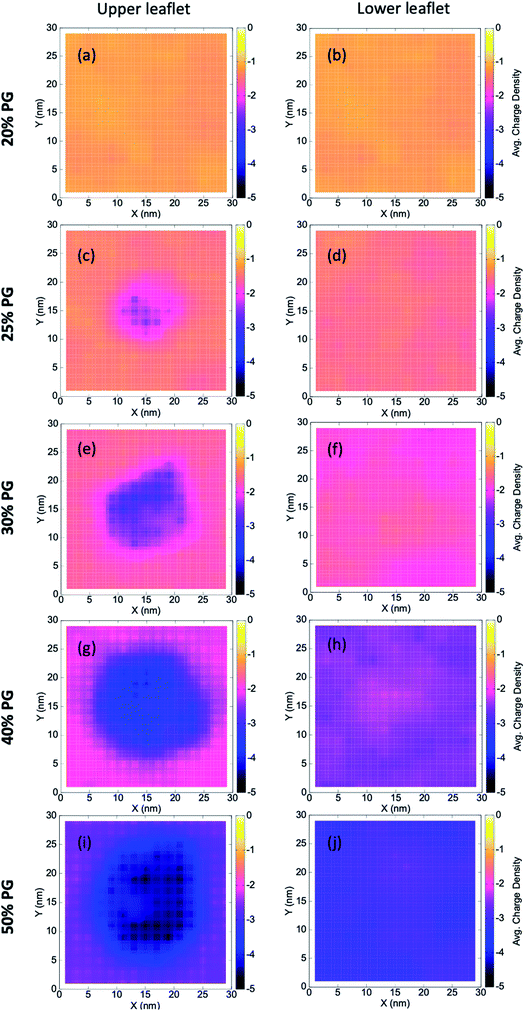
Multi-component lipid bilayers exhibit local heterogeneity that can get enhanced due to the presence of adsorbed polymers, bound proteins, or other macromolecules.^72–75 Local lipid demixing can eventually lead to an altered membrane morphology (due to different spontaneous curvatures of lipid components), which has far-reaching consequences in biology.

Here we find local demixing due to the adsorption of the coacervate on different bilayers. To quantitatively capture this, we compute grid-wise and time-averaged charge density (as given by eqn (4)) of lipid head groups by constructing a 15 × 15 grid in the XY plane along the bilayer [Fig. 2],

σ_ij = <n^POPG>_ij × (−1). (4)

Fig. 2 Wetting induced demixing in the lipid bilayers. The plots show grid-wise and time-averaged charge densities of the upper (left panel) and lower (right panel) leaflets. Significant demixing is observed at the upper leaflet where POPG molecules get accumulated near the contact region of the coacervate. Pure POPC and POPG systems are not shown as there is no demixing in these two systems.

Here, i and j are the grid indices, σ is the time-averaged charge density, and <n^POPG> is the time-averaged number of POPG heads in that particular grid. We characterize the upper and lower leaflet separately, where the former being the one in contact with the coacervate. We find a significant local demixing in the upper leaflet for lipid bilayers that form stable contacts with the IDPs (that is, from 25% to 50% POPG systems).

Our observations can be connected to the earlier mean-field theoretical studies of Ben-Shaul et al.⁷² They showed that local demixing of lipids is favored to achieve optimal charge matching, which compensates for the entropic penalty for demixing. When a charged sphere (of a fixed charge density, σ) and an oppositely charged planar surface (of a different but fixed charge density, σ′) approach each other, the interaction becomes rather repulsive at extremely short distances. This is because of the presence of a certain fraction of counterions trapped between these two surfaces. However, in the case of lipid membranes, charge redistribution is allowed through lateral diffusion. This makes the negatively charged POPG molecules concentrate near the contact region and eventually leads to local demixing.

3.3 Curvature generation

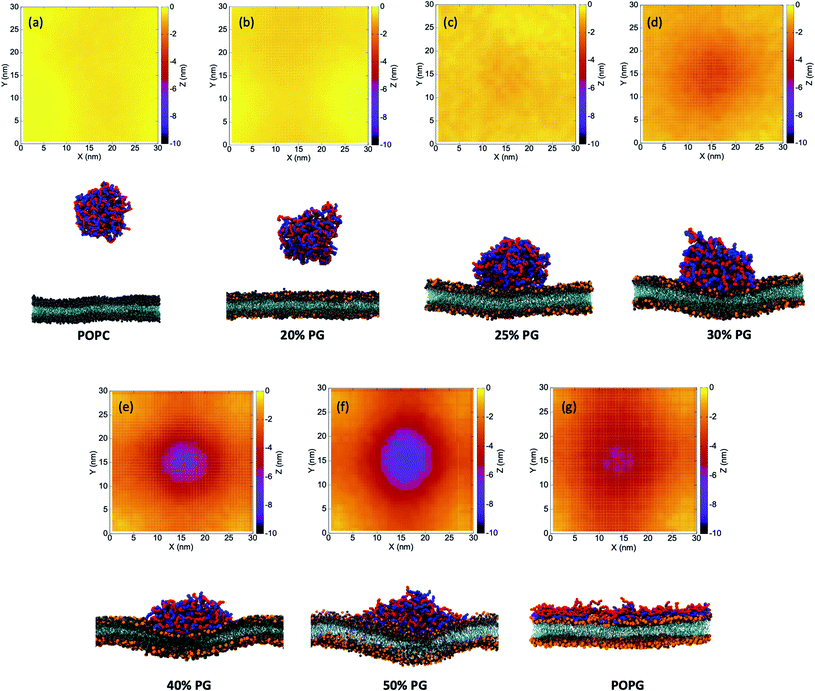
Curvature generation is an important biophysical process through which cell membranes can bend and adopt different configurations. This defines the morphology of the cell and is crucial for a diverse range of cellular functions such as membrane scission, fusion, cargo trafficking, motility, organelle shaping etc.⁷⁶ Membrane curvatures could arise because of the shapes of the constituent lipid molecules or due to the interaction with proteins/polymers.^77–82 The latter can be further divided into two broad classes of mechanisms: (i) hydrophobic insertion,⁸³ and (ii) coating/crowding of proteins.⁸⁴ In the case of curvature generation by insertion, the embedded peptide residues alter the area of membrane leaflets which leads to mechanical stress and steric repulsions.^83,85 On the other hand, curvature generation through coating/crowding occurs when proteins aggregate along the membrane surface, but without insertion. Such crowding and scaffolding generate steric pressure that drives the membrane deformation and leads to a positive curvature,⁸⁶ and the mechanism is particularly relevant to IDPs clustered at membrane surfaces.^86,87 However, the sign of the resulting curvature and morphology might depend on the chain flexibility and strength of adsorption.^81,88

We observe that E₃₀–K₃₀ coacervate induces negative curvatures at and around the region of contact. POPC and POPG exhibit zero spontaneous curvature due to their fairly cylindrical shapes.⁸⁹ The pure bilayer systems do not show any persistent spontaneous curvature under the same simulation protocols. This rules out the possibility of curvature generation due to the shape of the lipid molecules. During and after the process of curvature generation, we do not observe insertion of any E or K residues into the bilayer. The creation of negative curvatures allows the IDPs to interact strongly with the lipids which, in turn, leads to enthalpic stabilization.

In Fig. 3, we plot the time-averaged Z-surface (normal to the membrane) of the seven bilayer systems by translating the whole system with respect to the center of mass of the coacervate to the center of the box at each time step. We divide the XY-surface into 30 × 30 grids and calculate the time-averaged Z-coordinate for each grid. For the pure POPC and 20%-POPG systems, we do not observe any polyelectrolyte-lipid contact formation within the timescale of our CG simulations. Hence, there is no curvature as well [Fig. 3(a) and (b)]. However, for 25–50% POPG systems we observe persistent negative curvatures which gradually increase with the extent of wetting [Fig. 3(c)–(f)]. For the pure POPG system, expectedly there is no persistent curvature as the polyelectrolytes completely wet the bilayer surface [Fig. 3(g)].

Fig. 3 Contour plots of the Z-surface (Z is the direction of the membrane normal) and representative snapshots from simulations below each contour for: (a) pure POPC, (b) PC : PG = 80 : 20, (c) PC : PG = 75 : 25, (d) PC : PG = 70 : 30, (e) PC : PG = 60 : 40, (f) PC : PG = 50 : 50, and (g) pure POPG systems. In the two limiting cases, (a) and (g), there is no persistent curvature in the bilayer; in the former because of no contact and in the latter because of the completely dispersed state of the polyelectrolytes on the POPG membrane. Color codes: the backbone beads of E₃₀ and K₃₀ are shown in red and blue, respectively. POPC head-groups are shown in grey and those of POPG is shown in orange. Lipid tails are shown in cyan. For the clarity of representation, the water beads, ions, and polyelectrolyte side-chain beads are not shown.

These observations can be explained with the help of a theoretical model proposed by Kim and Sung.⁸¹ They established that weakly bound flexible polymers produce a positive curvature whereas a strongly bound flexible polymer produces a negative curvature, as observed in our simulations. For the latter, the order of the curvature (C) can be estimated qualitatively by eqn (5) as follows,

where T is the temperature, ε is the adsorption strength, κ is the bending modulus of the membrane, b is the range of polymer attraction that is comparable to the Debye length, and δ is a small positive number related to the thickness (ξ) of the polymer layer on the membrane; ξ = b(1 + δ). The typical values are as follows: b ∼1 nm, κ ∼10 k_BT,⁹⁰δ ∼0.1, and ε ∼10. With these numerical values fed into eqn (5), the order of the negative curvature yields as approximately 0.1 nm⁻¹. The estimated mean curvatures for our systems are also in the range of 0.1–0.2 nm⁻¹, which corroborate well with the above prediction (ESI, Table S1†). These values are one order of magnitude higher than those observed by Feig et al.⁹¹ in a simulation of protein clustering near the membrane surface. Lipowsky and co-workers also showed that an attractive interaction between the polymer and the membrane generates a negative curvature.⁸² On the other hand, a repulsive interaction between them leads to the generation of positive curvature. Later we show that the effective interaction between the polyelectrolytes and the membranes is indeed attractive and results in strong adsorption.

3.4 Deformation of the coacervate shape

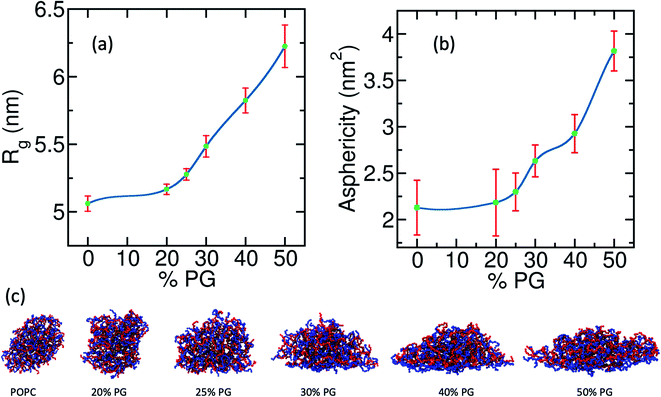
Upon adsorption on a membrane, the coacervate spreads and assumes an equilibrium shape that is different from those of the desorbed coacervates. To quantify the wetting-induced modulation of the droplet shape we calculate two time-averaged quantities, namely, radius of gyration(R_g) along the bilayer normal and asphericity (s̃), defined in eqn (6),⁹²

Here b₁, b₂, and b₃ are the eigenvalues of the gyration tensor with units of nm². The value of s̃ increases as the shape deviates from that of a sphere. In Fig. 4(a) and (b) we plot R_g and s̃ against the concentration of POPG in the bilayer. Both parameters show a non-linear monotonic increase with POPG concentration. In the cases of pure POPC and 20% POPG, the value of s̃ is around 2. This indicates that, even in the desorbed state, the shape of the coacervate is not spherical [Fig. 4(c)]. From a surface free-energy viewpoint, one might expect a spherical shape away from the membrane. However, these systems are far from the thermodynamic limit. Furthermore, there are dangling polyelectrolytes and density heterogeneity inside the coacervate that contributes to its asphericity in this lengthscale. The aspherical shape of the droplet in its desorbed state can also be realized from an entropic viewpoint. For an aspherical droplet, the effective volume of the coacervate and the number of possible configurations are higher than the spherical droplet. Both of these factors contribute to increased entropy. However, the thermodynamics of small systems can be quite different from that of a macroscopic system.⁹³

Fig. 4 Variation of the coacervate shape with respect to the fraction of POPG in the lipid membrane. (a) The radius of gyration of the polyelectrolyte coacervate along the Z-axis (membrane normal direction) quantifies the spread of the coacervate on the bilayer with increasing POPG concentration. (b) A measure of deviation from the spherical shape that captures the modulation in the shape of the droplet. (c) Representative snapshots of the coacervates in the presence of different lipid bilayers, viewed at normal to the Z-axis (The pure POPG system is not plotted as the polyelectrolyte coacervate completely wets the membrane surface and loses its globular shape).

We additionally look into the end-to-end distribution of single polymer chains in pure E₃₀–K₃₀ droplet and also in the presence of lipid bilayers. However, the single-chain end-to-end distributions of both E₃₀ and K₃₀ are found to be weakly dependent on the lipid composition and are mostly similar to the bulk distributions (ESI, Fig. S2†).

3.5 Energetics of wetting

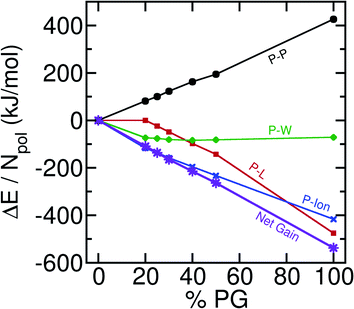
In our quest to understand the driving force for wetting and other subsequent events, we compute the component-wise interaction energy contributions between different pairs. In our multi-component systems (6 different molecules) there could be 21 distinct pairs. We obtain the sum of Lennard-Jones and electrostatic interaction energies for these pair interactions and only plot the significant contributions in Fig. 5 with respect to the % of POPG present in the system.

Fig. 5 Component-wise interaction energies against the concentration of anionic lipids in the bilayer. The energy values obtained from the pure POPC system are taken to be the reference. The self-interaction energy of polyelectrolytes increases with the negative charge concentration of the bilayer which indicates a destabilizing effect. On the other hand, the polyelectrolyte-lipid and polyelectrolyte-ion interaction energies decrease with the concentration of anionic lipids. These two stabilizing interactions produce a net gain in the enthalpy (The error bars are not shown to maintain the overall clarity of the figure).

As the total number of contacts decreases among the polyelectrolytes, there is a destabilizing effect from the polyelectrolyte–polyelectrolyte (P–P) interaction. However, there are two major stabilizing effects that arise from the polyelectrolyte-lipid (P-L) and polyelectrolyte-ion (P-Ion) interactions. It is interesting that the stabilization obtained through the increase in the P–L interactions is solely not enough to compensate for the destabilizing effect that enters through the P–P interaction energies. P-Ion and P–W attractive interactions play a major role in driving the bilayer wetting. This happens as the coacervate becomes more exposed to the water and ionic environment [Fig. 1(a), inset] after it comes in contact with the bilayer and spreads. Further decomposition of the interaction energies (ESI, Fig. S3†) for different sub-ensembles reveals that E–E interactions become stabilized with increasing wetting, but K–K and E-K interactions become more destabilized at the same time. K-POPG interactions are found to play a major role in stabilizing the P–L interactions. We note that we have focused on interaction energies in the analysis, while it has been suggested that entropic factors associated with counter ion release constitute a major driving force for coacervation in the bulk.⁴⁴ We have not analyzed the entropic component in detail here since coarse-grained models, in general, may not be able to capture the proper entropic components of the relevant free energies due to the reduction in the degrees of freedom of the system. For example, our previous study on the hydrophobic association between helical peptides⁹⁴ revealed that the MARTINI model could not capture an entropy-driven dimerization unless the CG water model features a quadrupole moment comparable to that of atomistic water clusters.⁹⁵ Interestingly, we find that Martini-3 can capture the enthalpy-entropy balance relatively well, in the context of polyelectrolyte association. Additionally, by comparing to a CHARMM36m⁹⁶ atomistic simulation, we find that Martini-3 can predict the right trend in the increase or decrease in interaction energetics among different sub-ensembles. A comparison of Martini-3 results with the new and previous simulations⁹⁷ is provided in the ESI (Section VI).† Nevertheless, systematic elucidation of entropic contributions⁹⁸ to coacervate–membrane interactions requires additional analysis using different CG or potentially atomistic models.

3.6 Kinetic aspects

The results discussed in the previous sections are based on simulations with a preformed coacervate. To study the sequence of dynamical events, we carry out several simulations starting from the relaxed bilayer surrounded by randomly placed E₃₀ and K₃₀ polypeptides, for bilayers that exhibit significant wetting. We monitor the time-evolution of the component-wise number of contacts as the systems emerge towards equilibrium. The change in the polyelectrolyte (backbone)-lipid (head) contacts (Q_P–L) are shown in Fig. 6(a) and the polyelectrolyte backbone self contacts Q_P–P) are shown in Fig. 6(b). We show several representative snapshots of the system from different time points in Fig. 7.

Fig. 6 Time evolution of (a) the total number of contacts between polyelectrolyte backbone beads and lipid heads, and (b) backbone–backbone self contacts. It is observed that the number of polyelectrolyte–polyelectrolyte contacts sharply increases within ∼100 ns, whereas the increase in the polyelectrolyte-lipid contacts is slower. The darker lines are running averages calculated for every 500 data points.

Fig. 7 Representative snapshots from different timepoints during the process of coacervate formation and wetting for all the four systems (30% to 100% POPG) where significant adsorption occurs. In all the cases, the coacervate formation precedes bilayer wetting.

For 30% and 40% POPG bilayers, we observe a gradual increase in Q_P–L followed by saturation. However, for 50% and 100% POPG systems, we observe two stages in the process of wetting. In the first stage (typically below 1 μs), the coacervate establishes contact with the lipid bilayer, followed by a spread over the bilayer at a later stage.

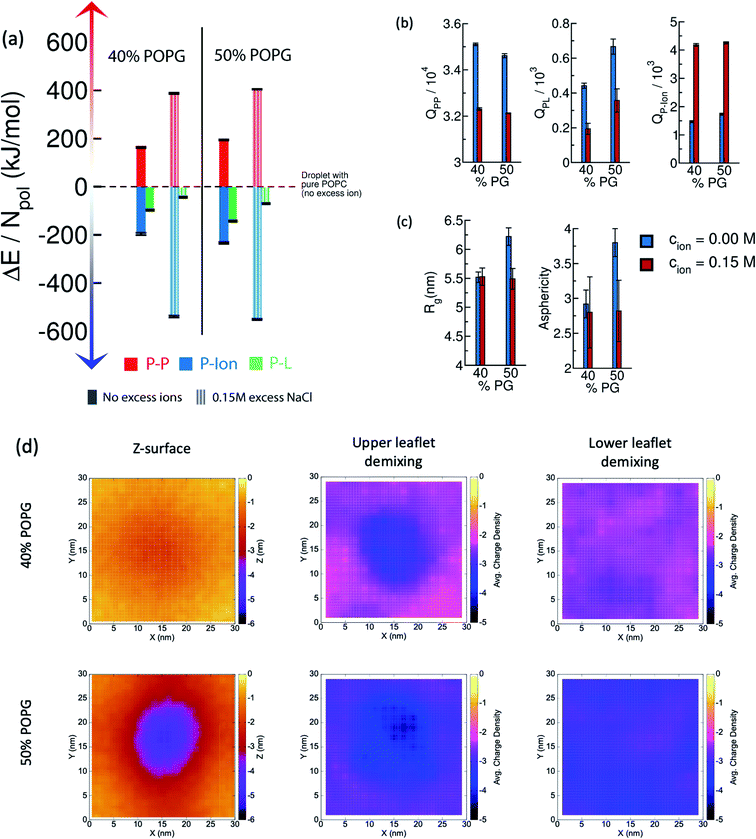
3.7 Effect of excess ions

The presence of excess ions is known to modulate the phase behavior of complex coacervates.⁴³ The results presented in the previous sub-sections include the effect of ions only required to maintain electrostatic neutrality. To understand the effect of excess ions we additionally study two systems, namely, 40% and 50% POPG, in 0.15 M NaCl solution. The results and comparisons among several quantities are shown in Fig. 8.

Fig. 8 Effect of excess ion concentration (0.15 M NaCl) on energetics, wetting, membrane remodeling, and coacervate deformation. Comparisons are drawn for two systems, namely, 40% POPG and 50% POPG. (a) Component-wise energies show that the polyelectrolyte–polyelectrolyte (red) and polyelectrolyte-lipid (green) interactions get more destabilized in the presence of excess ions, whereas polyelectrolyte-ion (blue) interactions become a substantial stabilizing factor. The energy values are subtracted from the respective values for the pure POPC system and thus are relative. (b) Time-averaged numbers of contacts between different components reveal a decrease in the polyelectrolyte–polyelectrolyte and polyelectrolyte-lipid contacts in the presence of excess ions. (c) The radius of gyration along the membrane normal (Z-axis) and asphericity parameter reveal a decreased spread of the droplet on 50% POPG membrane. (d) Polyelectrolyte-induced curvature generation and local demixing of lipids are observed, although the amplitude is attenuated in the presence of excess ions.

In Fig. 8(a), we show the interplay among the component-wise interaction energies. Compared to the systems with no-excess ion, a decrease in the polyelectrolyte–polyelectrolyte and polyelectrolyte-lipid interactions is observed, whereas there is a marked stabilization of the polyelectrolyte-ion interactions. The molecular origin of this can be clearly understood from the decrease in P–P and P–L contacts; and an increase in the P-Ion contacts [Fig. 8(b)]. Upon more microscopic analysis, we find that the E–K interchain contacts get substantially reduced, whereas the E–E and K–K contacts remain almost unchanged in these two cases. We provide the detailed decomposition of energetics and contact pair analysis for different components in the ESI (Table S2 and S3)†.

In Fig. 8(c), a comparison is drawn based on the shape of the poly-E/K coacervate in terms of R_g along the membrane normal and asphericity, s̃. It is found that, in the case of 40% POPG system, the shape of the droplet weakly depends on the excess 0.15 M salt concentration. On the other hand, in the case of 50% POPG system, the droplet exhibits less spreading over the bilayer, as identified by a decreased value of R_g and s̃. Coacervate induced negative curvature and local demixing are observed in the simulations with excess ions as well, although the magnitude of the curvature is attenuated [Fig. 8(d)].

We perform two more sets of simulations with 0.4 M and 0.6 M excess NaCl solution to check the catalytic effects (if any) of the charged bilayers. To this aim, we start with the same initial configuration with preformed droplet and replaced an appropriate number of water beads with ions. We find that both the P–P and P–L interactions get substantially screened. With the progress of time, the coacervate dissolves into the solution and the polyelectrolytes desorb from the membrane. The results are provided in ESI (Fig. S4†).

4 Concluding remarks

Interaction between phase-separated IDPs and biological membranes represents an emerging and important area of research considering its relevance to signal transduction and membrane remodeling.^{16–18,21,28} Here we use CG molecular dynamics simulations (with the MARTINI v3.0 force-field) to study the effect of complex coacervates on lipid bilayers. The choice of this particular model is partly driven by the previous study by Marrink et al.,³³ who captured the key characteristics of poly-E/K coacervation in the bulk, including the salt-dependence.⁴³ Our simulations reveal that the EK-coacervate can substantially modulate the structure and morphology of the membranes, without any peptide insertion. The membrane can also deform and modulate the structure of the coacervate. The extent of remodeling depends on the ratio of zwitterionic (POPC) and anionic (POPG) lipids. We find that at least more than 20% anionic lipid concentration is required for the coacervate to wet the membrane. Although it could be perceived as a fairly high anionic lipid concentration compared to physiological conditions, local fluctuations and density heterogeneity can produce lipid patches with a high fraction of anionic lipids.

There are several events that happen once the coacervate gets adsorbed on the membrane. The three key observations are as follows: (i) wetting of the membrane by the coacervate induces a negative curvature, (ii) the coacervate facilitates local demixing of lipids where the anionic lipids gather at and around the region of contact, and (iii) the coacervate gets deformed and spreads over the membrane surface. Our observations are in good agreement with existing theoretical models. For example, the phenomenon of negative curvature generation for such systems is well described by existing analytical theories^81,82 and the origin of local demixing upon wetting can also be explained with the help of earlier theoretical models.⁷² We perform several microscopic analyses to gain physical insights and elucidate the driving force that causes the aforementioned observations.

The earlier study by Stachowiak and co-workers, using a continuum mechanics framework, identified the increased overlap among the IDP residues as the driving force of membrane curvature generation.²¹ This is, however, not observed in the case of the polyelectrolyte coacervate-induced curvature generation. We observed that wetting of the bilayer reduces the total number of contacts among the polyelectrolytes. On the other hand, contacts between polyelectrolyte-lipid and polyelectrolyte-ion pairs show a marked increase. The curved membrane surface and the segregated anionic lipid heads near the coacervate, allow a larger number of contacts and thus lead to stronger ionic attractive interactions than a flat membrane surface. Our observations are in good agreement with the range of membrane curvatures predicted from the theoretical treatment of Kim and Sung [eqn. (5)] for strongly adsorbed polymers. The reduction in polyelectrolyte–polyelectrolyte contact is essentially led by a decrease in K–K and E–K contacts, whereas E–E contacts are found to slightly increase or remain the same. Hypothetically, in the case of a positively charged membrane, the reverse would have been observed. This is manifested in the energetics where the decrease in P–P interactions is compensated by an increase in the P–L and P-Ion interactions. Additionally, kinetic simulations reveal that the coacervate formation occurs before membrane wetting, at least for the polyelectrolyte concentrations explored in this study. The key trends are found to remain the same when an excess of 0.15 M NaCl is present in the system.

To conclude, the present study demonstrates that poly-glutamate and poly-lysine coacervate possesses a remarkable ability to remodel anionic lipid membranes; for example, the degree of membrane curvature observed in our analysis (∼0.1–0.2 nm⁻¹) falls in the range relevant to many realistic membrane remodeling processes in biology such as vesicle biogenesis.^76,99 The physical insight gained from this study could be helpful in understanding the potential use of synthetic IDPs in biology and medicine. Our analyses go beyond the conventional explanations of the origin of negative curvature generation and unravel the crucial role of counterions in curvature generation and demixing, for such highly charged systems. We believe that the present study raises several important questions such as how the sequence and/or charge distribution of the polyelectrolytes (or IDPs) get manifested in membrane remodeling. As the first computational study of LLPS on membranes, it could also serve as a prototype for future works in this field.

To study the related phenomena that involve more complex proteins and membranes and interpret their true implications in biology, simulations with larger length scales and longer time scales are required and would be computationally prohibitive even with the explicit solvent CG models used here. Although a number of solvent-free models are available for lipids and IDPs, accurate modeling of the lipid-IDP interactions remains a challenge. The future direction of our work shall focus on this aspect.

Data availability

The data that support the findings of this study are available in the main manuscript, the ESI† and also from the authors upon reasonable request.

Author contributions

Q. C. proposed the project. S. M. and Q. C. designed the research. S. M. performed the simulations and analyses. S. M. and Q. C. wrote the manuscript. Both the authors discussed, revised, and approved the final version of the manuscript.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

This work was supported in part by grant NSF-DMS-1661900 to QC. Computational resources from the Extreme Science and Engineering Discovery Environment (XSEDE¹⁰⁰), which is supported by NSF grant number ACI-1548562, are greatly appreciated; part of the computational work was performed on the Shared Computing Cluster which is administered by Boston University's Research Computing Services (URL: https://www.bu.edu/tech/support/research/).

References

1. A. A. Hyman, C. A. Weber and F. Jülicher, Annu. Rev. Cell Dev. Biol., 2014, 30, 39–58.
2. A. E. Posey, A. S. Holehouse and R. V. Pappu, Methods Enzymol., 2018, 611, 1–30.
3. J. McCarty, K. T. Delaney, S. P. Danielsen, G. H. Fredrickson and J.-E. Shea, J. Phys. Chem. Lett., 2019, 10, 1644–1652.
4. J. Dinic, A. B. Marciel and M. V. Tirrell, Curr. Opin. Colloid Interface Sci., 2021, 54, 101457.
5. C. P. Brangwynne, C. R. Eckmann, D. S. Courson, A. Rybarska, C. Hoege, J. Gharakhani, F. Jülicher and A. A. Hyman, Science, 2009, 324, 1729–1732.
6. S. Alberti and D. Dormann, Annu. Rev. Genet., 2019, 53, 171–194.
7. Y. Lin, D. S. Protter, M. K. Rosen and R. Parker, Mol. Cell, 2015, 60, 208–219.
8. S. F. Banani, H. O. Lee, A. A. Hyman and M. K. Rosen, Nat. Rev. Mol. Cell Biol., 2017, 18, 285–298.
9. S. Alberti, A. Gladfelter and T. Mittag, Cell, 2019, 176, 419–434.
10. A. Molliex, J. Temirov, J. Lee, M. Coughlin, A. P. Kanagaraj, H. J. Kim, T. Mittag and J. P. Taylor, Cell, 2015, 163, 123–133.
11. A. Bremer, M. Farag, W. M. Borcherds, I. Peran, E. W. Martin, R. V. Pappu and T. Mittag, Nat. Chem., 2022, 14, 196–207.
12. G. L. Dignon, W. Zheng, Y. C. Kim, R. B. Best and J. Mittal, PLoS Comput. Biol., 2018, 14, e1005941.
13. F. G. Quiroz and A. Chilkoti, Nat. Mater., 2015, 14, 1164–1171.
14. B. S. Schuster, G. L. Dignon, W. S. Tang, F. M. Kelley, A. K. Ranganath, C. N. Jahnke, A. G. Simpkins, R. M. Regy, D. A. Hammer and M. C. Good, et al. , Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 11421–11431.
15. S. Banjade and M. K. Rosen, eLife, 2014, 3, e04123.
16. L. B. Case, J. A. Ditlev and M. K. Rosen, Annu. Rev. Biophys., 2019, 48, 465–494.
17. H. Kusumaatmaja, A. I. May and R. L. Knorr, J. Cell Biol., 2021, 220, e202103175.
18. W. T. Snead and A. S. Gladfelter, Mol. Cell, 2019, 76, 295–305.
19. W. Y. C. Huang, S. Alvarez, Y. Kondo, Y. K. Lee, J. K. Chung, H. Y. M. Lam, K. H. Biswas, J. Kuriyan and J. T. Groves, Science, 2019, 363, 1098–1103.
20. L. B. Case, X. Zhang, J. A. Ditlev and M. K. Rosen, Science, 2019, 363, 1093–1097.
21. F. Yuan, H. Alimohamadi, B. Bakka, A. N. Trementozzi, K. J. Day, N. L. Fawzi, P. Rangamani and J. C. Stachowiak, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2017435118.
22. K. J. Day, G. Kago, L. Wang, J. B. Richter, C. C. Hayden, E. M. Lafer and J. C. Stachowiak, Nat. Cell Biol., 2021, 23, 366–376.
23. L.-P. Bergeron-Sandoval, S. Kumar, H. K. Heris, C. L. A. Chang, C. E. Cornell, S. L. Keller, P. Francois, A. G. Hendricks, A. J. Ehrlicher, R. V. Pappu and S. W. Michnick, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2113789118.
24. J. Agudo-Canalejo, S. W. Schultz, H. Chino, S. M. Migliano, C. Saito, I. Koyama-Honda, H. Stenmark, A. Brech, A. I. May, N. Mizushima and R. L. Knorr, Nature, 2021, 591, 142–146.
25. S. Botterbusch and T. Baumgart, Appl. Sci., 2021, 11, 1288.
26. J. K. Chung, W. Y. C. Huang, C. B. Carbone, L. M. Nocka, A. N. Parikh, R. D. Vale and J. T. Groves, Biophys. J., 2021, 120, 1257–1265.
27. L. B. Case, M. De Pasquale, L. Henry and M. K. Rosen, eLife, 2022, 11, e72588.
28. M. Rouches, S. L. Veatch and B. B. Machta, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2103401118.
29. R. K. Das and R. V. Pappu, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 13392–13397.
30. A. M. Rumyantsev, N. E. Jackson and J. J. De Pablo, Annu. Rev. Condens. Matter Phys., 2021, 12, 155–176.
31. C. E. Sing and S. L. Perry, Soft Matter, 2020, 16, 2885–2914.
32. K. T. Delaney and G. H. Fredrickson, J. Chem. Phys., 2017, 146, 224902.
33. M. Tsanai, P. W. Frederix, C. F. Schroer, P. C. Souza and S. J. Marrink, Chem. Sci., 2021, 12, 8521–8530.
34. L. Shih, M.-H. Shen and Y.-T. Van, Bioresour. Technol., 2006, 97, 1148–1159.
35. W.-C. Shen, Biochim. Biophys. Acta, Gen. Subj., 1990, 1034, 122–124.
36. I.-L. Shih, Y.-T. Van and M.-H. Shen, Mini-Rev. Med. Chem., 2004, 4, 179–188.
37. Y. Wang, L. Huang, Y. Shen, L. Tang, R. Sun, D. Shi, T. J. Webster, J. Tu and C. Sun, Int. J. Nanomedicine, 2017, 12, 7963.
38. A. Melnyk, J. Namieśnik and L. Wolska, Trends Anal. Chem., 2015, 71, 282–292.
39. W. C. Blocher and S. L. Perry, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2017, 9, e1442.
40. J. J. Hwang and S. I. Stupp, J. Biomater. Sci., Polym. Ed., 2000, 11, 1023–1038.
41. L. Richert, Y. Arntz, P. Schaaf, J.-C. Voegel and C. Picart, Surf. Sci., 2004, 570, 13–29.
42. J. M. Buescher and A. Margaritis, Crit. Rev. Biotechnol., 2007, 27, 1–19.
43. D. Priftis and M. Tirrell, Soft Matter, 2012, 8, 9396–9405.
44. A. N. Singh and A. Yethiraj, J. Phys. Chem. B, 2020, 124, 1285–1292.
45. J. T. G. Overbeek and M. Voorn, J. Cell. Comp. Physiol., 1957, 49, 7–26.
46. P. J. Flory, J. Chem. Phys., 1942, 10, 51–61.
47. M. L. Huggins, J. Phys. Chem., 1942, 46, 151–158.
48. Y.-H. Lin, J. Song, J. D. Forman-Kay and H. S. Chan, J. Mol. Liq., 2017, 228, 176–193.
49. S. Das, Y.-H. Lin, R. M. Vernon, J. D. Forman-Kay and H. S. Chan, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 28795–28805.
50. P. C. Souza, R. Alessandri, J. Barnoud, S. Thallmair, I. Faustino, F. Grünewald, I. Patmanidis, H. Abdizadeh, B. M. Bruininks and T. A. Wassenaar, et al. , Nat. Methods, 2021, 18, 382–388.
51. D. Ando, R. Zandi, Y. W. Kim, M. Colvin, M. Rexach and A. Gopinathan, Biophys. J., 2014, 106, 1997–2007.
52. S. Roberts, T. S. Harmon, J. L. Schaal, V. Miao, K. J. Li, A. Hunt, Y. Wen, T. G. Oas, J. H. Collier and R. V. Pappu, et al. , Nat. Mater., 2018, 17, 1154–1163.
53. A. P. Latham and B. Zhang, J. Chem. Theory Comput., 2019, 16, 773–781.
54. H. S. Samanta, D. Chakraborty and D. Thirumalai, J. Chem. Phys., 2018, 149, 163323.
55. V. Nguemaha and H.-X. Zhou, Sci. Rep., 2018, 8, 1–11.
56. M. Feric, N. Vaidya, T. S. Harmon, D. M. Mitrea, L. Zhu, T. M. Richardson, R. W. Kriwacki, R. V. Pappu and C. P. Brangwynne, Cell, 2016, 165, 1686–1697.
57. Z. Benayad, S. von Bulow, L. S. Stelzl and G. Hummer, J. Chem. Theory Comput., 2021, 17, 525–537.
58. L. A. Gruijs da Silva, F. Simonetti, S. Hutten, H. Riemenschneider, E. L. Sternburg, L. M. Pietrek, J. Gebel, V. Dötsch, D. Edbauer, G. Hummer, L. S. Stelzl and D. Dormann, EMBO J., 2022, e108443.
59. A. M. Rumyantsev, N. E. Jackson, B. Yu, J. M. Ting, W. Chen, M. V. Tirrell and J. J. De Pablo, ACS Macro Lett., 2019, 8, 1296–1302.
60. S. J. Marrink and D. P. Tieleman, Chem. Soc. Rev., 2013, 42, 6801–6822.
61. W. L. DeLano, et al. , CCP4 Newsl. Prot. Crystallogr., 2002, 40, 82–92.
62. T. A. Wassenaar, H. I. Ingólfsson, R. A. Bockmann, D. P. Tieleman and S. J. Marrink, J. Chem. Theory Comput., 2015, 11, 2144–2155.
63. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
64. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
65. H. J. Berendsen, J. v. Postma, W. F. Van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
66. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25.
67. G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613.
68. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
69. M. Bonomi, D. Branduardi, G. Bussi, C. Camilloni, D. Provasi, P. Raiteri, D. Donadio, F. Marinelli, F. Pietrucci and R. A. Broglia, et al., Comput. Phys. Commun., 2009, 180, 1961–1972.
70. A. Barducci, M. Bonomi, M. K. Prakash and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E4708–E4713.
71. P. Banerjee, S. Mondal and B. Bagchi, J. Chem. Phys., 2019, 150, 084902.
72. S. May, D. Harries and A. Ben-Shaul, Biophys. J., 2000, 79, 1747–1760.
73. T. Heimburg, B. Angerstein and D. Marsh, Biophys. J., 1999, 76, 2575–2586.
74. M. Das, U. Dahal, O. Mesele, D. Liang and Q. Cui, J. Phys. Chem. B, 2019, 123, 10547–10561.
75. B. H. Stumpf, P. Nowakowski, C. Eggeling, A. Maciołek and A.-S. Smith, Phys. Rev. Res., 2021, 3, L042013.
76. I. K. Jarsch, F. Daste and J. L. Gallop, J. Cell Biol., 2016, 214, 375–387.
77. T. Mandal, S. E. Spagnolie, A. Audhya and Q. Cui, Biophys. J., 2021, 120, 3211–3221.
78. H. Alimohamadi and P. Rangamani, Biomolecules, 2018, 8, 120.
79. H. T. McMahon and E. Boucrot, J. Cell Sci., 2015, 128, 1065–1070.
80. T. Baumgart, B. R. Capraro, C. Zhu and S. L. Das, Annu. Rev. Phys. Chem., 2011, 62, 483–506.
81. Y. W. Kim and W. Sung, Phys. Rev. E, 2001, 63, 041910.
82. C. Hiergeist, V. Indrani and R. Lipowsky, Europhys. Lett., 1996, 36, 491.
83. F. Campelo, H. T. McMahon and M. M. Kozlov, Biophys. J., 2008, 95, 2325–2339.
84. J. Zimmerberg and M. M. Kozlov, Nat. Rev. Mol. Cell Biol., 2006, 7, 9–19.
85. M. C. Lee, L. Orci, S. Hamamoto, E. Futai, M. Ravazzola and R. Schekman, Cell, 2005, 122, 605–617.
86. J. C. Stachowiak, E. M. Schmid, C. J. Ryan, H. S. Ann, D. Y. Sasaki, M. B. Sherman, P. L. Geissler, D. A. Fletcher and C. C. Hayden, Nat. Cell Biol., 2012, 14, 944–949.
87. D. J. Busch, J. R. Houser, C. C. Hayden, M. B. Sherman, E. M. Lafer and J. C. Stachowiak, Nat. Commun., 2015, 6, 1–11.
88. S. Liese and A. Carlson, Biophys. J., 2021, 120, 2482–2489.
89. A. Dickey and R. Faller, Biophys. J., 2008, 95, 2636–2646.
90. J. Eid, H. Razmazma, A. Jraij, A. Ebrahimi and L. Monticelli, J. Phys. Chem. B, 2020, 124, 6299–6311.
91. G. Nawrocki, W. Im, Y. Sugita and M. Feig, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 24562–24567.
92. J. Vymetal and J. Vondrasek, J. Phys. Chem. A, 2011, 115, 11455–11465.
93. T. L. Hill, J. Chem. Phys., 1962, 36, 3182–3197.
94. Z. Wu, Q. Cui and A. Yethiraj, J. Phys. Chem. Lett., 2011, 2, 1794–1798.
95. Z. Wu, Q. Cui and A. Yethiraj, J. Phys. Chem. B, 2010, 114, 10524–10529.
96. J. Huang, S. Rauscher, G. Nawrocki, T. Ran, M. Feig, B. L. De Groot, H. Grubmüller and A. D. MacKerell, Nat. Methods, 2017, 14, 71–73.
97. A. N. Singh and A. Yethiraj, J. Phys. Chem. B, 2020, 124, 1285–1292.
98. V. Vivcharuk and Y. Kaznessis, J. Phys. Chem. B, 2010, 114, 2790–2797.
99. A. L. Schuh and A. Audhya, Crit. Rev. Biochem. Mol. Biol., 2014, 49, 242–261.
100. J. Towns, T. Cockerill, M. Dahan, I. Foster, K. Gaither, A. Grimshaw, V. Hazelwood, S. Lathrop, D. Lifka, G. D. Peterson, R. Roskies, J. R. Scott and N. Wilkins-Diehr, Comput. Sci. Eng., 2014, 16, 62–74.

---

Footnote

† Electronic supplementary information (ESI) available: component wise analyses, end-to-end distributions of E₃₀ and K₃₀ chains, numerical values of curvature from spherical fits, comparison between systems with no vs. excess NaCl, and comparison with atomistic simulations. See https://doi.org/10.1039/d2sc02013k

---