Open Access Article
Open Access ArticleGa and Zn increase the oxygen affinity of Cu-based catalysts for the COx hydrogenation according to ab initio atomistic thermodynamics†
Andreas
Müller
 a,
Aleix
Comas-Vives
a,
Aleix
Comas-Vives
 *bc and
Christophe
Copéret
*bc and
Christophe
Copéret
 *a
*a
aDepartment of Chemistry and Applied Biosciences, ETH Zürich, 8093 Zurich, Switzerland. E-mail: ccoperet@ethz.ch; Tel: +41 44 633 93 94
bInstitute of Materials Chemistry, TU Wien, 1060 Vienna, Austria. E-mail: aleix.comas@tuwien.ac.at
cDepartament de Química, Universitat Autònoma de Barcelona, 08193 Cerdanyola del Vallès, Catalonia, Spain. E-mail: Aleix.Comas@uab.cat
First published on 8th November 2022
Abstract
The direct hydrogenation of CO or CO2 to methanol, a highly vivid research area in the context of sustainable development, is typically carried out with Cu-based catalysts. Specific elements (so-called promoters) improve the catalytic performance of these systems under a broad range of reaction conditions (from pure CO to pure CO2). Some of these promoters, such as Ga and Zn, can alloy with Cu and their role remains a matter of debate. In that context, we used periodic DFT calculations on slab models and ab initio thermodynamics to evaluate both metal alloying and surface formation by considering multiple surface facets, different promoter concentrations and spatial distributions as well as adsorption of several species (O*, H*, CO* and 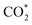 ) for different gas phase compositions. Both Ga and Zn form an fcc-alloy with Cu due to the stronger interaction of the promoters with Cu than with themselves. While the Cu–Ga-alloy is more stable than the Cu–Zn-alloy at low promoter concentrations (<25%), further increasing the promoter concentration reverses this trend, due to the unfavoured Ga–Ga-interactions. Under CO2 hydrogenation conditions, a substantial amount of O* can adsorb onto the alloy surfaces, resulting in partial dealloying and oxidation of the promoters. Therefore, the CO2 hydrogenation conditions are actually rather oxidising for both Ga and Zn despite the large amount of H2 present in the feedstock. Thus, the growth of a GaOx/ZnOx overlayer is thermodynamically preferred under reaction conditions, enhancing CO2 adsorption, and this effect is more pronounced for the Cu–Ga-system than for the Cu–Zn-system. In contrast, under CO hydrogenation conditions, fully reduced and alloyed surfaces partially covered with H* and CO* are expected, with mixed CO/CO2 hydrogenation conditions resulting in a mixture of reduced and oxidised states. This shows that the active atmosphere tunes the preferred state of the catalyst, influencing the catalytic activity and stability, indicating that the still widespread image of a static catalyst under reaction conditions is insufficient to understand the complex interplay of processes taking place on a catalyst surface under reaction conditions, and that dynamic effects must be considered.
) for different gas phase compositions. Both Ga and Zn form an fcc-alloy with Cu due to the stronger interaction of the promoters with Cu than with themselves. While the Cu–Ga-alloy is more stable than the Cu–Zn-alloy at low promoter concentrations (<25%), further increasing the promoter concentration reverses this trend, due to the unfavoured Ga–Ga-interactions. Under CO2 hydrogenation conditions, a substantial amount of O* can adsorb onto the alloy surfaces, resulting in partial dealloying and oxidation of the promoters. Therefore, the CO2 hydrogenation conditions are actually rather oxidising for both Ga and Zn despite the large amount of H2 present in the feedstock. Thus, the growth of a GaOx/ZnOx overlayer is thermodynamically preferred under reaction conditions, enhancing CO2 adsorption, and this effect is more pronounced for the Cu–Ga-system than for the Cu–Zn-system. In contrast, under CO hydrogenation conditions, fully reduced and alloyed surfaces partially covered with H* and CO* are expected, with mixed CO/CO2 hydrogenation conditions resulting in a mixture of reduced and oxidised states. This shows that the active atmosphere tunes the preferred state of the catalyst, influencing the catalytic activity and stability, indicating that the still widespread image of a static catalyst under reaction conditions is insufficient to understand the complex interplay of processes taking place on a catalyst surface under reaction conditions, and that dynamic effects must be considered.
1 Introduction
Today, a large effort is directed at finding solutions to decrease the emission of carbon dioxide (CO2) and its atmospheric concentration by conversion or sequestration processes since its atmospheric concentration directly relates to the observed climate change.1 One of the possible routes towards a carbon-neutral society is based on the so-called methanol economy,2–4 where CO2 is converted into methanol, a key chemical intermediate and a fuel additive, via hydrogenation using “green” H2, coming from renewable energy sources. This would lead to an overall decarbonisation of our economy (eqn (1)).5,6| CO2 + 3H2 ⇌ CH3OH + H2O; ΔH273K = −49.5 kJ mol−1 | (1) |
| CO2 + H2 ⇌ CO + H2O; ΔH273K = 41.25 kJ mol−1 | (2) |
| CO + 2H2 ⇌ CH3OH; ΔH273K = −90.5 kJ mol−1 | (3) |
| CO2 + 4H2 ⇌ CH4 + 2H2O; ΔH273K = −165.0 kJ mol−1 | (4) |
This reaction typically competes with the (reverse) water gas shift ((R)WGS) reaction (eqn (2)) as well as other reactions such as the hydrogenation of CO (eqn (3)) or the Sabatier (CO2 methanation) reaction (eqn (4)). The choice of catalysts is crucial to drive the efficient use of hydrogen and the reactions towards the desired product, e.g. methanol.7,8
In this context, some of the most promising catalysts are based on copper usually dispersed on or stabilized by oxide supports, e.g. Cu/ZnO/Al2O3. These catalysts were originally developed and are still used for the hydrogenation of CO to methanol. This process based on the conversion of syngas (mixture of H2/CO at ratios between 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 3
1 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) is carried out in the presence of small quantities of CO2 (a few %) at high temperatures (200 to 300 °C) and pressures (50 to 100 bar).9,10 The main advantage of such Cu-based catalysts is the absence of over-reduction of CO or CO2 to hydrocarbons via the Sabatier reaction (4), which would be thermodynamically favoured and would waste large quantities of hydrogen in the feedstock to produce methane, a greenhouse gas and a molecule of lower value than methanol.11
1) is carried out in the presence of small quantities of CO2 (a few %) at high temperatures (200 to 300 °C) and pressures (50 to 100 bar).9,10 The main advantage of such Cu-based catalysts is the absence of over-reduction of CO or CO2 to hydrocarbons via the Sabatier reaction (4), which would be thermodynamically favoured and would waste large quantities of hydrogen in the feedstock to produce methane, a greenhouse gas and a molecule of lower value than methanol.11
In recent years, large attention has been refocused on investigating these Cu-based catalysts for the hydrogenation of pure CO2 or CO2-rich gas feeds containing CO.12–54 This has led to the development of several processes towards large-scale application.55–59 Nevertheless, hydrogenation with CO2-rich feeds usually suffers from product inhibition, reducing the overall activity of the catalyst.60 Furthermore, low methanol selectivity is also observed in the low pressure range due to the competing RWGS-reaction.61 Finally, the production of large quantities of water causes catalyst deactivation, thus reducing the long-term catalyst stability.62
This has led to refocused research efforts to increase the activity, selectivity and stability of Cu-based catalysts.63,64 Detailed mechanistic studies using Surface Organometallic Chemistry (SOMC) and thermolytic molecular precursors (TMP),65,66 among others, have highlighted the role of the interface and specific promoters between Cu nanoparticles and the oxide supports.67–70
It was also shown that the presence of promoters like Ga or Zn can generate Cu–Ga- or Cu–Zn-alloy NPs upon treatment under H2. The addition of these promoters also greatly increases methanol selectivity, in particular at high conversion and low pressure. Detailed operando X-ray Absorption Spectroscopy was able to show that under reaction conditions (T = 230 °C, 15 bar H2, 5 bar CO2), full and partial dealloying takes place for Ga and Zn in a partially reversible process upon switching from a CO2/H2 to a pure H2 atmosphere, clearly showing that dynamic phenomena readily take place in these systems.71–74 Such process is reminiscent of what has been discussed for the Cu/ZnO/Al2O3 catalysts, further fuelling the debate regarding the nature of the catalytic active sites.75–81 Furthermore, it is consistent with the rich chemistry of Cu–Zn- and Cu–Ga-alloys, that display similar yet distinct alloying behaviour and phase diagrams (vide infra).82,83
In parallel, computational chemistry has emerged as a powerful technique for understanding heterogeneous catalysts84–91 and also helped unravel the role of the support in methanol synthesis.68,92 We aim to understand from first principles calculations the state of Cu–Ga- and Cu–Zn-based alloys under a broad range of reaction conditions, ranging from a pure hydrogen atmosphere under which catalysts are typically prepared, to typical CO/CO2 hydrogenation conditions. We will interrogate the stability of Cu–Ga- and Cu–Zn-alloys and their propensity to interact with multiple relevant adsorbates (O*, H*, CO*, 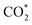 ) under these conditions, extending our previous work for pure Cu surfaces.93 We will focus our study on the most stable facets of Cu-based alloy NPs promoted with Ga and Zn by modelling the gas phase composition and temperature via ab initio atomistic thermodynamics. Since promoters are usually the minor species, we will consider a fcc-solid solution of both alloys under reaction conditions.
) under these conditions, extending our previous work for pure Cu surfaces.93 We will focus our study on the most stable facets of Cu-based alloy NPs promoted with Ga and Zn by modelling the gas phase composition and temperature via ab initio atomistic thermodynamics. Since promoters are usually the minor species, we will consider a fcc-solid solution of both alloys under reaction conditions.
2 Theoretical methods
2.1 Computational details
All Calculations were performed using the Vienna Ab initio Simulation Package (VASP)94–96 with a cut-off energy of 400 eV. The structures were optimized using the projector augmented wave (PAW) method (plane-wave basis set with pseudopotentials)97,98 using the official VASP pseudopotentials99 and the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional.100,101 Default settings were used for VASP if not stated otherwise. Electronic occupancies were determined according to a Methfessel–Paxton scheme with an energy smearing of 0.2 eV. The convergence criteria for the electronic SCF-loop (EDIFF) was set to 10−5 eV. The ionic relaxation was considered converged when the norms of all the forces were smaller than 10 meV Å−1 (EDIFFG = −0.01). The ions were relaxed via the conjugate gradient algorithm (IBRION = 2). The Monkhorst–Pack k-point mesh was used to sample the Brillouin zone; 11 × 11 × 11 for bulk, 3 × 3 × 1 for the slabs, and only at the Γ-point for molecules. Typical input files used for the calculations are attached to the ESI.† The slab models were illustrated using Visualization for Electronic and STructural Analysis (VESTA), a 3D visualisation program for structural models, volumetric data and crystal morphologies.1022.2 Ab initio thermodynamics
The stability of all surfaces considering the adsorption at given conditions was calculated using ab initio thermodynamics.103 We used the same approach as described in our last work (Müller et al.93). The configurational entropy can safely be neglected since its contribution to the Gibbs free energy is less than 3 meV Å−1 for transition metal surfaces and a surface area per surface site of around 10 Å2 as long as the temperature remains significantly lower than 1000 K.104 For a more detailed discussion than in the main text, we refer the reader to the ESI.†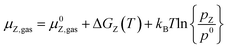 | (5) |
For gases consisting of multiple different atoms, such as CO2, the chemical potential of a single atom is defined as the difference of the chemical potential of the whole molecule and the chemical potential of the remaining molecule without that specific atom. For example, the chemical potential of O* in CO2 is the difference between the chemical potential of CO2 and the chemical potential of CO.
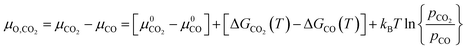 | (6) |
Thus, the chemical potential for any atom/molecule Z directly in the gas phase or a in gas containing Z can be represented by an equation of the following form:
| μZ,gas = aZ + bZ(T) + cZ(T,p) | (7) |
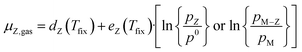 | (8) |
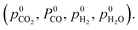 Assuming that only CO2 and H2O act as oxidising agents, eqn (9) can be used to calculate the total chemical potential of oxygen under reaction conditions (μO,tot):
Assuming that only CO2 and H2O act as oxidising agents, eqn (9) can be used to calculate the total chemical potential of oxygen under reaction conditions (μO,tot):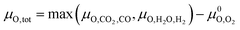 | (9) |
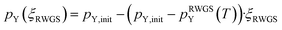 | (10) |
Since μO,tot only depends on the ratio of the partial pressures of CO2 to CO and H2O to H2 and μCO2, μCO, μH2O and μH depend linearly on the logarithm of the individual partial pressures (pCO2, pCO, pH2, pH2O; see eqn (8)), rather small changes are expected by changing the absolute pressures without changing the relative pressures. By doubling the pressures from the initial conditions (T = 230 °C, 15 bar H2, 5 bar CO2 to T = 230 °C, 30 bar H2, 10 bar CO2) we slightly increase the initial μH and μCO2 and thus the initial μO. Considering at least minimal RWGS conversion, μH and μCO2 decrease while μH2O and μCO increase resulting in practically the same observed chemical potentials as observed for the initial conditions (T = 230 °C, 15 bar H2, 5 bar CO2). The same trend is observed if the partial pressure is doubled again resulting in the industrially relevant conditions (T = 230 °C, 60 bar H2, 20 bar CO2, ptot = 80 bar). Since μO depends only on the ratio of CO2 to CO and H2O to H2, considering minimal RWGS conversion results in equal values for μO for the three different partial pressures since the ratios of pCO2 to pCO and pH2O to pH2 are equal in all three cases (compare eqn (8)). A selection of conditions with explicit values for the different chemical potentials are shown in Table S1 in the ESI,† while the changes for the oxygen chemical potentials for selected starting conditions are shown in the ESI (Fig. S1–S4†).
More significant changes are observed if the composition of the feedstock changes. If we replace some of the CO2 in the feedstock by CO, μO decreases. Fig. 1 shows μO under reaction conditions depending on the molar ratio of CO2 in the feedstock (XCO2) with the colour gradient indicating the progressing RWGS conversion: from low (yellow) to high (red). Unless a pure CO-feed is present, some CO2 and H2 are always converted to CO and H2O by the RWGS-reaction mainly due to the absence of H2O in the feedstock. Since H2O is a stronger oxidant than CO2 unless no CO is present in the feedstock, μO increases with increasing RWGS conversion.
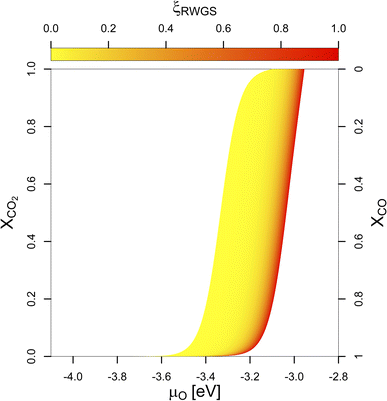 | ||
| Fig. 1 Chemical potential of oxygen (μO) under COx hydrogenation conditions depending on the molar ratio of CO2 in the feedstock (XCO2). The colour gradient from yellow to red indicates the progressing RWGS conversion (yellow indicates low conversion, red indicates higher RWGS conversion, respectively). μO does not depend linearly on the (R)WGS-conversion (compare Fig. S5 in the ESI†). For intermediate conditions (0.1 > XCO2 > 0.9), μO under reaction conditions depends linearly on XCO2. For a pure CO2-feed (XCO2 = 1), μO is much narrower and lies between −3.11 eV and −2.92 eV (corresponding to an equivalent O2 partial pressure below 10−48 bar at 500 K). For a pure CO-feed (XCO2 = 0), μO is much lower and lies between −4.07 to −3.93 eV (corresponding to an equivalent O2 partial pressure below 10−69 bar). Removing the last quantities of CO2 from the feedstock has the most drastic effect. | ||
If some of the CO2 in the feed is replaced by CO (50%), the initial μCO increases quite significantly. Since some CO2 is always converted into CO by the RWGS-reaction, μCO increases further due to the progressing RWGS, but this effect is smaller than the effect of changing the initial gas phase composition. For the mixed feed, the μH under reaction conditions increases slightly compared to the pure CO2 feed due to the lower consumption of H2 by the RWGS-reaction since large quantities of CO are already present in the feed gas. Moreover, less H2O is produced by the RWGS-reaction. Together with the lower CO2 partial pressure, this decreases μO from the range of −3.11 eV to −2.92 eV (corresponding to an equivalent O2 partial pressure below 10−48 bar at 500 K) to the range of −3.34 eV to −3.01 eV (corresponding to an equivalent O2 partial pressure below 10−50 bar). This results are again practically independent of the different initial pressures if minimal RWGS conversion is assumed (ξRWGS > 0.01). Thus, the reaction mixture becomes slightly less oxidising and as a result, less oxygen is expected to adsorb on the surface.
If the CO2 concentration further decreases to around 5%, the same trend continues for the active atmosphere under reaction conditions: μH increases very slightly, taking practically the same value as for the case of 50% CO, μCO increases quite strongly, favouring the CO adsorption on the surface and μO decreases from the range of −3.34 eV to −3.01 eV to the range of −3.47 eV to −3.13 eV (corresponding to an equivalent O2 partial pressure below 10−53 bar) due to a decrease of the CO2 partial pressure and reduced water formation due to the RWGS-reaction. Overall, this further decreases oxygen adsorption.
The biggest change in terms of oxygen adsorption is observed if the last 5% of CO2 is removed from the reaction conditions. In this case, the effect on μH and μCO are minimal. Nevertheless, due to the absence of both CO2 and H2O in the active atmosphere, the gas mixture becomes significantly less oxidising since no oxidant is present, with μO decreasing to a range of around −4.07 eV to −3.93 eV (corresponding to an equivalent O2 partial pressure below 10−69 bar). Moreover, under these conditions, the WGS-reaction occurs rather than RWGS one.
The effect of the composition of the feedstock on μO shows that small quantities of CO2 significantly increase μO under CO hydrogenation conditions. These results could explain why small quantities of CO2 are needed in the syngas-feedstock for efficient CO hydrogenation: CO2 can oxidise the promoter (Ga, Zn) under reaction conditions (vide infra), either directly as CO2 or, more likely, indirectly in the form of water produced by the RWGS-reaction, forming partial/full promoter surface oxides, with potential active sites for the CO2 hydrogenation reaction at the interface of the metallic phase with the promoter (sub)oxides.
2.3 Mixing energy
The mixing energy of a bulk structure is the energy change upon mixing two elements relative to the individual bulk chemical potentials: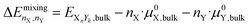 | (11) |
2.4 Surface energy
We used the same approach described in our last work (Müller et al.93) to calculate the surface energies of the evaluated systems (note that we calculate the Gibbs free surface energies). For a more detailed discussion, we refer the reader to the ESI.† The surface energy γ is defined as the energy needed to generate a surface from an equivalent bulk structure, normalized by the surface area of the resulting slab. It can be calculated for mono-metallic and multi-metallic systems: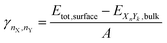 | (12) |
If an atom Z is adsorbed from the gas phase (the source of adsorbed Z), the chemical potential of the atom in the gas phase is subtracted to calculate the surface energy in the presence of the adsorbate Z.
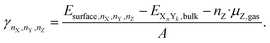 | (13) |
Inserting the expression in eqn (8) into (13) results in a expression depending linearly on the logarithm of the different partial pressures, obtaining the following equation:
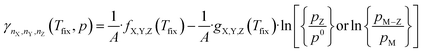 | (14) |
2.5 Cu-alloy phase diagrams
The phase diagrams for the Cu–Ga- and Cu–Zn-systems reveal some of their key properties. Both are fully miscible and form alloys (intermetallics and solid solutions) with different structures depending on the composition. The phase diagrams of the two bimetallic mixtures are shown in Fig. 2 with the different crystal structures explained in Table 1.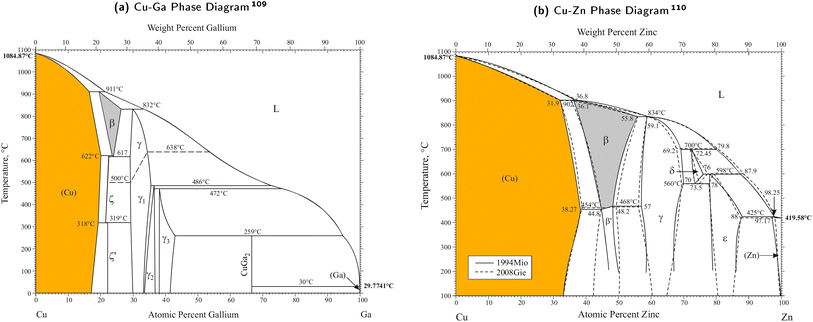 | ||
| Fig. 2 Phase diagrams of the two bimetallic mixtures for the Cu–Ga- and Cu–Zn-system. Figures taken and adapted from Okamoto109 (Cu–Ga phase diagram, (a)) and Okamoto110 (Cu–Zn phase diagram, (b)). For low concentrations of Ga/Zn, both structures crystallise in a solid solution with the fcc-structure of pure Cu modified by exchanging Cu with Ga/Zn (α-CuGa/-CuZn, coloured in orange). At higher concentrations, different crystal structures are obtained for the two systems (see Table 1). | ||
| Cu–Ga | Cu–Zn | ||
|---|---|---|---|
| Phase | Crystal structure | Phase | Crystal structure |
| (Cu) | fcc-Cu (with Ga) | (Cu) | fcc-Cu (with Zn) |
| β | bcc-Cu (with Ga) | β | bcc-Cu (with Zn, disordered) |
| ζ | hcp-Cu (with Ga) | β′ | bcc-Cu (with Zn, ordered) |
| ζ′ | Cu0.778Ga0.222 | γ | Cu5Zn8 |
| γ, γ1, γ2, γ3 | Cu9Ga4 (multiple variations) | δ | bcc-Zn (with Cu) |
| CuGa2 | CuGa2 | ε | hcp-Zn (with Cu) |
| (Ga) | Ga-structures | (Zn) | hcp-Zn |
For low promoter (Ga/Zn) concentrations, both structures crystallise in a solid solution in which the fcc-structure of pure Cu is modified by exchanging Cu with Ga/Zn. The Cu–Ga-system forms this stable fcc-solid solution up to a molar fraction of around 0.15 to 0.2 atomic% of Ga (α-CuGa, orange area in Fig. 2a), while the fcc-solid solution is much more stable for the Cu–Zn-systems up to a molar fraction of around 0.35 to 0.4 Zn (α-CuZn, orange area in Fig. 2b). For higher promoter concentrations, the effect of Ga/Zn becomes increasingly dominant, resulting in different crystal structures such as the bcc-solid solution (grey areas in Fig. 2a and b), the hcp-solid solutions, the stoichiometric ζ′-phase (Cu0.778Ga0.222) or even more complex systems at higher promoter concentrations (such as the γ-phase or its variations). In this article, we focus on evaluating the composition ranges within the α-phases of both systems (α-CuGa, orange area in Fig. 2a and α-CuZn, orange area in Fig. 2b).
3 Results and discussion
3.1 Bulk structures and alloy formation
We started by optimising the bulk structure of reference compounds, namely fcc-Cu, Cu2O, CuO, hcp-Zn, w-ZnO (Wurtzite ZnO), fcc-Cu3Zn, bcc-CuZn, β-Ga, β-Ga2O3, fcc-Cu3Ga, bcc-CuGa, hcp-CuGa and Cu9Ga4 as well as relevant gas phase molecules (CO2, CO, H2O, H2, O2). Then, the oxide formation energies of Cu2O, CuO, w-ZnO and β-Ga2O3 and the alloy formation energies for the fcc-Cu3Zn, bcc-CuZn, fcc-Cu3Ga bcc-CuGa, hcp-CuGa and Cu9Ga4 were calculated with respect to their constituents and compared with published computational and experimental results.The calculated formation enthalpies for copper(I) oxide (Cu2O) and copper(II) oxide (CuO) are ΔfH(Cu2O)calc = −1.25 eV (−121 kJ mol−1) and ΔfH(CuO)calc = −1.12 eV (−108 kJ mol−1), which are in acceptable agreement with the experimental data of ΔfH(Cu2O)exp = −1.76 eV (−170 kJ mol−1) and ΔfH(CuO)exp = −1.62 eV (−156 kJ mol−1).111 The calculated formation enthalpies for wurtzite-like zinc oxide (w-ZnO) and β-Ga2O3 are ΔfH(w-ZnO)calc = −2.91 eV (−280 kJ mol−1) and ΔfH(β-Ga2O3)calc = −9.41 eV (−908 kJ mol−1), which are again in acceptable agreement with experimental data of ΔfH(w-ZnO)exp = −3.63 eV (−351 kJ mol−1) and ΔfH(β-Ga2O3)exp = −11.29 eV (−1089 kJ mol−1).114
The differences between calculated and experimental formation energies (0.51 eV for Cu2O, 0.50 eV for CuO, 0.72 eV for w-ZnO and 1.88 eV for β-Ga2O3) are most likely due to the wrong description of the energy of the O2 molecule and metal oxides when using the GGA-based PBE exchange-correlation functional. As a consequence, the formation energies of transition metal oxides are underestimated by a mean absolute error of ca. 0.83 eV per oxygen atom, while the error in the formation energies of CuO, Cu2O and w-ZnO are 0.49, 0.53 and 0.77 eV per oxygen atom respectively in comparison to the reported values.115 The reported difference for the bulk formation energies per oxygen atom are almost identical to our results. Thus, since O2 is poorly described using the PBE exchange–correlation functional, adding 1 eV to the calculated energy of the O2 molecule decreases the difference between calculated and experimental formation energies to 0.01 eV for Cu2O (ΔfH(Cu2O)calc,cor = −1.75 eV), 0.00 eV for CuO (ΔfH(CuO)calc,cor = −1.62 eV), 0.22 eV for w-ZnO (ΔfH(w-ZnO)calc,cor = −3.41 eV) and 0.38 eV for β-Ga2O3 (ΔfH(β-Ga2O3)calc,cor = −10.91 eV); the error in the formation energies is reduced without over-stabilising the bulk oxides. For further analysis we will thus use the corrected energy of O2.
The calculated alloy formation enthalpies for fcc-Cu3Ga and fcc-Cu3Zn are ΔfH(fcc-Cu3Ga)calc = −0.39 eV (−37 kJ mol−1) and ΔfH(fcc-Cu3Zn)calc = −0.28 eV (−27 kJ mol−1). The formation of the fcc-Cu3Ga alloy is thus more favoured in comparison to the fcc-Cu3Zn one. The calculated alloy formation enthalpies for bcc-CuGa and bcc-CuZn are ΔfH(bcc-CuGa)calc = 0.014 eV (1.4 kJ mol−1) and ΔfH(bcc-CuZn)calc = −0.19 eV (−18 kJ mol−1). Only the formation energy of bcc-CuZn is negative, as expected from the alloy phase diagrams of the Cu–Ga- and the Cu–Zn-system (Fig. 2a and b).82,83 This indicates that bcc-CuZn is stable at low temperatures, while bcc-CuGa is only stable at high temperatures. The calculated alloy formation enthalpy for hcp-CuGa is ΔfH(hcp-CuGa)calc = −0.066 eV (−6.4 kJ mol−1), thus being more stable than the bcc-CuGa structure (as expected from the phase diagram in Fig. 2a). The calculated alloy formation enthalpy for Cu9Ga4 is ΔfH(Cu9Ga4)calc = −1.58 eV (−152 kJ mol−1), which makes Cu9Ga4 a remarkably stable alloy. The good agreement of the calculated alloy formation energies with the experimental phase diagrams gives confidence in the chosen computational methodology. The calculated structural parameters are also in good agreement with the experimental ones (see Table 2).
| Structure | Calculated structural parameters | Reference structural parameters |
|---|---|---|
| fcc-Cu | a = 3.630 Å | a = 3.597 ± 0.004 Å (ref. 111) |
| Cu2O | a = 4.272 Å | a = 4.268 Å (ref. 111) |
| CuO | a = 4.620 Å, b = 3.515 Å, c = 5.141 Å, β = 98.28° | a = 4.684 Å, b = 3.423 Å, c = 5.129 Å, β = 99.54° (ref. 111) |
| hcp-Zn | a = b = 2.683 Å, c = 4.812 Å | a = b = 2.665 Å, c = 4.947 Å (ref. 112) |
| α-Ga | a = 4.597 Å, b = 7.761 Å, c = 4.593 Å | a = 4.520 Å, b = 7.663 Å, c = 4.526 Å (ref. 113) |
| ZnO | a = b = 3.256 Å, c = 5.237 Å | a = b = 3.250 Å, c = 5.207 Å (ref. 114) |
| β-Ga2O3 | a = 12.280 Å, b = 3.070 Å, c = 5.867 Å, β = 103.78° | a = 12.225 Å, b = 3.040 Å, c = 5.809 Å, β = 103.8° (ref. 114) |
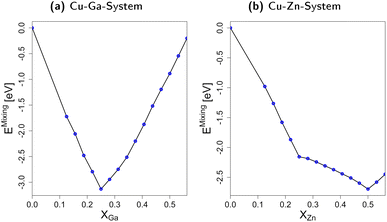
In short, we show that mixing fcc-Cu with either Zn or Ga by exchanging small amounts of Cu with Zn or Ga stabilises the system by decreasing its total energy when compared to the individual bulk structures. The interaction of Cu with Zn or Ga is thus significantly stronger than the Zn–Zn- and Ga–Ga-interactions. Moreover, the differences in the mixing energy for molar fractions above 0.25 clearly show that Ga–Ga-interactions are less favourable than the Zn–Zn-interactions. These trends and the associated thermodynamic implications can help rationalising the phase diagrams in Fig. 2: Ga–Ga-bonds are rather weak and destabilise the fcc-Cu3Ga structure. Thus, other crystal structures with less bonds in general, but also less Ga–Ga-bonds such as the ζ or ζ′ structure (see Fig. 2a) are observed rather than structures with a higher mean coordination for the metals. The discrepancy between the observed change of the crystal lattice and the expected change based on the mixing energy depending on the Ga molar fraction (Fig. 3a) is partially due to the Cu–Ga system being a solid solution instead of an intermetallic system. Accordingly, Ga is statistically distributed in the fcc-Cu-lattice meaning direct Ga–Ga-bonds are already expected for lower Ga molar fractions than in the ideal, fully ordered crystal. In contrast, the Zn–Zn-bonds are significantly more stable, resulting in the α-brass structure being observed for Zn molar fractions of up to around 0.35–0.4 (see Fig. 2b), when a transition to the bcc-structure (β-Brass) is observed.
3.2 Slab models
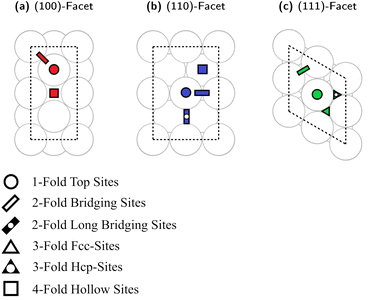
We recently generated Cu slab models representing the different surfaces of Cu nanoparticles (NPs).93 Here, we used an analogous approach to investigate Cu–Ga and Cu–Zn surface structures. The bulk structure of fcc-Cu3Ga (ideal structure of α-Cu3Ga) was cut at different crystal planes to generate specific surface facets, namely the low index (100)-, (110)- and (111)-facets. We ensured for each facet that the surface layer consists of four atoms. The slab model of all facets consists of 8 layers (4 atoms per layer, 32 atoms in total). Top-view images of the selected slabs and the specific adsorption sites evaluated are depicted in Fig. 4. A single colour is used for all atoms, since the atomic distribution changes for every facet.Each of the facets has different adsorption sites. The (100)-facet has three distinct adsorption sites (Fig. 4a): the first one is a hollow four-fold site on top of the subsurface atomic site (red square). The second site is on the top of an atom of the top-most surface (red circle) and the third site is a bridge site between two atoms of the top-most layer (red rectangle).
The (110)-facet has four distinct adsorption sites (Fig. 4b): the first one is a four-fold site on the hollow site of the top layer of the surface (blue square), the second site is on top of an atom of the top-most layer (blue circle), the third one is on the short bridging site between two atoms (blue rectangle), while the fourth site is on the long bridge site between two surface atoms of the top-most layer (blue rectangle with black point).
The (111)-facet has four distinct adsorption sites (Fig. 4c): the first one is a three-fold hollow fcc-site (green triangle), the second site is a three-fold hollow hcp-site (green triangle with black point), the third site is on top of an atom of the top-most layer (green circle), and the fourth site is a bridge site between two atoms of the top-most layer (green rectangle).
For all investigated facets, there are multiple variations of each distinct adsorption sites for different promoter concentrations and spatial distributions. For instance, if one atom in the surface layer of the (111)-facet is exchanged for Ga, there are now two different variations for each initial adsorption site (either adjacent to Ga or not adjacent to Ga). Similar variations exist for all investigated facets with multiple different variations for each adsorption site for all promoter concentrations, which must also be considered when investigating the different slabs.
Moreover, we also investigated slab models with different spatial distribution of the two metals inside the slab models for different promoter concentrations (i.e., partial or total separation of the two metals in the slab). This includes partial enrichment of the promoter on the relaxed surface (e.g., surface layers with 50% promoter concentrations instead of the only 25%), the diminishment of the promoters on the optimised surface (e.g., surface layers without promoters instead of the 25% in the ideal structure), or the formation of one or multiple surface layers of promoters on top of the pure copper structure or (sub)stoichiometric fcc-alloys, among others. This enabled us to better represent the possible slab models, including fully alloyed and dealloyed structures and intermediate situations.
We fixed the four bottom layers as either stoichiometric fcc-alloys (Cu3Ga, Cu3Zn, Cu- or Ga-/Zn-terminated) or pure fcc-Cu layers to correctly subtract the surface energy of the bottom layers. A selection of some of the used slab models for the Cu–Zn system is shown in Fig. 5. The Cu–Ga-system slab models are analogous to the Cu–Zn- ones with Zn exchanged for Ga and the lattice parameters modified according to the values obtained from bulk fcc-Cu3Ga, ensuring that the promoter concentration is not too high (lower or equal to 31.25% Ga).
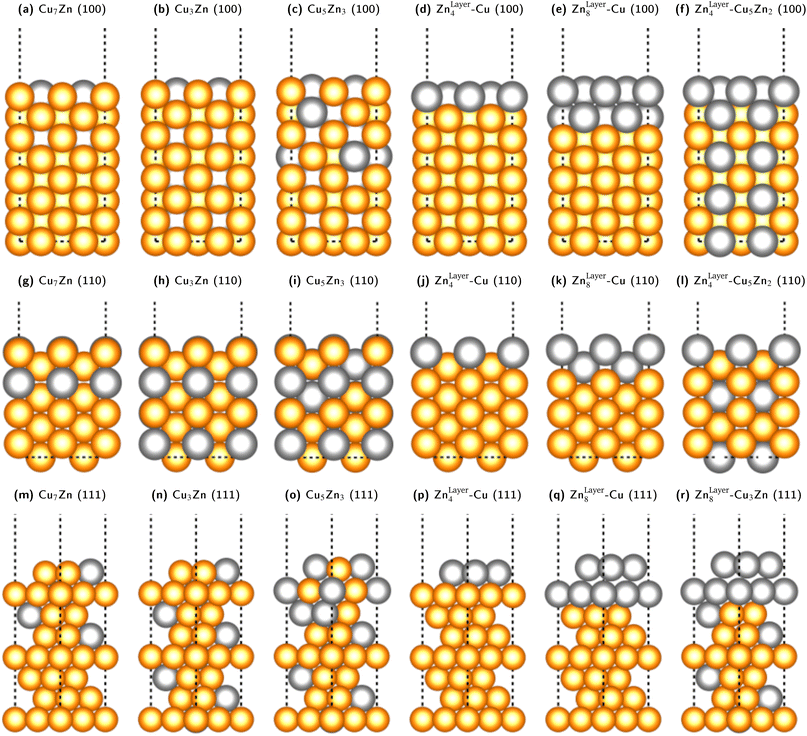 | ||
| Fig. 5 Selection of some of the used slab models for the Cu–Zn system with different promoter concentrations and distributions in the slab model for the (100)-, (110)- and (111)-facet. The same models with Zn exchanged for Ga were used for the Cu–Ga-system, but structures with Ga-content higher than 31% were not investigated since the bulk structure would not be fcc based on the mixing energy shown in Fig. 3. The depicted models are: (100)-facet: (a) substoichiometric fcc-Cu3Zn (12.5% Zn). (b) Stoichiometric fcc-Cu3Zn (25% Zn). (c) Superstoichiometric fcc-Cu3Zn (37.5% Zn). (d) One Zn-layer on pure fcc-Cu. (e) Two Zn-layers on pure fcc-Cu. (f) One Zn-layer on stoichiometric fcc-Cu3Zn. (110)-facet: (g) substoichiometric fcc-Cu3Zn (12.5% Zn). (h) Stoichiometric fcc-Cu3Zn (25% Zn). (i) Superstoichiometric fcc-Cu3Zn (37.5% Zn). (j) One Zn-layer on pure fcc-Cu. (k) Two Zn-layers on pure fcc-Cu. (l) One Zn-layer on stoichiometric fcc-Cu3Zn. (111)-facet: (m) substoichiometric fcc-Cu3Zn (12.5% Zn). (n) Stoichiometric fcc-Cu3Zn (25% Zn). (o) Superstoichiometric fcc-Cu3Zn (37.5% Zn). (p) One Zn-layer on pure fcc-Cu. (q) Two Zn-layers on pure fcc-Cu. (r) Two Zn-layers on stoichiometric fcc-Cu3Zn. | ||
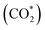 was investigated for all Cu–Ga and Cu–Zn surfaces by placing the adsorbate on a selection of the previously described surface sites while ensuring that the most distinct variations due to different promoter concentrations and spatial distributions were studied, followed by an optimisation. While studying all variations of all specific surface sites is not possible due to the high dimensionality of the accessible parameter space, we have ensured a good representation by selecting many structurally different surface sites, including different configurations of the same adsorption site. The adsorption of multiples of the same adsorbate to investigate different coverages was addressed analogously by testing multiple distinct structures. The total number of adsorbates for each structure was lower or equal to four H*/CO* adsorbed, which corresponds to a H*/CO* surface coverage between 0.25 and 1 monolayer (ML), lower or equal to one adsorbed
was investigated for all Cu–Ga and Cu–Zn surfaces by placing the adsorbate on a selection of the previously described surface sites while ensuring that the most distinct variations due to different promoter concentrations and spatial distributions were studied, followed by an optimisation. While studying all variations of all specific surface sites is not possible due to the high dimensionality of the accessible parameter space, we have ensured a good representation by selecting many structurally different surface sites, including different configurations of the same adsorption site. The adsorption of multiples of the same adsorbate to investigate different coverages was addressed analogously by testing multiple distinct structures. The total number of adsorbates for each structure was lower or equal to four H*/CO* adsorbed, which corresponds to a H*/CO* surface coverage between 0.25 and 1 monolayer (ML), lower or equal to one adsorbed 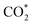 (corresponding to a
(corresponding to a 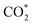 surface coverage of 0.25 ML) and lower or equal to six O* adsorbed, corresponding to an O* surface coverage between 0.25 and 1.5 ML. Since we assumed that oxygen could reconstruct the surface quite extensively, especially for high coverages, placing O* just onto the surfaces might not ensure the formation of these oxide-like overlayers. Thus, we also looked for subsurface variations of the previously explained O* adsorption sites to ensure extensive surface reconstruction: we placed oxygen atoms into different tetrahedral and octahedral sites of the subsurface layers of the alloy slab. We selected a large number of structurally distinct surface and subsurface sites for this purpose. The adsorption of the different adsorbates onto the same facets with different promoters M (M = Ga, Zn) will be discussed first.
surface coverage of 0.25 ML) and lower or equal to six O* adsorbed, corresponding to an O* surface coverage between 0.25 and 1.5 ML. Since we assumed that oxygen could reconstruct the surface quite extensively, especially for high coverages, placing O* just onto the surfaces might not ensure the formation of these oxide-like overlayers. Thus, we also looked for subsurface variations of the previously explained O* adsorption sites to ensure extensive surface reconstruction: we placed oxygen atoms into different tetrahedral and octahedral sites of the subsurface layers of the alloy slab. We selected a large number of structurally distinct surface and subsurface sites for this purpose. The adsorption of the different adsorbates onto the same facets with different promoters M (M = Ga, Zn) will be discussed first.
3.3 Surface stability diagrams – how chemical potential (gas phase composition) affects surface states
One-dimensional surface stability diagrams (SSDs) at 500 K (COx hydrogenation temperature) were constructed for each facet and promoter (Ga/Zn) atom distribution in the slab models considering the adsorption of oxygen (O*), hydrogen (H*), carbon monoxide (CO*) and carbon dioxide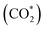 to evaluate the surface state of the different model systems in different atmospheres. The presence of O* is particularly relevant for the CO/CO2 hydrogenations71,72,116 in particular for a CO2 rich atmosphere as it is rather oxidizing for Ga and Zn (vide infra); we will thus start with discussing O* adsorption on the surfaces.
to evaluate the surface state of the different model systems in different atmospheres. The presence of O* is particularly relevant for the CO/CO2 hydrogenations71,72,116 in particular for a CO2 rich atmosphere as it is rather oxidizing for Ga and Zn (vide infra); we will thus start with discussing O* adsorption on the surfaces.
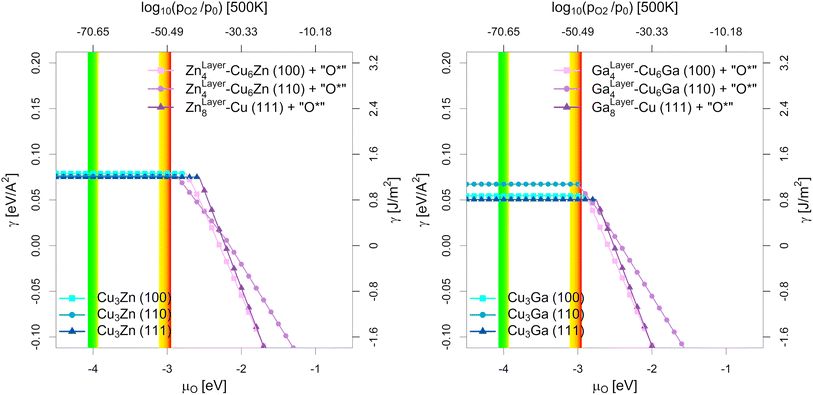 | ||
| Fig. 6 Most stable surfaces of the stoichiometric fcc-Cu3Ga/fcc-Cu3Zn alloys (25% Ga/Zn) depending on the chemical potential of oxygen (μO in eV) and the equivalent oxygen partial pressure at 500 K (Cu–Zn-system on the left, Cu-Ga-system on the right). The investigated systems are the unlayered structure with stoichiometric fcc-Cu3Ga/fcc-Cu3Zn alloy (see Fig. 5b, h and n), the partially layered structure with one Ga/Zn surface layer on substoichiometric fcc-Cu3Ga/fcc-Cu3Zn alloy and the fully layered structure with two Ga/Zn surface layers on pure fcc-Cu (see Fig. 5e, k and q). The yellow-red area indicates the expected oxygen chemical potential (μO) under CO2 hydrogenation conditions (−3.11 eV < μO < −2.92 eV, corresponding to an equivalent O2 partial pressure below 10−48 bar) while the green-yellow area indicates the expected μO under CO hydrogenation conditions (−4.07 eV < μO < −3.93 eV, equivalent to an O2 partial pressure below 10−69 bar) with the colour gradient indicating the progressing (R)WGS reaction (yellow for low conversion, red/green for high conversion; see Fig. 1 as well as Fig. S1, S4 and S5 in the ESI†). At low μO, the alloyed structures are more stable (blue part without incline), while the partially/fully layered structures are more stable at high μO due to surface oxidation (violet part with incline). | ||
As shown in Fig. 5, there are multiple configurations with different spatial distribution for the stoichiometric alloys (25% Ga/Zn): the fully alloyed structure with stoichiometric fcc-Cu3Ga/fcc-Cu3Zn alloy (compare Fig. 5b, h and n), the partially layered structure with one Ga/Zn surface layer on substoichiometric fcc-Cu3Ga/fcc-Cu3Zn alloy and the fully layered structure with two Ga/Zn surface layer on pure fcc-Cu (compare Fig. 5e, k and q). In vacuum (and thus under very low μO, such as CO hydrogenation conditions without CO2), the alloyed, unlayered structures are the most stable configurations independently of the investigated facet and used promoter, since the overall alloying energy is negative. If the gas phase becomes more oxidising (μO increases), the partially and fully alloyed structures show a significantly stronger stabilisation due to preferred interaction of the promoters with oxygen when compared to Cu. Thus, if μO increases enough (e.g. CO2 hydrogenation conditions), dealloying and surface (sub)oxide formation is observed for both promoters for all investigated surface facets.
Comparing the points of oxygen adsorption, and thus dealloying and surface (sub)oxide formation (formation of GaOx/ZnOx) reveals some key features of the two promoters. The surface energies of the alloyed structures are rather similar in vacuum conditions, with the surface energy of the (111)-facet being the lowest while the one of the (110)-facet being the highest, mirroring the results of pure Cu.93 Moreover, while both promoters stabilise oxygen adsorption, a stronger stabilisation of the dealloyed structure is observed for the Cu–Ga-system than for the Cu–Zn-system. The oxygen adsorption for the Cu–Ga-system is so strongly stabilised that full dealloying and surface oxidation becomes thermodynamically favoured under CO2 hydrogenation conditions, especially for the (110)-facet, while the Cu–Zn-system should remain fully alloyed. Nevertheless, the (110)-facet is also the easiest facet to oxidise for the Cu–Zn-system, and the point of oxygen adsorption is rather close to the μO expected under CO2 hydrogenation conditions.
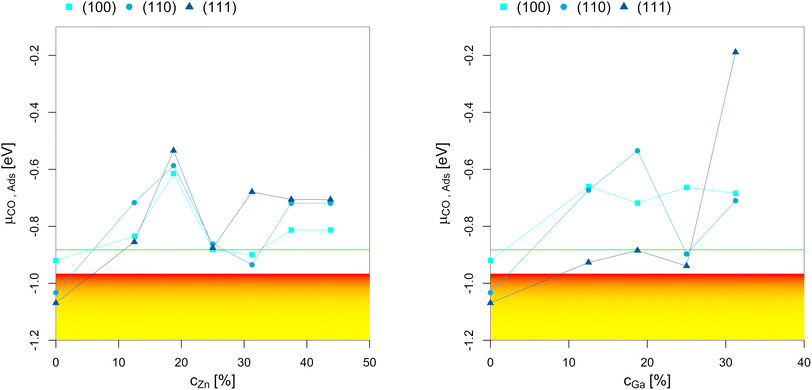
To better understand the dependency of the oxygen adsorption and (sub)oxide formation on the promoter concentration in the fcc-Cu crystal lattice, we plotted the points of oxygen adsorption (lowest μO where the slab model with one or multiple adsorbed O* is more stable than the clean surface) depending on the Zn-/Ga-concentration (Fig. 7). The yellow-red area indicates the expected μO under CO2 hydrogenation conditions (−3.11 eV < μO < −2.92 eV, corresponding to an equivalent O2 partial pressure below 10−48 bar). The expected μO under CO hydrogenation conditions (−4.07 eV < μO < −3.93 eV, equivalent to an O2 partial pressure below 10−69 bar) is not shown in the plots due to its low value. Fig. 7 shows that the point of oxygen adsorption generally decreases towards lower μO for increasing promoter concentrations, especially when compared to pure Cu as reported in our last article.93 The most stable surfaces of the alloys in an oxygen atmosphere with different stoichiometries and the individual surface stability diagrams in oxygen atmosphere are reported in the ESI.†
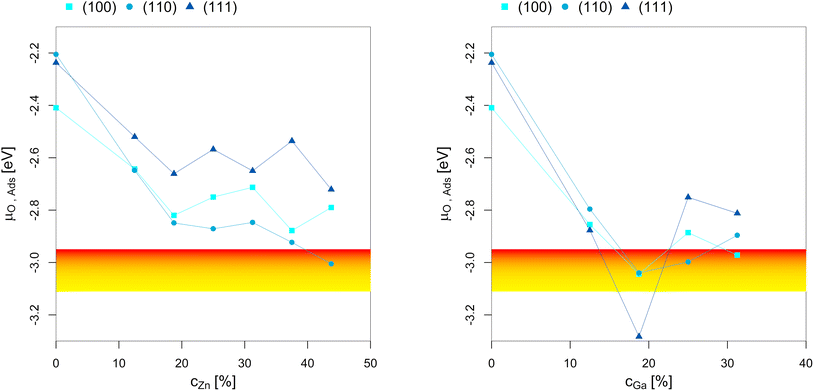 | ||
| Fig. 7 Points of oxygen adsorption (lowest μO where the slab model with one or multiple adsorbed O* is more stable than the clean surface), dealloying and surface oxidation depending on the Zn-/Ga-concentration in the fcc-Cu crystal lattice. The yellow-red area indicates the expected oxygen chemical potential (μO) under CO2 hydrogenation conditions (−3.11 eV < μO < −2.92 eV, corresponding to an equivalent O2 partial pressure below 10−48 bar). The expected μO under CO hydrogenation conditions (−4.07 eV < μO < −3.93 eV, equivalent to an O2 partial pressure below 10−69 bar) is so low that it is not shown in the plots. The point of oxygen adsorption generally decreases towards lower μO for increasing promoter concentrations. For the Cu–Zn-system, a plateau is reached for intermediate promoter concentrations (around 25% Zn), with and additional decrease observed for the highly superstoichiometric alloys (around 40% Zn). For the Cu–Ga-system, a minimum is reached for around 20% Ga, with the point of oxygen adsorption increasing for higher promoter concentrations. Data on pure Cu taken from Müller et al.93 | ||
For the Cu–Zn-system at low promoter concentration (0% < cZn < 20%), the point of oxygen adsorption decreases linearly as a function of the promoter concentration. The surface oxidation is especially stabilised for the (110)-facet, while the two other facets show rather similar behaviour for the point of oxygen adsorption. For intermediate promoter concentrations (20% < cZn < 40%), a plateau is reached, with the point of oxygen adsorption being mostly independent of the promoter concentration. When the promoter concentration is further increased (cZn > 40%), the point of oxygen adsorption decreases again, but only for the (110)-facet. The surface oxidation is so stabilized for this termination that partial dealloying is predicted under CO2 hydrogenation reaction conditions, while fully reduced/alloyed surfaces are expected under CO hydrogenation reaction conditions.
For the Cu–Ga-system at low promoter concentrations (0% < cGa < 20%), the point of oxygen adsorption again decreases linearly as a function of the promoter concentration. However, the Cu–Ga-system shows several key differences compared to the Cu–Zn-system. First, the linear decrease has a much steeper slope compared to the Cu–Zn-system, indicating that small quantities of Ga have a much stronger effect on stabilising the surface oxidation when compared to Zn. Thus, dealloying and surface oxidation under CO2 hydrogenation reaction conditions is expected for the Cu–Ga-system with a Ga-concentration of around 20% irrespective of the investigated facets, while the equivalent structures for the Cu–Zn-system remain alloyed and reduced under the same conditions. Second, while the trends for the (100)- and (110)-facet are equivalent for both the Cu–Zn- and Cu–Ga-systems, the (111)-facet shows such a strong stabilisation that fully oxidised surfaces are expected even at a μO lower than the one expected under CO2 hydrogenation reaction conditions.
If the promoter concentration increases further, the stabilisation is reversed: oxygen adsorption and surface oxidation becomes less favoured when increasing the promoter concentration, showing that the Cu–Ga-system has an optimal promoter concentration at around 18.75%; a similar effect has not been observed for the Cu–Zn-system. This shows that the Cu–Ga-system is more easily dealloyed and oxidised under CO2 hydrogenation conditions than the Cu–Zn-system; but while the oxygen adsorption on the Cu–Ga-system has a stronger dependency on the promoter (Ga) concentration, the Cu–Zn-system seems less affected by higher promoter (Zn) concentrations, which is similar to what has been observed for the alloy formation energies (Fig. 3) and mirrors again the results of the experimental phase diagrams (Fig. 2).
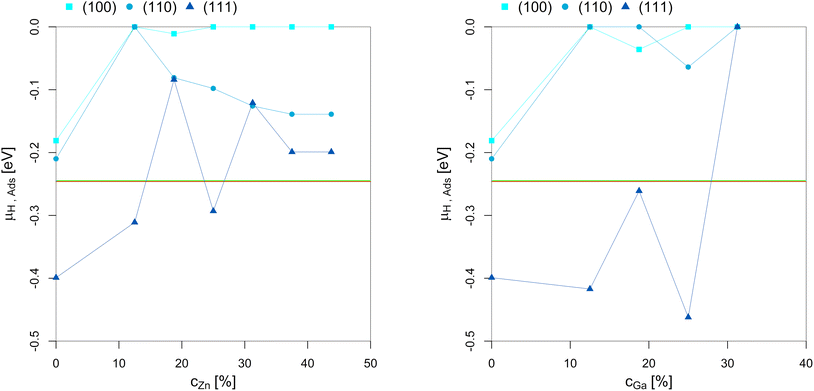 | ||
| Fig. 8 Points of hydrogen adsorption (lowest μH where the slab model with one or multiple adsorbed H* is more stable than the clean surface) depending on the Zn-/Ga-concentration in the fcc-Cu crystal lattice. The red/green line indicates μH expected under CO2 or CO hydrogenation conditions (−0.235 eV < μH < −0.234 eV). The overall dependency of the hydrogen adsorption on the promoter concentrations is rather low since H2 adsorption in the range of the μH expected under CO2 or CO hydrogenation conditions is exclusively located on the three-fold adsorption site on three Cu atoms on the (111)-facet.93 As long as this three-fold adsorption site is present on the (111)-facet (as long as the promoter concentration is 25% or lower), H* adsorption under reaction conditions is observed. Nevertheless, promoter atoms in close proximity still decrease hydrogen adsorption. | ||
Hydrogen adsorption under CO2 or CO hydrogenation conditions is exclusively located on the three-fold adsorption site on three Cu atoms on the (111)-facet, as shown for pure Cu.93 As a result, adsorption of H* on the (111)-facet is observed for both the Cu–Ga- and Cu–Zn-systems as long as the three-fold adsorption site on three Cu atoms is present. This adsorption is only observed for promoter concentrations up to 25% and if the promoters are not enriched on the top-most layer. Less hydrogen adsorption is expected for higher promoter concentrations since the promoters disfavour the formation of surface hydrides. But this effect is rather weak when compared to the effect of the promoters on oxygen adsorption. As a result, hydrogen adsorption is still expected under COx hydrogenation reaction conditions, but the amount of H* decreases as a function of the promoter concentration. Thus, increasing the hydrogen partial pressure results in realloying, favouring the formation of additional three-fold adsorption sites composed by three Cu atoms. Nevertheless, this only affects the (111)-facet since the other facets are not modified in the presence of H2.
In summary, while the promoters influence hydrogen adsorption, this effect is much weaker than the one observed for O*, since only one specific adsorption site of the Cu-based alloys adsorb H* under CO2 or CO hydrogenation conditions. Thus, the promoters reduce the total amount of adsorbed H*, but a partial H*-coverage is still observed under COx hydrogenation conditions.
The feedstock has a much stronger effect on the surface state: under only CO and H2, no surface oxidation and surface layer formation is observed, and only hydrogen is adsorbed. In contrast, if the feedstock contains large quantities of CO2 (and H2), surface oxidation and dealloying (by surface oxide layer formation) becomes possible for both promoters, and this effect is stronger for the Cu–Ga-alloys than for the Cu–Zn- ones; however, hydrogen adsorption and realloying is still possible under these conditions. Thus, both oxygen adsorption, surface oxidation and dealloying (by surface oxide layer formation) as well as hydrogen adsorption and realloying are thermodynamically feasible under CO2 hydrogenation conditions, which might result in a highly dynamic system under reaction conditions due to the competing oxidation and reduction processes. Such highly dynamic processes have already been observed experimentally using operando TEM while studying the oxidation of hydrogen on a Cu catalyst.117
CO adsorption shows a similar trend to hydrogen adsorption: CO* adsorbs almost excursively on the adsorption sites composed by only Cu, however, the facet-dependency is much weaker for CO adsorption than for hydrogen adsorption, i.e. CO adsorption is also observed for facets other than the (111)-facet. Similarly to hydrogen adsorption, the CO*-coverage on the surface decreases when the promoter contraction increases. Nevertheless, in contrast to the formation of surface H*, the promoters also influence the point of CO adsorption, predicting CO*-free surfaces for both the Cu–Ga- and Cu–Zn-systems under CO2 hydrogenation conditions for small quantities of either promoter. Higher promoter concentrations (>25%) further decrease CO adsorption, meaning CO*-free surfaces are predicted even under CO hydrogenation conditions.
CO adsorption on the other facets follows the same trend, but the initial decrease in CO adsorption upon adding promoters is stronger than for the (111)-facet. Again, this can be explained by the spatial distribution of the promoter in the slabs: Zn or Ga added to the (100)- and (110)-facet of Cu are preferentially located on the surface, preventing CO adsorption on the preferred sites composed by only Cu atoms. Thus, both the (100)- and (110)-facet of the CuGa- and CuZn-alloys are expected to remain free of adsorbed CO* even under CO hydrogenation reaction conditions, while the equivalent structure of pure Cu is expected to be covered with a substantial amount of CO*.
In summary, we showed that both Ga and Zn significantly decrease CO adsorption under COx hydrogenation reaction conditions, especially if the promoters are located on the outmost layer of the slab. The (111)-facet of the alloys is the only facet that can still adsorb CO* under COx hydrogenation reaction conditions for low promoter concentrations (<25%), and this adsorption is located exclusively on the three-fold adsorption site composed by three Cu atoms. Since hydrogen adsorption is also located on the same adsorption site, CO and hydrogen adsorption compete under reaction conditions, with the latter being thermodynamically slightly more favoured over CO adsorption. As a result, CO in the active atmosphere helps promoting realloying, and might increase the dynamics of the system under reaction conditions (both oxygen adsorption, surface oxidation and dealloying and hydrogen/CO adsorption and realloying being simultaneously possible). Nevertheless, if the atmospheric concentration of CO becomes to high, CO* can replace large quantities of adsorbed H* on the particle surface, thus presumably reducing the overall activity of the catalysts.
3.4 Effect of gas phase composition – comparing CO2vs. CO hydrogenation conditions
The oxygen chemical potential (μO) at which oxygen starts adsorbing depending on the promoter concentration (Fig. 7) shows that for μO corresponding to CO2 hydrogenation conditions (XCO2 = 1, XCO = 0, −3.11 eV < μO < −2.92 eV corresponding to pO2 < 10−48 bar at 500 K, yellow-red area), the surface facets of the Cu–Ga-alloy slabs are at least partially covered with O* under reaction conditions. Thus, while the pure Cu surfaces are expected to be fully reduced under reaction conditions,93 adding Ga to the slab significantly increases the oxygen affinity of the system. As a result, a partial or full Ga oxide overlayer is predicted under CO2 hydrogenation conditions for the Cu–Ga alloys. This can significantly influence the catalyst reactivity (from increased selectivity to reduced activity72). The formation of GaOx-island on metallic Cu under CO2 hydrogenation conditions has indeed been observed experimentally for selected model systems using STEM and XPS.118 In contrast, if μO decreases significantly, as predicted for pure CO hydrogenation conditions (XCO2 = 0, XCO = 1, −4.07 eV < μO < −3.93 eV, equivalent to pO2 < 10−69 bar at 500 K), oxygen adsorption is no longer favourable. For a mixture of CO2 and CO (0.1 < XCO2 < 0.9), μO increases linearly as a function of XCO2 (as described in Fig. 1). As a result, if small quantities of CO2 are present in the gas feed, oxygen adsorption is possible under reaction conditions, but depends quite strongly on XCO2.Zn shows a similar effect as Ga as a promoter in the slab; it significantly increases the oxygen affinity of the alloy when compared to pure Cu. But the Cu–Zn-system is more reluctant towards oxygen adsorption than the Cu–Ga-system. Thus, while the Cu–Zn-system is expected to form Zn (sub-)oxide layers on top of the slab models under CO2 hydrogenation reaction conditions, less surface oxidation is predicted based on our calculations. As a result, partially reduced Zn layers and alloyed surfaces are expected under CO2 hydrogenation conditions, which is consistent with experimental results.71 For the effect of the feedstock composition, the same trend as for the Cu–Ga-system is observed: Reducing the amount of CO2 in the feedstock decreases μO, which results in less adsorbed O* and more reduced surfaces.
The effect of the other adsorbates (H* and CO*) is opposite to O*: the μH/μCO at which hydrogen/CO starts adsorbing depends on the promoter concentration. Fig. 8 and 9 show that adding Ga or Zn to the slab surface decreases the adsorption of H* and CO* on the slab. In addition, since the adsorption is preferred on sites composed only by Cu, adding H2/CO to the feedstock decreases the dealloying and surface oxidation (as observed for oxygen adsorption) while stabilising the reduced and alloyed slabs. As a result, both dealloying and realloying processes are thermodynamically possible under COx hydrogenation conditions with the preferred state depending on the gas phase compositions (associated with μO, μH and μCO): more CO2 results in higher μO and more oxidised surfaces, while less CO2 leads to a lower μO and more reduced surfaces. Nevertheless, as shown in Fig. 1, the initial decrease in μO due to replacing CO2 with CO is rather small (the same applies to μH and μCO), resulting in small changes of the surface state of the catalyst if the gas phase still contains small quantities of CO2 (compare Table S1 in the ESI†). Thus, unless all CO2 is removed from the feedstock, surface oxidation remains possible under COx hydrogenation conditions.
3.5 Comparison of Ga and Zn as promoters
Comparing Ga and Zn as promoters for Cu reveals key similarities and differences. Solid solutions for both Ga and Zn in Cu are known, both having an fcc-crystal structure for high enough Cu concentrations (Fig. 2) with the promoters (Ga/Zn) being statistically distributed by randomly replacing Cu in the fcc-Cu crystal lattice with the promoters. The top-most layer of the surface is rich in Zn or Ga (in the respective alloys) and both promoters facilitate oxygen adsorption when compared to pure copper, favouring partial or full dealloying and forming partial or fully oxidized GaOx/ZnOx surface layers. Also, both promoters decrease hydrogen and CO adsorption, especially in the absence of surface sites composed only of Cu atoms.However, our study also highlights the differences between Zn and Ga as promoters. The stabilisation due to alloying is much larger for the fcc-CuGa solid solution in comparison to the equivalent fcc-CuZn solid solution for low promoter (Ga/Zn) concentration, as seen in the alloy energies in Fig. 3. But stabilisation due to the formation of a fcc-solid solution is only observed for Ga-contents below 25%, while there is a net stabilisation for the Cu–Zn-system up to a Zn-content of 50%. Partial or full surface oxidation under CO2 hydrogenation reaction conditions is expected for the Cu–Ga-system (depending on the feedstock compositions), while the Cu–Zn-system is expected to be partially oxidised at most.
4 Conclusions
In this article, we used DFT calculations in combination with ab initio atomistic thermodynamics to investigate the surface coverage of multiple key adsorbates on several surfaces for both the fcc-CuGa and fcc-CuZn solid solution with different stoichiometric compositions evaluating different spatial distributions of the two metals in the slab. Our calculations predict that both systems form fcc-solid solutions when the promoter concentration is low enough, with fcc-CuZn being stable for much higher Zn-concentrations than its corresponding Ga-equivalent, in agreement with the experimental phase diagrams. The outmost surface layers of the built surface models are the most impactful on the surface energy and surface coverage, while the subsurface layers have a rather low overall influence on them.We also show that when Ga and Zn are on the surface, oxygen adsorption is more favoured compared to pure copper due to formation of surface (sub)oxides. This is especially pronounced for the Cu–Ga-system, in which the stabilisation is so strong that under pure CO2 and mixed CO2/CO hydrogenation reaction conditions (small but significant quantities of CO2 present in the gas phase), partial to full dealloying and oxidation of all surface Ga to GaOx is possible. This effect is much weaker for the Cu–Zn-system, so that only partial dealloying and oxidation to surface ZnOx is possible under pure CO2 and mixed CO2/CO hydrogenation reaction conditions with some Zn retained in its metallic form, while all Ga is at least partially oxidised and no metallic Ga is expected. In contrast, the pure Cu-system was shown to be fully reduced under reaction conditions.93 This trend agrees well with experimental data, where Ga is fully oxidised and Zn is partially oxidised under pure CO2 and mixed CO2/CO hydrogenation reaction conditions.71,72
Regarding hydrogen/CO adsorption, we showed that the stability of surface H*/CO* is lower on both the fcc-CuGa and fcc-CuZn solid solutions in comparison to pure Cu, being especially pronounced in the absence of adsorption sites composed by only Cu atoms (observed for high promoter concentrations close to the surface), since both adsorbates exclusively adsorb on surface sites adjacent to multiple Cu atoms under CO2 and CO hydrogenation reaction conditions. As a result, both hydrogen and CO adsorption result in surface reduction and thus realloying of the surface slabs, but the stability of the resulting surface H*/CO* depends strongly on the active atmosphere. Finally, the adsorption of molecular CO2 is not observed on any of the investigated facets/stoichiometries.
Concerning the influence of the active atmosphere, we showed that the CO/CO2 hydrogenation conditions, usually perceived as rather reducing due to the presence of large quantities of hydrogen gas, are actually quite oxidising for both Zn and especially for Ga. This oxidising potential can be tuned by modifying the ratio of CO2 to CO in the feed gas. Only pure CO/H2-feeds are reducing enough so that fully reduced alloys are thermodynamically preferred under reaction conditions, while the addition of small quantities of CO2 increases the oxygen chemical potential (μO) so much that the formation of ZnOx and GaOx surface species become thermodynamically possible, likely forming a dynamic system enabling oxidation and reduction processes to occur at the same time.
The use of small quantities of CO2 to accelerate the hydrogenation of CO in an industrial setting is well-known and is mainly attributed to the influence of CO2 onto the reaction kinetics. We propose an alternative and complementary explanation based on thermodynamic properties: having small amounts of CO2 in the feed increases the oxygen chemical potential, resulting in a more oxidising atmosphere, which favours the formation of Zn or Ga (sub)oxides, and thereby generates interfacial sites between Cu and MOx directly on the metal surface, which could promote methanol formation similarly to the mechanism observed for the interface of Cu with non-reducible supports.68,92 This site formation depends on the gas phase composition, since the partial pressures of the individual adsorbates determine their specific chemical potentials under reaction conditions and thus their interplay with the catalytic surface. Without any CO2, no active sites are formed, while a pure CO2 feed is so oxidising that a closed oxide overlayer can form without any accessible Cu sites remaining, an aspect especially pronounced for Ga. Thus, carefully tuning the reaction conditions is of high importance for both the catalytic activity and stability under reaction conditions, at par with catalyst composition and particle preparation.
In conclusion, we found that Ga and Zn as promoters in Cu-based CO/CO2 hydrogenation significantly influence the interaction of the catalyst with the gas phase. Both fcc-CuGa and fcc-CuZn solid solutions show increased oxygen adsorption but reduced hydrogen and CO adsorption with respect to pure Cu, especially for high promoter concentrations. The gas phase composition can in return strongly interplay with the particle surface and form a dynamic equilibrium relevant for the reaction mechanism. Nevertheless, such effects are impossible to capture using static DFT, highlighting the need for dynamic calculations such as ab initio molecular dynamics of discrete Cu alloy particles to investigate the dynamics of the catalyst structure under reaction conditions. We are currently pursuing this effort and will disclose our work in due course.
Data availability
The data used in this manuscript (including structures as .cif-files, the corresponding energies in a .txt-file as well as typical INCAR and KPOINTS files used in the calculations) are available on Zenodo (a general-purpose open repository developed under the European OpenAIRE program and operated by CERN) at https://doi.org/10.5281/zenodo.7267564.Author contributions
CRediT (Contributor Roles Taxonomy)119 was used for standardised contribution descriptions: Andreas Müller: data curation, formal analysis, investigation, methodology, software, validation, visualization, writing (original draft), writing (review & editing). Aleix Comas-Vives: data curation, conceptualization, funding acquisition, methodology, supervision, validation, writing (review & editing). Christophe Copéret: conceptualization, funding acquisition, project administration, resources, supervision, writing (review & editing).Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This research is supported by the Sinergia Project of the Swiss National Science Fonds (SNSF fond number: CRSII5_183495). All DFT calculations were performed using the EULER cluster at ETH Zurich managed by the HPC team. Andreas Müller thanks Jan Alfke, Dr María Tejeda Serrano, Dr Gina Noh and Mélissa Zacharias for the discussion on the catalytic system and suggestions of further calculations and on the visual representation of the data. Aleix Comas-Vives thanks the Spanish MEC and the European Social Fund (RyC-2016-19930) and the Spanish “Ministerio de Ciencia, Innovación y Universidades” (PGC2018-100818-A-I00).Notes and references
- S. Solomon, G.-K. Plattner, R. Knutti and P. Friedlingstein, Proc. Natl. Acad. Sci., 2009, 106, 1704–1709 CrossRef CAS PubMed.
- G. A. Olah, Angew. Chem., Int. Ed., 2005, 44, 2636–2639 CrossRef CAS PubMed.
- A. Goeppert, M. Czaun, J.-P. Jones, G. K. Surya Prakash and G. A. Olah, Chem. Soc. Rev., 2014, 43, 7995–8048 RSC.
- S. Simon Araya, V. Liso, X. Cui, N. Li, J. Zhu, S. L. Sahlin, S. H. Jensen, M. P. Nielsen and S. K. Kær, Energies, 2020, 13, 596 CrossRef.
- A. Álvarez, A. Bansode, A. Urakawa, A. V. Bavykina, T. A. Wezendonk, M. Makkee, J. Gascon and F. Kapteijn, Chem. Rev., 2017, 117, 9804–9838 CrossRef PubMed.
- A. Álvarez, M. Borges, J. J. Corral-Pérez, J. G. Olcina, L. Hu, D. Cornu, R. Huang, D. Stoian and A. Urakawa, ChemPhysChem, 2017, 18, 3135–3141 CrossRef PubMed.
- K. Stangeland, H. Li and Z. Yu, Ind. Eng. Chem. Res., 2018, 57, 4081–4094 CrossRef CAS.
- C. V. Miguel, M. A. Soria, A. Mendes and L. M. Madeira, J. Nat. Gas Sci. Eng., 2015, 22, 1–8 CrossRef CAS.
- M. Behrens, F. Studt, I. Kasatkin, S. Kühl, M. Hävecker, F. Abild-Pedersen, S. Zander, F. Girgsdies, P. Kurr, B.-L. Kniep, M. Tovar, R. W. Fischer, J. K. Nørskov and R. Schlögl, Science, 2012, 336, 893–897 CrossRef CAS PubMed.
- S. Polierer, D. Guse, S. Wild, K. Herrera Delgado, T. N. Otto, T. A. Zevaco, M. Kind, J. Sauer, F. Studt and S. Pitter, Catalysts, 2020, 10, 816 CrossRef CAS.
- R. Horn and R. Schlögl, Catal. Lett., 2015, 145, 23–39 CrossRef CAS.
- S. Dang, H. Yang, P. Gao, H. Wang, X. Li, W. Wei and Y. Sun, Catal. Today, 2019, 330, 61–75 CrossRef CAS.
- K. Jalama, Catal. Rev., 2017, 59, 95–164 CrossRef CAS.
- H. Yang, C. Zhang, P. Gao, H. Wang, X. Li, L. Zhong, W. Wei and Y. Sun, Catal. Sci. Technol., 2017, 7, 4580–4598 RSC.
- O. A. Ojelade and S. F. Zaman, Catal. Surv. Asia, 2020, 24, 11–37 CrossRef CAS.
- O. Tursunov, L. Kustov and A. Kustov, Oil Gas Sci. Technol., 2017, 72, 30 CrossRef.
- W. Li, H. Wang, X. Jiang, J. Zhu, Z. Liu, X. Guo and C. Song, RSC Adv., 2018, 8, 7651–7669 RSC.
- A. Pustovarenko, A. Dikhtiarenko, A. Bavykina, L. Gevers, A. Ramírez, A. Russkikh, S. Telalovic, A. Aguilar, J.-L. Hazemann, S. Ould-Chikh and J. Gascon, ACS Catal., 2020, 10, 5064–5076 CrossRef CAS.
- A. Ramirez, L. Gevers, A. Bavykina, S. Ould-Chikh and J. Gascon, ACS Catal., 2018, 8, 9174–9182 CrossRef CAS.
- A. Dokania, A. Ramirez, A. Bavykina and J. Gascon, ACS Energy Lett., 2019, 4, 167–176 CrossRef CAS.
- D. Stoian, A. Bansode, F. Medina and A. Urakawa, Catal. Today, 2017, 283, 2–10 CrossRef CAS.
- A. Bansode and A. Urakawa, ACS Catal., 2014, 4, 3877–3880 CrossRef CAS.
- B. Tidona, C. Koppold, A. Bansode, A. Urakawa and P. Rudolf von Rohr, J. Supercrit. Fluids, 2013, 78, 70–77 CrossRef CAS.
- A. Álvarez, M. Borges, J. J. Corral-Pérez, J. G. Olcina, L. Hu, D. Cornu, R. Huang, D. Stoian and A. Urakawa, ChemPhysChem, 2017, 18, 3087 CrossRef.
- G. Liu, P. Poths, X. Zhang, Z. Zhu, M. Marshall, M. Blankenhorn, A. N. Alexandrova and K. H. Bowen, J. Am. Chem. Soc., 2020, 142, 7930–7936 CrossRef CAS PubMed.
- J.-Y. Liu, X.-Q. Gong, R. Li, H. Shi, S. B. Cronin and A. N. Alexandrova, ACS Catal., 2020, 10, 4048–4058 CrossRef CAS.
- J.-Y. Liu, X.-Q. Gong and A. N. Alexandrova, J. Phys. Chem. C, 2019, 123, 3505–3511 CrossRef CAS.
- W. J. Durand, A. A. Peterson, F. Studt, F. Abild-Pedersen and J. K. Nørskov, Surf. Sci., 2011, 605, 1354–1359 CrossRef CAS.
- E. L. Kunkes, F. Studt, F. Abild-Pedersen, R. Schlögl and M. Behrens, J. Catal., 2015, 328, 43–48 CrossRef CAS.
- M. S. Duyar, C. Tsai, J. L. Snider, J. A. Singh, A. Gallo, J. S. Yoo, A. J. Medford, F. Abild-Pedersen, F. Studt, J. Kibsgaard, S. F. Bent, J. K. Nørskov and T. F. Jaramillo, Angew. Chem., Int. Ed., 2018, 57, 15045–15050 CrossRef CAS PubMed.
- S. Polierer, J. Jelic, S. Pitter and F. Studt, J. Phys. Chem. C, 2019, 123, 26904–26911 CrossRef CAS.
- J. Tai, Q. Ge, R. J. Davis and M. Neurock, J. Phys. Chem. B, 2004, 108, 16798–16805 CrossRef CAS.
- J. Medina-Ramos, W. Zhang, K. Yoon, P. Bai, A. Chemburkar, W. Tang, A. Atifi, S. S. Lee, T. T. Fister, B. J. Ingram, J. Rosenthal, M. Neurock, A. C. T. van Duin and P. Fenter, Chem. Mater., 2018, 30, 2362–2373 CrossRef CAS.
- S. N. Steinmann, C. Michel, R. Schwiedernoch, J.-S. Filhol and P. Sautet, ChemPhysChem, 2015, 16, 2307–2311 CrossRef CAS PubMed.
- W. Guo, C. Michel, R. Schwiedernoch, R. Wischert, X. Xu and P. Sautet, Organometallics, 2014, 33, 6369–6380 CrossRef CAS.
- M. J. Kolb, D. Loffreda, P. Sautet and F. Calle-Vallejo, J. Catal., 2021, 395, 136–142 CrossRef CAS.
- V. D. Dasireddy and B. Likozar, Renewable Energy, 2019, 140, 452–460 CrossRef CAS.
- Y. Ma, J. Wang, K. R. Goodman, A. R. Head, X. Tong, D. J. Stacchiola and M. G. White, J. Phys. Chem. C, 2020, 124, 22158–22172 CrossRef CAS.
- J. Kim, B. B. Sarma, E. Andrés, N. Pfänder, P. Concepción and G. Prieto, ACS Catal., 2019, 9, 10409–10417 CrossRef CAS.
- W. Wang, Z. Qu, L. Song and Q. Fu, J. Catal., 2020, 382, 129–140 CrossRef CAS.
- M. S. Tameh, A. K. Dearden and C. Huang, J. Phys. Chem. C, 2018, 122, 17942–17953 CrossRef CAS.
- R. M. Palomino, P. J. Ramírez, Z. Liu, R. Hamlyn, I. Waluyo, M. Mahapatra, I. Orozco, A. Hunt, J. P. Simonovis, S. D. Senanayake and J. A. Rodriguez, J. Phys. Chem. B, 2018, 122, 794–800 CrossRef PubMed.
- G. Noh, E. Lam, D. T. Bregante, J. Meyet, P. Šot, D. W. Flaherty and C. Copéret, Angew. Chem., Int. Ed., 2021, 60, 9650–9659 CrossRef CAS PubMed.
- T. P. Araújo, A. H. Hergesell, D. Faust-Akl, S. Büchele, J. A. Stewart, C. Mondelli and J. Pérez-Ramírez, ChemSusChem, 2021, 14, 2914–2923 CrossRef PubMed.
- M. Zabilskiy, K. Ma, A. Beck and J. A. van Bokhoven, Catal. Sci. Technol., 2021, 11, 349–358 RSC.
- M. Zabilskiy, V. L. Sushkevich, D. Palagin, M. A. Newton, F. Krumeich and J. A. van Bokhoven, Nat. Commun., 2020, 11, 2409 CrossRef CAS PubMed.
- A. Ye, Z. Li, J. Ding, W. Xiong and W. Huang, ACS Catal., 2021, 11, 10014–10019 CrossRef CAS.
- C. Göbel, S. Schmidt, C. Froese, Q. Fu, Y.-T. Chen, Q. Pan and M. Muhler, J. Catal., 2020, 383, 33–41 CrossRef.
- Y. Lu, R. Zhang, B. Cao, B. Ge, F. F. Tao, J. Shan, L. Nguyen, Z. Bao, T. Wu, J. W. Pote, B. Wang and F. Yu, ACS Catal., 2017, 7, 5500–5512 CrossRef CAS.
- N. D. Nielsen, J. Thrane, A. D. Jensen and J. M. Christensen, Catal. Lett., 2020, 150, 1427–1433 CrossRef CAS.
- Z. Zhang, X. Chen, J. Kang, Z. Yu, J. Tian, Z. Gong, A. Jia, R. You, K. Qian, S. He, B. Teng, Y. Cui, Y. Wang, W. Zhang and W. Huang, Nat. Commun., 2021, 12, 4331 CrossRef CAS PubMed.
- C. Du, P. Lu and N. Tsubaki, ACS Omega, 2020, 5, 49–56 CrossRef CAS PubMed.
- S. Dey, G. C. Dhal, D. Mohan and R. Prasad, Adv. Compos. Hybrid Mater., 2019, 2, 626–656 CrossRef CAS.
- W. U. Khan, L. Baharudin, J. Choi and A. C. K. Yip, ChemCatChem, 2021, 13, 111–120 CrossRef CAS.
- Clariant, Clariant's MegaMax® 800 Catalyst Achieved ab Outstanding Performance at CNOOC’S Davy Methanol Plant in Hainan, China, 2021, https://www.clariant.com/en/Corporate/News/2021/07/Clariantrsquos-MegaMaxreg-800-catalyst-achieved-an-outstanding-performance-at-CNOOCrsquos-Davy-metha Search PubMed.
- K. Girod, H. Lohmann and S. Kaluza, Chem. Ing. Tech., 2021, 93, 850–855 CrossRef CAS.
- J. Matthey, Decarbonising Chemicals Production, 2021, https://matthey.com/en/about-us/transitions/decarbonising-chemicals-production Search PubMed.
- S. Energy, A New Hydrogen Reality: Fuel from Wind and Water, 2021, https://www.siemens-energy.com/global/en/offerings/renewable-energy/hydrogen-solutions/haru-oni.html Search PubMed.
- C. R. International, Recycling CO2 to Produce Methanol - A Question of Balance, 2021, https://www.carbonrecycling.is/co2-methanol Search PubMed.
- F. Studt, M. Behrens, E. L. Kunkes, N. Thomas, S. Zander, A. Tarasov, J. Schumann, E. Frei, J. B. Varley, F. Abild-Pedersen, J. K. Nørskov and R. Schlögl, ChemCatChem, 2015, 7, 1105–1111 CrossRef CAS.
- J. Nakamura, T. Fujitani and Y.-S. Choi, Top. Catal., 2003, 22, 277–285 CrossRef CAS.
- M. B. Fichtl, D. Schlereth, N. Jacobsen, I. Kasatkin, J. Schumann, M. Behrens, R. Schlögl and O. Hinrichsen, Appl. Catal., A, 2015, 502, 262–270 CrossRef CAS.
- A. Urakawa, Nat. Catal., 2021, 4, 447–448 CrossRef.
- A. Beck, M. Zabilskiy, M. A. Newton, O. Safonova, M. G. Willinger and J. A. van Bokhoven, Nat. Catal., 2021, 4, 488–497 CrossRef CAS.
- C. Copéret, A. Fedorov and P. A. Zhizhko, Catal. Lett., 2017, 147, 2247–2259 CrossRef.
- C. Copéret, Acc. Chem. Res., 2019, 52, 1697–1708 CrossRef PubMed.
- S. Tada, F. Watanabe, K. Kiyota, N. Shimoda, R. Hayashi, M. Takahashi, A. Nariyuki, A. Igarashi and S. Satokawa, J. Catal., 2017, 351, 107–118 CrossRef CAS.
- K. Larmier, W.-C. Liao, S. Tada, E. Lam, R. Verel, A. Bansode, A. Urakawa, A. Comas-Vives and C. Copéret, Angew. Chem., Int. Ed., 2017, 56, 2318–2323 CrossRef CAS PubMed.
- K. Fujiwara, S. Tada, T. Honma, H. Sasaki, M. Nishijima and R. Kikuchi, AIChE J., 2019, 65, e16717 CrossRef CAS.
- S. R. Docherty and C. Copéret, J. Am. Chem. Soc., 2021, 143, 6767–6780 CrossRef CAS PubMed.
- E. Lam, G. Noh, K. Larmier, O. V. Safonova and C. Copéret, J. Catal., 2021, 394, 266–272 CrossRef CAS.
- E. Lam, G. Noh, K. W. Chan, K. Larmier, D. Lebedev, K. Searles, P. Wolf, O. V. Safonova and C. Copéret, Chem. Sci., 2020, 11, 7593–7598 RSC.
- A. M. Hengne, D. J. Yuan, N. S. Date, Y. Saih, S. P. Kamble, C. V. Rode and K.-W. Huang, Ind. Eng. Chem. Res., 2019, 58, 21331–21340 CrossRef CAS.
- A. M. Hengne, K. D. Bhatte, S. Ould-Chikh, Y. Saih, J. M. Basset and K.-W. Huang, ChemCatChem, 2018, 10, 1360–1369 CrossRef CAS.
- V. D. Dasireddy and B. Likozar, Renewable Energy, 2019, 140, 452–460 CrossRef CAS.
- E. L. Kunkes, F. Studt, F. Abild-Pedersen, R. Schlögl and M. Behrens, J. Catal., 2015, 328, 43–48 CrossRef CAS.
- J. He, D. Laudenschleger, J. Schittkowski, A. Machoke, H. Song, M. Muhler, R. Schlögl and H. Ruland, Chem. Ing. Tech., 2020, 92, 1525–1532 CrossRef CAS.
- Y. Slotboom, M. Bos, J. Pieper, V. Vrieswijk, B. Likozar, S. Kersten and D. Brilman, Chem. Eng. J., 2020, 389, 124181 CrossRef CAS.
- J. Thrane, S. Kuld, N. D. Nielsen, A. D. Jensen, J. Sehested and J. M. Christensen, Angew. Chem., Int. Ed., 2020, 59, 18189–18193 CrossRef CAS PubMed.
- A. Pavlišič, M. Huš and B. Likozar, J. Cleaner Prod., 2020, 275, 122958 CrossRef.
- A. Pavlišič, M. Huš and B. Likozar, J. Cleaner Prod., 2020, 275, 122958 CrossRef.
- J.-B. Li, L. Ji, J. Liang, Y. Zhang, J. Luo, C. Li and G. Rao, Calphad, 2008, 32, 447–453 CrossRef CAS.
- M. Kowalski and P. J. Spencer, J. Phase Equilib., 1993, 14, 432–438 CrossRef CAS.
- B. W. J. Chen, L. Xu and M. Mavrikakis, Chem. Rev., 2021, 121, 1007–1048 CrossRef CAS PubMed.
- L. Grajciar, C. J. Heard, A. A. Bondarenko, M. V. Polynski, J. Meeprasert, E. A. Pidko and P. Nachtigall, Chem. Soc. Rev., 2018, 47, 8307–8348 RSC.
- C.-R. Chang, Z.-Q. Huang and J. Li, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 679–693 CAS.
- Á. Morales-García, F. Viñes, J. R. B. Gomes and F. Illas, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1530 Search PubMed.
- X. Zhang, T. E. Sewell, B. Glatz, S. Sarupria and R. B. Getman, Catal. Today, 2017, 285, 57–64 CrossRef CAS.
- N. Artrith, Matter, 2020, 3, 985–986 CrossRef.
- M. T. Darby, M. Stamatakis, A. Michaelides and E. C. H. Sykes, J. Phys. Chem. Lett., 2018, 9, 5636–5646 CrossRef CAS PubMed.
- X. Li, R. Chiong and A. J. Page, J. Phys. Chem. Lett., 2021, 12, 5156–5162 CrossRef CAS PubMed.
- E. Lam, J. J. Corral-Pérez, K. Larmier, G. Noh, P. Wolf, A. Comas-Vives, A. Urakawa and C. Copéret, Angew. Chem., Int. Ed., 2019, 58, 13989–13996 CrossRef CAS PubMed.
- A. Müller, A. Comas-Vives and C. Copéret, J. Phys. Chem. C, 2021, 125, 396–409 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Hafner, J. Phys.: Condens. Matter, 1994, 6, 8245–8257 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Paier, R. Hirschl, M. Marsman and G. Kresse, J. Chem. Phys., 2005, 122, 234102 CrossRef PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 035406 CrossRef.
- K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 045407 CrossRef.
- M. W. Chase, NIST-JANAF Thermochemical Tables, American Institute of Physics, 4th edn, 1998 Search PubMed.
- A. Roussey, P. Gentile, D. Lafond, E. Martinez, V. Jousseaume, C. Thieuleux and C. Copéret, J. Mater. Chem. C, 2013, 1, 1583–1587 RSC.
- T. Reichenbach, M. Walter, M. Moseler, B. Hammer and A. Bruix, J. Phys. Chem. C, 2019, 123, 30903–30916 CrossRef CAS.
- J. M. Moe, Chem. Eng. Prog., 1962, 58, 33–36 CAS.
- H. Okamoto, J. Phase Equilib. Diffus., 2016, 37, 350–362 CrossRef CAS.
- H. Okamoto, J. Phase Equilib. Diffus., 2018, 39, 87–100 CrossRef CAS.
- G. Brauer, Handbuch der Präparativen Anorganischen Chemie, Ferdinand Enke, Stuttgart, 1978, vol. 3 Search PubMed.
- A. F. Wells, Structural Inorganic Chemistry, Clarendon Press, Oxford University Press, 5th edn, 1984 Search PubMed.
- B. D. Sharma and J. Donohue, Z. Kristallogr. Cryst. Mater., 1962, 117, 293–300 CrossRef CAS.
- W. M. Haynes, CRC Handbook of Chemistry and Physics, CRC Press, 2nd edn, 2011 Search PubMed.
- J. Yan and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 245204 CrossRef.
- E. Frei, A. Gaur, H. Lichtenberg, L. Zwiener, M. Scherzer, F. Girgsdies, T. Lunkenbein and R. Schlögl, ChemCatChem, 2020, 12, 4029–4033 CrossRef CAS.
- X. Huang, T. Jones, A. Fedorov, R. Farra, C. Copéret, R. Schlögl and M.-G. Willinger, Adv. Mater., 2021, 33, 2101772 CrossRef CAS PubMed.
- J.-Q. Zhong, S. Shaikhutdinov and B. Roldan Cuenya, J. Phys. Chem. C, 2021, 125, 1361–1367 CrossRef CAS PubMed.
- CRediT – Contributor Roles Taxonomy, 2019, https://credit.niso.org/.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc03107h |
| This journal is © The Royal Society of Chemistry 2022 |