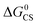Open Access Article
Open Access ArticleA long-lived charge-separated state of spiro compact electron donor–acceptor dyads based on rhodamine and naphthalenediimide chromophores†
Xiao
Xiao‡
 a,
Ivan
Kurganskii‡
b,
Partha
Maity‡
a,
Ivan
Kurganskii‡
b,
Partha
Maity‡
 c,
Jianzhang
Zhao
c,
Jianzhang
Zhao
 *ad,
Xiao
Jiang
*e,
Omar F.
Mohammed
*c and
Matvey
Fedin
*ad,
Xiao
Jiang
*e,
Omar F.
Mohammed
*c and
Matvey
Fedin
 *b
*b
aState Key Laboratory of Fine Chemicals, Frontiers Science Center for Smart Materials, School of Chemical Engineering, Dalian University of Technology, Dalian 116024, P. R. China. E-mail: zhaojzh@dlut.edu.cn
bInternational Tomography Center, SB RAS Institutskaya Str., 3A, and Novosibirsk State University, Pirogova str. 2, Novosibirsk 630090, Russia. E-mail: mfedin@tomo.nsc.ru
cDivision of Physical Sciences and Engineering, King Abdullah University of Science and Technology (KAUST), Thuwal 23955-6900, Kingdom of Saudi Arabia. E-mail: omar.abdelsaboor@kaust.edu.sa
dState Key Laboratory of Chemistry and Utilization of Carbon Based Energy Resources, College of Chemistry, Xinjiang University, Urumqi 830017, P. R. China
eKey Laboratory of Industrial Ecology and Environmental Engineering (Ministry of Education), School of Environmental Science and Technology, Dalian University of Technology, Dalian 116024, P. R. China. E-mail: xjiang@dlut.edu.cn
First published on 26th October 2022
Abstract
Spiro rhodamine (Rho)-naphthalenediimide (NDI) electron donor–acceptor orthogonal dyads were prepared to generate a long-lived charge separation (CS) state based on the electron spin control approach, i.e. to form the 3CS state, not the 1CS state, to prolong the CS state lifetime by the electron spin forbidden feature of the charge recombination process of 3CS → S0. The electron donor Rho (lactam form) is attached via three σ bonds, including two C–C and one N–N bonds (Rho-NDI), or an intervening phenylene, to the electron acceptor NDI (Rho-Ph-NDI and Rho-PhMe-NDI). Transient absorption (TA) spectra show that fast intersystem crossing (ISC) (<120 fs) occurred to generate an upper triplet state localized on the NDI moiety (3NDI*), and then to form the CS state. For Rho-NDI in both non-polar and polar solvents, a long-lived 3CS state (lifetime τ = 0.13 μs) and charge separation quantum yield (ΦCS) up to 25% were observed, whereas for Rho-Ph-NDI (τT = 1.1 μs) and Rho-PhMe-NDI (τT = 2.0 μs), a low-lying 3NDI* state was formed by charge recombination (CR) in n-hexane (HEX). In toluene (TOL), however, CS states were observed for Rho-Ph-NDI (0.37 μs) and Rho-PhMe-NDI (0.63 μs). With electron paramagnetic resonance (EPR) spectra, weak electronic coupling between the Rho and NDI moieties for Rho-NDI was proved. Time-resolved EPR (TREPR) spectra detected two transient species including NDI-localized triplets (formed via SOC-ISC) and a 3CS state. The CS state of Rho-NDI features the largest dipolar interaction (|D| = 184 MHz) compared to Rho-Ph-NDI (|D| = 39 MHz) and Rho-PhMe-NDI (|D| = 41 MHz) due to the smallest distance between Rho and NDI moieties. For Rho-NDI, the time-dependent e,a → a,e phase change of the CS state TREPR spectrum indicates that the long-lived CS state is based on the electron spin control effect.
Introduction
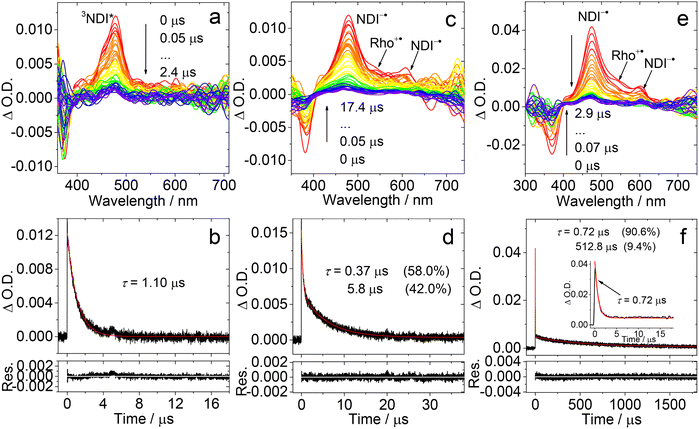
Charge separation (CS) is important in the study of fundamental photochemistry,1–10 and in the areas of artificial photosynthesis,11 photocatalysis and organic photovoltaics (OPVs),12–15etc. The interaction between the locally excited (LE) and CS states in electron donor–acceptor systems plays an important role in OPVs and organic light-emitting diodes (OLEDs).16 Concerning CS, a few key factors are the CS quantum yields (ΦCS), the CS state energy and the lifetimes.17–19 The intermolecular electron transfer initiated by the photo-generated CS state can be enhanced by higher CS state energy and longer CS state lifetime. The electron transfer rate constant, especially in weakly coupled systems, is described by eqn (1), based on Marcus theory for electron transfer: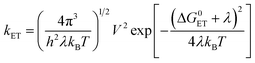 | (1) |
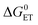 is the Gibbs free energy change of the electron transfer, λ is the total reorganization energy, and V is the electronic matrix element.
is the Gibbs free energy change of the electron transfer, λ is the total reorganization energy, and V is the electronic matrix element.
Based on the equation, a few methods have been studied to prolong the CS state lifetimes. In conventional electron donor–acceptor dyads containing a long linker and multiple donors (or acceptors), the electronic coupling is weak, and thus the CS state lifetime can be prolonged.4,20,21 The systems with this strategy also show high ΦCS.22,23 Another method to prolong the CS state lifetime is to exploit the so-called Marcus inverted region effect, i.e. to attain a CS state with high energy so that the Gibbs free energy change (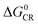 ) of the charge recombination (CR) process is larger than the reorganization energy (λ) (
) of the charge recombination (CR) process is larger than the reorganization energy (λ) (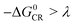 ). However, these conventional methods suffer from drawbacks. For instance, the large separation of the donor and the acceptor, or the use of multiple donors (or acceptors), makes the synthesis challenging, and the CS state may have a low energy. For the exploitation of the Marcus inverted region effect, a donor or acceptor with small λ is required, but the availability of such a donor or acceptor is limited (C60 is one example).4 On the other hand, the high CS state energy pushes the absorption wavelength to the blue or UV spectral range, and clearly these are disadvantages for the application of electron donor–acceptor dyads in photocatalysis and OPVs.1,24
). However, these conventional methods suffer from drawbacks. For instance, the large separation of the donor and the acceptor, or the use of multiple donors (or acceptors), makes the synthesis challenging, and the CS state may have a low energy. For the exploitation of the Marcus inverted region effect, a donor or acceptor with small λ is required, but the availability of such a donor or acceptor is limited (C60 is one example).4 On the other hand, the high CS state energy pushes the absorption wavelength to the blue or UV spectral range, and clearly these are disadvantages for the application of electron donor–acceptor dyads in photocatalysis and OPVs.1,24
Another less investigated method to prolong the CS state lifetimes is electron spin control in CS and CR processes.1,25–29 As other photophysical processes, the CS and CR processes are also electron spin selective, i.e. the electron spin is conserved in these processes. That is, the formation of the 1CS state with a localized singlet excited state (i.e.1LE state) as the precursor is bound to prevail compared to the formation of the 3CS state.1,25–30 On the other hand, the CR of 1CS → S0 is electron spin allowed, whereas the CR of 3CS → S0 is electron spin forbidden, and thus the 3CS state should be inherently longer lived than the 1CS state. Therefore, it is desired to attain the 3CS state, in order to prolong the CS state lifetime.1 However, the conventional electron donor–acceptor dyads have a large separation distance between the donor and acceptor, and thus the electron exchange integral (J) of the electrons in the frontier molecular orbitals of the CS state is extremely small (<0.01 cm−1), and as a result, no stable 1CS or 3CS states can be formed, and very often it is a spin-correlated radical pair (SCRP).1,25,31,32 Since a fraction of the population of SCRP is in the singlet state, the CR channel will shorten the lifetime of the CS state. The potential of the electron spin control method to prolong the CS state lifetime is not maximized under these circumstances. Moreover, it is critical to firstly produce the 3LE state precursor for the subsequent formation of the 3CS state.1 Thus, transition metal coordination frameworks (known for their ultrafast, efficient ISC)5,26,27,30,33 or organic chromophores with inherent ISC are required.19,28,34–38 However, these approaches suffer from high synthesis cost and limited availability of appropriate chromophores.
One method to tackle the above challenge is to prepare a compact electron donor–acceptor dyad, i.e. using a short linker between the donor and acceptor.1,39 Thus, the J value is larger compared with that of the dyads with a long distance between the donor and acceptor, and the formation of 1CS and 3CS states becomes possible. Only in this case the potential of the electron spin control for the prolongation of the CS state lifetime can be exploited.29 Concerning this circumstance, one critical issue is the production of the 3LE state firstly in these heavy atom-free compounds.3,24,40 Recently we used the electron spin control strategy in a compact rhodamine (Rho)-naphthalimide (NI) dyad to attain a long-lived 3CS state, with femtosecond, subnanosecond and nanosecond transient absorption spectroscopic methods, and we unravelled the photophysical processes as S0 → 1LE → 1CS → 3NI → 3CS → S0, and the CS state lifetime was determined to be 0.94 μs in fluid solution at room temperature.39 Recently we used pyromellitimide to prepare rhodamine derivatives, and a CS state lifetime of 2.6 μs was observed.41 It should be pointed out that the closed form of the Rho unit was rarely used as an electron donor for the preparation of compact electron donor–acceptor dyads. The advantage of this novel electron donor (EOX = +0.52 V, vs. Fc/Fc+) is the sterically congested microenvironment created by it,42 which is helpful for the donor and acceptor to adopt a rigid orthogonal geometry, beneficial for spin–orbit charge transfer intersystem crossing (SOCT-ISC), a novel method to generate the 3LE state as the precursor of CS, so that the 3CS state can be formed, and the electron spin control method can be implemented.24,39
In order to fully exploit this strategy, herein we prepared a series of Rho-naphthalenediimide (NDI) dyads (Scheme 1), to study the CS and CR processes, especially the effect of the molecular structure and geometry on the CS state lifetimes. In the three target dyads we prepared, the distance between the donor and acceptor is varied, by a direct connection of the donor and acceptor (Rho-NDI) or using an intervening phenyl link between the two units (Rho-Ph-NDI). Furthermore, the electronic coupling between the donor and acceptor is also varied via conformation restriction by the methyl groups on the intervening phenyl unit between the donor and acceptor (Rho-PhMe-NDI). Steady state and time-resolved transient optical and magnetic spectroscopic methods were used for the study of the photophysical properties of the dyads.
Results and discussion
Molecular structure design and synthesis
The closed form of Rho is an electron donor (EOX = +0.52 V, vs. Fc/Fc+). The unique feature is the spiro structure and the steric hindered microenvironment when an electron acceptor attached.39,42,43NDI was used as the electron acceptor (ERED = −1.02 V, vs. Fc/Fc+).44–46 The compact structure of Rho-NDI is beneficial for increasing the J magnitude, and to reduce the λ values.47 We also prepared two analogues with an intervening phenyl linker inserted between the donor and acceptor (Rho-Ph-NDI and Rho-PhMe-NDI). The larger distance between the donor and acceptor in these two dyads may increase the CS state energy.31 Moreover, the conformation restriction is also varied by the methyl groups attached on the intervening phenyl linker. This character may also have an effect on the CS, CR and the CS state lifetimes.The synthesis of the compounds is based on the routine derivatization chemistry of Rho and NDI chromophores.39,42 The yields are generally satisfactory. The molecular structures are verified by 1H NMR, 13C NMR, HR MS and Fourier transform infrared (FT-IR) spectral methods.
Single crystals of Rho-NDI were obtained by slow diffusion of n-hexane (HEX) into a tetrahydrofuran (THF) solution of the compound. X-ray diffraction shows that the centroid-to-centroid distance between xanthene and NDI units is 5.8 Å and the dihedral angle between the xanthene and NDI units is 52.9° (Fig. 1).
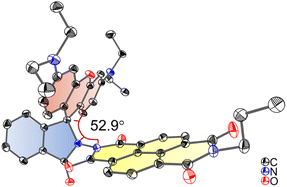 | ||
| Fig. 1 ORTEP view of the molecular structure of Rho-NDI determined by single-crystal X-ray diffraction. Hydrogen atoms are omitted for clarity. Thermal ellipsoids are set at 50% probability. Deposition number 2190442 contains the supplementary crystallographic data for this paper. Note that to grow a single crystal, we prepared the analogue of Rho-NDI with n-propylamine, instead of 2-ethylhexylamine, for better crystallizability. | ||
UV-visible absorption and luminescence emission studies
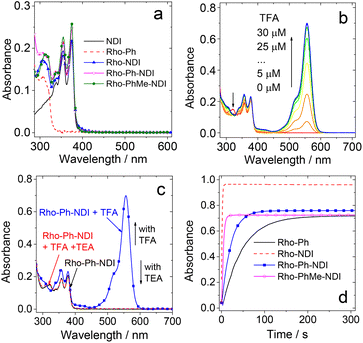
The UV-vis absorption spectra of the compounds were studied (Fig. 2a). NDI gives the featured absorption band in the range of 300–400 nm, which shows significant vibration progression. Rho-Ph shows absorption at 308 nm. All the dyads show UV-vis absorption spectra, which are identical to the sum of the absorption spectra of the NDI and the Rho-Ph units, and thus the electronic coupling between the donor and acceptor is negligible at the ground state,18,48–50 because the p-xylene linker is known to be able to electronically isolate the donor and acceptor.18 Given that the electronic coupling between the donor and acceptor was strong, a charge transfer (CT) absorption band (S0 → 1CT transition) should be observed.50–52 It is interesting that even for Rho-NDI, in which the donor and acceptor are separated by three σ bonds, and the electronic coupling at the ground state is weak.The Rho moiety is well known for the reversible spirolactam ↔ amide transformation in the presence of an acid or base.53–55 For Rho-Ph and the dyads, upon addition of trifluoroacetic acid (TFA), an absorption band at 557 nm appeared, which is attributed to the opened amide form of Rho derivatives (Fig. 2b). The absorption band of the open form of Rho decreased with the addition of a base such as triethylamine (TEA) (Fig. 2c), indicating that the opening-closure reaction in the presence of an acid or base is reversible. The reaction kinetics (i.e. the absorption variation of Rho-Ph and the dyads at 557 nm) with the addition of TFA were also studied (Fig. 2d). Rho-Ph shows the slowest kinetics of lactam → open form transformation, for which the apparent transformation rate constant is k = 2.2 × 10−2 s−1, followed by Rho-Ph-NDI (k = 4.6 × 10−2 s−1). Rho-NDI (k = 0.77 s−1) and Rho-PhMe-NDI (k = 0.22 s−1) which show relatively faster kinetics (these values may be dependent on the acid concentration).
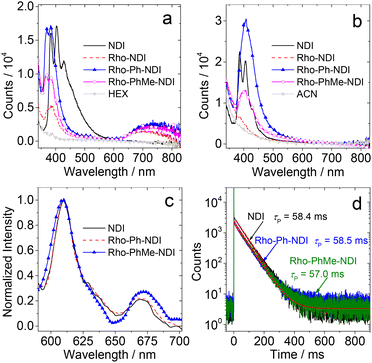
The photoluminescence of the compounds was studied (Fig. 3). In HEX, all the compounds show LE fluorescence emission bands in the range of 350–550 nm (Fig. 3a). The dyads give a broad and weak fluorescence emission band in the range of 650–850 nm. Neither the Rho nor the NDI unit gives a fluorescence emission band in this region, and thus it is attributed to a CS fluorescence emission band (1CS → S0), indicating the non-negligible electronic interaction of the radical anion and cation at the CS state. For Rho-NDI, the CS state decays with a biexponential feature, and the lifetime is 0.09 ns (91.2%)/2.91 ns (8.8%) in HEX (Fig. S20†). The biexponential decay of the CS state can be tentatively attributed to the existence of a dark 3CS state and the equilibrium between 1CS and 3CS states. The similar energy of 1CS and 3CS states can be verified by the small |J| value obtained by fitting TREPR spectra (see the later section). The species with a shorter lifetime is assigned to the prompt 1CS state. The minor species with a longer lifetime is tentatively assigned to the 1CS state originating from the dark 3CS state. Similar results were observed for the decay of the CS states of Rho-Ph-NDI and Rho-PhMe-NDI, and the lifetimes were determined to be 0.32 ns (60.3%)/3.13 ns (39.7%) and 0.40 ns (76.3%)/3.90 ns (23.7%), respectively. In acetonitrile (ACN), only the LE fluorescence band was observed (Fig. 3b). In toluene (TOL), much stronger fluorescence for NDI was observed. One possible reason is the formation of exciplexes of NDI with TOL (Fig. S19†).56 For the dyads, the fluorescence is very weak and no CS state fluorescence band was observed in TOL (Fig. S19†).
In order to determine the 3NDI* energy of the compounds, the phosphorescence emission spectra in frozen solution at 77 K were studied (Fig. 3c). Phosphorescence emission bands in the range of 600–700 nm were observed under these conditions. Based on the identical results observed for NDI and the dyads, the phosphorescence bands are assigned to the 3NDI* moiety. From the on-set of the phosphorescence band on the high energy side (can be approximated as the vibrational 00 transition of T1 → S0 radiative relaxation), the 3NDI* state energy is approximated to be 2.04 eV, which is consistent with the previously reported phosphorescence spectrum for NDI (substituted with n-hexyl at the N position) in 2-methyltetrahydrofuran (MeTHF) at 77 K (2.04 eV).57 The phosphorescence lifetimes were determined to be ca. 58 ms (Fig. 3d). However, no phosphorescence was observed for Rho-NDI at 77 K, even in the presence of ethyl iodide (in TOL/MeTHF/ethyl iodide, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, v/v), and the possible reason is that the 3CS state is the lowest-lying state rather than the 3NDI* state. This postulate is supported by the calculated CS state energy with the Rehm–Weller equation (see the later section). Note that the 3CS state should be weakly emissive, even at cryogenic temperature, due to the poor orbital overlap of the 3CS → S0 transition and the inhibited vibronic coupling. The photophysical parameters of the compounds are summarized in Table 1.
2, v/v), and the possible reason is that the 3CS state is the lowest-lying state rather than the 3NDI* state. This postulate is supported by the calculated CS state energy with the Rehm–Weller equation (see the later section). Note that the 3CS state should be weakly emissive, even at cryogenic temperature, due to the poor orbital overlap of the 3CS → S0 transition and the inhibited vibronic coupling. The photophysical parameters of the compounds are summarized in Table 1.
| Compounds | λ abs (εc) | λ F | Φ F | τ F | k r | k nr | λ P | τ P | Φ CS | |
|---|---|---|---|---|---|---|---|---|---|---|
| Lactam form | Open formd | |||||||||
| a In HEX. b Maximal UV-vis absorption wavelength. c = 1.0 × 10−5 M, in nm. c Molar absorption coefficient, in 104 M−1 cm−1. d In MeOH. e Maximal fluorescence emission wavelength, in nm. f Fluorescence quantum yields, in %. g Fluorescence lifetimes (λex = 340 nm) of NDI at 420 nm, Rho-NDI at 710 nm, Rho-Ph-NDI and Rho-PhMe-NDI at 750 nm. c = 1.0 × 10−5 M, in ns. h Radiative decay rate constant, in 107 s−1. i Nonradiative decay rate constant, in 109 s−1. j Maximal phosphorescence emission wavelength in MeTHF, in nm, at 77 K. k Phosphorescence lifetimes at 610 nm (λex = 370 nm), and c = 1.0 × 10−4 M, in ms, at 77 K. l CS quantum yields, in %. m Not applicable. n Literature values, ref. 25. o Not observed. p In ACN. | ||||||||||
| NDI | 375 (2.19)m | —m | 403 | 0.5 | 0.29 (93.5%)/3.22 (6.5%) | 1.04 | 2.07 | 609 | 58.4 | —m |
| Rho-Ph | 308 (1.35) | 556 (7.16) | 410n | 1.2n | 4.7n | 0.26 | 0.21 | —o | —o | —m |
| Rho-NDI | 374 (2.20) | 557 (9.61) | 388/730 | 0.2 | 0.09 (91.2%)/2.91 (8.8%) | 0.59 | 2.94 | —o | —o | 25 |
| Rho-Ph-NDI | 375 (2.48) | 557 (7.59) | 383/745 | 0.5 | 0.32 (60.3%)/3.13 (39.7%) | 0.51 | 1.01 | 609 | 58.5 | 19p |
| Rho-PhMe-NDI | 374 (2.59) | 557 (7.24) | 385/728 | 0.3 | 0.40 (76.3%)/3.90 (23.7%) | 0.24 | 0.81 | 610 | 57.0 | 17p |
Electrochemical studies
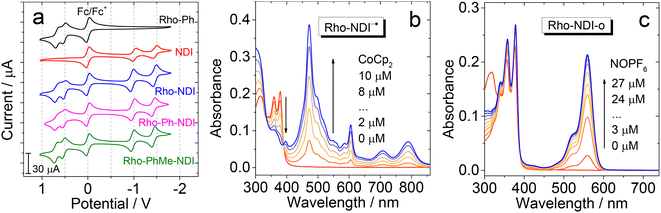
The redox potentials of the compounds were studied by using cyclic voltammograms (Fig. 4a). NDI shows two reversible reduction waves at −1.02 V and −1.46 V (vs. Fc/Fc+), respectively. No oxidation waves were observed in the redox potential window applied. These results are similar to previous reports on NDI.56 For Rho-Ph, two pseudo-reversible oxidation waves at +0.52 V and +0.66 V were observed (vs. Fc/Fc+), which is similar to a previously reported Rho-NI dyad.39 These results indicate that the Rho unit acts as an electron donor and the NDI moiety acts as an electron acceptor in the dyads upon photoexcitation. For the dyads, the reduction potential is similar to that of NDI, whereas the oxidation potential is similar to that of Rho, indicating that the electronic interaction between the two units at the ground state is weak. The redox potentials are summarized in Table 2.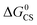 ) and the energy of the charge separated state (ECSS) of the compounds in different solventsa
) and the energy of the charge separated state (ECSS) of the compounds in different solventsa
| E OX (V) | E RED (V) | (eV)/ECSS (eV) | ||||
|---|---|---|---|---|---|---|
| HEX | TOL | THF | ACN | |||
| a Cyclic voltammetry in N2-saturated solvents containing 0.10 M Bu4N[PF6]. Pt electrode as the counter electrode, glassy carbon as the electrode working electrode, ferrocene (Fc/Fc+) as the internal reference (set as 0 V in the cyclic voltammograms), and Ag/AgNO3 couple as the reference electrode in dichloromethane. E00 = 3.28 eV for Rho-NDI, Rho-Ph-NDI and Rho-PhMe-NDI. E00 is the approximated energy with the cross point of UV-vis absorption and fluorescence emission of NDI after normalization in HEX. For Rho-Ph-NDI and Rho-PhMe-NDI, in HEX, ΔGS = 0.56 eV is used; in TOL, ΔGS = 0.40 eV is used. THF stands for tetrahydrofuran. b Not observed. c Not applicable. | ||||||
| NDI | —b | −1.02, −1.46 | —c | —c | —c | —c |
| Rho-Ph | +0.52, +0.66 | —b | —c | —c | —c | —c |
| Rho-NDI | +0.51, +0.67 | −0.96, −1.45 | −1.62/1.66 | −1.68/1.60 | −1.82/1.46 | −1.87/1.41 |
| Rho-Ph-NDI | +0.52, +0.66 | −0.98, −1.42 | −1.22/2.06 | −1.38/1.90 | −1.66/1.62 | −1.82/1.46 |
| Rho-PhMe-NDI | +0.53, +0.69 | −0.97, −1.42 | −1.22/2.06 | −1.38/1.90 | −1.66/1.62 | −1.82/1.46 |
Based on the electrochemical data, the spectral data and the theoretical computation results (see the later section), the driving force of the possible photo-induced CS, i.e. the Gibbs free energy changes of the CS (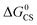 ), was calculated with the Rehm–Weller equation (for details, please refer to the ESI†):58
), was calculated with the Rehm–Weller equation (for details, please refer to the ESI†):58
For Rho-Ph-NDI and Rho-PhMe-NDI, with a large separation distance between the donor and acceptor, in HEX and TOL, eqn (2) does not give correct values for ΔGS because it overestimates the polarity of HEX and TOL. Therefore, we have used tentatively the value of ΔGS = 0.56 eV in HEX and ΔGS = 0.4 eV in TOL.59 The CS state energy (ECSS) in HEX (2.06 eV) obtained by this approximation also matches the energy obtained from the CS emission (Fig. 3a, 2.03 eV, estimated by 00 transition of 1CS → S0). For Rho-NDI, with a short separation distance between the donor and acceptor, the degree of overestimation for ΔGS from eqn (2) in HEX (0.19) and TOL (0.13) is negligible. The results (Table 2) show that the CS is thermodynamically allowed for all the dyads. The driving force for the CS of Rho-NDI is larger than that of the dyads with a large separation distance between the donor and acceptor (i.e.Rho-Ph-NDI and Rho-PhMe-NDI). The CS state energy (ECSS) was calculated with eqn (5). The results show that for Rho-NDI, the CS state energy is <2.0 eV, which means that the low-lying triplet state is a CS state, not a 3NDI* state, supported by nanosecond transient absorption (ns-TA) spectral studies (see the later section). For Rho-Ph-NDI and Rho-PhMe-NDI, the CS state energy is slightly higher than that of Rho-NDI in the same solvents. Thus, for these two dyads, the low-lying triplet state may probably be 3NDI* in HEX, but in polar solvents, the CS state may become lower in energy. These postulates were confirmed by ns-TA spectral studies (see the later section).
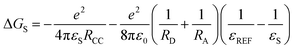 | (2) |
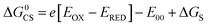 | (3) |
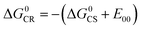 | (4) |
| ECSS = e[EOX − ERED] + ΔGS | (5) |
In order to facilitate the assignment of the CS state in the transient absorption spectra, the UV-vis absorption of the radical anion and radical cation forms of the dyads was studied, with either a chemical reduction or spectroelectrochemistry method (Fig. 4b and c). For Rho-NDI, upon reduction with cobaltocene (CoCp2), the absorption band centered at 375 nm is diminished, and new stronger absorption bands centered at 470 nm, 605 nm 707 nm and 790 nm emerge, which are attributed to the NDI−˙ species (Fig. 4b).60 These results are in agreement with the spectroelectrochemical studies (Fig. S25†). Similar results were observed for Rho-Ph-NDI and Rho-PhMe-NDI (Fig. S21†). The UV-vis spectra of NDI−˙ for Rho-NDI were also recorded by the TDDFT method (Fig. S51†), which support the experimental results. With the oxidant of nitrosonium hexafluorophosphate (NOPF6) added, intensive absorption bands centered at 520 nm and 560 nm appeared for Rho-NDI (Fig. 4c). These bands disappeared with the addition of TEA, which indicates that the new bands are attributed to the opened form of the Rho unit (Rho-NDI-o), not the radical cation of the Rho unit (Fig. S22†), although it is similar to the UV-vis spectra Rho+˙ of Rho-NDI calculated by the TDDFT method. This information is useful for the study of the femtosecond transient absorption (fs-TA) and the ns-TA spectra of the compounds, for instance the identification of the transient species observed with these spectroscopic methods, especially the CS state.
Femtosecond transient absorption (fs-TA) spectroscopy
To verify the photophysical processes involved in the dyads upon photoexcitation, the fs-TA spectra of the dyads were recorded. For NDI, the result of a target analysis of the fs-TA data with a scheme including S1/Tn state equilibrium is shown in Fig. S26.† The S1 state with an absorption band centered at 597 nm was populated after photoexcitation. Then the fast ISC process S1 → Tn (absorption at 467 nm) occurs (via spin orbit coupling ISC, SOC-ISC), and the Tn state has a lifetime of 2.6 ps, due to the similar energy of the two states of S1 (3.26 eV, based on the spectroscopic data) and Tn (3.24 eV, based on the DFT calculation). The reverse ISC of the Tn state to the S1 state (4.3 ps) competes with internal conversion to lower triplet states T1 (6.3 ps). The T1 state does not decay completely within the available time window of the fs-TA spectrometer, which is supported by the ns-TA spectra.61The fs-TA spectra of Rho-NDI and Rho-Ph-NDI in different solvents upon fs laser excitation at 375 nm are shown in Fig. 5. The species-associated difference spectra (SADS) of the dyads were obtained by global fitting with the sequential model. For Rho-NDI, two species were required for the satisfactory fitting of the spectra in HEX (Fig. 5b). The ground state bleaching (GSB) band was observed in the range of 330–400 nm, which is in agreement with the steady-state absorption spectrum (Fig. 2). The first species is assigned to the mixed state of S1 and a higher triplet state (Tn), showing excited state absorption (ESA) bands centered at 593 nm (S1) and 468 nm (Tn). ISC (<120 fs, response function time of the instrument) is too fast for the S1 and a higher triplet Tn state with similar energy to be isolated as two species from the fs-TA spectra. After 285 fs, the second species is formed, showing the typical absorption of NDI−˙ centered at 475 nm and 607 nm. Thus, the process upon photo-excitation can be summarized as 1NDI* → 3NDI* (an upper triplet state) → 3CS or 1NDI* → 1CS. Concerning the low charge separation efficiency of the 3CS (10–25%, see the later ns-TA section) for the dyads, the main pathway may be 1NDI* → 1CS, followed by 1CS → S0, which competes with the process of 1CS → 3CS. The lifetime of the CS state in fs TA spectra is determined to be 210 ps, although the signal can be observed in a longer time window (see the ns-TA section), which is likely due to the lower spectral resolution of the fs-TA spectrograph and a lower signal-to-noise ratio of the setup employed. In ACN, a similar EADS result was observed, CS (i.e., the lifetime of the first species) was determined to be 160 fs, and the CS state lifetime was 1.4 ps (Fig. 5c).
For Rho-Ph-NDI and Rho-PhMe-NDI, similar fs-TA spectra and SADS fitting results were observed (Fig. 5d–f and S26†) in both HEX and ACN. An upper excited triplet state, for which the energy is close to that of the S1 state, was generated by fast ISC (<120 fs). Then the CS process occurs to generate the CS state. Based on the electrochemical studies and DFT results, For Rho-Ph-NDI and Rho-PhMe-NDI, the low-lying triplet state is a LE state in HEX, and thus, we assume that 3NDI* was generated by the CR process from the CS state. The 3NDI* state was not obtained in fs-TA spectra, probably due to the slow CR process.
Nanosecond transient absorption (ns-TA) spectroscopy
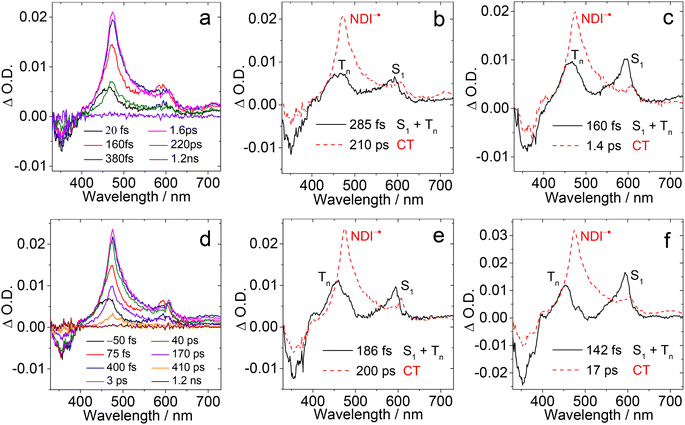
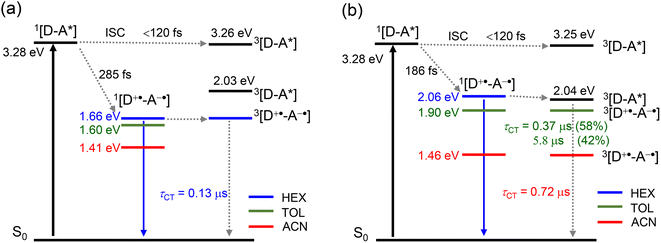
In order to study the long-lived species of the dyads formed upon photoexcitation, the ns-TA spectra of the compounds were recorded (Fig. 6). For Rho-NDI, a positive absorption band centered at 470 nm and a minor absorption band centered at 600 nm were observed upon nanosecond pulsed laser excitation (Fig. 6a). These absorption bands are attributed to NDI−˙, based on the chemical reduction results (Fig. 4). The weak absorption of Rho+˙ may be overshadowed by the strong absorption of NDI−˙.The decay of the transient species has a biexponential feature (Fig. 6b), and the shorter component has a lifetime of 0.13 μs (population rate 93.5%), and a longer component of 4.0 μs (6.5%). Based on the CS emission lifetime (0.09 ns (91.2%)/2.91 ns (8.8%), Fig. S20†), the first component is attributed to the 3CS state, not the 1CS state. The second component is attributed to intermolecular CR (see the later section). We recorded the ns-TA spectra of Rho-NDI in deaerated viscous solvent dimethyl silicone oil 500 (a solvent with low-polarity). Diffusion based photophysical processes, such as triplet–triplet annihilation or intermolecular electron transfer, should be inhibited in viscous solvent. Mono-exponential decay NDI−˙ of Rho-NDI was observed and the lifetime was determined to be 151.5 ns (Fig. S37†), which indicates that the second component of the decay traces of Rho-NDI in deaerated HEX and ACN (Fig. 6) is due to the intermolecular CR process. This is a long-lived CS state, considering that Rho-NDI is a compact dyad.35 Previously for a ZnPor-C60 dyad, the CS state lifetime was determined to be 530 ns.18
In polar solvent ACN, similar ns-TA spectra were obtained, but the lifetime of the first component was shortened to ca. 29 ns and the lifetime of the second component was reduced to 0.21 μs (Fig. 6c and d). In aerated HEX, the monoexponential decay NDI−˙ of Rho-NDI was observed and the lifetime was quenched to 91.1 ns (Fig. S31†).
These results show that the transient species are most likely in triplet spin multiplicity, i.e. the 3CS state was detected, not the 1CS state. Similarly, the lifetime of NDI−˙ was quenched to 20.8 ns with monoexponential decay in aerated ACN (Fig. S31†). In deaerated TOL, the signal of NDI−˙ is very weak with a lifetime of 0.39 μs (Fig. S30†), which is longer than that in HEX and ACN. The abnormal long-lived NDI−˙ is due to the intermolecular CT resulting from the high concentration of measurement.
We also recorded the ns-TA spectra of the reference compound NDI under similar conditions (Fig. 6e). A positive absorption band is located in the region <500 nm, which is attributed to the 3NDI* absorption (T1 → Tn transition). Moreover, the NDI* state lifetime was determined to be 23.6 μs (Fig. 6f). These results corroborate the assignment of the CS state in the ns-TA spectra of Rho-NDI. These results infer that the CS state has a lower energy than the 3NDI* state in Rho-NDI, which is in agreement with the electrochemical studies (Table 2).
The ΦCS was determined using the relative method (eqn (S1)†). The molar absorption coefficient of NDI−˙ (ε475 nm = 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 M−1 cm−1) was determined by the chemical reduction method and is similar to the reported value (ε475 nm = 40
700 M−1 cm−1) was determined by the chemical reduction method and is similar to the reported value (ε475 nm = 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1).46 The molar absorption coefficient of Rho+˙ was determined to be ca. 6600 M−1 cm−1 at 560 nm by spectroelectrochemistry. The strong absorption of the T1 state of anthracene (ε432 nm = 45
000 M−1 cm−1).46 The molar absorption coefficient of Rho+˙ was determined to be ca. 6600 M−1 cm−1 at 560 nm by spectroelectrochemistry. The strong absorption of the T1 state of anthracene (ε432 nm = 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 M−1 cm−1; ΦT = 0.71) was used as a standard to obtain the ΦCS, based on the absorption of NDI−˙.62,63 The ΦCS of Rho-NDI in HEX was determined to be 25% (Fig. S49†). It should be noted that the ΦCS is attributed to the 3CS state due to the long lifetime detected in ns-TA rather than total CS states (both 1CS and 3CS states).
500 M−1 cm−1; ΦT = 0.71) was used as a standard to obtain the ΦCS, based on the absorption of NDI−˙.62,63 The ΦCS of Rho-NDI in HEX was determined to be 25% (Fig. S49†). It should be noted that the ΦCS is attributed to the 3CS state due to the long lifetime detected in ns-TA rather than total CS states (both 1CS and 3CS states).
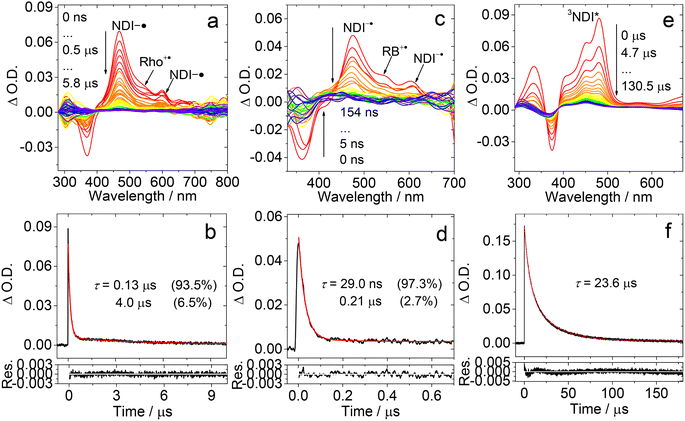
The ns-TA spectra of Rho-Ph-NDI were studied (Fig. 7). With the intervening phenyl linker, we anticipate that the CS state energy should increase as compared to that of Rho-NDI.31 In HEX, an intensive positive absorption band centered at 480 nm was observed, which is similar to that of NDI. Thus, it is attributed to the ESA band of the 3NDI* state. The lifetime was determined to be 1.10 μs (Fig. 7a and b). For Rho-Ph-NDI, the CS state energy in HEX is 2.06 eV, which is slightly higher than that of 3NDI* (2.04 eV), where they are in equilibrium. Therefore, for Rho-Ph-NDI, fast decay of 3NDI* (1.10 μs) is observed, but it is much shorter than the triplet state lifetime of native NDI (23.6 μs, Fig. 6f).
The ns-TA spectra of Rho-Ph-NDI in TOL were also recorded (Fig. 7c), and interestingly, positive absorption bands centered at 477 nm and 610 nm were observed, and thus the transient species was assigned to the CS state. The CS state lifetime was determined to be 0.37 μs (58%)/5.8 μs (42%) (Fig. 7d), which is longer than that of Rho-NDI (0.13 μs. In HEX). Note that the CS state lifetime is much longer than the CS state fluorescence lifetime (0.32 ns (60.3%)/3.13 ns (39.7%), Fig. S20†), and thus we assign the CS state observed in the ns-TA spectra to the 3CS state, not the emissive 1CS state. This longer CS state lifetime may be due to the weaker electronic coupling, as a result of the intervening phenyl linker. In polar solvent ACN, similar ns-TA spectra were observed, and the lifetime of the CS state was determined to be 0.72 μs (90.6%)/512.8 μs (9.4%) (Fig. 7e and f), which is also much longer than that of Rho-NDI (29 ns).
To clarify the longer-lived component of the decay of the transient of Rho-Ph-NDI in TOL, the ns-TA spectra of Rho-Ph-NDI in deaerated viscous solvent dimethylsilicone oil 500 (relative dielectric constant εr = 2.75, for which the polarity is similar to that of TOL, εr = 2.38) were recorded (Fig. S37†). Biexponential decay NDI−˙ of Rho-Ph-NDI was observed and the lifetime was determined to be 0.57 μs (88%)/7.4 μs (12%). Thus, the component with a longer lifetime is due to the close-lying CS state and the 3NDI* state rather than the diffusion controlled intermolecular CR, which is different from Rho-NDI. This conclusion is supported by the similar energy of the CS state (1.90 eV) calculated by electrochemistry and the 3NDI* state (2.04 eV, see the later section). In polar viscous solvent triacetin (ET(30) = 40.4 kcal mol−1), the CS state lifetime is 0.68 μs with monoexponential decay, which indicates that the second component of the fitting of the decay traces of Rho-Ph-NDI in ACN is attributed to the intermolecular charge recombination (Fig. S38†).
Rho-PhMe-NDI, with the attachment of methyl groups on the intervening phenyl linker, shows analogous spectra and triplet state lifetime compared with Rho-Ph-NDI (Fig. S34†). In HEX, the 3NDI* state (2.0 μs) was observed, which is almost two times that of Rho-Ph-NDI. In TOL, the CS state lifetime was determined to be 0.63 μs (70.4%)/5.4 μs (29.6%). In ACN, the CS state lifetime is 0.59 μs (87.4%)/595.1 μs (12.6%) similar to that of Rho-Ph-NDI, which is much longer than that of Rho-NDI. We tentatively attribute this longer CS state lifetime to the weaker electronic coupling in Rho-Ph-NDI and Rho-PhMe-NDI than that in Rho-NDI, as a result of the longer linker in the former. For Rho-Ph-NDI and Rho-PhMe-NDI, the ΦCS in TOL is low and determined to be 7% and 3%, respectively; the ΦCS in ACN was determined to be 19% and 17%, respectively (Fig. S49†), which is slightly lower than that of Rho-NDI in HEX (25%).
Steady state and time-resolved electron paramagnetic resonance (TREPR) spectroscopy
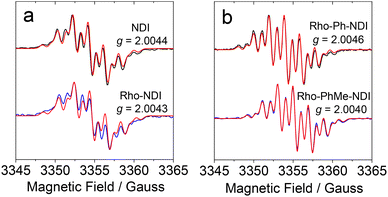
EPR experiments were performed to obtain information on the spin density distribution within the anion radicals of the compounds (Fig. 8). The radical anions of the compounds were prepared by chemical reduction with tetrabutylammonium fluoride (TBAF) in deaerated DMF.64,65Since NDI is N,N symmetrically disubstituted, the hydrogen atoms located on the aromatic core exist in equivalent environments. The hyperfine coupling (HFC) constants of NDI obtained by simulation of the experimental EPR spectra show two equivalent nitrogen atoms (0.98 G) and four equivalent protons (1.86 G), which are close to the values obtained by DFT calculations at the UB3LYP/EPR-II level (Table S3†).60,66 For Rho-Ph-NDI and Rho-PhMe-NDI, similar results and HFC constants observed as compared to NDI, which indicates that the electron donor Rho has negligible effect on the spin density distribution of NDI−˙ due to the linkers (phenyl and p-xylene, respectively) between the Rho and NDI units. However, for Rho-NDI, two pairs of equivalent nitrogen atoms (1.03 G/0.97 G) and protons (1.98 G/1.82 G) are needed to simulate the EPR spectra, revealing that a weak coupling of the N atoms of the Rho and the NDI moiety is present due to the direct link of the donor and acceptor. The HFC constants of Rho-NDI calculated by DFT also provide evidence for the asymmetry of spin density distribution of NDI−˙ (Table S3†).46 These results verify the fact mentioned above that weaker electronic coupling exists in Rho-Ph-NDI and Rho-PhMe-NDI than that in Rho-NDI, as a result of the longer linker in the former two dyads. Despite the slight differences between the spectra of Rho-NDI and other dyads, as well as NDI, NDI−˙ of the compounds has virtually identical g values (2.0044 for NDI, 2.0043 for Rho-NDI, 2.0046 for Rho-Ph-NDI, and 2.0040 for Rho-PhMe-NDI. Table 3). The isotropic hyperfine splitting parameters of NDI−˙ of the compounds based on EPR spectra are summarized in Table 3. Based on the above results, we propose that the J and the electron spin–spin interaction of Rho+˙-NDI−˙ (i.e. CS state) are stronger than those of Rho-Ph-NDI and Rho-PhMe-NDI.
| NDI | Rho-NDI | Rho-Ph-NDI | Rho-PhMe-NDI | ||
|---|---|---|---|---|---|
| a NDI−˙ of the compounds was generated by TBAF in deaerated DMF. c[Sample] = 1.0 × 10−4 M, c[TBAF] = 0.05 M, and 25 °C. Microwave frequency = 9.41 GHz, microwave power = 0.796 mW, and modulation amplitude = 1 G. b HFC constants. c The number of equivalent atoms. | |||||
| g | 2.0044 | 2.0043 | 2.0046 | 2.0040 | |
| α/Gb | 14N (nc) | 0.98 (2) | 1.03 (1)/0.97 (1) | 0.98 (2) | 0.98 (2) |
| 1H (nc) | 1.86 (4) | 1.98 (2)/1.82 (2) | 1.88 (4) | 1.88 (4) | |
| Linewidth/G | 0.103 | 0.105 | 0.090 | 0.094 | |
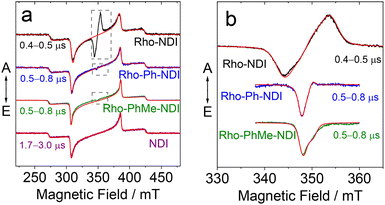
In order to understand the nature of the photoexcited states, we performed a series of time-resolved electron paramagnetic resonance (TREPR) spectroscopy measurements as shown in Fig. 9. All spectra were recorded in frozen solution at 80 K; the spectra recorded at higher temperatures (185 and 285 K, Fig. S53†) feature complex dynamics and will not be discussed in detail. Fig. 9 clearly shows that the spectra of Rho-NDI, Rho-Ph-NDI and Rho-PhMe-NDI consist of two overlapping signals: a dominant broader signal similar to the TREPR spectrum of the triplet state of NDI (see also Table 4) and a narrow weak signal in the center of the spectrum, most likely originating from a 3CS state, which can be described as a spin-correlated radical pair (SCRP).
| Compounds | |D| (MHz) | |E| (MHz) |
P
x
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Py Py![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pz Pz |
ΔP |
|---|---|---|---|---|
| NDI | 2121 | 34 | 0.46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
0.54 |
| Rho-NDI | 2075 | 34 | 0.76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
0.24 |
| Rho-Ph-NDI | 2115 | 29 | 0.51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
0.49 |
| Rho-PhMe-NDI | 2144 | 30 | 0.35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
0.65 |
Broad dominant signals shown in Fig. 9a are assigned to NDI-localized triplets formed via common SOC-ISC, because the native NDI gives the same signal. Subtle differences in the simulation parameters (Table 4) obtained for dyads and individual NDI can be attributed to the minor structural influence on a spin density distribution. The differences of this kind, e.g., in D-tensor parameters between a triplet of a pristine compound based on SOC-ISC and a triplet localized on it in a dyad based on SOCT-ISC have been reported previously.67–69
In principle, the weak and narrower signals shown in Fig. 9b can be assigned either to CS states [D+˙–A−˙] or to highly delocalized triplet states 3[D–A*] of the dyads. Narrow widths of the spectra infer that the two electrons are weakly coupled, i.e. both the zero-field splitting value and dipolar splitting are relatively small; therefore, the presence of a SCRP [D+˙–A−˙] is more likely.
Generally, a triplet state can be formed via common SOC-ISC, via SOCT-ISC, or via a radical pair ISC (RP-ISC). RP-ISC can provide an asymmetric polarization pattern in some cases,70,71 whereas SOC/SOCT-ISC always results in a symmetric one (assuming no anisotropic relaxation). None of these mechanisms alone can describe the patterns observed for dyads, e.g. asymmetric narrow signal with polarization type ea (e stands for emission and a – for absorption) for Rho-Ph-NDI (Fig. 9).
The signal originating from a charge-separated state has distinctive features given by weak spin coupling in its Hamiltonian and a resulting mixing of |S〉 and |T0〉 levels.31,32,72,73 Taking into account a dipolar interaction, both these factors provide a specific orientation dependence of a spectrum. To simulate such a spectral shape, we used a routine based on some functions of the EasySpin package for MatLab (note that exchange interaction in EasySpin is introduced within a spin Hamiltonian 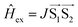 , whereas ref. 51 and 52 use
, whereas ref. 51 and 52 use 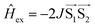 ).74
).74
The results of the simulations are given in Table 5. We used closely isotropic 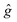 -tensors ≈2.003; hyperfine interaction was neglected. |D| in Table 5 stands for the absolute value of dipole interaction and it is consistent with the structures shown in Fig. 9, where Rho-NDI has the smallest distance between Rho and NDI moieties. Consequently, Rho-NDI must feature the largest value of dipolar interaction (|D| = 184 MHz) compared with Rho-Ph-NDI (|D| = 39 MHz) and Rho-PhMe-NDI (|D| = 41 MHz), and the assumption is consistent with the simulation result. Moreover, the |D|-values of the three dyads differ by a factor of ∼4–5, in agreement with estimations based on optimized ground state structures and point-dipole approximation.
-tensors ≈2.003; hyperfine interaction was neglected. |D| in Table 5 stands for the absolute value of dipole interaction and it is consistent with the structures shown in Fig. 9, where Rho-NDI has the smallest distance between Rho and NDI moieties. Consequently, Rho-NDI must feature the largest value of dipolar interaction (|D| = 184 MHz) compared with Rho-Ph-NDI (|D| = 39 MHz) and Rho-PhMe-NDI (|D| = 41 MHz), and the assumption is consistent with the simulation result. Moreover, the |D|-values of the three dyads differ by a factor of ∼4–5, in agreement with estimations based on optimized ground state structures and point-dipole approximation.
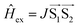 . |D| is the scalar parameter of zero-field splitting (|E| = 0). P−1, P0, P+1, and Ps are the representative populations of |T−1〉, |T0〉, |T+1〉, and |S〉 states, correspondingly
. |D| is the scalar parameter of zero-field splitting (|E| = 0). P−1, P0, P+1, and Ps are the representative populations of |T−1〉, |T0〉, |T+1〉, and |S〉 states, correspondingly
| Compounds | |J|/MHz | |D|/MHz |
P
−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P0 P0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P+1 P+1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ps Ps |
|---|---|---|---|
| Rho-NDI | 26 | 184 | 0.92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.92 0.92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
| Rho-Ph-NDI | 23 | 39 | 0.98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.90 0.90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
| Rho-PhMe-NDI | 28 | 41 | 0.80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
Thus, we succeeded to simulate weak features in the center of the spectra of all three dyads in a model of a CS state (SCRP) with weak electronic couplings. At the same time, we note that these features of Rho-NDI and Rho-PhMe-NDI can also be simulated as a superposition of two delocalized 3[D–A*] triplets: SOC-ISC triplet and RP-ISC triplet.70,71 However, in the case of Rho-Ph-NDI only the SCRP model provides satisfactory agreement. Therefore, most likely, we deal with CS states in the whole series of dyads, although for Rho-NDI and Rho-PhMe-NDI it cannot be proven by TREPR alone. Moreover, for the CS state of Rho-NDI, the e,a → a,e phase change of the CS state spectrum with increasing the delay time (Fig. S50 and S52†) is observed, which likely originates from the repopulation of the CS state from a singlet to a triplet state, i.e. the process 1NDI* → 1[Rho+˙–NDI−˙] → 3[Rho+˙–NDI−˙] in addition to 3NDI* → 3[Rho+˙–NDI−˙],75,76 which further supports that the long-lived CS state is due to the electron spin control effect. Similar phase change behaviors were observed for Rho-Ph-NDI and Rho-PhMe-NDI (e,a → a,e and e → a, correspondingly), although the TREPR signal of the CS state is weak (Fig. S50†). The spectral shapes of the observed CS state are determined by an interplay of D and J values, and only for Rho-NDI each of them can be reliably obtained (Table 5). In the cases of Rho-Ph-NDI and Rho-PhMe-NDI both |D| and |J| are rather small; however, their range agrees well with literature data in similar situations.19,25,28,31,77
Finally, it should be pointed out that TREPR spectral kinetics shows that the decay of the “minor feature” (Fig. S50†), associated with the CS state 3[D+˙–A−˙], is an order of magnitude (∼5–20 times) shorter than that of the NDI-localized SOC triplet (broad dominant component of the TREPR spectra). This fast decay of polarization makes the TREPR signal of this feature much weaker compared to the dominant signal; in addition, we note that the polarization formed by different mechanisms can differ strongly in intensity. Moreover, it is noteworthy that the spectra of spin-correlated radical pairs are the result of the mutual cancelling of an absorptive and an emissive signal if |J| and |D| both are relatively small.78 This is exactly the case for Rho-Ph-NDI and Rho-PhMe-NDI; therefore, the minor 3[D+˙–A−˙] signal of the Rho-NDI spectrum is much more intensive compared to 3[D+˙–A−˙] signals in Rho-Ph-NDI and Rho-PhMe-NDI. Saying that, we stress that the weak intensity of the 3[D+˙–A−˙] TREPR signal compared to the NDI-localized signal should not necessarily be interpreted as a small contribution of the former pathway compared to the latter one.
Theoretical computations
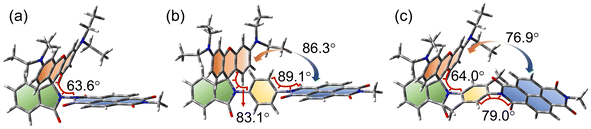
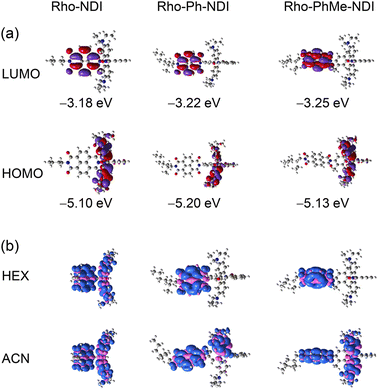
The ground state geometry of the compounds was optimized by DFT calculations (Fig. 10). For Rho-NDI, the dihedral angle between the π-conjugation planes of the xanthene moiety and NDI is 63.6°, which is slightly different from the molecular structure determined by the single crystal X-ray diffraction experiments (52.9°), and the difference probably results from the packing effect in the single crystal. The corresponding dihedral angles of Rho-Ph-NDI and Rho-PhMe-NDI between the xanthene and the NDI moieties are 86.3° and 76.9°, respectively, larger than that of Rho-NDI. For Rho-Ph-NDI, the dihedral angle of the xanthene moiety and the phenyl is 83.1°, and the dihedral angle between the phenyl and NDI moieties is 89.1°, which are all lager than that of Rho-PhMe-NDI (64.0° for xanthene and p-xylene and 79.0° for p-xylene and NDI, respectively). The centroid-to-centroid distances between the xanthene and the NDI moieties are 6.0 Å, 10.1 Å, and 9.9 Å, in Rho-NDI, Rho-Ph-NDI and Rho-PhMe-NDI, respectively.The frontier molecular orbitals (MOs) are presented in Fig. 11a. For the dyads, the highest occupied molecular orbital (HOMO) is localized on the Rho moiety and the lowest unoccupied molecular orbital (LUMO) is localized on the NDI moiety. There is negligible delocalization on two moieties for both MOs.
The electron spin density surfaces of the T1 state of the dyads in different polarity solvents were also studied (Fig. 11b). For Rho-NDI, the electron spin density of the T1 state is delocalized on the whole molecule in both TOL and ACN. These results are in agreement with the ns-TA spectral results that a CS state was observed for Rho-NDI. For Rho-Ph-NDI, the spin density of the T1 state is localized on the NDI moiety in low-polarity solvent HEX, but it is delocalized on the whole molecule in TOL and ACN, which is in agreement with the observation that the 3NDI state in HEX but a CS state was observed in TOL and ACN (Fig. 7). For Rho-PhMe-NDI, the spin density distribution was similar to that of Rho-Ph-NDI in HEX and ACN, which is also in accordance with the result of the ns-TA spectra.
Based on the above results, the energy diagrams of the dyads were constructed as shown in Schemes 2 and S1.† Upon photoexcitation of the NDI moiety, the singlet excited state of the dyads was populated. Then, fast ISC (<120 fs) produces an upper triplet state (Tn, whose energy approximately is equal to the energy of 1NDI*).
The CT process takes 186 fs for Rho-Ph-NDI and 175 fs for Rho-PhMe-NDI to generate the CS state. Concerning the low ΦCS of the triplet CS state (17–25%) for the dyads, the major pathway is CT from 1NDI* to generate the 1CS state, taking 285 fs. Subsequently, the process of 1CS → S0 competes with ISC from the 1CS state to the 3CS state to generate a long-lived 3CS state (0.13 μs in HEX for Rho-NDI). For Rho-Ph-NDI, the 3NDI* state with a lifetime of 1.1 μs was produced by CR in low-polarity solvent HEX due to the low-lying 3NDI* state, and the long-lived 3CS state was generated in TOL (0.37 μs (58%)/5.8 μs (42%)) and ACN (0.72 μs). For Rho-PhMe-NDI, a photophysical process similar to that of Rho-Ph-NDI was observed upon photoexcitation. In HEX, the CR process gives the 3LE state localized on the NDI moiety (2.0 μs). The 3CS state was produced with a lifetime of 0.63 μs (70%)/5.4 μs (30%) in TOL and 0.59 μs in ACN. For all dyads, a CS state with a long lifetime was generated by the electron spin control effect. Compared with Rho-NDI, the phenyl and p-xylene linkers of Rho-Ph-NDI and Rho-PhMe-NDI, leading to the weaker electronic coupling between the donor and acceptor, prolong the CS state lifetime.
Conclusions
In summary, we prepared three spiro electron donor–acceptor dyads, with the closed form of rhodamine (Rho) as the electron donor and naphthalenediimide (NDI) as the electron acceptor, to access the long-lived triplet charge separation (3CS) state based on the electron spin control effect. The distance and electronic coupling between the donor and acceptor are regulated by direct connection of Rho and NDI units for Rho-NDI or via an intervening phenyl or p-xylene linker between Rho and NDI units (Rho-Ph-NDI and Rho-PhMe-NDI, respectively). The dihedral angle (based on the optimized ground state geometry) between the xanthene and the NDI moieties is 63.6°, 86.3° and 76.9°, respectively. Compared to Rho-NDI, the longer distance between Rho and NDI moieties results in weaker electronic coupling for Rho-Ph-NDI and Rho-PhMe-NDI. Femtosecond transient absorption (fs-TA) spectra indicated that for all dyads fast ISC of the NDI unit takes less than 120 fs upon photoexcitation, and then charge separation (CS) from an upper 1NDI* and 3NDI* state takes hundreds of fs to generate the CS state. Nanosecond transient absorption (ns-TA) spectra show the formation of the 3CS state of Rho-NDI in different polarity solvents n-hexane (HEX), toluene (TOL) and acetonitrile (ACN). In HEX, the CS state lifetime is 0.13 μs, and the CS quantum yield (ΦCS) of the 3CS state is 25%. For Rho-Ph-NDI and Rho-PhMe-NDI, a triplet state localized on the NDI moiety (3NDI*) was observed in HEX, whereas long-lived CS states with a lifetime of 0.37 μs (58%)/5.8 μs (42%) for Rho-Ph-NDI and 0.63 μs (70.4%)/5.4 μs (29.6%) for Rho-PhMe-NDI were observed in TOL. The ΦCS of Rho-Ph-NDI was 19% and that of Rho-PhMe-NDI was 17%. The long-lived CS state of the dyads is based on the electron spin control effect, that is, to generate the final CS state with a triplet precursor (3NDI* state). With electron paramagnetic resonance (EPR) spectra, we prove the weak yet non-negligible electronic coupling between the Rho and NDI moieties for Rho-NDI. Time-resolved EPR (TREPR) spectra show that two transient species exist for the dyads upon photoexcitation. The dominant broader signals showing similar |D| and |E| values as compared to the triplet state of the native NDI are assigned to NDI-localized triplets formed via SOC-ISC. The weak and narrower signals in the middle of the spectra showing relatively small |J| and |D| values and |E| = 0 are assigned to the CS state. Rho-NDI features the largest value of dipolar interaction (|D| = 184 MHz) due to the smallest distance between Rho and NDI moieties compared with Rho-Ph-NDI (|D| = 39 MHz) and Rho-PhMe-NDI (|D| = 41 MHz). Moreover, for Rho-NDI, the time-dependent e,a → a,e phase change of the CS state spectrum is attributed to the population of the CS state from a singlet to a triplet state, respectively, which is evidence that the long-lived CS state results from the electron spin control effect.Experimental section
General method
All chemicals used in synthesis are analytically pure. Solvents for synthesis were dried before using. UV-vis spectra were recorded using a UV-2550 spectrophotometer (Shimadzu Ltd., Japan). Fluorescence emission spectra were recorded using an FS5 spectrofluorometer (Edinburgh Instruments Ltd., U.K.). Fluorescence lifetimes were recorded using an OB920 luminescence lifetime spectrometer (Edinburgh Instrument Ltd., U.K.), and a picosecond EPL laser was used for excitation. Fluorescence quantum yields (ΦF) were measured by using an absolute photoluminescence quantum yield spectrometer (Quantaurus-QY Plus C13534-11, Hamamatsu Ltd., Japan).Synthesis of Rho-NDI
Under a N2 atmosphere, compound 1 (37.9 mg, 0.10 mmol) and 4 (45.6 mg, 0.10 mmol) were dissolved in acetic acid (3 mL). The mixture was refluxed and stirred for 24 h. After the reaction was finished, the mixture was cooled to room temperature, and then ice water (10 mL) was added to the mixture. The pH of the resultant solution was adjusted to 8–9 by adding 1 M NaOH aqueous solution. A purple solid precipitate was formed and collected by filtration. The obtained solid was dried under vacuum at 50 °C. Then the crude product was purified by column chromatography (silica gel, EA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DCM = 1
DCM = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20, v/v) to give a grey solid (25.2 mg, yield: 31%). M.p. 124.1–124.6 °C. 1H NMR (400 MHz, DMSO-d6): δ 8.61 (d, J = 7.6 Hz, 2H), 8.36 (d, J = 7.6 Hz, 2H), 8.03 (d, J = 7.6 Hz, 1H), 7.85–7.76 (m, 2H), 7.42 (d, J = 7.4 Hz, 1H), 6.51 (d, J = 8.9 Hz, 2H), 6.42 (m, 2H), 6.03 (s, 2H), 4.01–3.94 (m, 2H), 3.31–3.21 (m, 8H), 1.84–1.82 (m, 1H), 1.36–1.24 (m, 8H), 1.02–1.00 (m, 12H), 0.88–0.84 (m, 6H). 13C NMR (125 MHz, DMSO-d6): δ 163.11, 162.69, 159.51, 153.82, 148.48, 148.38, 133.88, 130.79, 130.36, 130.03, 129.76, 129.28, 127.15, 126.47, 125.67, 125.08, 124.73, 123.18, 107.90, 104.77, 96.74, 67.22, 43.64, 43.58, 31.18, 29.95, 28.90, 28.62, 28.59, 23.36, 22.34, 21.99, 13.83, 12.13, 10.33. HRMS (EI), m/z: [M + H]+ calcd for C50H52N5O6: 818.3918; found: 818.3923.
20, v/v) to give a grey solid (25.2 mg, yield: 31%). M.p. 124.1–124.6 °C. 1H NMR (400 MHz, DMSO-d6): δ 8.61 (d, J = 7.6 Hz, 2H), 8.36 (d, J = 7.6 Hz, 2H), 8.03 (d, J = 7.6 Hz, 1H), 7.85–7.76 (m, 2H), 7.42 (d, J = 7.4 Hz, 1H), 6.51 (d, J = 8.9 Hz, 2H), 6.42 (m, 2H), 6.03 (s, 2H), 4.01–3.94 (m, 2H), 3.31–3.21 (m, 8H), 1.84–1.82 (m, 1H), 1.36–1.24 (m, 8H), 1.02–1.00 (m, 12H), 0.88–0.84 (m, 6H). 13C NMR (125 MHz, DMSO-d6): δ 163.11, 162.69, 159.51, 153.82, 148.48, 148.38, 133.88, 130.79, 130.36, 130.03, 129.76, 129.28, 127.15, 126.47, 125.67, 125.08, 124.73, 123.18, 107.90, 104.77, 96.74, 67.22, 43.64, 43.58, 31.18, 29.95, 28.90, 28.62, 28.59, 23.36, 22.34, 21.99, 13.83, 12.13, 10.33. HRMS (EI), m/z: [M + H]+ calcd for C50H52N5O6: 818.3918; found: 818.3923.
Synthesis of Rho-Ph-NDI
Under a N2 atmosphere, rhodamine B (120 mg, 0.27 mmol) was dissolved in dry DCM (7 mL), and then POCl3 (0.2 mL) was added dropwise. The solution was refluxed and stirred for 5 h. The solvent was evaporated under reduced pressure, and then crude product was dissolved in dry CH3CN (5 mL). The mixture was added dropwise to the solution of compound 2 (70.4 mg, 0.15 mmol) and Et3N (0.3 mL) in CH3CN (7 mL), and then the mixture was refluxed and stirred for 21 h. After the reaction was finished, the solvent was evaporated under reduced pressure, and the crude product was purified by column chromatography (silica gel, EA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DCM = 1
DCM = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, v/v) to give the product as a grey solid (72.4 mg, yield: 54%). M.p. 122.2–122.8 °C. 1H NMR (400 MHz, CDCl3): δ 8.77–8.72 (m, 4H), 8.01 (d, J = 7.6 Hz, 1H), 7.49–7.37 (m, 5H), 7.12–7.08 (m, 3H), 6.66 (s, 2H), 6.33 (d, J = 7.6 Hz, 3H), 4.20–4.09 (m, 2H), 3.33 (d, J = 7.6 Hz, 8H), 1.96–1.91 (m, 1H), 1.41–1.29 (m, 8H), 1.18–1.16 (m, 12H), 0.96–0.88 (m, 6H). 13C NMR (150 MHz, CDCl3): δ 168.26, 163.17, 162.85, 154.02, 152.76, 148.86, 137.92, 133.19, 131.26, 131.07, 129.62, 128.45, 126.99, 126.83, 126.71, 125.68, 123.75, 123.41, 108.33, 106.36, 98.00, 67.27, 44.65, 44.32, 37.94, 31.93, 30.71, 29.70, 29.66, 29.36, 28.63, 24.05, 23.04, 22.70, 14.07, 12.63, 10.60. HRMS (EI), m/z: [M]+ calcd for C56H55N5O6: 893.4152; found: 893.4141.
10, v/v) to give the product as a grey solid (72.4 mg, yield: 54%). M.p. 122.2–122.8 °C. 1H NMR (400 MHz, CDCl3): δ 8.77–8.72 (m, 4H), 8.01 (d, J = 7.6 Hz, 1H), 7.49–7.37 (m, 5H), 7.12–7.08 (m, 3H), 6.66 (s, 2H), 6.33 (d, J = 7.6 Hz, 3H), 4.20–4.09 (m, 2H), 3.33 (d, J = 7.6 Hz, 8H), 1.96–1.91 (m, 1H), 1.41–1.29 (m, 8H), 1.18–1.16 (m, 12H), 0.96–0.88 (m, 6H). 13C NMR (150 MHz, CDCl3): δ 168.26, 163.17, 162.85, 154.02, 152.76, 148.86, 137.92, 133.19, 131.26, 131.07, 129.62, 128.45, 126.99, 126.83, 126.71, 125.68, 123.75, 123.41, 108.33, 106.36, 98.00, 67.27, 44.65, 44.32, 37.94, 31.93, 30.71, 29.70, 29.66, 29.36, 28.63, 24.05, 23.04, 22.70, 14.07, 12.63, 10.60. HRMS (EI), m/z: [M]+ calcd for C56H55N5O6: 893.4152; found: 893.4141.
Synthesis of Rho-PhMe-NDI
Under a N2 atmosphere, rhodamine B (120 mg, 0.27 mmol) was dissolved in dry DCM (7 mL), and then POCl3 (0.2 mL) was added dropwise. The solution was refluxed and stirred for 5 h. The solvent was evaporated under reduced pressure, and then the crude product was dissolved in dry CH3CN (5 mL). The mixture was added to the solution of compound 3 (74.7 mg, 0.15 mmol) and Et3N (0.3 mL) in CH3CN (7 mL) dropwise under a N2 atmosphere, and then the mixture was refluxed and stirred for 21 h. After the reaction was finished, the solvent was evaporated under reduced pressure, and the crude product was purified by column chromatography (silica gel, EA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DCM = 1
DCM = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6, v/v) to give the product as a gray solid (70.6 mg, yield: 51%). M.p. 168.3–169.1 °C. 1H NMR (400 MHz, CDCl3): δ 8.80–8.77 (m, 4H), 8.07 (d, J = 6.2 Hz, 1H), 7.63–7.58 (m, 2H), 7.34–7.32 (m, 1H), 6.87 (s, 1H), 6.65–6.63 (m, 2H), 6.43–6.27 (m, 4H), 5.98 (s, 1H), 4.21–4.11 (m, 2H), 3.35–3.32 (m, 8H), 1.98–1.92 (m, 1H), 1.84 (s, 3H), 1.76 (s, 3H), 1.40–1.30 (m, 8H), 1.17–1.14 (m, 12H), 0.96–0.87 (m, 6H). 13C NMR (125 MHz, CDCl3): δ 165.74, 163.21, 162.12, 154.96, 153.94, 151.46, 148.95, 137.14, 135.32, 132.71, 131.40, 131.15, 131.05, 130.95, 129.95, 127.17, 126.89, 126.78, 124.46, 123.47, 108.20, 107.68, 107.30, 106.42, 98.01, 68.43, 44.65, 44.38, 37.95, 30.72, 29.70, 28.64, 24.06, 23.05, 18.07, 17.09, 14.08, 12.49, 10.62. HRMS (EI), m/z: [M]+ calcd for C58H59N5O6: 921.4465; found: 921.4487.
6, v/v) to give the product as a gray solid (70.6 mg, yield: 51%). M.p. 168.3–169.1 °C. 1H NMR (400 MHz, CDCl3): δ 8.80–8.77 (m, 4H), 8.07 (d, J = 6.2 Hz, 1H), 7.63–7.58 (m, 2H), 7.34–7.32 (m, 1H), 6.87 (s, 1H), 6.65–6.63 (m, 2H), 6.43–6.27 (m, 4H), 5.98 (s, 1H), 4.21–4.11 (m, 2H), 3.35–3.32 (m, 8H), 1.98–1.92 (m, 1H), 1.84 (s, 3H), 1.76 (s, 3H), 1.40–1.30 (m, 8H), 1.17–1.14 (m, 12H), 0.96–0.87 (m, 6H). 13C NMR (125 MHz, CDCl3): δ 165.74, 163.21, 162.12, 154.96, 153.94, 151.46, 148.95, 137.14, 135.32, 132.71, 131.40, 131.15, 131.05, 130.95, 129.95, 127.17, 126.89, 126.78, 124.46, 123.47, 108.20, 107.68, 107.30, 106.42, 98.01, 68.43, 44.65, 44.38, 37.95, 30.72, 29.70, 28.64, 24.06, 23.05, 18.07, 17.09, 14.08, 12.49, 10.62. HRMS (EI), m/z: [M]+ calcd for C58H59N5O6: 921.4465; found: 921.4487.
Single crystal X-ray diffraction
A single crystal of Rho-NDI was obtained via slow diffusion of HEX into THF solution of the compound. The single-crystal X-ray diffraction data for Rho-NDI were collected on a Bruker D8 Venture CMOS-based diffractometer (Mo-Kα radiation, λ = 0.71073 Å) using the SMART and SAINT programs. Final unit cell parameters were based on all observed reflections from the integration of all frame data. The structures were solved with the ShelXT structure solution program using intrinsic phasing and refined with the ShelXL refinement package using least squares minimization implanted in Olex2. All non-hydrogen atoms were refined anisotropically and the hydrogen atoms were located geometrically and fixed isotropic thermal parameters.Electrochemical studies
The cyclic voltammetry curves were recorded with a CHI610D electrochemical workstation (CHI instruments, Inc., Shanghai, China). The counter electrode is a platinum electrode; a glassy carbon electrode is the working electrode. The ferrocenium/ferrocene (Fc+/Fc) redox couple was used as an internal reference. Spectroelectrochemistry was performed using a 0.1 cm path length quartz electrochemical cell. A platinum gauze was the working electrode, and a platinum wire was the counter electrode. The potential was regulated with a CHI610D electrochemical workstation, and the spectra were recorded with an Agilent 8453 UV-vis spectroscopy system (Agilent Technologies Inc., USA). In both cases, Bu4N[PF6] was used as the supporting electrolyte, and the Ag/AgNO3 (0.1 M in ACN) couple was used as the reference electrode. Samples were deaerated with N2 for ca. 15 min before measurement, and the N2 atmosphere was kept during the measurement.Femtosecond transient absorption spectroscopy
Ultrafast pump probe spectroscopy measurements were performed on a Ti:sapphire laser amplifier-optical parametric amplifier system (Spectra Physics, Spitfre Pro XP, TOPAS) and a commercial setup of an ultrafast transient absorption spectrometer (Spectra Physics, Helios). The global fitting and target analysis were carried out with a sequential model using Glotaran software.79,80Nanosecond transient absorption spectroscopy
The nanosecond transient absorption spectra were studied on a LP920 laser flash photolysis spectrometer (Edinburgh Instruments, UK), and the signal was digitized with a Tektronix TDS 3012B oscilloscope. The samples were excited with a nanosecond pulsed laser (Quantel Nd: YAG nanosecond pulsed laser). The oxygen in the sample solution was removed by purging the solution with N2 for 15 minutes before measurement. The typical laser power is 65 mJ per pulse at 355 nm. The data were analyzed with L900 software.Steady-state and time-resolved electron paramagnetic resonance spectroscopy
Steady-state electron paramagnetic resonance (EPR) spectroscopy measurements were performed on an X-band (9.4 GHz) EPR ELEXSYS E500 spectrometer (Bruker, Germany) at 300 K. The radical anion of the compound was obtained by adding a reductant into deaerated N,N-dimethyl formamide (DMF), and then the EPR quartz tube was sealed with a H2/O2 torch under a N2 atmosphere. Time-resolved (TR) EPR measurements were performed on an X-band EPR spectrometer based on a Bruker EMX (Germany) at 80 K and 298 K. Samples were dissolved in TOL/MeTHF (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, v/v). The oxygen was removed with five freeze–pump–thaw cycles. The spectra were simulated using the EasySpin package based on Matlab.74
1, v/v). The oxygen was removed with five freeze–pump–thaw cycles. The spectra were simulated using the EasySpin package based on Matlab.74
DFT calculations
The geometries of the compounds, spin density surfaces, were optimized using density functional theory (DFT) with the B3LYP or CAM-B3LYP functional and 6-31G(d) basis set. There were no imaginary frequencies for all optimized structures. The triplet excited state energy of the compounds was calculated by time-dependent DFT (TDDFT) with the B3LYP functional and 6-31G(d) basis set based on the optimized ground-state geometry. The hyperfine coupling (HFC) constants were calculated using DFT with the UB3LYP functional and EPR-II basis set. All these calculations were performed with Gaussian 09.81Data availability
All relevant data are presented in the main text and ESI.†Author contributions
X. X., I. K. and P. M. contributed equally to this work.Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. Z. thanks the NSFC (U2001222), the State Key Laboratory of Fine Chemicals, the Fundamental Research Funds for the Central Universities (DUT22LAB610) and the Department of Education of the Xinjiang Uyghur Autonomous Region (Tian-Shan Chair Professor) for financial support. M. F. and I. K. thank the Ministry of Science and Higher Education of the Russian Federation (Grant No. 075-15-2020-779).Notes and references
- J. W. Verhoeven, J. Photochem. Photobiol., C, 2006, 7, 40–60 CrossRef CAS.
- J. W. Verhoeven, H. J. van Ramesdonk, M. M. Groeneveld, A. C. Benniston and A. Harriman, ChemPhysChem, 2005, 6, 2251–2260 CrossRef CAS PubMed.
- M. A. Filatov, Org. Biomol. Chem., 2020, 18, 10–27 RSC.
- D. M. Guldi, Chem. Commun., 2000, 321–327 RSC.
- N. Zarrabi, B. J. Bayard, S. Seetharaman, N. Holzer, P. Karr, S. Ciuti, A. Barbon, M. Di Valentin, A. van der Est, F. D'Souza and P. K. Poddutoori, Phys. Chem. Chem. Phys., 2021, 23, 960–970 RSC.
- S. Suzuki, M. Kozaki, K. Nozaki and K. Okada, J. Photochem. Photobiol., C, 2011, 12, 269–292 CrossRef CAS.
- S. Fukuzumi, Pure Appl. Chem., 2007, 79, 981–991 CrossRef CAS.
- E. Vauthey, ChemPhysChem, 2012, 13, 2001–2011 CrossRef CAS PubMed.
- J. H. Golden, L. Estergreen, T. Porter, A. C. Tadle, M. R. Daniel Sylvinson, J. W. Facendola, C. P. Kubiak, S. E. Bradforth and M. E. Thompson, ACS Appl. Energy Mater., 2018, 1, 1083–1095 CrossRef CAS.
- H. Song, H. Zhao, Y. Guo, A. M. Philip, Q. Guo, M. Hariharan and A. Xia, J. Phys. Chem. C, 2020, 124, 237–245 CrossRef CAS.
- S. Guo, K.-K. Chen, R. Dong, Z.-M. Zhang, J. Zhao and T.-B. Lu, ACS Catal., 2018, 8, 8659–8670 CrossRef CAS.
- C. K. Prier, D. A. Rankic and D. W. MacMillan, Chem. Rev., 2013, 113, 5322–5363 CrossRef CAS PubMed.
- D. P. Hari and B. König, Chem. Commun., 2014, 50, 6688–6699 RSC.
- D. Ravelli, M. Fagnoni and A. Albini, Chem. Soc. Rev., 2013, 42, 97–113 RSC.
- L. Shi and W. Xia, Chem. Soc. Rev., 2012, 41, 7687–7697 RSC.
- H. Imahori, Y. Kobori and H. Kaji, Acc. Mater. Res., 2021, 2, 501–514 CrossRef CAS.
- K. Ohkubo, H. Kotani, J. Shao, Z. Ou, K. M. Kadish, G. Li, R. K. Pandey, M. Fujitsuka, O. Ito, H. Imahori and S. Fukuzumi, Angew. Chem., Int. Ed., 2004, 43, 853–856 CrossRef CAS PubMed.
- T. Higashino, T. Yamada, M. Yamamoto, A. Furube, N. V. Tkachenko, T. Miura, Y. Kobori, R. Jono, K. Yamashita and H. Imahori, Angew. Chem., Int. Ed., 2016, 55, 629–633 CrossRef CAS PubMed.
- A. Karimata, S. Suzuki, M. Kozaki, K. Kimoto, K. Nozaki, H. Matsushita, N. Ikeda, K. Akiyama, D. Kosumi, H. Hashimoto and K. Okada, J. Phys. Chem. A, 2014, 118, 11262–11271 CrossRef CAS PubMed.
- D. I. Schuster, P. Cheng, P. D. Jarowski, D. M. Guldi, C. Luo, L. Echegoyen, S. Pyo, A. R. Holzwarth, S. E. Braslavsky, R. M. Williams and G. Klihm, J. Am. Chem. Soc., 2004, 126, 7257–7270 CrossRef CAS PubMed.
- K.-Y. Chen, C.-C. Hsieh, Y.-M. Cheng, C.-H. Lai, P.-T. Chou and T. J. Chow, J. Phys. Chem. A, 2006, 110, 12136–12144 CrossRef CAS PubMed.
- H. Imahori, D. M. Guldi, K. Tamaki, Y. Yoshida, C. Luo, Y. Sakata and S. Fukuzumi, J. Am. Chem. Soc., 2001, 123, 6617–6628 CrossRef CAS PubMed.
- H. Imahori, Y. Sekiguchi, Y. Kashiwagi, T. Sato, Y. Araki, O. Ito, H. Yamada and S. Fukuzumi, Chem.–Eur. J., 2004, 10, 3184–3196 CrossRef CAS PubMed.
- Y. Hou, X. Zhang, K. Chen, D. Liu, Z. Wang, Q. Liu, J. Zhao and A. Barbon, J. Mater. Chem. C, 2019, 7, 12048–12074 RSC.
- S. Suzuki, R. Sugimura, M. Kozaki, K. Keyaki, K. Nozaki, N. Ikeda, K. Akiyama and K. Okada, J. Am. Chem. Soc., 2009, 131, 10374–10375 CrossRef CAS PubMed.
- B. Geiβ and C. Lambert, Chem. Commun., 2009, 1670–1672 Search PubMed.
- S.-H. Lee, C. T.-L. Chan, K. M.-C. Wong, W. H. Lam, W.-M. Kwok and V. W.-W. Yam, J. Am. Chem. Soc., 2014, 136, 10041–10052 CrossRef CAS PubMed.
- A. Karimata, H. Kawauchi, S. Suzuki, M. Kozaki, N. Ikeda, K. Keyaki, K. Nozaki, K. Akiyama and K. Okada, Chem. Lett., 2013, 42, 794–796 CrossRef CAS.
- X. Zhang, X. Chen and J. Zhao, Dalton Trans., 2021, 50, 59–67 RSC.
- J. Hankache and O. S. Wenger, Chem. Commun., 2011, 47, 10145–10147 RSC.
- Z. E. X. Dance, Q. Mi, D. W. McCamant, M. J. Ahrens, M. A. Ratner and M. R. Wasielewski, J. Phys. Chem. B, 2006, 110, 25163–25173 CrossRef CAS PubMed.
- M. T. Colvin, R. Carmieli, T. Miura, S. Richert, D. M. Gardner, A. L. Smeigh, S. M. Dyar, S. M. Conron, M. A. Ratner and M. R. Wasielewski, J. Phys. Chem. A, 2013, 117, 5314–5325 CrossRef CAS PubMed.
- S. Chakraborty, T. J. Wadas, H. Hester, R. Schmehl and R. Eisenberg, Inorg. Chem., 2005, 44, 6865–6878 CrossRef CAS PubMed.
- D. Anglos, V. Bindra and A. Kuki, J. Chem. Soc., Chem. Commun., 1994, 213–215 RSC.
- S. Fukuzumi, H. Kotani, K. Ohkubo, S. Ogo, N. V. Tkachenko and H. Lemmetyinen, J. Am. Chem. Soc., 2004, 126, 1600–1601 CrossRef CAS PubMed.
- S. I. van Dijk, C. P. Groen, F. Hartl, A. M. Brouwer and J. W. Verhoeven, J. Am. Chem. Soc., 1996, 118, 8425–8432 CrossRef CAS.
- L. Hviid, A. M. Brouwer, M. N. Paddon-Row and J. W. Verhoeven, ChemPhysChem, 2001, 2, 232–235 CrossRef CAS PubMed.
- M. Murakami, K. Ohkubo, T. Nanjo, K. Souma, N. Suzuki and S. Fukuzumi, ChemPhysChem, 2010, 11, 2594–2605 CrossRef CAS PubMed.
- D. Liu, A. M. El-Zohry, M. Taddei, C. Matt, L. Bussotti, Z. Wang, J. Zhao, O. F. Mohammed, M. Di Donato and S. Weber, Angew. Chem., Int. Ed., 2020, 59, 11591–11599 CrossRef CAS PubMed.
- D. J. Gibbons, A. Farawar, P. Mazzella, S. Leroy-Lhez and R. M. Williams, Photochem. Photobiol. Sci., 2020, 19, 136–158 CrossRef CAS PubMed.
- X. Chen, A. A. Sukhanov, Y. Yan, D. Bese, C. Bese, J. Zhao, V. K. Voronkova, A. Barbon and H. G. Yaglioglu, Angew. Chem., Int. Ed., 2022, e202203758 CAS.
- M. Hu, A. A. Sukhanov, X. Zhang, A. Elmali, J. Zhao, S. Ji, A. Karatay and V. K. Voronkova, J. Phys. Chem. B, 2021, 125, 4187–4203 CrossRef CAS PubMed.
- Y. Cheng, L. Li, F. Wei and K. M.-C. Wong, Inorg. Chem., 2018, 57, 6439–6446 CrossRef CAS PubMed.
- G. P. Wiederrecht, W. A. Svec, M. R. Wasielewski, T. Galili and H. Levanon, J. Am. Chem. Soc., 2000, 122, 9715–9722 CrossRef CAS.
- Y. Mori, Y. Sakaguchi and H. Hayashi, J. Phys. Chem. A, 2002, 106, 4453–4467 CrossRef CAS.
- N. Pearce, E. S. Davies, R. Horvath, C. R. Pfeiffer, X.-Z. Sun, W. Lewis, J. McMaster, M. W. George and N. R. Champness, Phys. Chem. Chem. Phys., 2018, 20, 752–764 RSC.
- N. J. Turro, V. Ramamurthy and J. C. Scaiano, Principles of molecular photochemistry: an introduction, University Science Books, 2009 Search PubMed.
- Z. Wang, J. Zhao, M. Di Donato and G. Mazzone, Chem. Commun., 2019, 55, 1510–1513 RSC.
- X. Xiao, J. Pang, A. A. Sukhanov, Y. Hou, J. Zhao, M.-D. Li and V. K. Voronkova, J. Chem. Phys., 2020, 153, 184312 CrossRef CAS PubMed.
- S. Sasaki, K. Hattori, K. Igawa and G.-i. Konishi, J. Phys. Chem. A, 2015, 119, 4898–4906 CrossRef CAS PubMed.
- G. Tang, A. A. Sukhanov, J. Zhao, W. Yang, Z. Wang, Q. Liu, V. K. Voronkova, M. Di Donato, D. Escudero and D. Jacquemin, J. Phys. Chem. C, 2019, 123, 30171–30186 CrossRef CAS.
- X. Zhang, X. Liu, M. Taddei, L. Bussotti, I. Kurganskii, M. Li, X. Jiang, L. Xing, S. Ji, Y. Huo, J. Zhao, M. Di Donato, Y. Wan, Z. Zhao and M. V. Fedin, Chem.–Eur. J., 2022, 28, e202200510 CAS.
- X. Cui, J. Zhao, Z. Lou, S. Li, H. Wu and K.-l. Han, J. Org. Chem., 2015, 80, 568–581 CrossRef CAS PubMed.
- L. Yuan, W. Lin, Y. Xie, B. Chen and S. Zhu, J. Am. Chem. Soc., 2012, 134, 1305–1315 CrossRef CAS PubMed.
- X. Zhang, L. Chen, Z. Huang, N. Ling and Y. Xiao, Chem.–Eur. J., 2021, 27, 3688–3693 CrossRef CAS PubMed.
- K. Chen, J. Zhao, X. Li and G. G. Gurzadyan, J. Phys. Chem. A, 2019, 123, 2503–2516 CrossRef CAS PubMed.
- H. Matsuoka, Y. Shibano, I. Akimoto and Y. Kanzaki, Bull. Chem. Soc. Jpn., 2022, 95, 59–63 CrossRef CAS.
- R. Ziessel, B. D. Allen, D. B. Rewinska and A. Harriman, Chem.–Eur. J., 2009, 15, 7382–7393 CrossRef CAS PubMed.
- H. Imahori, K. Hagiwara, M. Aoki, T. Akiyama, S. Taniguchi, T. Okada, M. Shirakawa and Y. Sakata, J. Am. Chem. Soc., 1996, 118, 11771–11782 CrossRef CAS.
- S. Guha, F. S. Goodson, S. Roy, L. J. Corson, C. A. Gravenmier and S. Saha, J. Am. Chem. Soc., 2011, 133, 15256–15259 CrossRef CAS PubMed.
- O. Yushchenko, G. Licari, S. Mosquera-Vazquez, N. Sakai, S. Matile and E. Vauthey, J. Phys. Chem. Lett., 2015, 6, 2096–2100 CrossRef CAS PubMed.
- A. C. Marco Montalti, L. Prodi and M. Teresa Gandolfi, Handbook of Photochemistry, CRC Press, Boca Raton, 2006 Search PubMed.
- C. Luo, D. M. Guldi, H. Imahori, K. Tamaki and Y. Sakata, J. Am. Chem. Soc., 2000, 122, 6535–6551 CrossRef CAS.
- S. Guha and S. Saha, J. Am. Chem. Soc., 2010, 132, 17674–17677 CrossRef CAS PubMed.
- S. Guha, F. S. Goodson, L. J. Corson and S. Saha, J. Am. Chem. Soc., 2012, 134, 13679–13691 CrossRef CAS PubMed.
- V. V. Roznyatovskiy, D. M. Gardner, S. W. Eaton and M. R. Wasielewski, Org. Lett., 2014, 16, 696–699 CrossRef CAS PubMed.
- Y. Hou, I. Kurganskii, A. Elmali, H. Zhang, Y. Gao, L. Lv, J. Zhao, A. Karatay, L. Luo and M. Fedin, J. Chem. Phys., 2020, 152, 114701 CrossRef CAS PubMed.
- K. Chen, I. V. Kurganskii, X. Zhang, A. Elmali, J. Zhao, A. Karatay and M. V. Fedin, Chem.–Eur. J., 2021, 27, 7572–7587 CrossRef CAS PubMed.
- N. Rehmat, I. V. Kurganskii, Z. Mahmood, Q. L. Guan, J. Zhao, Y. H. Xing, G. G. Gurzadyan and M. V. Fedin, Chem.–Eur. J., 2021, 27, 5521–5535 CrossRef CAS PubMed.
- M. T. Colvin, A. B. Ricks, A. M. Scott, A. L. Smeigh, R. Carmieli, T. Miura and M. R. Wasielewski, J. Am. Chem. Soc., 2011, 133, 1240–1243 CrossRef CAS PubMed.
- M. T. Colvin, A. B. Ricks, A. M. Scott, D. T. Co and M. R. Wasielewski, J. Phys. Chem. A, 2012, 116, 1923–1930 CrossRef CAS PubMed.
- T. Fukuju, H. Yashiro, K. Maeda, H. Murai and T. Azumi, J. Phys. Chem. A, 1997, 101, 7783–7786 CrossRef CAS.
- C. D. Buckley, D. A. Hunter, P. J. Hore and K. A. McLauchlan, Chem. Phys. Lett., 1987, 135, 307–312 CrossRef CAS.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- K. Hasharoni, H. Levanon, S. R. Greenfield, D. J. Gosztola, W. A. Svec and M. R. Wasielewski, J. Am. Chem. Soc., 1995, 117, 8055–8056 CrossRef CAS.
- K. Hasharoni, H. Levanon, S. R. Greenfield, D. J. Gosztola, W. A. Svec and M. R. Wasielewski, J. Am. Chem. Soc., 1996, 118, 10228–10235 CrossRef CAS.
- R. Carmieli, A. L. Smeigh, S. M. Mickley Conron, A. K. Thazhathveetil, M. Fuki, Y. Kobori, F. D. Lewis and M. R. Wasielewski, J. Am. Chem. Soc., 2012, 134, 11251–11260 CrossRef CAS PubMed.
- M. D. E. Forbes, L. E. Jarocha, S. Sim and V. F. Tarasov, Adv. Phys. Org. Chem., 2013, 47, 1–83 CrossRef CAS.
- I. H. M. van Stokkum, D. S. Larsen and R. van Grondelle, Biochim. Biophys. Acta, Bioenerg., 2004, 1657, 82–104 CrossRef CAS PubMed.
- J. Snellenburg, S. Laptenok, R. Seger, K. Mullen, I. Van Stokkum, J. J. Snellenburg, S. Laptenok, R. Seger, K. M. Mullen and I. H. M. van Stokkum, J. Stat. Software, 2012, 49, 1–22 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian, Gaussian 09 (Revision A.01), Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: General experimental methods, synthesis of compounds, molecular structure characterization, X-ray crystallographic data, computational details and additional spectra. CCDC 2190442. For ESI and crystallographic data in CIF or other electronic format see https://doi.org/10.1039/d2sc04258d |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |