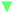Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electrostatic potential-derived charge: a universal OER performance descriptor for MOFs†
Xiangdong
Xue
 a,
Hongyi
Gao
a,
Hongyi
Gao
 *a,
Jiangtao
Liu
c,
Ming
Yang
d,
Shihao
Feng
a,
Zhimeng
Liu
a,
Jing
Lin
*a,
Jiangtao
Liu
c,
Ming
Yang
d,
Shihao
Feng
a,
Zhimeng
Liu
a,
Jing
Lin
 a,
Jitti
Kasemchainan
e,
Linmeng
Wang
a,
Qilu
Jia
a and
Ge
Wang
*ab
a,
Jitti
Kasemchainan
e,
Linmeng
Wang
a,
Qilu
Jia
a and
Ge
Wang
*ab
aBeijing Advanced Innovation Center for Materials Genome Engineering, Beijing Key Laboratory of Function Materials for Molecule & Structure Construction, School of Materials Science and Engineering, University of Science and Technology Beijing, Beijing, 100083, PR China. E-mail: hygao@ustb.edu.cn; gewang@ustb.edu.cn
bShunde Graduate School, University of Science and Technology Beijing, Shunde, 528399, PR China
cState Key Laboratory of Advanced Chemical Power Sources, Guizhou Meiling Power Sources Co., Ltd., Zunyi, Guizhou 563003, PR China
dDepartment of Applied Physics, The Hong Kong Polytechnic University, Hung Hom, Hong Kong SAR, China
eDepartment of Chemical Technology, Chulalongkorn University, Bangkok 10330, Thailand
First published on 18th October 2022
Abstract
Metal–organic frameworks (MOFs) provide opportunities for the design of high-efficiency catalysts attributed to their high compositional and structural tunability. Meanwhile, the huge number of MOFs poses a great challenge to experimental-intensive development of high-performance functional applications. By taking the computationally feasible and structurally representative trigonal prismatic secondary building units (SBUs) of MOFs as the entry point, we introduce a descriptor-based approach for designing high-performance MOFs for the oxygen evolution reaction (OER). The electrostatic potential-derived charge (ESPC) is identified as a robust and universal OER performance descriptor of MOFs, showing a distinct linear relationship with the onset potentials of OER elemental steps. Importantly, we establish an ESPC-based physical pattern of active site–intermediate binding strength, which interprets the rationality of ESPC as an OER performance descriptor. We further reveal that the SBUs with Ni/Cu as active site atoms while Mn/Fe/Co/Ni as spectator atoms have excellent OER activity through the variation pattern of ESPC along with metal composition. The universal correlation between ESPC and OER activity provides a rational rule for designing high-performance MOF-based OER electrocatalysts and can be easily extended to design functional MOFs for a rich variety of catalytic applications.
1. Introduction
Metal–organic frameworks (MOFs) are a class of materials assembled from SBUs and organic ligands according to a certain topological structure.1,2 Owing to their nature of large specific surface area, penetrating pore structures, abundant and atomically dispersed coordination unsaturated active sites (CUSs), flexible tunability of the composition and structure, etc., these materials have been extensively studied in molecular storage/sieving,3–7 catalysis,8–10 sensors,11–13 batteries,14,15 and phase transitions.16–18 During the past six years, over 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MOFs have been collected in the Cambridge Structural Database (CSD)19,20 and the number keeps on increasing dramatically. This, however, makes it challenging for conventional trial-and-error experiments to identify promising MOFs for high-performance functional applications.
000 MOFs have been collected in the Cambridge Structural Database (CSD)19,20 and the number keeps on increasing dramatically. This, however, makes it challenging for conventional trial-and-error experiments to identify promising MOFs for high-performance functional applications.
The development of high-throughput computational methods has provided a solution to screen high-performance MOFs efficiently and effectively.21–31 Many studies have focused on the screening of gas storage/sieving,28–30 using computationally cheap characterization for the relevant geometry (pore size distributions, pore diameters, surface area, pore volume, etc.) and molecular-level Grand Canonical Monte Carlo (GCMC)/molecular dynamics (MD) simulations. These efforts have greatly contributed to the development of high-performance MOFs by screening promising materials from tens of thousands or even half a million MOF structures. However, high-throughput computational screening is also called “brute-force screening,”32 meaning that it can only handle low-cost molecular-level simulations. Even with high-performance supercomputers, it is still difficult to deal with expensive electronic-level calculations. There are few electronic-level screening efforts involving specific catalytic reaction such as photocatalysis27 or thermocatalysis.22–26 Due to the costly quantum mechanics-based computational approach, the electronic structure or reaction barrier can only be calculated for a few tens to hundreds of MOFs even using an optimized workflow.
Herein, in order to break the barrier of traditional “brute-force screening” and achieve rational design of MOFs with little computational cost, we develop a promising descriptor-based pathway. Specifically, the pivotal reaction driving the transformation of energy structure, like the OER, was chosen as the target reaction, and the secondary building units (SBUs) that play a decisive role in catalytic performance were selected as a rational simplified scheme for MOFs. In particular, we selected the widespread trigonal prismatic SBUs possessing a small number of atoms as a case, whose characteristics such as universal atomic 5-coordination configuration and 3-metal coupling endow them with excellent transferability and compositional tunability, making them an ideal platform for mining descriptive models. With monometallic SBUs, we identify ESPC as a highly accurate, instructive, transferable, and readily available OER performance descriptor. The descriptor was then employed to predict the OER activity of SBUs with bimetallic composition, and the accuracy of the descriptive model was improved using DFT-derived data. Furthermore, by correlating ESPC with OER performance of SBUs with different structures and compositions, a universal linear scaling relationship between ESPC and OER performance was identified, illustrating the universality of ESPC as an OER performance descriptor. For the purpose of using ESPC to guide the actual experimental synthesis, we deeply analyzed the relationship between ESPC and bond order as well as band structure, established an ESPC-based physical pattern of active site–intermediate binding strength. Moreover, the variation regularity of ESPC with metal composition was revealed, which demonstrated that the MOFs with Ni/Cu as active sites and Mn/Fe/Co/Ni as spectator atoms have excellent OER activity.
2. Methods
Spin-polarized density functional theory (DFT) calculations were performed by using the linear combination of atomic orbitals (LCAO) method embedded in DMol3. A polarized basis set of double numerical polarization (DNP)33 was employed to ensure the computational accuracy as well as the descriptions of the hydrogen bond. The electronic exchange–correlation effect was described by the Perdew–Burke–Ernzerhof (PBE)34 functional of general gradient approximation (GGA) level. The large orbital cutoff of 6 Å was chosen for good convergence, and TS35 method was adopted for a long-range van der Waals (vdW) correction. For description of the electron–ion interaction, the DFT-based relativistic semi-core pseudopotentials (DSPPs)36 were adopted. For reliable adsorption energy, the basis set superposition error (BSSE) correction37 was adopted, by specifying the catalysts as Counterpoise 1 and adsorbed O-contained species as Counterpoise 2. During the geometric optimizations, all atoms were allowed to relax until the models reach the ground state without any imaginary frequency. The convergence criteria for self-consistent field (SCF) iteration and the max force on each atom were 10−8 Ha and 0.001 Ha Å−1, respectively.The method for bond order (BO) calculation used in this work was given by Mayer in 1986:38
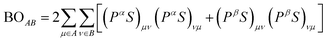 | (1) |
The widely studied four-electron mechanism is used to simulate the entire OER process:39,40
| * + OH− → HO* + e−, ΔG1 |
| HO* + OH− → O* + H2O + e−, ΔG2 |
| O* + OH− → HOO* + e−, ΔG3 |
| HOO* + OH− → * + H2O + O2 + e−, ΔG4 |
| ΔG = ΔE + ΔZPE − TΔS |
Based on the above Gibbs energy results, the Gibbs energy difference of the potential-limiting step is defined as follows:
| ΔGMAX = max{ΔG1, ΔG2, ΔG3, ΔG4} |
3. Results and discussion
3.1 Construction of an ESPC-based OER model
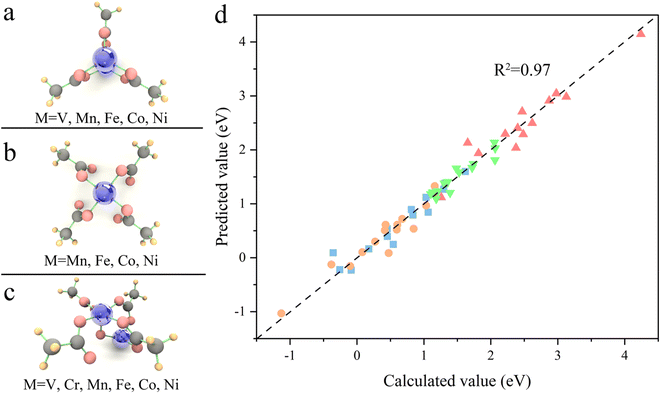
Due to the limitations imposed by the large number of atoms in MOFs for periodic DFT calculations, SBUs, which play a decisive role in the catalytic process, are usually selected as an alternative to MOFs for calculation.46,47 Among them, trigonal prismatic SBUs are a common class of SBUs (Fig. 1), whose few atoms make themselves feasible to be implemented in high-throughput calculations. In addition, the strong interaction of three metal atoms connected by a μ3 oxygen atom facilitates the fine-tuning of electronic structure by component orthogonalization. Moreover, the 6-coordinated metal atoms can readily desorb solvent molecules upon activation to form 5-coordinated unsaturated active sites that are widely present in MOFs, making the calculation-derived conclusions of such SBUs highly transferable. Therefore, we chose the trigonal prismatic SBUs as an entry point to study the general principles for the design of MOFs with high OER performance. In this study, the SBUs with monometallic components are labeled as Ma (Ma = V, Cr, Mn, Fe, Co, and Ni), and the SBUs with bimetallic components are labeled as Ma2Mb1 (Ma = V, Cr, Mn, Fe, Co and Ni; Mb = V, Cr, Mn, Fe, Co, Ni, and Cu). It is important to emphasize that we do not conduct specific screening, but rather pay attention to the descriptors of the OER onset potential by a proper amount of calculations. An adequate linear fitting requires data points with large variability, so we use Mb as the active site here since in Ma2Mb1 systems, the ESP-derived charge (ESPC) of Mb is expected to be more variable than that of Ma relative to the monometallic counterpart (due to the relatively low contents of Mb, more like the dopant).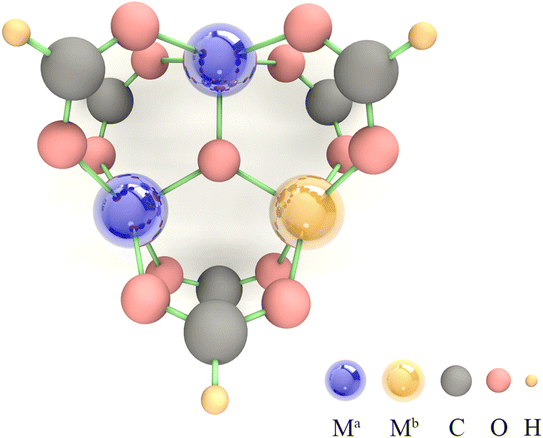 | ||
| Fig. 1 The model of the trigonal prismatic secondary building unit used in the DFT calculations, where Ma = V, Cr, Mn, Fe, Co, and Ni; Mb = V, Cr, Mn, Fe, Co, Ni, and Cu. | ||
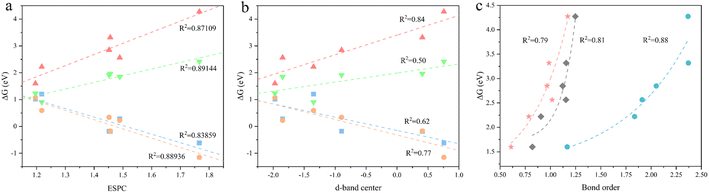
To obtain an accurate OER descriptive model, we comprehensively considered three most promising descriptors. They are electrostatic potential-derived charge (ESPC), density of states (DOS), and bond order (BO), which represents the spatial distribution of electrons, the energy distribution of electrons, and the chemical bond strength, respectively. Among them, we calculated the d-band center from the DOS for the convenience of quantification. For simplicity, we consider only one descriptor to correlate OER onset potentials. Additionally, we focus on the accuracy of the descriptors, while taking into account transferability, instructiveness, and computational simplicity. By correlating the Gibbs energy difference of the four primitive steps (target quantities) with the above candidates, we find that both ESPC and d-band center exhibit a linear scaling relationship with the target quantities with different accuracy (Fig. 2a and b). However, the BO shows an exponential scaling relationship with the target quantities, causing its predictive capacity drop sharply at larger values (Fig. 2c and S1†). Furthermore, the BO describing the binding strength of the adsorbed molecule to the active site cannot indicate the intrinsic properties of the material, leading to its poor transferability and instructiveness. Therefore, the BO was first excluded. For the d-band center, it requires expensive DOS calculation and may not be generalized well for MOFs possessing both metallic and semiconducting nature due to the common underestimation of the bandgap,48 and thus, it is not satisfactory in terms of transferability and computational simplicity. In contrast, ESPC can be obtained by fitting the charge distribution near the atom, which is computationally feasible. In addition, it is a physical quantity describing the properties of the atom with desirable transferability and instructiveness. Therefore, ESPC was finally chosen as the OER performance descriptor, and the ESPC-based OER descriptive model derived from six monometallic trigonal prismatic SBUs (Fig. 2a) is as follows:
| ΔG1 = −3.19ESPC + 4.81 |
| ΔG2 = −3.44ESPC + 5.07 |
| ΔG3 = 4.14ESPC − 3.12 |
| ΔG4 = 2.48ESPC − 1.84 |
3.2 Model testing and optimization
The OER performance of the SBUs with bimetallic composition was predicted by the proposed model and the results were validated by DFT calculations. The minor difference between the predicted values and the validated ones indicates the great accuracy (R2 ≈ 0.87) of the descriptive model (Fig. 3a). Furthermore, the improved model shows similar predictive ability (R2 ≈ 0.90) after being fed with the DFT data of SBUs with bimetallic composition (Fig. 3b), proving the effectiveness of fitting scaling relations using monometallic SBUs. In addition, the ESPC provides an excellent description (average R2 > 0.90) of the OER performance in the case of changing the active atoms while keeping the spectator atoms consistent (Fig. 4), which is of great significance for studying the doping and active site implanting systems. Moreover, the ESPC could also rationalise the experimentally tested OER activity well (Fig. S3 and S4†). The correlations between them are similar to the predictive model raised here, indicating the potential for practical applications.Based on the proposed model, the strong linear scaling relationships between ΔGi (i = 1, 2, 3, 4) and the ESPC are shown in Fig. 5 and Table S1,† where ΔG1 and ΔG2 are negatively correlated with the ESPC, while ΔG3 and ΔG4 show the opposite trends. This means that there is an onset potential minimum near the intersection of the four prediction lines. When the ESPC is less than 1.1, the height of the nearly coincident ΔG1 and ΔG2 prediction lines is higher than that of ΔG3 and ΔG4, indicating that the potential limiting step (PLS) is step 1 or 2 (* + H2O → HO* + H+ + e− or HO* + H2O → O* + H+ + e−), and when the ESPC is larger than 1.1, the height of the prediction line of ΔG3 is the highest, implying that the potential limiting step is step 3 (O* + H2O → HOO* + H+ + e−).
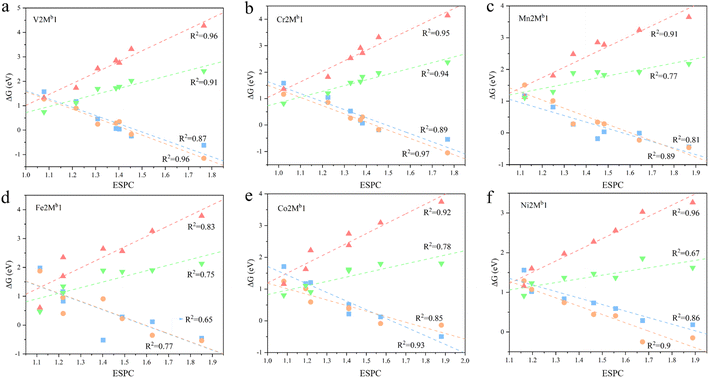
Transferability is another important criterion for evaluating a descriptive model, especially for MOFs with diverse compositions and structures, as designing material often involves adjusting composition and structure. Therefore, the ESPC was further employed to predict the OER performance of the SBUs with typical 3-, 4-, and 5-coordinated configurations and representative metals (Fig. 6a–c). Excitingly, the ESPC presents a near-perfect prediction (R2 = 0.97) of the OER performance of the catalysts (Fig. 6d and Table S2†), demonstrating the general applicability of the ESPC-based descriptive model. It is pointed out that the prediction accuracy of ESPC for OER activity of typical SBUs appears to be higher than that of trigonal prismatic SBUs. This is because we introduced component orthogonality in trigonal prismatic SBUs to accurately capture the effect of bimetallic coupling on the OER activity. And as can be seen in Fig. 4, in the case of fixed Ma metals, the prediction accuracy of the model for OER activity of the trigonal prismatic SBUs is similar to that of the typical SBUs.
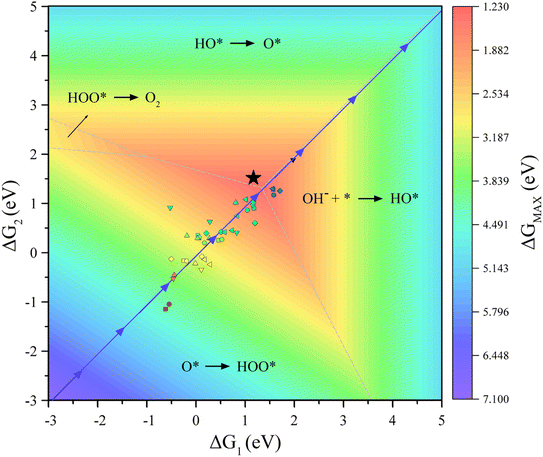
In addition, our goal is to find an optimal solution over a vast material space. To validate the proposed model, a 3D volcano plot of OER activity is constructed (Fig. 7, for more details see Fig. S2†), which shows the evolution trend of the OER performance under the ESPC guidance (blue arrows). It can be clearly seen that the predicted line just passes the top of the mountain, indicating that tuning the ESPC is a desirable option for designing MOFs with high OER performance.
3.3 Correlation analysis of ESPC and metal combination
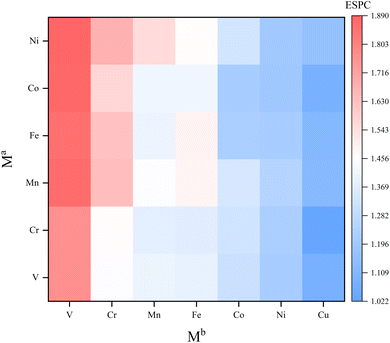
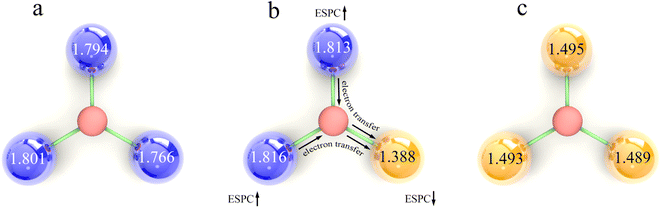
Uncovering the relationship between ESPC of the active site and metal composition is essential to fully utilize the descriptive model to guide the synthesis of high-performance materials. In view of this, we mapped the ESPC of active site onto the metal composition matrix (Fig. 8 and Table S3†). The result shows that the ESPC varies in a wide range of 1.0–1.9. When keeping the Ma metal unchanged, the ESPC varies with the Mb metals as following sequence V > Cr > Mn > Fe > Co > Ni > Cu. In addition, when Mb is fixed, the ESPC changes slightly with the difference of Ma metals, and the overall trend shifts towards larger values with the increase of the effective nuclear charge of Ma. The matrix shows that the ESPC is in the best interval when the spectator atoms are Mn/Fe/Co/Ni, and the active site atom is Cu or Ni. Among them, Ni atoms have been widely reported as OER active sites in various catalytic materials,49–51 such as carbon-based materials, transition metal sulfides and MOFs. This phenomenon is consistent with the finding in this study. While very few studies report Cu as the active site for OER, thus, results in this study may shed light on the design of future Cu-based OER catalysts. More importantly, by analyzing the related experimental studies,52–58 we obtained the OER performance ranking for MOFs containing different elements (i.e., Ni > Co > Fe, Fe > V, Fe > Mn), which is consistent with the findings of our results, demonstrating that the model proposed our work can capture the variation patterns of OER performance along with metal compositions.The variation trend of ESPC with metal composition can be explained by the difference of the element's electronegativity. For atoms in the same row of the periodic table, the distance between the valence electrons and the nucleus is similar. A bigger effective nuclear charge leads to stronger attraction to valence electrons, and the atom is less likely to lose electrons.59,60 In the single-metal systems, metals with larger electronegativity have higher electron retention and smaller ESPC (Fig. 9a and c). In bimetallic composition systems, the valence electrons of three metal atoms are redistributed through the μ3-O, and the electrons will flow to the atoms with larger electronegativity. For example, for atoms with less effective nuclear charge (like V), when they are combined with atoms with more effective nuclear charge (like Fe), their valence electrons tend to migrate to the counterpart, making the ESPC of Fe atoms in V2Fe1 less than that of Fe in the SBU with single Fe composition. In contrast, the ESPC of V atoms in V2Fe1 is larger than that of the V in the SBU with single V composition (Fig. 9b). It should be noted that this phenomenon is not distinct for systems in which Co, Ni, and Cu as Mb, probably due to their “harder” electron cloud stemming from relatively larger electronegativity.
3.4 Interpretability of ESPC as an OER activity descriptor
Since the ΔGtotal of the OER is a constant (4.92 eV), the ΔGi (i = 1, 2, 3, 4) actually has a trade-off relationship. Taking V, Co2Cu1 and Mn2Cu1 as examples (Fig. 10), high bonding strength of V atoms with OH and O species induces excessive bonding energy, even making ΔG1 and ΔG2 become negative values. This strong adsorption leads to little activity of O, so the thermodynamic barrier between the intermediate states of V–O and V–OOH is very high, leading to an ultra-high overpotential (4.27 eV). In contrast, for Co2Cu1, the lower bonding strength of Cu atoms with OH and O facilitates the bonding of OH on Cu–O, which makes ΔG1 and ΔG2 larger and is not desirable for the entire OER process. However, for Mn2Cu1, the adsorption strength of Cu with three oxygen species is moderate, and the balanced thermodynamic barrier is beneficial for obtaining excellent OER performance.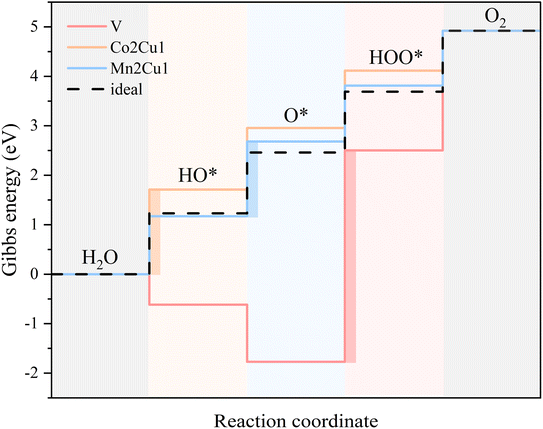 | ||
| Fig. 10 Gibbs energy diagram for V, Co2Cu1 and Mn2Cu1 systems calculated at 0 V vs. RHE. The color-filled rectangles denote the PLS. | ||
The relationship between ESPC and the adsorption strength of oxygen-containing intermediates can be revealed by BO. As shown in Fig. 11, with the increment of ESPC, the variation of BOM–OH and BOM–OOH is smaller than that of BOM![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O. This could be due to the fact that M–OH and M–OOH are always single bonds, whereas the M
O. This could be due to the fact that M–OH and M–OOH are always single bonds, whereas the M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond can be either a double or a single bond with a radical character, i.e., M–oxyl species. In fact, Fig. 11 shows that the bond order in M
O bond can be either a double or a single bond with a radical character, i.e., M–oxyl species. In fact, Fig. 11 shows that the bond order in M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O can adopt values ranging between ca. 1 and 2. The influence of the radical character in the M–O bond in OER catalysis has also been recently studied by García-Melchor et al., who also proposed different scaling relations for molecular systems exhibiting M–oxo or M–oxyl characters.61 In addition, the BOs between active site and three oxygen-containing intermediates exist saturation values, reaching the theoretical limitation (1 for M–OH and M–OOH, and 2 for M
O can adopt values ranging between ca. 1 and 2. The influence of the radical character in the M–O bond in OER catalysis has also been recently studied by García-Melchor et al., who also proposed different scaling relations for molecular systems exhibiting M–oxo or M–oxyl characters.61 In addition, the BOs between active site and three oxygen-containing intermediates exist saturation values, reaching the theoretical limitation (1 for M–OH and M–OOH, and 2 for M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) when ESPC is beyond 1.5. When ESPC is about 1.1, the BO difference among the metal–oxygen species is constant (about 0.25), which reflects the equilibrium adsorption of intermediates. When ESPC is less than 1.1, the BOM
O) when ESPC is beyond 1.5. When ESPC is about 1.1, the BO difference among the metal–oxygen species is constant (about 0.25), which reflects the equilibrium adsorption of intermediates. When ESPC is less than 1.1, the BOM![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O decreases rapidly, which indicates that the adsorption strength of the O intermediate is weak, and the PLS prefers to occur at the first or second elemental step. When ESPC is more than 1.1, the adsorption of the O intermediate is strong, and thus, the PLS occurs at the 3rd or 4th elemental step.
O decreases rapidly, which indicates that the adsorption strength of the O intermediate is weak, and the PLS prefers to occur at the first or second elemental step. When ESPC is more than 1.1, the adsorption of the O intermediate is strong, and thus, the PLS occurs at the 3rd or 4th elemental step.
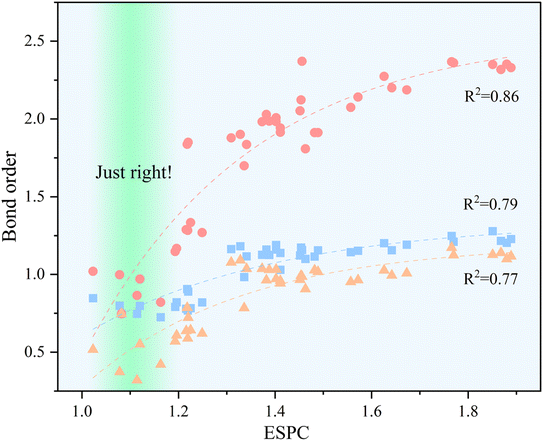 | ||
Fig. 11 Correlation between bond order and ESPC, the dashed lines provide guidance for eyes, the color blocks  , ,  , and , and  represent the M–OH bond, M–O bond, and M–OOH bond, respectively. represent the M–OH bond, M–O bond, and M–OOH bond, respectively. | ||
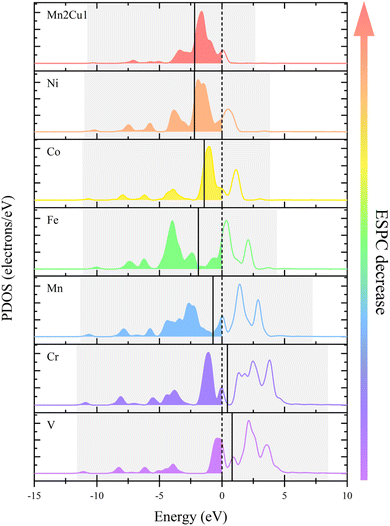
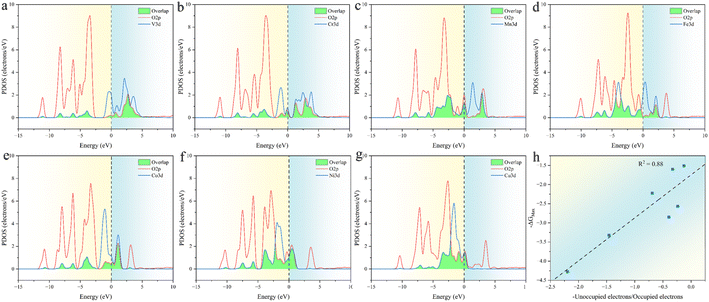
The relationship between ESPC and the adsorption strength of oxygen-containing intermediates can be understood more deeply from the perspective of band structure. As the decrease of ESPC, the d-band center becomes progressively lower relative to the Fermi level (Fig. 12), reducing the energy of the anti-bonding state formed between the adsorbed species and the catalyst. As a result, electrons flow more easily into the antibonding state, leading to an increase in the total energy and weakening the binding strength of intermediates on the catalyst. This weakening of the binding strength is particularly pronounced for O intermediates since the double bond nature of M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O is accompanied by more electron transfer during the adsorption. In addition, with the decrease of ESPC (the active site is from V to Cu, in the order of increasing atomic number), the overall energy of the orbitals that overlapping between the metal 3d orbital and the oxygen 2p orbital (green area in Fig. 13a–g) decreases, which improves the electron filling degree of the overlapping orbitals (Fig. 13h). The stability of the metals is gradually enhanced, indicating that the “bonding ability” of the metals is weakened and leads to the reduced adsorption strength of the OER intermediate on the metals. Thus, the ESPC can be used as a simple indicator to quantify the information of the band structure, which is directly related to the OER performance.
O is accompanied by more electron transfer during the adsorption. In addition, with the decrease of ESPC (the active site is from V to Cu, in the order of increasing atomic number), the overall energy of the orbitals that overlapping between the metal 3d orbital and the oxygen 2p orbital (green area in Fig. 13a–g) decreases, which improves the electron filling degree of the overlapping orbitals (Fig. 13h). The stability of the metals is gradually enhanced, indicating that the “bonding ability” of the metals is weakened and leads to the reduced adsorption strength of the OER intermediate on the metals. Thus, the ESPC can be used as a simple indicator to quantify the information of the band structure, which is directly related to the OER performance.
4. Conclusions
In summary, we unravel that ESPC, a universal descriptor, can describe the OER activity of MOFs containing diverse SBUs very well. By analyzing the variation of ESPC with combinations of different metals, a general design principle was further put forward to enhance the OER activity of MOFs, that is, the active sites should be Ni/Cu while the spectator atoms are Mn/Fe/Co/Ni. This principle is physically meaningful since ESPC indeed is a reflection of the bonding strength between metal and oxygen-containing intermediates. The appropriate metal configuration can optimize the d-electron distribution of the active site, which reduces the height of the anti-bonding state of the metal–oxygen species and weakens the bonding strength between them as well. All these effects synergistically contribute to the high-efficiency OER process. Our work demonstrates that the regulation of metal components of SBUs is a promising strategy for developing MOF-based energy conversion devices.Data availability
The structures and calculated data supporting the findings of this study are available in the ESI.†Author contributions
Xiangdong Xue: conceptualization, methodology, software, formal analysis, investigation, data curation, writing-original draft, and visualization. Hongyi Gao: methodology, validation, writing-review & editing, supervision, project administration, and funding acquisition. Jiangtao Liu: validation and formal analysis. Ming Yang: validation and formal analysis. Shihao Feng: validation and formal analysis. Zhimeng Liu: validation and formal analysis. Jing Lin: validation and formal analysis. Jitti Kasemchainan: validation and formal analysis. Linmeng Wang: validation and formal analysis. Qilu Jia: validation and formal analysis. Ge Wang: conceptualization, resources, writing-review & editing, supervision, project administration, and funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (no. 51972024), Natural Science Foundation of Guangdong Province of China (2022A1515010185), the State Key Laboratory of Advanced Chemical Power Sources, the Fundamental Research Funds for the Central Universities (QNXM20210012 and FRF-IDRY-20-004) and Scientific and Technological Innovation Foundation of Shunde Graduate School, University of Science and Technology Beijing (no. BK20AE003).Notes and references
- M. Eddaoudi, D. B. Moler, H. Li, B. Chen, T. M. Reineke, M. O'keeffe and O. M. Yaghi, Modular chemistry: secondary building units as a basis for the design of highly porous and robust metal–organic carboxylate frameworks, Acc. Chem. Res., 2001, 34, 319–330 CrossRef CAS PubMed.
- O. M. Yaghi, M. O'Keeffe, N. W. Ockwig, H. K. Chae, M. Eddaoudi and J. Kim, Reticular synthesis and the design of new materials, Nature, 2003, 423, 705–714 CrossRef CAS PubMed.
- A. Ahmed, S. Seth, J. Purewal, A. G. Wong-Foy, M. Veenstra, A. J. Matzger and D. J. Siegel, Exceptional hydrogen storage achieved by screening nearly half a million metal–organic frameworks, Nat. Commun., 2019, 10, 1–9 CrossRef CAS PubMed.
- N. Hanikel, M. S. Prévot and O. M. Yaghi, MOF water harvesters, Nat. Nanotechnol., 2020, 15, 348–355 CrossRef CAS PubMed.
- T. Tian, Z. Zeng, D. Vulpe, M. E. Casco, G. Divitini, P. A. Midgley, J. Silvestre-Albero, J.-C. Tan, P. Z. Moghadam and D. Fairen-Jimenez, A sol–gel monolithic metal–organic framework with enhanced methane uptake, Nat. Mater., 2018, 17, 174–179 CrossRef CAS PubMed.
- G. Liu, V. Chernikova, Y. Liu, K. Zhang, Y. Belmabkhout, O. Shekhah, C. Zhang, S. Yi, M. Eddaoudi and W. J. Koros, Mixed matrix formulations with MOF molecular sieving for key energy-intensive separations, Nat. Mater., 2018, 17, 283–289 CrossRef CAS PubMed.
- Y. Belmabkhout, P. M. Bhatt, K. Adil, R. S. Pillai, A. Cadiau, A. Shkurenko, G. Maurin, G. Liu, W. J. Koros and M. Eddaoudi, Natural gas upgrading using a fluorinated MOF with tuned H2S and CO2 adsorption selectivity, Nat. Energy, 2018, 3, 1059–1066 CrossRef CAS.
- T. Wang, L. Gao, J. Hou, S. J. Herou, J. T. Griffiths, W. Li, J. Dong, S. Gao, M.-M. Titirici and R. V. Kumar, Rational approach to guest confinement inside MOF cavities for low-temperature catalysis, Nat. Commun., 2019, 10, 1–9 CrossRef PubMed.
- M. Mon, R. Bruno, S. Sanz-Navarro, C. Negro, J. Ferrando-Soria, L. Bartella, L. Di Donna, M. Prejanò, T. Marino and A. Leyva-Pérez, Hydrolase-like catalysis and structural resolution of natural products by a metal–organic framework, Nat. Commun., 2020, 11, 1–9 CrossRef PubMed.
- C. S. Diercks, Y. Liu, K. E. Cordova and O. M. Yaghi, The role of reticular chemistry in the design of CO2 reduction catalysts, Nat. Mater., 2018, 17, 301–307 CrossRef CAS PubMed.
- M. Tchalala, P. Bhatt, K. Chappanda, S. Tavares, K. Adil, Y. Belmabkhout, A. Shkurenko, A. Cadiau, N. Heymans and G. De Weireld, Fluorinated MOF platform for selective removal and sensing of SO2 from flue gas and air, Nat. Commun., 2019, 10, 1–10 CrossRef CAS PubMed.
- S. Wu, H. Min, W. Shi and P. Cheng, Multicenter metal–organic framework-based ratiometric fluorescent sensors, Adv. Mater., 2020, 32, 1805871 CrossRef CAS PubMed.
- H.-Y. Li, S.-N. Zhao, S.-Q. Zang and J. Li, Functional metal–organic frameworks as effective sensors of gases and volatile compounds, Chem. Soc. Rev., 2020, 49, 6364–6401 RSC.
- S. Bi, H. Banda, M. Chen, L. Niu, M. Chen, T. Wu, J. Wang, R. Wang, J. Feng and T. Chen, Molecular understanding of charge storage and charging dynamics in supercapacitors with MOF electrodes and ionic liquid electrolytes, Nat. Mater., 2020, 19, 552–558 CrossRef CAS PubMed.
- S. Bai, X. Liu, K. Zhu, S. Wu and H. Zhou, Metal–organic framework-based separator for lithium–sulfur batteries, Nat. Energy, 2016, 1, 1–6 Search PubMed.
- D. G. Atinafu, S. J. Chang, K.-H. Kim, W. Dong and S. Kim, A novel enhancement of shape/thermal stability and energy-storage capacity of phase change materials through the formation of composites with 3D porous (3, 6)-connected metal–organic framework, Chem. Eng. J., 2020, 389, 124430 CrossRef CAS.
- T. Hu, S. Chang, H. Wu, L. Li and W. Yuan, Construction of high thermal conductivity MOFs composite phase change materials with reinforced light-to-thermal conversion, Sol. Energy Mater. Sol. Cells, 2021, 232, 111339 CrossRef CAS.
- J. Li, J. Yu, Z. Sun, H. Liu and X. Wang, Innovative Integration of Phase-Change Microcapsules with Metal–Organic Frameworks into an Intelligent Biosensing System for Enhancing Dopamine Detection, ACS Appl. Mater. Interfaces, 2021, 13, 41753–41772 CrossRef CAS PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, The Cambridge structural database, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- P. Z. Moghadam, A. Li, S. B. Wiggin, A. Tao, A. G. Maloney, P. A. Wood, S. C. Ward and D. Fairen-Jimenez, Development of a Cambridge Structural Database subset: a collection of metal–organic frameworks for past, present, and future, Chem. Mater., 2017, 29, 2618–2625 CrossRef CAS.
- Y. J. Colón and R. Q. Snurr, High-throughput computational screening of metal–organic frameworks, Chem. Soc. Rev., 2014, 43, 5735–5749 RSC.
- A. S. Rosen, J. M. Notestein and R. Q. Snurr, Identifying promising metal–organic frameworks for heterogeneous catalysis via high-throughput periodic density functional theory, J. Comput. Chem., 2019, 40, 1305–1318 CrossRef CAS PubMed.
- K. D. Vogiatzis, E. Haldoupis, D. J. Xiao, J. R. Long, J. I. Siepmann and L. Gagliardi, Accelerated computational analysis of metal–organic frameworks for oxidation catalysis, J. Phys. Chem. C, 2016, 120, 18707–18712 CrossRef CAS.
- P. Liao, R. B. Getman and R. Q. Snurr, Optimizing Open Iron Sites in Metal–Organic Frameworks for Ethane Oxidation: A First-Principles Study, ACS Appl. Mater. Interfaces, 2017, 9, 33484–33492 CrossRef CAS PubMed.
- D. R. Pahls, M. A. Ortuño, P. H. Winegar, C. J. Cramer and L. Gagliardi, Computational screening of bimetal-functionalized Zr6O8 MOF nodes for methane C–H bond activation, Inorg. Chem., 2017, 56, 8739–8743 CrossRef CAS PubMed.
- M. C. Simons, M. A. Ortuño, V. Bernales, C. A. Gaggioli, C. J. Cramer, A. Bhan and L. Gagliardi, C–H Bond Activation on Bimetallic Two-Atom Co-M Oxide Clusters Deposited on Zr-Based MOF Nodes: Effects of Doping at the Molecular Level, ACS Catal., 2018, 8, 2864–2869 CrossRef CAS.
- M. Fumanal, G. Capano, S. Barthel, B. Smit and I. Tavernelli, Energy-based descriptors for photo-catalytically active metal–organic framework discovery, J. Mater. Chem. A, 2020, 8, 4473–4482 RSC.
- F.-X. Coudert and A. H. Fuchs, Computational characterization and prediction of metal–organic framework properties, Coord. Chem. Rev., 2016, 307, 211–236 CrossRef CAS.
- H. Daglar and S. Keskin, Recent advances, opportunities, and challenges in high-throughput computational screening of MOFs for gas separations, Coord. Chem. Rev., 2020, 422, 213470 CrossRef CAS.
- A. H. Farmahini, S. Krishnamurthy, D. Friedrich, S. Brandani and L. Sarkisov, Performance-based screening of porous materials for carbon capture, Chem. Rev., 2021, 121, 10666–10741 CrossRef CAS PubMed.
- T. Yang, J. Zhou, T. T. Song, L. Shen, Y. P. Feng and M. Yang, High-throughput identification of exfoliable two-dimensional materials with active basal planes for hydrogen evolution, ACS Energy Lett., 2020, 5, 2313–2321 CrossRef CAS.
- S. Lee, B. Kim, H. Cho, H. Lee, S. Y. Lee, E. S. Cho and J. Kim, Computational Screening of Trillions of Metal–Organic Frameworks for High-Performance Methane Storage, ACS Appl. Mater. Interfaces, 2021, 13, 23647–23654 CrossRef CAS PubMed.
- P. Liu and J. A. Rodriguez, Catalysts for hydrogen evolution from the [NiFe] hydrogenase to the Ni2P (001) surface: the importance of ensemble effect, J. Am. Chem. Soc., 2005, 127, 14871–14878 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- A. Tkatchenko and M. Scheffler, Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- B. Delley, Hardness conserving semilocal pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 155125 CrossRef.
- F. B. Van Duijneveldt, J. G. van Duijneveldt-van de Rijdt and J. H. van Lenthe, State of the art in counterpoise theory, Chem. Rev., 1994, 94, 1873–1885 CrossRef CAS.
- I. Mayer, Bond orders and valences from ab initio wave functions, Int. J. Quantum Chem., 1986, 29, 477–483 CrossRef CAS.
- S. H. Ye, Z. X. Shi, J. X. Feng, Y. X. Tong and G. R. Li, Activating CoOOH porous nanosheet arrays by partial iron substitution for efficient oxygen evolution reaction, Angew. Chem., Int. Ed., 2018, 57, 2672–2676 CrossRef CAS PubMed.
- T. Ouyang, Y. Ye, C. Wu, K. Xiao and Z. Liu, Heterostructures comprised of Co/β-Mo2C-encapsulated N-doped carbon nanotubes as bifunctional electrodes for water splitting, Angew. Chem., Int. Ed., 2019, 58, 4923–4928 CrossRef CAS PubMed.
- X. R. Wang, J. Y. Liu, Z. W. Liu, W. C. Wang, J. Luo, X. P. Han, X. W. Du, S. Z. Qiao and J. Yang, Identifying the key role of pyridinic-N–Co bonding in synergistic electrocatalysis for reversible ORR/OER, Adv. Mater., 2018, 30, 1800005 CrossRef PubMed.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, Origin of the overpotential for oxygen reduction at a fuel-cell cathode, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- A. A. Peterson, F. Abild-Pedersen, F. Studt, J. Rossmeisl and J. K. Nørskov, How copper catalyzes the electroreduction of carbon dioxide into hydrocarbon fuels, Energy Environ. Sci., 2010, 3, 1311–1315 RSC.
- J. Rossmeisl, A. Logadottir and J. K. Nørskov, Electrolysis of water on (oxidized) metal surfaces, Chem. Phys., 2005, 319, 178–184 CrossRef CAS.
- Y. Ji, H. Dong, C. Liu and Y. Li, The progress of metal-free catalysts for the oxygen reduction reaction based on theoretical simulations, J. Mater. Chem. A, 2018, 6, 13489–13508 RSC.
- M. Barona and R. Q. Snurr, Exploring the tunability of trimetallic MOF nodes for partial oxidation of methane to methanol, ACS Appl. Mater. Interfaces, 2020, 12, 28217–28231 CrossRef CAS PubMed.
- P. Lyu and G. Maurin, Mechanistic Insight into the Catalytic NO Oxidation by the MIL-100 MOF Platform: Toward the Prediction of More Efficient Catalysts, ACS Catal., 2020, 10, 9445–9450 CrossRef CAS.
- P. Borlido, T. Aull, A. W. Huran, F. Tran, M. A. Marques and S. Botti, Large-scale benchmark of exchange–correlation functionals for the determination of electronic band gaps of solids, J. Chem. Theory Comput., 2019, 15, 5069–5079 CrossRef CAS PubMed.
- Y. Li, X. Bao, D. Chen, Z. Wang, N. Dewangan, M. Li, Z. Xu, J. Wang, S. Kawi and Q. Zhong, A Minireview on Nickel-Based Heterogeneous Electrocatalysts for Water Splitting, ChemCatChem, 2019, 11, 5913–5928 CrossRef CAS.
- Y. Chen, K. Rui, J. Zhu, S. X. Dou and W. Sun, Recent Progress on Nickel-Based Oxide/(Oxy)Hydroxide Electrocatalysts for the Oxygen Evolution Reaction, Chem.–Eur. J., 2019, 25, 703–713 CrossRef CAS PubMed.
- B. Xu, Y. Zhang, Y. Pi, Q. Shao and X. Huang, Research progress of nickel-based metal–organic frameworks and their derivatives for oxygen evolution catalysis, Acta Phys.-Chim. Sin., 2021, 37, 2009074 Search PubMed.
- W. Li, W. Fang, C. Wu, K. N. Dinh, H. Ren, L. Zhao, C. Liu and Q. Yan, Bimetal–MOF nanosheets as efficient bifunctional electrocatalysts for oxygen evolution and nitrogen reduction reaction, J. Mater. Chem. A, 2020, 8, 3658–3666 RSC.
- M. Xie, Y. Ma, D. Lin, C. Xu, F. Xie and W. Zeng, Bimetal–organic framework MIL-53 (Co–Fe): an efficient and robust electrocatalyst for the oxygen evolution reaction, Nanoscale, 2020, 12, 67–71 RSC.
- X. L. Wang, L. Z. Dong, M. Qiao, Y. J. Tang, J. Liu, Y. Li, S. L. Li, J. X. Su and Y. Q. Lan, Exploring the performance improvement of the oxygen evolution reaction in a stable bimetal–organic framework system, Angew. Chem., Int. Ed., 2018, 57, 9660–9664 CrossRef CAS PubMed.
- H. Guan, N. Wang, X. Feng, S. Bian, W. Li and Y. Chen, FeMn bimetallic MOF directly applicable as an efficient electrocatalyst for overall water splitting, Colloids Surf., A, 2021, 624, 126596 CrossRef CAS.
- L. Han, J. Xu, Y. Huang, W. Dong and X. Jia, High-performance electrocatalyst of vanadium-iron bimetal organic framework arrays on nickel foam for overall water splitting, Chin. Chem. Lett., 2021, 32, 2263–2268 CrossRef CAS.
- J. Li, W. Huang, M. Wang, S. Xi, J. Meng, K. Zhao, J. Jin, W. Xu, Z. Wang and X. Liu, Low-crystalline bimetallic metal–organic framework electrocatalysts with rich active sites for oxygen evolution, ACS Energy Lett., 2018, 4, 285–292 CrossRef.
- Z. Xue, Y. Li, Y. Zhang, W. Geng, B. Jia, J. Tang, S. Bao, H. P. Wang, Y. Fan and Z. w. Wei, Modulating electronic structure of metal–organic framework for efficient electrocatalytic oxygen evolution, Adv. Energy Mater., 2018, 8, 1801564 CrossRef.
- E. Babaev, Periodic law in chemistry and other sciences, Pure Appl. Chem., 2019, 91, 2023–2035 CrossRef CAS.
- A. L. Allred and E. G. Rochow, A scale of electronegativity based on electrostatic force, J. Inorg. Nucl. Chem., 1958, 5, 264–268 CrossRef CAS.
- M. J. Craig and M. García-Melchor, High-throughput screening and rational design to drive discovery in molecular water oxidation catalysis, Cell Rep. Phys. Sci., 2021, 2, 100492 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc04898a |
| This journal is © The Royal Society of Chemistry 2022 |