Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Guided discovery of chemical reaction pathways with imposed activation†
Cyrille
Lavigne
a,
Gabe
Gomesद
 *ab,
Robert
Pollice‡||
*ab,
Robert
Pollice‡||
 *ab and
Alán
Aspuru-Guzik
*abcdef
*ab and
Alán
Aspuru-Guzik
*abcdef
aDepartment of Computer Science, University of Toronto, 214 College St., Toronto, Ontario M5T 3A1, Canada. E-mail: gabegomes@cmu.edu; r.pollice@rug.nl; aspuru@utoronto.ca
bChemical Physics Theory Group, Department of Chemistry, University of Toronto, 80 St George St, Toronto, Ontario M5S 3H6, Canada
cDepartment of Chemical Engineering & Applied Chemistry, University of Toronto, 200 College St., Ontario M5S 3E5, Canada
dDepartment of Materials Science & Engineering, University of Toronto, 184 College St., Ontario M5S 3E4, Canada
eVector Institute for Artificial Intelligence, 661 University Ave Suite 710, Toronto, Ontario M5G 1M1, Canada
fLebovic Fellow, Canadian Institute for Advanced Research (CIFAR), 661 University Ave, Toronto, Ontario M5G, Canada
First published on 10th November 2022
Abstract
Computational power and quantum chemical methods have improved immensely since computers were first applied to the study of reactivity, but the de novo prediction of chemical reactions has remained challenging. We show that complex reaction pathways can be efficiently predicted in a guided manner using chemical activation imposed by geometrical constraints of specific reactive modes, which we term imposed activation (IACTA). Our approach is demonstrated on realistic and challenging chemistry, such as a triple cyclization cascade involved in the total synthesis of a natural product, a water-mediated Michael addition, and several oxidative addition reactions of complex drug-like molecules. Notably and in contrast with traditional hand-guided computational chemistry calculations, our method requires minimal human involvement and no prior knowledge of the products or the associated mechanisms. We believe that IACTA will be a transformational tool to screen for chemical reactivity and to study both by-product formation and decomposition pathways in a guided way.
Introduction
While a significant portion of the chemical reactions of scientific interest have half-lives on the order of seconds to days, the corresponding dynamic processes require time resolutions on the order of femtoseconds or even less for direct simulation. This difference of at least fifteen orders of magnitude in timescales makes brute force, large-scale computer simulations infeasible1 and, consequently, the prediction of chemical reactivity remains one of the most important challenges in computational chemistry. To tackle this challenge, many alternative approaches have been developed.2 In a recent review, these approaches have been classified with respect to the general strategy adopted for exploring potential energy surfaces.3 The three classes identified are (1) methods exploiting curvature information of the potential energy surface, (2) methods applying chemical heuristics, and (3) methods that rely on human intuition to guide the exploration.3 When methods combine multiple of these strategies they are classified based on the dominating one. Notably, we will limit this introduction to methods tackling forward explorations with an open end, i.e., we know the identity of the substrates and wish to find out how they react.4 Thus, we exclude methods assuming known product states.Among the approaches tackling open-ended forward explorations, heuristic approaches relying on human-derived rules for reactivity and stability5–13 are prominent and they largely belong to class 2 (vide supra). Predominantly mechanism-agnostic machine learning methods for product prediction based on experimental data14–21 are currently becoming increasingly popular and they formally belong to the same class as they simply utilize learned rather than human-derived rules. These approaches typically start with the prediction of likely intermediates and products allowing them to use methodology developed for start-to-end exploration4 thereafter for finding the corresponding reaction pathways.
In contrast, the prediction of potential reaction pathways starting from known minima leading to unknown products can also be tackled directly with ab initio simulations. In addition to the classification introduced above, the corresponding methods can be further grouped into several families. One of the simplest approaches is coordinate driving22 and it is one of the standard approaches used in contemporary user-guided potential energy surface exploration. The user decides on which, usually internal, coordinates are to be systematically modified and the corresponding energy profile is manually inspected. Accordingly, this method largely relies on human intuition and belongs to class 3. Based on the idea of coordinate driving, brute force approaches such as Grid Search,22 ValleyScan23 and the so-called single coordinate driving technique24,25 have been developed, which systematically explore all dimensions of the potential energy surface via exhaustive coordinate driving. Consequently, their computational expense increases steeply with the dimensionality of the system under study. These methods do not rely on human intuition anymore and solely utilize information from the potential energy surface which puts them into class 1.
To make exhaustive coordinate driving approaches more tractable, a combined molecular dynamics and coordinate driving (MD/CD) method26 has been developed which relies on molecular dynamics for systematic conformer sampling. Additionally, while still utilizing exhaustive coordinate driving for exploring reactivity, it allows users to define active atoms. Consequently, exhaustive coordinate driving is only applied to the active atoms thus reducing the dimensionality and scaling of the problem. Another variation of exhaustive coordinate driving has been realized in ZStruct2,27 which relies on the single-ended growing string method to construct reaction paths and find both transition states and the associated minima. It also allows for users to define active atoms to narrow down the space to be explored.
As an alternative to the previously discussed brute force approaches, class 1 methods like the gradient extremal walking algorithm (GEWA)28 and anharmonic downward distortion following (ADDF)29 directly exploit curvature information of the potential energy surface to identify paths leading to transition states and the corresponding connected minima. Nevertheless, exhaustive application of these approaches is still limited in scope and quickly becomes prohibitively expensive when the system size is increased. A different type of class 1 approach is the artificial force-induced reaction (AFIR) method.30 It applies an artificial force that pushes reactants together allowing reaction barriers to be overcome via ordinary energy minimization. By exploring many random initial reactant orientations, various alternative reaction pathways can be discovered. Notably, intramolecular reactions can also be explored by defining molecular fragments and user input can be utilized for the selection of suitable reactant pairs and active atoms within them.31
Arguably the most explored family of class 1 approaches relies on reactive molecular dynamics. Early examples include enhanced sampling techniques like metadynamics via local elevation32,33 and bias-potential-driven dynamics34,35 to overcome barriers between various conformers and between reactants and products. Additionally, reactions in molecular dynamics simulations can also be promoted by strong external electric fields,36 and by a virtual piston that periodically applies very high pressures to the simulated system to increase the frequency of collisions and thus the probability of barrier crossings, as realized in the so-called nanoreactor.37 The term nanoreactor has later also been used to describe metadynamics simulations of chemical reactions in confined spaces with time-independent wall potentials.38 Moreover, reactions can also be promoted by performing molecular dynamics with strongly vibrationally excited molecules as realized in the Transition State Search Using Chemical Dynamics Simulations (TSSCDS) approach.39,40 Notably, TSSCDS allows for the user-guided selection of vibrational modes to be excited to direct the reactivity to be explored.
Despite the plurality of existing approaches, current techniques for systematic prediction of chemical reactivity have significant drawbacks that curtail their general use, both in human-guided workflows and in fully automated settings.3 It is striking that many approaches for reaction pathway exploration show limited benefits from domain expert input. In fully automated settings, systematic and exhaustive reaction pathway searches are computationally prohibitive,41 and difficult to scale to larger molecules.24,26,42 Heuristics approaches can map extensive reaction networks43 but many of them in particular face issues when confronted with non-conventional bonding and organometallic species,3 which require alternative quantum chemistry-based strategies.8 Hence, there is room for a method that allows for both guided and systematic exploration of potential energy surfaces based on quantum chemistry simulations.
Herein, we introduce imposed activation (IACTA), a conceptually simple and general computational approach that semi-automatically and robustly explores chemical reaction pathways and their products. Additionally, it provides reasonable guess structures of the corresponding transition states. To do that, it requires as user input the identity of the substrates and selection of one reactive coordinate, which can be straightforward to choose for some systems but non-trivial for others, depending on the reactivity under study. Nevertheless, as the input does not require specific alignment of molecules or preliminary geometry optimization, it is operationally intuitive for human users and, in principle, also amenable to automated workflows. Specifically, we show that these pathways can be obtained by conformational exploration38 with a chemically activating constraint. This method provides meaningful suggestions for diverse reaction pathways together with an initial reaction feasibility assessment based on reaction energies and rough estimates of the associated barriers. Reactions of sizable molecules are found rapidly with only modest computational resources when employing state-of-the-art semi-empirical methods such as the GFN-xTB family.44,45 However, IACTA does not require the use of specific electronic structure methods and, thus, can be combined with any approach that computes energies based on 3-dimensional structures. Notably, while the separate ingredients of the workflow are well-established in computational chemistry, IACTA puts them together in a unique way that makes it both intuitive to use and computationally efficient by relying on user guidance. Despite introducing significant bias due to the requirement for user input, our results demonstrate that we are still able to discover many surprising reaction pathways. We present the capabilities of this approach on three main case studies with distinct challenges: (1) an epoxide-initiated stereoselective polyene tricyclization cascade with various side products, (2) a solvent-mediated Michael addition with a proton shuttle involving multiple water molecules, and (3) the late-stage oxidative addition of ten drug-like molecules with electronically unsaturated palladium phosphine complexes.
Results and discussion
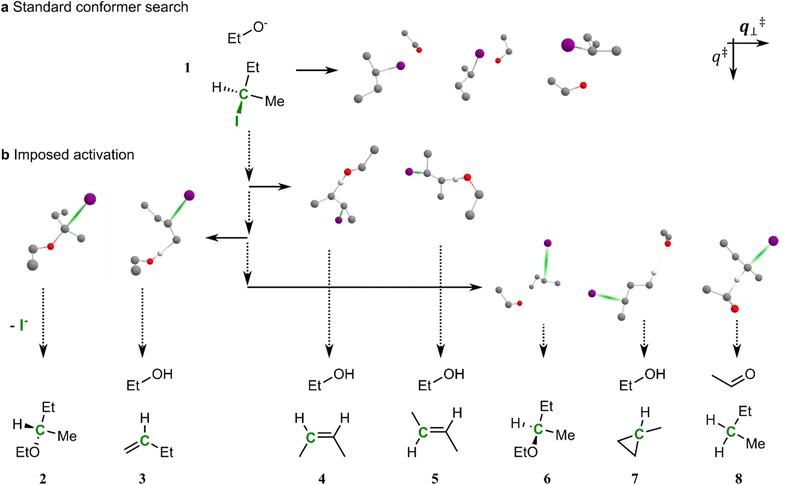
To initiate IACTA, a chemical coordinate (such as the length of a bond) is chosen as the activating coordinate q‡ (cf.Fig. 1). Subsequently, conformer generation38 is performed while constraining q‡ to a value between the initial reactant structure and possible product structures to explore the orthogonal coordinates q‡⊥. This corresponds to a search for local energy minima in the constrained space amidst the range of barriers separating products from reactants. These local energy minima, found by conformational exploration, are possible reaction pathways. A subsequent relaxed scan of q‡ pushes the molecule along discovered pathways to new products. We emphasize again that neither approximate transition structures, nor the identity of reaction products, nor any training data are required as input in the search, only the identity of the reactants and the choice of an activating coordinate. Overall, the workflow consists of four steps:1. The user selects an activating coordinate q‡ (i.e., an interatomic distance, a bending angle, or a torsional angle) and the initial structure of the reactants is optimized. With the reactive coordinate fixed at its equilibrium value q‡0, an initial conformer search is performed to obtain a diverse set of structures. A relaxed scan of the reactive coordinate follows, starting with one of the initially generated conformers, to an intermediate value between that of reactants and products q‡i.
2. A second, shorter and less exhaustive conformer search is undertaken with the reactive coordinate constrained at q‡i to explore the local energy landscape.
3. All the structures thereby generated are scanned from q‡ = q‡i to q‡N, with q‡N being the maximum scanned value, to obtain new reaction products. A backward scan from q‡i to q‡0 yields a complete trajectory back to a reactant conformation.
4. Finally, structures corresponding to energy minima of the trajectory (potential reactants and products conformations) are optimized without constraints to ensure stability.
Steps 2 to 4 above are then repeated for different values of q‡i to obtain an ensemble of reactive trajectories sampled from multiple transition structures.
As a concrete example, let us consider the various elimination and substitution reactions of (R)-2-iodobutane and ethoxide anion. Generating ground-state conformers for this system yields many loosely bound complexes (Fig. 1a). Reaction prediction starting from these structures following specific normal modes is challenging, as they are quite far from any connected transition states, such as those shown in Fig. 1b.
One standard approach used extensively by methods like coordinate driving and related approaches to traverse the mountain ranges of potential reactive modes is to pull together pairs of atoms via relaxed scans to form new bonds.26,42,46 Thus, they circumvent the issue of initial structures being too far from transition states by gradually guiding them into reactive conformations. For example, pulling together the ethoxide anion oxygen and the α-carbon of 2-iodobutane leads to the SN2 reaction. However, for predicting potential reaction outcomes without prior knowledge about which pairs of atoms are likely to react, a fully systematic search of all possible bond-forming pairs is necessary which scales quadratically with the number of atoms26 and generally can only be performed for relatively small systems.47 Additionally, if prior knowledge is available, this approach requires information about multiple sites that could potentially react with each other.
The key idea of our approach is to activate reactants using a single coordinate q‡ that can initiate many reactions of interest, thereby circumventing the scaling issues of searching for possible bond formation pairs systematically or heuristically. In the case of the (R)-2-iodobutane molecule depicted in Fig. 1, bond dissociation energies dictate that the carbon–iodine bond is readily broken,48 making it an excellent choice for q‡. Stretching the carbon–iodine bond, i.e., increasing q‡, creates activated and very electrophilic structures. A subsequent constrained conformer search in the orthogonal space q‡⊥ yields geometries close to the SN2 transition state, as the ethoxide oxygen stabilizes the structure when it lies close to the halogenated carbon. Relaxed scans along q‡ starting from one of these newly generated transition structures leads to the SN2 products (2 in Fig. 1).
Importantly, besides SN2, in a single run of our workflow, other activated conformers leading to different reaction products are also uncovered. Stretching the carbon–iodine bond of all the activated structures found also yields E2 and E1 elimination products (with both Hofmann49 product 3 and Zaitsev50 products 4 and 5), SN1 substitution reactions (with products 2 and 6), γ-elimination to methylcyclopropane 7 as well as a curious alkoxide hydride transfer51 forming 8. The latter two reactions, which have significantly higher estimated reaction barriers, are unlikely to occur in an experiment but, first, do represent known chemistry and thus are still reasonable, and second, demonstrate the complex pathways that can be obtained automatically from imposed activation with a single activating coordinate.
The reaction pathways discovered in coordinate scans are highly dependent on the corresponding starting geometries, especially when the scanned coordinate is not bond-forming. Indeed, for an iodine–carbon bond scan to generate a pathway towards compound 7via γ-elimination requires the ethoxide oxygen in very close proximity to the eliminated hydrogen, whereas it needs to be close to the α-carbon to proceed to the SN2 product 2. The diversity of products and reaction paths discovered by IACTA is made possible by bringing together two key concepts in a unique way. First, the activation of a single coordinate such as bond stretching generates a highly reactive species that can, in principle, undergo many transformations downhill in energy depending on its conformation. Second, the power of constrained conformer generation via metadynamics explores diverse reactive conformations of this species38,52 which are directly connected to a wide range of reaction pathways allowing subsequent relaxed scans to find new reaction products. Finally, these concepts are made practical and applicable to reasonable large molecular systems by relying on the computational efficiency and robustness of the GFN-xTB family of methods as computational workhorse.45 However, we would like to emphasize that IACTA does not require use of this specific family of methods but can be combined with any approach predicting energies from 3-dimensional structures.
To summarize the key features of IACTA and compare them with the main classes of alternative approaches, we again rely on the framework consisting of three distinct classes that was established in a recent review (vide supra).3 Specifically, we not only consider the main class of each method but also the extent to which they incorporate ideas of the other classes. Additionally, we assess how these approaches fulfill the main features demanded from systematic methods for potential energy surface exploration, as proposed in the same review.3 The corresponding results are summarized in Table 1. IACTA makes use of both curvature information and human intuition to explore reactivity and combines elements from both coordinate driving and reactive molecular dynamics approaches. Incorporation of heuristics, while currently not implemented, is possible, especially when aiming for a fully automated implementation testing alternative activating coordinates autonomously. Importantly, IACTA provides tractability at the cost of considerable thoroughness by relying on guidance based on user input. This provides IACTA with a prominent interactive component, unlike many alternative approaches. Overall, universal applicability of IACTA would require an automated method for selecting activating coordinates that could optionally supplement user choices enabling more thorough exploration. However, increasing thoroughness of IACTA will necessarily come at the cost of tractability.
| Feature | Coordinate driving | Exhaustive coordinate driving | AFIR | Reactive molecular dynamics | IACTA |
|---|---|---|---|---|---|
| a ✓ and ✗ indicate the presence and absence of a feature, respectively. ∼ indicates that realization of a feature within the algorithm is, in principle, possible but only with compromises. | |||||
| Curvature information | ✓ | ✓ | ✓ | ✓ | ✓ |
| Heuristics | ✗ | ∼ | ∼ | ∼ | ∼ |
| Human intuition | ✓ | ∼ | ∼ | ∼ | ✓ |
| Full automation | ✗ | ✓ | ✓ | ✓ | ∼ |
| Thoroughness | ✗ | ✓ | ✓ | ✓ | ∼ |
| Tractability | ✓ | ∼ | ∼ | ∼ | ✓ |
| Guidance | ✓ | ∼ | ∼ | ∼ | ✓ |
| Universal applicability | ✗ | ∼ | ∼ | ∼ | ∼ |
Apart from the reactions between (R)-2-iodobutane and ethoxide anion presented in Fig. 1, we used IACTA to explore reactivity in a diverse sample of similarly small molecules. The corresponding results are detailed in the ESI.† In the following sections, we apply IACTA to several more challenging examples inspired by recent literature studies to exemplify how IACTA can be applied to solve problems in chemistry.
Cyclization cascade in the synthesis of a natural product
A robust and automated reaction prediction approach can help to understand and rationalize complicated reactions with multiple outcomes. We demonstrate this based on the epoxide-initiated polycyclization of 9 to form 10 (cf.Fig. 2), an essential step in a concise total synthesis of the fungal meroterpenoid berkeleyone A.53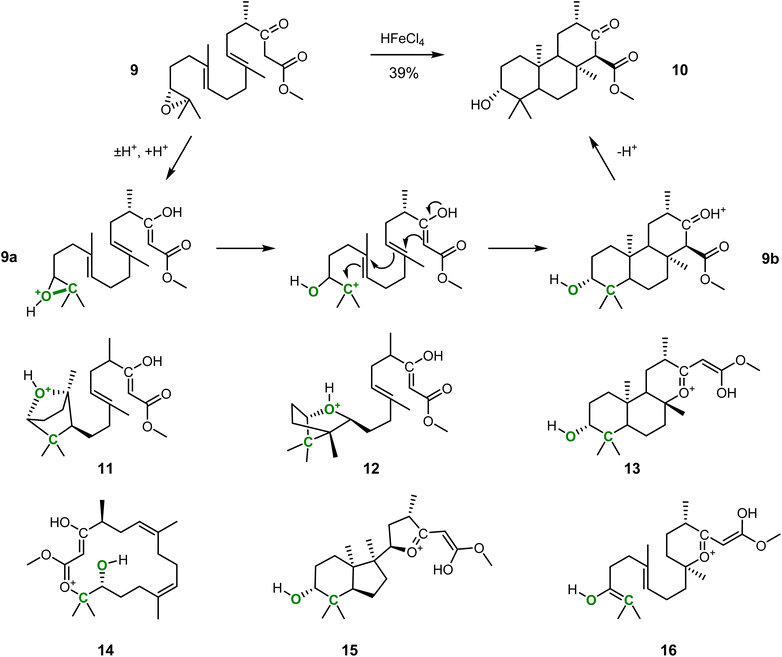 | ||
| Fig. 2 Epoxide-initiated β-keto ester-terminated triple cyclization reaction and the corresponding products and side-products predicted by IACTA. The polycyclization from 9 to 10 is a key step in a concise total synthesis of berkeleyone A described in the literature.53 We initiated an IACTA reaction search from protonated enol 9a using the epoxide C–O bond of the tertiary carbon indicated in green as the activating coordinate. Compounds 11–16 are a subset of the predicted side products. | ||
We selected this triple cyclization as it is a complex reaction, with the potential to form many by-products.54–57 Indeed, the yield of 39% reported in the literature53 was only achieved after extensive optimization of reaction conditions and hints towards significant by-product formation. Previous attempts at similar reactions yielded a range of mono- and polycyclic, fused and bridged products from ether formation by the epoxide and cyclization at the β-keto ester oxygen instead of the desired carbocyclization.58 We initiate IACTA from structure 9a, the reactive enol form of 9 protonated at the epoxide. Compound 9a is activated by opening the epoxide on the tertiary carbon side using the carbon–oxygen distance as the activating constraint (cf.Fig. 2, bond highlighted in green). More than 200 distinct reaction pathways are discovered, including many tautomerizations, high energy processes, and, most importantly, all experimentally reported modes of action.
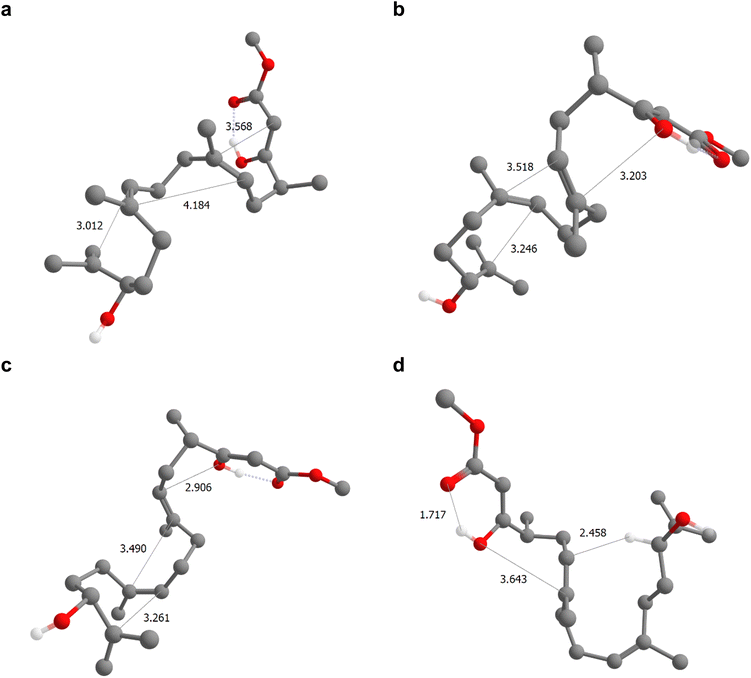
A subset of the thermodynamically favorable products with estimated activation energies below 35 kcal mol−1 is shown in Fig. 2. Notably, 9b is readily discovered by the reaction search from an epoxide-initiated triple cyclization cascade terminating at the β-keto ester which forms the desired product 10 after deprotonation. The transition structure, i.e., the transition state guess obtained from IACTA, for this reaction is depicted in Fig. 3a, with the three newly formed bonds shown with thin lines. We find this cyclization cascade to be barrier-free after this transition structure. Side products 11 and 12 result from 1,2-addition of the epoxide to the nearest alkene, forming bridged bicyclic ethers.54 Triple cyclization terminating at the β-keto ester oxygen forms 13, a major experimental by-product,58via a pathway that differs from the one forming 9b only by the nucleophilic atom initiating the cascade (cf.Fig. 3b). Direct nucleophilic epoxide opening by the same oxygen yields 14, which has a 16-membered ring. Product 15 is obtained like 13 except for the second stage of the cascade being formation of a five-membered rather than a six-membered ring (cf.Fig. 3c). Finally, the most surprising of the predicted products is 16, which is formed from the transfer of a proton from the epoxide (which forms an enol55) to the far alkene followed by an oxygen cyclization (Fig. 3c).
The straightforward initialization and short duration of our computational experiments employing IACTA are one of its crucial features. All the above reactions were obtained from a single run targeting compound 9a, which took only 6.3 hours on a single compute node. In this case, however, we note that success followed a failed search initiated from the less reactive keto form of 9a. Similarly, computations starting from another tautomer of 9, namely the enol of the ester, uncovered significantly fewer reactions and, to our surprise, failed to yield 9b. In practice, the sensitivity to the initial structures was solved by iteratively trying new tautomeric structures, an approach enabled by the fast turnaround times of the IACTA calculations, and the ease of tautomer generation using basic chemical rules,59 also making it amenable to automation.
Water-mediated Michael addition
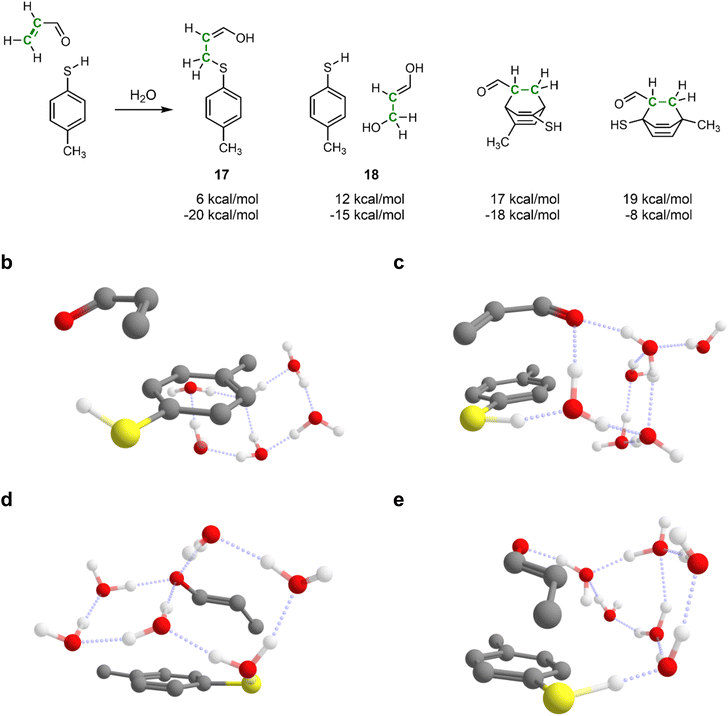
Automated reaction search is specifically needed when the reacting system consists of multiple loosely bound fragments with many possible arrangements. This is the case, for example, in solvent-mediated reactions, where specific solvation geometries play a major role in enabling various transition structures.60 Setting up traditional transition state calculations for such systems is very time-consuming and error-prone, as it requires carefully arranging fragments in various sometimes non-intuitive reactive geometries.61Therefore, next, we demonstrate IACTA on the water-mediated Michael addition of p-methylthiophenol to acrolein, shown in Fig. 4a, a case study inspired by a recent popular science article.62 Following this article, six explicit water molecules were added to the reacting system. Notably, as will be apparent from the following paragraphs, this choice of the explicit number of solvent molecules is non-trivial and strongly affects the outcome of the simulations. The addition reaction forming 17 was obtained as both thermodynamic and kinetic product upon stretching the carbon–carbon double bond of acrolein. By-products include hydration of acrolein to 3-hydroxypropanal (18), a biologically important process,63 and various Diels–Alder reactions between acrolein and 4-methylthiophenol that break aromaticity of the latter with higher estimated barriers.
This Michael addition involves proton transfer from the thiol to the carbonyl group of acrolein, which is facilitated in the simulations by a chain of hydrogen-bonded water molecules. Acrolein can have s-cis or s-trans configuration, and the reaction proceeds via the acrolein π-system either pointing towards the aromatic ring of the thiophenol (compact conformation) or away from it (expanded conformation). Among all the combinations of acrolein configurations and conformers, and the number of chained water molecules, IACTA identifies in a single run fourteen different pathways and distinct transition structures (Table 2), five of which are estimated to be faster than formation of 18. Thus, our method is excellent for screening potential pathways before embarking on extensive transition state optimization.
| Acrolein isomer | TS conformation | Number of H2O molecules in H+ transfer chain | ||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | ||
| a For each entry, the estimated activation energies at the GFN2-xTB level of theory in kcal mol−1 (bold, <12 kcal mol−1) and the number of occurrences are provided. Estimated ΔE†(kcal mol−1)|no. of occurrences. | ||||||
| s-cis | Compact | 21.2|6 | 8.7|20 | 11.2|8 | — | — |
| Expanded | — | 15.6|17 | 13.6|5 | 17.1|1 | — | |
| s-trans | Compact | — | 27.4|1 | 5.8|49 | 8.5|14 | 20.6|1 |
| Expanded | — | 23.3|4 | 9.8|41 | 17.1|11 | 16.6|1 | |
Reaction without hydrogen-bonding water molecules facilitating the proton transfer only occurs for the s-cis isomer, as it requires the carbonyl and thiol to be in proximity (Fig. 4b). The longer distance required for the proton transfer in the s-trans isomer favors proton shuttling by two or three water molecules. In contrast, addition of the s-cis isomer is efficiently mediated by one water molecule (Fig. 4c). The lowest activation energy is obtained for the s-trans isomer facilitated by two water molecules in the compact conformation (Fig. 4d). The longest identified water chain acting as proton shuttle comprises four water molecules (Fig. 4e) with a total of five distinct proton transfers. In the expanded conformation, only s-trans-acrolein with a two-water molecule bridge is favorable. We note that while computational studies can overemphasize the importance of intramolecular proton shuttles due to the difficulty of treating solute–solvent proton transfer steps,64 this is not a problem specific to IACTA but rather a general characteristic of computations not representing bulk solvent in an explicit manner.
Importantly, IACTA provides useful insight into complicated systems such as this Michael addition requiring minimal human labor at the cost of comparably moderate computational resources. Indeed, sampling of these pathways and the corresponding transition structures via IACTA took only 20 hours of wall-clock time on a single compute node. The search is fully automated and is successful even when starting from a structure far from the identified reactive pathways. While the obtained results in terms of estimated reaction barriers are only preliminary as they only stem from semi-empirical methods and are not based on actual transition states, the obtained energies can be used for high-throughput virtual screening65 as a qualitative guide to estimate the feasibility of the predicted pathways. Additionally, the corresponding transition structures are reasonable starting points for subsequent transition state optimization, offering significant potential to reduce the associated human labor compared to traditional approaches.
Oxidative addition complexes of drug-like compounds
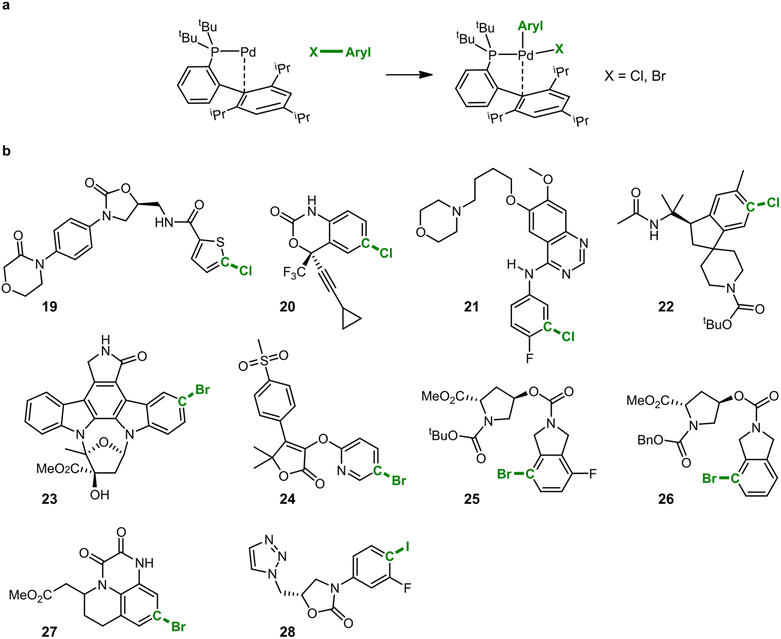
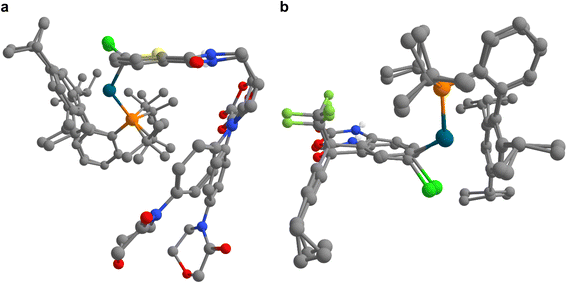
In addition to the exploration of reaction pathways and the prediction of potential by-products, IACTA can also reduce the human effort for setting up transition state calculations and diminish the entrance barrier to computational tools in chemistry by providing reasonable guess structures for subsequent transition state optimizations. We demonstrate this based on calculations for the oxidative addition of a palladium catalyst to a set of drug-like molecules.66 As demonstrated in the literature, forming oxidative addition complexes in this way provides a powerful means for late-stage diversification in experimental screening studies and avoids the sometimes inconsistent performance of catalytic Buchwald–Hartwig couplings with highly functionalized substrates.66Computational studies of organometallic catalysis typically tackle either complex ligands or complex substrates, but very rarely both, likely due to the required computational resources. Such studies are specifically challenging when revolving around designer catalysts such as tBuXPhosPd, which we studied here (cf.Fig. 5a), and functionalized ligands, due to the many possible coordination modes with the metal center.67
In this case study, we present transition state calculations enabled by IACTA for ten reactions with both complex catalysts and complex substrates. Because the aims of this section differ from those of the previous two (i.e., generating good transition state guess structures for a predetermined reaction as opposed to searching for new reactions), the calculations were set up in a more systematic way. Using automated structure generation, the activated catalyst was initially placed such that the Pd atom is approximately 5 angstroms away from the target halide. The halide-aryl bond was chosen as activating coordinate. The IACTA workflow was initiated with this structure and only the most accessible reaction pathway was selected. Finally, the lowest-energy reactant and product structures were re-optimized at the PBE-D3/def2-SVP level of theory. Transition states were obtained by relaxing the automatically obtained approximate transition structures at the PBE-D3/def2-SVP level of theory while constraining the aryl–halide bond, followed by a subsequent transition state optimization via the nudged elastic band method. Qualitative features of the transition states are well-reproduced by IACTA at the GFN2-xTB level of theory, as illustrated in Fig. 6.
The corresponding results are summarized in Table 3. The data show two general trends. First, as expected, activation energies tend to decrease when changing the halogen from chlorine to bromine to iodine.68,69 Secondly, electron-rich (hetero)aromatic rings seem to lead to more facile oxidative addition. This is in contrast to the expected trends for bisligated palladium(0) catalysts but in line with the results obtained for monoligated palladium(0), as the pre-reactive complexes of monoligated palladium(0) and aryl halide tend to be more tightly bound for electron-poor (hetero)aromatic rings.69,70 Furthermore, oxidative addition products with electron-poor (hetero)aromatic rings tend to be more thermodynamically favorable, as previously demonstrated.70,71 Moreover, all the estimated oxidative addition barriers are consistent with facile room temperature reactions, as observed in the original study.66 Looking at the contributions of London dispersion to the reaction energies, we find that larger Gibbs free energies of activation correlate with more repulsive dispersion contributions. This indicates that attractive interactions are lost during the oxidative addition, causing an overall higher barrier, and suggests that proper alignment of noncovalent interactions in the transition states is important in accelerating these reactions.72,73 While none of these findings in and of themselves are novel, the key point we wish to convey is the operational ease of obtaining these results with the help of IACTA.
| Substrate | N atoms | Halogen | Core aryl group | Reaction energies (kcal mol−1) | Compute time (node hours) | ||
|---|---|---|---|---|---|---|---|
| ΔG‡ | ΔG | IACTA | DFT optimizations | ||||
| a The first four columns provide the substrate identity, the total number of atoms in the system, the reacting halide identity, and the reacting aromatic system on the substrate. Gibbs free energies of activation ΔG‡ and Gibbs free energies of reaction ΔG are obtained from PBE-D3/def2-SVP calculations. The last two columns compare the compute times required (in node hours) for IACTA and subsequent DFT optimizations of product, reactant, and transition state geometries. | |||||||
| 19 | 123 | Cl | Thiophene | 13.5 | −12.2 | 10.6 | 4.5 |
| 20 | 106 | Cl | Benzoxazinone | 8.9 | −16.7 | 4.8 | 5.1 |
| 21 | 131 | Cl | Benzene | 16.0 | −6.7 | 10.3 | 3.7 |
| 22 | 141 | Cl | Indane | 4.4 | −15.8 | 10.5 | 4.5 |
| 23 | 132 | Br | Indole | 1.1 | −18.1 | 8.7 | 4.1 |
| 24 | 118 | Br | Pyridine | 12.2 | −12.1 | 7.6 | 3.9 |
| 25 | 130 | Br | Isoindoline | 7.6 | −9.6 | 9.6 | 4.1 |
| 26 | 131 | Br | Isoindoline | 8.0 | −5.6 | 10.7 | 4.6 |
| 27 | 110 | Br | Quinoxalinedione | 4.7 | −16.2 | 5.2 | 6.1 |
| 28 | 106 | I | Benzene | 6.0 | −2.1 | 4.9 | 4.3 |
Finally, we show in Table 3 that the computing demands of IACTA using GFN2-xTB are about twice as large as those of the subsequent PBE-D3/def2-SVP geometry optimizations, and thus are well within the realm of current high-throughput virtual screening capabilities74 allowing to perform reaction screening on a significantly larger scale than demonstrated here.
Conclusion and outlook
Virtual reaction prediction has significant potential to accelerate the search for novel catalysts, automatically flag detrimental reaction pathways (e.g., solvolysis or formation of side products), and help discover new reaction mechanisms. However, chemical reactions are extremely rare events not spontaneously captured by in silico dynamics. The complexity of all but the smallest molecules limits full, systematic searches of all possible bonding patterns and bonding transformations.In this work, we showed that the combination of two key concepts, namely the activation of a single coordinate such as bond stretching chosen by the user and the power of constrained conformer generation via metadynamics, is the foundation of a powerful method to explore chemical reaction pathways and provide the corresponding transition state guess structures. When implemented with robust and efficient semi-empirical quantum chemistry methods such as the GFN-xTB family of methods, it only requires modest computational resources while still providing meaningful results. Nevertheless, using IACTA with alternative electronic structure methods is straightforward. Leveraging user input for the selection of activating coordinates such as a bond to be broken allows us to bypass the quadratic scaling of all possible bond-forming processes encountered by more systematic approaches and explore pathways to be most likely for a given set of substrates or to be of most interest in a given situation. In essence, IACTA is analogous to starting a curly arrow mechanism by breaking one bond, and then computationally completing the mechanism by systematically finding the most energetically feasible responses. However, this comes at the cost of losing some rigor for the systematic exploration of reaction pathways by introducing user bias.
Importantly, while IACTA can in principle be combined with any level of theory, the use of IACTA with semi-empirical methods is sufficiently low-cost to be deployed in an exploratory fashion for medium-to high-throughput virtual screening, predicting, and studying the mechanisms behind by-product formation or catalyst decomposition, and exploring the role of explicit solvation in chemical reactions. Although the semi-empirical calculations used in this work are appropriate for qualitative discovery, they are not accurate enough for quantitative analysis.52 Yet the high degree of inherent parallelism present in our approach makes it scalable on distributed and cloud compute systems, which would compensate for the computational demands required even when higher levels of theory are employed.75 Alternatively, to increase the computational accuracy without sacrificing computational efficiency, machine-learning based computational chemistry methods such as the ANI family of methods76,77 offer huge potential for even more reliable exploration of reactivity together with IACTA. We are currently investigating the use of machine learning methods (such as Gaussian process regression78–80) to robustly refine the transition state guesses obtained from IACTA. Investigations are also underway to improve systematicity by automating the selection of potential activating coordinates. This could enable the study of complex chemical reaction networks3,81 by applying IACTA recursively over obtained products.43 Finally, the inclusion of automated (de)protonation and tautomerization capabilities82,83 would increase the range of chemistry that can be studied systematically by IACTA out of the box and we are testing their implementation as well.
Overall, we believe that IACTA sets the stage for a new approach to computational investigation of reactivity. Accordingly, we envision IACTA to be an important stepping stone towards a true virtual lab where reactivity can be explored in a similar manner as it is done in an experimental lab, without knowledge of the outcome, providing valuable ideas for subsequent in-depth investigations and entire research campaigns.
Methods
The results presented in this paper were obtained using the xTB package45,84 (version 6.3.0) and a custom interfacing and data analysis code. Additional results for the Buchwald–Hartwig coupling reactions were computed using ORCA (version 4.2.1),85 as described below. Timing data is reported for a single dual-socket compute node with two 20-core, 2.4 GHz Intel Skylake processors.Algorithmic details
For generating conformers, the metadynamics module integrated in xTB is used with parameters based on those of the highly reliable algorithm of Grimme et al.38 In effect, molecular dynamics are performed with regular snapshots, and these simulations are augmented with a biasing potential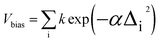 where Δi is the root-mean-square displacement (RMSD) between the current structure and the i-th previous snapshot, and k and α are numerical parameters. The biasing potential strongly drives the discovery of new structures. The obtained structures are then optimized, with similar structures being removed based on RMSD, rotational constant and energy thresholds.38 Finally, structures exceeding a maximum energy threshold are discarded. Numerical values for all parameters are given in the ESI.†
where Δi is the root-mean-square displacement (RMSD) between the current structure and the i-th previous snapshot, and k and α are numerical parameters. The biasing potential strongly drives the discovery of new structures. The obtained structures are then optimized, with similar structures being removed based on RMSD, rotational constant and energy thresholds.38 Finally, structures exceeding a maximum energy threshold are discarded. Numerical values for all parameters are given in the ESI.†
In the examples presented, the overall number of sampled trajectories varies between a few hundreds (such as the iodobutane example) and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (to obtain the results of Table 2), depending on the number of atoms and the chosen sampling parameters. The duration of metadynamics simulations, and thus the number of trajectories, is chosen proportional to the size of the system. A more thorough sampling is done for the 1,4-addition to explore many reactive geometries.
000 (to obtain the results of Table 2), depending on the number of atoms and the chosen sampling parameters. The duration of metadynamics simulations, and thus the number of trajectories, is chosen proportional to the size of the system. A more thorough sampling is done for the 1,4-addition to explore many reactive geometries.
For post-processing, the obtained trajectories are collected and parsed into reactions by transforming geometries of trajectory minima to canonical SMILES using Open Babel86 and identifying changes in the SMILES strings. For structures containing a metal complex, the metal atom is removed before conversion to eliminate spurious bond changes. The transition structure of a trajectory is taken to be the highest energy structure between reactants and products. The guess transition state for a given reaction is the lowest energy transition structure amongst all trajectories for this reaction, and the estimated activation energy is computed by subtracting the energy of the most stable identified reactant conformer from the energy of the approximate transition state.
Refinement of trajectories for oxidative addition complexes
Additional refinement of reaction trajectories was performed for the results shown in Table 3. The specific protocol described here broadly follows that of the computational study by Barder et al. involving a similar catalyst.87 We note that our study involves more substrates and that those substrates are more complex. DFT calculations were performed at the PBE-D3/def2-SVP level of theory.Approximate transition structures obtained from the reaction search were used to find transition states with Berny optimization at the GFN2-xTB level of theory. Here, performance is excellent, with every guess transition structure converging to a transition state. At this point, further transition state refinements were attempted using PBE-D3/def2-SVP, but GFN2-xTB was found to significantly overestimate the length of the aryl–halide bond in the transition state, hindering convergence and making the transition state poorly transferable to higher-level theory. Hence, a more sophisticated procedure was followed for transition state refinements. Specifically, a first transition state guess was obtained by geometry optimization of the xTB-obtained transition state, constraining the carbon–halogen bond. Unconstrained geometry optimization of the resulting structures resulted in the respective oxidative addition products in all cases. Subsequently, a relaxed scan of the carbon–halogen bond to 0.8 times the initial bond length starting from the geometry obtained after constrained optimization was carried out. In addition, a partially relaxed scan of the palladium–halogen bond to 1.5 times the initial bond length was performed by constraining the carbon–halogen bond length. Relaxed geometry optimization of either the last point of the first scan or the minimum energy structure of the second scan, whichever one was lower in energy, yielded the reactant structure. Next, nudged elastic band (NEB) calculations together with a subsequent transition state optimization (keywords NEB-TS or ZOOM-NEB-TS in Orca) was performed using the reactant as starting structure and the transition state guess from the constrained geometry optimization as product structure. Final optimizations of reactants, products and transition states were performed using exact initial Hessians to remove any residual imaginary frequencies. The transition states were verified by calculating both the forward and backward intrinsic reaction coordinates and comparing the resulting endpoint structures with the respective reactant and product structures.
Data availability
All the code used in this work can be downloaded from the following GitHub repository: https://github.com/aspuru-guzik-group/iacta (DOI: https://doi.org/10.5281/zenodo.7079486).Author contributions
C. L., G. P. G. and R. P. conceived the project based on an idea by C. L. C. L. designed and wrote the custom codes used in reaction discovery and data analysis. G. P. G. and R. P. provided scientific input to improve the custom codes. R. P. and C. L performed the DFT computations on oxidative addition complexes. All authors contributed to the analysis of generated data and to the writing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the Defense Advanced Research Projects Agency (DARPA) under the Accelerated Molecular Discovery Program under Cooperative Agreement No. HR00111920027 dated August 1, 2019. The content of the information presented in this work does not necessarily reflect the position or the policy of the Government. G. P. G gratefully acknowledges the Natural Sciences and Engineering Research Council of Canada (NSERC) for the Banting Postdoctoral Fellowship. A. A.-G. thanks Anders G. Frøseth for his generous support. A. A.-G. also acknowledges the generous support of Natural Resources Canada and the Canada 150 Research Chairs program.References
- O. T. Unke and M. Meuwly, Phys Net: A Neural Network for Predicting Energies, Forces, Dipole Moments, and Partial Charges, J. Chem. Theory Comput., 2019, 15(6), 3678–3693, DOI:10.1021/acs.jctc.9b00181.
- A. L. Dewyer, A. J. Argüelles and P. M. Zimmerman, Methods for Exploring Reaction Space in Molecular Systems, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(2), e1354, DOI:10.1002/wcms.1354.
- G. N. Simm, A. C. Vaucher and M. Reiher, Exploration of Reaction Pathways and Chemical Transformation Networks, J. Phys. Chem. A, 2019, 123(2), 385–399, DOI:10.1021/acs.jpca.8b10007.
- J. P. Unsleber and M. Reiher, The Exploration of Chemical Reaction Networks, Annu. Rev. Phys. Chem., 2020, 71(1), 121–142, DOI:10.1146/annurev-physchem-071119-040123.
- L. J. Broadbelt, S. M. Stark and M. T. Klein, Computer Generated Pyrolysis Modeling: On-the-Fly Generation of Species, Reactions, and Rates, Ind. Eng. Chem. Res., 1994, 33(4), 790–799, DOI:10.1021/ie00028a003.
- P. M. Zimmerman, Automated Discovery of Chemically Reasonable Elementary Reaction Steps, J. Comput. Chem., 2013, 34(16), 1385–1392, DOI:10.1002/jcc.23271.
- Y. Kim, S. Choi and W. Y. Kim, Efficient Basin-Hopping Sampling of Reaction Intermediates through Molecular Fragmentation and Graph Theory, J. Chem. Theory Comput., 2014, 10(6), 2419–2426, DOI:10.1021/ct500136x.
- M. Bergeler, G. N. Simm, J. Proppe and M. Reiher, Heuristics-Guided Exploration of Reaction Mechanisms, J. Chem. Theory Comput., 2015, 11(12), 5712–5722, DOI:10.1021/acs.jctc.5b00866.
- S. Habershon, Sampling Reactive Pathways with Random Walks in Chemical Space: Applications to Molecular Dissociation and Catalysis, J. Chem. Phys., 2015, 143(9), 094106, DOI:10.1063/1.4929992.
- Y. V. Suleimanov and W. H. Green, Automated Discovery of Elementary Chemical Reaction Steps Using Freezing String and Berny Optimization Methods, J. Chem. Theory Comput., 2015, 11(9), 4248–4259, DOI:10.1021/acs.jctc.5b00407.
- S. Szymkuć, E. P. Gajewska, T. Klucznik, K. Molga, P. Dittwald, M. Startek, M. Bajczyk and B. A. Grzybowski, Computer-Assisted Synthetic Planning: The End of the Beginning, Angew. Chem., Int. Ed., 2016, 55(20), 5904–5937, DOI:10.1002/anie.201506101.
- G. N. Simm and M. Reiher, Context-Driven Exploration of Complex Chemical Reaction Networks, J. Chem. Theory Comput., 2017, 13(12), 6108–6119, DOI:10.1021/acs.jctc.7b00945.
- D. Rappoport and A. Aspuru-Guzik, Predicting Feasible Organic Reaction Pathways Using Heuristically Aided Quantum Chemistry, J. Chem. Theory Comput., 2019, 15(7), 4099–4112, DOI:10.1021/acs.jctc.9b00126.
- J. N. Wei, D. Duvenaud and A. Aspuru-Guzik, Neural Networks for the Prediction of Organic Chemistry Reactions, ACS Cent. Sci., 2016, 2(10), 725–732, DOI:10.1021/acscentsci.6b00219.
- M. H. S. Segler and M. P. Waller, Neural-Symbolic Machine Learning for Retrosynthesis and Reaction Prediction, Chem.–Eur. J., 2017, 23(25), 5966–5971, DOI:10.1002/chem.201605499.
- P. Schwaller, T. Gaudin, D. Lányi, C. Bekas and T. Laino, Found in Translation: Predicting Outcomes of Complex Organic Chemistry Reactions Using Neural Sequence-to-Sequence Models, Chem. Sci., 2018, 9(28), 6091–6098, 10.1039/C8SC02339E.
- J. Bradshaw, M. J. Kusner, B. Paige, M. H. S. Segler and J. M. Hernández-Lobato, A Generative Model for Electron Paths, in International conference on learning representations, 2019 Search PubMed.
- C. W. Coley, W. Jin, L. Rogers, T. F. Jamison, T. S. Jaakkola, W. H. Green, R. Barzilay and K. F. Jensen, A Graph-Convolutional Neural Network Model for the Prediction of Chemical Reactivity, Chem. Sci., 2019, 10(2), 370–377, 10.1039/C8SC04228D.
- P. Schwaller, T. Laino, T. Gaudin, P. Bolgar, C. A. Hunter, C. Bekas and A. A. Lee, Molecular Transformer: A Model for Uncertainty-Calibrated Chemical Reaction Prediction, ACS Cent. Sci., 2019, 5(9), 1572–1583, DOI:10.1021/acscentsci.9b00576.
- P. Schwaller, R. Petraglia, V. Zullo, V. H. Nair, R. A. Haeuselmann, R. Pisoni, C. Bekas, A. Iuliano and T. Laino, Predicting Retrosynthetic Pathways Using Transformer-Based Models and a Hyper-Graph Exploration Strategy, Chem. Sci., 2020, 11(12), 3316–3325, 10.1039/C9SC05704H.
- M. D. Bajczyk, P. Dittwald, A. Wołos, S. Szymkuć and B. A. Grzybowski, Discovery and Enumeration of Organic-Chemical and Biomimetic Reaction Cycles within the Network of Chemistry, Angew. Chem., Int. Ed., 2018, 57(9), 2367–2371, DOI:10.1002/anie.201712052.
- M. Černohorský, M. Kutý and J. Koča, A Multidimensional Driver for Quantum Chemistry Program MOPAC, Comput. Chem., 1997, 21(1), 35–44, DOI:10.1016/S0097-8485(96)00004-6.
- G. Bringmann, S. Güssregen and H. V. S. Busse, A New Two-Bond Drive Technique for the Calculation of Potential Energy Surfaces with Less Computational Effort, J. Comput.-Aided Mol. Des., 1992, 6(5), 505–512, DOI:10.1007/BF00130400.
- J. Koča, A Mathematical Model of the Logical Structure of Chemistry. A Bridge between Theoretical and Experimental Chemistry and a General Tool for Computer-Assisted Molecular Design, Theor. Chim. Acta, 1991, 80(1), 29–50, DOI:10.1007/BF01114750.
- J. Koča, A Mathematical Model of the Logical Structure of Chemistry. A Bridge between Theoretical and Experimental Chemistry and a General Tool for Computer-Assisted Molecular Design, Theor. Chim. Acta, 1991, 80(1), 51–62, DOI:10.1007/BF01114751.
- M. Yang, J. Zou, G. Wang and S. Li, Automatic Reaction Pathway Search via Combined Molecular Dynamics and Coordinate Driving Method, J. Phys. Chem. A, 2017, 121(6), 1351–1361, DOI:10.1021/acs.jpca.6b12195.
- A. L. Dewyer and P. M. Zimmerman, Finding Reaction Mechanisms, Intuitive or Otherwise, Org. Biomol. Chem., 2017, 15(3), 501–504, 10.1039/C6OB02183B.
- P. Jørgensen, H. J. A. Jensen and T. Helgaker, A Gradient Extremal Walking Algorithm, Theor. Chim. Acta, 1988, 73(1), 55–65, DOI:10.1007/BF00526650.
- K. Ohno and S. Maeda, A Scaled Hypersphere Search Method for the Topography of Reaction Pathways on the Potential Energy Surface, Chem. Phys. Lett., 2004, 384(4), 277–282, DOI:10.1016/j.cplett.2003.12.030.
- S. Maeda and K. Morokuma, Finding Reaction Pathways of Type A + B → X: Toward Systematic Prediction of Reaction Mechanisms, J. Chem. Theory Comput., 2011, 7(8), 2335–2345, DOI:10.1021/ct200290m.
- W. M. C. Sameera, A. K. Sharma, S. Maeda and K. Morokuma, Artificial Force Induced Reaction Method for Systematic Determination of Complex Reaction Mechanisms, Chem. Rec., 2016, 16(5), 2349–2363, DOI:10.1002/tcr.201600052.
- T. Huber, A. E. Torda and W. F. van Gunsteren, Local Elevation: A Method for Improving the Searching Properties of Molecular Dynamics Simulation, J. Comput.-Aided Mol. Des., 1994, 8(6), 695–708, DOI:10.1007/BF00124016.
- A. Laio and M. Parrinello, Escaping Free-Energy Minima, Proc. Natl. Acad. Sci., 2002, 99(20), 12562–12566, DOI:10.1073/pnas.202427399.
- M. Iannuzzi, A. Laio and M. Parrinello, Efficient Exploration of Reactive Potential Energy Surfaces Using Car-Parrinello Molecular Dynamics, Phys. Rev. Lett., 2003, 90(23), 238302, DOI:10.1103/PhysRevLett.90.238302.
- C. Shang and Z.-P. Liu, Stochastic Surface Walking Method for Structure Prediction and Pathway Searching, J. Chem. Theory Comput., 2013, 9(3), 1838–1845, DOI:10.1021/ct301010b.
- A. M. Saitta and F. Saija Miller, Experiments in Atomistic Computer Simulations, Proc. Natl. Acad. Sci., 2014, 111(38), 13768–13773, DOI:10.1073/pnas.1402894111.
- L.-P. Wang, A. Titov, R. McGibbon, F. Liu, V. S. Pande and T. J. Martínez, Discovering Chemistry with an Ab Initio Nanoreactor, Nat. Chem., 2014, 6(12), 1044–1048, DOI:10.1038/nchem.2099.
- S. Grimme, Exploration of Chemical Compound, Conformer, and Reaction Space with Meta-Dynamics Simulations Based on Tight-Binding Quantum Chemical Calculations, J. Chem. Theory Comput., 2019, 15(5), 2847–2862, DOI:10.1021/acs.jctc.9b00143.
- E. Martínez-Núñez, An Automated Method to Find Transition States Using Chemical Dynamics Simulations, J. Comput. Chem., 2015, 36(4), 222–234, DOI:10.1002/jcc.23790.
- E. Martínez-Núñez, An Automated Transition State Search Using Classical Trajectories Initialized at Multiple Minima, Phys. Chem. Chem. Phys., 2015, 17(22), 14912–14921, 10.1039/C5CP02175H.
- S. Maeda and Y. Harabuchi, On Benchmarking of Automated Methods for Performing Exhaustive Reaction Path Search, J. Chem. Theory Comput., 2019, 15(4), 2111–2115, DOI:10.1021/acs.jctc.8b01182.
- E. Fadrná and J. Koča, Single-Coordinate-Driving Method Coupled with Simulated Annealing. An Efficient Tool To Search Conformational Space, J. Phys. Chem. B, 1997, 101(39), 7863–7868, DOI:10.1021/jp9710695.
- D. Rappoport, C. J. Galvin, D. Yu. Zubarev and A. Aspuru-Guzik, Complex Chemical Reaction Networks from Heuristics-Aided Quantum Chemistry, J. Chem. Theory Comput., 2014, 10(3), 897–907, DOI:10.1021/ct401004r.
- C. Bannwarth, S. Ehlert and S. Grimme, GFN2-XTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions, J. Chem. Theory Comput., 2019, 15(3), 1652–1671, DOI:10.1021/acs.jctc.8b01176.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Extended Tight-Binding Quantum Chemistry Methods, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, e01493, DOI:10.1002/wcms.1493.
- S. Maeda, Y. Harabuchi, M. Takagi, K. Saita, K. Suzuki, T. Ichino, Y. Sumiya, K. Sugiyama and Y. Ono, Implementation and Performance of the Artificial Force Induced Reaction Method in the GRRM17 Program, J. Comput. Chem., 2018, 39(4), 233–251, DOI:10.1002/jcc.25106.
- C. W. Lee, B. L. H. Taylor, G. P. Petrova, A. Patel, K. Morokuma, K. N. Houk and B. M. Stoltz, An Unexpected Ireland–Claisen Rearrangement Cascade During the Synthesis of the Tricyclic Core of Curcusone C: Mechanistic Elucidation by Trial-and-Error and Automatic Artificial Force-Induced Reaction (AFIR) Computations, J. Am. Chem. Soc., 2019, 141(17), 6995–7004, DOI:10.1021/jacs.9b01146.
- S. J. Blanksby and G. B. Ellison, Bond Dissociation Energies of Organic Molecules, Acc. Chem. Res., 2003, 36(4), 255–263, DOI:10.1021/ar020230d.
- A. W. V. Hofmann and J. Clark XIV, Researches into the Molecular Constitution of the Organic Bases, Philos. Trans. R. Soc. London, 1851, 141, 357–398, DOI:10.1098/rstl.1851.0017.
- A. Saytzeff, Zur Kenntniss Der Reihenfolge Der Analgerung Und Ausscheidung Der Jodwasserstoffelemente in Organischen Verbindungen, Justus Liebigs Ann. Chem., 1875, 179(3), 296–301, DOI:10.1002/jlac.18751790304.
- G. Tojo and M. Fernández, Oxidations by Hydride Transfer from Metallic Alkoxide, in Oxidation of Alcohols to Aldehydes and Ketones: A Guide to Current Common Practice; Basic Reactions in Organic Synthesis, Springer US, Boston, MA, 2006, pp. 255–279. DOI:10.1007/0-387-25725-X_6.
- M. H. Rasmussen and J. H. Jensen, Fast and Automatic Estimation of Transition State Structures Using Tight Binding Quantum Chemical Calculations, PeerJ Phys. Chem., 2020, 2, e15, DOI:10.7717/peerj-pchem.15.
- M. Elkin, S. M. Szewczyk, A. C. Scruse and T. R. Newhouse, Total Synthesis of (±)-Berkeleyone A, J. Am. Chem. Soc., 2017, 139(5), 1790–1793, DOI:10.1021/jacs.6b12914.
- E. J. Corey and M. Sodeoka, An Effective System for Epoxide-Initiated Cation-Olefin Cyclization, Tetrahedron Lett., 1991, 32(48), 7005–7008, DOI:10.1016/0040-4039(91)85025-Z.
- E. E. Van Tamelen, Bioorganic Chemistry: Sterols and Acrylic Terpene Terminal Expoxides, Acc. Chem. Res., 1968, 1(4), 111–120, DOI:10.1021/ar50004a003.
- E. E. Van Tamelen and J. P. McCormick, Terpene Terminal Epoxides. Mechanistic Aspects of Conversion to the Bicyclic Level, J. Am. Chem. Soc., 1969, 91(7), 1847–1848, DOI:10.1021/ja01035a042.
- K. B. Sharpless and E. E. Van Tamelen, Terpene Terminal Epoxides. Skeletal Rearrangement Accompanying Bicyclization of Squalene 2,3-Oxide, J. Am. Chem. Soc., 1969, 91(7), 1848–1849, DOI:10.1021/ja01035a043.
- V. K. Aggarwal, P. A. Bethel and R. Giles, A Formal Synthesis of (+)-Pyripyropene A Using a Biomimetic Epoxy-Olefin Cyclisation: Effect of Epoxy Alcohol/Ether on Cyclisation Efficiency, J. Chem. Soc., Perkin Trans. 1, 1999, 3315–3321, 10.1039/A906589J.
- D. K. Dhaked, W.-D. Ihlenfeldt, H. Patel, V. Delannée and M. C. Nicklaus, Toward a Comprehensive Treatment of Tautomerism in Chemoinformatics Including in InChI V2, J. Chem. Inf. Model., 2020, 60(3), 1253–1275, DOI:10.1021/acs.jcim.9b01080.
- B. Sunoj, R. Anand and M. Microsolvated, Transition State Models for Improved Insight into Chemical Properties and Reaction Mechanisms, Phys. Chem. Chem. Phys., 2012, 14(37), 12715–12736, 10.1039/C2CP41719G.
- E. Lyngvi and F. Schoenebeck, Oxidative Addition Transition States of Pd(0) Complexes in Polar Solvent—a DFT Study Involving Implicit and Explicit Solvation, Tetrahedron, 2013, 69(27), 5715–5718, DOI:10.1016/j.tet.2013.03.095.
- H. Rzepa, Choreographing a chemical ballet: a story of the mechanism of 1,4-Michael addition, Henry Rzep,’s Blog, https://www.ch.imperial.ac.uk/rzepa/blog/?p=22153, (accessed 2020-06-24) Search PubMed.
- C. Engels, C. Schwab, J. Zhang, M. J. A. Stevens, C. Bieri, M.-O. Ebert, K. McNeill, S. J. Sturla and C. Lacroix, Acrolein Contributes Strongly to Antimicrobial and Heterocyclic Amine Transformation Activities of Reuterin, Sci. Rep., 2016, 6, 36246, DOI:10.1038/srep36246.
- R. E. Plata and D. A. Singleton, A Case Study of the Mechanism of Alcohol-Mediated Morita Baylis-Hillman Reactions. The Importance of Experimental Observations, J. Am. Chem. Soc., 2015, 137, 3811–3826, DOI:10.1021/ja5111392.
- E. O. Pyzer-Knapp, C. Suh, R. Gómez-Bombarelli, J. Aguilera-Iparraguirre and A. Aspuru-Guzik, What Is High-Throughput Virtual Screening? A Perspective from Organic Materials Discovery, Annu. Rev. Mater. Res., 2015, 45(1), 195–216, DOI:10.1146/annurev-matsci-070214-020823.
- M. R. Uehling, R. P. King, S. W. Krska, T. Cernak and S. L. Buchwald, Pharmaceutical Diversification via Palladium Oxidative Addition Complexes, Science, 2019, 363(6425), 405–408, DOI:10.1126/science.aac6153.
- P. R. Melvin, A. Nova, D. Balcells, N. Hazari and M. Tilset, DFT Investigation of Suzuki–Miyaura Reactions with Aryl Sulfamates Using a Dialkylbiarylphosphine-Ligated Palladium Catalyst, Organometallics, 2017, 36(18), 3664–3675, DOI:10.1021/acs.organomet.7b00642.
- H. M. Senn and T. Ziegler, Oxidative Addition of Aryl Halides to Palladium(0) Complexes: A Density-Functional Study Including Solvation, Organometallics, 2004, 23(12), 2980–2988, DOI:10.1021/om049963n.
- B. A. Anjali and C. H. Suresh, Interpreting Oxidative Addition of Ph–X (X = CH3, F, Cl, and Br) to Monoligated Pd(0) Catalysts Using Molecular Electrostatic Potential, ACS Omega, 2017, 2(8), 4196–4206, DOI:10.1021/acsomega.7b00745.
- M. Ahlquist and P.-O. Norrby, Oxidative Addition of Aryl Chlorides to Monoligated Palladium(0): A DFT-SCRF Study, Organometallics, 2007, 26(3), 550–553, DOI:10.1021/om0604932.
- T. R. Kégl, L. Kollár and T. Kégl, DFT Study on the Oxidative Addition of 4-Substituted Iodobenzenes on Pd(0)-Phosphine Complexes, Adv. Phys. Chem., 2015, 2015, 985268, DOI:10.1155/2015/985268.
- J. P. Wagner and P. R. Schreiner, London Dispersion in Molecular Chemistry—Reconsidering Steric Effects, Angew. Chem., Int. Ed., 2015, 54(42), 12274–12296, DOI:10.1002/anie.201503476.
- E. Lyngvi, I. A. Sanhueza and F. Schoenebeck, Dispersion Makes the Difference: Bisligated Transition States Found for the Oxidative Addition of Pd(PtBu3)2 to Ar-OSO2R and Dispersion-Controlled Chemoselectivity in Reactions with Pd[P(IPr)(TBu2)]2, Organometallics, 2015, 34(5), 805–812, DOI:10.1021/om501199t.
- J. Hachmann, R. Olivares-Amaya, A. L. Jinich, A. A. Appleton, M. R. Blood-Forsythe, L. Seress, C. Román-Salgado, K. Trepte, S. Atahan-Evrenk, S. Er, S. Shrestha, R. Mondal, A. Sokolov, Z. Bao and A. Aspuru-Guzik, Lead Candidates for High-Performance Organic Photovoltaics from High-Throughput Quantum Chemistry – the Harvard Clean Energy Project, Energy Environ. Sci., 2014, 7(2), 698–704, 10.1039/C3EE42756K.
- C. A. Grambow, A. Jamal, Y.-P. Li, W. H. Green, J. Zádor and Y. V. Suleimanov, Unimolecular Reaction Pathways of a γ-Ketohydroperoxide from Combined Application of Automated Reaction Discovery Methods, J. Am. Chem. Soc., 2018, 140(3), 1035–1048, DOI:10.1021/jacs.7b11009.
- J. S. Smith, O. Isayev and A. E. Roitberg, ANI-1: An Extensible Neural Network Potential with DFT Accuracy at Force Field Computational Cost, Chem. Sci., 2017, 8(4), 3192–3203, 10.1039/C6SC05720A.
- X. Gao, F. Ramezanghorbani, O. Isayev, J. S. Smith and A. E. Roitberg, TorchANI: A Free and Open Source PyTorch-Based Deep Learning Implementation of the ANI Neural Network Potentials, J. Chem. Inf. Model., 2020, 60(7), 3408–3415, DOI:10.1021/acs.jcim.0c00451.
- A. Denzel and J. Kästner, Hessian Matrix Update Scheme for Transition State Search Based on Gaussian Process Regression, J. Chem. Theory Comput., 2020, 16(8), 5083–5089, DOI:10.1021/acs.jctc.0c00348.
- A. Denzel and J. Kästner, Gaussian Process Regression for Transition State Search, J. Chem. Theory Comput., 2018, 14(11), 5777–5786, DOI:10.1021/acs.jctc.8b00708.
- O.-P. Koistinen, V. Ásgeirsson, A. Vehtari and H. Jónsson, Nudged Elastic Band Calculations Accelerated with Gaussian Process Regression Based on Inverse Interatomic Distances, J. Chem. Theory Comput., 2019, 15(12), 6738–6751, DOI:10.1021/acs.jctc.9b00692.
- J. Proppe and M. Reiher, Mechanism Deduction from Noisy Chemical Reaction Networks, J. Chem. Theory Comput., 2019, 15(1), 357–370, DOI:10.1021/acs.jctc.8b00310.
- P. Pracht, C. A. Bauer and S. Grimme, Automated and Efficient Quantum Chemical Determination and Energetic Ranking of Molecular Protonation Sites, J. Comput. Chem., 2017, 38(30), 2618–2631, DOI:10.1002/jcc.24922.
- S. A. Grimmel and M. Reiher, The Electrostatic Potential as a Descriptor for the Protonation Propensity in Automated Exploration of Reaction Mechanisms, Faraday Discuss., 2019, 220, 443–463, 10.1039/C9FD00061E.
- XTB, Semiempirical Extended Tight-Binding Program Package, 2020 Search PubMed.
- F. Neese, ORCA (v. 6.2.1) Search PubMed.
- Open Babel, The Open Source Chemistry Toolbox (v. 3.1.1) Search PubMed.
- T. E. Barder, M. R. Biscoe and S. L. Buchwald, Structural Insights into Active Catalyst Structures and Oxidative Addition to (Biaryl)Phosphine−Palladium Complexes via Density Functional Theory and Experimental Studies, Organometallics, 2007, 26(9), 2183–2192, DOI:10.1021/om0701017.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional results for varied chemical reactions, values for every numerical parameter used in conformer generation and relaxed scans, and transition state geometries obtained for the oxidative addition of drug-like compounds are provided in the attached supplemental information. See DOI: https://doi.org/10.1039/d2sc05135d. |
| ‡ These authors contributed equally to this work. |
| § Current address: Department of Chemistry, Carnegie Mellon University, Pittsburgh, Pennsylvania, 15213, United States of America. |
| ¶ Current address: Department of Chemical Engineering, Carnegie Mellon University, Pittsburgh, Pennsylvania, 15213, United States of America. |
| || Current address: Stratingh Institute for Chemistry, University of Groningen, Nijenborgh 4, Groningen, 9747 AG, The Netherlands. |
| This journal is © The Royal Society of Chemistry 2022 |