High-throughput design of Na–Fe–Mn–O cathodes for Na-ion batteries†
Shipeng
Jia
a,
Jonathan
Counsell
b,
Michel
Adamič
a,
Antranik
Jonderian
a and
Eric
McCalla
 *a
*a
aDepartment of Chemistry, McGill University, Montreal, Canada. E-mail: eric.mccalla@mcgill.ca
bKratos Analytical Ltd., Wharfside, Trafford Wharf Road, Manchester, UK
First published on 2nd December 2021
Abstract
Na-ion batteries are considered to be environmentally favourable alternatives to Li-ion batteries, particularly in the extremely large-scale application of grid storage, given the abundance of Na. However, to date, the battery performance has not been competitive, and promising Na–Fe–Mn–O materials have been plagued by poor stability in air and unsatisfactory long-term cycling. Herein, high-throughput methods are used to systematically screen the entire pseudo-ternary system. The resulting phase diagram shows significant solid solution regions for 3 important layered-oxide phases: P2, P3 and O3. While only a few compositions were previously studied, we identified over 50 single-phase materials of potential interest for battery materials. The results help explain contradictions in the literature and resolve decisively the locations of each of these phases. The phase mappings were also interpreted within the context of the recently developed cationic potential approach, and we extend the approach to P3 materials for the first time and find that cationic potential cannot be used to distinguish all P2 and P3 materials. High-throughput XPS is used on aged samples to determine stability in air and demonstrates that the stability with both carbon dioxide and moisture is very sensitive to composition and structure (stability changes by an order of magnitude within the Na–Fe–Mn–O system). Importantly, the under-studied P3 and Mn-rich P2 regions show the best stability in air. High-throughput electrochemistry shows that the Mn-rich P2 material also shows the highest first discharge capacity of 206 mA h g−1 and excellent specific energy of 504 W h kg−1. The findings herein therefore provide many insights of importance for the further development of these promising and challenging materials.
1. Introduction
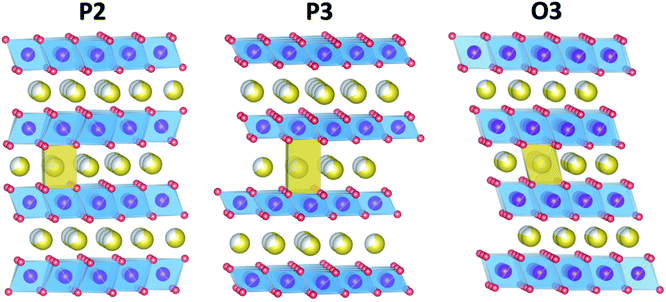
The battery plays a pivotal role in the storage, transfer, release, and usage of electric energy. With the wide application of Li-ion batteries, the huge demand for electric vehicles, and large-scale energy storage, there are more and more concerns about the sustainability of Li-ion batteries. Na-ion batteries, by contrast, could be the key to break the crisis by utilizing cheaper and environmentally friendly materials. Among them, sodium layered oxides are important cathode materials with good sodium mobilities and high specific capacities.1 Layered transition metal oxides NaxMO2 where M are mixtures of transition metals are constituted of layers of MO6 octahedra to preserve 2D transport channels for Na in the layers between the MO6 layers as illustrated in Fig. 1.2 For metal selections, M can be widely varied including: Fe,3 Mn,4 Co,5,6 Cr,7 Ni,6 Ti,8 V9 and their combinations.10–13 Interestingly, binary or ternary transition metal systems show better battery performance than materials with only a single transition metal,14 which makes composition studies imperative. Moreover, during cathode material design, metal combinations can achieve tunable properties with structure, electrochemical performance, and cycling stability. Herein, we focus on the Na–Fe–Mn–O system only, as a wide variety of compositions are possible and, as discussed extensively throughout, the resulting structural and electrochemical properties vary dramatically within the pseudoternary system.Due to the larger Na-ion radius, Na layered oxide can be stabilized into two main groups. According to the notation developed by Delmas et al.,15 P and O are used to represent the primary two layered structures based on the Na environment either in prismatic (P) or octahedral (O) sites, while a number is used to indicate the number of layers in the z-direction that must be stacked to obtain a repeating unit. P2, P3, and O3 are the most common layered structures for the cathode materials in Na-ion batteries as illustrated in Fig. 1. Importantly, all three of these structures have been reported previously in the Na–Fe–Mn–O system as shown in Fig. 2a,11,16–27 but at only a few compositions: four P2, one P3, and five O3 compositions (including one that was not phase pure and resulted in great confusion in the literature as discussed and resolved further herein). Fig. 2c shows our findings here, revealing that all 3 solid solutions are far larger than previously suspected in the literature, this alone justifies the use of high-throughput methods to study this system. The further importance of this system as being composed of earth-abundant environmentally benign elements also motivates this study.
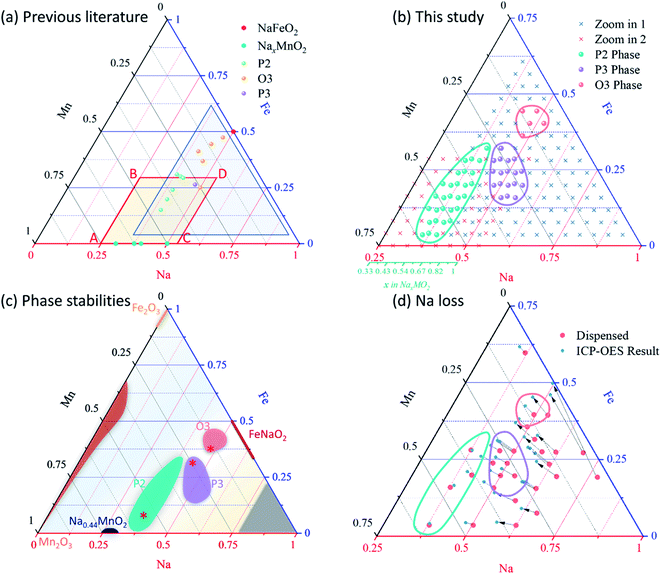 | ||
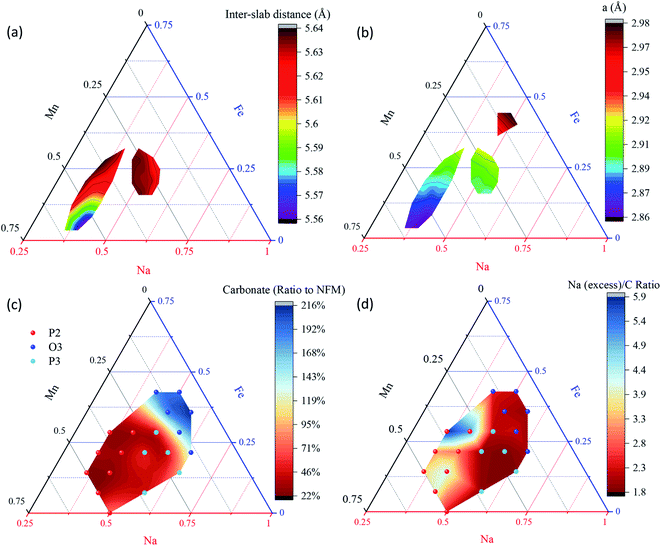
| Fig. 2 (a) The entire Na–Fe–Mn–O phase diagram with compositions previously studied in the literature, along with outlines of the two zoom-in regions studied here. (b) Compositions studied here along with boundaries for the P2, P3 and O3 regions. For all materials, XRD and electrochemistry were performed in high-throughput. Not shown are compositions in the entire phase diagram that were used to determine the phase stabilities in (c). The three * symbols in (c) indicate the three compositions studied more in depth later in Fig. 11. (d) A map of sodium loss during synthesis. All samples were heated at 850 °C. For ease of comparison to the rest of the literature, a secondary axis in turquoise is provided to indicate the Na content as x in NaxMO2. | ||
Let us briefly discuss the general trends seen in the P2, O3 and P3 structures in the literature with a particular emphasis on the limited number of pure phase Na–Fe–Mn–O materials (NFMO). Generally, the P2 structure shows superior Na-ion conductivity and higher capacity than the O3.11 However, the initial sodium content (typically x = 0.6–0.7) in P2 materials is lower than what is typically reported for O3 materials and this limits the first discharge capacity in full batteries.28 To achieve full capacity, P2 materials need to first be discharged below their open-circuit voltage in order to introduce more Na into the structure.
In 2012, Yabuuchi et al. sparked great interest in the Na–Fe–Mn–O materials with a P2–Na0.67Fe0.5Mn0.5O2 and a phase impure O3–NaFe0.5Mn0.5O2 material with capacities of 190 mA h g−1 and 110 mA h g−1, respectively. In that study, the P2 material shows higher capacity and better retention over the O3 material.11 However, the reported NaFe0.5Mn0.5O2 composition was not phase pure at the chosen synthesis temperature of 700 °C.11,29 Recently, Tripathi et al. reported a P3-material at a very nearby composition of Na0.9Fe0.5Mn0.5O2 by a solution-based synthesis. The P3 material showed a capacity of 155 mA h g−1,30 which provides a novel high-sodium phase in the Na–Fe–Mn–O system. However, the structure obtained from the XRD refinement assumes a Mn oxidation state of +3.2 while the XAS data clearly shows Mn is far closer to 4+ (>3.8+) and the resulting structure shows characteristics that we deem unphysical as shown in Fig. S1.† The structure shows a strong asymmetry in the z-direction with very short and very long Na–O distances even though the overall structure is symmetric in the z-direction. Although the material is undeniably P3, we find irregularities in the reported structure and so we revisit it herein with our own XRD data. It is also relevant to note that the P3 structure is often considered to be the sub-stable phase to P2 material only obtained at lower sintering temperatures.31 It is therefore highly relevant that in the current study all materials are obtained by the same synthesis and temperatures such that whether or not P2 or P3 is stabilized is a result of composition only.
Previously, a few pure phase O3 materials have also been made in this pseudoternary system as shown in Fig. 2a. They show a high Fe content, and also a high Na content (x = 0.8–1), where Na ions are stabilized at octahedra sites but with a higher energy barrier and phase transition at high voltage, resulting in a relatively low capacity and fast deterioration during cycling.32 There are other materials of interest within the Na–Fe–Mn–O system that warrant some attention here. O3-type α-NaFeO2 demonstrated electrochemical activity with a reversible capacity of 80 mA h g−1 with Fe3+/Fe4+ redox couple at higher voltage, which has not been found in Li-ion batteries.3 As-prepared P2 and O3 Na–Fe–Mn–O materials, however, have all contained Fe3+ only, demonstrated by Mössbauer spectroscopy16,33 and XAS analysis.11,17,34 For Na–Mn–O materials, due to Jahn–Teller distortion of Mn3+, various structures can be synthesized and lie on a binary in our system. These are: α-NaMnO2 (700 °C),35 β-NaMnO2 (950 °C),26 P2–Na0.67MnO2 (620 °C),27 P′2-Na0.67MnO2 (1100 °C),36 and tunnel-structure Na0.44MnO2 (850 °C).37 Among them, P2 and P′2 are the most attractive materials that can deliver high reversible capacities. P2–Na0.67MnO2 will start to transform into P′2 over 620 °C. P′2 is a distorted P2 phase stabilized with co-operative Jahn–Teller distortion (CJTD). Here, we synthesize all materials at 850 °C which favours the tunnel structure, and results in some co-existence between P2 and P′2 along the binary. It should be noted that even though Kumakura et al. reported P′2 can deliver 216 mA h g−1 for the first discharge capacity,36 the challenge in synthesizing them (e.g. quenching from above 1000 °C) makes them impractical. We therefore do not put much emphasis on these materials here except to determine the Fe content needed to suppress these structures forming.
Chemical stability against air/moisture is a major challenge for the practical application of layered oxides as cathodes for Na-ion batteries. P2 materials, in particular, are known to be unstable in air, reacting both with moisture and carbon dioxide: TOF-SIMS38 and TGA-MS39 have been used previously to analyze the species formed during reactions with air/moisture. Duffort et al. reported that the uptake of CO2 in P2–Na0.67Fe0.5Mn0.5O2 can form carbonate and oxidize Mn into 4+, which leads to a hysteresis on the first charge.39 However, due to the lack of systematic analysis, there are few satisfying methodologies developed to evaluate the composition impact on air/moisture stability. Here, we utilize high-throughput XPS to evaluate the stability of our materials and find good agreement with the mechanism established by Duffort et al. and extend the analysis to quantify the reactivity across the phase diagram.
A final aspect of the literature that is highly applicable to the current study is the recent development of the cationic potential approach. This method is an attempt to develop a predictive parameter that can determine whether or not a certain composition will take the P2 or O3 structures.40 This study plotted the cationic potential on the transition metal layers vs. the cationic potential on the sodium layer. The result was a clear straight line dividing the P2 and O3 materials for a high number of materials mined in the literature. However, no attempt was made to include P3 structures, such that herein we will extend the cationic potential approach to consider P2, O3 and P3 structures for the first time.
Clearly, the rational design of sodium cathode materials requires unravelling the complex relationship between metal compositions, structures, and the resulting battery properties. Herein, we utilize a high throughput (HTP) system to investigate the relationship amongst chemical compositions, crystal structures, electrochemical properties, and air/moisture stability. We utilize HTP methods developed by our group previously to make quality Na–Fe–Mn–O materials on the 3–5 mg scale and demonstrated high-quality HTP electrochemistry obtained from these materials.41Fig. 2 shows that there are significant previously ignored portions of the phase diagram worthy of careful study as potential battery materials. We therefore show careful HTP characterization with XRD, CV and XPS across the entire system. In particular, we introduce high-throughput XPS as a means to quantify air/moisture instability in these materials and find a strong compositional dependence. This serves as the first systematic study of an entire pseudoternary system of importance to Na-ion battery cathodes.
2. Experimental methods
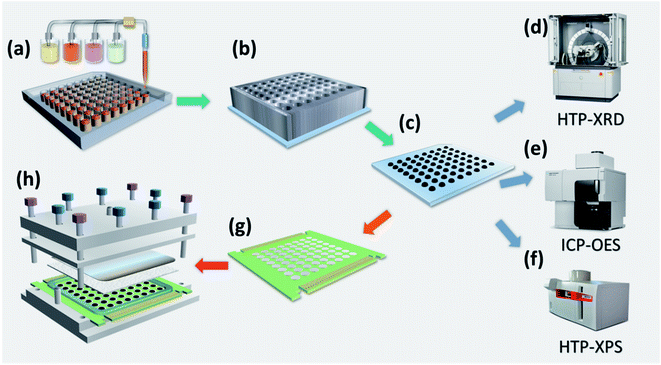
High-throughput approaches have been utilized for all synthesis and characterization herein, as shown schematically in Fig. 3. First, a sol–gel method was adopted for the synthesis to achieve combinatorial NFMO materials, as described in detail in ref. 41. Specifically, the samples were made by first dispensing varying volumes of 2 M solutions of NaNO3, Fe(NO3)3, and Mn(NO3)2 (all from Sigma-Aldrich) onto an 8 × 8 section of a standard 96-well plate with a total volume of 49 μL according to target stoichiometry (Fig. 3a). Citric acid (2 M) was then added as a chelating agent in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio to the total metal cations. Next, the gelation process was performed at 65 °C for 2 days to form homogeneous precursor gels through strong bonding from carboxylic groups. The resulting 8 × 8 set of samples were crushed and transferred onto an alumina plate equipped with an 8 × 8 aluminum smokestack as a combustion chamber to avoid cross-contamination during the off-gassing of citrate bi-products during the initial stages of heating (Fig. 3b). The samples were heated at 400 °C for 2 h (heating rate: 2 °C min−1) to decompose the nitrates and the citric acid in air. After lifting and removing the smokestack, the samples were further calcinated at 850 °C for 12 h in ambient air (heating and cooling rates were 5 °C min−1). The final products are illustrated in Fig. 3c. In total, 448 samples, each weighing about 3–5 mg, were synthesized through the above high-throughput method for further characterization, the compositions are shown in Fig. 2b and c.
1 molar ratio to the total metal cations. Next, the gelation process was performed at 65 °C for 2 days to form homogeneous precursor gels through strong bonding from carboxylic groups. The resulting 8 × 8 set of samples were crushed and transferred onto an alumina plate equipped with an 8 × 8 aluminum smokestack as a combustion chamber to avoid cross-contamination during the off-gassing of citrate bi-products during the initial stages of heating (Fig. 3b). The samples were heated at 400 °C for 2 h (heating rate: 2 °C min−1) to decompose the nitrates and the citric acid in air. After lifting and removing the smokestack, the samples were further calcinated at 850 °C for 12 h in ambient air (heating and cooling rates were 5 °C min−1). The final products are illustrated in Fig. 3c. In total, 448 samples, each weighing about 3–5 mg, were synthesized through the above high-throughput method for further characterization, the compositions are shown in Fig. 2b and c.
All samples were first characterized using high-throughput XRD. The XRD measurements were performed in the transmission mode using a Panalytical Empyrean diffractometer with a Mo target (60 kV, 40 mA) and GalaPIX area detector (Fig. 3d). For Mo Kα radiation (λ = 0.70926 Å for Kα1), a scattering angle range of 4–30° was selected (this corresponds to approximately 10–70° for Cu radiation). For all samples, the main peak intensity was well over 1000 counts for the 10 min scans, demonstrating that the data is suitable for Rietveld refinements. Each scan took <10 min and an entire batch of 64 samples took <10 h. For ease of comparison to the rest of the literature, all patterns shown herein have had the Mo-Kα2 peaks stripped, and scattering angles have been converted to those that would be obtained with Cu-Kα1 (λ = 1.54051 Å) as described in detail in ref. 42. All 448 samples were tested with XRD, and the resulting spectra were analyzed to map the phase stabilities. Home-written software was used to perform Pawley fits on all spectra in order to extract lattice parameters. To help answer some confusion in the literature regarding the structure of the P3 phase, we also performed Rietveld fits using the software Rietica on a single P3 material, Na0.9Mn0.5Fe0.5O2.
After XRD, 2 mg from each sample was then utilized for electrochemical testing. Combinatorial cells with 8 × 8 samples as cathode materials were used to test electrochemical properties as described in detail in ref. 41–43. Firstly, a custom-designed printed circuit board (PCB, Optima Tech) with 64 aluminum covered pads was used as illustrated in Fig. 3g. The composite cathode electrodes had 2 mg of active material and approximately 20 wt% carbon black and 20 wt% polyvinylidene fluoride (PVDF), both of which were added by drop-casting an N-methyl-2-pyrrolidone (NMP) solution. The PCB and electrodes were dried at 80 °C overnight to evaporate NMP. The assembly of the combinatorial cell was performed in an argon-filled glovebox. The electrolyte was 1 M sodium perchlorate in propylene carbonate with 2 wt% fluoroethylene carbonate. Na metal foil was used as the anode with a GF/D glass microfiber prefilter as a separator. The cell was then sealed using a 3M double-sided sealing tape as described in ref. 43. Cyclic voltammetry (CV) was performed with the voltage range 1.5 to 4.3 V vs. Na/Na+ at a scan rate of 0.1 V h−1 on a lab-built high-throughput electrochemical system based on ref. 44, which utilizes a quad voltage source (Keithley 213) and a multimeter with a multiplexer (Keithley 2750). 64 CVs were performed simultaneously. Data were processed to extract average voltages, and specific capacities over the multiple cycles performed. After a few cycles, a few of the cells were also cycled in the range 1.5–4.6 V vs. Na/Na+ (with 4.3–4.6 V being swept over 10 h) to determine if there is any activation at high potentials as obtained in Li-rich layered oxides at these potentials.
In order to quantify how much sodium was lost during synthesis throughout the phase diagram, certain samples were selected for inductively coupled plasma-optical emission spectrometry (ICP-OES). Samples were first dissolved by Aqua Regia in a 96-well plate overnight and diluted by deionized water. Blank control solutions were also prepared as a background to make sure there was no Na/Fe/Mn contamination source from the well plate. Agilent Technologies 5100 ICP-OES associated with the autosampler was used to analyze elemental compositions of combinatorial samples (Fig. 3e). With the help of the autosampler, the ICP-OES can run automatically with a throughput of about 20 samples per hour making it ideal for this study.
In order to obtain a measure of the instability of the NFMO samples in air, high-throughput X-ray photoemission spectroscopy (XPS) was performed using a Kratos Axis Nova spectrometer using a monochromatic Al K(alpha) source (15 mA, 15 kV) illustrated in Fig. 3f. The instrument work function was calibrated to give binding energy (BE) of 83.96 eV for the Au 4f7/2 line for metallic gold and the spectrometer dispersion was adjusted to give a BE of 932.62 eV for the Cu 2p3/2 line of metallic copper. The Kratos charge neutralizer system was used on all specimens. Survey scans were carried out with an analysis area of 300 × 700 microns and a pass energy of 160 eV. High-resolution scans were also performed for the Na 1s, Fe 2p, Mn 3s, and C 1s regions with a pass energy of 20/40 eV. Spectra have been charge-corrected to the mainline of the carbon 1s spectrum (adventitious carbon) set to 284.8 eV. Peak fitting was performed using the ESCApe software. Shirley backgrounds were applied to all 2p spectral areas with components fitted with constrained (Gaussian 70% to Lorentzian 30%) peaks. Survey scans were acquired in 120 s, while high-resolution spectra were acquired in various times (30–720 s) depending on the count rate. Quantification used relative sensitivity factors developed by Cant et al.45 The instrument is suited for high-throughput analysis as it is equipped with three sample holders each capable of mounting >100 samples.
It is important to note that all of the characterizations were performed on the same samples. After XRD, 2 mg were removed for electrochemical testing, leaving enough left for ICP-OES and/or XPS for the samples selected for those measurements.
3. Results and discussion
3.1 Structural phase diagram
To survey the phase distribution for Na–Fe–Mn–O pseudo ternary system, we synthesized 448 samples to both map out the entire Gibbs' triangle and to also focus in on the materials of highest interest for Na-ion batteries, as indicated in Fig. 2c. The reproducibility of this high-throughput system is excellent as demonstrated on these materials in ref. 42. Seven solid-solution regions were identified in the phase diagram: Mn2O3 (ICSD 159865), Fe2O3 (ICSD 154190), Na0.44MnO2 (ICSD 182617), β-FeNaO2 (ICSD 158330), and three layered oxide phases of interest for Na-ion cathodes: P2, P3, and O3 phases. Due to the high volatility of sodium oxides, no sample was obtained for the gray region shown in Fig. 2c near the sodium corner. The rest of the Gibbs' triangle is made up of multi-phase materials. The emphasis herein is on the layered oxides, such that a large number of samples were prepared in this region as shown in Fig. 2b where 184 target compositions were made (120 for zoom-in 1 and 64 for zoom-in 2) with 256 total samples (72 samples were triplicates to check reproducibility, which was found to be excellent as shown in ref. 42). In total, 256 XRD patterns were collected from samples in the zoom-in regions; all of which were visually compared to the reference patterns to identify phases present and subsequently fit using Pawley refinement. Fig. 4 and S5† show representative XRD patterns along with their fits. Fig. 4b shows the progression of the XRD patterns within the P2 single-phase region, illustrated by the red dashed line showing the shifting in peak position with composition. By contrast, Fig. 4c, d and S5† all demonstrate the progression of the XRD patterns through co-existence regions wherein secondary phases appear, and grow with composition. All XRD patterns are fully consistent with the phase stabilities shown in Fig. 2.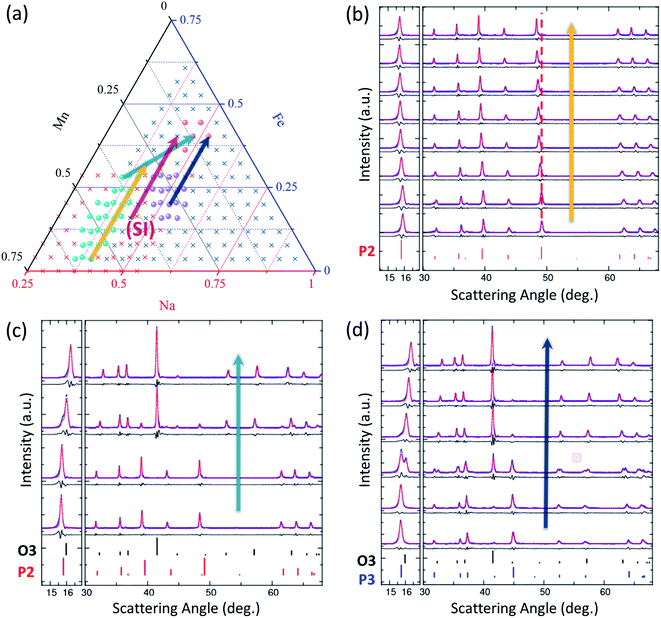 | ||
| Fig. 4 XRD patterns for P2, P3 and O3 structures to understand the phase evolution with chemical compositions. The four arrows in (a) indicate the compositions shown in (b–d) and S5.† (b)–(d) XRD patterns (blue points) along with results of Pawley fits (red) and difference plots black. Relevant reference patterns are shown at the bottom of each XRD stack. In (b), the vertical red dashed line is a guide to the eye to illustrate shifting peak positions with composition within the solid solution. | ||
The dense sampling used here enabled the precise determination of the boundaries to each single-phase region of interest. In total, 29 P2, 18 P3, and 5 O3 single phases are identified based on the XRD patterns. This study, therefore, represents the first investigation of the rich chemistry permitted in the Na–Fe–Mn–O system where only a few single-phase materials had been made previously as discussed in the introduction. The three solid-solution regions of greatest interest here (P2, P3, and O3) are shown in Fig. 2b on the Gibbs' triangle and illustrate the thermodynamic-stable regions for each phase at 850 °C following by slow cooling. In detail, the P2 solid solution takes an ellipse shape over a large range in Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn ratio (0.05–0.55 for Fe/(Fe + Mn)). To help with comparison to other literature, we present this solid solution region as a series of sodium solubility windows in Fig. 6a to illustrate the significant variations in Na solubility as a function of the Fe content (Fe/(Fe + Mn)) after taking Na-loss into account, and this applies to each of the 3 phases. The largest Na solubility window in the P2 structures is seen in the center of the ellipse where the sodium content varies from x = 0.49 to 0.71 for NaxMO2. Comparison to results from other literature46–50 shows that larger ranges in Na content have been enabled with substitutions such as Mg, Ni and Li. Further study following this project will involve further substitutions into the best NFMO structures obtained here.
Mn ratio (0.05–0.55 for Fe/(Fe + Mn)). To help with comparison to other literature, we present this solid solution region as a series of sodium solubility windows in Fig. 6a to illustrate the significant variations in Na solubility as a function of the Fe content (Fe/(Fe + Mn)) after taking Na-loss into account, and this applies to each of the 3 phases. The largest Na solubility window in the P2 structures is seen in the center of the ellipse where the sodium content varies from x = 0.49 to 0.71 for NaxMO2. Comparison to results from other literature46–50 shows that larger ranges in Na content have been enabled with substitutions such as Mg, Ni and Li. Further study following this project will involve further substitutions into the best NFMO structures obtained here.
To further put these solid solutions into context, we first note that it is well established in the literature that iron will take the Fe3+ state under these conditions and that Mn can occupy either the 3+ or 4+ state in the P2 materials. We therefore seek to understand what is the maximum composition range of the form 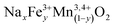 (i.e. we expect no vacancies on the transition metal layers). Charge balancing implies
(i.e. we expect no vacancies on the transition metal layers). Charge balancing implies 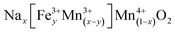 , which represents a triangular region in the Gibbs' triangle with vertices at Mn2O3, NaMnO2 and NaFeO2 as shown in Fig. S6.† Importantly, after accounting for Na loss during synthesis (Fig. 2d and S6†), all P2, P3 and O3 samples lie within the region defined by this formula. That is, all layered oxides made here are in principle consistent with fully occupied transition metal layers, and Fe3+ along with mixed Mn3,4+ balancing the charge, although we find this does not strictly hold for the P3 structures as discussed further below.
, which represents a triangular region in the Gibbs' triangle with vertices at Mn2O3, NaMnO2 and NaFeO2 as shown in Fig. S6.† Importantly, after accounting for Na loss during synthesis (Fig. 2d and S6†), all P2, P3 and O3 samples lie within the region defined by this formula. That is, all layered oxides made here are in principle consistent with fully occupied transition metal layers, and Fe3+ along with mixed Mn3,4+ balancing the charge, although we find this does not strictly hold for the P3 structures as discussed further below.
Interestingly, although the structures are related, there is a miscibility gap between the P2 and P′2 Na0.67MnO2 phases. Below the bottom of the P2 ellipse, P2 with trace P′2 is observed instead of the pure P2. The reason for this is explained by the behaviour of the P2 material Na0.67MnO2 that starts to transform into P′2 at temperatures above 620 °C as discussed in the introduction. According to our phase diagram, as little as 5% of Fe (i.e. NaxFe0.05Mn0.95O2) is sufficient to suppress the Jahn–Teller distortion and stabilize the P2 structure at moderate temperatures without quenching.
It is also important to note that a great deal of variety is permitted in the structures within the triangular region defined by Fe3+ and Mn3,4+. In particular, the P3 structure requires some attention as it has only recently been discovered in the Na–Fe–Mn–O system. Tripathi et al. reported P3–Na0.9Fe0.5Mn0.5O2 (implying an oxidation state of 3.2 for Mn).30 However, their EXAFS data clearly showed that Mn was far closer to the 4+ state, implying that the actual stoichiometry was closer to Na0.82Fe0.45Mn0.45O2. We have therefore performed Rietveld refinement on a P3 sample at this same composition, confirmed with ICP-OES. We consider 3 models: (1) Na0.9Fe0.5Mn0.5O2 as proposed by Tripathi et al., (2) Na0.82[Fe0.45Mn0.45]O2 (i.e. Mn4+ with vacancies on the TM layer), and (3) Na0.72[Na0.1Fe0.45Mn0.45]O2 (i.e. Mn4+ with no vacancies on the TM layer). Fig. S4† shows the results of fitting with each of these models and clearly shows that model 3 yields the smallest residual in the XRD pattern and also gives the best quality parameters for the fits, however the differences between models 2 and 3 are small given that Na scatters X-rays weakly. We therefore conclude that Mn in the P3 phase is in a high oxidation state (near 4+) and that some Na may occupy the TM layer thereby lowering the Na content on the Na layer closer to the 2/3 seen in other P3 materials in the literature.51–54 The occupation of Na on the transition metal layer will be explored in a follow-up study utilizing neutron powder diffraction. It is also significant to emphasize that the XRD patterns leave no doubt that the stable phase near the metal composition NaFe1/2Mn1/2 is in fact P3 and not O3 as originally reported in ref. 11 where Yabuuchi et al. reported a phase impure O3–NaFe0.5Mn0.5O2 synthesized at 700 °C. The impurity implies that the mixing in traditional solid state synthesis was insufficient for the materials to reach equilibrium at the temperatures used and thus the result was an O3 material co-existing with another phase (probably a P3 material based on our phase diagram though it is difficult to extrapolate to lower temperatures). In this work, however, with the help of well mixed metal-ions via the sol–gel method, we obtained a pure phase at this composition and have confirmed the findings of Tripathi et al. that a pure P3 material is the phase stabilized at high temperatures at this composition.
Regarding the O3 single-phase materials, the thermodynamically stable region was found with Fe-rich content as shown in Fig. 2. Delmas et al.23 have previously obtained pure O3–Na0.82Fe2/3Mn1/3O2 with high Fe content but failed with Fe/Mn = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio in complete agreement with our phase diagram. Nonetheless, the region where O3 materials can be stabilized is relatively small in the Na–Fe–Mn–O system. It should also be briefly mentioned that the fact we obtained β-NaFeO2 (orthorhombic) instead of α-NaFeO2 (O3, hexagonal) on the binary is expected given that α-NaFeO2 is a low-temperature phase, whereas β-NaFeO2 is stable above 750 °C.55 Therefore, this again creates a small miscibility gap between the O3 and β-NaFeO2 phase and also demonstrates that the addition of a small amount of Mn is needed to stabilize the α-NaFeO2 (O3) phase over the β-FeNaO2 phase at high temperatures.
1 ratio in complete agreement with our phase diagram. Nonetheless, the region where O3 materials can be stabilized is relatively small in the Na–Fe–Mn–O system. It should also be briefly mentioned that the fact we obtained β-NaFeO2 (orthorhombic) instead of α-NaFeO2 (O3, hexagonal) on the binary is expected given that α-NaFeO2 is a low-temperature phase, whereas β-NaFeO2 is stable above 750 °C.55 Therefore, this again creates a small miscibility gap between the O3 and β-NaFeO2 phase and also demonstrates that the addition of a small amount of Mn is needed to stabilize the α-NaFeO2 (O3) phase over the β-FeNaO2 phase at high temperatures.
Next, we examine the changes in structure with composition within the solid solutions by first looking at the lattice parameters plotted in Fig. 5 and S3.† Since all of the P2, P3, and O3 structures were fit with a hexagonal structure, the a parameter can all be compared easily, however the c parameter includes 3 slabs for P3 and O3 and only 2 for P2, so we plot the inter-slab distance (c/2 for P2 and c/3 for P3&O3) in Fig. 5a and S3a.† Usefully, as was the case for Li layered oxides,56 the contours for the two lattice parameters do not run in the same direction such that a set of lattice parameters may be used to identify a single composition using the contours. The contours also show that the inter-slab distance is correlated strongly to the sodium content: a higher sodium content has more Na–O bonding and shrinks the lattice in the c direction. Moreover, Fig. 5a and b also show that both a and c increase in the P2 materials as Fe content increases, which is not unexpected given that Fe3+ has a large ionic radius (0.645 Å), especially compared to the smaller Mn4+ (0.53Å).
As a final point of interest regarding the structures, we use our results to further refine the cationic potential approach recently used to predict whether given compositions will take the P2 or O3 structure.40 Although that study did not consider P3 structures, we extend the calculations to these structures here. We therefore use the same approach as in ref. 40 here and find that our results are dependent on what oxidation state we assign to Mn (Fe is maintained as 3+). Fig. 6b shows the result when we assume that the P2 and O3 structures have Mn in either the 3 or 4+ state and no vacancies on the TM layer, while for P3 we assume that Mn is in the 4+ and some Na goes to the TM layer to yield full occupancy of these layers as discussed in regards to our XRD data above. Interestingly, the 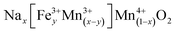 triangle discussed previously collapses to a parabola in the cationic potential plot (shown as ‘fitted line’ in Fig. 6b), such that the P2 and O3 materials lie on this line by definition. The P3 materials lie very close to both this line and the dividing line between P2 and O3 established in ref. 40, and interestingly they lie on the P2 side of the line. However, Fig. S7† shows that they lie on the O3 side of the line if we assume (incorrectly) that Mn can take predominantly the 3+ state in the P3 structure. This illustrates that although the cationic potential approach is useful to put the large body of work into context, it is not yet fully predictive as it takes the experimental determination of all oxidation states to correctly predict the structure based on cationic potential. It is also important to recognize that the space occupied here by P3 materials are occupied by other P2 materials in ref. 40 such that the cationic potential approach does not seem to distinguish P2 from P3 structures. By contrast, the calculated dividing sodium content x = 0.72 illustrated in Fig. 6b can successfully separate the P2 and O3 materials, where the maximum sodium content obtained in this study is 0.71.
triangle discussed previously collapses to a parabola in the cationic potential plot (shown as ‘fitted line’ in Fig. 6b), such that the P2 and O3 materials lie on this line by definition. The P3 materials lie very close to both this line and the dividing line between P2 and O3 established in ref. 40, and interestingly they lie on the P2 side of the line. However, Fig. S7† shows that they lie on the O3 side of the line if we assume (incorrectly) that Mn can take predominantly the 3+ state in the P3 structure. This illustrates that although the cationic potential approach is useful to put the large body of work into context, it is not yet fully predictive as it takes the experimental determination of all oxidation states to correctly predict the structure based on cationic potential. It is also important to recognize that the space occupied here by P3 materials are occupied by other P2 materials in ref. 40 such that the cationic potential approach does not seem to distinguish P2 from P3 structures. By contrast, the calculated dividing sodium content x = 0.72 illustrated in Fig. 6b can successfully separate the P2 and O3 materials, where the maximum sodium content obtained in this study is 0.71.
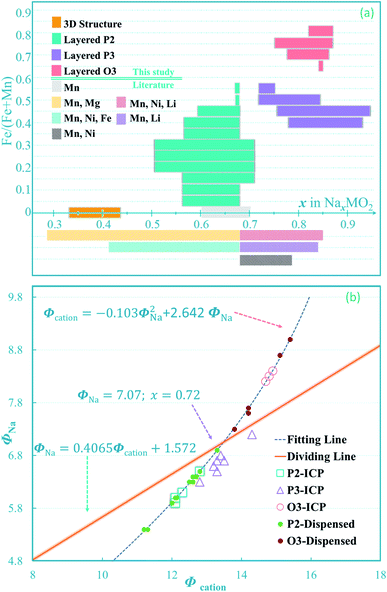 | ||
Fig. 6 (a) The solid solution regions are expressed as a series of sodium-solubility windows at various Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn ratios after taking Na-loss into account. Also shown are results from the literature.46–50 (b) Results of cationic potential analysis as described in ref. 40. The fitted line is described in the text, while the dividing line is defined in ref. 40 where it divides the P2 and O3 phases. For P3 materials that lie very near the boundary, only samples for which there was ICP data are shown so that exact compositions are used. Mn ratios after taking Na-loss into account. Also shown are results from the literature.46–50 (b) Results of cationic potential analysis as described in ref. 40. The fitted line is described in the text, while the dividing line is defined in ref. 40 where it divides the P2 and O3 phases. For P3 materials that lie very near the boundary, only samples for which there was ICP data are shown so that exact compositions are used. | ||
3.2 Stability in air
As discussed in the introduction, the electrochemical performance of NFMO cathodes is significantly limited by the material stability in air, and the poor stability of the P2 materials in particular are currently preventing these materials from being commercialized. Fig. S14† shows that samples obtained here for each of the three phases (P2, P3 and O3) show no significant changes in the XRD patterns after 6 months storage in air. We therefore utilize high-throughput XPS as shown in Fig. 7 and S8, S9† in order to systematically screen stability in air across the phase diagram and also determine oxidation states of Fe and Mn (though it is important to note that this is at the surface of particles only and after 6 months of exposure to air). We first performed survey scans to confirm the presence of Na, Fe, Mn, O and C; then high-resolution scans to quantify both the amounts of each of Na, Fe and Mn and also quantify the amounts of carbonate present. All peaks are fit for all samples, and labels identify them in Fig. S8.†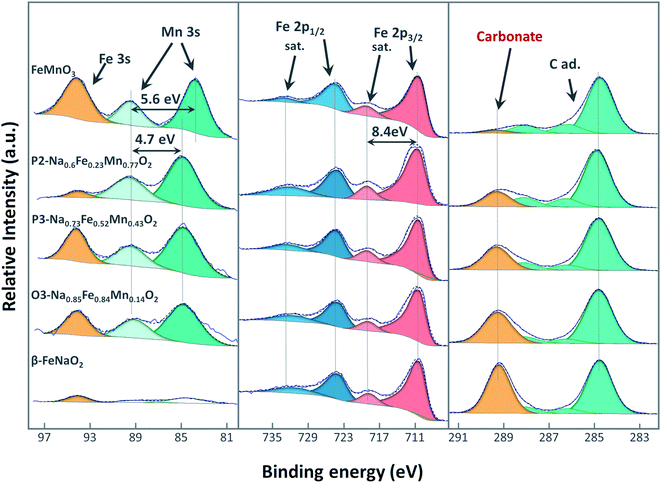 | ||
| Fig. 7 A partial set of XPS results of Mn 3s, Fe 2p and C1s for key samples. Of highest note here the yellow peak in the C 1s spectra represents carbonates. | ||
Systematically, we identify Fe in the 3+ state as determined by the Fe 2p3/2 peak position of ∼710.5 eV with a satellite peak splitting of ∼8.4 eV (ref. 57) consistent with NFMO materials from the literature. For Mn 2p3/2, all spectra are at similar locations at ∼642.0 eV except for FeMnO3 at 641.5 eV, where the Mn in FeMnO3 should be 3+ given that Fe is in the 3+ state. Another way to analyze the Mn oxidation state is by using the splitting between the two Mn 3s peaks. FeMnO3 shows 5.6 eV corresponding to 3+ (as per ref. 58). For all NFMO layered oxides studied here, the Mn 3s splitting energies were in the range 4.6–4.7 eV, indicating we have Mn4+. Again, as discussed in the introduction, this is consistent with Mn at the surface of particles being systematically oxidized to 4+ during reactions with moist air as discussed in ref. 39.
Although surface oxidation states are of interest, the main purpose of using XPS here is to quantify surface reactivity in NFMO materials as a function of composition. We therefore use XPS to determine the relative atomic concentrations on material's surface. First, the Fe/Mn molar ratio is investigated and is found to systematically be close to the dispensed values (within 5% on average). Thus, the Fe/Mn ratio on the particle surface appears to match that of the bulk. By contrast, the Na 1s peak at ∼1071 eV, shown in Fig. S9,† was consistently far larger than expected. Interestingly, the sodium content from the XPS quantification is systematically well above that obtained in ICP analysis and even well above the dispensed values, as shown in Fig. S3† and this deviation is well above the precision of the instrument. Based on the literature discussed in the introduction, we consider two mechanisms that can lead to an excess of sodium at the surface of particles: (1) sodium is extracted from the bulk by moisture to form NaOH, (2) sodium reacts with carbon dioxide in air to form Na2CO3. In both cases the sodium phase formed at the surface will absorb electrons, shielding the NFMO cores such that the Na content seen in the XPS is disproportionally high.
The C 1s peaks are therefore used to quantify the amount of carbonate formed on the surface. Two surface chemistries can be found for C 1s: the lower BE peaks (285–288 eV) are from adventitious carbon and are typically found in this relative ratio on almost all air-exposed samples. The low binding energy peak (C–C/C–H) is used as a charge reference. The peak near 289 eV indicates carbonates are present. The ratio between carbonate and NFM (Na + Fe + Mn) is calculated and presented in Fig. 5c. Importantly, the molar fraction of carbonate present varies from 22 to 216% clearly showing the dramatic impact that composition has on the surface reactivity. The carbonate content also shows a clear trend with composition across the 3 structures of interest here. For P2 and P3, less carbonate is found in comparison to O3 with an average of 35% and 55%, respectively. Thus, they appear more stable with air than the more Fe-rich O3 structures that have an average of 170% carbonate.
The ratio between the excess sodium and the carbonate is therefore expected to be 2.0 in mechanism 2 (reaction with carbon dioxide) above, and take a higher value when mechanism 1 (reaction with moisture) plays an important role. Fig. 5d shows the excess Na to carbon ratio is closest to 2 in the O3 and P3 materials, while considerably higher for P2 materials, which indicates P2 is prone to reactivity with water. It is also important to note that P2 materials with higher Mn content (e.g. NaxMn3/4Fe1/4O2) show better stability against moisture than P2 materials with higher Fe content (e.g. the most heavily studied P2 material Na2/3Mn1/2Fe1/2O2). This will prove to be highly significant in discussing the electrochemical performances below.
Given that this approach to quantify stability in air is new, we use two well-known materials in the literature to demonstrate its effectiveness: β-NaFeO2 and FeMnO3 that show carbonate contents of 220% and 1.5%, respectively. According to the literature, β-NaFeO2 is quite reactive with CO2 and this material is even used for CO2 capture,59 while FeMnO3 is quite stable under air and moisture.60 These two materials show dramatically different air stability from our quantified XPS results and illustrate that this method is accurate in quantifying stability in air. Furthermore, the excess Na to carbonate ratio for β-NaFeO2 was 1.92 which is very close to the expected value of 2 for this material given that it is known to form Na2CO3 when reacting with air.38 We therefore consider using the excess sodium content and the carbonate content together as a valid way to quantify both stability against moisture and carbon dioxide. Again, of greatest importance to this study, P2 materials do not all show the same instability against moisture as that seen in Na2/3Mn1/2Fe1/2O2, and P3 materials show improved stability both in air and moisture. Therefore, the air/moisture stability and the mechanism of degeneration are substantially determined by the structure and compositions of the layered oxides and not all NFMO materials are equally prone to air sensitivity.
3.3 Battery performance
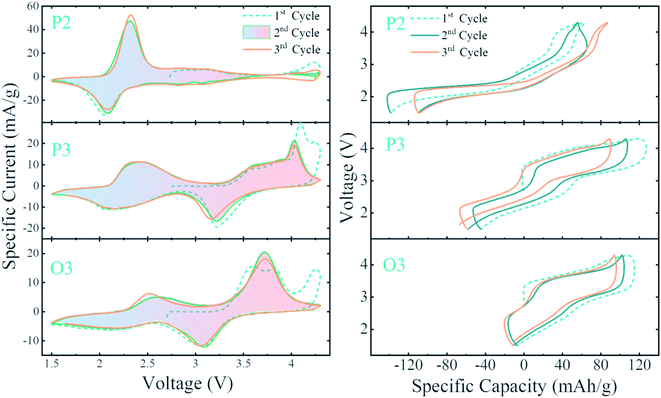
To investigate the electrochemical properties across all NFMO compositions, high-throughput cyclic voltammetry (CV) was performed for all samples in both zoom-in 1 and 2. The reproducibility of the high throughput electrochemistry on these Na-ion cathodes is excellent with standard deviations <1% for average voltages and 7.6% for discharge capacities as demonstrated in ref. 41. For zoom-in 1, we first cycled between 1.5 and 4.3 V at 0.1 V h−1 for 3 cycles then cycled up to 4.6 V. We found no signs of extra capacity when cycled up to 4.6 V, so we focus here on the cutoff to 4.3 V only. For zoom-in 2, performed after zoom-in 1, we cycle solely between 1.5 and 4.3 V for 15 cycles. We show the first 1.5 cycles for zoom-in 2 in Fig. 8 and 9 (this is the same data, Fig. 9 shows the voltage curves calculated from the CVs). The shaded regions highlight the single-phase materials, and we will discuss these in sequence below.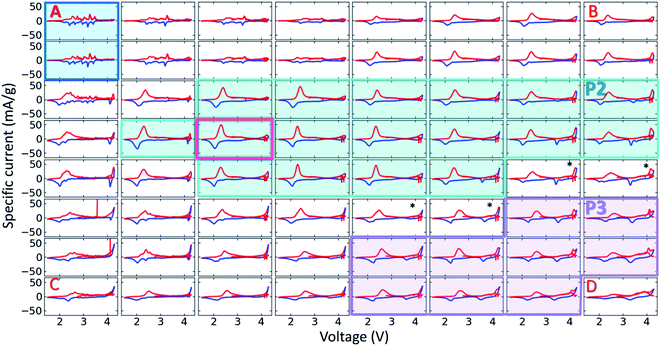 | ||
| Fig. 8 The first 1.5 cycles of the combinatorial cell made in zoom-in region 2. The four corners ABCD are shown in the phase diagram in Fig. 2a. Specifically, A has the most Mn, while A → B represents increasing Fe, and A → C represents increasing Na. Each of the single phase regions are highlighted (tunnel structure NaxMnO2 containing 2 samples, P2 and P3). The highest capacity material of all samples is in the pink rectangle and discussed extensively in the text. | ||
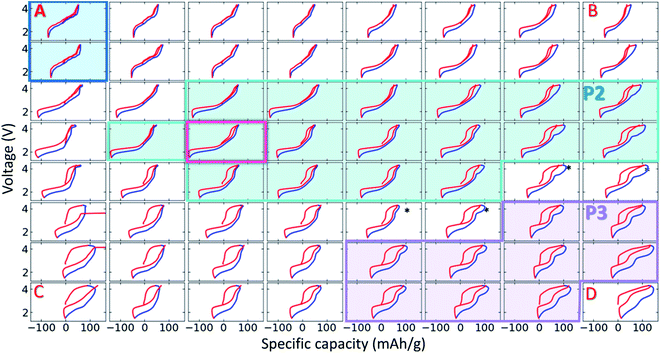 | ||
| Fig. 9 The first 1.5 cycles in zoom-in 2 shown as voltage curves. The four corners ABCD are labelled in Fig. 2a and the same colour coding is used as in Fig. 8 to highlight the various pure phases present. | ||
First, the two tunnel-structure NaxMnO2 materials (highlighted in blue in Fig. 8 and 9) show a high number of peaks in the CVs corresponding to the well-known high number of phase transitions during electrochemical cycling in Na0.44MnO2.67 These transitions are all systematically suppressed in both the P2 and P3 structures; this suppression of transitions is typically associated with an increase in cycling stability. The first cycle discharge capacities of these two materials are 125 and 123 mA h g−1, with capacity retentions of 88% and 89% after 15 cycles respectively, which shows an exceptional electrochemical performance with very close to the ref. 61 and the theoretical discharge capacity of 121 mA h g−1 calculated by Dai et al.62 This result demonstrates HTP synthesis with sol–gel method provides quality materials and good electrochemical performance consistent with that obtained in the literature (as also demonstrated in ref. 41).
In Fig. 8 and 9, the single-phase P2 and P3 materials are highlighted, while the stars in the panels indicate P2/P3 biphasic materials. Two main redox peaks are seen in the CVs: (1) 2.1 V(discharge)/2.4 V(charge) for Mn3+/Mn4+ which is activated by discharge to below the open-circuit voltage of 2.7 V and (2) 3.2 V(discharge)/4.0 V(charge) for Fe3+/Fe4+ redox activity. These peak attributions are well established in the literature.63,64 For Mn-rich P2 samples, we indeed predominantly see the Mn3+/Mn4+ peak, while the Fe3+/Fe4+ redox peak grows with more Fe content. Interestingly, at the boundary between the P2 and P3 regions (marked by *), CVs are consistent with being linear combinations of the nearby P2 and P3 pure phase CVs. Therefore, Fig. 8 clearly demonstrates that the relative amounts of Mn3+/Mn4+ and Fe3+/Fe4+ redox activity in P2 and P3 materials are highly dependent on compositions and not particularly influenced by the structure being P2 or P3.
Fig. 9 shows the voltage curves (voltage as a function of specific capacity) for the same zoom-in 2 samples. Although this is the same data as in Fig. 8, the voltage curves reveal important trends not evident in CVs, the most important of which is overpotential which appears as a vertical offset between the first charge and the first discharge. While this overpotential is very small for P2 materials with high Mn content (including the highest capacity material shown in the pink rectangle), it becomes quite significant in the Fe-rich P2 and all P3 materials. Interestingly, this trend in increasing overpotential is consistent with the trend in Na2CO3 content on the surface of particles shown in Fig. 5c. The high voltage on the first charge has been proposed to be due to the reactivity of surface Na2CO3 in ref. 39 and 65, and our findings are certainly consistent with this hypothesis. Furthermore, this higher overpotential in the P3 materials is not only seen in the first charge, but also can be found with a higher slope (voltage jump) at the capacity-voltage curve in Fig. 9. Delmas et al. also reported this polarization effect by GITT.18 At the stage with only Mn4+ and Fe3+ species in the material during the cycling, the charge transfer process is much slower. The general trend that the Mn3+/Mn4+ couple shows a lower overpotential (∼0.3 V) than the Fe3+/Fe4+ couple (0.8 V) is clearly maintained for both P2 and P3 materials across all compositions in Fig. 9.
In Fig. S10,† the first 5 cycles for zoom-in 2 are shown in order to illustrate that the charge endpoint slippage (which is caused by irreversible electrolyte consumption at the higher voltage66) varies greatly across the phase diagram. This test can demonstrate the cycling stability of the cathode material and even though we use the same electrolyte for the CV test, the different materials can show different effects on electrolyte oxidation. Of highest interest here, the slippage is very small in both Fe-rich P2 phases and the P3 phases. In fact, an Fe content of ∼16% (Fe/(Na + Fe + Mn)) is found to separate the samples with high slippage from those with low slippage. This demonstrates that Fe can effectively suppress the electrolyte oxidation and thereby stabilize the interface between the cathode materials with the electrolyte.
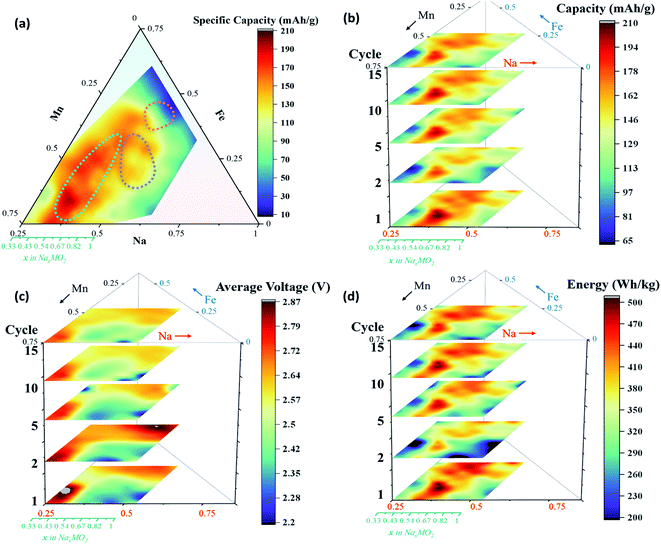
Having discussed the main features in the electrochemical data, we next explore the impact of composition on the important metrics for battery operation, all extracted from the CVs. Fig. 10a shows the first discharge capacities across both zoom-in plates, while Fig. 10b–d shows the discharge capacity, average discharge voltage, and energy across 15 cycles. Fig. S11 and S12† show the specific capacity and average voltage as a function of cycle number. Generally speaking, there is good capacity retention over the 15 cycles, and no signs of voltage fade. Overall, the P2 and P3 materials show higher capacities than the O3 and are therefore the main focus of this discussion. The energy contour plot in Fig. 10d shows the same trends as seen in capacity (Fig. 10b) implying that any change in average voltage is overshadowed by changes in capacity. Specifically, in the P2 materials, the average voltage decreases with increased manganese content as expected, but this decrease is more than compensated for by an increase in capacity, such that the highest energy P2 material is in fact quite rich in Mn (Na0.59Fe0.13Mn0.87O2) and this continues to be true through all 15 cycles.
3.4 Main consequences of this study on Na-ion cathode design
As a final point of focus regarding the battery performance, we summarize our findings by comparing the highest discharge capacity samples from each phase. These are: Na0.59Fe0.13Mn0.87O2 (P2, 206 mA h g−1), Na0.74Fe0.54Mn0.41O2 (P3, 180 mA h g−1), and Na0.85Fe0.70Mn0.30O2 (O3, 131 mA h g−1). Fig. 11 shows the cycling results for these 3 materials only. This figure certainly reinforces much of the above discussion: the Mn-rich P2 phase shows Mn-dominated redox activity and a great deal of activation below the open-circuit voltage as well as the smallest hysteresis. This material is both rich in Mn and slightly deficient in Na compared to the most heavily studied P2–Na0.67Fe0.5Mn0.5O2, such that this material is of particular interest for further study, especially given that it was found to be less reactive with moisture in the XPS results above. In particular, we consider studying the impact of further substitutions on the stability (both in air and in the electrolyte) to be of the highest priority. Given that its capacity retention in Fig. S11† was relatively noisy in the combinatorial cell, we made a Swagelok style cell with this material and it showed high capacity retention of 87% over 50 cycles (Fig. S13†). By contrast to this P2 material, the O3 material is of little interest given the low capacities and large overpotentials. Finally, the P3 material (slightly more Fe rich than the single P3 material previously studied in this system) is also of further interest. Not only is the capacity quite high and cycling retention good, but the stability with moisture was found to be better than P2 materials based on XPS. The high iron content also results in a higher average voltage than in the P2 material. Given that stability in air/moisture is considered the strongest hindrance to commercialization for this class of cathodes, we consider this P3 material of high interest for further study.To further understand the differences in performance of these 3 materials, SEM was performed on these 3 materials. Fig. S15† shows representative images for each of these phases. In all three samples the primary particles are in the range from 0.5 to 2 μm and form relatively porous secondary particles thereby giving easy access to electrolyte. We therefore see no correlation between electrochemical performance differences and morphology. Furthermore, to ensure that the selected voltage window did not bias the results in favor of the P2 and P3 phases, CVs were repeated on these 3 materials in the range 1.5–4.6 V as shown in Fig. S16.† The first discharge capacities did not change appreciably: 206 mA h g−1 for P2, 173 mA h g−1 for P3, and 136 mA h g−1 for O3. All 3 phases showed an increase in irreversible capacity consistent with an increase in electrolyte oxidation at such high potentials. Overall, the Mn-rich P2 and P3 phases continue to show the best electrochemistry even when a larger potential window is utilized.
This work clearly identifies two key compositions that warrant further exploration: the Mn-rich P2 phase and the P3 phase. Despite their improved performance, they continue to show some instability in air and further improvement of their extended cycling is certainly required in order to commercialize these materials. Both coatings and further substitutions are promising approaches to further improve both these important properties. Follow-up to this study will include a systematic screening of substitutions (>50 substituents are currently possible with our sol–gel synthesis approach) into both the Mn-rich P2 and the P3 materials in order to further improve the materials' stability and extended cycling. Utilizing those substituents to make a coating (or shell) is also of high interest for further development of these promising materials.
4. Conclusions
Newly developed high-throughput synthesis methods for Na-ion cathodes were used to make 448 Na–Fe–Mn–O materials. They were characterized with high-throughput XRD, XPS, ICP, and electrochemistry. The structural phase diagrams show that three phases are of interest as potential Na-ion battery cathodes: P2, P3 and O3, which all exist as 2D solid solutions within the phase diagrams. All 3 regions are larger than previously suspected in the literature, and the systematic study across compositions helped resolve some confusion in the literature such as whether O3 or P3 is made at the NaFe1/2Mn1/2O2 compositions. The phase mappings were also interpreted within the context of the recently developed cationic potential approach, and we found that the P3 materials lie on the P2 side of the dividing line, but they are not distinguishable from the P2 materials based on cationic potentials alone. Also of significance, the highest energy density materials in each of the 3 solid solution regions were found at novel compositions. In particular, the highest energy density P2 material is relatively rich in Mn and has a slight deficiency in Na compared to the most heavily studied P2 material. The best performing material showed capacity retention of 87% after 50 slow CV cycles (56 h per cycle) showing very promising cycling behavior for a Na half cell. Importantly, we also quantify the stability in air/moisture using XPS on aged samples across the entire phase diagram and find that the high manganese P2 and the under-explored P3 materials are in fact the most stable. A P3 material also showed both high capacities and good cycling performance. Given that instability with air is currently preventing the commercialization of P2 materials, we expect the results for both P3 and Mn-rich P2 materials here to help guide further development of these materials.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Natural Sciences and Engineering Research Council of Canada under the auspices of a Discovery grant. SJ also acknowledges a FRQNT graduate student scholarship.References
- Q. Liu, Z. Hu, M. Chen, C. Zou, H. Jin, S. Wang, S. L. Chou and S. X. Dou, Small, 2019, 15, 1805381 CrossRef.
- N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636–11682 CrossRef CAS PubMed.
- N. Yabuuchi, H. Yoshida and S. Komaba, Electrochemistry, 2012, 80, 716–719 CrossRef CAS.
- L. Bordet-Le Guenne, P. Deniard, P. Biensan, C. Siret and R. Brec, J. Mater. Chem., 2000, 10, 2201–2206 RSC.
- R. Berthelot, D. Carlier and C. Delmas, Nat. Mater., 2011, 10, 74–80 CrossRef CAS.
- C. Delmas, J.-J. Braconnier, C. Fouassier and P. Hagenmuller, Solid State Ionics, 1981, 3, 165–169 CrossRef.
- C.-Y. Yu, J.-S. Park, H.-G. Jung, K.-Y. Chung, D. Aurbach, Y.-K. Sun and S.-T. Myung, Energy Environ. Sci., 2015, 8, 2019–2026 RSC.
- A. Maazaz, C. Delmas and P. Hagenmuller, J. Inclusion Phenom., 1983, 1, 45–51 CrossRef CAS.
- M. Guignard, C. Didier, J. Darriet, P. Bordet, E. Elkaïm and C. Delmas, Nat. Mater., 2013, 12, 74–80 CrossRef CAS PubMed.
- D. H. Lee, J. Xu and Y. S. Meng, Phys. Chem. Chem. Phys., 2013, 15, 3304–3312 RSC.
- N. Yabuuchi, M. Kajiyama, J. Iwatate, H. Nishikawa, S. Hitomi, R. Okuyama, R. Usui, Y. Yamada and S. Komaba, Nat. Mater., 2012, 11, 512–517 CrossRef CAS PubMed.
- F. Tournadre, L. Croguennec, I. Saadoune, D. Carlier, Y. Shao-Horn, P. Willmann and C. Delmas, J. Solid State Chem., 2004, 177, 2790–2802 CrossRef CAS.
- Z.-Y. Li, R. Gao, L. Sun, Z. Hu and X. Liu, J. Mater. Chem. A, 2015, 3, 16272–16278 RSC.
- M. H. Han, E. Gonzalo, G. Singh and T. Rojo, Energy Environ. Sci., 2015, 8, 81–102 RSC.
- C. Delmas, C. Fouassier and P. Hagenmuller, Physica B+C, 1980, 99, 81–85 CrossRef CAS.
- J. Thorne, R. Dunlap and M. d. Obrovac, J. Electrochem. Soc., 2012, 160, A361 CrossRef.
- W. K. Pang, S. Kalluri, V. K. Peterson, N. Sharma, J. Kimpton, B. Johannessen, H. K. Liu, S. X. Dou and Z. Guo, Chem. Mater., 2015, 27, 3150–3158 CrossRef CAS.
- B. Mortemard de Boisse, D. Carlier, M. Guignard, L. Bourgeois and C. Delmas, Inorg. Chem., 2014, 53, 11197–11205 CrossRef CAS.
- B. Mortemard de Boisse, D. Carlier, M. Guignard, E. Guerin, M. Duttine, A. Wattiaux and C. Delmas, Chem. Mater., 2018, 30, 7672–7681 CrossRef CAS.
- T. Kodera and T. Ogihara, J. Ceram. Soc. Jpn., 2014, 122, 483–487 CrossRef.
- H. Hirsh, M. Olguin, H. Chung, Y. Li, S. Bai, D. Feng, D. Wang, M. Zhang and Y. S. Meng, J. Electrochem. Soc., 2019, 166, A2528 CrossRef CAS.
- H. Xu, J. Zong and X.-j. Liu, Ionics, 2018, 24, 1939–1946 CrossRef CAS.
- B. M. De Boisse, D. Carlier, M. Guignard and C. Delmas, J. Electrochem. Soc., 2013, 160, A569 CrossRef.
- S. Okada, Y. Takahashi, T. Kiyabu, T. Doi, J.-I. Yamaki and T. Nishida, ECS Meet. abstr., 2006, 4, 201 Search PubMed.
- A. Caballero, L. Hernan, J. Morales, L. Sanchez, J. S. Pena and M. Aranda, J. Mater. Chem., 2002, 12, 1142–1147 RSC.
- J. Billaud, R. J. Clément, A. R. Armstrong, J. Canales-Vázquez, P. Rozier, C. P. Grey and P. G. Bruce, J. Am. Chem. Soc., 2014, 136, 17243–17248 CrossRef CAS.
- J.-P. Parant, R. Olazcuaga, M. Devalette, C. Fouassier and P. Hagenmuller, J. Solid State Chem., 1971, 3, 1–11 CrossRef CAS.
- R. J. Clément, P. G. Bruce and C. P. Grey, J. Electrochem. Soc., 2015, 162, A2589 CrossRef.
- X. Lu, Y. Wang, P. Liu, L. Gu, Y.-S. Hu, H. Li, G. P. Demopoulos and L. Chen, Phys. Chem. Chem. Phys., 2014, 16, 21946–21952 RSC.
- A. Tripathi, S. Xi, S. R. Gajjela and P. Balaya, Chem. Commun., 2020, 56, 10686–10689 RSC.
- N.-A. Nguyen, K. Kim, K. H. Choi, H. Jeon, K. Lee, M.-H. Ryou and Y. M. Lee, J. Electrochem. Soc., 2016, 164, A6308 CrossRef.
- S. Komaba, N. Yabuuchi, T. Nakayama, A. Ogata, T. Ishikawa and I. Nakai, Inorg. Chem., 2012, 51, 6211–6220 CrossRef CAS.
- E. Lee, D. E. Brown, E. E. Alp, Y. Ren, J. Lu, J.-J. Woo and C. S. Johnson, Chem. Mater., 2015, 27, 6755–6764 CrossRef CAS.
- J. Zhao, J. Xu, D. H. Lee, N. Dimov, Y. S. Meng and S. Okada, J. Power Sources, 2014, 264, 235–239 CrossRef CAS.
- X. Ma, H. Chen and G. Ceder, J. Electrochem. Soc., 2011, 158, A1307 CrossRef CAS.
- S. Kumakura, Y. Tahara, K. Kubota, K. Chihara and S. Komaba, Angew. Chem., 2016, 128, 12952–12955 CrossRef.
- X. Zhou, A. Zhao, Z. Chen and Y. Cao, Electrochem. Commun., 2020, 106897 Search PubMed.
- Y. You, A. Dolocan, W. Li and A. Manthiram, Nano Lett., 2018, 19, 182–188 CrossRef PubMed.
- V. Duffort, E. Talaie, R. Black and L. F. Nazar, Chem. Mater., 2015, 27, 2515–2524 CrossRef CAS.
- C. Zhao, Q. Wang, Z. Yao, J. Wang, B. Sánchez-Lengeling, F. Ding, X. Qi, Y. Lu, X. Bai and B. Li, Science, 2020, 370, 708–711 CrossRef CAS PubMed.
- T. Adhikari, A. Hebert, M. Adamič, J. Yao, K. Potts and E. McCalla, ACS Comb. Sci., 2020, 22, 311–318 CrossRef CAS PubMed.
- E. McCalla, M. Parmaklis, S. Rehman, E. Anderson, S. Jia, A. Hebert, K. Potts, A. Jonderian, T. Adhikari and M. Adamič, Can. J. Chem., 2021 DOI:10.1139/cjc-2021-0111.
- K. P. Potts, E. Grignon and E. McCalla, ACS Appl. Energy Mater., 2019, 2, 8388–8393 CrossRef CAS.
- M. Fleischauer, T. Hatchard, G. Rockwell, J. Topple, S. Trussler, S. Jericho, M. Jericho and J. Dahn, J. Electrochem. Soc., 2003, 150, A1465 CrossRef CAS.
- A. G. Shard, J. D. Counsell, D. J. Cant, E. F. Smith, P. Navabpour, X. Zhang and C. J. Blomfield, Surf. Interface Anal., 2019, 51, 763–773 CrossRef CAS.
- N. Yabuuchi, R. Hara, M. Kajiyama, K. Kubota, T. Ishigaki, A. Hoshikawa and S. Komaba, Adv. Energy Mater., 2014, 4, 1301453 CrossRef.
- J. Cabana, N. A. Chernova, J. Xiao, M. Roppolo, K. A. Aldi, M. S. Whittingham and C. P. Grey, Inorg. Chem., 2013, 52, 8540–8550 CrossRef CAS.
- I. Hasa, D. Buchholz, S. Passerini and J. Hassoun, ACS Appl. Mater. Interfaces, 2015, 7, 5206–5212 CrossRef CAS PubMed.
- D. Buchholz, C. Vaalma, L. G. Chagas and S. Passerini, J. Power Sources, 2015, 282, 581–585 CrossRef CAS.
- D. Kim, S. H. Kang, M. Slater, S. Rood, J. T. Vaughey, N. Karan, M. Balasubramanian and C. S. Johnson, Adv. Energy Mater., 2011, 1, 333–336 CrossRef CAS.
- E. J. Kim, L. A. Ma, L. C. Duda, D. M. Pickup, A. V. Chadwick, R. Younesi, J. T. Irvine and A. R. Armstrong, ACS Appl. Energy Mater., 2019, 3, 184–191 CrossRef.
- S. Maddukuri, P. Valerie and V. V. Upadhyayula, ChemistrySelect, 2017, 2, 5660–5666 CrossRef CAS.
- B. Song, E. Hu, J. Liu, Y. Zhang, X.-Q. Yang, J. Nanda, A. Huq and K. Page, J. Mater. Chem. A, 2019, 7, 1491–1498 RSC.
- Y.-N. Zhou, P.-F. Wang, X.-D. Zhang, L.-B. Huang, W.-P. Wang, Y.-X. Yin, S. Xu and Y.-G. Guo, ACS Appl. Mater. Interfaces, 2019, 11, 24184–24191 CrossRef CAS.
- I. Grey and C. Li, J. Solid State Chem., 1987, 69, 116–125 CrossRef CAS.
- E. McCalla, A. Rowe, R. Shunmugasundaram and J. Dahn, Chem. Mater., 2013, 25, 989–999 CrossRef CAS.
- A. Grosvenor, B. Kobe, M. Biesinger and N. McIntyre, Surface and Interface Analysis: An International Journal devoted to the development and application of techniques for the analysis of surfaces, Interfaces and Thin Films, 2004, 36, 1564–1574 CAS.
- V. Galakhov, M. Demeter, S. Bartkowski, M. Neumann, N. Ovechkina, E. Kurmaev, N. Lobachevskaya, Y. M. Mukovskii, J. Mitchell and D. Ederer, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 113102 CrossRef.
- J. F. Gómez-García and H. Pfeiffer, J. Phys. Chem. C ., 2018, 122, 21162–21171 CrossRef.
- Z. Z. Vasiljevic, M. P. Dojcinovic, J. B. Krstic, V. Ribic, N. B. Tadic, M. Ognjanovic, S. Auger, J. Vidic and M. V. Nikolic, RSC Adv., 2020, 10, 13879–13888 RSC.
- X. Zhou, R. K. Guduru and P. Mohanty, J. Mater. Chem. A, 2013, 1, 2757–2761 RSC.
- K. Dai, J. Mao, X. Song, V. Battaglia and G. Liu, J. Power Sources, 2015, 285, 161–168 CrossRef CAS.
- M. H. Han, B. Acebedo, E. Gonzalo, P. S. Fontecoba, S. Clarke, D. Saurel and T. Rojo, Electrochim. Acta, 2015, 182, 1029–1036 CrossRef CAS.
- R. Viswanatha, B. Kishore, U. Bharath and N. Munichandraiah, J. Electrochem. Soc., 2018, 165, A263 CrossRef CAS.
- M. Sathiya, J. Thomas, D. Batuk, V. Pimenta, R. Gopalan and J.-M. Tarascon, Chem. Mater., 2017, 29, 5948–5956 CrossRef CAS.
- A. Rowe, J. Camardese, E. McCalla and J. Dahn, J. Electrochem. Soc., 2014, 161, A1189 CrossRef CAS.
- X. He, J. Wang, B. Qiu, E. Paillard, C. Ma, X. Cao, H. Liu, M. C. Stan, H. Liu and T. Gallash, Nano Energy, 2016, 27, 602–610 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta07940a |
| This journal is © The Royal Society of Chemistry 2022 |