Topological phase transition and skyrmions in a Janus MnSbBiSe2Te2 monolayer†
Zebin
Wu
ab,
Yufei
Xue
a,
Zhong
Shen
a and
Changsheng
Song
 *ac
*ac
aKey Laboratory of Optical Field Manipulation of Zhejiang Province, Department of Physics, Zhejiang Sci-Tech University, Hangzhou, 310018, China. E-mail: cssong@zstu.edu.cn
bSchool of Physics, University of Electronic Science and Technology of China, Chengdu, 611731, China
cLonggang Institute of Zhejiang Sci-Tech University, Wenzhou, 325802, China
First published on 18th November 2022
Abstract
Using first-principles calculations and micro-magnetic simulations, we propose a Janus MnSbBiSe2Te2 (MSBST) monolayer derived from the MnBi2Te4 (MBT) ferromagnet and investigate the influence of biaxial strain on the electronic structures, topological characteristics and spin textures. Different from pristine MBT with an out-of-plane easy axis, the anisotropy of MSBST prefers an in-plane direction. Intriguingly, switching the easy axis direction of MSBST will significantly modify the band structure. Topological phase transition can be achieved by applying a compressive strain, making MSBST become a topological insulator with 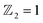 . Moreover, due to the inherent inversion asymmetry of Janus MSBST, a large Dzyaloshinskii–Moriya interaction (DMI) is induced for generating and stabilizing skyrmions. By micro-magnetic simulations, the results of spin textures show that the skyrmions phase can be achieved in MSBST with an external magnetic field of 0.8 T. Our findings provide guidelines for the development and application of spintronic devices with nontrivial topological properties and a large DMI.
. Moreover, due to the inherent inversion asymmetry of Janus MSBST, a large Dzyaloshinskii–Moriya interaction (DMI) is induced for generating and stabilizing skyrmions. By micro-magnetic simulations, the results of spin textures show that the skyrmions phase can be achieved in MSBST with an external magnetic field of 0.8 T. Our findings provide guidelines for the development and application of spintronic devices with nontrivial topological properties and a large DMI.
1. Introduction
Two-dimensional (2D) Janus ferromagnets with unidentical types of atoms on their opposite sides have received tremendous interest recently.1–3 Multiple theoretical4–6 and experimental7–9 studies have already proved the feasibility of Janus materials. Owing to their inherent inversion asymmetry and strong spin–orbit coupling (SOC) effect, some novel properties such as spin–valley splitting,10 Rashba splitting11 and especially a large Dzyaloshinskii–Moriya interaction (DMI)12,13 can be induced in Janus magnets when taking the magnetic proximity effect into account.14Among them, the DMI is a chiral interaction that usually exists in magnetic compounds lacking centrosymmetric or thin films with broken inversion symmetry.15,16 Meanwhile, the DMI is also a crucial factor in the creation, stabilization and manipulation of intrinsic magnetic skyrmions.17–19 The magnetic skyrmion is a topologically distinct spin texture, and many research studies have focused on modulating the DMI to reveal skyrmions, which has been realized in the interfaces of ferromagnet/heavy metal heterojunctions,20,21 weak ferromagnets,22 bilayer van der Waals heterojunctions23,24 and Janus materials, such as transition metal chalcogenides like MnSSe25 and CrSTe26 and transition metal iodides like Cr(I, Br)3.27 Due to their nanoscale size and low-threshold current drivability, skyrmions are promising candidates as information carriers for next-generation magnetic storage devices28 such as racetrack memory.29
Recently, MnBi2Te4 (MBT),30,31 as a topological insulator, provides a platform for the exploration of 2D magnetic topological spintronic devices due to its rich and tunable topological properties.32–34 However, the MBT monolayer is found to be a topological trivial insulator. A large indirect band gap30 and weak magnetic anisotropy35 prevent the occurrence of topological phase transition and skyrmions. In order to improve the performance of the MBT monolayer, great effort has been made by constructing heterojunctions,36 alloying,37 and applying an external field38 and strain.39,40 But it is still a challenge to realize a nontrivial topological phase in the MBT monolayer.
Inspired by the above study, we propose a 2D Janus ferromagnet with inversion asymmetry derived from the MBT monolayer, namely, MnSbBiSe2Te2 (MSBST), which is expected to achieve the coexistent phase of a nontrivial topological phase and skyrmions. In this work, we investigate the band structures, topological characteristics and spin textures of the Janus MSBST monolayer. The results show that switching the magnetic polarization direction of MSBST will significantly modify the band structure, inducing an indirect-to-direct band gap transition and a remarkable change of topological states. By applying a compressive strain, MSBST undergoes a topological phase transition and becomes a topological insulator with 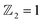 . In addition, we find that the Heisenberg exchange interactions and Curie temperature of MSBST are sensitive to biaxial strain, and a large DMI is obtained to generate a stable skyrmions phase with a suitable magnetic field of 0.8 T. The nontrivial topological properties and large DMI in our findings provide greater possibilities for spintronic devices.
. In addition, we find that the Heisenberg exchange interactions and Curie temperature of MSBST are sensitive to biaxial strain, and a large DMI is obtained to generate a stable skyrmions phase with a suitable magnetic field of 0.8 T. The nontrivial topological properties and large DMI in our findings provide greater possibilities for spintronic devices.
2. Methods and computational details
To investigate the electronic structures and magnetism, our first-principles calculations are performed using the Vienna Ab initio Simulation Package (VASP)41 with the projector augmented wave method.42 The exchange–correlation functional was described by the generalized gradient approximation (GGA) of the Perdew–Burke–Ernzerhof functional.43 To better describe the Coulomb interaction on Mn atoms, the GGA + U method44 is implemented with the effective Hubbard U set to 4.0 eV, which is consistent with recent studies.31,45,46 We also noticed that Otrokov et al.47 have tested the effect of different U values (3, 4 and 5.34 eV) and found all of them led to the same qualitative results. The cut-off energy is set to 400 eV. The atomic position is fully relaxed with an 11 × 11 × 1 Γ-centered Monkhorst–Pack k-point mesh until the convergence criteria for the total energy and Feynman–Hellmann force on each atom are less than 1 × 10−7 eV and 0.01 eV Å−1, respectively. SOC is included in the non-self-consistent calculations of band structures. To further explore the topological properties, we establish a tight-binding (TB) model by using the maximally localized Wannier functions (MLWF)48 implemented in WANNIER90.49 The surface states and Wannier charge center (WCC)50,51 are calculated using WANNIERTOOLS52 with iterative Green's function methods.53,54 The phonon dispersion is obtained by using Phonopy55 based on density functional perturbation theory. Based on the 2D Heisenberg model, the spin Hamiltonian can be described as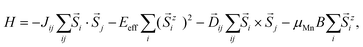 | (1) |
![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) ij represent the Heisenberg exchange interactions, effective magnetic anisotropy energy (MAE) and DMI vector, respectively. The last term is the Zeeman coupling of local magnetic moment μMn to vertical magnetic field of strength B, which is set to zero throughout this work, except in the skyrmions analysis.
ij represent the Heisenberg exchange interactions, effective magnetic anisotropy energy (MAE) and DMI vector, respectively. The last term is the Zeeman coupling of local magnetic moment μMn to vertical magnetic field of strength B, which is set to zero throughout this work, except in the skyrmions analysis. ![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) i and
i and ![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) j are the spin vector of each Mn atom at sites i and j, respectively, and are normalized to |
j are the spin vector of each Mn atom at sites i and j, respectively, and are normalized to |![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) | = 1. Here, the sign convention is that Jij > 0 favors ferromagnetic (FM) coupling, Eeff > 0 refers to the out-of-plane easy axis, and the modulus length of the DMI vector |
| = 1. Here, the sign convention is that Jij > 0 favors ferromagnetic (FM) coupling, Eeff > 0 refers to the out-of-plane easy axis, and the modulus length of the DMI vector |![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) ij| > 0 (|
ij| > 0 (|![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) ij| < 0) represent clockwise (CW) and anticlockwise (ACW) spin configurations, respectively. The DMI vector
ij| < 0) represent clockwise (CW) and anticlockwise (ACW) spin configurations, respectively. The DMI vector ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) ij can be expressed as
ij can be expressed as ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) ij = d‖(
ij = d‖(![[z with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_007a_20d1.gif) ×
× ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) ij) + d⊥
ij) + d⊥![[z with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_007a_20d1.gif) , where d‖ and d⊥ are the in-plane and out-of-plane components of the
, where d‖ and d⊥ are the in-plane and out-of-plane components of the ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) ij.
ij. ![[z with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_007a_20d1.gif) and
and ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) ij are the unit vectors pointing along the z direction and from site i to j. The detailed explanations for Jij, Eeff and
ij are the unit vectors pointing along the z direction and from site i to j. The detailed explanations for Jij, Eeff and ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) ij are presented in the ESI.† All necessary magnetic parameters were acquired by first-principles calculations, we then perform Monte Carlo (MC) and micro-magnetic simulations by using MCSOLVER56 and Vampire57 to explore the Curie temperature (TC) and spin textures of the MSBST monolayer.
ij are presented in the ESI.† All necessary magnetic parameters were acquired by first-principles calculations, we then perform Monte Carlo (MC) and micro-magnetic simulations by using MCSOLVER56 and Vampire57 to explore the Curie temperature (TC) and spin textures of the MSBST monolayer.
3. Results and discussion
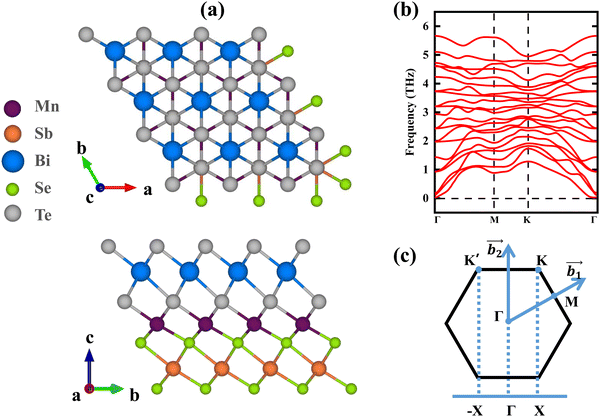
As illustrated in Fig. 1(a), like MBT (a = b = 4.36 Å), the MSBST monolayer shares the same hexagonal lattice but with a smaller lattice constant of a = b = 4.12 Å. The Janus MSBST is constructed by substituting the lower triple Te–Bi–Te layers of MBT with Se–Sb–Se layers. For a newly proposed 2D ferromagnet, the phonon dispersion with no imaginary frequency confirms its dynamic stability as shown in Fig. 1(b). Then, we applied a rational range of biaxial strain ε to explore the strain effect on MSBST. Here, ε is defined as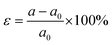 , where a0 and a are unstrained and strained lattice constants. In addition, the ground state of Janus MSBST is determined by calculating the energy of four possible spin configurations under different strains as illustrated in Fig. S1 (ESI†), where it prefers to be an FM within the strain range from −5% to 5%.
, where a0 and a are unstrained and strained lattice constants. In addition, the ground state of Janus MSBST is determined by calculating the energy of four possible spin configurations under different strains as illustrated in Fig. S1 (ESI†), where it prefers to be an FM within the strain range from −5% to 5%.
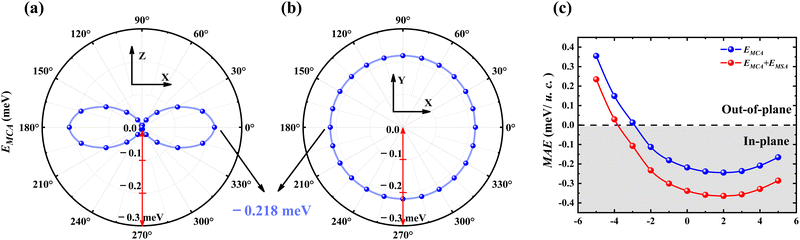
We now focus on MAE, which characterizes the dependence of energy on the orientation of magnetization. There are two origins of MAE: the first one is the SOC-driven magnetocrystalline anisotropy (MCA), and the second is magnetic shape anisotropy (MSA) originating from the dipole–dipole interaction. In ultrathin films, these two parts are typically comparable. Their competition determines the effective MAE (i.e., Eeff = EMCA + EMSA). Using the local magnetic moment of Mn and the lattice constant, we calculated the EMSA of Janus MSBST to be −0.12 meV per unit cell (u.c.), where the negative sign means that the MSA exhibits an in-plane magnetization.
The angular dependence of the MCA is illustrated in Fig. 2(a and b), which clearly shows that the MCA is isotropic in the XY plane, whereas it is strongly affected by the direction of magnetization in the XZ plane. One can find that both EMCA and EMSA favor the easy plane alignment of magnetization with no energetic barrier to rotate spins in the XY plane. As a result, the calculated Eeff of unstrained MSBST is −0.338 meV u.c.−1, which leads to an overall magnetic anisotropy favoring in-plane orientation of the moments. By applying a biaxial strain as shown in Fig. 2(c), the MSA does not change much under different strains, while the MCA changes parabolically and reaches an in-plane maximum (Eeff = −0.364 meV u.c.−1) at a strain of 2%. Moreover, the switching of MAE from in-plane to out-of-plane is observed when the compressive strain is about −4%, suggesting that the magnetization direction can be easily modulated by biaxial strain.
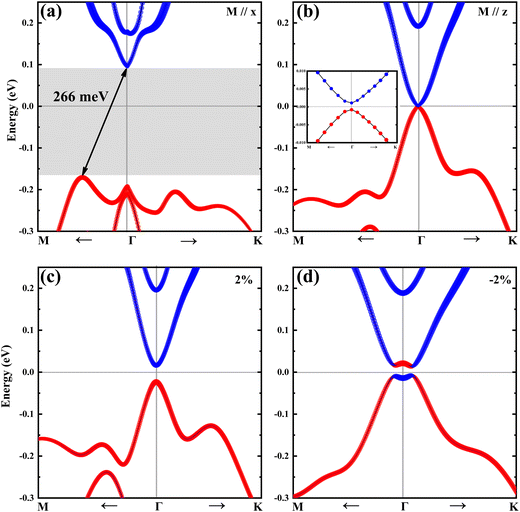
From the MAE analysis above, we know that the MAE of Janus MSBST prefers in-plane magnetization. We firstly consider a situation where the spin is oriented along the in-plane direction (M//x). The band structure of M//x in Fig. 3(a) proves that the pristine Janus MSBST system is an indirect gap semiconductor with a large bandgap of 266 meV. The element-resolved band structure tells us that the conduction band minimum (CBM) is mainly composed of the Sb-p orbital, while the valence band maximum (VBM) consists of Te-p. When a biaxial strain is applied, the band gap gradually decreases. Particularly, a remarkable change of an indirect-to-direct band gap transition occurs under a compressive strain. Due to the charge carrier transfers near the Fermi level without involving phonon scattering, the direct band gap semiconductor has potential applications in the field of photoelectric devices.58 There is no SOC-induced band inversion along M//x to prove that the MSBST with in-plane magnetization is a trivial insulator.
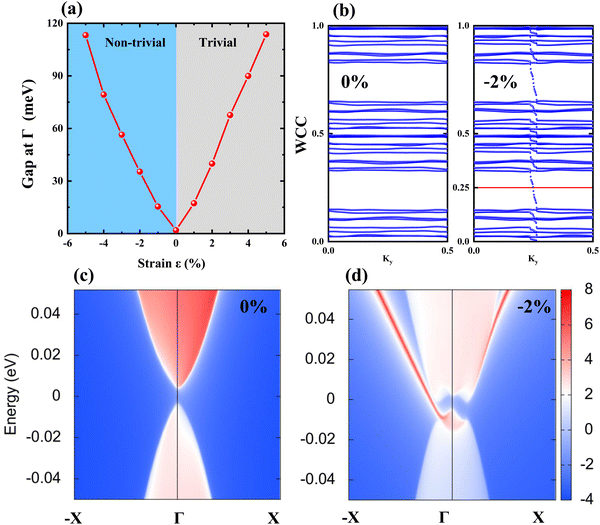
However, when the magnetic polarization is artificially switched to the z-axis (M//z), the direct band gap is significantly reduced to only 1.9 meV from 266 meV (M//x). Many theoretical33,58 and experimental59 results have confirmed the feasibility of turning the spin direction from in-plane to out-of-plane in 2D ferromagnets. In addition, the band gap of MSBST always increases no matter whether tensile or compressive strain is applied as shown in Fig. 4(a). Within the strain range from −5% to 5%, the bandgap firstly decreases from 113.2 to 1.9 meV (at a strain of 0%) and then increases up to 113.7 meV, suggesting that there is a critical point near 0% for the switching effect of band gap. As demonstrated in Fig. 3(d), different from the case of tensile strain or without strain, the −2% compressive strain pushes Sb-p orbitals down to contribute the VBM, while Te-p orbitals are raised to contribute to the CBM. That is to say, under a suitable compressive strain, an unexpected band inversion of Sb-p and Te-p states occurs to form a topological phase transition. Although it has been reported that changes in magnetic orientation can result in distinct symmetry selection rules and invoke different topological classifications,33,60 it is worth mentioning that, in the case of MSBST, changing the magnetic axis alone is not enough to induce the topological phase transition [Fig. 3(b)]. It is the further application of compressive strain that induces the band inversion around the Fermi level [Fig. 3(d)]. Similar phenomena of topological phase transition by applying appropriate pressure in MBT-family materials have also been reported.39,46
Due to the existence of intrinsic inversion asymmetry in Janus ferromagnets, the 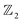 topological invariant by tracing the evolution of Wannier charge centers (WCCs) is calculated to ensure the existence of topological properties. As expected, the evolution of WCCs in Fig. 4(b) for MSBST along Ky illustrates that an arbitrary horizontal reference line (such as WCC = 0.25) crosses the evolution of WCCs only once with a compressive strain of −2% and zero times for the unstrained system. That is to say, the pristine Janus MSBST is a trivial insulator with
topological invariant by tracing the evolution of Wannier charge centers (WCCs) is calculated to ensure the existence of topological properties. As expected, the evolution of WCCs in Fig. 4(b) for MSBST along Ky illustrates that an arbitrary horizontal reference line (such as WCC = 0.25) crosses the evolution of WCCs only once with a compressive strain of −2% and zero times for the unstrained system. That is to say, the pristine Janus MSBST is a trivial insulator with 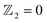 , while the compressed MSBST is a topological insulator with
, while the compressed MSBST is a topological insulator with 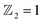 . Based on the TB models of MSBST with the MLWF method, we further confirm the existence of the topological surface state. The surface states along the projected −X–Γ–X high-symmetry path [Fig. 1(c)] are calculated in a semi-infinite MSBST thin film. As shown in Fig. 4(c), the local density at surface is still fully gapped in the trivial phase of pristine MSBST. In contrast, for the topological insulator with a compressive strain of −2%, a chiral edge state traverses across bulk gap and the Fermi level, connecting the valence and conduction bands, which verifies the topologically nontrivial nature of the compressed MSBST.
. Based on the TB models of MSBST with the MLWF method, we further confirm the existence of the topological surface state. The surface states along the projected −X–Γ–X high-symmetry path [Fig. 1(c)] are calculated in a semi-infinite MSBST thin film. As shown in Fig. 4(c), the local density at surface is still fully gapped in the trivial phase of pristine MSBST. In contrast, for the topological insulator with a compressive strain of −2%, a chiral edge state traverses across bulk gap and the Fermi level, connecting the valence and conduction bands, which verifies the topologically nontrivial nature of the compressed MSBST.
As we know, the non-trivial topological properties originate from the SOC effect. The effect of variational SOC strength on the band structure is shown in Fig. S4 (ESI†). The band gap can be closed and reopened by modulating the SOC strength, thereby leading to a topological phase transition. These interesting results are consistent with recent studies.31,38,39,61,62 In MSBST, the application of biaxial strain not only changes the lattice constant, but also modifies the SOC strength simultaneously, which can lead to a band inversion or its elimination.63 The distance between the neighbouring atoms is reduced by the compressive strain, leading to an enlargement of the hopping integral of electrons and the improvement of the overlapping of the conduction and valence bands. Briefly, band inversion occurs, resulting in the phase transition from a trivial to topological insulator. The opposite situation occurs when applying the tensile strain. The hopping integral of electrons is suppressed due to the increased atomic distance. The CBM and VBM move away from each other, causing the diminishing of band overlaps and eventually opening the full band gap. Modulating the topological phase transition between topological insulators and normal insulators can realize an on/off switch of spin current, which has potential application value in spintronic devices.
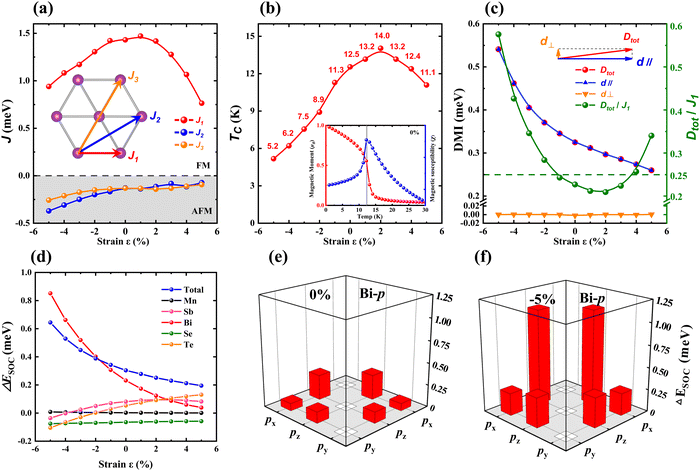
After proving the topologically nontrivial state of MSBST, we proceed to investigate its magnetic properties from the perspective of asymmetry. Based on the Hamiltonian (eqn (1)) above, as presented in Fig. 5, we calculate the Heisenberg exchange interactions and DMI under various biaxial strains. Here we take three different nearest neighbours of Heisenberg exchange interactions labeled as J1, J2, and J3 into account to obtain more accurate TC. As mentioned above, a positive value presents FM ordering. As shown in Fig. 5(a), with the strain ranging from −5% to 5%, the nearest neighbour J1 varies parabolically between 0.764 meV (5%) and 1.471 meV (1%) and dominates for the establishment of the FM ground state, while J2 and J3 exhibit a weak AFM coupling and monotonically weaken over the whole strain range. By Monte Carlo simulation, we estimated the TC of unstrained MSBST to be about 12.5 K,64 as shown in Fig. 5(b). The results show that the trend of TC is mainly affected by the dominant J1.
On the other hand, we calculated the energies of CW and ACW spin configurations with XY and XZ planes based on the chirality-dependent total energy difference method.15,20 Both the in-plane and out-of-plane components of DMI vector ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) ij can be obtained by d = (ECW − EACW)/12.26 As shown in Fig. 5(b), the in-plane component d‖ plays a dominant role in the modulus length of DMI vector
ij can be obtained by d = (ECW − EACW)/12.26 As shown in Fig. 5(b), the in-plane component d‖ plays a dominant role in the modulus length of DMI vector ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) ij (i.e., strength of the DMI, Dtot), while the value of the other component d⊥ is close to zero. This is because the sign of d⊥ for the six nearest neighbours changes staggeringly in the numerical derivation, leading to d⊥ neutralized in average, which is consistent with recent studies.65,66 The calculated Dtot of unstrained MSBST is 0.325 meV, which is larger than those of FeBrI (0.191 meV1), Cr(I, Br)3 (0.270 meV27) and MBST (0.285 meV67) reported in recent studies. Usually, a large value of the DMI leads to the formation and stabilization of more skyrmions with a smaller diameter.68–71 Besides, the compressive strain gives rise to an increase of the DMI to reach up to 0.541 meV at a strain of −5%, suggesting that the high sensitivity of the DMI on strain helps to create more stable skyrmions. To further explicate the origin of the enhanced DMI, the element- and orbital-resolved SOC energy difference (ΔESOC) between CW and ACW configurations is plotted in Fig. 5(d). In the absence of strain, all three hybridizations among px, py and pz orbitals provide small positive contributions to the DMI [Fig. 5(e)]. When the compressive strain is applied and reaches up to −5%, as shown in Fig. 5(f), the contributions of Bi-px/pz hybridized orbitals are greatly enhanced, which clearly shows that the enhancement of the DMI under the compressive strain is mainly associated with Bi-px/pz hybridized orbitals. The large ΔESOC of nonmagnetic Bi atoms, rather than that of Mn atoms, is responsible for the strong DMI in MSBST, and these results are similar to other recent studies.26,65,66
ij (i.e., strength of the DMI, Dtot), while the value of the other component d⊥ is close to zero. This is because the sign of d⊥ for the six nearest neighbours changes staggeringly in the numerical derivation, leading to d⊥ neutralized in average, which is consistent with recent studies.65,66 The calculated Dtot of unstrained MSBST is 0.325 meV, which is larger than those of FeBrI (0.191 meV1), Cr(I, Br)3 (0.270 meV27) and MBST (0.285 meV67) reported in recent studies. Usually, a large value of the DMI leads to the formation and stabilization of more skyrmions with a smaller diameter.68–71 Besides, the compressive strain gives rise to an increase of the DMI to reach up to 0.541 meV at a strain of −5%, suggesting that the high sensitivity of the DMI on strain helps to create more stable skyrmions. To further explicate the origin of the enhanced DMI, the element- and orbital-resolved SOC energy difference (ΔESOC) between CW and ACW configurations is plotted in Fig. 5(d). In the absence of strain, all three hybridizations among px, py and pz orbitals provide small positive contributions to the DMI [Fig. 5(e)]. When the compressive strain is applied and reaches up to −5%, as shown in Fig. 5(f), the contributions of Bi-px/pz hybridized orbitals are greatly enhanced, which clearly shows that the enhancement of the DMI under the compressive strain is mainly associated with Bi-px/pz hybridized orbitals. The large ΔESOC of nonmagnetic Bi atoms, rather than that of Mn atoms, is responsible for the strong DMI in MSBST, and these results are similar to other recent studies.26,65,66
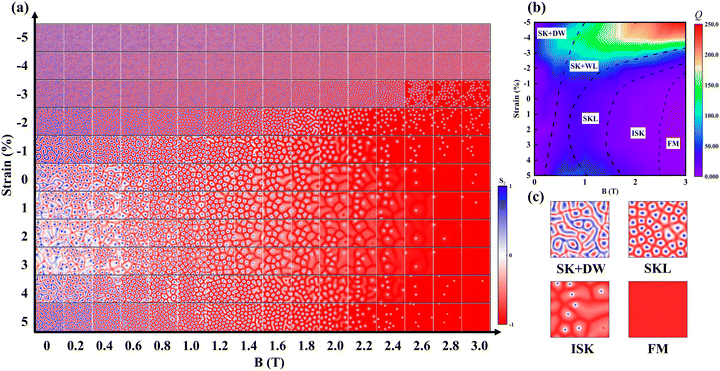
In fact, it is the large value of the ratio between Dtot and the exchange interaction J1 (i.e., Dtot/J1) that tends to a smaller diameter of skyrmions, which can be quantified by LD = 4πJ/D.72 Therefore, using the results of the first-principles calculations above, we performed micro-magnetic simulations to investigate their spin textures in the MSBST monolayer. The full periodic boundary conditions were used in the simulation. It is found that different types of spin textures can be formed and exist stably under various vertical magnetic fields B, namely, the mixed state with domain walls and Néel-type skyrmions (SK + DW), skyrmions lattice (SKL) states, isolated skyrmions (ISK) in a FM background, as well as the complete FM state [see Fig. 6(c)].
As shown in Fig. 6(a), when there exists neither strain nor a magnetic field, MSBST exhibits an SK + DW state, in which the domain walls are interconnected and filled in the main area. In addition, we have checked the types of skyrmions for our simulation by plotting the arrows in the spin textures. As shown in Fig. S9 (ESI†), all the skyrmions with a magnetic field of ∼0.8 T are of the Néel-like type. A recent study reports that Néel-type skyrmions are shown to be energetically preferred over collinear spin textures73 and thus can exist stably as the ground state in a large size material. Once the vertical magnetic field B is introduced and gradually increased, the spin textures of MSBST undergo an SK + DW–SKL–ISK–FM phase transition. Particularly when B is larger than 0.8 T, the worm-like domain walls completely disappear, inducing an SKL phase. As the magnetic field continues to increase, the diameter of skyrmions keeps decreasing and eventually they completely magnetized into the FM state at a B of 2.8 T.
Next, we proceed with the biaxial strain effect on the spin textures. As mentioned above, the diameter of skyrmion LD is closely related to the value between Dtot and the exchange interaction J1 (i.e., Dtot/J1). When the external magnetic field is absent, since the value of Dtot/J1 [the green line in Fig. 5(b)] changes with a parabolic shape. In the strain range of 0% to 3%, the Dtot/J1 values are small and change slowly, and the evolutions of spin textures are basically similar to those in the unstrained case. However, the Dtot/J1 ratio increases rapidly under larger tensile or compressive strains, then the skyrmions become smaller and denser. The density of skyrmions can be quantificationally reflected by the topological charge Q, which is described by 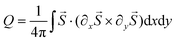 .73,74 The phase diagram of topological charge with magnetic field and strain is plotted in Fig. 6(b).
.73,74 The phase diagram of topological charge with magnetic field and strain is plotted in Fig. 6(b).
Based on the analysis above, we know that the domain walls can be diluted by the magnetic field. Interestingly, when the compressive strain is larger than −3%, the spin-up and spin-down densities are almost equal over the whole magnetic field range to show an AFM state with a very large Q. In addition, there is no FM state under a higher magnetic field of 3.0 T. When applying a compressive strain of −5%, the spin textures of the MSBST monolayer exhibit labyrinth-like magnetic domain walls with an extremely small LD. At this point, the modulating effect of vertical magnetic field is no longer significant. These changes in the spin textures are related to the switching of the easy axis in Fig. 2(c). The effect of vertical magnetic field is similar to that of intrinsic MAE,58 leading to constructive or destructive interference. With the perpendicular anisotropy under the large compressive strains, skyrmions favor a clear energy incentive to align the magnetization with the anisotropy axis.23,28 Finally, the evolutions of spin textures with temperatures have been studied as shown in Fig. S10 (ESI†). The thermal fluctuation increases with the increase of temperature. Then, if the temperature is beyond its TC, the magnetic moments orient randomly, which implies a disordered paramagnetic phase in MSBST.
4. Conclusion
In summary, we proposed a 2D Janus MSBST monolayer and systematically investigate its magnetism, topological properties and spin textures. We find that MSBST is a large indirect band gap semiconductor with an in-plane magnetic easy axis. Intriguingly, an unexpected topological phase transition occurs when the easy axis is turned to the z direction and a biaxial strain is applied. A topological insulator state with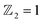 under compressive strain can be verified by the Wannier charge center and chiral edge states. Furthermore, strain-tunable MAE and an inherent large DMI are obtained, which can be used to generate and stabilize skyrmions. By micro-magnetic simulations, it is found that a vertical magnetic field can effectively modulate the size and density of skyrmions, turning the mixed spin textures of MSBST into a skyrmions lattice (at 0.8 T). Our work presents some interesting results for 2D Janus topological insulators, and it may provide useful guidelines for designing spintronic devices with the coexistence of nontrivial topological properties and a large DMI.
under compressive strain can be verified by the Wannier charge center and chiral edge states. Furthermore, strain-tunable MAE and an inherent large DMI are obtained, which can be used to generate and stabilize skyrmions. By micro-magnetic simulations, it is found that a vertical magnetic field can effectively modulate the size and density of skyrmions, turning the mixed spin textures of MSBST into a skyrmions lattice (at 0.8 T). Our work presents some interesting results for 2D Janus topological insulators, and it may provide useful guidelines for designing spintronic devices with the coexistence of nontrivial topological properties and a large DMI.
Conflicts of interest
The authors have no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 11804301), the Natural Science Foundation of Zhejiang Province (Grant No. LY21A040008), and the Fundamental Research Funds of Zhejiang Sci-Tech University (No. 2021Q043-Y and LGYJY2021015).References
- R. Li, J. Jiang, X. Shi, W. Mi and H. Bai, Two-Dimensional Janus FeXY (X, Y = Cl, Br, and I, X not equal Y) Monolayers: Half-Metallic Ferromagnets with Tunable Magnetic Properties under Strain, ACS Appl. Mater. Interfaces, 2021, 13(32), 38897–38905 CrossRef CAS
.
- P. Li and Z. X. Guo, The Dirac half-semimetal and quantum anomalous Hall effect in two-dimensional Janus Mn2X3Y3 (X, Y = F, Cl, Br, I), Phys. Chem. Chem. Phys., 2021, 23(35), 19673–19679 RSC
.
- M. Yagmurcukardes, Y. Qin, S. Ozen, M. Sayyad, F. M. Peeters, S. Tongay and H. Sahin, Quantum properties and applications of 2D Janus crystals and their superlattices, Appl. Phys. Rev., 2020, 7(1), 011311 CAS
.
- Y. Sun, Z. Shuai and D. Wang, Janus monolayer of WSeTe, a new structural phase transition material driven by electrostatic gating, Nanoscale, 2018, 10(46), 21629–21633 RSC
.
- X. Yang, D. Singh, Z. Xu, Z. Wang and R. Ahuja, An emerging Janus MoSeTe material for potential applications in optoelectronic devices, J. Mater. Chem. C, 2019, 7(39), 12312–12320 RSC
.
- J. Zhang, S. Jia, I. Kholmanov, L. Dong, D. Er, W. Chen, H. Guo, Z. Jin, V. B. Shenoy, L. Shi and J. Lou, Janus Monolayer Transition-Metal Dichalcogenides, ACS Nano, 2017, 11(8), 8192–8198 CrossRef CAS
.
- S.-W. Ng, N. Noor and Z. Zheng, Graphene-based two-dimensional Janus materials, NPG Asia Mater., 2018, 10(4), 217–237 CrossRef CAS
.
- L. Zhang, J. Yu, M. Yang, Q. Xie, H. Peng and Z. Liu, Janus graphene from asymmetric two-dimensional chemistry, Nat. Commun., 2013, 4(1), 1443 CrossRef
.
- A. Y. Lu, H. Y. Zhu, J. Xiao, C. P. Chuu, Y. Han, M. H. Chiu, C. C. Cheng, C. W. Yang, K. H. Wei, Y. Yang, Y. Wang, D. Sokaras, D. Nordlund, P. Yang, D. A. Muller, M. Y. Chou, X. Zhang and L. J. Li, Janus monolayers of transition metal dichalcogenides, Nat. Nanotechnol., 2017, 12(8), 744–749 CrossRef CAS
.
- W. Zhou, Z. Yang, A. Li, M. Long and F. Ouyang, Spin and valley splittings in Janus monolayer WSSe on a MnO(111) surface: Large effective Zeeman field and opening of a helical gap, Phys. Rev. B, 2020, 101(4), 045113 CrossRef CAS
.
- J. Liang, Q. Cui and H. Yang, Electrically switchable Rashba-type Dzyaloshinskii-Moriya interaction and skyrmion in two-dimensional magnetoelectric multiferroics, Phys. Rev. B, 2020, 102(22), 220409 CrossRef CAS
.
- I. Dzyaloshinsky, A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics, J. Phys. Chem. Solids, 1958, 4(4), 241–255 CrossRef CAS
.
- T. Moriya, Anisotropic Superexchange Interaction and Weak Ferromagnetism, Phys. Rev., 1960, 120(1), 91–98 CrossRef CAS
.
- A. Fert and P. M. Levy, Role of Anisotropic Exchange Interactions in Determining the Properties of Spin-Glasses, Phys. Rev. Lett., 1980, 44(23), 1538–1541 CrossRef CAS
.
- H. Yang, G. Chen, A. A. C. Cotta, A. T. N'Diaye, S. A. Nikolaev, E. A. Soares, W. A. A. Macedo, K. Liu, A. K. Schmid, A. Fert and M. Chshiev, Significant Dzyaloshinskii-Moriya interaction at graphene-ferromagnet interfaces due to the Rashba effect, Nat. Mater., 2018, 17(7), 605–609 CrossRef CAS
.
- F. Zhang, H. Zhang, W. Mi and X. Wang, Electronic structure, magnetic anisotropy and Dzyaloshinskii-Moriya interaction in Janus Cr2I3X3 (X = Br, Cl) bilayers, Phys. Chem. Chem. Phys., 2020, 22(16), 8647–8657 RSC
.
- A. N. Bogdanov and U. K. Rößler, Chiral Symmetry Breaking in Magnetic Thin Films and Multilayers, Phys. Rev. Lett., 2001, 87(3), 037203 CrossRef CAS PubMed
.
- M. Bode, M. Heide, K. von Bergmann, P. Ferriani, S. Heinze, G. Bihlmayer, A. Kubetzka, O. Pietzsch, S. Blügel and R. Wiesendanger, Chiral magnetic order at surfaces driven by inversion asymmetry, Nature, 2007, 447(7141), 190–193 CrossRef CAS
.
- Y. Zhang, C. Xu, P. Chen, Y. Nahas, S. Prokhorenko and L. Bellaiche, Emergence of skyrmionium in a two-dimensional CrGe(Se,Te)3 Janus monolayer, Phys. Rev. B, 2020, 102(24), 241107 CrossRef CAS
.
- H. Yang, A. Thiaville, S. Rohart, A. Fert and M. Chshiev, Anatomy of Dzyaloshinskii-Moriya Interaction at Co/Pt Interfaces, Phys. Rev. Lett., 2015, 115(26), 267210 CrossRef
.
- M. Raju, A. Yagil, A. Soumyanarayanan, A. K. C. Tan, A. Almoalem, F. Ma, O. M. Auslaender and C. Panagopoulos, The evolution of skyrmions in Ir/Fe/Co/Pt multilayers and their topological Hall signature, Nat. Commun., 2019, 10(1), 696 CrossRef CAS
.
- V. E. Dmitrienko, E. N. Ovchinnikova, S. P. Collins, G. Nisbet, G. Beutier, Y. O. Kvashnin, V. V. Mazurenko, A. I. Lichtenstein and M. I. Katsnelson, Measuring the Dzyaloshinskii–Moriya interaction in a weak ferromagnet, Nat. Phys., 2014, 10(3), 202–206 Search PubMed
.
- W. Sun, W. Wang, J. Zang, H. Li, G. Zhang, J. Wang and Z. Cheng, Manipulation of Magnetic Skyrmion in a 2D van der Waals Heterostructure via Both Electric and Magnetic Fields, Adv. Funct. Mater., 2021, 31(47), 2104452 CrossRef CAS
.
- Q. Cui, Y. Zhu, J. Jiang, J. Liang, D. Yu, P. Cui and H. Yang, Ferroelectrically controlled topological magnetic phase in a Janus-magnet-based multiferroic heterostructure, Phys. Rev. Res., 2021, 3(4), 043011 CrossRef CAS
.
- J. Yuan, Y. Yang, Y. Cai, Y. Wu, Y. Chen, X. Yan and L. Shen, Intrinsic skyrmions in monolayer Janus magnets, Phys. Rev. B, 2020, 101(9), 094420 CrossRef CAS
.
- Q. Cui, J. Liang, Z. Shao, P. Cui and H. Yang, Strain-tunable ferromagnetism and chiral spin textures in two-dimensional Janus chromium dichalcogenides, Phys. Rev. B, 2020, 102(9), 094425 CrossRef CAS
.
- C. Xu, J. Feng, S. Prokhorenko, Y. Nahas, H. Xiang and L. Bellaiche, Topological spin texture in Janus monolayers of the chromium trihalides Cr(I, X)3, Phys. Rev. B, 2020, 101(6), 060404 CrossRef CAS
.
- J. Sampaio, V. Cros, S. Rohart, A. Thiaville and A. Fert, Nucleation, stability and current-induced motion of isolated magnetic skyrmions in nanostructures, Nat. Nanotechnol., 2013, 8(11), 839–844 CrossRef CAS
.
- W. Kang, Y. Huang, C. Zheng, W. Lv, N. Lei, Y. Zhang, X. Zhang, Y. Zhou and W. Zhao, Voltage Controlled Magnetic Skyrmion Motion for Racetrack Memory, Sci. Rep., 2016, 6(1), 23164 CrossRef CAS PubMed
.
- M. M. Otrokov, I. P. Rusinov, M. Blanco-Rey, M. Hoffmann, A. Y. Vyazovskaya, S. V. Eremeev, A. Ernst, P. M. Echenique, A. Arnau and E. V. Chulkov, Unique Thickness-Dependent Properties of the van der Waals
Interlayer Antiferromagnet MnBi2Te4 Films, Phys. Rev. Lett., 2019, 122(10), 107202 CrossRef CAS PubMed
.
- J. Li, Y. Li, S. Du, Z. Wang, B. L. Gu, S. C. Zhang, K. He, W. Duan and Y. Xu, Intrinsic magnetic topological insulators in van der Waals layered MnBi2Te4-family materials, Sci. Adv., 2019, 5(6), eaaw5685 CrossRef CAS
.
- D. Zhang, M. Shi, T. Zhu, D. Xing, H. Zhang and J. Wang, Topological Axion States in the Magnetic Insulator MnBi2Te4 with the Quantized Magnetoelectric Effect, Phys. Rev. Lett., 2019, 122(20), 206401 CrossRef CAS
.
- J. H. Li, C. Wang, Z. T. Zhang, B. L. Gu, W. H. Duan and Y. Xu, Magnetically controllable topological quantum phase transitions in the antiferromagnetic topological insulator MnBi2Te4, Phys. Rev. B, 2019, 100(12), 121103 CrossRef CAS
.
- P. F. Zhu, X. G. Ye, J. Z. Fang, P. Z. Xiang, R. R. Li, D. Y. Xu, Z. M. Wei, J. W. Mei, S. Liu, D. P. Yu and Z. M. Liao, From negative to positive magnetoresistance in the intrinsic magnetic topological insulator MnBi2Te4, Phys. Rev. B, 2020, 101(7), 075425 CrossRef CAS
.
- Y. Li, Z. Jiang, J. Li, S. Xu and W. Duan, Magnetic anisotropy of the two-dimensional ferromagnetic insulator MnBi2Te4, Phys. Rev. B, 2019, 100(13), 134438 CrossRef CAS
.
- W. X. Zhu, C. Song, L. Y. Liao, Z. Y. Zhou, H. Bai, Y. J. Zhou and F. Pan, Quantum anomalous Hall insulator state in ferromagnetically ordered MnBi2Te4/VBi2Te4 heterostructures, Phys. Rev. B, 2020, 102(8), 085111 CrossRef CAS
.
- Y. S. Hou and R. Q. Wu, Alloying vanadium in MnBi2Te4 for robust ferromagnetic coupling and quantum anomalous Hall effect, Phys. Rev. B, 2021, 103(6), 064412 CrossRef CAS
.
- J. Y. You, X. J. Dong, B. Gu and G. Su, Electric field induced topological phase transition and large enhancements of spin-orbit coupling and Curie temperature in two-dimensional ferromagnetic semiconductors, Phys. Rev. B, 2021, 103(10), 104403 CAS
.
- P. Li, J. Y. Yu, Y. Wang and W. D. Luo, Electronic structure and topological phases of the magnetic layered materials MnBi2Te4, MnBi2Se4, and MnSb2Te4, Phys. Rev. B, 2021, 103(15), 155118 CAS
.
- Z. Wu, Z. Shen, Y. Xue and C. Song, Strain-induced topological phase transition and enhanced Curie temperature in MnBi2Te4/CrI3 heterojunction, Phys. Rev. Mater., 2022, 6(1), 014011 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186 CrossRef CAS PubMed
.
- P. E. Blochl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979 CrossRef
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS
.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA + U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57(3), 1505–1509 CrossRef CAS
.
- Z. Shen, Y. Xue, Z. Wu and C. Song, Spontaneous magnetic merons in a half-metallic Mn2I3Br3 monolayer with easy-plane anisotropy, Phys. Chem. Chem. Phys., 2022, 24, 27612–27618 RSC
.
- H. Zhang, W. Yang, Y. Wang and X. Xu, Tunable topological states in layered magnetic materials of MnSb2Te4, MnBi2Se4, and MnSb2Se4, Phys. Rev. B, 2021, 103(9), 094433 CrossRef CAS
.
- M. M. Otrokov, I. I. Klimovskikh, H. Bentmann, D. Estyunin, A. Zeugner, Z. S. Aliev, S. Gass, A. U. B. Wolter, A. V. Koroleva, A. M. Shikin, M. Blanco-Rey, M. Hoffmann, I. P. Rusinov, A. Y. Vyazovskaya, S. V. Eremeev, Y. M. Koroteev, V. M. Kuznetsov, F. Freyse, J. Sanchez-Barriga, I. R. Amiraslanov, M. B. Babanly, N. T. Mamedov, N. A. Abdullayev, V. N. Zverev, A. Alfonsov, V. Kataev, B. Buchner, E. F. Schwier, S. Kumar, A. Kimura, L. Petaccia, G. Di Santo, R. C. Vidal, S. Schatz, K. Kissner, M. Unzelmann, C. H. Min, S. Moser, T. R. F. Peixoto, F. Reinert, A. Ernst, P. M. Echenique, A. Isaeva and E. V. Chulkov, Prediction and observation of an antiferromagnetic topological insulator, Nature, 2019, 576(7787), 416–422 CrossRef CAS
.
- N. Marzari, A. A. Mostofi, J. R. Yates, I. Souza and D. Vanderbilt, Maximally localized Wannier functions: Theory and applications, Rev. Mod. Phys., 2012, 84(4), 1419–1475 CrossRef CAS
.
- A. A. Mostofi, J. R. Yates, G. Pizzi, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, An updated version of wannier90: A tool for obtaining maximally-localised Wannier functions, Comput. Phys. Commun., 2014, 185(8), 2309–2310 CrossRef CAS
.
- A. A. Soluyanov and D. Vanderbilt, Computing topological invariants without inversion symmetry, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83(23), 235401 CrossRef
.
- A. A. Soluyanov and D. Vanderbilt, Wannier representation of Z2 topological insulators, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83(3), 035108 CrossRef
.
- Q. Wu, S. Zhang, H.-F. Song, M. Troyer and A. A. Soluyanov, WannierTools: An open-source software package for novel topological materials, Comput. Phys. Commun., 2018, 224, 405–416 CrossRef CAS
.
- D. H. Lee and J. D. Joannopoulos, Simple scheme for surface-band calculations. I, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23(10), 4988–4996 CrossRef CAS
.
- D. H. Lee and J. D. Joannopoulos, Simple scheme for surface-band calculations. II. The Green's function, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23(10), 4997–5004 CrossRef
.
- A. Togo, F. Oba and I. Tanaka, First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78(13), 134106 CrossRef
.
- L. Liu, X. Ren, J. Xie, B. Cheng, W. Liu, T. An, H. Qin and J. Hu, Magnetic switches via electric field in BN nanoribbons, Appl. Surf. Sci., 2019, 480, 300–307 CrossRef CAS
.
-
VAMPIRE software package version 5.0 available from https://vampire.york.ac.uk/ Search PubMed
.
- P. Jiang, L. Li, Z. Liao, Y. X. Zhao and Z. Zhong, Spin Direction-Controlled Electronic Band Structure in Two-Dimensional Ferromagnetic CrI3, Nano Lett., 2018, 18(6), 3844–3849 CrossRef CAS PubMed
.
- Y. Deng, Y. Yu, Y. Song, J. Zhang, N. Z. Wang, Z. Sun, Y. Yi, Y. Z. Wu, S. Wu, J. Zhu, J. Wang, X. H. Chen and Y. Zhang, Gate-tunable room-temperature ferromagnetism in two-dimensional Fe3GeTe2, Nature, 2018, 563(7729), 94–99 CrossRef CAS
.
- A. P. Schnyder, S. Ryu, A. Furusaki and A. W. W. Ludwig, Classification of topological insulators and superconductors in three spatial dimensions, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78(19), 195125 CrossRef
.
- S. V. Eremeev, I. P. Rusinov, Y. M. Koroteev, A. Y. Vyazovskaya, M. Hoffmann, P. M. Echenique, A. Ernst, M. M. Otrokov and E. V. Chulkov, Topological Magnetic Materials of the (MnSb2Te4).(Sb2Te3)n van der Waals Compounds Family, J. Phys. Chem. Lett., 2021, 12(17), 4268–4277 CrossRef CAS PubMed
.
- Z. Li, J. H. Li, K. He, X. G. Wan, W. H. Duan and Y. Xu, Tunable interlayer magnetism and band topology in van der Waals heterostructures of MnBi2Te4-family materials, Phys. Rev. B, 2020, 102, 081107 CrossRef CAS
.
- C. Lin, M. Ochi, R. Noguchi, K. Kuroda, M. Sakoda, A. Nomura, M. Tsubota, P. Zhang, C. Bareille, K. Kurokawa, Y. Arai, K. Kawaguchi, H. Tanaka, K. Yaji, A. Harasawa, M. Hashimoto, D. Lu, S. Shin, R. Arita, S. Tanda and T. Kondo, Visualization of the strain-induced topological phase transition in a quasi-one-dimensional superconductor TaSe3, Nat. Mater., 2021, 20(8), 1093–1099 CrossRef CAS PubMed
.
- Y. Xue, Z. Shen, Z. Wu and C. Song, Theoretical prediction of Curie temperature in two-dimensional ferromagnetic monolayer, J. Appl. Phys., 2022, 132(5), 053901 CrossRef CAS
.
- J. H. Liang, W. W. Wang, H. Du, A. Hallal, K. Garcia, M. Chshiev, A. Fert and H. Yang, Very large Dzyaloshinskii-Moriya interaction in two-dimensional Janus manganese dichalcogenides and its application to realize skyrmion states, Phys. Rev. B, 2020, 101(18), 184401 CrossRef CAS
.
- S. Qi, J. Jiang, X. Wang and W. Mi, Valley polarization, magnetic anisotropy and Dzyaloshinskii-Moriya interaction of two-dimensional graphene/Janus 2H-VSeX (X = S, Te) heterostructures, Carbon, 2021, 174, 540–555 CrossRef CAS
.
- J. Jiang, X. Liu, R. Li and W. Mi, Topological spin textures in a two-dimensional MnBi2(Se, Te)4 Janus material, Appl. Phys. Lett., 2021, 119(7), 072401 CrossRef CAS
.
- B. Göbel, I. Mertig and O. A. Tretiakov, Beyond skyrmions: Review and perspectives of alternative magnetic quasiparticles, Phys. Rep., 2021, 895, 1–28 CrossRef
.
- A. Fert, V. Cros and J. Sampaio, Skyrmions on the track, Nat. Nanotechnol., 2013, 8(3), 152–156 CrossRef CAS PubMed
.
- N. S. Kiselev, A. N. Bogdanov, R. Schäfer and U. K. Rößler, Chiral skyrmions in thin magnetic films: new objects for magnetic storage technologies?, J. Phys. D: Appl. Phys., 2011, 44(39), 392001 CrossRef
.
- Z. Shen, C. Song, Y. Xue, Z. Wu, J. Wang and Z. Zhong, Strain-tunable Dzyaloshinskii-Moriya interaction and skyrmions in two-dimensional Janus Cr2X3Y3 (X, Y = Cl, Br, I, X≠Y) trihalide monolayers, Phys. Rev. B, 2022, 106(9), 094403 CrossRef CAS
.
- F. N. Rybakov, A. B. Borisov and A. N. Bogdanov, Three-dimensional skyrmion states in thin films of cubic helimagnets, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87(9), 094424 CrossRef
.
- Q. L. He, G. Yin, A. J. Grutter, L. Pan, X. Che, G. Yu, D. A. Gilbert, S. M. Disseler, Y. Liu, P. Shafer, B. Zhang, Y. Wu, B. J. Kirby, E. Arenholz, R. K. Lake, X. Han and K. L. Wang, Exchange-biasing topological charges by antiferromagnetism, Nat. Commun., 2018, 9(1), 2767 CrossRef
.
- N. Nagaosa and Y. Tokura, Topological properties and dynamics of magnetic skyrmions, Nat. Nanotechnol., 2013, 8(12), 899–911 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03860a |
| This journal is © the Owner Societies 2023 |

![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif)