Does liquid–liquid phase separation impact ice nucleation in mixed polyethylene glycol and ammonium sulfate droplets?†
Yao
Yao
ab,
Peter A.
Alpert
 c,
Andreas
Zuend
c,
Andreas
Zuend
 d and
Bingbing
Wang
d and
Bingbing
Wang
 *ab
*ab
aState Key Laboratory of Marine Environmental Science, Xiamen University, Xiamen 361102, China
bCollege of Ocean and Earth Sciences, Xiamen University, Xiamen 361102, China. E-mail: Bingbing.Wang@xmu.edu.cn
cLaboratory of Environmental Chemistry, Paul Scherrer Institute, 5232 Villigen, Switzerland
dDepartment of Atmospheric and Oceanic Sciences, McGill University, Montréal, Quebec, Canada
First published on 17th October 2022
Abstract
Particles can undergo different phase transitions in the atmosphere including deliquescence, liquid–liquid phase separation (LLPS), melting, and freezing. In this study, phase transitions of particles/droplets containing polyethylene glycol with a molar mass of 400 g mol−1 (PEG400) and ammonium sulfate (AS), i.e., PEG400-AS particles/droplets, were investigated at different organic-to-inorganic dry mass ratios (OIRs) under typical tropospheric temperatures and water activities (aw). The investigated droplets (60–100 μm) with or without LLPS in the closed system froze through homogeneous ice nucleation. At temperatures lower than 200 K, multiple ice nucleation events were observed within the same individual droplets at low aw. Droplets with and without LLPS shared similar lambda values at the same OIR according to the lambda approach indicating they form ice through the same mechanism. A parameterization of lambda values was provided which can be used to predict freezing temperature of aqueous PEG400-AS droplets. We found that adding AS reduces the temperature dependence of aw in aqueous PEG400 droplets. Assuming incorrectly that aw is temperature-independent for a constant droplet composition leads to a deviation between the experimental determined ice nucleation rate coefficients for droplets at OIR > 1 and the predicted values by the water-activity-based ice nucleation theory. We proposed a parameterization of temperature dependence of aw to minimize the deviations of the measured melting temperatures and nucleation rate coefficients from the corresponding predictions for aqueous PEG400-AS system.
1. Introduction
Aerosol particles are important atmospheric constituents as they play critical roles in air quality, cloud formation, and the Earth's radiative balance. They can impact the climate directly by interacting with light by scattering and absorbing incoming solar radiation and indirectly by acting as cloud condensation nuclei (CCN) and ice nuclei (IN). The composition of atmospheric particles is complex and a large fraction of particles generally contains both inorganic and organic compounds.1,2 Organic material contributes ∼20–50% to the total fine particle mass and up to 90% by mass to the sub-micrometer-sized particles.3 A significant fraction of these organic materials (∼20–70%) is water soluble.4 In the atmosphere, aerosol particles and droplets can undergo phase transitions as relative humidity (RH) and temperature change, such as deliquescence, efflorescence, freezing, melting, and glass formation.5–10 It has been found that non-ideal interactions among inorganic ions, organic compounds, and water may lead to the transition from one well-mixed liquid phase to two phase-separated liquid phases, which is termed liquid–liquid phase separation (LLPS).11–14 Previous studies showed that many types of ambient aerosol particles could undergo LLPS.15–18 For example, one study used micro-spectroscopy techniques and showed that particles collected from the Amazon region contained potassium salts as an inner core that was phase separated from biogenic organic materials as a coating.16 Li et al.18 observed phase separation between secondary inorganics and organic matter both in rural and suburban aerosol particles. Droplets with LLPS may display two, or in some cases three liquid phases19 and take on either core–shell or partially engulfed morphologies.20–24 Modelling the gas–particle partitioning of organic aerosol confirmed the importance of LLPS in particles for predicting the organic matter mass and composition.11,25,26 LLPS in droplets may affect their optical properties27 and heterogeneous chemistry.28,29 Recent studies have also shown that the formation of liquid phases has impacts on a particle's ability to serve as CCN.19,30–33 LLPS is also often observed in biological systems.34 Ice nucleation is an important process in cryobiology35 and biological systems.36,37 Some ice-binding proteins are the most efficient materials for controlling ice formation in living organisms.38The occurrence of LLPS depends on the type of inorganic salts or acids,39 the types and polarities of organics,24,40–43 and, in the ultrafine size range, the size of particles.44–48 Organic aerosols are ubiquitous in the atmosphere and can be directly emitted from different sources or form through the oxidation of volatile organic compounds.2 Sulfate is one of the most abundant inorganic species and often associated with organics in aerosol particles.49 For example, Heald et al. showed that the organic-to-sulfate mass ratio derived from 17 field campaigns ranges from 0.1 to close to 100 at different altitudes. The average elemental oxygen-to-carbon ratio (O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
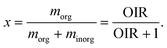
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C) of organic materials in the atmosphere ranges from close to zero for hydrocarbon-like organics to higher than one for low-volatility oxygenated organic aerosol particles.50 Previous studies often used O:C as a predictor for the presence of LLPS in particles because it serves as a proxy for the polarity of organic compounds and their miscibility with water and electrolytes.12,22,40,41,43,51 It has been shown in laboratory experiments that LLPS always occurs in mixed organic–inorganic particles containing substantial amounts of ammonium sulfate (AS) and organics with an average O:C < 0.56 and never occurs for O:C > 0.8, while the occurrence of LLPS depends on the composition and organic functional groups for 0.56 < O:C < 0.80.40 Particles containing organic material while free of inorganic salts can also undergo LLPS for O:C ≦ 0.58, depending on the spread in polarity among the organics.41,52 Phase separation was also shown to be influenced by the organic-to-inorganic dry mass ratio (OIR),53 which may result in different morphologies upon LLPS. The onset RH of LLPS in the investigated organics/AS/H2O droplets ranged from 60–90%.12,54,55 In these studies, onset is a term used to indicate the RH at which LLPS was first observed during a humidification or dehumidification, i.e. when RH was increased or decreased over time at a constant rate.
C) of organic materials in the atmosphere ranges from close to zero for hydrocarbon-like organics to higher than one for low-volatility oxygenated organic aerosol particles.50 Previous studies often used O:C as a predictor for the presence of LLPS in particles because it serves as a proxy for the polarity of organic compounds and their miscibility with water and electrolytes.12,22,40,41,43,51 It has been shown in laboratory experiments that LLPS always occurs in mixed organic–inorganic particles containing substantial amounts of ammonium sulfate (AS) and organics with an average O:C < 0.56 and never occurs for O:C > 0.8, while the occurrence of LLPS depends on the composition and organic functional groups for 0.56 < O:C < 0.80.40 Particles containing organic material while free of inorganic salts can also undergo LLPS for O:C ≦ 0.58, depending on the spread in polarity among the organics.41,52 Phase separation was also shown to be influenced by the organic-to-inorganic dry mass ratio (OIR),53 which may result in different morphologies upon LLPS. The onset RH of LLPS in the investigated organics/AS/H2O droplets ranged from 60–90%.12,54,55 In these studies, onset is a term used to indicate the RH at which LLPS was first observed during a humidification or dehumidification, i.e. when RH was increased or decreased over time at a constant rate.
Previous studies on homogeneous ice nucleation mainly focused on well-mixed aqueous droplets with homogeneous morphology (presence of one liquid phase). There are only a few studies that have investigated both the temperature dependence of LLPS in the low temperature range relevant to the middle and upper troposphere43 as well as the process of ice nucleation on phase-separated organic–sulfate particles.56 The potential impact of the occurrence of LLPS on ice nucleation in atmospheric particles or droplets required much more in-depth investigation. Due to the fact that LLPS can create a chemically and physically distinct interface, it could be suspected that ice nucleation could occur there aided by the interface itself. As such, we presented a study to test the hypothesis that the presence of a liquid–liquid interface may enhance the occurrence of heterogeneous ice nucleation.
The lambda approach and the water-activity-based approach have been widely used to describe homogenous ice nucleation in aqueous solutions or droplets. The lambda approach was formulated by MacKenzie57 and Rasmussen58 for the freezing depression of aqueous solutions and has since been used to describe the homogeneous ice nucleation of micrometer-sized samples.59–61 The lambda approach describes a linear relationship between the depressions of the melting point of ice and the homogeneous ice nucleation temperature of various types of aqueous samples.57,60,62–65 The water-activity-based approach describes freezing of supercooled aqueous droplets as depending only on a droplet's water activity (aw) and is independent of the nature of the solute.66 Although, we note that the nature of the solute affects the aw at a given mass fraction of solute in an aqueous solution; hence, solute properties are implicitly accounted for. It has been argued that the state of water hydrogen-bonding network in solutions constrains the ice nucleation process and it may be affected differently by different solutes and their concentrations.67 However, once aw is considered as a dimension of the state space, the homogeneous ice nucleation temperature follows to good approximation a single curve (function of aw) regardless of the solute's nature. The homogeneous ice nucleation curve is then parameterized with a constant shift of aw (i.e., Δaw) from the ice melting temperature curve. This parameterization was shown to be valid for a large set of homogeneous ice nucleation data, mainly comprised of single-solute-component aqueous solutions and pure water.66 The determined value of Δaw is about 0.313 for micrometer-sized droplets.67
There are a limited number of studies that have investigated the homogeneous ice nucleation of droplets containing multiple solute components. One study by Knopf and Rigg showed that homogeneous freezing of mixed levoglucosan and AS droplets at a fixed composition, in general, agreed with predictions of the water-activity-based homogeneous ice nucleation theory once the temperature dependence of aw was considered.68 Ice nucleation for atmospherically relevant organic aerosol systems have been investigated, such as in oxidation of volatile organic compounds that produce secondary organic aerosols.69 For example, α-pinene SOA particles were observed to nucleate ice homogeneously.70–72 Naphthalene–SOA in the glass state forms ice through heterogeneous nucleation, i.e. at lower RH and temperature relative to expected values for homogeneous ice nucleation.73 However, the composition of SOA are complex, multicomponent and less known at molecular level, therefore a definitive relation between LLPS in these previous studies70–73 and ice nucleation was not investigated. Here we focus on multicomponent systems of well-known chemical composition and their ability to nucleate ice either homogeneously or heterogeneously. Polyethylene glycol (PEG), a substance produced with various oligomer/polymer chain lengths corresponding to a range of molar masses, is commonly used as an excipient to increase the aqueous solubility of pharmaceutical drugs as well as in edible films in the food industry.74,75 PEG and AS are often used in laboratory model systems to represent properties of the organic and inorganic fractions in aerosol particles.53,64,76,77 PEG400 shares a similar molar masses of polymeric or oligomeric compounds routinely detected in atmospheric organics.78–80
Here, we study the LLPS behavior and ice nucleation of mixed PEG400-AS droplets. In our experiments, the OIR was varied from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 to 8
8 to 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to help elucidate the impacts of LLPS in ice cloud formation. Both LLPS presence and extent and ice nucleation were directly imaged with sensitivity to the location of where ice formed; nucleation in either of the phases or at the LLPS interface. The occurrence of LLPS in droplets at various aw in the range of 0.8–1.0 was investigated as well as their ice nucleation temperatures. The experimental data were analyzed using the lambda approach and the water-activity-based approach to describe ice nucleation of PEG400-AS droplets. Experimentally determined ice nucleation rate coefficients are presented according to the water-activity-based ice nucleation theory and a parameterization is discussed.
1 to help elucidate the impacts of LLPS in ice cloud formation. Both LLPS presence and extent and ice nucleation were directly imaged with sensitivity to the location of where ice formed; nucleation in either of the phases or at the LLPS interface. The occurrence of LLPS in droplets at various aw in the range of 0.8–1.0 was investigated as well as their ice nucleation temperatures. The experimental data were analyzed using the lambda approach and the water-activity-based approach to describe ice nucleation of PEG400-AS droplets. Experimentally determined ice nucleation rate coefficients are presented according to the water-activity-based ice nucleation theory and a parameterization is discussed.
2. Experimental methods
Particle samples were first prepared and used for two separated sets of experiments to determine: (1) the separation relative humidity (SRH), which denotes the RH of the onset of LLPS during a dehydration process starting from high RH, and efflorescence relative humidity (ERH) when efflorescence of AS occurs in the droplets; (2) the homogeneous freezing and melting temperatures of droplets. The methods are based on previous studies53,81–84 and described in detail elsewhere.53,84 They are briefly described in the following.2.1 Particle sample preparation
Particles were generated using a piezo-electric driven single droplet dispenser (MicroFab Tech. Inc., MJ-ABP-01) from aqueous AS solution, PEG400 solution, and solutions with different OIRs of PEG400 to AS (i.e., 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8, 1
8, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 1
2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8
1, 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). For each sample, a number of about 60–140 monodisperse particles were deposited onto a hydrophobic glass slide (Hampton, No. HR3-277). Particle generation was done in a clean bench to avoid contamination by ambient particles.
1). For each sample, a number of about 60–140 monodisperse particles were deposited onto a hydrophobic glass slide (Hampton, No. HR3-277). Particle generation was done in a clean bench to avoid contamination by ambient particles.
2.2 Observation of LLPS
A first set of experiments was conducted to observe the LLPS and determine the SRH and ERH. The prepared particle sample was transferred to an aerosol conditioning cell (ACC) and exposed to a humidified N2 (g) flow at 1.0 standard liter per minute. The ACC serves two purposes as a RH- and temperature-controlled (i) experimental chamber to observe the RH range over which phase transitions occur and (ii) flow chamber to prepare droplet samples at a desired aw and seal them for ice nucleation experiments (described later). The dew point (Tdew) of the humidified N2 (g) flow in the ACC was measured by a chilled mirror hygrometer (Buck Research Instruments, CR-1A) with an uncertainty of ±0.15 K. The particle or droplet temperature (Tdrop) was determined from a temperature sensor embedded in a custom-made cryo-cooling stage with an uncertainty of ±0.20 K. The sample was conditioned at a known Tdrop between 286 K and 288 K. Particles were cycled through hydration and dehydration over a wide RH range in order to observe LLPS. The sample was first exposed to a gas phase with a RH < 30% in the ACC for about 15 min. After that, it was cooled at a rate of 0.1 K min−1 (∼0.6% RH min−1) to change the RH from 35% to 98% as a hydration step and kept at 98% for at least 5 min. Then, the sample was heated at the same rate to decrease the RH down to 20% as a dehydration step. At least 3 independent samples were used for each OIR and the experiment was repeated 3 times for each independent sample. During the experiments, the images of samples were recorded by an optical microscope (OM) and used to visually confirm the appearance of LLPS. The SRH and ERH of the droplets were determined upon dehydration by the continuously monitored Tdew and Tdrop using the following equation for relative humidity with respect to liquid water: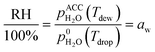 | (1) |
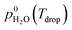 is the saturation vapor pressure over liquid water at the sample temperature, Tdrop, and
is the saturation vapor pressure over liquid water at the sample temperature, Tdrop, and 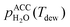 is the water vapor partial pressure in the ACC, which is calculated from Tdew.85
is the water vapor partial pressure in the ACC, which is calculated from Tdew.85
2.3 Droplet preparation and ice nucleation experiments
A second set of experiments was carried out to study ice nucleation of droplet samples at different aw. The prepared particle samples in the ACC were exposed to humidified air at a desired RH (i.e., a desired aw) and kept for a minimum of 15 min. This allowed sufficient diffusion of water in the droplets and equilibrium between droplets and water vapor. An OM was used to monitor the droplet size to ensure the droplets reached equilibrium with water vapor. In equilibrium, aw for these larger droplets with size between 60 and 100 μm was determined using Eq. (1). After conditioning, the droplet sample was sealed against ambient conditions using another hydrophobic glass slide and an aluminum foil spacer (∼200 μm thick) with vacuum grease. This resulted in a small air volume where the droplets were located so that during supercooling, any condensable water vapor resulted in an insignificant change in droplet composition.68,84 The sealed droplet sample was transferred to the ice nucleation apparatus consisting of a cryo-cooling stage (Linkam, THMS600) coupled with an OM (Olympus, BX53). The sample was cooled at a rate of 10 K min−1 until all droplets froze. After, the frozen particles were melted with a heating rate of 0.5 K min−1. For each aw, about 130–420 freezing events from at least two independent samples were recorded and analyzed. A digital camera (Olympus, DP74) recorded the images of the sample every 0.3 and 6 seconds corresponding to 0.05 K during cooling and heating, respectively. The images were used for the determination of freezing temperature (Tf) and melting temperature (Tm) of individual droplets along with their size. A high-speed camera (Phantom, v341) was used to capture the freezing of droplets for a few samples.2.4 Calibration and validation
The ACC was calibrated against the melting point of ice with respect to pure liquid water and also the deliquescence relative humidity (DRH) of NaCl particles. Uncertainty in RH due to the uncertainties in Tdew and Tdrop is less than 1% corresponding to an uncertainty of 0.01 in aw at 286 K to 288 K when the droplets were prepared. The temperature of the cryo-cooling stage for ice nucleation experiments was calibrated by the melting points of pure heptane (182.60 K), octane (216.33 K), decane (243.55 K), dodecane (263.58 K), and ice (273.15 K).86 The uncertainty of freezing temperature is less than 0.2 K.2.5 Chemicals
High purity N2 gas (99.999%) was used for sample preparation. All chemicals were purchased from Sigma and ware listed below with corresponding purities: NaCl (99.995%), (NH4)2SO4 (99.95%), decane (99%), dodecane (99+%), octane (98+%), heptane (99+%), and PEG400 (BioUltra). Millipore water (resistivity > 18.2 MΩ cm) was used for preparation of aqueous solutions.3. Results and discussion
3.1 Phase diagram of PEG400-AS-H2O system
The phase diagram of PEG400-AS-H2O samples used for ice nucleation experiments was first determined and validated as discussed below. Fig. 1 shows the combined RH/composition equilibrium and metastability phase diagram of the PEG400-AS-H2O ternary system at a temperature of 286–288 K. RH values for the phase transitions, determined in this study as a function of AS dry mass fraction (XAS) and OIR = (1 − XAS)/XAS, are compared with measurements from previous studies.21,53,76,87 The phase diagram is denoting four regions: (A) one-liquid phase, i.e., the whole droplet is in one liquid phase; (B) two-liquid phase, droplet with LLPS; (C1) two-liquid phase upon dehydration or (C2) two-phase state upon hydration (i.e., particles have one liquid and one solid phase); (D) two-phase state. Fig. S1 (ESI†) shows the phase transitions and typical morphologies of PEG400-AS particles during hydration and dehydration experiments.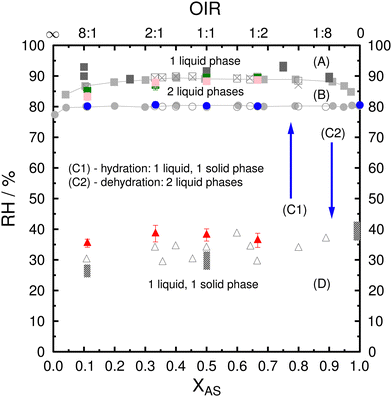 | ||
| Fig. 1 Phase diagram of PEG400-AS-H2O ternary system showing observations of LLPS as green and pink squares as a function of RH, AS dry mass fraction (XAS), and OIR, where OIR = (1 − XAS)/XAS. (A) one-liquid phase; (B) two-liquid phase; (C1) two-liquid phase upon dehydration or (C2) two-phase state upon hydration (i.e., one liquid and one solid phase); (D) two-phase state. Green and pink squares indicate LLPS upon hydration and dehydration, respectively. Blue circles are the complete deliquescence of AS in mixed PEG400-AS particles during hydration. Red triangles are AS efflorescence during dehydration. Error bars represent one standard deviation. Colored symbols indicate the data from this study. Gray symbols indicate data from previous studies including light grey87 and dark grey squares,21 open circles, squares, triangles and crosses,53 and columns.76 This figure has been adapted based on Fig. 5 of Ciobanu et al.53 | ||
At first, particles were all in the two-phase state initially at RH < 30% regardless their OIR, where AS crystals were surrounded by liquid phase rich in PEG400. Upon hydration, when the RH reached about 80% to 82%, AS crystals in the inner phase deliquesced, again independent of OIR. This is consistent with the DRH of pure AS which is 80–82% RH between 283–308 K.88 Upon deliquescence, we observed two liquid phases. The inner phase was likely to be AS-rich and the outer phase was PEG400-rich. Subsequently, upon further humidification, the two liquid phases started merging into one liquid phase after the complete deliquescence of AS. The formation of this single phase was observed to depend on OIR and RH. As shown in Fig. 1, it occurred at about 89% RH for OIR < 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and at about 85% RH for OIR of 8
1 and at about 85% RH for OIR of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, which is about 4–8% higher in RH than the complete deliquescence of AS in liquid PEG400. During the dehydration process, the droplets displayed only a one-liquid phase state for RH > 89%. Then, LLPS occurred at SRH of 88.7% and 83.3% for OIR = 1
1, which is about 4–8% higher in RH than the complete deliquescence of AS in liquid PEG400. During the dehydration process, the droplets displayed only a one-liquid phase state for RH > 89%. Then, LLPS occurred at SRH of 88.7% and 83.3% for OIR = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 to 2
2 to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and OIR = 8
1 and OIR = 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively. These observed SRH upon dehydration are similar to the RH when two liquid phases merged into a single liquid phase upon hydration. These results are consistent with observed SRH from previous studies.21,87 The two liquid phases persisted when further decreasing RH until the inner liquid phase effloresced when RH reached 35.4–38.6%. As a result, the particles showed an outer phase consisting mainly of PEG400 with small contributions of water and AS and inner phase consisting of AS crystals with some PEG400 trapped in the crystal.53,55 The observed ERH between 35.4–38.6% for the AS-rich phase was at the lower end of ERH for pure AS droplets between 33–48% (with different sizes).89,90 Ciobanu et al. observed lower ERH for the inner AS-rich phase in PEG400-AS droplets and showed a significant size dependence as compared to pure AS droplets.76 Our observations of the ERH are in general slightly higher than those from Ciobanu et al.76 at higher OIRs, which is likely due to the larger droplet size used in our experiments. Nucleation of pure AS leading to full efflorescence scales with the solution volume, meaning that larger AS solution droplets should effloresce at a higher RH than smaller droplets.87,89,90 Notice that the PEG400-AS droplets with diameters 60–100 μm used here had ERH slightly higher than those observed for micrometer-sized droplet from previous data.87
1, respectively. These observed SRH upon dehydration are similar to the RH when two liquid phases merged into a single liquid phase upon hydration. These results are consistent with observed SRH from previous studies.21,87 The two liquid phases persisted when further decreasing RH until the inner liquid phase effloresced when RH reached 35.4–38.6%. As a result, the particles showed an outer phase consisting mainly of PEG400 with small contributions of water and AS and inner phase consisting of AS crystals with some PEG400 trapped in the crystal.53,55 The observed ERH between 35.4–38.6% for the AS-rich phase was at the lower end of ERH for pure AS droplets between 33–48% (with different sizes).89,90 Ciobanu et al. observed lower ERH for the inner AS-rich phase in PEG400-AS droplets and showed a significant size dependence as compared to pure AS droplets.76 Our observations of the ERH are in general slightly higher than those from Ciobanu et al.76 at higher OIRs, which is likely due to the larger droplet size used in our experiments. Nucleation of pure AS leading to full efflorescence scales with the solution volume, meaning that larger AS solution droplets should effloresce at a higher RH than smaller droplets.87,89,90 Notice that the PEG400-AS droplets with diameters 60–100 μm used here had ERH slightly higher than those observed for micrometer-sized droplet from previous data.87
3.2 Imaging of the freezing of aqueous PEG400-AS droplets
Fig. 2 shows example OM images that demonstrate various freezing behaviors in PEG400-AS droplets with LLPS at OIR of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and aw of 0.849. Shown below the OM images are illustrations as a guide to where different liquid phases and ice were determined in these examples. We observed that ice nucleation occurs in phase-separated droplets in both the AS-rich and PEG400-rich phases, but surprisingly also at the interface between the two phases. As shown by OM image sequences in Fig. 2A during cooling, the phase-separated droplet at T > 196.4 K can be distinguished by the difference in opacity among the two liquid phases. As indicated by a change in opacity, ice nucleation started inside the AS-rich phase at 196.3 K. Within 0.1 K of further cooling, the ice crystal grew rapidly in the inner phase. As the droplet cooled below 196.3 K, ice continued to grow in the PEG400-rich phase, but slower than in the AS-rich phase. A second ice nucleation event occurred at 192.5 K in the PEG400-rich phase. This second event occurred in the PEG-rich phase seemingly unaffected by the ice growth from the first event. Then, freezing completed at 189.7 K. During ice formation of simple salt solutions, dissolved ions are expected to be expelled from locations becoming occupied by the growing ice crystal, creating a concentrated brine.91,92 Likewise, it is expected that concentrated brine of the AS-rich or a concentrated solution of the remaining PEG-rich phase may have formed during freezing. Images in Fig. 2 and Fig. S1 (ESI†) reveal that the contrasts generated due to solid and liquid phases are clearly detectable as rings or high light-absorbing dark areas. As the droplet in Fig. 2A freezes, several rings and regions of contrast appear, resulting in almost a “bull's-eye” target pattern at 189.7 K. We suspect this may be due to the formation and evolution of a variety of phases, i.e., ice and brine regions. However, a more thorough analysis would require an in situ dynamic and chemically selective investigation during freezing, which is beyond the scope of this work. Overall, our observation shows a complex freezing mechanism over time that should be the focus of future work. Fig. 2B and C shows two other examples of the freezing behavior. In Fig. 2B, it is likely that ice nucleation occurred at the interface between two liquid phases. Determining the exact location of nucleation needs 3-D imaging with higher resolution and high-speed camera. After nucleation, the ice crystal grew in a similar behavior as the case shown in Fig. 2A. In Fig. 2C, ice nucleation in yet another droplet occurred in the PEG400-rich phase. Ice crystal grew and contacted the inner AS-rich phase inducing freezing there. Later, three additional nucleation events occurred within 0.1 K in the PEG400-rich phase as temperature decreased. Fig. S2 (ESI†) provides additional examples at OIR = 1
1 and aw of 0.849. Shown below the OM images are illustrations as a guide to where different liquid phases and ice were determined in these examples. We observed that ice nucleation occurs in phase-separated droplets in both the AS-rich and PEG400-rich phases, but surprisingly also at the interface between the two phases. As shown by OM image sequences in Fig. 2A during cooling, the phase-separated droplet at T > 196.4 K can be distinguished by the difference in opacity among the two liquid phases. As indicated by a change in opacity, ice nucleation started inside the AS-rich phase at 196.3 K. Within 0.1 K of further cooling, the ice crystal grew rapidly in the inner phase. As the droplet cooled below 196.3 K, ice continued to grow in the PEG400-rich phase, but slower than in the AS-rich phase. A second ice nucleation event occurred at 192.5 K in the PEG400-rich phase. This second event occurred in the PEG-rich phase seemingly unaffected by the ice growth from the first event. Then, freezing completed at 189.7 K. During ice formation of simple salt solutions, dissolved ions are expected to be expelled from locations becoming occupied by the growing ice crystal, creating a concentrated brine.91,92 Likewise, it is expected that concentrated brine of the AS-rich or a concentrated solution of the remaining PEG-rich phase may have formed during freezing. Images in Fig. 2 and Fig. S1 (ESI†) reveal that the contrasts generated due to solid and liquid phases are clearly detectable as rings or high light-absorbing dark areas. As the droplet in Fig. 2A freezes, several rings and regions of contrast appear, resulting in almost a “bull's-eye” target pattern at 189.7 K. We suspect this may be due to the formation and evolution of a variety of phases, i.e., ice and brine regions. However, a more thorough analysis would require an in situ dynamic and chemically selective investigation during freezing, which is beyond the scope of this work. Overall, our observation shows a complex freezing mechanism over time that should be the focus of future work. Fig. 2B and C shows two other examples of the freezing behavior. In Fig. 2B, it is likely that ice nucleation occurred at the interface between two liquid phases. Determining the exact location of nucleation needs 3-D imaging with higher resolution and high-speed camera. After nucleation, the ice crystal grew in a similar behavior as the case shown in Fig. 2A. In Fig. 2C, ice nucleation in yet another droplet occurred in the PEG400-rich phase. Ice crystal grew and contacted the inner AS-rich phase inducing freezing there. Later, three additional nucleation events occurred within 0.1 K in the PEG400-rich phase as temperature decreased. Fig. S2 (ESI†) provides additional examples at OIR = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and aw = 0.852, where ice nucleation in one droplet occurred in the PEG400-rich phase and in the AS-rich phase in another droplet, similar to Fig. 2.
1 and aw = 0.852, where ice nucleation in one droplet occurred in the PEG400-rich phase and in the AS-rich phase in another droplet, similar to Fig. 2.
Fig. 3 shows another example of freezing in PEG400-AS droplets with LLPS at OIR of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and aw of 0.847 captured by a high-speed camera. Fig. 3A shows an example where ice nucleation occurred in the PEG400-rich phase and again 300 milliseconds later in the AS-rich phase of the same droplet. Fig. 3B shows ice nucleation started from the AS-rich phase and ice crystal grew rapidly in the inner phase. Bertram et al. showed that upon ice nucleation ice and AS could crystallize simultaneously in pure aqueous AS droplets.61 We speculated that this likely also occurred in the AS-rich phase of PEG400-AS droplets at low aw (Fig. 3B). As shown in Fig. 2A, B and 3B, the crystallization of ice and AS in the AS-rich phase is much faster than ice crystallization in the PEG400-rich phase. Crystallization in the AS-rich phase typically lasted 500 milliseconds, determined from high-speed imaging, while the ice crystal growth in the PEG400-rich phase took about 7 seconds. Longer ice crystallization times are partially due to the high viscosity and thus slower diffusion of water in the PEG400-rich phase at these investigated aw and T < 202 K. This temperature range coincides with the glass transition temperature of aqueous PEG400 solutions of different concentrations, 60–100 wt%, ranging from 184.2 K62 to 200.2 K.93 Huang et al.62 found that the glass transition temperature for the PEG400–H2O system is at about 190.7 K with a minimum value of 184.2 K at 0.6 mass fraction of PEG400 and maximum of 193.9 K at 0.8 mass fraction. This indicates that the PEG400-rich phase in this temperature range may have been highly viscous and in turn, the growth of ice crystals would have been limited by molecular diffusion.67,94,95 Here, multiple ice nucleation events were experimentally observed within the same, supermicron-sized droplets. We hypothesize that after the first nucleation occurs in either the AS-rich (Fig. 2A) or PEG400-rich phase (Fig. 3A), ice growth into the other phase is relatively slow so that sufficient water remains available for the formation of additional ice germs and thus more nucleation events to take place in the same droplet.
1 and aw of 0.847 captured by a high-speed camera. Fig. 3A shows an example where ice nucleation occurred in the PEG400-rich phase and again 300 milliseconds later in the AS-rich phase of the same droplet. Fig. 3B shows ice nucleation started from the AS-rich phase and ice crystal grew rapidly in the inner phase. Bertram et al. showed that upon ice nucleation ice and AS could crystallize simultaneously in pure aqueous AS droplets.61 We speculated that this likely also occurred in the AS-rich phase of PEG400-AS droplets at low aw (Fig. 3B). As shown in Fig. 2A, B and 3B, the crystallization of ice and AS in the AS-rich phase is much faster than ice crystallization in the PEG400-rich phase. Crystallization in the AS-rich phase typically lasted 500 milliseconds, determined from high-speed imaging, while the ice crystal growth in the PEG400-rich phase took about 7 seconds. Longer ice crystallization times are partially due to the high viscosity and thus slower diffusion of water in the PEG400-rich phase at these investigated aw and T < 202 K. This temperature range coincides with the glass transition temperature of aqueous PEG400 solutions of different concentrations, 60–100 wt%, ranging from 184.2 K62 to 200.2 K.93 Huang et al.62 found that the glass transition temperature for the PEG400–H2O system is at about 190.7 K with a minimum value of 184.2 K at 0.6 mass fraction of PEG400 and maximum of 193.9 K at 0.8 mass fraction. This indicates that the PEG400-rich phase in this temperature range may have been highly viscous and in turn, the growth of ice crystals would have been limited by molecular diffusion.67,94,95 Here, multiple ice nucleation events were experimentally observed within the same, supermicron-sized droplets. We hypothesize that after the first nucleation occurs in either the AS-rich (Fig. 2A) or PEG400-rich phase (Fig. 3A), ice growth into the other phase is relatively slow so that sufficient water remains available for the formation of additional ice germs and thus more nucleation events to take place in the same droplet.
3.3 Freezing behaviors of aqueous AS, PEG400, and PEG400-AS droplets
Ice nucleation experiments were conducted for PEG400-AS droplets of different OIRs along with water droplets and aqueous AS droplets for comparison. In total, more than 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 droplets were analyzed from the investigated samples. Fig. S3–S9 (ESI†) show the frozen fraction and probability density of ice nucleation events. The probability density histogram was normalized by the total number of analyzed droplets (Ntot) to better visualize the distribution of freezing frequency. Table S1 (ESI†) presents the median Tf with the corresponding 10th and 90th percentiles and mean Tm with one standard deviation for the investigated samples. Frozen fraction (f) was calculated by f(T) = Nice/Ntot where Nice is the number of droplets containing ice (i.e., frozen) at temperature T. Observations of homogenous freezing temperatures and melting temperatures of AS droplets and pure water droplets are shown in Fig. 4. The freezing temperatures determined here were consistent with the values reported by Knopf and Lopez84 using the same method and similar droplet size. Homogeneous freezing temperature curves given by Koop et al.66 determined for micrometer-size droplets (<10 μm) and by Knopf and Lopez84 for larger droplets (20–80 μm) are shown in Fig. 4; these curves corresponds to a Δaw of 0.305 and 0.295, respectively. Median Tf of water droplets determined here were about 236.2 K which is consistent with the prediction. Assuming no significant temperature dependence of aw, ice melting and freezing data for aqueous AS droplets fall well within the predictions.
000 droplets were analyzed from the investigated samples. Fig. S3–S9 (ESI†) show the frozen fraction and probability density of ice nucleation events. The probability density histogram was normalized by the total number of analyzed droplets (Ntot) to better visualize the distribution of freezing frequency. Table S1 (ESI†) presents the median Tf with the corresponding 10th and 90th percentiles and mean Tm with one standard deviation for the investigated samples. Frozen fraction (f) was calculated by f(T) = Nice/Ntot where Nice is the number of droplets containing ice (i.e., frozen) at temperature T. Observations of homogenous freezing temperatures and melting temperatures of AS droplets and pure water droplets are shown in Fig. 4. The freezing temperatures determined here were consistent with the values reported by Knopf and Lopez84 using the same method and similar droplet size. Homogeneous freezing temperature curves given by Koop et al.66 determined for micrometer-size droplets (<10 μm) and by Knopf and Lopez84 for larger droplets (20–80 μm) are shown in Fig. 4; these curves corresponds to a Δaw of 0.305 and 0.295, respectively. Median Tf of water droplets determined here were about 236.2 K which is consistent with the prediction. Assuming no significant temperature dependence of aw, ice melting and freezing data for aqueous AS droplets fall well within the predictions.
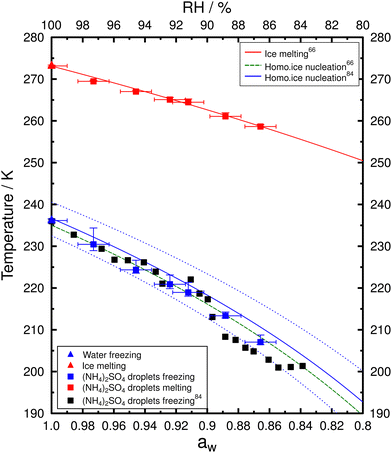 | ||
| Fig. 4 Median Tf with 20th and 80th percentiles and the corresponding mean Tm as a function of aw with uncertainty of ±0.01 for aqueous AS droplets (squares) and water droplets (triangles). Colored symbols show the data determined in this study. Black solid squares represent the median Tffor aqueous AS droplets by Knopf and Lopez.84 The red solid curve represents the ice melting boundary and the green dashed curve shows the homogeneous ice nucleation threshold with Δaw of 0.305 as given by Koop et al.66 The blue solid line represents the homogeneous ice nucleation threshold with Δaw of 0.295 and the blue dotted lines represent the pertaining uncertainty assuming δ(Δaw) of ±0.025 given by Knopf and Lopez.84 | ||
Fig. 5 presents the freezing and melting temperatures for aqueous PEG400 and mixed PEG400-AS droplets along with the initial conditioning temperature in the ACC when samples were sealed. Data for droplets in a one-liquid phase state, as well as for those containing two liquid phases right before freezing, are indicated by the solid and open circles, respectively. Tf with 10th and 90th percentiles and Tm with one standard deviation were plotted as a function of aw determined at the initial conditioning temperature assuming aw does not change with temperature. The predicted melting curve is the ice-liquid (solution) equilibrium line following a previous parameterization66 and the predicted freezing curve can be estimated using Δaw = 0.295 for droplets with diameters 20–80 μm. As expected, we observed that both Tm and Tf decreased with decreasing aw for all OIR investigated and for PEG400 without AS. Tm and Tf for PEG400-AS droplets at OIRs = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 and 1
8 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 were in agreement with the predicted melting and freezing values indicating that they froze through homogeneous ice nucleation. Deviations between the observed and predicted Tm and Tf were found for droplets at OIR = 1
2 were in agreement with the predicted melting and freezing values indicating that they froze through homogeneous ice nucleation. Deviations between the observed and predicted Tm and Tf were found for droplets at OIR = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 8
1 and 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, as well as for aqueous PEG400 droplets. The greater the organic content in droplets, the lower melting and freezing temperatures were compared to the predictions. For example, at OIR = 2
1, as well as for aqueous PEG400 droplets. The greater the organic content in droplets, the lower melting and freezing temperatures were compared to the predictions. For example, at OIR = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and aw = 0.848, Tf of 196.9 K is 9.5 K lower than the homogeneous freezing curve would suggest. For PEG400 without AS at aw = 0.949, Tf of 208.4 K is 19.6 K below the expected homogeneous freezing temperature. Additionally, for the same OIR value, deviations were greater at lower aw. This may be due to a substantial temperature dependence of aw for aqueous PEG40065,67 and the mixed PEG400-AS solutions, which becomes more evident as the organic mass fraction increases. This will be further discussed in Section 3.4.
1 and aw = 0.848, Tf of 196.9 K is 9.5 K lower than the homogeneous freezing curve would suggest. For PEG400 without AS at aw = 0.949, Tf of 208.4 K is 19.6 K below the expected homogeneous freezing temperature. Additionally, for the same OIR value, deviations were greater at lower aw. This may be due to a substantial temperature dependence of aw for aqueous PEG40065,67 and the mixed PEG400-AS solutions, which becomes more evident as the organic mass fraction increases. This will be further discussed in Section 3.4.
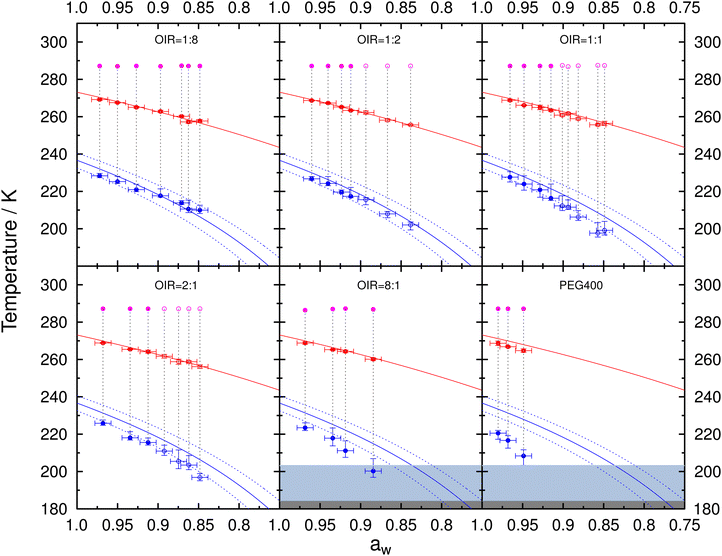 | ||
| Fig. 5 Median Tf with the corresponding 10th and 90th percentiles and mean Tm with one standard deviation are shown as blue and red circles, respectively, for aqueous PEG400-AS droplets at different OIR and salt-free PEG400 droplets. All data were plotted assuming that aw does not change with temperature indicated by the vertical gray dotted lines (i.e., at constant aw). Note that this assumption of constant aw is likely incorrect, as discussed in the main text. Solid and open circles indicate whether the droplets were in one-liquid or liquid–liquid phase-separated states at conditioning, respectively, immediately before freezing and after melting. OIR is indicated in each panel. Pink circles indicate the conditioning temperature and aw. Uncertainty in aw is ±0.01. Red and blue solid lines represent the ice melting66 and homogeneous ice nucleation curve for Δaw = 0.295,84 respectively. Dotted lines indicate the upper and lower limits of homogeneous ice nucleation assuming (Δaw) of ±0.025. Light gray and dark gray areas indicate glass transition temperatures between 200.2 K93 and 184.2 K62 for aqueous PEG400 solutions. | ||
As shown in Fig. 5, the droplets at OIR = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 freeze homogeneously following the homogeneous ice nucleation curve irrespective of droplets being homogenous or liquid–liquid phase-separated. The homogeneous and liquid–liquid phase-separated droplets at OIR = 1
2 freeze homogeneously following the homogeneous ice nucleation curve irrespective of droplets being homogenous or liquid–liquid phase-separated. The homogeneous and liquid–liquid phase-separated droplets at OIR = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 nucleated ice with a trend similar to the homogenous ice nucleation curve but at lower temperatures with the assumption of constant aw (Fig. 5). These droplets likely form ice through homogeneous nucleation irrespective of OIR or phase separation. In our experiments, the overall composition of each individual droplet with LLPS before freezing is fixed at the sample preparation conditions in the closed sandwich-type system with limited condensable water vapor. We conclude that LLPS likely had little to no impact on homogeneous ice nucleation of the investigated aqueous PEG400-AS droplets in our experiments, in which the overall composition of individual droplet remains unchanged during cooling. This is further supported by the similar supercooling tendency (λ values) for droplets with and without LLPS from the data analysis based on the lambda approach as discussed in Section 4.
1 nucleated ice with a trend similar to the homogenous ice nucleation curve but at lower temperatures with the assumption of constant aw (Fig. 5). These droplets likely form ice through homogeneous nucleation irrespective of OIR or phase separation. In our experiments, the overall composition of each individual droplet with LLPS before freezing is fixed at the sample preparation conditions in the closed sandwich-type system with limited condensable water vapor. We conclude that LLPS likely had little to no impact on homogeneous ice nucleation of the investigated aqueous PEG400-AS droplets in our experiments, in which the overall composition of individual droplet remains unchanged during cooling. This is further supported by the similar supercooling tendency (λ values) for droplets with and without LLPS from the data analysis based on the lambda approach as discussed in Section 4.
Upon cooling, ice nucleation was not observed in the PEG400 droplets at aw < 0.95 and the mixed PEG400-AS droplets with OIR = 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at aw < 0.88 (i.e., high PEG400 contents). For example, experiments with droplets having OIR = 8
1 at aw < 0.88 (i.e., high PEG400 contents). For example, experiments with droplets having OIR = 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at aw = 0.849 were first cooled without freezing down to 184 K. When the droplets were subsequently heated, freezing was observed at 198.5 K as shown in Fig. S10 (ESI†). As discussed in Section 3.2, the glass transition temperature for aqueous PEG400 was between 184.2 K and 200.2 K.62,93 At these low temperatures, the droplets with high PEG400 contents mentioned above are likely viscous or in the glass state. Thus, it is likely that ice nucleation was impeded when cooled because of high viscosity or even glass formation, and that water froze (devitrification) subsequent to warming.95,96 In other words, nucleation or critical cluster formation occurred at temperatures near the glass transition, but without crystal growth due to mass transfer limitations of water molecules. The high viscosity of the droplets at this low temperature also should have slowed the ice nucleation process.65 It is suggested that ice germs already formed during cooling in the glass or high viscosity solution, but ice nucleation was limited by the low molecular diffusion.95 Upon warming, the viscosity of droplets decreased sufficiently and ice growth was possible.91 The addition of AS in the solution would likely lower the glass transition temperature of the droplets, which is evident by the fact that this same behavior has not observed for droplets with lower OIRs.
1 at aw = 0.849 were first cooled without freezing down to 184 K. When the droplets were subsequently heated, freezing was observed at 198.5 K as shown in Fig. S10 (ESI†). As discussed in Section 3.2, the glass transition temperature for aqueous PEG400 was between 184.2 K and 200.2 K.62,93 At these low temperatures, the droplets with high PEG400 contents mentioned above are likely viscous or in the glass state. Thus, it is likely that ice nucleation was impeded when cooled because of high viscosity or even glass formation, and that water froze (devitrification) subsequent to warming.95,96 In other words, nucleation or critical cluster formation occurred at temperatures near the glass transition, but without crystal growth due to mass transfer limitations of water molecules. The high viscosity of the droplets at this low temperature also should have slowed the ice nucleation process.65 It is suggested that ice germs already formed during cooling in the glass or high viscosity solution, but ice nucleation was limited by the low molecular diffusion.95 Upon warming, the viscosity of droplets decreased sufficiently and ice growth was possible.91 The addition of AS in the solution would likely lower the glass transition temperature of the droplets, which is evident by the fact that this same behavior has not observed for droplets with lower OIRs.
3.4 Water activity of aqueous PEG400 and PEG400-AS droplets
As discussed previously, the deviation of observed Tf and Tm compared to predictions may be due to incorrectly assuming that aw remains constant as a function of temperature. Although, the droplet composition remained constant in our experiments, aw may still be temperature dependent to a non-negligible degree. From theory, in particular the Gibbs–Helmholtz equation, it is clear that activity coefficients and hence activities are (weak) functions of temperature (with the exception of so-called thermal mixtures).97,98 As summarized below, previous studies have also suggested that the temperature dependence of aw may explain Tm and Tf for aqueous PEG droplets64,65 as well as other organic compounds.62,66,68,98,99 There are no direct measurements of aw at supercooled temperatures available for metastable PEG solutions or PEG400-AS mixtures. It is also not straightforward to use a thermodynamic model like AIOMFAC to predict the temperature dependence, since the model's temperature dependence predictions of water and organic activities (e.g., for PEG400) usually need to be established from reliable experimental data covering the targeted temperature range, which is lacking in this case. Conversely, for improvements of models like AIOMFAC to lower temperatures, a key approach used in the past is to utilize the melting and homogeneous freezing data on the basis of the Δaw assumption (i.e., the water-activity-based approach) to tune the model.98 Therefore, we follow such approach used in previous studies64,98 in an attempt to parameterize aw(T) at constant pressure using 2 constraints. In the first, we assume that the aw of droplet samples at the conditioning temperature is certain. The second is that aw(Tm) and aw(Tf) exactly follow the predicted melting and homogeneous freezing curves.84 As shown in Fig. 6A, aw for aqueous PEG400 droplets must consequently exhibit a stronger, nonlinear temperature dependence, in agreement with previous work.65,67 The aw of aqueous PEG with a molar mass of 300 g mol−1 (PEG300) and 6000 g mol−1 (PEG6000) determined by Zobrist et al.64 are shown in Fig. 6B for comparison. The aw of all PEG solutions show a stronger temperature dependence for the lower aw range than at higher aw. The temperature effect on aw was more significant for PEG oligomers with higher molecular weight.62 The enhancement in intermolecular (hydrogen)-bonding of the oxygen-bearing ether and hydroxyl functionalities of PEG molecules with water molecules as temperature decreases is expected to lead to a reduction in the effective fraction of “free” water, as expressed by the mole fraction of water, and in turn a decrease in aw of the solution.100Fig. 6B also suggests a nonlinear temperature dependence of aw from the stable to the supercooled, metastable temperature range.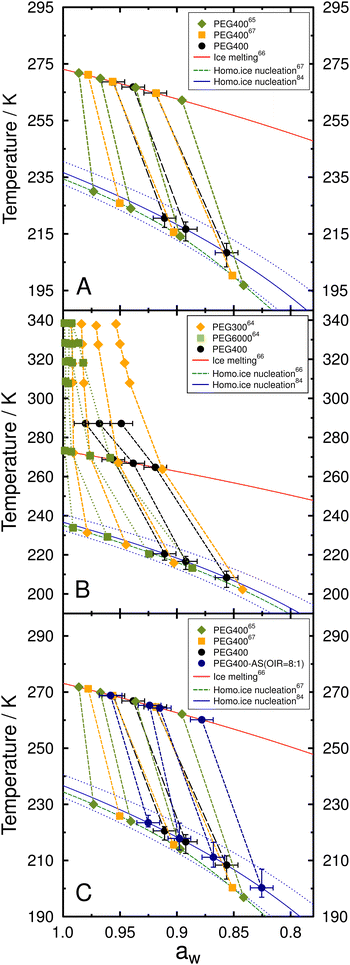 | ||
Fig. 6 (A) Observed melting and freezing temperature for aqueous PEG400 droplets, where aw was adjusted to match predictions. Color symbols show the data given by Koop and Zobrist67 and Kimizuka et al.65 (B) aw for various aqueous solutions of PEG300, PEG400, and PEG6000. PEG300 (diamonds) and PEG6000 (squares) data were given by Zobrist et al.64 PEG400 (circles) data are from this study. (C) PEG400-AS droplets at OIR = 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 data from this study were added alongside data from panel A. The lines connecting the data points are only for guidance. Uncertainty in aw is ±0.01 at 287 K. Error bars in temperature correspond to the 10th and 90th percentiles of freezing temperature. 1 data from this study were added alongside data from panel A. The lines connecting the data points are only for guidance. Uncertainty in aw is ±0.01 at 287 K. Error bars in temperature correspond to the 10th and 90th percentiles of freezing temperature. | ||
We suspect that the aqueous PEG400-AS droplets may also experience aw changes with decreasing temperature, similar to pure aqueous PEG400. As shown in Fig. 5, the deviation of Tf for the aqueous PEG400-AS droplets from predictions increased also as the content of PEG400 increased in droplets (i.e., higher OIRs). This implies that the corresponding aw for aqueous PEG400-AS droplets might also change with temperature, and that this effect is enhanced with increasing OIR. In aqueous droplets consisting of PEG400 and AS, the freezing data indicated that aw does not show strong temperature dependence at OIR of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 and 1
8 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. However, when OIR reaches 8
2. However, when OIR reaches 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the temperature dependence of aw is similar to PEG400 as shown in Fig. 6C. One way to explain these effects is via consideration of the temporary hydrogen-bonding network established in aqueous phases in its impact on aw. It is expected that the PEG400 hydroxyl groups may form hydrogen bonds with the oxygen of SO42− (when in close proximity) and there is also a weak binding between PEG400 and the sulfur of SO42−.101 For the samples with lower OIRs (i.e., enriched in SO42−), both of these temporary interactions might reduce the effect of temporary hydrogen bonding between PEG400 and surrounding water molecules, especially in the composition range where LLPS is absent. This facilitates the movement of more free water, which dampens nonideal mixing effects, resulting in insignificant changes of aw with temperature.100,101 However, for higher OIRs, the SO42− anions may only replace a relatively small portion of hydrogen bonds between PEG400 and water molecules.101 Thus, PEG400 would still be hydrogen bonded to water molecules in the PEG400-AS droplets at OIR between 1
1, the temperature dependence of aw is similar to PEG400 as shown in Fig. 6C. One way to explain these effects is via consideration of the temporary hydrogen-bonding network established in aqueous phases in its impact on aw. It is expected that the PEG400 hydroxyl groups may form hydrogen bonds with the oxygen of SO42− (when in close proximity) and there is also a weak binding between PEG400 and the sulfur of SO42−.101 For the samples with lower OIRs (i.e., enriched in SO42−), both of these temporary interactions might reduce the effect of temporary hydrogen bonding between PEG400 and surrounding water molecules, especially in the composition range where LLPS is absent. This facilitates the movement of more free water, which dampens nonideal mixing effects, resulting in insignificant changes of aw with temperature.100,101 However, for higher OIRs, the SO42− anions may only replace a relatively small portion of hydrogen bonds between PEG400 and water molecules.101 Thus, PEG400 would still be hydrogen bonded to water molecules in the PEG400-AS droplets at OIR between 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, resulting in a weaker temperature dependence of aw.
1, resulting in a weaker temperature dependence of aw.
Our results with PEG400-AS are compared with freezing temperatures of aqueous levoglucosan-AS droplets with various compositions determined by Knopf and Rigg.68 As shown in Fig. S11 (ESI†), the aw of aqueous levoglucosan droplets showed a strong temperature dependence.68,95 However, the observed Tf of aqueous levoglucosan-AS droplets with OIR ranging from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 to 10
10 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is in agreement with the predicted freezing temperature by water-activity-based ice nucleation theory within the experimental uncertainties.68 This indicates that the corresponding aw for aqueous levoglucosan-AS droplets did not change significantly with temperature regardless of the amount of AS in the droplets. This is in contrast with our results for PEG400-AS droplets as discussed above. The presence of AS in aqueous PEG or aqueous levoglucosan solutions reduces the temperature dependence of aw but in each to a different extent. The reason is not clear and further investigations are needed for a more quantitative and predictive understanding of the temperature dependence of aw in supercooled aqueous inorganic/organic mixtures.
1 is in agreement with the predicted freezing temperature by water-activity-based ice nucleation theory within the experimental uncertainties.68 This indicates that the corresponding aw for aqueous levoglucosan-AS droplets did not change significantly with temperature regardless of the amount of AS in the droplets. This is in contrast with our results for PEG400-AS droplets as discussed above. The presence of AS in aqueous PEG or aqueous levoglucosan solutions reduces the temperature dependence of aw but in each to a different extent. The reason is not clear and further investigations are needed for a more quantitative and predictive understanding of the temperature dependence of aw in supercooled aqueous inorganic/organic mixtures.
4. Parameterizations and implications
4.1 Lambda approach
The lambda approach has been used to described a linear relationship between the depressions of melting and freezing temperatures of micrometer-size samples including aqueous PEG.65,67,102 We apply this approach for the investigated droplets here. According to the lambda approach, the depression of the freezing temperature of an aqueous droplet can be described according to:| ΔThom = λ(s) × ΔTm | (2) |
Mean values of the determined λ when considering all droplets, homogeneous droplets (one-liquid phase), and liquid-liquid phase-separated droplets are summarized in Table 1. The uncertainties were determined from at least three different aw. The depressions of melting and freezing temperatures are also plotted in Fig. 7 for comparison. The determined λ for aqueous PEG400 droplets is 3.28 ± 0.22. This is in good agreement with λ of 3.44 reported by Kimizuka et al.,65 but lower than 4.21 ± 0.11 reported by Koop and Zobrist.67 For aqueous AS droplets, λ of 1.88 ± 0.17 is slightly lower than 2.1 reported by Bertram et al.61 and 2.29 ± 0.03 reported by Koop and Zobrist.67 The differences between our and previously reported values are likely due to the difference in the sample volumes (i.e., droplet sizes).67 As shown in Table 1, λ for PEG400-AS droplets changes from 1.80 ± 0.13 for OIR = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 to 2.71 ± 0.08 for OIR = 8
8 to 2.71 ± 0.08 for OIR = 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 when considering both one-liquid and phase-separated droplets. It has been shown that a variety of solutes falls into a range of 1.4 < λ < 2.267,103 indicated by the gray shaded area in Fig. 7. Although the λ values for OIR = 1
1 when considering both one-liquid and phase-separated droplets. It has been shown that a variety of solutes falls into a range of 1.4 < λ < 2.267,103 indicated by the gray shaded area in Fig. 7. Although the λ values for OIR = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8, 1
8, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 1
2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 2
1, and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 all fall into the shaded area, λ tends to increase with increasing OIR. It has been suggested that a solute with λ of about 2 indicates the solution does not exhibit any temperature dependence of aw, e.g., AS and H2SO4.104 Those solutes which show no or only weak temperature dependence of aw, especially inorganics with small molecular weights, likely fall within the range as mentioned above.105,106 Previous studies have proposed that a large variation of λ when comparing organics with different molecular weights is due to the differences either in the self-diffusion coefficients of the solutes106 or the hydrogen bonding interactions between water and solutes.64,104 As shown in Table 1, there are no significant differences in λ between homogeneous and phase-separated droplets with same OIR. This implies that these droplets likely form ice through the same mechanism, i.e., homogeneous ice nucleation in this case.
1 all fall into the shaded area, λ tends to increase with increasing OIR. It has been suggested that a solute with λ of about 2 indicates the solution does not exhibit any temperature dependence of aw, e.g., AS and H2SO4.104 Those solutes which show no or only weak temperature dependence of aw, especially inorganics with small molecular weights, likely fall within the range as mentioned above.105,106 Previous studies have proposed that a large variation of λ when comparing organics with different molecular weights is due to the differences either in the self-diffusion coefficients of the solutes106 or the hydrogen bonding interactions between water and solutes.64,104 As shown in Table 1, there are no significant differences in λ between homogeneous and phase-separated droplets with same OIR. This implies that these droplets likely form ice through the same mechanism, i.e., homogeneous ice nucleation in this case.
| All droplets | Homogeneous droplets | Liquid–liquid phase-separated dropletsa | |
|---|---|---|---|
| a The forward slash, “/”, denotes liquid–liquid phase separation was not observed in the investigated composition range in this study. | |||
| AS | 1.88 ± 0.17 | 1.88 ± 0.17 | / |
OIR = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8 |
1.80 ± 0.13 | 1.80 ± 0.13 | / |
OIR = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
1.98 ± 0.09 | 1.90 ± 0.04 | 2.03 ± 0.08 |
OIR = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
2.02 ± 0.16 | 1.90 ± 0.13 | 2.12 ± 0.11 |
OIR = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
2.28 ± 0.08 | 2.34 ± 0.04 | 2.23 ± 0.08 |
OIR = 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
2.71 ± 0.08 | 2.71 ± 0.08 | / |
| PEG400 | 3.28 ± 0.22 | 3.28 ± 0.22 | / |
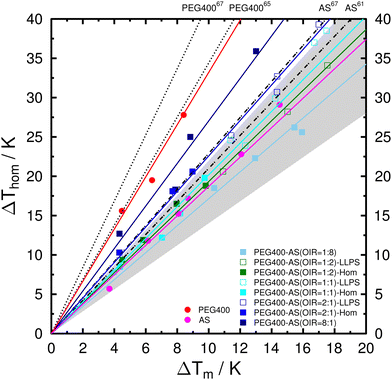 | ||
| Fig. 7 Observed depression of homogeneous ice nucleation temperature, ΔThom, as a function of the depression of melting temperature, ΔTm for the investigated systems. Color lines represent the mean λ when considering all droplets. Aqueous solution data taken from the literature: AS from Bertram et al.61 and Koop and Zobrist67 as gray dash-dotted lines. PEG400 from Kimizuka et al.65 and Koop and Zobrist67 as black dotted lines. Gray shaded area indicates the range of 1.4 < λ < 2.2 for a variety of solutes.67,103 | ||
4.2 Water-activity-based approach
The experimental ice nucleation data were used to derive homogeneous ice nucleation rate coefficients (Jhom). Jhom is defined as the number of nucleation events per volume and time with unit of cm−3 s−1. Methods for the analysis of the experimental data have been described in detail previously,84,107,108 they are briefly described in the following. For a given temperature interval (Ti) and a width (ΔT), different numbers of ice nucleation events may occur. Jhom as a function of temperature was derived using the following equation: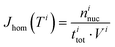 | (3) |
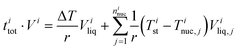 | (4) |
The experimentally determined Jhom (Jexphom) as a function of T and aw is presented in Fig. 8 for all investigated aqueous PEG400-AS and PEG400 droplets. They were compared with the predicted Jhom (Jprehom) from water-activity-based theory under the assumption that aw does not change with temperature. For each droplet composition and aw, Jexphom increases strongly as T decreases. Koop et al. showed that Jhom can change by 6 orders of magnitude when aw changes by about 0.025 according to the water-activity-based theory.66 As shown in Fig. 8, Jexphom at median freezing temperatures falls within the range of Jprehom employing an uncertainty of ±0.025 in aw at OIR < 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (also see the Fig. S12 and Table S1, ESI†). As OIR increases and aw decreases, Jexphom deviates more from the prediction. We suspect that these differences between Jexphom and Jprehom are explained by the changes in aw with temperature. This follows the same reasoning as the explanation for why Tf of the investigated aqueous PEG400-AS and PEG400 droplets which are lower than the expected homogeneous ice nucleation temperatures at higher OIRs and lower aw when a temperature dependence of aw is ignored.
1 (also see the Fig. S12 and Table S1, ESI†). As OIR increases and aw decreases, Jexphom deviates more from the prediction. We suspect that these differences between Jexphom and Jprehom are explained by the changes in aw with temperature. This follows the same reasoning as the explanation for why Tf of the investigated aqueous PEG400-AS and PEG400 droplets which are lower than the expected homogeneous ice nucleation temperatures at higher OIRs and lower aw when a temperature dependence of aw is ignored.
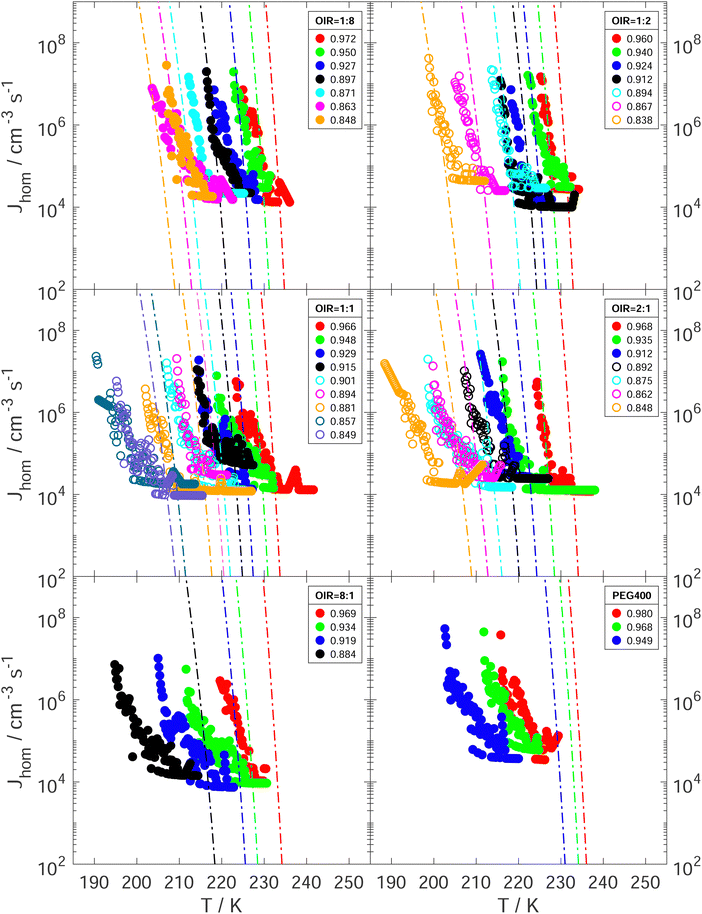 | ||
Fig. 8 Experimentally derived Jhom as a function of temperature and aw are given for aqueous PEG400-AS droplets with LLPS (open circles) and without LLPS (solid circles) at OIR of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8, 1 8, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 1 2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2 1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 1, 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and aqueous PEG400 droplets. Lines represent the corresponding predictions of Jhom from the water-activity-based ice nucleation theory for each initial aw with assumption that aw doesn’t change with temperature.66aw at sample preparation temperature is indicated by color with initial value in the legend. 1 and aqueous PEG400 droplets. Lines represent the corresponding predictions of Jhom from the water-activity-based ice nucleation theory for each initial aw with assumption that aw doesn’t change with temperature.66aw at sample preparation temperature is indicated by color with initial value in the legend. | ||
Fig. 5 and 8 show that measured Tf and Jexphom deviated from predictions when assuming the droplet's aw at the preparation temperature remains constant at lower temperature. A better agreement could be achieved if aw of a droplet with a fixed composition was temperature dependent, i.e. aw(T,x) where x is mass fraction of PEG400 related to the total mass of solutes. We consider a water activity offset, δaw, dependent on T and x with respect to the aw and T at the preparation conditions, aw,p and Tp, respectively, where
| aw(T,x) = aw,p − δaw, | (5) |
 | (6) |
| δaw = rx2(Tp − T)2, | (7) |
Fig. S13 (ESI†) shows Tf and Tm of individual droplets as a function of aw and Jhom as a function of Δaw applying eqn (5)–(7). As expected, aw is offset to lower values matching homogeneous ice nucleation temperatures, melting temperatures and homogeneous ice nucleation rate coefficients more closely. We note that, when deriving eqn (7), a first attempt was made to include linear terms in x and T with separate fitting constants. However, additional fitting constants contributed insignificantly to δaw and thus are not considered. Solution composition for aqueous AS, PEG400, and PEG400-AS droplets investigated here were fixed at all preparation conditions, meaning that the mass fraction of total solutes (mfs) did not change during ice nucleation experiments when T decreased as much as about 80 K. Often, the T dependence of aw at constant mfs is quadratic for many organic and mixed organic–inorganic solutions.110 The proposed parameterization of δaw (i.e., eqn (7)) reflects such T dependence. Fig. S13 (ESI†) shows that future studies aiming to relate mfs and aw should expect significant effects due to T and OIR, as in the case for the PEG400-AS system. Measurements of aw at supercooled region are needed for better constrains on the parameterization for such systems.
4.3 Implications of λ and δaw
The lambda approach provides an relatively simple way to predict the freezing temperature of a solution or droplet but requires the accurate melting temperature as a function of a large range of solute concentrations.67 Based on the determined λ values (Table 1 for all droplets), we provide a parameterization of λ for the PEG400-AS system with a wide range of OIRs as| λ = 1.887x2 − 0.617x + 1.878 | (8) |
5. Conclusions
We investigated the LLPS and ice nucleation of PEG400-AS droplets at different OIRs ranging from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 to 8
8 to 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 as a function of aw. The LLPS occurred at ∼80% RH and ∼89% RH in the mixed PEG400-AS particles upon hydration and dehydration, respectively. These were consistent with the observations from previous studies.53,87 For droplets with LLPS, ice nucleation occurred in the AS-rich phase, the PEG400-rich phase, and likely also in the interface between these two liquid phases. The freezing temperatures of droplets at OIR = 1
1 as a function of aw. The LLPS occurred at ∼80% RH and ∼89% RH in the mixed PEG400-AS particles upon hydration and dehydration, respectively. These were consistent with the observations from previous studies.53,87 For droplets with LLPS, ice nucleation occurred in the AS-rich phase, the PEG400-rich phase, and likely also in the interface between these two liquid phases. The freezing temperatures of droplets at OIR = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 followed the predictions of water-activity-based homogeneous ice nucleation theory within experimental uncertainties. For aqueous PEG400 and PEG400-AS droplets at OIR = 1
8 followed the predictions of water-activity-based homogeneous ice nucleation theory within experimental uncertainties. For aqueous PEG400 and PEG400-AS droplets at OIR = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8
1, 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, freezing temperatures were lower than the predictions when assuming no temperature dependence of aw and deviated more for droplets with higher PEG400 content. The addition of AS to aqueous PEG400 droplets reduces the temperature dependence of aw. We hypothesized that the presence of NH4+ cations and SO42− anions within an aqueous PEG400-rich phase might decrease the hydrogen bonding network among PEG and water molecules, thus resulting in a different temperature dependence of aw for different OIR. These findings are important to show that the addition of inorganic matter and its partial or complete miscibility with hygroscopic organics can reduce the deviation between observed freezing temperatures and predictions following a water-activity-based approach and using Δaw. However, for the case of mixed PEG400 and AS, equal or high organic content, in terms of OIR, imposes a strong nonlinear dependence of temperature, aw and composition. We suggest that this thermodynamic relationship needs to be quantified in more detail when predicting homogeneous ice nucleation temperatures for other mixed organic–inorganic aerosol systems in the atmosphere. For example, with the consideration of water activity, Kärcher and Koop used a detailed cloud microphysical model to study the effect of malonic acid on ice nucleation in sulfate particles.111
1, freezing temperatures were lower than the predictions when assuming no temperature dependence of aw and deviated more for droplets with higher PEG400 content. The addition of AS to aqueous PEG400 droplets reduces the temperature dependence of aw. We hypothesized that the presence of NH4+ cations and SO42− anions within an aqueous PEG400-rich phase might decrease the hydrogen bonding network among PEG and water molecules, thus resulting in a different temperature dependence of aw for different OIR. These findings are important to show that the addition of inorganic matter and its partial or complete miscibility with hygroscopic organics can reduce the deviation between observed freezing temperatures and predictions following a water-activity-based approach and using Δaw. However, for the case of mixed PEG400 and AS, equal or high organic content, in terms of OIR, imposes a strong nonlinear dependence of temperature, aw and composition. We suggest that this thermodynamic relationship needs to be quantified in more detail when predicting homogeneous ice nucleation temperatures for other mixed organic–inorganic aerosol systems in the atmosphere. For example, with the consideration of water activity, Kärcher and Koop used a detailed cloud microphysical model to study the effect of malonic acid on ice nucleation in sulfate particles.111
The experimental data were analyzed by the lambda approach and the water-activity-based approach. λ values for PEG400 and AS droplets are 3.36 and 1.88, respectively. These are consistent with previous studies.59,65,67λ values for PEG400-AS droplets increases from 1.80 for OIR = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 to 2.71 for OIR = 8
8 to 2.71 for OIR = 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The results show that homogeneous and phase-separated droplets with same OIR shared similar lambda values indicating they form ice through the same mechanism. A parameterization of lambda values was provided to predict freezing temperature of aqueous PEG400-AS droplets. Homogeneous ice nucleation rate coefficients were derived from the experimental data and compared to the predicted values from the water-activity-based approach. A new empirical parameterization was developed to estimate the ice nucleation rate coefficients for the PEG400-AS system accounting for changes in aw and temperature. The analysis based on the lambda approach and the water-activity-based approach confirms that there are no significant differences in the freezing process between homogeneously mixed and liquid–liquid phase-separated aqueous PEG400-AS droplets. We suggest further studies on more organic/inorganic mixtures to understand their temperature dependence of aw and impacts of LLPS on phase transitions.
1. The results show that homogeneous and phase-separated droplets with same OIR shared similar lambda values indicating they form ice through the same mechanism. A parameterization of lambda values was provided to predict freezing temperature of aqueous PEG400-AS droplets. Homogeneous ice nucleation rate coefficients were derived from the experimental data and compared to the predicted values from the water-activity-based approach. A new empirical parameterization was developed to estimate the ice nucleation rate coefficients for the PEG400-AS system accounting for changes in aw and temperature. The analysis based on the lambda approach and the water-activity-based approach confirms that there are no significant differences in the freezing process between homogeneously mixed and liquid–liquid phase-separated aqueous PEG400-AS droplets. We suggest further studies on more organic/inorganic mixtures to understand their temperature dependence of aw and impacts of LLPS on phase transitions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
B. W. and Y. Y. acknowledge the support by National Science Foundation of China (grant no. 41775133, 42075076), Fundamental Research Funds for the Central Universities (grant no. 20720160111, 20720190147). We thank Yongxiang Huang and Wanting Cheng for the assistant on operating the high-speed camera. A. Z. acknowledges support by the Natural Sciences and Engineering Research Council of Canada (NSERC; grant no. RGPIN-2021-02688).References
- K. A. Pratt and K. A. Prather, J. Geophys. Res.: Atmos., 2010, 115, D11305 CrossRef.
- J. L. Jimenez, M. R. Canagaratna, N. M. Donahue, A. S. H. Prevot, Q. Zhang, J. H. Kroll, P. F. DeCarlo, J. D. Allan, H. Coe, N. L. Ng, A. C. Aiken, K. S. Docherty, I. M. Ulbrich, A. P. Grieshop, A. L. Robinson, J. Duplissy, J. D. Smith, K. R. Wilson, V. A. Lanz, C. Hueglin, Y. L. Sun, J. Tian, A. Laaksonen, T. Raatikainen, J. Rautiainen, P. Vaattovaara, M. Ehn, M. Kulmala, J. M. Tomlinson, D. R. Collins, M. J. Cubison, E. J. Dunlea, J. A. Huffman, T. B. Onasch, M. R. Alfarra, P. I. Williams, K. Bower, Y. Kondo, J. Schneider, F. Drewnick, S. Borrmann, S. Weimer, K. Demerjian, D. Salcedo, L. Cottrell, R. Griffin, A. Takami, T. Miyoshi, S. Hatakeyama, A. Shimono, J. Y. Sun, Y. M. Zhang, K. Dzepina, J. R. Kimmel, D. Sueper, J. T. Jayne, S. C. Herndon, A. M. Trimborn, L. R. Williams, E. C. Wood, A. M. Middlebrook, C. E. Kolb, U. Baltensperger and D. R. Worsnop, Science, 2009, 326, 1525–1529 CrossRef CAS.
- M. Kanakidou, J. H. Seinfeld, S. N. Pandis, I. Barnes, F. J. Dentener, M. C. Facchini, R. Van Dingenen, B. Ervens, A. Nenes, C. J. Nielsen, E. Swietlicki, J. P. Putaud, Y. Balkanski, S. Fuzzi, J. Horth, G. K. Moortgat, R. Winterhalter, C. E. L. Myhre, K. Tsigaridis, E. Vignati, E. G. Stephanou and J. Wilson, Atmos. Chem. Phys., 2005, 5, 1053–1123 CrossRef CAS.
- S. Decesari, M. C. Facchini, S. Fuzzi and E. Tagliavini, J. Geophys. Res.: Atmos., 2000, 105, 1481–1489 CrossRef CAS.
- S. T. Martin, Chem. Rev., 2001, 221, 3403–3453 Search PubMed.
- C. F. Braban and J. P. D. Abbatt, Atmos. Chem. Phys., 2004, 4, 1451–1459 CrossRef CAS.
- M. T. Parsons, D. A. Knopf and A. K. Bertram, J. Phys. Chem. A, 2004, 108, 11600–11608 CrossRef CAS.
- S. D. Brooks, M. E. Wise, M. Cushing and M. A. Tolbert, Geophys. Res. Lett., 2002, 29, 1917 CrossRef.
- V. Varutbangkul, F. J. Brechtel, R. Bahreini, N. L. Ng, M. D. Keywood, J. H. Kroll, R. C. Flagan, J. H. Seinfeld, A. Lee and A. H. Goldstein, Atmos. Chem. Phys., 2006, 6, 2367–2388 CrossRef CAS.
- C. L. Badger, P. T. Griffiths, I. George, J. P. D. Abbatt and R. A. Cox, J. Phys. Chem. A, 2006, 110, 6986–6994 CrossRef CAS.
- A. Zuend, C. Marcolli, T. Peter and J. H. Seinfeld, Atmos. Chem. Phys., 2010, 10, 7795–7820 CrossRef CAS.
- A. K. Bertram, S. T. Martin, S. J. Hanna, M. L. Smith, A. Bodsworth, Q. Chen, M. Kuwata, A. Liu, Y. You and S. R. Zorn, Atmos. Chem. Phys., 2011, 11, 10995–11006 CrossRef CAS.
- M. A. Freedman, Chem. Soc. Rev., 2017, 46, 7694–7705 RSC.
- F.-M. Wu, X.-W. Wang, B. Jing, Y.-H. Zhang and M.-F. Ge, Atmos. Environ., 2018, 178, 286–292 CrossRef CAS.
- J. P. Patterson, D. B. Collins, J. M. Michaud, J. L. Axson, C. M. Sultana, T. Moser, A. C. Dommer, J. Conner, V. H. Grassian, M. D. Stokes, G. B. Deane, J. E. Evans, M. D. Burkart, K. A. Prather and N. C. Gianneschi, ACS Cent. Sci., 2016, 2, 40–47 CrossRef CAS PubMed.
- C. Pöhlker, K. T. Wiedemann, B. Sinha, M. Shiraiwa, S. S. Gunthe, M. Smith, H. Su, P. Artaxo, Q. Chen, Y. Cheng, W. Elbert, M. K. Gilles, A. L. D. Kilcoyne, R. C. Moffet, M. Weigand, S. T. Martin, U. Pöschl and M. O. Andreae, Science, 2012, 337, 1075–1078 CrossRef.
- Y. You, L. Renbaum-Wolff, M. Carreras-Sospedra, S. J. Hanna, N. Hiranuma, S. Kamal, M. L. Smith, X. Zhang, R. J. Weber, J. E. Shilling, D. Dabdub, S. T. Martin and A. K. Bertram, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 13188–13193 CrossRef CAS.
- W. Li, L. Liu, J. Zhang, L. Xu, Y. Wang, Y. Sun and Z. Shi, Environ. Sci. Technol., 2021, 55, 2234–2242 CrossRef CAS PubMed.
- Y. Huang, F. Mahrt, S. Xu, M. Shiraiwa, A. Zuend and A. K. Bertram, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2102512118 CrossRef CAS.
- M. Song, C. Marcolli, U. K. Krieger, A. Zuend and T. Peter, Atmos. Chem. Phys., 2012, 12, 2691–2712 CrossRef CAS.
- D. J. Stewart, C. Cai, J. Nayler, T. C. Preston, J. P. Reid, U. K. Krieger, C. Marcolli and Y. H. Zhang, J. Phys. Chem. A, 2015, 119, 4177–4190 CrossRef CAS PubMed.
- M. Song, P. Liu, S. T. Martin and A. K. Bertram, Atmos. Chem. Phys., 2017, 17, 11261–11271 CrossRef CAS.
- M. Song, A. M. Maclean, Y. Huang, N. R. Smith, S. L. Blair, J. Laskin, A. Laskin, W.-S. W. DeRieux, Y. Li, M. Shiraiwa, S. A. Nizkorodov and A. K. Bertram, Atmos. Chem. Phys., 2019, 19, 12515–12529 CrossRef CAS.
- Y.-C. Song, A. G. Be, S. T. Martin, F. M. Geiger, A. K. Bertram, R. J. Thomson and M. Song, Atmos. Chem. Phys., 2020, 20, 11263–11273 CrossRef CAS.
- A. Zuend and J. H. Seinfeld, Atmos. Chem. Phys., 2012, 12, 3857–3882 CrossRef CAS.
- A. Zuend and J. H. Seinfeld, Fluid Phase Equilib., 2013, 337, 201–213 CrossRef CAS.
- M. Z. Jacobson, Nature, 2001, 409, 695–697 CrossRef CAS.
- C. B. Robinson, G. P. Schill, K. J. Zarzana and M. A. Tolbert, Environ. Sci. Technol., 2013, 47, 13339–13346 CrossRef CAS.
- S. Brunamonti, U. K. Krieger, C. Marcolli and T. Peter, Geophys. Res. Lett., 2015, 42, 2532–2539 CrossRef CAS.
- J. Ovadnevaite, A. Zuend, A. Laaksonen, K. J. Sanchez, G. Roberts, D. Ceburnis, S. Decesari, M. Rinaldi, N. Hodas, M. C. Facchini, J. H. Seinfeld and C. O'Dowd, Nature, 2017, 546, 637–641 CrossRef CAS PubMed.
- M. B. Altaf, D. D. Dutcher, T. M. Raymond and M. A. Freedman, ACS Earth Space Chem., 2018, 2, 634–639 CrossRef CAS.
- P. Liu, M. Song, T. Zhao, S. S. Gunthe, S. Ham, Y. He, Y. M. Qin, Z. Gong, J. C. Amorim, A. K. Bertram and S. T. Martin, Nat. Commun., 2018, 9, 4076 CrossRef PubMed.
- J. F. Davies, A. Zuend and K. R. Wilson, Atmos. Chem. Phys., 2019, 19, 2933–2946 CAS.
- A. A. Hyman, C. A. Weber and F. Jülicher, Annu. Rev. Cell Dev. Biol., 2014, 30, 39–58 CrossRef CAS.
- I. Massie, C. Selden, H. Hodgson, B. Fuller, S. Gibbons and G. J. Morris, Tissue Eng., Part C, 2014, 20, 693–702 CrossRef CAS.
- K. E. Zachariassen and H. T. Hammel, Nature, 1976, 262, 285–287 CrossRef CAS.
- K. B. Storey and J. M. Storey, Sci. Am., 1990, 263, 92–97 CrossRef CAS PubMed.
- Z. Liu, X. Zheng and J. Wang, J. Am. Chem. Soc., 2022, 144, 5685–5701 CrossRef CAS.
- Y. You, L. Renbaum-Wolff and A. K. Bertram, Atmos. Chem. Phys., 2013, 13, 11723–11734 CrossRef.
- M. Song, C. Marcolli, U. K. Krieger, A. Zuend and T. Peter, Geophys. Res. Lett., 2012, 39, L19801 Search PubMed.
- M. Song, S. Ham, R. J. Andrews, Y. You and A. K. Bertram, Atmos. Chem. Phys., 2018, 18, 12075–12084 CrossRef CAS.
- L. Renbaum-Wolff, M. J. Song, C. Marcolli, Y. Zhang, P. F. F. Liu, J. W. Grayson, F. M. Geiger, S. T. Martin and A. K. Bertram, Atmos. Chem. Phys., 2016, 16, 7969–7979 CrossRef CAS.
- Y. You and A. K. Bertram, Atmos. Chem. Phys., 2015, 15, 1351–1365 CrossRef.
- T. M. Kucinski, J. N. Dawson and M. A. Freedman, J. Phys. Chem. Lett., 2019, 10, 6915–6920 CrossRef CAS PubMed.
- M. A. Freedman, Acc. Chem. Res., 2020, 53, 1102–1110 CrossRef CAS.
- E.-J. E. Ott and M. A. Freedman, J. Phys. Chem. B, 2020, 124, 7518–7523 CrossRef CAS PubMed.
- E.-J. E. Ott and M. A. Freedman, ACS Earth Space Chem., 2021, 5, 2320–2328 CrossRef CAS.
- M. B. Altaf, A. Zuend and M. A. Freedman, Chem. Commun., 2016, 52, 9220–9223 RSC.
- C. L. Heald, H. Coe, J. L. Jimenez, R. J. Weber and E. J. Dunlea, Atmos. Chem. Phys., 2011, 11, 25371–25425 CrossRef.
- M. R. Canagaratna, J. L. Jimenez, J. H. Kroll, Q. Chen, S. H. Kessler, P. Massoli, L. Hildebrandt Ruiz, E. Fortner, L. R. Williams, K. R. Wilson, J. D. Surratt, N. M. Donahue, J. T. Jayne and D. R. Worsnop, Atmos. Chem. Phys., 2015, 15, 253–272 CrossRef.
- E.-J. E. Ott, E. C. Tackman and M. A. Freedman, ACS Earth Space Chem., 2020, 4, 591–601 CrossRef CAS.
- F. Mahrt, Y. Huang, J. Zaks, A. Devi, L. Peng, P. E. Ohno, Y. M. Qin, S. T. Martin, M. Ammann and A. K. Bertram, Environ. Sci. Technol., 2022, 56, 3960–3973 CrossRef PubMed.
- V. G. Ciobanu, C. Marcolli, U. K. Krieger, U. Weers and T. Peter, J. Phys. Chem. A, 2009, 113, 10966–10978 CrossRef CAS PubMed.
- Y. You, M. L. Smith, M. Song, S. T. Martin and A. K. Bertram, Int. Rev. Phys. Chem., 2014, 33, 43–77 Search PubMed.
- R. E. O'Brien, B. Wang, S. T. Kelly, N. Lundt, Y. You, A. K. Bertram, S. R. Leone, A. Laskin and M. K. Gilles, Environ. Sci. Technol., 2015, 49, 4995–5002 CrossRef.
- G. P. Schill and M. A. Tolbert, Atmos. Chem. Phys., 2013, 13, 4681–4695 CrossRef.
- A. P. MacKenzie, Philos. Trans. R. Soc., B, 1977, 278, 167–189 CAS.
- D. H. Rasmussen, J. Cryst. Growth, 1982, 56, 56–66 CrossRef CAS.
- K. Sassen and G. C. Dodd, J. Atmos. Sci., 1988, 45, 1357–1369 CrossRef.
- C. M. Archuleta, P. J. DeMott and S. M. Kreidenweis, Atmos. Chem. Phys., 2005, 5, 2617–2634 CrossRef CAS.
- A. K. Bertram, T. Koop, L. T. Molina and M. J. Molina, J. Phys. Chem. A, 2000, 104, 584–588 CrossRef CAS.
- L. Huang and K. Nishinari, J. Polym. Sci., Part B: Polym. Phys., 2001, 39, 496–506 CrossRef CAS.
- B. Zuberi, A. K. Bertram, C. A. Cassa, L. T. Molina and M. J. Molina, Geophys. Res. Lett., 2002, 29, 449–455 CrossRef.
- B. Zobrist, U. Weers and T. Koop, J. Chem. Phys., 2003, 118, 10254–10261 CrossRef CAS.
- N. Kimizuka, C. Viriyarattanasak and T. Suzuki, Cryobiology, 2008, 56, 80–87 CrossRef CAS PubMed.
- T. Koop, B. P. Luo, A. Tsias and T. Peter, Nature, 2000, 406, 611–614 CrossRef CAS.
- T. Koop and B. Zobrist, Phys. Chem. Chem. Phys., 2009, 11, 10839–10850 RSC.
- D. A. Knopf and Y. J. Rigg, J. Phys. Chem. A, 2011, 115, 762–773 CrossRef CAS.
- D. A. Knopf, P. A. Alpert and B. Wang, ACS Earth Space Chem., 2018, 2, 168–202 CrossRef CAS.
- O. Möhler, S. Benz, H. Saathoff, M. Schnaiter, R. Wagner, J. Schneider, S. Walter, V. Ebert and S. Wagner, Environ. Res. Lett., 2008, 3, 025007 CrossRef.
- A. A. Piedehierro, A. Welti, A. Buchholz, K. Korhonen, I. Pullinen, I. Summanen, A. Virtanen and A. Laaksonen, Atmos. Chem. Phys., 2021, 21, 11069–11078 CrossRef CAS.
- L. A. Ladino, S. Zhou, J. D. Yakobi-Hancock, D. Aljawhary and J. P. D. Abbatt, J. Geophys. Res.: Atmos., 2014, 119, 9041–9051 CrossRef CAS.
- B. Wang, A. T. Lambe, P. Massoli, T. B. Onasch, P. Davidovits, D. R. Worsnop and D. A. Knopf, J. Geophys. Res.: Atmos., 2012, 117, D16209 Search PubMed.
- F. Debeaufort and A. Voilley, Cellulose, 1995, 2, 205–213 CrossRef CAS.
- G. Yang, L. Zhang and H. Feng, J. Membr. Sci., 1999, 161, 31–40 CrossRef CAS.
- V. G. Ciobanu, C. Marcolli, U. K. Krieger, A. Zuend and T. Peter, J. Phys. Chem. A, 2010, 114, 9486–9495 CrossRef CAS PubMed.
- S. B. Ushijima, E. Huynh, R. D. Davis and M. A. Tolbert, J. Phys. Chem. A, 2021, 125, 8668–8679 CrossRef CAS PubMed.
- E. R. Graber and Y. Rudich, Atmos. Chem. Phys., 2006, 6, 729–753 CrossRef CAS.
- M. D. Petters, S. M. Kreidenweis, J. R. Snider, K. A. Köhler, Q. Wang, A. J. Prenni and P. J. Demott, Tellus, Ser. B, 2006, 58, 196–205 CrossRef.
- S. Yang, F. Duan, Y. Ma, H. Li, J. Wang, Z. Du, Y. Xu, T. Zhang, L. Zhu, T. Huang, T. Kimoto, L. Zhang and K. He, Sci. Total Environ., 2020, 746, 141209 CrossRef CAS.
- T. Koop, H. P. Ng, L. T. Molina and M. J. Molina, J. Phys. Chem. A, 1998, 102, 8924–8931 CAS.
- P. A. Alpert, J. Y. Aller and D. A. Knopf, Atmos. Chem. Phys., 2011, 11, 5539–5555 CrossRef CAS.
- P. A. Alpert, J. Y. Aller and D. A. Knopf, Phys. Chem. Chem. Phys., 2011, 13, 19882–19894 RSC.
- D. A. Knopf and M. D. Lopez, Phys. Chem. Chem. Phys., 2009, 11, 8056–8068 RSC.
- D. M. Murphy and T. Koop, Q. J. R. Meteorol. Soc., 2005, 131, 1539–1565 CrossRef.
- D. A. Knopf, T. Koop, B. P. Luo, U. G. Weers and T. Peter, Atmos. Chem. Phys., 2002, 2, 207–214 CrossRef CAS.
- C. Marcolli and U. K. Krieger, J. Phys. Chem. A, 2006, 110, 1881–1893 CrossRef CAS PubMed.
- L. Greenspan, J. Res. Natl. Bur. Stand., 1977, 81A, 81–89 CrossRef.
- M. D. Cohen, R. C. Flagan and J. H. Seinfeld, J. Phys. Chem., 1987, 91, 4583–4590 CrossRef CAS.
- D. J. Cziczo, J. B. Nowak, J. H. Hu and J. P. D. Abbatt, J. Geophys. Res.: Atmos., 1997, 102, 18843–18850 CrossRef CAS.
- A. Bogdan, M. J. Molina, H. Tenhu, E. Bertel, N. Bogdan and T. Loerting, Sci. Rep., 2014, 4, 7414 CrossRef PubMed.
- A. Bogdan and M. J. Molina, J. Phys. Chem. A, 2017, 121, 3109–3116 CrossRef CAS PubMed.
- F. Debeaufort and A. Voilley, J. Agric. Food Chem., 1997, 45, 685–689 CrossRef CAS.
- T. Koop, J. Bookhold, M. Shiraiwa and U. Pöschl, Phys. Chem. Chem. Phys., 2011, 13, 19238–19255 RSC.
- B. Zobrist, C. Marcolli, D. A. Pedernera and T. Koop, Atmos. Chem. Phys., 2008, 8, 5221–5244 CrossRef CAS.
- M. Gemmei-Ide, T. Miyashita, S. Kagaya and H. Kitano, Langmuir, 2015, 31, 10881–10887 CrossRef CAS PubMed.
- J. M. Prausnitz, R. N. Lichtenthaler and E. G. D. Azevedo, Molecular Thermodynamics of Fluid-Phase Equilibria, Prentice Hall, 1999 Search PubMed.
- G. Ganbavale, A. Zuend, C. Marcolli and T. Peter, Atmos. Chem. Phys., 2015, 15, 447–493 CrossRef.
- G. Ganbavale, C. Marcolli, U. K. Krieger, A. Zuend, G. Stratmann and T. Peter, Atmos. Chem. Phys., 2014, 14, 9993–10012 CrossRef.
- E. E. Dormidontova, Macromolecules, 2002, 35, 987–1001 CrossRef CAS.
- J. Zhang, F. Han, X. Wei, L. Shui, H. Gong and P. Zhang, Ind. Eng. Chem. Res., 2010, 49, 2025–2030 CrossRef CAS.
- D. K. Lynch, K. Sassen, A. D. Genio, A. J. Heymsfield, P. Minnis, M. Platt, M. Quante, U. Schumann and H. Sundqvist, Cirrus, Oxford University Press, 2002 Search PubMed.
- P. Demott, Laboratory Studies of Cirrus Cloud Processes, Cirrus, 2002 Search PubMed.
- T. Koop, Zeitschrift für Physikalische Chemie, 2004, 218, 1231–1258 CrossRef CAS.
- P. W. Wilson and A. D. J. Haymet, Phys. Chem. Chem. Phys., 2009, 11, 2679–2682 RSC.
- N. Kimizuka and T. Suzuki, J. Phys. Chem. B, 2007, 111, 2268–2273 CrossRef CAS PubMed.
- T. Koop, B. P. Luo, U. M. Biermann, P. J. Crutzen and T. Peter, J. Phys. Chem. A, 1997, 101, 1117–1133 CrossRef CAS.
- D. A. Knopf, J. Phys. Chem. A, 2006, 110, 5745–5750 CrossRef CAS PubMed.
- B. Zobrist, T. Koop, B. P. Luo, C. Marcolli and T. Peter, J. Phys. Chem. C, 2007, 111, 2149–2155 CrossRef CAS.
- D. M. Lienhard, D. L. Bones, A. Zuend, U. K. Krieger, J. P. Reid and T. Peter, J. Phys. Chem. A, 2012, 116, 9954–9968 CrossRef CAS PubMed.
- B. Kärcher and T. Koop, Atmos. Chem. Phys., 2005, 5, 703–714 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04407b |
| This journal is © the Owner Societies 2023 |


