Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Large 31P-NMR enhancements in liquid state dynamic nuclear polarization through radical/target molecule non-covalent interaction†
Maik
Reinhard
 ab,
Marcel
Levien
ab,
Marcel
Levien
 ab,
Marina
Bennati
ab,
Marina
Bennati
 ab and
Tomas
Orlando
ab and
Tomas
Orlando
 *a
*a
aESR Spectroscopy Group, Max Planck Institute for Multidisciplinary Sciences, Am Faßberg 11, Göttingen, Germany. E-mail: tomas.orlando@mpinat.mpg.de
bDepartment of Chemistry, Georg-August-University, Tammannstraße 4, Göttingen, Germany
First published on 13th December 2022
Abstract
Dynamic nuclear polarization (DNP) is a method to enhance the low sensitivity of nuclear magnetic resonance (NMR) via spin polarization transfer from electron spins to nuclear spins. In the liquid state, this process is mediated by fast modulations of the electron-nuclear hyperfine coupling and its efficiency depends strongly on the applied magnetic field. A peculiar case study is triphenylphosphine (PPh3) dissolved in benzene and doped with BDPA radical because it gives 31P-NMR signal enhancements of two orders of magnitude up to a magnetic field of 14.1 T. Here we show that the large 31P enhancements of BDPA/PPh3 in benzene at 1.2 T (i) decrease when the moieties are dissolved in other organic solvents, (ii) are strongly reduced when using a nitroxide radical, and (iii) vanish with pentavalent 31P triphenylphosphine oxide. Those experimental observations are rationalized with numerical calculations based on density functional theory that show the tendency of BDPA and PPh3 to form a weak complex via non-covalent interaction that leads to large hyperfine couplings to 31P (ΔAiso ≥ 13 MHz). This mechanism is hampered in other investigated systems. The case study of 31P-DNP in PPh3 is an important example that extends the current understanding of DNP in the liquids state: non-covalent interactions between radical and target can be particularly effective to obtain large NMR signal enhancements.
Introduction
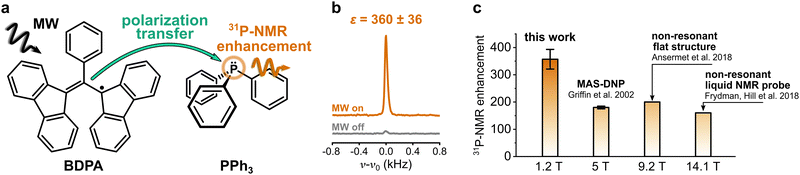
Nuclear magnetic resonance (NMR) spectroscopy is one of the most widely used methods in analytical chemistry. It relies on the detection of small energy splittings associated with the nuclear Zeeman level and therefore suffers from low sensitivity. To overcome this limitation and expand the class of viable NMR experiments, several methods to enhance the NMR signal have been developed. Those are known as hyperpolarization methods, and they usually involve the spin polarization transfer from a highly polarized spin system to the target nuclei.1 Among those methods, dynamic nuclear polarization (DNP) is one of the most versatile. It uses microwave (MW) irradiation to transfer spin polarization from unpaired electron spins, usually located on an organic radical, to the nuclear spins on a target molecule (Fig. 1a).In the liquid state, the polarization transfer is governed by a cross-relaxation process known as Overhauser effect.2–5 The efficiency of this process strongly depends on the choice of the polarizing agent (PA), i.e., the organic radical, and of the target molecule and nucleus, as well as on the applied magnetic field. The case of 1H as target nucleus for DNP is rather unfavorable: 1H-NMR signal enhancements for water at room temperature (<45 °C) are limited to |ε| ≲ 30 for magnetic fields B ≳ 9.4 T.6,7 The reason for this is the dominant dipolar relaxation between the nuclear spin of 1H and the electron spin of the radical, which decays rapidly for increasing magnetic fields.8 On the contrary, 13C-DNP is much more effective because the dipolar relaxation is counterbalanced and overcome by scalar relaxation, a mechanism that originates from the Fermi contact interaction between the radical and the target molecule.913C-NMR signal enhancements in liquids can be up to ε ∼ 1000 at a magnetic field of 3.4 T.10 Furthermore, recent reports showed that it is possible to obtain sizeable enhancements (>10) of 13C-NMR signals in a variety of small molecules at high magnetic field (9.4 T),11 even in water solutions.12 Those findings sparked new interest in the method, and now several groups are committed to tackle the open challenges to make DNP in the liquid state applicable to routine NMR spectroscopy.13–22 Within this context, it is important to design targets and PAs whose properties are specifically tailored to maximize the attainable NMR signal enhancements. To this aim, it is essential to identify the physical mechanisms that make the polarization transfer particularly effective.
DNP studies on target nuclei other than 1H and 13C have been only rarely reported. Here we consider the case of 31P, a target nucleus that is often used in NMR studies of phospholipids (e.g. mixtures, morphology), in metabolomics (e.g. ATP monitoring), and in structural investigations of DNA.23–25 Most studies of 31P-DNP date back to the early 80s, when MW and NMR technology limited the DNP measurements to magnetic fields below 1.2 T.26–30 The reported results show a strong dependence of 31P-DNP on the chemical environment of 31P; specifically, they observed enhancements dominated by scalar relaxation for sterically exposed trivalent phosphorus, while pentavalent phosphorus compounds show dipolar dominated enhancement.30 A unique case is the compound triphenylphosphine (PPh3) (Fig. 1a): when PPh3 is dissolved in benzene and doped with α,γ-Bisdiphenylene-β-phenylallyl radical (BDPA), 31P-NMR signal enhancements of two orders of magnitude are readily reachable, even at larger magnetic fields. 31P-NMR enhancements ε > 150 were reported for PPh3 at B ≈ 5 T,31 and more recently, up to ε ≈ 160 at 14.1 T (Fig. 1c).13,14 Notably, those enhancements show almost no dependence on the external magnetic field.
Here we compare the performance of two polarizing agents, BDPA and the nitroxide radical TEMPONE (TN) for enhancing 31P-NMR signal of PPh3, and of its oxidized counterpart, i.e. triphenylphosphine oxide (TPPO) (Scheme 1). Those systems were also tested in different organic solvents, which have a significant effect on the DNP outcome. DNP measurements performed on a hybrid EPR/NMR setup operating at 1.2 T allowed us to quantify the efficiency of the Overhauser effect and show that 31P-DNP is particularly favourable only for the system BDPA/PPh3 in benzene. With numerical calculations based on density functional theory (DFT), we rationalize this observation showing that BDPA and PPh3 form a weak complex that favors large hyperfine couplings. Our findings corroborate the model that the formation of a complex between radical and target molecule that leads to large hyperfine coupling values is crucial to obtain large NMR signal enhancements on small molecules in the liquid state.
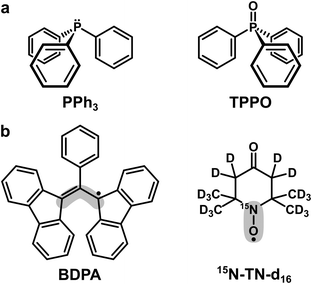 | ||
| Scheme 1 (a) Trivalent (PPh3) and pentavalent (TPPO) phosphorus compounds used as target molecules. (b) Organic radicals used as PAs. The grey areas mark the sites with the largest electron spin density: ∼40% for BDPA and ∼90% for 15N-TN-d16.18 | ||
Experimental methods
Triphenylphosphine (PPh3) and triphenylphosphine oxide (TPPO) were used as target molecules. As polarizing agents we utilized two organic radicals: BDPA (α,γ-Bisdiphenylene-β-phenylallyl, in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex with benzene) and TEMPONE (TN) in its deuterated and 15N-labeled version (15N-TN-d16, 4-Oxo-2,2,6,6-tetramethylpiperidine-d16,1-15N-1-oxyl). Both targets and PAs were purchased from Sigma-Aldrich and used without further purification. Organic solvents chloroform (CHCl3), tetrachloromethane (CCl4), benzene, pyridine and DMSO were purchased from Merck KGaA.
1 complex with benzene) and TEMPONE (TN) in its deuterated and 15N-labeled version (15N-TN-d16, 4-Oxo-2,2,6,6-tetramethylpiperidine-d16,1-15N-1-oxyl). Both targets and PAs were purchased from Sigma-Aldrich and used without further purification. Organic solvents chloroform (CHCl3), tetrachloromethane (CCl4), benzene, pyridine and DMSO were purchased from Merck KGaA.
The concentration of phosphorous compounds in the chosen solvent ranged between 1 M and 4 M. TPPO was soluble in CHCl3, pyridine and DMSO (1 M), while its solubility was too low in the less polar organic solvents benzene and CCl4 and prevented NMR detection at 1.2 T. The radical concentration was ∼8–10 mM and was calibrated for each sample with CW-EPR experiments. All samples were prepared in stocks of 100–550 μL, which were then degassed by freeze–pump–thaw cycles (three to five) to remove dissolved oxygen. The solutions were transferred into a glove box, where 4–4.5 μL were used to fill a quartz tube (1.6 mm outer diameter, Wilmad-LabGlass), which was then sealed with a flame. The sample preparation procedure results in an error in the radical concentration of 10% for tetrachloromethane, benzene, pyridine, and DMSO samples and 15% for chloroform samples, the latter due to a lower boiling point. Radical stability after sealing was monitored with CW-EPR. Radicals were stable in the tested solvents for the whole duration of the DNP, NMR, and EPR measurements (∼12 h).
31P-DNP measurements at 1.2 T were performed on a hybrid EPR/NMR system which combines a Bruker ElexSys E580 EPR spectrometer and a Bruker AVANCE III NMR console. We used a Bruker ER-5106QT/W resonator and a home built copper coil wrapped around the Q-Band quartz tube with 4 to 5 turns for NMR detection.11 With this arrangement, microwave and radio-frequency can be applied simultaneously, allowing for EPR, NMR, and DNP measurements on the same sample. The MW power was adjusted to avoid severe heating during MW irradiation.
Optimized geometries of the radical/target molecule pairs were computed with DFT using Orca 5.0.232 with B3LYP as functional, def2-TZVPP as basis set, and the dispersion correction D3BJ. Several structures (≥12) with different starting orientations of the PA and target molecule were computed for each system; the starting orientations were chosen to take into account different approaches of the two molecules (ESI†). For each optimized geometry, we assessed the non-covalent interactions by calculating the interaction energy Eint, defined as the difference between the electronic energy of the dimer and the electronic energy of the two monomers.33 The values were corrected for the basis set superposition error with the Boys-Bernardi procedure (ESI†).34–37 The calculations were performed in vacuum as well as with the implicit solvation model C-PCM38,39 for benzene and chloroform, using the same starting geometries. We calculated the isotropic hyperfine coupling to 31P using EPR-III basis set40 for H, C, N, and O atoms and IGLO-II41 for P atom.
Results and discussion
31P-NMR signals of PPh3 and TPPO in various solvents were recorded with (DNP) and without MW irradiation (thermal) at a magnetic field of 1.2 T. 31P-NMR signals were integrated to calculate the enhancements ε = IDNP·nthermal/(Ithermal·nDNP), where I is the integral and n is the number of scans. Fig. 2a reports the enhancements of the investigated systems. In PPh3, the highest 31P-NMR signal enhancement, i.e.31Pε = 360 ± 36, has been obtained in benzene and when using BDPA. The radical 15N-TN-d16 is not as efficient, and gives 31P-NMR signal enhancements that are a factor of 5 to 10 smaller, with a maximum of 31Pε = 21 ± 3 for PPh3 in benzene. No 31P-NMR signal enhancements were observed on the TPPO molecule with all utilized solvents and PAs. Earlier reports30 suggest that the large enhancements observed in PPh3 could be due to the lone pair of the trivalent 31P, which tends to coordinate with the unpaired electron of the radical. On the contrary, 31P in TPPO is in the pentavalent configuration, which hampers this mechanism.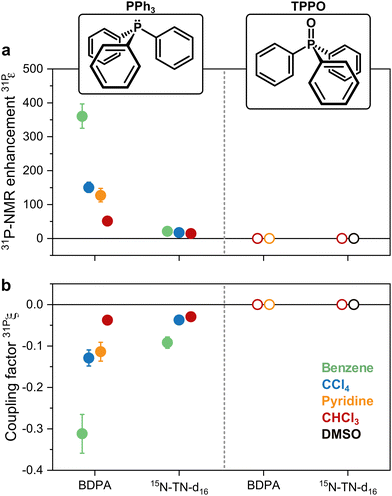 | ||
| Fig. 2 (a) 31P-NMR enhancements recorded at 1.2 T and (b) coupling factors calculated with eqn (1) for both PPh3 and TPPO doped with BPDA and 15N-TN-d16 in different solvents. | ||
The enhancements give only partial insight into the efficiency of 31P-DNP. Indeed, 31Pε is determined by several parameters, as given by the Overhauser equation:2,4
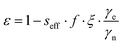 | (1) |
The leakage factor f depends on the nuclear relaxation times of the target nucleus measured with (T1,n) and without radical (T1,dia), and f = 1 − T1,n/T1,dia. f depends ultimately on the concentration of the PA (cPA) and for our samples is f ∼ 0.8 or larger for cPA ∼ 8–10 mM (Table 1). The effective saturation factor seff depends on the type of radical chosen as PA and can vary significantly. The EPR spectrum of BDPA shows a hyperfine structure that arises from the coupling to the protons on the diphenylene and phenyl rings (ESI† Fig. S2). At 34 GHz and cPA ∼ 10 mM the lines are merged into one and the total spectral width is ∼1 mT; this ensures an almost complete saturation of the EPR line when MW irradiation is applied on resonance with the center of the line. On the contrary, the spectrum of 15N-TN-d16 consists of two sharp lines separated by ∼2 mT stemming from the hyperfine coupling with the 15N nucleus. When one of the two lines is irradiated on resonance (as in a DNP experiment), the other line is only partially saturated via a mechanism known as ELDOR effect.44–46 The saturation factors were measured with an ELDOR (electron double resonance) experiment (ESI†) and, under similar experimental conditions, seff is seff > 0.8 for BDPA, while it is limited to seff < 0.35 for 15N-TN-d16 (Table 1). The leakage and the saturation factors together cannot explain the difference in enhancements among the tested systems.
| PA | Solvent | c PA (mM) | c PPh3 (M) | T 1,n (s) | T Buildup (s) | f | s eff | ε | ξ |
|---|---|---|---|---|---|---|---|---|---|
| a For this sample, the MW power was reduced to avoid excessive sample heating. | |||||||||
| BDPA | CHCl3 | 10 | 4 | 1.2 | 1.1 | 0.89 | 0.91 | 51 | −0.038 |
| BDPA | Pyridine | 10 | 2 | 3.7 | 3.8 | 0.83 | 0.82 | 127 | −0.114 |
| BDPA | CCl4 | 10 | 2 | 3.8 | 4.5 | 0.80 | 0.90 | 150 | −0.129 |
| BDPA | Benzene | 10 | 2 | 6.1 | 8.4 | 0.70 | 1.00 | 360 | −0.312 |
| 15N-TN-d16 | CHCl3 | 10 | 4 | 2.3 | 1.3 | 0.79 | 0.34 | 14 | −0.030 |
| 15N-TN-d16 | CCl4 | 10 | 2 | 2.3 | 2.0 | 0.88 | 0.30 | 17 | −0.037 |
| 15N-TN-d16 | Benzene | 8 | 2 | 3.5 | 3.4 | 0.83 | 0.16a | 21 | −0.092 |
With those values of f and seff and eqn (1), one can calculate the coupling factor 31Pξ (Fig. 2b). The quantification of this experimental parameter leads to three important observations: (1) BDPA is a better PA than 15N-TN-d16 for 31P and is characterized by a more efficient polarization transfer, i.e. |31PξBDPA| > |31PξTN|: this is rather surprising because nitroxide radicals are superior PAs both for 1H and 13C DNP;18 (2) no enhancements are observed on 31P-TPPO at 1.2 T and 31Pξ ∼ 0 independently of the solvent; (3) the solvent influences the 31P-DNP performance: in particular, benzene is the best solvent, while CCl4, pyridine, and chloroform follow in this order, for both BDPA and TN.
In the following, we rationalize those observations and investigate the interactions between target molecule and PA that could affect the polarization transfer process. From previous studies5,43 it is known that, when the enhancements are positive (31Pε > 0, and therefore 31Pξ < 0), the scalar (or Fermi contact) interaction between the electron and the nucleus is dominant over the dipolar one. The scalar interaction drives electron-nuclear cross-relaxation through modulation of the isotropic hyperfine coupling (Aiso) between the electron spin of the radical and the nuclear spin of the target. In the case of small molecules interacting with organic radicals in liquids at room temperature, those modulations arise from a collisional process.47 Particularly, one has Aiso ≠ 0 during the collision and Aiso = 0 when the two molecules diffuse apart. The collisional process is described by the following spectral density:47,48a
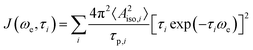 | (2) |
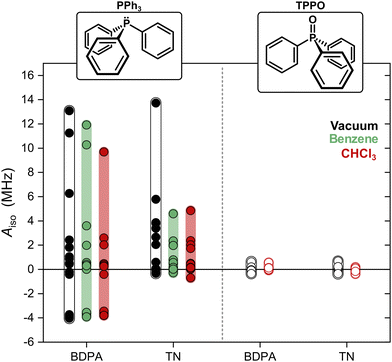
We computed optimized geometries (up to 15 optimized structures for each complex for each solvent) and isotropic hyperfine couplings of the complexes BDPA/PPh3, TN/PPh3, BDPA/TPPO, and TN/TPPO. The results are summarized in Fig. 3, where each point represents Aiso for each optimized structure in vacuum, benzene, and chloroform. When PPh3 interacts with the BDPA radical, Aiso spans the largest range, ΔAiso ∼ 17 MHz, going from negative (Aiso ∼ −4 MHz) to positive (Aiso > 10 MHz) in vacuum. The range is smaller for the system TN/PPh3, ΔAiso ∼ 14 MHz, and it is further reduced to ΔAiso ∼ 5 MHz when the solvent model is used. For TPPO, the hyperfine couplings are more than 10 times smaller and span the range −0.4 MHz < Aiso < 0.7 MHz.
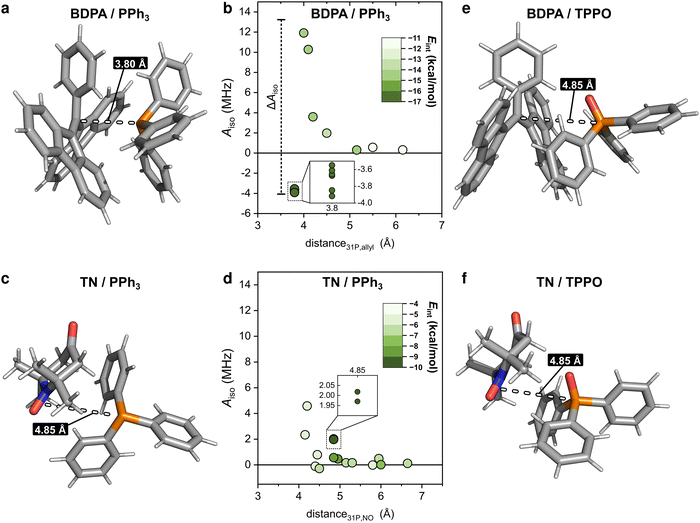
To clarify why the two radicals lead to a different Aiso to the 31P of PPh3, we took a closer look at the calculated geometries. By considering the pairs BDPA/PPh3, one notices that large hyperfine couplings (|Aiso| > 3 MHz) are observed when the lone pair of 31P is pointing directly to the allyl group of BDPA, which carries the majority of the electron spin density (∼40%) (Fig. 4a and Scheme 1).18 This configuration is unusual because the accessibility of the allyl group by small solvent molecule is limited.18 The interaction energy Eint calculated for each BDPA/PPh3 optimized structure show that complexes with short 31P-allyl group distances (d ≤ 4 Å) and large hyperfine couplings (|Aiso| > 3 MHz) are energetically favored over other geometries where 31P is further away from the allyl group (Fig. 4b and Fig. S4, ESI†). The same is found for calculations performed in vacuum, benzene, and chloroform.
We performed a similar analysis for the system TN/PPh3. In terms of distance, 31P cannot get as close to the electron spin density localized on the NO group of TN (d > 4.2 Å in benzene) (Fig. 4c). The interaction energy Eint has a minimum at distances d ∼ 4.85 Å, which corresponds to a hyperfine coupling |Aiso| ∼ 2 MHz (Fig. 4d and Fig. S4, ESI†). Therefore, TN/PPh3 show a non-covalent interaction that is less efficient in terms of hyperfine coupling. Additional calculations of Eint were performed with fixed values for the distance between 31P and the electron spin density (both for BDPA and TN), and confirm the tendency of PPh3 to approach BDPA, and specifically near the allyl group, while this is not the case for the pair TN/PPh3 (Fig. S6a, ESI†). Those results indicate that the large 31P-NMR enhancements observed on PPh3 doped with BDPA are facilitated by a non-covalent interaction that leads to large values of hyperfine coupling Aiso, which in turn renders the scalar relaxation from the collisional process more efficient (eqn (2)).
In regard to TPPO, the absence of enhancements must be a consequence of particularly small hyperfine couplings (Fig. 3). The oxygen atom bound to 31P hampers a close approach between the 31P of TPPO and BDPA (Fig. 4e) and leads to low hyperfine coupling values (|Aiso| < 0.7 MHz). In the case of TN, TPPO reaches a distance 31P-NO group d ≥ 4.2 Å in both vacuum and chloroform, which is similar to the distances obtained for PPh3 (Fig. 4f). Nevertheless, the hyperfine coupling |Aiso| remains below 0.7 MHz. As already observed for 13C-DNP of carbonyl groups,9c,d,10 the oxygen atom might be responsible for withdrawing electron spin density from 31P,49 which results in lower Aiso values thus decreasing the attainable enhancements.
The last remark concerns the role of the solvent. Recent experimental and theoretical studies on DNP mechanisms have been focused on the interaction of only two moieties, i.e the radical and a small molecule that is at the same time the solvent and the target molecule.7,9–11,48 Our experimental data show that a third player, i.e. the solvent, has a considerable effect in 31P-DNP and possibly contributes to the spin polarization transfer. In the context of DNP, the solvent (i) determines the degree of MW absorption, and (ii) when diffusivity increases, dipolar and scalar relaxations increase.50 The diffusion coefficient for benzene at 298 K is D = 2.2 × 105 cm2 s−1,51 while it is lower for CHCl3 (D = 2.14 × 105 cm2 s−1),17 CCl4 (D = 1.4 × 105 cm2 s−1),51 and pyridine (D = 1.54 × 105 cm2 s−1).52 Although a faster collision rate enabled by a larger D might favor 31P-DNP in benzene, the minor differences in D cannot explain the large differences observed in coupling factors. The solvent might affect the kinetics of the interaction between radical and target molecule, either stabilizing a non-covalent interaction or preventing its formation. Despite the presented numerical analysis considers the effect of the solvent through an implicit solvation model, it is not sufficient to gain insight in these mechanisms. To the best of our knowledge, more sophisticated simulations tools based on molecular dynamics and used for other systems48 are not yet available for large radicals like BDPA. Such investigations will be the subject of future works.
Conclusions
We investigated large 31P-NMR enhancements that have been observed from 1.2 T (this study) up to 14.1 T13,14,31 on the system BDPA/PPh3. Our DNP data recorded on a hybrid EPR/NMR instrument operating at 1.2 T show that those enhancements are attenuated when TEMPONE radical is used as a PA, and vanish when triphenylphosphine oxide (TPPO) is the target molecule. The experimental observations were interpreted in the context of the collisional model for scalar relaxation with the support of DFT calculations and show that PPh3 forms a weak complex with the polarizing agent BDPA, which favors large hyperfine couplings. This mechanism is precluded when 31P is in the pentavalent configuration or when a nitroxide is used. This finding provides a novel aspect within the context of DNP in the liquid state and shows how the choice of the optimal PA is strongly dependent on the chemical environment of the target nucleus. We foresee that the design of future PAs for liquid DNP, possibly supported by DFT calculations, will use non-covalent interactions between target molecule and PA as an effective strategy to boost the NMR enhancements.Data availability
Original data associated with Fig. 2 (ELDOR spectra, NMR spectra, NMR relaxation data), and output files of all geometries optimizations shown in Fig. 3 and 4 can be downloaded free of charge from the Göttingen Reseach Online website (DOI: 10.25625/A5WDZW).Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge Dr. Igor Tkac, Dr. Markus Hiller, and Dr. Andreas Meyer for the fruitful discussions. Financial support has been provided by the Max Planck Society, the ERC advanced grant Bio-enMR 101020262, and the Deutsche Forschungsgemeinschaft (DFG) – Project number 455993474. This work used the Scientific Compute Cluster at GWDG, the joint data center of Max Planck Society for the Advancement of Science (MPG) and University of Göttingen.Notes and references
- J. H. Ardenkjaer-Larsen, G. S. Boebinger, A. Comment, S. Duckett, A. S. Edison, F. Engelke, C. Griesinger, R. G. Griffin, C. Hilty, H. Maeda, G. Parigi, T. F. Prisner, E. Ravera, P. J. M. van Bentum, S. Vega, A. Webb, C. Luchinat, H. Schwalbe and L. Frydman, Angew. Chem., 2015, 54, 9162–9185 CrossRef CAS
.
- A. W. Overhauser, Phys. Rev., 1953, 92, 411–415 CrossRef CAS
.
- T. R. Carver and C. P. Slichter, Phys. Rev., 1953, 92, 212–213 CrossRef CAS
.
- I. Solomon, Phys. Rev., 1955, 99, 559–565 CrossRef CAS
.
-
H. H. Hausser and D. Stehlik, Dynamic nuclear polarization in liquids. In J. S. Waugh, ed., Advances in Magnetic Resonance, Academic Press, 1968, vol. 3, 79–139 Search PubMed
.
- C. Griesinger, M. Bennati, H. M. Vieth, C. Luchinat, G. Parigi, P. H. Engelke, S. J. Glaser, V. Denysenkov and T. F. Prisner, Prog. Nucl. Magn. Reson. Spectrosc., 2012, 64, 4–28 CrossRef CAS
.
- V. P. Denysenkov and T. F. Prisner, eMagRes, 2019, 41–54 CAS
.
- M. Bennati, C. Luchinat, G. Parigi and M.-T. Tuerke, Phys. Chem. Chem. Phys., 2010, 12, 5902–5910 RSC
.
-
(a) M. Bennati and T. Orlando, eMagRes, 2019, 8, 11–18 CAS
; (b) M. D. Lingwood and S. Han, J. Magn. Reson., 2009, 201, 137–145 CrossRef CAS
; (c) X. Wang, W. C. Isley, S. Salido, Z. Sun, L. Song, C. J. Cramer and H. Dorn, Chem. Sci., 2015, 6, 6482–6495 RSC
; (d) J. L. Russ, J. Gu, K.-H. Tsai, T. Glass, J. C. Duchamp and H. C. Dorn, J. Am. Chem. Soc., 2007, 129, 7018–7027 CrossRef CAS PubMed
.
- G. Liu, M. Levien, N. Karschin, G. Parigi, C. Luchinat and M. Bennati, Nat. Chem., 2017, 9, 676–680 CrossRef CAS PubMed
.
- T. Orlando, R. Dervisoglu, M. Levien, I. Tkach, T. F. Prisner, L. Andreas, V. Denysenkov and M. Bennati, Angew. Chem., Int. Ed., 2019, 58, 1402–1406 CrossRef CAS
.
- D. Dai, X. Wang, Y. Liu, X. Yang, C. Glaubitz, V. P. Denysenkov, X. He, T. Prisner and J. Mao, Nat. Commun., 2021, 12, 6880 CrossRef CAS PubMed
.
- D. Yoon, A. I. Dimitriadis, M. Soundararajan, C. Caspers, J. Genoud, S. Alberti, E. de Rijk and J.-P. Ansermet, Anal. Chem., 2018, 90, 5620–5626 CrossRef CAS PubMed
.
- T. Dubroca, A. N. Smith, K. J. Pike, S. Froud, R. Wylde, B. Trociewitz, J. McKay, F. Mentink-Vigier, J. van Tol, S. Wi, W. Brey, J. R. Long, L. Frydman and S. Hill, J. Magn. Reson., 2018, 289, 35–44 CrossRef CAS PubMed
.
- T. Dubroca, S. Wi, J. van Tol, L. Frydman and S. Hill, Phys. Chem. Chem. Phys., 2019, 21, 21200–21204 RSC
.
- V. P. Denysenkov, D. Dai and T. F. Prisner, J. Magn. Reson., 2022, 337, 107185 CrossRef CAS
.
- M. Levien, M. Hiller, I. Tkach, M. Bennati and T. Orlando, J. Chem. Phys. Lett., 2020, 11, 1629–1635 CrossRef CAS PubMed
.
- M. Levien, M. Reinhard, M. Hiller, I. Tkach, M. Bennati and T. Orlando, Phys. Chem. Chem. Phys., 2021, 23, 4480–4485 RSC
.
- M. G. Concilio, M. Soundararajan, L. Frydman and I. Kuprov, J. Magn. Reson., 2021, 326, 106940 CrossRef CAS
.
- M. G. Concilio, I. Kuprov and L. Frydman, Phys. Chem. Chem. Phys., 2022, 24, 2118–2125 RSC
.
-
(a) A. A. Kuzhelev, D. Dai, V. P. Denysenkov, I. A. Kirilyuk, E. G. Bagryanskaya and T. F. Prisner, J. Phys. Chem. C, 2021, 125, 25651–25659 CrossRef CAS
; (b) A. A. Kuzhelev, D. Dai, V. P. Denysenkov and T. F. Prisner, J. Am. Chem. Soc., 2022, 144, 1164–1168 CrossRef CAS
.
- T. J. Keller and T. Maly, Magn. Reson., 2021, 2, 117–128 CrossRef CAS
; Y. Rao, A. Venkatesh, P. Moutzouri and L. Emsley, J. Phys. Chem. Lett., 2022, 13, 7749–7755 CrossRef PubMed
.
- J. Schiller, M. Müller, B. Fuchs, K. Arnold and D. Huster, Curr. Anal. Chem., 2007, 3, 283–301 CrossRef CAS
.
- J. Abi-Ghanem, B. Heddi, N. Foloppe and B. Hartmann, Nucleic Acids Res., 2010, 38, 3 CrossRef
.
- F. Bhinderwala, P. Evans, K. Jones, B. R. Laws, T. G. Smith, M. Morton and R. Powers, Anal. Chem., 2020, 92, 9536–9545 CrossRef CAS PubMed
.
- R. A. Dwek and R. E. Richards, Chem. Commun., 1966, 581–582 RSC
.
- P. W. Atkins, R. A. Dwek, J. B. Reid and R. E. Richards, Mol. Phys., 1967, 13, 175–180 CrossRef CAS
.
- J. A. Potenza, P. J. Caplan and E. H. Poindexter, J. Chem. Phys., 1968, 49, 2461 CrossRef CAS
.
- E. H. Poindexter, R. A. Dwek and J. A. Potenza, J. Phys. Chem., 1969, 51, 628 CrossRef CAS
.
- J. A. Potenza, E. H. Poindexter, P. J. Caplan and R. A. Dwek, J. Am. Chem. Soc., 1969, 91(16), 4356–4360 CrossRef CAS
.
- N. M. Loening, M. Rosay, V. Weis and R. G. Griffin, J. Am. Chem. Soc., 2002, 124, 8808–8809 CrossRef CAS
.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS
.
- J. Řezáč and P. Hobza, Chem. Rev., 2016, 116, 5038–5071 CrossRef PubMed
.
- P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2013, 15, 11178 RSC
.
- J. Lapp and S. Scheiner, J. Phys. Chem. A, 2021, 125, 5069–5077 CrossRef CAS PubMed
.
- S. Scheiner and S. Hunter, ChemPhysChem, 2022, 202200011 Search PubMed
.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553 CrossRef CAS
.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105(8), 2999–3094 CrossRef CAS PubMed
.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102(11), 1995–2001 CrossRef CAS
.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(1), 73–78 CAS
.
-
W. Kutzelnigg, U. Fleischer and C. van Wüllen, Shielding Calculations: IGLO Method, in eMagRes, ed. R. K. Harris and R. L. Wasylishen, 2007 Search PubMed
.
- M. Bennati, C. Luchinat, G. Parigi and M. Türke, Phys. Chem. Chem. Phys., 2010, 12, 5902–5910 RSC
.
- E. Ravera, C. Luchinat and G. Parigi, J. Magn. Reson., 2016, 264, 78–87 CrossRef CAS PubMed
.
- J. S. Hyde, J. C. W. Chien and J. H. Freed, J. Chem. Phys., 1968, 48, 4226–4233 CrossRef
.
- M. T. Türke and M. Bennati, Phys. Chem. Chem. Phys., 2011, 13, 3630 RSC
.
- N. Enkin, G. Liu, M. del, C. Gimenez-Lopez, K. Porfyrakis, I. Tkach and M. Bennati, Phys. Chem. Chem. Phys., 2015, 17, 11144–11149 RSC
.
- W. Müller-Warmuth, R. Vilhjalmsson, P. Gerlof, J. Smidt and J. Trommel, Mol. Phys., 1976, 31, 1055–1067 CrossRef
.
-
(a) T. Orlando, I. Kuprov and M. Hiller, J. Magn. Reson. Open, 2022, 10–11, 100040 CrossRef
; (b) S. E. Küçük and D. Sezer, Phys. Chem. Chem. Phys., 2016, 18, 9353–9357 RSC
.
- M. Bennati, eMagRes, 2017, 6, 271–282 CAS
.
- S. G. J. van Meerten, M. C. D. Tayler, A. P. M. Kentgens and P. J. M. van Bentum, J. Magn. Reson., 2016, 267, 30–36 CrossRef CAS PubMed
.
- A. F. Collings and R. Mills, Trans. Faraday Soc., 1970, 66, 2761–2766 RSC
.
- M. Holz, X. Mao, D. Seiferling and A. Sacco, J. Chem. Phys., 1996, 104, 669–679 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04092a |
| This journal is © the Owner Societies 2023 |