Stable antiferromagnetism and semiconducting-to-metal transition in ALaCuOsO6 (A = Ba and Sr): strain modulations†
S.
Nazir
 *a and
Yingchun
Cheng
*a and
Yingchun
Cheng
 b
b
aDepartment of Physics, University of Sargodha, 40100 Sargodha, Pakistan. E-mail: safdar.nazir@uos.edu.pk; Tel: +92-334-9719060
bKey Laboratory of Flexible Electronics and Institute of Advanced Materials, Jiangsu National Synergetic Innovation Center for Advanced Materials, Nanjing Tech University, 30 South Puzhu Road, Nanjing 211816, China
First published on 9th December 2022
Abstract
Double perovskite oxides (DPO) with antiferromagnetic ground state have received much consideration as they exhibit small stray-field and ultra-fast spin dynamics, which is extremely convenient for high-density and high-frequency data storage devices. It is a well-established fact that strain can easily tune the physical properties of the materials; therefore, the electronic and magnetic properties of recently synthesized ordered ALaCuOsO6 (A = Ba and Sr) DPO under biaxial ([110]) strain are investigated using ab initio calculations. Our results revealed that the unstrained systems exhibit semiconducting states having energy band gaps (Eg) of 0.28 and 0.39 eV for A = Ba and Sr, respectively. Along with this, both structures exhibit AFM ground state due to a strong AFM coupling between partially filled high-energy Cu+ e1g↑ and low-energy empty Os+5 t02g↓ orbitals. The calculated partial spin moments of Cu and Os ions are 0.65/0.66 and 1.58/1.60μB in a Ba-/Sr-doped system having electronic configurations of 3d9 (t32g↑t32g↓e2g↑e1g↓) with S = 0.5 and 5d3 (t32g↑) with S = 1.5, respectively. The robustness of AFM spin ordering is affirmed under the strain effects. The most striking feature of the present study is that Ba- and Sr-doped systems demonstrate an electronic transition from semiconductor to metal at critical tensile strains of +4% and +5% along with improved magnetism as well as Néel temperature, respectively. However, the magnetic ground state remains robust against applied strains in both cases. Hence, the present study shows that strain engineering could be a practical tool to modulate the electronic and magnetic properties of DPO to further enhance their technological applications in spintronics.
1 Introduction
Double perovskite oxides (DPO) with the general formula A2BB′O6 based on B = 3d and B′ = 4/5d heavy transition metals often exhibit exotic electronic and magnetic characteristics due to the strong relationship among electronic correlation, spin–orbit coupling (SOC), and crystal field effects.1–6 As an octahedral distortion of the magnetic ions results in an exceptionally prosperous physics. Such as osmium ion having 5d5 electronic configuration has got much attention due to SOC-associated Mott-insulating (MI) antiferromagnetic (AFM) ground states that offer promising applications for high-density storage data devices with high frequency and ultrafast spin motions.7–9 In this respect, ordered DPO has attracted much attention as it is a well-known fact that magnetism in DPO substantially depends on B-site ordering. In most cases, AFM magnetic ordering is dominant due to the magnetic B-site cation, which leads the exchange coupling to the next nearest neighbor (NNN) ions.10–13 On the other hand, in the presence of both magnetic B and B′ cations, the magnetic interactions are governed by the nearest neighbor and NNN coupling, which leads the systems to a ferromagnetic (FM) or ferrimagnetic (FiM) spin state.Previously, it has been affirmed that DPO particularly having Cu+2 d9 and d0 cations at B and B′ sites, respectively, results in interesting low-dimensional magnetism14–16 due to John–Teller distortion. This is associated with elongation and shortening of Cu–O bond lengths along the c-axis and in the ab-plane, respectively. Moreover, it is also found that Cu in the a+2 state contains partially filled eg orbitals, which substantially improves the magnetic anisotropy of the system along the ab-plane. Very recently, Thakur et al.17 synthesised Cu+2 based DPO ALaCuOsO6 (A = Ba and Sr) which shows complete A- and B-site order having a tetragonal structure with space group no. 82 (I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) ). The authors observed that the A = Ba/Sr system displays AFM spin ordering as a magnetic ground state at low Néel temperature (TN) of 25 and 50 K, respectively. Furthermore, both Ba- and Sr-doped systems demonstrate semiconducting (SC) characteristics with an estimated energy band gap (Eg) of 0.26 and 0.34 eV, respectively.
). The authors observed that the A = Ba/Sr system displays AFM spin ordering as a magnetic ground state at low Néel temperature (TN) of 25 and 50 K, respectively. Furthermore, both Ba- and Sr-doped systems demonstrate semiconducting (SC) characteristics with an estimated energy band gap (Eg) of 0.26 and 0.34 eV, respectively.
To further improve the functionalities of DPOs, it is found that the strain strategy is one of the most common techniques. It is experimentally observed that Sr2FeMoO6 films deposited on the SrTiO3 substrate exhibit metallic behavior for thicknesses below 44 nm and become half-metal (HM) above this thickness.18 Similarly, Bark et al.19 found that when a biaxial compressive strain along the [110]-direction is applied on the LaAlO3/SrTiO3 structure, an electronic transition from insulator to metal occurs. In a similar fashion, Sr2CoNbO6 DPO demonstrates an increasing and decreasing trend in the electrical resistivity as well as in Eg values under the influence of tensile and compressive strains, respectively.20 In addition, an induced strain of 0.05% leads the Sr2CrReO6 epitaxial HM film to the SC state with an Eg of 0.21 eV at a very low temperature of 2 K when grown on the SrTiO3 substrate.21 Similar to experimental investigations, Yang et al., all-electron calculations show that application of a feasible strain value to an ordinary band insulator having heavy elements leads the system to a topological insulator.22 Along with this, a FM SC to metal and HM transition is confirmed in La2FeMnO6 for −8% compressive and +1% to +5% tensile strains, respectively.23 Similarly, a FiM SC to HM transition is observed in Lu2NiIrO6 DPO for −8% and −6% biaxial and hydrostatic strains, respectively.24 Equivalently, a FiM to FM magnetic transition occurs in the Sr2CrReO6 motif at +2% biaxial ([110]) and hydrostatic ([111]) strains.25 Very recently, Rubab et al. found an insulator-to-metal transition in a monoclinic LaSr1−xCaxNiReO6 DPO for x = 0.0 and 0.5 at −3% biaxial compressive strain. It is also confirmed that the combined effect of strong correlation and SOC is necessary to get the correct ground states (both electronic and magnetic) of the systems.26
Motivated by the above discussions, we investigate the impact of biaxial ([110]) strain on the electronic and magnetic properties of recently synthesized ALaCuOsO6 (A = Ba and Sr) DPO through density functional theory calculations. Our results indicate that both unstrained systems exhibit AFM SC state, which is in good agreement with the experiment. Interestingly, it is established that Ba- and Sr-doped systems display an electronic transition from SC to metal at a critical tensile strain of +4% and +5%, respectively. The robustness of the magnetic ground state is also affirmed under the strain effects. Furthermore, the computed moments of Cu and Os ions confirmed that they have S = 0.5 and S = 1.5 with electronic configurations of 3d9 (t32g↑t32g↓e2g↑e1g↓) and 5d3 (t32g↑), respectively. Moreover, the structural stability of the unstrained and strained systems is taken into account by computing the enthalpies of formation (ΔHf). Finally, the variation in the TN magnitude is studied as a function of strain.
2 Computational and structural details
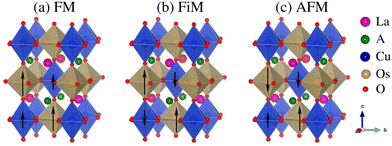
The present calculations were performed using the full-potential linearized augmented plane wave method (FP-LAPW) as implemented in the WIEN2K code.27 The generalized gradient approximation (GGA) is used on the exchange–correlation functional within the Wu-Cohen framework28 along with the inclusion of Hubbard parameter U of 7.5, 4.0, and 2.6 eV on the La 4f, Cu 3d, and Os 5d orbitals,29 respectively. Moreover, SOC effects are also attributed to the scalar relativistic form. A maximum value of lmax = 12 is chosen for the wave function expansion inside the atomic spheres, while the plane-wave cutoff is set to Rmt × Kmax = 7 with Gmax = 24. A 9 × 9 × 6 k-mesh having 84-points within the irreducible wedge of the Brillouin zone is found to be well converged. Along with this, the atomic positions of all doped systems are fully relaxed by minimizing the atomic forces up to 5 mRy au−1. Self-consistency is taken into account for a total charge/energy convergence of less than 10−5 C/10−5 Ry.Pristine ALaCuOsO6 (A = Ba and Sr) DPO crystallizes in a tetragonal cell of space group no. 82 (I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) ).17 The experimentally and theoretically calculated lattice parameters as well as atomic positions of both structures are listed in Table 1, which are a good match. The schematic representation of the ALaCuOsO6 DPO in three different magnetic states such as FM, FiM, and AFM spin ordering is shown in Fig. 1(a)–(c), respectively.
).17 The experimentally and theoretically calculated lattice parameters as well as atomic positions of both structures are listed in Table 1, which are a good match. The schematic representation of the ALaCuOsO6 DPO in three different magnetic states such as FM, FiM, and AFM spin ordering is shown in Fig. 1(a)–(c), respectively.
![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) )
)
| BaLaCuOsO6 (Ba-dop.) | SrLaCuOsO6 (Sr-dop.) | |||
|---|---|---|---|---|
| Exp.17 | Theo. | Exp.17 | Theo. | |
| A | 5.5230 | 5.5209 | 5.4728 | 5.4697 |
| c | 8.3773 | 8.3768 | 8.2905 | 8.2893 |
| A(x, y, z) | (0, 0.5, 0.25) | (0, 0.5, 0.25) | (0, 0.5, 0.25) | (0, 0.5, 0.25) |
| La(x, y, z) | (0, 0.5, 0.75) | (0, 0.5, 0.75) | (0, 0.5, 0.75) | (0, 0.5, 0.75) |
| Cu(x, y, z) | (0, 0, 0) | (0, 0, 0) | (0, 0, 0) | (0, 0, 0) |
| Os(x, y, z) | (0, 0, 0.5) | (0, 0, 0.5) | (0, 0, 0.5) | (0, 0, 0.5) |
| O1(x, y, z) | (0, 0, 0.265) | (0, 0, 0.263) | (0, 0, 0.265) | (0, 0, 0.262) |
| O1(x, y, z) | (0.281, 0.206, 0.029) | (0.276, 0.203, 0.027) | (0.281, 0.206, 0.029) | (0.279, 0.210, 0.028) |
| Cu–O1 | 2.217 | 2.220 | 2.156 | 2.149 |
| Cu–O2 | 1.938 | 1.951 | 1.898 | 1.901 |
| Os–O1 | 1.967 | 1.960 | 1.989 | 1.955 |
| Os–O2 | 2.036 | 1.977 | 2.013 | 1.977 |
| ΔHf | — | −21.6 | — | −20.4 |
3 Results and discussion
3.1 Unstrained systems
First, the structural stability of the systems is estimated by computing the ΔHf of ALaCuOsO6 (A = Ba and Sr) DPO as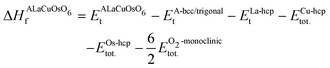 | (1) |
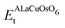 is the ground state total energy (Etot.) of the tetragonal phase of ALaCuOsO6. Similarly, EA-bcc/trigonalt, ELa-hcpt, ECu-hcptot., EOs-hcptot., and
is the ground state total energy (Etot.) of the tetragonal phase of ALaCuOsO6. Similarly, EA-bcc/trigonalt, ELa-hcpt, ECu-hcptot., EOs-hcptot., and  are the ground state Etot. of the fully relaxed crystal structures of Ba/Sr, La, Cu, Os atoms, and oxygen molecule having space group no. 229 (Im
are the ground state Etot. of the fully relaxed crystal structures of Ba/Sr, La, Cu, Os atoms, and oxygen molecule having space group no. 229 (Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m)/166 (R
m)/166 (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), 194 (P63/mmc), 225 (Fm
m), 194 (P63/mmc), 225 (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), 194 (P63/mmc), and 12 (C2/m), respectively. The calculated ΔHf for BaLaCuOsO6 and SrLaCuOsO6 systems are −21.6 and −20.4 eV (see Table 1), respectively. The “−” values of ΔHf support the exothermic reaction and confirm the structural stability of both motifs.
m), 194 (P63/mmc), and 12 (C2/m), respectively. The calculated ΔHf for BaLaCuOsO6 and SrLaCuOsO6 systems are −21.6 and −20.4 eV (see Table 1), respectively. The “−” values of ΔHf support the exothermic reaction and confirm the structural stability of both motifs.
Next, we analyze the magnetic ground state of the ALaCuOsO6 (A = Ba and Sr) DPO by supposing three types of magnetic structures such as FM (↑↑↑↑), FiM (↑↑↓↓), and AFM (↑↓↑↓) as shown in Fig. 1(a)–(c), respectively. Here, it is to be noted that small and large arrowhead lengths represent the Cu and Os spin moment amplitudes, respectively. The magnetic ground state of Ba- and Sr-doped La2CuOsO6 motifs is computed by comparing the Etot. of FM, FiM, and AFM spin ordering as ΔE1/ΔE2 = EAFM − EFM/EAFM − EFiM. The calculated values of ΔE1/ΔE2 are −112/−52 meV and −163/−48 meV for BaLaCuOsO6 and SrLaCuOsO6 motifs, respectively. The “−” sign of ΔE indicates that AFM spin ordering is more energetically stable than FM and FiM ordering in each case, which is in good agreement with the experimental observations.17 This means that a strong AFM coupling is dominant between Cu and Os ions in both in-plane and out-of-plane directions.
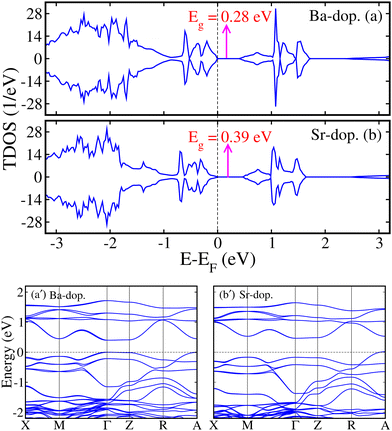
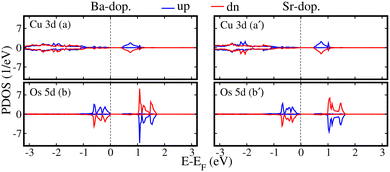
Regarding the electronic properties of unstrained ALaCuOsO6 DPO in a stable AFM spin ordering, we plotted the computed spin-polarized total density of states (TDOS) for Ba- and Sr-doped systems in Fig. 2(a) and (b), respectively. One can see that the spin-majority (N↑) and spin-minority (N↓) channels are degenerate and not crossing the Fermi level (EF) in both systems, which confirms the AFM SC state of Ba- and Sr-doped structures having Eg of 0.28 and 0.39 eV, which are in excellent agreement with the recent experimentally observed values of ∼0.26 and 0.34 eV,17 respectively. For a more deep understanding of the contribution of the electronic states near the Fermi level (EF), we plotted the spin-polarized spin-up (↑-blue color)/spin-down (↓-red color) Cu 3d and Os 5d states in Fig. 3(a, a′) and (b, b′) for ALaCuOsO6 (A = Ba (left column) and Sr (right column)) DPO. From Fig. 3, one can see that N↑ of Cu↑/Os↑ 3d/5d states (see the blue color) is equivalent to that of N↓ (see the red color) in the case of Cu↓/Os↓ 3d/5d states. Similarly, N↓ of Cu↑/Os↑ 3d/5d states (see the blue color) is identical to that of N↑ of Cu↓/Os↓ 3d/5d states (see the red color). This leads the systems into a perfect AFM state. Furthermore, it is found that the conduction band edges are mainly comprised of the Cu 3d states, while Os 5d orbitals are dominant at the valence band edges in both cases (see Fig. 3). In addition, the spin-polarized band structures within the GGA+U+SOC method are also plotted in Fig. 2(a′) and (b′) for further clear insight into the SC states in Ba- and Sr-doped motifs, respectively. Hence, the calculated band structures establish the fact that both systems display a well-defined Eg, which affirms the computed TDOS in Fig. 2.
 | ||
| Fig. 3 GGA+U+SOC calculated spin-polarized partial density of states of (a/a′) Cu 3d↑ (3d↓) and (b/b′) Os 5d↑ (5d↓) in Ba-/Sr-doped La2CuOsO6 double perovskite oxides. | ||
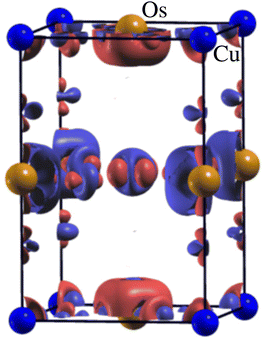
Now, we discuss the magnetism in these structures by analyzing the partial spin magnetic moments (ms) of the magnetic ions. The calculated ms of the Cu1/Cu2 and Os1/Os2 ions are +0.65/−0.65μB and +1.58/−1.58μB in the Ba-doped system, respectively. Similarly, the computed ms of the Cu1/Cu2 and Os1/Os2 ions are +0.66/−0.66μB and +1.60/−1.60μB in the Sr-doped system, respectively. Here, it is worth mentioning that the “−” and “+” signs of ms between Cu1 and Cu2 (Os1 and Os2) ions along with the same magnitudes confirm the AFM ordering between them in both doped systems. Cu and Os ions are in +2 and +5 states having electronic configurations of 3d9 (t32g↑t32g↓ e2g↑ e1g↓) with S = 0.5 and 5d3 (t32g↑t02g↓ e0g↑ e0g↓) with S = 1.5 in these motifs, respectively. Therefore, the only possible exchange coupling between the partially filled eg of Cu+2 and t2g of Os+5 ions via oxygen in ALaCuOsO6 DPO is shown in Fig. 4 as described in ref. 30. On the other hand, the higher energy Os e0g orbitals are empty and do not contribute to this exchange process. Similarly, t02g orbitals of Cu are occupied and also do not take part in interatomic exchange coupling. Hence, the electron hopping only occurs between partially filled high energy Cu e1g↑ and low energy t02g↓ states of Os ions via oxygen 2p2 orbitals as displayed in Fig. 4. Next, we plotted the three-dimensional spin magnetization density iso-surface plot having an iso-value of ±0.06 e Å−3 for the Ba-doped system in Fig. 5 for the direct observation of magnetism. The large densities around Os ions than that of Cu ions affirm that Os is the main contributor to magnetism along with a substantial contribution from Cu ions, which further confirms the calculated ms of these ions. Furthermore, Cu 3d9 is in a +2 state having the electronic configuration of t32g↑t32g↓e2g↑e1g↓; therefore, the eg orbital characteristics are manifested in the isosurfaces of both Cu ions. Similarly, the Os 5d3 ion remains in a +5 state with t32g↑t02g↓e0g↑e0g↓ electronic configuration; thus, only t2g orbital characteristics are evident in the isosurfaces of Os ions. Here, it is also worth noting that Cu1 and Cu2 ions have the same spin-density magnitudes but with different colors (see Fig. 5). This means that Cu spins are anti-aligned with each other, and a similar trend is also established for Os ions. Hence, the spin-magnetization density plot again verifies the AFM spin ordering in the Ba-doped motif as well.
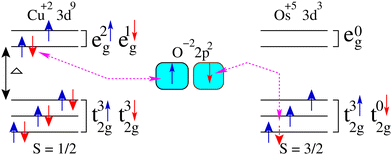 | ||
| Fig. 4 Superexchange mechanism is displayed between Cu 3d and Os 5d orbitals via oxygen 2p state by meditating the feasible Cu+2–O−2–Os+5 (e1g↑-2p2-t02g↓) coupling. | ||
Finally, we determined the TN of the Ba/Sr-doped La2CuOsO6 systems using the classical Heisenberg Hamiltonian:31
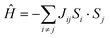 | (2) |
| Etot.(FM) = E0 + (S1(S1 + 1))1/2(S2(S2 + 1)1/2)(2J1 + 4J2) | (3) |
| Etot.(FiM) = E0 + (S1(S1 + 1))1/2(S2(S2 + 1)1/2)(−2J1 + 4J2) | (4) |
| Etot.(AFM) = E0 + (S1(S1 + 1))1/2(S2(S2 + 1)1/2)(−2J1 − 4J2) | (5) |
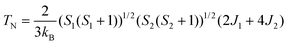 | (6) |
3.2 Strained systems
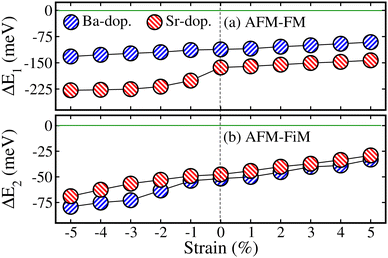
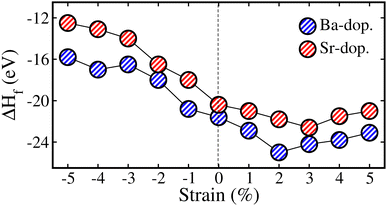
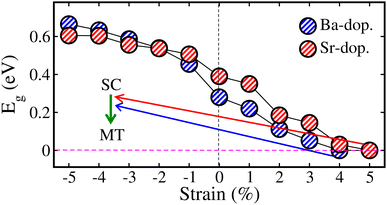
Here, we study the impact of biaxial (i.e., along the [110]-direction) strain on the physical properties of ALaCuOsO6 (A = Ba and Sr) DPO. The strain effects are realized by changing the lattice constants along the ab-plane, where the experimental lattice parameters are taken as a reference point (0% strain). The strain is constrained in the range of −5% to +5% as it is a well-known fact that a small lattice mismatch between the grown material and the substrate sufficiently reduces the possibility of the defect at the contact point.34 The “−” and “+” signs indicate the compressive and tensile strains, respectively. First, to confirm the dynamical stability of the ALaCuOsO6 (A = Ba and Sr) structures under biaxial ([110]) strain, the phonon band dispersion calculations have been performed at two extreme strain values of −5% (compressive) and +5% (tensile) strains. Therefore, the computed phonon band structures along the high symmetry directions in the BaLaCuOsO6 and SrLaCuOsO6 systems for −5%/+5% biaxial ([110]) strain are shown in Fig. S1 of the (ESI†), respectively. One can see that the phonon branches are free from any imaginary frequencies, which affirms the dynamical stability of both structures. Next, we investigate the stability of the magnetic ground state of the ALaCuOsO6 system against strain. To do this, we plotted the ΔE1 = EAFM − EFM and ΔE2 = EAFM − EFiM as a function of biaxial strains for Ba-/Sr-doped La2CuOsO6 structures in Fig. 6(a) and (b), respectively. The negative values of ΔE1 and ΔE2 in both cases affirm that the AFM structures emerge as the lowest energy state against applied strains as predicted in the case of unstrained ones. This confirms the robustness of AFM spin ordering in the Ba-/Sr-doped motif against considerable biaxial compressive and tensile strain. Now, the structural stability of the systems under biaxial strain is studied. Thus, we plotted the calculated values of ΔHf with respect to strain in Fig. 7 for Ba- and Sr-doped structures. Our results clearly established that all the motifs maintained negative values of ΔHf for both doped systems against each strain magnitude, which confirms their structural stability as well. However, systems show less stability when compressive strain is applied from −1% to −5% due to a lower negative amplitude of ΔHf than that of unstrained ones. On the other hand, tensile strained structures displayed more strength as they have higher negative ΔHf values as compared to unstrained motifs (see Fig. 7).Now, we study the strain-induced variations in the electronic properties of ALaCuOsO6 (A = Ba and Sr) DPO. Hence, first, we plotted the calculated Eg as a function of biaxial ([110]) strains ranging from −5% to +5% in the most stable AFM spin ordering of the Ba-/Sr-doped motif in Fig. 8. It is evident that Eg increases linearly for the compressively strained structures in each case. In contrast, the Eg magnitude continuously decreases for tensile strained systems and eventually becomes zero at +4/+5% for the Ba-/Sr-doped motif as displayed in Fig. 8. This means that an electronic transition from SC-to-metallic state occurs (see the arrowheads in Fig. 8) at these critical tensile strains. The increase/decrease in the Eg magnitude as a function of biaxial [110] compressive/tensile strain can be explained by considering the metal–anion bonding interactions using the Jaffe and Zunger ligand-field type model.35,36 From Fig. 3, one can see that the valence band edges mainly come from Os 5d states with a small contribution from Cu 3d states. On the other hand, the conduction band edges are mainly comprised of the Cu 3d states in both systems because they lie at high energy levels as compared to the other cations. Thus, Cu–O/Os–O bond length coupling results in bonding and anti-bonding states in the valence and conduction band edges, respectively, as discussed in ref. 37–39. Usually, it is well established that a strong bond length bonding increases the Eg between the bonding and anti-bonding states. Hence, the Cu–O/Os–O bond lengths become shortened as the compressive strain magnitude increases. This moves the anti-bonding states in the conduction band towards higher energies, which results in the increase in Eg. On the other hand, tensile strain lengthens the Cu–O/Os–O bond lengths, which shifts the anti-bonding states toward lower energies and reduces the Eg. So this is surely the valid reason for the variation of Eg with respect to metal–anion bonding.
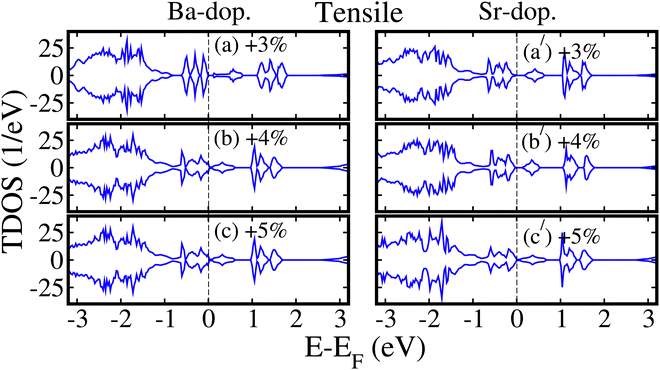
For quantitative analysis, we plotted the GGA+U+SOC calculated spin-polarized TDOS of ALaCuOsO6 (A = Ba and Sr) DPO in their most stable AFM spin ordering as a function of biaxial ([110]) compressive strain ranging from −1% to −5% in Fig. SS of the ESI.† One can see that conduction band edges of TDOS solely shift toward higher energies as the compressive strain increases from −1% to −5% (see Fig. S2(a–e) and 2S(a′–e′) (ESI†) for Ba- (left column) and Sr- (right column) doped motifs, respectively). This means that Eg increases in both cases and confirms the plotted data in Fig. 8. Similarly, the GGA+U+SOC computed spin-polarized TDOS of Ba- and Sr-doped systems in their most stable AFM spin ordering as a function of biaxial ([110]) tensile strains ranging from +3% to +5% is plotted in Fig. 9 (left column) and (right column), respectively. Our results revealed that as the tensile strain increases, the conduction band edges of TDOS substantially move towards lower energies (i.e., towards EF) in both cases. A small Eg exists for + 3% strain in the Ba-doped system as displayed in Fig. 9(a). Surprisingly, the Eg becomes zero at a critical strain of +4% (see Fig. 9(b), left column) in the Ba-doped system and a similar metallic behavior is also observed for +5% tensile strain (see Fig. 9(c)). In the case of the Sr-doped motif, both +3% and +4% tensile strained structures exhibit SC behavior (i.e., a small Eg exists between the conduction and valence band) as shown in Fig. 9(a′) and (b′) in the right column, respectively. Interestingly, an electronic phase transition from SC to metal occurs (i.e., Eg becomes zero) at +5% strain (see Fig. 9(c′), right column).
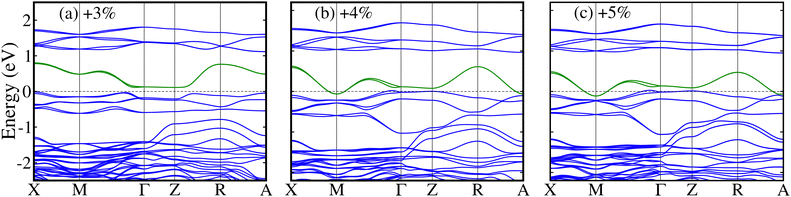
For more clarification of the electronic transitions, we plotted the GGA+U+SOC calculated spin-polarized band structures along with the high symmetry directions of the tetragonal Brillouin zone in Ba-doped La2CuOsO6 DPO for +3%, +4%, and +5% tensile strains in Fig. 10(a)–(c), respectively. It is evident that the system under +3% strain displays a SC behavior because a small Eg lies between the valence and conduction bands (see Fig. 10(a)) and confirms the calculated TDOS in Fig. 9(a). Interestingly, a few bands (green ones) emerge at the EF and Eg becomes zero for a +4% strain as displayed in Fig. 10(b), which further strengthens the calculated TDOS in Fig. 9(b). Moreover, a similar metallic nature is also predicted for the +5% strain-induced band structure (see Fig. 10(c)) as TDOS does in Fig. 9(c). Similarly, the calculated GGA+U+SOC spin-polarized band structures for the Sr-doped system for +3%, +4%, and +5% tensile strains are plotted in Fig. S3(a)–(c) of the ESI,† respectively. A SC nature is visible for +3% (see Fig. S3(a) of the ESI†) and +4% (see Fig. S3(b) of the ESI†) modulated band structures as TDOS does in Fig. 9(a′) and (b′), respectively. Interestingly, a SC-to-metal transition occurs (a few green bands appear at EF in Fig. S3(c) of the ESI†) in the +5% tensile strained band structure for the Sr-doped motif, which endorses the calculated TDOS in Fig. 9(c′).
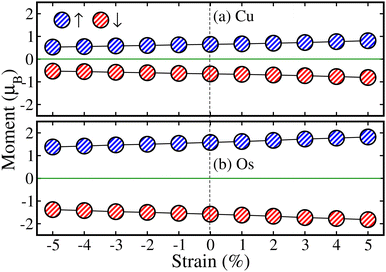
After that, we studied the impact of strain on the system magnetism. To do this, the calculated ms of Cu↑/Cu↓ and Os↑/Os↓ are plotted in Fig. 11(a) and (b) as a function of biaxial strain ranging from −5% to +5% along the [110]-direction in the most stable AFM spin ordering of Ba-doped La2CuOsO6 double perovskite oxide, respectively. One can see that the ms of Cu↑/Cu↓ and Os↑/Os↓ ms slightly decreases from 0.65 to 0.53μB and 1.58 to 1.38μB when the biaxial compressive strain is applied from 0% to −5% (see Fig. 11(a) and (b)), respectively. In contrast, the ms value increases from 0.65 to 0.81μB and 1.58 to 1.82μB when the biaxial tensile strain is applied from 0% to +5%, respectively. Here, it is very important to note that ms of both Cu ions have the same magnitude but are opposite in direction at each strain level, which results in a perfect AFM state. A similar trend of ms is also found versus strain for Os ions. Moreover, comparable variations in ms magnitudes with respect to strain are observed in Cu/Os ions for the Sr-doped system (which are not shown here). The decrease/increase in the ms amplitude due to compressive/tensile strain can be understood by taking the hybridization effects between ions. As the bond length between ions becomes shorter due to compressive strain, strong hybridization occurs among the neighboring ions. This leads to more charge transfer and the local ms value of each ion is decreased. In contrast, as the bond length between ions increases due to tensile strain, the ions are less hybridized. This restricts the charge transfer and results in the increase of ms of each ion.
Finally, we plotted the calculated TN in the ALaCuOsO6 (A = Ba and Sr) structure as a function of the biaxial ([110]) strain in Fig. S4 of the ESI.† One can see that as the magnitude of compressive and tensile strains increases, TN values are also enhanced in both cases (see Fig. S4 of the ESI†). This is due to the fact that the compression and elongation of the lattice constants along the [110]-direction (i.e., along the ab-plane) distorted the polyhedra in the c-out and c-in directions, respectively. Hence, distorted DPOs show higher TN amplitude than that of undistorted ones as discussed in ref. 40–42.
4 Conclusion
In summary, GGA+U+SOC spin-polarized calculations were performed to investigate the electronic and magnetic characteristics of ALaCuOsO6 (A = Ba and Sr) double perovskite oxide under the influence of biaxial ([110]) strain. The negative values of the formation of enthalpy confirm the structural stability of the motifs. Our results revealed that both unstrained systems displayed an antiferromagnetic (AFM) semiconducting state, which is attributed to a strong AFM coupling between partially filled high-energy Cu+2 e1g↑ and low-energy empty Os+5 t02g↓ orbitals. The computed partial spin moments of Cu and Os ions are 0.65/0.66 and 1.58/1.60μB in Ba-/Sr-doped systems having electronic configurations of 3d9 (t32g↑t32g↓e2g↑e1g↓) with S = 0.5 and 5d3 (t32g↑t02g↓e0g↑e0g↓) with S = 1.5, respectively. It is found that AFM spin ordering in both systems is a stable magnetic ground state under the influence of biaxial strain. Strikingly, Ba- and Sr-doped structures demonstrate an electronic transition from semiconductor to metal at a critical tensile strain of +4% and +5% along with improved magnetism as well as Néel temperature, respectively.Author contributions
S. Nazir: calculation, writing-original draft, editing, supervision, and validation. Yingchun Cheng: analysis and review.Conflicts of interest
We have no any conflict of interest.Acknowledgements
The computational work was supported by the University of Sargodha, Sargodha, Pakistan.Notes and references
- W. W. Krempa, G. Chen, B. Y. Kim and L. Balents, Annu. Rev. Condens. Matter Phys., 2014, 5, 57–82 CrossRef.
- Y. Du and X. Wan, Comput. Mater. Sci., 2016, 112, 416–427 CrossRef CAS.
- J. G. Rau, E. K.-H. Lee and H.-Y. Kee, Annu. Rev. Condens. Matter Phys., 2016, 7, 195–221 CrossRef CAS.
- R. Schaffer, E. K.-H. Lee, B.-J. Yang and Y. B. Kim, Rep. Prog. Phys., 2016, 79, 094504 CrossRef.
- C. Martins, M. Aichhorn and S. Biermann, J. Phys.: Condens. Matter, 2016, 29, 263001 CrossRef.
- G. Cao and P. Schlottmann, Rep. Prog. Phys., 2018, 81, 042502 CrossRef.
- T. Jungwirth, X. Marti, P. Wadley and J. Wunderlich, Nat. Nanotechnol., 2016, 11, 231 CrossRef CAS PubMed.
- V. Baltz, A. Manchon, M. Tsoi, T. Moriyama, T. Ono and Y. Tserkovnyak, Rev. Mod. Phys., 2018, 90, 015005 CrossRef CAS.
- H. Bai, X. Zhou, Y. Zhou, X. Chen, Y. You, F. Pan and C. Song, J. Appl. Phys., 2020, 128, 210901 CrossRef CAS.
- A. K. Paul, M. Jansen, B. Yan, C. Felser, M. Reehuis and P. M. Abdala, Inorg. Chem., 2013, 52, 6713–6719 CrossRef CAS.
- A. K. Paul, M. Reehuis, V. Ksenofontov, B. Yan, A. Hoser, D. M. Tobbens, P. M. Abdala, P. Adler, M. Jansen and C. Felser, Phys. Rev. Lett., 2013, 111, 167205 CrossRef.
- R. Morrow, J. R. Soliz, A. J. Hauser, J. C. Gallagher, M. A. Susner, M. D. Sumption, A. A. Aczel, J. Yan, F. Yang and P. M. Woodward, J. Solid State Chem., 2016, 238, 46–52 CrossRef CAS.
- O. N. Meetei, O. Erten, M. Randeria, N. Trivedi and P. Woodward, Phys. Rev. Lett., 2013, 110, 087203 CrossRef.
- D. Iwanaga, Y. Inaguma and M. Itoh, J. Solid State Chem., 1999, 147, 291–295 CrossRef CAS.
- S. Vasala, J. G. Cheng, H. Yamauchi, J. B. Goodenough and M. Karppinen, Chem. Mater., 2012, 24, 2764–2774 CrossRef CAS.
- V. Sami, S. Hassan, M. Elvezio, C. Omar, C. Ting-Shan, C. Jin-Ming, H. Ying-Ya, Y. Hisao and K. Maarit, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 134419 CrossRef.
- G. S. Thakur, H. L. Feng, W. Schnelle, C. Felser and M. Jansen, J. Solid State Chem., 2021, 293, 121784 CrossRef CAS.
- T. Fix, D. Stoeffler, S. Colis, C. Ulhaq, G. Versini, J. P. Vola, F. Huber and A. Dinia, J. Appl. Phys., 2005, 98, 023712 CrossRef.
- C. W. Bark, D. A. Felker, Y. Wang, Y. Zhang, H. W. Jang, C. M. Folkman, J. W. Park, S. H. Baek, H. Zhou, D. D. Fong, X. Q. Pan, E. Y. Tsymbal, M. S. Rzchowski and C. B. Eom, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 4720–4724 CrossRef CAS.
- K. Ajay, S. Rishabh, P. Akhilesh, D. Sandeep, M. Muralidhar, U. Kazuyuki, M. Masahiko and D. D. Rajendra, J. Appl. Phys., 2020, 128, 025303 CrossRef.
- A. J. Hauser, J. R. Soliz, M. Dixit, R. E. A. Williams, M. A. Susner, B. Peters, L. M. Mier, T. L. Gustafson, M. D. Sumption, H. L. Fraser, P. M. Woodward and F. Y. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 161201 CrossRef.
- K. Yang, W. Setyawan, S. Wang, M. B. Nardelli and S. A. Curtarolo, Nat. Mater., 2012, 11, 614 CrossRef CAS.
- Q. Yan, W. Haiping, K. ErJun, L. Jian, L. Ruifeng, L. Yuzhen, T. Weishi, X. Chuanyun and D. Kaiming, J. Appl. Phys., 2013, 114, 063713 CrossRef.
- S. Nazir, Phys. Chem. Chem. Phys., 2020, 22, 17969–17977 RSC.
- Q. U. Ain, S. Naseem and S. Nazir, Sci. Rep., 2020, 10, 13778 CrossRef CAS.
- F. Rubab and S. Nazir, Phys. Chem. Chem. Phys., 2022, 24, 17174–17184 RSC.
- P. Blaha, K. Schwarz, T. Fabien, R. Laskowski, G. K. H. Madsen and L. D. Marks, J. Chem. Phys., 2020, 152, 074101 CrossRef CAS PubMed.
- P. John, B. Kieron and E. Matthias, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef.
- E. C. Calderon, J. J. Plata, C. Toher, C. Oses, O. Levy, M. Fornari, A. Natan, J. M. Mehl, G. Hart, B. M. Nardelli and S. Curtarolo, Comput. Mater. Sci., 2015, 108, 233–238 CrossRef.
- S. Jana, P. Aich, A. P. Kumar, K. O. Forslund, E. Nocerino, V. Pomjakushin, M. Mansson, Y. Sassa, P. Svedlindh, O. Karis, V. Siruguri and S. Ray, Sci. Rep., 2019, 9, 18296 CrossRef PubMed.
- M. Pajda, J. Kudrnovsky, I. Turek, V. Drchal and P. Bruno, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 174402 CrossRef.
- M. D. I. Bhuyan, R. Hossain, F. Ara and M. A. Basith, Phys. Chem. Chem. Phys., 2022, 24, 1569–1579 RSC.
- W. Chen, J. George, G. B. Varley, G. M. Rignanese and G. Hautier, npj Comput. Mater., 2019, 5, 72 CrossRef.
- K. Yang, S. Nazir, M. Behtash and J. Cheng, Sci. Rep., 2016, 6, 34667 CrossRef CAS.
- J. E. Jaffe and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 5176–5179 CrossRef CAS.
- J. E. Jaffe and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 1882–1906 CrossRef CAS.
- K. Yoodee, J. C. Woolley and V. Sa-yakanit, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 5904–5915 CrossRef CAS.
- S.-H. Wei and A. Zunger, Phys. Rev. Lett., 1987, 59, 144–147 CrossRef CAS PubMed.
- P. Sainctavit, J. Petiau, A. M. Flank, J. Ringeissen and S. Lewonczuk, Physica B, 1989, 158, 623–624 CrossRef CAS.
- A. V. Powell, J. G. Gore and P. D. Battle, J. Alloys Compd., 1993, 201, 73–84 CrossRef CAS.
- R. C. Currie, J. F. Vente, E. Frikkee and D. J. W. IJdo, J. Solid State Chem., 1995, 116, 199–204 CrossRef CAS.
- T. Ferreira, G. Morrison, J. Yeon and H.-C. zur Loye, Cryst. Growth Des., 2016, 16, 2795–2803 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04548f |
| This journal is © the Owner Societies 2023 |