Hydrogen evolution reaction of Be_n + H₂O (n = 5–9) based on density functional theory

Abstract

The structural evolution of Be_n clusters with n = 5–9, the adsorption energy created by the Be_n@H₂O (n = 5–9) complex, and the mechanism of the hydrogen evolution reaction of Be_n + H₂O (n = 5–9) were all studied using DFT calculations based on the PBE0-D3/Def2TZVP level. Excluding the Be₇ cluster, the global minimum structures of beryllium clusters with n = 5–9 showed a higher point group pair formation. Be₇ clusters’ high point group symmetry is unstable. Be₉@H₂O released the greatest energy during the complex's creation (−1.45 eV). Exothermic hydrogen evolution occurs in Be_n + H₂O (n = 5–9), and all transition states, intermediate stages, and products have energies lower than the equilibrium constant (EC). More energy is released when an O–H bond in the Be_n@H₂O (n = 5–9) complex is broken, and the energy release results in a change in the cluster structure, which is more pronounced in the Be₇ + H₂O reaction. Interestingly, there are eight transition states in the Be₆ + H₂O hydrogen evolution reaction, with the second O–H bond break requiring more energy than the first. There are only three transition states in the Be₈ + H₂O hydrogen evolution reaction, and the reaction energy is the greatest (−4.13 eV).

---

1. Introduction

Burning fossil fuels produces carbon dioxide emissions, and they are the primary drivers of global warming (coal, oil, and natural gas). Intensification of the greenhouse effect will cause serious consequences to the earth. Carbon dioxide emissions and the search for clean energy to replace fossil fuels have become extremely urgent.¹ One of the most perfect renewable energy sources to replace conventional fossil fuels is hydrogen. Due to its high energy density (i.e., a low heating value of ∼120 MJ kg⁻¹), the combustion product of hydrogen is water, and power plants that can use the existing industrial infrastructure or fossil fuel power generation have attracted unprecedented attention around the world.^2–4 Separate water molecules are dissociated into H⁺ and OH⁻, and then hydrogen is generated,⁵ which requires 286 KJ mol⁻¹ of energy to generate hydrogen from liquid water.⁶

Beryllium metal exhibits many excellent properties, such as low density, high stiffness, and a low coefficient of thermal expansion, leading to alloys of beryllium metal that also have many excellent properties and exhibit unique quantum effects as the size of beryllium metal is reduced to the scale of clusters.^7–11 Special quantum size effects and high specific surface areas have considerable application potential in the realm of catalysis because of the distinct electronic structure of beryllium clusters. The molecular geometry and characteristics of pure beryllium clusters and doped beryllium clusters have drawn a lot of interest because beryllium clusters have a distinctive electronic structure.^12–17 Srinivas et al.¹² investigated the geometric structure and electronic properties of small beryllium clusters in the gradient-corrected density functional theory. The advantage of higher multiplicity was found in the low-energy isomers of larger clusters, and the influence of cluster size on the structure and electronic properties was analyzed. Abyaz et al.^13,14 used the USPEX method combined with density functional theory (DFT) calculations to obtain the global minimum structure of beryllium (Be_n, n = 3–25) clusters. Thermodynamic stability, photoelectric and photocatalytic capabilities, and bonding qualities are taken into account for the most stable clusters. Based on ELF (electronic localization function) analysis, it can be concluded that the Be–Be bond in small clusters is mainly van der Waals type, while the Be–Be bond in large clusters has metal properties. Zhang et al.¹⁵ obtained the global minimum structure of carbon-doped Be_n(n = 1–12) clusters at the B3PW91/6-311+G (d) level and compared it with that of pure beryllium clusters. The results show that the introduction of carbon doping strengthens the intra-cluster interaction of beryllium clusters. In addition, Be₃C and Be₈C clusters have special stability and are considered to be magic clusters in the Be_nC series. Li et al.¹⁶ obtained the lowest energy structure of oxygen-doped Be_n(n = 1–12) clusters at the B3PW91 level based on density functional theory. The energy and electronic properties of phenoxy clusters were systematically studied using the QCISD(T) method and compared with those of pure Be_n+1 clusters. Based on density functional theory, Ge et al.¹⁷ determined the minimum energy structure and electronic properties of MgBe_n (n = 2–12) clusters. It is found that MgBe₃ and MgBe₉ clusters have a higher binding energy and a larger HOMO–LUMO gap, which make them more stable than adjacent clusters. The stability of Be clusters is decreased by Mg doping, according to an analysis of the electrical characteristics of MgBe_n (n = 2–12) clusters.

In addition to investigating the lowest energy structure and electronic properties of beryllium clusters and doped beryllium clusters, the adsorption structure of beryllium clusters and doped beryllium clusters for small molecules and their related properties have been explored.^18–21 Orlando et al.¹⁸ studied the adsorption of hydrogen molecules on (BeO)_n (n = 2–7) clusters based on density functional theory. The effect of hydrogen doping on the beryllium cage structure was studied by Naumkin et al.¹⁹ Javad et al.²⁰ reported the adsorption energy, structure, energy gap (E_g), charge transfer and electronic properties of several adsorption states of carbon monoxide (CO) on primary, cationic Li⁻, Li⁻ and two kinds of Li⁻ coated fullerene beryllium oxides (Be₁₆O₁₆, Li⁺@Be₁₆O₁₆, Li@Be₁₆O₁₆, and 2Li@Be₁₆O₁₆, respectively), and the results have been explained by DFT calculations. As doped, Be atoms effectively improve the NLO reaction, thermodynamics, and hydrogen adsorption properties of Al₁₂N₁₂ nanoclusters, which were found in the study of Mehboob et al.²¹

Recent studies on two-dimensional structures, clusters and visible-light-driven photocatalytic hydrogen evolution reactions are also effective methods for developing hydrogen energy.^22–27 Vos et al.^28,29 reported a high level of single-reference and multi-reference ab initio calculations showing that Be₄ clusters exhibit very efficient Lewis acids when interacting with conventional Lewis bases such as ammonia, water, or hydrogen fluoride. The corresponding acid–base interactions trigger the sequential dissociation of all Lewis bases. Chakraborty et al.³⁰ investigated the possibility of CO oxidation on the Al₁₂Be cluster, dissociation, and addition of CH₃F and C₂H₅F, decomposition of the NAH bond in NH₃, dissociation of NO, and hydrogenation of C₂H₂.

Based on the above research, we studied the interaction between Be_n(n = 5–9) clusters and H₂O, including the lowest energy structure of Be_n(n = 5–9) clusters, the lowest energy structure of H₂O adsorbed by Be_n(n = 5–9) clusters, and the hydrogen evolution reaction (HER) of water molecules on the surface of beryllium clusters.

2. Computational methodology

The structure of many isomers of Be_n(n = 5–9) clusters was optimized, and the stability of the structure was analyzed by frequency analysis. The adsorption process of H₂O is carried out based on the lowest energy structure obtained by the above operation. In the adsorption process, the adsorption sites of H₂O were considered based on the symmetry of the lowest energy structure of the cluster. The structures after water molecule adsorption were optimized and frequency analyzed to determine the low-energy cluster adsorption structure. The HER of water molecules on the surface of beryllium clusters is conducted based on the lowest energy structure obtained after adsorption, which serves as the reactant of HER. The TS approach is used to determine the transition state in the hydrogen evolution reaction, and the intrinsic reaction coordinate (IRC) is used to determine the transition state. Considering the unique electronic structure of beryllium clusters, Perdew, Burke, and Ernzerhof (PBE) proposed in 1996 a pure functional,³¹ and Adamo created a hybrid functional PBE0³² density functional theory for simulation calculations. The PBE0 functional uses 25% exchange and 75% correlation weight. Focus is on the weak interaction between water molecules and beryllium clusters, increasing the functional dispersion correction. To make the calculation structure more accurate, the base sets were selected as def2-TZVP.^33–35 Finally, all the above operations were performed at the PBE0-D3/def2-TZVP level of Gaussian16.³⁶

To determine the mechanism underlying the hydrogen event, we thoroughly investigated the changes in electron distribution of the two interacting systems. For this purpose, we use the interaction region indicator function (IRI)³⁷ in the Multiwfn³⁸ program to provide the information we are looking for. Visualization of the information is completed by the VMD³⁹ and Gnuplot⁴⁰ programs.

During the formation of the Be_n@H₂O (n = 5–9) complex, the adsorption energy is a physical quantity that we are very concerned about. The formula for calculating the adsorption energy is as follows:

E_a = E_Ben@H2O − (E_Ben + E_H2O) (1)

where E_a is the adsorption energy, E_Be is the total energy of the Be_n clusters, E_H2O is the energy of H₂O, and E_Ben@H2O is the total energy of the Be_n cluster after adsorbing water.

The calculation formula for the energy barrier involved in the reaction process is as follows:

E_b = E_TS − E_r (2)

where E_b is the energy barrier, E_TS is the total energy of a transition state (e.g.: TS-A₁-B₁, TS-B₁-C₁…), and E_r represents the reactant's energy in this transition state. The formula for calculating the reverse energy barrier is as follows:

E_rb = E_p − E_TS (3)

where E_rb is the reverse energy barrier and E_TS is the total energy of a transition state (e.g.: TS-A₁-B₁, TS-B₁-C₁…), where E_p represents the energy generated in this transition state. The calculation formula for the reaction energy of Be_n@H₂O (n = 5–9) is as follows:

E_R = E_product − E_reaction (4)

where E_R is the reaction energy, E_product is the energy of the reaction product (e.g.: E₁, I₂, F₃…), and E_p represents the energy of the reactant in this transition state. E_reaction represents the energy of the whole reaction reactant (e.g.: A₁, A₂, A₃…). The formula for calculating the Gibbs free energy is as follows:

G = ε₀ + H_corr − TS_tot (5)

where ε₀ is the total electronic energy, H_corr is the thermal correction to enthalpy, T represents temperature, and S_tot is the entropy.

3. Results and discussion

3.1. Lowest-energy structures of Be_n(n = 5–9) clusters

The low-energy isomers of beryllium clusters (n = 5–9) and their symmetry and lowest frequency are shown in Fig. 1. The most stable structure of beryllium clusters and the magnetism of low-energy isomers were further studied. The spin-polarized DFT calculations show that the stable structures of beryllium clusters with n = 6,7 and n = 8,9 are the quintet ground state and triplet ground state, respectively, except that the clusters with n = 5 are favorable for the singlet ground state. These results are summarized in Fig. 1. As shown in Fig. 1, the Be₅ cluster has D_3h symmetry, and the Be–Be bond lengths are 2.01 Å and 2.06 Å, respectively (for bond length information see Table 1). The Be₆ cluster has O_h symmetry, and the Be–Be bond lengths are 2.91 Å and 2.06 Å, respectively. The Be₅ cluster has a tripartite structure and Be₆ has a diamond structure, which is consistent with the calculation results of Abyaz et al¹³ and Sulka et al.⁴¹ Our calculation results show that Be₇ has a pentagonal bipyramid shape with low symmetry, where the Be–Be bond lengths are 2.01 Å to 2.09 Å. It is worth noting that the highest symmetry of the pentagonal bipyramid structure of the Be₇ cluster should be D_5h, but our calculation results show that the symmetry of D_5h is unstable, which is consistent with the results of Abyaz et al¹³ and Srinivas et al.¹² According to our prediction, Be₈ has D_2d symmetry, and lateral bond lengths in the range of 1.89 Å to 2.72 Å. Be₉ is a tricapped trigonal prism with D_3h symmetry, in which the average Be–Be bond length in the trigonal prisms is about 2.15 Å.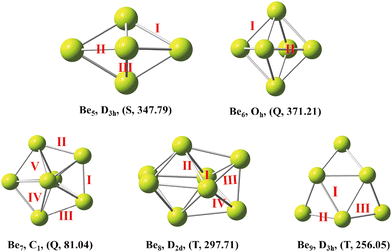

Fig. 1 The lowest-energy structures of Be_n(n = 5–9) clusters with exact symmetries, states (S = singlet, T = triplet and Q = quartet) and minimum vibrational frequency (cm⁻¹) in parentheses.

Table 1 The bond length (Å) of the most stable beryllium cluster. The structural performance was calculated using the PBE0-D3 method (see Fig. 1 for different bonds)

Cluster size n	I	II	III	IV	V
5	2.01	2.06
6	2.91	2.06
7	2.05	2.03	2.02	2.01	2.09
8	2.72	2.18	2.05	1.98
9	2.22	2.15	2.07

---

3.2. Be_n@H₂O (n = 5–9) complexes

The Be_n@H₂O (n = 5–9) complex structures formed by beryllium clusters and water molecules are shown in Fig. 2. On the one hand, the adsorption sites of water molecules, the spin multiplicity of the complex and the electron transfer between beryllium clusters and water molecules are discussed using NBO analysis (see Fig. 3 for specific information). Furthermore, the adsorption energy of the adsorption process is also sorted out (see Table 2 for specific information).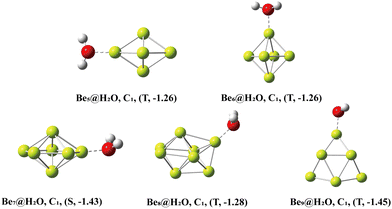

Fig. 2 The lowest-energy structures of Be_n@H2O (n = 5–9) clusters with exact symmetries, states (S = singlet, T = triplet and Q = quartet) and adsorption energy (eV) in parentheses.

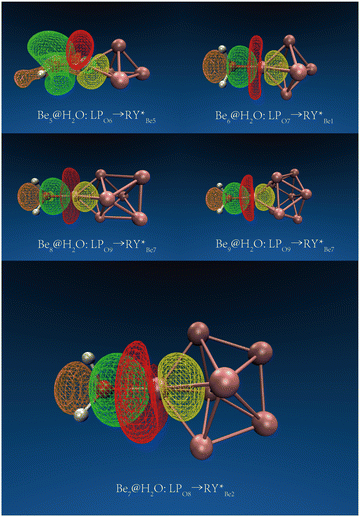Fig. 3 The main NBO donor–acceptor overlaps between H₂O and Be_n (n = 5–9). The orbit and direction of electron transfer.

Table 2 Adsorption and reaction energy of Be_n (n = 5–9) and H₂O molecule reactions

Cluster size n	5	6	7	8	9
Adsorption Energy (eV)	−1.26	−1.26	−1.43	−1.28	−1.45
Reaction Energy (eV)	−2.82	−2.86	−3.55	−4.13	−3.17

---

In NBO analysis, it was found that electron transfer occurred between two different OH bonds and an O atom to the clusters. The electron transfer between the O atom and Be atom at the adsorption site accounts for the main part of the electron transfer between water molecules and beryllium clusters. The second-order stabilization energy (E(2)) was positively correlated with the adsorption energy in the adsorption process.⁴² The adsorption energies of Be₅@H₂O and Be₆@H₂O complexes are about −1.26 eV. In NBO analysis, the E(2)s of Be₅@H₂O and Be₆@H₂O complexes are 2.00 kcal mol⁻¹ and 3.33 kcal mol⁻¹, respectively. The adsorption energies of Be₇@H₂O and Be₉@H₂O complexes are about −1.44 ev, and the E(2)s in the NBO analysis are 4.34 kcal mol⁻¹ and 3.99 kcal mol⁻¹, respectively. In NBO analysis, Be₈@H₂O has adsorption energy (−1.43 eV) and E(2) (3.84 kcal mol⁻¹). Our calculation results are consistent with the rule that the second-order stabilization energy and adsorption energy are positively correlated.

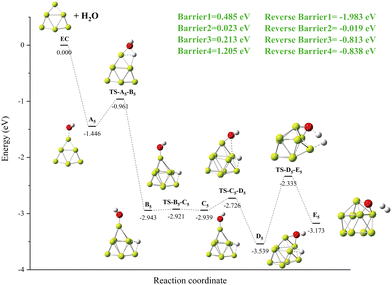
3.3. The reaction path between Be_n (n = 5–9) and H₂O molecule

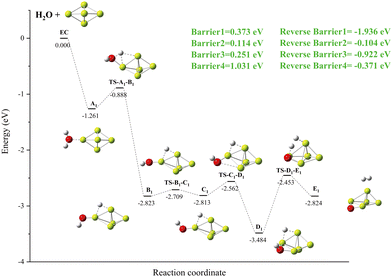
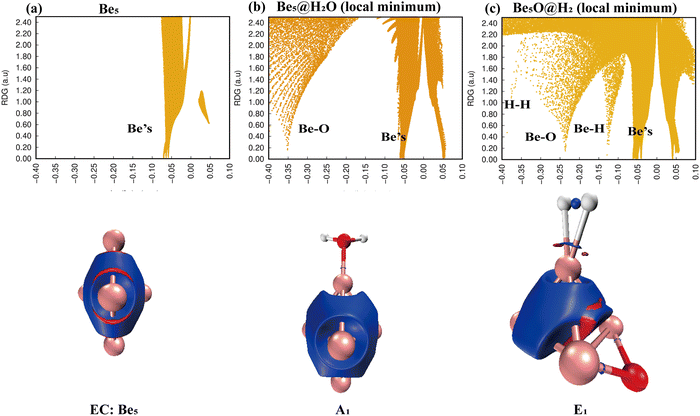
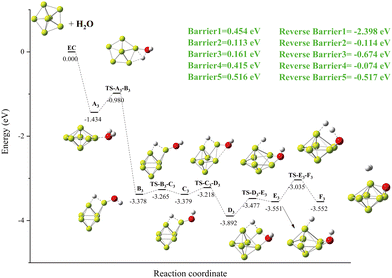
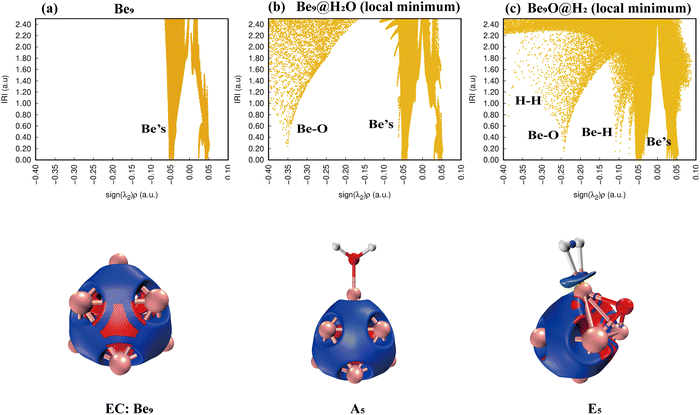
We concentrate on the modifications of chemical bonds in Be_n@H₂O (n = 5–9) complexes, the cleavage of OH bonds, the production of hydrogen molecules, the energy barriers in the dissociation process, and the reaction energy (see Table 2 for specific information) when predicting the reaction channels of Be_n (n = 5–9) clusters and H₂O molecules.

3.3.1. Reaction: Be₅ + H₂O. A new local minimum value A₂ with a Be–H–Be three-center bond results when an O–H bond breaks within the local minimum value of A₁. In this case, the H atom bridged between the two Be atoms of the Be₅ group (as shown in Fig. 4). The important finding is that, as we have just mentioned, the energy of the transition state (TS-A₁-B₁) and the new local minimum (B₁) related to this process are lower than those of the import channel EC. The OH group rotates 180° on the Be–O bond to obtain the local minimum C₁. A global minimum D₁ is produced when the OH group is deflected and drawn to another Be atom as a result of the H–O bond's spin. At D₁, the H–O bond breaks, drawing two hydrogen atoms to the surface of Be₅, where they combine to form hydrogen molecules.

Fig. 4 The energy diagram and the structures of the reactant A₁, intermediate states B₁, C₁, and D₁, and transition states TS-A₁-B₁, TS-B₁-C₁, TS-C₁-D₁, and TS-D₁-E₁, and product B₁, involved in the Be₅ + H₂O reaction. The energies are calculated at the PBE0-D3/Def2TZVP level.

Simply looking at the results shown in Fig. 5, we can clearly see that the electronic density of H₂O has undergone profound changes, because its initial geometric structure with two O–H bonds has been completely destroyed, and eventually formed a stable Be–O–Be three-center bond and H–H bond. The IRI 3D plot in Fig. 5(a) shows that the Be₅ double triangular pyramid cluster exhibits a structure, and five Be atoms share valence electron pairs, forming a typical metal bonding arrangement.

Fig. 5 Bonding characteristics of Be₅, the Be₅@H₂O complex and product Be₅O@H₂. The first line contains IRI 2D plots. The second line shows IRI 3D plots. In the IRI 3D plots, the blue color of the isosurface represents the chemical bond action, and the bright red color represents the strong steric hindrance here.

The symmetry of distribution is also reflected in the single spike in the corresponding IRI 2D plot. The IRI 3D plot around the Be₅ group is not significantly disturbed by the attachment of H₂O (Fig. 5(b)). This is well reflected in the IRI 2D plot. Two spikes have been clearly observed, one corresponding to the new Be–O bond and the other to the Be–Be interaction. The IRI 2D plot (Fig. 5(c)) clearly shows that the single spike observed by the Be₅ cluster (Fig. 5(a)) has now been split into several spikes: one Be–Be, two Be–H and Be–O spikes, and one H–H spike. It is very important that the intensity of these new Be–H, Be–O, and H–H spikes is much higher than that of the corresponding Be–Be bonds, indicating that the driving force for the systematic and total dissociation of the initial O–H bond of H₂O comes from the special intensity of the newly formed Be–O and Be–H bonds relative to the initial Be–Be bonds.

3.3.2. Reaction: Be₆ + H₂O. Details of the Be₆ + H₂O reaction channel are shown in Fig. 6. O–H bond breaking in A₂ also creates a new local minimum (B₂) with a tricentric bond. Due to the movement of the H atom on the surface of the Be₆ cluster and the rotation of OH groups, the geometric shape of the Be₆ cluster is changed, and the local minimum E₂ with a stable Be–O–Be three-center bond is formed. This process (B₂ to E₂) undergoes three transition states (TS-B₂-C₂, TS-C₂-D₂, TS-D₂-E₂) with lower energy barriers. The second O–H bond breaks, forming a global minimum F₂. In the global minimum F₂ to product I₂ process, after three transition states (TS-F₂-G₂, TS-G₂-H₂, TS-H₂-I₂), the geometric structure of the Be₆ cluster changes from biquarangular pyramid to pentagonal pyramid due to the formation of a hydrogen molecule by hydrogen atoms.

Fig. 6 The energy diagram and the structures of the reactant A₂, intermediate states B₂, C₂, D₂, E₂, F₂, G₂, and H₂, transition states TS-A₂-B₂, TS-B₂-C₂, TS-C₂-D₂, TS-D₂-E₂, TS-E₂-F₂, TS-F₂-G₂, TS-G₂-H₂, and TS-H₂-I₂, and product I₂, involved in the Be₆ + H₂O reaction. The energies are calculated at the PBE0-D3/Def2TZVP level.

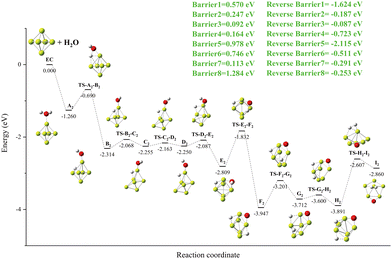
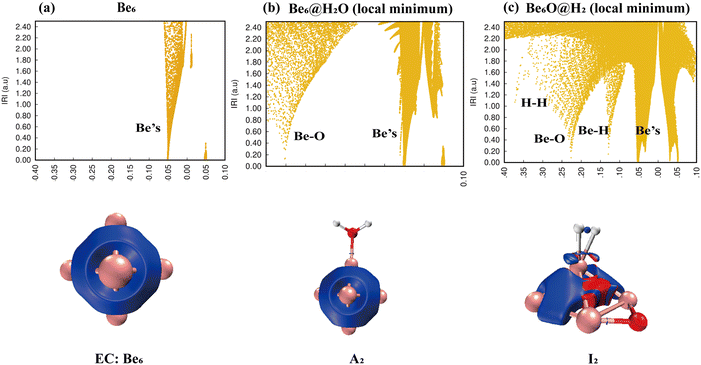
IRI analysis of the Be₆ + H₂O reaction is shown in Fig. 7. The electronic density of H₂O also changed dramatically on the surface of the Be₆ cluster. The cleavage of O–H bonds resulted in the formation of a stable Be–O–Be three-center bond and H–H bond. The IRI 3D plot in Fig. 7(a) shows that the Be₆ cluster presents a biquadrangular pyramid structure and forms a typical metal bond. It can be clearly seen in the IRI 3D plot (see Fig. 7(b)) that H₂O attached to the Be₆ cluster has little interference with the surroundings. This shows two spikes (Be–O, Be) in the IRI 2D plot.

Fig. 7 Bonding characteristics of Be₆, the Be₆@H₂O complex and product Be₆O@H₂. The first line contains IRI 2D plots. The second line shows IRI 3D plots. In the IRI 3D plots, the blue color of the isosurface represents the chemical bond action, and the bright red color represents the strong steric hindrance here.

The dissociation of H₂O on the surface of the Be₆ cluster leads to changes in the structure of the Be₆ cluster. This is evident in the IRI analysis. The single spike of Be splits into almost double spikes in the IRI 2D plot (Fig. 7(c)), and the geometry changes caused by the dissociation of H₂O can be clearly seen in the IRI 3D plot.

3.3.3. Reaction: Be₇ + H₂O. Details of the reaction mechanism of Be₇ + H₂O are shown in Fig. 8. In this reaction, there are five transition states, and there is no high energy barrier. The local minimum B₂ is created though an O–H bond in the local minimum A₃ breaks, which releases energy of around 2.398 eV (Fig. 8, Reverse Barrier 1). The reason for the change in the structure of B₃ may be the release of energy. In the process of B₃ to D₃, the OH group moves to form a relatively stable Be–O–Be three-center bond, and D₃ is the global minimum. In the process of D₃ to F₃, the second O–H bond was broken, and the hydrogen molecule was formed on the surface of the cluster. It is worth noting that the structure of the Be₇ cluster was restored to the pentagonal bipyramid structure, and O atom and one surface of the cluster formed a stable tetrahedral structure (F₃).

Fig. 8 The energy diagram and the structures of the reactant A₃, intermediate states B₃, C₃, D₃, E₃, and F₃, and transition states TS-A₃-B₃, TS-B₃-C₃, TS-C₃-D₃, TS-D₃-E₃, TS-E₃-F₃, and product F₃, involved in the Be₇ + H₂O reaction. The energies are calculated at the PBE0-D3/Def2TZVP level.

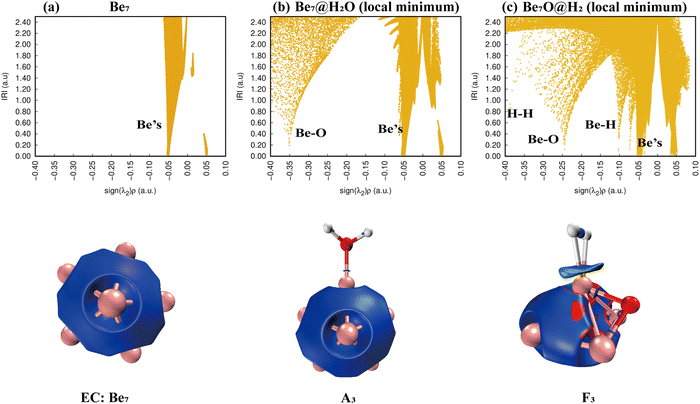
According to Fig. 9(a), only Be–Be bonds exist. Fig. 9(b) shows that the adsorption of a water molecule has little effect on the overall disturbance of Be₇ clusters. Fig. 9(c) shows that H–H bonds appear in the IRI plots of product F₃, whereas Be–H has two peaks, and the IRI 3D plot shows that the interaction between hydrogen molecules and the Be₇O cluster is weaker than chemical bonds. This shows that F₃ is easier to dehydrogenate than E₁ and I₂.

Fig. 9 Bonding characteristics of Be₇, the Be₇@H₂O complex and product Be₇O@H₂. The first line contains IRI 2D plots. The second line shows IRI 3D plots. In the IRI 3D plots, the blue color of the isosurface represents the chemical bond action, and the bright red color represents the strong steric hindrance here. Patina green indicates weaker chemical bonds.

3.3.4. Reaction: Be₈ + H₂O. The reaction mechanism of Be₈ + H₂O is shown in Fig. 10. Breaking of the O–H bond in A₄ releases an energy of −2.557 eV (Fig. 10, Reverse Barriers1) and forms a local minimum B₄ with the Be–H–Be triple center bond. The deflection of the remaining OH groups also forms the global minimum C₄ with the Be–O–Be triple center bond. The cleavage of the second O–H bond forms hydrogen molecules and the product D₄ at the same energy level as the C₄ structure. The energy barrier for the cleavage of O–H is the highest at 1.340 eV in the Be₈ + H₂O reaction (Fig. 10, Barrier3).

Fig. 10 The energy diagram and the structures of the reactant A₄, intermediate states B₄, C₄, and transition states TS-A₄-B₄, TS-B₄-C₄, TS-C₄-D₄, and product D₄, involved in the Be₈ + H₂O reaction. The energies are calculated at the PBE0-D3/Def2TZVP level.

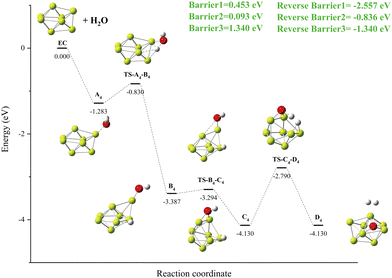
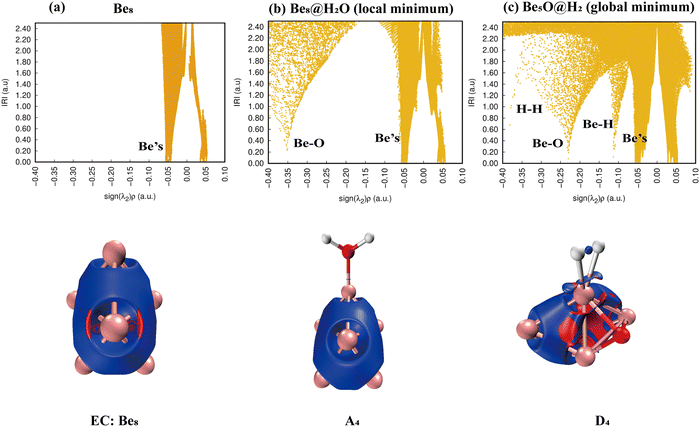
As shown in Fig. 11, the IRI 2D plot shows that Be₈ has a continuous peak belonging to the Be bond (Fig. 11(a)), and Be₈@H₂O has one more spike belonging to the Be–O bond (Fig. 11(b)). There are several obvious spikes for the product D₄ (Be₈O@H₂O), belonging to Be, Be–H, Be–O, and H–H, respectively, and the specific situation is shown in the IRI 3D plot (Fig. 11(c)). It is worth noting that the chemical bonding of the Be–H bond should be of a strong type, and the desorption of hydrogen molecules should be relatively difficult.

Fig. 11 Bonding characteristics of Be₈, the Be₈@H₂O complex and product Be₈O@H₂. The first line contains IRI 2D plots. The second line shows IRI 3D plots. In the IRI 3D plots, the blue color of the isosurface represents the chemical bond action, and the bright red color represents the strong steric hindrance here.

3.3.5. Reaction: Be₉ + H₂O. The specific details of the Be₉ + H₂O reaction mechanism are shown in Fig. 12. A local minimum B₅ is produced with one O–H bond in A₅ breaks, releasing −1.983 eV energy (Fig. 12 Reverse Barrier1). The process from B₅ to D₅ undergoes deflection of the OH group, forming the global minima D₅ structure of the Be–O–Be triple center bond. The second O–H bond is broken, and hydrogen molecules are formed on the surface of the cluster to give the product E₅. It is worth noting that the energy barrier of 1.205 eV to be overcome for the breaking of the second O–H bond is higher than that of the first O–H bond at 0.485 eV.

Fig. 12 The energy diagram and the structures of the reactant A₅, intermediate states B₅, C₅, and D₅, and transition states TS-A₅-B₅, TS-B₅-C₅, TS-C₅-D₅, and TS-D₅-E₅, and product E₅, involved in the Be₈ + H₂O reaction. The energies are calculated at the PBE0-D3/Def2TZVP level.

A strong steric hindrance effect appears in the center of the Be₉ cluster, as shown in Fig. 13(a). When an H₂O molecule is adsorbed on the Be₉ cluster, the steric hindrance effect in the face center disappears (Fig. 13(b)). The IRI 2D plot in Fig. 13(c) shows that there are multiple peaks, including Bes bonds, Be–O bonds, H–H bonds, and Be–H bonds. Notable among them is the Be–H bond, which has three peaks in the IRI 2D plot and a bronze isosurface in the IRI 3D plot, indicating that the interaction is weaker than the chemical bond.

Fig. 13 Bonding characteristics of Be₉, the Be₉@H₂O complex and product Be₉O@H₂. The first line contains IRI 2D plots. The second line shows IRI 3D plots. In the IRI 3D plots, the blue color of the isosurface represents the chemical bond action, and the bright red color represents the strong steric hindrance here. Patina green indicates weaker chemical bonds.

3.3.6. Gibbs free energy. We provide the Gibbs free energy of the reaction process so that it is feasible to directly compare with potential experiments. The specific outcomes are displayed in Table 3. The results show that the Gibbs free energy of reactants, transition states, intermediate states, and products in the Be_n + H₂O (n = 5–9) reaction are consistent with the changing trend of electron energy (energy above).

Table 3 Gibbs free energy of hydrogen evolution reaction of beryllium clusters (temperature 298.150 K, pressure 1.00000 Atm, n = 1–5, and the unit is electron volt)

Path	Be5	Be6	Be7	Be8	Be9
EC	0.000	0.000	0.000	0.000	0.000
An	−0.868	−0.877	−0.747	−0.825	−1.048
TS-An-Bn	−0.637	−0.433	−0.400	−0.497	−0.667
Bn	−2.549	−2.080	−2.735	−3.065	−2.649
TS-Bn-Cn	−2.482	−1.828	−2.655	−2.908	−2.621
Cn	−2.540	−2.000	−2.738	−3.701	−2.648
TS-Cn-Dn	−2.235	−1.937	−2.547	−2.487	−2.370
Dn	−3.083	−1.997	−3.182	−3.200	−3.123
TS-Dn-En	−2.191	−1.794	−2.829		−2.053
En	−2.605	−2.462	−2.914		−2.845
TS-En-Fn		−1.641	−2.439
Fn		−3.713	−2.970
TS-Fn-Gn		−2.993
Gn		−3.463
TS-Gn-Hn		−3.355
Hn		−3.642
TS-Hn-In		−2.502
In		−2.643

---

4. Conclusions

To investigate the structural evolution of Be_n clusters with n = 5–9, the adsorption energy produced by the complex generated by Be_n@H₂O (n = 5–9), and the mechanism of the hydrogen evolution process of Be_n + H₂O (n = 5–9), DFT calculations were conducted based on the PBE0-D3/Def2TZVP level. Our calculation results show that Be₅ and Be₉ clusters have D_3h point group symmetry, the Be₆ cluster has O_h point group symmetry, the Be₈ cluster has D_2d point group symmetry, and the Be₇ cluster has low C₁ point group symmetry. During the formation of the Be_n@H₂O (n = 5–9) complex, the formation and adsorption energies of Be₅@H₂O and Be₆@H₂O were −1.26 eV, −1.28 eV, −1.43 eV and −1.45 eV, respectively. The adsorption reaction between Be clusters and water molecules are a barrierless reaction, which indicates that water molecules are more easily adsorbed on the surface of Be clusters, and the adsorption energy is larger, which can also reflect that the adsorption structure is more stable.

The hydrogen evolution reaction in Be_n + H₂O (n = 5–9) is an exothermic reaction, and the energy of all transition states, intermediate states, and products is below EC.

When an O–H bond in the Be_n@H₂O (n = 5–9) complex is broken, more energy is released, and the release of energy brings about a change in the cluster structure, which is more obvious in the Be₇ + H₂O reaction. When the second O–H bond breaks, a high energy barrier needs to be overcome. It is worth noting that the hydrogen evolution reaction of Be₆ + H₂O has 8 transition states, and the second O–H bond breaks more energy than the first O–H bond breaks. The hydrogen evolution reaction of Be₈ + H₂O has only 3 transition states, and the reaction heat is the highest (−4.13 eV). It can be seen from the IRI analysis that the hydrogen molecules in the products of Be_n + H₂O (n = 5–9) are all adsorbed on the surface of the cluster in the form of chemical bonds. The weaker Be–H bond interaction in Be₇O@H₂ and Be₉O@H₂ is beneficial for the desorption of hydrogen molecules. The Gibbs free energy of the Be_n + H₂O (n = 5–9) reaction is consistent with the trend of electron energy change, revealing the spontaneity of the reaction to some extent, and can be compared with potential experiments.

Author contributions

Kai Diao: conceptualization, formal analysis, investigation, writing – original draft. Shun Ping Shi: conceptualization, writing – review & editing, supervision. Yong Song: supervision. Leilei Tang: data curation. Jiabao Hu: data curation. Zhanjiang Duan: writing – review & editing. Jing Jiang: writing – review & editing. De Liang Chen: software, resources.

Conflicts of interest

The authors declare that they have no known competing financial interests or relationships that could have appeared to influence the work reported in the paper.

Acknowledgements

This project is supported by the Open Research Fund of Computational Physics Key Laboratory of Sichuan Province, Yibin University (Grant No. YBXYJSWL-ZD-2020-005). This work is also supported by the Student's Platform for Innovation and Entrepreneurship Training Program (No. S202110616084 and G202210616030).

References

1. H. Song, S. Luo, H. Huang, B. Deng and J. Ye, ACS Energy Lett., 2022, 7, 1043–1065.
2. Y.-Q. Zou, N. von Wolff, A. Anaby, Y. Xie and D. Milstein, Nat. Catal., 2019, 2, 415–422.
3. S. Chu and A. Majumdar, Nature, 2012, 488, 294–303.
4. X. Liu, P. Wang, X. Liang, Q. Zhang, Z. Wang, Y. Liu, Z. Zheng, Y. Dai and B. Huang, Mater. Today Energy, 2020, 18, 100524.
5. P. Liao and E. A. Carter, Chem. Soc. Rev., 2013, 42, 2401–2422.
6. W.-L. Xie, Z.-H. Zhang, C.-L. Yang, M.-S. Wang and X.-G. Ma, Int. J. Hydrogen Energy, 2017, 42, 4032–4039.
7. S. Dong, Z. Wang, Y. Wang and J. zhang, J. Alloys Compd., 2017, 727, 1157–1164.
8. N. Gong, C. Deng, L. Wu, B. Wan, Z. Wang, Z. Li, H. Gou and F. Gao, J. Alloys Compd., 2019, 781, 371–377.
9. C. Li, Z. Fan, H.-L. Jia, C. Wang, P.-K. Ma, M.-W. Ren and H.-Y. Wang, J. Alloys Compd., 2021, 888, 161477.
10. M. D. Milosavljević, U. Burkhardt, A. Leithe-Jasper, Y. Grin and H. Borrmann, J. Alloys Compd., 2022, 890, 161420.
11. D. Zhu, Q. Zeng, Y. Liu, C. Li, L. Lu, T. Han, G. Xie and X. Shu, J. Alloys Compd., 2022, 919, 165780.
12. S. Srinivas and J. Jellinek, J. Chem. Phys., 2004, 121, 7243–7252.
13. B. Abyaz, Z. Mahdavifar, G. Schreckenbach and Y. Gao, Phys. Chem. Chem. Phys., 2021, 23, 19716–19728.
14. R. Kawai and J. H. Weare, Phys. Rev. Lett., 1990, 65, 80–83.
15. D.-D. Zhang, D. Wu, H. Yang, D. Yu, J.-Y. Liu, Z.-R. Li and Y. Li, Eur. J. Inorg. Chem., 2017, 2428–2434.
16. J.-Y. Li, D. Wu, Y. Li and Z.-R. Li, Chem. Phys. Lett., 2017, 674, 1–5.
17. G.-x Ge, Y.-l Yan, F.-z Ren, X.-l Lei, Z. Yang, W.-j Zhao, Q.-l Wang and Y.-h Luo, Chin. J. Chem. Phys., 2007, 20, 518–524.
18. O. Roberto-Neto and E. F. V. de Carvalho, Theor. Chem. Acc., 2020, 139, 93.
19. F. Y. Naumkin and D. J. Wales, Int. J. Quantum Chem., 2012, 112, 3068–3075.
20. J. Beheshtian and I. Ravaei, Struct. Chem., 2018, 29, 231–241.
21. M. Y. Mehboob, R. Hussain, Z. Irshad, U. Farwa, M. Adnan and S. Muhammad, J. Comput. Biophys. Chem., 2021, 20, 687–705.
22. R. Sun, C. L. Yang, M. S. Wang and X. G. Ma, J. Power Sources, 2022, 547 DOI:10.1016/j.jpowsour.2022.232008.
23. Q. Fu, F. Xin, X. Yin, Y. Song and Y. Xu, Int. J. Hydrogen Energy, 2021, 46, 22446–22453.
24. Q. K. Yin, C. L. Yang, M. S. Wang and X. G. Ma, J. Mater. Chem. C, 2021, 9, 12231–12238.
25. S. Jayachitra, D. Mahendiran, P. Ravi, P. Murugan and M. Sathish, Appl. Catal., B, 2022, 307 DOI:10.1016/j.apcatb.2022.121159.
26. L. L. Liu, B. W. Jiang, D. Sun, H. Y. Liu and Y. Xie, J. Mater. Chem. A, 2022, 10, 14060–14069.
27. M. Ge, C.-L. Yang, M.-S. Wang and X.-G. Ma, Int. J. Hydrogen Energy, 2022, 47(100) DOI:10.1016/j.ijhydene.2022.09.249.
28. E. Vos, I. Corral, M. M. Montero-Campillo, O. Mó, J. Elguero, I. Alkorta and M. Yáñez, Phys. Chem. Chem. Phys., 2021, 23, 6448–6454.
29. E. Vos, I. Corral, M. M. Montero-Campillo and O. Mó, J. Chem. Phys., 2021, 154, 044302.
30. D. Chakraborty and P. K. Chattaraj, J. Comput. Chem., 2018, 39, 535–545.
31. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
32. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
33. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
34. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
35. R. Peverati and D. G. Truhlar, Phys. Chem. Chem. Phys., 2012, 14(47), 16187–16191.
36. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
37. T. Lu and Q. Chen, Chem.: Methods, 2021, 1, 231–239.
38. T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592.
39. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics Modell., 1996, 14, 33–38.
40. C. K. Thomas Williams Gnuplot. An Interactive Plotting Program.
41. M. Šulka, D. Labanc, M. Kováč, M. Pitoňák, I. Černušák and P. Neogrády, J. Phys. B: At., Mol. Opt. Phys., 2012, 45, 085102.
42. B. Samanta, T. Sengupta and S. Pal, J. Phys. Chem. C, 2018, 122, 28310–28323.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04647d

---