By how much can closed-loop frameworks accelerate computational materials discovery?

Abstract

The implementation of automation and machine learning surrogatization within closed-loop computational workflows is an increasingly popular approach to accelerate materials discovery. However, the scale of the speedup associated with this paradigm shift from traditional manual approaches remains an open question. In this work, we rigorously quantify the acceleration from each of the components within a closed-loop framework for material hypothesis evaluation by identifying four distinct sources of speedup: (1) task automation, (2) calculation runtime improvements, (3) sequential learning-driven design space search, and (4) surrogatization of expensive simulations with machine learning models. This is done using a time-keeping ledger to record runs of automated software and corresponding manual computational experiments within the context of electrocatalysis. From a combination of the first three sources of acceleration, we estimate that overall hypothesis evaluation time can be reduced by over 90%, i.e., achieving a speedup of ∼10×. Further, by introducing surrogatization into the loop, we estimate that the design time can be reduced by over 95%, i.e., achieving a speedup of ∼15–20×. Our findings present a clear value proposition for utilizing closed-loop approaches for accelerating materials discovery.

---

1. Introduction

The discovery and optimization of materials is a central barrier to developing and deploying next-generation energy technologies.¹ In particular, decarbonizing chemical synthesis through electrochemistry requires the identification of new and efficient electrocatalysts.² One example of such decarbonization is to substitute the energy-intensive Haber–Bosch process used to synthesize ammonia by materials that can catalyze the reaction electrochemically,^3,4 at substantially lower energy costs. However, finding optimal candidates efficiently remains a challenge due to both the large size of the feasible candidate space⁵ and the computational cost of high-fidelity evaluation of each candidate. Development of methods to accelerate the candidate evaluation search, even within a well-defined and bounded design-space, is crucial to meet approaching climate goals.

These considerations have motivated significant research into new methods for accelerated materials discovery, both experimentally and computationally, tracing back to early work exploring autonomous experimentation.^6–9 We point the reader towards several comprehensive review articles and perspectives on this topic.^10–14 In the context of experimental screening, much research focus has taken the form of robotic experimentation for applications such as searching for battery electrolytes,^15,16 finding thermally stable perovskites,¹⁷ and optimizing battery charging protocols.¹⁸ These studies tend to employ a combination of robots to automate each experimental task and a learning agent that recommends the next experiment to perform based on the outputs of previous experiments, thereby “closing the loop”. However, the trade-off is that autonomous experimental setups are highly application-specific and do not typically probe the material under realistic device operating conditions. Thus, although experimental workflows show much promise, they are, at present, limited in terms of adaptability and bridging the device gap.¹⁹

In contrast, computational workflows promise to address a broad range of material discovery challenges as they are limited only by the availability of computational resources and the accuracy of the underlying methods.¹² In general, computational workflows share some similarities with closed-loop experimental workflows, especially around algorithms and approaches for iteratively selecting the next set of candidates to evaluate from a large design space. A notable difference, however, is that any new tasks or pipelines added to a computational workflow is limited only by computational requirements and not by the inventory of raw materials, supply logistics, instrumentation setup, laboratory space, and other considerations. This allows for improved modularity in existing closed-loop software frameworks as well as transferability between varying materials discovery workflows.

The use of an iterative informatics-driven search of the design space has demonstrated encouraging results in terms of speeding up materials discovery.^20–36 Similarly, informatics-driven closed-loop computational workflows have been shown to discover promising candidates faster than a random search, for applications such as catalyzing electrochemical CO₂ reduction and hydrogen evolution,³⁷ finding stable iridium oxide polymorphs,³⁸ and discovering stable binary and ternary systems.³⁹

While closed-loop computational frameworks with embedded guided design space search demonstrate a promising approach to accelerate materials discovery, quantification of their benefits over more traditional approaches remains challenging. Previous works have benchmarked the benefits of sequential learning as an overall accelerator for materials discovery.^33,40 However, the degree to which speedups from various components of a fully autonomous closed-loop framework, beyond design of experiments, combine to accelerate materials discovery remains unclear. Moreover, closed-loop frameworks can introduce multiple different accelerators such as automation.¹⁴ To our knowledge, a detailed quantitative breakdown of such sources of acceleration with relative estimates of the associated speedups has not been previously explored.

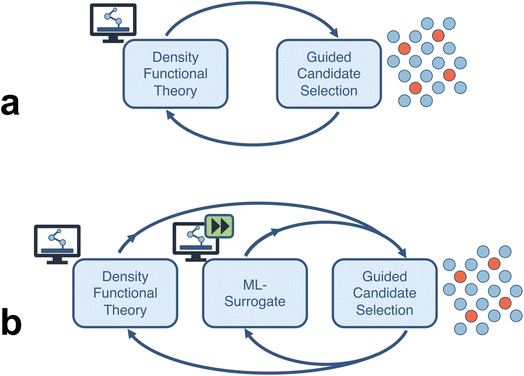
In this study, we quantify the acceleration estimates of a closed-loop computational framework for an electrocatalysis application. We probe two types of fully autonomous computational workflows (Fig. 1): (a) a closed-loop framework consisting of high-throughput density functional theory (DFT) calculations which feeds into a sequential learning (SL) algorithm that selects the next batch of candidate systems (thereby closing the loop), and (b) an extension of the previous framework where enough DFT data has been produced to train a machine learning (ML) surrogate to a desired accuracy and replace the expensive DFT calculations. We consider four categories of acceleration: (a) comprehensive end-to-end automation of computational workflows, (b) runtime improvements of individual compute tasks, (c) efficient search over vast design spaces using uncertainty-informed SL, and (d) surrogatization of time-consuming simulation tasks with ML models.

Fig. 1 Closed-loop materials discovery frameworks, (a) without, and (b) with machine learning surrogates for the density functional theory calculations, considered in this work for acceleration quantification.

Within each of the above categories, we estimate respective speedups and aggregate them into overall acceleration metrics. For end-to-end automation we estimate the attributed speedup through timing comparisons of automated tasks and their manual analogues. In addition, we introduce a human-lag model to simulate user-related delays associated with manual job management on a computational resource. For runtime improvements, we estimate speedups from using informed calculator settings as well as better initial structure guesses for DFT structural relaxations. This comparison is done in the context of calculations for relaxing the OH moeity onto the hollow sites of a sample single-atom alloy, Ni₁/Cu(111). For efficient design space search, we use a simulated SL-driven process on a representative problem of finding the bimetallic catalyst with the optimal surface binding energies for the CO moeity. For surrogatization with ML models, we estimate the speedup by calculating the DFT training set size needed to reach a desired model accuracy for adsorption energy (as opposed to generating the full dataset). Finally, we accumulate these results into an overall acceleration for workflows both excluding and including surrogatization. Through a combination of improvements in each of the above areas, we demonstrate a reduction in time to discover a new promising electrocatalytic material by 90–95% when compared to conventional approaches.

2. Results

Each of the forms of acceleration described above can synergize to provide an overall speedup in materials discovery. We benchmark the acceleration of each individual category through timing estimates of the relevant components both within a closed-loop automated workflow and for equivalent tasks when using a more traditional approach. For the automated workflow, we use the AutoCat, dftparse, and dftinputgen software packages in tandem. For the traditional workflow, we record timings for a researcher using the ASE (Atomic Simulation Environment⁴¹) software package for equivalent tasks. Additional details are provided in Section 5. As an example representative design space, we use the single-atom alloy (SAA) class of materials. SAAs are transition-metal hosts whose surface contains dispersed atoms of a different transition-metal species, and have shown much promise for electrocatalysis applications.⁴²

In the following subsections we discuss each of the individual acceleration categories and how their estimates were obtained. This is followed by acceleration estimates of the full workflow combining all sources of speedup to obtain a single acceleration estimate from the automated closed-loop approach relative to the traditional baseline.

2.1 Automation of computational tasks and workflows

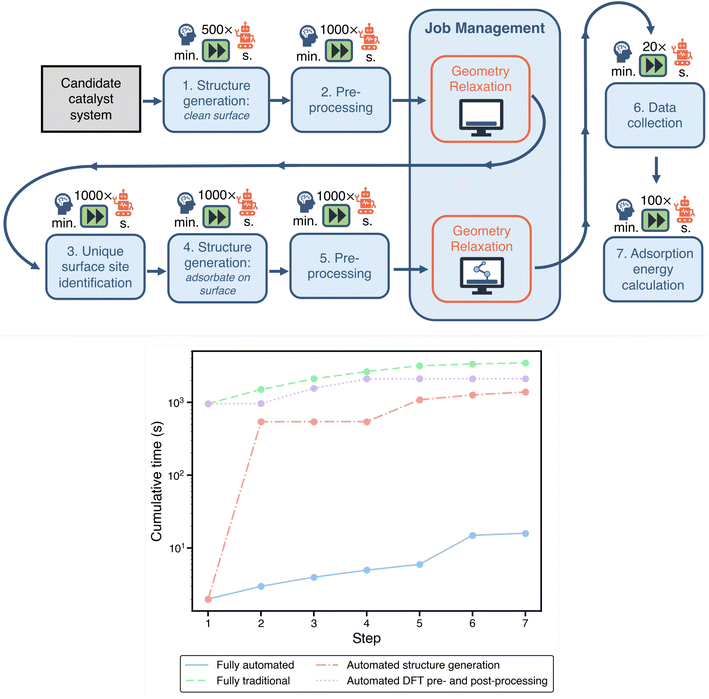
Within a standard computational study, there are many time-consuming tasks related to preparing, managing, and analyzing DFT calculations. In Fig. 2, we visualize a typical pipeline for a computational electrocatalysis study. Each of the boxes underneath the symbol of a brain represents a task where user involvement is required in the traditional paradigm. This includes structure generation, DFT pre-and post-processing, and job management on computational resources. Thus, every box in the pipeline that relies on user intervention is an opportunity for streamlining through automation.

Fig. 2 Top: a typical workflow for computational investigation of materials for electrocatalysis applications using density functional theory (DFT). Blue boxes indicate computational tasks which typically require researcher input. Factors above each task indicate potential acceleration through automation. Orange boxes are geometry optimizations via DFT calculations. Bottom: per-catalyst cumulative workflow evaluation times (excluding DFT runtimes). Each step corresponds to a component in the workflow above. Automating structure generation has a larger impact on acceleration than DFT pre- and post-processing.

To benchmark the traditional workflow against an automated one in a fair manner, we define the same objective for both paradigms: calculation of the adsorption energies of OH on the SAA of a Ni atom embedded on a Cu (111) surface, designated as Ni₁/Cu(111). This is further bounded to calculating adsorption only on three-fold sites on the surface (6 in total). The goal is to mimic the scenario where an activity descriptor has already been identified for a specific electrochemical reaction, thereby collapsing performance predictions to the surface binding energy of a single adsorbate, as reported in previous studies.³⁷ We have recently published methods to identify the most robust descriptors for a given reaction based on uncertainty quantification techniques,^43,44 and while we focus here on the binding energy alone, our acceleration estimation methodology is extensible to more complex descriptors equally well. As will be discussed later, this task of calculating the surface binding energy of an adsorbate species is integral to the representative problem of optimizing the binding energy across a set of possible SAAs using an SL-driven design of experiments. It should be noted that while automation generally replaces baseline tasks that are not very time-consuming in themselves, often on the order of seconds to minutes, the accelerations reported from this category free up the researcher to work on more analytical and constructive tasks, as elaborated in Section 3.

All of the necessary steps to obtain the specified adsorption energies are highlighted in Fig. 2. A comparison of the estimated time required for each task in the traditional approach and our automated approach is provided in Table 1. In the bottom panel of Fig. 2, we show the cumulative time for evaluating a single electrocatalyst using the above workflow (excluding the DFT runtimes) with varying degrees of automation. For this plot, the bounds emerge from the fully-automated and fully-manual (traditional) pipelines. We also consider two additional partially-automated “hybrid” scenarios: (1) automated structure generation with manual DFT pre- and post processing, and (2) manual structure generation with automated DFT pre- and post-processing. Automating structure generation has a larger impact on acceleration than automating DFT pre- and post-processing. Below we outline the potential acceleration for each of these individual tasks/workflow components via automation.

Table 1 Acceleration from automation of computational tasks and workflows. The timings listed in the traditional column represent completion of these tasks applying a manual approach. In contrast, the automated column demonstrates corresponding times using a streamlined automation approach. Comparing the traditional and automated values we can estimate acceleration factors as displayed in the acceleration column. It should be emphasized that while these factors sound exceptionally large, especially in comparison to the factors associated with the other acceleration sources, they are with respect to tasks that are on the order of seconds and minutes

Workflow step	Traditional	Automated	Acceleration
Catalyst structure generation
Clean surface	16 min	2 s	∼500×
Site identification	10 min	1 s	∼1000×
Adsorbate placement	9 min	1 s	∼1000×
DFT pre- and post-processing
Generating DFT input and job management scripts	9 min	1 s	∼1000×
Data collection	3 min	9 s	∼20×
Adsorption energy calculation	2 min	1 s	∼100×
DFT job submission and management
Job resubmission and error handling	9 h	—	—

---

2.1.1 Candidate structure generation. As an input, DFT requires atomic scale structural representations of the candidate systems to be evaluated. Structure generation in the context of electrocatalysis consists of generation of the catalyst structure without any reaction intermediates, identification of all of the possible adsorbate sites, and placement of the reaction intermediates on the sites of interest, along with the potential inclusion of the effect of water layer.⁴⁵ In this work, for simplicity, we do not consider solvation effects, but our analysis framework can be easily extended to include it. The first task corresponds to writing and executing scripts to generate the clean Ni₁/Cu(111) slab via either ASE or AutoCat (corresponding to the traditional and automated approaches, respectively), and recording the relative timings. While ASE has functions tailored for the generation of some classes of systems, additional user involvement is necessary for those that are not currently implemented. As an example, ASE does not currently have functions geared specifically towards SAAs, and thus additional scripts are necessary to dope host slabs. To generate each SAA the dopant site needs to be identified, the substitution made, and spin polarization added to both the host and dopant, as necessary. We can contrast this with automation software such as AutoCat which has a function, built on top of ASE functionalities, to streamline the generation of these SAA systems. Further, the implementation in AutoCat is suitable for generating multiple SAAs through a single function call by the user, including writing the generated structures to disk in an organized, predictable fashion. By leveraging tools for streamlined candidate structure generation, a speedup of approximately 500× over traditional manual approaches is observed.

The estimation of manual site identification for the second task of adsorbate placement requires measuring the time it takes a graduate researcher to identify all of the symmetrically unique surface sites of Ni₁/Cu(111). This task becomes increasingly challenging for the researcher as the candidate catalyst becomes more complex, particularly with broken surface symmetries. For example, in the case of SAAs, the presence of the single-atom breaks many of the symmetries, and correctly identifying all unique sites by hand is nontrivial. Some sites that are symmetrically equivalent on a non-doped surface no longer remain so after the substitution of the single-atom. In contrast, Delaunay triangulation provides a systematic automated approach to site identification that does not require user intervention.⁴⁶ A comparison of the time required for a graduate researcher to identify all of the sites relative to the automated approach shows a speedup by a factor of 1000×.

2.1.2 Density functional theory pre- and post-processing. For every catalyst structure generated, geometry optimizations via DFT calculations need to be performed. The total energies from these relaxed structures can then be used to estimate properties of interest, such as adsorbate binding energy. Preparation for each of these calculations involves writing DFT input files and scripts to submit these calculations to high-performance computing (HPC) resources. The DFT input files contain all of the calculation parameters to be used, such as the k-point density and the exchange–correlation functional. In addition, job submission scripts contain information about the requested computational resources on a HPC resource, including the number of compute cores needed and the walltime at which the job will be forcibly terminated. To obtain a baseline, we time a user performing both the above tasks, i.e., writing scripts to generate DFT input files as well as for submitting batch jobs to HPC resources. This is then compared to the time required for the equivalent tasks within a fully-automated framework (see Section 5 for details). The automated tasks are approximately 1000× faster than their traditional counterparts.

Additionally, once the DFT calculations have successfully completed, the compilation of results and data can consume a significant amount of time. The user must read through each of the DFT output files, extract the desired information, and collect and organize this data. When scaled up to a large number of systems, and thus calculation outputs, this can quickly become time-consuming. Here, we record the time taken to manually read all of the output files and collect all of the data into a single spreadsheet as well as for the parsing done by an automated framework (see Section 5 for details). A comparison of the recorded timings shows a speedup for data parsing and compilation step to be 20×.

Once the total energies of the reference states (the SAA surface with/without the adsorbate and the isolated adsorbate moeity) are extracted, the adsorbate binding energy can be calculated. We thus compare the time required to calculate these binding energies within a spreadsheet manually to that of automatically calculated via a software framework, resulting in a speedup of 100×. This final post-processing step of calculating the adsorbate binding energies is relatively quick regardless of the approach taken compared to the other steps considered in this workflow.

Note that while the speedups from the automation of tasks as described in the previous two sections are enormous, the baseline estimates for manual completion of these tasks are quite small, on the order of minutes. We reiterate that the impact of automation of these tasks is primarily on researcher productivity, allowing focus on the more analytical tasks rather than the more routine ones (see Section 3).

2.1.3 Workflow integration. In addition to the automation of candidate structure generation and DFT pre-/post-processing as described above, the automation of the submission of batch jobs to HPC clusters, status monitoring, and general job management provides opportunities for significant acceleration. DFT calculations of catalyst structures are computationally expensive and typically require active monitoring by a researcher. In particular, as these calculations can take variable lengths of time to complete, they may demand user intervention at unpredictable times. For example, this could be to fix errors or simply resubmit continuation jobs. The unpredictability associated with job management introduces “human lag” as it is not possible for the typical researcher to continuously monitor the status of all submitted DFT jobs at all times. Here, we estimate such a human lag via a simple Monte Carlo sampling approach. First, we divide days into three different windows representing typical working hours, hours where some monitoring may occur, and hours where usually no monitoring occurs, with “checkpoints” in time defined for each (see Section I in the ESI† for details). Next, we assume a uniform distribution for the job finishing on any day of the week, without any preference for weekdays or weekends. This assumption accounts for the fact that often a researcher has no control over the job queue/priority systems on HPC resources, and a specific already-submitted job may start whenever resources become available. Finally, we simulate the process of completion of a DFT job followed by research action at the nearest checkpoint in time, gathering statistics for a total of 10⁶ DFT jobs. In contrast, since job management within the fully-automated workflow is handled by a software framework, there is no equivalent human lag, which enables significant acceleration.

2.2 Calculation runtime improvements

In the next category of acceleration, we quantify the speedup of calculation runtimes (Table 2). Within our electrochemical materials discovery workflow, the primary physics-based simulation is DFT. As these calculations can be time-intensive, improving their runtimes is crucial in achieving significant acceleration.

Table 2 Acceleration from calculation runtime improvements. Here, the estimates in the traditional column refer to employing both a naive structure generation alongside naive calculator settings for OH adsorption on Ni₁/Cu(111). For comparison, the automated column refers to timing estimates on the same structures using chemically informed input structures and calculator settings. The acceleration column estimates the acceleration factors for each scenario. As mentioned previously, while these factors appear much smaller than the automation factors, they are with respect to significantly more time-consuming tasks

Workflow step	Traditional	Automated	Acceleration
DFT calculation settings and initial structure guess
Clean substrate relaxation	21 h	18.5 h	∼1.1×
Substrate + adsorbate relaxation	46 h	20 h	∼2.3×

---

In the case of adsorption structures, the initial guesses of the adsorbate geometry can play a key role. If the initial guess is far from the ground state geometry, more optimization steps will be required to reach equilibrium. Since each step requires a full self-consistent evaluation to obtain the energy and forces, the initial guess should ideally be as close to the equilibrium as possible to decrease the overall calculation runtime. The total runtimes of geometry optimizations via DFT can also be heavily influenced by the choice of calculator settings, such as initial magnetic moment. A poor guess of the initial magnetic moment can require more steps to achieve self-consistency and to converge on the final relaxed value of the magnetic moment.

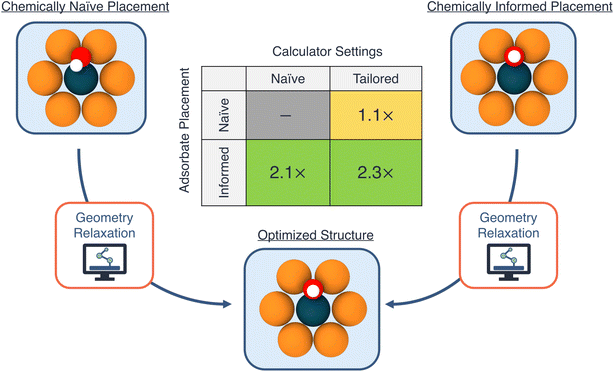
To decouple the influences of the initial geometry guess and the choice of calculator settings, we run four sets of relaxations for OH on all of the hollow sites of Ni₁/Cu(111). We use two initial geometry guesses: (a) a (chemically) “informed” configuration, in which the initial height of the adsorbate on the catalyst surface is guessed based upon the covalent radii of the nearest neighbors of the anchoring O atom, and (b) a “naive” configuration, in which the initial height of the adsorbate is set to 1.5 Å above the catalyst surface, and the OH bond angle is 45° with respect to the surface.

In addition to the different initial geometry guesses, we explore two choices for calculator settings, focusing here on the initial magnetic moment parameter: (a) a “tailored” setting, based on the ground-state magnetic moment of the single-atom dopant species from the ASE package (thus tailoring the initial guess for the magnetic moment to the specific SAA system being calculated), and (b) a “naive” setting, using an initial magnetic moment of 5.0 μ_B for the dopant atom in the SAA, regardless of its identity. In the specific case of Ni₁/Cu(111), since the structure prefers to be in a spin-paired state (i.e., without spin-polarization), the former approach provides an initial guess that is closer to the actual spin-polarization of the system. Note that our intention here is to highlight the impact of these choices on the acceleration of a DFT calculation, and the choices themselves can originate from deterministic algorithms, an ML model, or another approach entirely.

In Fig. 3 we visualize the accelerations of the DFT runtimes from both the choice of calculator settings as well as initial geometry guesses. Firstly, we observe relatively modest speedups from choice of calculator settings, approximately 1.1× for both the naive and informed geometry guesses. For these calculations, the system converges to the non-spin-polarized state within the first few iterations. Thus, the observed speedup from the choice of initial magnetic moment of the dopant atom is mainly a reflection of these initial iterations when the system reaches the appropriate spin state, which often also take the largest number of self-consistent steps. On the other hand, we observe a much larger acceleration from the initial geometry guess: a speedup of 2.1× and 2.3×, for the naive and tailored settings respectively.

Fig. 3 Estimated accelerations for density functional theory geometry optimization calculations. The effect of an initial geometry guess and choice of calculator settings are decoupled using four independent combinations of informed/naive initial geometry and tailored/naive settings. The largest factor of acceleration is observed when using an informed geometry guess with a tailored calculator settings.

The speedup from a good guess for the initial adsorbate geometry is mainly due to a reduction in the number of steps required to reach the equilibrium configuration within a fixed optimization scheme. For example, an average of approximately 33 and 16 geometry optimization steps using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm are required to reach equilibrium, when starting from the chemically-naive and informed geometries, respectively (with the tailored calculator settings). Thus, methods to reduce the number of steps required to reach equilibrium as well as shorten the DFT compute time at each geometry step (i.e., fewer steps to reach self-consistency) are highly desirable, and are an area of active research.^47–52 Overall, combining both the improved initial geometry guess as well as the choice of calculator settings yields the largest factor of runtime acceleration, 2.3×, thus motivating the consideration of both variables within automated workflows.

2.3 Efficient design space search

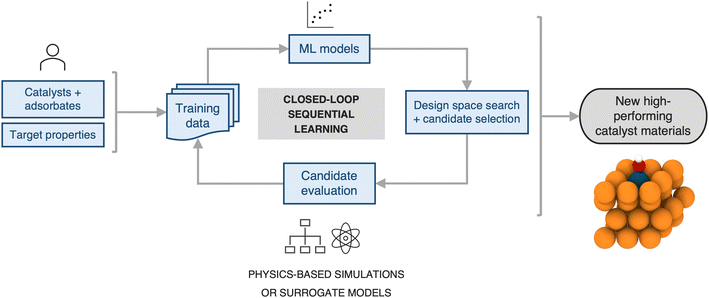
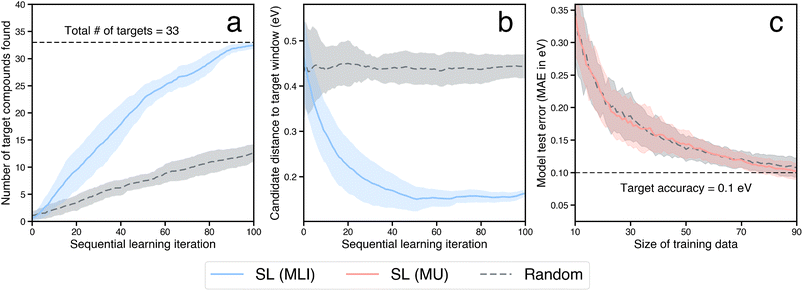
Next, we estimate the acceleration resulting from use of a sequential learning (SL) workflow for selecting and evaluating candidates in a design space of catalysts and compare it to that of traditional approaches. The SL workflow proceeds as follows: (1) collect an initial set of a small number of training examples of catalyst candidates and their properties, selected at random; (2) build ML models using the initial set of training examples and predict the objective properties of all the candidates in the design space of interest; (3) use an acquisition function that considers model predictions and uncertainties to select the next candidate to evaluate; (4) evaluate the selected candidate and add it, along with its newly obtained property values, to the training set; (5) iterate steps 2–4 in a closed-loop manner until a candidate, or a certain number of candidates, with the target properties has been discovered. A detailed schematic of this workflow is presented in Fig. 4. Such a strategy has been previously shown to be more efficient in sampling the design space to find novel candidates by a factor of 2–6× over traditional grid-based searches or random selection of candidates from the design space.^20–36

Fig. 4 A typical closed-loop sequential learning workflow for computational discovery of novel catalyst materials. First an initial training data set is collected at random. Second, this data is used to train a surrogate model for the objective properties. Next, both model predictions and uncertainties are fed into an acquisition function to select the next system for evaluation. From evaluating the selected candidate a new label is obtained and added to the dataset. The surrogate model is then re-trained and acquisition function scores iteratively recalculated, closing the loop.

For benchmarking the acceleration from SL for a typical catalyst discovery problem, we use a dataset of ∼300 bimetallic catalysts for CO₂ reduction.⁵³ The dataset contains ∼30 candidates with the target property of *CO adsorption energy on the catalyst surface inside a narrow window of [−0.7 eV, −0.5 eV]. We perform an SL simulation, starting with a small initial training set of 10 randomly selected examples from the above dataset, and iterate in a closed-loop as described above until all the target candidates in the design space have been identified successfully, and benchmark the acceleration against random search. We perform 20 independent trials of the full SL simulation to generate statistics. In particular, at each SL iteration, we build random forest-based models using the lolo software package,³⁰ and predict the *CO adsorption energies of all candidates, along with robust estimates of uncertainty in each prediction. The next candidate to evaluate is chosen based on the maximum likelihood of improvement (MLI) acquisition function. This function selects the system with the maximum likelihood of having an adsorption energy in the [−0.7 eV, −0.5 eV] window, when considering both the predicted value as well as its uncertainty. Overall we find that such an SL-based workflow successfully identifies all ∼30 target candidates 3× faster than random search (Fig. 5a). In addition, we note that the candidates surfaced by SL, on average, have properties closer to the target property window than those surfaced by random search, even when those candidates do not explicitly fall within the window (Fig. 5b). In other words, in addition to discovering target candidates considerably more efficiently than random search, an SL-based approach surfaces potentially interesting candidates near the target window much more frequently as well.

Fig. 5 A comparison of random search vs. sequential learning (SL)-driven approach to find new bimetallic catalysts with a target property. (a) Overall, the SL-driven approach identifies all the 33 target candidates in the dataset within 100 iterations, ∼3× faster than random search. (b) Candidates surfaced via SL lie much closer to the target window on average, when compared to those chosen via random search. (c) An SL-driven approach can help identify a much smaller number of examples that can be used to train ML surrogates to a desired accuracy, at a fraction of the overall dataset size. Here, the overall dataset has ∼300 candidates, and an ML model trained on only ∼25% of the candidates chosen via a SL-driven maximum uncertainty-based approach achieves the target accuracy. In each case, the shaded region in the plots represent variation in the reported quantities estimated over 20 independent trials.

2.4 Surrogatization of compute-intensive simulations

For the last category of acceleration, we estimate the extent of further possible speedup through the surrogatization of the most time-consuming tasks in the workflow. In particular, the rate determining step of the closed-loop framework considered here is the calculation of the binding energies of adsorbates using DFT. ML models can be used as surrogates for physics-based simulations of material properties often at a fraction of the compute cost and with marginal loss in accuracy. The primary cost of building such ML surrogates for materials properties often lies in the generation of training data where such data does not exist, especially when the data generation involves compute-intensive physics-based simulations such as DFT. Here we estimate the size of such training data required to build and train ML surrogates with a target accuracy, and in particular, when such training data is iteratively built using an SL-based strategy.

We use the dataset of bimetallic catalysts for CO₂ reduction mentioned in Section 2.3. within a SL workflow to simulate an efficient, targeted training set generation scheme. Similar to the SL workflow employed in the search for novel catalyst materials in a design space of interest, we employ a closed-loop iterative approach to generate the training data and address model accuracy. We consider a small initial training dataset of 10 systems chosen at random, build random forest models to predict adsorption energies, and iteratively choose the next candidate to build the training data. With model accuracy in mind, we employ an acquisition strategy that optimizes for the most accurate ML model on average by choosing candidates to evaluate from regions in the design space where the model is the least informed. In particular, at each iteration the candidate whose property prediction has the maximum uncertainty (MU) is selected to augment the training data. The inclusion of such a candidate results in the highest improvement in the overall accuracy of the ML model. Note that the aim of using the MU acquisition function is to build a minimal dataset that is nearly as informative as the full dataset. This is in contrast to the previously described strategy of using the MLI acquisition function for discovering the top-performing candidates as quickly as possible. Using an accuracy threshold of interest, we then determine the fraction of the overall training data necessary for building useful ML surrogates. For instance, with a threshold of 0.1 eV (the typical difference between DFT and experimental formation energy values⁵⁴), we estimate that accurate ML surrogates can be trained using a dataset generated via the above SL-strategy with ∼25% of the overall dataset size (Fig. 5c). The accuracy metric here is calculated on a test set of fixed size, via a bootstrapping approach, as described in the ESI.† Notably, the purely-exploratory random acquisition performs as well as MU for building minimal datasets, consistent with previous reports comparing model accuracy as a function of SL iteration using similar acquisition functions.⁵⁵ An expanded comparison of acquisition functions (including another baseline, a “space-filling” strategy, in addition to random search) for the three SL-related tasks of finding optimal candidates, surfacing high-quality candidates, and building minimal datasets for training ML surrogates, can be found in the ESI.†

2.5 Overall acceleration of the full end-to-end workflow

Finally, we aggregate the acceleration from the various steps in the workflow to estimate the overall speedup achieved in Table 3 and Fig. S2.† Here, we use the single-atom alloys (SAA) design space for calculating the overall estimates. We begin by estimating the size of such a design space. Limiting the design space to ∼30 transition metal hosts and dopants results in a total of ³⁰C₂ ≈ 900 SAA systems. For each SAA system, typically a few (3–5) low-index surface terminations are considered. Moreover, the considered adsorbate molecule can adsorb onto the catalyst surface at one of many possible symmetrically unique sites (up to 20–40 configurations), and all such possible intermediate configurations need to be considered in the design space. Overall, a typical SAA design space when fully enumerated can have up to 10⁵–10⁶ possibilities.

Table 3 Overall acceleration benchmarks for the end-to-end workflows, with and without surrogatization broken down into individual sources of acceleration. We demonstrate a speedup of up to 10× with automation of tasks and runtime improvements, and a speedup of up to 20× upon using ML surrogates for the most compute-intensive DFT tasks

Approach	Structure generation	Substrate calculation	Adsorbate placement	Catalyst calculation	Data usage	Post-processing	Design space search factor	Total acceleration
a i.c. = intermediate configuration (total # i.c. ≈200/catalyst system); “traditional” includes human lag estimates. b Estimate from bimetallic catalyst dataset of the relative amount of DFT training data needed to reach a target accuracy of 0.1 eV per adsorbate.
Traditional	16 min	21 h	18 min	72 h per i.c.^a	100%	5 min	1
Automated	2 s	18.5 h	2 s	20 h per i.c.^a	100%	10 s	0.33	10×
+ Surrogates	2 s	—	2 s	20 h per i.c.^a	10–25%^b	2 s	0.33	15–20×

---

Using the above SAA design space, we apply the estimated time for each step in our overall end-to-end catalyst workflow as described in the previous sections, using both traditional and automated closed-loop methods (with and without surrogates), and calculate the overall speedup. From the automation of tasks and workflows, and runtime improvements alone, an acceleration of ∼10× (a reduction of ∼90%) over traditional materials design workflows can be achieved. Further utilizing the ML surrogates (including the compute costs required to generate the training data) can result in an acceleration of up to ∼20× (a reduction of up to ∼95%) over traditional approaches.

3. Discussion

The results presented here have implications that reach beyond the reported factors of acceleration. It is helpful to make a distinction between project time and researcher time. We consider project time as the time necessary to carry a project to completion. In other words, this is an accumulation of all the time spent towards achieving the tasks to reach the project goal. Thus, all the acceleration factors quantified above are with respect to this project time. Therefore, the closed-loop workflows discussed here are anticipated to have a direct impact on time to project completion. In addition, by breaking down the acceleration factors for each component of the workflows, estimates for project time acceleration in the case of differing closed-loop framework topologies than those outlined here (e.g., a framework with multi-scale simulations in place of or in addition to DFT calculations) can be inferred.

On the other hand, researcher time can be interpreted as time spent from the frame of reference of the researcher on a given workday. The acceleration associated here is not directly quantified as with project time. The most obvious example of this influence is through task automation. In the traditional paradigm, these tasks can become time-consuming, particularly as the scale and throughput of the project increase. Automation frees up valuable researcher time that would normally be occupied by the more mundane tasks. This allows the researcher to instead focus on more intellectually demanding tasks such as surveying existing literature, refining the design space and project formulation, and improving research productivity.

The automation of job management has the benefit of impacting both project time and researcher time. Since this form of automation facilitates running computational jobs around-the-clock, the human-lag associated with monitoring and handling jobs manually is entirely removed. This decreases the project time as described above. In the context of researcher time, this automation also has the added benefit of decreasing the overhead of job monitoring at regular intervals.

We can make a few additional observations regarding the nature of the baselines used to estimate the speed of traditional approaches in this work. First, for estimation of task timings such as input file generation for simulations and script generation to submit jobs on HPC resources, we use time estimates from a single researcher. The timings of such tasks are inherently variable, depending on the exact nature of the task, the researcher performing it, as well as the environmental setup in which it is performed. Similarly, natural delays associated with monitoring and managing ongoing computational jobs depend on the working habits of the researcher, the time-scale associated with each computation (e.g., those that take hours opposed to days or weeks to complete), and the availability or connectivity of the computational resources (e.g., on-site resources versus those that can be accessed remotely). Lastly, to estimate the acceleration from an intelligent exploration of the design space using sequential learning, we use random sampling as the benchmark. While random sampling is an excellent exploratory acquisition function,⁵⁶ it is not a substitute for traditional methods of design space exploration. Typically, traditional search approaches are influenced by prior knowledge, research directions within the community at the time, available resources, among other factors. We use random search here, not least because a model to predict a traditional materials design trajectory does not exist, to our knowledge, but also because it is widely-used as an unbiased exploratory baseline.^{20–24,26–28,30–36}

We want to emphasize that, given some of the variability in the baselines as discussed above, the goal of this work is to highlight the approximate scale of acceleration that can be attributed to the several individual components in a closed-loop computational materials design workflow. Moreover, we also aim to highlight the challenges associated with estimating such factors of acceleration, versus attempting to maximize the accuracy of each timing estimate itself. Further methodological improvements for more precisely determining accelerations associated with each step in an automated workflow would be a valuable area for further study. Our work underscores the importance of data collection and sharing, especially around time spent on research tasks, monitoring and managing medium-to high-throughput computational projects, implementing traditional approaches of materials discovery and design trajectories, and handling failed computations and experiments. We recommend a community-driven initiative towards such data collection and sharing efforts to bolster our understanding of the traditional baselines as well as to further contextualize the significant benefits of automation and ML-guided strategies.

4. Conclusion

In this work we demonstrate that task automation and runtime improvements combined with a sequential learning-driven closed-loop search can accelerate a materials discovery effort by more than 10× (or more than 90% reduction in overall time/cost) over traditional approaches. Further, we estimate that such automation frameworks can have a significant impact on researcher productivity (20–1000× from task automation alone), direct compute costs (1.1–2.3× from runtime acceleration), and project/calendar time (>10–20× from overall acceleration). Using a comparison of recorded times for manual computational experiments versus fully-automated equivalents, we provide speedup estimates stemming from different components within a closed-loop workflow. The automation of tasks helps in streamlining, minimizing or completely eliminating the need for user intervention. We also identify that significant speedup in terms of simulation (here, DFT calculations) runtimes can be achieved through better initial prediction of the catalyst geometries as well as better choices for calculator settings. Moreover, the use of a sequential learning framework to guide the design of experiments can dramatically decrease the number of candidate evaluations required to achieve the target materials design goal. Finally, we extend this analysis to include replacement of time-consuming simulations with machine learning surrogates, another source of acceleration, and find an improvement in the overall speedup to >15–20× (or more than 95% reduction in the overall time/cost). We believe that our findings underscore the immense benefits of introducing automation, machine learning, and sequential learning into scientific discovery workflows, and motivate further widespread adoption of these methods.

5. Methods

5.1 Workflow topology

We consider two different closed-loop “topologies”. The first is a two-stage process consisting of DFT calculations to calculate adsorption energies which are then used in a sequential learning (SL) workflow to iteratively guide candidate selection (Fig. 1a). Each DFT calculation task, here, for an electrocatalysis problem, consists of multiple steps. Namely, a geometry relaxation of the “clean” catalyst surface (i.e., without reaction intermediates), followed by a geometry relaxation of all reaction intermediates adsorbed onto all symmetrically-unique sites on the (relaxed) catalyst surface. In an automated workflow, these DFT calculations are performed sequentially within a predetermined pipeline framework. Here, we use a combination of AutoCat (https://github.com/aced-differentiate/auto_cat) for automated generation of catalyst and adsorbate structures, and the dftinputgen and dftparse software for the DFT calculations. More details on these software packages are provided in Section 5.2.

Another topology we consider is an extension of that described above, with machine learning (ML) models used as surrogates for the DFT calculations (Fig. 1b). In this scenario, the first few overall SL iterations proceed the same as before, except now as the DFT data is generated, a surrogate ML model is trained on the resulting data until a threshold test accuracy is reached. For these first few “data generation” iterations, candidates are selected with the intent of improving overall prediction accuracy. Once the threshold accuracy for the surrogate model is met, all subsequent iterations of the loop will use the surrogate model only (instead of DFT calculations) to predict adsorption energies. From this point onward the candidate selection step in the SL workflow is then focused on identifying the most promising materials, as described above in the topology without surrogatization.

5.2 Automation software

To create the crystal structures for the DFT calculations, we use AutoCat, a software package with tools for structure generation and sequential learning for electrocatalysis applications. This package is built on top of the Atomic Simulation Environment (ASE)⁴¹ and pymatgen⁵⁷ to generate the catalyst structures en masse, and write them to disk following an organized directory structure. AutoCat has tailored functions for generation of single-atom alloy (SAA) surface structures, with optional parameters such as supercell dimensions, vacuum spacing, and number of bottom layers to be fixed during a DFT relaxation, with appropriate defaults for each parameter. Moreover, through the use of pymatgen's implementation of Delaunay triangulation,⁴⁶ the identification of all of the unique symmetry sites on an arbitrary surface is automated. Furthermore, initial heights of adsorbates are estimated using the covalent radii of the anchoring atom within a given adsorbate molecule as well as its nearest neighbors host atoms on the surface. As the development of this package is part of an ongoing work, additional details will be reported in a future publication.

Once the catalyst and adsorbate systems have been generated by AutoCat, the crystal structures are used as input to an automated DFT pipeline that (a) generates input files for a DFT calculator (here we use GPAW^58,59), (b) executes DFT calculation workflows, and (c) parses successfully completed calculations and extracts useful information.

5.2.1 Automatic DFT input generation. We leverage the Python-based dftinputgen package (https://github.com/CitrineInformatics/dft-input-gen) to automate the generation of DFT input files from a specified catalyst/adsorbate crystal structure. In particular, we extend the dftinputgen package to support GPAW. For a given input crystal structure, the package provides sensible defaults to use for commonly-used DFT parameters based on prior domain knowledge for novice users as well as fine-grained control over each parameter for more experienced DFT practitioners. The package also implements, “recipes”, sets of DFT parameters and values to be used as default depending on the properties of interest, e.g., ground-state geometry and electronic structure. The package outputs input files in a user-specified location that can be directly used by popular DFT packages as input for calculation.

5.2.2 Execution of DFT calculation workflows. We leverage the Python-based fireworks⁶⁰ package to both define complex sequences of DFT calculations necessary for electrocatalysis studies (e.g., clean surface relaxation followed by adsorption relaxation), and to create, submit, and monitor batch jobs on high performance compute (HPC) resources for each such calculation. These scripts are part of an ongoing study and will be open-sourced.

5.2.3 Parsing output from DFT. After the completion of DFT calculations of a large number of different candidate systems, key metrics such as total energy and forces need to be extracted. To accomplish this task we have extended the previously-developed dfttopif (https://github.com/CitrineInformatics/pif-dft) and dftparse (https://github.com/CitrineInformatics/dftparse) packages to parse output generated via GPAW. Functions written for this package can look for a .traj file resulting from a successful GPAW calculation in a specified directory. Once a .traj file has been identified, it can be read using ASE to extract calculated properties of interest. This includes not only results such as total energy and forces, but also calculator settings such as the exchange–correlation functional used. The extracted properties findings are then written into a Physical Information File (PIF)⁶¹ (https://citrine.io/pif), a general-purpose materials data schema, for every calculation conducted.

5.3 First-principles calculations

All DFT calculations are performed with the GPAW package^58,59via ASE.⁴¹ The projector-augmented wave method is used for the interaction of the valence electrons with the ion cores. A target spacing of 0.16 Å is applied for the real-space grid, with a Monkhorst–Pack⁶²k-mesh of 4 × 4 × 1 for all surface calculations. For improved self-consistent field convergence, a Fermi–Dirac smearing of 0.05 eV is applied. All geometry optimizations are conducted via the BFGS algorithm as implemented in ASE.

5.4 Machine learning models

We use ML models based on random forests⁶³ as described in the previously-reported FUELS framework.³⁰ The uncertainty in a model prediction is determined using jackknife-after-bootstrap and infinitesimal jackknife variance estimators.⁶⁴ All ML models and related analysis in this work use random forests and uncertainty estimates as implemented in the open-source lolo library.⁶⁵ Materials in the training dataset are transformed into the Magpie features,²⁴ a set of descriptors generated using only the material composition, as implemented in the matminer package.⁶⁶

Data availability

All data and Python scripts required to perform the analysis presented in this work are made available via the GitHub repository at https://github.com/aced-differentiate/closed-loop-acceleration-benchmarks. Data shared includes data processing and calculation timing records, crystal structure files, and a preexisting catalysts dataset used for benchmarking. Scripts shared include those for estimating human lag in job management, calculating acceleration from sequential learning, performing all related data aggregation, analysis, and reproduction of associated figures.

The versions of the open-source software used for this study are as follows: GPAW 20.1.0, ASE 3.19.1, AutoCat 2022.3.31, pymatgen 2022.11.1, fireworks 1.9.6, lolo 2.0.0, dftinputgen 0.1.2.

Author contributions

Conceptualization: B. M., L. K., V. H., V. V.; methodology: B. M., L. K., V. H., V. V.; software: E. M., L. K., V. H.; validation: L. K., V. H.; data curation: L. K., V. H.; writing – original draft: E. M., L. K., M. J., V. H.; writing – review & editing: all authors; visualization: L. K., V. H.; supervision: B. M., V. V.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work presented here was funded in part by the Advanced Research Projects Agency-Energy (ARPA-E), U.S. Department of Energy, under Award Number DE-AR0001211. L. K. acknowledges the support of the Natural Sciences and Engineering Research Council of Canada (NSERC). The authors thank Rachel Kurchin for helpful discussions around automation and acceleration estimation, and James E. Saal for providing comments on a previous version of this manuscript.

References

1. A. Mistry, A. A. Franco, S. J. Cooper, S. A. Roberts and V. Viswanathan, How machine learning will revolutionize electrochemical sciences, ACS Energy Lett., 2021, 6(4), 1422–1431.
2. Z. J. Schiffer and K. Manthiram, Electrification and decarbonization of the chemical industry, Joule, 2017, 1(1), 10–14.
3. B. H. R. Suryanto, H. L. Du, D. Wang, J. Chen, A. N. Simonov and D. R. MacFarlane, Challenges and prospects in the catalysis of electroreduction of nitrogen to ammonia, Nat. Catal., 2019, 2(4), 290–296.
4. D. Chanda, R. Xing, T. Xu, Q. Liu, Y. Luo and S. Liue, et al., Electrochemical nitrogen reduction: recent progress and prospects, Chem. Commun., 2021, 57, 7335–7349.
5. Y. Kim, E. Kim, E. Antono, B. Meredig and J. Ling, Machine-learned metrics for predicting the likelihood of success in materials discovery, npj Comput. Mater., 2020, 6(1), 131.
6. R. D. King, K. E. Whelan, F. M. Jones, P. G. Reiser, C. H. Bryant and S. H. Muggleton, et al., Functional genomic hypothesis generation and experimentation by a robot scientist, Nature, 2004, 427(6971), 247–252.
7. P. Nikolaev, D. Hooper, F. Webber, R. Rao, K. Decker and M. Krein, et al., Autonomy in materials research: a case study in carbon nanotube growth, npj Comput. Mater., 2016, 2(1), 1–6.
8. P. Nikolaev, D. Hooper, N. Perea-Lopez, M. Terrones and B. Maruyama, Discovery of wall-selective carbon nanotube growth conditions via automated experimentation, ACS Nano, 2014, 8(10), 10214–10222.
9. R. D. King, J. Rowland, S. G. Oliver, M. Young, W. Aubrey and E. Byrne, et al., The automation of science, Science, 2009, 324(5923), 85–89.
10. D. P. Tabor, L. M. Roch, S. K. Saikin, C. Kreisbeck, D. Sheberla and J. H. Montoya, et al., Accelerating the discovery of materials for clean energy in the era of smart automation, Nat. Rev. Mater., 2018, 3(5), 5–20.
11. R. Pollice, G. Dos Passos Gomes, M. Aldeghi, R. J. Hickman, M. Krenn and C. Lavigne, et al., Data-Driven Strategies for Accelerated Materials Design, Acc. Chem. Res., 2021, 54(4), 849–860.
12. C. W. Coley, N. S. Eyke and K. F. Jensen, Autonomous discovery in the chemical sciences part I: Progress, Angew. Chem., Int. Ed., 2020, 59(51), 22858–22893.
13. E. Stach, B. DeCost, A. G. Kusne, J. Hattrick-Simpers, K. A. Brown and K. G. Reyes, et al., Autonomous experimentation systems for materials development: A community perspective, Matter, 2021, 4(9), 2702–2726.
14. H. S. Stein and J. M. Gregoire, Progress and prospects for accelerating materials science with automated and autonomous workflows, Chem. Sci., 2019, 10(42), 9640–9649.
15. A. Dave, J. Mitchell, K. Kandasamy, H. Wang, S. Burke and B. Paria, et al., Autonomous Discovery of Battery Electrolytes with Robotic Experimentation and Machine Learning, Cell Rep. Phys. Sci., 2020, 1(12), 100264.
16. A. Dave, J. Mitchell, S. Burke, H. Lin, J. Whitacre and V. Viswanathan, Autonomous optimization of non-aqueous Li-ion battery electrolytes via robotic experimentation and machine learning coupling, Nat. Commun., 2022, 13(1), 1–9.
17. Y. Zhao, J. Zhang, Z. Xu, S. Sun, S. Langner and N. T. P. Hartono, et al., Discovery of temperature-induced stability reversal in perovskites using high-throughput robotic learning, Nat. Commun., 2021, 12(1), 1–9,  DOI:10.1038/s41467-021-22472-x.
18. P. M. Attia, A. Grover, N. Jin, K. A. Severson, T. M. Markov and Y. H. Liao, et al., Closed-loop optimization of fast-charging protocols for batteries with machine learning, Nature, 2020, 578(7795), 397–402.
19. M. M. Flores-Leonar, L. M. Mejía-Mendoza, A. Aguilar-Granda, B. Sanchez-Lengeling, H. Tribukait and C. Amador-Bedolla, et al., Materials acceleration platforms: On the way to autonomous experimentation, Curr. Opin. Green Sustainable Chem., 2020, 25, 100370.
20. M. K. Warmuth, J. Liao, G. Rätsch, M. Mathieson, S. Putta and C. Lemmen, Active learning with support vector machines in the drug discovery process, J. Chem. Inf. Comput. Sci., 2003, 43, 667–673.
21. A. Seko, T. Maekawa, K. Tsuda and I. Tanaka, Machine learning with systematic density-functional theory calculations: Application to melting temperatures of single-and binary-component solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 054303.
22. E. Pauwels, C. Lajaunie and J. P. Vert, A Bayesian active learning strategy for sequential experimental design in systems biology, BMC Syst. Biol., 2014, 8, 1–11.
23. S. Chen, K. R. G. Reyes, M. K. Gupta, M. C. McAlpine and W. B. Powell, Optimal learning in experimental design using the knowledge gradient policy with application to characterizing nanoemulsion stability, SIAM/ASA J. Uncertain. Quantification, 2015, 3, 320–345.
24. L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, A general-purpose machine learning framework for predicting properties of inorganic materials, npj Comput. Mater., 2016, 2, 1–7.
25. S. Kiyohara, H. Oda, K. Tsuda and T. Mizoguchi, Acceleration of stable interface structure searching using a kriging approach, Jpn. J. Appl. Phys., 2016, 55, 045502.
26. E. V. Podryabinkin and A. V. Shapeev, Active learning of linearly parametrized interatomic potentials, Comput. Mater. Sci., 2017, 140, 171–180.
27. A. M. Gopakumar, P. V. Balachandran, D. Xue, J. E. Gubernatis and T. Lookman, Multi-objective optimization for materials discovery via adaptive design, Sci. Rep., 2018, 8, 1–12.
28. R. Yuan, Z. Liu, P. V. Balachandran, D. Xue, Y. Zhou and X. Ding, et al., Accelerated discovery of large electrostrains in BaTiO3-based piezoelectrics using active learning, Adv. Mater., 2018, 30, 1702884.
29. R. E. Brandt, R. C. Kurchin, V. Steinmann, D. Kitchaev, C. Roat and S. Levcenco, et al., Rapid photovoltaic device characterization through Bayesian parameter estimation, Joule, 2017, 1, 843–856.
30. J. Ling, M. Hutchinson, E. Antono, S. Paradiso and B. Meredig, High-dimensional materials and process optimization using data-driven experimental design with well-calibrated uncertainty estimates, Integr. Mater. Manuf., 2017, 6, 207–217.
31. H. C. Herbol, W. Hu, P. Frazier, P. Clancy and M. Poloczek, Efficient search of compositional space for hybrid organic–inorganic perovskites via Bayesian optimization, npj Comput. Mater., 2018, 4, 1–7.
32. A. D. Sendek, E. D. Cubuk, E. R. Antoniuk, G. Cheon, Y. Cui and E. J. Reed, Machine learning-assisted discovery of solid Li-ion conducting materials, Chem. Mater., 2018, 31, 342–352.
33. B. Rohr, H. S. Stein, D. Guevarra, Y. Wang, J. A. Haber and M. Aykol, et al., Benchmarking the acceleration of materials discovery by sequential learning, Chem. Sci., 2020, 11, 2696–2706.
34. Z. Del Rosario, M. Rupp, Y. Kim, E. Antono and J. Ling, Assessing the frontier: Active learning, model accuracy, and multi-objective candidate discovery and optimization, J. Chem. Phys., 2020, 153, 024112.
35. A. G. Kusne, H. Yu, C. Wu, H. Zhang, J. Hattrick-Simpers and B. DeCost, et al., On-the-fly closed-loop materials discovery via Bayesian active learning, Nat. Commun., 2020, 11, 1–11.
36. A. E. Gongora, B. Xu, W. Perry, C. Okoye, P. Riley and K. G. Reyes, et al., A Bayesian experimental autonomous researcher for mechanical design, Sci. Adv., 2020, 6, eaaz1708.
37. K. Tran and Z. W. Ulissi, Active learning across intermetallics to guide discovery of electrocatalysts for CO2 reduction and H2 evolution, Nat. Catal., 2018, 1(9), 696–703,  DOI:10.1038/s41929-018-0142-1.
38. R. A. Flores, C. Paolucci, K. T. Winther, A. Jain, J. A. G. Torres and M. Aykol, et al., Active Learning Accelerated Discovery of Stable Iridium Oxide Polymorphs for the Oxygen Evolution Reaction, Chem. Mater., 2020, 32(13), 5854–5863.
39. J. H. Montoya, K. T. Winther, R. A. Flores, T. Bligaard, J. S. Hummelshøj and M. Aykol, Autonomous intelligent agents for accelerated materials discovery, Chem. Sci., 2020, 11(32), 8517–8532.
40. Q. Liang, A. E. Gongora, Z. Ren, A. Tiihonen, Z. Liu and S. Sun, et al., Benchmarking the performance of Bayesian optimization across multiple experimental materials science domains, npj Comput. Mater., 2021, 7(1), 188.
41. A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen and M. Dułak, et al., The atomic simulation environment—a Python library for working with atoms, J. Phys.: Condens. Matter, 2017, 29(27), 273002 . Available from: http://stacks.iop.org/0953-8984/29/i=27/a=273002.
42. R. T. Hannagan, G. Giannakakis, M. Flytzani-Stephanopoulos and E. C. H. Sykes, Single-Atom Alloy Catalysis, Chem. Rev., 2020, 120(21), 12044–12088.
43. L. Kavalsky and V. Viswanathan, Robust Active Site Design of Single-Atom Catalysts for Electrochemical Ammonia Synthesis, J. Phys. Chem. C, 2020, 124(42), 23164–23176,  DOI:10.1021/acs.jpcc.0c06692.
44. D. Krishnamurthy, V. Sumaria and V. Viswanathan, Maximal Predictability Approach for Identifying the Right Descriptors for Electrocatalytic Reactions, J. Phys. Chem. Lett., 2018, 9(3), 588–595.
45. V. Viswanathan, H. A. Hansen, J. Rossmeisl, T. F. Jaramillo, H. Pitsch and J. K. Nørskov, Simulating linear sweep voltammetry from first-principles: application to electrochemical oxidation of water on Pt (111) and Pt3Ni (111), J. Phys. Chem. C, 2012, 116(7), 4698–4704.
46. J. H. Montoya and K. A. Persson, A high-throughput framework for determining adsorption energies on solid surfaces, npj Comput. Mater., 2017, 3(1), 1–4.
47. J. Yoon and Z. W. Ulissi, Differentiable optimization for the prediction of ground state structures (DOGSS), Phys. Rev. Lett., 2020, 17, 173001,  DOI:10.1103/PhysRevLett.125.173001.
48. J. R. Boes, O. Mamun, K. Winther and T. Bligaard, Graph Theory Approach to High-Throughput Surface Adsorption Structure Generation, J. Phys. Chem. A, 2019, 123(11), 2281–2285.
49. E. Garijo Del Río, S. Kaappa, J. A. Garrido Torres, T. Bligaard and K. W. Jacobsen, Machine learning with bond information for local structure optimizations in surface science, J. Chem. Phys., 2020, 153(23), 234116,  DOI:10.1063/5.0033778.
50. S. Deshpande, T. Maxson and J. Greeley, Graph theory approach to determine configurations of multidentate and high coverage adsorbates for heterogeneous catalysis, npj Comput. Mater., 2020, 6(1), 1–6,  DOI:10.1038/s41524-020-0345-2.
51. J. Musielewicz, X. Wang, T. Tian and Z. Ulissi, FINETUNA: Fine-tuning Accelerated Molecular Simulations, arXiv, 2022, preprint, arXiv:220501223.
52. E. G. del Río, J. J. Mortensen and K. W. Jacobsen, Local Bayesian optimizer for atomic structures, Phys. Rev. B, 2019, 100, 104103.
53. X. Ma, Z. Li, L. E. Achenie and H. Xin, Machine-learning-augmented chemisorption model for CO2 electroreduction catalyst screening, J. Phys. Chem. Lett., 2015, 6, 3528–3533.
54. S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak and M. Aykol, et al., The Open Quantum Materials Database (OQMD): assessing the accuracy of DFT formation energies, npj Comput. Mater., 2015, 1, 1–15.
55. C. K. Borg, E. S. Muckley, C. Nyby, J. E. Saal, L. Ward and A. Mehta, et al., Quantifying the performance of machine learning models in materials discovery, Digi. Discov., 2023, 2(2), 327–338.
56. J. Bergstra and Y. Bengio, Random search for hyper-parameter optimization, J. Mach. Learn. Res., 2012, 13, 281–305.
57. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher and S. Cholia, et al., Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis, Comput. Mater. Sci., 2013, 68, 314–319.
58. J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Real-space grid implementation of the projector augmented wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035109.
59. J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dułak and L. Ferrighi, et al., Electronic structure calculations with GPAW: a real-space implementation of the projector augmented-wave method, J. Phys.: Condens. Matter, 2010, 22(25), 253202.
60. A. Jain, S. P. Ong, W. Chen, B. Medasani, X. Qu and M. Kocher, et al., FireWorks: a dynamic workflow system designed for high-throughput applications, Concurrency Comput. Pract. Ex., 2015, 27(17), 5037–5059.
61. K. Michel and B. Meredig, Beyond bulk single crystals: a data format for all materials structure–property–processing relationships, MRS Bull., 2016, 41, 617–623.
62. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13(12), 5188–5192 . Available from: http://link.aps.org/doi/10.1103/PhysRevB.13.5188%5Cnhttps://journals.aps.org/prb/abstract/10.1103/PhysRevB.13.5188.
63. L. Breiman, Random forests, Mach. Learn., 2001, 45, 5–32.
64. S. Wager, T. Hastie and B. Efron, Confidence intervals for random forests: The jackknife and the infinitesimal jackknife, J. Mach. Learn. Res., 2014, 15, 1625–1651.
65. Informatics C. Lolo. GitHub, 2017, https://github.com/CitrineInformatics/lolo.
66. L. Ward, A. Dunn, A. Faghaninia, N. E. Zimmermann, S. Bajaj and Q. Wang, et al., Matminer: An open source toolkit for materials data mining, Comput. Mater. Sci., 2018, 152, 60–69.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2dd00133k

‡ These authors contributed equally to this work.

---