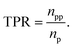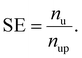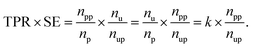Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular screening for solid–solid phase transitions by machine learning†
Daisuke
Takagi
a,
Kazuki
Ishizaki
 b,
Toru
Asahi
ab and
Takuya
Taniguchi
b,
Toru
Asahi
ab and
Takuya
Taniguchi
 *c
*c
aDepartment of Life Science and Medical Bioscience, Graduate School of Advanced Science and Engineering, Waseda University, 3-4-1 Okubo, Shinjuku-ku, Tokyo 169-8555, Japan
bDepartment of Advanced Science and Engineering, Graduate School of Advanced Science and Engineering, Waseda University, 3-4-1 Okubo, Shinjuku-ku, Tokyo 169-8555, Japan
cCenter for Data Science, Waseda University, 1-6-1 Nishiwaseda, Shinjuku-ku, Tokyo 169-8050, Japan. E-mail: takuya.taniguchi@aoni.waseda.jp
First published on 22nd June 2023
Abstract
The solid–solid phase transition in molecular crystals is generally found by chance empirically. In this study, we constructed a machine learning framework to screen molecules that will exhibit solid–solid phase transitions in their crystalline states, based on positive-unlabeled learning. We trained classification models using the positive dataset we constructed manually and the unlabeled data extracted from the Cambridge Structural Database. The best classifier works as a suggester, and 9 substances among the suggested 113 molecules were found to exhibit solid–solid phase transitions according to the literature and experiments. The finding probability of 8.0% is much higher than the probability of phase transition in the database, suggesting the effectiveness of molecular selection by this workflow. We also found that the molecular structure is weakly related to the transition temperature by regression analysis. The findings of this study are useful for designing functional molecular crystals with solid–solid phase transitions.
Introduction
The functionalities of molecular crystals can change in the solid–solid phase transition, defined as the reversal point of the minimum Gibbs free energy between at least two solid states.1 A solid–solid phase transition sometimes causes a significant and dynamic change2 in a property. For example, birefringence can change in a solid–solid phase transition due to the accompanying change in the electronic states of the crystal.3 As another example, macroscopic actuation occurs during the solid–solid phase transition upon temperature change.4–6 Solid–solid phase transitions of molecular crystals are caused not only by changes in temperature but also by other stimuli, such as pressure, light, force, vapor, grinding, and voltage, leading to the change or expression of various functions.7–10Despite the importance of solid–solid phase transitions, predicting their occurrence before actual experiments is currently difficult. Even though computational methods for crystal structure prediction have progressed,11 phase diagram investigations and predictions of solid–solid phase transitions based on molecular dynamics simulation have been limited to explaining known phase transitions of some specific substances.12–14 This is because it is computationally costly to accurately calculate the Gibbs free energy of (assumed) solid states. Therefore, theoretical calculations cannot uncover the occurrence of solid–solid phase transitions in molecular crystals before actual experiments; they are found by chance after many trial-and-error experiments.
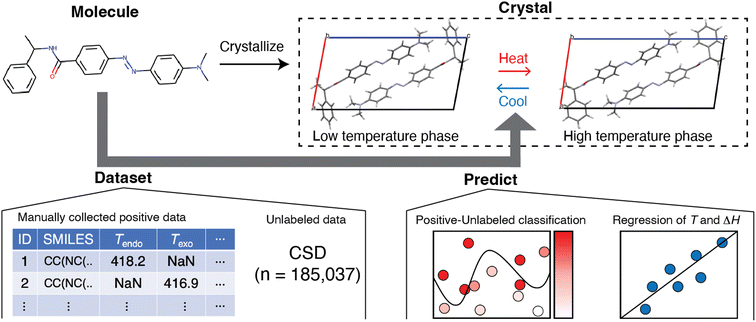
An inductive approach may solve this situation. The method in question, known as materials informatics, has been mainly applied to inorganic and polymeric materials15,16 and, recently, to molecular crystals as the next target.17,18 This motivated us to apply it to the search for a hidden trend of solid–solid phase transitions in molecular crystals (Fig. 1). We reduced the problem to using molecular structures without considering their crystal structures. Although this simplification introduces the limitation that we cannot incorporate the effect of intermolecular interactions, it has advantages for designing new molecules if we discover a relationship between a solid–solid phase transition and molecular structure.
In this work, we screened for the possibility of solid–solid phase transition using positive-unlabeled (PU) learning with molecular descriptors and found substances that exhibited solid–solid phase transitions in their crystalline states (Fig. 1). We accomplished this by constructing a positive dataset of thermally induced solid–solid phase transitions of molecular crystals, manually curated from published studies. The reason we focused on the thermally induced solid–solid transition was the number of available reports and the practical applications. Classification models were trained and then compared, and the best classifier suggested molecules that potentially exhibit solid–solid phase transitions. Among them, we found solid–solid phase transitions by literature search and our experiments. We also performed regression analysis and found that transition temperature was weakly related to molecular structure. These findings should be useful in designing molecular crystals that exhibit solid–solid phase transitions.
Materials and methods
Dataset preparation
The information on the phase transition of molecular crystals was collected based on the criteria that the phase transition has been confirmed by thermal analysis of differential scanning calorimetry (DSC) and/or X-ray crystallography. Here, the phase transition includes reversible and irreversible crystal-to-crystal phase transitions, and we did not care whether it was in a single-crystal-to-single-crystal manner. We did not focus on cryogenic temperatures and collected data at a temperature above 120 K under atmospheric pressure. We also added the condition that permitted atoms are H, B, C, N, O, F, Si, P, S, Cl, Br, and I atom species. A total of 297 datasetswere extracted from 91 papers, and the number of unique molecules was 88. The molecular structure corresponding to each dataset was downloaded from the Cambridge Crystal Database Centre (CCDC) in simplified molecular input line entry system (SMILES) format. The numeric information on phase transition, temperatures (Tendo and Texo), and enthalpies (ΔHendo and ΔHexo) at the endothermic and exothermic phase transitions, was also collected. When they were written as a specific value in the papers, the values were extracted. Instead, when they were written as a range in the papers, the average values were calculated. When they were not written as a value but shown in a figure in the papers, we read the values from the figures. We also collected crystal structure information: CCDC numbers and phase names, for future analysis.For molecular crystals that were not confirmed to show phase transitions, we searched the data in the CSD using the following conditions: no report on phase transition, R-factor ≤ 0.05, only organic, 3D coordinates determined, no disorder, not polymeric, and not the results of the powder study. We also added the condition that permitted atoms are H, B, C, N, O, F, Si, P, S, Cl, Br, and I atom species. This search was coded using the CSD Python API (v.3.0.14). The search raised 199![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 987 datasetsfrom the CSD (v.5.42). Then, the duplicate of SMILES was deleted within the unlabeled dataset and between the positive dataset and the unlabeled dataset. Finally, we obtained unlabeled data of 185
987 datasetsfrom the CSD (v.5.42). Then, the duplicate of SMILES was deleted within the unlabeled dataset and between the positive dataset and the unlabeled dataset. Finally, we obtained unlabeled data of 185![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 037 unique SMILESs.
037 unique SMILESs.
Machine learning implementation
Molecular structures represented as SMILESs were converted into vectors. We examined seven descriptors: Mordred, Extended-Connectivity Fingerprint (ECFP), Avalon, ErG, RDKit, MACCSKeys, and Estate.19–24For the classification task, we implemented positive-unlabeled (PU) and binary (BC) classifications. In both cases, we used random forest (RF), support vector machine (SVM), neural network (NN), and gradient boosting decision tree (GBDT) as prediction models. PU learning was implemented by the weighted Elkanoto method.25 The positive and unlabeled datasets were used for both PU and BC tasks.
Classification models were evaluated based on the product of true positive rate (TPR) and selection effect (SE) on the average of 10-fold cross-validation (CV). The TPR is defined as the proportion of the number of predicted positives in positive data (npp) to the number of positive data (np):
We defined the SE as the multiplier of the number of unlabeled data (nu) to the number of predicted positives in unlabeled data (nup) for the selection purpose:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 037, respectively. The product of TPR and SE is represented as
037, respectively. The product of TPR and SE is represented asWhen np and nu are fixed, this product depends on npp and nup. The better the performance of the model, the higher the npp should be, and the more useful the model as a suggester, the lower the nup should be. The model with a higher value of the product is expected to perform molecular screening. The rate of predicted positives in the unlabeled dataset, i.e., the reciprocal of the SE, was not used because the higher metric value (max. 1) does not mean better screening. This is why we used the product of TPR and SE as the score function even though the range of the metric was large. Hyperparameters of the prediction models are summarized in Table S1.†
For regression, we used the NN, RF, and transfer learning NN (TL-NN) as prediction models. A 5-fold CV was performed five times because the number of positive datasetswas small, and the results were influenced by the data split. The mean absolute error (MAE) was calculated on the average of five 5-fold CVs. Hyperparameters of the prediction models are summarized in Table S1.† In the TL-NN, the scratch model was trained on a larger dataset of melting points (n = 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 404)26 through hyperparameter optimization, and then transferred to learn transition temperature and enthalpy. Fine-tuning was performed by increasing the number of trainable layers from the nearest to the output.
404)26 through hyperparameter optimization, and then transferred to learn transition temperature and enthalpy. Fine-tuning was performed by increasing the number of trainable layers from the nearest to the output.
All the above computations were conducted on a computer (OS: Windows 10, memory: 16 GB, GPU: NVIDIA GeForce GTX 1650). We used rdkit (2022.03.02) and mordred (1.2.0), pulearn (0.0.7), scikit-learn (0.24.2), tensorflow (2.9.1), optuna (2.10.1), and shap (0.41.0) for the implementation in Python.
Material preparation and characterization
The compound 1,4-bis(3,5-di-tert-butyl-2-hydroxybenzylideneaminomethyl)benzene (the crystal of OCAPAK27 in the Results section) was synthesized by mixing 3,5-di-tert-butylsalicaldehyde and p-xylylenediamine in a molar ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in 2-propanol and by heating for 1 h at 423 K using a microwave. Differential scanning calorimetry was performed using a DSC 8500 (PerkinElmer) in the temperature range of 223–523 K at a speed of 10 K min−1. Powder X-ray diffraction analysis was performed using a Rigaku Ultima III diffractometer, equipped with monochromatic Cu Kα irradiation (λ = 1.54187 Å) at 40 kV and 40 mA. The solid appearance was observed using an optical microscope equipped with a camera (WRAYCAM-NF300, Wraymer).
1 in 2-propanol and by heating for 1 h at 423 K using a microwave. Differential scanning calorimetry was performed using a DSC 8500 (PerkinElmer) in the temperature range of 223–523 K at a speed of 10 K min−1. Powder X-ray diffraction analysis was performed using a Rigaku Ultima III diffractometer, equipped with monochromatic Cu Kα irradiation (λ = 1.54187 Å) at 40 kV and 40 mA. The solid appearance was observed using an optical microscope equipped with a camera (WRAYCAM-NF300, Wraymer).
Results and discussion
In the collected dataset, the total number of solid–solid phase transitions was n = 297, and the unique SMILES was n = 88. The molecular structures were well diverse (Fig. S1†). The transition temperatures and enthalpies of the collected positive data are also summarized in Fig. S2.† The unlabeled data, meaning the solid–solid phase transition in the molecular crystal not recognized in CSD, were collected from the CSD by filtering several conditions (see the Method section). The CSD search resulted in 185![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 037 unique SMILESs as the unlabeled dataset.
037 unique SMILESs as the unlabeled dataset.
Positive and unlabeled datasets were used for positive-unlabeled (PU) and binary (BC) classifications. BC is a task commonly used for determining a discriminant boundary between positive and negative data. However, this problem setting should not be appropriate for the current case because we do not know all the true negatives of the solid–solid phase transition. We cannot obtain the thermal analysis results of all molecular crystals in CSD. In this case, PU classification is a more reasonable setting to find a discriminant boundary between positive and unlabeled data. We can determine the possibility of solid–solid phase transition in unlabeled data by using the PU setting to predict the synthesizability of materials.28,29
First, we compared TPRs between PU and BC tasks to rationalize the PU setting (Table S2†). All combinations solved as PU yielded a much higher TPR than BC. This result indicated that the PU task is more reasonable in this work and that the discriminant boundary in BC failed to predict true positives due to improper problem setting and imbalanced size of positive and unlabeled data.
Among the PU results, Avalon-SVM was recognized as the best classifier and suggester based on the highest value of the product of TPR and SE (Table 1). There were some reasons why other models were worse than Avalon-SVM. For example, ECFP-SVM with the second highest metrics had a lower TPR, meaning less model validity (Table S3†). Mordred-GBDT and RDKit-GBDT showed higher TPRs, but the products with SEs were much lower due to low SEs (Table S3†). A low SE means that the model predicted most unlabeled molecules to be positive. In such a case, it is difficult for us to select candidate molecules to be investigated next in detail, and the model should not work as a suggester. Therefore, the Avalon-SVM was used for molecular selection. Here, we did not interpret the model due to the interpretability difficulties of Avalon and used it for the screening purpose.
The suggester must find molecules likely to exhibit solid–solid phase transitions. The unlabeled data were input into the trained 10 models obtained by 10-fold CV, and the number of times they were predicted to be positive divided by 10 was used as the probability of the solid–solid phase transition. Therefore, probabilities are obtained discretely such as 0.1, and 0.2. Most of the unlabeled data were predicted to have p = 0.1, while 113 substances resulted in higher probabilities of p ≥ 0.2 (Table 2). Therefore, the 113 substances were checked in detail to see if any phase transitions were reported in the literature that were not recognized in the CSD.
| p | Number of substances |
|---|---|
| 1.0 | 1 |
| 0.9 | 0 |
| 0.8 | 0 |
| 0.7 | 0 |
| 0.6 | 0 |
| 0.5 | 1 |
| 0.4 | 1 |
| 0.3 | 11 |
| 0.2 | 99 |
| 0.1 | 184![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 924 924 |
| 0 | 0 |
Among 14 molecules with p ≥ 0.3, three substances were identified to be positive, and one substance may probably exhibit the solid–solid phase transition (Fig. 2).30–32 For example, the crystal of KUDDUK02 (CSD code) has been reported to transform from α into β irreversibly at 342.9 K upon heating.31 In addition, we experimentally prepared the crystal reported as OCAPAK27 and found the irreversible crystal-to-crystal phase transition upon 450 K (Fig. S3†). This phase transition has not been reported anywhere, and the novel solid phase transition was found owing to the molecular screening. Furthermore, although the solid phase transition of the crystal of AREDIN has not been described in the literature,30 the DSC curve of the compound displayed a small endothermic peak upon heating without weight loss before decomposition, suggesting a potential phase transition.
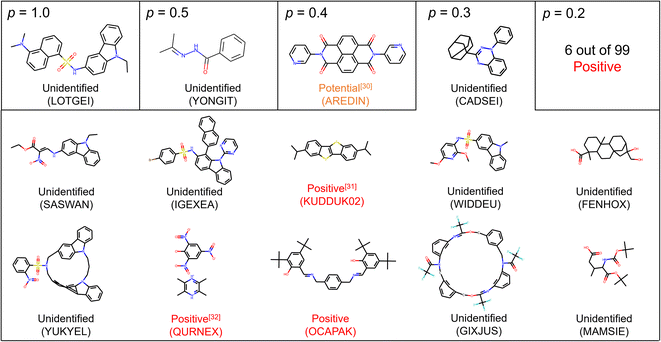 | ||
| Fig. 2 Suggested substances with p ≥ 0.2 by PU prediction. Unidentified means we did not find the DSC result of the crystal and we cannot conclude whether it is positive or negative. Positive means we confirmed the solid–solid phase transition of the crystal according to the literature and experiments. Potential means that the solid–solid phase transition was not reported in the literature, but the thermal profile of DSC showed peak-like behavior before reaching the melting point. CSD codes are also supplied to identify crystal data. Molecules with p = 0.2 are omitted due to the limitation of space and are supplied in the ESI.† | ||
For molecules with p = 0.2, we identified 6 substances as positive among 99 suggested molecules (Fig. S4†). We also identified 10 substances as being negative at least in the temperature range of DSC measurement. Determining whether positive or negative required the description and/or figure of DSC measurements. The reason why most substances are still unlabeled is that new crystal structures are often reported in papers focusing on organic synthesis. In such cases, the conduction of DSC measurement is rare, and a gap in the available amount of data between the crystal structure and thermal measurement is generated. This situation should also support the rationality of PU learning.
These above results showed that at least 3/14 (21.4%) compounds with p ≥ 0.3 and 9/113 (8.0%) compounds with p ≥ 0.2 were positive. These positive rates are higher than the positive rate used in model training (88/(185![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 037 + 88) = 0.05%). Moreover, the CSD contained 532 unique molecules assigned with the word “phase transition”, and the occurrence of phase transition in the CSD is 0.29% (=532/(185
037 + 88) = 0.05%). Moreover, the CSD contained 532 unique molecules assigned with the word “phase transition”, and the occurrence of phase transition in the CSD is 0.29% (=532/(185![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 037 + 532)), which is much lower than the occurrence from suggested substances. This insists that potential solid phase transitions are hidden even in known crystals, and the machine learning model constructed by PU learning provides us guidance for molecular selection.
037 + 532)), which is much lower than the occurrence from suggested substances. This insists that potential solid phase transitions are hidden even in known crystals, and the machine learning model constructed by PU learning provides us guidance for molecular selection.
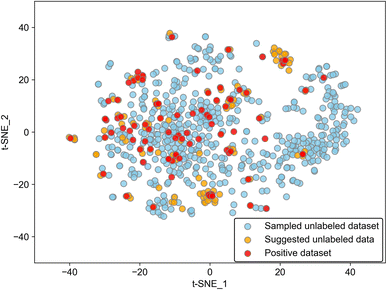
While the model worked well as a suggester as mentioned above, there is a limitation to the adaptability of the model. Because the discriminant boundary in PU learning is affected strongly by the positive data, the suggested substances among the unlabeled molecules should have similar features to positive ones. Data points of suggested molecules with p ≥ 0.2 are located near those of positive data as evidenced by the 2D visualization of the Avalon descriptor using t-distributed stochastic neighbor embedding (t-SNE), which is a typical method of manifold (Fig. 3). This result insists that the suggestion is limited to the known positive data. We calculated average distances between known positives and predicted positives and between known positives and the unlabeled data. The former was 1.68, and the latter was 4.71 in the embedding space, showing quantitatively that predicted positives are closer to known positives than other unlabeled data. From a different perspective, the addition of positive data will broaden the variety of suggested molecules. There is also a limitation in that the difference between polymorphs cannot be distinguished because molecular descriptors of the same molecule are encoded into the same vector. The incorporation of crystal structure information will improve model accuracy, and this kind of model extension should be tackled in the future.
Next, we performed the regression of transition temperature and enthalpy. The motivation was to determine whether transition temperature and enthalpy are related to the molecular structure. If this regression captures some hidden relationship, we can interpret which molecular substructure influences transition temperature and enthalpy and design molecules potentially expressing the solid–solid phase transition at an expected temperature. The positive dataset we manually collected made this analysis possible. In regression, target properties were endothermic and exothermic temperatures (Tendo and Texo) and the corresponding transition enthalpies (ΔHendo and ΔHexo). When multiple solid–solid phase transitions corresponded to a substance, the maximum and minimum values were used in independent regressions (denoted as, for example, Tendo(max) and Tendo(min)).
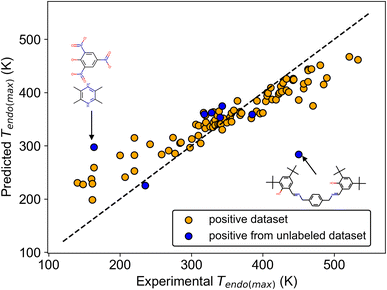
We show the regression results using the Mordred descriptor, which was better than other molecular descriptors in regression (Table S4†). For Tendo(max), the mean model resulted in a mean absolute error (MAE) = 75.4 (K), which is the criterion for no relationship between Tendo(max) and the molecular structure (Table 3). The NN and the transfer NN (TL-NN) models yielded worse metrics than the mean model (Table S4†), whereas RF outperformed the mean model (Table 3). The same trend, RF better than the mean model, was also observed for Tendo(min), Texo(max), and Texo(min) (Table S4†). These results suggested that Mordred-RF captured a hidden weak trend between transition temperature and molecular structure. The scatter plot of experimental and predicted values also supports this result because orange points are distributed almost along the reference line (Fig. 4). On the other hand, there was no clear trend for the regression of ΔHendo and ΔHexo (Tables 3 and S4†). Although enthalpy and entropy are directly related to transition temperature in thermodynamic physics, we did not obtain the relationship between transition enthalpy and molecular structure. This probably results from the relatively larger deviation of enthalpy and the smaller number (n ∼ 40) of datasets compared with that of the transition temperature (n ∼ 80).
| MAE | RF model | Mean model |
|---|---|---|
| T endo(max) (K) | 58.7 (8.1) | 75.4 |
| T exo(max) (K) | 66.2 (14.4) | 71.5 |
| ΔHendo(max) (kJ mol−1) | 5.3 (1.3) | 4.6 |
| ΔHexo(max) (kJ mol−1) | 3.6 (1.0) | 3.2 |
To further validate the regression results of the transition temperature, the generalization ability of the regression model was checked using positive data found in the unlabeled dataset. Among 9 substances found by molecular screening, 8 datasets were available for the inference of Tendo(max). A comparison of experimental and predicted values shows that 6 predicted values were well matched with the experimental values, although 2 predicted values resulted in larger errors (Fig. 4). Even though this inference afforded MAE = 57.1 (K), which is in good agreement with the regression result in Table 3, this validates that transition temperature is weakly related to the molecular structure.
To interpret which molecular substructure influences the transition temperature, we employed two different approaches for model interpretation. One is the feature importance obtained from the RF model, and important features can be identified by their magnitude in reducing the MAE. The other method is Shapley additive explanations (SHAP).33 This method calculates the SHAP value for each feature of each dataset, and the distribution of SHAP values for each feature affords which molecular feature has a positive or negative effect on the target variable.
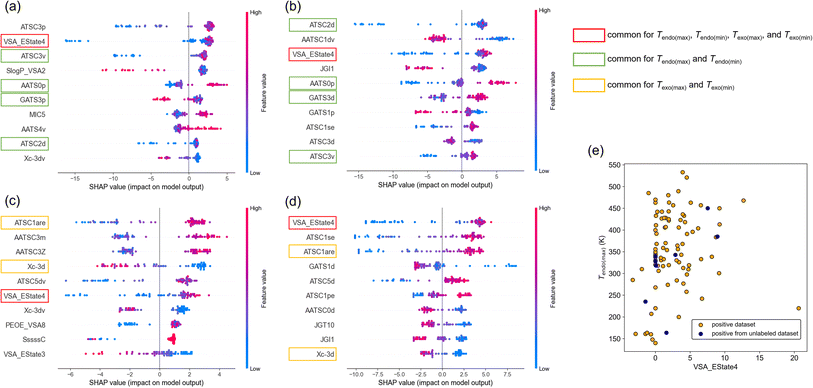
First, we show the distribution of SHAP values for Tendo(max), Tendo(min), Tendo(max), and Tendo(min) (Fig. 5a–d). Here, the top 10 features among 946 features after sorting by the averaged SHAP value are shown for each target variable. The commonly ranked feature was VSA_Estate4, which is defined as the sum of the electrotopological state values of atoms in the molecule with the van der Waals surface area between 5.41 and 5.74.24 In all cases, low feature values (shown as blue points) of VSA_EState4 tended to distribute in the negative region of SHAP values and high feature values (red points) tended to distribute in the positive region of SHAP values. This result suggests that higher VSA_EState4 tends to increase transition temperature. This interpretation can be rationalized by the scatter plot of VSA_EState4 and Tendo(max) (Fig. 5e). Although there is an outlier, a roughly positive correlation between VSA_EState4 and Tendo(max) was observed. The tendency is also applied to positive data found in the unlabeled dataset (Fig. 5e). VSA_EState4 was also ranked in the top 10 based on the feature importance of RF (Table S5†), and thus this feature should have the largest influence on the transition temperature.
There are 4 other features common for Tendo(max) and Tendo(min) and 2 features common for Texo(max) and Texo(min) based on SHAP values (Fig. 5a–d). Three out of 4 features common to Tendo(max) and Tendo(min) were also ranked in the top 10 based on the feature importance of RF (Table S5†). Thus, ATSC2d, AATS0p, and ATSC3v should affect the temperature of endothermic transition, and their effects should be positive based on SHAP values (Fig. 5a and b). In the same way, 2 features common to Texo(max) and Texo(min) raised by SHAP values were also ranked in the top 10 based on the feature importance of RF (Table S5†). ATSC1are and Xc-3d should affect the temperature of exothermic transition, and their effects should be positive and negative, respectively, based on SHAP values (Fig. 5c and d). Although intuitive chemical understanding is difficult for these important features, we can calculate each feature value of a molecule and obtain prior knowledge of whether the phase transition temperature is likely to be high or low.
Conclusions
In summary, we have successfully screened molecules for solid–solid phase transitions aided by PU learning and verified it by finding solid phase transitions of suggested substances. The positive rate of suggested substances was 8.0%, which is much higher than the rate used for model training and the rate in the database. This result validated the effectiveness of the current workflow, although there is a limitation in that the suggestions are around known positive data. We also found a hidden relationship between the molecular structure and transition temperature by regression. A feature, VSA_EState4, was raised as a commonly important feature for the temperatures of endothermic and exothermic transitions. The effect should be a positive relationship, and some other features were also found. Although this analysis neglected intermolecular interactions and 3-dimensional conformation, the obtained insight enables us to efficiently find molecules manifesting a solid–solid phase transition in the crystal. This work will aid in the design of functional molecular crystals for the future applications of organic optoelectronics and actuators.Data availability
(1) The code for executing the workflow of the paper can be found at https://github.com/takuyhaa/PUmolecules. The code was also archived to Zenodo with the following URL. https://doi.org/10.5281/zenodo.7710534.(2) Data and processing scripts for this paper are also available at GitHub and Zenodo at the above URLs.
(3) This study was carried out using a manually curated dataset and the Cambridge Structural Database v.5.42. The manually curated dataset has been uploaded as part of the ESI† and is also available at GitHub and Zenodo at the above URLs.
(4) The data analysis scripts of this paper are available in the interactive notebook, uploaded to GitHub and Zenodo at the above URLs.
Author contributions
D. T.: data curation, formal analysis, investigation, methodology, software, visualization, and writing – original draft; K. I.: data curation; T. A.: resources and supervision; T. T.: conceptualization, investigation, methodology, software, funding acquisition, project administration, supervision, writing – original draft, and writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was financially supported by JSPS Grant-in-Aid (19K23638, 20H04677, and 22K14747) and the Waseda University Grant for Special Research Projects (2019C-646, 2020C-530, 2021C-404, and 2022C-313). This work was also partly supported by the Cabinet Office, Government of Japan, Cross-ministerial Moonshot Agriculture, Forestry and Fisheries Research and Development Program “Technologies for Smart Bio-industry and Agriculture” (BRAIN).Notes and references
- J. Bernstein, Polymorphism in Molecular Crystals, Oxford University Press, 2007 Search PubMed.
- S. K. Park and Y. Diao, Chem. Soc. Rev., 2020, 49, 8287–8314 RSC.
- H. Chung, S. Chen, N. Sengar, D. W. Davies, G. Garbay, Y. H. Geerts, P. Clancy and Y. Diao, Chem. Mater., 2019, 31, 9115–9126 CrossRef CAS.
- T. Taniguchi, H. Sugiyama, H. Uekusa, M. Shiro, T. Asahi and H. Koshima, Nat. Commun., 2018, 9, 538 CrossRef PubMed.
- Y. Hagiwara, T. Taniguchi, T. Asahi and H. Koshima, J. Mater. Chem. C, 2020, 8, 4876–4884 RSC.
- S. C. Sahoo, M. K. Panda, N. K. Nath and P. Naumov, J. Am. Chem. Soc., 2013, 135, 12241–12251 CrossRef CAS PubMed.
- T. Taniguchi, H. Sato, Y. Hagiwara, T. Asahi and H. Koshima, Commun. Chem., 2019, 2, 1–10 CrossRef CAS.
- T. Taniguchi, K. Ishizaki, D. Takagi, K. Nishimura, H. Shigemune, M. Kuramochi, Y. C. Sasaki, H. Koshima and T. Asahi, Commun. Chem., 2022, 5, 1–10 CrossRef PubMed.
- S. Takamizawa and Y. Takasaki, Chem. Sci., 2016, 7, 1527–1534 RSC.
- M. Kato, H. Ito, M. Hasegawa and K. K. Ishii, Chemistry, 2019, 25, 5105–5112 CrossRef CAS PubMed.
- R. Nikhar and K. Szalewicz, Nat. Commun., 2022, 13, 3095 CrossRef CAS.
- C. Červinka and G. J. O. Beran, Chem. Sci., 2018, 9, 4622–4629 RSC.
- A. Mazurek, Ł. Szeleszczuk and D. M. Pisklak, Molecules, 2020, 25, 1584 CrossRef CAS PubMed.
- Y. A. Vaksler, A. Idrissi and S. V. Shishkina, New J. Chem., 2022, 46, 3856–3865 RSC.
- R. Ramprasad, R. Batra, G. Pilania, A. Mannodi-Kanakkithodi and C. Kim, npj Comput. Mater., 2017, 3, 1–13 CrossRef.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
- B. Olsthoorn, R. M. Geilhufe, S. S. Borysov and A. V. Balatsky, Adv. Quantum Technol., 2019, 2, 1900023 CrossRef.
- S. Wengert, G. Csányi, K. Reuter and J. T. Margraf, Chem. Sci., 2021, 12, 4536–4546 RSC.
- P. Gedeck, B. Rohde and C. Bartels, J. Chem. Inf. Model., 2006, 46, 1924–1936 CrossRef CAS PubMed.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS.
- N. Stiefl, I. A. Watson, K. Baumann and A. Zaliani, J. Chem. Inf. Model., 2006, 46, 208–220 CrossRef CAS PubMed.
- L. H. Hall and L. B. Kier, J. Chem. Inf. Comput. Sci., 1995, 35, 1039–1045 CrossRef CAS.
- J. L. Durant, B. A. Leland, D. R. Henry and J. G. Nourse, J. Chem. Inf. Comput. Sci., 2002, 42, 1273–1280 CrossRef CAS PubMed.
- H. Moriwaki, Y. S. Tian, N. Kawashita and T. Takagi, J. Cheminf., 2018, 10, 4 Search PubMed.
- C. Elkan and K. Noto, in KDD'08, Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Nevada, USA, ed., Y. Li, B. Liu and S. Sarawagi, Association for Computing Machinery, New York, 2008, pp. 213–220 Search PubMed.
- Enamine Ltd, http://www.enamine.net.
- D. M. Tooke, Y. Song, G. A. van Albada, J. Reedijk and A. L. Spek, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2004, 60, o1907–o1908 CrossRef CAS.
- J. Jang, G. H. Gu, J. Noh, J. Kim and Y. Jung, J. Am. Chem. Soc., 2020, 142, 18836–18843 CrossRef CAS PubMed.
- G. H. Gu, J. Jang, J. Noh, A. Walsh and Y. Jung, npj Comput. Mater., 2022, 8, 1–8 CrossRef.
- H. Zhu, P. Hao, Q. Shen, J. Shen, G. Li, G. Zhao, H. Xing and Y. Fu, CrystEngComm, 2021, 23, 3356–3363 RSC.
- H. Chung, S. Chen, B. Patel, G. Garbay, Y. H. Geerts and Y. Diao, Cryst. Growth Des., 2020, 20, 1646–1654 CrossRef CAS.
- A. Pawlukojć, J. Hetmańczyk, Ł. Hetmańczyk, J. Nowicka-Scheibe, J. K. Maurin, W. Schilf, D. Trzybiński and K. Woźniak, J. Mol. Struct., 2021, 1228, 129432 CrossRef.
- S. M. Lundberg and S. I. Lee, Advances in neural information processing systems, 2017, vol. 30 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the dataset, additional results of classification and regression, and experimental results. See DOI: https://doi.org/10.1039/d3dd00034f |
| This journal is © The Royal Society of Chemistry 2023 |