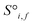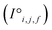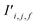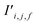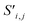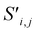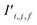Open Access Article
Open Access ArticleSite-Net: using global self-attention and real-space supercells to capture long-range interactions in crystal structures†
Michael
Moran
 ab,
Michael W.
Gaultois
ab,
Michael W.
Gaultois
 *ab,
Vladimir V.
Gusev
c and
Matthew J.
Rosseinsky
*ab,
Vladimir V.
Gusev
c and
Matthew J.
Rosseinsky
 ab
ab
aDepartment of Chemistry, University of Liverpool, Crown St, Liverpool, L69 7ZD, UK. E-mail: m.gaultois@liverpool.ac.uk
bLeverhulme Research Centre for Functional Materials Design, University of Liverpool, 51 Oxford Street, Liverpool, L7 3NY, UK
cDepartment of Computer Science, University of Liverpool, Ashton Street, Liverpool, L69 3BX, UK
First published on 1st August 2023
Abstract
Site-Net is a transformer architecture that models the periodic crystal structures of inorganic materials as a labelled point set of atoms and relies entirely on global self-attention and geometric information to guide learning. Site-Net processes standard crystallographic information files to generate a large real-space supercell, and the importance of interactions between all atomic sites is flexibly learned by the model for the prediction task presented. The attention mechanism is probed to reveal Site-Net can learn long-range interactions in crystal structures, and that specific attention heads become specialised to deal with primarily short- or long-range interactions. We perform a preliminary hyperparameter search and train Site-Net using a single graphics processing unit (GPU), and show Site-Net achieves state-of-the-art performance on a standard band gap regression task.
1 Introduction
The application of machine learning to materials science has enabled a new paradigm of high throughput property prediction for the screening and identification of new materials. Prediction pipelines based on machine learning models are significantly less computationally intensive than DFT and other physical simulations in much the same way that computational methods can be a faster and cheaper alternative to synthetic investigations.1,2 Consequently, the material discovery process can be significantly accelerated by initial screening and recommendation by machine learning models, which may lead to subsequent validation of promising candidates through physical modelling, and the final demonstration of discovery through preparation in the laboratory.3Machine learning models that rely only on the elemental composition have been widely successful and have been applied to a range of property prediction tasks.4,5 The elemental composition of materials is often the most well-characterised feature, and the fixed and limited number of elements mean that the compositions can be readily embedded as a fixed length vector that is amenable to most machine learning methods. However, many properties are strongly dependent on the crystal structure, and composition-based methods do not distinguish between materials with similar or identical compositions yet different crystal structures, such as polymorphs. A classic example is graphite and diamond, which both have a trivial elemental composition of pure carbon but have wildly different physical properties (e.g., band gap, electrical resistivity, thermal conductivity).6
The challenge of creating a suitable representation of the crystal structure prevents directly embedding crystal structures for use in property prediction tasks. Specifically, periodic crystal structures have an unbounded number of atoms, and the conventional methods used to describe periodic systems are challenging to represent appropriately for a machine learning algorithm. There is an infinite number of possible unit cells that can be chosen for a given crystal structure, and the varying number of atomic sites between the unit cells of different crystal structures makes it difficult to construct a representation using a fixed length vector. Further, any representation of the unit cell that uses a coordinate system must be invariant to rigid transformations, otherwise simple rotation and translation can lead to different predictions for different descriptions of the same crystal structure.7
Treating the crystal structure as a graph and using convolution neural networks has shown promising results for predicting properties,8–11 and such models now outperform composition-only models where sufficient structural data is available. However, these models rely on an explicitly defined cutoff distance or number of neighbours to define a meaningful interaction between atomic sites in the crystal structure. These graph learning methods were initially applied to molecules, which are of finite size.12 However, extended inorganic solids have many competing interactions at a range of length scales, and many functional properties arise from long-range features of the crystal structure.
In this report, we present Site-Net, a point-set model based on global self-attention augmented with pairwise interactions, where all atomic sites are free to interact with each other. Site-Net uses a physically motivated representation of the crystal structure as a point set of atomic sites, which is separated into “site features” containing chemical information (about elements), and “interaction features” containing geometric information (about positions). The set of atomic sites is directly ingested without any predefined connections, and the importance of interactions between all atomic sites is flexibly learned by the model through global self-attention. The attention mechanism is probed to reveal Site-Net learns long-range interactions, and that specific attention heads become specialised to deal with primarily short- or long-range interactions. This learning leads to state-of-the-art performance, which we assess using the band gap regression task from Matbench,13 where Site-Net achieves a mean absolute error of 0.234 eV on an 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 (train
20 (train![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) test) split of the dataset.
test) split of the dataset.
2 Methods
2.1 Representation construction and featurization
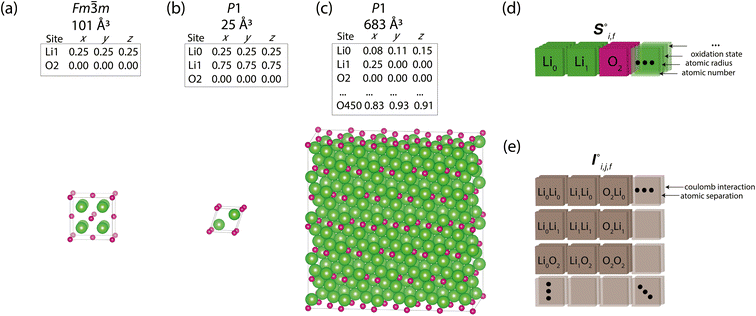
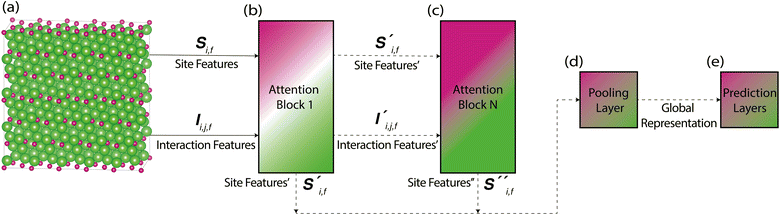
Periodic crystal structures have an infinite number of atoms and are thus commonly described in a more compact form by choosing an appropriate description that can be infinitely tiled in 3 dimensions (e.g., a unit cell). There are infinite possible choices of valid unit cells, and although there are several conventions for arriving at a unit cell useful to humans, defining a canonical unit cell for a given crystal structure that is robust to noise is a challenging problem.7 Unfortunately, the lack of a unique unit cell causes issues for training machine learning models, whereas model predictions for a given crystal structure should not be influenced by the arbitrary choice of unit cell. Notably, if the goal is to predict the properties of a crystal structure, two different choices of unit cell for the same crystal structure should lead to the same prediction. With Site-Net, we sidestep this problem by working with a large set of atoms without symmetry, and assume the set is large enough to capture most relevant features without suffering from finite size effects. Some models overcome the choice of unit cell by choosing a representation that is invariant to the unit cell, but this introduces additional hyperparameters, such as cutoff distances in some implementations of graphical neural networks.8,9Site-Net is able to ingest crystallographic information files (CIF) that are commonly used to represent crystal structures and generate an appropriate representation for training machine learning models (Fig. 1). Any conventional unit cell from a crystallographic database is transformed into a primitive unit cell in P1 (i.e., all symmetry constraints are removed, and the atoms are all listed explicitly). This minimal P1 unit cell is then iteratively tiled to generate a large set of atoms (Fig. 1c). While Site-Net avoids the need for a canonical choice of unit cell, there is nevertheless a soft requirement to provide each atomic site in the crystal the largest local environment possible. Accordingly, the aforementioned supercell is created to explicitly include longer range interactions with higher order images of the minimal P1 unit cell.
In this work, we show Site-Net performs well with a set of 500 atoms to work within the memory constraints of a single consumer graphics processing unit (GPU), though this is only a technical constraint, and the model performance should improve with increasing number of atoms and the consequently more rich structural context from considering longer range interactions. The set of atoms is generated by determining the optimal transformation of the minimal P1 unit cell to the largest possible supercell that is approximately cubic and contains less than 500 atoms. If exactly 500 atoms cannot be achieved, the supercell with the closest value to but not greater than 500 is used. The creation of appropriate supercells that are roughly cubic remains an open challenge,14 and most methods seek to optimise for a given volume, rather than number of atoms. As this work seeks to optimise for a given number of atoms, we perform supercell construction using an algorithm developed here for this task (Section S1†).
The resulting set of ∼500 atoms, roughly cubic in shape, is featurised into two distinct tensors that separately encode elemental information and spatial information. The elemental information is encoded as a vector of atomic site features (Fig. 1d), consisting of the identities of elements in the crystal structure, along with related properties of these elements. These elemental properties (e.g., atomic radius) can be manually defined, though we also include a learned embedding unique to each element, similar in concept to word embeddings with word2vec,15 where the tokens are chemical elements. For every chemical element, Site-Net stores a unique vector that is updated during model training; the length of the elemental vectors is a hyperparameter of the model (Table 1). In the present implementation of Site-Net, the raw site features are represented by a tensor of dimension [≤500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 101], comprising the number of sites (≤500), and the elemental features associated with each of the sites (101 for all models presented in this report). The spatial information is encoded in the interaction features using a full pairwise interaction matrix between these sites (Fig. 1e). The core of the interaction features is the full real-space Euclidean distance matrix of all atoms (respecting periodic boundary conditions), which ensures the spatial relationships of all atoms in the crystal structure are encoded.16,17
101], comprising the number of sites (≤500), and the elemental features associated with each of the sites (101 for all models presented in this report). The spatial information is encoded in the interaction features using a full pairwise interaction matrix between these sites (Fig. 1e). The core of the interaction features is the full real-space Euclidean distance matrix of all atoms (respecting periodic boundary conditions), which ensures the spatial relationships of all atoms in the crystal structure are encoded.16,17
| Hyperparameter | Value used | Range searched |
|---|---|---|
| Site features (from Pymatgen21 & Matminer22) | 101: Atomic number, atomic weight, row, column, first ionisation energy, electronegativity, atomic radius, density, oxidation state, learned embedding (92) | Fixed |
| Length of learned embedding | 92 | 1 to 128 dimensions |
| Site features length per attention head | 30 | 4 to 32 per attention head |
| Interaction features (from pymatgen21) | 2: Distance matrix, log(coulomb matrix) | Fixed |
| Interaction features length per attention head | 12 | 4 to 32 per attention head |
| Attention blocks | 2 | 1 to 3 blocks |
| Attention heads | 3 | 1 to 8 heads |
| Attention weights network (gW) [depth, width] | [1, 225] | 0 to 3 layers, 32 to 256 neurons per layer |
| Pre-pooling network [depth, width] | [1, 94] | 1 to 4 layers, 32 to 256 neurons per layer |
| Post-pooling network [depth, width] | [3, 200] | 1 to 4 layers, 32 to 256 neurons per layer |
| Activation function | Mish23 | Fixed |
| Optimizer | Adamw | Fixed |
| Learning rate | 8.12 × 10−4 | 5 × 10−5 to 10−2 |
| Normalization method | Layernorm24 | Batchnorm,25 layernorm,24 none |
| Global pooling function | Mean | Mean, max, self-attention |
| Batch size (unique sites) | 1200 unique sites | Fixed |
2.2 Self-attention as a mechanism to create context-enriched site features
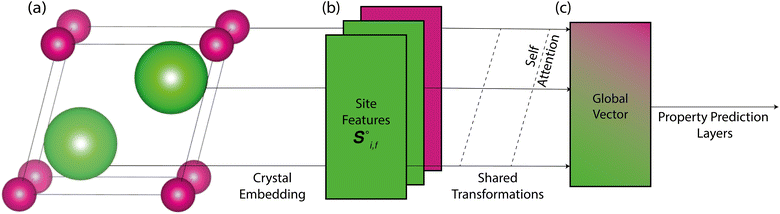
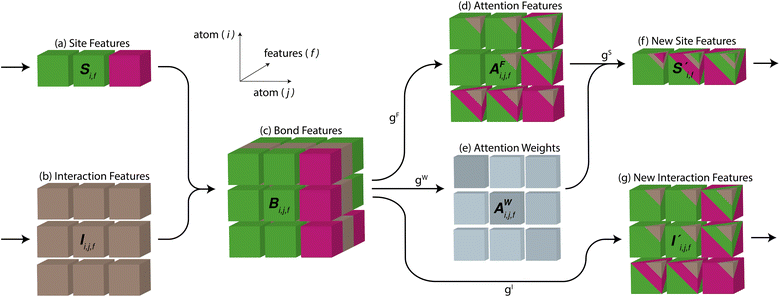
Site-Net is a set transformer18 architecture that takes a crystal structure, constructs a point set from the atomic sites in the unit cell, and processes the point set into a fixed length global feature vector representing the entire crystal structure, which is suitable for downstream property prediction (Fig. 2). Rather than encoding spatial information through a coordinate system (e.g., PointNet19), a matrix of pairwise interactions is incorporated into the custom attention mechanism to iteratively encode the spatial information into the point-set. Once a fixed length global vector has been attained, property prediction is performed through the application of standard dense neural network layers. However, the compression into a fixed length global feature vector necessary for property prediction is performed using permutation-invariant aggregation (here we use mean pooling), which leads to significant information loss. For example, taking the mean over the initial site features would destroy most relevant crystallographic information. Accordingly, Site-Net passes the initial site features through multiple attention layers to enrich the atomic site features with the context of their local chemical and structural environment (Fig. 3). These context-enriched site features retain enough structural information following aggregation to allow useful property predictions.Before being passed to an attention block, the raw site features 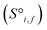 and raw interaction features
and raw interaction features 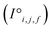 are reprocessed to an auxiliary embedding. Here, i and j are atomic site identities, and f is the factorisation dimension. The auxiliary embedding is likely to depend on the prediction task, so the lengths of the factorisation dimensions are tunable hyperparameters to allow the Site-Net model flexibility to find an optimal representation or dimensionality for a given task. This is accomplished by a single neural network layer preceding the first attention block, which ingests the raw site features
are reprocessed to an auxiliary embedding. Here, i and j are atomic site identities, and f is the factorisation dimension. The auxiliary embedding is likely to depend on the prediction task, so the lengths of the factorisation dimensions are tunable hyperparameters to allow the Site-Net model flexibility to find an optimal representation or dimensionality for a given task. This is accomplished by a single neural network layer preceding the first attention block, which ingests the raw site features 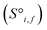 and interaction features
and interaction features 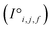 and generates processed analogues of the correct dimensionality. Specifically, the raw site feature tensor
and generates processed analogues of the correct dimensionality. Specifically, the raw site feature tensor 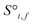 [≤500, 101] is transformed to Si,f [ ≤500, λ], and the raw interaction features tensor
[≤500, 101] is transformed to Si,f [ ≤500, λ], and the raw interaction features tensor 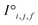 [≤500, ≤500, 2] is transformed to Ii,j,f [ ≤500, ≤500, μ]. These dimensions are consistent across the attention blocks for both input and output. In the final model presented here, the hyperparameters found after a preliminary search are λ = 90 and μ = 48 (Table 1).
[≤500, ≤500, 2] is transformed to Ii,j,f [ ≤500, ≤500, μ]. These dimensions are consistent across the attention blocks for both input and output. In the final model presented here, the hyperparameters found after a preliminary search are λ = 90 and μ = 48 (Table 1).
Starting from the raw site features in a crystal structure, site features enriched with the context of their local environment are constructed using a sequence of self-attention blocks, where the site features are iteratively replaced with a weighted aggregation of the pairwise interactions with all other atomic sites in the crystal structure representation (Fig. 4). This process replaces the purely elemental features of atomic sites with the aggregation of their local environment, and thus encodes information about the crystal structure into the context-enriched site features. This aggregation function does not depend on the ordering of atomic sites, and is thus permutation-invariant in the same way the global feature vector is produced from the site features. At a conceptual level, self-attention is a learned permutation-invariant function that prioritises the most important interactions when constructing the new enriched site features.
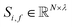 | (1) |
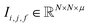 | (2) |
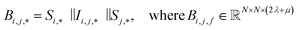 | (3) |
To begin, the site features Si,f (eqn (1)) and interaction features Ii,j,f (eqn (2)) for each pair of atoms are concatenated to create bond features Bi,j,f (eqn (3)). The bond feature vector Bi,j,* captures interactions between atomic sites i and j, and is an ordered combination of a site vector Si,*, followed by the interaction vector Ii,j,*, and then Sj,*. Here, an asterisk (*) denotes the span of an index. Importantly, because the order of the atom pairs is preserved, these bond features are directional (Bi,j,* ≠ Bj,i,*). Assembling all the bond feature vectors into the complete bond features tensor Bi,j,f leads to a unified representation of the crystal structure (Fig. 4c). This is carried forward and subsequently used to derive new context-enriched site features 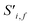 and new context-enriched interaction features
and new context-enriched interaction features 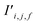 (Fig. 4).
(Fig. 4).
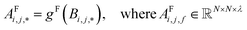 | (4) |
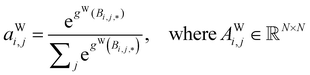 | (5) |
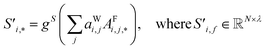 | (6) |
Global self-attention is used to generate new context-enriched site features 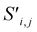 . In this implementation, we introduce intermediate attention features AFi,i,f (Fig. 4d and eqn (4)), and attention weights aWi,i (Fig. 4e and eqn (5)). The vectors
. In this implementation, we introduce intermediate attention features AFi,i,f (Fig. 4d and eqn (4)), and attention weights aWi,i (Fig. 4e and eqn (5)). The vectors 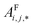 have the same dimension as site feature vectors and are obtained from bond vectors Bi,j,* by means of a fully connected neural network
have the same dimension as site feature vectors and are obtained from bond vectors Bi,j,* by means of a fully connected neural network 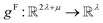 . The relative importance of site j to i based on their interaction is captured by the scalar attention weights aWi,j (Fig. 4e and eqn (5)), which are computed using another fully connected neural network
. The relative importance of site j to i based on their interaction is captured by the scalar attention weights aWi,j (Fig. 4e and eqn (5)), which are computed using another fully connected neural network 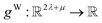 . The number of layers and the number of neurons per layer for gW are hyperparameters of the model. The resulting scalar values gW(Bi,j,*) are normalised using the softmax function (eqn (5)). For every atomic site i, this softmax normalisation ensures that the weights aWi,j over all atomic sites j sum to 1. As a consequence of the softmax normalisation to generate attention weights aWi,j, the resulting distribution of weights is conceptually similar to a probability distribution over all neighbours, where the attention weights aWi,j represent the significance of neighbour j to i. Critically, the exponential nature of the softmax normalisation is likely important to discard many of the negligible contributions that will be present when considering all pairwise interactions in Site-Net.
. The number of layers and the number of neurons per layer for gW are hyperparameters of the model. The resulting scalar values gW(Bi,j,*) are normalised using the softmax function (eqn (5)). For every atomic site i, this softmax normalisation ensures that the weights aWi,j over all atomic sites j sum to 1. As a consequence of the softmax normalisation to generate attention weights aWi,j, the resulting distribution of weights is conceptually similar to a probability distribution over all neighbours, where the attention weights aWi,j represent the significance of neighbour j to i. Critically, the exponential nature of the softmax normalisation is likely important to discard many of the negligible contributions that will be present when considering all pairwise interactions in Site-Net.
Finally, the new context-enriched site feature vector 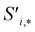 (eqn (6)) is a sum of vectors
(eqn (6)) is a sum of vectors 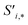 weighted by scalars aWi,j, followed by simple transformation by gS into a new basis. In simple terms, each atomic site has a vector representing its chemical and geometric configuration, which is subsequently replaced by the mean of all vectors for every neighbour and itself. This mean is modified by the relative importance of every site. As a consequence, the new site features are no longer a descriptor of a single site. Rather, they are representations of every local environment in the crystal structure. With repeated attention blocks, the representation of each individual site feature becomes more abstract.
weighted by scalars aWi,j, followed by simple transformation by gS into a new basis. In simple terms, each atomic site has a vector representing its chemical and geometric configuration, which is subsequently replaced by the mean of all vectors for every neighbour and itself. This mean is modified by the relative importance of every site. As a consequence, the new site features are no longer a descriptor of a single site. Rather, they are representations of every local environment in the crystal structure. With repeated attention blocks, the representation of each individual site feature becomes more abstract.
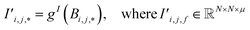 | (7) |
The bond features are also used to produce new interaction features 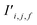 (eqn (7)). In comparison to the bond features, obtaining new interaction features is straightforward. The new interaction features and the bond features are of the same dimension, so new interaction features
(eqn (7)). In comparison to the bond features, obtaining new interaction features is straightforward. The new interaction features and the bond features are of the same dimension, so new interaction features 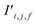 are obtained by passing the bond features through a single feed forward layer (gI) so they are of the expected dimensionality (eqn (7)). These new interaction features contain the information of the two sites connected by that interaction and serve a similar role to residual connections, as they preserve this information for subsequent attention blocks.
are obtained by passing the bond features through a single feed forward layer (gI) so they are of the expected dimensionality (eqn (7)). These new interaction features contain the information of the two sites connected by that interaction and serve a similar role to residual connections, as they preserve this information for subsequent attention blocks.
With respect to the overall architecture, we have described the process of performing single-headed attention. This process can be generalised to multi-headed attention, where multiple sets of attention feature and attention weight tensors are independently computed inside the same attention block and then concatenated. The use of more attention heads allows more attention operations to be performed in parallel, where each head can focus on a specific group of interactions. Similarly, the number of attention blocks can be increased to achieve more abstract features, as attention is performed on the outputs of the last attention block. The preliminary hyperparameter search performed on the band gap prediction task revealed that 2 attention blocks and 3 attention heads is a reasonable balance able to achieve state-of-the-art performance (Table 1).
2.3 Post-attention processing and pooling
The new site features and interaction features generated by the attention block are fed into the next attention block to repeat this process of contextual enrichment through the construction of higher-level features. After passing through all attention blocks, the separate site feature outputs from each and every attention block are concatenated together in preparation for pooling to a fixed length global feature vector by taking the mean of all sites. Further, a final pre-pooling step is performed to minimise the information loss of the subsequent pooling. Here, a simple neural network whose size is a hyperparameter of the model is used to process the concatenated site features from the attention blocks to an auxiliary embedding for pooling, much in the same way that a single neural network layer was used to reprocess the raw site features and interaction features to an auxiliary embedding for performing attention. After taking the mean of all sites to produce the fixed length global feature vector, obtaining a property prediction is a straightforward process with a sequence of feed forward neural network layers. An explicit process flow diagram for the entire architecture can be found in the ESI (Fig. S6).†2.4 Implementation
To generate the representations of the crystals, CIF files are first converted into Pymatgen structure objects.21 From these Pymatgen structure objects, the crystal structure can be featurised using featurization libraries such as matminer22 and describe.26 The models were developed using pytorch27 combined with the use of the pytorch lightning framework28 to provide automatic GPU training and data management.Hyperparameter tuning was handled via hyperopt29 using the Ray Tune20 distributed hyperparameter tuning framework as a front end. The hyperparameters that performed best on the validation set when trained on the training dataset are benchmarked on the holdout dataset. The hyperparameter search was performed on the Barkla compute cluster using a single Tesla P100 GPU with 16 GB of VRAM; the batch size was limited by the available VRAM. A preliminary hyperparameter search was performed by sequentially training 30 models for 24 hours each, using previous models to inform future hyperparameter choices. The best set of hyperparameters was then carried forward for longer training of the final models presented here (Table 1). The model is sensitive to the choice of hyperparameters, and based on the limited search performed here, these hyperparameters are likely far from optimal and will allow considerable model improvement in the future.
3 Results and discussion
The performance of Site-Net was primarily assessed using the band gap regression task from Matbench, a materials benchmarking test suite.13 The first fold of the preset cross validation pipeline was used for this benchmarking, and consists of 106![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 113 crystal structures and associated band gap energies. The training set was 80% of the available data and the test set was 20%. Within the training data, 80% was used for training, while 20% of the training data was used for a validation score for hyperparameter optimisation. As training was done using a single GPU, it was computationally unfeasible to run a separate hyperparameter search over all five Matbench data folds. Further, using a single hyperparameter set on all five folds would be unsuitable owing to data leakage, as training data from the first fold—on which hyperparameters are determined—is cycled into test data of the other 4 folds.
113 crystal structures and associated band gap energies. The training set was 80% of the available data and the test set was 20%. Within the training data, 80% was used for training, while 20% of the training data was used for a validation score for hyperparameter optimisation. As training was done using a single GPU, it was computationally unfeasible to run a separate hyperparameter search over all five Matbench data folds. Further, using a single hyperparameter set on all five folds would be unsuitable owing to data leakage, as training data from the first fold—on which hyperparameters are determined—is cycled into test data of the other 4 folds.
The Matbench band gap dataset poses unique challenges as it contains a smooth continuum of positive band gap energies together with a large number of zeros. We employ a custom activation function to address this unique property of the dataset, wherein negative predictions of band gap were clamped to zero while preserving the gradient to allow the model to recover from false zero predictions. Given negative band gaps are non-physical, we thus treat negative predictions as a level of confidence in the classification of zero rather than an “overshoot” that needs to be corrected.
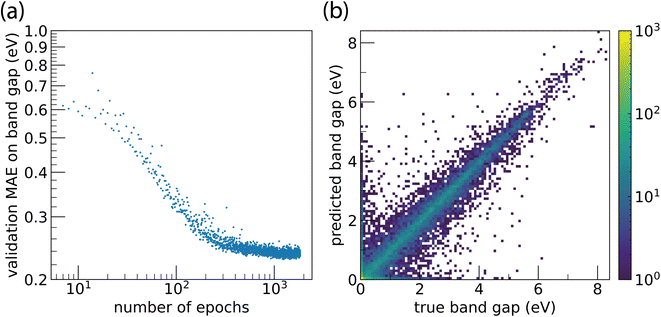
Training Site-Net on the band gap regression task leads to a smooth, monotonic learning curve that steadily converges to a plateau; models did not exhibit divergent overtraining behaviour (Fig. 5a). Despite its complexity, the Site-Net model trains to a stable state and does not suffer from problems typically encountered with continued training, where the validation score begins to diverge. Site-Net achieves a mean absolute error (MAE) of 0.234 eV on the band gap regression task, and performance of the model is consistent across band gap values (Fig. 5b). Even with only a preliminary hyperparameter search, Site-Net currently demonstrates competitive performance with the highest performing algorithms on the leaderboard. For example, CGCNN8 has a reported MAE of 0.297 eV as of this report, and ALIGNN,10 which considers the angles between atomic pairs in addition to pairwise interactions, is the highest performing algorithm with a reported MAE of 0.186 eV.
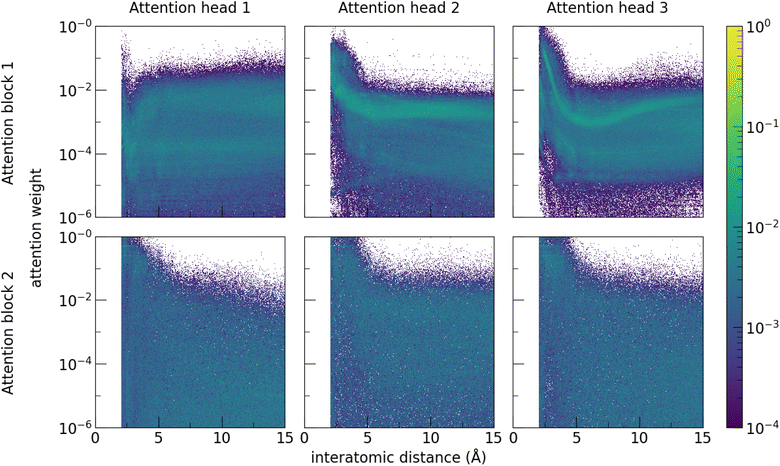
Examining the attention weights of the trained band gap model for all pairs of atomic sites in the test dataset allows interrogation of the model to investigate the importance of pairwise atomic interactions at different distances (Fig. 6). Attention heads of the first attention block generally focus on atomic sites that are close together (<5 Å), which is consistent with local interactions being important to material properties. The first attention head within the first block notably contains more long-range interactions, suggesting that model training specialised the attention head for this purpose while other heads were more focused on the local environment. Enforcing a cutoff limit of 5 Å on the range of the attention and retraining the model decreases performance (MAE 0.273 eV), confirming that interactions beyond this distance meaningfully contribute to model predictions. Decreasing the number of atoms in the supercell and retraining the model also degrades model performance (Table 2).
| Atoms in supercell (N) | Test MAE (eV) |
|---|---|
| 50 | 0.294(3) |
| 100 | 0.246(3) |
| 500 | 0.234(3) |
| 500 (5 Å attention) | 0.273(5) |
Meanwhile, the attention weights of the second attention block are less dependent on distance. This is consistent with focusing on higher-order correlations, as features entering the second attention head are more context-enriched after passing through the first attention block. Notably, the model learns that the majority of significant interactions are at short range but is able to nevertheless capture significant interactions at longer distances, without having to define beforehand what constitutes a meaningful interaction. This is consistent with the decrease in performance seen when a cutoff distance is enforced. Enforcing a 5 Å distance cutoff limit to the attention in Site-Net decreases model performance to levels to graph-based models with the same cutoff (MAE 0.273 eV).
Several different Site-Net models were trained to determine the influence of the quantity of training information on model performance (measured using MAE on the test data). This was probed by varying the number of crystal structures (training data points) and the size of the supercell used (Table 3). Crystal structures where the minimal P1 unit cell has more atoms than the chosen supercell size limit were not used in training, but were still included during testing and performance evaluation. Consequently, the model is penalised if it cannot learn about larger structures when training on smaller unit cells.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 890) in the training data. When less training data are used, the size of the supercell does not significantly affect model performance (test MAE, in eV), whereas using more training data (e.g., ∼105) leads to improved performance with larger supercells. Errors on the test scores were estimated by taking the standard deviation of the validation score during the last 100 epochs of training (after the model had converged)
890) in the training data. When less training data are used, the size of the supercell does not significantly affect model performance (test MAE, in eV), whereas using more training data (e.g., ∼105) leads to improved performance with larger supercells. Errors on the test scores were estimated by taking the standard deviation of the validation score during the last 100 epochs of training (after the model had converged)
| Supercell (N) | Data points | ||
|---|---|---|---|
| Test MAE (eV) | |||
| 103 | 104 | ∼105 | |
| 50 | 0.75(5) | 0.47(3) | 0.294(3) |
| 100 | 0.78(5) | 0.49(3) | 0.246(3) |
| 500 | 0.74(5) | 0.47(3) | 0.234(3) |
Models were trained with 103, 104 and ∼105 (84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 890) crystal structures in the training data, and with supercells of 50, 100, and 500 atoms (as well as 500 atoms with a 5 Å attention cutoff). Model performance varies strongly with the number of crystal structures used. When fewer training data are used, the size of the supercell does not significantly affect model performance. Using more training data (e.g., ∼105) leads to improved performance with larger supercells, which suggests the model is in a data-limited regime even with 104 data points. This is expected, as deep learning models are recognised to benefit from large datasets. Importantly, overtraining was not observed when using fewer training data, suggesting there is no disadvantage to using larger representations employed in Site-Net. This is true even with larger supercells, so there is no disadvantage to using large supercells, even with smaller datasets.
890) crystal structures in the training data, and with supercells of 50, 100, and 500 atoms (as well as 500 atoms with a 5 Å attention cutoff). Model performance varies strongly with the number of crystal structures used. When fewer training data are used, the size of the supercell does not significantly affect model performance. Using more training data (e.g., ∼105) leads to improved performance with larger supercells, which suggests the model is in a data-limited regime even with 104 data points. This is expected, as deep learning models are recognised to benefit from large datasets. Importantly, overtraining was not observed when using fewer training data, suggesting there is no disadvantage to using larger representations employed in Site-Net. This is true even with larger supercells, so there is no disadvantage to using large supercells, even with smaller datasets.
While Site-Net demonstrates excellent performance on the band gap prediction task, not all tasks are expected to benefit from identical model features. Accordingly, most model features of Site-Net used in this report were deliberately chosen to be tunable hyperparameters that can be learned (e.g., the learned elemental embedding), but some initial site features and interaction features were defined manually and may not be optimal. For example, construction of models without the Coulomb matrix in the interaction features resulted in marginal decrease in model performance on the band gap regression task, while models trained without the real-distance matrix led to reasonable training but poor test set performance.
To measure the relative importance of long-range interactions in a Site-Net model prediction for a particular crystal structure, we introduce a simple scalar metric referred to as the long-range coefficient. First, for every attention head we compute the maximum of the products between every attention weight (aWi,j) and the corresponding interatomic distances (di,j). This computed maximum value across all products for a given crystal structure captures the long-range affinity of a particular attention head. Second, in order to get an overall influence of the long-range interactions, the maximum value for each attention head is summed over the N = 3 attention heads in the second attention block. The second attention block is chosen as it contains context-enriched local environments rather than purely elemental features. The long-range coefficient is formally written as follows, where ⊙ denotes the Hadamard matrix product:
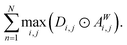 | (8) |
Observe that the long-range coefficient is large when there are long interatomic distances within a crystal structure that correspond to large attention weights in the attention heads. In short, when the long-range coefficient is large, Site-Net assigns more importance to longer-range interactions to make a prediction. Consequently, the long-range coefficient can be used to investigate the importance of long-range interactions, which are expected to depend on the chemistry of the system (e.g. the crystal structure) and the prediction task.
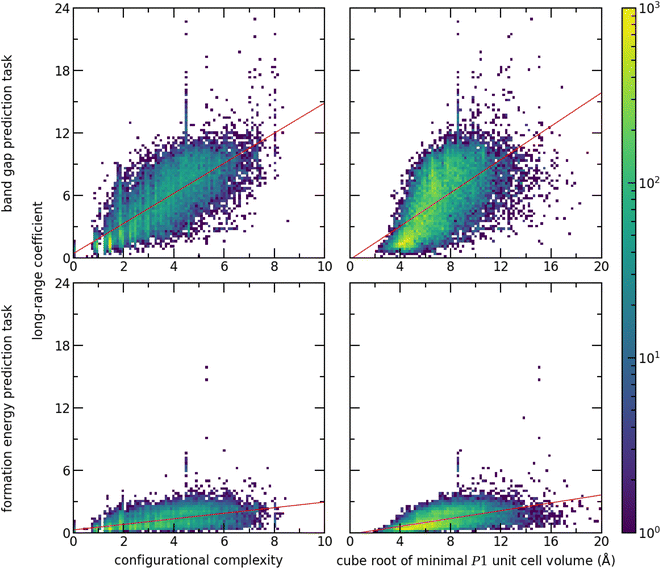
To evaluate the impact of the chemistry on the importance of long-range interactions, we use the long-range coefficient to investigate the crystal structures in the test dataset based on two proxies for unit cell complexity. These are the configurational complexity30 as computed by CrystIT,31 and the cube root of the minimal P1 unit cell volume (Fig. 7). To evaluate the influence of the prediction task on the importance of long-range interactions, we perform a second prediction task: formation energy, taken from the Matbench dataset.13 We trained and tested a Site-Net model with an identical architecture to the band gap model. Despite the lack of hyperparameter optimisation, the formation energy model nevertheless demonstrates competitive performance with the leader board, attaining a test MAE of 0.034 eV and highlighting the flexibility of the Site-Net architecture. (For comparison, as of this report, CGCNN has a reported MAE of 0.033 eV on the same task8).
The importance of long-range interactions in Site-Net is probed by examining the long-range coefficient for all crystal structures using both measures of crystal structure complexity and prediction tasks (Fig. 7). Increasing structural complexity is positively correlated with the long-range coefficient for both prediction tasks. In a simple crystal structure with short periodicity, most information will be available using the nearest neighbours, whereas more complex structures require longer-range interactions. Meanwhile, the prediction task has a dominant role in determining the importance of long-range interactions. The long-range coefficients are globally much lower for the formation energy prediction task, suggesting that Site-Net relies less on longer range interactions for prediction tasks where local interactions are expected to dominate. Notably, the formation energy calculated by density functional theory is understood to rely on short range interactions.32,33 Provided the nearest neighbour interactions are correct, the bulk of the formation energy will be accounted for. Importantly, Site-Net is flexible and robust enough to deal with these many cases, and the self-attention mechanism implemented in Site-Net is able to take advantage of long-range interactions when they are relevant and to ignore them when they are not.
We have shown throughout this work that Site-Net is effective at operating on ordered crystal structures, but owing to the construction of a large supercell and removal of symmetry, the same process can also be used to examine disordered crystal structures. Disordered materials could either be treated directly (e.g., using the raw atom positions from a molecular dynamics simulation), or treated by constructing multiple ordered supercells (e.g., using Pymatgen21) and generating predictions for all supercell approximates. We note the predictions on the set of ordered supercells could be aggregated and subsequently interrogated using simple statistics to infer the reliability of the predictions.
3.1 Implementation considerations and scalability
Explicitly computing all pairwise interactions is computationally intensive, and has a quadratic dependence on the number of atoms in the crystal in terms of VRAM and computational load. If operating in this fashion, Site-Net can ingest unit cells of 100 atoms and be trained using ∼14 GB of VRAM, which can run on a single desktop GPU. Even when running explicitly computing all pairwise interactions and operating as above, Site-Net demonstrates competitive performance on the Matbench band gap regression task (MAE 0.246 eV). >97% of crystal structures in the Matbench band gap dataset have unit cells with less than 100 atoms (Fig. S1†); however, the limit of 100 atoms should also be appropriate on more general tasks using other datasets. Similar examination of ∼200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 crystal structures in the Inorganic Crystal Structure Database (ICSD) demonstrates a limit of 100 atoms would allow training on 92% of the crystal structures in the ICSD (Fig. S5†). A limit of 100 atoms provides a balance by having sufficiently large local environment for any atomic site as well as including nearly all of the data in the training set, while avoiding prohibitive batch sizes and training times.
000 crystal structures in the Inorganic Crystal Structure Database (ICSD) demonstrates a limit of 100 atoms would allow training on 92% of the crystal structures in the ICSD (Fig. S5†). A limit of 100 atoms provides a balance by having sufficiently large local environment for any atomic site as well as including nearly all of the data in the training set, while avoiding prohibitive batch sizes and training times.
Although Site-Net performs well in the most limiting case where all pairwise interactions are calculated using brute force, we introduce several modifications to overcome this limitation and significantly increase the accessible model size and training speed. Importantly, these modifications are purely computational tricks to improve efficiency, and they do not fundamentally change the model, in that they still lead to complete attention across the supercell.
The first modification involves considering symmetry to efficiently treat equivalent atomic sites generated in the supercell. Rather than calculating the attention weights explicitly on all atomic sites in the supercell, calculation of the attention weights and training is performed for only the unique atomic sites in the initial minimal P1 unit cell. Specifically, in the interaction features tensor Ii,j,f, the length of i is equal to the number of atomic sites in the minimal P1 unit cell, and the length of j would be equal to the total number of atoms in the supercell.
The second modification to increase model size and training speed involves better handling of the tensors in the model. The use of fixed-length or regular tensors is essential on current hardware, as GPUs rely on the regularity of the tensor for matrix multiplications. However, crystal structures have a varying number of atoms, so generating a fixed-length tensor for every crystal structure requires adding dummy atoms (i.e., zero-padding) to all crystal structures to match the number of atoms in the largest crystal structure used in training. Consequently, the largest crystal in the dataset dictates the VRAM and computational requirements. Further, the model must then be constructed to account for and prune this junk data from downstream aggregations to prevent it from influencing model predictions.
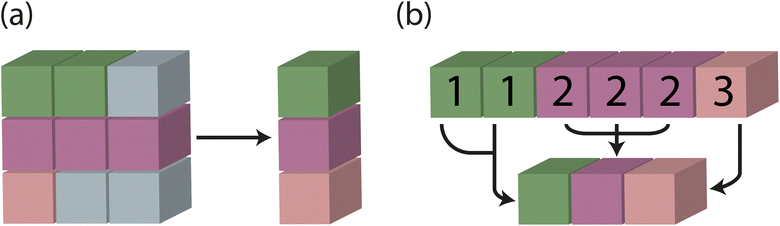
In traditional batching methods with zero padding, global feature vectors are obtained by taking the mean of each supercell and including logic to identify and eliminate the influence of junk data from zero padding. In the modified batching method developed and implemented in Site-Net, batching is performed along an existing tensor rank and a separate index tensor is created to keep track of which atomic sites are associated with a particular crystal. The mean for each crystal in the batch is taken independently using the index tensor, and the results are concatenated (Fig. 8). The size of the fixed-length tensor is then defined as a hyperparameter of the model (Table 1), which determines how many unique sites from minimal P1 unit cells are considered in a single batch. Importantly, the consideration of symmetry and efficient treatment of the interaction features tensor described in the first modification leads to variable length tensors, which are then dealt with the modified batching method implemented here.
The removal of redundant calculations through the inclusion of symmetry and the removal of the zero padding through the use of modified batching reduce the number of computations and required VRAM per batch by a factor of 20, and thus allow access to considerably larger models and quicker training. The final Site-Net model reported here uses a 500 atom limit for the supercell, as 500 atoms is larger than any minimal P1 unit cell in the Matbench band gap dataset (Fig. S1†), and a model using 500 atoms can be trained comfortably using a single desktop GPU. Further, a limit of 500 atoms allows generation of well-behaved pseudo-cubic supercells (Fig. S4†) with a large number of atoms to encode long-range interactions (Fig. S2†).
While there is no fundamental limit to the size of a supercell that Site-Net can consider, several further modifications can be made to increase the scale of Site-Net. In the most simple case, larger supercells could be handled by running on a larger GPU, for example using a high-performance computing cluster with a 128 GB GPU. Straightforward changes to the architecture can also be made to achieve larger models. The first is to split the parameters of the model across multiple GPUs to increase the available VRAM and speed up training. Alternatively, parameters of the model could be offloaded from VRAM to system RAM or even high speed solid state drives.34 These methodologies combined would allow a Site-Net implementation to scale to a local environment of arbitrary size. The ability of Site-Net to access larger scale models increases the scope of potential applications, such as the examination of disordered materials, which could be included in the same dataset as ordered materials.
3.2 Invariance under unit cell transformations
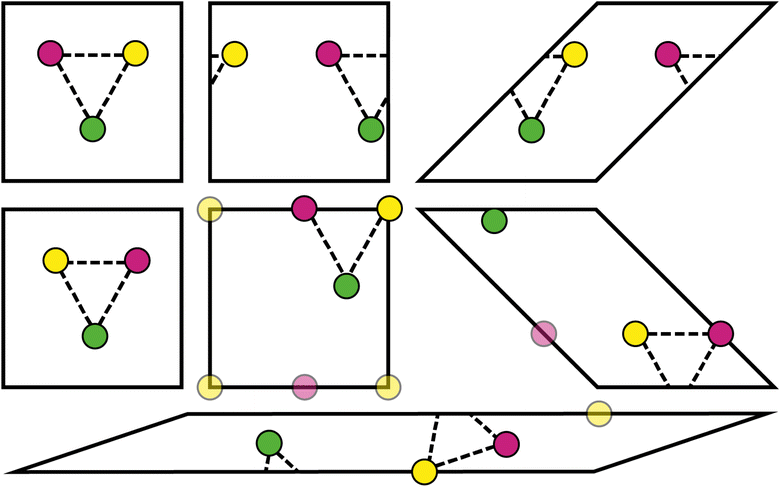
Every physical crystal structure can be represented using many possible unit cells or supercells. For example, the choice of unit cell setting in triclinic crystal systems is not straightforward,35 and non-standard representations can be preferred in some circumstances (e.g., the use of hexagonal unit cells as opposed to primitive rhombohedral unit cells36). Transforming between unit cells changes various parameters in the CIF, such as the atomic coordinates and unit cell parameters. If these parameters form part of the input of a machine learning model, then the choice of unit cell can lead to different predictions. This issue has gained recent attention in the literature and has prompted assessment of existing models.7,37,38The design of the Site-Net model ensures that model predictions do not change under translations and unimodular transformations, described below. These transformations do not change the volume of the unit cell or supercell, but they nevertheless lead to unit cells that are very distinct (Fig. 9). Importantly, the types and quantities of crystallographic sites remain unchanged by these transformations, so while the order of crystallographic sites may change, the same set of inputs Si,f and Ii,j,f will be processed by a model that is invariant to permutations.
In the case of translation, which is more straightforward, the number of crystallographic sites Sti,f in the translated unit cell and their identities remain the same, but their ordering might change. Formally, it means that there is a permutation π over the sites such that Si,f and Stπ(i),f are equal. Furthermore, since the distances are computed under periodic boundary conditions (i.e., the distance between any two sites is always the distance between an atomic site and the closest site from any self or image unit cell), the resulting interaction features Iti,j,f will be identical to Ii,j,f after the rearrangement Itπ(i),π(j),f. Thus, the tensors Bi,j,f and Bti,j,f, which constitute the only input to Site-Net, are identical up to a permutation. Since all operations performed in Site-Net are permutation-invariant, we arrive at the same predictions.
The same reasoning applies in the case of unimodular transformations (i.e., a volume-preserving shear of the unit cell), where we show that the number of crystallographic sites and their identities are preserved. A crystallographic lattice defined by the lattice vectors V = [![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) ,
,![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) ,
,![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif) ] can be generated using different sets of vectors. A classical result from lattice theory states that multiplication of V by a unimodular matrix U (i.e., a matrix with integer coefficients and the determinant ±1) leads to vectors V′ = VU that also generate the initial lattice.39 As the point lattices before and after transformation are identical, both unit cells (as fundamental domains) will have the same volume and contain a unique representative of every crystallographic site. Therefore, the new sites Sui,f of the unit cell after a unimodular transformation are identical to the original sites Sπ(i),f after application of a suitable permutation π of indices. Similarly to the case of translations, we can conclude that the tensors Bi,j,f and Buπ(i),π(j),f are the same, which leads to identical predictions produced by the Site-Net model.
] can be generated using different sets of vectors. A classical result from lattice theory states that multiplication of V by a unimodular matrix U (i.e., a matrix with integer coefficients and the determinant ±1) leads to vectors V′ = VU that also generate the initial lattice.39 As the point lattices before and after transformation are identical, both unit cells (as fundamental domains) will have the same volume and contain a unique representative of every crystallographic site. Therefore, the new sites Sui,f of the unit cell after a unimodular transformation are identical to the original sites Sπ(i),f after application of a suitable permutation π of indices. Similarly to the case of translations, we can conclude that the tensors Bi,j,f and Buπ(i),π(j),f are the same, which leads to identical predictions produced by the Site-Net model.
Finally, it is important to note that Site-Net is, by design, not invariant to scale. Site-Net is designed to update its predictions by incorporating increasingly long-range interactions. Accordingly, as the supercell size is increased, attention heads will be able to examine more interactions at longer radial distances, and we expect convergence at some sufficiently long distance when all meaningful interactions are considered.
4 Conclusions
We present Site-Net, a transformer model for learning structure–property relationships in extended inorganic solids. Site-Net processes standard crystallographic information files, and uses a physically motivated representation of the crystal structure as a point set of atomic sites. As many physical phenomena in extended inorganic solids arise from long-range interactions and features of the crystal structure, we build a large supercell to encode this information explicitly. Critically, the set of atomic sites is directly ingested without any predefined connections, and the importance of interactions between all atomic sites is flexibly learned by the model for the prediction task presented.The relevant structural information will differ between property prediction tasks, and the use of a custom global self-attention mechanism on all pairwise interactions of atomic sites allows Site-Net to identify important interactions and effectively deal with the all-to-all connectivity that would otherwise be overwhelming. The attention mechanism in Site-Net works by iteratively replacing the atomic sites with context-enriched versions of themselves, which are created by aggregating the most important structural information from all other atomic sites in the crystal structure present in the supercell.
The use of attention in Site-Net allows interrogation of the learning by examining the weights assigned to interactions at different interatomic distances. We show that for the band gap prediction task performed here, Site-Net learns from interactions that are beyond the nearest neighbour atomic sites, and that attention heads performing the attention calculations become specialised to deal with primarily short- or long-range interactions. Further, training Site-Net where the attention has an artificial distance cutoff limit of 5 Å decreases model performance, confirming that including longer range interactions within a crystal structure meaningfully contributes to property predictions of extended inorganic materials.
To measure the importance of long-range interactions in the predictions of Site-Net, we develop a scalar metric, the long-range coefficient. Through examining proxies for crystal structure complexity and comparing between the prediction tasks of band gap and formation energy, we use this metric to show the importance of long-range interactions in Site-Net property predictions depends both on the chemistry and the prediction task. Notably, the self-attention mechanism implemented in Site-Net is sufficiently robust to take advantage of long-range interactions when they are relevant and to ignore them when they are not.
We demonstrate the effectiveness of Site-Net through a band gap prediction task, as this task is heavily studied and commonly used as a benchmark for model performance. As a proof of concept, we build supercells of 500 atoms and train Site-Net using a single consumer graphics processing unit (GPU). Site-Net achieves a mean absolute error (MAE) of 0.234 eV using the Matbench band gap regression dataset, and performance of the model is consistent across band gap values. Even after only a preliminary hyperparameter search and using supercells of 500 atoms, Site-Net demonstrates competitive performance with the highest performing algorithms on the Matbench leaderboard. The performance of Site-Net is likely to improve following a more extensive hyperparameter search and through the use of larger supercells. Both paths to improvement can be easily accommodated through changes to the way calculations are handled internally as well as through the use of larger or parallel GPUs.
Importantly, we show that explicit incorporation of long-range interactions through the use of supercells can improve the performance of machine learning models that use crystal structure to predict properties of extended inorganic solids. Given that many physical properties result from long-range features and/or the extended nature of a crystal structure, the performance of other models on many prediction tasks may also be improved through similar methods.
Data availability
The code for Site-Net can be found at https://github.com/lrcfmd/Site-Net. The data used in this study was the publicly available band gap data from matbench and can be found at https://matbench.materialsproject.org/Leaderboards%20Per-Task/matbench_v0.1_matbench_mp_gap/ and https://matbench.materialsproject.org/Leaderboards%20Per-Task/matbench_v0.1_matbench_mp_gap/, the version of the dataset used is V0.1.Code availability
The code developed for this work is available at https://github.com/lrcfmd/Site-Net.Conflicts of interest
There are no competing interests to declare.Acknowledgements
Work was performed using Barkla, part of the High Performance Computing facilities at the University of Liverpool, UK. The authors thank the Leverhulme Trust for funding via the Leverhulme Research Centre for Functional Materials Design. MWG thanks the Ramsay Memorial Fellowships Trust for funding through a Ramsay Trust Memorial Fellowship.Notes and references
- G. R. Schleder, A. C. M. Padilha, C. M. Acosta, M. Costa and A. Fazzio, J. Phys. Mater., 2019, 2, 032001 CrossRef CAS.
- K. Choudhary, B. DeCost, C. Chen, A. Jain, F. Tavazza, R. Cohn, C. W. Park, A. Choudhary, A. Agrawal, S. J. L. Billinge, E. Holm, S. P. Ong and C. Wolverton, npj Comput. Mater., 2022, 8, 59 CrossRef.
- R. Pollice, G. dos Passos Gomes, M. Aldeghi, R. J. Hickman, M. Krenn, C. Lavigne, M. Lindner-D'Addario, A. Nigam, C. T. Ser, Z. Yao and A. Aspuru-Guzik, Acc. Chem. Res., 2021, 54, 849–860 CrossRef CAS PubMed.
- A. Y.-T. Wang, S. K. Kauwe, R. J. Murdock and T. D. Sparks, npj Comput. Mater., 2021, 7, 77 CrossRef.
- D. Jha, L. Ward, A. Paul, W.-k. Liao, A. Choudhary, C. Wolverton and A. Agrawal, Sci. Rep., 2018, 8, 17593 CrossRef PubMed.
- B. I. Kharisov and O. V. Kharissova, Carbon allotropes: metal-complex chemistry, properties and applications, Springer, 2019 Search PubMed.
- J. Ropers, M. M. Mosca, O. Anosova and V. Kurlin, Acta Crystallogr., Sect. A: Found. Adv., 2021, 77, C671 Search PubMed.
- T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301 CrossRef CAS PubMed.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Chem. Mater., 2019, 31, 3564–3572 CrossRef CAS.
- K. Choudhary and B. DeCost, npj Comput. Mater., 2021, 7, 1–8 CrossRef.
- S.-Y. Louis, Y. Zhao, A. Nasiri, X. Wang, Y. Song, F. Liu and J. Hu, Phys. Chem. Chem. Phys., 2020, 22, 18141–18148 RSC.
- S. Kearnes, K. McCloskey, M. Berndl, V. Pande and P. Riley, J. Comput.-Aided Mol. Des., 2016, 30, 595–608 CrossRef CAS PubMed.
- A. Dunn, Q. Wang, A. Ganose, D. Dopp and A. Jain, npj Comput. Mater., 2020, 6, 138 CrossRef.
- Y. Hinuma, Sci. Technol. Adv. Mater.: Methods, 2022, 2, 266–279 CAS.
- T. Mikolov, K. Chen, G. Corrado and J. Dean, arXiv, 2013, preprint, arXiv: 1301.3781, DOI:10.48550/arXiv.1301.3781.
- I. Dokmanic, R. Parhizkar, J. Ranieri and M. Vetterli, IEEE Signal Process. Mag., 2015, 32, 12–30 Search PubMed.
- L. Liberti, C. Lavor, N. Maculan and A. Mucherino, SIAM Rev., 2014, 56, 3–69 CrossRef.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser and I. Polosukhin, Advances in Neural Information Processing Systems, 2017 Search PubMed.
- R. Q. Charles, H. Su, M. Kaichun and L. J. Guibas, 2017 IEEE Conference on Computer Vision and Pattern Recognition, CVPR, 2017, pp. 77–85 Search PubMed.
- R. Liaw, E. Liang, R. Nishihara, P. Moritz, J. E. Gonzalez and I. Stoica, arXiv, 2018, preprint, arXiv: 1807.05118, DOI:10.48550/arXiv.1807.05118.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- L. Ward, A. Dunn, A. Faghaninia, N. E. R. Zimmermann, S. Bajaj, Q. Wang, J. Montoya, J. Chen, K. Bystrom, M. Dylla, K. Chard, M. Asta, K. A. Persson, G. J. Snyder, I. Foster and A. Jain, Comput. Mater. Sci., 2018, 152, 60–69 CrossRef.
- D. Misra, arXiv, 2019, preprint, arXiv:1908.08681, DOI:10.48550/arXiv.1908.08681.
- J. L. Ba, J. R. Kiros and G. E. Hinton, arXiv, 2016, preprint, arXiv:1607.06450, DOI:10.48550/arXiv.1607.06450.
- S. Ioffe and C. Szegedy, Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 2015, pp. 448–456 Search PubMed.
- L. Himanen, M. O. J. Jäger, E. V. Morooka, F. Federici Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke and A. S. Foster, Comput. Phys. Commun., 2020, 247, 106949 CrossRef CAS.
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Kopf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai and S. Chintala, Advances in Neural Information Processing Systems 32, Curran Associates, Inc., 2019, pp. 8024–8035 Search PubMed.
- W. Falcon and The PyTorch Lightning team, 2019 Search PubMed.
- J. Bergstra, B. Komer, C. Eliasmith, D. Yamins and D. D. Cox, Comput. Sci. Discov., 2015, 8, 014008 CrossRef.
- W. Hornfeck, Acta Crystallogr., Sect. A: Found. Adv., 2020, 76, 534–548 CrossRef CAS PubMed.
- C. Kaußler and G. Kieslich, J. Appl. Crystallogr., 2021, 54, 306–316 CrossRef PubMed.
- E. Prodan and W. Kohn, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 11635–11638 CrossRef CAS PubMed.
- W. Kohn, Phys. Rev. Lett., 1996, 76, 3168–3171 CrossRef CAS PubMed.
- J. Rasley, S. Rajbhandari, O. Ruwase and Y. He, Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, New York, NY, USA, 2020, pp. 3505–3506 Search PubMed.
- J. D. H. Donnay, Am. Mineral., 1943, 28, 507–511 CAS.
- G. Burns and A. Glazer, Space Groups for Solid State Scientists, Academic Press, Oxford, 3rd edn, 2013, pp. 45–64 Search PubMed.
- N. Thomas, T. Smidt, S. Kearnes, L. Yang, L. Li, K. Kohlhoff and P. Riley, arXiv, 2018, preprint, arXiv:1802.08219, DOI:10.48550/arXiv.1802.08219.
- D. E. Worrall, S. J. Garbin, D. Turmukhambetov and G. J. Brostow, arXiv, preprint, 2016, arXiv:1612.04642, DOI:10.48550/arXiv.1612.04642.
- D. Micciancio and S. Goldwasser, in Complexity of Lattice Problems: a cryptographic perspective, Kluwer Academic Publishers, Boston, Massachusetts, 2002, vol. 671, ch. 1 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00005b |
| This journal is © The Royal Society of Chemistry 2023 |