Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Chemical design with GPU-based Ising machines†
Zetian
Mao
a,
Yoshiki
Matsuda
bc,
Ryo
Tamura
*ade and
Koji
Tsuda
 *ade
*ade
aGraduate School of Frontier Sciences, The University of Tokyo, 5-1-5 Kashiwanoha, Kashiwa 2778561, Japan. E-mail: tamura.ryo@nims.go.jp; tsuda@k.u-tokyo.ac.jp
bFixstars Corporation, 3-1-1 Shibaura, Minato-ku, Tokyo 108-0023, Japan
cGreen Computing System Research Organization, Waseda University, 27 Wasedacho, Shinjuku-ku, Tokyo 162-0042, Japan
dCenter for Basic Research on Materials, National Institute for Materials Science, 1-1 Namiki, Tsukuba, Ibaraki 305-0044, Japan
eRIKEN Center for Advanced Intelligence Project, 1-4-1 Nihonbashi, Chuo-ku, Tokyo 103-0027, Japan
First published on 23rd June 2023
Abstract
Ising machines are hardware-assisted discrete optimizers that often outperform purely software-based optimization. They are implemented, e.g., with superconducting qubits, ASICs or GPUs. In this paper, we show how Ising machines can be leveraged to gain efficiency improvements in automatic molecule design. To this end, we construct a graph-based binary variational autoencoder to obtain discrete latent vectors, train a factorization machine as a surrogate model, and optimize it with an Ising machine. In comparison to Bayesian optimization in a continuous latent space, our method performed better in three benchmarking problems. Two types of Ising machines, a qubit-based D-Wave quantum annealer and GPU-based Fixstars Amplify, are compared and it is observed that the GPU-based one scales better and is more suitable for molecule generation. Our results show that GPU-based Ising machines have the potential to empower deep-learning-based materials design.
Introduction
Molecule design with deep learning has become an essential tool to navigate through the vast chemical space.1–4 So far, automatic molecule design methods have been successfully applied to develop, e.g., DDR1 kinase prohibitors,5 fluorescent molecules,6 electrets7 and ligands for supramolecular gate modulation.8 Among the large variety of deep learning models, latent space-based models such as variational autoencoders9 and transformers10 constitute a major category. In their pioneering study, Gómez-Bombarelli et al.1 proposed the use of a variational autoencoder to create a latent space and generate molecules by applying Bayesian optimization11 to the latent space. This approach has been extended in a number of ways to grammar VAE,2 syntax directed VAE3 and junction tree VAE (JTVAE).4These methods employ a continuous-valued vector as the latent representation to enable smooth navigation with gradient information. However, the fitness functions in the latent space are rich in local minima and may not be optimized completely.12 Although the optimization performance is hard to measure, we suspect that the performance of latent space-based models is affected adversely by local minima. A dilemma here is that increasing the latent space dimensionality leads to better expressivity but causes difficulty in optimization. If a powerful optimizer is available, it may be exploited to break out of this dilemma.
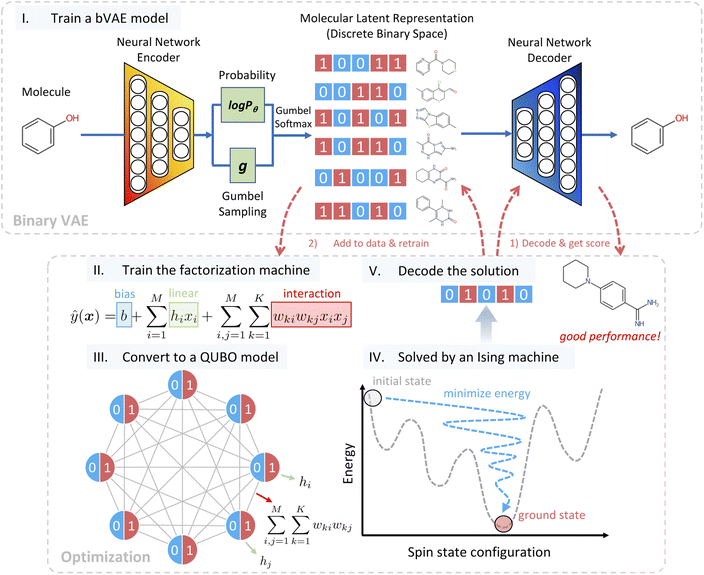
Ising machines are specialized hardware that can solve quadratic unconstrained binary optimization (QUBO).13 QUBO with M bits is described as
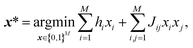 | (1) |
Highly efficient global optimization of QUBO can be achieved by various physical platforms other than superconducting qubits. Examples include an ASIC-based digital annealer,17 coherent Ising machine18 and quantum approximate optimization algorithm (QAOA) implemented on gate-based quantum computers.19 Among them, we focus on a GPU-based Ising machine called a Fixstars Amplify Annealing Engine20 (referred to as Amplify later on). It is based on simulated annealing and uses multi-level parallel processing on multiple GPUs to find optimal solutions. Amplify relies on conventional semiconductor technologies, but can handle large scale problems up to 130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bits with full connection.
000 bits with full connection.
In this paper, we construct a discrete latent space-based molecule generation framework by combining an adaptation of JTVAE and Amplify. We evaluate the expressivity of our discrete latent space in comparison to the continuous counterpart and elucidate how many bits are necessary to accurately represent the fitness functions and optimize them. It turns out that the number of required bits is around 300, which is beyond the limit of the D-Wave Advantage. Our approach was tested in three different benchmarking problems, and we observed that it outperformed the combination of continuous VAE and Bayesian optimization in three different benchmarking problems. Our results show that the combination of a discrete latent space and a powerful discrete optimizer is a viable approach to solve various molecular design problems.
Method
Our algorithm called bVAE-IM assumes an oracle that returns the property of a given molecule. In real-world materials design tasks, the oracle can correspond to synthesis experiments or numerical simulations such as density functional theory calculations. In addition, two kinds of training examples are given: nu unlabeled examples and nl labeled examples. An unlabeled example is a molecule without any properties, while a labeled example is the pair of a molecule and its property. In most cases, these examples are collected from public databases like ZINC21 and PubChem.22 Our algorithm repeatedly generates a molecule and calls the oracle to obtain its property. The efficiency of bVAE-IM is measured by the best property values among the molecules generated with a predetermined number of oracle calls.The workflow of bVAE-IM is detailed in Fig. 1. First, a binary junction tree VAE (bJTVAE) is trained with the unlabeled examples to construct a latent space. We obtain bJTVAE by modifying the junction tree VAE4 with the Gumbel softmax reparametrization16 such that the latent representation is a bit vector. We selected junction tree VAE as our base model, because it can deal with graph representations of molecules without relying on string representations like SMILES.23 As a result, we obtain a decoder that translates a bit vector to a molecular graph.
After the latent space is obtained, our task of generating a molecule boils down to finding the best bit vector in the latent space. In a continuous latent space, a commonly used method is to employ a Gaussian process surrogate model and choose the best latent representation by optimizing an acquisition function.1 In our case, we employ a factorization machine24 as the surrogate model and the best bit vector is selected by optimizing the trained FM with an Ising machine. The functional form of FM is described as
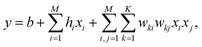 | (2) |
Results
Expressivity of latent spaces
The reconstruction accuracy of VAEs is measured by how accurately input examples are reconstructed as output examples. To achieve high accuracy for a wide variety of molecules, the dimensionality of the latent space must be sufficiently high to ensure that the latent representation is expressive enough. We show that the binary latent space of bJTVAE has comparable expressivity in comparison to the continuous counterpart, JTVAE. To this end, 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules were sampled from ZINC and divided into 220
000 molecules were sampled from ZINC and divided into 220![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 training and 30
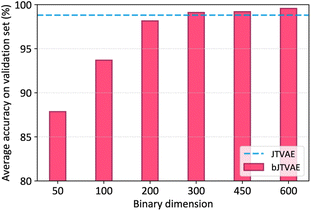
000 training and 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 validation examples. Six bJTVAE models with different latent dimensionalities, d = 50, 100, 200, 300, 450, and 600, were trained, while the dimensionality of JTVAE was fixed to 56 as in the literature.4 The reconstruction accuracy is defined as the fraction of exactly reconstructed molecules in the validation examples. The validity of generated molecules by bJTVAE is always 100%, because the decoder of JTVAE is utilized.
000 validation examples. Six bJTVAE models with different latent dimensionalities, d = 50, 100, 200, 300, 450, and 600, were trained, while the dimensionality of JTVAE was fixed to 56 as in the literature.4 The reconstruction accuracy is defined as the fraction of exactly reconstructed molecules in the validation examples. The validity of generated molecules by bJTVAE is always 100%, because the decoder of JTVAE is utilized.
In Fig. 2, the average reconstruction accuracies over 10 runs are shown. The accuracy of bJTVAE grows monotonically up to d = 300 and starts to saturate after d > 300. At d = 300, the accuracy of bJTVAE is roughly on par with that of JTVAE, indicating that the binary latent space is capable of encoding molecules without much information loss. It also implies that molecular generators need a high dimensional latent space beyond the limit of D-Wave annealers.
Optimization performance
We tested bVAE-IM with the following three computational oracles. (1) Penalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P2: octanol–water partition coefficient (log
P2: octanol–water partition coefficient (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P) penalized by the synthetic accessibility (SA) score and the number of rings that have more than 6 atoms. (2) Topological polar surface area (TPSA): total surface area of all polar atoms including their attached hydrogen atoms. (3) GSK3β + JNK3 + QED + SA:26 score unifying the predicted inhibition levels against c-Jun N-terminal kinase 3 (JNK3) and glycogen synthase kinase-3 beta (GSK-3β), QED (drug-likeliness) and SA. The first and second properties are computed with RDKit,27 while the code provided at MolEvol28 was used to compute the third.
P) penalized by the synthetic accessibility (SA) score and the number of rings that have more than 6 atoms. (2) Topological polar surface area (TPSA): total surface area of all polar atoms including their attached hydrogen atoms. (3) GSK3β + JNK3 + QED + SA:26 score unifying the predicted inhibition levels against c-Jun N-terminal kinase 3 (JNK3) and glycogen synthase kinase-3 beta (GSK-3β), QED (drug-likeliness) and SA. The first and second properties are computed with RDKit,27 while the code provided at MolEvol28 was used to compute the third.
As the unlabeled data, we employed nu = 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 randomly selected molecules from ZINC. The labeled data are created by adding the properties to nl = 10
000 randomly selected molecules from ZINC. The labeled data are created by adding the properties to nl = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 randomly selected molecules from ZINC using the computational oracles. To investigate extrapolative performances, we intentionally limited our labeled data to those with poor properties: penalized log
000 randomly selected molecules from ZINC using the computational oracles. To investigate extrapolative performances, we intentionally limited our labeled data to those with poor properties: penalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P∈[−3,3], TPSA∈[0,100] and GSK3-β + JNK3 + QED + SA∈[0,0.5]. As a baseline method, we employ a standard approach called VAE-BO consisting of JTVAE and Gaussian process-based Bayesian optimization as implemented in Kusner et al.2 Note that the Gaussian process is initially trained with the same set of labeled data and retrained whenever a molecule is generated. Additionally, we compared our method with random sampling in discrete and continuous latent spaces, which are denoted as bVAE-Random and VAE-Random, respectively. See Section 2 in the ESI† for details about training.
P∈[−3,3], TPSA∈[0,100] and GSK3-β + JNK3 + QED + SA∈[0,0.5]. As a baseline method, we employ a standard approach called VAE-BO consisting of JTVAE and Gaussian process-based Bayesian optimization as implemented in Kusner et al.2 Note that the Gaussian process is initially trained with the same set of labeled data and retrained whenever a molecule is generated. Additionally, we compared our method with random sampling in discrete and continuous latent spaces, which are denoted as bVAE-Random and VAE-Random, respectively. See Section 2 in the ESI† for details about training.
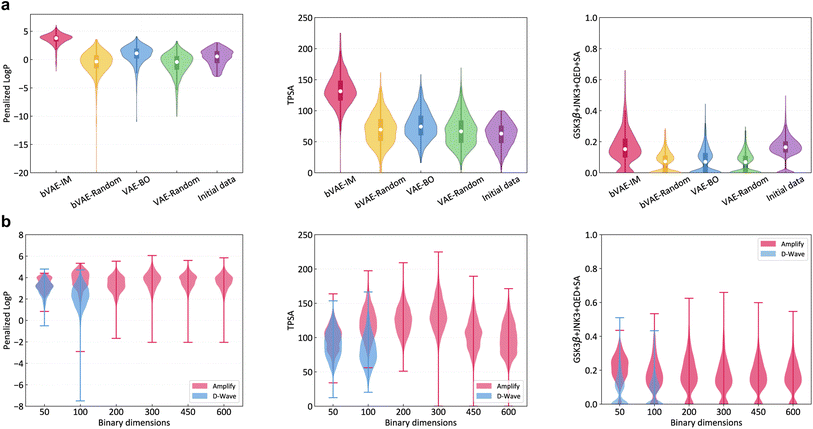
VAE-BO and bVAE-IM are applied up to the point that 300 molecules are generated. This is repeated five times with different random seeds. bVAE-IM employed Amplify and the dimensionality of the latent space is set to 300. The property distributions of the generated molecules are shown in Fig. 3a. In all of the three cases, the top molecules of bVAE-IM were better than those of VAE-BO and the initial labeled data. See Table 1 for detailed statistics and Fig. S2 in the ESI† for examples of generated molecules. Note that the experimental results for three additional properties are shown in Section 4 in the ESI.† This result implies that, using a high performance discrete optimizer, it is possible to construct a competitive molecular generator. The performance improvement of bVAE-IM from bVAE-Random is larger than that of VAE-BO from VAE-Random. It may serve as evidence that the superiority of bVAE-IM results from better optimization, not from better expressivity of the latent space. However, the adversarial effect of local minima in the continuous latent space of VAE-BO is hard to measure precisely, because guaranteed global optimization in a high dimensional space is extremely hard.
| Property | Method | Maximum | Mean of top 5% | Mean of top 10% | Runtime (h) |
|---|---|---|---|---|---|
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P P |
bVAE-IM | 5.606 ± 0.263 | 5.144 ± 0.089 | 4.948 ± 0.067 | 4.96 ± 0.44 |
| bVAE-Random | 3.263 ± 0.245 | 2.359 ± 0.091 | 2.061 ± 0.093 | — | |
| VAE-BO | 3.699 ± 0.138 | 3.303 ± 0.185 | 3.120 ± 0.235 | 9.46 ± 3.86 | |
| VAE-Random | 2.888 ± 0.331 | 2.135 ± 0.173 | 1.836 ± 0.130 | — | |
| Initial data | 2.999 | 2.640 | 2.445 | — | |
| TPSA | bVAE-IM | 221.552 ± 5.430 | 192.030 ± 4.433 | 181.276 ± 3.541 | 5.32 ± 0.39 |
| bVAE-Random | 149.338 ± 10.748 | 125.319 ± 2.758 | 116.168 ± 2.175 | — | |
| VAE-BO | 148.908 ± 7.452 | 127.947 ± 3.351 | 119.713 ± 2.574 | 8.38 ± 1.67 | |
| VAE-Random | 149.320 ± 11.146 | 122.744 ± 1.973 | 114.105 ± 1.736 | — | |
| Initial data | 99.990 | 95.832 | 92.691 | — | |
| GSK3β + JNK3 + QED + SA | bVAE-IM | 0.637 ± 0.028 | 0.444 ± 0.018 | 0.386 ± 0.021 | 7.90 ± 0.32 |
| bVAE-Random | 0.264 ± 0.017 | 0.203 ± 0.008 | 0.179 ± 0.006 | — | |
| VAE-BO | 0.388 ± 0.029 | 0.265 ± 0.012 | 0.230 ± 0.007 | 10.25 ± 4.37 | |
| VAE-Random | 0.272 ± 0.028 | 0.198 ± 0.007 | 0.177 ± 0.006 | — | |
| Initial data | 99.990 | 95.832 | 92.691 | — |
The runtime for generating a molecule involves an oracle call, retraining of the surrogate model, optimization of the surrogate model, and decoding. Ising models are expected to accelerate the optimization part, but the impact on the total runtime is limited, because the other parts take substantially more time. Table 1 shows the total runtime for bVAE-IM and VAE-BO. BVAE-IM was more efficient, but the difference is less pronounced when the oracle takes more time (i.e., GSK3β + JNK3 + QED + SA).
Fig. 3b shows the property distributions under different latent space dimensions. At 50 and 100 dimensions, the D-Wave quantum annealer (Advantage 4.1) was applied as well, but Amplify outperformed D-Wave in these cases. This is probably due to the limitation of current qubit technologies such as fast annealing time and Hamiltonian control errors.29 Although the GPU-based Ising machine is clearly a better choice at present, the situation might change as qubit technologies improve.
Discussion
The binary junction tree variational autoencoders developed in this paper are of independent interest in the chemoinformatics community, because the latent representation serves as an alternative fingerprint of molecules. See Section 1 of the ESI† for related discussions. Our method employs a factorization machine as the surrogate model, but alternative choices are possible. See Section 3 of the ESI† for details.Latent spaces provided by deep learning models have revolutionized how molecules are generated. Complex valence rules can now be learned from data and need not be implemented explicitly. Nevertheless, modeling molecular properties in the latent space and optimizing them are not straightforward. We have shown how molecule generators can be improved by powerful optimizers such as Ising machines. The development of deep learning methods is rapid, and the variational autoencoders employed in this paper may no longer be among the best methods. However, our approach can basically be applied to newer models with latent spaces such as transformers.10
Current quantum-based optimizers have a scalability problem as pointed out in this paper. In addition, environmental noise often prevents quantum-based optimizers from reaching the global minimum. Nevertheless, quickly developing technologies of Ising machines may solve these problems to the point that quantum-based ones are preferred over GPU-based methods.
Data availability
The code is available at https://github.com/tsudalab/bVAE-IM. The data to reproduce the results of this paper is available at https://zenodo.org/badge/latestdoi/608057945. As of March 2023, Fixstars Amplify is available via Python API free of charge.Author contributions
R. T. and K. T. conceived the idea and designed the research. Z. M. implemented the code and conducted all experiments. Y. M. offered technical support about Fixstars Amplify. Z. M., R. T. and K. T. wrote the manuscript. All authors confirmed the manuscript.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This work is supported by AMED JP20nk0101111, JST CREST JPMJCR21O2, JST ERATO JPMJER1903 and MEXT JPMXP1122712807.References
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed
.
-
M. J. Kusner, B. Paige and J. M. Hernández-Lobato, International conference on machine learning, 2017, pp. 1945–1954 Search PubMed
.
- H. Dai, Y. Tian, B. Dai, S. Skiena and L. Song, arXiv, 2018, preprint, arXiv:1802.08786, DOI:10.48550/arXiv.1802.08786.
- W. Jin, R. Barzilay and T. S. Jaakkola, arXiv, 2018, preprint, arXiv:1802.04364, DOI:10.48550/arXiv.1802.04364.
- A. Zhavoronkov, Y. A. Ivanenkov, A. Aliper, M. S. Veselov, V. A. Aladinskiy, A. V. Aladinskaya, V. A. Terentiev, D. A. Polykovskiy, M. D. Kuznetsov and A. Asadulaev,
et al.
, Nat. Biotechnol., 2019, 37, 1038–1040 CrossRef CAS PubMed
.
- M. Sumita, K. Terayama, N. Suzuki, S. Ishihara, R. Tamura, M. K. Chahal, D. T. Payne, K. Yoshizoe and K. Tsuda, Sci. Adv., 2022, 8, eabj3906 CrossRef CAS PubMed
.
- Y. Zhang, J. Zhang, K. Suzuki, M. Sumita, K. Terayama, J. Li, Z. Mao, K. Tsuda and Y. Suzuki, Appl. Phys. Lett., 2021, 118, 223904 CrossRef CAS
.
- H. Lambert, A. Castillo Bonillo, Q. Zhu, Y.-W. Zhang and T.-C. Lee, npj Comput. Mater., 2022, 8, 1–8 CrossRef
.
- D. P. Kingma and M. Welling, arXiv, 2013, preprint, arXiv:1312.6114, DOI:10.48550/arXiv.1312.6114.
- E. Castro, A. Godavarthi, J. Rubinfien, K. Givechian, D. Bhaskar and S. Krishnaswamy, Nat. Mach. Intell., 2022, 4, 840–851 CrossRef
.
- B. Shahriari, K. Swersky, Z. Wang, R. P. Adams and N. De Freitas, Proc. IEEE, 2015, 104, 148–175 Search PubMed
.
-
B. Choffin and N. Ueda, 2018 IEEE 28th International Workshop on Machine Learning for Signal Processing, MLSP, 2018, pp. 1–6 Search PubMed
.
- N. Mohseni, P. L. McMahon and T. Byrnes, Nat. Rev. Phys., 2022, 4, 363–379 CrossRef
.
- M. W. Johnson, M. H. Amin, T. Gildert, S. an d Lanting, F. Hamze, N. Dickson, R. Harris, A. J. Berkley, J. Johansson and P. Bunyk, Nature, 2011, 473, 194 CrossRef CAS PubMed
.
- B. A. Wilson, Z. A. Kudyshev, A. V. Kildishev, S. Kais, V. M. Shalaev and A. Boltasseva, Appl. Phys. Rev., 2021, 8, 041418 CAS
.
- E. Jang, S. Gu and B. Poole, arXiv, 2016, preprint, arXiv:1611.01144, DOI:10.48550/arXiv.1611.01144.
- M. Aramon, G. Rosenberg, E. Valiante, T. Miyazawa, H. Tamura and H. G. Katzgraber, Front. Phys., 2019, 7, 48 CrossRef
.
- T. Inagaki, Y. Haribara, K. Igarashi, T. Sonobe, S. Tamate, T. Honjo, A. Marandi, P. L. McMahon, T. Umeki and K. Enbutsu,
et al.
, Science, 2016, 354, 603–606 CrossRef CAS PubMed
.
- E. Farhi, J. Goldstone and S. Gutmann, arXiv, 2013, preprint, arXiv:1411.4028, DOI:10.48550/arXiv.1411.4028.
- Fixstars Amplify, https://amplify.fixstars.com/en/, accessed 04-Mar-2023.
- J. J. Irwin, T. Sterling, M. M. Mysinger, E. S. Bolstad and R. G. Coleman, J. Chem. Inf. Model., 2012, 52, 1757–1768 CrossRef CAS PubMed
.
- S. Kim, J. Chen, T. Cheng, A. Gindulyte, J. He, S. He, Q. Li, B. A. Shoemaker, P. A. Thiessen and B. Yu,
et al.
, Nucleic Acids Res., 2021, 49, D1388–D1395 CrossRef CAS PubMed
.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS
.
-
S. Rendle, ACM Transactions on Intelligent Systems and Technology (TIST), 2012, 3, 1–22 Search PubMed
.
- K. Kitai, J. Guo, S. Ju, S. Tanaka, K. Tsuda, J. Shiomi and R. Tamura, Phys. Rev. Res., 2020, 2, 013319 CrossRef CAS
.
-
B. Chen, T. Wang, C. Li, H. Dai and L. Song, International Conference on Learning Representation, ICLR, 2021 Search PubMed
.
- RDKit: Open-source cheminformatics, http://www.rdkit.org, Online; accessed 04-March-2023.
- MolEvol, https://github.com/binghong-ml/MolEvol, Online; accessed 04-March-2023.
- A. Pearson, A. Mishra, I. Hen and D. A. Lidar, npj Quantum Inf., 2019, 5, 107 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00047h |
| This journal is © The Royal Society of Chemistry 2023 |