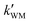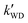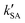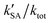A possible atmospheric source of HNO3: the ammonolysis reaction of t-N2O4 in the presence of water monomer, water dimer, and sulfuric acid†
Received
24th June 2023
, Accepted 3rd August 2023
First published on 16th August 2023
Abstract
Although the ammonolysis of t-N2O4 is one of the potential sources of HNO3 formation, the available studies have only focused on its naked reaction. Herein, the effect of important neutral and acidic trace gases, water monomer, water dimer, and sulfuric acid, on the formation of HNO3 from the ammonolysis of t-N2O4 was studied by the quantum chemical method of CCSD(T)/aug-cc-pVTZ//B3LYP-D3/6-311++G(3df,2pd) and the Master equation/Rice–Ramsperger–Kassel–Marcus (ME/RRKM) rate calculations. The quantum chemical results revealed that the ammonolysis of t-N2O4 with (H2O)2 and H2SO4 are barrierless or nearly barrierless reactions, potentially lowering the energy barrier to 3.4–4.1 kcal mol−1. The calculated effective rate constant illustrates that (H2O)2 (100% RH) dominates over H2O and H2SO4 within the range of 280–320 K (0 km), with an effective rate constant that is 1–3 orders of larger magnitude, whereas H2SO4 (108 mol cm−3) is the most favorable catalyst within the troposphere between 5 and 30 km. However, the contributions of H2O, (H2O)2, and H2SO4 are not apparent in the gas-phase ammonolysis of t-N2O4 within the range of 213–320 K and 0–30 km because their effective rate constants were at least 4 orders of magnitude lower than the corresponding rate constant of the ammonolysis of t-N2O4. In general, the current findings shed fresh light on neutral (H2O and (H2O)2) and acidic (H2SO4) catalysts that not only affect energy barriers but also have an impact on the ammonolysis of t-N2O4 in neutral and acidic conditions.
Environmental significance
Nitrogen tetroxide (N2O4) is considered to be a dimer of nitrogen dioxide (NO2) and plays an important role in the formation of acid rain. The fact is that the ammonolysis of t-N2O4 is one of the potential sources of HNO3 formation; thus, the effort of water monomer, water dimer, and sulfuric acid on the ammonolysis of t-N2O4 was studied by quantum chemical method and Master equation rate calculations. The quantum chemical results reveal that the ammonolysis of t-N2O4 with (H2O)2 and H2SO4 are barrierless or nearly barrierless reactions. In terms of the effective rate constant, (H2O)2 outperforms the other catalysts in the temperature range 280–320 K (0 km). Moreover, the effect of H2SO4 on the ammonolysis reaction of t-N2O4 is obvious at higher altitudes of 5–30 km. In general, this work will give a new insights into how the neutral and acidic catalysts affect the formation of HNO3.
|
1. Introduction
Nitrogen dioxide (NO2),1 as one of the most significant NOx, is not only a precursor to the photochemical formation of ozone in the troposphere,2 but it can also contribute to the formation of photochemical smog and cause significant health and environmental hazards.3 Nitrogen tetroxide (N2O4), a dimer of nitrogen dioxide (NO2),4 can be used for nitration, nitrosation, and oxidation.5 In addition, N2O4 is an oxidizing agent for auto-igniting fuels and plays an important role in the formation of acid rain.6 Due to the fact that N2O4 is a highly toxic chemical species that hinders experimental studies,7 quantum calculations are a trend in current research to probe the N2O4-related reaction mechanisms. As the most major loss route of N2O4 in the atmosphere, the hydrolysis of N2O4 is potentially important in the lower atmosphere and plays an important role in the formation of HONO, a major source of OH pollution in the urban atmosphere.8,9
Several investigations have shown that the less stable t-N2O4 (trans-N2O4) is substantially more reactive than s-ONONO2 (symmetric N2O4); hence, it was selected as a starting point for studying the hydrolysis of NO2 dimers.9–12 The reaction barrier for the hydrolysis of t-N2O4 to form HONO was in the range of 10.8–11.9 kcal mol−1 at different theoretical levels.9,11,12 Several groups reported that using H2O and (H2O)2 as catalysts stabilized the reactant complexes by 3.5–6.9 kcal mol−1 and reduced the energy barrier to 6.2 kcal mol−1. Consequently, Zhang et al.9 revealed that, for the hydrolysis of t-N2O4, the H2SO4 catalyst is more effective than H2O and (H2O)2 catalysts, resulting in not only a higher binding energy of 15.0 kcal mol−1 for the reactant complex but also a lower energy barrier of 3.8 kcal mol−1.
In the atmosphere, the hydrolysis of t-N2O4 to produce HONO is the most major loss route of t-N2O4.10,11 As a complement to the loss of t-N2O4, the ammonolysis reaction of t-N2O4 can form HNO3,13 which could be competitive with the main source of HNO3, the gas-phase reaction of NO2 with the hydroxyl (OH) radical8,14 during the day and the hydrolysis reaction of N2O5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15–17 at night, in polluted areas of NH3. The ammonolysis of t-N2O4 (shown in eqn (1) and (2)) investigated by Lin et al.13 reveals that the energy barrier of the t-N2O4 + NH3 reaction was determined to be 5.3 kcal mol−1 and the corresponding rate constant at low temperature was not pressure-dependent. As far as we know, the effect of neutral and acidic gases on the ammonolysis of t-N2O4, which plays a significant catalytic role in hydrogen abstraction reactions,9,15,18–37 has not been explored.
15–17 at night, in polluted areas of NH3. The ammonolysis of t-N2O4 (shown in eqn (1) and (2)) investigated by Lin et al.13 reveals that the energy barrier of the t-N2O4 + NH3 reaction was determined to be 5.3 kcal mol−1 and the corresponding rate constant at low temperature was not pressure-dependent. As far as we know, the effect of neutral and acidic gases on the ammonolysis of t-N2O4, which plays a significant catalytic role in hydrogen abstraction reactions,9,15,18–37 has not been explored.
| | | t-N2O4 + NH3 → HNO3 + NH2NO | (2) |
As in the previous studies on N2O4 + H2O,11,12 HO2 + NO2,38 H2CO + NH3,39 and SO2 + NO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 reactions, water molecules were found to play an essential role in enhancing the stability of pre-reactive complexes and lowering the apparent activation energies of the transition states. In addition to water monomer, some recent works addressed the potential role of water dimer,18,41 which may play a significant catalytic role in hydrogen abstraction reactions because its concentrations can reach 9 × 1014 mol cm−3.42,43 Aside from water monomer and water dimer, acidic9,15,30–37 gas species in the atmosphere may also be effective in lowering the energy barriers for hydrogen transfer reactions30–34 and atmospheric hydrolysis reactions9,15,35–37 in the gas phase. The presence of H2SO4
40 reactions, water molecules were found to play an essential role in enhancing the stability of pre-reactive complexes and lowering the apparent activation energies of the transition states. In addition to water monomer, some recent works addressed the potential role of water dimer,18,41 which may play a significant catalytic role in hydrogen abstraction reactions because its concentrations can reach 9 × 1014 mol cm−3.42,43 Aside from water monomer and water dimer, acidic9,15,30–37 gas species in the atmosphere may also be effective in lowering the energy barriers for hydrogen transfer reactions30–34 and atmospheric hydrolysis reactions9,15,35–37 in the gas phase. The presence of H2SO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37,44 in the atmosphere was considered to be a more effective catalyst than neutral catalysts,25,28–30,33,45 which not only greatly reduces the energy barriers27,28,33 but also facilitates the transfer of hydrogen,30–33,46 and thus, H2SO4 was regarded as either good acceptors or good donors of H in the catalytic gas reactions. These situations stimulated our interest in studying the ammonolysis of t-N2O4 by neutral (H2O and (H2O)2) and acidic (H2SO4) gases.
37,44 in the atmosphere was considered to be a more effective catalyst than neutral catalysts,25,28–30,33,45 which not only greatly reduces the energy barriers27,28,33 but also facilitates the transfer of hydrogen,30–33,46 and thus, H2SO4 was regarded as either good acceptors or good donors of H in the catalytic gas reactions. These situations stimulated our interest in studying the ammonolysis of t-N2O4 by neutral (H2O and (H2O)2) and acidic (H2SO4) gases.
In this work, using global minimum searching combined with quantum chemical methods, we first obtained the stable structures of the reactant complexes of t-N2O4⋯NH3⋯X (X = H2O, (H2O)2, and H2SO4). The ammonolysis of t-N2O4 in the presence of X was then studied using the stable molecular clusters t-N2O4⋯NH3⋯X. Finally, the effective rate constant for the ammonolysis of t-N2O4 with X was estimated at temperatures ranging from 213 to 320 K and altitudes ranging from 0 to 30 km.
2. Calculation details
2.1 Electronic structure calculations
The molecular geometries of the isolated reactants, pre-reactive complexes, transition states, post-reactive complexes, and products of the ammonolysis reaction of t-N2O4 without and with X were optimized using the B3LYP-D3 method47–53 with 6-311++G(3df,2pd) basis set in Gaussian 09 suites.54 The D3 method has been reliably utilized to describe the noncovalent interaction and the equilibrium structure of atmospheric clusters and reactions.51,55 Notably, the keyword “stable = opt” is added in the calculations at the B3LYP-D3/6-311++G(3df,2pd) level to ensure that all the geometries are stable. Frequency calculations were calculated at the same level for all stationary points to check that all transition states have the same character as a first-order saddle point with a single imaginary frequency and that other stationary points correspond to minima on potential energy surfaces (PESs). The scaling factor employed to adjust the ZPEs was 0.969.56,57 To ensure that the optimized transition state connects the desired pre- and post-reactive complexes, intrinsic reaction coordinate (IRC) calculations58–60 were performed at the same level. To improve the accuracy of the relative energies, single-point energy calculation was performed at the CCSD(T)/aug-cc-pVTZ61–63 level by using the Gaussian 09 software.54 It was noted that the T1 diagnostic values for closed-shell in Table S3† were 0.02 less than the standard value,64,65 showing the multireference calculations for recovering non-dynamical correlation were not a problem, and the single reference method of CCSD(T)/aug-cc-pVTZ is reliable to single point energy calculation.
Global minimum searching combined with quantum chemical methods was employed to obtain the most stable structures of the reactant complexes of t-N2O4⋯NH3⋯X. Initially, 500 structures with low energies were auto-produced by ABCluster software66,67 with TIP4P68,69 model for H2O, (H2O)2, and CHARMM70 force field for t-N2O4, NH3, and H2SO4. Then, pre-optimized by the semi-empirical method of PM7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 71 in MOPAC 2016.72 Next, the structures with the N(t-N2O4)⋯N(NH3) interaction of electron donor–acceptor (EDA) and facilitating the transfer of hydrogen atom from t-N2O4 to NH3 were selected to optimize at the B3LYP-D3/6-311+G(d,p) level. Subsequently, 50 isomers with an order of electronic energies were chosen to optimize at the level of B3LYP-D3/6-311+G(2d,2p). Finally, the global minimum isomers within 5.0 kcal mol−1 (the electric energy) were re-optimized at the B3LYP-D3/6-311++G(3df,2pd) level.
71 in MOPAC 2016.72 Next, the structures with the N(t-N2O4)⋯N(NH3) interaction of electron donor–acceptor (EDA) and facilitating the transfer of hydrogen atom from t-N2O4 to NH3 were selected to optimize at the B3LYP-D3/6-311+G(d,p) level. Subsequently, 50 isomers with an order of electronic energies were chosen to optimize at the level of B3LYP-D3/6-311+G(2d,2p). Finally, the global minimum isomers within 5.0 kcal mol−1 (the electric energy) were re-optimized at the B3LYP-D3/6-311++G(3df,2pd) level.
2.2 Rate constant calculations
The rate constants for the ammonolysis reaction of t-N2O4 without and with X were calculated in two steps. First, the high-pressure-limit (HPL) rate constants were calculated by using the VRC-VTST calculations in Polyrate 2017 software.73 The details of VRC-VTST can be seen in Table S7 of the ESI.† Then, based on the HPL rate constants, the rate constants for the ammonolysis reaction of t-N2O4 without and with X at different temperatures and pressures were calculated using the Master Equation Solver for Multi-Energy Well Reactions (MESMER) program.74 The Inverse Laplace Transform (ILT) approach was used to analyze the barrierless step from distinct reactants to the pre-reactive complex.75,76 Meanwhile, the transition step from the pre-reactive complex to the post-reactive complex occurring through the transition state was applied to the RRKM theory.77,78 ILT methods and RRKM theory can be, respectively, expressed in eqn (3) and (4).| | 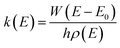 | (3) |
| | 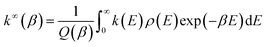 | (4) |
In eqn (3) and (4), where W(E − E0) is the rovibrational sum of states (SOS) at the optimized transition state (TS) geometry, E0 is the reaction threshold energy, h is Planck's constant, ρ(E) is the density of rovibrational states of the reactant, and Q(β) is the corresponding canonical partition function. Moreover, the electronic geometries, vibrational frequencies, and rotational constants were calculated at the B3LYP-D3/6-311++G(3df,2pd) level, and single-point energy calculations were refined at the CCSD(T)/aug-cc-pVTZ level for the modeling. The one-dimensional asymmetric Eckart potential was used to treat the tunneling effect in the RRKM calculation. In addition, the Lennard-Jones (L-J) parameters ε/kB = 71.4 K and σ = 3.798 Å were used for N2,79ε/kB = 200.0 K and σ = 3.50 Å were used for t-N2O4,80 while ε/kB = 481.0 K and σ = 2.92 Å were estimated for NH3.80
3. Results and discussions
The pre-reactive complex in each reaction channel was denoted by “IM” followed by a number, whereas the transition state and post-reactive complexes were denoted by “TS” and “IMF”, respectively. Species in the presence of H2O, (H2O)2, and H2SO4 were denoted by the suffixes “WM”, “WD”, and “SA”.
3.1 Mechanism and rate constants for the ammonolysis reaction of t-N2O4
The ammonolysis reaction of t-N2O4 has been extensively investigated from the theoretical viewpoint.13 Here, this reaction has been reinvestigated at the CCSD(T)/aug-cc-pVTZ//B3LYP-D3/6-311++G(3df,2pd) level to check the catalytic effect of X. Our results shown in Fig. 1 were found to be very mechanistically and energetically similar to the work reported by Lin et al.13 All the relative energy values qualitatively matched (see Table S2†). As seen in Fig. 1, the t-N2O4 + NH3 reaction occurred through a ring formation mechanism, resulting in the formation of a six-membered ring complex t-N2O4⋯NH3 with a binding energy of 0.5 kcal mol−1. Then, the terminal O1 atom of t-N2O4 abstracts the H atom of NH3 along with the N–N bond formation to form the product complex HNO3⋯NH2NO. From an energy point of view, the barrier height of the t-N2O4 + NH3 reaction was 3.7 kcal mol−1, revealing that t-N2O4 can easily react with NH3 in the gas phase.
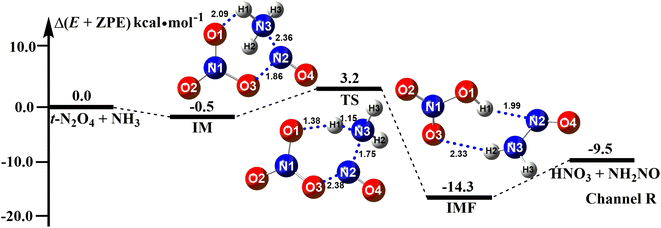 |
| | Fig. 1 Potential energy profiles for the t-N2O4 + NH3 → HNO3 + NH2NO reaction at the CCSD(T)/aug-cc-pVTZ//B3LYP-D3/6-311++G(3df,2pd) level. | |
The calculated rate constants for the ammonolysis reaction of t-N2O4 are listed in Table 1. In the ammonolysis reaction of t-N2O4, the hindered internal rotation (HIR)77,81–86 correction at 760 Torr has a moderate effect, increasing the rate constants by a factor of 1.25 to 1.28. Meanwhile, the almost unchanged rate constants for the ammonolysis reaction of t-N2O4 at different atmospheric pressures revealed that the pressure (10–760 Torr)87 has little effect on the ammonolysis reaction of t-N2O4 within the temperature range of 280–320 K.88,89
Table 1 The rate constants (kR) (cm3 mol−1 s−1) for the t-N2O4 + NH3 reaction without and with HIR treatments within the temperature range of 280–320 K and pressure range of 10–760 Torr
|
T (K) |
HIR impacta |
Pressure impact |
| With HIR treatments |
Without HIR treatments |
Factorb |
10 Torr |
50 Torr |
100 Torr |
300 Torr |
760 Torr |
|
HIR impact represents the hindered internal rotations treatment.
Factor denotes the rate ratio between with HIR treatments and without HIR treatments.
|
| 280 |
6.67 × 10−17 |
5.20 × 10−17 |
1.28 |
5.03 × 10−17 |
5.14 × 10−17 |
5.16 × 10−17 |
5.18 × 10−17 |
5.20 × 10−17 |
| 290 |
7.81 × 10−17 |
6.13 × 10−17 |
1.27 |
5.90 × 10−17 |
6.07 × 10−17 |
6.10 × 10−17 |
6.12 × 10−17 |
6.13 × 10−17 |
| 298 |
8.80 × 10−17 |
6.95 × 10−17 |
1.27 |
6.65 × 10−17 |
6.88 × 10−17 |
6.92 × 10−17 |
6.94 × 10−17 |
6.95 × 10−17 |
| 300 |
9.06 × 10−17 |
7.17 × 10−17 |
1.26 |
6.84 × 10−17 |
7.09 × 10−17 |
7.13 × 10−17 |
7.16 × 10−17 |
7.17 × 10−17 |
| 310 |
1.04 × 10−16 |
8.32 × 10−17 |
1.26 |
7.84 × 10−17 |
8.20 × 10−17 |
8.26 × 10−17 |
8.30 × 10−17 |
8.32 × 10−17 |
| 320 |
1.19 × 10−16 |
9.57 × 10−17 |
1.25 |
9.40 × 10−17 |
9.40 × 10−17 |
9.55 × 10−17 |
9.55 × 10−17 |
9.57 × 10−17 |
3.2 Mechanism and rate constants for the ammonolysis reaction of t-N2O4 with H2O and (H2O)2
Fig. 2a and b show the ammonolysis reaction of t-N2O4 assisted by H2O (Channel WM) and (H2O)2 (Channel WD), where both H2O and (H2O)2 served as a “bridge” to promote hydrogen atom transfer from the N3 atom of NH3 to the terminal O1 atom of t-N2O4. In the case of Channel WM, the reaction can occur either (a) between NH3 and monohydrated t-N2O4 (t-N2O4⋯H2O) or (b) between hydrated NH3 (NH3⋯H2O) and t-N2O4. The binding energy of t-N2O4⋯H2O was 2.9 kcal mol−1, which was consistent with the previously calculated value of 3.5 kcal mol−1 at the CCSD(T)-F12a/cc-pVDZ-F12//M06-2X/6-311++G(3df,2pd) level.9 The binding energy of NH3⋯H2O was 4.4 kcal mol−1, which agreed well with the calculated values of 4.4–4.6 kcal mol−1.90,91 The stability of NH3⋯H2O was 1.5 kcal mol−1 higher than that of t-N2O4⋯H2O. So, the ammonolysis of t-N2O4 in the presence of H2O mainly takes place via the collision of NH3⋯H2O with t-N2O4 to form the quasi-planar eight-membered ring reactant complex IM_WM1. The energy of the reactant complex IM_WM1 was 4.7 kcal mol−1 lower than that of the isolated reactants t-N2O4 + H2O + NH3. In the complex IM_WM1, H2O played the roles of a single acceptor and donor of hydrogen bonds. After the formation of the complex IM_WM1, the reaction proceeded to form a hydrogen-bonded complex, HNO3⋯H2O⋯NH2NO (denoted IMF_WM), through the transition state TS_WM, with an energy barrier of 4.2 kcal mol−1.
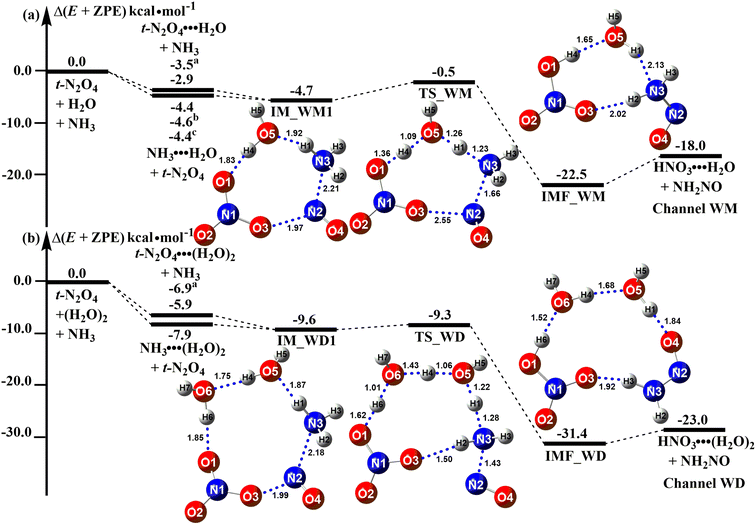 |
| | Fig. 2 Potential energy profiles for the t-N2O4 + NH3 → HNO3 + NH2NO reaction catalyzed by H2O and (H2O)2 at the CCSD(T)/aug-cc-pVTZ//B3LYP-D3/6-311++G(3df,2pd) level (a–c) denotes the values respectively reported from ref. 9, 90, and 91. | |
The reaction t-N2O4 + NH3 + (H2O)2 can be initiated by the reactant complex IM_WD1, which can be formed from t-N2O4⋯(H2O)2 + NH3 or t-N2O4 + NH3⋯(H2O)2. It is clear from Fig. 2b that NH3 was most likely bound to (H2O)2 prior to t-N2O4. The reactant complex IM_WD1 has a quasi-planar structure similar to that of complex IM_WM1 and can be regarded as H2O in IM_WM1, which was replaced by (H2O)2. The binding energy of IM_WD1 was 1.7 kcal mol−1 from t-N2O4 + NH3⋯(H2O)2. After complex IM_WD1, the ammonolysis reaction of t-N2O4 with (H2O)2 can form the product complex HNO3⋯(H2O)2⋯NH2NO (labeled as IMF_WD) through the transition state TS_WD with an energy barrier of 0.3 kcal mol−1. Three hydrogen atom transfer mechanisms occurred at TS_WD, as well as the simultaneous formation of the N(2)⋯N(3) bond. In comparison to H2O in Channel WM, (H2O)2 in Channel WD played a more obvious catalytic role in promoting the ammonolysis reaction of t-N2O4. When (H2O)2 was used as a catalyst in Channel WD, it stabilized the reactant complex by a further 4.9 kcal mol−1 and decreased the reaction barrier by 3.9 kcal mol−1. The more pronounced catalytic effect of (H2O)2 could be attributed to two factors. On the one hand, (H2O)2 may improve the N(t-N2O4)⋯N(NH3) interaction compared to H2O. For example, in the reactant complex IM_WD1, the strengthening of the N(t-N2O4)⋯N(NH3) interaction was shown by the shortening of the bond distance N(2)⋯N(3) (2.18 Å, shown in Fig. 2b), which is less than the corresponding value in the reactant complex IM_WM1 (2.21 Å, shown in Fig. 2a). On the other hand, when H2O was replaced by (H2O)2, however, the transition state extended from an eight-member ring (TS_WM) to a ten-member ring (TS_WD). This structural change reduces the ring tension of the transition state to a certain extent, lowering the reaction energy barrier.
As shown in Table 2, within the range of 213–320 K and 0–30 km,88,89 the rate constant for the ammonolysis reaction of t-N2O4 assisted by H2O (kWM) was predicted to be 3.94 × 10−20 to 1.93 × 10−19 cm3 mol−1 s−1, which was 2–3 orders of magnitude lower than that of the naked ammonolysis reaction of t-N2O4. The calculated rate constant for the ammonolysis reaction of t-N2O4 assisted by (H2O)2 (kWD) was 3.66 × 10−16 to 1.98 × 10−15 cm3 mol−1 s−1, which was 1–2 orders of magnitude greater than the naked ammonolysis reaction of t-N2O4. The ammonolysis reaction of t-N2O4 assisted by (H2O)2 was more kinetically favorable than the ammonolysis reaction of t-N2O4 with H2O, with a rate constant that was 3–5 orders of magnitude greater.
Table 2 Calculated rate constants (k, cm3 mol−1 s−1) for the t-N2O4 + NH3 reaction with H2O, (H2O)2, and H2SO4 calculated by master equation within the range of 213–320 K and 0–30 kma,b
| Altitude |
T (K) |
k
R
|
k
WM
|
k
WD
|
k
SA
|
|
k
R, kWM, kWD, and kSA were respectively denoted the rate constants for the t-N2O4 + NH3, t-N2O4 + NH3⋯H2O, t-N2O4 + NH3⋯(H2O)2, and t-N2O4 + NH3⋯H2SO4 reactions.
The 0–30 km data were reported from ref. 88 and 89.
|
| 0 km |
280 |
5.20 × 10−17 |
1.16 × 10−19 |
6.05 × 10−16 |
1.49 × 10−16 |
| 290 |
6.13 × 10−17 |
1.33 × 10−19 |
5.29 × 10−16 |
1.50 × 10−16 |
| 298 |
6.95 × 10−17 |
1.48 × 10−19 |
4.76 × 10−16 |
1.50 × 10−16 |
| 300 |
7.17 × 10−17 |
1.52 × 10−19 |
4.64 × 10−16 |
1.51 × 10−16 |
| 310 |
8.32 × 10−17 |
1.72 × 10−19 |
4.11 × 10−16 |
1.52 × 10−16 |
| 320 |
9.57 × 10−17 |
1.93 × 10−19 |
3.66 × 10−16 |
1.54 × 10−16 |
| 5 km |
259.3 |
3.59 × 10−17 |
8.59 × 10−20 |
8.30 × 10−16 |
1.48 × 10−16 |
| 10 km |
229.7 |
1.92 × 10−17 |
5.32 × 10−20 |
1.40 × 10−15 |
1.51 × 10−16 |
| 15 km |
212.6 |
1.24 × 10−17 |
3.94 × 10−20 |
1.98 × 10−15 |
1.56 × 10−16 |
| 20 km |
215.5 |
1.28 × 10−17 |
4.15 × 10−20 |
1.86 × 10−15 |
1.55 × 10−16 |
| 25 km |
218.6 |
1.37 × 10−17 |
4.38 × 10−20 |
1.74 × 10−15 |
1.54 × 10−16 |
| 30 km |
223.7 |
1.55 × 10−17 |
4.79 × 10−20 |
1.57 × 10−15 |
1.53 × 10−16 |
3.3 Mechanism and rate constants for the ammonolysis reaction of t-N2O4 with H2SO4
As shown in Fig. S3,† nine geometrical isomers of the reactant complex t-N2O4⋯NH3⋯H2SO4 (labeled as IM_SAn, n = 1–9) were found at the B3LYP-D3/6-311++G(3df,2pd) level, with complex IM_SA1 being the most stable. Based on complex IM_SA1, Fig. 3 presents the potential energy surface (PES) for the ammonolysis of t-N2O4 in the presence of H2SO4 (Channel SA). In the case of Channel SA, the reaction can occur (a) between NH3 and t-N2O4⋯H2SO4 or (b) between t-N2O4 and NH3⋯H2SO4. The binding energy of NH3⋯H2SO4 was 14.7 kcal mol−1, which was in good agreement with the previously reported value.92 The large binding energy of NH3⋯H2SO4 indicates that in the reaction of t-N2O4 + NH3 + H2SO4, NH3 is easily bound to the isolated H2SO4. In this sense, the ammonolysis reaction of t-N2O4 with H2SO4 mainly takes place via the collision of t-N2O4 with NH3⋯H2SO4, resulting in the reactant complex IM_SA1.
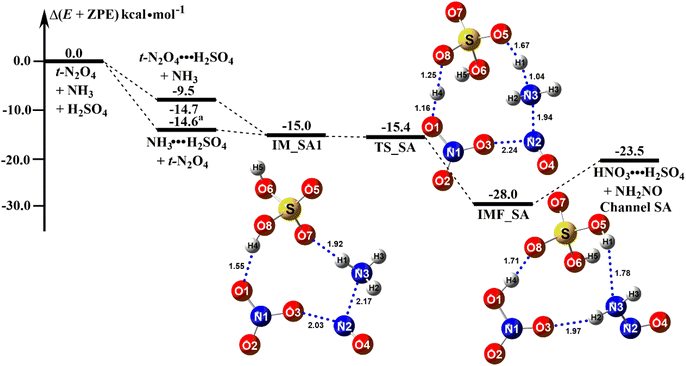 |
| | Fig. 3 Potential energy profiles for the t-N2O4 + NH3 → HNO3 + NH2NO reaction catalyzed by H2SO4 at the CCSD(T)/aug-cc-pVTZ//B3LYP-D3/6-311++G(3df,2pd) level (a) The values was reported from ref. 92. | |
The energy of the reactant complex IM_SA1 was 15.0 kcal mol−1 lower than that of the separate reactants t-N2O4, NH3, and H2SO4. In the complex IM_SA1, H2SO4 served as a single donor and acceptor of hydrogen bonds to form a ring-like structure with the binary complex of t-N2O4⋯NH3. The stability of complex IM_SA1 increased by 5.4–10.3 kcal mol−1 when compared to the reactant complexes IM_WM1 and IM_WD1, with the distance of the N(t-N2O4)⋯N(NH3) bond reduced by 0.01–0.04 Å. After the formation of the complex IM_SA1, Channel SA proceeded through the transition state TS_SA to form a ten-membered ring hydrogen-bonded complex HNO3⋯H2SO4⋯NH2NO (labeled as IMF_SA). Similar to the transition state TS_WM described above, TS_SA was in the middle of a double hydrogen atom transfer process, with the H2SO4 moiety serving as a bridge for the hydrogen transfer. From the viewpoint of the energy barrier height, Channel SA was a barrierless process. In comparison to H2O and (H2O)2, H2SO4 could lower the energy barrier, at least by 0.7–4.6 kcal mol−1. Complex IMF_SA showed a ten-membered ring structure. It had a binding energy of 28.0 kcal mol−1 to the separate reactants t-N2O4, NH3, and H2SO4, which was 13.0 kcal mol−1 lower than the reactant complex IM_SA1. The rate constant of the t-N2O4 + NH3⋯H2SO4 reaction is one order of magnitude more than that of the ammonolysis reaction of t-N2O4 without a catalyst, as shown in Table 2. This result revealed that H2SO4 in the t-N2O4 + NH3⋯H2SO4 reaction plays a favorable catalytic role in promoting the ammonolysis reaction of t-N2O4. Thus, the ammonolysis reaction of t-N2O4 assisted by (H2O)2 and H2SO4 was more kinetically favorable than the reaction with H2O.
3.4 Kinetics and implication in atmospheric chemistry
According to previous reports,93–96 it is clear that the rate constant listed in Table 2 is insufficient to predict the atmospheric importance of the ammonolysis reaction of t-N2O4 assisted by (H2O)2 and H2SO4. To understand the atmospheric effect of (H2O)2 and H2SO4 on the ammonolysis reaction of t-N2O4, we introduced the effective rate constants (k′) to calculate the relative efficiency of neutral and acid trace gases affecting the atmospheric reaction97–100 and to compare the rate constant for the naked reaction.
On the basis of the rate constant for Channels WM, WD, and SA, the equilibrium constant for the bimolecular formation (NH3⋯H2O, NH3⋯(H2O)2, and NH3⋯H2SO4) and the concentrations of H2O, (H2O)2, and H2SO4 are listed in Tables S4-6,† as stated in eqn (5)–(7).
| | 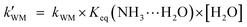 | (5) |
| | 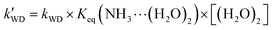 | (6) |
| | 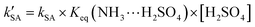 | (7) |
where
kWM,
kWD, and
kSA are the bimolecular rate constants for Channel WM, Channels WD, and SA, respectively;
Keq(NH
3⋯H
2O),
Keq(NH
3⋯(H
2O)
2), and
Keq(NH
3⋯H
2SO
4) are the equilibrium constants for the formation of complexes NH
3⋯H
2O, NH
3⋯(H
2O)
2, and NH
3⋯H
2SO
4. [H
2O], [(H
2O)
2], and [H
2SO
4] represent the concentrations of H
2O, (H
2O)
2, and H
2SO
4 taken from previous reports.
44,87 The
k′ for the ammonolysis reaction of
t-N
2O
4 with X at 0 km altitude and at different altitudes (5–30 km) in the troposphere was calculated.
3.4.1 Zero kilometer altitude.
As seen in Table 3, the calculated value of 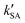 can compete with
can compete with 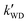 at 280 K. With increasing temperature, the calculated
at 280 K. With increasing temperature, the calculated 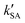 was ∼1–3 orders of magnitude smaller than the values of
was ∼1–3 orders of magnitude smaller than the values of 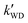 , showing that the ammonolysis reaction of t-N2O4 was superior to that of an acidic (H2SO4) catalyst in the presence of neutral (H2O and (H2O)2) catalysts. However, the H2SO4-catalyzed reaction can be neglected because its calculated
, showing that the ammonolysis reaction of t-N2O4 was superior to that of an acidic (H2SO4) catalyst in the presence of neutral (H2O and (H2O)2) catalysts. However, the H2SO4-catalyzed reaction can be neglected because its calculated 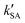 was at least 4 orders of magnitude lower than the corresponding value of kR in the naked reaction of the ammonolysis reaction of t-N2O4. This indicated that the contributions of H2SO4 to the ammonolysis reaction of t-N2O4 in atmospheric chemistry are not obvious within the temperature range of 280–320 K (at 0 km altitude).
was at least 4 orders of magnitude lower than the corresponding value of kR in the naked reaction of the ammonolysis reaction of t-N2O4. This indicated that the contributions of H2SO4 to the ammonolysis reaction of t-N2O4 in atmospheric chemistry are not obvious within the temperature range of 280–320 K (at 0 km altitude).
Table 3 The effective rate constants (k′, cm3 molecule−1 s−1) for the t-N2O4 + NH3 reaction assisted by H2O, (H2O)2, and H2SO4 within the temperature range of 280–320 Ka,b (0 km)
| Catalysts |
T/K |
280 K |
290 K |
298 K |
300 K |
310 K |
320 K |
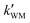 , , 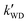 , and , and 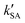 were respectively denoted the effective rate constants for the t-N2O4 + NH3⋯H2O, t-N2O4 + NH3⋯(H2O)2, and t-N2O4 + NH3⋯H2SO4 reactions.
The values of temperature were reported from ref. 88 and 89.
The values of concentrations were reported from ref. 44 and 87. were respectively denoted the effective rate constants for the t-N2O4 + NH3⋯H2O, t-N2O4 + NH3⋯(H2O)2, and t-N2O4 + NH3⋯H2SO4 reactions.
The values of temperature were reported from ref. 88 and 89.
The values of concentrations were reported from ref. 44 and 87.
|
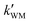
|
100% RHc |
4.29 × 10−22 |
6.96 × 10−22 |
1.02 × 10−21 |
1.11 × 10−21 |
1.70 × 10−21 |
2.49 × 10−21 |
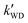
|
100% RHc |
2.45 × 10−21 |
3.68 × 10−21 |
5.16 × 10−21 |
5.46 × 10−21 |
7.70 × 10−21 |
1.02 × 10−20 |
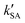
|
[H2SO4]c = 108 mol cm3 |
1.39 × 10−21 |
5.49 × 10−22 |
2.72 × 10−22 |
2.32 × 10−22 |
1.03 × 10−22 |
4.71 × 10−23 |
3.4.2 Higher altitudes.
The k′ for the ammonolysis reaction of t-N2O4 with H2O, (H2O)2, and H2SO4 were calculated within the 5–30 km altitude range, and the calculated k′ is listed in Table 4. It can be seen in Table 4 that the contribution of H2SO4 was most obvious in the catalysts of H2O, (H2O)2, and H2SO4 within the altitude range of 5–30 km, since the value of 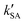 was larger by 1–8 orders of magnitude than that of
was larger by 1–8 orders of magnitude than that of 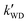 . In order to quantitatively assess the impact of H2SO4 on the ammonolysis reaction of t-N2O4, the total rate constant ktot can be calculated using eqn (8). The branching ratio for
. In order to quantitatively assess the impact of H2SO4 on the ammonolysis reaction of t-N2O4, the total rate constant ktot can be calculated using eqn (8). The branching ratio for 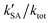 in Table 4 was calculated to be 3.11 × 10−5–5.06 × 10−4 at 5–30 km. This indicates that the contribution of the H2SO4-assisted ammonolysis reaction of t-N2O4 can be negligible in atmospheric gas-phase chemistry.
in Table 4 was calculated to be 3.11 × 10−5–5.06 × 10−4 at 5–30 km. This indicates that the contribution of the H2SO4-assisted ammonolysis reaction of t-N2O4 can be negligible in atmospheric gas-phase chemistry.| | 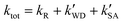 | (8) |
Table 4 The effective rate constants (k′, cm3 molecule−1 s−1) for the t-N2O4 + NH3 reaction with H2O, (H2O)2, and H2SO4 at different altitudes in tropospherea
4. Summary and conclusions
In this work, the favorable route for the ammonolysis reaction of t-N2O4 in the presence of neutral (H2O and (H2O)2) and acidic (H2SO4) catalysts was investigated using the quantum chemical method of CCSD(T)/aug-cc-pVTZ//B3LYP-D3/6-311++G(3df,2pd) and the master equation. The calculated results show that the energy barrier for the ammonolysis reaction of t-N2O4 increased when H2O was present, but when (H2O)2 was present, the reaction energy barrier decreased to 0.3 kcal mol−1, which was 3.4 kcal mol−1 lower than the ammonolysis reaction of t-N2O4 without the catalyst, especially when H2SO4 was directly involved in the reaction that is a barrierless process. In terms of the effective rate constant, (H2O)2 outperforms the other catalysts in the temperature range of 280–320 K (0 km). Moreover, the effect of H2SO4 on the ammonolysis reaction of t-N2O4 is obvious at higher altitudes of 5–30 km. Overall, this work will give a new insight into how the neutral and acidic catalysts affect the formation of HNO3 from the ammonolysis reaction of t-N2O4. As HNO3 is an important source of acid rain, the present work will provide a potential formation pathway for HNO3, which plays a crucial role in the formation of acid rain.
Author contributions
Ruxue Mu: investigation, data curation, visualization, writing – original draft. Weixin Zhou: supervision, writing – review and editing, project administration. Zhaozhao Hong: visualization, data curation. Rui Wang: writing – review and editing, project administration. Quan Liu: visualization, data curation. Qiang Zhang: formal analysis. Min Jiang: formal analysis. Balaganesh Muthiah: supervision, writing – review and editing. Tianlei Zhang: writing – review and editing, project administration.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (no. 22073059, 22203052); the Natural Science Foundation of Shaanxi Province (no. 2023-YBGY-486, 2022JM-133); the Funds of Graduate Innovation of Shaanxi University of Technology (no. SLGYCX2304); the authors also thank Prof. Mark A. Blitz (from University of Leeds) for providing the use of the MESMER program.
References
- M. T. Martins-Costa, J. M. Anglada, J. S. Francisco and M. F. Ruiz-López, Theoretical investigation of the photoexcited NO2 + H2O reaction at the air-water interface and its atmospheric implications, Chem. – Eur. J., 2019, 25, 13899–13904 CrossRef CAS PubMed
 .
.
- A. Bacak, M. Cooke, M. Bardwell, M. McGillen, A. Archibald, L. Huey, D. Tanner, S. Utembe, M. Jenkin and R. Derwent, Kinetics of the HO2 + NO2 Reaction: On the impact of new gas-phase kinetic data for the formation of HO2NO2 on HOx, NOx and HO2NO2 levels in the troposphere, Atmos. Environ., 2011, 45, 6414–6422 CrossRef CAS
 .
.
-
J. H. Seinfeld and S. N. Pandis, Atmospheric Chemistry and Physics: from Air Pollution to Climate Change, John Wiley & Sons, 2016 Search PubMed
 .
.
- W.-G. Liu and W. A. Goddard III, First-principles study of the role of interconversion between NO2, N2O4, cis-ONO-NO2, and trans-ONO-NO2 in chemical processes, J. Am. Chem. Soc., 2012, 134, 12970–12978 CrossRef CAS PubMed
 .
.
- C. Nonnenberg, I. Frank and T. M. Klapötke, Ultrafast cold reactions in the bipropellant monomethylhydrazine/nitrogen tetroxide: CPMD simulations, Angew. Chem., Int. Ed., 2004, 43, 4586–4589 CrossRef CAS PubMed
 .
.
- L. Dejun, T. Gan, Y. Zhengwei, J. Guofeng, W. ZHANG, W. Yin and W. Huali, Stress corrosion behavior of 2195-T8 Al-Li alloy with an artificial pit exposed to a 30vol% HNO3 solution, Chin. J. Aeronaut., 2023, 36, 304–315 CrossRef
 .
.
- Y. Guo, Z. Huang, G. Tian, W. Wu, J. Lin and X. Chang, Isomerization and reaction process of N2O4(H2O)n, RSC Adv., 2023, 13, 12469–12475 RSC
 .
.
-
B. J. Finlayson-Pitts and J. N. Pitts Jr, Chemistry of the Upper and Lower Atmosphere: Theory, Experiments, and Applications, Elsevier, 1999 Search PubMed
 .
.
- T. Zhang, M. Wen, X. Cao, Y. Zhang, Z. Zeng, X. Guo, C. Zhao, M. Lily and R. Wang, The hydrolysis of NO2 dimer in small clusters of sulfuric acid: A potential source of nitrous acid in troposphere, Atmos. Environ., 2020, 243, 117876 CrossRef CAS
 .
.
- L. Li, Z. Duan, H. Li, C. Zhu, G. Henkelman, J. S. Francisco and X. C. Zeng, Formation of HONO from the NH3-promoted hydrolysis of NO2 dimers in the atmosphere, Proc. Natl. Acad. Sci., 2018, 115, 7236–7241 CrossRef CAS PubMed
 .
.
- R. Zhu, K.-Y. Lai and M.-C. Lin, Ab initio chemical kinetics for the hydrolysis of N2O4 isomers in the gas phase, J. Phys. Chem. A, 2012, 116, 4466–4472 CrossRef CAS PubMed
 .
.
- R. Putikam and M. C. Lin, A novel mechanism for the isomerization of N2O4 and its implication for the reaction with H2O and acid rain formation, Int. J. Quantum Chem., 2018, 118, e25560 CrossRef
 .
.
- H. P. Trac, T. Le Huyen and M.-C. Lin, A Computational Study on the Redox Reactions of Ammonia and Methylamine with Nitrogen Tetroxide, J. Phys. Chem. A, 2020, 124, 9923–9932 CrossRef CAS PubMed
 .
.
- K. Mondal, S. Biswas, A. Chattopadhyay, P. Chatterjee and T. Chakraborty, Gas-phase oxidation of NO2 to HNO3 by phenol: atmospheric implications, ACS Earth Space Chem., 2021, 5, 2131–2141 CrossRef CAS
 .
.
- M. Wen, R. Li, T. Zhang, C. Ding, Y. Hu, R. Mu, M. Liang, T. Ou and B. Long, A potential source of tropospheric secondary organic aerosol precursors: The hydrolysis of N2O5 in water dimer and small clusters of sulfuric acid, Atmos. Environ., 2022, 287, 119245 CrossRef CAS
 .
.
- J. G. Calvert, A. Lazrus, G. L. Kok, B. G. Heikes, J. G. Walega, J. Lind and C. A. Cantrell, Chemical mechanisms of acid generation in the troposphere, Nature, 1985, 317, 27–35 CrossRef CAS
 .
.
- J. I. Steinfeld, Atmospheric chemistry and physics: from air pollution to climate change, Environ Sci Policy, 1998, 40, 26 Search PubMed
 .
.
- L. P. Viegas and A. n. J. Varandas, Role of (H2O)n (n = 2-3) Clusters on the HO2 + O3 Reaction: A Theoretical Study, J. Phys. Chem. B, 2016, 120, 1560–1568 CrossRef CAS PubMed
 .
.
- B. Long, J. L. Bao and D. G. Truhlar, Unimolecular reaction of acetone oxide and its reaction with water in the atmosphere, Proc. Natl. Acad. Sci. U.S.A., 2018, 115, 6135–6140 CrossRef CAS PubMed
 .
.
- X. Chen, C. Tao, L. Zhong, Y. Gao, W. Yao and S. Li, Theoretical study on the atmospheric reaction of SO2 with the HO2 and HO2···H2O complex formation HSO4 and H2SO3, Chem. Phys. Lett., 2014, 608, 272–276 CrossRef CAS
 .
.
- R. J. Buszek, J. S. Francisco and J. M. Anglada, Water effects on atmospheric reactions, Int. Rev. Phys. Chem., 2011, 30, 335–369 Search PubMed
 .
.
- C. Iuga, J. R. Alvarez-Idaboy, L. Reyes and A. Vivier-Bunge, Can a single water molecule really catalyze the acetaldehyde + OH reaction in tropospheric conditions?, J. Phys. Chem. Lett., 2010, 1, 3112–3115 Search PubMed
 .
.
- B. Du and W. Zhang, Theoretical study on the water-assisted reaction of NCO with HCHO, J. Phys. Chem. A, 2013, 117, 6883–6892 CrossRef CAS PubMed
 .
.
- P. S. Peters, D. Duflot, A. Faure, C. Kahane, C. Ceccarelli, L. Wiesenfeld and C. Toubin, Theoretical investigation of the isomerization of trans-HCOH to H2CO: an example of a water-catalyzed reaction, J. Phys. Chem. A, 2011, 115, 8983–8989 CrossRef CAS PubMed
 .
.
- B. Long, J. L. Bao and D. G. Truhlar, Atmospheric chemistry of Criegee intermediates: Unimolecular reactions and reactions with water, J. Am. Chem. Soc., 2016, 138, 14409–14422 CrossRef CAS PubMed
 .
.
- F. Xu, X.-F. Tan, Z.-G. Dong, D.-S. Ren and B. Long, Hydrolysis of ketene catalysed by nitric acid and water in the atmosphere, Environ. Chem., 2020, 17, 457–467 CrossRef CAS
 .
.
- K. Li, X. Song, T. Zhu, C. Wang, X. Sun, P. Ning and L. Tang, Mechanistic and kinetic study on the catalytic hydrolysis of COS in small clusters of sulfuric acid, Environ. Pollut., 2018, 232, 615–623 CrossRef CAS PubMed
 .
.
- B. Long, X.-F. Tan, C.-R. Chang, W.-X. Zhao, Z.-W. Long, D.-S. Ren and W.-J. Zhang, Theoretical studies on gas-phase reactions of sulfuric acid catalyzed hydrolysis of formaldehyde and formaldehyde with sulfuric acid and H2SO4···H2O complex, J. Phys. Chem. A, 2013, 117, 5106–5116 CrossRef CAS PubMed
 .
.
- X.-F. Tan, B. Long, D.-S. Ren, W.-J. Zhang, Z.-W. Long and E. Mitchell, Atmospheric chemistry of CH3CHO: the hydrolysis of CH3CHO catalyzed by H2SO4, Phys. Chem. Chem. Phys., 2018, 20, 7701–7709 RSC
 .
.
- R. J. Buszek, A. Sinha and J. S. Francisco, The isomerization of methoxy radical: intramolecular hydrogen atom transfer mediated through acid catalysis, J. Am. Chem. Soc., 2011, 133, 2013–2015 CrossRef CAS PubMed
 .
.
- J. Elm, M. Bilde and K. V. Mikkelsen, Influence of nucleation precursors on the reaction kinetics of methanol with the OH radical, J. Phys. Chem. A, 2013, 117, 6695–6701 CrossRef CAS PubMed
 .
.
- A. Karton, Inorganic acid-catalyzed tautomerization of vinyl alcohol to acetaldehyde, Chem. Phys. Lett., 2014, 592, 330–333 CrossRef CAS
 .
.
- M. Torrent-Sucarrat, J. S. Francisco and J. M. Anglada, Sulfuric acid as autocatalyst in the formation of sulfuric acid, J. Am. Chem. Soc., 2012, 134, 20632–20644 CrossRef CAS PubMed
 .
.
- Y. Zhang, Y. Cheng, T. Zhang, R. Wang, J. Ji, Y. Xia, M. Lily, Z. Wang and B. Muthiah, A computational study of the HO2 + SO3 → HOSO2 + 3O2 reaction catalyzed by a water monomer, a water dimer and small clusters of sulfuric acid: kinetics and atmospheric implications, Phys. Chem. Chem. Phys., 2022, 24, 18205–18216 RSC
 .
.
- T. Zhang, Y. Zhang, S. Tian, M. Zhou, D. Liu, L. Lin, Q. Zhang, R. Wang and B. Muthiah, Possible atmospheric source of NH2SO3H: the hydrolysis of HNSO2 in the presence of neutral, basic, and acidic catalysts, Phys. Chem. Chem. Phys., 2022, 24, 4966–4977 RSC
 .
.
- Y. Cheng, R. Wang, Y. Chen, S. Tian, N. Gao, Z. Zhang and T. Zhang, Hydrolysis of SO3 in Small Clusters of Sulfuric Acid: Mechanistic and Kinetic Study, ACS Earth Space Chem., 2022, 6, 3078–3089 CrossRef CAS
 .
.
- J. Liu, S. Fang, Z. Wang, W. Yi, F.-M. Tao and J.-y. Liu, Hydrolysis of sulfur dioxide in small clusters of sulfuric acid: Mechanistic and kinetic study, Environ. Sci. Technol., 2015, 49, 13112–13120 CrossRef CAS PubMed
 .
.
- T. Zhang, R. Wang, H. Chen, S. Min, Z. Wang, C. Zhao, Q. Xu, L. Jin, W. Wang and Z. Wang, Can a single water molecule really affect the HO2 + NO2 hydrogen abstraction reaction under tropospheric conditions?, Phys. Chem. Chem. Phys., 2015, 17, 15046–15055 RSC
 .
.
- S. Sarkar and B. Bandyopadhyay, Aldehyde as a potential source of aminol in troposphere: Influence of water and formic acid catalysis on ammonolysis of formaldehyde, Atmos. Environ., 2019, 213, 223–230 CrossRef CAS
 .
.
- Z. Wang, C. Zhang, G. Lv, X. Sun, N. Wang and Z. Li, Synergistic reaction of SO2 with NO2 in presence of H2O and NH3: A potential source of sulfate aerosol, Int. J. Mol. Sci., 2019, 20, 3746 CrossRef CAS PubMed
 .
.
- B. Du and W. Zhang, The effect of (H2O)n (n = 1–2) or H2S on the hydrogen abstraction reaction of H2S by OH radicals in the atmosphere, Comput. Theor. Chem., 2015, 1069, 77–85 CrossRef CAS
 .
.
- T. Zhang, W. Wang, P. Zhang, J. Lü and Y. Zhang, Water-catalyzed gas-phase hydrogen abstraction reactions of CH3O2 and HO2 with HO2: a computational investigation, Phys. Chem. Chem. Phys., 2011, 13, 20794–20805 RSC
 .
.
- M. E. Dunn, E. K. Pokon and G. C. Shields, Thermodynamics of forming water clusters at various temperatures and pressures by Gaussian-2, Gaussian-3, complete basis set-QB3, and complete basis set-APNO model chemistries; implications for atmospheric chemistry, J. Am. Chem. Soc., 2004, 126, 2647–2653 CrossRef CAS PubMed
 .
.
- H. Zhang, O. Kupiainen-Määttä, X. Zhang, V. Molinero, Y. Zhang and Z. Li, The enhancement mechanism of glycolic acid on the formation of atmospheric sulfuric acid-ammonia molecular clusters, J. Chem. Phys., 2017, 146, 184308 CrossRef
 .
.
- L. Zhang and B. Long, Hydrolysis of formyl fluoride catalyzed by sulfuric acid and formic acid in the atmosphere, ACS Omega, 2019, 4, 18996–19004 CrossRef CAS PubMed
 .
.
- R. Asatryan and E. Ruckenstein, Dihydrogen catalysis: a remarkable avenue in the reactivity of molecular hydrogen, Catal. Rev., 2014, 56, 403–475 CrossRef CAS
 .
.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed
 .
.
- J. Witte, M. Goldey, J. B. Neaton and M. Head-Gordon, Beyond energies: Geometries of nonbonded molecular complexes as metrics for assessing electronic structure approaches, J. Chem. Theory Comput., 2015, 11, 1481–1492 CrossRef CAS PubMed
 .
.
- J. Rezac, Non-covalent interactions atlas benchmark data sets 2: Hydrogen bonding in an extended chemical space, J. Chem. Theory Comput., 2020, 16, 6305–6316 CrossRef CAS PubMed
 .
.
- J. Řezáč, An integrative framework for computational chemistry,
J. Comput. Chem.
, 2016, 37, 1230–1237 CrossRef PubMed
 .
.
- J. Elm, M. Bilde and K. V. Mikkelsen, Assessment of density functional theory in predicting structures
and free energies of reaction of atmospheric prenucleation clusters, J. Chem. Theory Comput., 2012, 8, 2071–2077 CrossRef CAS PubMed
 .
.
- N. Mardirossian and M. Head-Gordon, How accurate are the Minnesota density functionals for noncovalent interactions, isomerization energies, thermochemistry, and barrier heights involving molecules composed of main-group elements?, J. Chem. Theory Comput., 2016, 12, 4303–4325 CrossRef CAS PubMed
 .
.
- A. T. Pereira, A. J. Ribeiro, P. A. Fernandes and M. J. Ramos, Benchmarking of density functionals for the kinetics and thermodynamics of the hydrolysis of glycosidic bonds catalyzed by glycosidases, Int. J. Quantum Chem., 2017, 117, e25409 CrossRef
 .
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson and et al., Gaussian09, 1, Gaussian, Inc., Wallingford CT, 2009, 121, pp. 150–166 Search PubMed
 .
.
- J. Elm, M. Bilde and K. V. Mikkelsen, Assessment of binding energies of atmospherically relevant clusters, Phys. Chem. Chem. Phys., 2013, 15, 16442–16445 RSC
 .
.
- A. F. Rodrigues-Oliveira, F. W. M. Ribeiro, G. Cervi and T. C. Correra, Evaluation of common theoretical methods for predicting infrared multiphotonic dissociation vibrational spectra of intramolecular hydrogen-bonded ions, ACS Omega, 2018, 3, 9075–9085 CrossRef CAS PubMed
 .
.
- M. Kieninger and O. N. Ventura, Calculations of the infrared and Raman spectra of simple thiols and thiol-water complexes, Int. J. Quantum Inf., 2011, 111, 1843–1857 CAS
 .
.
- H. Hratchian and H. Schlegel, Using Hessian updating to increase the efficiency of a Hessian based predictor-corrector reaction path following method, J. Chem. Theory Comput., 2005, 1, 61–69 CrossRef CAS PubMed
 .
.
- H. P. Hratchian and H. B. Schlegel, Accurate reaction paths using a Hessian based predictor-corrector integrator, J. Chem. Phys., 2004, 120, 9918–9924 CrossRef CAS PubMed
 .
.
- S. Maeda, Y. Harabuchi, Y. Ono, T. Taketsugu and K. Morokuma, Intrinsic reaction coordinate: Calculation, bifurcation, and automated search, Int. J. Quantum Chem., 2015, 115, 258–269 CrossRef CAS
 .
.
- J. Pople, R. Krishnan, H. Schlegel and J. Binkley, Electron correlation theories and their application to the study of simple reaction potential surfaces, Int. J. Quantum Chem., 1978, 14, 545–560 CrossRef CAS
 .
.
- Y. S. Lee, S. A. Kucharski and R. J. Bartlett, A coupled cluster approach with triple excitations, J. Chem. Phys., 1984, 81, 5906–5912 CrossRef
 .
.
- R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS
 .
.
- T. J. Lee and P. R. Taylor, A diagnostic for determining the quality of single-reference electron correlation methods, Int. J. Quantum Chem., 1989, 36, 199–207 CrossRef
 .
.
- T. J. Lee, Comparison of the T1 and D1 diagnostics for electronic structure theory: a new definition for the open-shell D1 diagnostic, Chem. Phys. Lett., 2003, 372, 362–367 CrossRef CAS
 .
.
- J. Zhang and M. Dolg, ABCluster: the artificial bee colony algorithm for cluster global optimization, Phys. Chem. Chem. Phys., 2015, 17, 24173–24181 RSC
 .
.
- J. Zhang and M. Dolg, Global optimization of clusters of rigid molecules using the artificial bee colony algorithm, Phys. Chem. Chem. Phys., 2016, 18, 3003–3010 RSC
 .
.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS
 .
.
- D. J. Wales and M. P. Hodges, Global minima of water clusters (H2O)n, n ≤ 21, described by an empirical potential, Chem. Phys. Lett., 1998, 286, 65–72 CrossRef CAS
 .
.
- A. D. MacKerell Jr, D. Bashford, M. Bellott, R. L. Dunbrack Jr, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo and S. Ha, All-atom empirical potential for molecular modeling and dynamics studies of proteins, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef PubMed
 .
.
- J. J. Stewart, Optimization of parameters for semiempirical methods VI: more modifications to the NDDO approximations and re-optimization of parameters, J. Mol. Model., 2013, 19, 1–32 CrossRef CAS PubMed
 .
.
-
J. Stewart, MOPAC2016 Stewart Computational Chemistry, Colorado Springs, CO, OpenMOPAC, 2016 Search PubMed
 .
.
-
Y. Chuang, J. Corchado, P. Fast, J. Villa, E. Coitino, W. Hu, Y. Liu, G. Lynch, K. Nguyen and C. Jackels, Polyrate-version 8.2, University of Minnesota, Minneapolis, 1999 Search PubMed
 .
.
- D. R. Glowacki, C.-H. Liang, C. Morley, M. J. Pilling and S. H. Robertson, MESMER: an open-source master equation solver for multi-energy well reactions, J. Phys. Chem. A, 2012, 116, 9545–9560 CrossRef CAS PubMed
 .
.
- G. Horváth, I. Horváth, S. A.-D. Almousa and M. Telek, Numerical inverse Laplace transformation using concentrated matrix exponential distributions, Perform. Evaluation, 2020, 137, 102067 CrossRef
 .
.
- A. Kumar, S. Mallick and P. Kumar, Oxidation of HOSO˙ by Cl˙: a new source of SO2 in the atmosphere?, Phys. Chem. Chem. Phys., 2021, 23, 18707–18711 RSC
 .
.
- T. V.-T. Mai, M. V. Duong, H. T. Nguyen and L. K. Huynh, Ab initio kinetics of the HOSO2 + 3O2 → SO3 + HO2 reaction, Phys. Chem. Chem. Phys., 2018, 20, 6677–6687 RSC
 .
.
- S. Mallick, A. Kumar and P. Kumar, Oxidation of HOSO by NH2: A new path for the formation of an acid rain precursor, Chem. Phys. Lett., 2021, 773, 138536 CrossRef CAS
 .
.
- H. Hippler, J. Troe and H. Wendelken, Collisional deactivation of vibrationally highly excited polyatomic molecules. II. Direct observations for excited toluene, J. Chem. Phys., 1983, 78, 6709–6717 CrossRef CAS
 .
.
-
R. J. Kee, G. Dixon-Lewis, J. Warnatz, M. E. Coltrin and J. A. Miller, A Fortran computer code package for the evaluation of gas-phase multicomponent transport properties, Sandia National Laboratories Report SAND86-8246, 1986, vol. 13, pp. 80401–81887 Search PubMed
 .
.
- T. V.-T. Mai, H. T. Nguyen and L. K. Huynh, Ab initio dynamics of hydrogen abstraction from N2H4 by OH radicals: an RRKM-based master equation study, Phys. Chem. Chem. Phys., 2019, 21, 23733–23741 RSC
 .
.
- T. V.-T. Mai, H. T. Nguyen and L. K. Huynh, Kinetics of hydrogen abstraction from CH3SH by OH radicals: An ab initio RRKM-based master equation study, Atmos. Environ., 2020, 242, 117833 CrossRef CAS
 .
.
- X. T. Le, T. V.-T. Mai, M. v. Duong and L. K. Huynh, Kinetics of hydrogen abstraction from desflurane by OH and Cl radicals–A theoretical study, Chem. Phys. Lett., 2019, 728, 142–147 CrossRef CAS
 .
.
- T. V.-T. Mai, P. Raghunath, X. T. Le, L. K. Huynh, P.-C. Nam and M.-C. Lin, Ab initio chemical kinetics for the HCCO + OH reaction, Chem. Phys. Lett., 2014, 592, 175–181 CrossRef CAS
 .
.
- T. V.-T. Mai, M. v. Duong, H. T. Nguyen, K. C. Lin and L. K. Huynh, Ab initio chemical kinetics of the CH2OO + C2F4 reaction, Chem. Phys. Lett., 2018, 706, 280–284 CrossRef CAS
 .
.
- T. V.-T. Mai and L. K. Huynh, Ab initio kinetics of the C2H2 + NH2 reaction: a revisited study, Phys. Chem. Chem. Phys., 2019, 21, 17232–17239 RSC
 .
.
- J. M. Anglada, G. J. Hoffman, L. V. Slipchenko, M. M. Costa, M. F. Ruiz-Lopez and J. S. Francisco, Atmospheric significance of water clusters and ozone-water complexes, J. Phys. Chem. A, 2013, 117, 10381–10396 CrossRef CAS PubMed
 .
.
- B. Bandyopadhyay, P. Kumar and P. Biswas, Ammonia catalyzed formation of sulfuric acid in troposphere: the curious case
of a base promoting acid rain, J. Phys. Chem. A, 2017, 121, 3101–3108 CrossRef CAS PubMed
 .
.
- S. Mallick, S. Sarkar, B. Bandyopadhyay and P. Kumar, Effect of ammonia and formic acid on the OH˙ + HCl reaction in the troposphere: Competition between single and double hydrogen atom transfer pathways, J. Phys. Chem. A, 2018, 122, 350–363 CrossRef CAS PubMed
 .
.
- T. Zhang, K. Zhai, Y. Zhang, L. Geng, Z. Geng, M. Zhou, Y. Lu, X. Shao and M. Lily, Effect of water and ammonia on the HO + NH3 → NH2 + H2O reaction in troposphere: Competition between single and double hydrogen atom transfer pathways, Comput. Theor. Chem., 2020, 1176, 112747 CrossRef CAS
 .
.
- S. Sarkar and B. Bandyopadhyay, Theoretical investigation of the relative impacts of water and ammonia on the tropospheric conversion of N2O5 to HNO3, Phys. Chem. Chem. Phys., 2021, 23, 6651–6664 RSC
 .
.
- B. Long, X. F. Tan, Y. B. Wang, J. Li, D. S. Ren and W. J. Zhang, Theoretical Studies on Reactions of OH with H2SO4···NH3 Complex and NH2 with H2SO4 in the Presence of Water, ChemistrySelect, 2016, 1, 1421–1430 CrossRef CAS
 .
.
- S. Sarkar, S. Mallick, P. Kumar and B. Bandyopadhyay, Isomerization of methoxy radical in the troposphere: competition between acidic, neutral and basic catalysts, Phys. Chem. Chem. Phys., 2017, 19, 27848–27858 RSC
 .
.
- R. J. Buszek, M. Torrent-Sucarrat, J. M. Anglada and J. S. Francisco, Effects of a single water molecule on the OH + H2O2 reaction, J. Phys. Chem. A, 2012, 116, 5821–5829 CrossRef CAS PubMed
 .
.
- J. Gonzalez, J. M. Anglada, R. J. Buszek and J. S. Francisco, Impact of water on the OH + HOCl reaction, J. Am. Chem. Soc., 2011, 133, 3345–3353 CrossRef CAS PubMed
 .
.
- A. Parandaman, J. E. Perez and A. Sinha, Atmospheric decomposition of trifluoromethanol catalyzed by formic acid, J. Phys. Chem. A, 2018, 122, 9553–9562 CrossRef CAS PubMed
 .
.
- G. Shen, M. Suto and L. Lee, Reaction rate constant of SO3 + CH3OH in the gas phase, Int. J. Chem. Kinet., 1990, 22, 633–639 CrossRef CAS
 .
.
- L. Liu, J. Zhong, H. Vehkamäki, T. Kurtén, L. Du, X. Zhang, J. S. Francisco and X. C. Zeng, Unexpected quenching effect on new particle formation from the atmospheric reaction of methanol with SO3, Proc. Natl. Acad. Sci., 2019, 116, 24966–24971 CrossRef CAS PubMed
 .
.
- J. Gonzalez, M. Torrent-Sucarrat and J. M. Anglada, The reactions of SO3 with HO2 radical and H2O⋯HO2 radical complex. Theoretical study on the atmospheric formation of HSO5 and H2SO4, Phys. Chem. Chem. Phys., 2010, 12, 2116–2125 RSC
 .
.
- Y.-Q. Sun, X. Wang, F.-Y. Bai and X.-M. Pan, Theoretical study of the hydrolysis of HOSO + NO2 as a source of atmospheric HONO: effects of H2O or NH3, Environ. Chem., 2016, 14, 19–30 CrossRef
 .
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ea00095h |
| ‡ Ruxue Mu and Weixin Zhou have contributed equally to this work. |
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Quan
Liu
a,
Quan
Liu
 a,
Qiang
Zhang
a,
Qiang
Zhang
 a,
Min
Jiang
a,
Balaganesh
Muthiah
a,
Min
Jiang
a,
Balaganesh
Muthiah
 b and
Tianlei
Zhang
b and
Tianlei
Zhang
 *a
*a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15–17 at night, in polluted areas of NH3. The ammonolysis of t-N2O4 (shown in eqn (1) and (2)) investigated by Lin et al.13 reveals that the energy barrier of the t-N2O4 + NH3 reaction was determined to be 5.3 kcal mol−1 and the corresponding rate constant at low temperature was not pressure-dependent. As far as we know, the effect of neutral and acidic gases on the ammonolysis of t-N2O4, which plays a significant catalytic role in hydrogen abstraction reactions,9,15,18–37 has not been explored.
15–17 at night, in polluted areas of NH3. The ammonolysis of t-N2O4 (shown in eqn (1) and (2)) investigated by Lin et al.13 reveals that the energy barrier of the t-N2O4 + NH3 reaction was determined to be 5.3 kcal mol−1 and the corresponding rate constant at low temperature was not pressure-dependent. As far as we know, the effect of neutral and acidic gases on the ammonolysis of t-N2O4, which plays a significant catalytic role in hydrogen abstraction reactions,9,15,18–37 has not been explored.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 reactions, water molecules were found to play an essential role in enhancing the stability of pre-reactive complexes and lowering the apparent activation energies of the transition states. In addition to water monomer, some recent works addressed the potential role of water dimer,18,41 which may play a significant catalytic role in hydrogen abstraction reactions because its concentrations can reach 9 × 1014 mol cm−3.42,43 Aside from water monomer and water dimer, acidic9,15,30–37 gas species in the atmosphere may also be effective in lowering the energy barriers for hydrogen transfer reactions30–34 and atmospheric hydrolysis reactions9,15,35–37 in the gas phase. The presence of H2SO4
40 reactions, water molecules were found to play an essential role in enhancing the stability of pre-reactive complexes and lowering the apparent activation energies of the transition states. In addition to water monomer, some recent works addressed the potential role of water dimer,18,41 which may play a significant catalytic role in hydrogen abstraction reactions because its concentrations can reach 9 × 1014 mol cm−3.42,43 Aside from water monomer and water dimer, acidic9,15,30–37 gas species in the atmosphere may also be effective in lowering the energy barriers for hydrogen transfer reactions30–34 and atmospheric hydrolysis reactions9,15,35–37 in the gas phase. The presence of H2SO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37,44 in the atmosphere was considered to be a more effective catalyst than neutral catalysts,25,28–30,33,45 which not only greatly reduces the energy barriers27,28,33 but also facilitates the transfer of hydrogen,30–33,46 and thus, H2SO4 was regarded as either good acceptors or good donors of H in the catalytic gas reactions. These situations stimulated our interest in studying the ammonolysis of t-N2O4 by neutral (H2O and (H2O)2) and acidic (H2SO4) gases.
37,44 in the atmosphere was considered to be a more effective catalyst than neutral catalysts,25,28–30,33,45 which not only greatly reduces the energy barriers27,28,33 but also facilitates the transfer of hydrogen,30–33,46 and thus, H2SO4 was regarded as either good acceptors or good donors of H in the catalytic gas reactions. These situations stimulated our interest in studying the ammonolysis of t-N2O4 by neutral (H2O and (H2O)2) and acidic (H2SO4) gases.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 71 in MOPAC 2016.72 Next, the structures with the N(t-N2O4)⋯N(NH3) interaction of electron donor–acceptor (EDA) and facilitating the transfer of hydrogen atom from t-N2O4 to NH3 were selected to optimize at the B3LYP-D3/6-311+G(d,p) level. Subsequently, 50 isomers with an order of electronic energies were chosen to optimize at the level of B3LYP-D3/6-311+G(2d,2p). Finally, the global minimum isomers within 5.0 kcal mol−1 (the electric energy) were re-optimized at the B3LYP-D3/6-311++G(3df,2pd) level.
71 in MOPAC 2016.72 Next, the structures with the N(t-N2O4)⋯N(NH3) interaction of electron donor–acceptor (EDA) and facilitating the transfer of hydrogen atom from t-N2O4 to NH3 were selected to optimize at the B3LYP-D3/6-311+G(d,p) level. Subsequently, 50 isomers with an order of electronic energies were chosen to optimize at the level of B3LYP-D3/6-311+G(2d,2p). Finally, the global minimum isomers within 5.0 kcal mol−1 (the electric energy) were re-optimized at the B3LYP-D3/6-311++G(3df,2pd) level.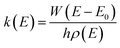
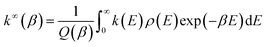



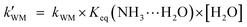
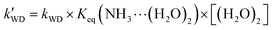
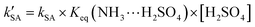
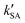 can compete with
can compete with 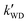 at 280 K. With increasing temperature, the calculated
at 280 K. With increasing temperature, the calculated 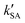 was ∼1–3 orders of magnitude smaller than the values of
was ∼1–3 orders of magnitude smaller than the values of 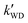 , showing that the ammonolysis reaction of t-N2O4 was superior to that of an acidic (H2SO4) catalyst in the presence of neutral (H2O and (H2O)2) catalysts. However, the H2SO4-catalyzed reaction can be neglected because its calculated
, showing that the ammonolysis reaction of t-N2O4 was superior to that of an acidic (H2SO4) catalyst in the presence of neutral (H2O and (H2O)2) catalysts. However, the H2SO4-catalyzed reaction can be neglected because its calculated 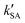 was at least 4 orders of magnitude lower than the corresponding value of kR in the naked reaction of the ammonolysis reaction of t-N2O4. This indicated that the contributions of H2SO4 to the ammonolysis reaction of t-N2O4 in atmospheric chemistry are not obvious within the temperature range of 280–320 K (at 0 km altitude).
was at least 4 orders of magnitude lower than the corresponding value of kR in the naked reaction of the ammonolysis reaction of t-N2O4. This indicated that the contributions of H2SO4 to the ammonolysis reaction of t-N2O4 in atmospheric chemistry are not obvious within the temperature range of 280–320 K (at 0 km altitude).
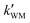 ,
, 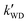 , and
, and 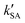 were respectively denoted the effective rate constants for the t-N2O4 + NH3⋯H2O, t-N2O4 + NH3⋯(H2O)2, and t-N2O4 + NH3⋯H2SO4 reactions.
b The values of temperature were reported from ref. 88 and 89.
c The values of concentrations were reported from ref. 44 and 87.
were respectively denoted the effective rate constants for the t-N2O4 + NH3⋯H2O, t-N2O4 + NH3⋯(H2O)2, and t-N2O4 + NH3⋯H2SO4 reactions.
b The values of temperature were reported from ref. 88 and 89.
c The values of concentrations were reported from ref. 44 and 87.
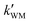
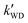
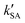
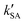 was larger by 1–8 orders of magnitude than that of
was larger by 1–8 orders of magnitude than that of 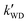 . In order to quantitatively assess the impact of H2SO4 on the ammonolysis reaction of t-N2O4, the total rate constant ktot can be calculated using eqn (8). The branching ratio for
. In order to quantitatively assess the impact of H2SO4 on the ammonolysis reaction of t-N2O4, the total rate constant ktot can be calculated using eqn (8). The branching ratio for 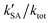 in Table 4 was calculated to be 3.11 × 10−5–5.06 × 10−4 at 5–30 km. This indicates that the contribution of the H2SO4-assisted ammonolysis reaction of t-N2O4 can be negligible in atmospheric gas-phase chemistry.
in Table 4 was calculated to be 3.11 × 10−5–5.06 × 10−4 at 5–30 km. This indicates that the contribution of the H2SO4-assisted ammonolysis reaction of t-N2O4 can be negligible in atmospheric gas-phase chemistry.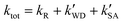
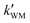 ,
, 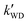 , and
, and 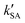 were respectively denoted the effective rate constants for the t-N2O4 + NH3⋯H2O, t-N2O4 + NH3⋯(H2O)2, and t-N2O4 + NH3⋯H2SO4 reactions; ktot = kR +
were respectively denoted the effective rate constants for the t-N2O4 + NH3⋯H2O, t-N2O4 + NH3⋯(H2O)2, and t-N2O4 + NH3⋯H2SO4 reactions; ktot = kR + 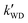 +
+ 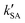 .
b The values of altitude, temperature and pressure were reported from ref. 87, 88 and 89.
.
b The values of altitude, temperature and pressure were reported from ref. 87, 88 and 89.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.