Comment on the “Discovery of high-performance thermoelectric copper chalcogenide using modified diffusion-couple high-throughput synthesis and automated histogram analysis technique” by T. Deng, T. Xing, M. K. Brod, Y. Sheng, P. Qiu, I. Veremchuk, Q. Song, T.-R. Wei, J. Yang, G. J. Snyder, Y. Grin, L. Chen and X. Shi, Energy Environ. Sci., 2020, 13, 3041

Abstract

The recent paper by Deng et al. showed that a copper sulphide with Cu₇Sn₃S₁₀ composition is a promising thermoelectric material reaching a figure of merit ZT of 0.8 at 750 K via Cl doping. However, structural reinvestigations of the Cu₇Sn₃S₁₀ sample (i.e., Cu_2.10Sn_0.90S₃) prepared in the reported conditions show that the phase of interest is not tetragonal (space group I4̄2m, a_t = 5.4164 Å, c_t = 10.832 Å), but crystallizes in the cubic symmetry (space group P4̄3n, a_c = 10.832 Å) with a composition close to Cu₂₂Sn₁₀S₃₂ similar to the results published by Pavan Kumar et al. These observations indicate that the main phase around the composition Cu₇Sn₃S₁₀ is cubic, and a revision needs to be imposed for the understanding of the relationships between the structure and thermoelectric properties in this family.

---

Broader context

The past few years have seen a renewed interest in thermoelectric sulphides as the earth-abundance of sulphur is one critical aspect to encourage the large-scale production of thermoelectric devices with a potentially meaningful impact on mitigating climate change. Following reports of excellent properties in ternary and quaternary sulphides, the performance of cost-efficient sulphides has become closer to that of well-established state-of-the-art materials such as selenides, tellurides, clathrates, skutterudites, Zintl phases, silicides etc.… with ZT values now reaching unity (A. V. Powell, J. Appl. Phys., 2019, 126, 100901).

In a recent article, Deng et al.¹ discovered a high-performance thermoelectric with the composition Cu₇Sn₃S₁₀ and demonstrated that it is a promising material with ultralow thermal conductivity, moderate band gap, and high electrical conductivity. A figure of merit ZT of 0.8 at 750 K was indeed achieved via Cl doping. In the structural analysis of this material by powder X-ray diffraction, considering stannite-like structural models (i.e., tetragonal superstructure of the sphalerite-type with the space group I4̄2m, a = 5.4164 Å, c = 10.832 Å), Deng et al. reported difficulties in the refinement getting either chemical composition Cu_39.3Sn_10.7S_50.0 far from the nominal one Cu₃₅Sn₁₅Sn₅₀, also confirmed by EDXS (model 1), or large spread of the atomic displacement parameters (model 2). A further structural model was mentioned (model 3) assuming chemically improbable mixed cation/anion occupancies of the positions, but yielding expected chemical composition and reasonable values of the atomic displacement parameters. Finally, the authors decided to postpone the clarification of this issue to a separate study, and structural model 2 was considered for the interpretation of the attractive thermoelectric properties of this material.

In a posterior study of the Cu–Sn–S system, Pavan Kumar et al.² synthesized a low thermal conductivity degenerate semiconductor with a rather close composition, Cu₂₂Sn₁₀S₃₂ (i.e. Cu_2.0625Sn_0.9375S₃), and showed that this sulphide also exhibits attractive thermoelectric properties with a figure of merit ZT of 0.55 at 700 K via Sb for Sn substitution. For the structure solution in the tetragonal symmetry, the authors met with the first step difficulties similar to those encountered by Deng et al. and refined chemical composition far from the nominal one. However, considering the fact that the c parameter is rigorously double the a parameter in the tetragonal structure of the I4̄2m space group, Pavan Kumar et al. reported that it may imply a cubic supercell (a_c = 2a_t = c_t).² Note that refinements reported in Deng et al.¹ article lead also to a cell parameters ratio c_t/a_t of 2. Using a combination of synchrotron powder X-ray diffraction, single crystal X-ray diffraction, ¹¹⁹Sn Mössbauer spectroscopy, and transmission electron microscopy, Pavan Kumar et al.² demonstrated that the phase of interest crystallizes in fact in a cubic superstructure sphalerite-type with the space group P4̄3n. Further the group demonstrated that the as-prepared phase is characterized by a semi-ordered cationic distribution: the Cu–Sn disorder being localized on one crystallographic site (see Table 1).

Table 1 Crystallographic data of the Cu₇Sn₃S₁₀ sample from the Rietveld refinement of the powder X-ray diffraction data considering the cubic Cu₂₂Sn₁₀S₃₂ structural model²

P4̄3n, a = 10.8365(1) Å, Cu22.2(1)Sn9.8(1)S32
Atom	Site	x	y	z	B iso (Å^2)	SOF
Sn1	6c	¼	½	0	1.28(8)	1.00
Cu2	6d	¼	0	½	1.09(4)	1.00
Cu3	8e	0.251(1)	x	x	1.23(5)	1.00
Cu4/Sn4	12f	0.244(1)	0	0	0.95(7)	0.68(1)/0.32(1)
S1	8e	0.127(1)	x	x	0.78(26)	1.00
S2	24i	0.378(1)	0.370(1)	0.129(1)	0.72(9)	1.00

---

Based on the comparison of these results showing strong similitudes between Cu₇Sn₃S₁₀ and Cu₂₂Sn₁₀S₃₂, we have analysed a sample provided by the group of X. Shi and prepared in the conditions reported in their paper (i.e., heat treatments at 723 K, 1223 K, and 1073 K, followed by ball-milling process, and SPS treatment at 923 K) to revisit the structural analysis of the materials around the composition Cu₇Sn₃S₁₀ (i.e. Cu_2.10Sn_0.90S₃). The aim of the present comment is to draw attention to the crystal chemistry of the thermoelectric chalcogenides, which requires detailed structural studies to elucidate complex order–disorder phenomena and its impact on the understanding of their transport properties.

Rietveld refinements considering the tetragonal stannite-like (i.e. model 2) and the cubic Cu₂₂Sn₁₀S₃₂ structural models, reported by Deng et al.¹ and Pavan Kumar et al.,² respectively, have been performed on long duration (48 h) powder X-ray diffraction data collected at CRISMAT laboratory using a Bruker D8 Advance Vario A two-circle diffractometer (θ–2θ Bragg–Brentano mode) equipped with a Ge(111) monochromator (Johansson type), a Lynx Eye detector and a Cu X-ray tube (λ = 1.5406 Å). Similar to the description provided by Deng et al.,¹ the Rietveld refinement considering the tetragonal stannite-like structural model (I4̄2m) gives at first sight an apparent high-quality refinement and some correct reliability factors (Fig. 1, top panel). However, a careful analysis of the refinement reveals the presence of additional non-indexed diffraction peaks of weak intensity as clearly evidenced in the top panel of Fig. 2 with intensity in the logarithmic scale. These weak intensity diffraction peaks can be indexed as superstructure diffraction reflections in a larger cubic cell similar to that previously observed by Pavan Kumar et al.² for Cu₂₂Sn₁₀S₃₂. The reinvestigation of the crystal structure of the Cu₇Sn₃S₁₀ sample was then carried out with the cubic structural model reported for Cu₂₂Sn₁₀S₃₂,² assuming that a homogeneity range with rather close compositions may exist. Rietveld refinement of the powder X-ray diffraction data considering the cubic structural model (space group P4̄3n) of the Cu₂₂Sn₁₀S₃₂ phase² also provides very low reliability factors (Fig. 1, bottom panel). Moreover, in contrast to the tetragonal unit cell,¹ the cubic structural model allows a perfect fit of all the diffraction peaks, including the weak intensity superstructure reflections (Fig. 2, bottom panel). Importantly, it leads to refined structural parameters and chemical composition Cu_22.2(1)Sn_9.8(1)S₃₂ (Table 1) in fair agreement with those reported for the cubic phase Cu₂₂Sn₁₀S₃₂.² The refined composition (i.e., Cu_2.08Sn_0.92S₃), slightly different from the nominal one Cu_2.10Sn_0.90S₃, is supported by the existence of a broad diffraction peak, detected at 2θ = 26.5° (Fig. 2), which may be assigned to a binary copper sulphide present in a minor amount in the sample. Note that the refinement of the atomic parameters (Table 1) results in the composition Cu_22.2(1)Sn_9.8(1)S₃₂, which – in combination with the refined lattice parameter of 10.8234(2) Å and chemical composition of Cu_21.8(1)Sn_10.2(1)S₃₂ reported by Pavan Kumar et al.² from synchrotron PXRD data – may indicate a small homogeneity range of the cubic phase.

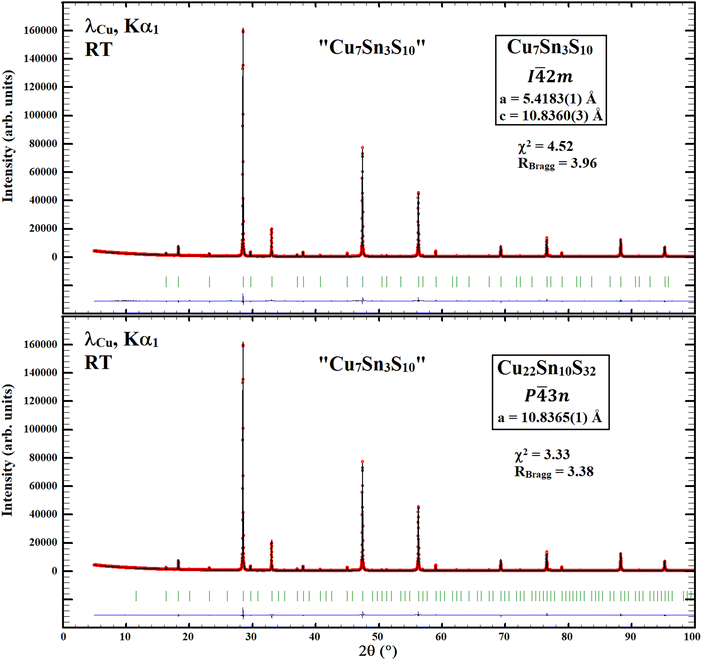Fig. 1 Rietveld refinement of the Cu₇Sn₃S₁₀ sample considering (i) the tetragonal structural model (I4̄2m) proposed by Deng et al.¹ (top panel) and (ii) the cubic Cu₂₂Sn₁₀S₃₂ structural model (P4̄3n) proposed by Pavan Kumar et al.² (bottom panel).

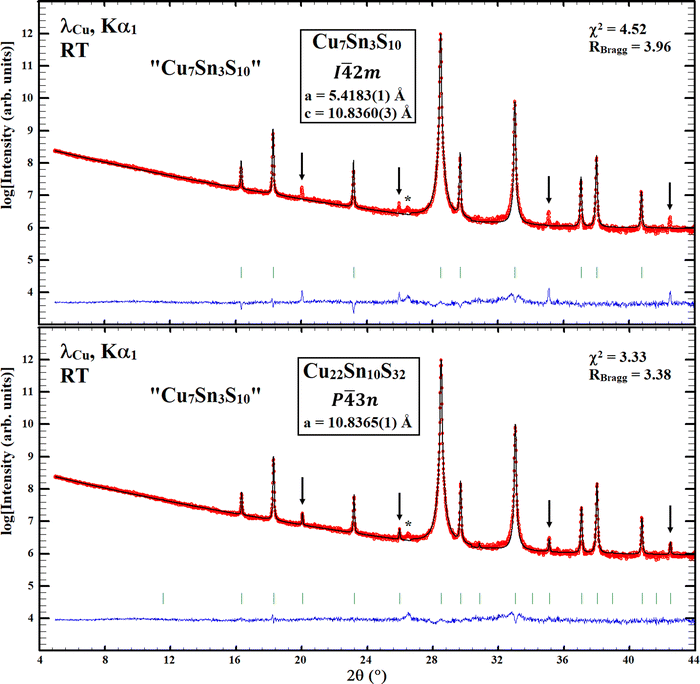Fig. 2 Magnified Rietveld refinement of the Cu₇Sn₃S₁₀ sample, with intensity in the logarithmic scale, considering (i) the tetragonal structural model (I4̄2m) proposed by Deng et al.¹ (top panel) and (ii) the cubic Cu₂₂Sn₁₀S₃₂ structural model (P4̄3n) proposed by Pavan Kumar et al.² (bottom panel). * refers to copper sulphide impurity.

Moreover, it is worth pointing out that the local transmission electron microscopy analysis previously reported by Deng et al. (Fig. 4b in ref. 1) for “Cu₇Sn₃S₁₀” is erroneous and incompatible with the proposed cell and space group I4̄2m. Indeed, several low-intensity extra reflections in the [110] zone axis pattern, for example between the transmitted beam (000) and the reflection indexed 1 − 10, cannot be indexed in the I4̄2m space group, however, could be well indexed with the cubic cell (a ∼ 10.8 Å) and the space group P4̄3n (Fig. 3)

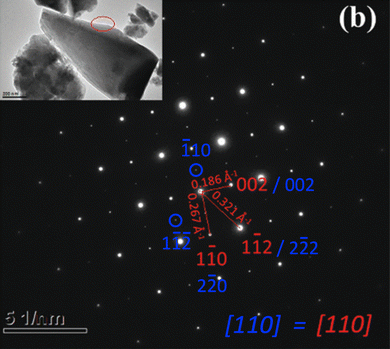Fig. 3 Selected area electron diffraction (SAED) pattern of the sample Cu₇Sn₃S₁₀ presented by Deng et al.¹ in Fig. 4. The spots with high intensity (red) were indexed by Deng et al. in the tetragonal cell (I4̄2m) with 2 × a_t = c_t, while additional spots of weak intensity (blue) were not and cannot be indexed in this tetragonal cell. The present indexation, in blue, shows that the additional weak intensity spots are indexed in the cubic cell (P4̄3n) with a_c = 2 × a_t.

Thus, these results demonstrate without any ambiguity that the samples of composition Cu₇Sn₃S₁₀ prepared in the conditions reported by Deng et al.¹ (i.e. heat treatments at 723 K, 1223 K, and 1073 K, followed by ball-milling process and SPS treatment at 923 K) are biphasic and that the observed majority phase is not tetragonal with composition Cu₇Sn₃S₁₀ but cubic with composition Cu₂₂Sn₁₀S₃₂.

As a consequence, the crystal chemistry results, reported by Deng et al.,¹ cannot be used to explain the thermoelectric properties of the pristine Cu₇Sn₃S₁₀ sample. The fact that the structure of the pristine sample is cubic and not tetragonal significantly influences the interpretation previously proposed for the lattice thermal conductivity of pristine and Cl-substituted SPS-treated Cu₇Sn₃S_10−xCl_x materials, which can no more be compared on the basis of a tetragonal-cubic conversion neither the disappearance of the distorted non-cubic framework due to the Cl-substitution.¹ The fact that the pristine composition exhibits lower lattice thermal conductivity than those of disordered Cl-substituted materials remains also still quite unexpected. Indeed, Cl-substituted samples exhibit a cubic fully-disordered sphalerite structure, while the pristine composition Cu₇Sn₃S₁₀ (in fact cubic Cu_22.2(1)Sn_9.8(1)S₃₂) has a partially ordered structure. The pristine compound should then exhibit a larger lattice thermal conductivity than the Cl-doped compounds. Full cationic disorder, induced by Cl-substitution, stoichiometry deviation, or process effect, are well known to strongly enhance phonon scattering and to reduce the lattice thermal conductivity in copper-based sphalerite derivative compounds.^3,4 Attention must be drawn to the extremely low value of the lattice thermal conductivity of the pristine phase. A possible explanation may be in the estimation of the latter by the expression κ_L = κ − LσT, where L is the Lorenz number calculated by the single parabolic band (SPB) model.^5,6 Unfortunately, this model is inadequate for L calculation due to the multiband nature of the valence band structure of this highly metallic degenerate semiconductor. It results in too high L values leading to a substantial underestimation of κ_L. This difficulty in determining the lattice contribution has been highlighted in the degenerate semiconductor Cu₅Sn₂S₇,^3,7 and several thermoelectric materials, such as SnTe, for which the presence of several electronic bands tends to lower the L values despite the strongly degenerate nature of the compound.^8–11

To summarize, our present structural investigations clearly demonstrate that the stable structure around the composition Cu_2.1Sn_0.9S₃ is not tetragonal with composition Cu₇Sn₃S₁₀ but cubic with the space group P4̄3n and the composition Cu₂₂Sn₁₀S₃₂, requiring the revision of the understanding of structure-transport properties relationships of this system. Moreover, we demonstrate once again that the order–disorder phenomena in copper sulphides are very complex and very difficult to detect. In-depth structural analyses should be then systematically performed to elucidate the subtle influence of crystal chemistry on the electrical and thermal properties of these materials.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the group of X. Shi for having provided a sample prepared in the conditions reported in their paper (i.e. heat treatments at 723 K, 1223 K and 1073 K, followed by ball-milling process and SPS treatment at 923 K). See their experimental section.¹

References

1. T. Deng, T. Xing, M. K. Brod, Y. Sheng, P. Qiu, I. Veremchuk, Q. Song, T.-R. Wei, J. Yang, G. J. Snyder, Y. Grin, L. Chen and X. Shi, Energy Environ. Sci., 2020, 13, 3041–3053.
2. V. Pavan Kumar, P. Lemoine, V. Carnevali, G. Guélou, O. I. Lebedev, B. Raveau, R. Al Rahal Al Orabi, M. Fornari, C. Candolfi, C. Prestipino, D. Menut, B. Malaman, J. Juraszek, K. Suekuni and E. Guilmeau, Inorg. Chem., 2021, 60, 16273–16285.
3. G. Guélou, V. Pavan Kumar, V. Carnevali, O. I. Lebedev, B. Raveau, C. Couder, C. Prestipino, P. Lemoine, B. Malaman, J. Juraszek, C. Candolfi, B. Lenoir, R. Al Rahal Al Orabi, M. Fornari and E. Guilmeau, Chem. Mater., 2021, 33, 9425–9438.
4. P. Lemoine, G. Guélou, B. Raveau and E. Guilmeau, Angew. Chem., Int. Ed., 2022, 61, e202108686.
5. Thermal Conductivity Theory, Properties, and Applications, ed. T. M. Tritt, Kluwer Academic/Plenum Publishers, New York, 2004.
6. A. F. May and J. G. Snyder, in Thermoelectrics and its energy harvesting, ed. D. M. Rowe, CRC Press, Boca Racon, 2012, ch. 11, pp. 1–18.
7. V. Pavan Kumar, P. Lemoine, V. Carnevali, G. Guélou, O. I. Lebedev, P. Boullay, B. Raveau, R. Al Rahal Al Orabi, M. Fornari, C. Prestipino, D. Menut, C. Candolfi, B. Malaman, J. Juraszek and E. Guilmeau, J. Mater. Chem. A, 2021, 9, 10812–10826.
8. R. W. McKinney, P. Gorai, V. Stevanović and E. S. Toberer, J. Mater. Chem. A, 2017, 5, 17302–17311.
9. M. Thesberg, H. Kosina and N. Neophytou, Phys. Rev. B, 2017, 95, 125206.
10. L. V. Prokof’eva, A. A. Shabaldin, V. A. Korchagin, S. A. Nemov and Y. I. Ravich, Semiconductors, 2008, 42, 1161.
11. S. Misra, B. Wiendlocha, J. Tobola, F. Fesquet, A. Dauscher, B. Lenoir and C. Candolfi, J. Mater. Chem. C, 2020, 8, 977–988.

---