Clumped methane isotopologues (13CH3D and 12CH2D2) of natural samples measured using a high-resolution mass spectrometer with an improved pretreatment system†
Xinchu
Wang
 a,
Cong-Qiang
Liu
a,
Cong-Qiang
Liu
 *a,
Naizhong
Zhang
*a,
Naizhong
Zhang
 b,
Sheng
Xu
a,
Zhiyong
Pang
b,
Sheng
Xu
a,
Zhiyong
Pang
 a,
Si-Liang
Li
a,
Si-Liang
Li
 a,
Hu
Ding
a,
Jianfa
Chen
c,
Zengye
Xie
a,
Hu
Ding
a,
Jianfa
Chen
c,
Zengye
Xie
 d and
Rob M.
Ellam
a
d and
Rob M.
Ellam
a
aInstitute of Surface-Earth System Science, School of Earth System Science, Tianjin University, Tianjin 300072, China. E-mail: liucongqiang@tju.edu.cn
bEarth-Life Science Institute, Tokyo Institute of Technology, Tokyo 152-8551, Japan
cState Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum, Beijing 102249, China
dPetroChina Research Institute of Petroleum Exploration & Development, Beijing 100083, China
First published on 16th November 2022
Abstract
Doubly-substituted methane isotopologues (13CH3D and 12CH2D2) can provide unique information to resolve the origin, transport, and conversion of environmental methane. We used a high-resolution mass spectrometer (Thermo Fisher Scientific 253 Ultra) to precisely determine Δ13CH3D and Δ12CH2D2 (precision and accuracy of ∼0.35‰ and ∼1.35‰ (1σ), respectively) in this study. The impacts of temperature, humidity, and slit quality are found to be critical for the reproducibility of the results, while the fragmentation rate and bellows effects on the clumped isotope results were negligible. A heating equilibrium experiment performed at 500 °C, 400 °C and 300 °C (n = 19) calibrates the results to an absolute reference. A pretreatment system that can extract methane having concentrations from ∼15% to ∼99.8% is proposed, while the fractionation produced throughout the pretreatment is negligible within precision (Δ13CH3D = +0.16 ± 0.32‰ and Δ12CH2D2 = +0.14 ± 1.12‰ (n = 16)). Analyses of natural gases from shale basins and variable methane-rich gases emitted from artificial lakes validate the capability of the current pretreatment and spectrometer systems to determine methane clumped isotopes in a wide range of natural environmental samples.
1. Introduction
Methane (CH4) is the primary component of natural gas and hence a critical energy source, but also the most potent anthropogenic greenhouse gas emission.1,2 The origin of environmental methane is usually classified into three types: thermogenic, biogenic, and abiotic.3 Methane bulk isotope compositions (δ13C-CH4 and δD-CH4) can be diagnostic,4,5 and are used to trace the fate and source of methane in the carbon cycle.6,7 However, there is partial overlap between CH4 of different origins, and the subsequent migration and conversion processes also affect the stable isotopic compositions making conventional C and H isotope data inconclusive.8 The abundances of methane clumped (doubly substituted) isotopologues (13CH3D and 12CH2D2) record the formational conditions and provide reliable apparent temperatures in the equilibrium state,9–12 and trace the causes of disequilibrium characteristics caused by kinetic effects in the generation and/or post-generation process.13–19In practice, due to the low abundance (proportional relative abundance of 10−6 and 10−7, while the most abundant 12CH4 is ∼9.88 × 10−1) and similar masses (18.041 amu and 18.044 amu) of 13CH3D and 12CH2D2, resolved measurements of abundance of doubly substituted methane isotopologues are challenging.12 The recent development of high-resolution isotope ratio mass spectrometry has facilitated the measurement of doubly-substituted methane isotopologues.10,16,20 However, detailed commissioning data and the influence of a variety of potential analytical factors (e.g., temperature, humidity, slit quality, fragmentation rate, and bellows effects) have not been widely reported.
The introduction of HR-IRMS also requires confirmation that sample pre-treatment methods are robust to the standards of the enhanced measurement capability. In the pre-treatment of natural samples, two alternative methods are generally used: (i) cryogenic purification (at 45 K) and 5 Å molecular sieve collection (at 70 K)10,12 or (ii) gas chromatography (GC) purification and a silica gel collection method.13,19 The Δ18 (abundance of both 13CH3D and 12CH2D2 relative to a random isotopic distribution) fractionation of 5 Å molecular sieve collection-release is ∼+0.49‰.12,13 GC systems typically exhibit no fractionation, but are variably efficient in water removal,21 which becomes important in methane isotopologue measurements because the common 1H216O (18.011 amu) molecule is approximately isobaric with doubly-substituted methane isotopologues. In particular, 13CH5 might lead to CH4 18 amu isobaric interferences. The 1H216O peak was used for the tailing correction procedure in 12CH2D2 measurement.22 Previously reported10,23–26 pretreatment methods have been shown to be effective for methane-dominated samples of relatively high purity (e.g., natural gas) and a limited number of samples with relatively low methane purity (e.g., natural water emitted gases with a CH4 concentration of <20%). Efficient purification and collection of methane from low concentration environmental samples is necessary for clumped isotope measurements in natural systems.
Here, we report a one-year dataset of high-resolution mass spectrometry measurements in our laboratory, including the δ13C-CH4, δD-CH4, δ13CH3D, and δ12CH2D2 results. The precision, accuracy, and four potentially important factors which may influence measurements are discussed and compared to those of previous studies. Using the temperature scale from catalyzed equilibration experiments at 500 °C, 400 °C and 300 °C, the working gas results (δ13CH3D and δ12CH2D2) can be calibrated and converted to an absolute reference frame (Δ13CH3D and Δ12CH2D2). We present a cryogenic purification (at 50 K) and silica gel collection (at 75 K) pretreatment system with demonstrably negligible isotope fractionation. A series of synthetic and natural samples with large isotopic (bulk and clumped) differences have been successfully measured using this system.
2. Experimental section
2.1 Mass spectrometer commissioning
The high-resolution isotope ratio mass spectrometer (253 Ultra, Thermo Fisher Scientific, Germany), installed at the School of Earth System Science, Tianjin University, China, has a mass resolving power (MRP; 5% and 95% edge definition) of 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–50
000–50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 with the HR+ mode (high-resolution slit with a width of 5 μm and an additional mechanical aperture for higher resolution combination27). The spectrometer is equipped with nine Faraday cup (L4–L1, Center, H1–H4) detectors. Three of the Faraday cups (H2, H3, and H4) are co-mounted with miniature compact discrete dynode (CDD) electron multipliers designed to quantify low intensity signals.
000 with the HR+ mode (high-resolution slit with a width of 5 μm and an additional mechanical aperture for higher resolution combination27). The spectrometer is equipped with nine Faraday cup (L4–L1, Center, H1–H4) detectors. Three of the Faraday cups (H2, H3, and H4) are co-mounted with miniature compact discrete dynode (CDD) electron multipliers designed to quantify low intensity signals.
L1 [13CH4+], L4 [12CH4+], H3 CDD [13CH3D+], and H4 CDD [12CH2D2+] are used in methane clumped isotope measurement. The resulting mass scans for δ13C, δD, Δ13CH3D, and Δ12CH2D2 are shown in Fig. 1.
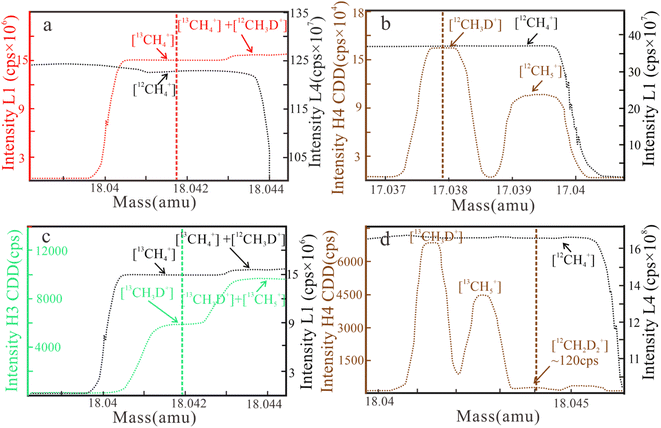 | ||
| Fig. 1 Mass scan results of ion intensity for δ13C (a), δD (b), Δ13CH3D (c), and Δ12CH2D2 (d) measurements on April 29, 2022. Δ13CH3D and δ13C are simultaneously analyzed (cps = counts per second). | ||
Measurements are ordered as Δ13CH3D and δ13C, δD, Δ12CH2D2, and peak tailing corrections, with a complete cycle measurement of about 30 h (complete 2 days of measurement is shown as a flow chart in Fig. S1†). The samples were thoroughly mixed over 20 cycles of bellows compression and relaxation (100–20% software settings) to ensure homogeneous isotope distribution before introduction to the mass analyser.12,13
2.2 Methane bulk and clumped isotopes
The bulk isotope compositions of CH4 are expressed as:| δ13CVPDB = [(13C/12C)sample/(13C/12C)VPDB − 1] × 1000 | (1) |
| δDSMOW = [(D/H)sample/(D/H)VSMOW − 1] × 1000 | (2) |
The clumped isotope compositions of CH4 are expressed below:
| Δ13CH3D = [(13CH3D/12CH4)sample/(13CH3D/12CH4)stochastic − 1] × 1000 | (3) |
| Δ12CH2D2 = [(12CH2D2/12CH4)sample/(12CH2D2/12CH4)stochastic − 1] × 1000 | (4) |
To establish a temperature scale for our laboratory, the in-house standard was ascribed a Δ value of zero, and measurements are performed within the ‘working gas reference frame’. Then, by independent calibration of the internal standard gain from the heated equilibrium experiments, the measured results for samples are converted to an ‘absolute thermodynamic reference frame’ (details of the calculation process in ESI Text S1†).
| (13CH3D/12CH4)stochastic = 4 × (13C/12C)sample × (D/H)sample | (5) |
| (12CH2D2/12CH4)stochastic = 6 × (D/H)sample × (D/H)sample | (6) |
2.3 Methane clumped isotope thermometer
Methane clumped isotope signatures (Δ12CH2D2 and Δ13CH3D) are reliable independent intramolecular thermometers at thermodynamic equilibrium, based on the following thermodynamic equilibrium equations for methane isotopic exchange reactions:13CH4 + 12CH3D ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) 12CH4 + 13CH3D 12CH4 + 13CH3D | (7) |
2 12CH3D ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) 12CH4 + 12CH2D2 12CH4 + 12CH2D2 | (8) |
The equilibrium constants K13CH3D and K12CH2D2 of reactions (7) and (8) are directly related to temperature (T). The relationship between T and Δ12CH2D2 and Δ13CH3D can be theoretically calculated using previous studies adopting two distinct approaches. Young et al. used ab initio calculations13 to derive:
| K13CH3D = 1 + 0.0355502/T – 433.038/T2 + 1270210.0/T3 − 5.9804 × 108/T4 + 1.196630 × 1011/T5 − 9.07230 × 1012/T6 | (9) |
| (8/3) K12CH2D2 = 1 + 0.183798/T – 785.483/T2 + 1056280.0/T3 + 9.37307 × 107/T4 – 8.919480 × 1010/T5 + 9.901730 × 1012/T6 | (10) |
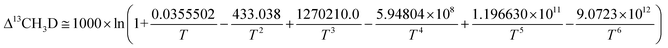 | (11) |
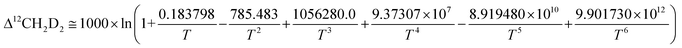 | (12) |
Subsequently, comparison of the Bigeleisen and Mayer/Urey (BMU) model and the path integral Monte Carlo (PIMC) model allowed Eldrige et al. to obtain the PIMC theoretical results:22
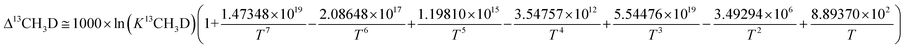 | (13) |
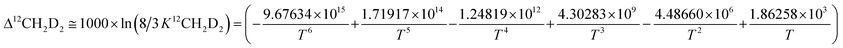 | (14) |
2.4 Sample preparation
Instrument internal precisions (±1 s.e.) and external precision (±1 s.d.) were determined using commercially purchased pure methane used as working standard gases. The first (HL) was obtained from Tianjin Haolun Gas Co., Ltd (CH4 purity 99.999%) and the second (JH) is from Suzhou Jinhong Gas Co., Ltd (CH4 purity 99.999%). Both in-house methane working standards are stored in high-pressure cylinders (∼2 MPa) and connected directly to the spectrometer's inlet system via a 1/4 inch needle connection.Samples for heated gas equilibration experiments used a Pyrex tube filled with silica gel (∼2–5 mm granules) and a nickel catalyst (65 wt% nickel dispersed on a silica/alumina support; Sigma Aldrich). The tube was packed with glass wool (Thermo Fisher) and pre-evacuated (<10−1 Pa) in a vacuum line system. ∼300 torr methane cylinder gas was transferred into the Pyrex tube and subsequently flame sealed. Gas samples were heated in a muffle furnace (Yamato) at fixed temperatures (300 °C, 400 °C, and 500 °C) for a fixed period (1.5–90 h). We removed the samples at high temperatures and quenched them to room temperature. Then, the gas sample was collected in a Kimble glass bottle after purification.
Natural gas samples were collected from a natural gas well head in the Gaoshiti-Moxi (Gao-Mo) area, Sichuan Basin, and stored in high-pressure cylinders (∼3 MPa). The Gao-Mo methane samples exceed 95% purity and contain only trace amounts of H2S, H2, and other impurities. The lake emitted samples were collected from artificial lakes, Qingnian Lake (39°06′42.1′′N, 117°10′16.7′′E), Youyi Lake (39°06′27.6′′N, 117°10′10.4′′E), and Aiwan Lake (39°06′33.8′′N, 117°10′09.0′′E), on the Tianjin University campus (TJU), Tianjin. Samples were collected by submerged, umbrella-style gas bubble traps from surface water, with a methane purity of 15–30%.
2.5 Methane pretreatment system
Pure methane (purity > 99%) samples at 70–110 mbar were required for the dual-inlet isotopic measurement. A pretreatment system with stainless steel tubing joined with Swagelok valves was used for purification and collection (Fig. 2) using previously described methods.10,12 Before starting sample processing, the whole system was evacuated to <10−1 Pa. The gas sample was introduced using a gas-tight syringe or a one-quarter-inch needle directly into the vacuum line and then passed into a liquid N2 trap to remove H2O, CO2, and H2S (Fig. 2). The headspace gases, including CH4, O2, and N2, were transferred into a 20 K liquid-helium cryostat trap (Lanhai Keyi Instrument Co., Ltd, Tianjin, China) for 10 minutes and residual He and H2 in the headspace were pumped away for about 3 minutes. The cold trap was then heated to 80 K and cooled to 45 K, while pumping the headspace gas until the pressure was <2.67 Pa at 45 K, when the theoretical purity of CH4 is >99.8%.10 After completing each sample pretreatment, the liquid-helium cryostat was heated to room temperature and the whole system was required to attain a vacuum level of <10−1 Pa before the next sample pretreatment.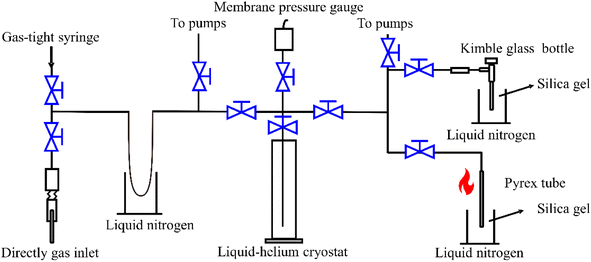 | ||
| Fig. 2 Cryogenic vacuum line purification and silica-gel collection pretreatment systems. The black lines and blue switches represent stainless steel tubes and Swagelok valves, respectively. | ||
Two methods were utilised for final gas collection. One used a conventional flame-seal tube technique in which a Pyrex break-seal tube containing silica-gel at liquid N2 temperature was sealed using an oxy-hydrogen welding torch. The second method used a silica-gel-filled high-vacuum high-boron glass bottle (Kimble, America) or a stainless cold finger submerged in liquid N2, which can directly collect methane gas to avoid flame sealing. Both collection methods required heating for 5 minutes with a heat gun or a 50 °C water bath before introduction to the sample bellows.
All heated gas, natural gas samples, and lake source point samples were measured within a half-day of the pre-treatment process. We note that in the pre-treatment of the source point samples, the purification pumping temperature was set to 50 K and the collection temperature was set to 75 K due to the low methane purity.
3. Results and discussion
3.1 Precision and accuracy
The optimization and commissioning of the spectrometer started in November 2020. δ13C and δ13CH3D measurements achieved an internal precision of ±0.01‰ and ±0.36‰ (±1 s.e.), respectively after basic commissioning (Fig. S2†). δD has a higher requirement for the MRP; from December 2020 until April 2021, the HR+ mode of instrument operation reached a MRP of ∼45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, with internal precision (±1 s.e.) for achieving δD ∼±0.1‰. The detail of δ12CH2D2 commissioning is shown in Text S2 and Fig. S3.† HR+ mode (high resolution slit with an aperture) has higher MRP but low sensitivity ([12CH2D2+] ∼ 55 cps). HR mode (high resolution slit but without the additional aperture) gave better sensitivity but the lower MRP necessitated a tailing correction procedure. Nonetheless, the tailing correction appears to be successful and facilitates improved analytical precision consistent with the increased sensitivity. Thus, HR mode with a tailing correction procedure was used for δ12CH2D2 giving an internal precision (±1 s.e.) for δ12CH2D2 of ∼±1.35‰. This illustrates the play-off between MRP and sensitivity that needs to be optimized to achieve the most precise measurements.
000, with internal precision (±1 s.e.) for achieving δD ∼±0.1‰. The detail of δ12CH2D2 commissioning is shown in Text S2 and Fig. S3.† HR+ mode (high resolution slit with an aperture) has higher MRP but low sensitivity ([12CH2D2+] ∼ 55 cps). HR mode (high resolution slit but without the additional aperture) gave better sensitivity but the lower MRP necessitated a tailing correction procedure. Nonetheless, the tailing correction appears to be successful and facilitates improved analytical precision consistent with the increased sensitivity. Thus, HR mode with a tailing correction procedure was used for δ12CH2D2 giving an internal precision (±1 s.e.) for δ12CH2D2 of ∼±1.35‰. This illustrates the play-off between MRP and sensitivity that needs to be optimized to achieve the most precise measurements.
The in-house methane showed the instrument internal precisions (±1 s.e.) in complete 2 days of measurements to be: δD = ±0.08‰, δ13C = ±0.01‰, δ13CH3D = ±0.31‰, and δ12CH2D2 = ±1.44‰ (±1 s.e.) (Table 1). However, this dataset includes the results obtained before the δ12CH2D2 commissioning was fully optimized and the precision of optimized δ12CH2D2 measurements is slightly lower, close to ∼±1.35‰ (Tables S1 and S2;† the 21 heated gas samples have a precision mean value of ∼±1.32‰).
| Methane type | n | δD(wg) (‰) | 1 s.e. | 1 s.d. | δ13C(wg) (‰) | 1 s.e. | 1 s.d. | Δ13CH3D(wg) (‰) | 1 s.e. | 1 s.d. | Δ12CH2D2(wg) (‰) | 1 s.e. | 1 s.d. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a All processed pure HL gases, including different types of purification and collection. | |||||||||||||
| HL gas | 14 | 0.0 | 0.06 | 0.07 | 0.06 | 0.02 | 0.07 | −0.01 | 0.33 | 0.35 | 0.21 | 1.59 | 1.20 |
| p-HL gasa | 11 | 0.68 | 0.07 | 0.24 | −0.17 | 0.01 | 0.40 | 0.18 | 0.32 | 0.40 | 0.06 | 1.45 | 1.34 |
| JH gas | 4 | −32.52 | 0.08 | 0.07 | 8.06 | 0.01 | 0.01 | 0.08 | 0.28 | 0.10 | 0.08 | 1.39 | 0.56 |
The external precision (±1 s.d.) represents reproducibility between samples. The external precision for each indicator of “raw” HL gas (n = 14) was δD = ±0.07‰, δ13C = ±0.07‰, Δ13CH3D = ±0.35‰, and Δ12CH2D2 = ±1.20‰. Processed HL gas (n = 11; including 5 variations of collecting and releasing procedures) gave external precisions of: δD = ±0.24‰, δ13C = ±0.40‰, Δ13CH3D = ±0.40‰, and Δ12CH2D2 = ±1.34‰. JH gas, replicated 4 times, gave external precisions of: δD = ±0.07‰, δ13C = ±0.01‰, Δ13CH3D = ±0.10‰, and Δ12CH2D2 = ±0.56‰ (Table 1).
The precision and accuracy results in this study are comparable to those reported at Caltech,10 UC Berkeley,22 and the Tokyo Institute of Technology19 using similar instruments. All individual replicate measurements are provided in Table S1† and the comparison results are shown in Table S2.†
3.2 Factors influencing the measurements of clumped methane isotopologues
| Data | M/H ratioa | [12CH2D2+] intensityb (cps) | 1 s.e.c (‰) | 1 s.d.d (‰) |
|---|---|---|---|---|
| a Estimated from the intensity ratio of [12CH4+] recorded by L4 in MR mode and HR mode. b Initial gas volume is 100–110 mbar and the ion source pressure is below 2 × 10−7 mbar (cps = counts per second). c Represents the internal precision (±1 s.e.) of δ12CH2D2 in 8 cycles × 30 blocks. d Represents the external precision (±1 s.d.) of Δ12CH2D2 from 2022/2/22–2022/3/1 and 2022/4/13–2022/5/15. e The results were measured immediately after the slit was changed on 2022/4/21. | ||||
| 2022/2/25 | 4.5 | 110 | 1.44 | 1.04 |
| 2022/4/10 | 6.7 | 80–90 | 1.53 | 0.56 |
| 2022/4/19 | 7.9 | 60–70 | 1.86 | |
| 2022/4/26e | 3.4 | 140–150 | 1.25 | |
| F = [12CH3+]/[12CH4+] = [13CH3+]/[13CH4+] | (15) |
In this study, the measured F value is ∼0.78 and range of six-month measurements’ external accuracy (±1 s.d.) was about ±0.03.
The introduction of the F value would change the calculation process to some extent and affect the results of δ13CVPDB, δDSMOW, Δ13CH3D, and Δ12CH2D2 values (see details in Text S1†). The F values of this mass spectrometer are mostly in the range of 0.7 to 0.8 and comparable with those of previous studies using similar instruments.12,22 To explore the effect of F on clumped isotope (Δ13CH3D and Δ12CH2D2) calculations, we performed simulations of F values from 0 to 1 in increments of 0.01 (i.e., different F values were assigned during the calculations of the samples). The results of two sets of cylinder gases (HL and JH), a sample gas (GS8), and a mixed gas (MG) were considered. During this process, the other measurement factors and the calculation process remain unchanged. In the working gas reference frame, the HL, JH, and GS8 results show almost no change (<0.01‰), and the results of the MG Δ13CH3D(wg) changed by ∼0.04‰, and Δ12CH2D2(wg) changed ∼0.18‰ (Fig. S8†).
Compared with the internal precision (±1 s.e.) of Δ13CH3D (±0.35‰) and Δ12CH2D2 (±1.35‰) measurements, this change is negligible and the process can be incorporated into the entire measurement and used as validation of the calculations and instrument performance stability.
JH gas (sample, in the left bellows) and HL gas (reference, in the right bellows) were used to make a bellows effect comparison. We adjusted the initial gas volume (mbar) and compression (%) of the bellows, and ten blocks of measurements were performed to verify the possible effect of the bellows leaking process on the δD results (details of the gas leakage experiments are shown in Text S4†). The results show that measured δD(wg) values do not correlate with the initial gas volume, compression ratio, or measured gas volume (Table S4†). All the results (including measurement on 2022/4/24 without compression) had an external precision (±1 s.d.) of ∼±0.08‰, which is acceptable, both for the subsequent calculation procedure involving δD and the internal precision (±1 s.e. ∼ ±0.1‰). This study showed that any pressure-dependent isotope fractionation during gas leakage can be effectively canceled by the Ultra 253 dual inlet. To avoid possible fractionation, it is recommended that the sample be released quickly and have a relatively high initial pressure (>100 mbar),30 and that a uniform isotopic distribution of the gas be established prior to measurement by repeated compression and relaxation of the bellows.12
3.3 Pretreatment process: purity and fractionation
We have refined pretreatment procedures for methane clumped isotope analysis in two significant respects. (1) To analyze samples in the surface environment, we combined aspects of two previous pretreatment protocols12,13 and used a new cryogenic purification and silica gel collection method (Fig. 2); (2) in previous studies purification and collection steps were performed at 45 K and 70 K, respectively.10,12,32 Our method increased purification and collection temperatures by 5 K. In our method a large amount of headspace gas (N2 and O2) was pumped away at 50 K, leaving a level of sample purity (headspace pressure < 2.67 Pa and purity > 99.8%) achieved at 45 K in previous studies. The collection temperature of 75 K (compared to 70 K in previous studies) similarly does not appear to induce deleterious effects and facilitated the collection of copious quantities of gas from the cryostat quickly.Methane clumped isotopes measurements require 3 ml pure (∼99%) sample,14 so removing impurity gases is the first step for pretreatment. It was verified that pumping at 45 K or 50 K and collecting at 70 K or 75 K does not change the purity of the final collected gas. The natural gas sample from Sichuan basin (GS8, initial methane content of ∼90%) and lake source point sample from Aiwan Lake (initial methane content of ∼15%) were measured after purification, collection, and release procedures. To determine the purity of the methane sample, we used three constraints: (i) the purity of methane samples in the pre-treatment process is generally considered to be greater than 99.8% at 45 K with a headspace pressure of <2.67 Pa.10,12,32 In our sample pre-treatment process this pressure is usually <1 Pa; (ii) the intensity of mass-28 was compared to the intensity of mass-16 to indicate the air content.27 After the samples were introduced into the 253 Ultra, a mass scan was carried out first, which verified an air (mass-28 content) content lower than ∼0.2% (Fig. S10†); (iii) the signal values of mass-16 of the purified samples and HL cylinder gases (CH4 purity 99.999%) under the same pressure were compared; the ratios were >0.998, and finally the verified purity of the purified samples was obtained. These constraints mean that the methane purity was ∼99.8% and met the measurement requirements.
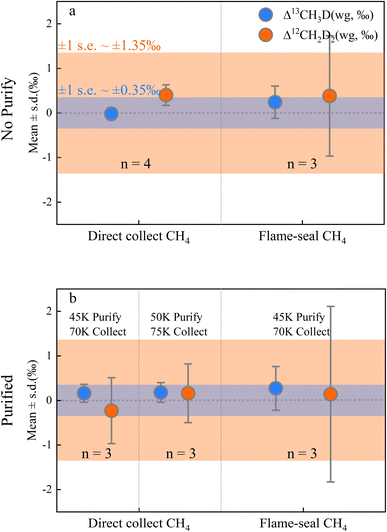
Clearly it is necessary to demonstrate that the pretreatment process is not responsible for artefactual isotopic fractionation. Overall, the cryogenic purification and silica gel collection method may have produced a slight shift in δD and δ13C, but this was negligible for both the conventional isotope analysis,19 and Δ13CH3D (mean ± s.d. = +0.16 ± 0.32‰) and Δ12CH2D2 (mean ± s.d. = +0.14 ± 1.12‰) and did not vary significantly for pre-treated in-house methane samples (n = 16; Table S3†). A comparison of Fig. 3a and b shows that the presence or absence of the purification process had no significant effect on the isotope results. The results of the direct collection method show higher precision, and the flame-sealed collection method appeared to show an increased uncertainty (Fig. 3) that has not been reported in previous studies.12,22 The additional uncertainty is thought to be operator-induced variability in the flame-sealing process. We suggest that the conventional flame-seal method is necessary for samples that require long-term storage which ensures the reliability of the sample preservation. However, direct collection is preferable if the samples can be measured promptly. After changing the purification and collection temperatures to 50 K & 75 K respectively, there is almost no significant difference in fractionation compared to fractionation at 45 K & 70 K (Fig. 3) supporting the contention that isotopic fractionation resulting from changes in the pre-treatment strategy is negligible.
3.4 Temperature scale calibration
Two independent theoretical predictions exist to describe the temperature dependence of isotopically equilibrated methane doubly substituted isotopologue abundances based upon ab initio and PIMC calculations respectively,13,22 but they largely predict concordant relationships (Fig. 4). In the range of 0–1000 °C, the two sets of predictions are highly correlated (correlation analysis: P value (2 tailed) <0.001) and not significantly different (ANOVA: P value (2 tailed) ∼0.96) (Table S5†). In this study, all results were calculated using the ab initio model prediction.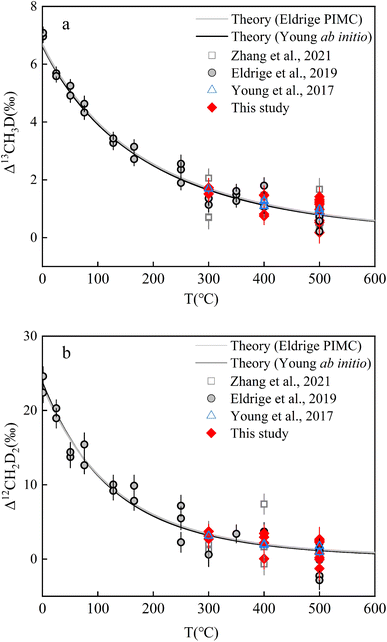 | ||
| Fig. 4 Experimental and theoretical values of equilibrium CH4 clumped isotopologues as a function of temperature: (a). Δ13CH3D values versus T (°C) and (b). Δ12CH2D2 values versus T (°C). Error bars for experimental data points here represent the internal precision (±1 s.e.) of replicates (i.e., experimental reproducibility). Data of CH4 double substituted isotopologues heating experiments result from previous studies.13,19,22 | ||
The results after heating both JH and HL gases at different temperatures (500 °C, 400 °C, and 300 °C; the reasons for selecting the three temperatures are shown in Text S5†) are summarized in Table 3 (see Fig. 4 and Table S6† for the individual results). The internal precision (±1 s.e.) for all heated gas samples was Δ13CH3D ∼ ±0.35‰ and Δ12CH2D2 ∼ ±1.35‰. The external precision (±1 s.d.) for the samples at 500 °C (n = 11; heating durations from 1.5–24 h) was Δ13CH3D = ±0.39‰ and Δ12CH2D2 = ±1.35‰. The external precision (±1 s.d.) of the sample heated at 400 °C (n = 4; heating durations from 5–20 h) was Δ13CH3D = ±0.34‰ and Δ12CH2D2 = ±1.30‰. The external precision (±1 s.d.) of the samples heated at 300 °C (n = 4; heating durations from 40–90 h) was Δ13CH3D = ±0.08‰ and Δ12CH2D2 = ±0.35‰. To establish a temperature scale, the results are indistinguishable at the same heating temperature, indicating that intramolecular equilibrium is comparable with the previous temperature scale data13,19,22 (Fig. 4; a detailed discussion of the validation of isotopologues reaching intramolecular equilibrium after heating is given in Text S5, Table S7†).
| Heated temperaturea | Durationb (h) | Δ13CH3D(wg) (‰) | 1 s.e. | 1 s.d. | Δ12CH2D2(wg) (‰) | 1 s.e. | 1 s.d. | n |
|---|---|---|---|---|---|---|---|---|
| a The 500 °C, 400 °C, and 300 °C represent the samples heated temperature of equilibrated gas experiments. b The duration time represents the heated gas experiment duration (hours) at a certain temperature. | ||||||||
| 500 °C | 1.5–24 | −1.34 | 0.33 | 0.39 | −2.15 | 1.35 | 1.35 | 11 |
| 400 °C | 5–20 | −1.14 | 0.30 | 0.34 | −1.31 | 1.23 | 1.30 | 4 |
| 300 °C | 40–90 | −0.62 | 0.30 | 0.08 | −0.30 | 1.21 | 0.35 | 4 |
The measured results (mean ± s.d.) were fitted linearly with the ab initio theoretical results at 500 °C, 400 °C, and 300 °C (Fig. S11†). A linear trend with a slope of 1 and an intercept of Δ13CH3D ∼ −2.27 ± 0.019 (1σ; R2 ∼ 0.98) and Δ12CH2D2 ∼ −3.51 ± 0.06 (1σ; R2 ∼ 0.97) implied a ‘true’ Δ13CH3D value of +2.27‰ and a Δ12CH2D2 value of +3.51‰ for the reference gas (HL working gas) in the SESS laboratory, relative to the random isotope distribution. A weighted least-squares regression of the data results in slopes for Δ13CH3D ∼ 0.89 ± 0.08 (1σ; R2 ∼ 0.99) and Δ12CH2D2 ∼ 0.86 ± 0.07 (1σ; R2 ∼ 0.99), which are comparable with the previous temperature scaling results,12,19 and at a 95% confidence interval are indistinguishable from the results for slope = 1. Theoretical calculations provide a reference frame that, when combined with the obtained results of heating gas to equilibrium at different temperatures, can help correct the CH4 clumped isotope compositions (Δ13CH3D and Δ12CH2D2) for the working gas in the ‘absolute thermodynamic reference frame’. Using the ‘true values’ of the working gas, the measured samples can be converted to the absolute reference frame (see Text S1† for details of the calculations). The accuracy of our temperature calibration results was tested by inter-laboratory comparisons of the same samples (STD-A and STD-C). Our results were comparable to those of TIT,19 further validating the accuracy of the entire method including the temperature scale results.
3.5 Natural environmental samples
The bulk and clumped isotope signatures of the laboratory in-house methanes (HL and JH), the heated equilibrium gas, and the two sets of natural samples (natural gases and lake emission gases) are shown in Fig. 4. HL and JH have different bulk isotope compositions of δ13CVPDB = −45.16‰ and δDSMOW = −162.81‰, and δ13CVPDB = −37.41‰ and δDSMOW = −190.04‰, respectively, but similar clumped isotope compositions of Δ13CH3D = +2.27‰ and Δ12CH2D2 = +3.51‰ and Δ13CH3D = +2.35‰ and Δ12CH2D2 = +3.59‰ (Table S1;† corrected by temperature scale), respectively. The industrial production processes of the two in-house methanes were close, and the clumped isotope signatures indicated that they formed at temperatures of ∼200–250 °C. The results of heated gas at 300 °C, 400 °C, and 500 °C are shown in Table 4. The process of heating methane using 65 wt% nickel dispersed on a silica/alumina support catalyst is essentially C–H bond activation and hydrogen isotope exchange.22 The high temperature and the presence of a catalyst can drive methane to intra-species equilibrium.13 As shown in Fig. 5, this process can be regarded as a re-equilibrium process that produced equilibrated clumped isotope signatures at a specific temperature.| Sample | δDVSMOW (‰) | 1 s.e. (‰) | δ13CVPDB (‰) | 1 s.e. (‰) | Δ13CH3D (‰) | 1 s.e. (‰) | T-Δ13CH3Da (°C) | Δ12CH2D2 (‰) | 1 s.e. (‰) | T-Δ12CH2D2a (°C) |
|---|---|---|---|---|---|---|---|---|---|---|
| a Estimated temperatures were derived from Δ13CH3D and Δ12CH2D2 using the ab initio model prediction. | ||||||||||
| GS8-D4-DOWN | −143.45 | 0.12 | −34.10 | 0.01 | 1.68 | 0.37 | 296.8 | 3.59 | 1.42 | 281.4 |
| GS8-D4-UP | −138.76 | 0.07 | −34.08 | 0.01 | 1.91 | 0.27 | 264.3 | 6.06 | 1.26 | 193.6 |
| GS11-D2 | −138.37 | 0.06 | −29.54 | 0.01 | 2.01 | 0.28 | 252.5 | 4.45 | 1.30 | 244.5 |
| MX17-D2 | −143.67 | 0.07 | −33.83 | 0.01 | 2.79 | 0.29 | 174.4 | 5.00 | 1.31 | 224.9 |
| MX8-LWM | −132.00 | 0.10 | −33.96 | 0.01 | 2.77 | 0.30 | 176.4 | 6.57 | 1.43 | 180.9 |
| MX18-LWM | −131.22 | 0.09 | −33.88 | 0.01 | 1.87 | 0.25 | 269.0 | 3.54 | 1.24 | 284.2 |
| Qingnian lake | −349.70 | 0.06 | −60.51 | 0.01 | 0.02 | 0.22 | — | −33.33 | 0.94 | — |
| Youyi lake | −303.96 | 0.06 | −66.96 | 0.01 | 0.11 | 0.28 | −24.60 | 1.01 | ||
| Aiwan lake | −342.41 | 0.06 | −67.81 | 0.01 | −0.27 | 0.27 | −35.69 | 0.92 | ||
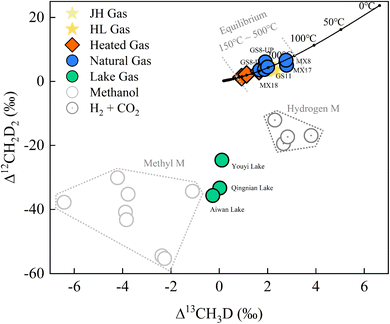 | ||
| Fig. 5 Clumped isotope results of methane for natural gas (GS- and MX-), lake gas (Youyi, Aiwan, and Qingnian Lake), and heated gas (mean values of 500 °C, 400 °C and 300 °C) plotted as the Δ13CH3D versus Δ12CH2D2 plot. Hydrogenotrophic and methylotrophic methanogenesis culturing experiment data from previous studies.13,24,40 | ||
The Gao-Mo area is the main natural gas-producing area in the Sichuan Basin of southwestern China, having the Sinian Dengying Formation and the Cambrian Longwangmiao Formation (LWM) as important gas reservoirs.33 The results show that δDVSMOW of Dengying Fm (D2 and D4) was lighter relative to that of LWM Fm (Table 4). This might be related to the difference in aqueous medium conditions in the depositional environment.34,35 Previous thermochemical sulfate reduction (TSR) studies in the Gao-Mo area suggest that the CH4 bulk isotopes might be due to different degrees of TSR.36 However, Δ13CH3D and Δ12CH2D2 signatures fitted well with the equilibrium curve and do not show a distribution that varies with bulk isotope composition (Fig. 5). The paired clumped isotope results showed that GS8-D4-UP was located on the upper side of the equilibrium line, suggesting gas diffusion from the lower to upper formation when compared with the GS8-D4-DOWN results; MX17-D2 was located on the lower side of the equilibrium line, which might be influenced by exotic organisms or post-generation processes. However, overall, methane clumped isotopes indicate that formation (or re-equilibration) temperature of natural gas in the Gao-Mo area ranged from 174.6 to 296.3 °C (T-Δ13CH3D = 174.6–296.3 °C and T-Δ12CH2D2 = 180.9–284.1 °C). The highest temperature experienced by the Sinian formations exceeded 240 °C (Ro ∼ 3.5‰).37 Bulk isotope reversal of methane and ethane suggested that the natural gas in the study area originated from high-over maturity shale and is a mixture of two thermogenic gases.34 Generally, the kinetic process controlled the thermogenic gases' bulk isotope compositions,38 and the clumped isotope compositions reflect 13C–D and D–D clumping in the methyl precursor at the cracking temperature.39 The methane-clumped isotope thermometer gives additional reliable temperature information at equilibrium. Combining the results of the methane bulk and clumped isotopes places new additional constraints on the formation and evolution of the thermogenic gas.
The results of doubly substituted isotopologues of methane released from natural water environments have not been extensively reported in previous studies. The samples released from the artificial lakes (Qingnian Lake, Youyi Lake, and Aiwan Lake in TJU) had δ13CVPDB values from −60.51‰ to −67.81‰ and δDSMOW values from −303.69‰ to −349.70‰. The bulk isotopes were consistent with the isotopic source signatures of microbial methyl-type fermentation on ‘Whiticar plots’.6 The lake samples’ clumped isotope results (Δ13CH3D from −0.27‰ to +0.11‰ and Δ12CH2D2 from −24.60‰ to −35.69‰) showed a clear disequilibrium characteristic (Fig. 5). The results of the Youyi Lake sample lie between previously reported hydrogenotrophic and methylotrophic methanogenic culturing experimental results.13,24,40 Qingnian and Aiwan Lake were closer to the methylotrophic methanogenic pathway and the results of their samples are similar to the results reported by Young et al. using Methanosarcina barkeri incubated at 30 °C (Δ13CH3D = −1.11‰ and Δ12CH2D2 = −34.33‰).13 However, as the paired clumped isotope results for acetoclastic methanogenesis were not reported, only the Δ13CH3D (from −1.70‰ to −3.10‰) can be compared.41 The data from the culture experiments need to be further refined, but the methane production pathway can be characterized by using clumped isotopes. In combination with other environmental parameters, the results can be used as a proxy to explore kinetic processes in methane release,24e.g., biogeochemical processes and their connection with sediment components.25
4. Conclusions
We present a new measurement protocol for methane clumped isotopes and bulk isotopes, with an MRP of 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–50
000–50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. The following conclusions can be reached:
000. The following conclusions can be reached:
(1) The high-resolution mass spectrometer could separate adjacent methane peaks and achieved internal precision of δ13C = ±0.01‰, δD = ±0.08‰, δ13CH3D = ±0.35‰, and δ12CH2D2 = ±1.35‰ (±1 s.e.). The external precision of the samples was δ13C = ±0.01‰, δD = ±0.10‰, Δ13CH3D = ±0.35‰, and Δ12CH2D2 = ±1.35‰ (±1 s.d.).
(2) It is recommended to maintain relatively constant ambient laboratory temperature (±1 °C) and humidity (±5%) for the spectrometer. It was found that slit quality directly influenced signal intensity and further determined the stability of measurement, and a relatively minor impact on the clumped isotope results (Δ13CH3D and Δ12CH2D2) was associated with the fragmentation rate. In addition, a gas leakage experiment showed that in the dual-inlet system, any bellows effect, previously observed in low resolution IRMS measurements, has a negligible impact on the measurement results.
(3) Cryogenic purification at 50 K and silica gel collection at 75 K remove impurity gases from low methane concentration samples, resulting in a methane purity of ∼99.8%, and both flame-sealed and direct collection are acceptable. The system does not produce isotopic fractionation during either purification collection or release, and no additional correction of the results is necessary.
(4) The heated equilibrium gas experiments at 500 °C, 400 °C and 300 °C provide a reliable temperature scale for correcting the relative equilibrium 13CH3D and 12CH2D2 abundances of the working gas to convert the dataset to an absolute reference frame. The results from industrial tank gas (in-house methane), heated re-equilibrium gas, natural gas, and lake emission samples showed 150–500 °C equilibrium and microbially dominated disequilibrium clumped isotope signatures, which support the measurement possibilities for broad environmental samples. This study demonstrated an improved efficient purification, collection, and clumped isotope analysis method for natural methane with a wide range of concentrations.
Author contributions
Xinchu Wang: methodology, investigation, data curation, writing – original draft, review and editing. Cong-Qiang Liu: funding acquisition, supervision, project administration, and writing – review and editing. Naizhong Zhang: methodology, validation. Sheng Xu: supervision, writing – review and editing. Zhiyong Pang: methodology, visualization. Si-Liang Li: supervision, writing – review and editing. Hu Ding: supervision, conceptualization, resources. Jianfa Chen: supervision, validation Zengye Xie: validation. Rob M. Ellam: methodology, writing – review and editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This research was funded by the National Natural Science Foundation of China [grant number 41925002, 41971123, and 42150710532]; the National Science & Technology Fundamental Resources Investigation Program of China (Grant No. 2021FY101000); Tianjin Municipal Science and Technology Bureau [20ZLGCGX00030]; National Key R&D Program of China (Grant No. 2018YFC1800306). We thank Zhifeng Yan and Xueqi Niu for sampling. We also thank Hao Xie and Li Lu for the use of the instrument.References
- E. J. Dlugokencky, E. G. Nisbet, R. Fisher and D. Lowry, Philos. Trans. R. Soc., A, 2011, 369, 2058–2072 CrossRef CAS PubMed.
- A. R. Brandt, G. A. Heath, E. A. Kort, F. O'Sullivan, G. Pétron, S. M. Jordaan, P. Tans, J. Wilcox, A. M. Gopstein, D. Arent, S. Wofsy, N. J. Brown, R. Bradley, G. D. Stucky, D. Eardley and R. Harriss, Science, 2014, 343, 733–735 CrossRef CAS PubMed.
- R. K. Thauer, Microbiology, 1998, 144, 2377–2406 CrossRef CAS.
- B. B. Bernard, J. M. Brooks and W. M. Sackett, Earth Planet. Sci. Lett., 1976, 31, 48–54 CrossRef CAS.
- M. Schoell, Chem. Geol., 1988, 71, 1–10 CrossRef CAS.
- M. J. Whiticar, Chem. Geol., 1999, 161, 291–314 Search PubMed.
- J. L. France, M. Cain, R. E. Fisher, D. Lowry, G. Allen, S. J. O'Shea, S. Illingworth, J. Pyle, N. Warwick, B. T. Jones, M. W. Gallagher, K. Bower, M. Le Breton, C. Percival, J. Muller, A. Welpott, S. Bauguitte, C. George, G. D. Hayman, A. J. Manning, C. L. Myhre, M. Lanoisellé and E. G. Nisbet, J. Geophys. Res.: Atmos., 2016, 121, 14257–214270 CAS.
- P. M. J. Douglas, D. A. Stolper, J. M. Eiler, A. L. Sessions, M. Lawson, Y. Shuai, A. Bishop, O. G. Podlaha, A. A. Ferreira, E. V. Santos Neto, M. Niemann, A. S. Steen, L. Huang, L. Chimiak, D. L. Valentine, J. Fiebig, A. J. Luhmann, W. E. Seyfried, G. Etiope, M. Schoell, W. P. Inskeep, J. J. Moran and N. Kitchen, Org. Geochem., 2017, 113, 262–282 CrossRef CAS.
- R. L. Tyne, P. H. Barry, M. Lawson, D. J. Byrne, O. Warr, H. Xie, D. J. Hillegonds, M. Formolo, Z. M. Summers, B. Skinner, J. M. Eiler and C. J. Ballentine, Nature, 2021, 600, 670–674 CrossRef CAS PubMed.
- N. Thiagarajan, N. Kitchen, H. Xie, C. Ponton, M. Lawson, M. Formolo and J. Eiler, Geochim. Cosmochim. Acta, 2020, 275, 188–208 CrossRef CAS.
- O. Warr, E. D. Young, T. Giunta, I. E. Kohl, J. L. Ash and B. S. Lollar, Geochim. Cosmochim. Acta, 2021, 294, 315–334 CrossRef CAS.
- D. A. Stolper, A. L. Sessions, A. A. Ferreira, E. V. Santos Neto, A. Schimmelmann, S. S. Shusta, D. L. Valentine and J. M. Eiler, Geochim. Cosmochim. Acta, 2014, 126, 169–191 CrossRef CAS.
- E. D. Young, I. E. Kohl, B. S. Lollar, G. Etiope, D. Rumble, S. Li, M. A. Haghnegahdar, E. A. Schauble, K. A. McCain, D. I. Foustoukos, C. Sutclife, O. Warr, C. J. Ballentine, T. C. Onstott, H. Hosgormez, A. Neubeck, J. M. Marques, I. Pérez-Rodríguez, A. R. Rowe, D. E. LaRowe, C. Magnabosco, L. Y. Yeung, J. L. Ash and L. T. Bryndzia, Geochim. Cosmochim. Acta, 2017, 203, 235–264 CrossRef CAS.
- J. J. Jautzy, P. M. J. Douglas, H. Xie, J. M. Eiler and I. D. Clark, Earth Planet. Sci. Lett., 2021, 562, 116841 CrossRef CAS.
- J. Labidi, E. D. Young, T. Giunta, I. E. Kohl, J. Seewald, H. Tang, M. D. Lilley and G. L. Früh-Green, Geochim. Cosmochim. Acta, 2020, 288, 248–261 CrossRef CAS.
- Y. Shuai, H. Xie, S. Zhang, Y. Zhang and J. M. Eiler, Earth Planet. Sci. Lett., 2021, 566, 116960 CrossRef CAS.
- D. T. Wang, D. S. Gruen, B. S. Lollar, K.-U. Hinrichs, L. C. Stewart, J. F. Holden, A. N. Hristov, J. W. Pohlman, P. L. Morrill and M. Könneke, Science, 2015, 348, 428–431 CrossRef CAS.
- D. T. Wang, E. P. Reeves, J. M. McDermott, J. S. Seewald and S. Ono, Geochim. Cosmochim. Acta, 2018, 223, 141–158 CrossRef CAS.
- N. Zhang, G. T. Snyder, M. Lin, M. Nakagawa, A. Gilbert, N. Yoshida, R. Matsumoto and Y. Sekine, Geochim. Cosmochim. Acta, 2021, 315, 127–151 CrossRef CAS.
- D. A. Stolper, M. Lawson, C. L. Davis, A. A. Ferreira, E. S. Neto, G. S. Ellis, M. D. Lewan, A. M. Martini, Y. Tang and M. Schoell, Science, 2014, 344, 1500–1503 CrossRef CAS.
- S. Ono, D. T. Wang, D. S. Gruen, B. Sherwood Lollar, M. S. Zahniser, B. J. McManus and D. D. Nelson, Anal. Chem., 2014, 86, 6487–6494 CrossRef CAS PubMed.
- D. L. Eldridge, R. Korol, M. K. Lloyd, A. C. Turner, M. A. Webb, T. F. Miller and D. A. Stolper, ACS Earth Space Chem., 2019, 3, 2747–2764 CrossRef CAS.
- Y. Shuai, G. Etiope, S. Zhang, P. M. J. Douglas, L. Huang and J. M. Eiler, Earth Planet. Sci. Lett., 2018, 482, 213–221 CrossRef CAS.
- P. M. J. Douglas, R. G. Moguel, K. M. W. Anthony, M. Wik, P. M. Crill, K. S. Dawson, D. A. Smith, E. Yanay, M. K. Lloyd, D. A. Stolper, J. M. Eiler and A. L. Sessions, Geophys. Res. Lett., 2020, 47, e2019GL086756 CrossRef CAS.
- J. L. Ash, M. Egger, T. Treude, I. Kohl, B. Cragg, R. J. Parkes, C. P. Slomp, B. S. Lollar and E. D. Young, Geochem. Perspect. Lett., 2019, 10, 26–30 CrossRef.
- T. Giunta, J. Labidi, I. E. Kohl, L. Ruffine, J. P. Donval, L. Géli, M. N. Çağatay, H. Lu and E. D. Young, Earth Planet. Sci. Lett., 2021, 553 Search PubMed.
- J. M. Eiler, M. Clog, P. Magyar, A. Piasecki, A. Sessions, D. Stolper, M. Deerberg, H.-J. Schlueter and J. Schwieters, Int. J. Mass Spectrom., 2013, 335, 45–56 CrossRef CAS.
- T. W. Boutto, Carbon isotope techniques, 1991, vol. 1, p. 155 Search PubMed.
- X.-C. Zhang, A.-Y. Zhang, Z.-F. Zhang, F. Huang and H.-M. Yu, Rapid Commun. Mass Spectrom., 2018, 32, 1026–1030 CrossRef CAS.
- H. Yan, Y. Peng and H. Bao, Rapid Commun. Mass Spectrom., 2022, 36, e9290 CAS.
- F. Sharipov and V. Seleznev, J. Phys. Chem. Ref. Data, 1998, 27, 657–706 CrossRef CAS.
- P. M. J. Douglas, D. A. Stolper, D. A. Smith, K. M. Walter Anthony, C. K. Paull, S. Dallimore, M. Wik, P. M. Crill, M. Winterdahl, J. M. Eiler and A. L. Sessions, Geochim. Cosmochim. Acta, 2016, 188, 163–188 CrossRef CAS.
- Y. Yang, L. Wen, B. Luo, W. Wang and S. Shan, Pet. Explor. Dev., 2016, 43, 197–207 CrossRef.
- S. Zhang, K. He, G. Hu, J. Mi, Q. Ma, K. Liu and Y. Tang, Mar. Pet. Geol., 2018, 89, 68–82 CrossRef CAS.
- W. Guoqi, X. Zengye, B. Guilin, L. Jian, W. Zhihong, L. Aiguo and L. Zhisheng, Nat. Gas Ind., 2014, 1, 66–71 Search PubMed.
- C. Cai, C. Zhang, H. He and Y. Tang, Mar. Pet. Geol., 2013, 48, 100–110 CrossRef CAS.
- C. Zou, J. Du, C. Xu, Z. Wang, B. Zhang, G. Wei, T. Wang, G. Yao, S. Deng, J. Liu, H. Zhou, A. Xu, Z. Yang, H. Jiang and Z. Gu, Pet. Explor. Dev., 2014, 41, 306–325 CrossRef.
- Y. Ni, Q. Ma, G. S. Ellis, J. Dai, B. Katz, S. Zhang and Y. Tang, Geochim. Cosmochim. Acta, 2011, 75, 2696–2707 CrossRef CAS.
- D. A. Stolper, M. Lawson, M. J. Formolo, C. L. Davis, P. M. J. Douglas and J. M. Eiler, Geological Society, London, Special Publications, 2018, vol. 468, pp. 23–52 Search PubMed.
- T. Giunta, E. D. Young, O. Warr, I. Kohl, J. L. Ash, A. Martini, S. O. C. Mundle, D. Rumble, I. Pérez-Rodríguez, M. Wasley, D. E. LaRowe, A. Gilbert and B. Sherwood Lollar, Geochim. Cosmochim. Acta, 2019, 245, 327–351 CrossRef CAS.
- D. S. Gruen, D. T. Wang, M. Könneke, B. D. Topçuoğlu, L. C. Stewart, T. Goldhammer, J. F. Holden, K.-U. Hinrichs and S. Ono, Geochim. Cosmochim. Acta, 2018, 237, 339–356 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Datasets include all measurement results; process of δ and Δ value calculations; experimental details; measurement flowcharts, schematic data results; additional figures and tables (PDF). See DOI: https://doi.org/10.1039/d2ja00315e |
| This journal is © The Royal Society of Chemistry 2023 |