Open Access Article
Open Access ArticleNanowires exfoliated from one-dimensional van der Waals transition metal trihalides and quadrihalides†
Chuanxun
Su
 *ab and
Lixin
He
*ab and
Lixin
He
 *ab
*ab
aCAS Key Laboratory of Quantum Information, University of Science and Technology of China, Hefei, 230026, Anhui, People's Republic of China. E-mail: sucx@ustc.edu.cn; helx@ustc.edu.cn
bSynergetic Innovation Center of Quantum Information and Quantum Physics, University of Science and Technology of China, Hefei, 230026, People's Republic of China
First published on 4th March 2023
Abstract
The exfoliation of van der Waals (vdW) materials has been widely used to fabricate two-dimensional (2D) materials. However, the exfoliation of vdW materials to isolate atomically thin nanowires (NWs) is an emerging research topic. In this letter, we identify a large class of transition metal trihalides (TMX3), which have one-dimensional (1D) vdW structures, i.e., they comprise columns of face-sharing TMX6 octahedral chains, whereas the chains are bound by weak vdW forces. Our calculations show that the single-chain and multiple-chain NWs constructed from these 1D vdW structures are stable. The calculated binding energies of the NWs are relatively small, suggesting that it is possible to exfoliate NWs from the 1D vdW materials. We further identify several 1D vdW transition metal quadrihalides (TMX4) that are candidates for exfoliation. This work opens a paradigm for exfoliating NWs from 1D vdW materials.
Introduction
The exfoliation of van der Waals (vdW) materials to isolate atomically thin films is widely used by experimentalists to produce two-dimensional (2D) materials.1,2 The vdW materials that are successfully exfoliated can be natural or synthetic. First-principles calculations predicted a large number of vdW materials that can be exfoliated to build 2D materials by screening databases of crystal structures.3–6 These data provide valuable guidance to experimentalists for discovering novel 2D materials.One-dimensional (1D) vdW materials are made up of strongly bonded 1D atomic chains with weak inter-chain vdW forces. A previous experimental study verified the existence of vdW forces between atomic chains in 1D vdW material Tellurium by Raman spectroscopy.7 It is possible that 1D vdW materials can be exfoliated into nanowires (NWs), which provides a top-down approach to fabricate NWs. Quantum effects will be strong in atomically thin NWs, which may host exotic physics. However, the research on the exfoliation of vdW materials down to atomically thin NWs is still very limited.8 Freestanding atomically thin transition metal trihalide (TMX3) NW structures have been reported to be stable by previous studies. For example, a recent theoretical study investigated the magnetic and electronic properties of 3d transition-metal tribromide NWs, i.e. TMBr3 (TM = Sc, Ti, V, Cr, Co, and Cu), and half-metallicity was reported in ferromagnetic (FM) VBr3 and CuBr3 NWs.9 Guo et al.10 systematically studied vanadium-trihalide VX3 (X= F, Cl, Br, I) NWs and found that a single-chain VI3 NW is a FM semiconductor. The metal ions in TMX3 may have local magnetic moments, which may host new physical phenomena and could be useful for future spintronic applications. However, these previously reported NWs do not have a corresponding 1D vdW bulk phase for exfoliation.
In this study, we present computational research on the exfoliation of 1D vdW TMX3 and transition metal quadrihalides (TMX4). We first show that TiI311 is a 1D vdW material that can be exfoliated down to NWs consisting of a single chain or multiple chains of TiI6 octahedra. We demonstrate that the NWs are thermodynamically stable. To find more exfoliable 1D vdW materials, we use the structure prototype analysis package (SPAP)12 to search for structures that are similar to the TiI3 structure prototype in the Crystallography Open Database (COD).13 We identify a large class of 1D vdW TMX3 materials, including β-TiCl3,14 RuBr3,15,16 β-RuCl3,15 TcBr3,17 MoBr3,16,18 and ZrI3.19 These 1D vdW materials all have relatively small binding energies and therefore are potentially exfoliable. We further examine the magnetism, stability, and electronic structures of the NWs. We also find a series of 1D vdW TMX4 materials, including PtI4,20 OsBr4,21 TcCl4,22 TcF4,23 ZrCl4,24 HfCl4,25 TiI4,26 and UI4,27 which are candidates for exfoliation. This work opens a new path to fabricate NWs by a top-down approach.
Results and discussion
TiI3 nanowires
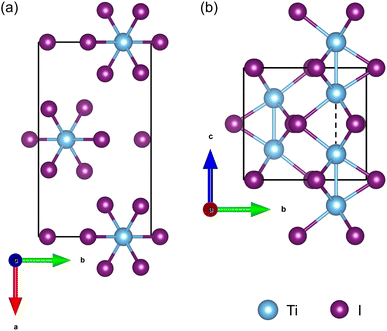
As shown in Fig. 1, the orthorhombic low-temperature phase of TiI3 (space group Pmmn)11 comprises parallel infinite columns of face-sharing TiI6 octahedra and the Ti atoms form dimers within the chains. In a unit cell, each chain contains 2 transition metal Ti atoms, which have a regular alternation of short and long inter-Ti distances as shown in Fig. 1(b). The TiI3 structure is a typical 1D vdW material. We construct 1 chain, 3 chains, and 7 chains of freestanding NWs from orthorhombic bulk TiI3, as shown in Fig. 2. The NW structures are then fully relaxed.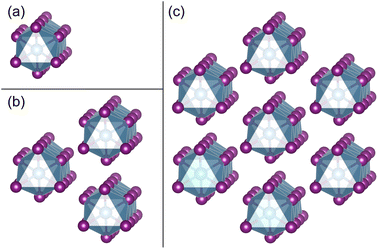 | ||
| Fig. 2 (a)–(c) NWs consist of 1 chain, 3 chains, and 7 chains of face-sharing octahedra exfoliated from the bulk phase of TiI3, respectively. | ||
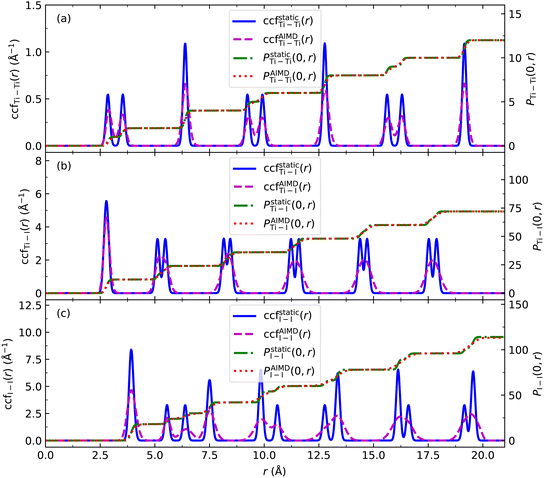
We use the coordination characterization function (CCF) to characterize the 1-chain TiI3 NW. Details about the CCF are provided in the Methods section. For the 1-chain TiI3 NW, the alternating short and long inter-Ti distances lead to alternating splitting and non-splitting peaks of ccfstaticTi–Ti(r) in Fig. 3. We define the pair function Pij(r1,r2) to characterize the number of atomic pairs for 2 formula units of TiI3 within a certain range between r1 and r2, such that
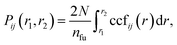 | (1) |
To determine the magnetic ground state of the NWs, we compare the total energies of different magnetic configurations for each NW structure. The total energies for various magnetic configurations are listed in Table S2 in the ESI.† All TiI3 NWs are nonmagnetic (NM). We calculate the binding energy (per atom) of a NW relative to its bulk material as
 | (2) |
| Compound | Space group | System | E b (eV per atom) | Magnetism | M (μB) | Band gap (eV) |
|---|---|---|---|---|---|---|
| TiI3 | Pmmn | Bulk | NM | 0.0 | 0.1 | |
| TiI3 | 1-Chain | 0.1643 | NM | 0.0 | 0.3 | |
| TiI3 | 3-Chain | 0.1114 | NM | 0.0 | 0.2 | |
| TiI3 | 7-Chain | 0.0725 | NM | 0.0 | 0.2 | |
| β-TiCl3 | Pmmn | Bulk | NM | 0.0 | 0.1 | |
| TiCl3 | 1-Chain | 0.1152 | NM | 0.0 | 0.2 | |
| TiCl3 | Monolayer | 0.0792 | NM | 0.0 | 0.2 | |
| MoBr3 | Pmmn | Bulk | AFM | 1.8 | 1.0 | |
| MoBr3 | 1-Chain | 0.1358 | AFM | 1.8 | 1.2 | |
| β-RuCl3 | Pmmn | Bulk | NM | 0.0 | 0.1 | |
| RuCl3 | 1-Chain | 0.1153 | NM | 0.0 | 0.3 | |
| RuBr3 | Pmmn | Bulk | NM | 0.0 | 0.1 | |
| RuBr3 | 1-Chain | 0.1342 | NM | 0.0 | 0.5 | |
| ZrI3 | Pmmn | Bulk | NM | 0.0 | 0.0 | |
| ZrI3 | 1-Chain | 0.1636 | NM | 0.0 | 0.3 | |
| CrI3 | P63/mcm | Bulk | FM | 3.4 | 0.1 | |
| CrI3 | 1-Chain | 0.1558 | AFM | 3.3 | 0.8 | |
| CrI3 | 3-Chain | 0.1068 | FM | 3.4 | 0.5 | |
| CrI3 | 7-Chain | 0.0697 | FM | 3.4 | 0.3 | |
| TcBr3 | Pmmn | Bulk | FM | 0.9 | 0.1 | |
| TcBr3 | 1-Chain | 0.1421 | FM | 0.8 | 0.2 | |
| TcBr4 | Pbca | Bulk | AFM | 2.1 | 0.6 | |
| TcBr4 | 1-Chain | 0.1394 | AFM | 2.2 | 0.9 |
To investigate the stability of the NWs, we recorded the phonon spectra of the 1-chain TiI3 NW, and no imaginary phonon frequencies are found, which indicates that it is dynamically stable. Since 3- and 7-chain TiI3 NWs have lower Ebs than 1-chain TiI3 NWs, they are expected to be more stable. This expectation is supported by our phonon spectrum calculations (Fig. S5 in the ESI†). To further check the stability of the NWs at finite temperatures, we perform ab initio molecular dynamics (AIMD) simulations of the 1-chain NW at 300 K. We calculate the CCFs of 3168 structures taken from the AIMD trajectories in the time range between 0.5 and 10.0 ps, and the averaged CCFs are shown in Fig. 3. We see that the CCFs of the 1-chain TiI3 at 300 K only have minor changes compared to those at zero temperature. The double-peak feature of CCFs is still preserved. The CCFs of Ti–I and I–I pairs are more smeared, and some double peaks merge into single peaks, which indicates that the I atoms move more vigorously. The platforms of ground state pair functions Pstaticij(0,r) and PAIMDij(0,r) at 300 K match very well. Importantly, the CCFs at 300 K still have the well organized periodicity, suggesting that the NW structure preserves the long range ordering (i.e., the crystal structure).
TMX3 nanowires
Since we have shown that TiI3 is exfoliable to stable NWs, we aim to find more materials similar to TiI3 for exfoliation, with even lower Eb and possibly being magnetic. We use the SPAP code12 to calculate the structural distance (d) between the orthorhombic phase of (bulk) TiI3 and structures with composition type AB3 sourced from the COD.13 The structures are first adjusted to an atom number density that is the same as that of the target TiI3 structure, before calculating the d. The structural distance d is a dimensionless quantity which can be obtained by comparing the similarity of the CCFs of the structures. The detailed methodology is introduced in the ESI.† A structure with smaller d is more similar to the target structure. We select 1153 AB3 structures from the COD and calculate the structural distances between the TiI3 structure and the adjusted AB3 structures. The structures are ordered by the increase in the structural distance, and the first 42 structures are listed in Table 2. Usually, structures with distances smaller than 0.075 in this framework are regarded as similar structures. We identity a series of 1D vdW materials that have structural distances smaller than 0.100 with TiI3, including β-TiCl3,14 RuBr3,15,16 β-RuCl3,15 TcBr3,17 MoBr3,16,18 and ZrI3.19| Compound | No. | d | Compound | No. | d |
|---|---|---|---|---|---|
| a The structures are sorted in the ascending order of distances. No. represents the sequence number of the structure. Only the first 42 structures are listed. | |||||
| TiI3 | 1 | 0.000 | CrF3 | 22 | 0.112 |
| MoBr3 | 2 | 0.021 | RhF3 | 23 | 0.113 |
| TiI3 | 3 | 0.032 | Fe3N | 24 | 0.119 |
| RuBr3 | 4 | 0.039 | Zr3O | 25 | 0.122 |
| ZrI3 | 5 | 0.043 | ReO3 | 26 | 0.123 |
| RuBr3 | 6 | 0.044 | IrF3 | 27 | 0.132 |
| MoBr3 | 7 | 0.056 | BiI3 | 28 | 0.133 |
| TiCl3 | 8 | 0.060 | CrF3 | 29 | 0.135 |
| RuCl3 | 9 | 0.063 | Fe3N | 30 | 0.141 |
| RuBr3 | 10 | 0.065 | FeF3 | 31 | 0.142 |
| RuBr3 | 11 | 0.069 | PdF3 | 32 | 0.147 |
| YI3 | 12 | 0.074 | FeF3 | 33 | 0.151 |
| RuBr3 | 13 | 0.075 | Fe3N | 34 | 0.152 |
| TcBr3 | 14 | 0.076 | CrF3 | 35 | 0.156 |
| RuCl3 | 15 | 0.079 | CrF3 | 36 | 0.161 |
| BiI3 | 16 | 0.082 | FeF3 | 37 | 0.165 |
| Zr3O | 17 | 0.091 | CrF3 | 38 | 0.165 |
| ScCl3 | 18 | 0.100 | Ni3C | 39 | 0.169 |
| Ti3O | 19 | 0.102 | FeF3 | 40 | 0.174 |
| SbI3 | 20 | 0.104 | TiCl3 | 41 | 0.198 |
| RuF3 | 21 | 0.106 | TiCl3 | 42 | 0.205 |
We construct NWs from the 1D vdW bulk structures found in the database. The space group of the bulk materials, the NW binding energy Eb, the magnetic ground state, the magnetic moments of transition metals, etc., are listed in Table 1. The 1-chain TiCl3, MoBr3, RuCl3, RuBr3, and TcBr3 NWs have Eb below 0.1500 eV per atom, indicating that they are likely to be exfoliated in experiments. Among them, the 1-chain TiCl3 NW has the lowest Eb of 0.1152 eV per atom, which is most promising for synthesis. The low Eb of monolayer TiCl3 (0.0792 eV per atom) indicates that the monolayer can also be obtained by exfoliation. Even if some freestanding NWs cannot be synthesized, they still have the possibility to stabilize on substrates.
Since the FM monolayer CrI3 was successfully fabricated in 2017,31 this material has gained growing attention. However, the ground state structure of CrI3 (rhombohedral structure, space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , BiI3 structure type)32 is not of the 1D vdW structure. To check whether CrI3 may have a meta-stable 1D vdW structure, we perform structure prediction calculations, which use the crystal structure prototype database to generate candidate structures.12 The details of this method are given in the ESI.† The structure with the lowest energy among the predicted structures is the experimental R
, BiI3 structure type)32 is not of the 1D vdW structure. To check whether CrI3 may have a meta-stable 1D vdW structure, we perform structure prediction calculations, which use the crystal structure prototype database to generate candidate structures.12 The details of this method are given in the ESI.† The structure with the lowest energy among the predicted structures is the experimental R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) structure. However, we find a meta-stable structure with the space group P63/mcm, which is only 0.0352 eV per atom higher than the R
structure. However, we find a meta-stable structure with the space group P63/mcm, which is only 0.0352 eV per atom higher than the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) structure, consisting of face-sharing CrI6 octahedral chains. Phonon spectra calculation shows that the P63/mcm CrI3 is dynamically stable. The structure is similar to that of the high temperature phase of TiI3, and is of the 1D vdW structure type. The P63/mcm CrI3 structure is also FM. We calculate the binding energies of the CrI3 NWs constructed from the P63/mcm CrI3 structures, and the results are given in Table 1. The Eb of the 1-chain CrI3 NW is approximately 0.156 eV per atom, and the Eb decreases as the NW becomes thicker, as expected.
structure, consisting of face-sharing CrI6 octahedral chains. Phonon spectra calculation shows that the P63/mcm CrI3 is dynamically stable. The structure is similar to that of the high temperature phase of TiI3, and is of the 1D vdW structure type. The P63/mcm CrI3 structure is also FM. We calculate the binding energies of the CrI3 NWs constructed from the P63/mcm CrI3 structures, and the results are given in Table 1. The Eb of the 1-chain CrI3 NW is approximately 0.156 eV per atom, and the Eb decreases as the NW becomes thicker, as expected.
Table 1 also shows the calculated magnetism of these materials. TiI3, TiCl3, RuCl3, RuBr3, and ZrI3 are NM for both bulk and NW phases. The NWs and bulk MoBr3 are antiferromagnetic (AFM) and the projected magnetic moment for Mo is 1.8 μB. The TcBr3 system turns out to be FM. Interestingly, the thickness of the NW may change its magnetism. For example, the bulk, 3-chain, and 7-chain CrI3 are FM, whereas the 1-chain CrI3 is AFM. The change of magnetism through the thickness of a 1D material provides an effective way to tune the magnetism of NWs.
The electronic band structure and density of states calculations show that all the TMX3 NWs are semiconductors. The band gaps of the NWs are listed in Table 1 compared to that of the bulk phase. The 1-chain MoBr3 has the largest band gap of 1.2 eV, whereas the 3- and 7-chain TiI3, 1-chain TiCl3, and 1-chain TcBr3 have the smallest band gap of 0.2 eV. The increase in the thickness of a NW reduces its band gap, due to quantum confinement effects. For example, 1-chain and 3-chain TiI3 have band gaps of 0.3 and 0.2 eV, respectively, and the band gaps for 1-chain, 3-chain, and 7-chain CrI3 NWs are 0.8, 0.5, and 0.3 eV, respectively. The bulk 1D vdW TMX3 has smaller band gaps compared to its respective NWs. In particular, the metallic bulk ZrI3 transforms to a semiconductor in the 1-chain NW.
To verify the dynamic and thermodynamic stabilities of the freestanding NWs, we recorded the phonon spectrum and performed AIMD simulations. The 1-chain TiI3, TiCl3, MoBr3, RuCl3, CrI3, and 3-chain CrI3, TiI3, and 7-chain TiI3 NWs have no or negligible imaginary phonon frequencies, indicating that they are dynamically stable. The phonon spectra of 1-chain RuBr3, ZrI3, and TcBr3 NWs have slightly softened modes near the Γ point (see the ESI†). However, the AIMD simulations show that all these NWs are thermodynamically stable at 300 K. The 1-chain RuBr3, ZrI3, and TcBr3 NWs are presumably stabilized by the free energy at room temperature (Fig. S7 and S8 in the ESI†).
1D vdW TMX4 materials
In addition to TMX3 materials, we also find a series of 1D vdW TMX4 materials that are potentially exfoliable into NWs. Bulk TcBr3 and TcBr4 were synthesized by reaction between technetium metal and bromine and characterized by single crystal XRD.17 Interestingly, both TcBr3 and TcBr4 are 1D vdW materials. As shown in Fig. 4(a), the TcBr4 comprises chains of edge-sharing TcBr6 octahedra. The TcBr4 atomic chains are bonded through weaker inter-chain vdW forces in the bc plane. We exfoliate the freestanding TcBr4 NWs, presented in Fig. 4(b), from its bulk phase. The low binding energy (0.1394 eV per atom) verifies that the TcBr4 NW is exfoliable. The AIMD simulations at 300 K show that the NW is thermodynamically stable. The bulk and NW structures of TcBr4 are both AFM. Using the SPAP to search structures similar to bulk TcBr4 in the COD, we find more 1D vdW materials, including TcF4, TcCl4, ZrCl4, HfCl4, OsBr4, TiI4, PtI4, and UI4. These materials are all potentially exfoliable to produce NWs. We leave these materials for future investigations. | ||
| Fig. 4 (a) The experimental bulk phase Pbca of TcBr4 viewed along the chains of edge-sharing TcBr6 octahedra. (b) 1 chain of TcBr4 exfoliated from its bulk phase. | ||
Conclusion
We identify a large class of TMX3 materials (TiI3, β-TiCl3, RuBr3, β-RuCl3, TcBr3, MoBr3, ZrI3, etc.), which have 1D vdW structures and are exfoliable to NWs, using first-principles calculations. Our calculations show that the single-chain and multiple-chain NWs constructed from these 1D vdW structures are stable. The calculated binding energies of the NWs are relatively small, which is promising for exfoliation. We further identify several 1D vdW TMX4 materials which are candidates for exfoliation. This work opens a top-down approach to fabricate NWs from 1D vdW materials.Methods
Computational details
The first-principles calculations are performed within density functional theory using the projector augmented wave pseudopotentials33,34 as implemented in the Vienna ab initio simulation package.35 We utilize the optimized exchange van der Waals functional B86b of the Becke (optB86b vdW) functional to handle the effect of van der Waals interactions.36 An energy cutoff of 500 eV is applied in the expansion of the wave function into plane waves, and Monkhorst–Pack k point meshes with a grid smaller than 0.2 Å−1 are used to sample the Brillouin zone. For the NW calculations, we leave a vacuum space larger than 16 Å around the NWs to eliminate the fictitious interactions between the NW and its periodic images. The structures are relaxed until the forces are less than 1 meV Å−1. For compounds with Ru and Cr elements, we use the DFT + U method.37 We use U = 3.5 eV and J = 1.0 eV for Ru element, in which the relaxed bulk β-RuCl3 and RuBr3 structures are close to the experimental structures. We use U = 3.9 eV and J = 1.1 eV for Cr.38 AIMD simulations are performed with a supercell, which is extended 4 times the unit cell along the atomic chain, at 300 K for 10 ps. The phonon spectra are recorded using a supercell approach39 implemented in the PHONOPY package.40 We use the VESTA code to visualize structural images.41Coordination characterization function
The CCF identifies the fingerprint of a structure on the basis of its interatomic distances. For pairs of atomic types i and j, | (3) |
 . We use f(rninj) = 1 and rcut = 20 Å for the calculation of CCFs shown in Fig. 3.
. We use f(rninj) = 1 and rcut = 20 Å for the calculation of CCFs shown in Fig. 3.
Structure prototype analysis package
The SPAP12 analyzes symmetry and compares the similarity of different atomic structures. It can cluster a large number of atomic structures according to the physical features, such as symmetry, composition type, and structural distance. The SPAP allows us to find structures in the database that are similar to the target structure. The detailed method of the SPAP can be found in the ESI.†Author contributions
Chuanxun Su: conceptualization, calculation, data curation, software, and writing – original draft. Lixin He: supervision, validation, funding acquisition, and writing – review & editing.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was funded by the Chinese National Science Foundation (No. 12134012). The numerical calculations were performed on the USTC HPC facilities.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D.-e. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- R. Frisenda, Y. Niu, P. Gant, M. Muñoz and A. Castellanos-Gomez, npj 2D Mater. Appl., 2020, 4, 1–13 CrossRef.
- S. Lebègue, T. Björkman, M. Klintenberg, R. M. Nieminen and O. Eriksson, Phys. Rev. X, 2013, 3, 031002 Search PubMed.
- N. Mounet, M. Gibertini, P. Schwaller, D. Campi, A. Merkys, A. Marrazzo, T. Sohier, I. E. Castelli, A. Cepellotti and G. Pizzi, et al. , Nat. Nanotechnol., 2018, 13, 246–252 CrossRef CAS PubMed.
- Y. Zhu, X. Kong, T. D. Rhone and H. Guo, Phys. Rev. Mater., 2018, 2, 081001 CrossRef CAS.
- P. M. Larsen, M. Pandey, M. Strange and K. W. Jacobsen, Phys. Rev. Mater., 2019, 3, 034003 CrossRef CAS.
- Y. Du, G. Qiu, Y. Wang, M. Si, X. Xu, W. Wu and P. D. Ye, Nano Lett., 2017, 17, 3965–3973 CrossRef CAS PubMed.
- Y. Zhu, D. A. Rehn, E. R. Antoniuk, G. Cheon, R. Freitas, A. Krishnapriyan and E. J. Reed, ACS Nano, 2021, 15, 9851–9859 CrossRef CAS PubMed.
- S.-s. Li, Y.-p. Wang, S.-j. Hu, D. Chen, C.-w. Zhang and S.-s. Yan, Nanoscale, 2018, 10, 15545–15552 RSC.
- Z. Guo, Q. Chen, J. Yuan, K. Xia, X. Wang and J. Sun, J. Phys. Chem. C, 2019, 124, 2096–2103 CrossRef.
- J. Angelkort, A. Schönleber and S. van Smaalen, J. Solid State Chem., 2009, 182, 525–531 CrossRef CAS.
- C. Su, J. Lv, Q. Li, H. Wang, L. Zhang, Y. Wang and Y. Ma, J. Phys.: Condens. Matter, 2017, 29, 165901 CrossRef PubMed.
- S. Gražulis, A. Daškevič, A. Merkys, D. Chateigner, L. Lutterotti, M. Quiros, N. R. Serebryanaya, P. Moeck, R. T. Downs and A. Le Bail, Nucleic Acids Res., 2012, 40, D420–D427 CrossRef PubMed.
- G. Natta, P. Corradini and G. Allegra, J. Polym. Sci., 1961, 51, 399–410 CrossRef CAS.
- H. Hillebrecht, T. Ludwig and G. Thiele, Z. Anorg. Allg. Chem., 2004, 630, 2199–2204 CrossRef CAS.
- S. Merlino, L. Labella, F. Marchetti and S. Toscani, Chem. Mater., 2004, 16, 3895–3903 CrossRef CAS.
- F. Poineau, E. E. Rodriguez, P. M. Forster, A. P. Sattelberger, A. K. Cheetham and K. R. Czerwinski, J. Am. Chem. Soc., 2009, 131, 910–911 CrossRef CAS PubMed.
- D. Babel, J. Solid State Chem., 1972, 4, 410–416 CrossRef CAS.
- A. Lachgar, D. S. Dudis and J. D. Corbett, Inorg. Chem., 1990, 29, 2242–2246 CrossRef CAS.
- K. Brodersen, G. Thiele and B. Holle, Z. Anorg. Allg. Chem., 1969, 369, 154–160 CrossRef CAS.
- G. Thiele, H. Wochner and H. Wagner, Z. Anorg. Allg. Chem., 1985, 530, 178–186 CrossRef CAS.
- M. Elder and B. R. Penfold, Inorg. Chem., 1966, 5, 1197–1200 CrossRef CAS.
- P. F. Weck, E. Kim, F. Poineau, E. E. Rodriguez, A. P. Sattelberger and K. R. Czerwinski, Inorg. Chem., 2009, 48, 6555–6558 CrossRef CAS PubMed.
- R. Borjas Nevarez, S. M. Balasekaran, E. Kim, P. Weck and F. Poineau, Acta Crystallogr., Sect. C: Struct. Chem., 2018, 74, 307–311 CrossRef CAS PubMed.
- R. Niewa and H. Jacobs, Z. Krystallog., 1995, 210, 687 CAS.
- S. Troyanov, Zh. Neorg. Khim., 1993, 38, 226–229 CAS.
- J. Levy, J. Taylor and A. Waugh, Inorg. Chem., 1980, 19, 672–674 CrossRef CAS.
- A. K. Singh, K. Mathew, H. L. Zhuang and R. G. Hennig, J. Phys. Chem. Lett., 2015, 6, 1087–1098 CrossRef CAS PubMed.
- B. C. Revard, W. W. Tipton, A. Yesypenko and R. G. Hennig, Phys. Rev. B, 2016, 93, 054117 CrossRef.
- M. Ashton, J. Paul, S. B. Sinnott and R. G. Hennig, Phys. Rev. Lett., 2017, 118, 106101 CrossRef PubMed.
- B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire and D. H. Cobden, et al. , Nature, 2017, 546, 270–273 CrossRef CAS PubMed.
- M. A. McGuire, H. Dixit, V. R. Cooper and B. C. Sales, Chem. Mater., 2015, 27, 612–620 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- J. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131 CrossRef.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- P. Jiang, C. Wang, D. Chen, Z. Zhong, Z. Yuan, Z.-Y. Lu and W. Ji, Phys. Rev. B, 2019, 99, 144401 CrossRef CAS.
- K. Parlinski, Z. Li and Y. Kawazoe, Phys. Rev. Lett., 1997, 78, 4063 CrossRef CAS.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Method to query structures in the database, structure prediction for CrI3, electronic band structure and density of states, phonon spectra, ab initio molecular dynamics simulations, and structures for the NWs and bulk P63/mcm CrI3. See DOI: https://doi.org/10.1039/d2na00877g |
| This journal is © The Royal Society of Chemistry 2023 |