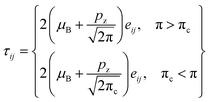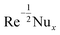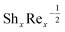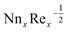DOI:
10.1039/D3NA00400G
(Paper)
Nanoscale Adv., 2023,
5, 6560-6571
Interaction of gyrotactic moment of microorganisms and nanoparticles for magnetized and chemically reactive shear-thinning fluid with stratification phenomenon
Received
9th June 2023
, Accepted 4th September 2023
First published on 3rd November 2023
Abstract
Nanotechnology has gained substantial attention on account of its vast applications in food manufacturing, heat exchanges, electronic cooling systems, medical treatment, coolant processes, energy production, biotechnology, transportation, biochemistry, nuclear reactors, and metrology. Currently, the phenomenon of bioconvection using nanomaterials has found wide industrial and technical implementations. Contemporary nanofluids are a dynamic source for illuminating heat transport systems related to engineering as well as industrial phenomena. Bioconvection has numerous applications in bio-micro-systems, owing to the augmentation in mass renovation besides collaborating, which are vital complications in diverse micro-systems. This study intended to model and examine an incompressible, unsteady 3D Casson fluid nanofluid with bioconvection on a stretching surface. A model by means of these characteristics is beneficial in applications, such as in nuclear reactors, coolants in automobiles, metallurgical procedures, energy construction, micro-manufacturing, industrial engineering, and geophysical fluid mechanics along with dynamics. The performance of the Brownian motion along with thermophoresis diffusion is assumed through an extraordinary effect of thermal radiation in the temperature equation of the fluid movement. This model was created by using PDE, which was then converted into an ODE system. The somatic behavior of substantial parameters was investigated graphically. Similarly, tables were interpreted to display the effect of the control of physical quantities on the local Nusselt number, local Sherwood number, and motile density. Consequently, it was determined that the temperature of Casson fluid grew exponentially with higher estimates of the magnetic parameter and the thermal Biot number. At the same time, we detected that augmented estimation of the Lewis number decreases the Casson fluid concentration. For growing values of the parameters, Biot number and the stretching parameter, there is a direct reaction for the microorganism profile.
1. Introduction
Recently, nanoparticles have attracted the attention of researchers owing to their growing significance in food, biomaterials, bioengineering, electronic devices, and the mechanical industry. Nanofluids further offer considerable assistance in biomedical sciences. Examples include cancer therapeutics, magnetic resonance, nano-cryosurgery, localized therapy, labeling of cancerous tissues, magnetic resonance imaging (MRI), bacteriostatic activity, and nano-drug delivery. The word nanofluid indicates nanomaterials suspended in a traditional liquid to enhance the joint heat and mass conversion process. It is a well-defined circumstance that in refrigeration and thermal systems, fluids transient over microfluidic procedures rely exclusively on heat transfer molecules carried by nanomaterials. Therefore, nanofluid dynamics is the key term that must be involved in all fields related to non-molecular suspension in every way to endeavor for optimal routine. Nanofluid exists as a subgroup of fluid consisting of (1–100) nanometer-sized materials. Choi1 presented the elementary conception of these nanomaterials using enhanced thermophysical possessions, which has been popularized by many researchers. Buongiorno2 discussed the seven sliding developments in nanoparticle movement including Brownian motion and thermophoresis effects. The thermal conductivity of nanoparticles is higher than that of conventional liquids. The nanometer-sized solid particles intensify the transportation rate of heat of conventional fluids. The nanofluid has many potential applications for heat conversion, such as in industrial procedures, cooling systems, chiller, temperature reduction, hybrid-energy appliances, refrigerators, microchips, and fuel cells. Today's world is a fast technological world. The cooling of electronic materials is one of the main requirements of the contemporary industry. Today's standard heat transfer fluids cannot offer adequate cooling in industrial processes. Such conditions have led to the development of a present technology called nanotechnology. The practice of nanofluids in place of an extra effective cooling medium in nuclear power plants means that present coolant can be utilized more efficiently to cool hot surfaces. A thermostatic valve is employed to control heat transfer in nanofluid implementations. Its ability to transfer heat quickly can be used for cooling purposes. Oncologists treat cancer patients by inserting medication as well as radiation into a device involving iron-based nanofluid. Nanofluids are used, for example, as a coolant in an extensive range of automatic cooling usages containing vehicle radiators, PC servers, and warm sun-based accumulators. Abu-Nada, and Oztop studied the properties of Cu-water nanofluid,3 while Shahzad et al.4 considered the entropy concept for the cross nanofluid with radiation. The entropy optimization in the hybrid nanofluid was presented by Khan et al.5 Furthermore, Khan et al.,6 Ali et al.,7 Khan et al.,8,9 and Anjum et al.10 reported the nanofluid behavior in different fluid models.
The bioconvection of nanofluids circumstance is an alternative extraordinary field of research that has many applications, such as in pharmaceutical engineering, sedimentary waterways, micro-fluidics machines, gas-bearing, model construction, lubrication ingredients, fuel, hydrodynamics systems, polymer construction, microbial augmented oil recovery, and hydrodynamics production. The phenomenon of bioconvection occurs owing to the upward swimming of microorganisms in a definite track within the fluid. Consequently, the density of the fluid in the upper part grows causing the drop of microorganisms. They swim back upward and thus proceed with the development of bioconvection. The bioconvection advances through active swimming and the disorganized movement of motile microorganisms that remain denser in comparison with water. Presently, numerous efforts have been undertaken to study the movement of motile gyrotactic microorganisms in fluid flow due to their important applications in biomedicine, fertilizers, ethanol, biofuel, bio-microsystems, and biotechnology. Because of the gathering appropriate to the already stated microorganisms, a dense cover of bacteria appears beside the top exterior of the lighter fluid. Microorganisms transport an organic fluid upstairs happening some way due toward its lower density associated with water. Biochemical nanomaterials are transparent aqueous and non-aqueous fluids containing gyrotactic motile microorganisms, comprising metal-acquired nanomaterials. The term bioconvection was first familiarized by Platt11 in an extemporaneous evolutionary process in the association of swimming motile microorganisms. Numerous usages of bioconvection by means of microorganisms and nanoparticles in the region of mechanical energy, biosensors, manufacturing, bioinformatics, and biosensors have attained the consideration of scholars in the direction of this field. Owing to the irregular and unsteady configuration, microbes swim in the superior area. When the microbe has nothing on the top surface, the top area becomes unbalanced due to the high layer density. Microbes float unrestrained in the marine environment, for instance, canyons and rivers and ponds along oceans. The idea of nanofluids in bioconvection is to bring into concentration work defining the evolution of burst formation and density stratification performed with the simultaneous edge of self-propelled microorganisms, nanoparticles, besides drag forces. Functioning micro-organisms may comprise gyrotaxis, gravitaxis, and oxytaxis organisms. Supporting gyrotactic microorganisms in the bulk conversion of liquid enrichment nanofluids, mixing on a small scale, fully within microvolumes, and increasing the stability of nanofluids. Biomedical engineering applies the procedure of bioconvection in bioreactors, fuel cell engineering, and diesel fuel products. Lately, various researchers have employed bioconvection as seen from the literature reports. Some of the foremost and contemporary study on the bioconvection of diverse nanofluidic models by gyrotactic microorganisms can be established in the studies of Kuznetsov,12 Usman,13 Chu,14 and Anjum.15
In modern applied sciences, such as geothermal engineering, astrophysical bio-fluid, geophysical, and petroleum sectors, the analysis of non-Newtonian fluids, the studies done by Khan et al.,16 Hayat et al.,17 Khan et al.,18–20 Irfan21,22 and Bhatti et al.23,24 have received significant consideration. The implementations established on non-Newtonian fluids' connection comprise ceramic products, wire coating, certain oils, printing, fiber engineering, and petroleum industries. Modern technological development calls for revolutionary progress in the field of temperature transference. Even with the complications of non-Newtonian fluids, applied theoreticians and manufacturing scientists are connected in non-Newtonian fluid dynamics, subsequently the flow and heat transfer properties of these fluids are significant for abundant systems and diverse applications in pharmacy, chemical engineering, and bio-technology. In summary, non-Newtonian models have a non-linear bounding affiliation between stress and strain rate. The mechanical properties of non-Newtonian fluids, whether they are shear thinness and/or thickness, normal stress variances, and viscoelastic interactions, may not be described using conservation theory; consequently, advanced and operative forecasting is essential. Several fluid models have been proposed to analyze the transportation rate of heat and mass, among these models Casson model have the wide range of applications. Casson's model is sustained by structural modeling of the reactive nature of solids along with liquid phases for biphasic suspensions. Casson25 was the leading scientist who exhibited a mathematical model of this class of liquids. Subsequently, many researchers have shifted their considerations to the flow properties of Casson fluids. Several well-known examples of Casson fluids include honey, tomato pastes, jellies, and soups to concentrated fruit extracts. Human blood can also be deliberated as Casson's fluid as many substances, such as fibrinogens, proteins, and globulins, in aqueous disreputable plasmas besides human red blood cells are present in it. It is requested that this rheological model is superior for some liquids than the viscoelastic model. This model is appropriate for chocolate and blood rheology. Casson fluid is the thin shear fluid that is a type of non-Newtonian fluid since it shows an elastic limit. If a shear stress less than the yield stress is provided, the fluids act like solids, i.e., no flows occur and vanish if the shear stresses are greater than the produced stresses. In the thick shear fluid model, it is assumed to have infinite viscosity near which the shear rate vanishes, resulting in pressures lower than no flow and the viscosity vanishes at an infinite shear rate. A Casson fluid sample consists of the bonds or interactions between the liquid and solid phases. When the elastic limit becomes mandatory and is less than the shear stress, Casson fluids perform resembling solids. Casson's model of fluids has become a non-Newtonian fluid for explorers since those applications have a wide scope in energy construction, industrial and biomedical engineering, geo-physical fluid mechanics besides dynamics. Specific investigations of Casson fluid can be found in ref. 26–32.
The novelty of this analysis is to estimate the significance of thermal radiation on the MHD flow of three-dimensional Casson nanofluids with bioconvection in excess of a stretching sheet. Firstly, MHD flow has gained a lot of attention from scholars for the reason that there are various applications in industries along with engineering. For example, in metallurgical procedures, definite practices involve the cooling of many continuous strips by extracting electrically conductive fluids subject to magnetic fields. It allows one to control the speed of cooling to obtain the desired results. Secondly, the use of bioconvection has across-the-board uses in bio-micro and organic structures casing microbial-better-quality oil retrieval structures, enzyme bio-sensors, and bio-machines. The bio-convection presence is interrelated to organic solutions and microbes. Third, the theory of nanofluids is working in a number of engineering uses, including the refrigeration of electronics, the change of solar thermal energy, and refined developed methods. Furthermore, the assessment of Casson liquids has attracted the attention of various researchers owing to their uses in medicinal, biological work, and biomedical sciences. The production ink, shampoos, fluxes, pastes, and mixtures are the few ingredients explaining the non-Newtonian nature.
1. The purpose of this study is to improve the rate of heat and mass transfer by providing activation energy.
2. Besides, the effects of chemical reactions and double stratification conditions are also taken into account.
3. The basic equations of this problem are updated to a dimensionless system by using appropriate transformations.
4. The system of ordinary differential equations is numerically processed using the bvp4c algorithm in the MATLAB computer program.
5. Numerical calculations are acclimated to study the characteristics of essential parameters.
2. Mathematical modeling
Consider an incompressible, unsteady flow of 3D Casson nanofluid over a stretching sheet with bioconvection. In this study, we deliberated double stratification boundary conditions and thermal radiation. Additionally, the aspects of activation energy, chemical reaction, and MHD are assimilated. Thermophoretic and Brownian dispersion are incorporated for the reason of nanoparticles. The velocity constituents (u = ax, v = by) of Casson nanofluid are reserved beside x and y directions and T = Tw = T0 + e1x, C = Cw = C0 + e2x, N = Nw = N0 + e3x represent surface temperature, concentration, and microorganism respectively. The diagram of the Casson nanofluid together with gyrotactic motile microorganisms is shown in Fig. 1.
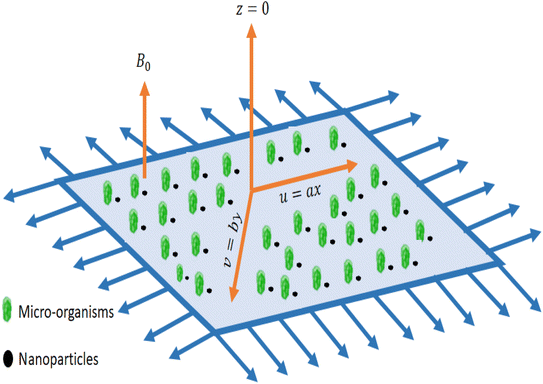 |
| | Fig. 1 Physical representation of the flow model. | |
The rheological equation of state for the incompressible and isotropic flow of a Casson nanofluid is given by:
where (
τij,
eij, π,
μB, π
c) denote the shear stress, deformation rate component (
i,
j)
th, the product of the component of deformation, yield stress and critical value of π =
eijeijpz, respectively. By using conservation laws, the basic transport equations for the Casson fluid model in vector form are
| | | ρf(V·∇)V = −∇p + ∇·τij + J × B, | (2) |
| | 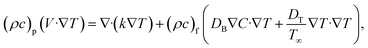 | (3) |
| | 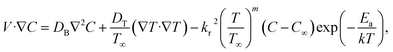 | (4) |
| | 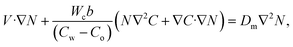 | (5) |
Underneath these assumptions, the governing boundary layer system of the equations can be assembled for instance:
| | 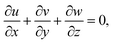 | (6) |
| | 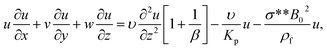 | (7) |
| | 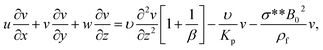 | (8) |
| | 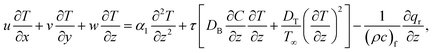 | (9) |
| | 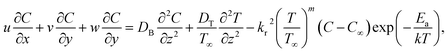 | (10) |
| | 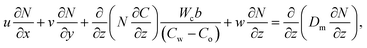 | (11) |
with
| | 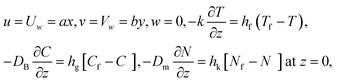 | (12) |
| | 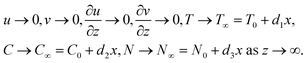 | (13) |
By using the Rosseland approximation, we find the radiative heat flux as,
| | 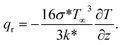 | (14) |
Considering:
| | 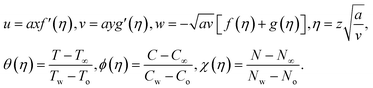 | (15) |
We have
| | 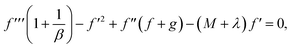 | (16) |
| | 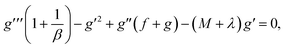 | (17) |
| | 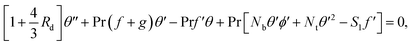 | (18) |
| | 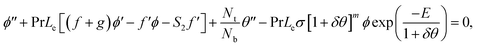 | (19) |
| | | χ′′ + Lbχ′[f + g] − Lb(S3 + χ)f′ − Pe[ϕ′′(χ + Ω) + ϕ′χ′] = 0, | (20) |
| | | f(0) = 0, f′(0) = 1, f′(∞) → 0, | (21) |
| | | g(0) = 0, g′(0) = α, g′(∞) → 0, | (22) |
| | | θ′(0) = −γ1[1 − S1 − θ(0)], θ(∞) → 0, | (23) |
| | | ϕ′(0) = −γ2[1 − S2 − ϕ(0)], ϕ(∞) → 0, | (24) |
| | | χ′(0) = −γ3[1 − S3 − χ(0)], χ(∞) → 0, | (25) |
where
| | 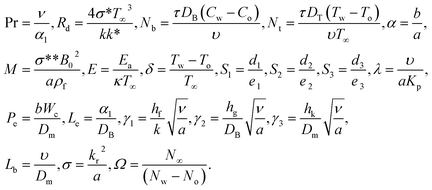 | (26) |
Precisely, expressions for Nusselt and Sherwood numbers (Nux, Shx) and density of the microbe (Nnx) in dimensional type are:
| | 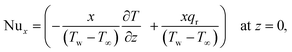 | (27) |
| | 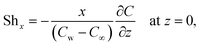 | (28) |
| | 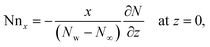 | (29) |
| | 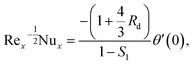 | (30) |
| | 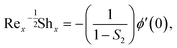 | (31) |
| | 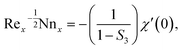 | (32) |
where
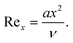
3. Results and discussion
This segment is systematized to examine the performance of 3D steady incompressible flow of a Casson nanomaterial model considering bioconvection along with stratifications. The scheme used in this problem is bvp4c.33–35 The graphical pictures of the following parameters are described. The influences of Pr the Prandtl number and stretching parameter α on θ(η) are interpreted in Fig. 2(a) and (b). From these diagrams, we observe the θ(η) decreases for the higher estimations of Pr the Prandtl number and stretching parameter α. From a mathematical perspective, the Prandtl quantity has contrariwise association with heat diffusivity, and higher estimate of Pr decay temperature, as shown in the diagram. Fig. 3(a) and (b) displays the results of the magnetic parameter M and γ1 the thermal Biot number on θ(η). It should be seen from these sketches that both the parameters have a direct relation with the temperature profile. Furthermore, superior estimations of the magnetic parameter M produce more resistive forces between the liquid particles. Consequently, the temperature of the Casson nanofluid is exaggerated. Fig. 4(a) and (b) elucidates the characteristics of the radiation parameter Rd along with the porosity parameter λ on θ(η). It should be perceived from these figures that both the parameters have a direct relation with the temperature profile. Thermal-radiation procedures yield extra heat inside the functioning fluid thus Rd and connected thermal-layer viscosity enhances. Extraordinary development in thermal-radiation, Rd improves the temperature field. The features of Lewis number Le and S2 mass stratified variable on ϕ(η) are displayed in Fig. 5(a) and (b). From these figures, we perceive that ϕ(η) decreases with growing values of both the parameters. It is perceived that for prevailing estimates of the concentration of Casson nanofluid Le contracts. In fact, owing to the reverse fraction amongst Le and Brownian diffusion coefficient displays a decline in the diffusion coefficient, consequently Le drops. The outcomes of the magnetic parameter M and the reaction constant σ on ϕ(η) are exhibited in Fig. 6(a) and (b). These figures exhibited that both the parameters are inversely related to the concentration profile. The influences of the Brownian motion parameter Nb and stretching parameter α on ϕ(η) are displayed in Fig. 7(a) and (b). As of these diagrams, we identify that the concentration profile decays with growing estimates of both the parameters. The developed flying nano-particle collisions through greater Nb upshot in conflict to species diffusion, which reduces ϕ(η) besides a feeble thickness of the concentration layer. Fig. 8(a) and (b) express the significance of the thermophoresis parameter Nt and γ2 concentration Biot number on ϕ(η). These figures display that both the parameters have a direct relation with concentration profile. From the mathematical viewpoint, the mass transferal coefficient declines as soon as γ2 is augmented. Hence, ϕ(η) for superior assessment of γ2. Furthermore, amplifying thermophoretic influence Nt encourages the immigration of nanomaterial underneath the current rise in the way of cooler regions then this advances the concentration of nanomaterial intended for such purpose produces a sophisticated boundary layer thickness. Fig. 9(a) and (b) illuminate the inspirations of the activation energy E and the porosity parameter λ possessions on ϕ(η). Fig. 10(a) and (b) interprets the impacts of the stretching parameter α and Ω the microorganism difference parameter distinction on χ(η). These figures revealed that both the parameters have the same contradictory relation with concentration profile. These figures revealed that both the parameters have the same contradictory relation with microorganism profile. Fig. 11(a) and (b) exhibit the effects of γ3 microorganisms Biot number and S3 the microorganisms stratified variable on χ(η). These figures display that both the parameters are inversely related with microorganism profile. Fig. 12(a) and (b) demonstrate the significances of Pe Peclet number along with Lb bioconvection Lewis number on χ(η). These figures demonstrated that the microorganism profile decreases for improving estimates of Pe Peclet number along with Lb bioconvection Lewis number. By improving the Peclet number we found a decrease in the micro-organism profile. Actually this parameter narrates the advection rate of micro-organisms boosted due to the flow in the direction of the rate of χ(η) diffusion. Naturally Peclet number is related through convection heat transference procedures and also usually designates the heat transport. This parameter conspicuously changes flow designs of χ(η). The greater value of Peclet number corresponds to enhanced speediness of swimming that declines their concentration. The converse influence is perceived at subordinate Peclet number and their growth relaxed acquiescent sophisticated concentrations. At this point, the noteworthy decrease of microorganisms distribution function χ(η) is achieved in contrast to better involvements of bioconvection Lewis number Lb, which is reciprocal to mass diffusivity of microorganisms.
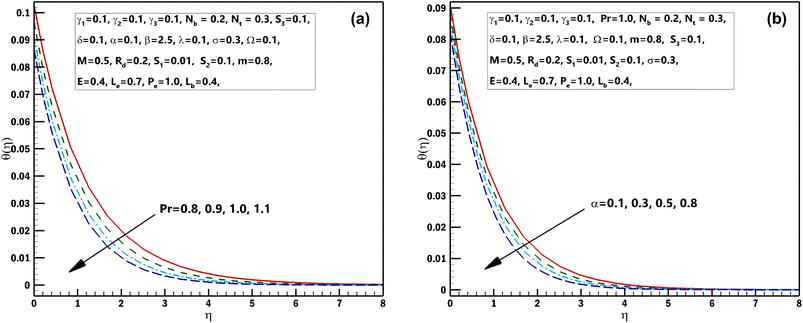 |
| | Fig. 2 (a and b) Influence of numerous approximations of [Pr] and [α] on θ(η). | |
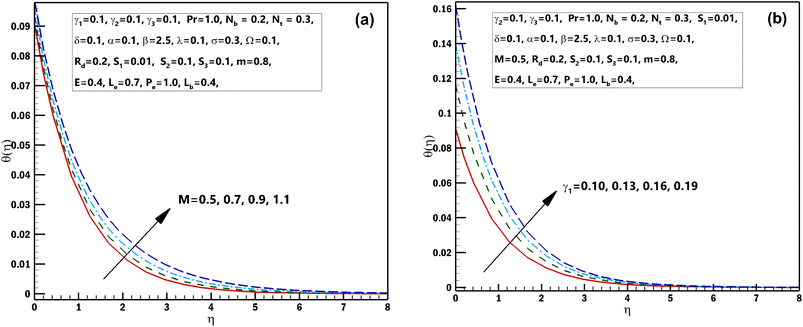 |
| | Fig. 3 (a and b) Influence of numerous approximations of [M] and [γ1] on θ(η). | |
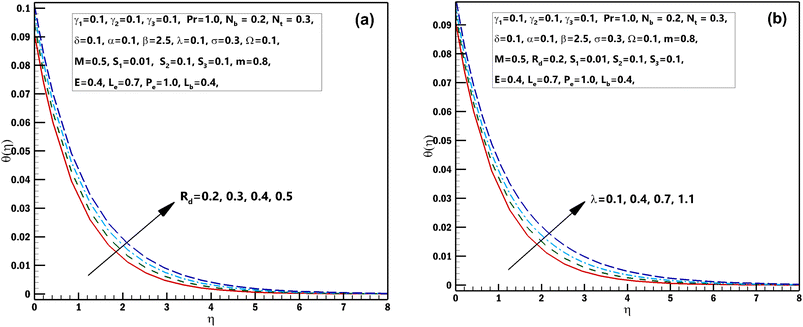 |
| | Fig. 4 (a and b) Influence of numerous approximations of [Rd] and [λ] on θ(η). | |
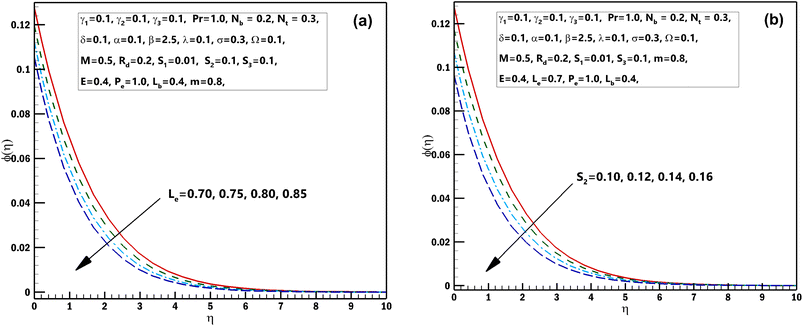 |
| | Fig. 5 (a and b) Influence of numerous approximations of [Le] and [S2] on ϕ(η). | |
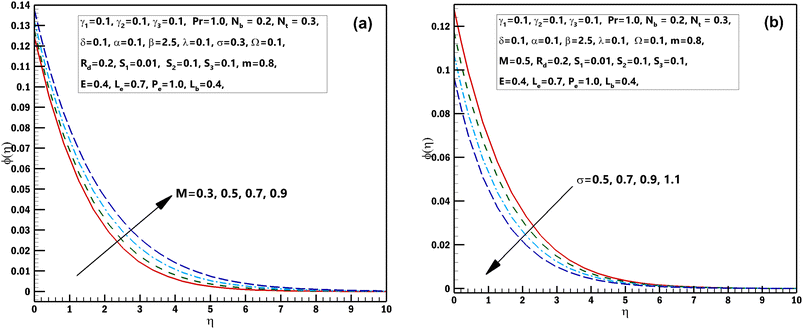 |
| | Fig. 6 (a and b) Influence of numerous approximations of [M] and [σ] on ϕ(η). | |
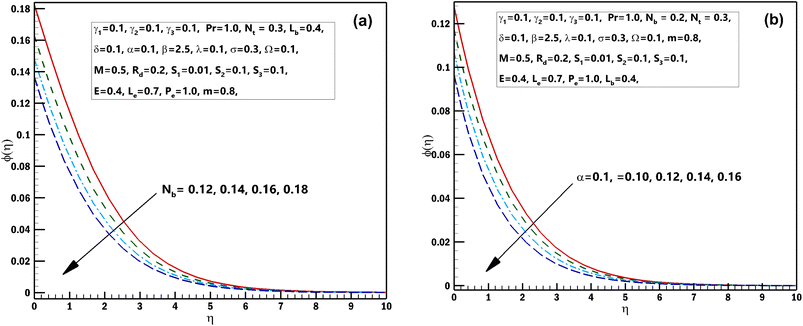 |
| | Fig. 7 (a and b) Influence of numerous approximations of [Nb] and [α] on ϕ(η). | |
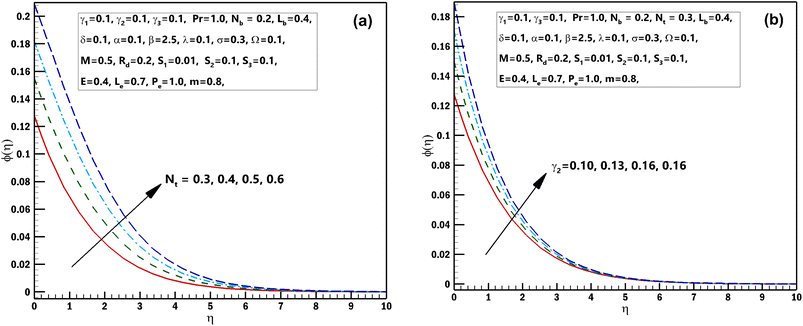 |
| | Fig. 8 (a and b) Influence of numerous approximations of [Nt] and [γ2] on ϕ(η). | |
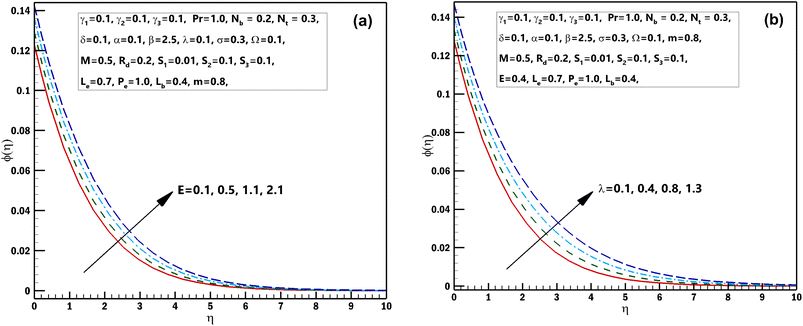 |
| | Fig. 9 (a and b) Influence of numerous approximations of [E] and [λ] on χ(η). | |
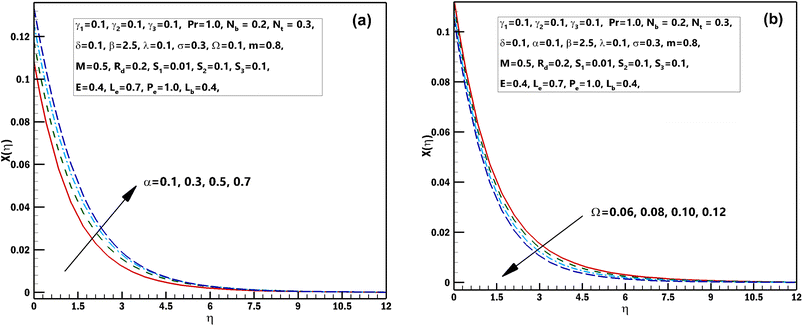 |
| | Fig. 10 (a and b) Influence of numerous approximations of [α] and [Ω] on χ(η). | |
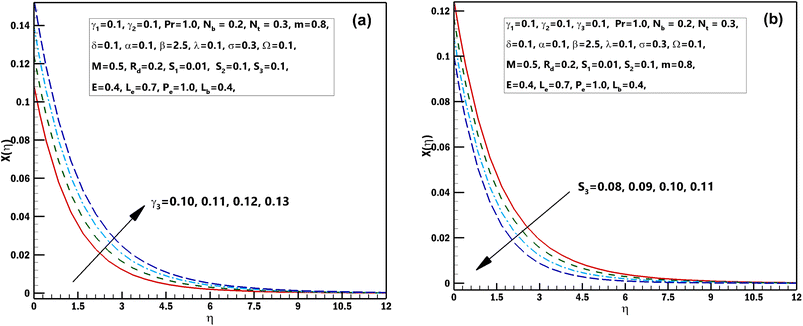 |
| | Fig. 11 (a and b) Influence of numerous approximations of [γ3] and [S3] on χ(η). | |
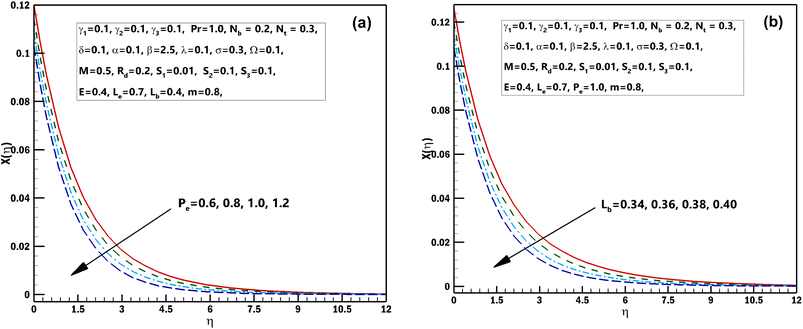 |
| | Fig. 12 (a and b) Influence of numerous approximations of [Pe] and [Lb] on χ(η). | |
Table 1 reports a brilliant comparison with those of Akbar et al.36 and Waqas et al.26 for various values of M on CfxRex0.5. Table 2, estimates the dissimilarities in 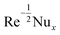 developing parameters Pr, γ1, S1 and Rd. It is inspected that the deviance of
developing parameters Pr, γ1, S1 and Rd. It is inspected that the deviance of 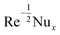 growths by increasing the approximations of parameters Pr, γ1, S1 and Rd. Table 3, scrutinizes the variations in
growths by increasing the approximations of parameters Pr, γ1, S1 and Rd. Table 3, scrutinizes the variations in 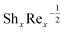 with several evaluations of captivating parameters Nt, Le, Nb and γ2. It can be perceived that by growing the parameters Le, Nb and γ2 an intensification in
with several evaluations of captivating parameters Nt, Le, Nb and γ2. It can be perceived that by growing the parameters Le, Nb and γ2 an intensification in 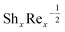 is originated. A contradictory performance can be appreciated Nt. The different values of Ω, Lb, Pe and S3 against
is originated. A contradictory performance can be appreciated Nt. The different values of Ω, Lb, Pe and S3 against 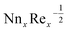 are demonstrated in Table 4, we noticed that
are demonstrated in Table 4, we noticed that 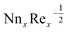 decreases by refining S3. While
decreases by refining S3. While 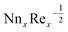 increases for the parameters Ω, Lb, Pe.
increases for the parameters Ω, Lb, Pe.
Table 1 Comparison of M for CfxRex0.5 when β = ∞, λ = α = 0
|
M
|
C
fxRex0.5 |
| Akbar et al.36 |
Waqas et al.26 |
Present bvp4c |
| 0 |
1 |
1 |
1 |
| 0.3 |
|
1.0440 |
1.04402 |
| 0.5 |
1.11803 |
1.1180 |
1.11801 |
| 0.7 |
|
1.2206 |
1.22064 |
| 1.0 |
1.41421 |
1.4141 |
1.41413 |
Table 2
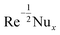 for different Pr, γ1, S1 and Rd
for different Pr, γ1, S1 and Rd
| Pr |
γ
1
|
S
1
|
R
d
|
bvp4c technique |
| 1.0 |
0.1 |
0.02 |
0.1 |
0.115020 |
| 1.1 |
|
|
|
0.115607 |
| 1.2 |
|
|
|
0.116114 |
| 1.3 |
|
|
|
0.116557 |
|
|
0.2 |
|
|
0.210228 |
|
|
0.3 |
|
|
0.290457 |
|
|
0.4 |
|
|
0.359029 |
|
|
0.5 |
|
|
0.418268 |
|
|
|
0.03 |
|
0.116458 |
|
|
|
0.04 |
|
0.117172 |
|
|
|
0.05 |
|
0.117900 |
|
|
|
0.06 |
|
0.118644 |
|
|
|
|
0.2 |
0.115071 |
|
|
|
|
0.3 |
0.126694 |
|
|
|
|
0.4 |
0.138244 |
|
|
|
|
0.5 |
0.149725 |
Table 3
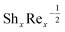 for different Nt, Le, Nb and γ2
for different Nt, Le, Nb and γ2
|
N
t
|
L
e
|
N
b
|
γ
2
|
bvp4c technique |
| 0.3 |
0.4 |
0.1 |
0.3 |
0.0807154 |
| 0.4 |
|
|
|
0.0780301 |
| 0.5 |
|
|
|
0.0753527 |
| 0.6 |
|
|
|
0.0726832 |
|
|
0.5 |
|
|
0.0763572 |
|
|
0.6 |
|
|
0.0788308 |
|
|
0.7 |
|
|
0.0807154 |
|
|
0.8 |
|
|
0.0822065 |
|
|
|
0.2 |
|
0.0822065 |
|
|
|
0.3 |
|
0.0846472 |
|
|
|
0.4 |
|
0.0858676 |
|
|
|
0.5 |
|
0.0865998 |
|
|
|
|
0.4 |
0.258338 |
|
|
|
|
0.5 |
0.301387 |
|
|
|
|
0.6 |
0.339054 |
|
|
|
|
0.7 |
0.372288 |
Table 4
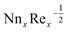 for different Ω, Lb, Pe and S3
for different Ω, Lb, Pe and S3
|
Ω
|
L
b
|
P
e
|
S
3
|
bvp4c technique |
| 0.2 |
0.3 |
1.0 |
0.01 |
0.0726217 |
| 0.3 |
|
|
|
0.0738469 |
| 0.4 |
|
|
|
0.075072 |
| 0.5 |
|
|
|
0.0762972 |
|
|
0.4 |
|
|
0.0726217 |
|
|
0.5 |
|
|
0.0745206 |
|
|
0.6 |
|
|
0.0759949 |
|
|
0.7 |
|
|
0.0771863 |
|
|
|
1.1 |
|
0.0729859 |
|
|
|
1.2 |
|
0.0733404 |
|
|
|
1.3 |
|
0.0736855 |
|
|
|
1.4 |
|
0.0740217 |
|
|
|
|
0.02 |
0.0804444 |
|
|
|
|
0.03 |
0.0794543 |
|
|
|
|
0.04 |
0.0784678 |
|
|
|
|
0.05 |
0.0774847 |
4. Major findings
The research analysed the implications of bioconvection, magnetic field, Brownian motion, thermophoresis diffusion, and Arrhenius activation energy on Casson's fluid flow in the existence of nanoparticles along with microorganisms. We examined thermal and solutal stratification boundary conditions for this study. Furthermore, thermal radiation was exploited to designate the heat transportation mechanism. An efficient numerical technique was utilized to solve the model equations and verify the experimental work. Numerical experiments for parametric analysis were carried out. The performance of temperature, mass concentration, and microorganism was revealed by using graphs and tables. The results can be outlined as follows:
1. The temperature field of Casson fluid rises for greater approximations of Rd the radiation parameter and the porosity parameter λ.
2. By improving the values of Prandtl number Pr and stretching parameter α decay the Casson fluid temperature.
3. The Lewis number Le and S2 mass stratified variable have diminishing performance for the concentration field.
4. The concentration field has a contradictory tendency with the deviation of thermophoresis Nt and reaction constant σ in the flow of Casson nanofluid.
5. The Peclet number Pe and bioconvection Lewis number Lb have decreasing behavior for microorganism profiles.
6. We observed a conflicting behavior for γ3 microorganisms Biot number, and S3 the microorganisms stratified variable in the Casson microorganism profile.
Abbreviations
| (x, y, z) | Coordinate axis (m) |
| (ρc)f | Fluid's heat capacity (J K−1) |
| (u, v, w) | velocity coordinates (m s−1) |
|
B
| Magnetic induction (kg s−2 m−2) |
|
D
T
| Thermophoresis diffusion coefficient (m2 s−1) |
|
C
| Fluid concentration profile (kg m−3) |
|
α
1
| Thermal diffusivity (m2 s−1) |
|
T
| Fluid temperature (K) |
|
c
p
| Specific heat capacity (J kg−1 K−1) |
|
ν
| Kinematic viscosity (m2 s−1) |
|
σ** | Electrical conductivity (S m−1) |
|
D
B
| Brownian diffusion coefficient (m2 s−1) |
|
k* | Mean absorption coefficient (m−1) |
|
ρ
| Fluid density (kg m−3) |
|
σ* | Stefan–Boltzmann constant (W m−2 K−4) |
|
k
| Thermal conductivity (W m−1 K−1) |
|
C
∞
| Ambient concentration (kg m−3) |
|
N
w
| Motile gyrotactic microorganism surface |
|
T
∞
| Ambient temperature (K) |
|
T
w
| Wall temperature (K) |
|
q
r
| Radiative heat flux (kg s−3) |
|
W
c
| Maximum cell swimming speed (m s−1) |
|
D
m
| Diffusivity of microorganism (m2 s−1) |
|
U
w
| Stretching velocity (m s−1) |
| Nnx | Local density of microbe |
|
E
a
| Wall shear stress |
|
d
1, d2, d3 | Positive constants |
|
N
b
| Brownian motion parameter |
|
θ
| Dimensionless temperature |
|
K
| Porous medium permeability |
|
σ
| Chemical reaction parameter |
|
η
| Non-dimensional variable |
|
N
| Gyrotactic microorganism |
|
β
| Casson fluid parameters |
| Nux | Nusselt number |
|
N
∞
| Ambient motile organism density |
|
C
w
| Concentration on elastic sheet surface |
|
λ
| Porosity parameter |
|
γ
3
| Microorganism stratification Biot number |
|
L
e
| Lewis number |
|
γ
2
| Mass stratification Biot number |
|
S
3
| Microorganism stratification parameter |
|
L
b
| Bioconvection Schmidt number |
|
S
1
| Thermal stratification parameter |
| Shx | Local Sherwood number |
|
γ
1
| Thermal stratification Biot number |
|
δ
| Temperature difference parameter |
|
S
2
| Mass stratification parameter |
| Pr | Prandtl number |
|
P
e
| Bio-convection Peclet number |
|
Ω
| Microorganisms difference parameter |
|
N
b
| Brownian movement parameter |
|
R
d
| Thermal radiation parameter |
|
M
| Magnetic parameter |
|
α
| Stretching ratio parameter |
|
χ
| Dimensionless microorganism field |
|
N
t
| Thermophoresis parameter |
|
E
| Activation energy |
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia for funding this work through Large Groups Project under grant number RGP.2/329/44.
References
-
S. U. Choi and J. A. Eastman, Enhancing thermal conductivity of fluids with nanoparticles, Argonne. National. Lab., IL, United States, 1995 Search PubMed.
-
J. Buongiorno, Convective transport in nanofluids, 2006, pp. 240–250 Search PubMed.
- E. Abu-Nada and H. F. Oztop, Effects of inclination angle on natural convection in enclosures filled with Cu-water nanofluid, Int. J. Heat Fluid Flow, 2009, 30, 669–678 CrossRef CAS.
- M. Shahzad, H. Sun, F. Sultan, W. A. Khan, M. Ali and M. Irfan, Transport of radiative heat transfer in dissipative Cross nanofluid flow with entropy generation and activation energy, Phys. Scr., 2019, 94, 115224 CrossRef CAS.
- M. I. Khan, S. A. Khan, T. Hayat, M. Waqas and A. Alsaedi, Modeling and numerical simulation for flow of hybrid nanofluid (SiO2/C3H8O2) and (MoS2/C3H8O2) with entropy optimization and variable viscosity, Int. J. Numer. Methods Heat Fluid Flow, 2020, 22, 3939–3955 Search PubMed.
- S. A. Khan, T. Hayat, A. Alsaedi and B. Ahmad, Melting heat transportation in radiative flow of nanomaterials with irreversibility analysis, Renewable Sustainable Energy Rev., 2021, 140, 110739 CrossRef CAS.
- M. Ali, F. Sultan, W. A. Khan and M. Shahzad, Exploring the physical aspects of nanofluid with entropy generation, Appl. Nanosci., 2020, 10, 3215–3225 CrossRef CAS.
- S. A. Khan, T. Hayat and A. Alsaedi, Thermal conductivity performance for ternary hybrid nanomaterial subject to entropy generation, Energy Rep., 2022, 8, 9997–10005 CrossRef.
- S. A. Khan, T. Hayat and A. Alsaedi, Entropy optimization for nanofluid flow with radiation subject to a porous medium, J. Pet. Sci. Eng., 2022, 217, 110864 CrossRef CAS.
- N. Anjum, W. A. Khan, M. Ali, I. Hussain, M. Waqas and M. Irfan, Thermal performance analysis of Sutterby nanoliquid subject to melting heat transportation, Int. J. Mod. Phys. B, 2022, 2350185 Search PubMed.
- J. R. Platt, Bioconvection Patterns in Cultures of Free-Swimming Organisms, Science, 1961, 133, 1766–1767 CrossRef CAS PubMed.
- A. V. Kuznetsov, The onset of nanofluid bioconvection in a suspension containing both nanoparticles and gyrotactic microorganisms, Int. Commun. Heat Mass Transfer, 2010, 37, 1421–1425 CrossRef CAS.
- Usman, M. M. Bhatti, A. Ghaffari and M. H. Doranehgard, The role of radiation and bioconvection as an external agent to control the temperature and motion of fluid over the radially spinning circular surface: a theoretical analysis via Chebyshev spectral approach, Math. Methods Appl. Sci., 2023, 11523–11540 CrossRef.
- Y. M. Chu, S. Jakeer, S. R. R. Reddy, M. L. Rupa, Y. Trabelsi, M. I. Khan, H. A. Hejazi, B. M. Makhdoum and S. M. Eldin, Double diffusion effect on the bio-convective magnetized flow of tangent hyperbolic liquid by a stretched nano-material with Arrhenius Catalysts, Case Stud. Therm. Eng., 2023, 44, 102838 CrossRef.
- N. Anjum, W. A. Khan, M. Azam, M. Ali, M. Waqas and I. Hussain, Significance of bioconvection analysis for thermally stratified 3D Cross nanofluid flow with gyrotactic microorganisms and activation energy aspects, Therm. Sci. Eng. Prog., 2023, 38, 101596 CrossRef CAS.
- W. A. Khan, M. Irfan, M. Khan, A. S. Alshomrani, A. K. Alzahrani and M. S. Alghamdi, Impact of chemical processes on magneto nanoparticle for the generalized burgers fluid, J. Mol. Liq., 2017, 234, 201–208 CrossRef CAS.
- T. Hayat, S. A. Khan, A. Alsaesi and H. M. Fardoun, Heat transportation in electro- magnetohydrodynamic flow of Darcy-Forchheimer viscous fluid with irreversibility analysis, Phys. Scr., 2020, 95, 105214 CrossRef CAS.
- S. A. Khan, T. Hayat and A. Alsaedi, Simultaneous features of Soret and Dufour in entropy optimized flow of Re iner-Rivlin fluid considering thermal radiation, Int. Commun. Heat Mass Transfer, 2022, 137, 106297 CrossRef CAS.
- S. A. Khan, T. Hayat and A. Alsaedi, Numerical study for entropy optimized radiative unsteady flow of Prandtl liquid, Fuel, 2022, 319, 123601 CrossRef CAS.
- S. A. Khan, T. Hayat, A. Alsaedi and M. S. Alhodaly, Thermal analysis for radiative flow of Darcy–Forchheimer nanomaterials subject to entropy generation, J. Comput. Des. Eng., 2022, 9, 1756–1764 Search PubMed.
- M. Irfan, Influence of thermophoretic diffusion of nanoparticles with Joule heating in flow of Maxwell nanofluid, Numer. Methods Part. Differ. Equ., 2023, 39(2), 1030–1041 CrossRef.
-
M. Irfan, Energy transport phenomenon via Joule heating and aspects of Arrhenius activation energy in Maxwell nanofluid, Waves Random Complex media, 2023, DOI:10.1080/17455030.2023.2196348.
- M. M. Bhatti, A. Shahid, L. E. Sarris and O. A. Beg, Spectral relaxation computation of Maxwell fluid flow from a stretching surface with quadratic convection and non-Fourier heat flux using Lie symmetry transformations, Int. J. Mod. Phys. B, 2023, 37, 2350082 CrossRef CAS.
- M. M. Bhatti, O. A. Beg, R. Ellahi and T. Abbas, Natural Convection Non-Newtonian EMHD Dissipative Flow Through a Microchannel Containing a Non-Darcy Porous Medium: Homotopy Perturbation Method Study, Qual. Theory Dyn. Syst., 2022, 21 DOI:10.1007/s12346-022-00625-7.
- N. Casson, A flow equation for the pigment oil suspension of the printing ink type, Rheol. Disperse Syst., 1959, 84–102 CAS.
- M. Waqas, W. A. Khan, A. A. Pasha, N. Islam and M. M. Rahman, Dynamics of bioconvective Casson nanoliquid from a moving surface capturing gyrotactic microorganisms, magnetohydrodynamics and stratifications, Therm. Sci. Eng. Prog., 2022, 36, 101492 CrossRef CAS.
- A. Shahid, W. Wei, M. M. Bhatti, O. A. Bég and T. A. Bég, Mixed convection Casson polymeric flow from a nonlinear stretching surface with radiative flux and non-Fourier thermal relaxation effects: Computation with CSNIS, ZAMM, 2023, 103(10), e202200519 CrossRef.
- U. Ali, M. Irfan, N. S. Akbar, K. U. Rehman and W. Shatanawi, Dynamics of Soret–Dufour effects and thermal aspects of Joule heating in multiple slips Casson–Williamson nanofluid, Int. J. Mod. Phys. B, 2023 DOI:10.1142/S0217979224502060.
- J. Qing, M. M. Bhatti, M. A. Abbas, M. M. Rashidi and M. E. S. Ali, Entropy Generation on MHD Casson Nanofluid Flow over a Porous Stretching/Shrinking Surface, Entropy, 2016, 18(4), 123 CrossRef.
- K. Bhattacharyya, MHD Stagnation-Point Flow of Casson Fluid and Heat Transfer over a Stretching Sheet with Thermal Radiation, J. Thermodyn., 2013, 2013, 169674 CrossRef.
- G. Mahanta and S. Shaw, 3D Casson fluid flow past a porous linearly stretching sheet with convective boundary condition, Alexandria Eng. J., 2015, 54, 653–659 CrossRef.
- U. Ali and M. Irfan, Thermal aspects of multiple slip and Joule heating in a Casson fluid with viscous dissipation and thermo-solutal convective conditions, Int. J. Mod. Phys. B, 2023, 37, 2350043 CrossRef CAS.
- M. Khan, M. Irfan, W. A. Khan and A. S. Alshomrani, A new modeling for 3D Carreau fluid flow considering nonlinear thermal radiation, Results Phys., 2017, 7, 2692–2704 CrossRef.
- Z. Hussain, W. A. Khan, T. Muhammad, H. A. Alghamdi, M. Ali and M. Waqas, Dynamics of gyrotactic microorganisms for chemically reactive magnetized 3D Sutterby nanofluid flow comprising non-uniform heat sink-source aspects, J. Magn. Magn. Mater., 2023, 587, 170798 CrossRef.
- Z. Hussain, M. M. Alam, A. A. Pasha, W. A. Khan, M. Ali and A. I. Khan, Gyrotactic microorganisms analysis for radiative 3D Carreau nanofluid flow configured by activation energy and viscous dissipation, Therm. Sci. Eng. Prog., 2023, 42, 101898 CrossRef CAS.
- N. S. Akbar, S. Nadeem, R. U. Haq and Z. H. Khan, Numerical solutions of Magnetohydrodynamic boundary layer flow of tangent hyperbolic fluid towards a stretching sheet, Indian J. Phys., 2013, 87, 1121–1124 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
M.
Irfan
b,
Taseer
Muhammad
c,
Sayed M.
Eldin
d,
M.
Waqas
ef and
P. V. Satya
Narayana
*g
a,
M.
Irfan
b,
Taseer
Muhammad
c,
Sayed M.
Eldin
d,
M.
Waqas
ef and
P. V. Satya
Narayana
*g
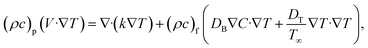
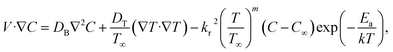
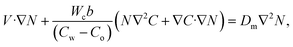
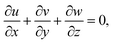
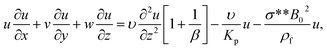
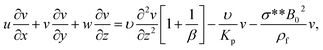
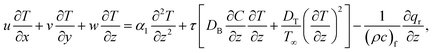
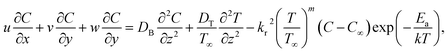
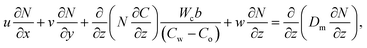
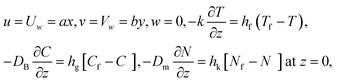
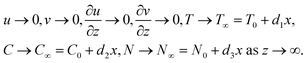
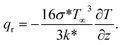
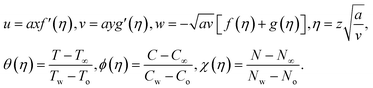
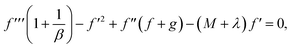
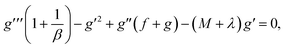
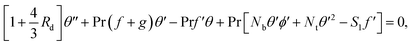
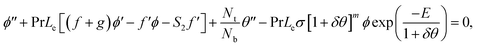
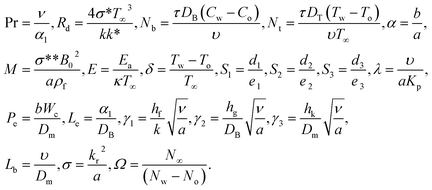
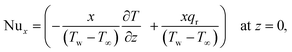
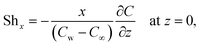
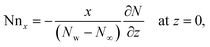
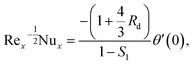
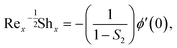
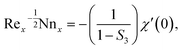
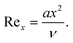
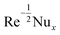 developing parameters Pr, γ1, S1 and Rd. It is inspected that the deviance of
developing parameters Pr, γ1, S1 and Rd. It is inspected that the deviance of 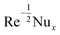 growths by increasing the approximations of parameters Pr, γ1, S1 and Rd. Table 3, scrutinizes the variations in
growths by increasing the approximations of parameters Pr, γ1, S1 and Rd. Table 3, scrutinizes the variations in 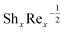 with several evaluations of captivating parameters Nt, Le, Nb and γ2. It can be perceived that by growing the parameters Le, Nb and γ2 an intensification in
with several evaluations of captivating parameters Nt, Le, Nb and γ2. It can be perceived that by growing the parameters Le, Nb and γ2 an intensification in 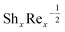 is originated. A contradictory performance can be appreciated Nt. The different values of Ω, Lb, Pe and S3 against
is originated. A contradictory performance can be appreciated Nt. The different values of Ω, Lb, Pe and S3 against 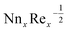 are demonstrated in Table 4, we noticed that
are demonstrated in Table 4, we noticed that 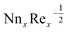 decreases by refining S3. While
decreases by refining S3. While 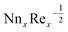 increases for the parameters Ω, Lb, Pe.
increases for the parameters Ω, Lb, Pe.