Open Access Article
Open Access ArticleModel systems for dye-sensitized solar cells: cyanidin-silver nanocluster hybrids at TiO2 support†
Margarita Bužančić Milosavljević a,
Antonija Mravak
a,
Antonija Mravak a,
Martina Perić Bakulić
a,
Martina Perić Bakulić *a and
Vlasta Bonačić-Koutecký
*a and
Vlasta Bonačić-Koutecký *abc
*abc
aCenter of Excellence for Science and Technology-Integration of Mediterranean Region (STIM), Faculty of Science, University of Split, Ruđera Boškovića 33, 21000 Split, Croatia. E-mail: margarita@stim.unist.hr; antonija@stim.unist.hr; martina@stim.unist.hr
bInterdisciplinary Center for Advanced Science and Technology (ICAST) at University of Split, Meštrovićevo šetalište 45, 21000 Split, Croatia
cDepartment of Chemistry, Humboldt Universität zu Berlin, Brook-Taylor-Strasse 2, 12489 Berlin, Germany. E-mail: vbk@cms.hu-berlin.de
First published on 17th February 2023
Abstract
Theoretical study of structural, optical, and photovoltaic properties of novel bio-nano hybrids (dye-nanocluster), as well as at TiO2 surface model support is presented in the context of the application for dye-sensitized solar cells (DSSC). A group of anthocyanidin dyes (pelargonidin, cyanidin, delphinidin, peonidin, petunidin, and malvidin) represented by cyanidin covalently bound to silver nanoclusters (NCs) with even or odd number of valence electrons have been investigated using DFT and TDDFT approach. The key role of nanoclusters as acceptors in hybrids cyanidin-NC has been shown. The nanoclusters with an even number of valence electrons are suitable as acceptors in hybrids. The interaction of bio-nano (cyanidin-NC) hybrid with the TiO2 surface model has been investigated in the context of absorption in near-infrared (NIR) and charge separation due to donor and acceptor subunits. Altogether, the theoretical concept serves to identify the key steps in the design of novel solar cells based on bio-nano hybrids at TiO2 surface for DSSC application.
1 Introduction
In a search for a photovoltaic cell that would be commercially more attractive due to better energy conversion efficiency, Grätzel et al. proposed a dye-sensitized solar cell (DSSC),1–3 based on light harvesting dye that sensitizes the transparent TiO2 semiconductor film. Since then, a significant experimental and theoretical effort has been invested into finding the optimal sensitizer.4–8 Transition metal compounds, specifically Ru-complexes, have emerged as highly efficient DSSC dye candidates with promising photovoltaic properties.3,9 However, the search for new materials has led to natural dyes,10–12 that are non-toxic for both humans and the environment,13 and easily available through plant extraction.14 The reported efficiency of these dyes is rather small (maximum value of over 4%12). Nevertheless, their modification by small silver nanoclusters (NCs) opens a route to design new systems with donor–acceptor properties. These properties have been previously studied within sensitizers15 based on ruthenium,16,17 porphyrin18 complexes, and metal-free19 organic dyes.Anthocyanidins, a subclass of flavonoids, have absorption maxima lying ∼500 nm20 and are extensively investigated in the context of the DSSC application.21–23 However, they have low stability24 and low efficiency as solar cell sensitizers (maximum around 1%25). Also, they do not satisfy the donor–acceptor condition.
Although several properties of the DSSC system can be tuned to improve efficiency, our approach is the modification of the sensitizer by introducing the donor–acceptor concept through bio-nano hybrid. A variety of modified natural dyes based on bio-nano hybrids have been investigated. Those include but are not limited to complexes of two or more natural dyes,25,26 natural and synthetic dyes27 and multilayered natural dyes DSSC.28 Also, the addition of metal atoms to natural dye (e.g. iron–cyanidin complex) has been reported to improve optical properties compared to pure pigments.29
Furthermore, the silver nanoclusters (NCs) forming bio-nano hybrids substantially increase optical absorption of pure biomolecules due to the interaction between intense excitations within the cluster and π–π* excitations within aromatic rings of biomolecule.30 This opens a route for enhancing the optical properties as well as improving the light-harvesting efficiency of natural dyes through interaction with silver NCs which introduces donor–acceptor subunits. Previous work has demonstrated that ligated noble metal NCs31,32 as well as noble metal nanoparticles (NPs)33,34 can contribute towards more efficient sensitizers.
The anchoring of the dye on the TiO2 surface is critical for ensuring electron injection from the dye to the semiconductor, which is one of the important conditions for DSSC efficiency.35 Therefore, anchoring the cyanidin-NC on the TiO2 semiconductor has been investigated by modeling the complex {cyanidin-NC}-TiO2. Such hybrids have not been investigated previously in the context of DSSC application.
In the present paper, we focus on the theoretical study of the dye and silver NC (cyanidin-NC) hybrids by their opto-electronic and DSSC properties within the DFT and TDDFT methods. Results involve theoretical prediction of structural and linear optical properties (one-photon absorption, OPA) of bio-nano hybrids, in order to find out how the overall efficiency depends on selected NCs. Calculations of nonlinear optical properties (two-photon absorption, TPA) on chosen example have also been performed. Anchoring of the bio-nano hybrids on the semiconductor surface of TiO2 model is addressed in the context of charge separation and shift in near-infrared (NIR) regime for a potential application.
2 Molecular models for dye-NC hybrids anchored on TiO2 surface
The basic concept behind the proposed DSSC system is that light is captured by sensitizer dye-NC hybrid which is coupled to the semiconductor allowing electron injection into its conduction band after which dye is regenerated via electrolyte.36 Photovoltaic parameters (light harvesting efficiency, LHE and driving force for electron injection, ΔGinject), defined in the supplement, serve as an indication for the appropriate choice of hybrid sensitizer.Anthocyanidins as salt derivatives of flavylium cation belong to the group of natural pigments.37 The most common naturally produced anthocyanidins are pelargonidin, cyanidin, delphinidin, peonidin, petunidin, and malvidin38,39 (cf. Scheme 1). However, they do not contain acceptor–donor subunits. For this purpose, the silver nanoclusters serve to offer one of the needed subunits. Among structures from this family of natural pigments, we have chosen cyanidin to study the interaction with the NCs whose sizes have been selected according to their electronic properties. Structural and optical properties, as well as DSSC parameters of cyanidin-NCs with silver clusters containing 2, 4, 8, and 20 valence electrons, have been compared with hybrids involving clusters with an odd number of valence electrons. All of them have discrete energy levels and belong to the size regime <2 nm in which each atom counts.30 It is well known that the pure nanoclusters with an even number of electrons are more stable than those with an odd number of electrons.40
A TiO2 semiconductor was used as a surface model to investigate the anchoring of cyanidin-Ag9 hybrid. Anatase is the most widely used crystal type of TiO2 for DSSC application since it has a large band gap and conduction band edge energy.4,41 Consequently, the 2-layer anatase model of TiO2 (100) adapted from Koch et al. was selected.42,43 The anchoring on the surface was modeled by hydroxyl groups (–OH) through dissociative binding, which is more energetically favorable than the undissociative one.44 The link between the cyanidin-Ag9 hybrid and the surface is established by two titanium–oxygen bonds. In addition, binding over Ag9 and over both Ag9 and cyanidin has been also studied. However, the energies of all studied isomers are very close.
3 Computational
The structural and optical properties of cyanidin and cyanidin-NC hybrids have been determined using density functional theory (DFT) and its time-dependent version (TDDFT) in Gaussian 16 program.45 The ground state geometries of all systems were optimized with the Perdew–Burke–Ernzerhof (PBE) functional.46,47 For cyanidin-NC hybrids, an extensive search for the lowest energy isomer has been carried out using simulated annealing as implemented in TURBOMOLE.48 The Coulomb-attenuated version of Becke's three-parameter nonlocal exchange functional together with the Lee–Yang–Parr gradient-corrected correlation functional (CAM-B3LYP)49 has been employed to calculate optical properties due to its accurate assessment of silver NCs excitation energies.50,51 For all atoms, split valence polarization atomic basis set (SVP) has been used.52 For the silver atoms, the 19-e− relativistic effective core potential (19-e− RECP) from the Stuttgart group taking into account scalar relativistic effects has been employed.53 Nonlinear optical properties; TPA spectra and cross sections (σ)54 were obtained using either single residue or double residue quadratic response procedure55,56 implemented in Dalton electronic structure program57,58The fragment representing semiconductor TiO2 contains 30 TiO2 units saturated with 12 hydrogen atoms forming (TiO2)30O6H12. Systems of similar sizes have been already used for such applications.59 The considered surface model is {cyanidin-Ag9}-TiO2, where TiO2 fragment is interacting with a cyanidin-Ag9 hybrid. The complex was optimized within the Gaussian 16 program45 using the PBE exchange–correlation functional. The SVP basis set was used for all atoms, with the addition of a 19-e− RECP for Ag atoms.52,60 Due to the size of the complex, the density fitting Weigend-06 (W06) was employed with the GGA functional to speed up computations. The calculation of the absorption spectrum was performed at the same level of theory as for the hybrids.
4 Results and discussion
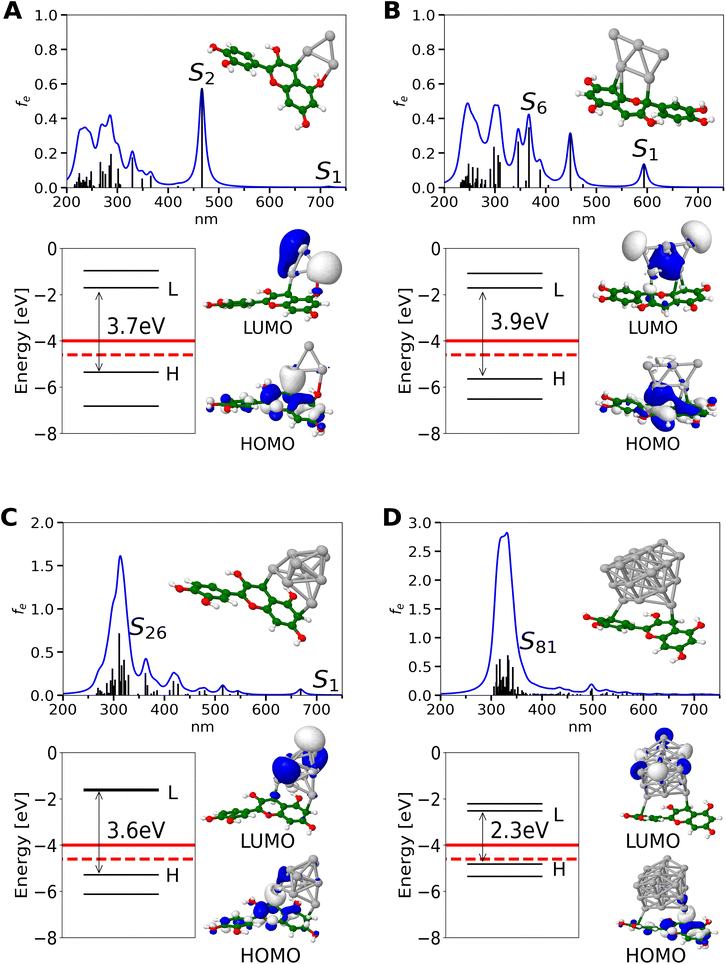
None of the anthocyanidin dyes including selected cyanidin satisfy conditions for photovoltaic parameters needed for DSSC applications (cf. Fig. S1†). HOMO and LUMO orbitals of pure anthocyanidin dyes are delocalized over all three aromatic rings as presented by cyanidin creating characteristic bright π–π* transition (cf. Fig. S2†). In order to form bio-nano hybrids as sensitizers for solar cells, adequate HOMO and LUMO energy levels are needed. The HOMO of the dye-NC should be lower than I−/I3− redox potential allowing for system regeneration. In addition, to ensure conditions for charge generation the LUMO of the system should be higher than TiO2 conduction band.36 Both HOMO and LUMO energy levels of the anthocyanidin dyes lie below the electrolyte redox potential and semiconductor conduction band, thus requiring correction which is possible by silver NCs (cf. Fig. S1†).The inclusion of silver NC of the given size and number of valence electrons shifts HOMO and LUMO energy levels to higher values allowing them to satisfy photovoltaic parameters. Absorption spectra for cyanidin-Agn (n = 3, 5, 9, 21 with 2, 4, 8, 20 valence electrons) together with MO energies as well as values for TiO2 conduction band edge and I−/I3− redox potential are shown in Fig. 1. Notice that the binding energy of NC's to dye is ∼ −12 eV (cf. Table 1). In contrast, for cyanidin-Agn (n = 6, 12) with an odd number of valence electrons (5, 11) HOMO, LUMO energy levels lie above TiO2 conduction band edge and I−/I3− redox potential, due to their lower stability (cf. Fig. S3† and Table 1).
| Smax | λmax [nm] | femax | −HOMO [eV] | LHE | ΔGinject [eV] | Eb [eV] | ||
|---|---|---|---|---|---|---|---|---|
| I | Cyanidin+ | S1 | 459 | 0.60 | 10.52 | 0.75 | 3.815 | |
| Cyanidin-Ag3 | S2 | 467 | 0.57 | 5.35 | 0.73 | −1.304 | −12.45 | |
| Cyanidin-Ag5 | S6 | 367 | 0.34 | 5.65 | 0.55 | −1.730 | −12.56 | |
| Cyanidin-Ag9 | S26 | 311 | 0.71 | 5.28 | 0.80 | −2.706 | −11.73 | |
| Cyanidin-Ag21 | S81 | 332 | 0.68 | 4.82 | 0.79 | −2.908 | −11.07 | |
| II | (Cyanidin-Ag6)− | S10 | 393 | 0.49 | 2.47 | 0.68 | −4.683 | −8.26 |
| (Cyanidin-Ag12)− | S30 | 360 | 0.68 | 2.69 | 0.79 | −4.750 | −8.97 |
For dye-Agn hybrids containing silver cluster with an even number of valence electrons, the HOMO, LUMO energy levels are shifted in the right direction where HOMO level is lower than electrolyte redox potential and LUMO is higher than the TiO2 conduction band, making them capable for electron injection and system regeneration (cf. Fig. 1). The decrease of the HOMO–LUMO gap with increasing cluster size shifts the absorption band towards the red regime which is suitable for efficiency.61 Dye-Agn (n = 3, 5, 9, 21) hybrids containing an even number of valence electrons have much smaller HOMO–LUMO energy gaps (3.9 eV–2.3 eV) in comparison with cyanidin dye (4.8 eV, cf. Fig. 1 and Fig. S2†). Furthermore, the HOMO energy level of cyanidin-Ag9 hybrids remains similar to the cyanidin-Ag3 systems, but the HOMO–LUMO gap of the cyanidin-Ag21 hybrid is further reduced due to considerably larger cluster size. Overall, the silver NC interacting with the dye sensitizer influences the energy gap in the following manner: cyanidin > cyanidin-Ag3, Ag5, Ag9, > cyanidin-Ag21. This suggests that the cyanidin-Ag9 and the cyanidin-Ag21 are preferable in the context of DSSC application. From the experimental point of view, in the gas phase, only the charged species (cyanidin-Agn)+/− can be identified.
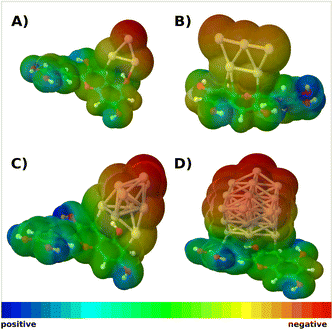
A slight difference in the steric configuration (dihedral angle (θ) and the bond length) of dye-NC hybrids with even and odd numbers of electrons is shown in Fig. S4.† HOMO orbitals of hybrids are delocalized mainly within cyanidin, whereas LUMO orbitals are delocalized within nanoclusters, as shown in Fig. 1. Absorption spectra of hybrids are characterized by two groups of transitions. The first one is ∼600 nm and below with low intensities and the second one is ∼300 nm with higher intensities. For the latter one with a higher intensity, clusters with a given number of valence electrons are responsible. This is illustrated in Fig. S5† in which absorption spectra obtained for pure cationic clusters with an even number of electrons are shown. Cluster structures have been taken from optimized hybrids. In fact, donor–acceptor properties of cyanidin-NCs are illustrated in molecular electrostatic potential surfaces (cf. Fig. 2), where clusters correspond to acceptors and cyanidin to donors.
In this contribution, two photon absorption (TPA) of cyanidin and cyanidin-Ag9 is also presented (cf. Fig. S6†). The addition of Ag9 cluster to cyanidin dye produces a large cross section only in near-infrared due to the resonance of OPA S1 and TPA S34 state. MOs presented for the S34 state demonstrate the donor–acceptor nature of the cyanidin-Ag9 system indicating charge transfer between cyanidin and Ag9 NC. This increases transition dipole moments causing the enhancement of TPA cross sections. The enlarged NIR region of calculated TPA spectra is shown also in Fig. S6†. For cyanidin-Ag9 cross sections are several orders of magnitude larger compared to cyanidin dye which extends the TPA spectrum in the near-infrared range (notice the σ values for 600–1100 nm). Investigation of the nonlinear optical properties is needed for the evaluation of the solar cells since their enhancement is connected with better photovoltaic performance.62,63
A design of novel materials with desirable linear and nonlinear optical properties can induce in solar cells a better harvesting of photons in the visible and near-infrared region.
Photovoltaic parameters such as LHE and ΔGinject are important for influencing incident photon to the conversion efficiency (IPCE) of the solar cell. LHE of the sensitizer is directly connected with the oscillator strength of absorption maximum.
The increasing size of the NC enhances the intensity of the absorption spectra of the hybrids in a region ∼300 nm consisting of multiple transitions with similar intensities. In contrast, the maximum absorption of cyanidin dye is characterized by a single transition. For this reason, regardless of hybrids having larger absorption intensity, LHE values of both cyanidin dye and hybrids remain similar (cf. Table 1). Cyanidin dye has the LUMO below the TiO2 conduction band which is reflected in the positive value of the ΔGinject, and the low possibility of the electron injection. In contrast, the interaction with the small silver NC containing an even number of electrons shifts the HOMO and LUMO energy levels matching the TiO2 conduction band and I−/I3− redox potential. This produces negative values of the ΔGinject favoring spontaneous electron injection from the excited state of the sensitizer to the semiconductor conduction band. The trend for the lowering ΔGinject is further supported by the increased size of the nanocluster.
Anchoring of cyanidin-Ag9 on TiO2 semiconductor has been investigated due to the importance of the efficient charge transfer from the sensitizer to the semiconductor. The details of the model system are described in the Sections 2 and 3.
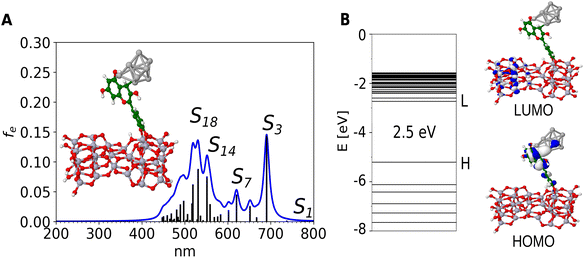
The isomers bound to surface over silver cluster have very low oscillator strengths (cf. Fig. S7A and B†). Therefore, we have selected the isomer bound over cyanidin which exhibits stronger interaction (cf. Fig. 3A). The structure of selected cyanidin-Ag9 forms two covalent bonds with the TiO2 model, which results in the adsorption energy (Eads, defined in the supplement) of the hybrid by −2.1 eV. The calculation of the binding energy of cyanidin to TiO2 has a similar value (−2.13 eV). This ensures the formation of the complex necessary for the electron injection from the hybrid cyanidin-Ag9 to the semiconductor.
The calculated absorption spectrum of the cyanidin-Ag9 anchored on TiO2 reveals a bathochromic shift (cf. Fig. 3A) compared to the spectrum of the cyanidin-Ag9. It also reveals two distinct regions, one ∼ 500 nm and the other one ∼ 700 nm. Both regions consist of transitions with low intensities. The HOMO of the anchored hybrid is delocalized on the cyanidin and two silver atoms. Also, it is energetically close to the HOMO of the hybrid without support. In contrast, the LUMO is entirely delocalized on the TiO2 model, as reported previously.64 The HOMO and LUMO orbitals (cf. Fig. 3B) along with the analysis of transitions corresponding to the largest absorption peaks (cf. Table S1 and Fig. S8†) demonstrate charge separation between the hybrid and TiO2 semiconductor which is a prerequisite for efficient DSSC performance. Altogether, the hybrid cyanidin-Ag9 anchored on the TiO2 surface serves as a model for stabilization of the bio-nano hybrid at the semiconductor surface.
5 Conclusion
Theoretical investigation of optical properties of model systems including the direct estimate of photovoltaic parameters is an important step in the context of improvement of DSSC performance. In the present paper, we have proposed bio-nano donor–acceptor hybrids as photosensitizers for DSSC application. These systems are formed by the interaction of silver NCs with the most common anthocyanidin dyes represented by cyanidin. The proposed strategy is based on a simple concept of bringing together natural dye and silver metal nanoclusters to form a donor–acceptor hybrid. The hybrids containing NC with an even number of valence electrons are more stable than those with an odd number of valence electrons. Therefore, NCs of selected sizes (with 2, 4, 8, 20 valence electrons) play a key role for the optical properties of cyanidin-NC hybrids as well as for determining photovoltaic parameters. In contrast to pure anthocyanidin dyes, bio-nano hybrids reveal the improvement of the overall efficiency (cf. LHE and ΔGinject). The interaction of the hybrid with TiO2 semiconductor model confirms the stability of the bio-nano system.We have demonstrated that silver NCs due to their unique electronic and optical properties introduce acceptor subunits interacting with natural pigments as donors. In summary, these findings serve to stimulate experimental investigation of optical and photovoltaic properties of bio-nano hybrids at TiO2 support, in order to realize novel materials at the nanoscale to improve DSSC's efficiency.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the project STIM – REI, Contract Number: KK.01.1.1.01.0003, funded by the European Union through the European Regional Development Fund – the Operational Programme Competitiveness and Cohesion 2014–2020 (KK.01.1.1.01). M. B. M., A. M. and M. P. B. acknowledge computational facilities of the HPC computer within the STIM-REI project, Doctoral study of Biophysics at the University of Split, as well as thank Professor Miroslav Radman at MedILS and Split-Dalmatia County. Also, the authors would like to thank Dr Rodolphe Antoine for his helpful comments.Notes and references
- B. O'Regan and M. Grätzel, Nature, 1991, 353, 737–740 CrossRef.
- M. Grätzel, Nature, 2001, 414, 338–344 CrossRef PubMed.
- M. Grätzel, J. Photochem. Photobiol., C, 2003, 4, 145–153 CrossRef.
- A. Hagfeldt, G. Boschloo, L. Sun, L. Kloo and H. Pettersson, Chem. Rev., 2010, 110, 6595–6663 CrossRef CAS PubMed.
- V. Sugathan, E. John and K. Sudhakar, Renewable Sustainable Energy Rev., 2015, 52, 54–64 CrossRef CAS.
- K. Sharma, V. Sharma and S. Sharma, Nanoscale Res. Lett., 2018, 13, 1–46 CrossRef CAS PubMed.
- F. De Angelis, S. Fantacci and A. Sgamellotti, Theor. Chem. Acc., 2007, 117, 1093–1104 Search PubMed.
- M. Pastore, E. Mosconi, S. Fantacci and F. De Angelis, Curr. Org. Synth., 2012, 9, 215–232 Search PubMed.
- N. Tomar, A. Agrawal, V. S. Dhaka and P. K. Surolia, Sol. Energy, 2020, 207, 59–76 CrossRef CAS.
- A. Kay and M. Grätzel, J. Phys. Chem., 1993, 97, 6272–6277 CrossRef CAS.
- H. Hug, M. Bader, P. Mair and T. Glatzel, Appl. Energy, 2014, 115, 216–225 CrossRef CAS.
- N. Mariotti, M. Bonomo, L. Fagiolari, N. Barbero, C. Gerbaldi, F. Bella and C. Barolo, Green Chem., 2020, 22, 7168–7218 RSC.
- S. Ito, Solar Cells-Dye-Sensitized Devices, 2011, pp. 19–48 Search PubMed.
- G. Richhariya, A. Kumar, P. Tekasakul and B. Gupta, Renewable Sustainable Energy Rev., 2017, 69, 705–718 CrossRef CAS.
- A. Carella, F. Borbone and R. Centore, Front. Chem., 2018, 6, 2296–2646 Search PubMed.
- J.-H. Yum, I. Jung, C. Baik, J. Ko, M. K. Nazeeruddin and M. Grätzel, Energy Environ. Sci., 2009, 2, 100–102 RSC.
- I. M. Abdellah, A. I. Koraiem and A. El-Shafei, Sol. Energy, 2019, 177, 642–651 CrossRef CAS.
- J. Lu, S. Liu and M. Wang, Front. Chem., 2018, 6, 541 CrossRef CAS PubMed.
- Z. Yao, M. Zhang, H. Wu, L. Yang, R. Li and P. Wang, J. Am. Chem. Soc., 2015, 137, 3799–3802 CrossRef CAS PubMed.
- J. Harborne, Biochem, 1958, 70, 22 CrossRef CAS PubMed.
- K. Tennakone, A. Kumarasinghe, G. Kumara, K. Wijayantha and P. Sirimanne, J. Photochem. Photobiol., A, 1997, 108, 193–195 CrossRef CAS.
- S. Hao, J. Wu, Y. Huang and J. Lin, Sol. Energy, 2006, 80, 209–214 CrossRef CAS.
- I. C. Maurya, A. K. Gupta, P. Srivastava and L. Bahadur, J. Sol. Energy Eng., 2016, 138, 051006 CrossRef.
- J. Fleschhut, F. Kratzer, G. Rechkemmer and S. Kulling, Eur. J. Nutr., 2006, 51, 1461–1471 Search PubMed.
- R. Ramamoorthy, N. Radha, G. Maheswari, S. Anandan, S. Manoharan and R. V. Williams, J. Appl. Electrochem., 2016, 46, 929–941 CrossRef CAS.
- E. C. Prima, A. Nuruddin, B. Yuliarto, G. Kawamura and A. Matsuda, New J. Chem., 2018, 42, 11616–11628 RSC.
- D. D. Pratiwi, F. Nurosyid, A. Supriyanto and R. Suryana, IOP Conf. Ser.: Mater. Sci. Eng., 2017, 176, 012012 Search PubMed.
- N. Kumara, P. Ekanayake, A. Lim, L. Y. C. Liew, M. Iskandar, L. C. Ming and G. Senadeera, J. Alloys Compd., 2013, 581, 186–191 CrossRef CAS.
- A. Purwoko, V. Setiawati and S. Hadisaputra, IOP Conf. Ser.: Mater. Sci. Eng., 2019, 509, 012130 CAS.
- V. Bonačić-Koutecký, A. Kulesza, L. Gell, R. Mitrić, R. Antoine, F. Bertorelle, R. Hamouda, D. Rayane, M. Broyer, T. Tabarin and P. Dugourd, Phys. Chem. Chem. Phys., 2012, 14, 9282–9290 RSC.
- M. S. Kim, M. A. Abbas and J. H. Bang, Bull. Korean Chem. Soc., 2016, 37, 791–792 CrossRef CAS.
- M. A. Abbas, T.-Y. Kim, S. U. Lee, Y. S. Kang and J. H. Bang, J. Am. Chem. Soc., 2016, 138, 390–401 CrossRef CAS PubMed.
- S. Sreeja and B. Pesala, Sci. Rep., 2020, 10, 1–17 CrossRef PubMed.
- N. Bakr, A. Ali and S. Jassim, J. Adv. Phys., 2017, 6, 370–374 CrossRef.
- W.-C. Chen, S. Nachimuthu and J.-C. Jiang, Sci. Rep., 2017, 7, 1–13 CrossRef PubMed.
- W. Fan, D. Tan and W.-Q. Deng, ChemPhysChem, 2012, 13, 2051–2060 CrossRef CAS PubMed.
- S. C. Moldoveanu, Pyrolysis of Organic Molecules, Elsevier, 2nd edn, 2019, pp. 715–762 Search PubMed.
- F. J. Francis, Crit. Rev. Food. Sci. Nutr., 1989, 28, 273–314 CrossRef CAS PubMed.
- J.-M. Kong, L.-S. Chia, N.-K. Goh, T.-F. Chia and R. Brouillard, Phytochemistry, 2003, 64, 923–933 CrossRef CAS PubMed.
- V. Bonačić-Koutecky, L. Češpiva, P. Fantucci and J. Koutecky, J. Chem. Phys., 1993, 98, 7981–7994 CrossRef.
- N. Martsinovich, D. R. Jones and A. Troisi, J. Phys. Chem. C, 2010, 114, 22659–22670 CrossRef CAS.
- R. Koch, A. S. Lipton, S. Filipek and V. Renugopalakrishnan, J. Mol. Model., 2011, 17, 1467–1472 CrossRef CAS PubMed.
- E. Marcano, Energy Harvest. Syst., 2018, 5, 29–38 CrossRef.
- F. De Angelis, S. Fantacci, A. Selloni, M. Grätzel and M. K. Nazeeruddin, Nano Lett., 2007, 7, 3189–3195 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision A.03, Gaussian Inc, Wallingford CT, 2016 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- TURBOMOLE V7.5 2020, A Development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com Search PubMed.
- T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- F. Rabilloud, J. Phys. Chem. A, 2013, 117, 4267–4278 CrossRef CAS PubMed.
- B. Anak, M. Bencharif and F. Rabilloud, RSC Adv., 2014, 4, 13001–13011 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- L. Frediani, Z. Rinkevicius and H. Ågren, J. Chem. Phys., 2005, 122, 244104 CrossRef PubMed.
- N. H. List, R. Zaleśny, N. A. Murugan, J. Kongsted, W. Bartkowiak and H. Ågren, J. Chem. Theory Comput., 2015, 11, 4182–4188 CrossRef CAS PubMed.
- P. Norman, Phys. Chem. Chem. Phys., 2011, 13, 20519–20535 RSC.
- Dalton, A Molecular Electronic Structure Program, Release Dalton2020.alpha, 2020, http://daltonprogram.org Search PubMed.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansík, H. J. A. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Sałek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, WIRES Comput. Mol. Sci., 2014, 4, 269–284 CrossRef CAS PubMed.
- M. J. Lundqvist, M. Nilsing, P. Persson and S. Lunell, Int. J. Quantum Chem., 2006, 106, 3214–3234 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- R. Ma, P. Guo, H. Cui, X. Zhang, M. K. Nazeeruddin and M. Grätzel, J. Phys. Chem. A, 2009, 113, 10119–10124 CrossRef CAS PubMed.
- A. Guillén-López, C. Delesma, C. Amador-Bedolla, M. Robles and J. Muñiz, Theor. Chem. Acc., 2018, 137, 1–15 Search PubMed.
- Z. Hu, V. Khadka, W. Wang, D. Galipeau and X. Yan, J. Mol. Model., 2012, 18, 3657–3667 CrossRef CAS PubMed.
- J. K. Roy, S. Kar and J. Leszczynski, J. Phys. Chem. C, 2019, 123, 3309–3320 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra00165b |
| This journal is © The Royal Society of Chemistry 2023 |