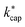Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Proton-transfer rate constants for the determination of organic indoor air pollutants by online mass spectrometry†
Tunga Salthammer *a,
Uwe Hohm
*a,
Uwe Hohm b,
Marcel Stahn
b,
Marcel Stahn c and
Stefan Grimme
c and
Stefan Grimme c
c
aFraunhofer WKI, Department of Material Analysis and Indoor Chemistry, 38108 Braunschweig, Germany. E-mail: tunga.salthammer@wki.fraunhofer.de
bInstitute of Physical and Theoretical Chemistry, University of Braunschweig – Institute of Technology, 38106 Braunschweig, Germany
cMulliken Center for Theoretical Chemistry, Institute for Physical and Theoretical Chemistry, University of Bonn, 53115 Bonn, Germany
First published on 13th June 2023
Abstract
Proton transfer reaction mass spectrometry (PTR-MS) has become an indispensable analytical tool for indoor related sciences. With high-resolution techniques not only is the online monitoring of the selected ions in the gas phase possible, but also, with some limitations, the identification of substance mixtures without chromatographic separation. The quantification is carried out with the help of kinetic laws, which require knowledge of the conditions in the reaction chamber, the reduced ion moblilities and the reaction rate constant kPT under these conditions. Ion–dipole collision theory can be used to calculate kPT. One approach is an extension of Langevin's equation and is known as average dipole orientation (ADO). In a further development, the analytical solution of ADO was replaced by trajectory analysis, which resulted in capture theory. The calculations according to ADO and capture theory require precise knowledge of the dipole moment and the polarizability of the respective target molecule. However, for many relevant indoor related substances, these data are insufficiently known or not known at all. Consequently, the dipole moment μD and polarizability α of 114 organic compounds that are frequently found in indoor air had to be determined using advanced quantum mechanical methods. This required the development of an automated workflow that performs conformer analysis before computing μD and α using density functional theory (DFT). Then the reaction rate constants with the H3O+ ion are calculated according to the ADO theory (kADO), capture theory (kcap) and advanced capture theory 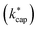 for different conditions in the reaction chamber. The kinetic parameters are evaluated with regard to their plausibility and critically discussed for their applicability in PTR-MS measurements.
for different conditions in the reaction chamber. The kinetic parameters are evaluated with regard to their plausibility and critically discussed for their applicability in PTR-MS measurements.
1 Introduction
A milestone in the analytical chemistry of the gas phase was the development of online mass spectrometry, which is, inter alia, suitable for numerous applications in food control, medicine and environmental research.1,2 The method was developed for very volatile and volatile organic compounds (VVOCs and VOCs) and is preferably used when their concentration has to be determined down to the ppt range and with high time resolution. The first applications in atmospheric chemistry aimed to examine ambient air.3–5 However, the suitability of online mass spectrometry for indoor applications was quickly recognized.6,7 A basic distinction is made between selected ion flow tube mass spectrometry (SIFT-MS)8 and proton-transfer-reaction mass spectrometry (PTR-MS),9,10 with the latter being mainly established in indoor air sciences.7 The use of PTR-MS to analyze human respiratory gas has been known for many years.11–13 Other successful areas of PTR-MS application and other mass spectrometry techniques with indoor-related questions involve ozone-initiated chemistry,6,14–16 photocatalytic reactions,17,18 measurements in museums,19,20 exposure under living conditions21–23 and gas phase/particle partitioning.24However, online mass spectrometry has pros and cons. The coverage of a wide mass range and the high time resolution are often offset by calibration problems. In addition, only molecules whose proton affinity is greater than that of water can be studied, since H3O+ is the preferred reagent for proton transfer. Ions of the same nominal mass cannot be distinguished with a low-resolution quadrupole mass filter without disproportionate effort, their selective analysis requires a time-of-flight (ToF) detector. Not all molecules can be detected via the [M + 1]+ ion but rather fragment in the reaction tube, which makes both qualification and quantification more difficult.25,26
In a PTR-MS system quantification takes place from the signals of the ions involved, the device settings and the reaction constant of the proton transfer kPT. However, it is a fundamental problem of the PTR-MS method that reliable kPT values are only available for a comparatively small number of molecules. On the other hand, kPT can theoretically be calculated. The theory of ion–polar molecule collisions developed by Su and Bowers,27,28 also called average orientation dipole – ADO theory, is well suited for a reasonable estimation of reaction constants. In later works, Su and Chesnavich29 have taken an alternative route. The results of trajectory calculations were parameterized to give expressions which allow the calculation of kPT. This approach is known as capture theory. Finally, Su30 parameterized the trajectory calculations for the relative kinetic energy dependence of the rate constant at various temperatures. The ADO and the capture theory were discussed and compared by Ellis and Mayhew.31
Whichever theory is used, precise data on the dipole moment and polarizability of the target compound under the current reaction conditions are always required. The most critical quantity is the dipole moment. Even for a small and rigid molecule like acetaldehyde, the results of quantum mechanical calculations are between 2.65 D,32 2.88 D33 and 2.94 D (this work), depending on the level of theory. Generally, the span between these quantum chemically calculated dipole moments increases with molecular size and flexibility, which can be attributed to routinely considering only a single molecular geometry. This ignores conformational flexibility and thermal effects, which is far from reality. These effects can significantly impact geometries and geometry-dependent properties like dipole moments (see below). For many molecules that play a role in the indoor environment, no reliable gas phase dipole moments are known at all.
In this work, we provide quantum chemically calculated, thermally averaged ensemble dipole moments and polarizabilities for 114 organic molecules. On that basis, we calculate and discuss rate constants for proton transfer reactions of organic compounds with H3O+ ions according to ADO theory and capture theory. Particular attention is paid to Su's30 advanced capture theory, because this allows the calculation of kPT as a function of the electric field strength in the PTR-MS reaction chamber. We believe that these data are of particular value for the reliable determination of organic indoor air pollutants.
2 Methods
2.1 Software
The program OriginPro 2021b (64-bit) (OriginLab, Northampton, MA) was used for all non-quantum mechanical calculations, non-linear regression analyses, statistical evaluations and the drawing of some images. ChemDraw 16.0.1.4 (PerkinElmer Informatics Inc.) was used for drawing chemical structures. DFT calculations were performed using the program package TURBOMOLE 7.5.1.342.2 Quantum chemical calculations
Density functional theory (DFT) is routinely used to calculate dipole moments and polarizabilities for organic molecules. However, these calculations need reasonable starting geometries for all investigated compounds as input. Getting these geometries by hand for 114 organic compounds is tedious work and would limit further up-scaling of the developed workflow for an even larger number of compounds. Therefore, a workflow had to be developed as a first step that allows the automatic calculation of the relevant properties from more readily available inputs, such as CAS numbers.The PubChem35 database provides with its Power User Gateway (PUG) an URL-based API (application programming interface) for programmatic access to its contents. Using a simple command-line program dubbed PubGrep, we were able to get reasonable starting structures for all molecules by translating the given input to a PubChem Compound Identification (CID) first and afterward getting the corresponding 3D structure information from the database. If no 3D structure information was available, the 2D structure information was taken instead and converted into a 3D structure using the 2D to 3D structure converter included in our xTB program suite. Because dipole moments are highly dependent on the geometric structure of the molecule, a conformational sampling was performed using the program CREST36 with the GFN2-xTB37 semiempirical method. The resulting conformer ensemble was re-ranked with the program CENSO38 and the r2SCAN-3c39 composite DFT method with an energy threshold of 2.0 kcal mol−1 (8.4 kJ mol−1). These conformer ensembles were finally used to calculate the dipole moments and polarizabilities with the ωB97X-V40 DFT method. This functional is reported to perform very well for dipole moments with an RMS regularized error (RMSE) of just over 5% for small organic or inorganic molecules.41 A simplified schematic of this workflow is visualized in Fig. 1. Due to the rapid convergence of the computed dipole moment with the size of the applied AO basis (remaining completeness effects of about 0.1%), the def2-TZVPP basis set was chosen for computational efficiency. Instead of just using the lowest lying conformer for these calculations, the properties were calculated as a Boltzmann-weighted average over all conformers in the DFT refined ensemble at 298.15 K up to a Boltzmann threshold of 99% as
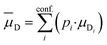 | (1) |
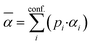 | (2) |
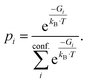 | (3) |
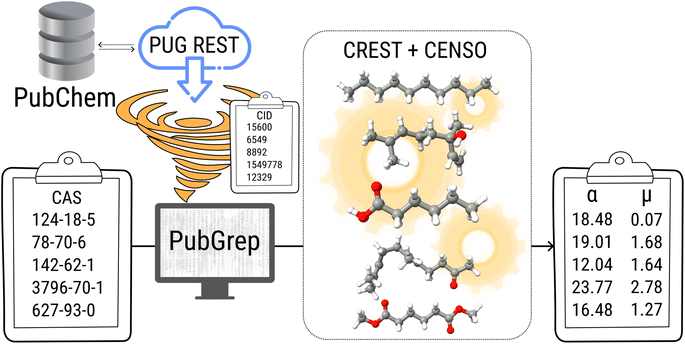 | ||
| Fig. 1 Simplified schematic of the automated calculation workflow including PubGrep, CREST and CENSO. | ||
3 Fundamentals of PTR-MS
The principle of PTR-MS is based on chemical ionization of organic molecules. H3O+ ions are generated as primary reagents in an ion source. These enter the drift reaction chamber, where they collide with the sample gas molecules. In this process, a proton is transferred, resulting in the formation of ionized organic molecules and water as shown in eqn (4). Organic compounds, whose proton affinity is higher than the proton affinity of water (691 kJ mol−1)42 can be measured according to this principle.| R + H3O+ → RH+ + H2O | (4) |
For [H3O+] >> [RH+] the VOC concentration [R] can be obtained from eqn (5) if the drift time tr and the proton transfer constant kPT are known.9,10,31
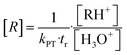 | (5) |
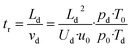 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325 Pa and T0 = 273.15 K are the pressure and temperature at standard conditions, respectively. The conditions inside the drift tube are expressed by the ratio E/N of the electric field strength E = Ud/Ld to the number density N. Assuming ideal gas behaviour we have N = pd/kBTd and N0 = p0/kBT0, kB is the Boltzmann constant. The drift velocity vd from eqn (6) is given by eqn (7).
325 Pa and T0 = 273.15 K are the pressure and temperature at standard conditions, respectively. The conditions inside the drift tube are expressed by the ratio E/N of the electric field strength E = Ud/Ld to the number density N. Assuming ideal gas behaviour we have N = pd/kBTd and N0 = p0/kBT0, kB is the Boltzmann constant. The drift velocity vd from eqn (6) is given by eqn (7).
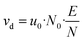 | (7) |
Usually, the ratio E/N is expressed in Townsend (Td) where 1 Td = 10−21 V m2. The values of u0 for H3O+ ions and the H3O+·(H2O) cluster were experimentally determined by Dotan et al.43 as a function of E/N. Note that these data can also be found as a graph in Warneke et al.3 and in the book of Ellis and Mayhew.31 In both publications, the data from Dotan et al.43 are discussed in detail and assessed as valid. Clusters only occur with small E/N values. For 100 Td the H3O+·(H2O)/H3O+ concentration ratio is 1.1 and for 120 Td it is 0.023.31 Table 1 shows values for u0, vd and tr at different E/N with a drift tube length Ld = 9.6 cm. Clusters are not discussed further, the data are given in Table 1 for comparison. Small molecules have similar rate constants for H3O+ and H3O+·(H2O).44 The E/N value not only affects the energy of the ions in the drift chamber, but also the fragmentation behavior of the molecules. In chemical ionization, the [M + 1]+ ions are often formed preferentially, but many molecules tend to fragment, a well-studied example being terpenoids.25,45 Normally, molecules fragment more with higher E/N. A comprehensive fragment ion database is provided by Pagonis et al.46
| Ion | E/N Td | u0 cm2 (V s)−1 | vd m s−1 | tr μs | KEion 10−20 J | KEion eV |
|---|---|---|---|---|---|---|
| H3O+ | 80 | 2.73 | 587 | 164 | 2.10 | 0.13 |
| H3O+ | 90 | 2.74 | 663 | 145 | 2.47 | 0.15 |
| H3O+ | 100 | 2.75 | 739 | 130 | 2.90 | 0.18 |
| H3O+ | 110 | 2.80 | 828 | 116 | 3.45 | 0.22 |
| H3O+ | 120 | 2.81 | 906 | 106 | 3.99 | 0.25 |
| H3O+ | 130 | 2.85 | 996 | 96 | 4.67 | 0.29 |
| H3O+ | 140 | 2.89 | 1087 | 88 | 5.42 | 0.34 |
| H3O+·H2O | 80 | 2.32 | 499 | 193 | 1.72 | 0.11 |
| H3O+·H2O | 90 | 2.36 | 571 | 168 | 2.02 | 0.13 |
| H3O+·H2O | 100 | 2.41 | 648 | 148 | 2.40 | 0.15 |
| H3O+·H2O | 110 | 2.44 | 721 | 133 | 2.80 | 0.17 |
4 Determination of kPT values
4.1 Calculation of the reaction rate constant kADO from dipole orientation theory
A widely used approach to calculate kPT follows the ion–dipole collision theory developed by Su and Bowers.27 Eqn (8) is an extension of Langevin's approach. The term kL describes the classical Langevin rate coefficient for the interaction of an ion with a non-polar molecule. The contribution of the interaction between ion and dipole is given by kμD.
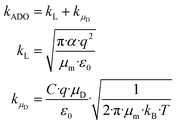 | (8) |
4.2 The locking parameter C
C is a function of the dipole moment μD and the square root of the polarizability α of the neutral molecule. For an entirely non-polar molecule, C = 0 and then eqn (8) corresponds to the classical Langevin approach. Temperature-dependent values for C as a function of μD/α1/2 were published by Su and Bowers47 and Su et al.48 The data sets for 300 K and 350 K were fitted with the empirical eqn (9) in order to be able to calculate kADO for the respective target molecules. The fit parameters are presented in Table 2, the fit curves are shown in Fig. 2 and the data are provided in the ESI (Appendix A).†
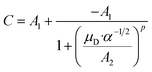 | (9) |
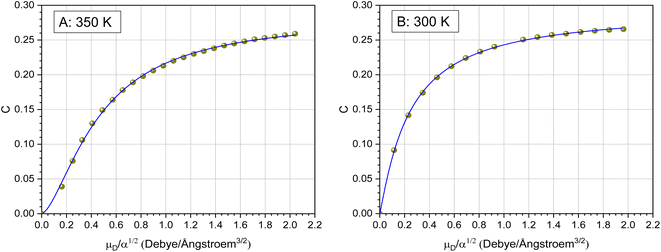 | ||
| Fig. 2 Plot of the locking parameter C versus μD/α1/2 and fitting curve with eqn (9). The data for 350 K (A) are from Su and Bowers47 and the 300 K data (B) are from Su et al.48 | ||
Extending their ADO theory, Su et al.48 developed an approach that takes into account the moment of inertia of a molecule. The authors explain that, strictly speaking, their extended theory only provides exact values for small linear molecules with a moment of inertia I ≤ 10−39 g cm2. Moreover, Su et al.48 mention that the temperature dependent C values from Su and Bowers47 contain a “minor error”. Unfortunately, corrected data for 350 K were not presented, only for 300 K (see Fig. 2B). We therefore used the data from Su and Bowers47 in our work in order to be able to make comparisons with other kPT values.
4.3 Calculation of the collision rate constant kcap by trajectory analysis
An alternative to analytical expressions for calculating rate coefficients for ion–molecule interactions is to model reaction processes by trajectory calculations. Su and Chesnavich29 have published corresponding parameterizations of this method, known as capture theory, with which temperature-dependent rate constants can be determined. First, the reaction rate kL according to Langevin (see eqn (8) with C = 0) is determined. In order to obtain the capture rate coefficient kcap, kL is multiplied by the parameterized quantity Kcap according to eqn (10) and (11).| kcap = kL·Kcap(TR) | (10) |
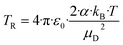 | (11) |
All quantities are given in SI units. The full trajectory analysis method for Kcap is provided with the respective units in the ESI (Appendix B).† It is a disadvantage of Su and Chesnavich's29 capture theory that only for small molecules Kcap is a function of TR and independent of the moment of inertia I. Ellis and Mayhew31 state that for the reactions taking place in the PTR-MS, Kcap is insensitive to the moment of inertia. In principle, however, this must be checked individually for each molecule. The question whether the conditions of the capture theory are fulfilled depends not only on I but also on μD and α. We have not performed a rigorous analysis of all the compounds being relevant here, as kcap is presented and calculated for comparison purposes only.
4.4 Calculation of the collision rate constant 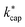 by advanced trajectory analysis
by advanced trajectory analysis
In a later work, Su30 presented improved parameterizations that cover a wider temperature range. This takes into account the effect that the temperature of the ions traveling along a drift tube is higher than the drift tube temperature Td because they experience additional energy from the electric field. Eqn (12) for the total mean ion kinetic energy KEion was originally developed by Wannier49 and later discussed by de Gouw et al.5 in relation to PTR-MS applications.
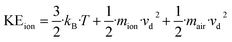 | (12) |
For T = 353 K and different E/N ratios, KEion values of H3O+ and H3O+·H2O are listed in Table 1. The collision energy of an ion–molecule reaction is then obtained from eqn (13). This is the kinetic energy KECM relative to the center of mass of the colliding system that is available for the reaction process.31
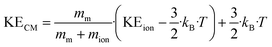 | (13) |
In eqn (12) and (13) mion is the mass of the respective ion H3O+ or H3O+·H2O, mair is the average mass of dry air and mm is the mass of the target molecule. The reaction constant 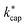 is then obtained according to eqn (14) from the Langevin constant kL and the factor KC, which according to Su30 depends on the parameters τ and ε to be calculated from the dipole moment μD, polarizability α and KECM.
is then obtained according to eqn (14) from the Langevin constant kL and the factor KC, which according to Su30 depends on the parameters τ and ε to be calculated from the dipole moment μD, polarizability α and KECM.
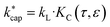 | (14) |
The full trajectory analysis method is provided in the ESI (Appendix C).† The influence of the kinetic energy on the reaction constant is discussed by Ellis and Mayhew31 using acetone at 300 K as an example. The difference to thermal energy is also significant for the increased temperature in a PTR-MS drift tube (353 K was assumed here). A value of KECM = 0.20 eV then results for acetone at E/N = 120 Td, the thermal energy from 3/2·kB·T accounts to 0.05 eV. As already pointed out in detail by Cappellin et al.,50 the particular advantage of 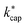 is that it can be used over a wide temperature range. Moreover, there is a direct connection with the electric field in the drift tube via the drift velocity vd, see eqn (7). This allows the rate constants to be calculated as a function of the E/N value for the respective drift tube temperature.
is that it can be used over a wide temperature range. Moreover, there is a direct connection with the electric field in the drift tube via the drift velocity vd, see eqn (7). This allows the rate constants to be calculated as a function of the E/N value for the respective drift tube temperature.
5 Results and discussion
5.1 Dipole moments
The essential parameters for calculating kADO, kcap and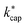 are the dipole moment μD and the polarizability α. Both quantities are linked to the molar polarization via the Debye equation.51 For PTR-MS measurements, values are required for the complete, thermally averaged conformer ensemble in the gas phase, because changes in the molecular geometry affect the dipole moment in particular. This effect has not been considered so far in our context. It has already been mentioned that published values can vary considerably. For gas phase 2-butoxyethanol, we calculate a dipole moment of 2.42 D after conformer analysis, while Iglesias et al.52 published 2.13 D for this molecule in cyclohexane. For 2-ethyl-1-hexanol with a calculated gas phase dipole moment of 1.61 D and a measured dipole moment in cyclohexane of 1.69 D at 298 K53 the difference is less pronounced. Nevertheless, it should be noted that the geometry of a molecule significantly impacts the dipole moment, and solvent interactions can influence the conformational distribution.38 Therefore, values measured in solution are not useful for flexible molecules. For example, the absolute difference between the dipole moment for the thermally averaged conformer ensemble and the lowest-lying conformer (ΔμD) of 2-ethyl-1-hexanol is 0.21 D. The mean deviation of the ΔμD values for all of the investigated compounds is with 0.13 D significant. The deviations are more pronounced for non-rigid molecules, such as 2-butoxyethylacetate (0.43 D), geranylacetone (0.45 D) or dimethylsebacate (1.4 D). The maximum ΔμD value is as high as 2.62 D for dimethyl phthalate. Moreover, tabulated data often has the disadvantage that the experimental conditions are unknown. Reliable data are only tabulated for a limited number of molecules,54,55 but quantum chemical tools for their calculation are nowadays routinely available.50 In this respect, quantum mechanical calculations computed for conformer ensembles appear as the only reasonable alternative, especially in the case of large and non-rigid molecules. The polarizabilities are much less susceptible to conformer changes than the dipole moments. Since the quality of many of the dipole moments available in the literature could not be evaluated and in order to avoid inconsistencies, only dipole moments and polarizabilities that were determined quantum mechanically according to the method described in Section 2 were used to calculate kADO, kcap and
are the dipole moment μD and the polarizability α. Both quantities are linked to the molar polarization via the Debye equation.51 For PTR-MS measurements, values are required for the complete, thermally averaged conformer ensemble in the gas phase, because changes in the molecular geometry affect the dipole moment in particular. This effect has not been considered so far in our context. It has already been mentioned that published values can vary considerably. For gas phase 2-butoxyethanol, we calculate a dipole moment of 2.42 D after conformer analysis, while Iglesias et al.52 published 2.13 D for this molecule in cyclohexane. For 2-ethyl-1-hexanol with a calculated gas phase dipole moment of 1.61 D and a measured dipole moment in cyclohexane of 1.69 D at 298 K53 the difference is less pronounced. Nevertheless, it should be noted that the geometry of a molecule significantly impacts the dipole moment, and solvent interactions can influence the conformational distribution.38 Therefore, values measured in solution are not useful for flexible molecules. For example, the absolute difference between the dipole moment for the thermally averaged conformer ensemble and the lowest-lying conformer (ΔμD) of 2-ethyl-1-hexanol is 0.21 D. The mean deviation of the ΔμD values for all of the investigated compounds is with 0.13 D significant. The deviations are more pronounced for non-rigid molecules, such as 2-butoxyethylacetate (0.43 D), geranylacetone (0.45 D) or dimethylsebacate (1.4 D). The maximum ΔμD value is as high as 2.62 D for dimethyl phthalate. Moreover, tabulated data often has the disadvantage that the experimental conditions are unknown. Reliable data are only tabulated for a limited number of molecules,54,55 but quantum chemical tools for their calculation are nowadays routinely available.50 In this respect, quantum mechanical calculations computed for conformer ensembles appear as the only reasonable alternative, especially in the case of large and non-rigid molecules. The polarizabilities are much less susceptible to conformer changes than the dipole moments. Since the quality of many of the dipole moments available in the literature could not be evaluated and in order to avoid inconsistencies, only dipole moments and polarizabilities that were determined quantum mechanically according to the method described in Section 2 were used to calculate kADO, kcap and 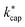 . All dipole moments, polarizabilities and calculated
. All dipole moments, polarizabilities and calculated 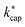 values are listed in Table 3. The kADO and kcap values are listed in the ESI† (Appendix D).
values are listed in Table 3. The kADO and kcap values are listed in the ESI† (Appendix D).
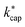 at 353 K in dependence of E/N for the reaction of organic compounds with H3O+ ions in the PTR-MS drift tube according to Su's30 capture theory. Other parameters and rate constants are listed in the ESI
at 353 K in dependence of E/N for the reaction of organic compounds with H3O+ ions in the PTR-MS drift tube according to Su's30 capture theory. Other parameters and rate constants are listed in the ESI
| Compound | CAS | μD D | α 10−24 cm3 | 10−9 cm3 s−1 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (E/N) = 80 Td | 90 | 100 | 110 | 120 | 130 | 140 | ||||
| Aliphatic and cyclic hydrocarbons | ||||||||||
| n-Hexane | 110-54-3 | 0.04 | 11.30 | 1.99 | 1.99 | 1.99 | 1.99 | 1.99 | 1.99 | 1.99 |
| n-Heptane | 142-82-5 | 0.08 | 13.09 | 2.12 | 2.12 | 2.12 | 2.12 | 2.12 | 2.12 | 2.12 |
| n-Octane | 111-65-9 | 0.06 | 14.87 | 2.24 | 2.24 | 2.24 | 2.24 | 2.24 | 2.24 | 2.24 |
| n-Nonane | 111-84-2 | 0.08 | 16.66 | 2.35 | 2.35 | 2.35 | 2.35 | 2.35 | 2.35 | 2.35 |
| n-Decane | 124-18-5 | 0.07 | 18.48 | 2.46 | 2.46 | 2.46 | 2.46 | 2.46 | 2.46 | 2.46 |
| Cyclohexane | 110-82-7 | 0.00 | 10.36 | 1.91 | 1.91 | 1.91 | 1.91 | 1.91 | 1.91 | 1.91 |
| Methylcyclohexane | 108-87-2 | 0.12 | 12.17 | 2.05 | 2.05 | 2.05 | 2.05 | 2.05 | 2.05 | 2.05 |
| 4-Vinyl cyclohexene (4-VCH) | 100-40-3 | 0.30 | 13.82 | 2.17 | 2.17 | 2.17 | 2.17 | 2.17 | 2.17 | 2.17 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| Aromatic hydrocarbons | ||||||||||
| Benzene | 71-43-2 | 0.00 | 10.07 | 1.90 | 1.90 | 1.90 | 1.90 | 1.90 | 1.90 | 1.90 |
| Toluene | 108-88-3 | 0.39 | 12.00 | 2.04 | 2.04 | 2.04 | 2.04 | 2.04 | 2.04 | 2.04 |
| Ethylbenzene | 100-41-4 | 0.42 | 13.80 | 2.17 | 2.17 | 2.17 | 2.17 | 2.17 | 2.17 | 2.17 |
| o-Xylene | 95-47-6 | 0.66 | 13.85 | 2.24 | 2.17 | 2.17 | 2.17 | 2.17 | 2.17 | 2.17 |
| m-Xylene | 108-38-3 | 0.37 | 13.95 | 2.18 | 2.18 | 2.18 | 2.18 | 2.18 | 2.18 | 2.18 |
| p-Xylene | 106-42-3 | 0.00 | 14.00 | 2.18 | 2.18 | 2.18 | 2.18 | 2.18 | 2.18 | 2.18 |
| 1,2,3-Trimethylbenzene | 526-73-8 | 0.73 | 15.70 | 2.36 | 2.29 | 2.29 | 2.29 | 2.29 | 2.29 | 2.29 |
| 1,2,4-Trimethylbenzene | 95-63-6 | 0.40 | 15.85 | 2.30 | 2.30 | 2.30 | 2.30 | 2.30 | 2.30 | 2.30 |
| 1,3,5-Trimethylbenzene | 108-67-8 | 0.00 | 15.91 | 2.31 | 2.31 | 2.31 | 2.31 | 2.31 | 2.31 | 2.31 |
| Isopropylbenzene | 98-82-8 | 0.39 | 15.56 | 2.28 | 2.28 | 2.28 | 2.28 | 2.28 | 2.28 | 2.28 |
| Styrene | 100-42-5 | 0.17 | 14.43 | 2.22 | 2.22 | 2.22 | 2.22 | 2.22 | 2.22 | 2.22 |
| Chlorobenzene | 108-90-7 | 1.86 | 12.25 | 2.86 | 2.75 | 2.65 | 2.56 | 2.49 | 2.42 | 2.37 |
| 1,2-Dichlorobenzene | 95-50-1 | 2.65 | 14.32 | 3.51 | 3.43 | 3.33 | 3.20 | 3.08 | 2.94 | 2.84 |
| 1,4-Dichlorobenzene | 106-46-7 | 0.00 | 14.56 | 2.18 | 2.18 | 2.18 | 2.18 | 2.18 | 2.18 | 2.18 |
| 4-Phenyl cyclohexene (4-PCH) | 4994-16-5 | 0.28 | 20.06 | 2.55 | 2.55 | 2.55 | 2.55 | 2.55 | 2.55 | 2.55 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| Polycyclic aromatic hydrocarbons | ||||||||||
| Naphthalene | 91-20-3 | 0.00 | 17.37 | 2.40 | 2.40 | 2.40 | 2.40 | 2.40 | 2.40 | 2.40 |
| 1-Methylnaphthalene | 90-12-0 | 0.36 | 19.25 | 2.51 | 2.51 | 2.51 | 2.51 | 2.51 | 2.51 | 2.51 |
| 1-Chloronaphthalene | 90-13-1 | 1.79 | 19.50 | 3.03 | 2.96 | 2.89 | 2.83 | 2.79 | 2.75 | 2.72 |
| Anthacene | 120-12-7 | 0.00 | 26.19 | 2.89 | 2.89 | 2.89 | 2.89 | 2.89 | 2.89 | 2.89 |
| Phenanthrene | 85-01-8 | 0.01 | 24.89 | 2.82 | 2.82 | 2.82 | 2.82 | 2.82 | 2.82 | 2.82 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| Terpenoids | ||||||||||
| Isoprene | 78-79-5 | 0.27 | 9.88 | 1.91 | 1.91 | 1.91 | 1.91 | 1.91 | 1.91 | 1.91 |
| α-Pinene | 80-56-8 | 0.18 | 16.51 | 2.33 | 2.33 | 2.33 | 2.33 | 2.33 | 2.33 | 2.33 |
| β-Pinene | 127-91-3 | 0.72 | 16.70 | 2.41 | 2.34 | 2.34 | 2.34 | 2.34 | 2.34 | 2.34 |
| 3-Carene | 13466-78-9 | 0.17 | 16.74 | 2.35 | 2.35 | 2.35 | 2.35 | 2.35 | 2.35 | 2.35 |
| D-Limonene | 5989-27-5 | 0.57 | 17.45 | 2.39 | 2.39 | 2.39 | 2.39 | 2.39 | 2.39 | 2.39 |
| α-Phellandrene | 4221-98-1 | 0.24 | 17.42 | 2.39 | 2.39 | 2.39 | 2.39 | 2.39 | 2.39 | 2.39 |
| Myrcene | 123-35-3 | 0.44 | 18.73 | 2.48 | 2.48 | 2.48 | 2.48 | 2.48 | 2.48 | 2.48 |
| β-Caryophyllene | 87-44-5 | 0.50 | 25.07 | 2.81 | 2.81 | 2.81 | 2.81 | 2.81 | 2.81 | 2.81 |
| Terpinolene | 586-62-9 | 0.24 | 17.81 | 2.42 | 2.42 | 2.42 | 2.42 | 2.42 | 2.42 | 2.42 |
| Linalool | 78-70-6 | 1.68 | 19.01 | 2.95 | 2.88 | 2.82 | 2.77 | 2.73 | 2.69 | 2.67 |
| α-Terpineol | 98-55-5 | 1.52 | 18.02 | 2.79 | 2.74 | 2.69 | 2.65 | 2.62 | 2.59 | 2.57 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| Alcohols | ||||||||||
| Methanol | 67-56-1 | 1.70 | 3.14 | 2.37 | 2.33 | 2.30 | 2.26 | 2.23 | 2.18 | 2.13 |
| Ethanol | 64-17-5 | 1.73 | 4.90 | 2.47 | 2.43 | 2.39 | 2.33 | 2.27 | 2.19 | 2.11 |
| 1-Propanol | 71-23-8 | 1.68 | 6.64 | 2.51 | 2.46 | 2.40 | 2.31 | 2.23 | 2.14 | 2.06 |
| 2-Propanol | 67-63-0 | 1.69 | 6.66 | 2.52 | 2.47 | 2.41 | 2.32 | 2.24 | 2.15 | 2.07 |
| 1-Butanol | 71-36-3 | 1.68 | 8.39 | 2.59 | 2.52 | 2.43 | 2.33 | 2.25 | 2.18 | 2.12 |
| 2-Butanol | 75-65-0 | 1.69 | 8.37 | 2.59 | 2.53 | 2.44 | 2.34 | 2.26 | 2.19 | 2.13 |
| 2-Methyl-1-propanol | 78-83-1 | 1.61 | 8.37 | 2.53 | 2.46 | 2.37 | 2.27 | 2.20 | 2.14 | 2.08 |
| 1-Pentanol | 71-41-0 | 1.65 | 10.17 | 2.64 | 2.53 | 2.44 | 2.36 | 2.30 | 2.24 | 2.19 |
| 1-Hexanol | 111-27-3 | 1.66 | 11.96 | 2.69 | 2.59 | 2.51 | 2.44 | 2.38 | 2.33 | 2.29 |
| 1-Heptanol | 111-70-6 | 1.66 | 13.75 | 2.74 | 2.65 | 2.58 | 2.51 | 2.47 | 2.42 | 2.38 |
| 2-Ethyl-1-hexanol | 104-76-7 | 1.61 | 15.37 | 2.75 | 2.68 | 2.62 | 2.56 | 2.52 | 2.48 | 2.45 |
| Benzyl alcohol | 100-51-6 | 1.62 | 12.68 | 2.67 | 2.58 | 2.51 | 2.44 | 2.40 | 2.35 | 2.31 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| Aldehydes | ||||||||||
| Acetaldehyde | 75-07-0 | 2.94 | 4.45 | 3.40 | 3.33 | 3.26 | 3.19 | 3.13 | 3.07 | 3.02 |
| Propanal | 123-38-6 | 2.85 | 6.14 | 3.35 | 3.29 | 3.23 | 3.17 | 3.12 | 3.05 | 2.99 |
| Butanal | 123-72-8 | 2.83 | 7.90 | 3.39 | 3.34 | 3.29 | 3.22 | 3.16 | 3.08 | 2.99 |
| 2-Methylpropanal | 78-84-2 | 2.91 | 7.88 | 3.45 | 3.39 | 3.34 | 3.27 | 3.21 | 3.14 | 3.05 |
| Pentanal | 110-62-3 | 2.85 | 9.68 | 3.49 | 3.43 | 3.37 | 3.30 | 3.22 | 3.12 | 3.00 |
| Hexanal | 66-25-1 | 2.83 | 11.45 | 3.55 | 3.49 | 3.43 | 3.33 | 3.24 | 3.12 | 2.98 |
| Heptanal | 111-71-7 | 2.86 | 13.25 | 3.66 | 3.59 | 3.51 | 3.40 | 3.29 | 3.15 | 3.01 |
| Octanal | 124-13-0 | 2.85 | 15.04 | 3.72 | 3.65 | 3.55 | 3.43 | 3.30 | 3.15 | 3.03 |
| Nonanal | 124-19-6 | 2.85 | 16.84 | 3.79 | 3.71 | 3.60 | 3.46 | 3.32 | 3.18 | 3.07 |
| Decanal | 112-31-2 | 2.85 | 18.66 | 3.86 | 3.76 | 3.64 | 3.49 | 3.35 | 3.22 | 3.12 |
| Acrolein (trans) | 107-02-8 | 3.43 | 6.34 | 3.84 | 3.76 | 3.68 | 3.60 | 3.54 | 3.47 | 3.41 |
| Acrolein (cis) | 107-02-8 | 2.81 | 6.14 | 3.33 | 3.27 | 3.22 | 3.16 | 3.11 | 3.04 | 2.97 |
| trans-2-Butenal | 123-73-9 | 4.20 | 8.40 | 4.48 | 4.38 | 4.29 | 4.19 | 4.11 | 4.03 | 3.95 |
| trans-2-Hexenal | 6728-26-3 | 4.37 | 12.02 | 4.68 | 4.59 | 4.50 | 4.41 | 4.33 | 4.24 | 4.15 |
| Furfural (trans) | 98-01-1 | 3.60 | 9.82 | 3.99 | 3.91 | 3.85 | 3.77 | 3.70 | 3.62 | 3.53 |
| Furfural (cis) | 98-01-1 | 4.31 | 9.88 | 4.51 | 4.41 | 4.32 | 4.22 | 4.15 | 4.07 | 3.98 |
| Glyoxal (cis) | 107-22-2 | 3.68 | 4.64 | 3.87 | 3.77 | 3.68 | 3.58 | 3.51 | 3.43 | 3.36 |
| Benzaldehyde | 100-52-7 | 3.42 | 12.53 | 4.01 | 3.95 | 3.88 | 3.79 | 3.71 | 3.60 | 3.47 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| Ketones | ||||||||||
| Acetone | 67-64-1 | 3.11 | 6.15 | 3.55 | 3.48 | 3.42 | 3.35 | 3.29 | 3.23 | 3.16 |
| 2-Butanone (MEK) | 78-93-3 | 2.97 | 7.86 | 3.49 | 3.44 | 3.38 | 3.31 | 3.25 | 3.18 | 3.09 |
| 4-Methyl-2-pentanone (MIBK) | 108-10-1 | 2.87 | 11.36 | 3.58 | 3.52 | 3.45 | 3.36 | 3.27 | 3.15 | 3.01 |
| Cyclohexanone | 108-94-1 | 3.45 | 10.57 | 3.93 | 3.86 | 3.79 | 3.72 | 3.65 | 3.56 | 3.45 |
| 6-Methyl-5-heptene-2-one (6-MHO) | 110-93-0 | 2.88 | 15.12 | 3.75 | 3.68 | 3.58 | 3.46 | 3.34 | 3.18 | 3.05 |
| 4-Oxopentanal (4-OPA) | 626-96-0 | 2.95 | 9.73 | 3.51 | 3.45 | 3.39 | 3.32 | 3.24 | 3.14 | 3.03 |
| Geranylacetone | 3796-70-1 | 2.78 | 23.77 | 3.98 | 3.85 | 3.69 | 3.54 | 3.44 | 3.34 | 3.25 |
| 3-Octanone | 106-68-3 | 2.71 | 14.90 | 3.62 | 3.53 | 3.44 | 3.31 | 3.18 | 3.04 | 2.93 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| Esters | ||||||||||
| Methyl acetate | 79-20-9 | 1.88 | 6.77 | 2.61 | 2.56 | 2.50 | 2.42 | 2.34 | 2.23 | 2.14 |
| Ethyl acetate | 141-78-6 | 2.03 | 8.59 | 2.82 | 2.76 | 2.69 | 2.59 | 2.49 | 2.39 | 2.30 |
| n-Butyl acetate | 123-86-4 | 2.06 | 12.13 | 3.00 | 2.92 | 2.81 | 2.69 | 2.60 | 2.52 | 2.45 |
| 2-Ethylhexyl acetate | 103-09-3 | 1.84 | 19.01 | 3.04 | 2.95 | 2.88 | 2.82 | 2.77 | 2.73 | 2.69 |
| Dimethyl phthalate | 131-11-3 | 2.93 | 19.46 | 3.91 | 3.81 | 3.68 | 3.52 | 3.39 | 3.26 | 3.15 |
| Diethylphthalate | 84-66-2 | 2.60 | 23.06 | 3.79 | 3.63 | 3.50 | 3.37 | 3.28 | 3.19 | 3.12 |
| Dimethyl succinate | 106-65-0 | 1.30 | 12.80 | 2.38 | 2.33 | 2.29 | 2.25 | 2.22 | 2.20 | 2.17 |
| Dimethyl adipate | 627-93-0 | 1.27 | 16.48 | 2.55 | 2.52 | 2.48 | 2.46 | 2.43 | 2.41 | 2.40 |
| Dimethyl sebacate | 106-79-6 | 1.50 | 23.76 | 3.01 | 2.97 | 2.93 | 2.90 | 2.88 | 2.86 | 2.84 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| Glycols | ||||||||||
| 2-Ethoxyethanol | 110-80-5 | 2.45 | 9.20 | 3.16 | 3.10 | 3.04 | 2.95 | 2.87 | 2.76 | 2.63 |
| 1-Methoxy-2-propanol | 107-98-2 | 2.33 | 9.16 | 3.07 | 3.01 | 2.95 | 2.86 | 2.77 | 2.65 | 2.53 |
| 1,2-Propanediol | 57-55-6 | 2.34 | 7.29 | 2.97 | 2.93 | 2.87 | 2.80 | 2.74 | 2.64 | 2.54 |
| 2-Butoxyethanol | 111-76-2 | 2.42 | 12.70 | 3.30 | 3.22 | 3.13 | 3.01 | 2.89 | 2.77 | 2.68 |
| 2-Butoxyethoxyethanol | 54446-78-5 | 2.81 | 16.93 | 3.74 | 3.65 | 3.54 | 3.39 | 3.26 | 3.13 | 3.02 |
| Phenoxyethanol | 122-99-6 | 1.67 | 15.41 | 2.79 | 2.71 | 2.64 | 2.58 | 2.54 | 2.50 | 2.46 |
| 2-Butoxyethyl acetate | 112-07-2 | 1.73 | 16.36 | 2.85 | 2.77 | 2.70 | 2.64 | 2.59 | 2.55 | 2.52 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| Acids | ||||||||||
| Formic acid | 64-18-6 | 1.56 | 3.30 | 2.13 | 2.10 | 2.07 | 2.02 | 1.98 | 1.92 | 1.86 |
| Acetic acid | 64-19-7 | 1.80 | 5.01 | 2.44 | 2.40 | 2.35 | 2.29 | 2.23 | 2.15 | 2.06 |
| Propionic acid | 79-09-4 | 1.69 | 6.72 | 2.46 | 2.41 | 2.34 | 2.25 | 2.17 | 2.08 | 2.01 |
| Hexanoic acid | 142-62-1 | 1.64 | 12.04 | 2.64 | 2.55 | 2.47 | 2.40 | 2.35 | 2.30 | 2.26 |
| Isobutyric acid | 79-31-2 | 1.74 | 8.45 | 2.59 | 2.52 | 2.44 | 2.33 | 2.25 | 2.18 | 2.11 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| Phenones | ||||||||||
| Acetophenone | 98-86-2 | 3.16 | 14.20 | 3.90 | 3.84 | 3.76 | 3.65 | 3.55 | 3.41 | 3.25 |
| Benzophenone | 119-61-9 | 3.11 | 22.62 | 4.19 | 4.08 | 3.95 | 3.77 | 3.63 | 3.49 | 3.38 |
| Darocur 1173 | 7473-98-5 | 3.89 | 18.41 | 4.55 | 4.47 | 4.38 | 4.27 | 4.16 | 4.01 | 3.84 |
| Irgacure 184 | 947-19-3 | 3.42 | 22.90 | 4.40 | 4.30 | 4.17 | 4.01 | 3.85 | 3.68 | 3.54 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| Siloxanes | ||||||||||
| D4 | 556-67-2 | 0.60 | 28.26 | 2.94 | 2.94 | 2.94 | 2.94 | 2.94 | 2.94 | 2.94 |
| D5 | 541-02-6 | 0.86 | 35.16 | 3.26 | 3.26 | 3.26 | 3.26 | 3.26 | 3.26 | 3.26 |
| D6 | 540-97-6 | 0.74 | 42.11 | 3.56 | 3.56 | 3.56 | 3.56 | 3.56 | 3.56 | 3.56 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| Other | ||||||||||
| Acetonitrile | 75-05-8 | 4.06 | 4.34 | 4.39 | 4.28 | 4.17 | 4.05 | 3.96 | 3.86 | 3.77 |
| Ethylamine | 75-04-7 | 1.37 | 5.55 | 2.27 | 2.21 | 2.15 | 2.07 | 2.00 | 1.93 | 1.87 |
| Diethylamine | 109-89-7 | 0.99 | 9.17 | 2.07 | 2.04 | 2.01 | 1.98 | 1.96 | 1.94 | 1.93 |
| Triethylamine | 121-44-8 | 0.68 | 12.56 | 2.15 | 2.14 | 2.07 | 2.07 | 2.07 | 2.07 | 2.07 |
| Dimethyl sulfide | 75-18-3 | 1.68 | 7.27 | 2.56 | 2.50 | 2.43 | 2.33 | 2.25 | 2.17 | 2.10 |
| 1,3-Benzothiazol | 95-16-9 | 1.31 | 15.49 | 2.56 | 2.51 | 2.48 | 2.44 | 2.42 | 2.40 | 2.38 |
| N-Methyl-2-pyrrolidon | 872-50-4 | 4.12 | 10.28 | 4.38 | 4.29 | 4.21 | 4.12 | 4.05 | 3.97 | 3.88 |
| 2-Butanonoxim | 96-29-7 | 1.04 | 9.54 | 2.09 | 2.05 | 2.02 | 1.99 | 1.97 | 1.95 | 1.94 |
| Phenol | 108-95-2 | 1.29 | 10.87 | 2.33 | 2.28 | 2.23 | 2.19 | 2.15 | 2.12 | 2.10 |
However, if one refers to the literature, the question now arises as to how precisely the dipole moment of a molecule is available for the conditions prevailing here and what range has to be expected when calculating the reaction constants. For example, experimental values of 1.84 D55 and 1.87 D56 in the liquid state have been published for n-butyl acetate. Our calculations resulted in a value of μD = 2.06 D. The difference between experiment (liquid phase) and theory (gas phase) is striking but not surprising. Dipole moments in gas phase and liquid phase are hardly comparable. Molecular geometries are impacted by dispersion and solvent interactions and will therefore often look very different in these phases, changing the resulting dipole moments.
Attig et al.57 calculated dipole moments of n-butyl acetate using quantum mechanical methods with 18 different levels of theory. The minima and maxima were 1.97 D and 2.35 D, respectively. However, these values are obtained only for the lowest-lying conformer and are not directly comparable to our thermally averaged results over a conformer ensemble. The computed dipole moment for the lowest-lying conformer in our ensemble is 2.15 D, i.e., very close to the calculated value of Attig et al.57 (2.18 D) using the B3LYP/6-311++G(d,p) level of theory, which is arguably the best of their methods. A more recent benchmark study on the accuracy of dipole moments for DFT calculations41 suggests a root mean square error (RMSE) of about 5% for the here employed method (see Section 2.1) which is quite close to the assumption by Cappellin et al.50 regarding the uncertainty in the quantum chemical calculation for the dipole moment.
Fig. 3 shows the dependence of the kPT values, which were calculated with the three methods presented, on the dipole moment using the example of n-butyl acetate. For comparison with our value of 2.06 D, the experimentally determined dipole moments in cyclohexane55,56 and calculated dipole moments by Attig et al.57 for three assigned conformers were taken. Regardless of the calculation method, the rate constants for this molecule vary by 5–10% when the dipole moments differ by about 10%. However, it should be noted that uncertainties in the polarizability were not considered. For n-butyl acetate, Fig. 3 shows reasonable values for the dependence of kPT on the dipole moment. However, the results must not be generalized, since higher dipole moments have a greater influence on kPT. The differences between the calculation methods are discussed in Section 5.2.
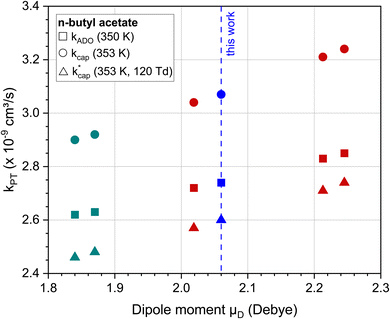 | ||
Fig. 3 Rate constants kADO, kcap and  for the reaction of n-butyl acetate with H3O+ ions as a function of the dipole moment. For all calculations the polarizability was α = 12.13·10−24 cm3. The values of 1.84 D55 and 1.87 D56 (green) are in cyclohexane (note: these data are used for purposes of comparison only); 2.06 D (blue) is this work; 2.02 D, 2.21 D and 2.25 D (red) are calculated data from Attig et al.57 for three assigned conformers. for the reaction of n-butyl acetate with H3O+ ions as a function of the dipole moment. For all calculations the polarizability was α = 12.13·10−24 cm3. The values of 1.84 D55 and 1.87 D56 (green) are in cyclohexane (note: these data are used for purposes of comparison only); 2.06 D (blue) is this work; 2.02 D, 2.21 D and 2.25 D (red) are calculated data from Attig et al.57 for three assigned conformers. | ||
The reliability of theoretical kPT calculations stands and falls not only with the precision of the dipole moment and the polarizability, but it is also important to get the “right” molecule. The question may therefore arise as to which isomer a dipole moment is to be calculated for. A good example is furfural shown in Fig. 4, whose dominant trans isomer at 298.15 K has a calculated dipole moment of 3.60 D, while 4.31 D is given for the cis isomer.58 Moreover, the energy of the trans isomer is 3.1 kJ mol−1 lower than that of the cis isomer.59 A similar case concerns acrolein with the more abundant cis isomer60 (μD(cis) = 2.81 D). The dipole moment of the trans isomer is μD(trans) = 3.43 D. Acrolein was already discussed in a previous publication.61
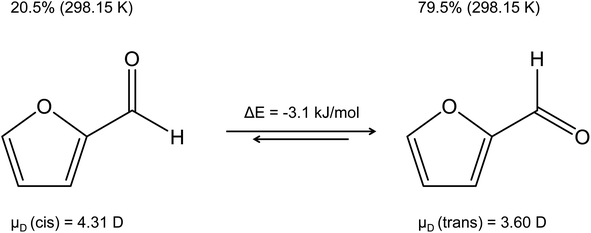 | ||
| Fig. 4 Dipole moments of the cis and trans isomers of furfural in the gas phase,58 percent of each isomer, and the energy difference between the two conformers.59 | ||
5.2 Reaction rate constants
Application of the ion–dipole collision theory is the most common method for determining kPT in PTR-MS and SIFT measurements. It should only be mentioned at this point that other formulas can be used to calculate reaction constants in related techniques such as multiple-ion laminar flow tube spectrometry (MIFT).62,63Zhao and Zhang32 provide kADO values at 300 K for a total of 136 substances. However, Cappellin et al.33 doubt that these data can be used for PTR-MS applications and argue with the electric field strength, which induces far more energetic collisions than those at room temperature. Blake et al.10 point out that the ADO theory tends to result in lower rate constants than experimentally determined kPT values. With reference to Wannier49 it is assumed that the effective temperature for ion–molecule collisions is higher than the temperature in the drift tube. For an ion with a drift velocity in the range of 900 m s−1, the thermal energy accounts for only a small part of the total kinetic energy. The calculation of the kADO data listed in the ESI† was carried out according to Su and Bowers27,28 using their data for the locking parameter C at 350 K,47 a common temperature for PTR-MS measurements. It was already mentioned that Su et al. critically discussed these data in a later publication.48
Ellis and Mayhew31 also state that the ADO theory underestimates experimental kPT values at 300 K, but found good agreement with kcap values calculated according to Su and Chesnavich.29 This is not surprising, because only molecules with small moments of inertia I were included in the comparisons. The molecule with the highest molecular weight was toluene. Nevertheless, Ellis and Mayhew31 come to the reasonable conclusion that the theoretical values are just as reliable as the experimental values and that uncertainties of 20–30% must generally be expected. The kcap values for the 114 target compounds of this work are listed in the ESI† (Appendix D) and were calculated for 353 K according to Su and Chesnavich.29 The parameterizations for determining Kcap(TR) are also listed in the ESI.†
The ion–dipole collision theories used here have already been discussed by several authors,9,10,31,50 but essentially for small molecules. Tsikritea et al.64 state that the ADO theory and the capture theory according to Su and Chesnavich29 are appropriate when the rotational constants of the molecules are high. Calculated kPT of larger molecules relevant for the indoor environment has only rarely been compared with experimental data, but the available results are satisfactory. Strictly speaking, on account of their symmetry, none of the molecules relevant to indoor analysis as well as those listed in Table 3 meet the preconditions of Su and Chesnavich.29 However, assuming the molecules to be linear rotors, the parameterization provided by Su30 is reasonable and the calculation of  should yield reliable results. The calculated values show the expected E/N dependent deviation from kcap (see Fig. 5).
should yield reliable results. The calculated values show the expected E/N dependent deviation from kcap (see Fig. 5).
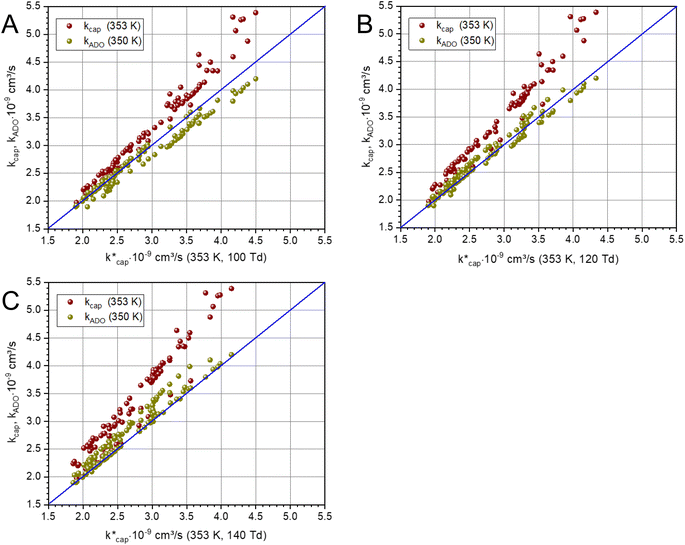 | ||
Fig. 5 Plot of kADO and kcap versus 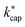 at a temperature of 353 K (350 K for kADO) for E/N values of 100 Td (A), 120 Td (B), and 140 Td (C). The data were taken from Table 3 and from the ESI.† at a temperature of 353 K (350 K for kADO) for E/N values of 100 Td (A), 120 Td (B), and 140 Td (C). The data were taken from Table 3 and from the ESI.† | ||
In general, one must be very careful and critical when comparing calculated and experimentally determined kPT values. The rate constants depend not only on the temperature Td in the reaction chamber, but also on the pressure pd and in particular on the electric field in the drift tube, because these variables have a direct influence on the ion mobility. The advanced capture theory takes these aspects into account. The ion energies KEion required to calculate the 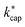 values listed in Table 3 are based on the ion mobilities measured by Dotan et al.43 (see Table 1). The details of the parameterization for calculating
values listed in Table 3 are based on the ion mobilities measured by Dotan et al.43 (see Table 1). The details of the parameterization for calculating 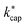 from KC(τ, ε) can be found in the ESI.† In total,
from KC(τ, ε) can be found in the ESI.† In total, 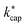 was calculated for seven different E/N values between 80 Td and 140 Td at a temperature of 353 K. The advantages of Su's30 advanced capture theory over ADO theory and the original capture theory were discussed in detail by Cappellin et al.50 Using the example of seven sulfur compounds, it was also shown that the
was calculated for seven different E/N values between 80 Td and 140 Td at a temperature of 353 K. The advantages of Su's30 advanced capture theory over ADO theory and the original capture theory were discussed in detail by Cappellin et al.50 Using the example of seven sulfur compounds, it was also shown that the 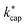 values are larger than the kADO values. In a later work, Cappellin et al.33 measured kPT values at E/N = 120 Td and Td = 363 K for 11 substances that also play a role indoors. Excellent agreement with the calculated
values are larger than the kADO values. In a later work, Cappellin et al.33 measured kPT values at E/N = 120 Td and Td = 363 K for 11 substances that also play a role indoors. Excellent agreement with the calculated 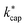 values for these conditions was found. In all cases, the deviations between theory and experiment were less than 10%. Cappellin et al.33 also provide an extensive table of calculated
values for these conditions was found. In all cases, the deviations between theory and experiment were less than 10%. Cappellin et al.33 also provide an extensive table of calculated 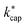 values of organic compounds at 363 K as a function of E/N. Table 3 in this work essentially extends the list of Cappellin et al.33 with a large number of indoor-related compounds. In addition, as already mentioned, the applied quantum mechanical method for calculating dipole moments and polarizabilities is superior to previous approaches.
values of organic compounds at 363 K as a function of E/N. Table 3 in this work essentially extends the list of Cappellin et al.33 with a large number of indoor-related compounds. In addition, as already mentioned, the applied quantum mechanical method for calculating dipole moments and polarizabilities is superior to previous approaches.
As far as our results are concerned, there is the expected good agreement with the data of Cappellin et al.33 The small deviations (≤5%) are due to the different data for dipole moment and polarizability as well as the different temperature (353 K vs. 363 K). The deviations in furfural are due to the fact that Cappellin et al.33 confused the dipole moments for the cis and trans isomer. The rate constants for glyoxal in Cappellin et al.33 are for the trans isomer and in our work for the cis isomer.
Of particular interest is the comparison of the different theories. For this purpose, kADO and kcap are plotted versus 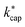 in Fig. 5, for 100 Td, 120 Td and 140 Td, respectively. The blue line represents the 1
in Fig. 5, for 100 Td, 120 Td and 140 Td, respectively. The blue line represents the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. It can be seen that at 100 Td the kADO values are slightly below the
1 ratio. It can be seen that at 100 Td the kADO values are slightly below the 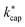 values from about 3.0 × 10−9 cm3 s−1. At 120 Td the agreement between
values from about 3.0 × 10−9 cm3 s−1. At 120 Td the agreement between 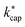 and kADO is excellent, at 140 Td the kADO values deviate slightly upwards. Referring to the values shown in Fig. 5, the highest differences between
and kADO is excellent, at 140 Td the kADO values deviate slightly upwards. Referring to the values shown in Fig. 5, the highest differences between 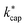 and kADO for 100 Td and 140 Td are in the range of 10%, for 120 Td they are ≤5%. In this respect, for our assumed conditions and substances, we cannot confirm the statement by Ellis and Mayhew31 that ADO theory generally tends to underestimate the rate coefficients.
and kADO for 100 Td and 140 Td are in the range of 10%, for 120 Td they are ≤5%. In this respect, for our assumed conditions and substances, we cannot confirm the statement by Ellis and Mayhew31 that ADO theory generally tends to underestimate the rate coefficients.
A different picture emerges for kcap. In the three cases displayed, the calculated kcap values are well above the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 line and show the expected systematic deviations from
1 line and show the expected systematic deviations from 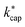 . However, in the case of u0 = constant, both kcap and
. However, in the case of u0 = constant, both kcap and 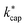 do well agree within ≈±10% in the limit E/N → 0. Hence, the advanced trajectory analysis and its parametrization with a field dependent kinetic energy term has proven to be a sound and reasonable extension of the capture theory. In contrast to kADO, the deviations of kcap to
do well agree within ≈±10% in the limit E/N → 0. Hence, the advanced trajectory analysis and its parametrization with a field dependent kinetic energy term has proven to be a sound and reasonable extension of the capture theory. In contrast to kADO, the deviations of kcap to 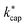 increase with increasing rate constant and E/N. The highest deviations of about 30% occur at 140 Td with strongly polar substances such as acetonitrile, N-methyl-2-pyrrolidone and cis-furfural. In general, it is clear that deviations become more likely with increasing polarity and moment of inertia of the substance. For μD → 0 all theories merge into the Langevin equation. In addition, the capture theory according to Su and Chesnavich29 has methodological weaknesses when applied to larger molecules. In the calculation of the trajectories Chesnavich et al.65 have approximated all molecules as linear rotors irrespective of their effective symmetry. This means at least that the individual moments of inertia of the three mutually perpendicular axes of the molecule are averaged, which is a rough approximation for large molecules.
increase with increasing rate constant and E/N. The highest deviations of about 30% occur at 140 Td with strongly polar substances such as acetonitrile, N-methyl-2-pyrrolidone and cis-furfural. In general, it is clear that deviations become more likely with increasing polarity and moment of inertia of the substance. For μD → 0 all theories merge into the Langevin equation. In addition, the capture theory according to Su and Chesnavich29 has methodological weaknesses when applied to larger molecules. In the calculation of the trajectories Chesnavich et al.65 have approximated all molecules as linear rotors irrespective of their effective symmetry. This means at least that the individual moments of inertia of the three mutually perpendicular axes of the molecule are averaged, which is a rough approximation for large molecules.
6 Conclusion
Proton transfer rate constants, which are necessary for the quantitative determination of airborne organic compounds in PTR-MS measurements, were calculated for 114 indoor air pollutants using ion–dipole collision theory at different levels. It was shown that this requires reliable dipole moments and polarizabilities, which are accessible for the respective ensemble containing the energetically lowest conformers in the gas phase via quantum mechanical calculations. The automation of these methods is necessary in order to be able to process a large number of molecules in a reasonable amount of time. In agreement with earlier work we conclude that the advanced capture theory according to Su30 provides the most reliable rate constants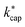 , since the conditions in the PTR-MS reaction chamber are taken into account with the energy of the ions KEion, as is the E/N ratio. However, the ion mobilities in the reaction chamber as a function of E/N are required for the calculation.3,43 For Td = 353 K and E/N = 120 Td, the ADO theory also provides reasonable values.
, since the conditions in the PTR-MS reaction chamber are taken into account with the energy of the ions KEion, as is the E/N ratio. However, the ion mobilities in the reaction chamber as a function of E/N are required for the calculation.3,43 For Td = 353 K and E/N = 120 Td, the ADO theory also provides reasonable values.
After analyzing the available experimental and theoretical data, we also agree with previous estimates that the rate constants can be determined with an accuracy of 10–25%. The uncertainties increase with the size of the molecule and increasing dipole moment. For more precise assessments, round-robin tests with certified gas standards are also required, which are not yet available for PTR-MS measurements.
Author contributions
TS: conceptualization, methodology, investigation, formal analysis, visualization, writing – original draft; UH: methodology, investigation, formal analysis, verification, writing – original draft; MS: methodology, investigation, formal analysis, visualization, software, writing – original draft; SG: investigation, methodology, writing – review & editing.Conflicts of interest
The authors have no conflicts of interest to declare.Acknowledgements
TS is grateful to Dr Jens Herbig (IONICON Analytik GmbH), Dr Erik Uhde (Fraunhofer WKI) and Christian Fauck (Fraunhofer WKI) for providing information on the PTR-MS device. The 3D structure images in Fig. 1 were taken from PubChem (CID: 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600, 6549, 8892, 1549778, 12329) https://pubchem.ncbi.nlm.nih.gov/.
600, 6549, 8892, 1549778, 12329) https://pubchem.ncbi.nlm.nih.gov/.
References
- W. Lindinger, A. Hansel and A. Jordan, On-line monitoring of volatile organic compounds at pptv levels by means of proton-transfer-reaction mass spectrometry (PTR-MS) medical applications, food control and environmental research, Int. J. Mass Spectrom. Ion Processes, 1998, 173, 191–241 CrossRef CAS.
- A. Hansel, A. Jordan, R. Holzinger, P. Prazeller, W. Vogel and W. Lindinger, Proton transfer reaction mass spectrometry: on-line trace gas analysis at the ppb level, Int. J. Mass Spectrom. Ion Processes, 1995, 149–150, 609–619 CrossRef.
- C. Warneke, C. van der Veen, S. Luxembourg, J. de Gouw and A. Kok, Measurements of benzene and toluene in ambient air using proton-transfer-reaction mass spectrometry: calibration, humidity dependence, and field intercomparison, Int. J. Mass Spectrom., 2001, 207, 167–182 CrossRef CAS.
- A. Tani, S. Hayward and C. Hewitt, Measurement of monoterpenes and related compounds by proton transfer reaction-mass spectrometry (PTR-MS), Int. J. Mass Spectrom., 2003, 223–224, 561–578 CrossRef CAS.
- J. de Gouw, C. Warneke, T. Karl, G. Eerdekens, C. van der Veen and R. Fall, Sensitivity and specificity of atmospheric trace gas detection by proton-transfer-reaction mass spectrometry, Int. J. Mass Spectrom., 2003, 223–224, 365–382 CrossRef CAS.
- A. Wisthaler, G. Tamás, D. P. Wyon, P. Strøm-Tejsen, D. Space, J. Beauchamp, A. Hansel, T. D. Märk and C. J. Weschler, Products of ozone-initiated chemistry in a simulated aircraft environment, Environ. Sci. Technol., 2005, 39, 4823–4832 CrossRef CAS PubMed.
- T. Schripp, S. Etienne, C. Fauck, F. Fuhrmann, L. Märk and T. Salthammer, Application of proton-transfer-reaction-mass-spectrometry for indoor air quality research, Indoor Air, 2014, 24, 178–189 CrossRef CAS PubMed.
- D. Smith and P. Španěl, Selected ion flow tube mass spectrometry (SIFT-MS) for on-line trace gas analysis, Mass Spectrom. Rev., 2005, 24, 661–700 CrossRef CAS PubMed.
- J. de Gouw and C. Warneke, Measurements of volatile organic compounds in the earth's atmosphere using proton-transfer-reaction mass spectrometry, Mass Spectrom. Rev., 2007, 26, 223–257 CrossRef CAS PubMed.
- R. S. Blake, P. S. Monks and A. M. Ellis, Proton-transfer reaction mass spectrometry, Chem. Rev., 2009, 109, 861–896 CrossRef CAS PubMed.
- J. Herbig, M. Müller, S. Schallhart, T. Titzmann, M. Graus and A. Hansel, On-line breath analysis with PTR-TOF, J. Breath Res., 2009, 3, 027004 CrossRef PubMed.
- K. Schwarz, W. Filipiak and A. Amann, Determining concentration patterns of volatile compounds in exhaled breath by PTR-MS, J. Breath Res., 2009, 3, 027002 CrossRef CAS PubMed.
- U. Riess, U. Tegtbur, C. Fauck, F. Fuhrmann, D. Markewitz and T. Salthammer, Experimental setup and analytical methods for the non-invasive determination of volatile organic compounds, formaldehyde and NO in exhaled human breath, Anal. Chim. Acta, 2010, 669, 53–62 CrossRef CAS PubMed.
- C. J. Weschler, A. Wisthaler, S. Cowlin, G. Tamás, P. Strøm-Tejsen, A. T. Hodgson, H. Destaillats, J. Herrington, J. J. Zhang and W. W. Nazaroff, Ozone-initiated chemistry in an occupied simulated aircraft cabin, Environ. Sci. Technol., 2007, 41, 6177–6184 CrossRef CAS PubMed.
- A. Wisthaler and C. J. Weschler, Reactions of ozone with human skin lipids: Sources of carbonyls, dicarbonyls, and hydroxycarbonyls in indoor air, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 6568–6575 CrossRef CAS PubMed.
- Y. Liu, P. K. Misztal, C. Arata, C. J. Weschler, W. W. Nazaroff and A. H. Goldstein, Observing ozone chemistry in an occupied residence, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2018140118 CrossRef CAS PubMed.
- J. Mo, Y. Zhang, Q. Xu, Y. Zhu, J. J. Lamson and R. Zhao, Determination and risk assessment of by-products resulting from photocatalytic oxidation of toluene, Appl. Catal., B, 2009, 89, 570–576 CrossRef CAS.
- B. Kolarik, P. Wargocki, A. Skorek-Osikowska and A. Wisthaler, The effect of a photocatalytic air purifier on indoor air quality quantified using different measuring methods, Build. Environ., 2010, 45, 1434–1440 CrossRef.
- D. Pagonis, D. J. Price, L. B. Algrim, D. A. Day, A. V. Handschy, H. Stark, S. L. Miller, J. de Gouw, J. L. Jimenez and P. J. Ziemann, Time-resolved measurements of indoor chemical emissions, deposition, and reactions in a university art museum, Environ. Sci. Technol., 2019, 53, 4794–4802 CrossRef CAS PubMed.
- D. J. Price, D. A. Day, D. Pagonis, H. Stark, A. V. Handschy, L. B. Algrim, S. L. Miller, J. A. de Gouw, P. J. Ziemann and J. L. Jimenez, Sources of Gas-Phase Species in an Art Museum from Comprehensive Real-Time Measurements, ACS Earth Space Chem., 2021, 5, 2252–2267 CrossRef CAS.
- K. Kristensen, D. M. Lunderberg, Y. Liu, P. K. Misztal, Y. Tian, C. Arata, W. W. Nazaroff and A. H. Goldstein, Sources and dynamics of semivolatile organic compounds in a single-family residence in northern California, Indoor Air, 2019, 29, 645–655 CAS.
- Y. Liu, P. K. Misztal, J. Xiong, Y. Tian, C. Arata, R. J. Weber, W. W. Nazaroff and A. H. Goldstein, Characterizing sources and emissions of volatile organic compounds in a northern California residence using space- and time-resolved measurements, Indoor Air, 2019, 29, 630–644 CAS.
- D. M. Lunderberg, P. K. Misztal, Y. Liu, C. Arata, Y. Tian, K. Kristensen, R. J. Weber, W. W. Nazaroff and A. H. Goldstein, High-resolution exposure assessment for volatile organic compounds in two California residences, Environ. Sci. Technol., 2021, 55, 6740–6751 CrossRef CAS PubMed.
- L. B. Algrim, D. Pagonis, J. A. Gouw, J. L. Jimenez and P. J. Ziemann, Measurements and modeling of absorptive partitioning of volatile organic compounds to painted surfaces, Indoor Air, 2020, 30, 745–756 CrossRef CAS PubMed.
- S. D. Maleknia, T. L. Bell and M. A. Adams, PTR-MS analysis of reference and plant-emitted volatile organic compounds, Int. J. Mass Spectrom., 2007, 262, 203–210 CrossRef CAS.
- P. Misztal, M. Heal, E. Nemitz and J. Cape, Development of PTR-MS selectivity for structural isomers: Monoterpenes as a case study, Int. J. Mass Spectrom., 2012, 310, 10–19 CrossRef CAS.
- T. Su and M. T. Bowers, Theory of ion–polar molecule collisions. Comparison with experimental charge transfer reactions of rare gas ions to geometric isomers of difluorobenzene and dichloroethylene, J. Chem. Phys., 1973, 58, 3027–3037 CrossRef.
- T. Su and M. T. Bowers, Ion–Polar molecule collisions: the effect of ion size on ion–polar molecule rate constants; the parameterization of the average-dipole-orientation theory, Int. J. Mass Spectrom. Ion Phys., 1973, 12, 347–356 CrossRef CAS.
- T. Su and W. J. Chesnavich, Parametrization of the ion–polar molecule collision rate constant by trajectory calculations, J. Chem. Phys., 1982, 76, 5183–5185 CrossRef CAS.
- T. Su, Parametrization of kinetic energy dependences of ion–polar molecule collision rate constants by trajectory calculations, J. Chem. Phys., 1994, 100, 4703 CrossRef CAS.
- A. M. Ellis and C. A. Mayhew, Proton Transfer Reaction Mass Spectrometry: Principles and Applications, John Wiley & Sons, Chichester, 2013 Search PubMed.
- J. Zhao and R. Zhang, Proton transfer reaction rate constants between hydronium ion (H3O+) and volatile organic compounds, Atmos. Environ., 2004, 38, 2177–2185 CrossRef CAS.
- L. Cappellin, T. Karl, M. Probst, O. Ismailova, P. M. Winkler, C. Soukoulis, E. Aprea, T. D. Märk, F. Gasperi and F. Biasioli, On quantitative determination of volatile organic compound concentrations using proton transfer reaction time-of-flight mass spectrometry, Environ. Sci. Technol., 2012, 46, 2283–2290 CrossRef CAS PubMed.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Electronic structure calculations on workstation computers: The program system turbomole, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- S. Kim, J. Chen, T. Cheng, A. Gindulyte, J. He, S. He, Q. Li, B. A. Shoemaker, P. A. Thiessen, B. Yu, L. Zaslavsky, J. Zhang and E. E. Bolton, PubChem in 2021: new data content and improved web interfaces, Nucleic Acids Res., 2021, 49, D1388–D1395 CrossRef CAS PubMed.
- P. Pracht, F. Bohle and S. Grimme, Automated exploration of the low-energy chemical space with fast quantum chemical methods, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB – An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- S. Grimme, F. Bohle, A. Hansen, P. Pracht, S. Spicher and M. Stahn, Efficient quantum chemical calculation of structure ensembles and free energies for nonrigid molecules, J. Phys. Chem. A, 2021, 125, 4039–4054 CrossRef CAS PubMed.
- S. Grimme, A. Hansen, S. Ehlert and J.-M. Mewes, r2SCAN-3c: A “Swiss army knife” composite electronic-structure method, J. Chem. Phys., 2021, 154, 064103 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, ωb97X-V: A 10-parameter, range-separated hybrid, generalized gradient approximation density functional with nonlocal correlation, designed by a survival-of-the-fittest strategy, Phys. Chem. Chem. Phys., 2014, 16, 9904–9924 RSC.
- D. Hait and M. Head-Gordon, How accurate is density functional theory at predicting dipole moments? An assessment using a new database of 200 benchmark values, J. Chem. Theory Comput., 2018, 14, 1969–1981 CrossRef CAS PubMed.
- E. P. L. Hunter and S. G. Lias, Evaluated gas phase basicities and proton affinities of molecules: an update, J. Phys. Chem. Ref. Data, 1998, 27, 413–656 CrossRef CAS.
- I. Dotan, D. L. Albritton, W. Lindinger and M. Pahl, Mobilities of CO2+, N2H+, H3O+, H3O+H2O and H3O+(H2O)2 ions in N2, J. Chem. Phys., 1976, 65, 5028–5030 CrossRef CAS.
- D. K. Bohme, G. I. Mackay and S. D. Tanner, An experimental study of the gas-phase kinetics of reactions with hydrated H3O+ ions (n = 1–3) at 298 K, J. Am. Chem. Soc., 1979, 101, 3724–3730 CrossRef CAS.
- A. Tani, Fragmentation and reaction rate constants of terpenoids determined by proton transfer reaction–mass spectrometry, Environ. Control Biol., 2013, 51, 23–29 CrossRef CAS.
- D. Pagonis, K. Sekimoto and J. de Gouw, A library of proton-transfer reactions of H3O+ ions used for trace gas detection, J. Am. Soc. Mass Spectrom., 2019, 30, 1330–1335 CrossRef CAS PubMed.
- T. Su and M. T. Bowers, Parameterization of the average dipole orientation theory: temperature dependence, Int. J. Mass Spectrom. Ion Phys., 1975, 17, 211–212 CrossRef CAS.
- T. Su, E. C. F. Su and M. T. Bowers, Ion–polar molecule collisions. Conservation of angular momentum in the average dipole orientation theory. The AADO theory, J. Chem. Phys., 1978, 69, 2243–2250 CrossRef CAS.
- G. H. Wannier, On the motion of gaseous ions in a strong electric field, Phys. Rev., 1951, 83, 281–289 CrossRef CAS.
- L. Cappellin, M. Probst, J. Limtrakul, F. Biasioli, E. Schuhfried, C. Soukoulis, T. D. Märk and F. Gasperi, Proton transfer reaction rate coefficients between H3O+ and some sulphur compounds, Int. J. Mass Spectrom., 2010, 295, 43–48 CrossRef CAS.
- P. W. Atkins, J. Paula and J. Keeler, Physical Chemistry, Oxford University Press, Oxford, 2018 Search PubMed.
- T. P. Iglesias, Â. F. S. Santos, F. J. V. Santos, M. L. C. J. Moita, I. M. S. Lampreia and J. C. R. Reis, Dipole moments of isomeric alkoxyalcohols in cyclohexane. Comparison of Hedestrand and Fröhlich procedures with a new formula, Phys. Chem. Chem. Phys., 2012, 14, 16400 RSC.
- A. Ghanadzadeh, H. Ghanadzadeh, R. Sariri and L. Ebrahimi, Dielectric study of molecular association in the binary mixtures (2-ethyl-1-hexanol+alcohol) and (cyclohexane+alcohol) at 298.2 K, J. Chem. Thermodyn., 2005, 37, 357–362 CrossRef CAS.
- R. D. Nelson, D. R. Lide and A. A. Maryott, Selected values of electric dipole moments for molecules in the gas phase, National Bureau of Standards: Washington D.C., 1967 Search PubMed.
- C. L. Yaws and P. K. Narasimhan, Dipole moment—Organic compounds, in Thermophysical Properties of Chemicals and Hydrocarbons, ed. C. L. Yaws, William Andrew Publishing, Norwich, NY, 2009, pp. 672–682 Search PubMed.
- J. R. Rumble, T. J. Bruno and M. J. Doa, Handbook of Chemistry and Physics, CRC Press, Boca Raton, 101st edn, 2020 Search PubMed.
- T. Attig, L. Sutikdja, R. Kannengießer, I. Kleiner and W. Stahl, The microwave spectrum of n-butyl acetate, J. Mol. Spectrosc., 2013, 284–285, 8–15 CrossRef CAS.
- K. K. Baldridge, V. Jonas and A. D. Bain, Ground state gas and solution phase conformational dynamics of polar processes: Furfural systems, J. Chem. Phys., 2000, 113, 7519–7529 CrossRef CAS.
- H. Ashish and P. Ramasami, Rotational barrier and thermodynamical parameters of furfural, thiofurfural, and selenofurfural in the gas and solution phases: theoretical study based on density functional theory method, Mol. Phys., 2008, 106, 175–185 CrossRef CAS.
- C. E. Blom, G. Grassi and A. Bauder, Molecular structure of s-cis- and s-trans-acrolein determined by microwave spectroscopy, J. Am. Chem. Soc., 1984, 106, 7427–7431 CrossRef CAS.
- A. Schieweck, E. Uhde and T. Salthammer, Determination of acrolein in ambient air and in the atmosphere of environmental test chambers, Environ. Sci.: Processes Impacts, 2021, 23, 1729–1746 RSC.
- B. Huang, H. Wu, M. Yang and Z. Luo, An integrated instrument of a tandem quadrupole mass spectrometer for cluster reaction and soft-landing deposition, Rev. Sci. Instrum., 2022, 93, 113307 CrossRef CAS PubMed.
- B. Huang, W. Gan, K. Hansen and Z. Luo, What determines the drastic reactivity of Nbn+ clusters with nitric oxide under thermalized conditions?, J. Phys. Chem. A, 2022, 126, 4801–4809 CrossRef CAS PubMed.
- A. Tsikritea, J. A. Diprose, T. P. Softley and B. R. Heazlewood, Capture theory models: An overview of their development, experimental verification, and applications to ion–molecule reactions, J. Chem. Phys., 2022, 157, 060901 CrossRef CAS PubMed.
- W. J. Chesnavich, T. Su and M. T. Bowers, Collisions in a noncentral field: A variational and trajectory investigation of ion–dipole capture, J. Chem. Phys., 1980, 72, 2641–2655 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra01705b |
| This journal is © The Royal Society of Chemistry 2023 |