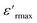Open Access Article
Open Access ArticleEffect of lithium doping on the structural, conduction mechanism and dielectric property of MnNbO4
Samia Aydia,
Souad Chkoundalia,
Abderrazek Oueslati b and
Abdelhedi Aydi
b and
Abdelhedi Aydi *a
*a
aLaboratory of Multifunctional Materials and Applications (LaMMA), LR16ES18, Faculty of Sciences, University of Sfax, B. P. 1171, 3000 Sfax, Tunisia. E-mail: aydi_abdelhedi@yahoo.fr
bLaboratory of Spectroscopic and Optical Characterization of Materials (LaSCOM), Faculty of Sciences, University of Sfax, B. P. 1171, 3000 Sfax, Tunisia
First published on 4th July 2023
Abstract
The development of multifunctional materials is an exceptional research area, which is aimed at enhancing the versatility of materials according to their wide fields of application. Special interest was devoted here to lithium (Li)-doped orthoniobate ANbO4 (A = Mn), in particular, the new material Li0.08Mn0.92NbO4. This compound was successfully synthesized by a solid-state method and characterized using various techniques, including X-ray diffraction (XRD), which confirmed the successful formation of an ABO4 oxide with an orthorhombic structure and the Pmmm space group. The morphology and elemental composition were analyzed by scanning electron microscopy (SEM) and energy dispersive X-ray spectroscopy (EDX). The vibrational study (Raman) at room temperature confirmed the existence of the NbO4 functional group. The effects of frequency and temperature on the electrical and dielectric properties were studied using impedance spectroscopy. In addition, the diminishing of the radius of semicircular arcs in the Nyquist plots (–Z′′ vs. Z′) showed the semiconductor behavior of the material. The electrical conductivity followed Jonscher's power law and the conduction mechanisms were identified. The electrical investigations showed the dominant transport mechanisms in the different frequency and temperature ranges, proposing the correlated barrier hopping (CBH) model in the ferroelectric phase and the paraelectric phase. The temperature dependence in the dielectric study revealed the relaxor ferroelectric nature of Li0.08Mn0.92NbO4, which correlated the frequency–dispersive dielectric spectra with the conduction mechanisms and their relaxation processes. The results demonstrate that Li-doped Li0.08Mn0.92NbO4 could be used both in dielectric and electrical applications.
1. Introduction
Multifunctional ceramics represent an important class of advanced materials owing to their stability, low cost, low toxicity, useful photophysical properties and wide range of technological applications.1 They also display interesting electrical, magnetic, optical, thermal, and other properties and consequently have become a hotspot for research in modern materials science.2 The performance of ceramic materials depends on their structure, microstructure, and high-temperature properties. Many ceramic materials, e.g., ABO4 (fergusonites, scheelites, and wolframites),3 ABO3 (perovskites),4 and AB2O4 (spinels),5 undergo structural phase transitions. Since the structural phase transitions are important phenomena when it comes to the analysis of the materials properties, structural studies need to be carried out.6Among the ceramics, ternary ABO4 oxides have attracted considerable interest in both fundamental and applied research.7 One of the most interesting groups is formed by scheelite-type compounds.8 Such structures are closely and simply related via their crystallographic operations9 because of their compositional diversity and structural simplicity. The crystal structure of scheelites consists of a framework of edge-sharing AO8 polyhedra connected to isolated BO4 tetrahedra via corner-sharing. There are two groups of four A–O distances in scheelites. All four B–O distances are equal; however, the tetrahedron is somewhat distorted as shown by two sets of three O–B–O angles being significantly smaller or larger than the ideal tetrahedral bond angle. Scheelites are related to fergusonite (standard space group C2/c, while the non-standard space groups I2/a or I2/c are often used for comparison with scheelites) via small cation displacements and more significant changes in the anion positions.10–12
Among these, orthoniobates with the formula ANbO4 (where A is a trivalent cation) are receiving increasing attention from researchers due to their technologically important properties; for instance, low thermal conductivity, high-temperature ionic conductivity, magnetic nature, and chemical and radiation stability.13 They can be also used as laser-host materials, photocatalysts, and microwave dielectric materials.14 Among the elements of this family, MnNbO4 presents good mechanical behavior and dielectric properties.15 All these properties make MnNbO4 an interesting material for several technological applications, but it remains necessary to improve the conductivity of MnNbO4 to employ this material in commercial applications, which can be obtained through modifications in the lattice.16
The doping process is widely used in materials science to improve or provide a new characteristic to a material using an appropriate dopant, and this can be obtained without great changes in the lattice of the host material when the dopant has a charge and ionic radius close to the ion that will be replaced.17 Many studies have demonstrated that the insertion of dopants into the A-site influences the structural and electrical properties of orthoniobates, whereas introducing metal ions into this site is mainly employed to study new technological properties.18
For the manufacture of materials with a scheelite structure, several synthetic approaches have been developed to prepare spinel ferrite nanoparticles, including sol–gel,19 hydrothermal,20 novel combustion,21 auto-combustion,22 and the solid-state reaction route.23 However, the majority of these synthesis methods are economically impracticable for large-scale production. Hence, the solid-state reaction has attracted much attention from the scientific community and has proven its effectiveness over several years due to its simplicity, high crystallinity, homogeneity of the product, and its low cost compared with other synthesis methods.24 Also, it was successfully developed for the preparation of Li0.08Mn0.92NbO4. In this article, the main objective of our research work was to study the doping effect of MnNbO4 with the Li element on the Mn site and to discuss the results of the structural, dielectric, and electrical studies of Li0.08Mn0.92NbO4, belonging to the group of ABO4 oxides. Particular effort was devoted to studying Li0.08Mn0.92NbO4 as a new material.
2. Experimental section
The new sample with the formula Li0.08Mn0.92NbO4 was synthesized using the conventional solid-state method, with the aim of obtaining a sample sufficiently homogenous and well crystallized with exceptional and reasonable final properties.Stoichiometric amounts of dried Li2CO3, MnO, and Nb2O5 with a purity of not less than 99% were used. In the first stage, the starting precursors were weighed. In the next step, the mixed powder was ground neatly in an agate mortar for 2 h to reduce the size of the grains. The powder was then pulverized and pressed into pellets with a diameter of 13 mm and a thickness of 1 mm, under a pressure of 5 tons per cm2. Then, the resulting mixture was calcinated at 700 °C for 4 h in order to eliminate the volatile compounds (CO2). Once the reaction was completed, the obtained powder was ground for 1 h and pressed into a circular disc shape 8 mm in diameter and 1 mm in thickness. To obtain a high-density ceramic and a perfect crystallization, the pellet was sintered at 800 °C for 1 h in an electric muffle furnace and slowly cooled to room temperature. After the preparation was complete, we placed the resulting compound in a desiccator to prevent it from reacting with moisture. Before performing any analysis at room temperature, we heated the sample for at least 8 h at a temperature of 200 °C to ensure the pure and dry chemical formula of the studied compound.
In order to identify the crystal phase formation of our material, we used X-ray diffraction (XRD) patterns, which were recorded on a Bruker D8 powder X-ray diffractometer using Cu (Ka) radiation (λ = 1.5406 Å) with a step size of 0.02° for 13.5 s over a 2 h range from 13° to 70°. The data were fitted using the FullProf software with the Rietveld powder diffraction profile fitting technique.25 The morphological study was carried out by scanning electron microscopy (SEM, Merlin) to identify the morphological characteristics of the synthesized material. A qualitative study of the chemical composition of our material was carried out by energy dispersive X-ray spectrometry (EDX) to confirm the presence in a stoichiometric quantity of all the chemical elements of the sample.
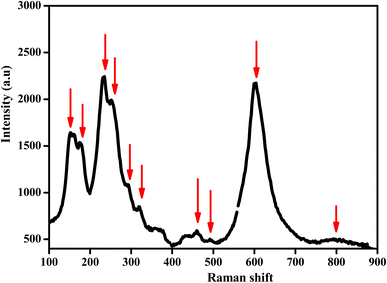
Raman spectroscopy was performed, with the spectra recorded at room temperature in the wavenumber range of 100–1000 cm−1 using a Renishaw Invia Reflex spectrometer.
Electrical measurements were performed over a wide range of frequencies at various temperatures using a using 1260 Solartron impedance analyzer. To obtain good contact, the pellet was coated with thin gold films on both flat faces and then placed between two copper electrodes. These measurements were performed on a cylindrical pellet characterized by a diameter of 8 mm and a thickness of 1.1 mm by installing silver electrodes as contacts on both sides and then mounting in a temperature control system.
3. Results and discussion
3.1. Structural study
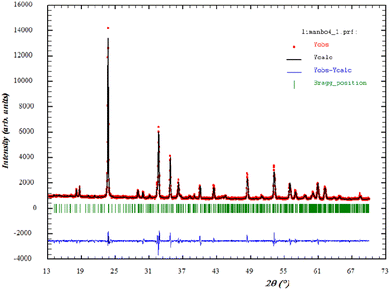
In order to verify the purity of the synthesized sample, powder X-ray diffraction (XRD) patterns were recorded at room temperature (Fig. 1) In addition, the diffractogram showed the Bragg peaks could be successfully indexed and showed the presence of a single phase. This confirmed the superior purity of the prepared sample. Consequently, data Rietveld refinement was successfully performed using an orthorhombic phase (JCPDS Card No. 80-1976) as the initial crystal structure model. The cell parameters and the Rietveld refinement results are shown in Table 1. These values are higher than those given in the literature, which was attributed to the higher ionic radius of Mn compared to that of Li.26 Moreover, the XRD analysis showed that Li-doping stabilized the orthorhombic structure. The influence of Li-doping on the structure of MnNbO4 was in a good agreement with previous studies. These results were also consistent with a phase diagram describing the structure of ABO4 compounds as related to the ionic radii ratios of the cations and the anion.27 The quality factor indicated the concurrence between the observed and the calculated profiles χ2.| Formula | Li0.08 Mn0.92NbO4 at room temperature |
| Crystalline system | Orthorhombic |
| Space group | Pmmm |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Lattice parameter (Å) | |
| a = | 19.809 |
| b = | 16.142 |
| c = | 6.147 |
| α = β = δ (°) | 90 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Reliability factors (%) | |
| Rp (%)/Rwp (%)/Rexp (%) | 10.67/26.1/20.7 |
| χ2 | 3.71 |
By analogy to the similar peaks observed in the powder XRD patterns of a similar orthoniobate-doped compound in the literature,28 the XRD data obtained at room temperature confirmed that Li0.08Mn0.92NbO4 occurred as a scheelite-type phase.29
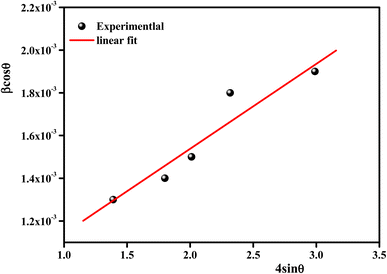
According to the XRD results, the average crystallite size D and the constraint ε of the Li0.08Mn0.92NbO4 sample could be estimated using the Williamson–Hall (W–H) approach:30
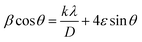 | (1) |
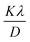 represents the enlargement due to the crystallite size and 4ε
represents the enlargement due to the crystallite size and 4ε![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ represents the enlargement due to the distortion of the crystal lattice. The linear plot of β
θ represents the enlargement due to the distortion of the crystal lattice. The linear plot of β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ versus 4
θ versus 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ yields the intercept as the crystallite size and the slope as the strain, as shown in Fig. 2. The observed positive slope confirmed the tensile strain experienced in the smaller sized grain. The values of D and ε were calculated from the y-intercept and slope of the fitted line, respectively. Moreover, the found values were D = 64 nm and ε = 1.28 × 10−3. These values of lattice distortion were comparable with those previously reported for the ABO4 structure.31
θ yields the intercept as the crystallite size and the slope as the strain, as shown in Fig. 2. The observed positive slope confirmed the tensile strain experienced in the smaller sized grain. The values of D and ε were calculated from the y-intercept and slope of the fitted line, respectively. Moreover, the found values were D = 64 nm and ε = 1.28 × 10−3. These values of lattice distortion were comparable with those previously reported for the ABO4 structure.31
3.2. Morphological study
Fig. 3(a) and (b) display the SEM images of the particle-size distribution of the title compound. It could be clearly been seen that the grains were dense and homogeneously distributed over the entire sample. Similar microstructures were reported for Ca-, Sr-, and Ba-doped LaNbO4.32–35 By comparing the average size of the crystallites obtained from XRD and the particle size of the SEM analysis, we can deduce that every grain was almost monocrystalline, which confirmed the nanometric size of our sample. | ||
| Fig. 3 SEM image of the Li0.08Mn0.92NbO4 compound at scale 5 μm size (a). SEM image of the Li0.08Mn0.92NbO4 compound at scale 50 μm size (b). | ||
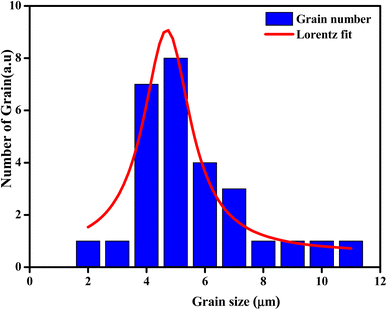
The average grain size of the particles (DSEM) was deduced by fitting the histogram (Fig. 4) by employing the image analyzer software Image J. DSEM was about 4.68 μm. This means that the grains had a polycrystalline structure, compared with the low crystallite size obtained from the XRD study. To check their size, the particle-size distribution was fitted by the Lorentz function, and the median grain size was found to be in the range of 5 μm.
3.3. Chemical analysis
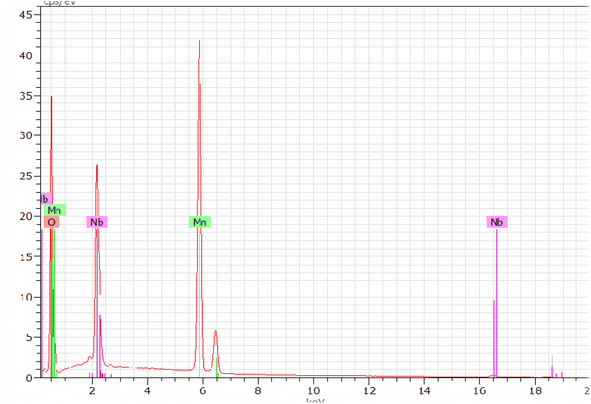
Fig. 5 shows the characteristic peaks of the constituent elements, namely manganese (Mn), niobium (Nb), and oxygen (O), without any impurity. Nevertheless, the small atomic number (Z) of lithium element, which was less than the sensitivity of EDX to the element's atomic number, could explain their invisibility in the spectrum.36 It was highlighted that all the elements were approximately uniformly distributed at the micrometer scale in the sample, and the small differences could be ascribed to the different crystallographic orientations. The proportions of the constituents obtained as an atomic percentage are given in Tables 2 and 3. The EDX results indicated that the preparation had good stoichiometries property and denoted that the compositions of the experimental sample were similar to the theoretical compositions. Consequently, the EDX results indicated that the preparation displayed an interesting surface morphology of the sample.| Elemen | Series | unn. | C norm. | C atom | C error (3 sigma) |
|---|---|---|---|---|---|
| [wt%] | [wt%] | [at%] | [wt%] | ||
| Oxygen | K-series | 47.59 | 47.97 | 78.64 | 15.45 |
| Manganese | K-series | 33.92 | 34.18 | 16.32 | 2.71 |
| Niobium | L-series | 17.71 | 17.85 | 5.04 | 2.05 |
| Total | 99.22 | 100.00 | 100.00 | ||
| Li0.08Mn0.92NbO4−δ 100% Atomic | ||
|---|---|---|
| Theoretical values | Experimental values (EDX) | |
| Li | 14.31 | — |
| Nb | 4.31 | 5.04 |
| Mn | 13.98 | 16.32 |
| O | 67.40 | 78.64 |
3.4. Raman spectroscopy
Vibrational study by Raman spectroscopy is very useful to confirm the presence of the NbO4 group. The Raman spectrum was collected at room temperature in the spectral range of 100 to 900 cm−1 and is presented in Fig. 6. Group theory analysis predicted a total number of 12 modes. In this case, the reported Raman modes were consistent with the modes we detected at 150, 175, 234, 260, 295, 320, 374, 464, 600, and 795 cm−1, which agreed with the literature data reported for similar doped orthoniobates.37–41 The low-frequency mode at ≤ 200 cm−1 is an unexpected mode always observed in this material, which could be Raman active due to the cationic disorder that induced a breakdown of the translation symmetry.42 This mode is tentatively related to the stretching mode of Li in the octahedral coordination.43 The other modes corresponded to the allowed Raman active modes. In particular, the Raman bands located at about 234 and 260 cm−1 were the symmetric Mn–O stretching vibrations of MnO4 groups.44 The Raman peaks at 374 and 600 cm−1 were assigned to Nb–O anti-symmetric and symmetric modes of the NbO4 tetrahedral structure, respectively.45 Previous to our study, only the strong mode (at 600 cm−1 in our experiment) was detected in synthetic Li0.08Mn0.92NbO4−δ. In previous experiments, a weak mode was observed at 850 cm−1,46 which was not observed in our experiments. The Raman peaks observed at 260, 374, and 600 cm−1 represented the absence of any impurity phase, agreeing with the XRD study.47–49These modes of Raman data confirmed the ABO4 structure with a similar space gathering of samples with the addition of Li ions.
3.5. Impedance spectroscopy
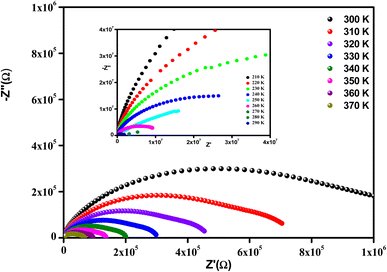
It is clear that the radii of the corresponding semicircular arcs decreased with the increasing temperature (Fig. 7), which revealed that the resistance of the sample decreased with temperature and that conductivity is a thermally activated process. In fact, this resulted in a significant increase in continuous conduction.51
All the spectra were modeled by the same equivalent circuit formed by a series of two parallel combinations (R1//CPE1) and (R2//CPE2) to characterize, respectively, the grains and grain boundaries effects. Fig. 8 shows the good conformity between the experimental data of impedance at 300 K and the theoretical ones obtained using the proposed equivalent circuit.
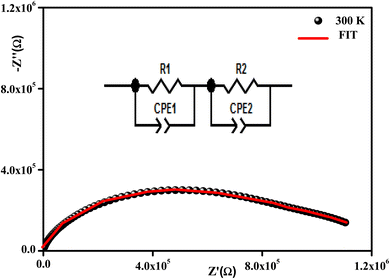 | ||
| Fig. 8 Complex impedance spectra in the Nyquist plane with an electrical equivalent circuit (inset) at 380 K. | ||
The following relation gives the constant phase element (CPE) impedance (ZCPE):52
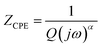 | (2) |
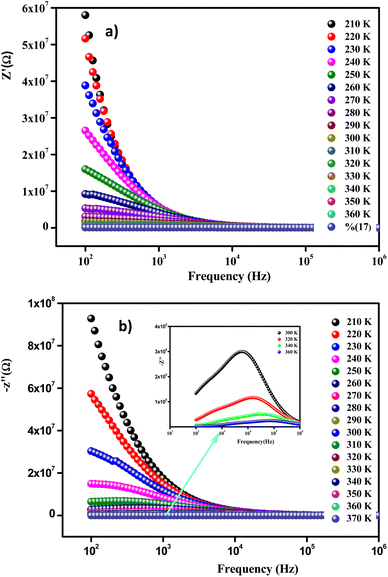
Fig. 9(a) displays the variation versus frequency of the real part of the impedance (Z′) at several temperatures of the Li0.08Mn0.92NbO4 compound studied. The amplitude of (Z′) was typically greater at low frequencies and gradually decreased with increasing frequency, indicating the increase in conductivity of the material.53 On the other hand and in relation to the insertion of Li, this decrease could be observed, demonstrating that doping led to a decrease in the resistive character of Li0.08Mn0.92NbO4.54
At high frequencies (f > 104Hz), the spectra merged and became stable. This behavior is related to the liberation of a space charge. Therefore, the latter resulted in the reduction of the charge barrier of the studied compound. This behavior, consistent with ABO4 materials, can be explained by the space charge, which occurs when the potential barrier of a material has been reduced due to the increase in temperature. Hence, a possible improvement in the conductivity of the material with temperature at high frequencies could be strongly expected and is consistent with the results.55
Fig. 9(b) illustrates the variation of the imaginary part of the impedance (−Z′′) with frequency at different temperatures. For the sample studied, we can use this to understand the frequency-dependent behavior of the charge carriers and the relaxation process. The appearance of a peak in the imaginary part of the impedance (−Z′′) indicates the presence of relaxation in the material. Added to that, the relaxation process may be due to the presence of immobile species at low temperatures and defects at higher ones.56 It should also be noted that as the temperature increases, the maximum peaks moved toward the high-frequency region, indicating a decrease in the resistance of the sample.
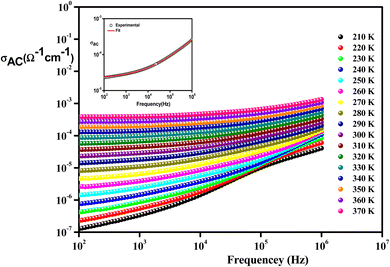 | ||
| Fig. 10 Frequency variation of conductivity at selected temperatures of Li0.08Mn0.92NbO4 compound. The inset is s typical example at 300 K. | ||
From these curves, we could detect two distinct regions. At lower frequencies (102–104 Hz), the conductivity spectra displayed nearly constant values (σdc), because the random distribution of the charges carriers gave rise to frequency-independent conductivity. It was clear that dc conductivity was thermally activated, which can display a semiconductor behavior, by the leap of the localized load carrier, where the holes jumped between Mn2+ and Mn3+ cations and the electrons hopped between Nb2+ and Nb5+ ions.57 The semiconductor nature indicated that this compound may be promising in certain applications, such as optoelectronics, photodetectors, and photovoltaics.58 At higher frequencies (>104 Hz), the conductivity increased with increasing frequency. This can be explained by the important contribution of the charge carrier and the jumping mechanism. This region was attributed to the alternating conductivity (σac). This behavior conformed to Jonscher's universal power law, expressed as follows:59
| σac = σdc + AωS | (3) |
For comparison, the insertion of doping ions on the orthoniobate resulted in increased conductivity (Table 4) due to the generation of oxygen vacancies and other charge carriers originating from a change in the oxidation states of the doped material.60,61
In the literature, different conduction models have been reported. These different theoretical models include quantum mechanical tunneling (QMT),62 correlated barrier hopping (CBH),63 non-overlapping small polaron tunneling (NSPT),64 and the overlapping large polaron tunneling (OLPT) model.65
These models have been proposed to correlate the conduction mechanism of ac conductivity with the power exponent “s” behavior as a function of temperature.
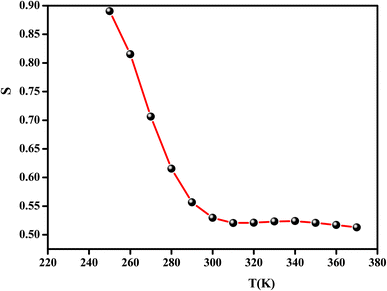
According to the CBH model, the value of the exponent (s) decreases with the increase in temperature. This is in good agreement with the obtained result for the studied compound, as shown in Fig. 11.
For the CBH model, the exponent s is given by:66
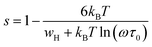 | (4) |
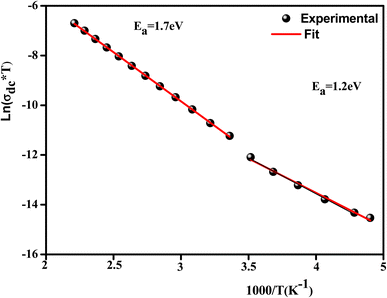
Fig. 12 illustrates the logarithmic variation of the conductivity ln(σdc × T) versus the inverse of the temperature. This curve can be described according to the Arrhenius relation:67
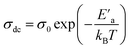 | (5) |
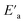 is the minimum amount of energy to activate a process, and KB is the Boltzmann constant.
is the minimum amount of energy to activate a process, and KB is the Boltzmann constant.
A change in the slope of the dc conductivity curve was observed around T = 300 K. The activation energies calculated (least squares linear regressions) from the linear temperature dependence of the conductivity in regions I and II were Ea (I) = 1.12 eV and Ea (II) = 1.7 eV, respectively. These values are comparable to those found for other oxide semiconductor compounds.68
 | ||
Fig. 13 Real (a) and imaginary (b) parts of the permittivity vs. temperature at selected frequencies and (c) 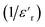 , as a function of temperature at a fixed frequency of 10 , as a function of temperature at a fixed frequency of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz. 000 Hz. | ||
It was clearly observed that the dielectric parameters (ε′) below 240 K were independent of temperature. Also, up to 240 K, the dielectric permittivity gradually increased as the temperature rose. This behavior can be explained by orientational polarization, where the dipoles align themselves along the electric field direction and fully contribute to the total polarization.69 When the temperature was raised above 240 K, the permittivity began to increase abnormally. Due to the ferroelectric–paraelectric transition, the fluctuation of the dielectric constant as a function of temperature showed the existence of a peak at a specific temperature (Tmax), thus confirming that the dielectric constant had a relaxor thermal evolution. The relaxor behavior was caused by temperature effects on Nb5+ ions, which resulted in a substantial shift in the electric dipole moment related to polarization. Similar observations have been reported for other ceramics.70
Moreover, the values of ε′ for the doped system demonstrated higher values than for MnNbO4, which could be justified because Li ions present smaller ionic radii than Mn, thereby enhancing the polarizability effect on the NbO4 tetrahedral groups and consequently increasing the polarization in the doped materials.71 In comparison with another orthoniobate, we noticed that the insertion of the dopant ions caused an increase in the permittivity of the orthoniobate ceramic (Table 4) due to the enhancement of the polarization in the doped materials.72,73
In addition, the curve of the imaginary part ε′′ (Fig. 13(b)) revealed that the values of ε′′ were almost constant for T < 280 K. This behavior can be interpreted by the halting of the atomic motion, induced by the low thermal energy of the charge carriers, leaving them unable to follow the direction of the electric field. However, above 280 K, the values of ε′′ started to increase with the increase in temperature, indicating that the charge carriers had gained sufficient thermal energy to follow the direction of the electric field.74
The broadened peak that appeared in the real part ε′ indicated that the transition was of the diffuse type, which is an important feature of a disordered compound. Fig. 13(c) presents the plot of 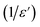 as a function of temperature at a fixed frequency of 10
as a function of temperature at a fixed frequency of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz. The latter appears as a straight line just above the temperature of the phase transition.
000 Hz. The latter appears as a straight line just above the temperature of the phase transition.
Permittivity measurements were performed to investigate the dielectric properties of the prepared sample. The complex dielectric permittivity can be expressed according to Mott's theory by the following equation:75
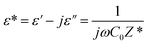 | (6) |
Fig. 14(a) and (b) show the frequency and temperature dependence of the real and imaginary parts of the dielectric permittivity of Li0.08Mn0.92NbO4 compound. It can be noted that ε′ decreased with increasing frequency and temperature; this result indicated a strong dielectric dispersion. Indeed, the high value of ε′ at low frequencies was mainly linked to the contribution of electronic and ionic charges, which are generally accompanied by the appearance of dielectric relaxation. Therefore, the dielectric dispersion observed in the low-frequency region was attributed to interfacial polarization, since the electronic and atomic polarizations remained unchanged in this frequency range.76 The experimental data of the dielectric constant (ε′) was fitted using the modified Debye function given by the following expression:77
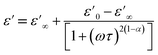 | (7) |
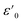 is the dielectric constant at low frequency, and
is the dielectric constant at low frequency, and 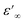 is the dielectric constant at high frequency.
is the dielectric constant at high frequency.
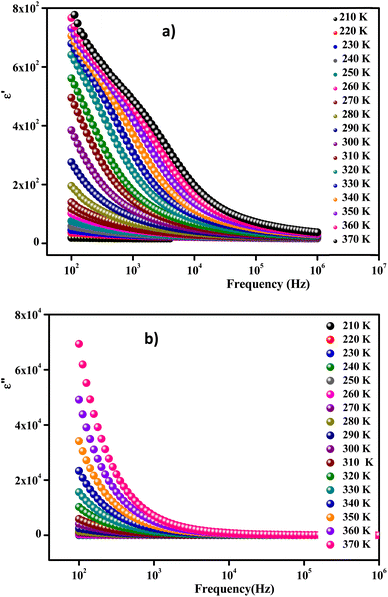 | ||
| Fig. 14 Frequency-dependent real part ε′ (a) and imaginary part ε′′ of the dielectric constant measured at different temperatures (b). | ||
Fig. 14(b) exhibits the variation of the imaginary part (ε′′) of the complex permittivity versus the frequency at different temperatures for the compound. It is clear that ε′′ presented high values in the low-frequency region and decreased rapidly with increasing frequency within the presence of any relaxation peak. This feature is indicative of a non-Debye behavior. In this context, these results suggest that the sample can be used in various technological applications, including fuel cells, ceramic technology, and microwave technology.78
The analyses of the electrical modulus provide insights into the electrode polarization and relaxation times of the conductivity as a function of frequency and temperature. The complex electric modulus M* is represented by:79
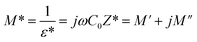 | (8) |
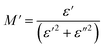 | (9) |
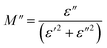 | (10) |
To gain insights into the dielectric relaxation procedure in Li0.08Mn0.92NbO4 compound, the detailed complex modulus (M* = M′ + jM′′) spectra were studied. Fig. 15 shows the behavior of the real part of the modulus (M′) versus frequency and temperature. In the low-frequency region, it was observed that the M′ values were very small for the sample. This confirmed that the polarization of the electrode had a negligible contribution on the materials. With increasing frequency, a continuous increase in M′ values was observed, and the values tended to saturate at an asymptotic maximum value in the high-frequency region. This could be due to the short-range mobility of the charge carriers.80
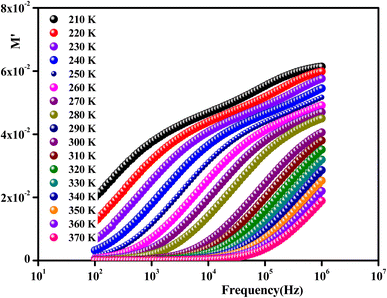 | ||
| Fig. 15 Frequency dependence of the real part of the complex modulus as a function of temperature for Li0.08Mn0.92NbO4. | ||
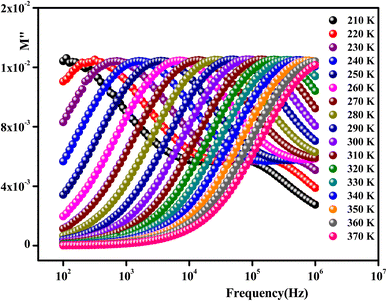
The imaginary part of the electric modulus M′′ as a function of frequencies in the studied temperature range is reported in Fig. 16. It was observed that the peak maximum  was shifted to higher frequencies with increasing temperature. These spectra revealed the presence of a single peak only, confirming the studied material's single relaxation phenomenon. These findings were in good agreement with those of the Nyquist plots. The observed peaks were slightly asymmetric at each temperature, and they were rather wider than the Debye peaks.81 The enlargement indicated the spread of relaxation with different meantime constants, confirming the non-Debye relaxation of the Li0.08Mn0.92NbO4. In addition, with the increase in temperature, the position of the peaks marked a shift toward higher frequencies. These observations were confirmed by the analysis of the single peak characteristic using the Bergman equation, which can be stated as follows:82
was shifted to higher frequencies with increasing temperature. These spectra revealed the presence of a single peak only, confirming the studied material's single relaxation phenomenon. These findings were in good agreement with those of the Nyquist plots. The observed peaks were slightly asymmetric at each temperature, and they were rather wider than the Debye peaks.81 The enlargement indicated the spread of relaxation with different meantime constants, confirming the non-Debye relaxation of the Li0.08Mn0.92NbO4. In addition, with the increase in temperature, the position of the peaks marked a shift toward higher frequencies. These observations were confirmed by the analysis of the single peak characteristic using the Bergman equation, which can be stated as follows:82
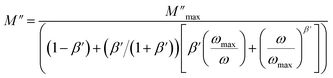 | (11) |
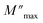 is the modulus maximum associated with the frequency noted by ωmax, and β′ is known as the Kohlrausch parameter (0 < β′ < 1).
is the modulus maximum associated with the frequency noted by ωmax, and β′ is known as the Kohlrausch parameter (0 < β′ < 1).
4. Conclusion
In summary, we studied the structural and electrical properties of Li-doped MnNbO4 prepared by a solid-state route. The high crystalline quality of the obtained particles was confirmed by XRD measurements. Li0.08Mn0.92NbO4 crystallized in the orthorhombic phase of the Pmmm space group. Furthermore, the EDX results confirmed the good stochiometric property of the preparation and proved the homogeneous chemical composition. The assignments of the Raman bands were in good agreement with those found in the literature.A detailed analysis of the impedance data revealed the grain and the grain boundary contribution. In addition, the ac conductivity was successfully described through Jonscher's power law. The variation of the deduced s (T) indicated that the CBH model could best interpret the charge-transport mechanism in the sample prepared. The activation energy was calculated using the alternating current conduction σdc to confirm the phase transition.
As for the dielectric study as a function of temperature, it brings arguments for the existence of ferroelectricity, revealing the relaxor nature of the studied material. Finally, the presented results provide insights into the correlation between the various properties of this material.
These results reveal that Li0.08Mn0.92NbO4 was prepared and characterized as a multifunctional material, which opens up new possibilities for developing functional materials, which is desirable to meet the rapidly increasing demand for new and more advanced technological applications. Nevertheless, the optic and magnetic properties as a function of temperature in Li0.08Mn0.92NbO4 are perspectives that are still needed in order to complete this work.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This work is financially supported by the Ministry of Higher Education and Scientific Research of Tunisia.References
- D. Errandonea and F. J. Manjon, Prog. Mater. Sci., 2008, 53, 711–773 CrossRef CAS.
- D. Errandonea and A. B. Garg, Prog. Mater. Sci., 2018, 97, 123–169 CrossRef CAS.
- S. Injac, A. K. L. Yuen, M. Avdeev, C.-H. Wang, P. Turner, H. E. A. Brand and B. Kennedy, J. Inorg. Chem., 2020, 59, 2791–2802 CrossRef CAS PubMed.
- M. Ferriol and S. Lecocq, Eur. J. Solid State Inorg. Chem., 1998, 35, 707–714 CrossRef CAS.
- I. L. Shukaev, A. A. Pospelov and A. A. Gannochenko, J. Solid State Chem., 2007, 180, 2189–2193 CrossRef CAS.
- S. Devesa, P. S. P. da Silva, M. P. Graça, L. C. Costa and J. A. Paixão, J. Sol-Gel Sci. Technol., 2020, 96(1), 143–152 CrossRef CAS.
- H. Nyman, B. G. Hyde and S. Andersson, Acta Crystallogr., Sect. B: Struct. Sci., 1984, 40, 441 CrossRef.
- O. Fukunaga and S. Yamaoka, Phys. Chem. Miner., 1979, 5, 167 CrossRef CAS.
- J. P. Bastide, J. Solid State Chem., 1987, 71, 115 CrossRef CAS.
- M. De Los Reyes, R. Aughterson, D. Gregg, S. Middleburgh, N. Zaluzec, P. Huai, C. Ren and G. Lumpkin, J. Am. Ceram. Soc., 2020, 103(10), 5502–5514 CrossRef CAS.
- A. H. Krumpel, P. Boutinaud, E. van der Kolk and P. Dorenbos, J. Lumin., 2010, 130(8), 1357–1365 CrossRef CAS.
- M. K. Patel, D. K. Avasthi, P. K. Kulriya, S. Kailas, J. C. Pivin and A. K. Tyagi, et al., Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 42–48 CrossRef CAS.
- P. Barpanda, K. Djellab, N. Recham, M. Armand and J. M. Tarascon, J. Mater. Chem., 2011, 21, 10143–10152 RSC.
- W. Zuo, M. Luo, X. Liu, J. Wu, H. Liu, J. Li, M. Winter, R. Fu, W. Yang and Y. Yang, Energy Environ. Sci., 2020, 13(12), 4450–4497 RSC.
- H. Li, W. Zhang, K. Sun, J. Guo, K. Yuan, J. Fu, T. Zhang, X. Zhang, H. Long, Z. Zhang, Ya. Lai and H. Sun, Adv. Energy Mater., 2021, 11(25), 2100867 CrossRef CAS.
- R. Marom, S. F. Amalraj, N. Leifer, D. Jacob and D. Aurbach, J. Mater. Chem., 2011, 21, 9938–9954 RSC.
- S. K. Hong, S. I. Mho, I. H. Yeo, Y. K. Kang and D. W. Kim, Electrochim. Acta, 2015, 156, 29–37 CrossRef CAS.
- W. B. Luo, J. Alloys Compd., 2015, 636, 24–28 CrossRef CAS.
- M. Steinhauer, S. Risse, N. Wagner and K. A. Friedrich, Electrochim. Acta, 2017, 228, 652–658 CrossRef CAS.
- N. P. W. Pieczonka, Z. Y. Liu, P. Lu, K. L. Olson, J. Moote, B. R. Powell and J. H. Kim, J. Phys. Chem. C, 2013, 117, 15947–15957 CrossRef CAS.
- C. M. Julien and M. Massot, Mater. Sci. Eng., B, 2003, 97, 217–230 CrossRef.
- X. Li, J. Liang, X. Yang, K. R. Adair, C. Wang, F. Zhao and X. Sun, Sci, 2020, 13, 1429–1461 CAS.
- C. Wang, J. Liang, J. Luo, J. Liu, X. Li, F. Zhao, R. Li, H. Huang, S. Zhao, L. Zhang, J. Wang and X. Sun, Sci. Adv., 2021, 7(37), 1–9 Search PubMed.
- G. B. Mullens, M. S. Múzquiz, F. P. Marlton, M. Avdeev, H. E. A. Brand, S. Mondal, G. Vaitheeswaran, J. Brendan and K. Beyond, J. Alloys Compd., 2023, 930, 167399 CrossRef.
- T. Roisnel and J. Rodriguez-Carvajal, FullProf suite program V.1.10, laboratoire Lyeon Brillouin (CEA-CNRS), 2009 Search PubMed.
- H. Yang, S. Zhang, H. Yang, Y. Yuan and E. Li. Bond, Ceram. Int., 2019, 45(14), 16940–16947 CrossRef CAS.
- X. Zhang, S. Tang and Y. Du, J. Phys. Chem. C, 2011, 115(6), 2644–2649 CrossRef CAS.
- J. E. Auckett, L. Lopez-Odriozola, S. J. Clarkb and I. R. Evans, J. Mater. Chem. A, 2021, 9, 4091 RSC.
- H. Ji, X. Tang, H. Zhang, X. Li and Y. Qian, Coatings, 2021, 11, 383 CrossRef CAS.
- L. Li, J. Deng, J. Chen, X. Sun, R. Yu, G. Liu and X. X. Wire, Chem. Mater., 2009, 21(7), 1207–1213 CrossRef CAS.
- L. Liang, X. Kang, Y. Sang and H. Liu, Adv. Sci., 2016, 3(7), 1500358 CrossRef PubMed.
- T. Mokkelbost, I. Kaus, R. Haugsrud, T. Norby, T. Grande and M. A. Einarsrud, J. Am. Ceram. Soc., 2008, 91, 879–886 CrossRef CAS.
- L. Jian, C. M. Huang, G. B. Xu and C. M. Wayman, Mater. Lett., 1994, 21, 105e10 Search PubMed.
- O. Prytz and J. Tafto, Accurate determination of domain boundary orientation in LaNbO4, Acta Mater., 2005, 53, 297–302 CrossRef CAS.
- T. Takagi, Y. H. Choa, T. Sekino and K. Niihara. Sci Eng Ceram Book Ser: Key Energy Mater. 1999, vol. 161, p. 181e4 Search PubMed.
- T. Ouahrani, A. B. Garg, R. Rao, P. R-Hernández, A. Muñoz, M. Badawi and D. Errandonea, J. Phys. Chem. C, 2022, 126(9), 4664–4676 CrossRef CAS.
- J. Ruiz-Fuertes, D. Errandonea, S. Lopez-Moreno, J. González, O. Gomis, R. Vilaplana, F. J. Manjon, A. Muñoz, P. Rodriguez- Hernandez and A. Friedrich, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 2011,(83), 214112 CrossRef.
- W. G. Fateley, F. R. Dollish, N. T. McDevitt and F. F. Bentley, Infrared and Raman selection rules for molecular and lattice vibrations: the correlation method, Wiley & Sons, New York, 1972 Search PubMed.
- S.-J. Hwang, D.-H. Park, J.-H. Choy and G. Campet, J. Phys. Chem. B, 2004, 108(34), 12713–12717 CrossRef CAS.
- R. B. Hadjean and J. P. Pereira-Ramos, Chem. Rev., 2010, 110, 1278–1319 CrossRef PubMed.
- D. Errandonea and A. B. Garg, Prog. Mater. Sci., 2018, 97, 123–169 CrossRef CAS.
- M. F. Lu, C. P. Zhou, Q. Q. Li, C. L. Zhang and H. F. Shi, Mater. Sci. Eng., 2018, 292, 012020 Search PubMed.
- H. Ji, X. Tang, H. Zhang, X. Li and Y. Qian, Coatings, 2021, 11, 383 CrossRef CAS.
- J. Ruiz-Fuertes, D. Errandonea, S. Lopez-Moreno, J. González, O. Gomis, R. Vilaplana, F. J. Manjon, A. Muñoz, P. Rodriguez- Hernandez and A. Friedrich, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 214112 CrossRef.
- K. P. F. Siqueira, R. L. Moreira and A. Dias, Chem. Mater., 2010, 22, 668 CrossRef.
- M. Yang, X. Zhao, Y. Ji, F. Liu, W. Liu, J. Sun and X. Liu, New J. Chem., 2014, 38, 4249 RSC.
- J. M. Jehng and I. E. Wachs, Chem. Mater., 1991, 3, 100 CrossRef CAS.
- U. Balachandran and N. G. Eror, J. Mater. Sci., 1982, 1, 374 CAS.
- X. Huang, K. Wang, J. S. Church and Y. Ch Li, Electrochim. Acta, 1999, 44, 2571 CrossRef.
- A. T. Aldred, Acta Crystallogr., 1984, B40, 569–574 Search PubMed.
- H. Yang, S. Zhang, H. Yang, Y. Yuan and E. Li, Ceram. Int., 2019, 45(3), 3620–3626 CrossRef CAS.
- H. W. Choi, S. J. Kim, Y.-H. Rim and Y. S. Yang, J. Phys. Chem. C, 2015, 119(49), 27192–27199 CrossRef CAS.
- K. Ozawa, Lithium Ion Rechargeable Batteries: Materials, Technology, and New Applications, WILEY-VCH Verlag GmbH & Co, 2009 Search PubMed.
- M. Wu, B. Xu and Ch. Ouyang, Chin. Phys. B, 2016, 25(1), 018206 CrossRef.
- D. Lu, W. Li, X. Zuo, Z. Yuan and Q. Huang, J. Phys. Chem. C, 2007, 111(32), 12067–12074 CrossRef CAS.
- X.- Gui Xin, J.-Q. Shen and S.-Q. Shi, Chin. Phys. B, 2012, 21(12), 128202 CrossRef.
- P. Aitchison, B. Ammundsen, T. Bell, D. Jones, J. Rozière, G. Burns, H. Berg, R. Tellgren and J. Thomas, Phys. B, 2000, 276, 847–848 CrossRef.
- M. Kamran and M. Anis-ur-Rehman, Ceram. Int., 2023, 49(4), 7017–7029 CrossRef CAS.
- K. L. Routray and D. Behera, J. Mater. Sci.: Mater. Electron., 2018, 29(16), 14248–14260 CrossRef CAS.
- D. V. M. Paiva, M. A. S. Silva, A. S. B. Sombra and P. B. A. Fechine, J. Alloys Compd., 2018, 748, 766 CrossRef CAS.
- R. G. M. Oliveira, D. B. Freitas, G. S. Batista, J. E. V. de Morais, V. C. Martins, M. M. Costa, M. A. S. Silva, D. X. Gouvêa, C. Singh and A. S. B. Sombra, J. Mater. Sci.: Mater. Electron., 2018, 29, 16248 CrossRef CAS.
- S. Chakrabarty, M. Pal and A. Dutta, Ceram. Int., 2018, 44(12), 14652–14659 CrossRef CAS.
- I. Soudani, K. B. Brahim, A. Oueslati, H. Slimi, A. Aydi and K. Khirouni, RSC Adv., 2022, 12(29), 18697–18708 RSC.
- S. O. Mansour, B. Louati and K. Guidara, Opt. Quantum Electron., 2017, 9, 49 Search PubMed.
- R. A. Young, P. E. Mackie and R. B. Dreele, J. Appl. Crystallogr., 1977, 10, 262–269 CrossRef.
- I. Gharbi, A. Oueslati, A. Bulou and M. Gargouri, Mater. Res. Bull., 2021, 139, 111250 CrossRef CAS.
- M. Ram, J. Alloys Compd., 2011, 509(18), 5688–5691 CrossRef CAS.
- A. Djemal, B. Louati and K. Guidara, J. Alloys Compd., 2016, 683, 610–618 CrossRef CAS.
- M. Ennefati, B. Louati, K. Guidara, M. Rasheed and R. Barillé, J. Mater. Sci.: Mater. Electron., 2018, 29, 171–179 CrossRef.
- Z. Zou, J. Ye and H. Arakawa, Chem. Phys. Lett., 2000, 332, 271–277 CrossRef CAS.
- K. P. F. Siqueira, R. L. Moreira and A. Dias, Chem. Mater., 2010, 22, 2668–2674 CrossRef CAS.
- J. M. S. Filho, C. A. Rodrigues Junior, D. G. Sousa, R. G. M. Oliveira, M. M. Costa, G. C. Barroso and A. S. B. Sombra, J. Electron. Mater., 2017, 46, 4344 CrossRef CAS.
- D.-W. Kim, D.-K. Kwon, S. H. Yoon and K. S. Hong, J. Am. Ceram. Soc., 2006, 89, 3861 CrossRef CAS.
- R. Haugsrud and T. Norby, Solid State Ionics, 2006, 177, 1129–1135 CrossRef CAS.
- L. Hakimova, A. Kasyanova, A. Farlenkov, J. Lyagaeva, D. Medvedev, A. Demin and P. Tsiakaras, Ceram. Int., 2019, 45, 209–215 CrossRef CAS.
- R. Haugsrud, B. Ballesteros, M. Lira-Cantu and T. Norby, J. Electrochem. Soc., 2006, 153, J87–J90 CrossRef CAS.
- D. Nguyen, Y. H. Kim, J. S. Lee and J. G. Fisher, Mater. Chem. Phys., 2017, 202, 320–328 CrossRef CAS.
- A. D. Brandão, N. Nasani, A. A. Yaremchenko, A. V. Kovalevsky and D. P. Fagg, Int. J. Hydrogen Energy, 2018, 56, 18682–18690 CrossRef.
- S. Wachowski, A. Mielewczyk-Gryn, K. Zagorski, C. Li, P. Jasinski, S. J. Skinner, R. Haugsrud and M. Gazda, J. Mater. Chem. A, 2016, 4, 11696–11707 RSC.
- A. Mielewczyk-Gryn, S. Wachowski, K. Zagórski, P. Jasinski and M. Gazda, Ceram. Int., 2015, 41, 7847–7852 CrossRef CAS.
- A. Mielewczyk-Gryn, K. Gdula, T. Lendze, B. Kusz and M. Gazda, Cryst. Res. Technol., 2010, 45, 1225–1228 CrossRef CAS.
- R. Haugsrud and T. Norby, Nat. Mater., 2006, 5, 193–196 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |