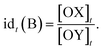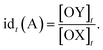Open Access Article
Open Access ArticleTemporal logic circuits implementation using a dual cross-inhibition mechanism based on DNA strand displacement†
Yuan Liu a,
Xiaokang Zhang
a,
Xiaokang Zhang a,
Xun Zhanga,
Xin Liu
a,
Xun Zhanga,
Xin Liu a,
Bin Wangb,
Qiang Zhang
a,
Bin Wangb,
Qiang Zhang *a and
Xiaopeng Wei*a
*a and
Xiaopeng Wei*a
aSchool of Computer Science and Technology, Dalian University of Technology, Dalian 116024, China. E-mail: zhangq@dlut.edu.cn; xpwei@dlut.edu.cn
bKey Laboratory of Advanced Design and Intelligent Computing, Ministry of Education, School of Software Engineering, Dalian University, Dalian 116622, China
First published on 11th September 2023
Abstract
Molecular circuits crafted from DNA molecules harness the inherent programmability and biocompatibility of DNA to intelligently steer molecular machines in the execution of microscopic tasks. In comparison to combinational circuits, DNA-based temporal circuits boast supplementary capabilities, allowing them to proficiently handle the omnipresent temporal information within biochemical systems and life sciences. However, the lack of temporal mechanisms and components proficient in comprehending and processing temporal information presents challenges in advancing DNA circuits that excel in complex tasks requiring temporal control and time perception. In this study, we engineered temporal logic circuits through the design and implementation of a dual cross-inhibition mechanism, which enables the acceptance and processing of temporal information, serving as a fundamental building block for constructing temporal circuits. By incorporating the dual cross-inhibition mechanism, the temporal logic gates are endowed with cascading capabilities, significantly enhancing the inhibitory effect compared to a cross-inhibitor. Furthermore, we have introduced the annihilation mechanism into the circuit to further augment the inhibition effect. As a result, the circuit demonstrates sensitive time response characteristics, leading to a fundamental improvement in circuit performance. This architecture provides a means to efficiently process temporal signals in DNA strand displacement circuits. We anticipate that our findings will contribute to the design of complex temporal logic circuits and the advancement of molecular programming.
Introduction
DNA nanotechnology has brought forth novel methods and techniques for computation and manufacturing at the molecular and nanoscale levels.1,2 DNA molecules, harnessed in ways unseen in nature, are employed to fabricate chemical reaction networks,3,4 molecular computers,5,6 information storage media,7,8 and further utilized to drive nanomachines,9,10 control molecular systems,11,12 process information,13,14 and construct molecular security systems.15,16 Among all applications, DNA circuits play a vital role, which can be realized through diverse approaches including DNA strand displacement,17,18 pH-regulation,19,20 lighting control,21,22 DNA self-assembly,23,24 and more.25,26DNA combinational logic circuits possess the inherent capability to process information through the utilization of transient values from inputs.27,28 As a consequence, these circuits demonstrate proficient analysis of multiple input signals,29 effectively catering to diverse requirements encompassing computing,30,31 sensing,32,33 and self-assembly control.34,35 However, they encounter significant challenges when it comes to processing temporal information related to input order or historical inputs, which is ubiquitous in nature, spanning from the molecular level36 to cellular,37 tissue,38 and organismal levels.39
Temporal logic circuits, incorporating time as a factor in their operations, offer unique advantages compared to combinational logic circuits.40,41 On the one hand, temporal logic circuits exhibit dynamic behavior and can respond to changes in inputs over time, which enables temporal circuits to model and simulate real-world systems that involve time-dependent behaviors, such as control systems, communication protocols, or signal processing algorithms. On the other hand, temporal logic circuits can incorporate memory elements, allowing them to store information about previous states or events and perform tasks that require memory, including state retention, temporal logic operations, and more. These advantageous features make the construction of temporal logic circuits capable of performing temporal information of great significance.
In recent years, temporal logic circuits have been realized using a variety of approaches. Notably, genetic circuits have been employed to create temporal logic gates capable of sensing and recording temporal information, encompassing the order of inputs, the timing between inputs, and the duration of input pulses.40 Furthermore, DNA strand displacement has been adopted as a viable method to construct DNA reaction networks, which exhibit the capacity to process temporal information owing to their programmability and predictability. In the realm of theoretical research, DNA reaction networks integrated with memory units present a promising avenue for computational tasks that involve the verification of specific temporal relationships within time-varying input signals.42 Such networks, designed with temporal specificity, can discern and respond to specific time patterns in the concentration parameters of signals.41 In the realm of experimentation, a temporal memory strategy has been proposed to construct temporal logic circuits capable of encoding and retaining all input information, thereby facilitating intelligent decision-making from a comprehensive perspective.43 Additionally, another strategy known as cross-inhibition has been employed to realize temporal logic circuits, enabling time-based responses and swift decision-making based on the timing of consecutive events.44 Moreover, the DNA self-assembly technique serves as the computing platform to implement finite-state machines with temporal resolution, endowing them with the ability to perceive and process inputs with temporal ordering.45
Among the above strategies, cross-inhibition is fundamentally a dynamic process that utilizes chemical reaction networks to enable interactive inhibition between two or more signals or components.44 In the process, the presence or activation of one signal leads to the suppression or reduction of other signals, creating a regulatory feedback loop. Due to its ability to process and control signals and events within biochemical systems at the nanoscale, the cross-inhibition mechanism can be utilized for decision-making and molecular cryptography.
By cascading with DNA combinational logic circuits, the cross-inhibition mechanism can be harnessed for decision-making in tic-tac-toe games.44 Through the input of a sequence representing the game process, the outcome of the game can be determined. Combined with enzyme-controlled techniques, the cross-inhibition mechanism can be employed to construct a molecular encryption system based on an enzyme-controlled cross-inhibition network, where the progressive unlocking of the network in a specific sequence is achievable only by inputting the password in the correct order.46 Otherwise, the inhibitory factors within the network will be activated to block the unlocking pathway and make the system sealed. Furthermore, the expanded multi-node cross-inhibition mechanism can be utilized to realize symmetric encryption systems, wherein different input sequences activate distinct inhibitory nodes that convert the input temporal information into encrypted data according to the arrangement of the inhibitory nodes.47
Despite the existence of various methods for constructing versatile components of temporal logic circuits, such as the temporal AND gate, there still remains a notable scarcity of such versatile components in temporal logic circuits. The diversity of such versatile components is of utmost importance for the construction of complex temporal circuits. At present, the lack of available and versatile temporal logic circuit components severely limits the construction and application of complex temporal logic circuits, thus hindering their full potential. In comparison to combinational circuits, temporal logic circuits necessitate the consideration of time factors, making the design and implementation of versatile temporal circuit components a persistent challenge.
To tackle this challenge, we have proposed a novel DNA temporal logic circuit capable of functioning as temporal OR gate. The core of the temporal logic circuits lies in the dual cross-inhibition mechanism, which resolves two key issues of the traditional cross-inhibition mechanism. On one hand, through interface-based design, it resolves the issue of the traditional cross-inhibition mechanism being unable to cascade with other circuits. On the other hand, by designing two inhibition pathways, it significantly enhances inhibition degree of the circuit, thereby improving the reliability and precision. Furthermore, we have proposed a method to improve the temporal logic circuit by incorporating an annihilation mechanism, which can substantially increase the inhibition degree at the expense of a minor reduction in the output signal. Notably, the system we designed is an all-DNA system, wherein both the input and output signals are composed of single-stranded DNA, thereby enabling seamless cascading with various types of DNA circuits. Within such an all-DNA system, the intrinsic programmability and scalability render the circuit highly compatible with diverse chemical reaction networks, particularly those reliant on time-dependent processes.
Results and discussion
Design and implementation of temporal logic circuits
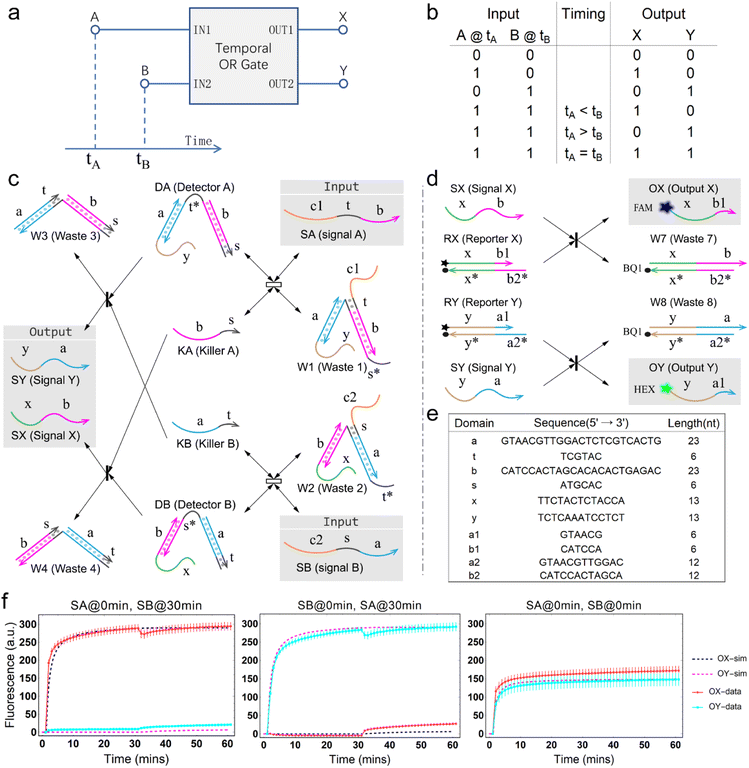
The concept of a temporal OR gate is shown as Fig. 1a. Port A and port B serve as input while port X and port Y serve as output. Like a traditional OR gate, if either input A or input B (or both) is true, the output is also true. Only when both inputs A and B are false, the output will be false. However, unlike a traditional OR gate, there is one more column describing the temporal order of the two inputs A and B in the truth table (Fig. 1b), which leads to a greater number of input combinations for a two-input temporal OR gate compared to the four input combinations of the traditional OR gate. This distinction arises due to the involvement of relative timing of signals, which represents a crucial aspect of temporal information. Similar to the temporal AND gate,43 in a temporal OR gate, the operation is influenced by the relative order of the two inputs when both input values are true. This means that the design of the temporal OR gate needs to take the sequence of the signals into account.The principle of the temporal OR gate implemented by DNA strand displacement is designed as shown in Fig. 1c. The operation of the temporal OR gate depends on the dual cross-inhibition mechanism. Previous work on cross-inhibition mechanism tended to focus on reporting the results of a cross-inhibition process. However, the output signals were designed as three-strand complexes, making it impossible to cascade with other types of DNA circuits or act as an upstream circuit in chemical reaction networks.
The dual cross-inhibition mechanism we proposed can effectively address this issue, in which two inhibition pathways are engineered to synergistically inhibit target signal and after inhibition a DNA single strand is generated for cascading. The reporter mechanism is employed to receive the single strand to demonstrate the cascading ability and produce detectable fluorescence signals (Fig. 1d). As shown in Fig. 1c, the main inhibition process is performed by the two detectors. Their cooperative operation enables the processing of temporal information composed of two input signals in a specific order. When the signal is input, the corresponding detector is activated, initiating a toehold exchange reaction and triggering the release of the “killer” strand. The killer strand invalidates the other detector while generating an output signal. The output signal consists of two parts: the linking domain bound to the detector and the displacement domain used for branch migration of the reporter. The linker domain contains a hidden toehold that is arranged 6 nt away from the end of the detector to reduce leakage reactions.
We model this chemical reaction network as follows:
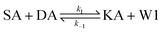 | (1) |
 | (2) |
 | (3) |
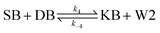 | (4) |
 | (5) |
 | (6) |
From the model, it can be seen that the chemical reaction network is highly symmetrical. In the case of Signal A (SA) input first, Detector A (DA) receives SA, then takes domain t and domain s as the toeholds, and domain b as the branch migration domain, carries out the toehold exchange reaction, while releasing Killer A (KA). Then KA takes domain s as the toehold, and domain b as the branch migration domain, undergo a strand displacement reaction with DB, releasing output Signal X (SX). The domain b of SX contains a hidden toehold 5′-CTAGCA-3′ (its complementary domain is the 6 nt sequence at the 5′ end of the b2* domain, which is the toehold of Reporter X. The abbreviation for Reporter X is RX), which can undergo strand displacement reaction with RX using the domain x as the branch migration domain. The final output signal is expressed through the fluorophore attached to RX. The process of inputting SB first, followed by SA, can be achieved through the symmetry of this system.
The sequence information of each key domain in the circuit is depicted in Fig. 1e. Here, the domains c1 and c2 in the circuit represent functional domains that participate in upstream biochemical reactions, and their sequences are determined by the specific experimental requirements. As long as there is no interference with the sequences of other parts of the system, the sequences of domains c1 and c2 have no observable impact on the kinetic process.44
Fig. 1f (and ESI Fig. S1†) presents the results of real-time fluorescence experiments, accompanied by simulated results. The curves OX-data and OY-data in the figure represent the data of real-time fluorescence experiments, while the dashed lines OX-sim and OY-sim represents the simulated results. DA, DB, RX, and RY were pre-added as substrates and scanned at initial points. The time interval between SA and SB was 30 minutes. (Demonstrations of real-time fluorescent experiments and simulation results at the time intervals of 10 min and 20 min are shown in ESI Fig. S2†) It is evident that upon introducing any signal into the system, the signal promptly propagates through the chemical reaction pathway, leading to a swift augmentation of fluorescence intensity. Furthermore, subsequent input signals are noticeably suppressed, albeit with a minor deviation from the simulated theoretical values, indicating a slight leakage. The reaction rate constants, fitted based on experimental data, are as follows: k1 = 7.5 × 104 M−1 s−1, k−1 = 1.7 × 105 M−1 s−1, k2 = 1.7 × 105 M−1 s−1, k3 = 4 × 105 M−1 s−1. In this case, due to the use of similar sequences, k1 and k−1 were referenced from the reaction rate constants of the cross-inhibitor,44 and k3 was referenced from the rate of reporter krox.48 Due to the approximate symmetry,48 we assume k−1 = k2. Given the symmetry of the DNA circuit, the reaction rate constants can be theoretically designed to be extremely close. Therefore, for biochemical reactions with the symmetric process, we assume that the reaction rate constants in the symmetric positions are equal, that is, k1 = k4, k−1 = k−4, k2 = k5, k3 = k6.
Time–response characteristics of the dual cross-inhibition mechanism
The relative timing of signals is a significant aspect of temporal information, especially in fields like neuroscience. It implies that there are specific time intervals between signals, which impose requirements on the time–response characteristics of temporal circuits. For the dual cross-inhibition mechanism, this requirement manifests in the need for effective inhibition of signals with different time intervals. To facilitate the quantification and comparison of inhibition effectiveness, the concept of inhibition degree was introduced,44 which is defined as follows:The formula indicates that the inhibition degree to which signal SB is inhibited by SA at time t is equal to the ratio of the concentration of OX to that of OY at that moment. Correspondingly, the inhibition degree to which signal SA is inhibited by SB at time t is equal to the ratio of the concentration of OY to that of OX at the moment, i.e.,
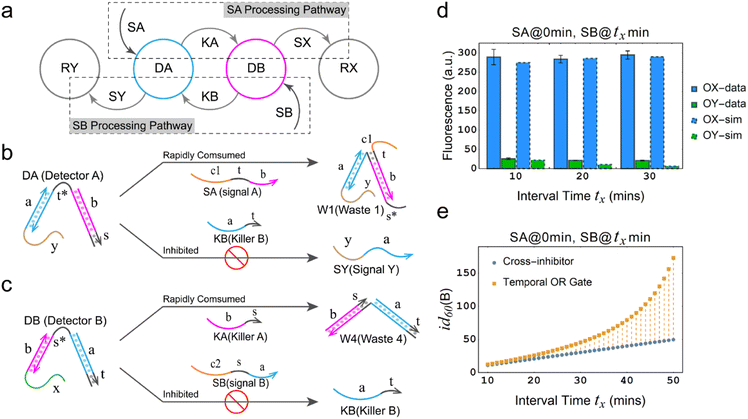
The dual cross-inhibition mechanism not only exhibits effective signal inhibition but also demonstrates a higher inhibition degree at different time intervals compared to previous work on cross-inhibition mechanism, which means that utilizing the dual cross-inhibition mechanism enables the realization of specific functions while generating and transmitting more precise signals. Fig. 2a depicts schematic diagram elucidating the dual cross-inhibition mechanism employed in the temporal OR gate. It is illustrated that two signal processing pathways intersect at nodes DA and DB. At each node, signal processing within one pathway inhibits the other, thus giving rise to a distinctive inhibition pathway which we refer to as DA inhibition pathway (at node DA) or DB inhibition pathway (at node DB). Due to the dual action of both pathways, we coined the term dual cross-inhibition mechanism to encapsulate this unique characteristic. Specifically, we take the inhibition of SB by SA as an example.
In the DA inhibition pathway (Fig. 2b), the generation of SY necessitates the presence of DA. However, due to the rapid consumption of DA by SA, KB is unable to react with DA to produce SY, thus achieving the inhibitory effect. To elaborate further, the reaction between DA and SA involves a strand displacement reaction with toehold exchange, leading to the rapid consumption of DA by SA and the formation of W1 and KA. Since the subsequent reaction involving KA is a unidirectional strand displacement reaction, the rapid consumption of generated KA promotes the reaction between SA and DA to proceed in the forward direction and further accelerating the consumption of DA.
In the DB inhibition pathway (Fig. 2c), the generation of SY necessitates the presence of DB, which is rapidly consumed by the products KA from SA and DA, converting DB into W4. As a result, it becomes extremely difficult for SB to react with W4. While there is a potential for leakage between SB and W4, the presence of the domain b in W4 makes it challenging for the domain s in SB to attach to the domain s* in W4, which effectively block the leakage. Due to the presence of these two pathways, when SB is input after SA, it is very difficult for SY to be generated through the chemical reaction networks to trigger the generation of fluorescence from reporter RY.
From the perspective of chemical reaction networks, the dual cross-inhibition mechanism offers improvements in signal processing, which expands the functionality of the inhibition strand within the dual cross-inhibition mechanism. The inhibition strand not only hampers reactions by rendering the substrates invalid but also serves as a vital signaling pathway for displacing the output strand from the substrates. In the specific chemical reaction network, it is observed that the generation of an output (OY) from the inhibited latter input signal (e.g., SB) requires two steps. Firstly, the inhibited signal must undergo toehold exchange with the residual detector (DB) that receives the signal. Secondly, it necessitates the displacement of the inhibition strand (KB) generated through the toehold exchange with the other detector (DA). Therefore, both toehold exchange with DB and displacement of KB are crucial factors in generating the output and serve as the focal points that are inhibited.
Under the effective inhibition of the two pathways, experimental and simulation results show that the temporal logic OR gate based on the dual cross-inhibition mechanism can perform accurate signal processing (Fig. 2d). SA can significantly inhibit the subsequent input signal SB at time intervals of 10 min, 20 min, and 30 min, preventing the establishment of a signaling pathway between SB and the reporter RY. Moreover, the experimental and simulation results are consistent. To observe the signal inhibition in a broader range and compare the performance with the cross-inhibitor, we simulated the inhibition degree of the temporal OR gate and the cross-inhibitor at intervals ranging from 10 min to 50 min.
As shown in Fig. 2e, the orange data points represent the correlation between inhibition degree and time interval for the temporal OR gate, while the blue data points represent the relationship for the cross-inhibitor. Both the temporal OR gate and the cross-inhibitor exhibit an increase in inhibition degree as the time interval extends. However, there is a notable difference that the temporal OR gate demonstrates an exponential-like pattern with the time interval, whereas the cross-inhibitor shows a linear relationship. This discrepancy suggests that the dual cross-inhibition mechanism employed in the temporal OR gate is more effective compared to a single-step reaction of the cross-inhibitor, where the input signal directly converts to the output signal. The presence of the dual cross-inhibition mechanism enhances the gate's time response characteristics, enabling it to respond more sensitively to changes in time intervals.
In conclusion, the temporal OR gate based on the dual cross-inhibition mechanism provides cascading function, robust temporal response characteristics and exceptional signal processing capabilities. These attributes offer significant assurance for signal accuracy, particularly in conditions where longer time intervals are involved.
Enhancing temporal logic OR gates using annihilation gates
The annihilation mechanism utilizes cooperative hybridization to mutually annihilate two specified signals,49 and is thus used in winner-take-all neural networks to ensure the preservation of a single winner.50 We introduce this mechanism into the temporal OR gate to enhance the inhibitory effect and ensure the preservation of effective signals.Fig. 3a illustrates the difference between the temporal OR gates with and without the incorporation of the annihilation gate (AG). As shown, SA is input prior to SB at a time interval of 2 min, leading to the output OX increasing sharply. However, in the left plot where AG is not incorporated into the temporal circuit, the undesired production of OY reaches the half of the amount of OX, leading to a seriously distorted output signal. In contrast, in the right plot of Fig. 3a, where AG was incorporated into the temporal circuit, the latter input SB is significantly inhibited at a cost of a small amount of OX, generating a small amount of OY. In the Fig. 3b, it can be seen that the inhibition degree of the temporal OR gate with AG is increased three-fold than that of the temporal OR gate without AG, which means that the proportion of the leakage signal has decreased from approximately one-half to one-sixth, which is a significant improvement. In order to specifically investigate the role of AG, it is necessary to establish a specific definition in this context, excluding AG as a substrate. Therefore, the substrates considered in this study are restricted to DA, DB, RX, and RY, while AG is not included.
 | ||
Fig. 3 Demonstration of the temporal logic gate with the incorporation of the annihilation gate. (a) Comparison of the simulations of temporal OR gates with and without the incorporation of the annihilation gate. “−AG” indicates that the annihilation gate is not incorporated, while “+AG” indicates that the annihilation gate is incorporated. [DA] = [DB] = [RX] = [RY] = 150 nM, [SA] = [SB] = 300 nM. DA, DB, RX and RY are pre-added as substrates. (b) Comparison of the inhibition degrees in (a). “−AG” and “+AG” represent the absence and presence of the annihilation gate. (c) Architecture design of the chemical reaction network of temporal OR gate with the incorporation of the annihilation gate. The reaction process of the reporter mechanism is the same as shown in Fig. 1a. (d) Simulation results of the inhibition degree in a temporal OR gate with the incorporation of the annihilation gate at different orders of magnitude for the reaction rate constant ka. (e) Simulation results of the three-dimensional surface plot illustrating the inhibition degree id60(B) (Z-axis) as a function of the reaction rate constant k1 (X-axis), and the ratio of rate constants k2 to k1 (Y-axis) for the temporal OR gate with the incorporation of the annihilation gate. (f) Simulation depicting the inhibition degree under different concentrations of AG, with the X-axis representing AG concentration and the Y-axis representing the inhibition degree. The graph includes three curves representing substrate concentrations of 100 nM, 200 nM, and 300 nM. In all cases, the input-to-substrate ratio is maintained at 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. (g) Time response characteristics of temporal OR gate with the incorporation of annihilation gate. (f) Comparison of time response characteristics between temporal OR gates with and without the incorporation of the annihilation gate. In (d)–(h), all substrates and AG, except for the variables and the specifically annotated, were at a concentration of 300 nM, while the input signals were twice the concentration of the substrates. 1. (g) Time response characteristics of temporal OR gate with the incorporation of annihilation gate. (f) Comparison of time response characteristics between temporal OR gates with and without the incorporation of the annihilation gate. In (d)–(h), all substrates and AG, except for the variables and the specifically annotated, were at a concentration of 300 nM, while the input signals were twice the concentration of the substrates. | ||
The principle of a temporal OR gate with the incorporation of AG is shown in Fig. 3c and is mainly used to eliminate the killers (Killer A and Killer B) in the pathway that generates the output signal. The annihilating process involving the elimination of KA and KB is modeled as follows:
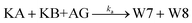 | (7) |
The annihilation gate contains domains within KA and KB, which can trigger the annihilation reaction only when both of KA and KB are present, resulting in the production of W5 and W6 that no longer participate in any reactions in the circuit. We conducted a detailed study of temporal OR gate with the incorporation of the annihilation gate using the CRN-Simulator. Keeping other parameters constant, we first investigated ka at different orders of magnitude, which determines the effectiveness of the annihilation gate. As shown in Fig. 3d, as ka increases from 106 to 1014, the annihilation effect rapidly increases when the exponent reaches around 12. At the exponent of 13, a highly effective inhibition is already achieved. Therefore, in subsequent studies, we assumed ka = 1013 (which implies the lengths of toehold t and s are approximately 7 nt). Next, we studied the rate constants k1 and k−1, which collectively determine the production rate of KA and also represent the speed at which the temporal circuit receive the upstream signals (SA and SB). As shown in ESI Fig. S3,† a smaller k1 leads to a lower inhibition degree and exhibits an approximately linear relationship, while a smaller k−1 leads to a higher inhibition degree, showing a similar exponential relationship. Furthermore, we assumed that k−1 is n times as large as k1 to study the impact of the relationship between k1 and k−1 on the inhibition degree. As a collaborative parameter, k1 ranges in two orders of magnitude. From Fig. 3e, it can be observed that when n is less than 2, the inhibition degree increases with the increase of k1. However, when n is greater than 2, the inhibition degree decreases significantly, and regardless of how k1 changes, it remains at a low level (the slice plots of Fig. 3e are shown in ESI Fig. S4†). This means that if k−1 is much greater than k1, temporal OR gate will lose its information processing functionality.
After studying the intrinsic properties of the circuit determined by k1 and k−1, we further investigated the effect of the concentration factors on the inhibition degree. When the global concentration increases (keeping a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio between input and substrate), the inhibition degree of the system significantly enhances, indicating that the higher the concentration of the system that incorporates this circuit, the better performance can be achieved (ESI Fig. S5†). When only the concentration of AG is increased (Fig. 3f) or only the ratio of input to substrate is increased (ESI Fig. S6†), the inhibition degree shows a noticeable rise, showing that these parameters can be adjusted individually based on the specific system into which the temporal circuits are integrated. However, due to the inability to consume excess strands, the improvement in circuit performance associated with an increase in excess concentration comes at the cost of potential leakage risk. Therefore, when designing circuits, it is not recommended to prioritize strategies that enhance circuit performance by elevating excess concentrations. Theoretically, it is recommended to use an AG concentration that is equal to the substrate concentration (i.e., [DA] = [DB] = [AG]) such that the annihilation gate is capable of annihilating almost all of the killers. Practically, a moderate increase in concentration may be performed in experiments if necessary.
1 ratio between input and substrate), the inhibition degree of the system significantly enhances, indicating that the higher the concentration of the system that incorporates this circuit, the better performance can be achieved (ESI Fig. S5†). When only the concentration of AG is increased (Fig. 3f) or only the ratio of input to substrate is increased (ESI Fig. S6†), the inhibition degree shows a noticeable rise, showing that these parameters can be adjusted individually based on the specific system into which the temporal circuits are integrated. However, due to the inability to consume excess strands, the improvement in circuit performance associated with an increase in excess concentration comes at the cost of potential leakage risk. Therefore, when designing circuits, it is not recommended to prioritize strategies that enhance circuit performance by elevating excess concentrations. Theoretically, it is recommended to use an AG concentration that is equal to the substrate concentration (i.e., [DA] = [DB] = [AG]) such that the annihilation gate is capable of annihilating almost all of the killers. Practically, a moderate increase in concentration may be performed in experiments if necessary.
Interestingly, it has been observed that maintaining constant concentrations of AG and input while increasing substrate concentration actually results in a reduction in inhibition (ESI Fig. S7†). This finding suggests that, when aiming to enhance circuit performance, the interplay between AG and substrate concentrations holds greater significance than simply regulating one of them independently. Notably, when solely the concentration of the input signal remains constant and both AG and substrate concentrations rise simultaneously, leading to an initial increase followed by a subsequent decrease in the inhibition degree (Fig. 3g). Therefore, an optimal solution lies within the range of these concentrations. If the system in which the circuit is integrated allows, selecting the optimal concentration solution becomes feasible.
Finally, we studied and compared the time response characteristics of the temporal OR gates with and without the incorporation of AG. As shown in Fig. 3h, the temporal OR gate with the incorporation of AG exhibited a significantly enhanced inhibition degree. Even with relatively short intervals between signals, the circuit was able to respond sensitively.
Among all the aforementioned cases, compared to the circuits with incorporated AG, circuits without incorporated AG exhibited very minimal changes in inhibition degree, indicating that the strategy of integrating annihilation mechanism can significantly enhance circuit performance, particularly within a time interval of only 2 minutes. Thus, the improvements implemented with this strategy have been proven to be highly effective, demonstrating the vital role of the annihilation mechanism in the circuit, greatly expanding the application scope of the proposed temporal circuit.
Above all, circuits without incorporated AG demonstrated minimal changes in the inhibition degree when compared to circuits with incorporated AG. This observation highlights the effectiveness of integrating an annihilation mechanism in enhancing circuit performance, particularly within a short time interval of only two minutes. Consequently, the improvements implemented through this strategy have been proven to be effective, underscoring the crucial role of the annihilation mechanism in the circuit. This advancement significantly broadens the application potential of the proposed temporal circuit.
Experimental
Materials and reagents
All DNA samples with specific sequences were purchased from GenScript Biotech Co., Ltd. (Nanjing, China). All the unmodified DNA strands were gel-purified using the polyacrylamide gel electrophoresis (PAGE), while the modified DNA strands were purified using high-performance liquid chromatography (HPLC). The two fluorophores immobilized on the reporters were FAM and HEX, and their corresponding quenchers were both BHQ1. All oligonucleotides were dissolved in 1× tris–acetate–EDTA–Mg2+ (1× TAE/Mg2+) buffer. The 1× TAE/Mg2+ buffer contains 40 mM tris, 20 mM acetic acid, 1 mM EDTA2Na and pH balanced to 8.0 with the addition of 12.5 mM Mg(OAc2) and is stored at 4 °C. The DNA sample concentrations were measured using a NanoDrop 2000 spectrophotometer (Thermo Fisher Scientific Inc., Waltham, MA, USA), with the absorption wavelength set at λ = 260 nm. All the involved reagents were of analytical grade without further purification. All solutions were prepared using ultrapure water. Note that there are no more purifications were applied in our experiments.Assembly procedure
All DNA complexes (ESI S8†) were formed by mixing the corresponding single strands with equal molar concentrations of 4 μM in a total volume of 50 μL in 1× TAE/Mg2+ buffer. Subsequently, all samples were then annealed using a polymerase chain reaction (PCR) thermal cycler C1000 Touch (Bio-Rad Laboratories, Inc., Hercules, CA, USA). The annealing process involved heating the samples to 95 °C for 5 minutes, followed by a gradual temperature decrease at a rate of −0.8 °C per minute until reaching 23 °C.DNA sequence design
The sequences of all strands used in the experiment, as listed in (ESI S8†), were designed through the following process: the sequence design of the dual cross-inhibition mechanism was guided by the sequence provided in the cross-inhibitor.44 The reporter component was designed based on the sequence and methods employed in the catalytic system.48 The remaining sequences were generated using NUPACK and underwent manual modifications before being concatenated to meet the desired specifications. These modified sequences were further examined using NUPACK to ensure the absence of unexpected hybridization structures (ESI Tables S1 and S2†) and minimize crosstalk between unrelated domains.51,52Fluorescence kinetics
All spectrofluorometric measurements were conducted at 37 °C using a real-time PCR system (CFX96 Deep Well, Bio-Rad Laboratories, Inc., Hercules, CA, USA) equipped with a 96-well fluorescence plate reader. Prior to the experiments, all samples related to fluorescence experiments were kept at room temperature. The volume of each DNA sample used was 26.67 μL.Simulation
The simulation and dynamic analysis were conducted using CRNSimulator, a programming platform for engineered chemical systems that runs on Wolfram Mathematica 12.0. Before running the program, the CRNSimulator Mathematica Package (CRNSimulator.m) and its extensions (CRNSimulator-Extensions.m) were loaded. The stochastic perturbation method was applied in the Fig. 3a and b, where all reaction rate constants were subjected to random perturbations with a range of positive and negative 30%. The codes used in the program is listed in ESI S9.†Conclusions
In this study, we have incorporated time as a key factor to design and implement DNA strand-displacement circuits capable of processing specific types of temporal information. The pivotal component of the temporal logic circuit is the dual cross-inhibition mechanism, which allows the circuit to achieve high levels of inhibition and low levels of leakage. By introducing a toehold-hidden strategy, the interface-based design enables the circuit to seamlessly cascade with other DNA-based molecular circuits. Additionally, leveraging the annihilation mechanism, we have proposed a method that can trade a small amount of output signal for a high degree of inhibition, effectively enhancing the circuit's overall performance.The molecular system we propose possesses two important characteristics. Firstly, the system is an all-DNA system, with DNA single-strands as both inputs and outputs. This feature facilitates the integration of this system with other existing types of molecular circuits, including combinational logic circuits and temporal logic circuits. Secondly, the system is symmetric, implying that by increasing the number of inhibition nodes, the number of input and output interfaces can be theoretically expanded.
However, in our proposed system, the inhibition pathways are point-to-point, meaning that one inhibition signal inhibits one substrate. To address this limitation, a signal-restoration mechanism, akin to the winner-take-all neural networks,50 can be introduced to achieve the one-to-many effect, enabling the construction of a multi-node inhibitory network and facilitating the realization of more complex temporal information processing systems. Additionally, our research has shown that reaction rate constants significantly impact circuit performance. Thus, further research can introduce various rate regulation mechanisms, like mismatch strategies, to provide fine-tuning capabilities.
As a type of temporal logic circuit, the circuits proposed in this study are envisaged to have utilities in the design of time-related information processing systems, specifically in the development of event-driven systems and systems that necessitate precise timing and synchronization. Specifically, based on the time–responsive characteristics, the circuits we proposed could be applied to design time-aware devices and integrated with time-related sensors. This feature provides opportunities for developing advanced systems that dynamically respond to temporal changes and synchronize with specific events.
Moreover, the adaptability and robustness of our temporal logic circuit offer potential applications in the field of molecular robotics and nanomachines. By leveraging its ability to process temporal inputs and make precise decisions, our circuit can act as a control module for constructing molecular machines with sophisticated functionalities, which could autonomously perform complex molecular computations and carry out precise tasks at the nanoscale.
In conclusion, with the incorporation of a dual cross-inhibition mechanism as the core component, we have achieved an effective and reliable circuit capable of distinguishing temporal patterns of molecular signals. Its capacity holds promise for potential applications in synthetic biology, time-aware sensors, molecular robotics, and other areas. As we continue our exploration and endeavor to harness the potential of temporal information in molecular systems, our temporal logic circuit may serve as a foundational stepping stone, offering possibilities for the development of innovative and intelligent molecular technologies.
Author contributions
Conceptualization, methodology, writing – original draft preparation, software, Y. L.; writing – review and editing, data curation, formal analysis, X. Z. (Xiaokang Zhang); investigation, X. Z. (Xun Zhang); validation, X. L.; supervision, B. W.; project administration, Q. Z.; funding acquisition, X. W. and Q. Z. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by 111 Project (No. D23006), the National Natural Science Foundation of China (No. 62272079, 61972266), Liaoning Revitalization Talents Program (No. XLYC2008017), Natural Science Foundation of Liaoning Province (No. 2021-MS-344, 2021-KF-11-03, 2022-KF-12-14), the Postgraduate Education Reform Project of Liaoning Province (No. LNYJG2022493), the Dalian Outstanding Young Science and Technology Talent Support Program (No. 2022RJ08).Notes and references
- A. Lacroix and H. F. Sleiman, ACS Nano, 2021, 15, 3631–3645 CrossRef CAS PubMed.
- C. M. Platnich, F. J. Rizzuto, G. Cosa and H. F. Sleiman, Chem. Soc. Rev., 2020, 49, 4220–4233 RSC.
- S. S. Wang and A. D. Ellington, Chem. Rev., 2019, 119, 6370–6383 CrossRef CAS PubMed.
- H. W. van Roekel, B. J. Rosier, L. H. Meijer, P. A. Hilbers, A. J. Markvoort, W. T. Huck and T. F. de Greef, Chem. Soc. Rev., 2015, 44, 7465–7483 RSC.
- L. Qian, E. Winfree and J. Bruck, Nature, 2011, 475, 368–372 CrossRef CAS PubMed.
- L. Qian and E. Winfree, Science, 2011, 332, 1196–1201 CrossRef CAS PubMed.
- F. Farzadfard, Nat. Biotechnol., 2020, 38, 31–32 CrossRef CAS PubMed.
- L. Organick, S. D. Ang, Y. J. Chen, R. Lopez, S. Yekhanin, K. Makarychev, M. Z. Racz, G. Kamath, P. Gopalan, B. Nguyen, C. N. Takahashi, S. Newman, H. Y. Parker, C. Rashtchian, K. Stewart, G. Gupta, R. Carlson, J. Mulligan, D. Carmean, G. Seelig, L. Ceze and K. Strauss, Nat. Biotechnol., 2018, 36, 242–248 CrossRef CAS PubMed.
- J. Dong, M. P. O'Hagan and I. Willner, Chem. Soc. Rev., 2022, 51, 7631–7661 RSC.
- L. Zhou, M. X. Gao, W. L. Fu, Y. X. Wang, D. Luo, K. Chang and M. Chen, Sci. Adv., 2020, 6, eabb0695 CrossRef CAS PubMed.
- A. J. Thubagere, W. Li, R. F. Johnson, Z. Chen, S. Doroudi, Y. L. Lee, G. Izatt, S. Wittman, N. Srinivas, D. Woods, E. Winfree and L. Qian, Science, 2017, 357, eaan6558 CrossRef PubMed.
- D. Y. Zhang, R. F. Hariadi, H. M. Choi and E. Winfree, Nat. Commun., 2013, 4, 1965 CrossRef PubMed.
- F. Wang, H. Lv, Q. Li, J. Li, X. Zhang, J. Shi, L. Wang and C. Fan, Nat. Commun., 2020, 11, 121 CrossRef CAS PubMed.
- W. Y. Lv, C. H. Li, F. F. Yang, Y. F. Li, S. J. Zhen and C. Z. Huang, Angew Chem. Int. Ed. Engl., 2022, 61, e202115561 CrossRef CAS PubMed.
- Y. Zhang, F. Wang, J. Chao, M. Xie, H. Liu, M. Pan, E. Kopperger, X. Liu, Q. Li, J. Shi, L. Wang, J. Hu, L. Wang, F. C. Simmel and C. Fan, Nat. Commun., 2019, 10, 5469 CrossRef PubMed.
- Z. Q. Bu, Q. F. Yao, Q. Y. Liu, M. X. Quan, J. Y. Lu and W. T. Huang, ACS Appl. Mater. Interfaces, 2022, 14, 8311–8321 CrossRef CAS PubMed.
- J. Bucci, P. Irmisch, E. Del Grosso, R. Seidel and F. Ricci, J. Am. Chem. Soc., 2022, 144, 19791–19798 CrossRef CAS PubMed.
- F. C. Simmel, B. Yurke and H. R. Singh, Chem. Rev., 2019, 119, 6326–6369 CrossRef CAS PubMed.
- D. Mariottini, D. Del Giudice, G. Ercolani, S. Di Stefano and F. Ricci, Chem. Sci., 2021, 12, 11735–11739 RSC.
- A. Amodio, A. F. Adedeji, M. Castronovo, E. Franco and F. Ricci, J. Am. Chem. Soc., 2016, 138, 12735–12738 CrossRef CAS PubMed.
- C. Xing, Z. Chen, J. Dai, J. Zhou, L. Wang, K. L. Zhang, X. Yin, C. Lu and H. Yang, ACS Appl. Mater. Interfaces, 2020, 12, 6336–6342 CrossRef CAS PubMed.
- M. P. O'Hagan, Z. Duan, F. Huang, S. Laps, J. Dong, F. Xia and I. Willner, Chem. Rev., 2023, 123, 6839–6887 CrossRef PubMed.
- F. Hong, F. Zhang, Y. Liu and H. Yan, Chem. Rev., 2017, 117, 12584–12640 CrossRef CAS PubMed.
- P. Zhan, A. Peil, Q. Jiang, D. Wang, S. Mousavi, Q. Xiong, Q. Shen, Y. Shang, B. Ding, C. Lin, Y. Ke and N. Liu, Chem. Rev., 2023, 123, 3976–4050 CrossRef CAS PubMed.
- F. Li, J. Li, B. Dong, F. Wang, C. Fan and X. Zuo, Chem. Soc. Rev., 2021, 50, 5650–5667 RSC.
- J. Wang, Y. Li and G. Nie, Nat. Rev. Mater., 2021, 6, 766–783 CrossRef CAS PubMed.
- L. Zhu, L. Yu and X. Yang, ACS Appl. Mater. Interfaces, 2021, 13, 42250–42257 CrossRef CAS PubMed.
- G. Chatterjee, N. Dalchau, R. A. Muscat, A. Phillips and G. Seelig, Nat. Nanotechnol., 2017, 12, 920–927 CrossRef CAS PubMed.
- P. Miao and Y. Tang, ACS Cent. Sci., 2021, 7, 1036–1044 CrossRef CAS PubMed.
- B. Groves, Y. J. Chen, C. Zurla, S. Pochekailov, J. L. Kirschman, P. J. Santangelo and G. Seelig, Nat. Nanotechnol., 2016, 11, 287–294 CrossRef CAS PubMed.
- W. Li, Y. Yang, H. Yan and Y. Liu, Nano Lett., 2013, 13, 2980–2988 CrossRef CAS PubMed.
- P. Zhang, Z. Li, H. Wang, Y. Zhuo, R. Yuan and Y. Chai, Nanoscale, 2017, 9, 2310–2316 RSC.
- L. Song, Y. Zhuge, X. Zuo, M. Li and F. Wang, Adv. Sci., 2022, 9, e2200327 CrossRef PubMed.
- M. Zheng, Z. Li, L. Liu, M. Li, V. E. Paluzzi, J. Hyun Choi and C. Mao, J. Am. Chem. Soc., 2021, 143, 20363–20367 CrossRef CAS PubMed.
- K. He, Y. Li, B. Xiang, P. Zhao, Y. Hu, Y. Huang, W. Li, Z. Nie and S. Yao, Chem. Sci., 2015, 6, 3556–3564 RSC.
- Y. Lin, C. H. Sohn, C. K. Dalal, L. Cai and M. B. Elowitz, Nature, 2015, 527, 54–58 CrossRef CAS PubMed.
- C. A. Ortmann, D. G. Kent, J. Nangalia, Y. Silber, D. C. Wedge, J. Grinfeld, E. J. Baxter, C. E. Massie, E. Papaemmanuil, S. Menon, A. L. Godfrey, D. Dimitropoulou, P. Guglielmelli, B. Bellosillo, C. Besses, K. Dohner, C. N. Harrison, G. S. Vassiliou, A. Vannucchi, P. J. Campbell and A. R. Green, N. Engl. J. Med., 2015, 372, 601–612 CrossRef PubMed.
- Y. Xie, P. Y. Hu, J. R. Li, J. W. Chen, W. B. Song, X. J. Wang, T. M. Yang, S. Dehaene, S. M. Tang, B. Min and L. P. Wang, Science, 2022, 375, 632–639 CrossRef CAS PubMed.
- D. J. Berry and P. Palladino, J. Hist. Biol., 2019, 52, 223–243 CrossRef PubMed.
- V. Hsiao, Y. Hori, P. W. Rothemund and R. M. Murray, Mol. Syst. Biol., 2016, 12, 869 CrossRef PubMed.
- J. O'Brien and A. Murugan, ACS Synth. Biol., 2019, 8, 826–832 CrossRef PubMed.
- M. R. Lakin and D. Stefanovic, presented in part at the Unconventional Computation and Natural Computation, UCNC 2017, Fayetteville, AR, USA, 2017, vol. 6 Search PubMed.
- A. P. Lapteva, N. Sarraf and L. Qian, J. Am. Chem. Soc., 2022, 144, 12443–12449 CrossRef CAS PubMed.
- C. Liu, Y. Liu, E. Zhu, Q. Zhang, X. Wei and B. Wang, Nucleic Acids Res., 2020, 48, 10691–10701 CrossRef CAS PubMed.
- L. Liu, F. Hong, H. Liu, X. Zhou, S. X. Jiang, P. Sulc, J. H. Jiang and H. Yan, Sci. Adv., 2022, 8, eabm9530 CrossRef CAS PubMed.
- X. Zhang, Q. Zhang, Y. Liu, B. Wang and S. Zhou, Comput. Struct. Biotechnol. J., 2020, 18, 2107–2116 CrossRef CAS PubMed.
- S. Zhao, Y. Liu, X. Zhang, R. Qin, B. Wang and Q. Zhang, Nanomaterials, 2023, 13, 903 CrossRef CAS PubMed.
- D. Y. Zhang, A. J. Turberfield, B. Yurke and E. Winfree, Science, 2007, 318, 1121–1125 CrossRef CAS PubMed.
- D. Y. Zhang, J. Am. Chem. Soc., 2011, 133, 1077–1086 CrossRef CAS PubMed.
- K. M. Cherry and L. Qian, Nature, 2018, 559, 370–376 CrossRef CAS PubMed.
- B. R. Wolfe, N. J. Porubsky, J. N. Zadeh, R. M. Dirks and N. A. Pierce, J. Am. Chem. Soc., 2017, 139, 3134–3144 CrossRef CAS PubMed.
- M. E. Fornace, N. J. Porubsky and N. A. Pierce, ACS Synth. Biol., 2020, 9, 2665–2678 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra03995a |
| This journal is © The Royal Society of Chemistry 2023 |