Pressure threshold for inhibition of dense granular film opening

Abstract

Controlling the stability of a granular film is essential in a wide range of industrial applications, from aerated building materials to recovering ore by flotation and treating wastewater. We therefore carry out experiments of granular film opening where particles of hundred of micrometers above random close packing zip the two interfaces of a soap film which liquid pressure is controlled. We create a hole at the center of this dense granular film and, surprisingly, we observe that the opening is not always inhibited. Different behaviours are identified: total bursting of the granular film, intermittent opening and jammed state for which the hole does not evolve. The liquid pressure drives the transition from one opening behaviour to another. Lower is the liquid pressure, more jammed is the system. The critical pressure transition scales as the surface tension over the particle size until the finite size of the granular film is only few tens of the particle size. Ultimately we evidence that spontaneous hole in thin film between particle do not lead to the granular film failure.

---

1. Introduction

Since the pioneering works of Ramsden¹ and Pickering,² it is known that the stability of oil-in-water emulsion can be drastically increased by resorting to hydrophobic solid particles. For more than a century, many applications, from cosmetic, medical to food industries, have been developed on the principle that particles can be adsorbed at fluid interfaces to create armor-like protective layers, either for single droplets or bubbles encapsulation purposes,^3,4 for stabilizing assemblies of droplets or bubbles as emulsions or foams respectively.⁵ One of the potential applications of this three-phases systems are aerated material with hierarchical structure (liquid films, particles assembly, bubbles assembly) which present interesting physical properties, in addition to their low density: thermal and acoustic insulation. Such physical properties depend on the opening of the membrane separating bubbles. Other potential applications are flotation processes, used in a wide range of industries from deinking and wastewater treatment to plastics, minerals and coal recovery,⁶ particles are separated according to their wetting properties. In general, the particles of interest are attached to the rising bubbles that form a foam at the top of the tank. The stability of the particle-laden films separating the bubbles determines particle recovery.

Indeed, liquid foams are ephemeral due to three main destabilization mechanisms: the liquid drainage due to gravity or capillarity, the coarsening due to gas diffusion from small to large bubbles and the coalescence of films between bubbles.⁷ This mechanisms are generally coupled. The liquid films between the bubbles thin under the effect of gravitational or capillary drainage (or evaporation) and tend to break; the thinner they are, the more unstable they are. The stability of particle-laden foams is either associated to reduction of aging due to surface elasticity that inhibit bubbles coarsening,⁸ to particles confinement in liquid network that stop liquid drainage,^9,10 or to large stability of films that prevent coalescence. The stability of films in the presence of particles is influenced by their size and hydrophobicity¹¹ and is thus a delicate balance of particle-interface, surfactant-interface and particle–surfactant interactions that are highly susceptible to system change, see ref. 5, 12 and 13 for review. In a similar way to emulsions, particle laden foams stability is based on the principle of particles creating a steric barrier to coalescence, but the range of particle size and contact angle are smaller (within 60°–70°). Studying particle-laden films with controlled physico-chemical parameters is thus essential.

Few experiments have been conducted at the film scale. Stability of thin liquid films containing hydrophilic colloidal particles is explained by layered structure and a critical film size below which the colloidal particles show no tendency of leaving the film.¹⁴ Recently, for manually ruptured films made of colloidal particles right after its formation, it has been shown that hole opens in a manner similar to Newtonian fluids film.¹⁵ When allowed to rupture spontaneously after thinning, the same dense colloidal films exhibit exotic instabilities reminiscent of a wrinkling fabric on the film surface which could be caused by competition of its thickness with the colloidal particle size. For manually ruptured films made of large particles (grains larger thant 10 μm typically) partially non wetting and thus positioned at the interfaces of liquid soap film,¹⁶ Timounay et al. have shown that hole opening depends on the position of the particles in relation to the two interfaces of the film. Indeed, for films with particles attached to a single interface, full opening is observed at a constant retraction velocity that can be modeled by Taylor–Culick-like theory, balancing liquid and particles inertia against surface tension. But, this approach is only valid up to a critical value of particle coverage, presumably due to the interplay between the interfaces and the friction between particles. When the particles bridge the two interfaces (monolayer configuration) the hole opens intermittently and hole opening can be inhibited once the packing is sufficiently dense. Moreover it has been shown that the viscosity of such granular film diverges at the approach of the random close packing of the 2D discs assembly ϕ ≃ 0.84.¹⁷ In the light of these last decade experimental studies of manually triggered rupture of particle laden soap film, one can conclude that its opening is similar to classical soap film as long as the particle assembly is small and the particles are not affected by the confinement. Otherwise, the particle film exhibit behaviour similar to that of a solid membrane and particle film opening can be inhibited.

This experiments challenge the assumption made by numerical works, that a particle film would burst at low liquid pressure due to spontaneous rupture of thin liquid film between particles.^13,18 Indeed, Morris et al. have modeled the stability of particle laden film by assuming that spontaneous opening occurs at the appearance of a liquid film with zero thickness in between the particles. Thanks to static simulations with Surface Evolver, they obtained the 3D equilibrium configuration of the liquid around the particles as a function of liquid pressure, particle surface fraction and contact angle. They have shown that liquid pressure has to be lower than a critical (capillary) pressure to form a liquid film of zero thickness, which absolute value decreases with particles separation (increases with particle surface fraction) and contact angle. Thus they have concluded that the thin liquid films with particles have a longer lifetime, producing a more stable froth because higher capillary depressure is required to generate its spontaneous rupture.

In previous hole-opening experiments with particulate soap films, the liquid pressure was neither controlled nor measured.^15,16 Nevertheless liquid pressure inside a liquid foam varies due to gravity, so to compare an experiment on an isolated film with a film in the bulk of a foam, it is essential to be able to control this liquid pressure. Studying its influence on film opening is of interest for applications relating to the performance of aerated materials or the recovery of particles by flotation. In the present work, we want to study the influence of the liquid pressure on hole opening for dense granular film. To this end, we have developed an original experimental setup to control liquid pressure in a dense granular film, inspired from the thin film liquid-pressure balance.^19,20

First, in ‘Materials and methods’ section, we detail this set-up and experimental protocols developed to trigger the rupture in a dense granular film. Second, we present the different opening behaviors and study their dependence with liquid pressure and particle size. Finally we conclude and discuss our results in view of other film opening behavior (soap film or elastic membrane) as well as applications.

2. Materials and methods

2.1. Surfactant solution

Tetradecyltrimethylammonium bromide (TTAB) is used at 10 g L⁻¹ in deionized water. It is a cationic surfactant with a Critical Micelle Concentration (CMC) about 1.5 g L⁻¹. For visualization purposes, we add fluorescein sodium at 0.2 g L⁻¹. From pendant drop method, we measured the liquid–gas surface tension of our solution, γ = 34 mN m⁻¹.

2.2. Particles

We use polystyrene spherical particles from Microbeads (Dinoseeds®) with a density of 1.05 g cm⁻³ of different sizes and similar contact angle.

We ensured that the size distribution was reduced by sieving particles. The size distribution is analyzed by laser diffraction with Mastersizer 3000 with Red light source (Max. 4 mW He–Ne, 632.8 nm), the results are summarized in the Table 1.

Table 1 Particles characteristics. D_p: average particle diameter; ΔD_p: standard deviation of the particle size; θ: particle contact angle with surfactant solution; Δθ: standard deviation of the measurement

Dp [μm]	ΔDp/Dp [%]	θ [°]	Δθ [°]
80	10	74	2
141	8	80	3
250	12	81	4
590	10	70	3

---

The particles surface was chemically treated with silane (1H,1H,2H,2H-perfluorodode cyltrichlorosilane from Sigma-Aldrich, CAS No. 102488-49-3) to change their wetting properties. From the attachment of a bead to the surface of a pendant drop,²¹ the wetting angle θ is estimated on at least 10 different particles of each size. We performed the measurement by identifying the intersection between a particle and the droplet, next fitted two circles: one at the droplet apex and a second on the particle contour. We then calculate the angle between the tangents of the two circles at the intersection points. The wetting characteristics of the different particles are summarized in the Table 1. The contact angle with the surfactant solution is in the range θ = 75° ± 6° for all particle sizes, and we can consider that all particles have the same contact angle.

Each granular film is formed with one size of particle, we studied the case of monodisperse granular films.

2.3. Granular film pressure balance set-up

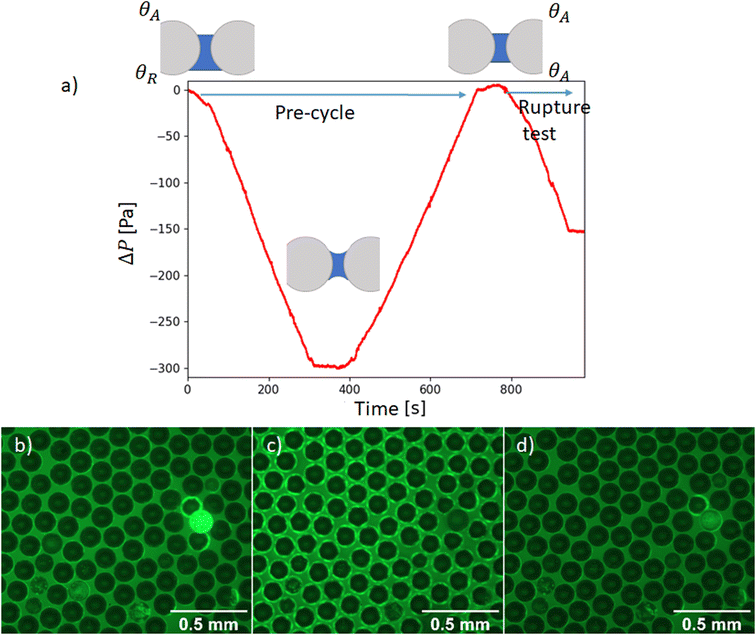
The experimental set-up we developed was inspired on the thin film liquid-pressure balance.^19,20 It allows us to form a centrimetric circular film loaded with particles and to vary its liquid pressure. To this end, we use a cylindric sintered borosillicate porous disc with a centrimetric hole at the middle to sustain the film. The porous disc we use has pore sizes ranging from 16 to 40 μm (nomenclature P3), it is saturated with surfactant solution and relies on a tank of this solution. The reservoir under the porous disk is connected to a system that consists of a syringe on a syringe pump (Harvard Appartus PHD ULTRA™) permitting us to pump or inject air into a bottle containing the liquid solution. This system is symbolized by “Q2” on Fig. 1. By varying the air pressure in this bottle, we vary the pressure forces applied to the liquid which vary the liquid pressure of the reservoir under the porous and by extension that of the liquid in the porous. When a granular film rests on the porous pellet, the pressure of the liquid within the film is the same as that of the porous. Varying the liquid pressure in the porous medium is therefore equivalent to varying the pressure in the film P_liq. Injecting air in the bottle, the liquid pressure in the granular film increases and pumping air decreases the film liquid pressure. We use differential pressure sensors (MPX5010 DP from NXP) to measure and monitor in real time the pressure variations in our system. The pressure sensor gives us the difference between the ambient air pressure (P_atm, in the experiment room) and the pressure in a gas pipe that is equal to the liquid pressure at equilibrium P_res in a reservoir. This liquid pressure is equal to the liquid pressure in the granular film plus the hydrostatic pressure due to the differential height (h) between the free surface in the reservoir and the film P_res = P_liq + ρgh. First, we identify the liquid pressure of reference P_res0 for which porous disc relax after oversaturation (apparition of a thin liquid layer) corresponding to P_liq = P_atm. We introduce the following notation: ΔP = P_res − P_res0 = P_liq − P_atm. Differential pressure sensors can measure approximately 500 pressure values per second which considerably reduces the measurement noise by averaging the pressure over one second, we have a measurement uncertainty to within 1 Pa. ΔP = 0 means that the film is at atmospheric pressure and when we lower the liquid pressure, ΔP decreases.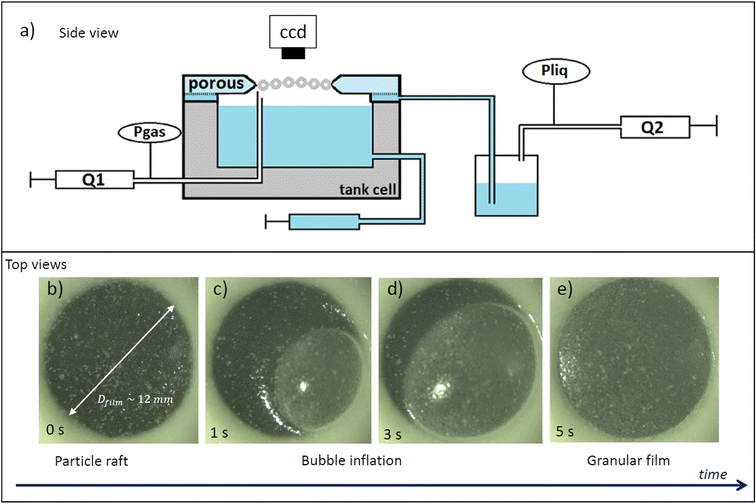

Fig. 1 (a) Sketch of a side view of the granular film pressure balance. (b–e) Top view pictures illustrating the creation of a granular film attached to a porous plate from the granular raft.

Varying the liquid pressure causes the air–liquid interfaces of the pores to curve. We can vary the liquid pressure of the porous disc without desaturation (no air penetration in the pores) in a range of ΔP ∈ [−900; 0] Pa.

During the experiment, we capture images of the films with a CCD camera. We can record the opening of the films at a maximum rate of 20 fps.

2.4. Granular film creation

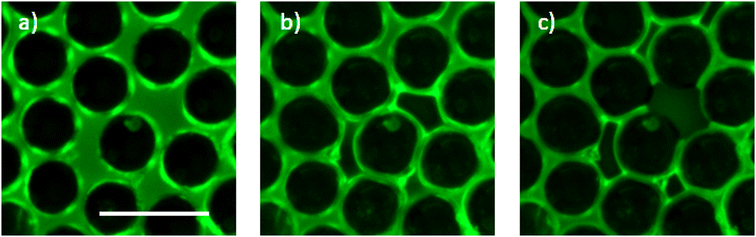
To form a granular film, we start by saturating the sintered porous disc with the surfactant solution. Then, we raise the water level in the cell so that the vertical air pipe is not submerged. Polystyrene beads are poured onto the interface between the solution and the air in the tank cell. Care is taken to completely cover the interface in order to obtain a compact granular raft. Subsequently, air is blown at a constant flow rate of Q₁ = 10 mL min⁻¹ using a syringe pump through the air hose of 400 μm diameter. The granular raft is made to slightly rise above this pipe (Fig. 1b), a bubble is then blown which size grows (Fig. 1c) and the film is formed by being attached to the porous disc (Fig. 1d and e). The water level in the cell is then lowered so that it is no longer in contact with the porous medium. We make sure that the film is flat by disconnecting the gas pipe (Q₁ circuit) so the gas pressure above and below the film is the same. We can observe the film as the photo example of Fig. 2 on the camera. The film appears as a dark circle in the middle of the picture surrounded by the porous disc. The bright dots we see on the film are particles that emits more light than the other, they are likely on top of other particles in the film (so outside of the film's plane) or can be porous and emit more light. In the film, the particles appear dark while the liquid is brighter. The contrast between particles and liquid helps us measure the surface density of particles. If a film appears dense and homogeneously laden in particles we finally can start the experiments. Moreover we note that the camera is well focused all over the granular film, which attest that the surface of the film does not deviate from an horizontal plane and thus that gravity is negligible on the initial state of the film.

Fig. 2 (a) Top view of a granular film made of 141 μm particles illuminated with blue light, the scale bar is 5 mm. (b) Illustration of particles detection algorithm in the dotted square drawn on (a). Detected particles are circled in by red or blue circle depending on size detection, the particle fraction ϕ_s ≃ 0, 87, the scale bar is 1 mm.

2.5. Pressure pre-cycle

In order to symmetrize the position of the particle in the median plan of the film, a pressure pre-cycle is applied (Fig. 3). The creation of the granular film is asymmetric as the two contact angles of particles at the upper and bottom interfaces are expected to be different due to hysteresis of contact angle: on top, we presume that it is an advancing angle θ_A because particles are wetted when they are poured on the liquid, whereas at the bottom, we presume that it is a receding angle θ_R because particles are dewetted when the bubble is inflated from below. As θ_R is lower or equal to θ_A, the lower hemisphere of the particles are expected to be more covered by liquid than its upper part. Consequently when the pressure of the liquid is lower than the atmospheric pressure (interfaces are curved), the particle center is pulled towards the center of the liquid film and the granular film will be more symmetrical with respect to a median plane. A pressure pre-cycle is performed by lowering the liquid pressure in the film at a rate of variation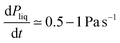 so that the liquid flow is quasi-static. It is verified with the pressure sensor: when we stop the syringe pump, there is no more pressure variation. By performing this pressure pre-cycle, the material is prepared to gain repeatability and erase the memory of its preparation. This will be confirmed in the next part presenting the results. It can also help densify the film in particles if there is enough space for some particles out of the plane, see Fig. 3b–d where a bright particle enter the liquid film and appear black after precycle.

Fig. 3 (a) Pressure variation versus time along a so-called pressure pre-cycle, sketches illustrate the deformation of the interfaces and asymmetric position of the particles: top left, the interfaces are flat and the particles are not centered; bottom, the interfaces are curved and the particles are centered; top right, the interfaces are flat and the particles are centered. (b–d) Top view images of the granular film with particle diameter of 141 μm, the particles are black, the fluid is green: (b) ΔP = 0 Pa, (c) ΔP = −300 Pa, halos are signature of interfaces curvature around the particle, (d) ΔP = 0 Pa.

2.6. Particle surface fraction of granular films

We measure the surface fraction of particles in the film thanks to the intensity gradient between liquid and particles. We performed the measurement with a circle recognition algorithm (Fig. 2b) and thus calculate an average particle surface fraction packing ϕ_s ≃ 87 ± 2%. This particle surface fraction is above the jamming expected at 84% for such monodisperse 2D packing of spheres.¹⁷ We also note that this value is relatively close to the maximal value for close packing in perfectly 2D and monodispersed system corresponding to hexagonal arrangement and equal to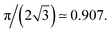 We thus suspect that the granular film is quasi-2D in a sense that the mid plane of the particles do not perfectly lies on the same plane as previously noticed for granular raft.²²

3. Results

In this study, the film can break in two ways: spontaneously or manually triggered.

3.1. Spontaneous rupture of a granular film

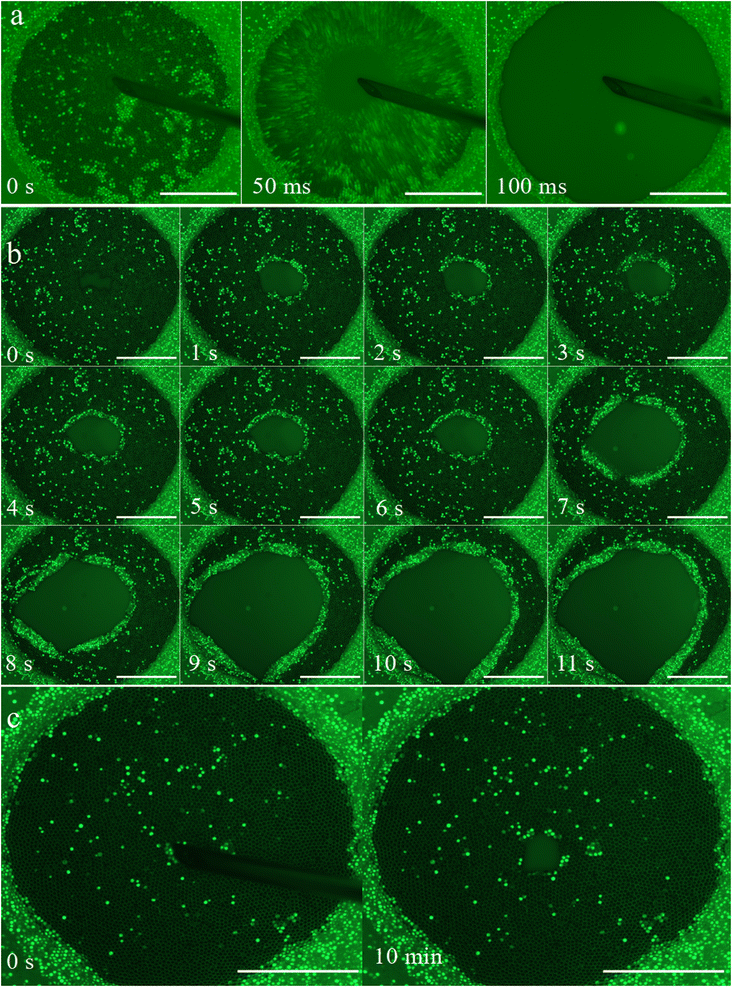
When decreasing the liquid pressure, the interfaces of liquid film between particles bend, bringing them closer together. A thin flat liquid film forms in the defect area where the particles are furthest apart (see Fig. 4a and b). We note that for our soap solution made with TTAB above the CMC, the liquid film should be stable and could sustain high depression larger than thousand of Pa.²³ Nevertheless a soap never last forever and some perturbations due to ambient atmosphere might be the reasons of thin film failure. Thus spontaneous ruptures of the thin film between grains occur below a certain liquid pressure that depends on the size of particle. We observe that this is a very local event, the resulting hole is of the size of the interstice and does not propagate, the rest of the film is intact (see Fig. 4c).

Fig. 4 Granular film made with 590 μm illustrating the distribution of liquid between particles, scale bar is 1 mm. As the liquid contains fluorescein, the greener the film, the thicker it is. From (a) to (b), as the liquid pressure decreases from 0 to −400 Pa, the films become thinner. Depending on the arrangement of the particles, the thinner the liquid film between the particles, the further apart they are. (c) Spontaneous opening of the liquid film between particles ΔP = −400 Pa.

This experimental result is very interesting because it calls into question Morris et al.’s hypothesis¹⁸ that the granular film ruptures completely as soon as the liquid–gas interfaces touch. While this assumption was necessary in the numerical study to define a stability criterion based on the configuration of the liquid around the particles, it is not verified experimentally.

3.2. Opening behavior after triggered rupture

For spontaneous rupture at high liquid depression, we have seen that the film always remains stable by blocking its opening. We then want to see how universal this behavior is, due to our high particle surface fraction i.e. does the film will remain jammed if we trigger rupture at a lower depression? More generally, we want to study the influence of liquid pressure on the stability of a granular film.

As explained before, after the formation of a granular film a liquid pressure pre-cycle is applied. Then, the liquid pressure is reduced again at the same rate until the desired value is reached and the rupture of liquid film between the particles is triggered manually with a needle (stainless steel, 0.8 mm of radius) by forming a hole in the particle network about the size of 3–5 particles of diameter at the center of the granular film (Section 3.2). We then pierce the liquid film at the center of the film.

When liquid pressure and particle diameter are varied, different types of hole opening in granular film are observed. We consider a film to be open when the opening front touches the porous disk locally or completely. We identified three behaviors that we named bursting, intermittent and jamming.

3.2.1 Bursting film. We classified a hole opening as bursting when the granular film opens completely in the blink of an eye, similarly to liquid film and elastic membrane under tension. We recorded this kind of film opening at 20 fps as illustrated in Fig. 5a where the pictures are successive. On the first image, we see the needle positioned to pierce the granular film, on the second image, the image is blurred all over the circular hole, meaning that the granular film is opening, then on the third image, we see the hole without any granular film, the needle is still in position (the experimentalist has not yet removed it). Note that, the opening step on the second image is not visible for all bursting we made, for most of the experiments (80%) the two successive images are recorded before and after the bursting. From the acquisition frame rate, the opening time is below 50 ms. The opening velocity is thus larger than 0.1 m s⁻¹.

Fig. 5 Different types of granular film opening with an interval of time between images Δt. All scale bars represent 4 mm. (a) Bursting film, Δt = 50 ms, (b) intermittent opening, Δt = 4 s (c) jammed film Δt = 10 min.

3.2.2 Jammed film. We classified a hole opening as jammed when the hole does not evolve (Fig. 5c), the granular film can stay for hours with the hole at its center, the rupture is inhibited, similarly to a solid sheet.

3.2.3 Intermittent film opening. We also observed films that retract step by step i.e. its behavior alternates between the bursting regime and the jammed regime until reaching the edges of the porous (Fig. 5b). The retraction is localized at the periphery of the hole. A kind of rim is visualized by bright zone. At the beginning the perimeter seems almost circular whereas at the end, its perimeter can partially be drawn by straight lines. An intermittent opening lasts for 1–5 s.

On Fig. 6 we report all the opening types we observed for 141 μm diameter particles when the liquid depression ΔP is varied from 0 to −325 Pa. We can note that the different types are correlated to liquid depression. For low depression all the granular films open by bursting whereas for high depression all granular films are jammed. In between, the three types of opening can occur. The opening behaviors are dispersed in the range of ΔP from −125 to −180 Pa: a granular film can either burst, open intermittently or be jammed (see vertical dotted lines of Fig. 6a). In order to reduce the dispersion that might be due to the preparation of the sample, we apply a pre-cycle to symmetrize the geometry of the granular film (see Section 2.5). The chosen value of the pre-cycle ΔP_PC141 is such that, if we open a film at this value of depression, we will always observe a jamming behavior, i.e. ΔP_PC141 = −300 Pa. With a pre-cycle, the opening behaviors are less dispersed, indeed bursting and jammed behaviors cannot be observed for the same ΔP (see vertical dotted line of Fig. 6b).

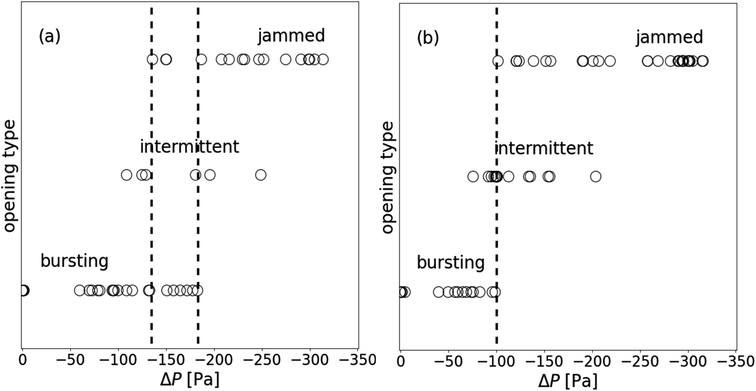Fig. 6 Opening type observed as a function of the imposed ΔP at the puncture, for granular film with D_p = 141 μm: (a) right after their formation; (b) after a pre-cycle ΔP_PC = −300 [Pa].

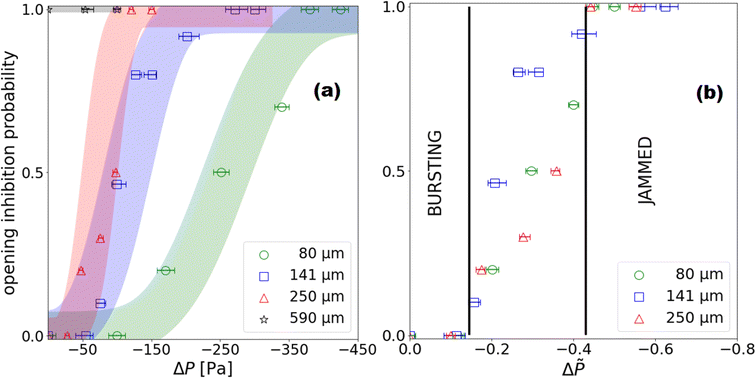
Quantitatively, we affect the values 0, 0.5 and 1 respectively to the bursting, intermittent and jamming classes for each experiment, and calculate average values of classes and ΔP values over five to ten experiments where the range of ΔP varies over approximately ten Pascals. These average values are analogue to the probability of inhibiting the total opening of a granular film. All averages i.e. opening inhibition probability (OIP) obtained for granular film made with particles of 141 μm are plotted in Fig. 7a. The horizontal error bars assigned to these average data represent the interval over which the average pressure is calculated. Even if the data are scattered, a clear trend is observed and an error function is plotted as a guide for the eye. Lower is the liquid pressure, more likely the hole opening is inhibited. All experiments (one hundred percent) for which ΔP ≤ −300 Pa result in a jamming state, after puncturing the center, the created hole remains forever. We punctured at other position in the granular film and we observed a static hole, even for holes closer than 5 beads of another hole. On the opposite, all experiments for which ΔP ≥ −50 Pa result in a total opening of the granular film. In the middle range of depressure −300 Pa ≤ ΔP ≤ −50 Pa, the probability of inhibiting the opening of granular film increases monotonically with decreasing ΔP.

Fig. 7 Opening inhibition probability (OIP) for different particle sizes as a function of liquid pressure: (a) OIP vs. absolute pressure ΔP (Pa); (b) (OIP) vs. normalized liquid pressure ΔP̃ = ΔP/(2γ/D_p). Average of opening values is calculated over experiments in the a range of depression represented by horizontal bar.

3.3. Influence of particle size on the critical pressures: signature of capillary pressure and effect of granular film size effect

To test the influence of particle size, we repeat the experiments for particles of diameter 80 μm, 250 μm and 590 μm independently.

Just as we prepared the films with 141 μm particles, we need to perform pressure pre-cycle for all particle size. Preliminary experiments have shown that for films formed with 250 μm particles, lowering the liquid pressure at ΔP = ΔP_PC141 = −300 Pa leads to spontaneous ruptures. We therefore need a dedicated pre-cycle value for each particle size for which the liquid film is stable over the whole sample. We adapt the criterion for 141 μm particle laden films to the other particle sizes assuming that, for our systems made of grains and soap film, the pressure scales with the capillary pressure calculated from the surface tension (γ) and grain radius (D_p/2) i.e. 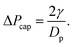From ΔP_PC = −300 Pa for D_p = 141 μm, we deduce ΔP_PC/ΔP_cap ≃ 2/3. Pre-cycle pressure values ΔP_PC for given particle diameter D_p are reported in Table 2. We made sure that for these pre-cycle values no spontaneous rupture is observed and that triggered opening at ΔP = ΔP_PC always leads to jammed state.

Table 2 Pre-cycle pressure values ΔP_PC for given particle diameter D_p

Dp (μm)	80	141	250	590
ΔPPC (Pa)	−560	−300	−180	−90

---

We therefore carried out experiments of triggered opening of granular films for all bead sizes at different depression after the dedicated pre-cycle. All results are presented on Fig. 7a, where points for any particle size are averaged over five to ten experiments in the range of depression represented by horizontal bars. Similarly to data discussed for granular film with 141 μm diameter beads, the larger is the depression, the more likely the hole opening is inhibited. Moreover, the smaller is the particle size, the larger is the depression threshold and the wider is the transition between the bursting and the jamming regime. Furthermore we notice a particular case for the 590 μm beads: no transition in the opening behavior with pressure variation, we only witness jammed films after triggered rupture. We assume that for this large particle size, which is one tenth of the granular film radius, arches and force chains might prevent the hole from opening.

As previously written, according to dimensional analyses for monodisperse granular and capillary systems, one expects a scaling of the pressure with 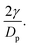Thus we plot all previous data as a function of dimensionless pressure 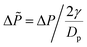in Fig. 7b. All data collapse on a same curve. For ΔP̃ ≥ −0.15, all granular films burst when exposed to puncture. For ΔP̃ ≤ −0.45, all granular films are jammed and hole opening is totally inhibited.

4. Discussion and conclusion

In this work we have evidenced for the first time that the triggered opening of a dense granular film (where particles zip the two interfaces) transit from a total opening to a jammed state as the liquid pressure is decreased inside the film. This transition is reminiscent of the classic behaviour of granular media which can behave like a liquid or like a solid depending on the stress.²⁴ Nevertheless, the liquid like opening is somehow surprising as the granular packing is above the random close packing in 2D.

At low liquid depression, the granular film opens very fast like a soap film but also like stretched membrane. On one hand, a kind of rim forms at the periphery of the hole in a similar way of liquid soap film (see Fig. 5b). On another hand, some vertical granular film sheets dip down in a similar way of stretched membrane that bursts.²⁵ Such behavior is also reminiscent of the exotic instabilities observed for spontaneous rupture of colloidal films.¹⁵ In the case of a dense granular film (above random close packing of the 2D assembly discs) we suspect that elasticity will play a role but in a different way to that of a classical soap film because the elasticity is not due to surfactants accumulation at the tip of the rim but due to grain network interaction via liquid meniscus like in a granular raft.^22,26 In addition, the accumulation of grains at the periphery of the hole, for tightly packed grains, might requires out-of-plane displacement and total wetting of the grains, which are sources of dissipation. To elucidate which of the scenarios is correct (retraction of a liquid film or fragmentation of a stretched membrane), or whether a mixture of the two happens, high speed recording of hole opening is required but out of the scope of this paper.

For large depressions, the creation of a hole in granular film will not lead to its rupture, as the granular film remains at rest, like creating a hole in a solid with no stress. This result extends the stability of particle foams beyond the critical pressure at which the liquid film between the particles has zero thickness.¹³ In fact, even a spontaneous rupture might occurs at very low liquid pressure, the granular film stay at rest and thus the foam do not collapse. To explain this opening inhibition, the radial force pulling on the hole periphery must increase more slowly with liquid depression than internal cohesion. What is most intriguing about this system is that the radial force and the cohesion of the granular skeleton have the same capillary origin. This is why it would be particularly interesting to use numerical simulations, using Surface Evolver for example, to access to these interparticle forces.

Moreover, we show that the pressure of transition scales with the capillary pressure calculated as ratio of surface tension over particle size. For dimensionless pressure ΔP̃ ≤ −0.45, the probability to inhibit hole opening is equal to one. This inhibition is observed before the “spontaneous opening” i.e. the formation of thin film with the particles which is expected for ΔP̃ ≃ −1 for closely packed particulate film.¹⁸ Thus, spontaneous film opening obtained for very low pressure, cannot be responsible of bursting as the opening is inhibited in this range of pressure.

Finally, the resistance of granular film to triggered rupture is more effective the lower the liquid pressure, which is contrary to soap film for which low liquid pressure implies a thinner film, less stable and faster bursting.⁷ Due to gravity, hydrostatic equilibrium imposes a lower liquid pressure at the top than at the bottom of foams, therefore, we expect that in foams composed of partially hydrophobic particles bridging both interfaces of the films separating the bubbles, the collapse of the foam due to films burst avalanches would not start from the top as in liquid foams. In regards to flotation issues, the larger the froth height, the more stable the top layer, which means that particles recovery from the foam will be more difficult. One method is to re-wet the foam to increase the amount of liquid and thus reduce the stability of the particulate films. Importantly, this means that in Pickering foams where the bubbles are confined by such granular film, some spontaneous thin liquid film rupture may occur in between of the grains at very low liquid pressure but this will not cause the foam to collapse as the hole will not open.

Author contributions

Conceptualization, methodology, writing – original draft preparation, Y. K., N. R. and F. R.; data curation, Y. K., and N. R.; investigation, N. R.; writing – review and editing, Y. K. and F. R. All authors have read and agreed to the published version of the manuscript.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors thank Paul Gauthier for conduction some complementary experiments during his internship. They acknowledge David Hautemayou, Cédric Mézière and Christophe Courrier for mechanical and electronical conceptions. They are also grateful to Xavier Chateau, Georges Gauthier and Olivier Pitois for discussions. This research was supported by the French Agence Nationale de la Recherche (ANR), under grant ANR-19-CE30-0009 – PhyGaMa and ANR-11-LABX-022 – labex MMCD.

References

1. W. Ramsden, Separation of solids in the surface-layers of solutions and ‘suspensions’ (observations on surface-membranes, bubbles, emulsions, and mechanical coagulation)—Preliminary account, Proc. R. Soc. London, 1904, 72(477–486), 156–164.
2. Spencer Umfreville Pickering, Cxcvi.—emulsions, J. Chem. Soc., Trans., 1907, 91, 2001–2021.
3. P. Aussillous and D. Quéré, Liquid marbles, Nature, 2001, 411.
4. Y. Timounay, O. Pitois and F. Rouyer, Gas marbles: Much stronger than liquid marbles, Phys. Rev. Lett., 2017, 118, 228001.
5. S. H. Tommy, Foams and foam films stabilised by solid particles, Curr. Opin. Colloid Interface Sci., 2008, 13(3), 134–140.
6. A. Nguyen and H. J. Schulze, Colloidal science of flotation, CRC Press, 2003.
7. I. Cantat, S. Cohen-Addad, F. Elias, F. Graner, R. Höhler, O. Pitois, F. Rouyer and A. Saint-Jalmes, Liquids Foams: Structure and Dynamic, Oxford University Press, 2013.
8. A. Stocco, W. Drenckhan, E. Rio, D. Langevin and B. P. Binks, Particle-stabilised foams: an interfacial study, Soft Matter, 2009, 5, 2215–2222.
9. B. Haffner, Y. Khidas and O. Pitois, The drainage of foamy granular suspensions, J. Colloid Interface Sci., 2015, 458, 200–208.
10. J. Yang, A. Wang and Q. Zheng, Ultra-long lifetime water bubbles stabilized by negative pressure generated between microparticles, Soft Matter, 2017, 13, 8202–8208.
11. G. I. Johansson and R. J. Pugh, The influence of particle size and hydrophobicity on the stability of mineralized froths, Int. J. Miner. Process., 1992, 34(1), 1–21.
12. T. N. Hunter, R. J. Pugh, G. V. Franks and G. J. Jameson, The role of particles in stabilising foams and emulsions, Adv. Colloid Interface Sci., 2008, 137(2), 57–81.
13. G. Morris, K. Hadler and J.-J. Cilliers, Particles in thin liquid films and at interfaces, Curr. Opin. Colloid Interface Sci., 2015, 20(2), 98–104.
14. G. N. Sethumadhavan, A. D. Nikolov and D. T. Wasan, Stability of liquid films containing monodisperse colloidal particles, J. Colloid Interface Sci., 2001, 240(1), 105–112.
15. P. Shah, E. Ward, S. Arora and M. M. Driscoll, Rupture dynamics of flat colloidal films, Phys. Rev. Fluids, 2023, 8, 024002.
16. Y. Timounay, E. Lorenceau and F. Rouyer, Opening and retraction of particulate soap films, EPL, 2015, 111(2), 26001.
17. Y. Timounay and F. Rouyer, Viscosity of particulate soap films: approaching the jamming of 2d capillary suspensions, Soft Matter, 2017, 13, 3449–3456.
18. G. Morris, M. R. Pursell, S. J. Neethling and J. J. Cilliers, The effect of particle hydrophobicity, separation distance and packing patterns on the stability of a thin film, J. Colloid Interface Sci., 2008, 327(1), 138–144.
19. A. Scheludko and D. Exerowa, Instrument for interferometric measuring of the thickness of microscopic foam layers, Commun. Inst. Chem. Bulg. Acad. Sci., 1959, 7, 123–131.
20. K. J. Mysels and M. N. Jones, Direct measurement of the variation of double-layer repulsion with distance, Discuss. Faraday Soc., 1966, 42, 42–50.
21. Y. Timounay, Rhéologie d'interface liquide/air chargées de grains : vers la consolidation d'un milieu aéré, PhD thesis, Université Paris-Est, 2016.
22. C. Planchette, E. Lorenceau and A.-L. Biance, Surface wave on a particle raft, Soft Matter, 2012, 8, 2444–2451.
23. B. Vance, Disjoining pressures and film stability of alkyltrimethylammonium bromide foam films, Langmuir, 1997, 13(13), 3474–3482.
24. A. J. Liu and S. R. Nagel, Jamming is not just cool any more, Nature, 1998, 396, 21–22.
25. S. Moulinet and M. Adda-Bedia, Popping balloons: A case study of dynamical fragmentation, Phys. Rev. Lett., 2015, 115, 184301.
26. D. Vella, P. Aussillous and L. Mahadevan, Elasticity of an interfacial particle raft, Europhys. Lett., 2004, 68(2), 212.

---