Open Access Article
Open Access ArticleRole of the solvent polarity on the optical and electronic characteristics of 1-iodoadamantane
Aravindhan R.a,
Jianping Hu*b and
M. Ummal Momeen *a
*a
aMagnetic Instrumentation and Applied Optics Laboratory, Department of Physics, School of Advanced Sciences, Vellore Institute of Technology, Vellore-632014, India. E-mail: ummalmomeen@gmail.com
bThe College of Nuclear Technology and Automation Engineering, Chengdu University of Technology, Chengdu, P. R. China. E-mail: profjianpinghu@hotmail.com
First published on 9th October 2023
Abstract
The natural absorbance caused by the chromophore and chemical behavior of 1-iodoadamantane is highly influenced by the polarity of different solvent environments. This gives rise to the solvatochromatic shifts in the optical absorption and electronic structure and the experimentally measured UV-vis absorption spectra show significant solvatochromic shifts with respect to the solvent polarity. The absorption shift for both σ to σ*and n to σ* electronic transitions are more dominant in polar solvents than in nonpolar solvents. To obtain a better understanding of the impact of solvent polarity on the 1-iodoadamantane at the molecular level, computational calculations were carried out through implicit solvation. According to this, changes in the HOMO and LUMO energies and electron density distributions of various solvent continuums demonstrate the influence of solvent polarity on the HOMO and LUMO energy levels of the chemical system. This also shows an increment in the HOMO–LUMO gap with respect to the polarity of the solvent.
Introduction
The impact of carbon-based materials in modern technology thrives the fascination towards carbon-based materials in the contemporary situation. Diamondoids are found to be the one among this intriguing group. Small saturated hydrocarbon molecules with cyclohexane rings fused in the form of diamond clusters are called diamondoids. Diamondoids are known for the three-dimensional array of diamond lattice, which combines many beneficial properties of inorganic materials and hydrocarbon molecules at the nanoscale. This makes diamondoids exceptional in terms of structural and electronic properties with high thermal stability.1,2 Adamantane is found to be the simplest diamondoid in nature, which is composed of cyclohexane rings in the chair conformation. It contains a single aliphatic tetrahedral carbon cage with a molecular formula of C10H16.3–5Functionalized adamantane derivatives are of great interest in many applications ranging from materials chemistry to composite materials and 3D porous networks.6,7 The inclusion of halogens and functional groups, such as amines and esters, on the tertiary carbons is increasingly in demand for the materials technologies.4,5 The possibility of tuning the band gap in lower dimensional materials is attractive in nanoscale research. Rigid strain-free ring systems of diamondoids are also offering this luxury. Adamantane functionalization is more eclectic than functionalization in polymantanes for the existence of two kinds of C–H bonds. This is found to be an effective choice for tuning the electronic properties of lower diamondoids when compared to the other substituted diamondoids from many perspectives.8 In this study, the monosubstituted derivative of adamantane with iodine in the bridgehead tertiary carbon atom, namely, 1-iodoadamantane (IAD) is considered. An enduring interest in the solvent effects on the optical properties of the solute paved the way for our findings.9 It is noticed that the electronic spectra of the compound in the gas phase was completely different in comparison with the solvation. Our study demonstrates significant solvent effects on the electronic absorption of IAD through the experimental UV-vis spectra. Also, computationally noticeable changes are obtained from the HOMO and LUMO energies, and electronic density distribution of the IAD molecule in different solvent media.
Computational methods
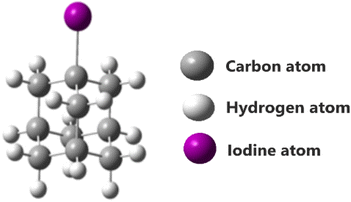
Complex excited state geometry and nearly degenerate excited states of halogen-substituted adamantane encounter challenging issues for the theoretical calculations of 1-iodoadamantane (Fig. 1). In many cases, lowest-lying excited states are one of the reasons for the inaccurate predictions of potential energy surfaces in quantum chemical calculations.10 To overcome this drawback, the employment of high electron correlation methods and large zeta basis sets is found to be an effective option. The coupled cluster singles and doubles (CCSD) method can account for high electron correlation.11,12The framework of coupled clusters provides an infinite perturbation theory in the form of an exponential cluster operator for a better description of electronic wavefunctions.13,14 The equation of motion-coupled cluster singles and doubles (EOM-CCSD) is a form of coupled cluster theory introduced for the robust description of the excited states. EOM-CCSD is preferred to attain the exact excited state and potential energy surfaces for bond-breaking conditions.15,16 In the case of EOM-CCSD, the excited state wavefunctions are attained using an excitation operator.17–19 To achieve exact excited state energies, all the calculations were carried out with EOM-CCSD high electron correlated methods in Gaussian 16 and for visualization, Gauss View 6 was used.20,21 Choosing a proper basis set is tedious for the molecules consisting of heavy atoms such as iodine to attain better accuracy. Smaller basis sets, which are used for providing the correct description of the electronic structure of molecules in the self-consistent field (SCF) are majorly not adequate to account for both intra- and interatomic distance in equal proportion. Due to the high atomic energies of iodine, small basis sets are not suitable for providing the complete description of the molecular system.22 As such, for the accurate description of IAD, we carried out our calculations with the set of effective core potential (ECP), and all-electron basis sets were named LanL2DZ and MidiX.23–27
Solvation effects are computationally included by means of the solvent model density (SMD) solvation model developed by Marenich et al. through the self-consistent reaction field (SCRF) formalism.28,29 SMD model is applicable to all charged and uncharged solutes. Further, dielectric constant, refractive index, bulk surface tension, acidity, and basicity are taken as key descriptors for the solvents. In the SMD model, the charge density of the solute induces the polarization in the solvent dielectric medium and the self-consistent interaction between the charge density of the solute and the polarization field of the solvent continuum confers the free energy of solvation.28 In solvation, a standard-state free energy of transfer from the gas phase to the condensed phase are partitioned and shown as
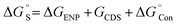 | (1) |
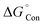 represents the concentration change between the gaseous state and the liquid state.28 Solvents in our study were selected based on the fundamental descriptors, namely dielectric constant (ε), relative polarity, and Kamlet–Taft solvatochromatic parameters (α, β, π*).28,30–34
represents the concentration change between the gaseous state and the liquid state.28 Solvents in our study were selected based on the fundamental descriptors, namely dielectric constant (ε), relative polarity, and Kamlet–Taft solvatochromatic parameters (α, β, π*).28,30–34
Experimental procedures
To measure the UV-vis absorption spectra, homogenous solutions of 1-iodoadamantane were prepared in both nonpolar (cyclohexane, hexane, and carbon tetrachloride (CCL4)) and polar solvents (cyclohexanone and dimethyl sulfoxide (DMSO)). Solvents with different dielectric constants for this study were chosen and classified as polar and nonpolar solvents with respect to the polarity.35–37 Homogenous IAD solutions were prepared in 10 mg ml−1, 20 mg ml−1, 50 mg ml−1, 80 mg ml−1, and 100 mg ml−1 concentrations in both polar and nonpolar solvents. Solvent effects on the UV-vis spectra were measured using the Jasco V-670 spectrophotometer at a concentration of 10 mg ml−1, which is shown in Fig. 3. The experimental results were compared with the computed absorption spectra, as shown in Fig. 4. The solvent concentration effects of the IAD in various solvents are also shown in Fig. 4.Results and discussion
The experimental and theoretical results of this study demonstrated the crucial solvent effect on the photophysical and electronic properties of IAD. This causes a significant color change between the polar and non-polar solvents, as shown in Fig. 2.Solvent effects on absorption spectra
Absorption spectra of IAD have two possible absorption bands.38,39 The absorption band in the vacuum UV region corresponds to the σ to σ* transition and the absorption band at 450 nm corresponds to the n to σ* electronic transition. In the solvation phase, all nonpolar solvents exhibit red shift for absorption due to σ to σ* transition and n to σ* transition by the higher stabilization of the excited state (Fig. 3). In polar solvents, an increase in the solvent polarity makes the ground state more stabilized than the excited state and causes a blue shift for both σ to σ* transition and n to σ* transition.36–41 Large dipole moments of polar solvents cause significant stabilization of the iodine atom.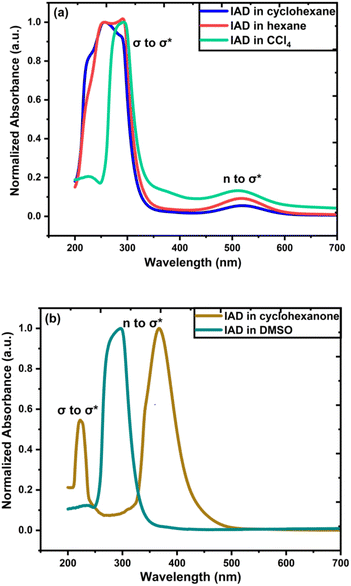 | ||
| Fig. 3 (a) Effects of solvent on experimental UV-vis spectra for IAD in nonpolar solvents, and (b) solvent effects on experimental UV-vis for IAD in polar solvents. | ||
Solvent effects are more significant in polar solvents due to the change in the charge density of the solute caused by the solvent, which alters the electronic distribution of IAD and results in the solvatochromatic shifts.33,35 These changes are less in the nonpolar solvents due to the small dielectric constant possessed by the solvents. The strength of the electronic transitions is illustrated by the oscillator strength, which allowed us to clearly examine a band with a lower absorption intensity. A less intense peak in the nonpolar solvents approximately at 500 nm was identified computationally by the values of oscillator strength for the electronic transition. In addition to the solvent effects, absorption of IAD in different solvents also undergoes significant variations with respect to the concentration of IAD irrespective of the polarity of solvents. The noticeable difference obtained between the experimentally measured and computed absorption, as shown in Table 1 and Fig. 4, is due to the exclusion of temperature, vibronic effects, and limitations of the theoretical model.
| Solvents | Experimental | Computed |
|---|---|---|
| Cyclohexane | 256 nm, 515 nm | 336 nm, 526 nm |
| Hexane | 290 nm, 517 nm | 345 nm, 548 nm |
| CCL4 | 293 nm, 519 nm | 330 nm, 509 nm |
| Cyclohexanone | 223 nm, 366 nm | 194 nm, 296 nm |
| DMSO | 297 nm | 194 nm, 291 nm |
 | ||
| Fig. 4 Comparison of computed (dotted line) and experimental (solid line) IAD absorption spectra and concentration effects for all solvents. | ||
Solvent effect through computational analysis
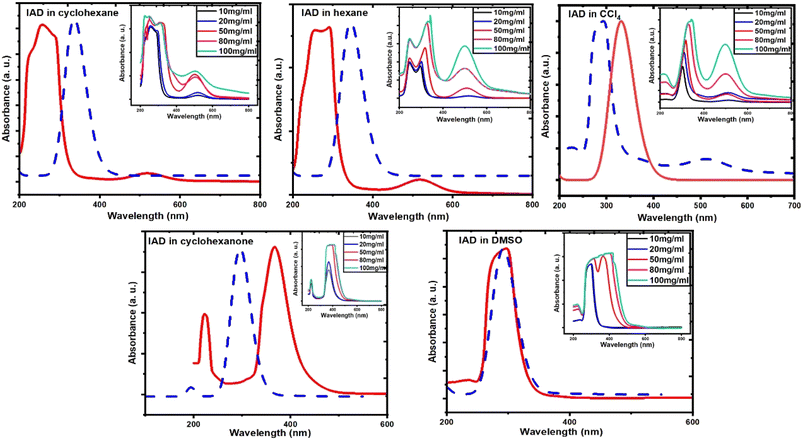
To acquire a qualitative understanding of the measured solvent-induced shift in the electronic absorption, solvent influences were studied computationally by means of implicit solvation with various solvent dielectric continuums. According to this, when IAD encounters different solvent media, electron density distribution is highly influenced by the charge distribution provided by the dielectric medium with specific values of the dielectric constant for each solvation, which causes the change in the electronic absorbance. In particular, the electron density of the states experiences an energy shift and change in the occupancy. This was found to be more in polar solvents because the bonding energies of C–C bonds are sensitive to the substituents and environments, thus affecting the σ to σ* transition and it also causes significant influence on the n to σ* transition. In addition to this, partial density of states (PDOS) and total density of states (TDOS) were obtained using the Multiwfn 3.8 software,42 as shown in Fig. 5. PDOS suggests that all the atoms are highly affected by the solvent polarity, this in turn causes substantial influence on the TDOS of IAD. The density of states for both polar and nonpolar solvents is affected, which alters the Fermi energies for both polar and nonpolar solvation. | ||
| Fig. 5 TDOS and PDOS spectra of (a) IAD in the gas phase, (b) IAD in cyclohexane, (c) IAD in hexane, (d) IAD in CCL4, (e) IAD in cyclohexanone and (f) IAD in DMSO. | ||
With a maximum probable percentage of electron densities, natural bonding orbital (NBO) analysis provides a natural tenable Lewis structure of the wavefunction, which in turn provides information on the filled and virtual orbitals.43,44 Each donor and acceptor interaction is calculated from the second order perturbation interaction energy E(2), which are evaluated using the equation
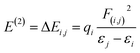 | (2) |
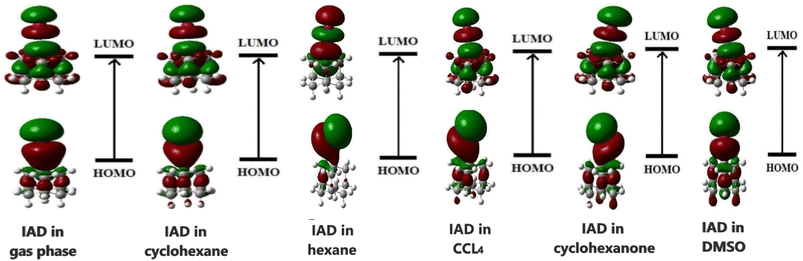
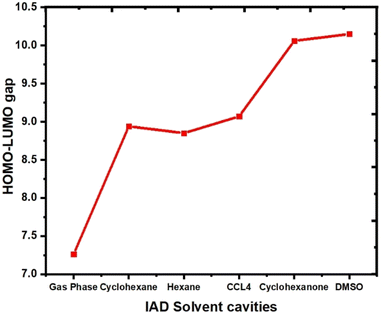
The HOMO and LUMO of the molecules play a vital role in the chemical reactivity and stability of the molecular system.37 The ability of a molecule to donate or accept an electron determines the electron densities of HOMO and LUMO in both ground and excited states. In the excited state, both HOMOs and LUMOs at the gas phase are localized over the entire molecular surface of IAD. In all the non-polar solvent continuum, electron densities are not significantly altered. In polar media, with respect to the polarity, HOMOs are more localized on the molecular surface, as shown in Fig. 6. This evidence of solvent-induced stabilization and notable changes in the electron densities of HOMOs and LUMOs results in the red and blue shifts in absorption due to major changes in HOMO–LUMO energies.1,2 As a result of this, the HOMO–LUMO gap increases when the polarity of the solvent continuum increases, which is shown in Fig. 7.
The HOMO–LUMO energies of IAD are high in polar media and low in nonpolar media, and the electron densities of the HOMO and LUMO orbitals are depicted in Fig. 6. To obtain a clear insight into the active electrophilic and nucleophilic sites of IAD in different solvent media, the molecular electrostatic potential (MEP) was computed. Different colors in the reactivity maps of the MEP represented different values of the electrostatic potential (Table 3). The electron-rich region around iodine was identified as a suitable site for nucleophilic attack in the gas phase and nonpolar media, which is represented in red color. Regions suitable for electrophilic attack and zero electrostatic potentials are represented in blue and green color. The high polarity possessed by DMSO and cyclohexanone neutralizes the electrostatic potential around the iodine atom in both ground and excited states. This justified the measured blue shifts in the absorption of the polar solvents. A positive potential (σ-hole) was found in the gaseous state46 and in all non-polar solvation media, which were unaffected by the influence of the solvent charge distribution. Due to the neutralization of the polar solvents, a σ-hole is not generated in the electrostatic potential map. Variation in the surface maxima and minima also depicts the influence of the solvent on the charge distribution of all the dielectric continuum.
| Solvents | Core | Valence Lewis | Total Lewis | Valence non-Lewis | Rydberg non-Lewis | Total non-Lewis |
|---|---|---|---|---|---|---|
| IAD in gas phase | 65.98764 | 61.41606 | 127.40370 | 0.48787 | 0.10843 | 0.59630 |
| IAD in cyclohexane | 65.98735 | 61.44055 | 127.42791 | 0.46493 | 0.10716 | 0.57209 |
| IAD in hexane | 65.98738 | 61.43830 | 127.42568 | 0.46708 | 0.10724 | 0.57432 |
| IAD in CCL4 | 65.98732 | 61.44211 | 127.42943 | 0.46346 | 0.10711 | 0.57057 |
| IAD in cyclohexanone | 65.99256 | 61.20936 | 127.20192 | 0.62171 | 0.17637 | 0.79808 |
| IAD in DMSO | 65.99256 | 61.20953 | 127.20209 | 0.62141 | 0.17651 | 0.79791 |
Conclusions
We demonstrated significant solvatochromatic shifts in the measured absorption spectra of IAD in both polar and non-polar solvents, which is well supported by the computed results, such as HOMO and LUMO energies, electron density distribution, electrostatic potentials, and bonding orbital analysis from a molecular perspective. In this study, we found that polar solvents with relatively large dielectric constants strongly influence the electronic structure of IAD. Correspondingly, nonpolar solvents with small dielectric constant also exhibit a notable influence. A significant color change obtained for the polar solvents also supports these claims. This study elaborates on the crucial role of charge distributions provided by each solvent in determining various optical and electronic properties of the molecular system. Our attempt to expose the solvent effects was successful with experimental measurements and validated the computational calculations.Author contributions
The conceptualization of this work was made by JH and MUM. Data collection and analysis were performed by AR. Writing and editing were performed by AR, JH, and MUM.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the financial support provided by DST-SERB through Grant No. EMR/2016/005575 and SPG/2021/002905.References
- G. A. Mansoori, Diamondoid molecules, Adv. Chem. Phys., 2007, 136, 207–258 CrossRef CAS.
- F. Yang, et al., Effects of molecular geometry on the properties of compressed diamondoid crystals, J. Phys. Chem. Lett., 2016, 7(22), 4641–4647 CrossRef CAS PubMed.
- O. Pirali, et al., Rotationally resolved infrared spectroscopy of adamantane, J. Chem. Phys., 2012, 136(2), 024310 CrossRef CAS PubMed.
- F. Marsusi and K. Mirabbaszadeh, Altering the electronic properties of diamondoids through encapsulating small particles, J. Phys.: Condens. Matter, 2009, 21(21), 215303 CrossRef PubMed.
- B. Adhikari and M. Fyta, Towards double-functionalized small diamondoids: selective electronic band-gap tuning, Nanotechnology, 2014, 26(3), 035701 CrossRef PubMed.
- L. Wanka, K. Iqbal and P. R. Schreiner, The lipophilic bullet hits the targets: medicinal chemistry of adamantane derivatives, Chem. Rev., 2013, 113(5), 3516–3604 CrossRef CAS PubMed.
- H. Nasrallah and J.-C. Hierso, Porous materials based on 3-dimensional Td-directing functionalized adamantane scaffolds and applied as recyclable catalysts, Chem. Mater., 2018, 31(3), 619–642 CrossRef.
- M. A. Gunawan, et al., Diamondoids: functionalization and subsequent applications of perfectly defined molecular cage hydrocarbons, New J. Chem., 2014, 38(1), 28–41 RSC.
- H. E. Ungnade, The effect of solvents on the absorption spectra of aromatic compounds, J. Am. Chem. Soc., 1953, 75(2), 432–434 CrossRef CAS.
- E. Papajak, et al., Perspectives on basis sets beautiful: seasonal plantings of diffuse basis functions, J. Chem. Theory Comput., 2011, 7(10), 3027–3034 CrossRef CAS PubMed.
- C. D. Sherrill, An introduction to configuration interaction theory, School of Chemistry and Biochemistry, Georgia Institute of Technology, 1995 Search PubMed.
- S. N. Datta, A Coupled Cluster Theory Based on Quantum Electrodynamics, arXiv, 2019, preprint, arXiv:1904.11956.
- J. B. Foresman, et al., Toward a systematic molecular orbital theory for excited states, J. Phys. Chem., 1992, 96(1), 135–149 CrossRef CAS.
- I. Y. Zhang and A. Grüneis, Coupled cluster theory in materials science, Front. Mater., 2019, 6, 123 CrossRef.
- J. J. Goings, et al., Assessment of low-scaling approximations to the equation of motion coupled-cluster singles and doubles equations, J. Chem. Phys., 2014, 141(16), 164116 CrossRef PubMed.
- Y. Ohtsuka, et al., Active-space symmetry-adapted-cluster configuration-interaction and equation-of-motion coupled-cluster methods for high accuracy calculations of potential energy surfaces of radicals, J. Chem. Phys., 2007, 126(16), 164111 CrossRef PubMed.
- A. B. Sannigrahi and S. D. Peyerimhoff, Extended Gaussian basis sets for iodine and their preliminary applications in abinitio configuration interaction calculations, J. Chem. Phys., 1990, 93(4), 2956–2957 CrossRef CAS.
- J. F. Stanton and R. J. Bartlett, The equation of motion coupled-cluster method. A systematic biorthogonal approach to molecular excitation energies, transition probabilities, and excited state properties, J. Chem. Phys., 1993, 98(9), 7029–7039 CrossRef CAS.
- A. Asthana, J. Liu and L. Cheng, Exact two-component equation-of-motion coupled-cluster singles and doubles method using atomic mean-field spin-orbit integrals, J. Chem. Phys., 2019, 150(7), 074102 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- D. Roy, T. A. Keith and J. M. Millam, GaussView, Version 6, Semichem Inc., Shawnee Mission, KS, 2016 Search PubMed.
- A. B. Sannigrahi and S. D. Peyerimhoff, Extended Gaussian basis sets for iodine and their preliminary applications in abinitio configuration interaction calculations, J. Chem. Phys., 1990, 93(4), 2956–2957 CrossRef CAS.
- D. Feller, et al., Performance of coupled cluster theory in thermochemical calculations of small halogenated compounds, J. Chem. Phys., 2003, 118(8), 3510–3522 CrossRef CAS.
- K. Sayin and D. Karakaş, Method and basis set investigation for trans-platinum (II)oxime complex, Cumhuriyet Science Journal, 2015, 36(2), 1–10 Search PubMed.
- L. Li, et al., Theoretical Studies on Structures, Properties and Dominant Debromination Pathways for Selected Polybrominated Diphenyl Ethers, Int. J. Mol. Sci., 2016, 17(6), 927 CrossRef PubMed.
- J. Li, C. J. Cramer and D. G. Truhlar, MIDI! basis set for silicon, bromine, and iodine, Theor. Chem. Acc., 1998, 99(3), 192–196 Search PubMed.
- R. E. Easton, et al., The MIDI! basis set for quantum mechanical calculations of molecular geometries and partial charges, Theor. Chim. Acta, 1996, 93(5), 281–301 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions, J. Phys. Chem. B, 2009, 113(18), 6378–6396 CrossRef CAS PubMed.
- E. L. M. Miguel, et al., How accurate is the SMD model for predicting free energy barriers for nucleophilic substitution reactions in polar protic and dipolar aprotic solvents?, J. Braz. Chem. Soc., 2016, 27(11), 2055–2061 CAS.
- M. Reta, C. Rosa and J. J. Silber, Kamlet–Taft's solvatochromic parameters for nonaqueous binary mixtures between n-hexane and 2-propanol, tetrahydrofurane, and ethyl acetate, J. Solution Chem., 2001, 30(3), 237–252 CrossRef CAS.
- B. U. Emenike, et al., Quantitative model for rationalizing solvent effect in noncovalent CH–Aryl interactions, Chem. Sci., 2016, 7(2), 1401–1407 RSC.
- K. M. Solntsev, D. Huppert and A. Noam, Photochemistry of “super”-photoacids. Solvent effects, J. Phys. Chem. A, 1999, 103(35), 6984–6997 CrossRef CAS.
- T. Islam, et al., Kamlet Taft Parameters: A Tool to Alternate the Usage of Hazardous solvent in Pharmaceutical and Chemical Manufacturing/Synthesis-A Gateway towards Green Technology, Anal. Chem. Lett., 2020, 10(5), 550–561 CrossRef CAS.
- A. Eilmes, Solvatochromic probe in molecular solvents: implicit versus explicit solvent model, Theor. Chem. Acc., 2014, 133(9), 1–13 Search PubMed.
- T.-J. Bi, et al., Solvent effects on excitation energies obtained using the state-specific TD-DFT method with a polarizable continuum model based on constrained equilibrium thermodynamics, Phys. Chem. Chem. Phys., 2017, 19(48), 32242–32252 RSC.
- M. Yoosefian and N. Etminan, The role of solvent polarity in the electronic properties, stability and reactivity trend of a tryptophane/Pd doped SWCNT novel nanobiosensor from polar protic to non-polar solvents, RSC Adv., 2016, 6(69), 64818–64825 RSC.
- H. C. Georg, K. Coutinho and S. Canuto, Solvent effects on the UV-visible absorption spectrum of benzophenone in water: A combined Monte Carlo quantum mechanics study including solute polarization, J. Chem. Phys., 2007, 126(3), 034507 CrossRef PubMed.
- W. Kemp, Organic Spectroscopy, Bloomsbury Publishing, 2017 Search PubMed.
- E. Pretsch, et al. Structure Determination of Organic Compounds, Springer-Verlag, Berlin, 2000 Search PubMed.
- N. Mora-Diez, L. A. Montero and J. Fabian, Molecular orbital modeling of solvent effects on excited states of organic molecules, J. Mol. Struct.: THEOCHEM, 1998, 453(1–3), 49–57 CrossRef CAS.
- A. Julià-López, et al., Solid materials with tunable reverse photochromism, ACS Appl. Mater. Interfaces, 2019, 11(12), 11884–11892 CrossRef PubMed.
- T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33(5), 580–592 CrossRef CAS PubMed.
- A. E. Reed, L. A. Curtiss and W. Frank, Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint, Chem. Rev., 1988, 88(6), 899–926 CrossRef CAS.
- A. J. Pounds, Valency and Bonding: A Natural Bond Orbital Donor–Acceptor Perspective, Frank (Weinhold and Clark Landis), 2007, p. 43 Search PubMed.
- F. Weinhold and E. D. Glendening, Comment on “natural Bond Orbitals and the Nature of the Hydrogen Bond”, J. Phys. Chem. A, 2018, 122(2), 724–732 CrossRef CAS PubMed.
- R. Aravindhan, M. Ummal Momeen and J. Hu, Halogenation effects on the bridgehead position of the adamantane molecule, Chem. Phys. Lett., 2023, 140746 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |