DOI:
10.1039/D3RA05360A
(Paper)
RSC Adv., 2023,
13, 30071-30085
Retracted Article: Novel hybrid QSPR-GPR approach for modeling of carbon dioxide capture using deep eutectic solvents†
Received
7th August 2023
, Accepted 3rd October 2023
First published on 13th October 2023
Abstract
In recent years, deep eutectic solvents (DESs) have garnered considerable attention for their potential in carbon capture and utilization processes. Predicting the carbon dioxide (CO2) solubility in DES is crucial for optimizing these solvent systems and advancing their application in sustainable technologies. In this study, we presented an evolving hybrid Quantitative Structure-Property Relationship and Gaussian Process Regression (QSPR-GPR) model that enables accurate predictions of CO2 solubility in various DESs. The QSPR-GPR model combined the strengths of both approaches, leveraging molecular descriptors and structural features of DES components to establish a robust and adaptable predictive framework. Through a systematic evolution process, we iteratively refined the model, enhancing its performance and generalization capacity. By incorporating experimental CO2 solubility data in varied DES compositions and temperatures, we trained the model to capture the intricate solubility behaviour precisely. The analytical capability of the evolving hybrid model was validated against an extensive dataset of experimental CO2 solubility values, demonstrating its superiority over individual QSPR and GPR models. The model achieves high accuracy, capturing the complex interactions between CO2 and DES components under varying thermodynamic conditions. The versatility of the evolving hybrid model was highlighted by its ability to accommodate new experimental data and adapt to different DES compositions and temperatures. The proposed QSPR-GPR model presented a powerful tool for predicting CO2 solubility in DES, providing valuable insights for designing and optimizing solvent systems in carbon capture technologies. The model's remarkable performance enhances our understanding of CO2 solubility mechanisms and contributes to sustainable solutions for mitigating greenhouse gas emissions. As research in DESs progresses, the evolving hybrid QSPR-GPR model offers a versatile and accurate means for predicting CO2 solubility, supporting advancements in carbon capture and utilization processes towards a greener and more sustainable future.
1. Introduction
Carbon dioxide (CO2) plays a substantial role in generating greenhouse gases, contributing to global warming.1–3 To address the urgent issue of global warming, scholars have focused on understanding and reducing CO2 emissions.4–6 Up until now, a multitude of methodologies, including detention, operation, and trap, have been devised to decrease CO2 emissions.7 Various CO2 capture technologies, including chemical-solvent scrubbing or physical and pressure-swing adsorption, are under investigation. However, these technologies often face challenges such as high energy demands, elevated costs, and secondary pollution due to gas complexity.8–10 Consequently, developing new capture technologies is urgently required, which could involve designing novel processes and solvents. Ionic liquids (ILs) have gained significant attention as possible solvents for CO2 removal thanks to their distinctive and appealing characteristics.11 While the surprising properties of ILs have made them highly sought-after solvents, their expensive nature poses a significant challenge. The complex synthesis and purification processes involved in IL production require specialized equipment and expertise, increasing the overall expense. Additionally, the raw materials used in IL synthesis can be costly. These factors limit the widespread adoption of ILs, especially in large-scale industrial applications.12 Deep eutectic solvents (DESs) have emerged as promising substitutes for ILs across multiple areas of investigation and industries.13 Their eco-conscious nature, cost-efficiency, and adaptability render them alluring choices for applications like CO2 separations, biomass utilization, nanoscience, extraction methodologies, electrochemical processes, and catalytic reactions.14–16 DESs possess unique characteristics that set them apart. These include reduced vapour pressure and enhanced stability by lowering volatility and evaporation. DESs also exhibit high conductivity for efficient charge transfer, high thermal and chemical stability, ensuring structural integrity in various conditions, non-combustibility for fire safety, non-toxicity for human and environmental well-being, and compatibility with a wide range of solutes. Compared to ILs, DESs offer advantages such as simplified and economical synthesis without additional purification steps, reducing costs, and improving production efficiency.16,17 The structural multiplicity of DESs arises from the arrangement of hydrogen bond donor (HBD) and hydrogen bond acceptor (HBA) components. The resulting mixture undergoes a phase transition, forming a liquid phase driven by intermolecular solid interactions between HBA and HBD.18,19 Additionally, DESs have the potential to utilize cost-effective and renewable compounds, aligning with sustainability principles in green chemistry by optimizing resources and minimizing environmental impact, contributing to the development of eco-friendly and economically viable chemical processes.20 DESs demonstrate promising potential as solvents for the separation of CO2.21–23 However, experimental methods have been limited to studying only a small set of potential DES options. This restriction exists because DESs come in a wide range of structures, making it possible to consider around ten combinations that could improve CO2 capture. However, testing all these combinations in real-life experiments is practically impossible.24 Consequently, a surging interest in developing computational models arises, aiming to predict CO2 solubilities within DESs. These models present a cost-effective and time-efficient approach to identifying efficacious solvent systems for carbon capture and utilization. By simulating CO2-DES interactions, researchers can effectively screen and identify promising candidates.25 Computational models provide valuable insights into how molecules interact, aiding in a more profound comprehension of solvation mechanisms and the variables that impact CO2 adsorption.26 Moreover, these models allow for an extended exploration of DES compositions and structural variations that surpass the experimental realm. Virtual screening techniques facilitate the identification of DES combinations endowed with amplified CO2 adsorption capacities and selectivity. The development of dependable computational models for predicting CO2 solubilities in DESs stands as an increasing and highly coveted area of research, as these models expedite the discovery and optimization of DES-based solvent systems, propelling the development of efficient and sustainable solutions for CO2 emissions mitigation.27–29
Currently, diverse thermodynamic models comprising UNIQUAC Functional-group Activity Coefficients (UNIFAC),30 UNIversal QUAsi Chemical (UNIQUAC),31 and Non-Random Two-Liquid (NRTL),32 in conjunction with an equation of state techniques like Peng–Robinson state equation (PR-EoS),33 Cubic-Plus Association (CPA),34 soft-SAFT,35 and perturbed chain statistical associating fluid theory (PC-SAFT),36 have been effectively employed to estimated gas solubility in systems including DESs. These thermodynamic models offer valuable tools for estimating gas solubility in DES-containing systems. The NRTL, UNIQUAC, and UNIFAC models, which rely on calculations of activity coefficients, provide insights into the behaviour of DESs in the presence of gases. Conversely, equation-of-state methods such as PC-SAFT, soft-SAFT, CPA, and PR-EoS employ equations representing the system's intermolecular interactions to predict gas solubility in DESs. Researchers can derive informed gas solubility predictions in DES-containing systems using these models.
However, these methods require access to experimental data to calibrate mixing parameters and detailed binary interaction at the molecular level. This requirement imposes limitations on the applicability of these methods, mainly when dealing with innovative solvent systems like DESs and ILs. In recent times, there have been a significant researches focus on employing molecular dynamics (MD), Monte Carlo (MC), and quantum chemical (QC) methods to explore the molecular simulation characteristics of CO2 within the structures of ILs37–40 and deep DESs.25,41–43 These computational techniques offer valuable insights into the behaviour and interactions of CO2 molecules within the intricate frameworks of ILs and DESs. However, the convergence of issues related to the creation of force field parameters and the substantial computational resources demanded for MD, MC, and explicit QC calculations places significant constraints on the practicality of performing extensive simulations for DESs and emerging ionic combinations. Consequently, researchers often focus on specific systems or resort to simplified models and approximations to explore the behaviour of CO2 in ILs and DESs. Fortunately, researchers have extensively employed a pioneering thermodynamic framework derived from a quantum chemical principles model called COnductor, like Screening MOdel for Real Solvents (COSMO-RS). This model has exhibited its significance as an essential instrument for evaluating solvents and predicting gas solubilities with acceptable precision.44,45 COSMO-RS operates on the principles of QC and statistical thermodynamics to calculate the solvation properties of molecules in a solvent.46–50 It utilizes QC descriptors to characterize solute and solvent molecules' electronic structure and charge distribution. By considering these factors, COSMO-RS can estimate solvation energies and predict the solubility of gases in various solvents, including ILs and DESs. While COSMO-RS calculations generally require only molecular structure information and offer a convenient approach to predicting solubilities, recent studies have revealed limitations in accurately predicting gas solubilities in DESs.42,51 The complex structures and interactions within DESs challenge the assumptions of the COSMO-RS model, resulting in over- or under-predictions. Nonetheless, these investigations overlooked the consideration of HBA and HBD conformers in their COSMO-RS predictions. In contrast, MD and MC simulations have proven to be dependable computational approaches for forecasting thermodynamic and phase equilibrium characteristics, encompassing gas solubility in solvents.25,52 However, it is worth noting that these techniques come with a substantial computational cost, rendering them less feasible for addressing the extensive range of solvent-gas variations encountered in DESs.
A promising approach to evaluating CO2 solubility and DES properties lies in developing machine learning (ML) models derived from quantitative structure–property relationships (QSPR).53 These models offer the potential for accurate and cost-effective assessment, accompanied by insightful observations on molecular–level interactions. These models' continuous evolution and improvement are promising for industries, including those involved in CO2 capture and utilization. By leveraging the capabilities of ML, scientists and professionals can advance our understanding of solubility phenomena, fine-tune the properties of DESs, and pave the way for innovative approaches to tackle environmental and industrial issues.24 Meeting specific prerequisites is essential to ensure the efficacy of QSPR models. Among these requirements, COSMO-RS-based descriptors assume great significance, mainly the region of charge distribution termed the Sigma profile (Sσ-profile). This descriptor depicts the likelihood distribution of a molecular surface segment characterized by a particular charge density. Its reliability has been established in accurately predicting solvent properties, including those of ILs and DESs, making it a dependable molecular-specific input feature for QSPR models. To create an ML model capable of envisaging density, aqueous solubility and refractive index, the input variables consisted of Sσ-profile features derived from COSMO-RS calculations. Lemaoui et al. undertook an in-depth exploration wherein they utilized the Sσ-profile regions derived from COSMO-RS as essential input parameters for developing QSPR forms. These models aimed to predict a range of thermodynamic characteristics, including pH, electrical conductivity, surface tension, viscosity, density and, with a specific focus on DESs.54,55 Additionally, Nordness et al. established an ML framework to estimate the IL thermophysical characteristics.56 The model effectively utilized Sσ-profile as input features, demonstrating their proficiency in capturing the necessary data to achieve accurate predictions. This study constitutes a significant advancement in ML approaches to property prediction in ILs, consequently highlighting the pivotal role of Sσ-profile as indispensable descriptors in such modelling endeavours.
Considering the limitations of multilinear and linear models, which often struggle to accurately characterize the complex and non-linear behaviour of various thermophysical properties,57 there has been a growing trend toward utilizing ML algorithms. These traditional models may fail to capture intricate relationships within data, especially when dealing with nonlinearity, high dimensionality, or intricate dependencies. By contrast, ML algorithms offer a more flexible and data-driven approach, making them increasingly appealing for tackling such challenges in thermophysical property modelling.58 These algorithms have gained popularity as they offer the ability to construct more intricate non-linear QSPR models, enabling the prediction of various physicochemical and phase equilibrium properties with enhanced accuracy. This shift towards ML-based approaches signifies the recognition of the need for more sophisticated and flexible models to capture the complexities inherent in these properties. Artificial neural networks (ANNs) are materialized as practical resources for simulating various phenomena, making them highly promising in modelling complex processes.59–66 Extensive literature reports substantiate ANN models' consistent demonstration of particular accuracy in predicting thermodynamic properties based on molecular descriptors.67,68 This extensive body of evidence highlights the ability of ANNs to effectively capture the intricate correlations between molecular features and thermodynamic properties, solidifying their position as a valuable approach for achieving precise property predictions. Ghareh Bagh et al. studied phosphonium and ammonium salt-based DES electrical conductivity.69 An ANN model successfully predicted the conductivity, yielding a Normalized Mean Square Error of 0.0010 and confirming the model's reliability with a 4.40% absolute relative deviation. Adeyemi et al. considered three amine-based DESs with varying choline chloride-to-amine molar ratios. Experimental measurements were taken for thermal stability, surface tension, pH, conductivity, viscosity, and density. Density predictions using conventional methods showed high deviations, but the bagging ANN approach achieved better accuracy with normalized mean square errors of 5.820 × 10−4 and 2.799 × 10−7 for conductivity and density, respectively.70 The commendable performance of ANN-based models in predicting thermodynamic properties has been well-documented. However, there is a dearth of research on developing an ANN model exclusively for predicting CO2 solubility. Consequently, an extensive and systematic exploration of a diverse range of DESs is essential to facilitate the creation of a wide-ranging ANN model tailored to predict CO2 solubility accurately.
In this investigation, a four-kernel algorithm for Gaussian process regression (i.e., rational quadratic, Matern, squared exponential and exponential) was formulated to accurately estimate the solubility of CO2 within a diverse array of DESs across wide temperature and pressure ranges. The solubility was estimated according to descriptors obtained from COSMO-RS approach and operational parameters (temperature and pressure) by Gaussian process regression strategy. It is crucial to highlight the specific focus on CO2 solubility within physically driven DESs. In these systems, the capacity for CO2 adsorption aligns with selectivity and Henry's constant, intricately associated with the structure of the HBD and HBA. An exhaustive inspection was carried out to analyze the available experimental outcomes concerning the solubility of CO2 in various physical-based DESs under particular experimental situations. Modelling based on COSMO-RS, a DES's CO2 solubility was computationally determined, and the resultant values were then juxtaposed with the complementary experimental CO2 solubilities. Furthermore, the COSMO-RS calculations enabled the extraction of Sσ-profile descriptors corresponding to the HBA and HBD moieties within the DESs. The abovementioned ML algorithm was developed and validated by incorporating data from DES's input features derived from the COSMO-RS literature database. Leveraging this model, novel combinations of HBAs and HBDs are suggested to enhance the DES's CO2 solubility.
2. Methodology
2.1. Gaussian process regression (GPR)
A highly influential managed ML algorithm, GPR, has emerged as a formidable model with probabilistic and nonparametric abilities. Its extraordinary ability to model intricate non-linear problems positions it as a potent tool applicable across various domains.71 The GPR method leverages the Gaussian process to conduct regression analysis. This approach is particularly appealing due to its inherent flexibility in characterizing uncertainty, which stands as one of its primary advantageous features.72 In the context of GPR modelling, as a general practice, we consider two sets of data: one for testing (T) and another for training (L). These data sets, T and L, are selected randomly and consist of pairs {xL,i,yL,i}i=1n, and {xT,i,yT,i}i=1n respectively, where x represents the input variables, and y represents the corresponding outcome variables. The GPR modelling initiates by considering the following equation as its foundation:| | |
yL,i = f(xL,i) + εL,i, i = 1,2,3,…,n
| (1) |
In this context, xL represents the independent variables, while yL denotes the outcomes associated with the training data points. Additionally, the observation noise is denoted by ε, while the variance of the noise is indicated by σnoise2, In is the unit array. Likewise, we can express the following for the test data set:| | |
yT,i = f(xT,i) + εT,i, i = 1,2,3,…,n
| (3) |
The symbols uphold the identical interpretations as previously defined, albeit about the test data set. Consequently, the Gaussian noise model establishes a linkage between each calculated outcome (y) and the corresponding function under consideration, f(x). Following the GPR model, the function f(x) is considered a random function or a stochastic, characterized by its associated mean m(x) and covariance k(x,x′) (commonly referred to as the kernel) functions.
| | |
f(xL,i) ∼ GP(m(x)·k(x,x′))
| (4) |
The determination of the mean function m(x) could be accomplished by utilizing explicit basis functions; nevertheless, for simplification and ease in calculations, it is frequently assumed to be zero.73
| | |
f(xL,i) ∼ GP(0,k(x,x′))
| (5) |
The y distribution could be obtained by combining eqn (1) and (5).
| | |
y ∼ N(0,k(x,x′) + σnoise2In)
| (6) |
Based on the aforementioned criteria and variables, the following can be inferred:
| |
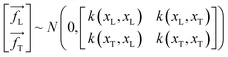 | (7) |
| |
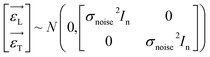 | (8) |
In addition to the latest two equations, the subsequent Gaussian expression can be derived:
| |
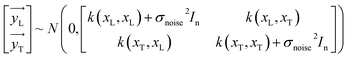 | (9) |
The variable yT distribution can be attained by applying the conditioning principle of Gaussian:
| | |
ΣT = k(xT,xT) = k(xT,xT) + σnoise2In − k(xT,xL)(k(xL,xL) + σnoise2In)−1k(xL,xT)
| (11) |
| |
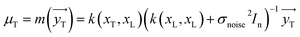 | (12) |
The covariance (ΣT) and mean value (μT) have their respective roles in this context. The strength and resilience of the predictive capability of the ultimate GPR model can be altered by the choice of a kernel function that incorporates a symmetric invertible matrix. In order to determine the optimal kernel function, four distinct choices, including rational quadratic, Matern, squared exponential, and exponential, have been made. The presentation of the chosen kernel functions is provided below:
Rational quadratic kernel function:
| |
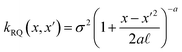 | (13) |
Matern kernel function:
| |
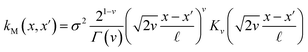 | (14) |
Squared exponential kernel function:
| |
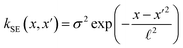 | (15) |
Exponential kernel function:
| |
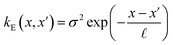 | (16) |
Within this framework, the variables
α,
σ,
σ2, and
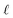
signify scale-mixture, amplitude, variance, and length scale, respectively. Moreover, the
Kv,
Γ, and
v symbols denote the modified Bessel function, gamma function, and a positive parameter, respectively.
2.2. COSMO-RS approach
To evaluate the CO2 solubility in DESs, COSMO-RS computations were performed. The Avogadro software74,75 was utilized to create the molecular geometries of all the examined species, including cations of salts, anions, and CO2. The molecular structures under investigation underwent widespread optimization using the Gaussian09 software suite.76–78 This detailed optimization procedure, conducted at the B3LYP level of theory with the 6-311++G(d,p) basis set, accurately determines the most energetically favourable conformations. QC calculations were performed on triethylene glycol to compare the single-point energies obtained from the B3LYP/6-311++G(d,p) calculations. The calculations were conducted using a theory level of B3LYP, incorporating the Grimme empirical dispersion GD3BJ correction and basis set 6-311++G(d,p). Detailed results of this comparison can be found in the ESI.† The energy comparison between the B3LYP and B3LYP-D3 principles yielded no substantial deviation. This implies that the two approaches produced similar results. Moreover, the ESI† contains all molecules' adjusted geometry coordinates considered in this report, including HBDs, HBAs, and CO2, supporting a detailed representation of their spatial arrangement. The generation of the COSMO files was accomplished by implementing the “scrf = COSMORS” keyword and employing a basis set and theories such as BVP86, TZVP, and DGA1.79 In order to investigate HBD and HBA conformational spaces, a detailed analysis was performed utilizing the BIOVIA COSMOconfX2022 package and Turbomole software.80 These software tools incorporate advanced algorithms designed to automatically detect and select relevant conformers, which are then utilized in subsequent COSMO-RS computations. This systematic approach ensures an inclusive exploration of molecular flexibility and aids in achieving accurate solvation predictions. Steady COSMO conformers were obtained through COSMO computations employed within COSMOConf via the basis set and BP-TZVP approach. Following the creation of COSMO conformers, these conformers were effectively employed as input within the COSMOtherm package, which was executed using the BP_TZVP_19 parametrization. This package included in-depth calculations to determine HBD and HBA Sσ-profile. Furthermore, the DESs' CO2 solubility and activity coefficient (γ) were accurately computed, providing valuable insights into their solvation behaviour.81 Following is an equation that determines the gas's solubility.82
In the given scenario, ‘pj’ signifies a compound ‘j’'s partial pressure, while ‘p0j’ represents the pure compound's vapour pressure. Additionally, the mole fraction or solubility of CO2 in the liquid phase is denoted by ‘xj’, and the activity coefficient is referred to as ‘γj’. The activity coefficient (γ) of component ‘j’ can be attributed to the chemical potential γj, and the subsequent equation can mathematically describe it:
| |
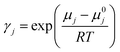 | (18) |
The given equation incorporates the chemical potential (μ0j) of the pure component ‘j’, with T denoting the absolute temperature and R representing the value of the real gas constant. Fig. S1 and S2† depict HBDs and HBAs chemical structures utilized in this study. In order to generate COSMO files for all the molecules under investigation, we meticulously followed the procedural guidelines presented in the introductory paragraph of Section 2.2.
3. Model development
3.1. Data collection
The primary focus of this investigation was to explore the solubility characteristics of CO2 in an extensive selection of 132 physically-based DESs.25,34,83–99 A meticulous data collection process was conducted to achieve this goal, acquiring 1973 data points from relevant literature sources. The collected data covered a wide range of experimental conditions, including an extensive temperature range spanning from 293.15 K to 348.15 K. Additionally, the investigation considered a broad pressure range, ranging from 26.3 kPa to 7620 kPa, allowing for the inclusion of various pressure conditions. The molar ratios, ranging from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16, also exhibited variations, enabling an extensive examination of the solubility behaviour of CO2 in DESs. Fig. S1 and S2† comprehensively summarize all the constituents involved in the DESs, including 25 HBDs and 23 HBAs. These figures offer an overview of the different components of the DESs studied. For a more in-depth analysis, Table S1† contains detailed information on temperatures, DES compositions (molar ratios, HBD, and HBA), CO2 solubility data, pressures, and the corresponding references. Researchers interested in exploring the specifics of this study are encouraged to refer to the ESI,† where inclusive data and references can be found.
16, also exhibited variations, enabling an extensive examination of the solubility behaviour of CO2 in DESs. Fig. S1 and S2† comprehensively summarize all the constituents involved in the DESs, including 25 HBDs and 23 HBAs. These figures offer an overview of the different components of the DESs studied. For a more in-depth analysis, Table S1† contains detailed information on temperatures, DES compositions (molar ratios, HBD, and HBA), CO2 solubility data, pressures, and the corresponding references. Researchers interested in exploring the specifics of this study are encouraged to refer to the ESI,† where inclusive data and references can be found.
3.2. COSMO-RS-derived molecular descriptors
The COSMO-RS theory employs a virtual conductor methodology to predict thermodynamic characteristics. This technique involves generating a virtual conductor around each molecule and conducting calculations to determine the wide-ranging analysis involved in the assessment of two critical parameters for each segment residing on the conductor's surface: the surface area, which quantifies the extent of exposure to the surrounding environment, and the screening charge density, which characterizes the charge distribution and interactions at the molecular level. The Sσ-profile, which depicts the charge distribution, are derived using these computations.100 As elucidated in Section 2.2, the molecules under investigation underwent the generation of COSMO files, which were subsequently employed to calculate thermodynamic properties. HBDs and HBAs were calculated based on their polarity distributions (Sσ-profile) using COSMOthermX,82 utilizing the created molecular surfaces. At the core of molecular analysis lies the Sσ-profile, a pivotal statistical distribution that significantly contributes to quantitatively evaluating the probability of each molecular surface segment possessing a specific screening charge density.101 As an outcome, Sσ-profiles cumulative area can be employed to provide an account of the molecular surface, commonly known as Sσ-profile. The Sσ-profiles factor in QC characterizes atom concentration and types within a σ-range, offering insights into spatial distribution and chemical identity. Refer to Torrecilla et al.102 for complete information on its significance in understanding molecular properties. Significant differences are observed in the distribution patterns of Sσ-profile within the regions of hydrogen bond donors and acceptors, along with variations in the areas covered by the Sσ-profile. These findings underscore each molecule's individual and characteristic Sσ-profile properties.103 Within molecular surface analysis, the Sσ-profile undergo a thorough partitioning process, classifying them into three distinct regions. The first region, characterized as non-polar, encompasses molecular surface segments with charge densities between −1e nm−2 and +1e nm−2. The second region, involving hydrogen bond donors, comprises segments with charge densities below −1e nm−2, while the third region, housing hydrogen bond acceptors, comprises segments with charge densities above 1e nm−2. To define Sσ-profile input descriptors for the ML models, a segmentation process was applied to the Sσ-profile of the constituents within DESs. This involved dividing the Sσ-profile into ten fractions, labelled as S1 to S10, by performing integrations of the Sσ-profile Px (σ) across the entire range of screening charge density, σ. The segmented fractions that emerge offer an improved depiction of how electric charges are distributed among the components of DESs. These fractions can be employed as input descriptors for ML models, enhancing their ability to make more precise predictions regarding specific properties or behaviors. These profiles undergo thorough analysis, leading to their classification into five distinct classes based on the screening charge densities they exhibit. The classification is as follows: (1) the strong donor region, encompassing segments denoted as S1 and S2, characterized by substantial charge densities indicative of significant donor properties; (2) the weak donor region, represented by segment S3, featuring charge densities associated with relatively feeble donor characteristics; (3) the non-polar region, containing segments S4, S5, S6, and S7, characterized by charge densities suggesting non-polar interactions; (4) the weak acceptor region, represented by segment S8, featuring charge densities corresponding to relatively feeble acceptor attributes; and finally, (5) the strong acceptor region, encompassing segments denoted as S9 and S10, with charge densities signifying potent acceptor properties. This all-inclusive classification scheme supports researchers in discerning distinct molecular interactions, providing valuable insights into the charge distributions and functional characteristics of various molecular segments, paving the way for advanced research in various scientific applications. This classification allows for a thorough characterization of the charge density distributions within the Sσ-profiles, enabling a better understanding of the molecules under investigation's hydrogen bonding capabilities and non-polar characteristics. In order to characterize the Sσ-profile of the modelled DESs, a fundamental step involves calculating the molar weighted average of their constituent molecules. This approach, widely accepted and applied in the scientific literature, provides a standard method for defining the Sσ-profile of DESs.104–108 By incorporating the contributions of each constituent in a weighted manner, the resulting Sσ-profile offers insights into the DES system's collective charge distribution and solvation behaviour.54 The equation is formulated in the following manner:| |
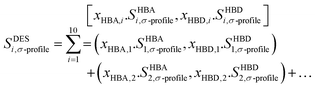 | (19) |
The terms xHBA and xHBD in the equation signify the mole fractions of the hydrogen bond acceptor (HBA) and hydrogen bond donor (HBD), respectively. Furthermore, Sσ-profile functions imply a sigma-profile descriptor located in the ‘i’ region, including S1 through S10.
3.3. Outlier detection
The disputed or outlier data exhibit dissimilar behaviour compared to the remaining data points. The emergence of such data can often be attributed to errors occurring during the experimental process or instrumental limitations. Detecting potentially problematic data within a dataset is vital to prevent incorrect interpretations of the established model and optimize its performance. To accomplish this, the leverage method was implemented, defining the Hat matrix as stated below:
The matrix U possesses dimensions i × j, wherein i corresponds to the parameter count and j signifies the training data point numbers. A graphical representation called William's plot is created to evaluate the accuracy of the dataset. This plot showcases the standardized residuals plotted against the Hat values. A defined region within this plot is considered reliable, and any data points located outside this region are regarded as suspected data. In order to establish a reliable zone, the range of standardized residuals is constrained from −3 to 3, while the Hat values are limited from 0 to the critical leverage limit.109,110
| |
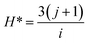 | (21) |
The crucial threshold, an essential parameter for this calculation, is derived using the provided formula. This delineation of the reliable zone aids in identifying the data points that conform to expected patterns and lie within the boundaries of statistical reliability, thereby contributing to the accurate assessment and interpretation of the dataset. Fig. 1 presents William's plot of the CO2 solubility data bank, offering crucial insights into the reliability of the data points utilized in the analysis. It is evident that a significant majority of the data points, out of the total 1973, exhibit reliability. Specifically, a limited number of outliers are identified: 47 outliers for the GPR-Matern model, 50 outliers for the GPR-exponential model, 52 outliers for the GPR-squared exponential model, and 60 outliers for the GPR-rational quadratic model. These outliers warrant further examination and consideration due to their deviation from the expected patterns observed in most of the dataset.
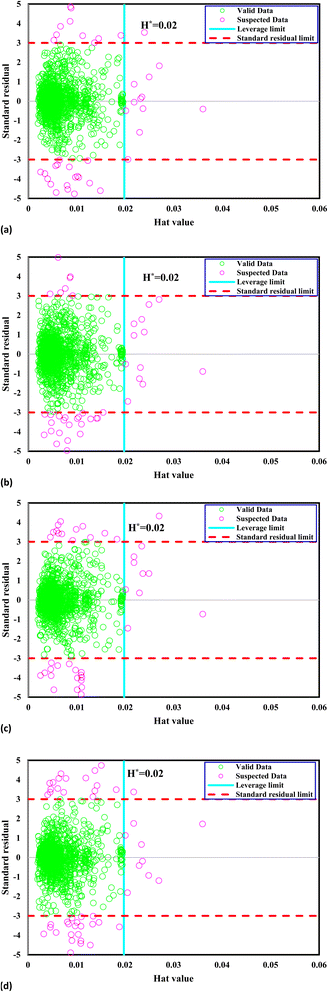 |
| | Fig. 1 William's plot of the CO2 solubility data bank to find outliers for Kernel-based GPR model of (a) Matern, (b) exponential, (c) squared exponential, (d) rational quadratic. | |
3.4. Statistical evaluations
A range of statistical parameters were calculated to determine the effectiveness of the developed ML models in predicting outcomes. These parameters included average absolute relative deviation (AARD), mean absolute error (MAE), root mean square error (RMSE), and the determination coefficient (R2). Model fit adequacy can be evaluated by considering R2, where a higher R2 value signifies a more favourable model fit. The AARD, MAE, and RMSE values, in conjunction with the provided statistical parameter expressions (eqn (22)–(25)), serve as means to assess the disparity between experimentally measured and predicted CO2 solubility in DES. These parameters effectively characterise actual and predicted solubility deviations, contributing to the total calculation and assessment of the model's accuracy and performance.| |
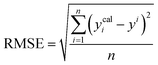 | (22) |
| |
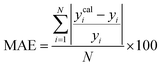 | (23) |
| |
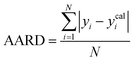 | (24) |
| |
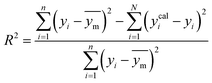 | (25) |
In the given equation, N denotes the total data points available. Within this equation, yi signifies the experimental solubility of CO2 in DES, 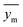 represents the experimental dataset average, and ycali represents the calculated CO2 solubility derived from both the ML or COSMO-RS models.
represents the experimental dataset average, and ycali represents the calculated CO2 solubility derived from both the ML or COSMO-RS models.
4. Results and discussions
4.1. Analysis of sensitivity
To develop an accurate model, it is imperative to ascertain the impacts of the input variables on the solubility of CO2 in DES. An inherent requirement for assessing the significance of individual input parameters is the implementation of a sensitivity analysis, yielding the relevancy factor, which can be determined subsequently:| |
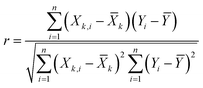 | (26) |
The variables Xk,i, ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) k, Yi, and Ȳ are defined as follows: Xk,i represents the ‘k’-th input,
k, Yi, and Ȳ are defined as follows: Xk,i represents the ‘k’-th input, ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) k denotes the average of inputs, Yi corresponds to the ‘i’-th output, and Ȳ represents averaging outputs. A greater ‘r’ value associated with an input parameter signifies heightened effectiveness in influencing CO2 solubility, whereas a smaller value indicates reduced impact. In this study, Fig. 2 offers a visually compelling depiction of great importance, providing valuable insights into the correlation between the input variable and the solubility of CO2. Through an in-depth sensitivity analysis, the pivotal input variables leading to CO2 solubility estimation have been discerned, and the results are outlined as follows: among the various input factors, the pressure, S5, and S6 exhibit substantial influence, signifying ‘r’ values of 0.65, 0.41, and 0.38, respectively. An intricate interplay exists between the inputs and CO2 solubility, as evidenced by their direct relationship. It is fascinating to highlight the ‘r’ value corresponding to temperature, which appears relatively small compared to other input variables.
k denotes the average of inputs, Yi corresponds to the ‘i’-th output, and Ȳ represents averaging outputs. A greater ‘r’ value associated with an input parameter signifies heightened effectiveness in influencing CO2 solubility, whereas a smaller value indicates reduced impact. In this study, Fig. 2 offers a visually compelling depiction of great importance, providing valuable insights into the correlation between the input variable and the solubility of CO2. Through an in-depth sensitivity analysis, the pivotal input variables leading to CO2 solubility estimation have been discerned, and the results are outlined as follows: among the various input factors, the pressure, S5, and S6 exhibit substantial influence, signifying ‘r’ values of 0.65, 0.41, and 0.38, respectively. An intricate interplay exists between the inputs and CO2 solubility, as evidenced by their direct relationship. It is fascinating to highlight the ‘r’ value corresponding to temperature, which appears relatively small compared to other input variables.
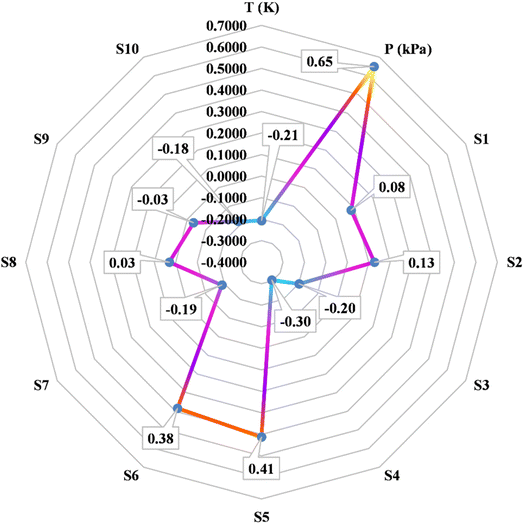 |
| | Fig. 2 The investigation focuses on assessing the sensitivity of input parameters concerning CO2 solubility in DES. | |
4.2. Modeling results
A set of matching statistical parameters assumes great importance in the pursuit of a thorough assessment of the proposed model's performance. These parameters act as a reliable means to quantify the level of agreement between the experimentally measured CO2 solubility values and those predicted by the model. These factors' values are computed and documented in Table 1. An insightful evaluation of the GPR models employing diverse kernel functions has yielded essential R2 values. Specifically, the Matern kernel function exhibits remarkable performance with an R2 value of 1.00, signifying optimal data-model fit. The exponential kernel function follows with an R2 value of 0.998, underscoring its notable capability to capture the underlying CO2 solubility behaviour. Furthermore, the squared exponential and rational quadratic kernel functions both demonstrate robust performance, exhibiting R2 values of 0.997 each. These high R2 values reflect the strong alignment between the predicted and experimental CO2 solubility values, validating the efficacy of the respective GPR models.
Table 1 The statistical metrics of the GPR models proposed in this study
| Model |
Group |
R2 |
MRE (%) |
MSE |
RMSE |
STD |
| Matern |
Train data |
0.9983 |
1.0314 |
0.0026 |
0.0505 |
0.0373 |
| Test data |
0.9978 |
1.0196 |
0.0035 |
0.0592 |
0.0479 |
| Total data |
0.9982 |
1.0285 |
0.0028 |
0.0592 |
0.0402 |
| Exponential |
Train data |
0.9981 |
1.1711 |
0.0030 |
0.0545 |
0.0396 |
| Test data |
0.9975 |
1.1900 |
0.0040 |
0.0631 |
0.0477 |
| Total data |
0.9979 |
1.1758 |
0.0032 |
0.0631 |
0.0418 |
| Squared exponential |
Train data |
0.9963 |
1.6176 |
0.0057 |
0.0754 |
0.0555 |
| Test data |
0.9958 |
1.5243 |
0.0068 |
0.0824 |
0.0654 |
| Total data |
0.9962 |
1.5943 |
0.0060 |
0.0824 |
0.0582 |
| Rational quadratic |
Train data |
0.9939 |
2.0755 |
0.0094 |
0.0969 |
0.0714 |
| Test data |
0.9926 |
2.1358 |
0.0119 |
0.1092 |
0.0851 |
| Total data |
0.9936 |
2.0906 |
0.0100 |
0.1092 |
0.0750 |
A broad evaluation of the error parameters, including STD, RMSE, MSE, and MRE, has provided valuable insights into the training performance of the proposed GPR models. The analysis reveals that the models have effectively captured the underlying patterns and trends within the training data, as evidenced by the acceptable precision reflected in these error metrics. In predictive modelling, evaluating a model's performance extends beyond its accuracy in predicting the training data. Equally crucial is assessing the model's ability to generalize and forecast CO2 solubility for previously unseen data points. This aspect assumes particular importance as it reflects the model's capacity to capture underlying trends and patterns in the data rather than merely memorizing the specific instances from the training set. To estimate the predictive performance of the proposed models on unseen data, accurate evaluation was conducted using the testing dataset. Notably, matern kernel in the GPR model emerged as the top performer, showcasing excellent accuracy in forecasting CO2 uptake for previously unobserved instances. This is evident from the noteworthy values of various statistical metrics, including a very high R2 value of 0.998, denoting an almost perfect model fit to unknown data. Additionally, the low values of MRE (1.02%), MSE (0.004), RMSE (0.059), and STD (0.048) further reinforce the model' s superior predictive capabilities. These metrics indicate minimal errors and deviations in the model's predictions, underscoring its robustness and generalization ability beyond the training data. The exemplary performance of the GPR model with the exponential kernel function affirms its efficacy in capturing the underlying complexities of CO2 solubility in DES, thus promoting its potential applications in carbon capture and utilization research.
In Fig. 3, the predicted and experimental CO2 solubility values are concomitantly displayed, providing additional validation of the accuracy achieved by the confirmed models. A precise examination of the data reveals a remarkable alignment between the experimental CO2 solubility and the varied GPR models under consideration. This notable agreement substantiates the models' ability to capture and predict the CO2 solubility behaviour within DES faithfully. A widespread analysis of the proposed models highlights a striking correspondence between the predicted CO2 adsorption values and the experimental CO2 solubility. This close agreement stands as a testament to the exemplary predictive capability of the GPR models in estimating CO2 solubility within DES. The precise alignment between the predicted and experimental values underscores the models' ability to accurately capture the intricate solubility phenomena, with potential implications in carbon capture, storage, and utilization applications. GPR models' significant performance advances the field of predictive modelling as researchers gain confidence in employing these models to make informed decisions and optimize processes related to CO2 solubility.
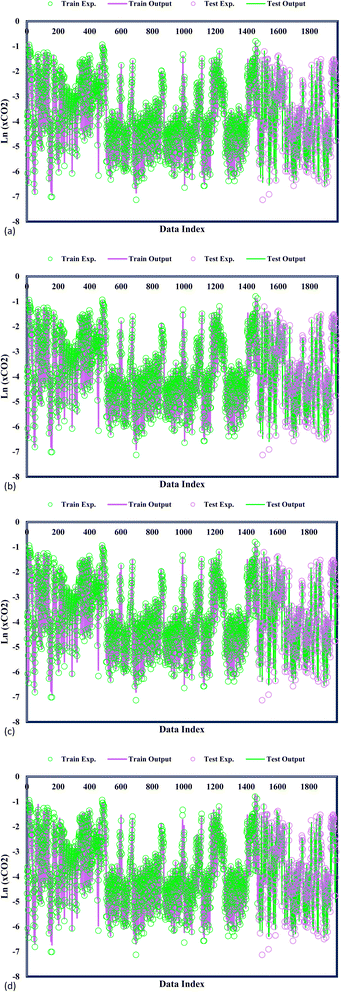 |
| | Fig. 3 Model and experimental outputs of kernel-based GPR model of (a) Matern, (b) exponential, (c) squared exponential, (d) rational quadratic. | |
In Fig. 4, the predicted values for CO2 solubility presentation are accompanied by the corresponding experimental data visualization, providing an in-depth overview of the model's performance. Each data point is accurately plotted, with the fitting lines superimposed to accentuate the correlation between the predicted and experimental values. Strikingly, all the predicted CO2 solubility values closely align with their respective experimental counterparts, leading to fitting lines boasting correlation coefficients surpassing 0.98. This high level of correlation signifies the models' remarkable accuracy in capturing the intricate solubility behaviours. An influential visual representation of the GPR models' predictive performance is depicted by the fitting lines intersecting with the 45° line in the graph. This alignment illustrates the models' precision in predicting the experimental CO2 solubility data, representing remarkable accuracy. When the predicted values closely mirror the experimental data along this diagonal reference line, it implies that the models can precisely capture the underlying solubility patterns and trends. This alignment supports confidence in the model's ability to accurately represent CO2 solubility behaviours in DES, enhancing their applicability in various scientific and industrial applications, including carbon capture technologies. As researchers interpret this graph, they gain valuable insights into the reliability and efficacy of the GPR models in predicting CO2 solubility, contributing to advancements in the field and informing decision-making processes in related research and engineering endeavours. The bisector line, representing a critical standard for precision in established models, serves as an essential reference in assessing their accuracy and predictive capabilities. Among the array of models under consideration, one model stands out for its unique precision—the GPR model equipped with the Matern kernel function. This model attains a correlation coefficient of 1, indicating a perfect match between the predicted and experimental CO2 solubility values. The impeccable alignment along the bisector line reflects the model's remarkable ability to precisely capture the intricate solubility behaviours, thus presenting an invaluable tool for predicting CO2 solubility within DES.
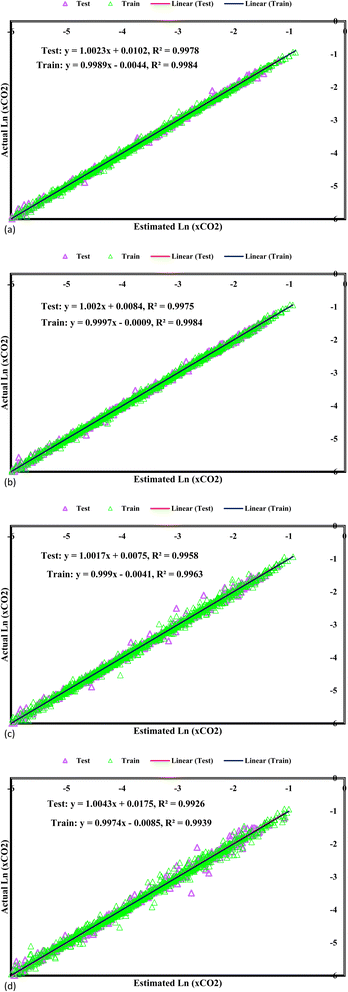 |
| | Fig. 4 Cross plots of Kernel-based GPR model of (a) Matern, (b) exponential, (c) squared exponential, (d) rational quadratic. | |
Fig. 5 reveals fundamental understandings of the GPR models' predictive efficacy, prominently exhibiting the relative disparities between the experimentally measured CO2 solubility and the estimated values. The visual depiction highlights the model's accuracy in capturing the actual solubility values, represented by the absolute deviation points. Notably, the GPR models employing the exponential, squared exponential, and rational quadratic kernel functions exhibit remarkable accuracy, with the highest level deviation below 30%. This finding indicates that these models closely match the predicted and experimental CO2 solubility values, further bolstering their credibility and reliability for CO2 solubility prediction in DES. In particular, the Matern kernel function surpasses in accuracy, showcasing deviation points below 20%, emphasizing its superior precision in capturing the underlying solubility behaviour. By providing a wide-ranging assessment of the model's predictive prowess, these insights guide researchers in selecting the most suitable GPR models for specific applications, ultimately supporting advances in carbon capture and utilization research and enhancing sustainable solutions for mitigating greenhouse gas emissions.
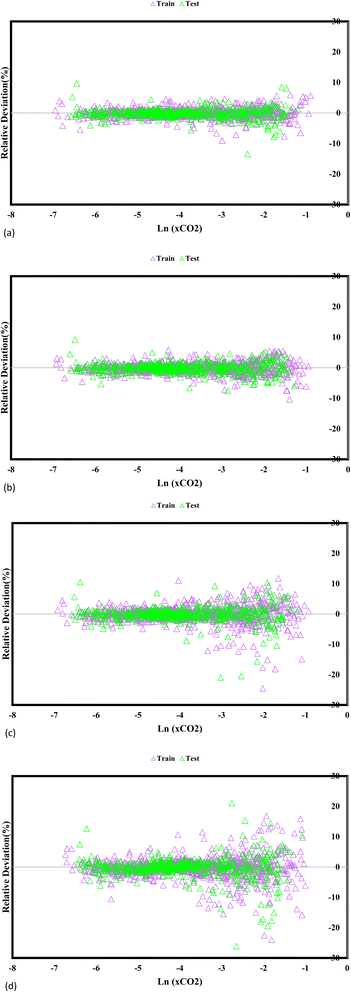 |
| | Fig. 5 A comparative analysis of the evaluation of the predictive capabilities of the GPR models employing distinct kernel functions, namely (a) exponential, (b) Matern, (c) squared exponential, and (d) rational quadratic, against the experimental data. | |
The assessment of the results reveals the appropriate performance of the proposed GPR models in predicting CO2 solubility within DES. In addition to other influential factors, Fig. 6 highlights the pivotal role of temperature in determining CO2 solubility within DES. The discovery of a negative correlation between temperature and CO2 solubility is another finding, as elevated temperatures result in decreased CO2 solubility due to the exothermic nature of the process. This insight has important implications for various applications, especially in carbon capture processes, where temperature control is crucial in enhancing CO2 solubility efficiency. Interestingly, the predictive capability of the Matern kernel function stands out prominently, demonstrating a remarkable fitness with the experimental data. This high level of agreement underscores the Matern kernel's superior capacity to capture the intricate solubility variations influenced by temperature changes. Such precision is invaluable for researchers and engineers seeking to optimize carbon capture technologies and improve the overall performance of CO2 solubility processes.
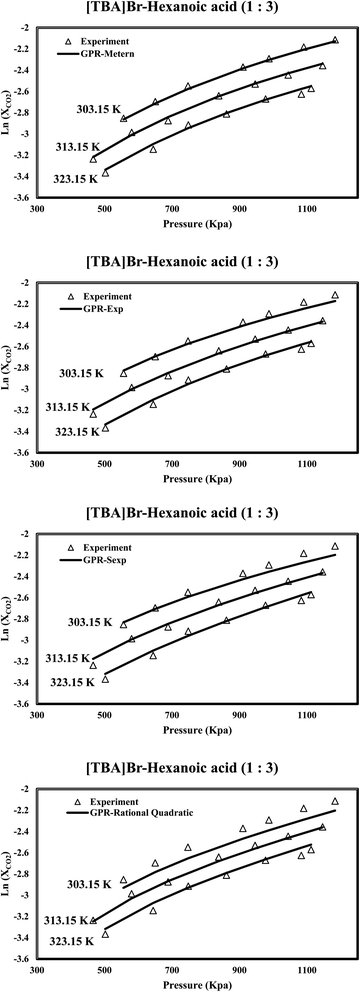 |
| | Fig. 6 The investigation examines the predicted CO2 solubility in [TBA]Br-hexanoic acid (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) concerning pressure variations at different temperatures. 3) concerning pressure variations at different temperatures. | |
5. Conclusion
The evaluation of GPR models using various kernel functions yielded essential R2 values. The Matern kernel function demonstrated high performance with an R2 value of 0.998, closely followed by the exponential kernel function with an R2 value of 0.998. The squared exponential and rational quadratic kernel functions also performed robustly, achieving R2 values of 0.996 and 0.993, respectively. Evaluation of error parameters (STD, RMSE, MSE, and MRE) confirmed the models' precision in capturing underlying patterns within the training data. The Matern kernel function-based GPR model exhibited extraordinary accuracy, with an impressive R2 value of 0.998 and notably low values for MRE (1.02%), MSE (0.004), RMSE (0.059), and STD (0.048). These results highlight the model is astonishing predictive capabilities and potential applicability in carbon capture and utilization research. A thorough data analysis further confirmed a remarkable alignment between experimental CO2 solubility and various GPR models, validating their faithful prediction of CO2 solubility within DES.
The complete assessment emphasized a striking correspondence between the predicted and experimental CO2 solubility values, underscoring the exemplary predictive capability of the models. The precise alignment between predicted and experimental values underscored the models' accuracy in capturing intricate solubility phenomena, potentially benefiting carbon capture, storage, and utilization endeavours. Among these models, the GPR model utilizing the Matern kernel function stood out due to its excellent precision, making it a valuable tool for predicting CO2 solubility within DES. The visual representation emphasized the accuracy of GPR models employing exponential, squared exponential, and rational quadratic kernels, with deviations from valid solubility values remaining below 30% at various points. The Matern kernel demonstrated superior precision with deviation points below 20%, further accentuating its efficacy. These insights aid in selecting the appropriate model for specific applications, thereby advancing carbon capture research and promoting sustainable solutions for mitigating greenhouse gases. The evolving hybrid QSPR-GPR model emerges as a versatile and accurate means for predicting CO2 solubility in DES, playing a pivotal role in advancements within carbon capture and utilization processes. Its invaluable contributions steer us towards a greener and more sustainable future, paving the way for innovative solutions to address the pressing challenges of greenhouse gas mitigation. As research in DESs continues to progress, the QSPR-GPR model remains an essential tool for researchers and engineers seeking to optimize solvent systems and enhance the efficiency of carbon capture technologies.
Conflicts of interest
There are no conflicts to declare.
References
- I. Salahshoori, M. N. Jorabchi, M. Asghari, S. Ghasemi and S. Wohlrab, J. Mater. Res. Technol., 2023, 23, 1862–1886 CrossRef CAS.
- T. R. Anderson, E. Hawkins and P. D. Jones, Endeavour, 2016, 40, 178–187 CrossRef PubMed.
- I. Salahshoori, A. Babapoor and A. Seyfaee, Polym. Bull., 2022, 79, 3595–3630 CrossRef CAS.
- L. Chen, G. Msigwa, M. Yang, A. I. Osman, S. Fawzy, D. W. Rooney and P.-S. Yap, Environ. Chem. Lett., 2022, 20, 2277–2310 CrossRef CAS PubMed.
- I. Salahshoori, M. Asghari, M. Namayandeh Jorabchi, S. Wohlrab, M. Rabiei, M. Raji and M. Afsari, Arabian J. Chem., 2023, 16, 104792 CrossRef CAS.
- I. Salahshoori, I. Cacciotti, A. Seyfaee and A. Babapoor, J. Polym. Res., 2021, 28, 223 CrossRef CAS.
- W. Gao, S. Liang, R. Wang, Q. Jiang, Y. Zhang, Q. Zheng, B. Xie, C. Y. Toe, X. Zhu, J. Wang, L. Huang, Y. Gao, Z. Wang, C. Jo, Q. Wang, L. Wang, Y. Liu, B. Louis, J. Scott, A.-C. Roger, R. Amal, H. He and S.-E. Park, Chem. Soc. Rev., 2020, 49, 8584–8686 RSC.
- M. R. Ketabchi, S. Babamohammadi, W. G. Davies, M. Gorbounov and S. Masoudi Soltani, Carbon Capture Sci. Technol., 2023, 6, 100087 CrossRef CAS.
- O. H. Gunawardene, C. A. Gunathilake, K. Vikrant and S. M. Amaraweera, Atmosphere, 2022, 13(3), 397 CrossRef CAS.
- A. Dubey and A. Arora, J. Cleaner Prod., 2022, 373, 133932 CrossRef CAS.
- W. Faisal Elmobarak, F. Almomani, M. Tawalbeh, A. Al-Othman, R. Martis and K. Rasool, Fuel, 2023, 344, 128102 CrossRef CAS.
- N. Nasirpour, M. Mohammadpourfard and S. Zeinali Heris, Chem. Eng. Res. Des., 2020, 160, 264–300 CrossRef CAS.
- J. Płotka-Wasylka, M. de la Guardia, V. Andruch and M. Vilková, Microchem. J., 2020, 159, 105539 CrossRef.
- Y. P. Mbous, M. Hayyan, A. Hayyan, W. F. Wong, M. A. Hashim and C. Y. Looi, Biotechnol. Adv., 2017, 35, 105–134 CrossRef CAS PubMed.
- E. L. Smith, A. P. Abbott and K. S. Ryder, Chem. Rev., 2014, 114, 11060–11082 CrossRef CAS PubMed.
- B. B. Hansen, S. Spittle, B. Chen, D. Poe, Y. Zhang, J. M. Klein, A. Horton, L. Adhikari, T. Zelovich, B. W. Doherty, B. Gurkan, E. J. Maginn, A. Ragauskas, M. Dadmun, T. A. Zawodzinski, G. A. Baker, M. E. Tuckerman, R. F. Savinell and J. R. Sangoro, Chem. Rev., 2021, 121, 1232–1285 CrossRef CAS PubMed.
- P. Dehury, U. Mahanta, R. Singh and T. Banerjee, J. Mol. Liq., 2023, 379, 121700 CrossRef CAS.
- P. K. Naik, D. Kundu, P. Bairagya and T. Banerjee, Chem. Thermodyn. Thermal Anal., 2021, 3–4, 100011 CrossRef.
- M. Mohan, P. K. Naik, T. Banerjee, V. V. Goud and S. Paul, Fluid Phase Equilib., 2017, 448, 168–177 CrossRef CAS.
- M. del Mar Contreras-Gámez, Á. Galán-Martín, N. Seixas, A. M. da Costa Lopes, A. Silvestre and E. Castro, Bioresour. Technol., 2023, 369, 128396 CrossRef PubMed.
- C. Ma, S. Sarmad, J.-P. Mikkola and X. Ji, Energy Procedia, 2017, 142, 3320–3325 CrossRef CAS.
- Y. Gu, Y. Hou, S. Ren, Y. Sun and W. Wu, ACS Omega, 2020, 5, 6809–6816 CrossRef CAS PubMed.
- I. Cichowska-Kopczyńska, B. Nowosielski and D. Warmińska, Molecules, 2023, 28(14), 5293 CrossRef PubMed.
- M. Mohan, O. Demerdash, B. A. Simmons, J. C. Smith, M. K. Kidder and S. Singh, Green Chem., 2023, 25, 3475–3492 RSC.
- J. Wang, H. Cheng, Z. Song, L. Chen, L. Deng and Z. Qi, Ind. Eng. Chem. Res., 2019, 58, 17514–17523 CrossRef CAS.
- A. Hatami, I. Salahshoori, N. Rashidi and D. Nasirian, Chin. J. Chem. Eng., 2020, 28, 2267–2284 CrossRef CAS.
- A. Dashti, M. Raji, P. Amani, A. Baghban and A. H. Mohammadi, Sep. Sci. Technol., 2021, 56, 2351–2368 CrossRef CAS.
- M. Heydari Dokoohaki and A. R. Zolghadr, J. Phys. Chem. B, 2021, 125, 10035–10046 CrossRef CAS PubMed.
- D. V. Wagle, L. Adhikari and G. A. Baker, Fluid Phase Equilib., 2017, 448, 50–58 CrossRef CAS.
- H. S. Esfahani, A. Khoshsima, G. Pazuki and A. Hosseini, J. Mol. Liq., 2023, 381, 121641 CrossRef CAS.
- T. Amini, A. Haghtalab and J. Y. Seyf, J. Chem. Eng. Data, 2022, 67, 3252–3267 CrossRef CAS.
- M. Moghimi, A. Roosta, J. Hekayati and N. Rezaei, J. Mol. Liq., 2023, 371, 121126 CrossRef CAS.
- H. Ghanbari-Kalajahi and A. Haghtalab, J. Mol. Liq., 2023, 375, 121310 CrossRef CAS.
- R. Haghbakhsh, M. Keshtkar, A. Shariati and S. Raeissi, Fluid Phase Equilib., 2022, 561, 113535 CrossRef CAS.
- K. Parvaneh, R. Haghbakhsh, A. R. C. Duarte and S. Raeissi, Front. Chem., 2022, 10, 909485 CrossRef CAS PubMed.
- G. Yu, N. F. Gajardo-Parra, M. Chen, B. Chen, G. Sadowski and C. Held, AIChE J., 2023, 69, e18053 CrossRef CAS.
- A. R. Shaikh, M. Ashraf, T. AlMayef, M. Chawla, A. Poater and L. Cavallo, Chem. Phys. Lett., 2020, 745, 137239 CrossRef CAS.
- R. Biswas, J. Mol. Model., 2022, 28, 231 CrossRef CAS PubMed.
- Y. Zeng, K. Li, Q. Zhu, J. Wang, Y. Cao and S. Lu, Chem. Eng. Sci., 2018, 192, 94–102 CrossRef CAS.
- A. R. Shaikh, H. Karkhanechi, E. Kamio, T. Yoshioka and H. Matsuyama, J. Phys. Chem. C, 2016, 120, 27734–27745 CrossRef CAS.
- O. Alioui, Y. Benguerba and I. M. Alnashef, J. Mol. Liq., 2020, 307, 113005 CrossRef CAS.
- J. Wang, Z. Song, L. Chen, T. Xu, L. Deng and Z. Qi, Green Chem. Eng., 2021, 2, 431–440 CrossRef.
- A. Gutiérrez, S. Rozas, P. Hernando, R. Alcalde, M. Atilhan and S. Aparicio, J. Mol. Liq., 2022, 366, 120285 CrossRef.
- N. Islam, H. Warsi Khan, A. A. Gari, M. Yusuf and K. Irshad, Fuel, 2022, 330, 125540 CrossRef CAS.
- Y. Wang, Y. Xin, F. Gao, S. Jiang, M. Li, S. Zhang, Y. Hu and Z. Liu, Ind. Eng. Chem. Res., 2022, 61, 1503–1513 CrossRef CAS.
- I. Salahshoori, M. Namayandeh Jorabchi, S. Ghasemi, A. Ranjbarzadeh-Dibazar, M. Vahedi and H. A. Khonakdar, Process Saf. Environ. Prot., 2023, 175, 473–494 CrossRef CAS.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- I. Salahshoori, M. Namayandeh Jorabchi, S. Ghasemi, M. Golriz, S. Wohlrab and H. A. Khonakdar, Sep. Purif. Technol., 2023, 319, 124081 CrossRef CAS.
- I. Salahshoori, M. N. Jorabchi, S. Ghasemi, M. Golriz, S. Wohlrab and H. A. Khonakdar, Desalination, 2023, 559, 116654 CrossRef CAS.
- I. Salahshoori, M. Namayandeh Jorabchi, S. Ghasemi, S. M. S. Mirnezami, M. A. L. Nobre and H. A. Khonakdar, J. Water Process. Eng., 2023, 55, 104081 CrossRef.
- Y. Liu, H. Yu, Y. Sun, S. Zeng, X. Zhang, Y. Nie, S. Zhang and X. Ji, Front. Chem., 2020, 8, 82 CrossRef PubMed.
- H. S. Salehi, R. Hens, O. A. Moultos and T. J. H. Vlugt, J. Mol. Liq., 2020, 316, 113729 CrossRef CAS.
- Y. Tian, X. Wang, Y. Liu and W. Hu, J. Mol. Liq., 2023, 383, 122066 CrossRef CAS.
- T. Lemaoui, A. Boublia, A. S. Darwish, M. Alam, S. Park, B.-H. Jeon, F. Banat, Y. Benguerba and I. M. AlNashef, ACS Omega, 2022, 7, 32194–32207 CrossRef CAS PubMed.
- T. Lemaoui, A. Boublia, S. Lemaoui, A. S. Darwish, B. Ernst, M. Alam, Y. Benguerba, F. Banat and I. M. AlNashef, ACS Sustain. Chem. Eng., 2023, 11, 9564–9580 CrossRef CAS.
- O. Nordness, P. Kelkar, Y. Lyu, M. Baldea, M. A. Stadtherr and J. F. Brennecke, J. Mol. Liq., 2021, 334, 116019 CrossRef CAS.
- M. J. Tillotson, N. I. Diamantonis, C. Buda, L. W. Bolton and E. A. Müller, Phys. Chem. Chem. Phys., 2023, 25, 12607–12628 RSC.
- A. Maleki, A. Haghighi and I. Mahariq, J. Mol. Liq., 2021, 322, 114843 CrossRef CAS.
- O. I. Abiodun, A. Jantan, A. E. Omolara, K. V. Dada, N. A. Mohamed and H. Arshad, Heliyon, 2018, 4, e00938 CrossRef PubMed.
- M. H. Ahmadi, A. Baghban, M. Ghazvini, M. Hadipoor, R. Ghasempour and M. R. Nazemzadegan, J. Therm. Anal. Calorim., 2020, 139, 2381–2394 CrossRef CAS.
- A. Baghban, P. Abbasi and P. Rostami, Pet. Sci. Technol., 2016, 34, 1698–1704 CrossRef CAS.
- A. Baghban, T. Kashiwao, M. Bahadori, Z. Ahmad and A. Bahadori, Pet. Sci. Technol., 2016, 34, 891–897 CrossRef CAS.
- A. Baghban, M. Bahadori, Z. Ahmad, T. Kashiwao and A. Bahadori, Pet. Sci. Technol., 2016, 34, 933–939 CrossRef CAS.
- A. Bemani, A. Baghban and A. H. Mohammadi, J. Pet. Sci. Eng., 2020, 184, 106459 CrossRef CAS.
- A. Bahadori, A. Baghban, M. Bahadori, M. Lee, Z. Ahmad, M. Zare and E. Abdollahi, Appl. Therm. Eng., 2016, 102, 432–446 CrossRef CAS.
- A. Bemani, A. Baghban, A. Mosavi and S. Shahab, Eng. Appl. Comput. Fluid Mech., 2020, 14(1), 818–834 Search PubMed.
- F. Masi, I. Stefanou, P. Vannucci and V. Maffi-Berthier, J. Mech. Phys. Solids, 2021, 147, 104277 CrossRef.
- J. Yang, M. J. Knape, O. Burkert, V. Mazzini, A. Jung, V. S. J. Craig, R. A. Miranda-Quintana, E. Bluhmki and J. Smiatek, Phys. Chem. Chem. Phys., 2020, 22, 24359–24364 RSC.
- F. S. Ghareh Bagh, K. Shahbaz, F. S. Mjalli, I. M. AlNashef and M. A. Hashim, Fluid Phase Equilib., 2013, 356, 30–37 CrossRef.
- I. Adeyemi, M. R. M. Abu-Zahra and I. M. AlNashef, J. Mol. Liq., 2018, 256, 581–590 CrossRef CAS.
- N.-D. Hoang, A.-D. Pham, Q.-L. Nguyen and Q.-N. Pham, Adv. Civ. Eng., 2016, 2016, 2861380 Search PubMed.
- C. E. Rasmussen, in Advanced Lectures on Machine Learning: ML Summer Schools 2003, Canberra, Australia, February 2–14, 2003, Tübingen, Germany, August 4–16, 2003, Revised Lectures, ed. O. Bousquet, U. von Luxburg and G. Rätsch, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, pp. 63–71, DOI:10.1007/978-3-540-28650-9_4.
- Q. Fu, W. Shen, X. Wei, P. Zheng, H. Xin and C. Zhao, Inf. Process. Agric., 2019, 6, 396–406 Search PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17 CAS.
- I. Salahshoori, N. Montazeri, A. Yazdanbakhsh, M. Golriz, R. Farhadniya and H. A. Khonakdar, ACS Appl. Mater. Interfaces, 2023, 15, 31185–31205 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C. 01, 2016 Search PubMed.
- I. Salahshoori, A. Mohseni, M. Namayandeh Jorabchi, S. Ghasemi, M. Afshar and S. Wohlrab, J. Mol. Liq., 2023, 375, 121286 CrossRef CAS.
- I. Salahshoori, M. Namayandeh Jorabchi, K. Valizadeh, A. Yazdanbakhsh, A. Bateni and S. Wohlrab, J. Mol. Liq., 2022, 363, 119793 CrossRef CAS.
- M. Mohan, T. Banerjee and V. V. Goud, J. Chem. Eng. Data, 2016, 61, 2923–2932 CrossRef CAS.
- F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, WIREs Comput. Mol. Sci., 2014, 4, 91–100 CrossRef CAS.
- Y. Li and Y. Jin, Renewable Energy, 2015, 77, 550–557 CrossRef CAS.
- F. Eckert and A. Klamt, AIChE J., 2002, 48, 369–385 CrossRef CAS.
- X. Li, M. Hou, B. Han, X. Wang and L. Zou, J. Chem. Eng. Data, 2008, 53, 548–550 CrossRef CAS.
- A. Alhadid, J. Safarov, L. Mokrushina, K. Müller and M. Minceva, Front. Chem., 2022, 10, 864663 CrossRef CAS PubMed.
- L. F. Zubeir, D. van Osch, M. A. A. Rocha, F. Banat and M. C. Kroon, J. Chem. Eng. Data, 2018, 63, 913–919 CrossRef CAS PubMed.
- R. B. Leron and M.-H. Li, Thermochim. Acta, 2013, 551, 14–19 CrossRef CAS.
- S. Sarmad, Y. Xie, J.-P. Mikkola and X. Ji, New J. Chem., 2017, 41, 290–301 RSC.
- G. Li, D. Deng, Y. Chen, H. Shan and N. Ai, Int. J. Greenhouse Gas Control, 2014, 75, 58–62 CAS.
- L. F. Zubeir, M. H. Lacroix and M. C. Kroon, J. Phys. Chem. B, 2014, 118, 14429–14441 CrossRef CAS PubMed.
- M. B. Haider, D. Jha, B. Marriyappan Sivagnanam and R. Kumar, J. Chem. Eng. Data, 2018, 63, 2671–2680 CrossRef CAS.
- F. Luo, X. Liu, S. Chen, Y. Song, X. Yi, C. Xue, L. Sun and J. Li, ACS Sustain. Chem. Eng., 2021, 9, 10250–10265 CrossRef CAS.
- Y. Ji, Y. Hou, S. Ren, C. Yao and W. Wu, Fluid Phase Equilib., 2016, 429, 14–20 CrossRef CAS.
- M. Lu, G. Han, Y. Jiang, X. Zhang, D. Deng and N. Ai, Int. J. Greenhouse Gas Control, 2015, 88, 72–77 CAS.
- Y. Chen, N. Ai, G. Li, H. Shan, Y. Cui and D. Deng, J. Chem. Eng. Data, 2014, 59, 1247–1253 CrossRef CAS.
- X. Liu, B. Gao, Y. Jiang, N. Ai and D. Deng, J. Chem. Eng. Data, 2017, 62, 1448–1455 CrossRef CAS.
- D. Deng, Y. Jiang, X. Liu, Z. Zhang and N. Ai, Int. J. Greenhouse Gas Control, 2016, 103, 212–217 CAS.
- H. Ghaedi, M. Ayoub, S. Sufian, A. M. Shariff, S. M. Hailegiorgis and S. N. Khan, J. Mol. Liq., 2017, 243, 564–571 CrossRef CAS.
- E. Ali, M. K. Hadj-Kali, S. Mulyono and I. Alnashef, Int. J. Greenhouse Gas Control, 2016, 47, 342–350 CrossRef CAS.
- Z. Song, X. Hu, H. Wu, M. Mei, S. Linke, T. Zhou, Z. Qi and K. Sundmacher, ACS Sustain. Chem. Eng., 2020, 8, 8741–8751 CrossRef CAS.
- A. Klamt, WIREs Comput. Mol. Sci., 2011, 1, 699–709 CrossRef CAS.
- M. Mohan, J. D. Keasling, B. A. Simmons and S. Singh, Green Chem., 2022, 24, 4140–4152 RSC.
- J. S. Torrecilla, J. Palomar, J. Lemus and F. Rodríguez, Green Chem., 2010, 12, 123–134 RSC.
- D. O. Abranches, Y. Zhang, E. J. Maginn and Y. J. Colón, Chem. Commun., 2022, 58, 5630–5633 RSC.
- A. Mouffok, D. Bellouche, I. Debbous, A. Anane, Y. Khoualdia, A. Boublia, A. S. Darwish, T. Lemaoui and Y. Benguerba, J. Mol. Liq., 2023, 375, 121321 CrossRef CAS.
- A. González de Castilla, J. P. Bittner, S. Müller, S. Jakobtorweihen and I. Smirnova, J. Chem. Eng. Data, 2020, 65, 943–967 CrossRef.
- I. I. I. Alkhatib, D. Bahamon, F. Llovell, M. R. M. Abu-Zahra and L. F. Vega, J. Mol. Liq., 2020, 298, 112183 CrossRef CAS.
- D. K. Mishra, G. Pugazhenthi and T. Banerjee, ACS Sustain. Chem. Eng., 2020, 8, 4910–4919 CrossRef CAS.
- Z. Sumer and R. C. Van Lehn, ACS Sustain. Chem. Eng., 2023, 11, 187–198 CrossRef CAS.
- X. Zhou, F. Zhou and M. Naseri, Sci. Rep., 2021, 11, 7203 CrossRef CAS PubMed.
- R. Razavi, A. Bemani, A. Baghban, A. H. Mohammadi and S. Habibzadeh, Fuel, 2019, 243, 133–141 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *d and
Amirhosein Yazdanbakhshe
*d and
Amirhosein Yazdanbakhshe
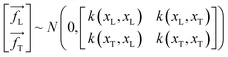
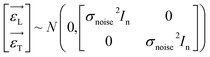
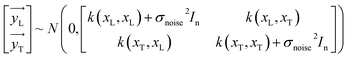
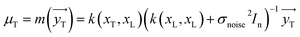
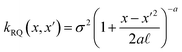
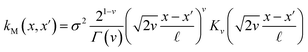
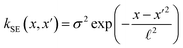
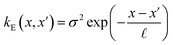
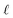 signify scale-mixture, amplitude, variance, and length scale, respectively. Moreover, the Kv, Γ, and v symbols denote the modified Bessel function, gamma function, and a positive parameter, respectively.
signify scale-mixture, amplitude, variance, and length scale, respectively. Moreover, the Kv, Γ, and v symbols denote the modified Bessel function, gamma function, and a positive parameter, respectively.
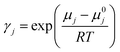
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16, also exhibited variations, enabling an extensive examination of the solubility behaviour of CO2 in DESs. Fig. S1 and S2† comprehensively summarize all the constituents involved in the DESs, including 25 HBDs and 23 HBAs. These figures offer an overview of the different components of the DESs studied. For a more in-depth analysis, Table S1† contains detailed information on temperatures, DES compositions (molar ratios, HBD, and HBA), CO2 solubility data, pressures, and the corresponding references. Researchers interested in exploring the specifics of this study are encouraged to refer to the ESI,† where inclusive data and references can be found.
16, also exhibited variations, enabling an extensive examination of the solubility behaviour of CO2 in DESs. Fig. S1 and S2† comprehensively summarize all the constituents involved in the DESs, including 25 HBDs and 23 HBAs. These figures offer an overview of the different components of the DESs studied. For a more in-depth analysis, Table S1† contains detailed information on temperatures, DES compositions (molar ratios, HBD, and HBA), CO2 solubility data, pressures, and the corresponding references. Researchers interested in exploring the specifics of this study are encouraged to refer to the ESI,† where inclusive data and references can be found.
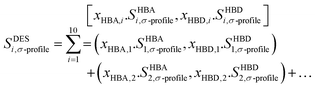

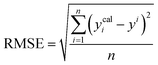

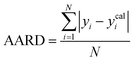
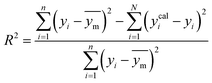
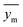 represents the experimental dataset average, and ycali represents the calculated CO2 solubility derived from both the ML or COSMO-RS models.
represents the experimental dataset average, and ycali represents the calculated CO2 solubility derived from both the ML or COSMO-RS models.
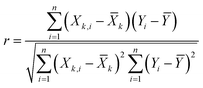
![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) k, Yi, and Ȳ are defined as follows: Xk,i represents the ‘k’-th input,
k, Yi, and Ȳ are defined as follows: Xk,i represents the ‘k’-th input, ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) k denotes the average of inputs, Yi corresponds to the ‘i’-th output, and Ȳ represents averaging outputs. A greater ‘r’ value associated with an input parameter signifies heightened effectiveness in influencing CO2 solubility, whereas a smaller value indicates reduced impact. In this study, Fig. 2 offers a visually compelling depiction of great importance, providing valuable insights into the correlation between the input variable and the solubility of CO2. Through an in-depth sensitivity analysis, the pivotal input variables leading to CO2 solubility estimation have been discerned, and the results are outlined as follows: among the various input factors, the pressure, S5, and S6 exhibit substantial influence, signifying ‘r’ values of 0.65, 0.41, and 0.38, respectively. An intricate interplay exists between the inputs and CO2 solubility, as evidenced by their direct relationship. It is fascinating to highlight the ‘r’ value corresponding to temperature, which appears relatively small compared to other input variables.
k denotes the average of inputs, Yi corresponds to the ‘i’-th output, and Ȳ represents averaging outputs. A greater ‘r’ value associated with an input parameter signifies heightened effectiveness in influencing CO2 solubility, whereas a smaller value indicates reduced impact. In this study, Fig. 2 offers a visually compelling depiction of great importance, providing valuable insights into the correlation between the input variable and the solubility of CO2. Through an in-depth sensitivity analysis, the pivotal input variables leading to CO2 solubility estimation have been discerned, and the results are outlined as follows: among the various input factors, the pressure, S5, and S6 exhibit substantial influence, signifying ‘r’ values of 0.65, 0.41, and 0.38, respectively. An intricate interplay exists between the inputs and CO2 solubility, as evidenced by their direct relationship. It is fascinating to highlight the ‘r’ value corresponding to temperature, which appears relatively small compared to other input variables.



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) concerning pressure variations at different temperatures.
3) concerning pressure variations at different temperatures.
