Open Access Article
Open Access ArticleElectron density mapping of boron clusters via convolutional neural networks to augment structure prediction algorithms†
Pinaki Saha a and
Minh Tho Nguyen
a and
Minh Tho Nguyen *bc
*bc
aSchool of Physics, Engineering and Computer Science, University of Hertfordshire, UK
bLaboratory for Chemical Computation and Modelling, Institute for Artificial Intelligence, Van Lang University, Ho Chi Minh City, Vietnam
cFaculty of Applied Technology, School of Technology, Van Lang University, Ho Chi Minh City, Vietnam. E-mail: minhtho.nguyen@vlu.edu.vn
First published on 19th October 2023
Abstract
Determination and prediction of atomic cluster structures is an important endeavor in the field of nanoclusters and thereby in materials research. To a large extent the fundamental properties of a nanocluster are mainly governed by its molecular structure. Traditionally, structure elucidation is achieved using quantum mechanics (QM) based calculations that are usually tedious and time consuming for large nanoclusters. Various structural prediction algorithms have been reported in the literature (CALYPSO, USPEX). Although they tend to accelerate the structure exploration, they still require the aid of QM based calculations for structure evaluation. This makes the structure prediction process quite a computationally expensive affair. In this paper, we report on the creation of a convolutional neural network model, which can give relatively accurate energies for the ground state of nanoclusters from the promolecule density on the fly and could thereby be utilized for aiding structure prediction algorithms. We tested our model on dataset consisting of pure boron nanoclusters of varying sizes.
1. Introduction
Nanoscience involves the study of structures and properties of nanomaterials. An important class of nanomaterials is nanoclusters. Nanoclusters are defined as atomic aggregates that exist in the nanoscale. Transition metal clusters, with diameters ranging from 1 to 10 nm, are of significant theoretical and practical interest due to their actual and potential use in ultrahigh density magnetic recording materials, catalytic particles in the synthesis of chemical compounds, carbon nanotubes and several applications in electronics and optics.1–10 The geometrical structure plays an important role in the determination of several physico-chemical properties of nanoclusters.1,2 Theoretically, structure determination is conventionally done via electronic structure calculations using a variety of quantum mechanics (QM) based methods based on molecular orbital theory (wavefunction) and density functional theory (DFT). This is often a tedious, slow and computationally expensive process for medium and large size systems.An alternate solution for speeding up calculations is the use of parameterized molecular mechanics (MM) based force fields that treat atoms and bond as classical objects and use Newtonian mechanics to estimate the energy and forces of the system. MM based force field calculations are much faster than quantum chemical ones by a large order of magnitude. While the MM force field approaches have successfully been employed for simulations and analysis of organic molecules,11 their applicability is limited in nanoclusters due to the presence of inherently non-classical bonds and extensive electron delocalization in nanoclusters. In this context, the machine learning based potentials instead have been propositioned as an alternative that could be applied to nanoclusters.
Machine learning (ML) is a powerful emerging technique for the construction of molecular transferrable and non-transferrable potentials. In the field of computational chemistry, ML has currently and extensively been implemented to solve problems in a variety of chemical subjects such as, among others, the prediction of structures, reaction pathways, formation energies, nuclear magnetic resonance (NMR) shift, prediction of HOMO–LUMO gap and glass transition temperature.12,13 Several ML algorithms have already been reported in the recent literature that deal with molecular systems including the neural networks, support vector machine (SVM) based classification/regression, ridge regression, Gaussian progression regression (GPR), partial least square (PLS) based regression, random forest/XG boost etc.
In our case, we have utilized neural networks for our machine learning analysis. Neural networks form a class of ML algorithms which are gaining prominence due to their efficiency, effectiveness and ability to handle a diverse range of problems.14–16 Of the neural networks that have been designed for molecular systems, the Behler–Parrinello neural network (BPNN)17 relies on division of a molecule into its atomic constituent where a feed-forward neural network infers the atomic contributions for the total molecular property. The atomic contributions are then combined to get the total molecular property. In the BPNN scheme, symmetry is preserved by mapping the coordinates onto a large set of two- and three-body symmetry functions. Fixing these symmetry functions is a painstaking endeavour for molecules containing many elements. BPNN is sensitive to the choice of input features used to describe the molecular system, and selection of the most relevant features is usually a time-consuming and challenging task.
Another important machine learning based potential is the gradient domain machine learning (GDML).18 In the GDML scheme, the symmetry is preserved by mapping the coordinates onto the eigenvalues of the Coulomb matrix whose elements are the inverse distances between all distinct pairs of atoms. However, GDML has up to now only been used for relatively small organic molecules.19
In lieu of the aforementioned shortcomings, we set out to look at other approaches in devising a new methodology involving neural networks. It has been shown that the neural network consisting of single hidden layer can approximate any continuous function and hence neural networks are also termed universal function approximators.20 This makes neural networks particularly suitable for regression problems. It is well known that the deep convolutional networks can approximate any continuous function.21 Featureless learning is the unique ability of convolutional neural network (CNN) to utilize training data, especially images, directly for modelling without feature extraction.22 Featureless learning is also expected to be useful for the creation of a regression model which not only predicts energy but also multiple properties of molecular systems.
Currently, featureless learning is not restricted to convolutional neural networks, graph neural networks are also utilized for featureless learning in molecular systems. Graph neural network, as the name suggests, works on graph-structured data. Their architecture allows them to directly work on the natural representations of molecules hence displaying featureless learning for molecules.23 A molecule can be treated as a undirected graph where the nodes and the vertices of the graph correspond to the atoms and bond of a molecule. The graph network utilized for molecular systems are message passing graph neural networks (MPNN). In the MPNN framework, a node level embedding of a molecule is generated using message passing where information of node is relayed in form of messages through graph edges to neighbouring nodes. Upon completion of this step for the whole molecular graph we get an embedding which is then propagated to classic deep neural architecture for either classification or regression tasks. Graph neural networks are also system agnostic and can be utilized for organic, inorganic, crystalline and nanostructure.23 In case of boron clusters, especially larger boron clusters where a large amount of delocalized multi center bonding exists it is not straightforward to encode such structures accurately as molecular graphs and hence would not be suitable for graph neural networks. Electron density based machine learning paradigm on the other hand can deal with such delocalized nanoclusters.
It is well known that in density functional theory (DFT), the Hohenberg & Kohn theorem24 states that the electron density of a molecule ρ(r) uniquely determines the ground state electronic energy. A unique energy functional E[ρ(r)] is required for mapping the electron density to the ground state electronic energy eqn (1):
| E = E[ρ(r)] | (1) |
In the case of DFT based calculations for molecules, a trial electron density is assigned to a molecular system, and the use of a suitable functional along with an atomic basis set leads to the total energy of the molecule being calculated. Instead of utilization of a density functional, we can now map the electron density to the ground state electronic energy using convolutional neural network eqn (2):
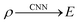 | (2) |
Recently Zhao et al.25 reported a study regarding 3D-CNN which utilizes the electron localization function (ELF) for prediction of various properties for materials. The ELF does capture both the localization and delocalization of the electron density. Generation of an ELF map requires quantum chemical calculations. A fast ML algorithm would require rapid calculation of electron density which is not possible by using traditional QM based calculations. The solution to this problem is the construction of promolecule densities for the clusters/molecules examined. For a better understanding of the promolecule density, we need to know about the Hirshfeld partitioning scheme. The Hirshfeld partitioning scheme is basically a partitioning method where the molecular electron density is divided into its constituent atomic density. In this scheme, a promolecule density is assigned to a molecule by superposition of precalculated electron densities of the atomic constituents of the molecule considered. Then this electron density is partitioned by giving weightage to the atomic constituents proportionated to their contribution to the electron density.26,27 The promolecule density (ρ°(r)) can be written as a weighed summation of atomic densities eqn (3):
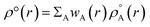 | (3) |
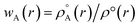 | (4) |
This promolecule density is akin to the initial trial density utilized in DFT calculations. However, unlike trial density in DFT calculations, there is no occurrence of iterative process just the straightforward mapping of promolecule density to energy. One caveat of this approach is since we are not using the actual ground state energy for mapping but promolecule density, thus the energy obtained from the model is not expected to be highly accurate. The purpose of the present machine learning model is to predict energy trends amongst the molecular systems, not the actual energy itself. Ultimately, we want to augment the machine learning algorithm with structure prediction codes, thus the neural network should be able to correctly predict the ordering of structural isomers for a particular molecular system. The model can thus successfully predict the energy ordering of isomers but it will not predict the exact ground state energy of the isomers. The density can be mapped to the ground state energy of a system by using convolutional neural network (CNN) model. The promolecule approach is also limited to neutral systems this is because, the reference atomic density used for construction of promolecule density are of neutral atoms.28 The Hirshfeld method has been proved not to be very accurate for charged systems. Due to the aforementioned reasons, our method exclusively applies only to neutral nanocluster systems.
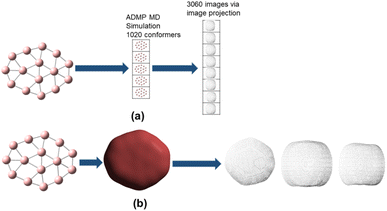
The promolecule density is a three-dimensional (3D) quantity and thus cannot be utilized in a traditional CNN. CNNs are typically used for two dimensional (2D) images; in that regard we have to first convert the three dimensional promolecule density to a 2D quantity. We can achieve this by projecting the 3D density to 2D planes, namely the xy, yz and xz planes. Via this 2D projection we obtain three projected datapoints from a single 3D datapoint. This 2D projection thus leads to a data augmentation (artificial increase of the dataset size) and minimizes loss of information. The dataset required for our model is mainly sourced from the current literature (including reviews on nanoclusters).29 Majorly the neutral boron structures ranging from size 4 to 40 (Bn: n = 4–40) were taken from the review authored by Barroso et al.29a Boron clusters from size 31 to 50 (Bn: n = 31–50) were taken from the research paper authored by Wu et al.29b There were certain neutral boron clusters (Bn: n = 26–30) which were not reported in the aforementioned papers we sourced the structures from two papers earlier published by our research group (Tai et al.29d & H. T. Pham et al.29e). We further carried out calculations on the PBE0/6-311+G level of theory to ascertain as to whether the reported structures were truly global minimum. Our calculations indeed ascertain the structures reported in the literature are global minima.
Hirshfeld surfaces have already been utilized for machine learning purposes especially via convolutional neural networks. Logan et al.30a have utilized deep learning to predict formation energy and lattice structure parameters30b using Hirshfeld fingerprints as inputs for the CNNs. Hirshfeld surface can be availed for crystal structure but not for discrete molecules. Promolecule densities are thus required for deep learning predictions of nanoclusters. As the CNN approaches tend to require a large dataset for accurate prediction, we are using a data augmentation technique to increase the data size. Data augmentation is a way of creating new training data from existing training data. In our case, we can use molecular dynamics (MD) simulations to achieve data augmentation, in which the numerous conformational isomers/poses generated by MD simulations are used for augmenting our dataset. MD simulations are accordingly performed using ab initio molecular dynamics simulation (ADMP MD simulation). The ADMP simulation turns out to be a robust and computationally efficient method of data augmentation as compared to the random generation of particles and computing the energies of the generated particles.31 As far as we are aware, prediction of total energies of molecular systems via ML algorithm using the promolecule density has not yet been reported in the current literature.
As for the dataset, we build up our neural network models on boron nanoclusters. Boron clusters show a wide complexity in their structures that it can adopt a variety of geometrical motifs including the planar, quasi-planar, bowl, ribbon, cage, core–shell, fullerene and tubular structures etc. The bonding phenomenon of these clusters is not straightforward as it contains extensive delocalized bonding in both 2D and 3D structures.32–36 Boron clusters thus form a challenging dataset for ML problem. Following a successful implementation of deep learning model on boron clusters we would plan to expand the model on other nanoclusters.
In the present study, we utilize pure boron clusters Bn ranging from the size B4 to B40 to establish the dataset for our machine learning based study. This is due to the fact the structures for the Bn clusters in the size range of n = 4–40 have been relatively well established. Some larger clusters (Bn, with n > 40) still do not have well-established global minimum structures. For example, the B70 boron cluster was postulated to be quasi-planar by Rahane et al.37 but subsequent studies pointed out that both tubular and bilayer structures have lower energy and are positioned as the global minimum for the B70 cluster.38,39 Large clusters can take up a myriad number of configurations and thus it is quite difficult to ascertain the global minimum structures. Our present training dataset for the Bn boron clusters is thus limited up to the size of B40.
2. Computational details
Calculations on boron clusters are carried out using the PBE0 functional and the Gaussian 09 program40 in conjunction with the 6-311+G basis set. Calculations to verify global minimum structure of the boron clusters are also done using PBE0/6-311+G level of theory. These structures are then used as initial structures for MD simulations. Promolecule densities of the clusters are generated using the Crystal Explorer software.27 Automation of the Crystal Explorer processes is done via Microsoft's Power automate tool. The convolutional neural network (CNN) models are created using the MATLAB R2021b suite. In house bash/python scripts are also utilized for small data processing tasks. Details are given in the ESI.† We also put the relevant codes in Github: https://github.com/314111953/Featureless-learning-using-Promolecular-Density/tree/main.3. Results and discussion
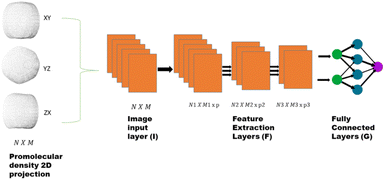
We utilize a CNN based regression model that takes a regular convolutional neural network which is succeeded by regression layer at the end of the network. The feature extraction layers contain convolution, RELU and pooling layers.Convolution neural networks (CNN) are well known in the field of image recognition. The underlying assumption is that the complex geometrical features of an image are an ensemble of smaller and simpler patterns. CNN uses small filters that extract local features and progressively reduce the size of the input variable with each layer. The number of layers in CNN increases with an increase in the size of the input image. Consider the input image X of size N × M (Fig. 1). Each convolution + RELU and pooling layer produce the feature maps of reduced dimension as compared to its input. Additionally, the pooling layers produce an output map that is invariant to small changes within pooling window. The model is trained using a regression loss function which is given by the following eqn (5):
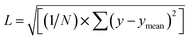 | (5) |
We utilize regression loss function as our model will be trained to capture the trend of energy distribution amongst various diverse boron nanocluster. As explained earlier our model based on promolecule density can only approximate the energy, thus we are utilizing our model to gauge the energy distribution which will be helpful in case of a potential energy landscape exploration. The model utilizes the Adam optimizer for the purpose of back-propagation. The model is trained on AMD Ryzen-7 PRO 4750U CPU, 16 GB RAM with RADEON graphics card using the MATLAB R2021B.
As stated above, the dataset used for training the model is generated from boron clusters ranging from the size of B4 to B40. Ab initio based molecular dynamics simulations (ADMP) are performed on all these clusters considered. Each ADMP trajectory gives a set of molecular clusters along with their corresponding energies. There are thus 37 clusters in the dataset and each cluster generates 1020 structures along with their corresponding energies, thus we obtain 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 structures. For each of these 37
740 structures. For each of these 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 structures, we generate the corresponding promolecule density for each structure using the Crystal Explorer (Fig. 2a). The promolecule density is a 3D quantity and cannot be utilized by 2D CNN; of course there do exist 3D CNNs which can directly work with the promolecule density but we do not use 3D CNNs as they possess an inherent disadvantage, that is, they have high computational complexity and excessive memory usage.41 We thus limit our study to 2D CNN to utilize the promolecule density for our model we project this 3D quantity to three axes X, Y & Z to get 2D images in the YZ, XZ and XY plane respectively (cf. Fig. 2b).
740 structures, we generate the corresponding promolecule density for each structure using the Crystal Explorer (Fig. 2a). The promolecule density is a 3D quantity and cannot be utilized by 2D CNN; of course there do exist 3D CNNs which can directly work with the promolecule density but we do not use 3D CNNs as they possess an inherent disadvantage, that is, they have high computational complexity and excessive memory usage.41 We thus limit our study to 2D CNN to utilize the promolecule density for our model we project this 3D quantity to three axes X, Y & Z to get 2D images in the YZ, XZ and XY plane respectively (cf. Fig. 2b).
Projection of the surface on the three orthogonal planes ensure that we are capturing maximum data from the 3D surface. Projection of the promolecule density to images is done via a pointcloud2image Matlab script.42 Thus, from 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 structures generated, we get 113
740 structures generated, we get 113![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 220 projected images, hence we obtain a dataset of a size of 113
220 projected images, hence we obtain a dataset of a size of 113![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 220.
220.
The dataset obtained consists of projected images from planar, quasi planar, bowl, tubular, cage and fullerene structure (cf. Table 1). A quite complicated growth pattern is seen as we move from B4 to B40. Planar, quasiplanar and bowl structures are predominant (67.6%) followed by tubular (18.9%), cage (8.1%) and fullerene (5.4%) structures. The dataset is divided into the training, validation and test set in the following proportions of 60, 20 and 20%, respectively.
| Planar, quasiplanar, bowl | Tubular | Fullerene | Cage |
|---|---|---|---|
| B4, B5, B6, B7, B8, B10, B11, B12, B13, B15, B16, B17, B18, B19, B21, B23, B25, B28, B29, B30, B33, B35, B36, B37, B38 | B20, B22, B24, B26, B27, B32, B39 | B14, B40 | B9, B31, B34 |
We construct the test set to include the planar, quasi-planar, bowl, tubular fullerene and cage structures. Table 2 shows the distribution of training, validation and test dataset.
| Training dataset clusters | Validation dataset clusters | Test dataset clusters |
|---|---|---|
| B7, B8, B10, B12, B13, B16, B18, B19, B23, B26, B27, B28, B30, B31, B32, B33, B34,B35, B36, B38, B39, B40 | B4, B6, B9, B15, B20, B21, B22, B29 | B5, B11, B14, B17, B24, B25, B37 |
Accordingly, the training dataset consists of 22 boron clusters which generate 67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 320 data points. Validation dataset consists of 8 boron clusters which corresponds to 24
320 data points. Validation dataset consists of 8 boron clusters which corresponds to 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 data points. The test dataset consists of 7 boron clusters which corresponds to 21
480 data points. The test dataset consists of 7 boron clusters which corresponds to 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420 data points. Distribution of the datasets is presented in Table 3.
420 data points. Distribution of the datasets is presented in Table 3.
| Planar, quasiplanar, bowl | Tubular | Fullerene | Cage | |
|---|---|---|---|---|
| Training | 68.2% | 18.2% | 4.5% | 9.1% |
| Validation | 62.5% | 25.0% | 12.5% | |
| Test | 71.4% | 14.3% | 14.3% |
The model is trained using Matlab, and the data is trained for 50 epochs. The initial learning rate is kept at 0.002 and the learning rate is lowered after 20 epochs, with a learn-rate drop factor of 0.1. Early stopping is utilized to avoid an overfitting. In early stopping, the variation between the evolving trend of the loss on training and validation is seen, then the training is stopped when the variation increases between training and validation increases by a large margin. The time required to train the model amounts to 1100 minutes (∼18.3 hours). The architecture of the CNN model constructed is given in the ESI.†
To further assess our model, we use two well-known quantities in machine learning realm: correlation coefficient R and regression coefficient R2. The Pearson correlation coefficient captures how similar is the data distribution of predicted response to the actual response, whereas the R2 coefficient is a scale independent quantity used for assessing a regression model. Since our model is trained on regression loss, R2 is pertinent for gauging the model performance. The R2 and Pearson correlation coefficient value of 1 are for a perfect model which accurately predicts all data points correctly. We also utilize these two quantities as they are ideal for capturing the distribution or trend of energy distribution amongst different molecular systems, thus it will allow us to gauge how well the model can capture the ordering of the clusters with respect to their energies. The R2 regression coefficients amount to 0.86 and 0.89, respectively, and the correlation coefficients are 0.93 and 0.94 for the validation and test data set, respectively (cf. Table 4). The CNN model is thus able to learn from the projected images of the electronic densities and able to map the density features obtained from the images to evaluate the total energies quite accurately.
| R2 | R | |
|---|---|---|
| Regression coefficient | Correlation coefficient | |
| Validation | 0.86 | 0.93 |
| Test | 0.89 | 0.94 |
Fig. 3 displays the results demonstrating that the CNN model predicts quite well for each of the clusters, though a large variance is observed for B14 and B17 clusters. This figure may not be very intuitive to the readers as it includes up to 1020 conformational isomers for certain large clusters considered, and thus for each corresponding cluster a spread of predicted energy values is seen. While the predicted energies vary over a range for the configurations of a particular cluster, with exception of one cluster B17, most of the values of the configuration of a particular cluster are clustered towards the mean; the presence of outliers at both ends of distribution is akin to a bell distribution, where most of the values congregate around the mean and outlier are present at both ends of the Gaussian distribution. The mean of the values gives us the approximate value of the cluster, similar to a Gaussian distribution. A better way of visualization is plotting the average conformational isomer energies of nanocluster with respect to the average predicted energy for each cluster as presented in Fig. 4.
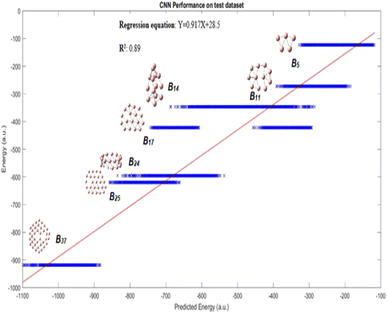 | ||
| Fig. 3 Performance on test dataset is illustrated by the graph, good R2 and R values of 0.89 and 0.94, respectively for this complex dataset are obtained. | ||
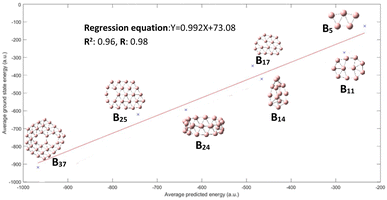 | ||
| Fig. 4 The performance on test dataset is illustrated by the graph, we get a good R2 and R value of 0.96 and 0.98 respectively. | ||
We can see in Fig. 4 that all the three values of R2 and R are improved, with an exception for the B17 cluster; all the average predicted energies lie close to regression line. The average energy of conformational isomer (Eavg_conformers) of a particular nanocluster is roughly equivalent to the ground state energy of nanocluster Egs (Eavg_conformers ≈ Egs).
The energy of a conformational isomer A (EconfA) with respect to the ground state system's energy (Egs) can be written as eqn (6):
| EconfA = Egs + ΔEA | (6) |
The average of all the conformational isomer for a particular nanocluster can thus be written as eqn (7)–(9):
| Eavg_conf = (∑nEgs + ∑nΔEn)/n | (7) |
| Eavg_conf = Egs + ΔEavg | (8) |
Hence:
| Eavg_conf ≈ Egs | (9) |
Overall, by taking the average of the energies predicted by the CNN model, we can evaluate the ground state total energy of a particular boron cluster in the test dataset with a certain accuracy. This approach is not foolproof though, as we are utilizing projections, it is not sensitive to rotational invariance. Since we are utilizing the promolecule density and not the actual ground state electron density, the energy which is got from the CNN, will not be the exact ground state energy I but a higher energy E′. Thus, the machine learning paradigm considered here will thus not give accurate energy but is useful for a quick potential energy landscape exploration of nanoclusters. Our model is thus well suited for capturing the energy trend, hence we believe our model is better suited for classification-based tasks. Regression model can be converted to classification model by utilizing thresholds i.e. class can be assigned to particular molecule depending whether their predicted energy is above the certain threshold or not. For the classification task, we use a test dataset containing boron clusters ranging from B41 to B50. We also include the B70 structure in our test dataset. The global minimum of B70 was purported to be quasiplanar and later it was purported to be tubular structure but recently it was shown to be a bilayer structure. Ascertaining the global minimum structure for such large clusters is a difficult task even after using QM based calculations. B70 structure would be thus a challenging case for our model. The global minimum structures and few of their higher energy constitutional isomeric structures are used in this task. We again perform the MD simulation, generating 50 conformational isomers each for the global minimum and their higher energy isomeric counterparts (Table 5). We reduce the number of conformational isomers for the classification test dataset as we only require the conformational isomers for getting the average energy of particular nanoclusters for the purpose of classification, also it is less computationally expensive process.
The promolecule densities are subsequently calculated, and their two-dimensional projection are utilized by CNN to obtain predicted energies. Consequently, we take the average of the energy over the 50 conformational isomers for each constitutional isomer to reach the predicted ground state energy. Hence, we obtain ground state energy for each of the constitutional isomers of each nanocluster. The ground state energies of the isomers are then normalized using max–min normalization (eqn (10)).
| Ȳ = (Y − Ymin)/Ymax | (10) |
The purpose of a max–min normalization is to ensure that the constitutional isomer with lowest energy gets the value zero while the isomer with the highest energy gets the value 1. Using our neural network model we obtain the following normalized score for the classification test dataset (Table 6).
| Minmax normalized score for global minimum | Minmax normalized score for constitutional isomer 1 | Minmax normalized score for constitutional isomer 2 | |
|---|---|---|---|
| B41 | 0 | 0.46 | 1 |
| B42 | 0 | 1 | — |
| B43 | 0 | 1 | — |
| B44 | 0 | 1 | 0.1 |
| B45 | 1 | 0 | — |
| B46 | 0 | 1 | — |
| B47 | 0 | 1 | — |
| B48 | 0 | 1 | — |
| B49 | 0 | 0.81 | 1 |
| B50 | 0 | 1 | — |
| B70 | 0 | 0.73 | 1 |
Consequently, we go on to perform binary classification with this data by taking the threshold t as greater than zero as inactive for the normalized score. Thus, for t > 0 the class non global minimum is assigned as is for the rest class global minimum. Using this threshold, we obtain the following confusion matrix for our classification problem (Table 7).
| Predicted global minimum | Predicted non global minimum | |
|---|---|---|
| True global minimum | 10 (TP) | 1 (FP) |
| True non global minimum | 1 (FN) | 14(TN) |
The Matthew's correlation coefficient (MCC) is written in the expression (11):
| MCC = {(TP × TN − FP × FN)/sqrt[(TP + FP) × (TP + FN) × (TN + FP) × (TN + FN)]} × 100 | (11) |
The MCC in this case results in 84.2%, which is a respectable score. In this sense, the CNN classification paradigm is successful in separating out the global minimum out of the different configurational isomers except for one misclassification. This CNN classification paradigm can be then further implemented to augment the efficiency of structure prediction algorithms.
4. Concluding remarks
Conversion of electron density of a molecular system to its ground state energy has traditionally been carried out by using quantum chemical programs utilizing DFT functionals. In the present study, we attempted a different approach for such a purpose: We utilize neural networks for mapping the electron density of a molecule to its ground state energy using its promolecule density. Our approach consists of a utilization of 2D convolutional neural network (CNN) with projected images of promolecule density to predict ground state energy. In case of 2D convolutional neural network, we have the aspect of featureless learning: the images are directly utilized by the CNN model to predict the energies of the boron clusters. Boron nanoclusters ranging from B4 to B40 are used for the training set. The dataset of projected images is divided into training, test and validation sets (with a split percentage: 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20%). The 2D-CNN model obtained shows a good R2 value of 0.89 on the test set.
20%). The 2D-CNN model obtained shows a good R2 value of 0.89 on the test set.
The model thus meets our goal for the utilization in exploration of a potential energy landscape. The model cannot predict the ground state energy with prediction of the geometric shapes of the stable clusters with, which high accuracy as we are mapping the promolecule density to energy instead of the actual electron density. What is important is the ability of the neural network to get the distribution correctly which our model successfully does. This will be important for potential energy landscape (PES) exploration studies of nanocluster, we can quickly find the initial local minimum structures using our neural network. These structures will be subsequently subjected to quantum chemical calculations to ascertain, or to search further, the global minimum. Overall, our approach shows that the mapping of electron density of a molecule to its ground state energy is possible with the use of neural networks, and such neural network models can be augmented with the available structure prediction codes. A following step of this study which is more interesting but also more challenging, effectively entails both generation of nanoclusters using a generative model and using discriminative model to assess the structures.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work of MTN is funded by VinGroup (Vietnam) and supported by VinGroup Innovation Foundation (VinIF) under project code VinIF.2020.DA21.References
- S. Goedecker, W. Hellmann and T. Lenosky, Global minimum determination of the Born-Oppenheimer surface within density functional theory, Phys. Rev. Lett, 2005, 95, 055501, DOI:10.1103/PhysRevLett.95.055501.
- S. Nouemo, F. Tchoffo, J. M. B. Ndjaka and S. Domngang, Global minima of iron clusters described by Gupta potential, J. Taibah Univ. Sci., 2016, 10, 430–436, DOI:10.1016/j.jtusci.2015.06.014.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, CALYPSO: a method for crystal structure prediction, Comput. Phys. Commun., 2012, 183, 2063–2070, DOI:10.1016/j.cpc.2012.05.008.
- C. W. Glass, A. R. Oganov and N. Hansen, USPEX—evolutionary crystal structure prediction, Comput. Phys. Commun., 2006, 175, 713–720, DOI:10.1016/j.cpc.2006.07.020.
- P. Entel, M. E. Gruner, G. Rollmann, A. Hucht, S. Sahoo, A. T. Zayak, H. C. Herper and A. Dannenberg, First-principles investigations of multimetallic transition metal clusters, Philos. Mag., 2008, 88, 2725–2738, DOI:10.1080/14786430802398040.
- H. Dai, A. G. Rinzler, P. Nikolaev, A. Thess, D. T. Colbert and R. E. Smalley, Single-wall nanotubes produced by metal-catalyzed disproportionation of carbon monoxide, Chem. Phys. Lett., 1996, 260, 471–475, DOI:10.1016/0009-2614(96)00862-7.
- J. A. Elliott, M. Hamm and Y. Shibuta, A multiscale approach for modeling the early stage growth of single and multiwall carbon nanotubes produced by a metal-catalyzed synthesis process, J. Chem. Phys., 2009, 130, 034704, DOI:10.1063/1.3058595.
- R. S. Berry and D. J. Wales, Freezing, melting, spinodals, and clusters, Phys. Rev. Lett., 1989, 63, 1156, DOI:10.1103/PhysRevLett.63.1156.
- Y. Shibuta and T. Suzuki, Melting and nucleation of iron nanoparticles: a molecular dynamics study, Chem. Phys. Lett., 2007, 445, 265–270, DOI:10.1016/j.cplett.2007.07.098.
- I. M. Billas, A. Châtelain and W. A. de Heer, Magnetism of Fe, Co and Ni clusters in molecular beams, J. Magn. Magn. Mater., 1997, 168, 64–84, DOI:10.1016/S0304-8853(96)00694-4.
- K. Vanommeslaeghe and O. Guvench, Molecular mechanics, Curr. Pharm. Des., 2014, 20, 3281–3292, DOI:10.2174/13816128113199990600.
- N. Sukumar, M. Krein, Q. Luo and C. Breneman, MQSPR modeling in materials informatics: a way to shorten design cycles?, J. Mater. Sci., 2012, 47, 7703–7715, DOI:10.1007/s10853-012-6639-0.
- L. Ward and C. Wolverton, Atomistic calculations and materials informatics: a review, Curr. Opin. Solid State Mater. Sci., 2017, 21, 167–176, DOI:10.1016/j.cossms.2016.07.002.
- J. Gasteiger and J. Zupan, Neural networks in chemistry, Angew. Chem., Int. Ed., 1993, 32, 503–527, DOI:10.1002/anie.199305031.
- I. I. Baskin, D. Winkler and I. V. Tetko, A renaissance of neural networks in drug discovery, Expert Opin. Drug Discovery, 2016, 11, 785–795, DOI:10.1080/17460441.2016.1201262.
- S. Ekins, The next era: deep learning in pharmaceutical research, Pharm. Res., 2016, 33, 2594–2603, DOI:10.1007/s11095-016-2029-7.
- J. Behler and M. Parrinello, Generalized neural-network representation of high-dimensional potential-energy surfaces, Phys. Rev. Lett., 2007, 98, 146401, DOI:10.1103/PhysRevLett.98.146401.
- S. Chmiela, A. Tkatchenko, H. E. Sauceda, I. Poltavsky, K. T. Schütt and K. R. Müller, Machine learning of accurate energy-conserving molecular force fields, Sci. Adv., 2017, 3, e1603015, DOI:10.48550/arXiv.1611.04678.
- L. Zhang, J. Han, H. Wang, R. Car and E. Weinan, Deep potential molecular dynamics: a scalable model with the accuracy of quantum mechanics, Phys. Rev. Lett., 2018, 120, 143001, DOI:10.1103/PhysRevLett.120.143001.
- G. Cybenko, Approximation by superpositions of a sigmoidal function, Math. Control Signals Syst., 1989, 2, 303–314, DOI:10.1007/BF02551274.
- D. X. Zhou, Universality of deep convolutional neural networks, Appl. Comput. Harmon. Anal., 2020, 48, 787–794, DOI:10.48550/arXiv.1805.10769.
- N. Aloysius and M. Geetha, A review on deep convolutional neural networks, Internat. Conf. Commun. Signal Proc. (ICCSP), Academic Publishers: IEEE, Chennai, India, 6–8 April 2017, pp. 0588–0592, DOI:10.1109/ICCSP.2017.8286426.
- P. Reiser, M. Neubert, A. Eberhard, L. Torresi, C. Zhou, C. Shao, H. Metni, C. van Hoesel, H. Schopmans, T. Sommer and P. Friederich, Graph neural networks for materials science and chemistry, Commun. Mater., 2022, 3, 93, DOI:10.1038/s43246-022-00315-6.
- P. Hohenberg and W. Kohn, Inhomogeneous electron gas, Phys. Rev., 1964, 136, B864, DOI:10.1103/PhysRev.136.B864.
- Y. Zhao, K. Yuan, Y. Liu, S. Y. Louis, M. Hu and J. Hu, Predicting elastic properties of materials from electronic charge density using 3D deep convolutional neural networks, J. Phys. Chem. C, 2020, 124, 17262–17273, DOI:10.1021/acs.jpcc.0c02348.
- F. L. Hirshfeld, Bonded-atom fragments for describing molecular charge densities, Theor. Chim. Acta, 1977, 44, 129–138, DOI:10.1007/BF00549096.
- P. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, CrystalExplorer: a program for Hirshfeld surface analysis, visualization and quantitative analysis of molecular crystals, J. Appl. Crystallogr., 2021, 54, 1006–1011, 10.1039/B704980C.
- E. R. Davidson and S. Chakravorty, A test of the Hirshfeld definition of atomic charges and moments, Theor. Chim. Acta, 1992, 83, 319 CrossRef CAS.
- (a) J. Barroso, S. Pan and G. Merino, Structural transformations in boron clusters induced by metal doping, Chem. Soc. Rev., 2022, 51, 1098–1123, 10.1039/D1CS00747E; (b) X. Wu, L. Sai, S. Zhou, P. Zhou, M. Chen, M. Springborg and J. Zhao, Competition between tubular, planar and cage geometries: a complete picture of structural evolution of Bn (n= 31–50) clusters, Phys. Chem. Chem. Phys., 2020, 22, 12959–12966, 10.1039/D0CP01256D; (c) Z. A. Piazza, I. A. Popov, W. L. Li, R. Pal, X. Cheng Zeng, A. I. Boldyrev and L. S. Wang, A photoelectron spectroscopy and ab initio study of the structures and chemical bonding of the B25− cluster, J. Chem. Phys., 2014, 141, 034303, DOI:10.1063/1.4879551; (d) T. B. Tai and M. T. Nguyen, Electronic structure and photoelectron spectra of Bn with n=26–29: an overview of structural characteristics and growth mechanism of boron clusters, Phys. Chem. Chem. Phys., 2015, 17, 13672–13679, 10.1039/C5CP01851J; (e) H. T. Pham, L. V. Duong, N. M. Tam, M. P. Pham-Ho and M. T. Nguyen, The boron conundrum: bonding in the bowl B30 and B36, fullerene B40 and triple ring B42 clusters, Chem. Phys. Lett., 2014, 608, 295, DOI:10.1016/j.cplett.2014.05.069.
- (a) L. Williams, A. Mukherjee, A. Dasgupta and K. Rajan, Monitoring the role of site chemistry on the formation energy of perovskites via deep learning analysis of Hirshfeld surfaces, J. Mater. Chem. C, 2021, 34, 11153–11162, 10.1039/d1tc01972d; (b) L. Williams, A. Mukherjee and K. Rajan, Deep learning based prediction of perovskite lattice parameters from Hirshfeld surface fingerprints, J. Phys. Chem. Lett., 2020, 17, 7462–7468, DOI:10.1021/acs.jpclett.0c02201.
- H. B. Schlegel, J. M. Millam, S. S. Iyengar, G. A. Voth, A. D. Daniels, G. E. Scuseria and M. J. Frisch, Ab initio molecular dynamics: propagating the density matrix with Gaussian orbitals, J. Chem. Phys., 2001, 114, 9758–9763, DOI:10.1063/1.1372182.
- H. J. Zhai, A. N. Alexandrova, K. A. Birch, A. I. Boldyrev and L. S. Wang, Hepta- and octacoordinate boron in molecular wheels of eight-and nine-atom boron clusters: observation and confirmation, Angew. Chem., Int. Ed., 2003, 42, 6004–6008, DOI:10.1002/anie.200351874.
- B. Kiran, S. Bulusu, H. J. Zhai, S. Yoo, X. C. Zeng and L. S. Wang, Planar-to-tubular structural transition in boron clusters: B20 as the embryo of single-walled boron nanotubes, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 961–964, DOI:10.1073/pnas.0408132102.
- W. Huang, A. P. Sergeeva, H. J. Zhai, B. B. Averkiev, L. S. Wang and A. I. Boldyrev, A concentric planar doubly π-aromatic B19− cluster, Nat. Chem., 2010, 2, 202–206, DOI:10.1038/nchem.534.
- I. A. Popov, Z. A. Piazza, W. L. Li, g L. S. Wan and A. I. Boldyrev, A combined photoelectron spectroscopy and ab initio study of the quasi-planar B24− cluster, J. Chem. Phys., 2013, 139, 144307, DOI:10.1063/1.4824156.
- E. Oger, N. R. Crawford, R. Kelting, P. Weis, M. M. Kappes and R. Ahlrichs, Boron cluster cations: transition from planar to cylindrical structures, Angew. Chem., Int. Ed., 2007, 46, 8503–8506, DOI:10.1002/anie.200701915.
- A. B. Rahane and V. Kumar, B84: a quasi-planar boron cluster stabilized with hexagonal holes, Nanoscale, 2015, 7, 4055–4062, 10.1039/C4NR06026A.
- L. Pei, Q. Q. Yan and S. D. Li, Predicting the Structural Transition in Medium-Sized Boron Nanoclusters: From Bilayer B64, B66, B68, B70, and B72 to Core-Shell B74, Eur. J. Inorg. Chem., 2021, 2618–2624, DOI:10.1002/ejic.202100328.
- Q. Q. Yan, L. Pei and S. D. Li, Predicting bilayer B50, B52, B56, and B58: structural evolution in bilayer B48–B72 clusters, J. Mol. Model., 2021, 27, 1–9, DOI:10.1007/s00894-021-04954-3.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, et al., Gaussian 09, rev. A.1, Gaussian. Inc, Wallingford, CT, 2009 Search PubMed.
- D. Kim, H. Cho, H. Shin, S. C. Lim and W. Hwang, An efficient three-dimensional convolutional neural network for inferring physical interaction force from video, Sensors, 2019, 19, 3579, DOI:10.3390/s19163579.
- B. Vahid, pointcloud2image(x,y,z,numr,numc), https://www.mathworks.com/matlabcentral/fileexchange/55031-pointcloud2image-x-y-z-numr-numc, MATLAB Central File Exchange, 2023 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra05851d |
| This journal is © The Royal Society of Chemistry 2023 |