Open Access Article
Open Access ArticleIntegration of machine learning in 3D-QSAR CoMSIA models for the identification of lipid antioxidant peptides†
Thi Thanh Nha Tran *,
Thi Dieu Thuan Tran
*,
Thi Dieu Thuan Tran and
Thi Thu Thuy Bui
and
Thi Thu Thuy Bui
Faculty of Chemical Engineering, Industrial University of Ho Chi Minh City, 12 Nguyen Van Bao, Ho Chi Minh City, 700000, Vietnam. E-mail: tranthithanhnha@iuh.edu.vn
First published on 17th November 2023
Abstract
The comparative molecular similarity indices analysis (CoMSIA) method is a widely used 3D-quantitative structure–activity relationship (QSAR) approach in the field of medicinal chemistry and drug design. However, relying solely on the Partial Least Square algorithm to build models using numerous CoMSIA indices has, in some cases, led to statistically underperforming models. This issue has also affected 3D-CoMSIA models constructed for the ferric thiocyanate (FTC) dataset from linoleic antioxidant measurements. In this study, a novel modeling routine has been developed incorporating various machine learning (ML) techniques to explore different options for feature selection, model fitting, and tuning algorithms with the ultimate goal of arriving at optimal 3D-CoMSIA models with high predictivity for the FTC activity. Recursive Feature Selection and SelectFromModel techniques were applied for feature selection, resulting in a significant improvement in model fitting and predictivity (R2, RCV2, and R2_test) of 24 estimators. However, these selection methods did not fully address the problem of overfitting and, in some instances, even exacerbated it. On the other hand, hyperparameter tuning for tree-based models resulted in dissimilar levels of model generalization for four tree-based models. GB-RFE coupled with GBR (hyperparameters: learning_rate = 0.01, max_depth = 2, n_estimators = 500, subsample = 0.5) was the only combination that effectively mitigated overfitting and demonstrated superior performance (RCV2 of 0.690, R2_test of 0.759, and R2 of 0.872) compared to the best linear model, PLS (with RCV2 of 0.653, R2_test of 0.575, and R2 of 0.755). Therefore, it was subsequently utilized to screen potential antioxidants among a range of Tryptophyllin L tripeptide fragments, leading to the synthesis and testing of three peptides: F-P-5Htp, F-P-W, and P-5Htp-L. These peptides exhibited promising activity levels, with FTC values of 4.2 ± 0.12, 4.4 ± 0.11, and 1.72 ± 0.15, respectively.
Introduction
The delicate balance between the production and neutralization of reactive species including reactive oxygen species (ROS), reactive nitrogen species (RNS), and reactive sulfur species (RSS) is essential to life.1,2 On the one hand, these reactive species participate in a variety of physiological processes within the mitochondria.3 On the other hand, the overproduction of these species, also known as oxidative stress, has been found to cause damage to many biomolecules including proteins, DNA (deoxyribonucleic acid), RNA (ribonucleic acid), and lipids.4 The supplement of external antioxidants has been suggested to maintain this delicate balance,5,6 with antioxidants being defined as “any substance that when present at low concentrations compared to that of an oxidizable substrate would significantly delay or prevent oxidation of that substrate”.7,8Antioxidant peptides have been extensively investigated in recent decades using both experimental and statistical approaches. A variety of antioxidant assays have been employed for peptide testing, with some commonly used including ABTS+ radical scavenging assay,9,10 ferric ion reducing antioxidant power (FRAP),11,12 2,2-diphenyl-1-picrylhydrazyl radical-scavenging capacity (DPPH),13,14 oxygen radical absorbance capacity (ORAC),15 and the FTC method.16 Consequently, several datasets of antioxidant peptides have been made available to the public through databases.17 Three of these datasets have been frequently utilized for constructing QSAR models due to their favorable attributes in terms of peptide structure and bioassay homogeneity, which are typically required for statistical modeling. These datasets include the TEAC dataset consisting of 108 synthesized tripeptides, the FTC dataset containing 214 tripeptides,18 and the FRAP dataset comprising 172 tripeptides.19 Only a few studies have explored the application of other datasets with varying peptide lengths and bioassays for studying QSAR of antioxidant peptides, as these datasets necessitate special treatment to extract molecular features.20,21
QSAR modeling has emerged as an alternative approach to overcome the time and resource-intensive nature of biochemical methods, thereby contributing to the exploration of the chemical space of antioxidants.2,5,6 Among the various QSAR techniques, CoMFA and CoMSIA, have been widely utilized in studies exploring the QSAR of antioxidant peptides. In a notable study conducted in 2019, Y. Wang and colleagues developed 3D-QSAR CoMFA and 4-field CoMSIA models utilizing the FTC dataset comprising 198 peptides.22 Similarly, R. Zhang's group constructed CoMSIA models using a TEAC dataset of only 54 tryptophan-containing peptides.23 Both studies utilized the Sybyl software with built-in Tripos force field and Gasteiger-Hückel charge for model derivation.
Our group has also employed CoMFA and CoMSIA techniques with the OPLS_2005 (Optimized Potentials for Liquid Simulations) force field to build 3D-QSAR models for predicting TEAC values. These models were subsequently employed to screen various tripeptide fragments derived from Tryptophyllin L peptides.24,25 This is a peptide family that possesses a characteristic Pro–Trp sequence extracted from the dorsal skin of the frog Litoria rubella, an Australian frog occupying a large area of central and northern Australia. Details of the extraction, structures and antioxidant activities of some peptides from this peptide family can be found in the following ref. 26 and 27 and also in our recent publications.24,25
In our previous study, a Gaussian-based 3D-QSAR model constructed using the dataset of ABTS+ radical scavenging tripeptides was employed in a combined statistical and experimental approach to identify a range of antioxidant Tryptophyllin L peptides. These peptides exhibited excellent ABTS+, DPPH radical scavenging and reducing power. However, neither our research group nor any other has conducted an investigation into the lipid antioxidant properties of these peptides.
During exploration of the TEAC and FTC datasets, we observed a phenomenon that certain peptides displayed significant ABTS+ scavenging activity but showed negligible activity in the FTC assay, and vice versa (e.g. PWY, PWE, LHG).18,28 This observation prompted us to consider the reliability of relying solely on a single model built from just one dataset to predict antioxidant peptides within the Tryptophyllin L family. Consequently, we initiated our investigation into FTC 3D-QSAR modeling and experimental study of antioxidant Tryptophyllin L peptides. This study therefore aims to uncover potential lipid antioxidant Tryptophyllin L peptides that might have been overlooked by previous TEAC models and experiments.
Despite the notable accomplishments thus far, both CoMFA and CoMSIA methods suffer from inherent weaknesses. One such weakness is the excessive number of descriptors typically involved (often several thousands). Among these numerous descriptors, a significant portion is uninformative and irrelevant to biological activities, essentially introducing noise into the models. Without appropriate feature-selection techniques, the models' efficacy is compromised. Furthermore, the linear PLS estimator used as default in these methods, may not adequately capture the nonlinear nature of certain datasets, leading to subpar statistical performance and predictive power.29
Looking at the field of ML based 3D-QSAR, it can be seen that support vector machine (SVM) has been the most frequently utilized non-linear algorithm for developing field-based models. Several notable studies can be mentioned, such as the analysis of naphthyridone derivatives as ATAD2 bromodomain inhibitors, which employed least squares-support vector machine (LS-SVM) models based on CoMFA-field descriptors.30 Additionally, investigations on reversible acetyl cholinesterase inhibitors were conducted using CoMFA and ligand protein interaction fingerprints.31 More recently, G. Floresta and V. Abbate constructed 3D-QSAR models to establish correlations between field descriptors calculated from the extended electron distribution (XED) force field and 5-HT2AR activity. They employed four algorithms, namely k-nearest neighbor (kNN), SVM, random forest (RF), and relevance vector machine (RVC), provided by Forge software.32 To the best of our knowledge, there has been no previous research utilizing non-linear machine learning (ML) algorithms to construct 3D-QSAR CoMSIA models in the context of antioxidant activity.
Due to the aforementioned reasons, in this study, we have developed a more flexible approach to constructing 3D-CoMSIA regression models using the FTC dataset. The process of building the models, from data cleaning to feature selection and model construction, will be managed mainly through the utilization of Python scripts. A comprehensive comparison between traditional CoMSIA models and ML-based CoMSIA models will also be conducted. The former will be derived from two different force fields, namely OPLS_2005 and Tripos force fields. The latter will employ ML techniques to select field-similarity-index features and build models using the FTC dataset. The top-performing model will be employed to predict and guide the synthesis and subsequent evaluation of potential lipid antioxidant peptides from Tryptophyllin L family.27 This investigation will also help determine the potential benefits and extent of applying different ML algorithms to 3D-CoMSIA QSAR models.
Material and methods
Data collection, optimization and alignment
The FTC dataset consisting of 214 peptides was collected from the published articles and presented in Table 1.18,28 The FTC values were shown as relative activities by adjusting the control to 1.0 (please see the Experimental section for more detail). The duplicates and values of less than 0.1 were then removed resulting in a dataset of 197 peptides.| No. | Peptide | Activity | No. | Peptide | Activity | No. | Peptide | Activity | No. | Peptide | Activity |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | LHA | 3.918 | 51 | PHT | 6.247 | 101 | RWN | 2.404 | 151 | RYY | 2.257 |
| 2 | LHD | 3.593 | 52 | PHV | 3.335 | 102 | RWQ | 0.606 | 152 | AYY | 3.071 |
| 3 | LHE | 6.136 | 53 | PHW | 6.535 | 103 | RWR | 2.384 | 153 | IYY | 3.071 |
| 4 | LHF | 3.628 | 54 | PHY | 4.227 | 104 | RWS | 0.808 | 154 | LYY | 3.071 |
| 5 | LHG | 6.697 | 55 | PWA | 1.396 | 105 | RWT | 3.818 | 155 | FYY | 1.911 |
| 6 | LHH | 4.836 | 56 | PWD | 1.096 | 106 | RWV | 0.606 | 156 | WYY | 1.911 |
| 7 | LHI | 6.531 | 57 | PWE | 1.096 | 107 | RWW | 2.707 | 157 | GYY | 5.071 |
| 8 | LHK | 4.225 | 58 | PWF | 0.919 | 108 | RWY | 0.808 | 158 | NYY | 5.071 |
| 9 | LHL | 5.920 | 59 | PWG | 2.687 | 109 | DHH | 0.905 | 159 | QYY | 5.071 |
| 10 | LHM | 4.504 | 60 | PWH | 1.184 | 110 | EHH | 0.905 | 160 | MYY | 1.991 |
| 11 | LHN | 5.148 | 61 | PWI | 1.396 | 111 | AHH | 2.020 | 161 | SYY | 3.070 |
| 12 | LHQ | 4.136 | 62 | PWK | 0.407 | 112 | IHH | 2.020 | 162 | TYY | 3.070 |
| 13 | LHR | 5.184 | 63 | PWL | 1.096 | 113 | FHH | 1.803 | 163 | CYY | 0.470 |
| 14 | LHS | 4.293 | 64 | PWM | 0.796 | 114 | WHH | 1.803 | 164 | YDY | 3.047 |
| 15 | LHT | 5.584 | 65 | PWN | 2.104 | 115 | YHH | 1.803 | 165 | YEY | 3.047 |
| 16 | LHV | 3.481 | 66 | PWQ | 1.202 | 116 | GHH | 1.089 | 166 | YHY | 9.886 |
| 17 | LHW | 6.791 | 67 | PWR | 2.705 | 117 | NHH | 1.089 | 167 | YKY | 9.886 |
| 18 | LHY | 4.203 | 68 | PWS | 1.096 | 118 | QHH | 1.089 | 168 | YRY | 9.886 |
| 19 | LWA | 1.192 | 69 | PWT | 2.598 | 119 | MHH | 2.015 | 169 | YAY | 3.607 |
| 20 | LWD | 1.717 | 70 | PWV | 1.008 | 120 | SHH | 1.320 | 170 | YIY | 3.607 |
| 21 | LWE | 1.717 | 71 | PWW | 2.899 | 121 | THH | 1.320 | 171 | YLY | 3.607 |
| 22 | LWF | 1.414 | 72 | PWY | 1.114 | 122 | CHH | 0.937 | 172 | YFY | 2.233 |
| 23 | LWG | 1.313 | 73 | RHA | 5.205 | 123 | HDH | 1.477 | 173 | YWY | 2.233 |
| 24 | LWH | 3.212 | 74 | RHD | 3.304 | 124 | HEH | 1.477 | 174 | YGY | 3.366 |
| 25 | LWI | 1.111 | 75 | RHE | 5.096 | 125 | HAH | 0.952 | 175 | YNY | 3.366 |
| 26 | LWK | 1.899 | 76 | RHF | 3.300 | 126 | HIH | 0.952 | 176 | YQY | 3.366 |
| 27 | LWL | 0.606 | 77 | RHG | 5.725 | 127 | HLH | 0.952 | 177 | YMY | 1.780 |
| 28 | LWM | 1.394 | 78 | RHH | 3.296 | 128 | HFH | 2.026 | 178 | YSY | 3.447 |
| 29 | LWN | 1.313 | 79 | RHI | 4.806 | 129 | HWH | 2.026 | 179 | YTY | 3.447 |
| 30 | LWQ | 2.505 | 80 | RHK | 2.694 | 130 | HYH | 2.026 | 180 | YCY | 3.087 |
| 31 | LWR | 2.909 | 81 | RHL | 3.501 | 131 | HGH | 0.832 | 181 | YYD | 4.116 |
| 32 | LWS | 2.020 | 82 | RHM | 3.218 | 132 | HNH | 0.832 | 182 | YYE | 4.116 |
| 33 | LWT | 2.020 | 83 | RHN | 5.713 | 133 | HQH | 0.832 | 183 | YYH | 5.303 |
| 34 | LWV | 1.616 | 84 | RHQ | 3.108 | 134 | HMH | 0.873 | 184 | YYK | 5.303 |
| 35 | LWW | 3.515 | 85 | RHR | 4.302 | 135 | HSH | 0.730 | 185 | YYR | 5.303 |
| 36 | LWY | 2.222 | 86 | RHS | 3.386 | 136 | HTH | 0.730 | 186 | YYA | 3.344 |
| 37 | PHA | 5.793 | 87 | RHT | 5.987 | 137 | HCH | 0.975 | 187 | YYI | 3.344 |
| 38 | PHD | 4.622 | 88 | RHV | 3.206 | 138 | HHD | 0.188 | 188 | YYL | 3.344 |
| 39 | PHE | 6.152 | 89 | RHW | 5.878 | 139 | HHE | 0.188 | 189 | YYF | 4.050 |
| 40 | PHF | 3.916 | 90 | RHY | 3.378 | 140 | HHF | 3.612 | 190 | YYW | 4.050 |
| 41 | PHG | 5.197 | 91 | RWA | 1.212 | 141 | HHW | 3.612 | 191 | YYG | 2.996 |
| 42 | PHH | 6.051 | 92 | RWD | 0.909 | 142 | HHY | 3.612 | 192 | YYN | 2.996 |
| 43 | PHI | 4.916 | 93 | RWE | 1.091 | 143 | HHG | 0.317 | 193 | YYQ | 2.996 |
| 44 | PHK | 3.426 | 94 | RWF | 0.909 | 144 | HHN | 0.317 | 194 | YYM | 2.103 |
| 45 | PHL | 5.311 | 95 | RWG | 1.717 | 145 | HHQ | 0.317 | 195 | YYS | 3.983 |
| 46 | PHM | 3.714 | 96 | RWH | 1.091 | 146 | HHC | 0.128 | 196 | YYT | 3.983 |
| 47 | PHN | 6.061 | 97 | RWI | 1.232 | 147 | DYY | 3.417 | 197 | YYC | 0.637 |
| 48 | PHQ | 3.718 | 98 | RWK | 0.606 | 148 | EYY | 3.417 | |||
| 49 | PHR | 4.751 | 99 | RWL | 3.212 | 149 | HYY | 2.257 | |||
| 50 | PHS | 4.042 | 100 | RWM | 0.727 | 150 | KYY | 2.257 |
The structures of 197 peptides were generated using ChemDraw Professional 15.1 software. Subsequently, each structure underwent optimization using the PM7 method from the Molecular Orbital Package (MOPAC) quantum chemistry program, as described in detail in the ref. 24.
In FTC dataset, three peptides YHY, YKY and YRY display the same highest lipid antioxidant activities (9.886) and share a common structure of two tyrosine at the first and the third amino acid and one basic amino acid at the second amino acid. As the structure alignment is of pivotal importance for 3D-QSAR modeling, in this study, two sets of aligned structures were prepared, employing either YRY or YHY as the reference molecule.
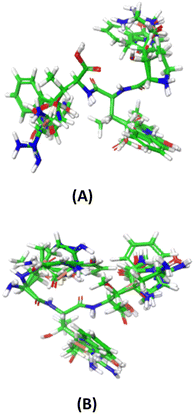
To align the optimized structures, the Flexible Ligand Alignment Panel in Maestro 11.5 software was utilized. Common scaffolds among the ligands were superimposed using the maximum common substructure and SMARTS, taking into account conformational variations in the side chains. A round of manual alignment was then performed to ensure proper alignment of side chains not covered by the template molecule. The alignments of all 197 peptides with respect to YRY and YHY are illustrated in Fig. 1A and B.
For model development, the dataset was divided into a training set comprising 158 peptides (80%) and a test set comprising 39 peptides (20%). Different random seeds were employed to assess the reproducibility of the results (refer to ESI 1† for the train-set splits corresponding to different random seeds).
Construction of 3D-CoMSIA models with OPLS_2005 and Tripos force fields
To assess the impact of two different force fields on the statistical performance of the models, we employed the OPLS_2005 and Tripos force fields on each set of aligned structures to generate CoMSIA models, referred to as OPLS-based and Tripos-based CoMSIA models, respectively. The construction of the OPLS-based models followed the procedure outlined in,24,25 while the construction of the Tripos-based models was guided by the Release Notes integrated into Sybyl X 2.1.In brief, all aligned peptides were positioned within a 3D cubic lattice. Molecular similarity indices were calculated by comparing the similarity of each molecule to a common probe atom, placed at lattice points of the cubic lattice, which had a radius of 1 Å, a charge of +1, and a hydrophobicity of +1. The calculation involved five fields: steric, electrostatic, hydrophobic, hydrogen-bond donor, and hydrogen-bond acceptor. Energy values were truncated at a cutoff of 30 kcal mol−1.
For the OPLS-based models, variables with a standard deviation less than 0.01, an absolute t-value smaller than 2, or within a distance of 2.0 Å from any training set atom were eliminated. For the Tripos-based models, the common dataset, exported from Maestro software as sdf files, was imported into Sybyl software. The CoMSIA descriptors were calculated using the calculate properties dialog, with the following parameters: charge calculation using Gasteiger-Hückel, attenuation set to 0.3, and automatic region creation. The models were constructed using the Partial Least Square Analysis module in the QSAR section in the MDE toolbar.
The optimal number of factors for constructing OPLS or Tripos models was determined following specific instructions in the respective software. Using Maestro, a series of 20 models was created, gradually varying the number of PLS factors from 1 to 20 for each train-test split (random seed). The statistical metrics obtained from each model were compared to identify the most statistically reliable and robust model. These metrics encompassed the coefficient of determination (R2), the cross-validation coefficient achieved through a leave-one-out approach (RLOO2), the external validation correlation coefficient (Q2), the F value, the root-mean-square error in test set predictions (RMSE), and Rscramble2, which is the coefficient of determination derived from a randomization test. While higher R2, RCV2 (RLOO2), Q2, and F values correspond to the higher reliability and predictability of the models, larger values of the remaining metrics suggest the opposite. Consequently, the optimal number of factors was selected to achieve a harmonious balance between these two sets of metrics.
In the case of the Tripos-based models, the optimal number of PLS factors was determined automatically by the software based on the best cross-validation result from 20 models. This optimal PLS number was then employed for all subsequent PLS analyses.
The formulas for the determination of all the aforementioned statistical parameters were presented in ESI 2.† To ensure the consistency of any comparisons, these formulas were employed uniformly for all models developed in this work, unless otherwise stated.
ML based CoMSIA models
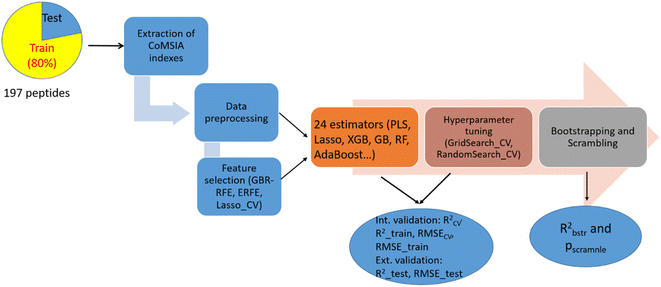
The process of constructing ML-based CoMSIA models is depicted in Fig. 2. The model building was performed using Python 3.10.11 on a computer (HP 340S G7 Notebook PC) equipped with an Intel Core i7 1.30 GHz CPU. All subsequent steps, from data pre-processing to model building, were carried out in Jupyter Notebook using various Python modules from the Sklearn library.Feature extraction
The peptide YRY was chosen in further ML based modeling as it has the longest side-chain at the second amino acid making the alignment more consistent at this position compared to YKY and YHY (two other peptides having the same FTC values).The CoMSIA descriptors were extracted using the Manage CoMFA module of the QSAR Menubar in Sybyl X 2.1. A total of 6480 CoMSIA variables were collected (see ESI 3†) and served as the independent variables for building the ML models. These variables were organized into feature columns, with columns 1–1296 corresponding to the steric field, columns 1297–2592 to the electrostatic field, columns 2593–3888 to the hydrophobic field, columns 3889–5184 to the hydrogen-bond acceptor field, and columns 5185–6480 to the hydrogen-bond donor field. Each column was marked to track the contribution of its respective field to the final models. All the required features and estimators were imported from the scikit-learn (https://scikit-learn.org/) and XGBoost package (https://xgboost.readthedocs.io/en/stable/) for implementation.33,34
Data pre-processing
Several pre-processing steps were applied to the CoMSIA-variable dataset. Firstly, any column with missing values was dropped from the dataset. Additionally, columns containing fewer than 5 values were also removed. Next, a correlation analysis was conducted to identify features (variables) with a correlation greater than 0.95. Among these highly correlated features, the ones that had the least correlation with the target variable were eliminated from the dataset.Feature selection
Following the data pre-processing step, two feature selection approaches were employed: SelectFromModel-LassoCV and GradientBoosting-Recursive Feature Elimination (GB-RFE). These two methods were deliberately chosen to assess the impact of LassoCV, known for its linear supportiveness, and RFE, which relies on feature importance or coefficient attributes, on the statistical performance of the models.The SelectFromModel-LassoCV method is a feature selection technique in scikit-learn that selects important features from a dataset based on the coefficients derived from the LassoCV (Lasso Cross-Validation) algorithm. LassoCV is a variant of Lasso regression that incorporates cross-validation to automatically select the regularization parameter. On the other hand, GradientBoosting Recursive Feature Elimination (GB-RFE) is a feature selection technique that combines the Gradient Boosting algorithm with a recursive feature elimination process. It aims to identify and select the most important features by iteratively training a Gradient Boosting model and eliminating the least significant features (using feature importance attributes).
Construction of ML based CoMSIA models
After the data splitting into X_train and X_test, the training set (X_train) was utilized to construct models. During each iteration of the cross-validation loop, a pipeline consisting of a StandardScaler and an estimator was employed to build the models. The cross_val_score function was used to split the X_train dataset into internal training and testing subsets for the current fold. The StandardScaler within the pipeline performed two operations on the internal training and testing subsets. Firstly, it fit the scaler on the internal training data (X_train_internal) and then transformed it to obtain the scaled version. Next, it applied the same scaling transformation on the internal testing data (X_test_internal) using the parameters learned from the internal training data. The scaled X_train_internal and X_test_internal were used for training and evaluating the model, respectively, within the current fold of cross-validation. This ensured that the scaling was performed independently for each fold and prevented any data leakage from the testing set to the training set, which is crucial for proper evaluation during cross-validation.In this study, three groups of models were constructed sequentially, each serving different analytical purposes that will be discussed in the Result and discussion section. The first group of models was built after the data pre-processing step using 24 estimators with default hyperparameters and without any feature selection (Script S1†). The second group of models was constructed using one of the aforementioned feature selection methods (Script S2.1–2.2†). In the first two groups, several parameters, including RCV2, Root Mean Squared Error (RMSE), Std_RMSE, and R2 (coefficient of determination for the training set), were computed to compare the performance and generalization of the models. R2_test (coefficient of determination for the test set) was used to assess their predictability.
Finally, several models with the best cross-validation (CV) statistics from the second group were selected for hyperparameter tuning, leading to the creation of the third group of models (Script S3.1–3.4†). Grid search and random search techniques were employed, along with five-fold cross-validation, to identify the optimal hyperparameters for the models. These models were trained and evaluated on the inner folds of the training set using different hyperparameter combinations, and the best hyperparameters were chosen based on their CV performance. GridSearch_CV has also been used to derive the optimum number of PLS components using each phase of feature selection (Script S4.1–4.4†).
RFE selection methods utilizing different estimators including RandomForest, XGBoost, and AdaBoost (Embedded-RFE of RF, XGB, Ada), were executed to assess the impact of these selection methods on the overall model performance (Script S5.1–5.3†). Bootstrapping (Rbstr2) and scrambling (p value) evaluation were also performed to assess the robustness and reliability of the ML-based models (Script S6.1–6.2†).
Experimental
Materials
All peptides were prepared using L-isomers of each amino acid by solid-phase synthesis with the fluorenylmethoxycarbonyl (Fmoc) strategy. The synthesis was conducted by GL Biochem Co., Ltd. The purities were approximately 95% as evidenced by high-performance liquid chromatography (HPLC) and mass spectrometry (MS) data. Linoleic acid (∼95%) was purchased from Sigma Chemical (St. Louis, MO). Ammonium thiocyanate, ferrous chloride and other reagents were obtained with the analytical grade. Thermo Scientific Genesys 20 served as the equipment in all UV-Vis measurements.Ferric thiocyanate assay
The ferric thiocyanate assay was conducted following the procedure described in the ref. 18. Test samples dissolved in 0.5 mL of deionized water were combined with linoleic acid emulsion (1.0 mL, 50 mM) and phosphate buffer (1.0 mL, 0.1 M) in 5 mL glass test tubes. The final concentration of test sample is 40 μM. The test tubes were tightly sealed with silicon rubber caps and placed in a dark environment at 60 °C. Throughout the incubation period, small aliquots (50 μL) of the reaction mixtures were extracted at various intervals.To assess the extent of oxidation, sequential additions of ethanol (2.35 mL, 75%), ammonium thiocyanate (50 μL, 30%), and ferrous chloride (50 μL, 20 mM in 3.5% HCl) were made to the extracted reaction mixtures. After allowing the mixture to stand for 3 minutes, the absorbance of the solution was measured at 500 nm. A control sample, excluding the peptides but containing the same components as the test sample, was prepared. The induction period, denoting the time required to reach an absorbance of 0.3, was calculated. The relative activities of the test samples were determined by dividing their respective induction periods by that of the control sample. All experiments were conducted in triplicate, and the average values were recorded.
Result and discussion
Data distribution
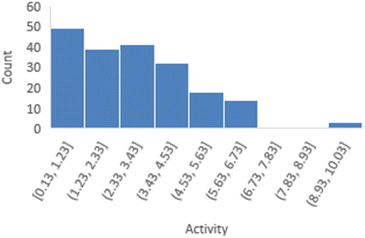
The distribution of activities for 197 peptides in the FTC dataset was shown in Fig. 3, revealing a right-skewed pattern with a skewness of 0.943, where the number of peptides with lower activities is significantly higher than those with larger activities.However, it is important to note that linear regression remains robust to deviations from normality in the target variable itself, as long as the residuals or prediction errors meet the assumption of a normal distribution. This robustness is supported by the Central Limit Theorem, making it less necessary for the target variable to follow a normal distribution.35 Therefore, in the case of skewness less than 1, we have chosen not to transform the target variable as it will complicate the explanation of the predicted results, and we will discuss the distribution of prediction errors in the next section.
OPLS-based CoMSIA models
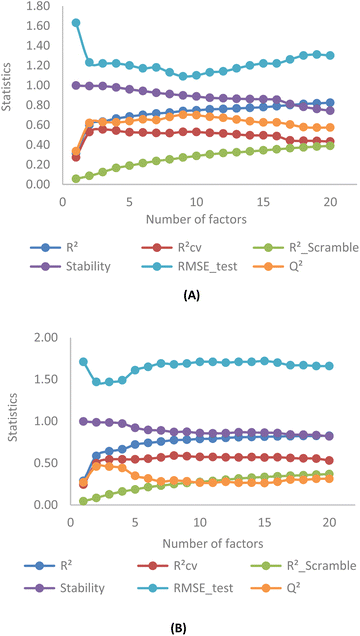
Fig. 4 illustrates the correlation between key statistical parameters obtained from OPLS-3D-CoMISA models as the number of factors varied from 1 to 20. A compromise is achieved between the highest R2, RCV2 (RLOO2), Q2 values, and the lowest RScramble2 and RMSE_test values at 3 factors for both YHY (Fig. 4A) and YRY (Fig. 4B) aligned datasets, using the same random seed.The R2, RCV2, Q2 values for the first superimposed set of structures are 0.63, 0.55, and 0.63, while RScramble2 and RMSE_test are 0.12 and 1.22, respectively. Similarly, for the YRY aligned dataset, the R2, RCV2, and Q2 values are 0.64, 0.54, and 0.46, with RScramble2 and RMSE_test at 0.13 and 1.47, respectively. These results indicate the performances of the OPLS-based models are moderate for both superimposed datasets in terms of model fitting and predictivity.
The correlation pattern remains generally consistent across five different data splits for each aligned set, resulting in all OPLS-based CoMSIA models having a common number of 3 PLS factors for optimal statistics. Observation of cross-validation (RCV2) and prediction coefficients (Q2) for 5 random seeds in both YHY and YRY alignments reveals that the change in the molecular template does not affect the statistical results of OPLS-based models substantially, and these values do not mutually exceed 0.6. This reaffirms the moderate performance of all OPLS-based models. For detailed statistical information related to factor selection and PLS analysis in OPLS-based models, please refer to ESI 4.†
To assess the reliability of the 3-factor-CoMSIA models, distribution plots and skewness calculations for prediction errors were conducted using various random seeds. Fig. 5 depicts a distribution plot of prediction errors for random seed 1 (YHY-reference). This distribution illustrates a general normal distribution centered around 0 but still exhibits a long left tail, highlighting two primary characteristics of this model type: the reliability of statistical inference, and the model's limitation in adequately predicting structures with extreme activities. Similar distribution patterns were also observed for five other train-test splits, as presented in ESI 1.†
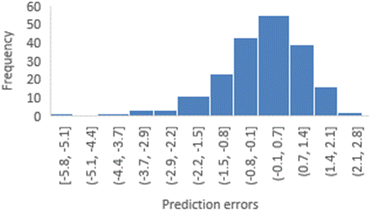 | ||
| Fig. 5 Distribution of prediction errors derived from the 3-factor-CoMSIA model with YRY as the reference. | ||
Tripos-based CoMSIA models
It is important to note that the cross-validation coefficient is denoted in this study as RLOO2 instead of QLOO2, as provided by the Sybyl X software's output. This choice was made to prevent any potential confusion with the variance explained in external prediction, which is also referred to as Q2. Additionally, the evaluation of a model based only on R2 and QLOO2 as reported by a number of studies22,23 is insufficient as it could not represent the performance of the model on the unseen data.36–38 For that reason, in this study, parameters for both internal and external assessment were evaluated to arrive at conclusions regarding each model's performance.To facilitate direct comparison between the OPLS and Tripos-based CoMSIA models, all the Tripos models were constructed using the same random seed used for OPLS models ranging from 1 to 5, thereby maintaining consistent train-test compositions (ESI 1†). The statistical results for two of the Tripos-based CoMSIA models built with random seed 1 are presented in Table 2.
| Tripos-CoMSIA model | Optimal factor | R2 | RLOO2 | Rbstr2 | SEP | Q2 |
|---|---|---|---|---|---|---|
| a SEP: standard error of prediction. | ||||||
| YHY_ref | 11 | 0.756 | 0.446 | 0.781 | 1.432 | 0.547 |
| YRY_ref | 18 | 0.828 | 0.531 | 0.684 | 1.350 | 0.339 |
As the optimal number of factors (PLS number) was determined solely based on RCV2, the PLS number in Tripos-based CoMSIA models is significantly higher than that in OPLS models when using the same random seed and molecular template. This method of PLS factor optimization also leads to variation in the PLS number across different random seeds, as it responds promptly to changes in the composition of the training set.
Furthermore, the Tripos-based CoMSIA models tend to exhibit overfitting, as indicated by substantial discrepancy between R2 (0.756 and 0.828) and RCV2 (0.446 and 0.531) for YHY and YRY aligned sets, respectively. For comprehensive statistical details regarding Tripos-based models generated with five different random seeds during factor selection and PLS analysis, please refer to ESI 5.†
Predictability plots for the OPLS and Tripos based models
The predictability plots for the OPLS models are illustrated in Fig. 6, while those for the Tripos force field are displayed in Fig. 7. These plots indicate that both models have inadequate predictive performance, severely underestimating the FTC values of peptides in the high activity range. The root-mean-square error in the test-set predictions from the OPLS model reaches as high as 1.460, which is similar to the standard error of prediction from the Tripos model (1.432). These errors are considered significant considering the range of FTC activity in the dataset only up to nearly 10. All prediction performances of OPLS and Tripos-based models can be found in ESI 4 and 5.† To the best of our knowledge, the only study constructing 3D-CoMSIA models using the FTC dataset was implemented with YRY being the alignment template using the Sybyl X software. The models were evaluated based on only two statistical parameters (R2 of 0.914 and Q2 of 0.733) and no evaluation of external prediction was concluded.22 Thus, in our opinion, there are no reliable 3D-CoMSIA models for this data set have been reported before this study.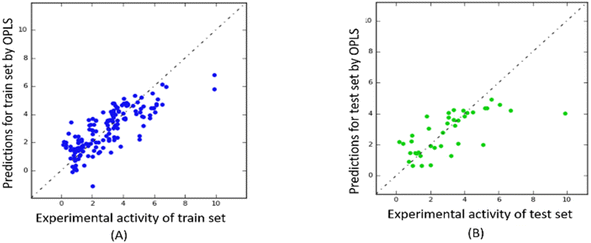 | ||
| Fig. 6 Predictability plots of the OPLS models for the training set (A) and for test set (B), random seed 1, YRY reference. | ||
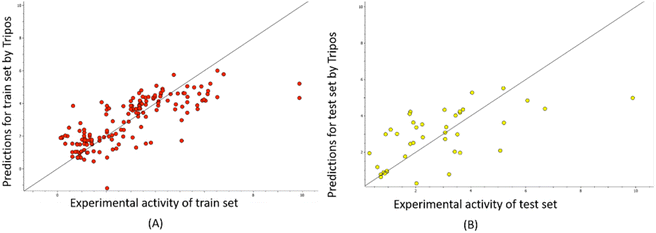 | ||
| Fig. 7 Predictability plots of the Tripos models for the training set (A) and for test set (B), random seed 1, YRY reference. | ||
ML based CoMSIA models without variable selection
The primary reason for using Python scripts, instead of fixed functions within commercial software, to construct 3D-CoMSIA models for the FTC dataset was to allow for more flexibility in experimenting with various feature selection methods and regression algorithms. This approach aimed to mitigate the impact of the abundant number of CoMSIA variables and the imbalanced distribution of the FTC activities that could not be handled successfully by the traditional PLS modeling routine.The training dataset containing 6840 CoMSIA variables underwent preprocessing, resulting in 1282 variables that were used as inputs for the first group of models. The statistics of these models are presented in Table 3. Without employing any feature selection method, all the models performed below statistical expectations. The primary factor contributing to this poor performance is the high dimensionality of the features and the small sample size.
| Regression algorithm | RCV2 | RMSE_CV | R2_test | RMSE_test | R2 | RMSE |
|---|---|---|---|---|---|---|
| GradientBoostingRegressor() | 0.500 | 1.290 | 0.812 | 0.872 | 0.995 | 0.125 |
| RandomForestRegressor() | 0.465 | 1.332 | 0.812 | 0.870 | 0.930 | 0.489 |
| Lasso(alpha = 0.1) | 0.415 | 1.391 | 0.534 | 1.371 | 0.719 | 0.979 |
| BayesianRidge() | 0.413 | 1.377 | 0.688 | 1.123 | 0.760 | 0.904 |
| HistGradientBoostingRegressor() | 0.400 | 1.400 | 0.754 | 0.996 | 0.970 | 0.319 |
| TweedieRegressor() | 0.371 | 1.420 | 0.666 | 1.161 | 0.807 | 0.811 |
| AdaBoostRegressor() | 0.344 | 1.442 | 0.824 | 0.844 | 0.866 | 0.675 |
| SVR(epsilon = 0.2) | 0.306 | 1.520 | 0.309 | 1.670 | 0.589 | 1.183 |
| PLSRegression(n_components = 3) | 0.301 | 1.500 | 0.646 | 1.195 | 0.702 | 1.008 |
| BaggingRegressor(base_estimator = SVR()) | 0.297 | 1.531 | 0.292 | 1.691 | 0.568 | 1.213 |
| XGBRegressor(booster = None) | 0.230 | 1.569 | 0.832 | 0.824 | 1.000 | 0.000 |
| ElasticNet() | 0.221 | 1.603 | 0.190 | 1.808 | 0.272 | 1.575 |
| DecisionTreeRegressor() | 0.122 | 1.669 | 0.504 | 1.415 | 1.000 | 0.000 |
| KNeighborsRegressor(n_neighbors = 2) | 0.032 | 1.749 | 0.497 | 1.426 | 0.657 | 1.081 |
| NuSVR(nu = 0.1) | 0.018 | 1.789 | 0.103 | 1.903 | 0.186 | 1.666 |
| QuantileRegressor() | −0.042 | 1.850 | 0.000 | 2.010 | −0.002 | 1.848 |
| MLPRegressor() | −0.372 | 1.964 | 0.628 | 1.226 | 0.999 | 0.052 |
| HuberRegressor() | −0.835 | 2.246 | 0.219 | 1.776 | 0.845 | 0.727 |
| GaussianProcessRegressor() | −2.700 | 3.430 | −2.175 | 3.580 | 1.000 | 0.000 |
| XGBRegressor(booster = ‘gblinear’) | −3.393 | 3.328 | −0.270 | 2.265 | 0.885 | 0.625 |
| Ridge() | −6.160 | 3.901 | −0.918 | 2.782 | 0.897 | 0.593 |
| KernelRidge() | −8.350 | 4.958 | −2.352 | 3.679 | −1.580 | 2.965 |
| LinearSVR(random_state = 1, tol = 1 × 10−5) | −8.630 | 4.607 | −0.903 | 2.772 | 0.852 | 0.710 |
| LinearRegression() | −702.889 | 40.070 | −116.058 | 21.739 | 1.000 | 0.000 |
Among 24 regression estimators, the GradientBoostingRegressor (GBR) exhibited the best performance, with an RCV2 value of 0.500 and a Root Mean Square Error for cross-validation (RMSECV) of 1.326. Generally, the tree-based, Lasso and Bayesian Ridge outperformed other regressors, which can be attributed to the inherent feature-selection nature of these algorithms. This feature has helped to mitigate the impact of the high number of CoMSIA indices derived from the FTC dataset. The PLS model with 3 components demonstrated less effective cross-validation estimation compared to the OPLS_2005 and Tripos models, achieving an RCV2 of 0.301 and an RMSECV of 1.515.
Interestingly, the coefficients of determination for the test set (R2_test) and training set (R2) were remarkably higher than the RCV2 for most models, particularly for the tree models. This suggests the presence of overfitting in these models. For example, the GBR model exhibited an RCV2 of 0.500 and an R2 of 0.995, indicating the need for feature selection to achieve more reliable models.
ML based CoMSIA models with feature selection
The GB-RFE method was applied to the 1282 variables obtained from the data preprocessing step for feature selection from the YRY-aligned structure set. The elimination of variables was performed iteratively, with 20 features being removed at each iteration. No significant difference was observed in the resulting models when varying the number of variables eliminated at a time (20, 10, or 5). To optimize computational efficiency, the removal of 20 features per iteration was chosen. This recursive process continued until the desired number of features was reached. Among the pruned dataset, twelve variables (feature columns) were selected for the training dataset, specifically columns [2240, 2946, 3077, 3251, 3257, 4857, 5566, 5657, 5688, 5831, 5961, and 5987]. These variables corresponded to the lowest Root Mean Square Error (RMSE) for the associated GBR model, indicating the importance of hydrophobicity and hydrogen-bond donor in relation to FTC activity.Furthermore, the SelectFromModel-LassoCV method with a threshold of 0.01 identified 37 variables that contributed significantly to the Lasso models. Among these variables, the variable corresponding to the hydro-bond donor field still showed essential importance. Additionally, less impacts on FTC activity were observed for 3 other fields including electrostatic, hydrophobic and hydro-bond acceptor, as indicated by the ratios of selected variables representing these fields. The selected variables were as follows: [209, 664, 693, 913, 1414, 1458, 1582, 1833, 1906, 1928, 2216, 2345, 3060, 3191, 3251, 3299, 3442, 3535, 3620, 4262, 4463, 4664, 4723, 4747, 4866, 5277, 5421, 5545, 5566, 5670, 5831, 5843, 5855, 5891, 6004, 6125, and 6403].
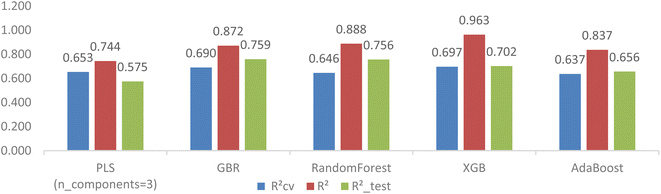
The top ten models selected based on their cross-validation RCV2 and RMSECV for each feature selection method are presented in Table 4. Several noteworthy points can be highlighted. Firstly, the implementation of feature selection has improved the cross-validation estimation of all models. Secondly, the GB-RFE feature selection method has yielded advantages for tree-based models (GradientBoosting, RandomForest, XGBoost, and AdaBoost), while the SelectFromModel-LassoCV has shown benefits for linear models (PLS, Lasso, and BayesianRidge). The GBR model stood out as the best performer in the first group, achieving an RCV2 of 0.644, RMSECV of 1.072, R2_test of 0.756, and R2 of 0.977. In the second group, the PLS model showcased the highest RCV2 of 0.653, RMSECV of 1.058, R2_test of 0.575, and R2 of 0.755. However, there was a significant overlap of estimators between the two top-ten model groups, indicating that these estimators are suitable for developing 3D CoMSIA models of FTC dataset.
| GB-RFE | RCV2 | RMSECV | R2_test | RMSE_ test | R2 | RMSE |
|---|---|---|---|---|---|---|
| GradientBoostingRegressor(random_state = 1) | 0.644 | 1.072 | 0.756 | 0.993 | 0.977 | 0.280 |
| RandomForestRegressor() | 0.638 | 1.094 | 0.760 | 0.985 | 0.950 | 0.413 |
| XGBRegressor(booster = None) | 0.624 | 1.095 | 0.721 | 1.061 | 1.000 | 0.001 |
| AdaBoostRegressor() | 0.607 | 1.131 | 0.629 | 1.224 | 0.853 | 0.708 |
| HistGradientBoostingRegressor() | 0.529 | 1.245 | 0.668 | 1.158 | 0.916 | 0.535 |
| BaggingRegressor(base_estimator = SVR()) | 0.449 | 1.358 | 0.331 | 1.643 | 0.565 | 1.218 |
| SVR(epsilon = 0.2) | 0.447 | 1.360 | 0.337 | 1.636 | 0.578 | 1.200 |
| Lasso(alpha = 0.1) | 0.377 | 1.416 | 0.472 | 1.461 | 0.509 | 1.293 |
| BayesianRidge() | 0.355 | 1.420 | 0.476 | 1.454 | 0.542 | 1.249 |
| KNeighborsRegressor(n_neighbors = 2) | 0.328 | 1.484 | 0.510 | 1.406 | 0.783 | 0.860 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| SelectFromModel_LassoCV | ||||||
| PLSRegression(n_components = 3) | 0.653 | 1.058 | 0.575 | 1.310 | 0.744 | 0.934 |
| TweedieRegressor() | 0.649 | 1.068 | 0.596 | 1.277 | 0.598 | 1.170 |
| BayesianRidge() | 0.621 | 1.112 | 0.646 | 1.196 | 0.662 | 1.074 |
| GradientBoostingRegressor() | 0.514 | 1.252 | 0.700 | 1.101 | 0.974 | 0.300 |
| RandomForestRegressor() | 0.514 | 1.266 | 0.727 | 1.049 | 0.934 | 0.473 |
| Lasso(alpha = 0.1) | 0.506 | 1.278 | 0.617 | 1.244 | 0.606 | 1.158 |
| KNeighborsRegressor(n_neighbors = 2) | 0.503 | 1.263 | 0.434 | 1.511 | 0.800 | 0.825 |
| MLPRegressor() | 0.495 | 1.245 | 0.666 | 1.162 | 0.655 | 1.084 |
| XGBRegressor(booster = None) | 0.485 | 1.300 | 0.667 | 1.159 | 1.000 | 0.001 |
| AdaBoostRegressor() | 0.476 | 1.316 | 0.597 | 1.276 | 0.803 | 0.819 |
Among the 24 distinct regression techniques examined, non-linear regression methods consistently demonstrated superior fitting performance when assessed across the two feature selection methods. This underscores the presence of non-linearity in predicting antioxidant activity and, in turn, provides an explanation for the subpar model performance observed in the previous section and prior studies that relied on linear regression methods.22
For a small dataset like FTC, the superior performance of GB-RFE tree-based models compared to Lasso-PLS can be attributed to their intrinsic algorithms. PLS is particularly sensitive to outliers because the linear regression line is directly influenced by the mean of the target variable during fitting. In contrast, extreme target values only affect local trees and the local splitting decisions in tree-based models, resulting in an improved overall perform for GBR, RandomForest, XGBoost, and AdaBoost.
ML based CoMSIA models with hyperparameter tuning
The disparity of RCV2, R2_test, and R2 in Table 4 suggests that the feature selection only improved the cross-validation performance but still could not fix the problem of overfitting completely for tree-based models. Hyperparameter tuning using GridsearchCV was carried out on hundreds of hyperparameter combinations to explore the improvement of generalization ability for the four tree-based models.Fig. 8 visually illustrates the superior performance of tree-based models when compared to the LassoCV-PLS model (with n = 3 components). Specifically, while the cross-validation RCV2 of the PLS model is comparable to that of the four tree-based models, the tree-based models with tuned hyperparameters clearly outperform the LassoCV-PLS model in predictivity.
After hyperparameter tuning, the GBR model with specific settings (learning_rate = 0.01, max_depth = 2, n_estimators = 500, subsample = 0.5) showed the most significant improvement in model generalization, with notable reductions in the differences between RCV2, R2 and R2_test (0.690, 0.872, and 0.759, respectively). Likewise, the RMSECV, RMSE and RMSE_test values for the GBR model decreased to 1.042, 0.66, and 0.987, respectively.
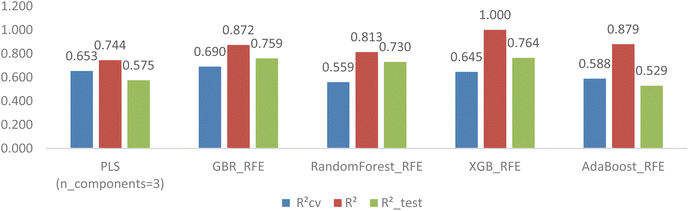
On the other hand, the other tree-based models, including RandomForest, XGB, and AdaBoost, unexpectedly did not achieve the same level of improvement, as indicated by larger disparities between their coefficients. There are various reasons contributing to the dissimilar response between GBR and the other three models to hyperparameter tuning, with common factors being feature selection, data size, and incomplete hyperparameter tuning. Since testing all possible measures is not feasible, we conducted an additional experiment involving Embedded RFE (ERFE) feature selection coupled with hyperparameter tuning with GridSearchCV.
The ERFE feature selection was applied with three different estimators (RF, XGB, and Ada). However, the results indicated that the ERFE method did not improve the overfitting issue; in fact, it exacerbated it, as shown in Fig. 9. The application of the Embedded XGB model revealed a notable escalation in overfitting, evidenced by a rise in R2 to 1.000. This increase further widened the gap between this parameter and RCV2 (0.645) as well as R2_test (0.764). Similar trends were observed in the RF and Ada models, where the discrepancy of these coefficients also intensified.
Bootstrapping and Y-scrambling evaluation for the GB-RFE GBR model
The bootstrapping evaluation has generated Rbstr2 of 0.703 (standard deviation (SD): 0.056), average MSE: 1.200 (SD: 0.227). These results are similar to R2_test of the GBR model, indicating that the model's performance is consistent, robust, and not dependent on the specific sample of data used for training.The result of Y-scrambling activity for the GBR model has shown a p value <0.001 after 100 iterations, suggesting that the model's performance is not due to random chance and strengthening its reliability and applicability.
Predictability of the GB-RFE GBR model for the FTC dataset
Fig. 10 shows the correlation between predicted and experimental FTC values for the training and test sets obtained from the GBR model. The plot demonstrates the excellent fitting of the GBR model compared to the Tripos and OPLS-based CoMSIA models for the training set, even at the highest activity levels. However, its performance was comparatively less efficient for the test set, particularly in the activity range higher than 6 (please refer to ESI 6† for all the predictions on the FTC dataset using the RFE-GBR model with the optimized hyperparameters).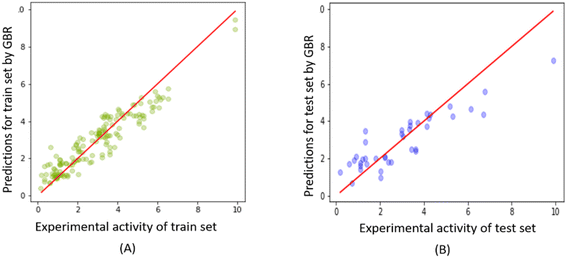 | ||
| Fig. 10 Experimental versus predicted FTC values derived from the GBR model for (A) FTC training and (B) test set. | ||
Predictions of FTC activity of Tryptophyllin L tripeptides
The GBR model, employing the GB-RFE selection method and specific hyperparameters (learning_rate = 0.01, max_depth = 2, n_estimators = 500, subsample = 0.5), was identified as the most optimal 3D-CoMSIA model constructed using FTC data, and therefore was used to predict the lipid antioxidant activity of 13 Tryptophyllin L peptide fragments.The two most important field effects on lipid antioxidant capability, including hydrophobicity and hydrogen bond donor, were illustrated in Fig. 11. A notable observation is the positive impact of hydrophobicity in the first amino acid position on overall activity, but interestingly, this effect reverses when the hydrophobic amino acid is in the second position. Additionally, hydrogen-bond donor groups are found to be beneficial to FTC activity when located on the second and third amino acid positions, while they have a mixed effect on the first amino acid.
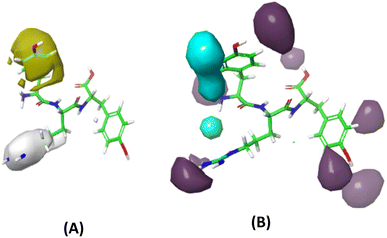 | ||
| Fig. 11 Contour maps of field contribution to lipid antioxidant activity (A) hydrophobicity (yellow: positive, white: negative) and (B) hydrogen-bond donor (purple: positive, cyan: negative). | ||
Structures of 13 Tryptophyllin L tripeptides superimposed on the YRY reference are displayed in Fig. 12. The CoMSIA indices from these peptides were subjected to the RFE-GBR model to predict the FTC activities of these peptide fragments (ESI 7†). Table 5 presents 13 Tryptophyllin L tripeptides along with their corresponding predicted FTC values. Based on the predictions from the GBR models, the peptides F-P-W and F-P-5Htp were identified as the highest FTC activities.
| No. | Title | FTC predictions by GBR model |
|---|---|---|
| a 5Htp: 5 hydroxytryptophan, pE: pyroglutamic acid. | ||
| 1 | FPW | 3.882 |
| 2 | pEFP | 3.476 |
| 3 | FPF | 2.556 |
| 4 | IPW | 3.225 |
| 5 | FLP | 1.996 |
| 6 | PWF | 1.287 |
| 7 | PWF(NH2) | 1.304 |
| 8 | FHR(NH2) | 2.119 |
| 9 | PWP | 1.772 |
| 10 | PFP | 1.755 |
| 11 | WFH | 2.443 |
| 12 | P-5Htp-L | 1.818 |
| 13 | F-P-5Htp | 3.694 |
The most interesting observation from the predictions on Tryptophyllin L tripeptides was the combined effect of phenylalanine at the first amino acid and tryptophan at the third amino acid on the FTC activity. This combination provides hydrophobicity for the first position and hydrogen-bond donor for the C-terminal leading to the highest FTC activity in the list. The FTC value does not change significantly when tryptophan is replaced by 5-hydroxytryptophan (5Htp) explained by the subtle difference in hydrogen-bond donor ability of 5Htp compared with that of tryptophan.
Three tripeptides were synthesized and tested using the FTC assay, including FPW, F-P-5Htp, and P-5Htp-L. The latter two tripeptides are derived from the Tryptophyllin L F-P-5Htp-L, is of special interest as containing 5-Htp one of the tryptophan metabolites. Experimental results yielded FTC values of 4.2 ± 0.12, 4.4 ± 0.11, and 1.72 ± 0.15 for F-P-5Htp, F-P-W, and P-5Htp-L, respectively. These experimental results generally align with the predictions of the RFE-GBR model, suggesting the potential lipid antioxidant properties of these three peptides.
Conclusion
In conclusion, this study conducted a comprehensive comparison of two modeling approaches to determine the most statistically reliable and robust model for predicting the lipid antioxidant activities of tripeptides. The first approach utilized the traditional PLS algorithm within Maestro 11.5 and Sybyl X 2.1, while the second approach employed various machine learning algorithms for model selection.The analysis of the FTC CoMSIA dataset using traditional methods revealed several key findings. Firstly, changing the molecular template for alignment had no significant impact on the CoMSIA models' statistics. However, switching between force fields resulted in notable differences. OPLS-based models exhibited more stable PLS numbers and statistical parameters compared to Tripos force field models, which displayed variations in PLS numbers across different data splits and tended to overfit. Secondly, the CoMSIA models from both force fields showed low predictive capability (Q2) with a strong inclination to underestimate FTC activity, particularly in the high activity range.
The ML-based modelling routine was intentionally designed to process the data into three stages. The ML-based 3D-CoMSIA models without feature selection have revealed better performances for four tree-based regressors (RandomForest, XGB, AdaBoost and GBR), Lasso and Bayesian Ridge Regressor as a result of the feature self-selected nature of these estimators. This feature is beneficial greatly in alleviating the detrimental impact of the abundance of CoMSIA indices on the models.
Out of the 24 distinct regression techniques investigated, non-linear regression methods consistently exhibited better model fitting than the linear methods when evaluated using the two feature selection methods GBR-RFE and SelectFromModel_LassoCV. This highlights the presence of non-linearity in predicting antioxidant activity, thus offering an explanation for the less favorable performance of linear models previously.
The competition of four tree-based models at the final stage of hyperparameter tuning has revealed different levels of generalization for these tree-based models, although improvement in terms of cross-validation and predictivity were observed for all of these models. Among those, the GBR model with the GBR-RFE selection method and specific hyperparameters (learning_rate = 0.01, max_depth = 2, n_estimators = 500, subsample = 0.5) was selected as the best model for predicting the FTC activity of tripeptides when displaying smallest disparity in internal and external statistics. It is therefore statistically reliable to be used for screening of lipid-antioxidant tripeptides.
Overall, the ML-based modeling approach has demonstrated greater efficiency compared to the traditional CoMSIA method when modeling 3D-field similarity models for the FTC dataset. This conclusion is based not only on the comparison of models constructed in this study but also on a review of results from previous research.
The predicted FTC values of 13 Tryptophyllin L peptide fragments by the RFE-GBR model have guided the experimental testing of three tripeptides, yielding FTC values of 4.2 ± 0.12, 4.4 ± 0.11, and 1.72 ± 0.15 for F-P-5Htp, F-P-W, and P-5Htp-L, respectively. The experimental results generally aligned with the model predictions, suggesting that these peptides have great potential as lipid antioxidants and should be further tested on food-based samples.
Finally, this study offers a collection of adaptable Python scripts (please refer to the attached Script S1–S6† for relevant code) that can be used to model various bioactivities or properties, requiring only an input CoMSIA dataset as a minimum requirement. These scripts enable model construction using 24 estimators, both with and without feature selection. Notably, the scripts incorporate features such as variable selection (GBR-RFE, ERFE, and SelectFromModel) and hyperparameter tuning through GridSearch_CV and RandomSearch_CV, scrambling and bootstrapping evaluation, allowing the estimation of model consistency and reliability.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We express our gratitude to the Faculty of Chemical Engineering at the Industrial University of Ho Chi Minh City for their generous provision of instruments and invaluable support during the antioxidant testing conducted in this study.Notes and references
- N. Wiernsperger, Oxidative stress as a therapeutic target in diabetes: revisiting the controversy, Diabetes Metab., 2003, 29(6), 579–585 CrossRef CAS PubMed.
- M. Carocho and I. C. Ferreira, A review on antioxidants, prooxidants and related controversy: natural and synthetic compounds, screening and analysis methodologies and future perspectives, Food Chem. Toxicol., 2013, 51, 15–25 CrossRef CAS PubMed.
- M. Ebadi, Antioxidants and free radicals in health and disease: an introduction to reactive oxygen species, oxidative injury, neuronal cell death and therapy in neurodegenerative diseases, Crit. Rev. Toxicol., 2001, 38, 13–71 Search PubMed.
- H. Sies, C. Berndt and D. P. Jones, Oxidative stress, Annu. Rev. Biochem., 2017, 86, 715–748 CrossRef CAS PubMed.
- C. Vassalle, M. Maltinti and L. Sabatino, Targeting oxidative stress for disease prevention and therapy: where do we stand, and where do we go from here, Molecules, 2020, 25(11), 2653 CrossRef CAS PubMed.
- H. J. Forman and H. Zhang, Targeting oxidative stress in disease: promise and limitations of antioxidant therapy, Nat. Rev. Drug Discovery, 2021, 20(9), 689–709 CrossRef CAS PubMed.
- B. Halliwell, M. A. Murcia, S. Chirico and O. I. Aruoma, Free radicals and antioxidants in food and in vivo: what they do and how they work, Crit. Rev. Food Sci. Nutr., 1995, 35(1–2), 7–20 CrossRef CAS PubMed.
- B. Halliwell and M. Whiteman, Measuring reactive species and oxidative damage in vivo and in cell culture: how should you do it and what do the results mean?, Br. J. Pharmacol., 2004, 142(2), 231–255 CrossRef CAS PubMed.
- R. Re, N. Pellegrini, A. Proteggente, A. Pannala, M. Yang and C. Rice-Evans, Antioxidant activity applying an improved ABTS radical cation decolorization assay, Free Radicals Biol. Med., 1999, 26(9–10), 1231–1237 CrossRef CAS PubMed.
- L. Zheng, M. Zhao, C. Xiao, Q. Zhao and G. Su, Practical problems when using ABTS assay to assess the radical-scavenging activity of peptides: Importance of controlling reaction pH and time, Food Chem., 2016, 192, 288–294 CrossRef CAS PubMed.
- I. F. Benzie and J. J. Strain, The ferric reducing ability of plasma (FRAP) as a measure of “antioxidant power”: the FRAP assay, Anal. Biochem., 1996, 239(1), 70–76 CrossRef CAS PubMed.
- C. Sonklin, N. Laohakunjit and O. Kerdchoechuen, Assessment of antioxidant properties of membrane ultrafiltration peptides from mungbean meal protein hydrolysates, PeerJ, 2018, 6, e5337 CrossRef PubMed.
- O. P. Sharma and T. K. Bhat, DPPH antioxidant assay revisited, Food Chem., 2009, 113(4), 1202–1205 CrossRef CAS.
- M. S. Blois, Antioxidant determinations by the use of a stable free radical, Nature, 1958, 181, 1199–1200 CrossRef CAS.
- P. Manual, OxiSelect™ Oxygen Radical Antioxidant Capacity (ORAC) Activity Assay, Cell Biolabs, Inc Search PubMed.
- R. Chapman and K. Mackay, The estimation of peroxides in fats and oils by the ferric thiocyanate method, J. Am. Oil Chem. Soc., 1949, 26(7), 360–363 CrossRef CAS.
- P. Minkiewicz, J. Dziuba, A. Iwaniak, M. Dziuba and M. Darewicz, BIOPEP database and other programs for processing bioactive peptide sequences, J. AOAC Int., 2008, 91(4), 965–980 CrossRef CAS PubMed.
- K. Saito, D.-H. Jin, T. Ogawa, K. Muramoto, E. Hatakeyama and T. Yasuhara, et al., Antioxidative properties of tripeptide libraries prepared by the combinatorial chemistry, J. Agric. Food Chem., 2003, 51(12), 3668–3674 CrossRef CAS PubMed.
- M. Tian, B. Fang, L. Jiang, H. Guo, J. Cui and F. Ren, Structure-activity relationship of a series of antioxidant tripeptides derived from β-Lactoglobulin using QSAR modeling, Dairy Sci. Technol., 2015, 95, 451–463 CrossRef CAS.
- T. H. Olsen, B. Yesiltas, F. I. Marin, M. Pertseva, P. J. García-Moreno and S. Gregersen, et al., AnOxPePred: using deep learning for the prediction of antioxidative properties of peptides, Sci. Rep., 2020, 10(1), 21471 CrossRef CAS PubMed.
- Y.-W. Li and B. Li, Characterization of structure–antioxidant activity relationship of peptides in free radical systems using QSAR models: key sequence positions and their amino acid properties, J. Theor. Biol., 2013, 318, 29–43 CrossRef CAS PubMed.
- H. Guo, Y. Wang, Q. He, Y. Zhang, Y. Hu and Y. Wang, et al., In silico rational design and virtual screening of antixoidant tripeptides based on 3D-QSAR modeling, J. Mol. Struct., 2019, 1193, 223–230 CrossRef CAS.
- W. Yan, G. Lin, R. Zhang, Z. Liang and W. Wu, Studies on the bioactivities and molecular mechanism of antioxidant peptides by 3D-QSAR, in vitro evaluation and molecular dynamic simulations, Food Funct., 2020, 11(4), 3043–3052 RSC.
- T. T. N. Tran, D. P. Tran, V. C. Nguyen, T. D. T. Tran, T. T. T. Bui and J. H. Bowie, Antioxidant activities of major tryptophyllin L peptides: a joint investigation of Gaussian-based 3D-QSAR and radical scavenging experiments, J. Pept. Sci., 2021, 27(4), e3295 CrossRef CAS PubMed.
- T. T. N. Tran, D. P. Tran, T. M. A. Nguyen, T. H. Tran, N. N. A. Phan and V. C. Nguyen, et al., Virtual screening and rational design of antioxidant peptides based on tryptophyllin L structures isolated from the Litoria rubella frog, J. Pept. Sci., 2022, 28(4), e3380 CrossRef CAS PubMed.
- S. T. Steinborner, P. A. Wabnitz, R. J. Waugh, J. H. Bowie, C. Gao and M. J. Tyler, et al., The structures of new peptides from the Australian red tree frog'Litoria rubella'. The skin peptide profile as a probe for the study of evolutionary trends of amphibians, Aust. J. Chem., 1996, 49(9), 955–963 CrossRef CAS.
- T. T. N. Tran, Structural and mechanistic studies of post-translationally modified peptides and proteins, School of Chemistry and Physics: The University of Adelaide, 2014 Search PubMed.
- Y.-W. Li, B. Li, J. He and P. Qian, Quantitative structure–activity relationship study of antioxidative peptide by using different sets of amino acids descriptors, J. Mol. Struct., 2011, 998(1–3), 53–61 CrossRef CAS.
- J. B. Ghasemi and H. Tavakoli, Improvement of the prediction power of the CoMFA and CoMSIA models on histamine H3 antagonists by different variable selection methods, Sci. Pharm., 2012, 80(3), 547–566 CrossRef CAS PubMed.
- B. Sepehri, Z. Rasouli, Z. Hassanzadeh and R. Ghavami, Molecular docking and QSAR analysis of naphthyridone derivatives as ATAD2 bromodomain inhibitors: application of CoMFA, LS-SVM, and RBF neural network, Med. Chem. Res., 2016, 25, 2895–2905 CrossRef CAS.
- H. Ghafouri, M. Ranjbar and A. Sakhteman, 3D-QSAR studies of some reversible Acetyl cholinesterase inhibitors based on CoMFA and ligand protein interaction fingerprints using PC-LS-SVM and PLS-LS-SVM, Comput. Biol. Chem., 2017, 69, 19–27 CrossRef CAS PubMed.
- G. Floresta and V. Abbate, Machine learning vs. field 3D-QSAR models for serotonin 2A receptor psychoactive substances identification, RSC Adv., 2021, 11(24), 14587–14595 RSC.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion and O. Grisel, et al., Scikit-learn: Machine learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- T. Chen and C. Guestrin, Xgboost: A scalable tree boosting system, Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2016 Search PubMed.
- S. G. Kwak and J. H. Kim, Central limit theorem: the cornerstone of modern statistics, Korean J. Anesthesiol., 2017, 70(2), 144–156 CrossRef PubMed.
- V. Consonni, D. Ballabio and R. Todeschini, Comments on the definition of the Q 2 parameter for QSAR validation, J. Chem. Inf. Model., 2009, 49(7), 1669–1678 CrossRef CAS PubMed.
- R. Veerasamy, H. Rajak, A. Jain, S. Sivadasan, C. P. Varghese and R. K. Agrawal, Validation of QSAR models-strategies and importance, Int. J. Drug Des. Discovery, 2011, 3, 511–519 Search PubMed.
- P. Gramatica, On the development and validation of QSAR models, Comput. Toxicol., 2013, 499–526 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra06690h |
| This journal is © The Royal Society of Chemistry 2023 |