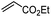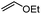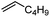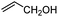Open Access Article
Open Access ArticleCobalt-catalyzed radical-mediated carbon–carbon scission via a radical-type migratory insertion†
Jian-Biao
Liu
*a,
Xiao-Jun
Liu
 a,
João C. A.
Oliveira
b,
De-Zhan
Chen
a,
João C. A.
Oliveira
b,
De-Zhan
Chen
 a and
Lutz
Ackermann
a and
Lutz
Ackermann
 *b
*b
aCollege of Chemistry, Chemical Engineering and Materials Science, Shandong Normal University, Jinan 250014, China. E-mail: jianbiaoliu.thu@sdnu.edu.cn
bInstitut für Organische und Biomolekulare Chemie, Wöhler Research Institute for Sustainable Chemistry (WISCh), Georg-August-Universität Göttingen, Tammannstraße 2, 37077 Göttingen, Germany. E-mail: Lutz.Ackermann@chemie.uni-goettingen.de
First published on 28th February 2023
Abstract
Migratory insertions of alkenes into metal–carbon (M–C) bonds are elementary steps in diverse catalytic processes. In the present work, a radical-type migratory insertion that involves concerted but asynchronous M–C homolysis and radical attack was revealed by computations. Inspired by the radical nature of the proposed migratory insertion, a distinct cobalt-catalyzed radical-mediated carbon–carbon (C–C) cleavage mechanism was proposed for alkylidenecyclopropanes (ACPs). This unique C–C activation is key to rationalizing the experimentally observed selectivity for the coupling between benzamides and ACPs. Furthermore, the C(sp2)–H activation in the coupling reaction occurs via the proton-coupled electron transfer (PCET) mechanism rather than the originally proposed concerted metalation–deprotonation (CMD) pathway. The ring opening strategy may stimulate further development and discovery of novel radical transformations.
Introduction
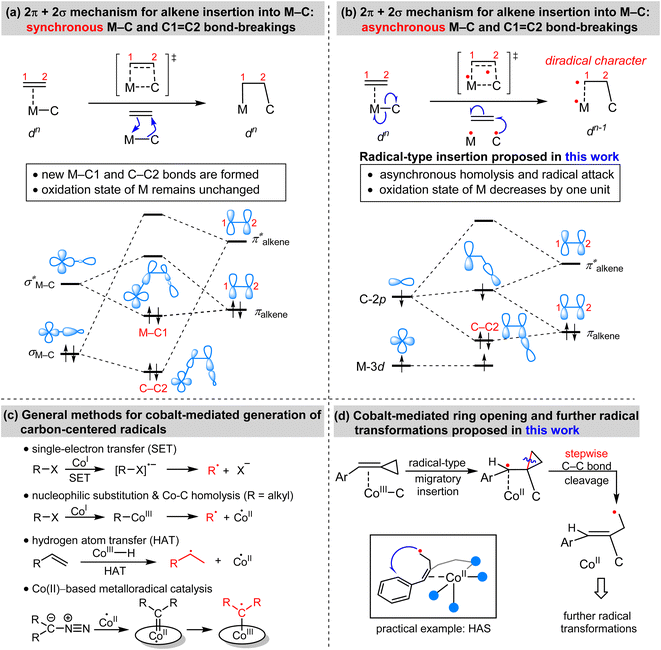
Migratory insertion reactions are fundamental elementary steps involved in a variety of commonly practiced catalytic reactions. Numerous investigations have been conducted to identify the detailed mechanism and the kinetic and thermodynamic behavior of these transformations to disclose the basic principles and to design more efficient catalysts.1 Among the various insertions, migratory insertion of alkenes into metal–carbon (M–C) bonds is one of the most efficient methods to form new carbon–carbon (C–C) bonds (Scheme 1a). Prominent examples include the palladium-catalyzed Mizoroki–Heck coupling2 as well as the catalytic insertion polymerization.3 The generally accepted mechanism for alkene insertion relies on a four-center transition state. During this 2π + 2σ reaction, the occupied σM–C and πalkene orbitals interact with the vacant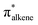 and
and 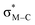 orbitals, respectively, leading to the formation of new M–C and C–C bonds.4
orbitals, respectively, leading to the formation of new M–C and C–C bonds.4
Adenosylcobalamin, also known as coenzyme B12, is a naturally occurring organometallic complex that plays a pivotal role in a number of metalloenzyme-catalyzed radical reactions.5 The low bond-dissociation energy (BDE) of the axial Co–C bond in coenzyme B12 results in its facile homolytic cleavage, which plays an important role in the observed biological activities. Utilizing this kind of one-electron reactivity of cobalt and other first-row transition metals, synthetic chemists have explored different highly controlled radical reactions.6 Inspired by the one-electron reactivity of first-row transition metals, we anticipated that the alkene insertion may proceed via a concerted but asynchronous M–C homolysis and radical attack (Scheme 1b), which is distinct from the synchronous M–C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond-breakings. This radical-type insertion involves a three-orbital interaction. Meanwhile, the insertion products exhibit a diradical character with a decrease of the physical oxidation state of the metal. To the best of our knowledge, this radical-type migratory insertion has thus far proven elusive, while it could provide an efficient access to carbon-centered radicals.
C bond-breakings. This radical-type insertion involves a three-orbital interaction. Meanwhile, the insertion products exhibit a diradical character with a decrease of the physical oxidation state of the metal. To the best of our knowledge, this radical-type migratory insertion has thus far proven elusive, while it could provide an efficient access to carbon-centered radicals.
Transition-metal-mediated radical reactions have provided various innovative catalysis protocols for organic synthesis.7 In this context, the contribution of cobalt in radical chemistry is remarkable because of its cost effectiveness and unique catalytic reactivity.8 In general, the methods for the cobalt-mediated generation of carbon-centered radicals can be classified into the following types: single-electron transfer (SET), nucleophilic substitution and Co–C homolysis, hydrogen atom transfer (HAT), and metalloradical catalysis (Scheme 1c).9 Based on detailed consideration of the mechanistic information of the aforementioned radial-type migratory insertion as well as the classical radical clock reactions, we were wondering whether alkylidenecyclopropanes (ACPs) could exhibit new reactivity patterns. As a result, we, herein, demonstrate an unprecedented strain-release generation of radicals via a cobalt-catalyzed radical-mediated C–C bond cleavage/functionalization strategy (Scheme 1d). The resulting homoallyl radical can enable aromatic C–H functionalization such as homolytic aromatic substitution (HAS) reactions, as illustrated by an example of cobalt-catalyzed coupling between benzamides and ACPs.10 This cobalt-mediated ring opening reaction represents a fundamentally distinct strategy to generate carbon-centered radicals, with considerable potential for the development of new types of radical transformation.
Results and discussion
Mechanism for migratory insertion of ethylene into Co–C bonds
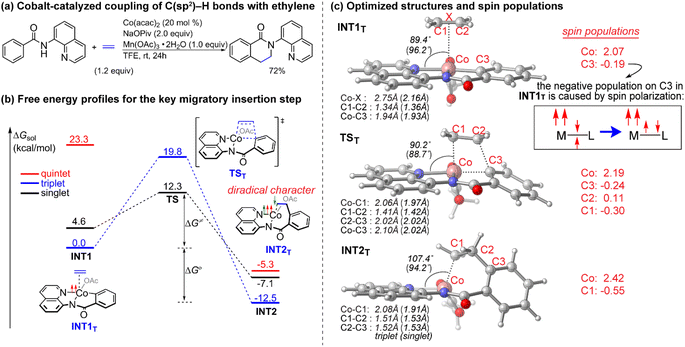
Since the pioneering discovery of the 8-aminoquinoline-directed Co-catalyzed C–H alkenylation,11 diverse cobalt-catalyzed C(sp2)–H annulations with alkenes, alkynes, allenes, and heterocycles were realized by different groups.12–17 We initiated our investigation by exploring the cobalt-catalyzed coupling of C(sp2)–H bonds with ethylene as the model reaction, as was reported by Daugulis12a (Fig. 1a). The calculated reaction profiles of migratory insertion of alkene are depicted in Fig. 1b. Additional computational results are given in Fig. S1–S8 in the ESI.† All three possible spin states of Co(III) were investigated, i.e., the singlet (S = 0), triplet (S = 1), and quintet (S = 2) states. For the alkene-coordinated complex INT1, the medium-spin triplet is the ground state, which lies below the low-spin singlet and high-spin quintet states by 4.6 kcal mol−1 and 23.3 kcal mol−1, respectively. The migratory insertion transition state TS, however, exhibits a different energy ordering, with the closed-shell singlet being 7.5 kcal mol−1 more stable than the triplet. Attempts to locate the corresponding quintet transition state from the π complex were unsuccessful. The relative energy of the resulting triplet insertion product INT2T is lower than the other two states, which results in larger reaction energy of the triplet state. The reaction pathway of the alkene insertion into Co–C bond has the characteristic features of a two-state reactivity (TSR) scenario,18 in which the initially medium-spin triplet crosses over through the singlet transition state to generate the insertion intermediate.The optimized structures of the intermediates and transition states are shown in Fig. 1c. The Mulliken atomic spin populations, representing the excess of positive (α) or negative (β) spin on an atomic site, are also provided. For the alkene-coordinated complex INT1, the metal–olefin bond distance in the triplet is significantly longer than that of the singlet. The spin population for Co in INT1T is 2.07, very close to the number of unpaired electrons (2 electrons with α-spin) for the complex. The negative spin population for C3 atom in INT1T is caused by spin polarization,19 which makes the bonding electron pair of equatorial Co–C3 polarized. Consequently, a certain amount of the positive spin density of the bonding electron pair gets close to the metal atom, whereas some negative spin densities are induced at the atoms bonded to the metal. In the transition state TST, the absolute values of spin population on Co and C3 atoms both increase as compared to that in INT1T. Furthermore, in TST an excess on the spin density distribution of 0.11 for the α-spin and 0.30 for the β-spin was found on C2 and C1 atoms, respectively. For the resulting insertion intermediate, it is noteworthy that the Co–C1 bond in the INT2T is 0.17 Å longer than that in the INT2S with the carbon atom presenting a slight deviation from the axial position (Fig. 2c). More interestingly, spin population analysis revealed a 0.55 excess of the β-spin at the C1 atom and a significant spin density of 2.42 located on the cobalt metal center.
The radical-type migratory insertion
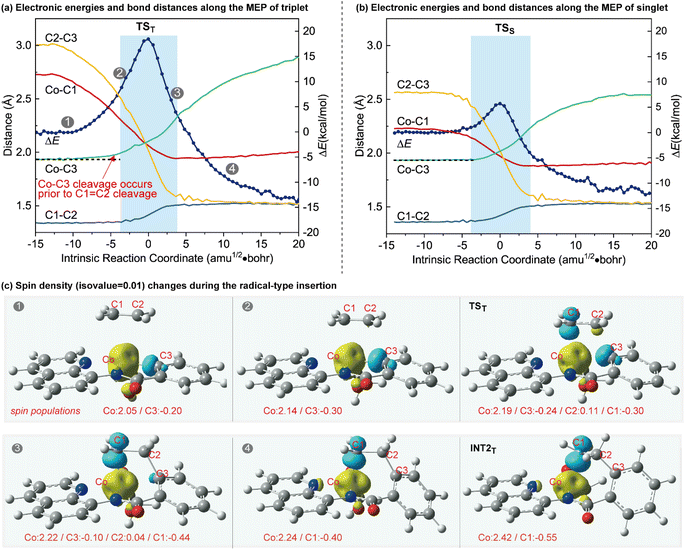
To further illustrate the distinctions between the proposed radical-type migratory insertion and the conventional process, the key bond distances along the minimum energy path (MEP) were examined in detail (Fig. 2). The results of the triplet and singlet states correspond to the radical-type and the classical synchronous mechanisms, respectively. Herein, we focus on the breaking of C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C2 and Co–C3 bonds to inspect the beginning of the insertion process. A comparison of the bond distance changes during the two different mechanisms reveals that they are both energetically concerted but the C1
C2 and Co–C3 bonds to inspect the beginning of the insertion process. A comparison of the bond distance changes during the two different mechanisms reveals that they are both energetically concerted but the C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C2 and Co–C3 bond-breakings in the radical-type migratory insertion are asynchronous20 (Fig. 2a). The homolytic Co–C3 bond breaking occurs prior to the C1
C2 and Co–C3 bond-breakings in the radical-type migratory insertion are asynchronous20 (Fig. 2a). The homolytic Co–C3 bond breaking occurs prior to the C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C2 breaking in the radical-type mechanism (Fig. 2a), which is distinct from bond breaking events occurring synchronously in Fig. 2b. The differences between the two mechanisms are also well reflected by the changes of the aromaticity. The aromaticity decreases along the MEP for the conventional mechanism on the basis of the calculated nucleus-independent chemical shift (NICS) values at the ring center NICS(0).21 However, in the radical-type mechanism, the aromaticity first gradually increases before the highest energy point following a decrease during the insertion process (Fig. S4†). The spin density changes along the MEP of the triplet state shown in Fig. 2c clearly demonstrate the electron-transfer process during the concerted but asynchronous Co–C homolysis and radical attack, which is in good agreement with the orbital interaction analysis in Scheme 1b. The spin density contour and spin population for INT2T show an unpaired spin density on the Co and the C1 atoms, with opposite signs, suggesting that this intermediate presents a diradical character.22 Accordingly, the stable INT2T complex can be better described as a quartet cobalt(II) antiferromagnetically coupled with a carbon-centered radical.
C2 breaking in the radical-type mechanism (Fig. 2a), which is distinct from bond breaking events occurring synchronously in Fig. 2b. The differences between the two mechanisms are also well reflected by the changes of the aromaticity. The aromaticity decreases along the MEP for the conventional mechanism on the basis of the calculated nucleus-independent chemical shift (NICS) values at the ring center NICS(0).21 However, in the radical-type mechanism, the aromaticity first gradually increases before the highest energy point following a decrease during the insertion process (Fig. S4†). The spin density changes along the MEP of the triplet state shown in Fig. 2c clearly demonstrate the electron-transfer process during the concerted but asynchronous Co–C homolysis and radical attack, which is in good agreement with the orbital interaction analysis in Scheme 1b. The spin density contour and spin population for INT2T show an unpaired spin density on the Co and the C1 atoms, with opposite signs, suggesting that this intermediate presents a diradical character.22 Accordingly, the stable INT2T complex can be better described as a quartet cobalt(II) antiferromagnetically coupled with a carbon-centered radical.
To investigate the substituent effect on the feasibility of the radical-type insertion mechanism, the computed activation free energies and free energy changes during the migratory insertion step of various monosubstituted alkenes as well as cyclopentene and allene are summarized in Table 1. There exists site selectivity for unsymmetrical alkenes because of different insertion fashions, and the orientation of the substituents would establish different stereo-centers. Here, we only considered the pathway that leads to the formation of experimentally observed products. The free energy profiles of different substituted alkenes (see Fig. S9–S11†) are similar with that of ethylene as shown in Fig. 1b, except for styrene, in which the quintet insertion product INT2Q becomes more stable. There are two dominant contributions to the thermodynamic driving force for the radical-type migratory insertion, i.e., the homolytic bond dissociation energy of Co–C bond and exergonicity of the addition of the carbon-centered radical to alkenes. The insertion reaction for all studied alkenes are thermodynamically favorable (Table 1), consistent with previous results of alkene insertion into M–C bonds of other transition-metal complexes.4a
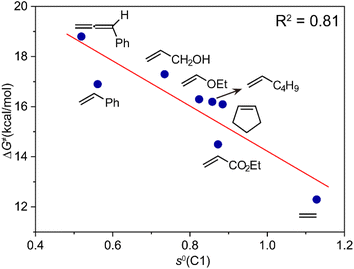
For the activation barriers of the migratory insertion of different alkenes into the same M–C bond, the values are mainly determined by the reactivity of radical addition. To rationalize the steric and electronic effects of the substituents on the activation barriers and to develop a predictable model for the reactivity of different types of coupling partners, we calculated the condensed local softness s0, the values of which can be viewed as quantitative measures of the chemical reactivity of the different atoms in the molecule and are suited for studies of radical attack.23 A relatively good correlation between the activation free energy of the migratory insertion and the condensed local softness of the C1 atom that coordinates to cobalt is observed (Fig. 3). The results again demonstrate the inherent radical character of the migratory insertion proposed. Other possible factors influencing the activation barriers are discussed in the ESI (Fig. S12–S14).† Apart from cobalt, the radical-type migratory insertion might also compete with classical insertion for other first-row transition metals that have smaller M–C bond dissociation energies in specific complexes.24
The transition-metal-mediated ring opening strategy
Having established the radical-type insertion mechanism, we were particularly interested in its potential application to organic synthesis. The C–C activation catalyzed by transition metal complexes is a field of major interest, since it offers an efficient approach for the construction of organic compounds.25 The highly strained, yet readily accessible alkylidenecyclopropanes can undergo a variety of ring-opening reactions and different modes of activation were observed.26 Considering the diradical character of the insertion products generated in the aforementioned radical-type mechanism, we questioned whether the presence of cyclopropyl ring could enable new modes of C–C bond cleavage.Despite the vast development of transition-metal-catalyzed ring-opening reactions and cycloadditions of ACPs, there are still limited reactions merging C–H activation and C–C bond cleavage.27–29 Kwong and co-workers recently reported cobalt-catalyzed coupling between benzamides and ACPs via one-pot sequential activation of C–H/C–C/C–H bonds, generating the dihydronaphthalene skeletons (Scheme 2).10 Based on a series of experimental mechanistic studies, Kwong proposed a plausible mechanism that involves N–H deprotonation, first C(sp2)–H activation, alkene insertion, β-C elimination, second C(sp2)–H activation via concerted metalation–deprotonation (CMD),30 C–C reductive elimination and catalyst regeneration. Interestingly, our calculations show that, instead of the originally proposed CMD-type C–H activation, an unconventional proton-coupled electron transfer (PCET) is found to be the most favorable one. The cyclometallic intermediate formed by β-C elimination proceeds via unexpected Co–C homolysis to afford a cobalt(II) complex, which undergoes consecutive radical cyclization and PCET to afford the final product. In this proposed mechanism, we disclosed a new pattern of transition metal-mediated ring-opening process, which is the key step controlling the reaction selectivity.
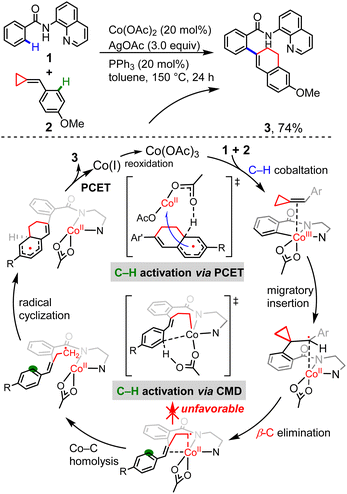 | ||
| Scheme 2 The Co-catalyzed coupling reaction between benzamides and ACPs, and the originally proposed CMD mechanism together with the unconventional PCET mechanism proposed in this work. | ||
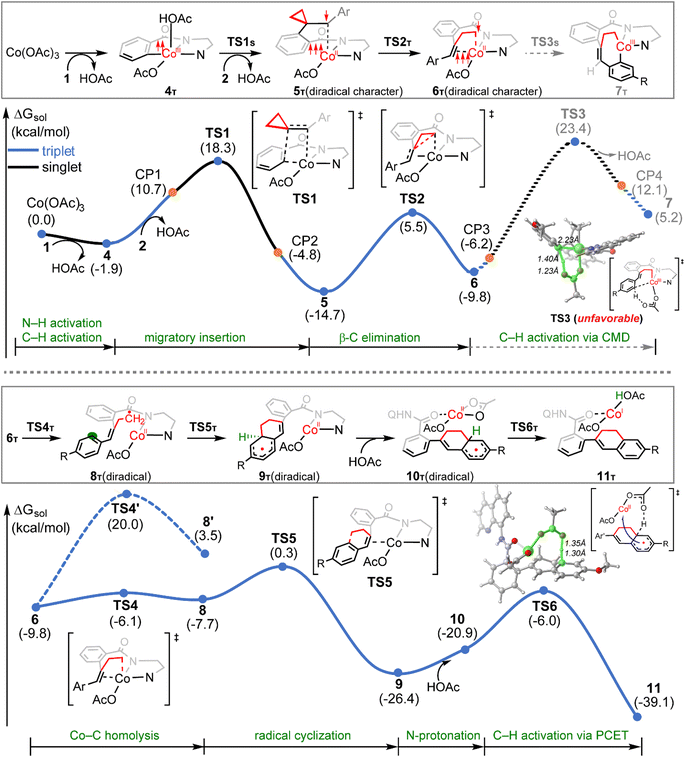
The calculated reaction profiles for the cobalt-catalyzed chelation-assisted tandem C–H activation/C–C cleavage/C–H cyclization of aromatic amides with ACPs are depicted in Fig. 4. The possible roles of PPh3 were not considered, since the product yield was indeed only slightly increased in the presence of ligand.10 The three possible spin states of cobalt(III) were again investigated. Our calculations show that the reaction mainly proceeds on the singlet- and triplet-state surfaces, whereas the quintet-state is solely involved in the first N–H deprotonation. Previously, both experimental and computational studies demonstrated that an additional aminoquinoline-benzamide can coordinate with the metal center as a bis-chelating ligand.15b,31 However, our calculations reveal that the migratory insertion of the ACP cannot take place from such bis-ligated intermediate, due to the significant steric repulsion between ACP and the additional amide unit (Fig. S15–S17†). The regioselectivity during the migratory insertion and the competition between C–N reductive elimination and ring opening via β-C elimination of the seven-membered cobaltacycle intermediate were also considered. The additional results are given in Fig. S18–S33.†
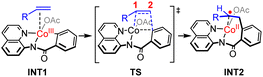
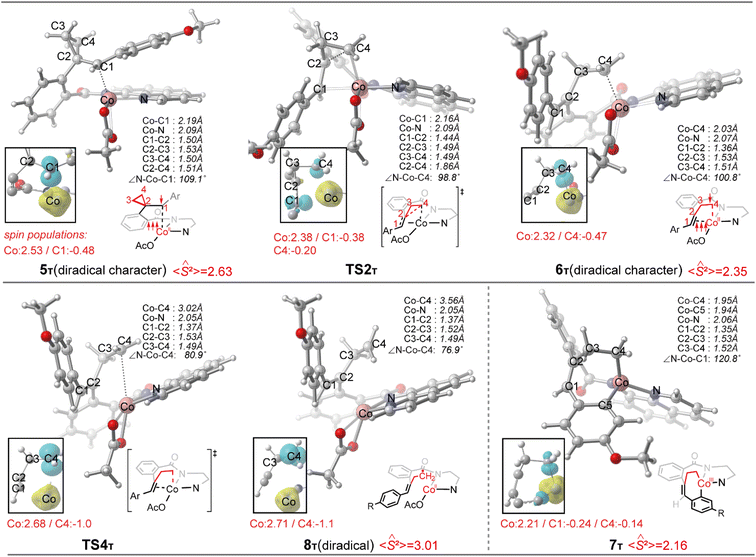
Initially, coordination of the amide nitrogen atom of the 1 to the active catalyst Co(OAc)3 generates the substrate-coordinated intermediate. Then, facile N–H deprotonation and the first C(sp2)–H activation via base-assisted intramolecular electrophilic-type substitution (BIES)32 take place to yield intermediate 4, with the triplet state (4T) as the ground state. The effective activation barrier for the first C(sp2)–H activation is calculated to be 17.0 kcal mol−1 (Fig. S15†). From complex 4T, the substrate–ligand exchange with 2 and the following radical-type insertion of alkene insertion into the newly formed Co–C bond lead to the formation of cobalt(II) intermediate 5T, in which significant diradical character was observed (Fig. 5). Analogous to the results of alkenes shown in Fig. 1 and Table 1, a spin surface crossing through a minimum energy crossing point (MECP; CP1 or CP2 in current case) between the triplet and singlet takes place prior to or after the migratory insertion transition state TS1S (Fig. 4). Subsequently, the β-C elimination takes place viaTS2T, wherein cleavage of a β-C–C σ-bond and formation of axial Co–C bond occur with concomitant generation of a π-bond. The corresponding optimized structures are depicted in Fig. 5. Upon formation of the eight-membered intermediate 6T, the second C(sp2)–H activation was originally proposed to proceed via the CMD-type transition state TS3s, in which the coordinated acetate anion acts as the base for deprotonation via an inner-sphere mechanism. However, on the basis of our computational results, this process is kinetically unfavorable due to the relatively high energy barrier (TS3s, ΔG‡ = 38.1 kcal mol−1 relative to 5T in Fig. 4). The feasibility of CMD mechanism can be further ruled out by considering that the transition state of the competing C–N reductive elimination from 6T even lies below TS3s by 10.0 kcal mol−1 (see Fig. S29†). Hong and co-workers recently found that the cobalt(IV) intermediate could be involved in both electro-chemical and chemical oxidation processes.33 To address this possibility, a cobalt(IV) intermediate potentially generated from the oxidation of complex 6 by AgOAc was considered during the second C(sp2)–H activation. However, the Co(IV)-catalyzed C(sp2)–H activation is highly disfavored due to the significantly higher barrier (ΔG‡ = 45.4 kcal mol−1 for the quartet states, see Fig. S27†). In addition, we also considered the possible roles of silver acetate,34 but attempts to locate the corresponding transition states of bimetallic activation modes did not meet with success.
The pseudo-octahedral geometry of intermediate 6 and the existing ring strain prompted us to investigate the possible reaction pathway involving axial Co–C homolysis, analogous to the behavior observed in coenzyme B12.5 Interestingly, as shown in Fig. 4, Co–C homolysis from 6T is very facile, with a fairly low energy barrier. The resulting intermediate 8T is a diradical, in which one of the unpaired electrons is located at the alkyl position (C4 atom, see Fig. 5) and the other three unpaired electrons are on the cobalt(II) center. The participation of this kind of complex is strongly supported by the radical quenching experiments, in which the yield of the product was significantly decreased, when 2,2,6,6-tetramethyl-1-piperidinyloxy (TEMPO) was added to the reaction medium and a compound generated by the radical–radical cross coupling reaction between intermediate 8T and TEMPO was isolated.10 Our calculations also revealed that the diradical 8T cannot be directly formed via a single-step C–C cleavage from intermediate 5T.
Instead, the abovementioned stepwise process involving β-C elimination (5T → 6T) and the subsequent Co–C homolysis (6T → 8T) is required. To achieve a deeper understanding of the cobalt-catalyzed radical-mediated carbon–carbon scission, the spin density distribution and the expectation value of the total spin 〈Ŝ2〉 are used to assess the extent of the diradical character during this stepwise process (Fig. 5). As compared to 8T, intermediate 5T exhibit significant diradical character based on the relatively large spin densities distribution and the 〈Ŝ2〉 values. Furthermore, the diradical character decreases from intermediate 5T to 6T and then increases from 6T to 8T. In the diradical 8T, the distance between the cobalt(II) and the C4 atom is significantly long (up to 3.56 Å) with the alkyl radical pointing towards the phenyl ring.
From 8T, an intramolecular cyclization by attack of the primary radical to phenyl ring via a favored six-membered transition state (TS5) proceeds to afford the ring-closed intermediate 9T. Prior to the second C(sp2)–H activation, protonation is required for the cyclized intermediate 9T. The proton is transferred from an additional HOAc to the anionic N(sp3) atom of quinoline-based directing group, which only requires a barrier of 9.2 kcal mol−1 (see Fig. S20†). The subsequent conformational changes make the O atom of 8-aminoquinoline rather than the N,N-bidentate directing group to become coordinated with cobalt(II) in 10T. The following C(sp2)–H activation requires 14.9 kcal mol−1 from 10T to generate the product-coordinated complex 11T. Re-aromatization is realized via the PCET transition state TS6T, which involves proton transfer from the sp3 carbon to acetate and electron transfer from the cyclohexadienyl radical to the metal center. Compared to the results of the CMD mechanism (33.2 kcal mol−1 for 6T to TS3s), the C(sp2)–H activation via PCET (20.4 kcal mol−1 for 9T to TS6T) is significantly more favorable. Furthermore, the activation barrier of C(sp2)–H activation via PCET is 5.3 kcal mol−1 lower than that of the competing C–N reductive elimination that produces spirocyclopropanes (Fig. S31†). This result successfully explains why the corresponding annulated product with conservation of the cyclopropyl ring was not observed in the experiments.10 Finally, the cobalt(I) species dissociating from 11T is reoxidized into cobalt(III) to complete the catalytic cycle.
From 6T, we have located two different pathways for the homolytic cleavage of the Co–C bond, while the alternative Co–C homolysis via (Fig. 4) is 26.1 kcal mol−1 less favorable than that viaTS4T. The formation of radical intermediate
(Fig. 4) is 26.1 kcal mol−1 less favorable than that viaTS4T. The formation of radical intermediate 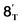 is also less thermodynamically favorable. The differences of the underlying electronic structure changes for the Co–C homolysis via the two pathways are illustrated in Scheme 3. For cobalt(II) complex 6T, the electronic structure can be described as (dxz)2(dyz)2(dxy)1(dz2)1(dx2–y2)0. For the homolysis via transition state TS4T, an electron transfer from σCo–C orbital to the unoccupied dx2–y2-based molecular orbital is calculated to be more favorable. The electron transfer to the antibonding orbital weakens the Co–C bond and lowers the corresponding reaction barrier. In the case of
is also less thermodynamically favorable. The differences of the underlying electronic structure changes for the Co–C homolysis via the two pathways are illustrated in Scheme 3. For cobalt(II) complex 6T, the electronic structure can be described as (dxz)2(dyz)2(dxy)1(dz2)1(dx2–y2)0. For the homolysis via transition state TS4T, an electron transfer from σCo–C orbital to the unoccupied dx2–y2-based molecular orbital is calculated to be more favorable. The electron transfer to the antibonding orbital weakens the Co–C bond and lowers the corresponding reaction barrier. In the case of  , the electron transfer to the half-filled dxy orbital results in considerable Coulomb repulsions, thus making this pathway unfavorable.
, the electron transfer to the half-filled dxy orbital results in considerable Coulomb repulsions, thus making this pathway unfavorable.
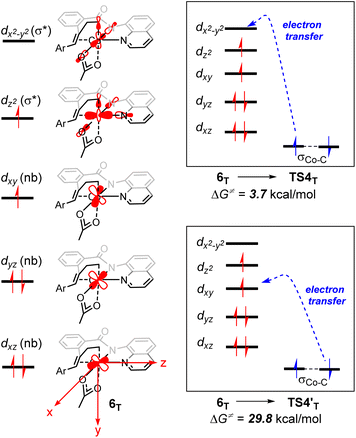 | ||
| Scheme 3 Schematic molecular orbital diagrams with the electronic structure changes for the Co–C homolysis via two different pathways. | ||
The organocobalt(III) complexes (CoIII–R) and their radical activation reactions have been investigated for more than half a century. Cleavage of the Co–C bond via photolysis, electrochemistry, or thermolysis, producing the radicals in a controlled manner, is the fundamental step during such transformations.6b The strategy proposed herein (Scheme 4) clearly demonstrates that the strength of the Co–C bond is the key parameter that can lead to divergent reactivities as compared to the second- and third-row transition-metal complexes. Depending on the ligands and the alkyl group R, the single-electron pathway might be dominant for the cobalt complex. Furthermore, due to the persistent radical effect of Co(III)–R, which significantly extends the lifetime of the generated carbon-centered radicals, further selective inter- or intramolecular radical reactions could be developed on the basis of ring opening strategy.
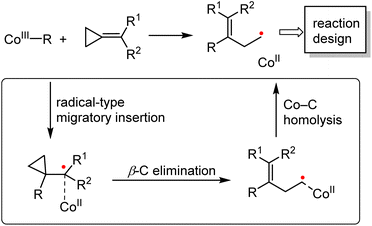 | ||
| Scheme 4 Summary of the cobalt-catalyzed radical-mediated C–C bond cleavage/functionalization strategy. | ||
Conclusions
In summary, we have uncovered a radical-type migratory insertion mediated by cobalt(III) complex. The unprecedented radical-type insertion proceeds via concerted but asynchronous Co(III)–C homolysis and radical attack, which results in an insertion intermediate exhibiting diradical character. Depending on the coordination geometry as well as the oxidation and spin states, the radical-type insertion might compete favorably with the classical mechanism for the other first-row transition metals.In combination with the use of alkylidenecyclopropanes, a new and fundamentally distinct cobalt-mediated ring opening strategy was further proposed. The strategy for C–C bond cleavage involves the radical-type addition of organocobalt(III) complexes into alkylidenecyclopropanes, β-carbon elimination and Co–C homolysis. This single-electron pathway is different from the behavior previously observed for palladium, nickel or rhodium-catalyzed C–C cleavages, in which redox-neutral β-carbon elimination usually occurs. Our mechanistic studies reveal that this cobalt-catalyzed radical-mediated C–C bond cleavage plays a key role in controlling the selectivity of cobalt-catalyzed coupling between benzamides and ACPs. Interestingly, the resulting carbon-centered radical undergoes facial intramolecular cyclization, followed by C(sp2)–H activation via PCET. The Co(III)/Co(II)/Co(I) catalytic scenario is significantly favored as compared to the originally proposed Co(III)/Co(I) pathway.
Finally, our results suggest that the low BDE of the Co–C bonds as well as the persistent radical effect with cobalt complexes can lead to distinct mechanisms for cobalt-catalyzed reactions, providing opportunities for achieving new reactivities that are inaccessible with other transition metals. We hope that our mechanistic insights will serve as an inspiration for further development of catalytic radical-type transformations.
Computational details
All the geometries of the intermediates and transition states were optimized by Gaussian 09![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 in the corresponding solvent at the B3LYP36-D3(BJ)37/6-31G(d,p)/ECP10MDF(Co) level of theory with the corresponding Stuttgart/Dresden (SDD) effective core potential (ECP) on cobalt. Frequency calculations were performed at the same theoretical level to verify the nature of the stationary points and to obtain the thermal Gibbs free energy corrections (ΔGcorr) at 423.15 K (for ACPs) or 298.15 K (for the other alkenes). The intrinsic reaction coordinate (IRC)38 calculations have been performed to confirm whether the obtained transition state is connected with two local minimum structures for a target reaction. Single point calculations at B3LYP-D3(BJ)/def2-TZVP39 were carried out in solvent to obtain more accurate electronic energies. The continuum solvation model SMD40 was utilized to consider the bulk solvent effects. Toluene is used as the solvent for ACPs and 2,2,2-trifluoroethanol (TFE) is used as the solvent for the other alkene coupling partners. The correction caused by the different standard states in the gas phase and in solution was added to the free energies of all species. Numerical integrations were performed with the ultrafine grid during the calculations. The 3D diagrams of molecules and the spin density isosurface maps were prepared by CYLview41 and GaussView5.0 respectively. The condensed local softness, atomic charges and spin densities were calculated by Multiwfn 3.8.42
35 in the corresponding solvent at the B3LYP36-D3(BJ)37/6-31G(d,p)/ECP10MDF(Co) level of theory with the corresponding Stuttgart/Dresden (SDD) effective core potential (ECP) on cobalt. Frequency calculations were performed at the same theoretical level to verify the nature of the stationary points and to obtain the thermal Gibbs free energy corrections (ΔGcorr) at 423.15 K (for ACPs) or 298.15 K (for the other alkenes). The intrinsic reaction coordinate (IRC)38 calculations have been performed to confirm whether the obtained transition state is connected with two local minimum structures for a target reaction. Single point calculations at B3LYP-D3(BJ)/def2-TZVP39 were carried out in solvent to obtain more accurate electronic energies. The continuum solvation model SMD40 was utilized to consider the bulk solvent effects. Toluene is used as the solvent for ACPs and 2,2,2-trifluoroethanol (TFE) is used as the solvent for the other alkene coupling partners. The correction caused by the different standard states in the gas phase and in solution was added to the free energies of all species. Numerical integrations were performed with the ultrafine grid during the calculations. The 3D diagrams of molecules and the spin density isosurface maps were prepared by CYLview41 and GaussView5.0 respectively. The condensed local softness, atomic charges and spin densities were calculated by Multiwfn 3.8.42
Data availability
Additional computational results supporting this work's conclusions are available in the ESI.†Author contributions
J.-B. L. and L. A. conceived the study, analyzed the results, and wrote the paper. J.-B. L., X.-J. L. and D.-Z. C. carried out the calculations. J. C. A. O. provided helpful discussions. All authors discussed the results and edited the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from Natural Science Foundation of Shandong Province (ZR2019YQ11) is gratefully acknowledged. L. A. thanks the DFG (Gottfried-Wilhelm-Leibniz-Preis to L. A. and SPP2363) and the European Union (ERC Advanced Grant No. 101021358).Notes and references
- For selected reviews and examples, see: (a) K. J. Cavell, Coord. Chem. Rev., 1996, 155, 209–243 CrossRef CAS; (b) S. A. Macgregor and G. W. Neave, Organometallics, 2003, 22, 4547–4556 CrossRef CAS; (c) P. Wucher, L. Caporaso, P. Roesle, F. Ragone, L. Cavallo, S. Mecking and I. Göttker-Schnetmann, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 8955–8959 CrossRef CAS PubMed; (d) P. S. Hanley and J. F. Hartwig, Angew. Chem., Int. Ed., 2013, 52, 8510–8525 CrossRef CAS PubMed; (e) G. Lu, C. Fang, T. Xu, G. Dong and P. Liu, J. Am. Chem. Soc., 2015, 137, 8274–8283 CrossRef CAS PubMed; (f) G. Huang and P. Liu, ACS Catal., 2016, 6, 809–820 CrossRef CAS; (g) C. P. Richers, S. Roediger, V. Laserna and J. F. Hartwig, Chem. Sci., 2020, 11, 10449–10456 RSC.
- (a) R. F. Heck, Acc. Chem. Res., 1979, 12, 146–151 CrossRef CAS; (b) I. P. Beletskaya and A. V. Cheprakov, Chem. Rev., 2000, 100, 3009–3066 CrossRef CAS PubMed; (c) C. Amatore and A. Jutand, Acc. Chem. Res., 2000, 33, 314–321 CrossRef CAS PubMed.
- (a) R. H. Grubbs and G. W. Coates, Acc. Chem. Res., 1996, 29, 85–93 CrossRef CAS; (b) S. Mecking, Angew. Chem., Int. Ed., 2001, 40, 534–540 CrossRef CAS; (c) V. C. Gibson and S. K. Spitzmesser, Chem. Rev., 2003, 103, 283–316 CrossRef CAS PubMed.
- (a) S. Niu and M. B. Hall, Chem. Rev., 2000, 100, 353–406 CrossRef CAS PubMed; (b) X. Zhu, Y. Zheng and J. Liu, J. Phys. Chem. A, 2021, 125, 5031–5039 CrossRef CAS PubMed.
- For selected reviews, see: (a) K. Gruber, B. Puffer and B. Kräutler, Chem. Soc. Rev., 2011, 40, 4346–4363 RSC; (b) M. Giedyk, K. Goliszewska and D. Gryko, Chem. Soc. Rev., 2015, 44, 3391–3404 RSC.
- For selected reviews, see: (a) S. W. M. Crossley, C. Obradors, R. M. Martinez and R. A. Shenvi, Chem. Rev., 2016, 116, 8912–9000 CrossRef CAS; (b) J. Demarteau, A. Debuigne and C. Detrembleur, Chem. Rev., 2019, 119, 6906–6955 CrossRef CAS; (c) K. P. S. Cheung, S. Sarkar and V. Gevorgyan, Chem. Rev., 2022, 122, 1543–1625 CrossRef.
- S. H. Kyne, G. Lefèvre, C. Ollivier, M. Petit, V. Ramis Cladera and L. Fensterbank, Chem. Soc. Rev., 2020, 49, 8501–8542 RSC.
- (a) M. Moselage, J. Li and L. Ackermann, ACS Catal., 2016, 6, 498–525 CrossRef CAS; (b) P. Gandeepan, T. Müller, D. Zell, G. Cera, S. Warratz and L. Ackermann, Chem. Rev., 2019, 119, 2192–2452 CrossRef CAS PubMed; (c) P. Gandeepan, L. H. Finger, T. H. Meyer and L. Ackermann, Chem. Soc. Rev., 2020, 49, 4254–4272 RSC.
- (a) W. I. Dzik, X. Xu, X. P. Zhang, J. N. H. Reek and B. de Bruin, J. Am. Chem. Soc., 2010, 132, 10891–10902 CrossRef CAS PubMed; (b) H. Lu, W. I. Dzik, X. Xu, L. Wojtas, B. de Bruin and X. P. Zhang, J. Am. Chem. Soc., 2011, 133, 8518–8521 CrossRef CAS; (c) C. F. Harris, C. S. Kuehner, J. Bacsa and J. D. Soper, Angew. Chem., Int. Ed., 2018, 57, 1311–1315 CrossRef CAS PubMed; (d) M. Ociepa and D. Gryko, in Cobalt Catalysis in Organic Synthesis, ed. M. Hapke and G. Hilt, Wiley-VCH, Weinheim, Germany, 2020, pp. 417–451 Search PubMed; (e) X. Cheng, X. Liu, S. Wang, Y. Hu, B. Hu, A. Lei and J. Li, Nat. Commun., 2021, 12, 4366 CrossRef CAS.
- M. Li and F. Y. Kwong, Angew. Chem., Int. Ed., 2018, 57, 6512–6516 CrossRef CAS.
- L. Grigorjeva and O. Daugulis, Angew. Chem., Int. Ed., 2014, 53, 10209–10212 CrossRef CAS.
- (a) L. Grigorjeva and O. Daugulis, Org. Lett., 2014, 16, 4684–4687 CrossRef CAS PubMed; (b) L. Grigorjeva and O. Daugulis, Org. Lett., 2014, 16, 4688–4690 CrossRef CAS; (c) T. T. Nguyen, L. Grigorjeva and O. Daugulis, ACS Catal., 2016, 6, 551–554 CrossRef CAS PubMed.
- (a) W. Ma and L. Ackermann, ACS Catal., 2015, 5, 2822–2825 CrossRef CAS; (b) R. Mei, H. Wang, S. Warratz, S. A. Macgregor and L. Ackermann, Chem.–Eur. J., 2016, 22, 6759–6763 CrossRef CAS PubMed; (c) N. Sauermann, T. H. Meyer, C. Tian and L. Ackermann, J. Am. Chem. Soc., 2017, 139, 18452–18455 CrossRef CAS; (d) C. Tian, L. Massignan, T. H. Meyer and L. Ackermann, Angew. Chem., Int. Ed., 2018, 57, 2383–2387 CrossRef CAS; (e) R. Mei, N. Sauermann, J. C. A. Oliveira and L. Ackermann, J. Am. Chem. Soc., 2018, 140, 7913–7921 CrossRef CAS PubMed; (f) U. Dhawa, C. Tian, W. Li and L. Ackermann, ACS Catal., 2020, 10, 6457–6462 CrossRef CAS.
- (a) D. Kalsi and B. Sundararaju, Org. Lett., 2015, 17, 6118–6121 CrossRef CAS; (b) D. Kalsi, S. Dutta, N. Barsu, M. Rueping and B. Sundararaju, ACS Catal., 2018, 8, 8115–8120 CrossRef CAS.
- (a) N. Thrimurtulu, A. Dey, D. Maiti and C. M. R. Volla, Angew. Chem., Int. Ed., 2016, 55, 12361–12365 CrossRef CAS; (b) S. Maity, R. Kancherla, U. Dhawa, E. Hoque, S. Pimparkar and D. Maiti, ACS Catal., 2016, 6, 5493–5499 CrossRef CAS; (c) A. Dey, N. Thrimurtulu and C. M. R. Volla, Org. Lett., 2019, 21, 3871–3875 CrossRef CAS PubMed.
- Z. Zhang, Y. Han, B. Zhan, S. Wang and B. Shi, Angew. Chem., Int. Ed., 2017, 56, 13145–13149 CrossRef CAS PubMed.
- (a) L. Zhang, X. Hao, Z. Liu, X. Zheng, S. Zhang, J. Niu and M. Song, Angew. Chem., Int. Ed., 2015, 54, 10012–10015 CrossRef CAS; (b) P. Gandeepan, P. Rajamalli and C. Cheng, Angew. Chem., Int. Ed., 2016, 55, 4308–4311 CrossRef CAS PubMed; (c) P. Williamson, A. Galván and M. J. Gaunt, Chem. Sci., 2017, 8, 2588–2591 RSC; (d) S. Tang, D. Wang, Y. Liu, L. Zeng and A. Lei, Nat. Commun., 2018, 9, 798 CrossRef; (e) S. Kathiravan and I. A. Nicholls, Org. Lett., 2019, 21, 9806–9811 CrossRef CAS PubMed; (f) Y. Ban, L. You, T. Wang, L. Wu and Q. Liu, ACS Catal., 2021, 11, 5054–5060 CrossRef CAS; (g) H. Zhai, M. Liu, C. Wang, S. Qiu, J. Wei, H. Yang and Y. Wu, J. Org. Chem., 2021, 86, 14915–14927 CrossRef CAS.
- (a) D. Schröder, S. Shaik and H. Schwarz, Acc. Chem. Res., 2000, 33, 139–145 CrossRef; (b) Y. Sun, H. Tang, K. Chen, L. Hu, J. Yao, S. Shaik and H. Chen, J. Am. Chem. Soc., 2016, 138, 3715–3730 CrossRef CAS.
- E. Ruiz, J. Cirera and S. Alvarez, Coord. Chem. Rev., 2005, 249, 2649–2660 CrossRef CAS.
- For selected examples, see: (a) D. A. Singleton, B. E. Schulmeier, C. Hang, A. A. Thomas, S. W. Leung and S. R. Merrigan, Tetrahedron, 2001, 57, 5149–5160 CrossRef CAS; (b) O. M. Gonzalez-James, E. E. Kwan and D. A. Singleton, J. Am. Chem. Soc., 2012, 134, 1914–1917 CrossRef CAS PubMed; (c) Y. J. Hong, R. Ponec and D. J. Tantillo, J. Phys. Chem. A, 2012, 116, 8902–8909 CrossRef CAS PubMed; (d) S. R. Neufeldt, G. Jiménez-Osés, J. R. Huckins, O. R. Thiel and K. N. Houk, J. Am. Chem. Soc., 2015, 137, 9843–9854 CrossRef CAS PubMed.
- (a) P. V. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. van Eikema Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318 CrossRef CAS PubMed; (b) Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. R. Schleyer, Chem. Rev., 2005, 105, 3842–3888 CrossRef CAS PubMed.
- (a) N. Kumar, M. Alfonso-Prieto, C. Rovira, P. Lodowski, M. Jaworska and P. M. Kozlowski, J. Chem. Theory Comput., 2011, 7, 1541–1551 CrossRef CAS PubMed; (b) G. M. Lee, A. S. C. Leung, D. J. Harrison, I. Korobkov, R. P. Hughes and R. T. Baker, Organometallics, 2017, 36, 2853–2860 CrossRef CAS; (c) P. Ma and H. Chen, ACS Catal., 2019, 9, 1962–1972 CrossRef CAS; (d) N. P. van Leest and B. de Bruin, Inorg. Chem., 2021, 60, 8380–8387 CrossRef CAS PubMed.
- W. Yang and R. G. Parr, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 6723–6726 CrossRef CAS PubMed.
- (a) B. de Bruin, W. I. Dzik, S. Li and B. B. Wayland, Chem.–Eur. J., 2009, 15, 4312–4320 CrossRef CAS PubMed; (b) O. Gutierrez, J. C. Tellis, D. N. Primer, G. A. Molander and M. C. Kozlowski, J. Am. Chem. Soc., 2015, 137, 4896–4899 CrossRef CAS PubMed; (c) M. Yuan, Z. Song, S. O. Badir, G. A. Molander and O. Gutierrez, J. Am. Chem. Soc., 2020, 142(15), 7225–7234 CrossRef CAS.
- (a) C. Jun, Chem. Soc. Rev., 2004, 33, 610–618 RSC; (b) F. Chen, T. Wang and N. Jiao, Chem. Rev., 2014, 114, 8613–8661 CrossRef CAS; (c) L. Souillart and N. Cramer, Chem. Rev., 2015, 115, 9410–9464 CrossRef CAS; (d) P. Chen, B. A. Billett, T. Tsukamoto and G. Dong, ACS Catal., 2017, 7, 1340–1360 CrossRef CAS PubMed; (e) L. Deng and G. Dong, Trends Chem., 2020, 2, 183–198 CrossRef CAS; (f) M. Murakami and N. Ishida, Chem. Rev., 2021, 121, 264–299 CrossRef CAS PubMed.
- (a) A. Masarwa, D. Didier, T. Zabrodski, M. Schinkel, L. Ackermann and I. Marek, Nature, 2014, 505, 199–203 CrossRef CAS PubMed; (b) A. Brandi, S. Cicchi, F. M. Cordero and A. Goti, Chem. Rev., 2014, 114, 7317–7420 CrossRef CAS PubMed; (c) D. S. Müller and I. Marek, Chem. Soc. Rev., 2016, 45, 4552–4566 RSC; (d) G. Fumagalli, S. Stanton and J. F. Bower, Chem. Rev., 2017, 117, 9404–9432 CrossRef CAS PubMed; (e) Y. Cohen, A. Cohen and I. Marek, Chem. Rev., 2021, 121, 140–161 CrossRef CAS.
- (a) S. I. Kozhushkov, D. S. Yufit and L. Ackermann, Org. Lett., 2008, 10, 3409–3412 CrossRef CAS PubMed; (b) L. Ackermann, S. I. Kozhushkov and D. S. Yufit, Chem.–Eur. J., 2012, 18, 12068–12077 CrossRef CAS PubMed.
- S. Cui, Y. Zhang and Q. Wu, Chem. Sci., 2013, 4, 3421–3426 RSC.
- Y. Liang, V. Müller, W. Liu, A. Münch, D. Stalke and L. Ackermann, Angew. Chem., Int. Ed., 2017, 56, 9415–9419 CrossRef CAS.
- (a) D. Lapointe and K. Fagnou, Chem. Lett., 2010, 39, 1118–1126 CrossRef; (b) D. Balcells, E. Clot and O. Eisenstein, Chem. Rev., 2010, 110, 749–823 CrossRef CAS; (c) L. Ackermann, Chem. Rev., 2011, 111, 1315–1345 CrossRef CAS; (d) D. L. Davies, S. A. Macgregor and C. L. McMullin, Chem. Rev., 2017, 117, 8649–8709 CrossRef CAS.
- L. Xu, E. E. L. N. Liu, J. Bacsa, C. E. MacBeth and D. G. Musaev, Chem. Sci., 2020, 11, 6085–6096 RSC.
- (a) W. Ma, R. Mei, G. Tenti and L. Ackermann, Chem.–Eur. J., 2014, 20, 15248–15251 CrossRef CAS PubMed; (b) D. Zell, M. Bursch, V. Müller, S. Grimme and L. Ackermann, Angew. Chem., Int. Ed., 2017, 56, 10378–10382 CrossRef CAS; (c) E. Tan, O. Quinonero, M. E. Orbe and A. M. Echavarren, ACS Catal., 2018, 8, 2166–2172 CrossRef CAS; (d) L. Wang and B. P. Carrow, ACS Catal., 2019, 9, 6821–6836 CrossRef CAS; (e) C. Zhu, R. Kuniyil, B. B. Jei and L. Ackermann, ACS Catal., 2020, 10, 4444–4450 CrossRef CAS . See also Fig. S19† for details..
- X. Chen, S. Zhang, T. H. Meyer, C. Yang, Q. Zhang, J. Liu, H. Xu, F. Cao, L. Ackermann and X. Hong, Chem. Sci., 2020, 11, 5790–5796 RSC.
- (a) M. D. Lotz, N. M. Camasso, A. J. Canty and M. S. Sanford, Organometallics, 2017, 36, 165–171 CrossRef CAS; (b) B. Bhaskararao, S. Singh, M. Anand, P. Verma, P. Prakash, A. C, S. Malakar, H. F. Schaefer and R. B. Sunoj, Chem. Sci., 2020, 11, 208–216 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision D.01), Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- (a) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- (a) K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS; (b) H. P. Hratchian and H. B. Schlegel, J. Chem. Phys., 2004, 120, 9918–9924 CrossRef CAS.
- (a) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC; (b) F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- C. Y. Legault, CYLview, 1.0b, Université de Sherbrooke, Canada, 2009, https://www.cylview.org Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional computational results, calculated energies and imaginary frequencies, and Cartesian coordinates of optimized structures. See DOI: https://doi.org/10.1039/d2sc05200h |
| This journal is © The Royal Society of Chemistry 2023 |