Experimental and computational insights into the mechanism of FLP mediated selective C–F bond activation

Abstract

Frustrated Lewis pairs (FLP) comprising of B(C₆F₅)₃ (BCF) and 2,4,6-triphenylpyridine (TPPy), P(o-Tol)₃ or tetrahydrothiophene (THT) have been shown to mediate selective C–F activation in both geminal and chemically equivalent distal C–F sites. In comparison to other reported attempts of C–F activation using BCF, these reactions appear surprisingly facile. We investigate this reaction through a combination of experimental and computational chemistry to understand the mechanism of the initial C–F activation event and the origin of the selectivity that prevents subsequent C–F activation in the monoactivated salts. We find that C–F activation likely occurs via a Lewis acid assisted S_N1 type pathway as opposed to a concerted FLP pathway (although the use of an FLP is important to elevate the ground state energy), where BCF is sufficiently Lewis acidic to overcome the kinetic barrier for C–F activation in benzotrifluorides. The resultant intermediate salts of the form [ArCF₂(LB)][BF(C₆F₅)₃] (LB = Lewis base) are relatively thermodynamically unstable, and an equilibrium operates between the fluorocarbon/FLP and their activation products. As such, the use of a fluoride sequestering reagent such as Me₃SiNTf₂ is key to the realisation of the forward C–F activation reaction in benzotrifluorides. Selectivity in this reaction can be attributed to both the installation of bulky Lewis bases geminal to residual C–F sites and from electronic re-ordering of kinetic barriers (of C–F sites in products and starting materials) arising from the electron withdrawing nature of the pyridinium, phosphonium and sulfonium groups.

---

Introduction

Selective functionalization of a single C–F bond in difluoro and trifluoromethyl groups is a simple strategy to access a vast array of fluorocarbon products. However, this approach is complicated by the fact that the resulting singly functionalized products contain weaker C–F bonds than their starting materials and a mixture of ‘over-reaction’ products is commonly obtained.¹

A number of solutions have been offered to address this problem, however, most are limited in fluorocarbon substrate and functionalization scope. For example, electron poor benzotrifluorides and trifluoromethylamides can be functionalised via SET reactions,² CF₃ and CF₂H groups vicinal to carbonyl or vinyl groups are able to generate fluoroalkene products with thermodynamically stable sp² C–F bonds,³ and monoselective nucleophilic substitution of aromatic CF₃ and CF₂H groups ortho to hydrosilyl groups is possible.⁴

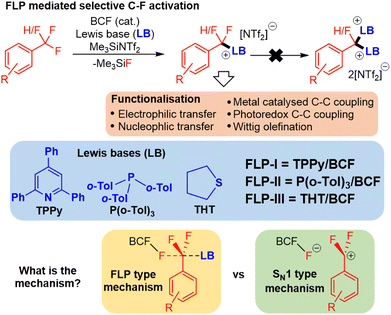
Recently, frustrated Lewis pairs (FLPs) have been used to selectively activate aliphatic polyfluorocarbons.⁵ Notably, we have been able to employ a combination of B(C₆F₅)₅ (BCF) with triarylphosphines, 2,4,6-triphenylpyridine (TPPy) and dialkylsulfides to enable selective activation of CF₃ and CF₂H groups (Fig. 1).^5a–d This reaction can be run with catalytic Lewis acid in the presence of Me₃SiNTf₂. Indeed, the reaction performs much better under catalytic conditions.

Fig. 1 FLP mediated C–F bond activation allows single fluoride functionalisation in difluoromethyl and trifluoromethyl groups. TPPy = 2,4,6-triphenylpyridine, THT = tetrahydrothiophene, BCF = tris(pentafluorophenyl)borane.

The observed activity of this FLP mediated C–F bond activation reaction is surprising given past reports that have failed to activate benzotrifluorides using BCF alone.⁶ Indeed, other reports of FLP mediated C–F bond activation have employed stoichiometric silylium and dicationic phosphonium, both of which are very strong Lewis acids.^5e,f Computational evidence that BCF and TPPy exhibit FLP type cooperative activity was recently reported by Fernández (and later Chattaraj) (Fig. 1), whose calculations suggested that the TPPy base plays an important role in lowering the activation barrier for the Lewis acid mediated C–F scission.⁷ Despite the insight that Fernández's model offered, it relied upon stabilizing π–π stacking interactions between arenes on the benzotrifluoride substrate and TPPy base that would not be present in other Lewis bases that are competent in FLP C–F activation. In addition, computational examination of the initial C–F activation event does not explain the high selectivity that these FLPs have for controlled single fluoride abstraction in polyfluoroalkanes, nor the enhanced reactivity observed under catalytic conditions (as opposed to stoichiometric reactions).

In an effort to illuminate unexplored mechanistic aspects of the selective C–F activation FLP reaction, we have undertaken a combined computational and experimental study. In addition to the BCF/TPPy FLP system studied by Fernández,^7a we have expanded the study to include sulfide and phosphine FLP systems, which have also been reported to facilitate selective C–F activation.^5a,c Importantly, we are able to benchmark our computational results to experimentally obtained kinetic and thermodynamic data, which corroborate each other in suggesting that the reaction mirrors a Lewis acid assisted S_N1 reaction (independent of Lewis base) more closely than an FLP cooperative reaction (as suggested by Fernández).

Results and discussion

The initial FLP mediated C–F activation event

We chose to examine three FLPs that have previously demonstrated selective C–F activation; namely BCF/TPPy (FLP-I), BCF/P(o-Tol)₃ (FLP-II) and BCF/THT (THT = tetrahydrothiophene) (FLP-III) (Fig. 1).^5a–c Based upon Fernández's report,^7a we expected to observe a reaction rate dependence directly proportional to the concentration of substrate (fluorocarbon), Lewis acid (BCF) and Lewis base used, consistent with a Lewis acid assisted S_N2 (FLP type) mechanism. A first-order rate dependence was established for both substrate and BCF, however, we found that the reaction rate was independent of the concentration of Lewis base used. For example, the activation of 4-Me-C₆H₄CF₃ (1a) with FLP-I or FLP-II showed no increase in rate with increasing base concentration. Indeed, if anything a slight inhibition was observed at very high TPPy and P(o-Tol)₃ concentrations.

We reasoned that an FLP type mechanism was still viable if the apparent base independence (or inhibition) resulted from a competing equilibrium of FLP and Lewis adduct forms of FLP-I and FLP-II, where higher concentrations of Lewis base favoured the inactive Lewis adduct form. As such, we undertook a Hammett plot analysis⁸ for the activation of a series of benzotrifluorides with FLP-I and FLP-II, the results of which would not be affected by any FLP/Lewis adduct equilibrium (Table 1).

Table 1 Hammett plot analysis ρ-values for FLP systems FLP-I, FLP-II and FLP-III^a

Entry	FLP system	Substrate	ρ-Value	ρ ^+-Value
a N.R. = No reaction observed with any of ArCF3 substrates.
1	FLP-I	ArCF3	−3.0 ± 0.3	−2.6 ± 0.5
2	FLP-II	ArCF3	−4.8 ± 0.7	−4.2 ± 0.4
3	FLP-III	ArCF3	N.R.	N.R.
4	FLP-I	ArCF2H	−3.1 ± 0.4	−2.8 ± 0.2
5	FLP-II	ArCF2H	−7.0 ± 1.2	−6.6 ± 0.9
6	FLP-III	ArCF2H	−3.5 ± 0.7	−3.2 ± 0.5

---

We observed a ρ-value of −3.0 ± 0.3 for FLP-I, indicative of a significant positive charge accumulation at the benzylic position (Table 1, entry 1). Such a value is common for S_N1 transition states, but could also be due to an open or early transition state S_N2 process.⁹ Repeating the Hammett plot analysis with FLP-II gave an even lower ρ-value of −4.8 ± 0.7, clearly indicative of an S_N1 type process (Table 1, entry 2). A Hammett plot analysis of FLP-III with benzotrifluorides was not possible due to no observed reaction in this system (Table 1, entry 3).

Hammett plot analyses were also carried out for FLP-I, FLP-II and FLP-III for difluoromethylarene substrates, where the ρ-values were indicative of S_N1 processes (Table 1, entries 4–6). In theory, for an S_N1 process the observed ρ-values for each FLP system should be identical for either of the substrates sets (i.e. ArCF₃ or ArCF₂H). In practice we would expect error in these measurements, but given the wide spread of ρ-values, we suspect that secondary intermolecular interactions in the transition states – such as H-bonding or π–π stacking – may have subtle influences on the ρ-value for each FLP system (see ESI, Fig. S47†).

We also modelled these data using σ⁺ values (Table 1). The corresponding ρ⁺-values cannot be directly compared to ρ-values, however, a better Hammett plot fit of rate constants to σ⁺ values is indicative of an S_N1 type process. In all cases, the calculated standard error for the σ⁺ plots was lower than their σ plot counterparts, except in the case of FLP-I with benzotrifluorides (Table 1).

The intermediary ρ-value of −3.0 ± 0.3 for FLP-I taken with its poorer fit to σ⁺ values does not allow conclusive assignment of FLP-I to an S_N1 mechanism or an FLP type mechanism as proposed by Fernández. To clarify the situation, we decided to conduct our own theoretical analysis at DFT level. Geometry optimisations and transition state locations were performed at the level of PCM(DCM)-B3LYP-D3/Def2SVP. The reported Gibbs free energies in our study were obtained by combining PCM(DCM)-B3LYP-D3/def2TZVPP electronic energies with the thermal and entropic contributions computed at the PCM(DCM)-B3LYP-D3/Def2SVP level followed by quasi-harmonic correction (for more details on testing different DFT functionals, solvation models and dispersion corrections see Computational studies section in ESI†). Considering the large conformational space that a Lewis base may occupy, a thorough conformational study was performed to obtain the lowest energy transition state. Additionally, various conformers were assessed for the FLP adducts and different ion pairs.

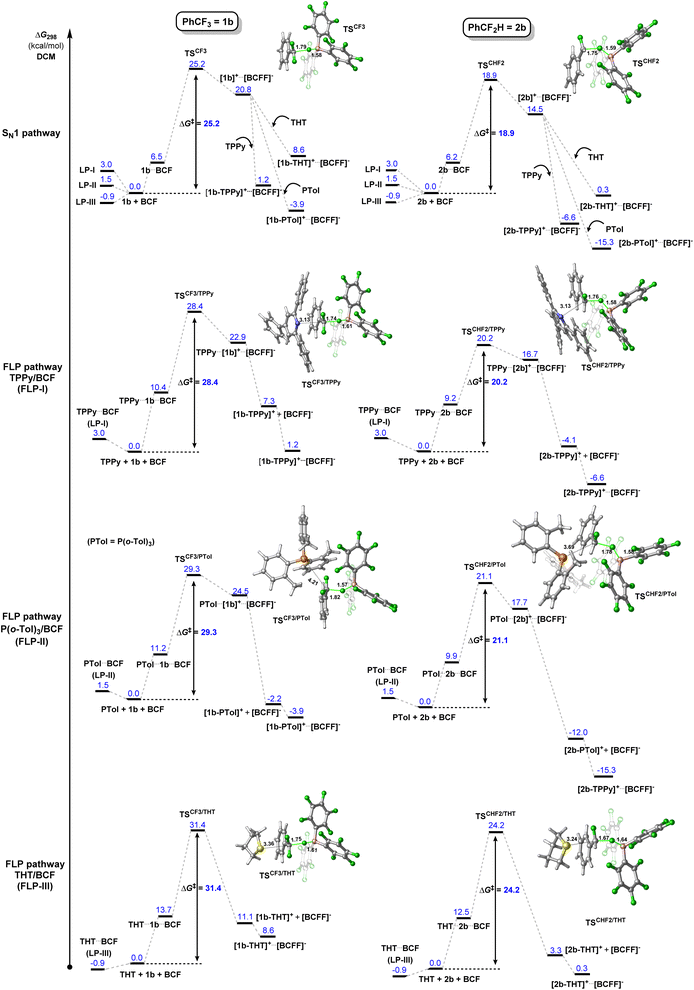
The FLP systems (FLP-I, FLP-II, FLP-III) were computationally interrogated with two model substrates; PhCF₃ (1b) and PhCF₂H (2b) (Fig. 2). We investigated two possible pathways for the C–F activation reaction. Namely, a stepwise S_N1 type reaction where BCF abstracts fluoride from the fluorocarbon to form a carbocation intermediate (S_N1 pathway) and a concerted FLP type activation involving both Lewis acid and base in the transition state, similar to that reported by Fernández (FLP pathway). Fernández calculated that an S_N2 pathway in the absence of Lewis acid has a barrier of over 80 kcal mol⁻¹,^7a and therefore this mechanism was not considered in our studies.

Fig. 2 Calculated S_N1 and FLP reaction pathways for the reactions of FLP-I, FLP-II and FLP-III with PhCF₃ (1b, left hand side) and PhCF₂H (2b, right hand side). Note: PTol = P(o-Tol)3, LP = Lewis pair/adduct. Level of theory: PCM(DCM)-B3LYP-D3/Def2TZVPP//PCM(DCM)-DB3LYP-D3/Def2SVP (quasi-harmonic entropic correction). Displayed calculated bond distances given in Å.

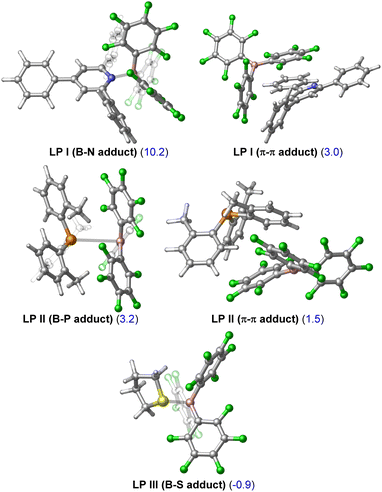
The first computational result of note is that calculated equilibria between Lewis pair/adduct (LP) and FLP forms greatly favour the FLP forms in FLP-I and FLP-II (Table 2). The classical B–N adduct form of FLP-I is thermodynamically disfavoured by 10.2 kcal mol⁻¹ in comparison to the FLP form and the lowest energy adduct conformer (an arene π–π stacking adduct) is disfavoured by 3.0 kcal mol⁻¹. Similarly, the lowest energy B–P adduct form of FLP-II located is disfavoured by 3.2 kcal mol⁻¹ as compared to the FLP form, however, once again the lowest energy adduct conformer found corresponded to an arene π–π stacking adduct, which was disfavoured by 1.5 kcal mol⁻¹. In the case of FLP-III, the classical B–S adduct represented the lowest energy isomer, and (in contrast to FLP-I and FLP-II) was slightly thermodynamically preferred by 0.9 kcal mol⁻¹.¹⁰ The consequences of these calculated equilibria are that (i) if there is no base dependence arising in the rate determining step, then higher concentrations of base that perturb the FLP/LP equilibria will result in an inverse observed rate, and that (ii) the ground state of FLP-III is likely the Lewis adduct form (i.e.LP-III), and the additional energy required to break this adduct will result in higher observed kinetic barriers for reactions involving FLP-III.

Table 2 Calculated free energy differences between FLP and Lewis pair (LP)/adduct forms of FLP-I, FLP-II and FLP-III, and representations of their lowest energy conformers

Entry	FLP system	Conformer	Calc. ΔG^0298 (kcal mol^−1)
1	FLP-I/LP-I	B–N adduct	+10.2
2	FLP-I/LP-I	π–π adduct	+3.0
3	FLP-II/LP-II	B–P adduct	+3.2
4	FLP-II/LP-II	π–π adduct	+1.5
5	FLP-III/LP-III	B–S adduct	−0.9

---

Calculated differences in free energies of FLP and adduct forms of FLP-I, FLP-II and FLP-III could not be verified experimentally due to fast dynamic exchange between the two forms that could not be resolved through ¹⁹F NMR spectroscopy upon cooling. However, in support of the adduct form of FLP-III being thermodynamically viable, the solid state molecular structure for this adduct has been reported.¹¹

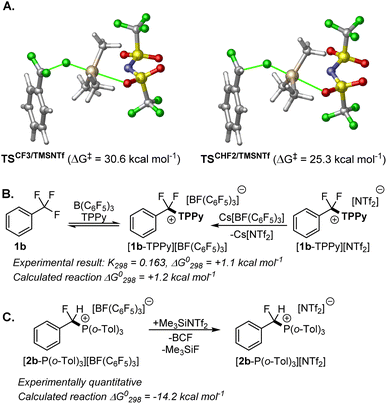
Turning our attention to the initial C–F activation event, in the case of FLP-I, calculated barriers for C–F activation in 1b show that an S_N1 pathway (25.2 kcal mol⁻¹) is slightly favourable to an FLP pathway (28.4 kcal mol⁻¹). The ordering of these energy barriers is the reverse of that which Fernández reported and they are more aligned to a slow ambient temperature reaction. We found that the previously reported relative Gibbs free energy profile by Fernández lacks single-point refinements with a larger basis set (the indicated relative free energies were computed at the PCM(DCM)-B3LYP-D3/def2SVP level). Besides, thorough conformational analysis for transition states was not performed.

Even higher kinetic barriers are calculated for the activation of 1b with FLP-II and FLP-IIIvia FLP pathways, corroborating with experimental data that suggest a preferred S_N1 pathway for FLP-II, while no product is observed experimentally in the case of FLP-III.

For C–F activation in benzodifluoride 2b, FLP-I was calculated to have similar kinetic barriers for S_N1 and FLP reaction pathways, with an S_N1 pathway slightly preferred by 1.3 kcal mol⁻¹. The S_N1 pathway was clearly preferred over FLP pathways for FLP-II and FLP-III. The barrier for C–F activation in CF₂H groups was found to be lowered by as much as ca. 2 kcal mol⁻¹ through a hydrogen-bonding interaction between the CF₂H hydrogen and an ortho-fluoroaryl group present on the BCF catalyst. These computational data support an S_N1 mechanism for C–F activation reactions of 1b and 2b in all FLP systems studied.

A series of kinetic experiments under catalytic conditions were undertaken to obtain experimental ΔG^‡ values for the C–F activation event in difluoromethyl and trifluoromethyl arenes (listed in Table 3). Using the substrate 4-Me-C₆H₄-CF₃ (1a), ΔG^‡ was determined to be 22.4 ± 2.3 kcal mol⁻¹ for FLP-I and 22.9 ± 1.7 kcal mol⁻¹ for FLP-II, with the calculated barrier for S_N1 activation of 1a found to be 24.4 kcal mol⁻¹ (see ESI, Fig. S54†). Substrates 2a and 2b were found to react too quickly under our standard conditions, so 2-Br-C₆H₄-CF₂H (2c) was employed to obtain experimental kinetic data. With 2c, ΔG^‡ was determined to be 20.7 ± 1.3 kcal mol⁻¹ for FLP-I, 21.1 ± 0.7 kcal mol⁻¹ for FLP-II and 22.2 ± 0.6 kcal mol⁻¹ for FLP-III, against calculated values of 19.3 kcal mol⁻¹ for FLP-I and FLP-II, and 20.2 kcal mol⁻¹ for FLP-III (Fig. 4 and S61†).

Table 3 Experimental (exp.) and calculated (calc.) ΔG^‡ values for activation of substrates 1a (4-Me-C₆H₄-CF₃), 1b (PhCF₃), 2b (PhCF₂H), 2c (4-Br-C₆H₄-CF₂H) and 3b (1,4-(CF₂H)₂C₆H₄) by FLP-I, FLP-II and FLP-III

Entry	FLP system	Substrate	ΔG^‡ (kcal mol^−1)
1	FLP-I	1a	22.4 ± 2.3 (exp.)
2	FLP-II	1a	22.9 ± 1.7 (exp.)
3	FLP-I, FLP-II	1a	24.4 (calc.)
4	FLP-III	1a	25.3 (calc.)
5	FLP-I, FLP-II	1b	25.2 (calc.)
6	FLP-III	1b	26.1 (calc.)
7	FLP-I, FLP-II	2b	18.9 (calc.)
8	FLP-III	2b	19.8 (calc.)
9	FLP-II	[2b-P(o-Tol)3][NTf2]	27.1 (calc.)
10	FLP-I	2c	20.7 ± 1.3 (exp.)
11	FLP-II	2c	21.1 ± 0.7 (exp.)
12	FLP-III	2c	22.2 ± 0.6 (exp.)
13	FLP-I, FLP-II	2c	19.3 (calc.)
14	FLP-III	2c	20.2 (calc.)
15	FLP-I	3b	19.3 (calc.)
16	FLP-I	[3b-TPPy][NTf2]	20.3 (calc.)
17	FLP-III	3b	20.2 (calc.)
18	FLP-III	[3b-THT][NTf2]	24.0 (calc.)

---

The similar activation barrier values for FLP-I and FLP-II for each substrate strongly support an S_N1 process with a common transition state, and verify the calculated activation barriers in the S_N1 pathway. Additionally, the higher experimental activation barrier for FLP-III with 2c (as compared to FLP-I and FLP-II) agrees with the adduct form of FLP-III being thermodynamically preferred. Indeed, a control experiment where 1b was reacted with FLP-I under standard catalytic conditions but with the addition of 1.5 equivalents of THT resulted in no activation occurring after 48 hours, confirming that the presence of THT inhibits activation of benzotrifluorides through the formation of a thermodynamically preferred Lewis adduct.

The role of Me₃SiNTf₂

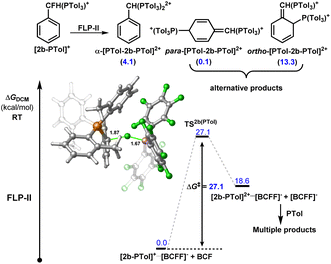
As our catalytic protocol includes the use of Me₃SiNTf₂, we attempted to calculate pathways involving Me₃SiNTf₂ in the rate determining C–F activation step. Such attempts resulted in higher kinetic barriers for both 1b and 2b as compared to C–F activation by BCF alone with the lowest energy transition states located for Me₃SiNTf₂ mediated C–F bond cleavage of 1b and 2b 5.4 kcal mol⁻¹ and 6.4 kcal mol⁻¹ (respectively) higher in energy than those mediated by BCF (Fig. 3A). Interestingly, the lowest energy transition states for Me₃SiNTf₂ mediated C–F activation involved oxygen bridged Me₃SiNTf₂ (see ESI, Fig. S55†), similar to tin bistriflimide isomers reported by Pápai and Ashley.¹² The non-active role of Me₃SiNTf₂ in the C–F activation step was confirmed through kinetic experiments that varied the concentration of Me₃SiNTf₂ in reactions of FLP-I with 1a and 2c, and FLP-II with 2c, all of which showed no rate dependence on Me₃SiNTf₂ concentration (see ESI, Fig. S7 and S8†).

Fig. 3 (A) Lowest energy transition states for C–F activation of 1b and 2b by Me₃SiNTf₂. (B) Experimental and computational analysis for the equilibrium between FLP-I/1b and their activation product. (C) Experimental and computational evidence supporting the role of Me₃SiNTf₂ in abstracting fluoride from [BF(C₆F₅)₃]⁻ and providing thermodynamic preference to the reaction products.

In the absence of Me₃SiNTf₂, calculated free energies of the starting materials and the FLP activation products revealed that very little thermodynamic gradient existed in FLP-I with 1b, with the product, [1b-TPPy][BF(C₆F₅)₃], a mere 1.2 kcal mol⁻¹ less stable than the starting materials (Fig. 3B). These comparable free energies, combined with the low kinetic barrier, result in an equilibrium between FLP-I and 1b with their activation products. The equilibrium constant for this reaction was determined from both reaction directions through stoichiometric reaction of FLP-I with 1b and then with stoichiometric reaction of Cs[BF(C₆F₅)₃] with [PhCF₂(TPPy)][NTf₂], that provided an equilibrium constant of K₂₉₈ = 0.163, corresponding to an experimentally derived free energy difference of ΔG₂₉₈ = +1.1 kcal mol⁻¹ and agreeing with computed energies remarkably well (Fig. 3B).

In the case of FLP-II, the equilibrium lies well in the direction of the products and the kinetic barrier for the reverse reaction is consequently higher. However, the possibility of the reverse reaction using FLP-II with certain benzotrifluoride substrates was confirmed through reaction of [4-OMe-C₆H₄CF₂(P(o-Tol)₃)][NTf₂] with Cs[BF(C₆F₅)₃] to generate 4-OMe-C₆H₄CF₃. It is proposed in the presence of Me₃SiNTf₂ that the anion [BF(C₆F₅)₃]⁻ is quickly converted to BCF and Me₃SiF, preventing the reverse reaction and improving reaction rate and yield.

In support of this assertion, a control reaction between [2b-P(o-Tol)₃][BF(C₆F₅)₃] and Me₃SiNTf₂ resulted in the fast generation of BCF, Me₃SiF and [2b-P(o-Tol)₃][NTf₂] (Fig. 3C). The calculated free energy change for the reaction of Me₃SiNTf₂ with [2b-P(o-Tol)₃][BF(C₆F₅)₃] shows a significantly exergonic reaction (ΔG₂₉₈ = −14.2 kcal mol⁻¹) (see ESI, Fig. S53†). Providing further evidence that the main role of Me₃SiNTf₂ is to sequester fluoride from the reaction, thermodynamically driving it in a productive direction whilst regenerating the BCF catalyst.

Indication that Me₃SiNTf₂ can play a more direct role in the activation reaction was observed in the activation of 2c with FLP systems FLP-I and FLP-II. In these reactions, the formation of an intermediate was observed, assigned as [2-Br-C₆H₄-CFH(NTf₂)] (2c-NTf₂), that formed quickly and was then consumed to generate the final product [2c-LB][NTf₂] (LB = TPPy, P(o-Tol)₃). In the case of FLP-III, this intermediate was not observed. The intermediate was easily identifiable via a distinct shift in the bistriflimide ¹⁹F NMR signal from δ_F −80.0 to −71.5 that is characteristic for N-alkyl bistriflimide adducts.¹³ Additionally, a signal for the benzylic fluoride was observed at δ_F −143.8 and the intermediate's composition was confirmed via ESI-MS. Repeating the activation reaction in the absence of Lewis base provided 2c-NTf₂ as the sole product in 60% NMR yield. However, the instability of this compound prevented its isolation.

The rate of reaction of 2c-NTf₂ with Lewis bases followed the order TPPy > P(o-Tol)₃, and was concentration dependent, implying an S_N2 type mechanism for NTf₂ substitution (see ESI, Fig. S22 and S23†). DFT calculations supported this observation with S_N2 pathways at least 1.2 kcal mol⁻¹ lower in energy than the calculated S_N1 pathway and following the ordering of TPPy < THT < P(o-Tol)₃ in the transition barrier height (Fig. 4).

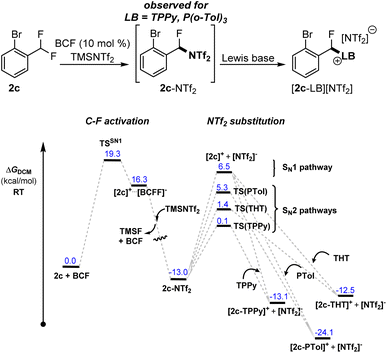Fig. 4 Calculated reaction profiles for formation and nucleophilic substitution of 2-NTf₂ with TPPy, P(o-Tol)₃ and THT.

The transient detection of 2c-NTf₂ under standard reaction conditions implies that (i) Me₃SiNTf₂ (or [NTf₂]⁻) reacts with the carbocation [2c]⁺ faster than TPPy and P(o-Tol)₃ and (ii) the barrier for the substitution of [NTf₂]⁻ with TPPy/P(o-Tol)₃ is similar to the barrier for C–F activation (and formation of 2c-NTf₂).¹⁴ Our calculations support the similar barriers between C–F activation and substitution steps, with substitution with P(o-Tol)₃ only 0.4 kcal mol⁻¹ lower in energy than C–F activation and substitution with TPPy 5.4 kcal mol⁻¹ lower in energy.

In the case of FLP-III, intermediate 2c-NTf₂ was not observed. This could be due to either THT reacting with the carbocation intermediate [2c]⁺ faster than Me₃SiNTf₂/[NTf₂]⁻ or due to a relatively higher C–F activation barrier as compared to the substitution barrier arising from the need to dissociate the Lewis adduct (LP-III) prior to C–F activation. Similarly, in benzotrifluoride and benzodifluoride substrates 1 and 2 (other than 2c), 1-NTf₂ and 2-NTf₂ are not observed under standard reactions, however, this does not discount their formation if the C–F activation step is significantly higher in energy than NTf₂ substitution. The veracity of bistriflimide adducts as a universal intermediate in the C–F activation reaction is dependent on the kinetic barriers for combination of intermediate carbocations [1]⁺ and [2]⁺ with Lewis bases (TPPy, P(o-Tol)₃, THT) as compared to with [NTf₂]⁻.

Attempts to computationally model nucleophilic attack of the free carbocations [1]⁺ and [2]⁺ by NTf₂, TPPy, THT and P(o-Tol)₃ failed to provide a definitive ordering of relative kinetic barriers. However, the calculations did suggest that carbocation combination with THT was a barrierless processes, while nucleophilic attack with TPPy and P(o-Tol)₃ had barriers similar to that of the S_N1 C–F activation event (based upon endergonic ion separation) (see ESI, Fig. S57–S60†). Observations that 2c-NTf₂ forms preferentially to [2c-TPPy]⁺ and [2c-P(o-Tol)₃]⁺ but is not observed with FLP-III support our calculations, and imply that the barrier to nucleophilic attack by Me₃SiNTf₂ lies between those of THT and TPPy/P(o-Tol)₃. However, our failure to locate convergent transition states for the addition of both TPPy and P(o-Tol)₃ to the free carbocations points towards a more complicated nucleophilic substitution process that is beyond the scope of this study. Unfortunately, the facile substitution reactions of bistriflimide, THT and TPPy adducts to form thermodynamic products also precludes any experimentally determined relative distribution of initial kinetic products formed immediately after C–F activation.

Although the formulation of bistriflimide adducts as intermediates in cannot be discounted, C–F activation of benzodifluorides using FLP-I, FLP-II and FLP-III has been reported in the absence of Me₂SiNTf₂ (i.e. under stoichiometric conditions). Thus, the formation of 2-NTf₂ is not necessary for C–F activation and might only occur in cases where the barrier for Lewis base combination with the carbocation fragment [2]⁺ is greater than that for [NTf₂]⁻.

The observed difference in reaction rates of bases with the carbocation fragment arising from the S_N1-type C–F activation of 2c may help explain other anecdotal observations made in related systems which did not observe C–F activation using BCF. For example, Ozerov reported that BCF does not catalyse the hydrodefluorination reaction between benzotrifluorides and Et₃SiH, and Stephan reported BCF does not catalyse the Friedel–Crafts arylation of benzotrifluorides.^6a,b Our studies suggest that BCF is capable of S_N1-type C–F activation in benzotrifluorides and that it is the subsequent kinetic barrier arising from reaction with poorer nucleophilic reagents¹⁵ (e.g. hydrosilane, arene) that prevented any observable reaction occurring in these cases. That is, C–F activation is kinetically accessible with BCF but the thermodynamic instability of the initial product (i.e. [ArCF₂][BF(C₆F₅)₃]) may hinder the ability of weak nucleophiles to overcome the barrier for combination with the carbocation fragment.

Subsequent C–F activation (from where selectivity arises)

Pertinent to the development of FLP mediated selective C–F activation is obtaining an understanding of why the reaction is monoselective. Most substitutions of fluoride in CF₂R groups (R = H or F) result in dramatic decreases in remaining C–F bond activation energies in the products. For example, the BCF mediated C–F activation energy barrier in 2b is calculated to be 18.9 kcal mol⁻¹ (Fig. 2), while in BnF (the initial product of hydrodefluorination for 2b) it is calculated to be only 13.5 kcal mol⁻¹ (see ESI, Fig. S56†).

In the cases of secondary C–F activation at geminal positions in substrates with installed bulky TPPy and P(o-Tol)₃ groups, it might be expected that the approach of BCF would be sterically hindered resulting in an increase in the kinetic barrier, however, THT is an unassuming base, and we have shown that chemically equivalent distal C–F sites may also undergo selective activation using our approach. Thus, we suspected that the substitution of a fluoride in polyfluorocarbons with a neutral Lewis base might re-order the kinetic barriers for C–F activation in the starting materials and products through electronic factors.

To investigate the second C–F activation event (i.e. C–F activation of the monoactivated products) we utilised 2b and 1,4-(CF₂H)₂C₆H₄ (3b) as model substrates for (de)activation at geminal and distal sites respectively. The first activation of 2b is described above (Fig. 2) and we have previously reported on the selective activation of 3b to generate [1-CF₂H-4-CFH(LB)C₆H₄][NTf₂] {[3b-LB][NTf₂]} (LB = TPPy, THT).^5c Of note in previous reports, no diactivation side products were observed in the case of 2b, whereas we have observed small amounts of diactivation products when employing distal polyfluorides 3a and 3b (Fig. 5).

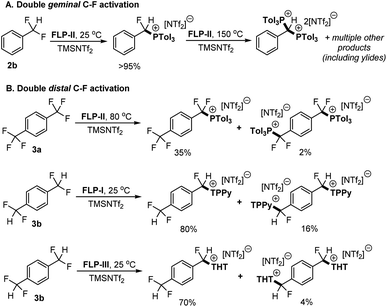Fig. 5 (A) Sequential activation of 2b by FLP-II. The initial activation product was isolated before the second activation reaction was undertaken. (B) Examples of diactivation occurring in distal (and chemically equivalent) C–F positions in substrates 3a and 3b. The mono and diactivation products were observed in the same reaction (in the yields indicated).^5a,c, Yields determined by ¹⁹F and/or ³¹P NMR spectroscopy.

Although we do not observe double C–F activation of 2b under ambient temperatures, subjecting the isolated salt [2-P(o-Tol)₃][NTf₂] to more forcing conditions (130–150 °C) resulted in further C–F activation and formation of bisphosphonium salt [2-(P(o-Tol)₃)₂][NTf₂]₂ (Fig. 5A). ³¹P NMR spectroscopy revealed that multiple products are present once [2-P(o-Tol)₃][NTf₂] is consumed. ESI-MS confirmed the presence of [2-(P(o-Tol)₃)₂][NTf₂]₂ in solution, however, a number of isomers of [2-(P(o-Tol)₃)₂][NTf₂]₂ are possible, with the incoming P(o-Tol)₃ foreseeably attacking the α-carbon position to generate [α-2-(P(o-Tol)₃)₂][NTf₂]₂ or the aryl ring at the ortho or para positions to generate [ortho-2-(P(o-Tol)₃)₂][NTf₂]₂ or [para-2-(P(o-Tol)₃)₂][NTf₂]₂ (Fig. 6). In addition to the dication, a major signal is observed at 697.97 m/z with a monocationic isotopic distribution pattern and attributed to ylide formation from deprotonation of [2-(P(o-Tol)₃)₂][NTf₂]₂. As such, [2-(P(o-Tol)₃)₂][NTf₂]₂ could not be isolated, but it is shown to be kinetically accessible (albeit with difficulty).

Fig. 6 Calculated energy profile for the reaction of [PhCHFP(o-Tol)₃][BF(C₆F₅)₃] {[2b-PTol][BCFF]} with FLP-II. Note: P(o-Tol)₃ is represented by PTol in figure. The relative stabilities of possible products are shown in parentheses in kcal mol⁻¹. Displayed calculated bond distances given in Å.

To understand the origin of the higher kinetic barrier for the second C–F activation event in 2b, we modelled the second activation event computationally for FLP-II. A transition state corresponding to an S_N1 C–F activation was located 27.1 kcal mol⁻¹ higher in energy than the ground state {i.e. [2-P(o-Tol)₃]⁺⋯[BF(C₆F₅)₃]⁻} (Fig. 6), representing an increase in activation barrier of 8.2 kcal mol⁻¹ as compared to the initial C–F activation event in 2b, and 13.6 kcal mol⁻¹ greater than in benzyl fluoride (as a comparison to another monofluoride substrate).

Much of this increase in barrier may be attributed to the steric profile of P(o-Tol)₃, hindered access of BCF to the remaining fluoride position and dissociation of the ion pair. In contrast, distal C–F positions are equally accessible in starting materials and monoactivation products. As stated above, we do see diactivation products in the case of distal fluorides, however, these are minor products as compared to the desired monoactivated salts, suggesting that the initial activation products are less reactive than the starting materials.

Modelling the double C–F bond activation of 3b with FLP-I, we found that the initial C–F activation is calculated to have a kinetic barrier of 19.3 kcal mol⁻¹ (Fig. 7, for a detailed energy profile see Fig. S63†). This value is slightly higher than in 2b, as would be expected with the inclusion of an additional electron withdrawing para-CF₂H group. The second barrier for C–F bond activation (i.e. C–F activation of [3b-TPPy][NTf₂]) was calculated to be 20.3 kcal mol⁻¹. Although the increase in activation barrier from 3b to [3b-TPPy][NTf₂] is small, under controlled reaction conditions, a high yield of the monoactivation product can be obtained when using stoichiometric amounts of TPPy.

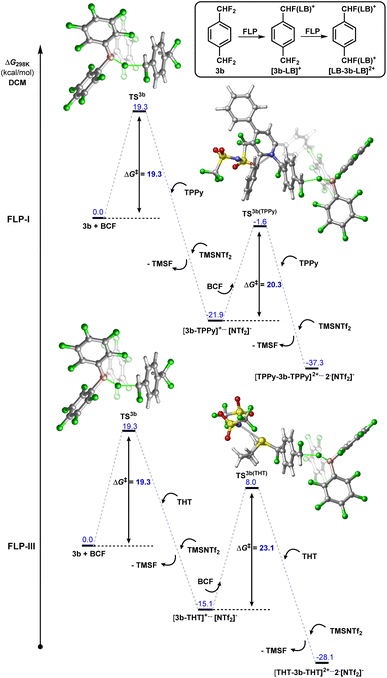Fig. 7 Calculated energy profile for the 1^st and 2^nd C–F activation events between 1,4-(CF₂H)₂-C₆H₄ (3b) and FLP-I or FLP-III.

In contrast, we found that the barrier for the second C–F activation using FLP-III (i.e. C–F activation of [3b-THT][NTf₂]) was 23.1 kcal mol⁻¹, representing a barrier increase of 3.8 kcal mol⁻¹ as compared to 3b (Fig. 8). The result of this is corroborated with experimental observations, where we generally see much higher selectivity of the monoactivation product over the diactivation product (Fig. 5B). In both cases, the effect of installing a neutral Lewis base is similar to the conversion of CF₂H to a slightly more electron withdrawing group, providing an electronic deterrent for further C–F activation in the product.

Fig. 8 Calculated atom NBO charges for fluorine atoms and HOMO for [3b-TPPy]⁺ and [3b-THT]⁺.

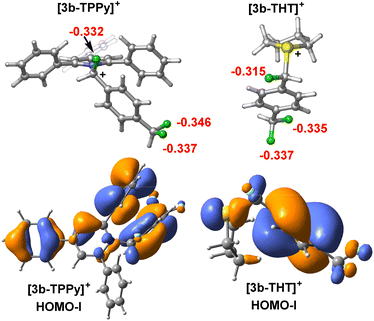
To understand from where the difference in 1^st and 2^nd C–F activation barrier heights between FLP-I and FLP-III arises, we generated frontier orbitals and charge assignments for [3b-LB]⁺ (LB = TPPy, THT) (Fig. 8 and S67†). The charge assignment for the geminal and distal fluorides in [3b-THT]⁺ are more positive than in [3b-TPPy]⁺ meaning that there is potentially less electrostatic interaction between the BCF catalyst and fluoride positions in [3b-THT]⁺. Examining the HOMO-I (and LUMO-I) of [3b-TPPy]⁺ and [3b-THT]⁺, it is clear that the frontier orbitals are significantly delocalised throughout the TPPy motif, whereas the frontier orbitals have little occupancy on the THT backbone. This can be interpreted as a delocalisation of positive charge throughout the TPPy fragment in [3b-TPPy]⁺, whereas in [3b-THT]⁺ the positive charge is maintained on the sulfonium position and throughout the fluorocarbon fragment. So the cationic charge that inhibits further C–F activation is more prevalent in the ‘3b⁺’ fragment in [3b-THT]⁺, resulting in a higher activation barrier for subsequent fluoride abstraction as compared to [3b-TPPy]⁺.

It is also apparent from the frontier orbitals of [3b-TPPy]⁺ that significant π–π stacking occurs between one of the TPPy ortho phenyl substituents and the ‘3b’ aromatic fragment. By modelling a single phenyl substituent on TPPy (i.e. monophenylpyridine) in the 2, 4 and 6 positions, inductive and through space stabilization provided by the phenyl substituents could be estimated (for details see Fig. S68†). It was found that π–π stacking of the phenyl group stabilized the diactivation product [3b′-TPPy]²⁺ by up to 2.7 kcal mol⁻¹, and as such, it might be expected to also stabilise the transition state for the second C–F activation event in [3b-TPPy]⁺. This effect would not be active in [3b-THT]⁺, resulting in a higher transition state barrier.

Conclusions

The results of this study suggest that C–F activation in benzotrifluorides (1) and benzodifluorides (2) occurs via an S_N1 type mechanism as opposed to a concerted FLP mechanism. Although this is not a classical FLP activation mechanism involving both the FLP components in the activation transition state, the use of an FLP system is an important aspect of the reaction given that thermodynamically preferred Lewis adducts (as in the case of FLP-III) can increase the kinetic activation barriers and suppress C–F activation. Indeed, given that BCF has become a mainstay of main group catalysis,¹⁶ a number of facets of this system are important to consider in other FLP and C–F activation systems. In addition to ‘reversible’ FLPs¹⁷ suffering from an energy penalty to dissociate the adduct form, this study suggests that steps that occur after the C–F activation event can be reaction limiting. This finding will be of interest to main group chemists who employ BCF in C–F and other bond activation chemistry.

We have also shown that the inclusion of Me₃SiNTf₂ is important for the thermodynamic stabilization of C–F activation products. Indeed, the reverse reaction (attack of the activation product by [BF(C₆F₅)₃]⁻ anion) is thermodynamically preferred for FLP-I with 1a and 1b in the absence of Me₃SiNTf₂. However, despite Me₃SiNTf₂ being a competent Lewis acid, we have found that it does not affect the kinetic barrier for C–F activation.

Lastly, we have provided mechanistic evidence of where the monoselective C–F activation reaction arises. We have shown that subsequent C–F activation events incur a higher kinetic barrier (as compared to the initial C–F activation step), and that this is true for geminal and distal fluorides (i.e. selectivity has an electronic component). Moreover, we have shown that the Lewis bases incorporated into the activation products affect the kinetic barriers for subsequent C–F activation, and that this should be a consideration when choosing FLP for monoselective C–F activation.

Data availability

Experimental and computational data are available in the accompanying ESI.†

Author contributions

RG and KL performed all experimental procedures including the collection and processing of kinetic data. DC performed all of the computations. RDY wrote the manuscript and devised the project. RG, DC, KL and RDY planned the experiments.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

We thank the Singapore Agency for Science, Technology and Research for funding (A*STAR grant no. A1983c0033 and M21K2c0111) and Dr Jason B. Harper for helpful discussions.

Notes and references

1. (a) F. Jaroschik, Chem.–Eur. J., 2018, 24, 14572; (b) D. O'Hagan, Chem. Soc. Rev., 2008, 37, 308.
2. (a) K. Chen, N. Berg, R. Gschwind and B. Konig, J. Am. Chem. Soc., 2017, 139, 18444; (b) H. Wang and N. T. Jui, J. Am. Chem. Soc., 2018, 140, 163; (c) D. B. Vogt, C. P. Seath, H. Wang and N. T. Jui, J. Am. Chem. Soc., 2019, 141, 13203; (d) C. Luo and J. S. Bandar, J. Am. Chem. Soc., 2019, 141, 14120; (e) Y.-C. Luo, F.-F. Tong, Y. Zhang, C.-Y. He and X. Zhang, J. Am. Chem. Soc., 2021, 143, 13971; (f) Y.-J. Yu, F.-L. Zhang, T.-Y. Peng, C.-L. Wang, J. Cheng, C. Chen, K. N. Houk and Y.-F. Wang, Science, 2021, 371, 1232; (g) J.-H. Ye, P. Bellotti, C. Heusel and F. Glorius, Angew. Chem., Int. Ed., 2021, 61, e202115456.
3. (a) G. Meißner, K. Kretschmar, T. Braun and E. Kemnitz, Angew. Chem., Int. Ed., 2017, 56, 16338; (b) M. Bergeron, T. Johnson and J.-F. Paquin, Angew. Chem., Int. Ed., 2011, 50, 11112; (c) L. Tang, Z.-Y. Liu, W. She and C. Feng, Chem. Sci., 2019, 10, 8701; (d) T. Xiao, L. Li and L. Zhou, J. Org. Chem., 2016, 81, 7908; (e) S. B. Lang, R. J. Wiles, C. B. Kelly and G. A. Molander, Angew. Chem., Int. Ed., 2017, 56, 15073; (f) T. Ichitsuka, T. Fujita and J. Ichikawa, ACS Catal., 2015, 5, 5947; (g) S.-S. Yan, D.-S. Wu, J.-H. Ye, L. Gong, X. Zeng, C.-K. Ran, Y.-Y. Gui, J. Li and D.-G. Yu, ACS Catal., 2019, 9, 6987; (h) X. Lu, X.-X. Wang, T.-J. Gong, J.-J. Pi, S.-J. He and Y. Fu, Chem. Sci., 2019, 10, 809; (i) Y. Lan, F. Yang and C. Wang, ACS Catal., 2018, 8, 9245; (j) Z. Lin, Y. Lan and C. Wang, ACS Catal., 2019, 9, 775; (k) Z. Lin, Y. Lan and C. Wang, Org. Lett., 2019, 21, 8316; (l) Z. Liu, X.-S. Tu, L.-T. Guo and X.-C. Wang, Chem. Sci., 2020, 11, 11548; (m) J.-P. Bégué, D. Bonnet-Delpon and M. H. Rock, Synlett, 1995, 659; (n) J. P. Bégué, D. Bonnet-Delpon and M. H. Rock, Tetrahedron Lett., 1995, 36, 5003; (o) J. Ichikawa, H. Fukui and Y. Ishibashi, J. Org. Chem., 2003, 68, 7800; (p) J. Yang, A. Mao, Z. Yue, W. Zhu, X. Luo, C. Zhu, Y. Xiao and J. Zhang, Chem. Commun., 2015, 51, 8326; (q) J. Ichikawa, J. Synth. Org. Chem., Jpn., 2010, 68, 1175; (r) K. Fuchibe, M. Takahashi and J. Ichikawa, Angew. Chem., Int. Ed., 2012, 51, 12059; (s) T. Fujita, M. Takazawa, K. Sugiyama, N. Suzuki and J. Ichikawa, Org. Lett., 2017, 19, 588; (t) K. Fuchibe, H. Hatta, K. Oh, R. Oki and J. Ichikawa, Angew. Chem., Int. Ed., 2017, 56, 5890; (u) M. Bergeron, D. Guyader and J.-F. Paquin, Org. Lett., 2012, 14, 5888.
4. (a) S. Yoshida, K. Shimomori, Y. Kim and T. Hosoya, Angew. Chem., Int. Ed., 2016, 55, 10406; (b) Y. Kim, K. Kanemoto, K. Shimomori, T. Hosoya and S. Yoshida, Chem.–Eur. J., 2020, 26, 6136; (c) R. Idogawa, Y. Kim, K. Shimomori, T. Hosoya and S. Yoshida, Org. Lett., 2020, 22, 9292.
5. (a) D. Mandal, R. Gupta and R. D. Young, J. Am. Chem. Soc., 2018, 140, 10682; (b) D. Mandal, R. Gupta, A. K. Jaiswal and R. D. Young, J. Am. Chem. Soc., 2020, 142, 2572; (c) R. Gupta, D. Mandal, A. K. Jaiswal and R. D. Young, Org. Lett., 2021, 23, 1915; (d) R. Gupta, A. K. Jaiswal, D. Mandal and R. D. Young, Synlett, 2020, 31, 933; (e) S. Khanapur, K. Lye, D. Mandal, X. J. Wee, E. G. Robins and R. D. Young, Angew. Chem., Int. Ed., 2021, 61, e202210917; (f) I. Mallov, A. J. Ruddy, H. Zhu, S. Grimme and D. W. Stephan, Chem.–Eur. J., 2017, 23, 17692; (g) P. Mehlmann, T. Witteler, L. F. B. Wilm and F. Dielmann, Nat. Chem., 2019, 11, 1139.
6. (a) V. J. Scott, R. Celenligil-Cetin and O. V. Ozerov, J. Am. Chem. Soc., 2005, 127, 2852; (b) J. Zhu, M. Perez, C. B. Caputo and D. W. Stephan, Angew. Chem., Int. Ed., 2016, 55, 1417; (c) H.-J. Ai, X. Ma, Q. Song and X.-F. Wu, Sci. China: Chem., 2021, 64, 1630.
7. (a) J. J. Cabrera-Trujillo and I. Fernández, Chem.–Eur. J., 2021, 27, 3823; (b) M. Ghara, S. Giri, P. Das and P. K. Chattaraj, J. Chem. Sci., 2022, 134, 14.
8. H. M. Yau, A. K. Croft and J. B. Harper, Chem. Commun., 2012, 48, 8937.
9. H. Tinnermann, S. Sung, D. Csókás, Z. H. Toh, C. Fraser and R. D. Young, J. Am. Chem. Soc., 2021, 143, 10700.
10. The ground state for FLP-III is −0.9 kcal. Kinetic barriers should be calculated from this point, however, to compare with FLP-I and FLP-II, we have taken the FLP state (i.e. fully dissociated) as the ground state.
11. F. Schaper and H.-H. Brintzinger, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2002, 58, o77.
12. J. S. Sapsford, D. Csókás, R. C. Turnell-Ritson, L. A. Parkin, A. D. Crawford, I. Pápai and A. E. Ashley, ACS Catal., 2021, 11, 9143.
13. (a) A. K. Jaiswal, P. K. Kishore and R. D. Young, Chem.–Eur. J., 2019, 25, 6290; (b) R. Gupta and R. D. Young, Synthesis, 2022, 54, 1671.
14. If the barrier for [NTf₂]⁻ substitution was much less than C–F activation then the rate of formation of 2c-NTf₂ would be less than its consumption at all observable concentrations. If the barrier for [NTf₂]⁻ substitution was much greater than C–F activation then 2c would be consumed before formation of [2c-LB][NTf₂] was observed. If the barrier for [NTf₂]⁻ substitution was similar to (or slightly less than) C–F activation, then the rate of formation of 2c-NTf₂ would exceed its consumption assuming that the consumption rate of 2c-NTf₂ is dependent on [2c-NTf₂] and that [2c-NTf₂] ≪ [2c].
15. Mayr nucleophilic parameters: pyridine: N = 12.90, s_N = 0.67; P(o-Tol)₃: N = 8.56, s_N = 0.70; THT: N = 13.10, s_N = 0.72; Et₃SiH: N = 3.58, s_N = 0.70; toluene: N = −4.36, s_N = 1.77. See: (a) F. Brotzel, B. Kempf, T. Singer, H. Zipse and H. Mayr, Chem.–Eur. J., 2006, 13, 336; (b) J. Ammer, C. Nolte and H. Mayr, J. Am. Chem. Soc., 2012, 134, 13902; (c) H. Mayr and A. R. Ofial, J. Phys. Org. Chem., 2008, 21, 584.
16. G. Kumar, S. Roy and I. Chatterjee, Org. Biomol. Chem., 2021, 19, 1230.
17. T. C. Johnstone, G. N. J. H. Wee and D. W. Stephan, Angew. Chem., Int. Ed., 2018, 57, 5881.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc05632a

‡ These authors contributed equally.

---