Open Access Article
Open Access ArticleCombining structural and coevolution information to unveil allosteric sites†
Giuseppina
La Sala‡
 *a,
Christopher
Pfleger‡
b,
Helena
Käck
c,
Lisa
Wissler
c,
Philip
Nevin
d,
Kerstin
Böhm
d,
Jon Paul
Janet
a,
Marianne
Schimpl
e,
Christopher J.
Stubbs
e,
Marco
De Vivo
f,
Christian
Tyrchan
g,
Anders
Hogner
a,
Holger
Gohlke
*a,
Christopher
Pfleger‡
b,
Helena
Käck
c,
Lisa
Wissler
c,
Philip
Nevin
d,
Kerstin
Böhm
d,
Jon Paul
Janet
a,
Marianne
Schimpl
e,
Christopher J.
Stubbs
e,
Marco
De Vivo
f,
Christian
Tyrchan
g,
Anders
Hogner
a,
Holger
Gohlke
 *bh and
Andrey I.
Frolov
*bh and
Andrey I.
Frolov
 *a
*a
aMedicinal Chemistry, Research and Early Development, Cardiovascular, Renal and Metabolism (CVRM), BioPharmaceuticals R&D, AstraZeneca, Gothenburg, Sweden. E-mail: giuseppina.lasala@astrazeneca.com; andrey.frolov@astrazeneca.com
bMathematisch-Naturwissenschaftliche Fakultät, Institut für Pharmazeutische und Medizinische Chemie, Heinrich-Heine-Universität Düsseldorf, 40225 Düsseldorf, Germany. E-mail: gohlke@uni-duesseldorf.de
cMechanistic and Structural Biology, Discovery Sciences, BioPharmaceuticals R&D, AstraZeneca, Gothenburg, Sweden
dDiscovery Biology, Discovery Sciences, BioPharmaceuticals R&D, AstraZeneca, Gothenburg, Sweden
eMechanistic and Structural Biology, Discovery Sciences, BioPharmaceuticals R&D, AstraZeneca, Cambridge, UK
fLaboratory of Molecular Modeling and Drug Design, Istituto Italiano di Tecnologia, Via Morego 30, 16163, Genoa, Italy
gMedicinal Chemistry, Research and Early Development, Respiratory & Immunology (R&I), BioPharmaceuticals R&D, AstraZeneca, Gothenburg, Sweden
hJohn von Neumann Institute for Computing (NIC), Jülich Supercomputing Centre (JSC), Institute of Biological Information Processing (IBI-7: Structural Biochemistry), Institute of Bio- and Geosciences (IBG-4: Bioinformatics), Forschungszentrum Jülich GmbH, 52425, Jülich, Germany
First published on 8th June 2023
Abstract
Understanding allosteric regulation in biomolecules is of great interest to pharmaceutical research and computational methods emerged during the last decades to characterize allosteric coupling. However, the prediction of allosteric sites in a protein structure remains a challenging task. Here, we integrate local binding site information, coevolutionary information, and information on dynamic allostery into a structure-based three-parameter model to identify potentially hidden allosteric sites in ensembles of protein structures with orthosteric ligands. When tested on five allosteric proteins (LFA-1, p38-α, GR, MAT2A, and BCKDK), the model successfully ranked all known allosteric pockets in the top three positions. Finally, we identified a novel druggable site in MAT2A confirmed by X-ray crystallography and SPR and a hitherto unknown druggable allosteric site in BCKDK validated by biochemical and X-ray crystallography analyses. Our model can be applied in drug discovery to identify allosteric pockets.
Introduction
Complex biomolecular networks regulate the cellular processes in a living organism, which are often regulated by allosteric mechanisms.1 Allosteric modulators display several advantages over orthosteric ligands that render them a useful modality for drug discovery.2 Hence, identifying new druggable allosteric sites is of utmost importance in pharmaceutical research,3 and many approaches have been developed to study allosteric regulation in biomolecules.4–6 However, the complex nature of allosteric regulation challenges the development of generally applicable methods. Allosteric regulation can be induced by structural processes, ranging from global or local conformational changes to only changes in protein dynamics.7,8 Furthermore, identifying allosteric sites may be hampered if they are occluded in static experimental protein structures.9,10Experimental methods provide excellent tools to detect allosteric sites and investigate allosteric mechanisms in biomolecules,11–17 however, they are often time-consuming.18 Of computational methods, molecular dynamics (MD) simulations allow for insights into allosteric regulation by studying structural signals from the sampling of conformational states,19–21 but may require exhaustive sampling to obtain significant signal-to-noise ratios.22 Another application of MD is to identify hidden allosteric pockets,23–25 often using cosolvent-based simulations to facilitate pocket opening.26 Graph-based network approaches help to identify allosteric signaling pathways between remote sites and the orthosteric site.27 Within these networks, the residues/atoms of the protein are represented as nodes connected by edges that are defined by physical contact-based28–32 or interaction energy-based33–35 criteria. Computational decoupling of a bound ligand from its binding site perturbs the network and reveals how this perturbation percolates through the network to the distant protein sites.30 To overcome issues of robustness, the application of network approaches to conformational ensembles has been introduced.36–39 Sequence-based approaches, such as statistical coupling analysis (SCA), allow for predicting allosteric sites in proteins from multiple sequence alignments (MSA).40 While evolutionarily conserved amino acids are essential for structural integrity and function,41 amino acid positions with evolutionarily correlated mutations, i.e., coevolving amino acids, are essential for preserving allosteric mechanisms.42 Mutually coevolving amino acids can build contiguous structural networks, termed “sectors”. These “sectors” might include residues from distant sites in proteins and are used to study allosteric mechanisms.42–45 However, results from sequence-based approaches strongly depend on the availability of homologous sequences. Finally, the wealth of structural information and the increase of computational power paved the way for the development of robust and fast machine learning (ML) predictive models with many fitted parameters.46,47 Although fast and efficient, such models may suffer when allosteric sites are hidden in the input structure. To alleviate this issue, some ML models incorporate dynamic effects through Normal Mode Analysis (NMA).48,49
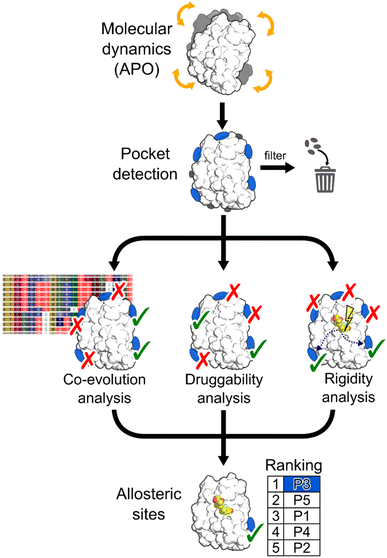
In this work, we aimed at integrating local binding site information, coevolutionary information, and information on dynamic allostery30,50 into a generally applicable structure-based three-parameter model to identify potentially hidden allosteric sites in structural ensembles of holo proteins for which the orthosteric ligand is known (Fig. 1). We demonstrate that our three-parameter model overcomes the shortcomings of each method when they are executed individually. With it, we identify a novel druggable site in MAT2A confirmed by X-ray crystallography and SPR and a hitherto unknown allosteric site in BCKDK validated by biochemical and X-ray crystallography analysis. Furthermore, we scrutinize the scope of our method on five proteins with known allosteric mechanisms and identify experimentally validated allosteric pockets as ranked in the top three positions for each protein. Thus, our model should be valuable for pocket prioritization in drug discovery campaigns.
Results and discussion
To assess our three-parameter model, we selected a dataset of five soluble proteins with already known allosteric sites, including the Glucocorticoid Receptor (GR), the Mitogen-Activated Protein Kinase 14 (MAPK14 or p38-α), the Branched Chain Ketoacid Dehydrogenase Kinase (BCKDK), Lymphocyte Function-associated Antigen 1 (LFA-1), and Methionine Adenosyl Transferase 2A (MAT2A). We chose these proteins because (i) studies probing allosteric regulation mechanisms of these proteins are available and (ii) they belong to different protein families, ensuring structural diversity in our dataset.Identifying hidden pockets in proteins
We applied the Fpocket detection algorithm to the X-ray structures that served as input for the analyses (see ESI, Fig. S1†). Over all systems, between 7 and 29 pockets were identified (Table S1†). In two out of five cases, the allosteric site is already present in the apo state, and, compared with results from the detected pockets in the corresponding holo states, shows almost identical volumes (Table S2†).To facilitate the identification of allosteric pockets hidden in static X-ray structures, we generated structural ensembles from conventional MD simulations starting from the apo state of each system. The MDpocket algorithm was applied to ensembles extracted from MD trajectories of 500 ns length (see ESI†). All pockets have an opening frequency >20%, and the number of identified pockets is almost doubled for all systems compared to the X-ray structure analysis (Table S1†). After filtering (see ESI†), nine, six, and nine pockets remained for GR, LFA-1, and p38-α, respectively (Fig. S2 and Table S2†). Remarkably, for all three systems, the allosteric pockets became detectable by MDpocket, which was not possible from the X-ray structure analysis (Fig. S1†). Our results demonstrate that despite the conformational rearrangement involved in the opening of the allosteric pockets in p38-α and LFA-1 (local RMSD > 2 Å),51,52 the MD simulations sampled the respective movements (Fig. S3†). However, compared to the known allosteric modulator-bound X-ray structures, the pockets along the MD simulations are only partially open, which is reflected by the smaller pocket volumes (Table S2†). For p38-α, pockets located in the D-groove and noncanonical sites already present in the X-ray structure (Fig. S1†) remained stable during the MD simulations (Fig. S2†). In the case of GR, we observed the opening of a small pocket in the co-regulator allosteric site (AF-2) during the MD simulations, which was not visible in the apo X-ray structure. Finally, allosteric pockets in BCKDK and MAT2A were already detected in the apo X-ray structures (Fig. S1†) and remained open during the MD trajectories (Fig. S2†). In contrast to LFA-1 and p38-α, these pockets have larger volumes during the MD simulations, being 457 ± 170 Å3 and 2285 ± 383 Å3 for BCKDK and MAT2A, respectively.
Overall, conventional MD simulations retained the allosteric pockets already present in the X-ray structures in BCKDK and MAT2A and led to the identification of allosteric pockets in p38-α, LFA-1, and GR that were undetectable in the X-ray structures.
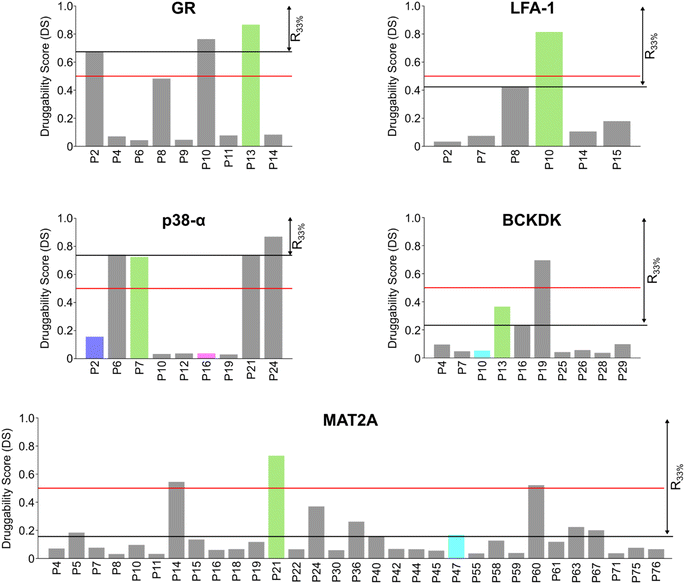
Scoring pockets with druggability score
In most cases in drug discovery it is important to focus on those pockets with a high likelihood of binding to a bioavailable small molecule. This can narrow the search for allosteric pockets in the ensemble of pockets identified in our MD simulations. We estimated the druggability using the druggability score (DS)53 (see ESI†). The DS ranges from 0 to 1, with pockets being likely druggable if the DS is between 0.5 and 1.The experimentally validated allosteric pockets in GR and MAT2A identified during the MD simulations have DS values >0.5 and, thus, are correctly considered druggable (Fig. 2). Though only partially open, the algorithm recognizes the allosteric pockets in LFA 1 and p38-α also as potentially druggable (DS > 0.5). The allosteric pockets are ranked according to DS within the first third (R33%) for LFA-1, GR, and MAT2A (Fig. 2) but only within the second third for p38-α. The two pockets of p38-α with the highest DS (P24 and P6) have been cocrystallized with small fragments,13 but evidence for their role in kinase function has not been reported. For BCKDK, the DS indicates that the known allosteric pocket is not druggable (Fig. 2), although small molecules can bind to this site.54 By contrast, in p38-α, both detected pockets in the D-groove and noncanonical site are not predicted as druggable, though both sites are targeted by proteins and small fragments.13
Overall, the experimentally validated allosteric pockets in GR, LFA-1, and MAT2A are correctly predicted as druggable and are in the first third of the ranking. By contrast, for p38-α and BCKDK, the allosteric pockets are not predicted as druggable or not ranked in the first third. These results indicate that, while valuable in most cases, the druggability assessment may lead to falsely negatively ranked allosteric pockets.
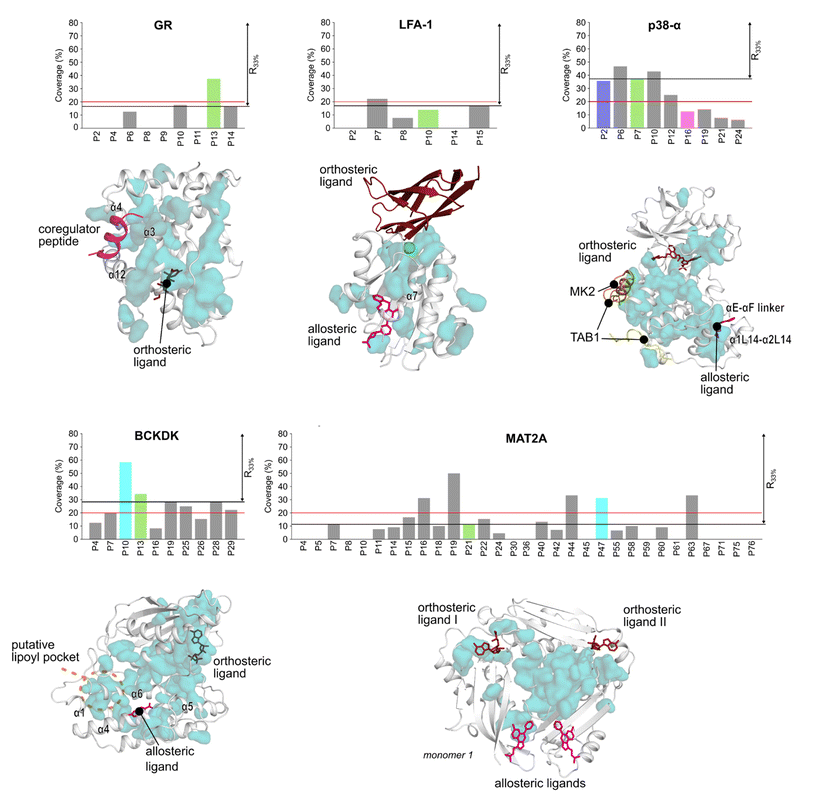
Detecting functional pockets via coevolution analysis
We used the Statistical Coupling Analysis (SCA) method to identify coevolving amino acids involved in functional pockets, such as allosteric pockets and other regulatory sites (see ESI†). Higher values of the coverage score (CS), the percentage of coevolving amino acids within pockets identified during the MD simulations, indicate that the pocket is chiefly composed of coevolving amino acids and, thus, likely important for the protein function.Over all systems, clusters of coevolving amino acids are found in the proteins' orthosteric pockets, which have the highest CS values (20–50%) compared to other pockets (Fig. S4 and Table S3†). We ranked the pockets found in our MD simulations according to the CS and focused on those occupying the first third of the ranking (R33%). For GR, the α-helices 3 and 4 (Fig. 3) have several coevolving amino acids, which might be relevant for propagating allosteric signals, as shown by NMR experiments55 and MD simulations.56 The known allosteric pocket shows a CS value of 37.5% (Fig. 3 and Table S3†). The allosteric pockets of GR, BCKDK, and p38-α have CS > 20% and are ranked within R33% (Fig. 3). In MAT2A, the known allosteric pocket has a low CS value of 11.3%, but still is ranked within the best R33% of all pockets (Fig. 3). Finally, for LFA-1, the known allosteric pocket is not within the R33% and has a CS value of 13.6%, thus, this pocket is falsely classified by the SCA method (Fig. 3). Although the coevolving amino acids in the β strand region of LFA-1 (Fig. 3) suggest that the allosteric signal is conveyed through the core of the protein, in agreement with previous computational studies,30 the allosteric pocket is not directly populated by coevolving amino acids.
We also identified clusters of coevolving amino acids between the orthosteric and the allosteric pockets that connect distant sites, which has also been reported for other systems.43 In p38-α, the majority of coevolving amino acids are in the C-lobe, in the αC helix, and nearby the ATP pocket (Fig. 3). These residues connect the orthosteric site with the MAPK insert, including the known allosteric pocket and two pockets in the D-groove and the noncanonical site, in agreement with reported findings.57 The pockets in the D-groove and the noncanonical site have CS values of 12.5% and 35.7%, respectively, and have been targeted by substrates, modulators,58 and small molecules.13 The many coevolving amino acids found in the C-lobe (Fig. 3) suggest that multiple pathways are intertwined throughout the C-lobe to convey the signal between the different functional sites and the orthosteric site in p38-α. In BCKDK, the orthosteric ATP-binding pocket is connected via a network of coevolving amino acids with both the allosteric pocket and the putative lipoyl pocket located in the N-terminal domain (Fig. 3). The connection between these three sites is proposed to be key for allosteric regulation in BCKDK.54 In MAT2A, coevolving amino acids are located in the core of the protein at the dimerization interface, and consequently, the pockets identified in MD simulations have an overall low CS: only 5 out of 31 pockets have a CS > 20%. The central position of coevolving amino acids suggests that they can preserve the homodimers' structural stability and mediate the cross-talk between the orthosteric and the allosteric sites.
Overall, these analyses show that the CS ranks the known allosteric pockets of GR, BCKDK, p38-α, and MAT2A in R33%. Hence, SCA is valuable for identifying allosteric pockets and investigating the allosteric signal transmission. SCA failed, however, to identify the allosteric pocket in LFA-1. This is likely because most coevolving amino acids are located in the core of the protein (Fig. 3).
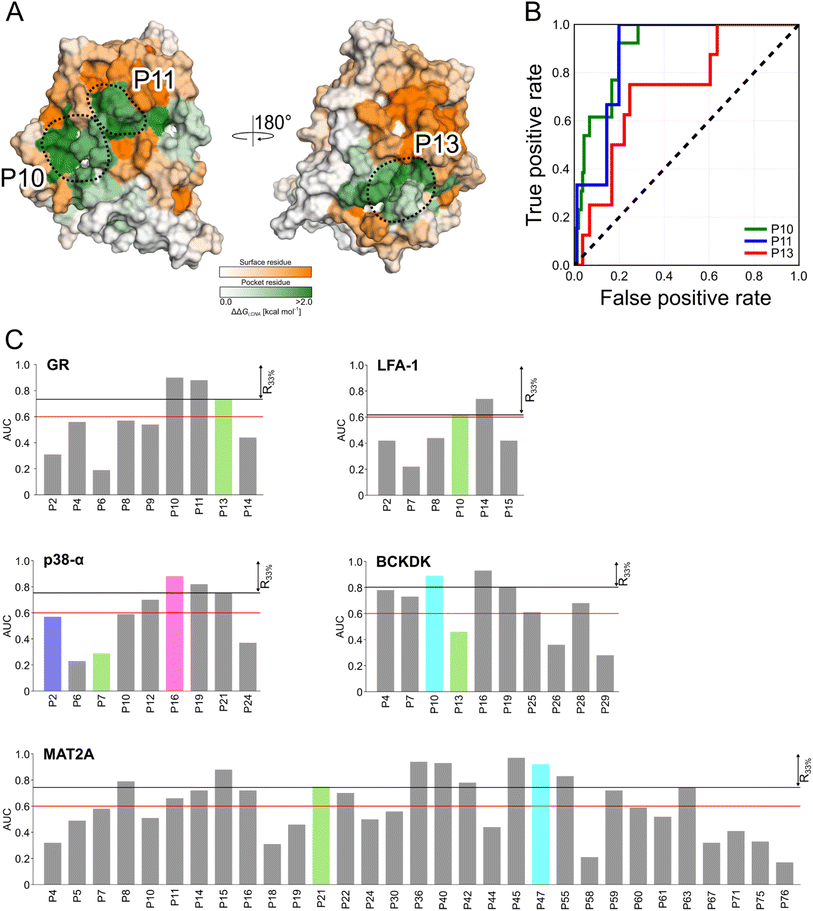
Detecting functional pockets from rigidity analysis
We probed how the binding of orthosteric ligands affects the identified pockets using an ensemble- and rigidity theory-based free-energy perturbation approach.30 Allosteric effects due to ligand binding are described with the free-energy measure ΔGi,CNA (see ESI eqn (S4)†).59–61 The per-residue ΔGi,CNA values from individual trajectories correlate well for each system, indicating robust and consistent results were obtained across the independent MD trajectories (Table S4†). We performed receiver operating characteristic (ROC) analyses to evaluate whether the pockets identified in our MD simulations comprise more residues with larger ΔGi,CNA values than other surface regions (Fig. S5 and Table S5†). The area under the curve (AUC) serves as a measure for the enrichment of larger ΔGi,CNA values within the pockets (Fig. 4B and S5†). Because the entire pocket does not need to be involved in the allosteric response, we already consider an AUC > 0.6 as an acceptable threshold.For GR, three pockets show enrichments with AUC > 0.6 (Fig. 4A and C). The 3rd-ranked pocket matches the co-regulator pocket (AF-2), which forms a dynamic allosteric communication pathway with the orthosteric site ∼15 Å away.55,56 In LFA-1, only two pockets have AUC > 0.6, with the experimentally validated allosteric pocket (AUC = 0.62) ranked at the 2nd position and within R33% (Fig. 4C). For MAT2A, we identified 15 pockets with AUC > 0.6 (Fig. 4C). The known allosteric pocket is ranked at the 9th position and within the R33% threshold and has AUC = 0.75. For p38-α, we identified four pockets with AUC > 0.6 (Fig. 4C). The top-ranked pocket (AUC = 0.93) corresponds to the D-groove for protein substrate (MK1) or modulator (TAB1) binding.62 However, we observed no enrichment of residues with larger ΔGi,CNA values (AUC = 0.29) for the allosteric site in the MAPK insert. For BCKDK, we identified ten pockets with seven pockets showing AUC > 0.6 (Fig. 4C). Good enrichment (AUC > 0.7) is found for the four pockets located at the intersection of the two kinase lobes and close to the putative lipoyl pocket.63 We also observe moderate per-residue ΔGi,CNA values for the α6 helix in the N-terminal domain (Fig. S6†), which is involved in the experimentally validated allosteric pocket in BCKDK's N-terminal domain. However, the identified pocket that matches the allosteric site shows no enrichment (AUC = 0.46).
Our ensemble-based perturbation approach shows that pocket-lining residues have larger ΔGi,CNA values than other surface residues in each system. For GR, LFA-1, and MAT2A, the allosteric pockets are ranked within the R33% threshold and have AUC > 0.6. For BCKDK and p38-α, seven and four pockets are ranked at high positions, but the results from rigidity analysis show no or only weak effects for the known allosteric sites. Our perturbation approach focuses on the entropic nature of allostery because it excludes conformational changes upon perturbation of the system.64 Hence, this lack of consideration of conformational rearrangements might underlie the missing detection of allosteric signaling between orthosteric and allosteric sites for both systems. In turn, the strength of this approach is to track how orthosteric site ligands influence biomolecular stability and how the influence percolates through the structure, thus, providing mechanistic insights into the allosteric signaling.
Integrating druggability, coevolution, and rigidity analysis into a ranking model
The above results showed that none of the three approaches outperformed the others in ranking the known allosteric pockets in the top positions. Only in the case of GR and MAT2A all three methods correctly place the known allosteric pocket within the R33% of all identified pockets. For all other systems, only one or two of the used approaches rank the known allosteric pockets within the R33% (Table S6†). Thus, we linearly combined the results from the three approaches (see ESI, eqn (S6)†). The resulting three-parameter model correctly places the known allosteric pockets for each system in the R33% and ranks them at the 1st position in the cases of GR, MAT2A, and LFA-1, 2nd position for p38-α, and 3rd position for BCKDK (Fig. 5). P6 and P19 are at the top of the ranking for p38-α and BCKDK, respectively. While fragments binding to P6 have been identified, their role in modulating p38-α function has not been investigated.13 P19 is close to BCKDK's lipoyl site. Notably, a recently published work reports putative allosteric inhibitors binding to this pocket, supporting our predictions.65 Other known functionally relevant sites in p38-α, such as the noncanonical site and the D-groove, are not placed in the R33%, being ranked at the 6th and 8th position, respectively (Fig. 5). This result is mainly due to the low druggability estimates for both sites. Unlike the aforementioned allosteric pockets, these sites are relatively shallow protein–protein interaction sites, making them considerably less druggable than traditional active site targets.66 Thus, our three-parameter model performs better for allosteric pockets than regulatory sites that involve protein–protein interactions. Removing the druggability contribution from our model, the noncanonical site and the D-groove are ranked in the 2nd and 4th position (Table S6†), respectively. This finding suggests that combining the rankings from SCA and rigidity analysis alone provides a good indicator for identifying potential new surface regulatory sites but might not be sufficient to find better druggable allosteric pockets.We also tested the two-method combinations (Table S6†). Combining SCA and rigidity analysis, as well as rigidity analysis and DS, ranked three and four pockets, respectively, out of seven in R33%, and thus, indicated a worse performance than the three-parameter model. Like the three-parameter model, the SCA and DS model combination places five pockets out of seven in the R33%. However, the allosteric pockets are ranked lower than in the three-parameter model (see average rank in Table S6†), evidencing a better performance when all three approaches are combined.
Prediction of a novel binding pocket in MAT2A
We performed an experimental validation to assess whether additional, high ranking MAT2A pockets according to our three-parameter model have a functional role. First, we conducted a fragment-based screening campaign coupled with X-ray crystallography intending to identify new ligands binding to those sites. We found that compound 1 binds to P47 (or P16 in the second monomer, Fig. S2†), corresponding to the second pocket in our ranking (Fig. 5). P47 is located on the outer surface of MAT2A and compound 1 binds via an H-bond with Glu148 and hydrophobic interactions (Fig. 6A). Importantly, P47 was not predicted as druggable, as the DS is lower than 0.5 (Fig. 2). In contrast, both SCA and rigidity analysis yielded high scores (CS = 31%, AUC = 0.92 Fig. 3 and 4). The agreement between the coevolution and rigidity analyses led us to hypothesize that P47 is important for the modulation of the protein's function. Due to the low binding affinity of compound 1 measured via SPR (Kd = 550 ± 75 μM, Fig. S7†), we could not successfully functionally characterize this fragment. Instead, we performed a rigidity analysis to investigate if MAT2A can be allosterically regulated by compound 1, similar to other studies.30,61 In brief, through this methodology, we can detect the presence of an allosteric signal triggered by compound 1 and identify the network of residues affected by the removal of the fragment. Fig. S8† shows that the removal of compound 1 led to overall weak stability changes, mainly centered to the core of the monomer. The weak changes are likely associated with the poor binding affinity of compound 1. Nevertheless, the stability changes percolate to both the orthosteric and allosteric pockets, indicating an allosteric cross-talk between P47 and the known functional sites (Fig. S8†). Although further investigations are needed to confirm the functional role of compound 1, our preliminary data indicate that targeting P47 might be a promising strategy to regulate the function of MAT2A. | ||
| Fig. 6 Novel pockets in MAT2A and in BCKDK. (A) X-ray structure of MAT2A in complex with compound 1 (orange sticks) bound to P47 (chain A) and P16 (chain B). S-Adenosylmethionine (SAM, yellow sticks) is bound to the orthosteric pocket of the two chains (PDB code: 8OOG). The inset highlights the binding mode of compound 1. H-bonds are represented as black dashes. (B) X-ray structure of the human BCKDK in complex with compound 5 (orange sticks) (PDB code: 7ZPE), lacking the loop region due to missing electron density. The inset highlights the binding mode of the compound. H-bonds are represented as black dashes. (C) Representative frame from MD simulations of BCKDK with the predicted pocket (P10, light green surface) and the long loop region connecting the two lobes (green cartoon). (D) The X-ray structure containing compound 5 (orange sticks) is superimposed onto the representative frame from MD simulations showing the presence of a new subpocket (P0MD) when the loop region is removed. (E) Concentration–response curves for compound 5 measured in an enzymatic BCKDK LC-MS assay at different concentrations of ATP and peptide substrates: low ATP, 5 μM; high ATP, 500 μM; low peptide, 20 μM; high peptide, 400 μM. Data are from three independent replicates. | ||
Prediction and experimental validation of a novel allosteric pocket in BCKDK
Our three-parameter model correctly identified the experimentally validated allosteric site at the N-terminal lobe of BCKDK (i.e., P13) at rank 3 (Fig. 5 and Table S6†). Interestingly, a spatially close pocket (P10 Fig. S2†) was ranked 2nd (Fig. 5). P10 is located between the ATP and the known allosteric pocket P13 and it is part of the long loop region connecting the two lobes (see green carton in Fig. 6C). P10 was predicted as not druggable with DS < 0.5 (Fig. 2), but both SCA and rigidity analysis yielded high scores (CS = 58%, AUC = 0.89) (Fig. 3 and 4). The consensus of SCA and rigidity analysis led us to hypothesize that the region comprising P10 is a critical hotspot for kinase function, which, to our knowledge, has not been reported before.In order to validate our predictions a small fragment library was screened against BCKDK using X-ray crystallography. A new X-ray structure of human BCKDK kinase was generated in complex with compound 5 (Table S7†), a fragment recently reported by Bertrand et al. as an inhibitor of mitochondrial branched-chain aminotransferase (BCATm, pIC50 = 5.7).67 Electron density corresponding to compound 5 was detected in a cleft between the α-helices 7 and 8, in proximity to P10. The triazolopyrimidinone scaffold of compound 5 interacts with Lys 248 of α-helix 8 via an H-bond, while the p-chloro benzyl moiety sits in a small pocket (referred to as P0X-ray, Fig. S9B†), interacting with Lys 215 of α-helix 7 through a cation–π interaction (Fig. 6B). Like in the publicly available rat BCKDK X-ray structures, the long loop in the proximity of the nucleotide pocket connecting the two lobes cannot be detected in the electron density, suggesting that it is highly flexible. No binding was observed within the ATP pocket.
While P10 is adjacent to P0X-ray and they share a few residues (Fig. S10†), P0X-ray could not be fully detected in our MD simulations because Met333 occupies the cleft between α-helices 7 and 8 (Fig. 6C and S9C†). Similarly, P0X-ray was not detected in the X-ray structure used as the starting point of our simulations because Met333 sits in the cavity (loop modeled using as template the PDB code 1GKZ, Fig. S9A†). Nevertheless, such a pocket can be identified in our MD simulations after manually removing the long loop from our trajectories (referred to as P0MDFig. 6D and S9D†). Notably, the three-parameter model ranked the new P0MD in the R33% (Table S6†), further suggesting that this region of the kinase is important for the protein function. To experimentally validate this prediction, we performed an additional in vitro study. We used an LC-MS assay to measure BCKDK-catalyzed phosphorylation of an E1-derived peptide substrate in the presence of various amounts of compound 5 and at two different ATP concentrations (see ESI†). At both high and low ATP concentrations, the pIC50 was similar (5.07 ± 0.10 and 4.90 ± 0.23 for high and low [ATP], respectively, Fig. 6E and Table S8†), indicating that compound 5 inhibits the phosphorylation of the E1-derived peptide with a non-competitive mechanism with respect to ATP binding, in agreement with X-ray crystallography. To exclude the possibility that compound 5 inhibits the kinase function by competing with the substrate peptide, we performed a second LC-MS experiment, this time varying the substrate peptide concentration (see ESI†). The pIC50 of compound 5 is unaffected by the concentration of the peptide (pIC50 = 5.07 ± 0.10 and 5.01 ± 0.17 for low and high [peptide], respectively, Fig. 6E and Table S8†), indicating that the ligand is not competing with the substrate. Taken together, these in vitro experiments demonstrate that compound 5 binds to a yet unreported pocket (P0X-ray or P0MD) that partially overlaps with the predicted pocket (P10) identified in the full-length model of BCKDK, and confirm that compound 5 acts as an allosteric inhibitor of the kinase function in agreement with the predictions of the three-parameter model.
We hypothesize that compound 5 alters the conformation of the loop in the nucleotide binding pocket, affecting either the substrate binding or the catalytic function. Without compound 5, the loop can intercalate between α-helices 7 and 8 via Met333 (Fig. S9†). This might be the optimal loop configuration for the correct functioning of the protein. Compound 5 displaces Met333, forcing the loop to adopt another conformation that might not be competent with the protein function. A recent work also reports the importance of the loop's spatial orientation for the modulation of BCKDK's function.65 Our pocket analyses also suggest that compound 5 can be chemically modified to better fit the predicted pocket and directly interact with the loop region.
These results show that the pocket detection is affected by the choice of the initial structural coordinates and the sampling method.68 We chose PDB code 1GKZ as starting point for modeling BCKDK because it contained the longest resolved loop among available structures. In our MD simulations, Met333 remained anchored in the cleft, hampering the initial detection of the crystallographic pocket occupied by compound 5. To facilitate pocket opening, one could adopt enhanced sampling simulations26,69 or use different X-rays as starting point. However, it is encouraging to see that the three-parameter model is sensitive enough to detect the region of the protein around P0X-ray as functionally relevant. This indicates that the three-parameter model can provide useful insights even in the cases of partial opening of the pockets during the MD simulations.
Conclusion
While great progress has been made in prediction of orthosteric pockets, it remains challenging to identify and characterize other functional sites, such as allosteric pockets. In this work, we developed a three-parameter model to highlight new potential allosteric sites from a set of identified pockets and used it to predict a novel allosteric pocket in BCKDK.Firstly, we first performed 500 ns long conventional MD simulations to aid the opening of hidden pockets and analyzed the trajectories to detect pockets exposed over time. The MD simulations aided the early detection of allosteric pockets that were occluded in the unbound protein X-ray structure, further demonstrating that simulations are a valuable tool for identifying hidden pockets.68 Other schemes, such as enhanced sampling simulations in combination with co-solvents, could replace conventional MD simulations when the opening of a hidden pocket is governed by a larger protein conformational rearrangement.70 Secondly, we evaluated which pockets are more likely to be allosteric using a ranking model that combines druggability, coevolution and rigidity analysis information. The two latter parameters have been used separately before to scrutinize allosteric signaling.30,42 We tested the three-parameter model on five allosterically regulated proteins belonging to different families (LFA-1, p38-α, GR, MAT2A, and BCKDK). Remarkably, our three-parameter model successfully ranked all experimentally validated allosteric pockets for all systems in the top three positions. Combining only two of the parameters led to inferior performance.
Finally, we validated our three-parameter model on MAT2A and BCKDK, performing in vitro experiments to characterize the role of unreported pockets that were predicted as allosteric by our approach. In MAT2A, X-ray crystallography showed that compound 1 binds a novel pocket located on the outer surface of the protein. The potential functional role of this pocket was highlighted by the rigidity analysis. In BCKDK, X-ray crystallography showed that a small molecule BCAT inhibitor (compound 5) binds in a cavity that partially overlaps with the predicted pocket from our approach. This new cavity is only visible in the MD simulations when the loop comprising Met333 was not modeled, and it was also predicted as allosteric by our three-parameter model. LC-MS biochemical assays showed that compound 5 allosterically inhibits BCKDK, corroborating our predictions. These results suggest that our model can be prospectively applied in the early stages of drug discovery projects to identify novel allosteric pockets.
Data availability
All the data are available upon reasonable request.Author contributions
GLS and CP contributed equally.Conflicts of interest
The authors declare the following competing financial interest(s): GLS, HK, LW, PN, KB, JPJ, MS, CJS, CT, AH and AIF are employees of AstraZeneca and own stock options.Acknowledgements
The authors acknowledge Jenny Gunnarsson for her help with protein expression and Elizabeth Underwood for reagent generation. GLS is a fellow of the AstraZeneca R&D postdoc program. GLS and MDV acknowledge ISCRA C for awarding access to Marconi computational facilities based in Italy at Cineca (Project IcC72_alloMD). Parts of the study were supported by the German Federal Ministry of Education and Research (BMBF) through funding number 031B1342A “LipoBiocat” to HG. We are grateful for computational support and infrastructure provided by the “Zentrum für Informations- und Medientechnologie” (ZIM) at the Heinrich Heine University Düsseldorf and the computing time provided by the John von Neumann Institute for Computing (NIC) to HG on the supercomputer JUWELS at Jülich Supercomputing Centre (JSC) (user ID: HKF7, VSK33, LIPASES).References
- R. Nussinov, C.-J. Tsai and B. Ma, Annu. Rev. Biophys., 2013, 42, 169–189 CrossRef CAS PubMed.
- A. Chatzigoulas and Z. Cournia, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1529 CAS.
- S. Lu, M. Ji, D. Ni and J. Zhang, Drug Discovery Today, 2018, 23, 359–365 CrossRef CAS PubMed.
- J. R. Wagner, C. T. Lee, J. D. Durrant, R. D. Malmstrom, V. A. Feher and R. E. Amaro, Chem. Rev., 2016, 116, 6370–6390 CrossRef CAS PubMed.
- G. M. Verkhivker, S. Agajanian, G. Hu and P. Tao, Front. Mol. Biosci., 2020, 7, 136 CrossRef CAS PubMed.
- O. Schueler-Furman and S. J. Wodak, Curr. Opin. Struct. Biol., 2016, 41, 159–171 CrossRef CAS PubMed.
- R. Nussinov, Chem. Rev., 2016, 116, 6263–6266 CrossRef PubMed.
- C.-J. Tsai and R. Nussinov, PLoS Comput. Biol., 2014, 10, e1003394 CrossRef PubMed.
- R. Nussinov and C. J. Tsai, Curr. Opin. Struct. Biol., 2015, 30, 17–24 CrossRef CAS PubMed.
- A. Cooper and D. T. F. Dryden, Eur. Biophys. J., 1984, 11, 103–109 CrossRef CAS PubMed.
- S. Lu, X. He, D. Ni and J. Zhang, J. Med. Chem., 2019, 62, 6405–6421 CrossRef CAS PubMed.
- T. Mühlethaler, D. Gioia, A. E. Prota, M. E. Sharpe, A. Cavalli and M. O. Steinmetz, Angew. Chem., Int. Ed., 2021, 60, 13331–13342 CrossRef PubMed.
- C. Nichols, J. Ng, A. Keshu, G. Kelly, M. R. Conte, M. S. Marber, F. Fraternali and G. F. De Nicola, J. Med. Chem., 2020, 63, 7559–7568 CrossRef CAS PubMed.
- D. A. Erlanson, B. J. Davis and W. Jahnke, Cell Chem. Biol., 2019, 26, 9–15 CrossRef CAS PubMed.
- J. Schiebel, N. Radeva, S. G. Krimmer, X. Wang, M. Stieler, F. R. Ehrmann, K. Fu, A. Metz, F. U. Huschmann, M. S. Weiss, U. Mueller, A. Heine and G. Klebe, ACS Chem. Biol., 2016, 11, 1693–1701 CrossRef CAS PubMed.
- S. Grutsch, S. Brüschweiler and M. Tollinger, PLoS Comput. Biol., 2016, 12, e1004620 CrossRef PubMed.
- B. VanSchouwen and G. Melacini, Proc. Natl. Acad. Sci., 2016, 113, 9407–9409 CrossRef CAS PubMed.
- M. G. Carneiro, A. B. Eiso, S. Theisgen and G. Siegal, Essays Biochem., 2017, 61, 485–493 CrossRef PubMed.
- G. Collier and V. Ortiz, Arch. Biochem. Biophys., 2013, 538, 6–15 CrossRef CAS PubMed.
- G. Song, D. Yang, Y. Wang, C. de Graaf, Q. Zhou, S. Jiang, K. Liu, X. Cai, A. Dai, G. Lin, D. Liu, F. Wu, Y. Wu, S. Zhao, L. Ye, G. W. Han, J. Lau, B. Wu, M. A. Hanson, Z.-J. Liu, M.-W. Wang and R. C. Stevens, Nature, 2017, 546, 312–315 CrossRef CAS PubMed.
- G. La Sala, L. Riccardi, R. Gaspari, A. Cavalli, O. Hantschel and M. De Vivo, J. Chem. Theory Comput., 2016, 12, 5563–5574 CrossRef CAS PubMed.
- C. L. McClendon, G. Friedland, D. L. Mobley, H. Amirkhani and M. P. Jacobson, J. Chem. Theory Comput., 2009, 5, 2486–2502 CrossRef CAS PubMed.
- G. La Sala, S. Decherchi, M. De Vivo and W. Rocchia, ACS Cent. Sci., 2017, 3, 949–960 CrossRef CAS PubMed.
- J. A. Hardy and J. A. Wells, Curr. Opin. Struct. Biol., 2004, 14, 706–715 CrossRef CAS PubMed.
- S. Lu, M. Ji, D. Ni and J. Zhang, Drug Discovery Today, 2018, 23, 359–365 CrossRef CAS PubMed.
- D. Schmidt, M. Boehm, C. L. McClendon, R. Torella and H. Gohlke, J. Chem. Theory Comput., 2019, 15, 3331–3343 CrossRef CAS PubMed.
- N. V. Dokholyan, Chem. Rev., 2016, 116, 6463–6487 CrossRef CAS PubMed.
- B. R. C. Amor, M. T. Schaub, S. N. Yaliraki and M. Barahona, Nat. Commun., 2016, 7, 1–13 Search PubMed.
- J. Wang, A. Jain, L. R. McDonald, C. Gambogi, A. L. Lee and N. V. Dokholyan, Nat. Commun., 2020, 11, 1–13 CrossRef PubMed.
- C. Pfleger, A. Minges, M. Boehm, C. L. McClendon, R. Torella and H. Gohlke, J. Chem. Theory Comput., 2017, 13, 6343–6357 CrossRef CAS PubMed.
- A. Ghosh and S. Vishveshwara, Proc. Natl. Acad. Sci., 2007, 104, 15711–15716 CrossRef CAS PubMed.
- C. Chennubhotla and I. Bahar, Mol. Syst. Biol., 2006, 2, 36 CrossRef PubMed.
- M. S. Vijayabaskar and S. Vishveshwara, Biophys. J., 2010, 99, 3704–3715 CrossRef CAS PubMed.
- A. A. S. T. Ribeiro and V. Ortiz, J. Chem. Theory Comput., 2014, 10, 1762–1769 CrossRef CAS PubMed.
- G. Kar, O. Keskin, A. Gursoy and R. Nussinov, Curr. Opin. Pharmacol., 2010, 10, 715–722 CrossRef CAS PubMed.
- H. Gohlke, L. A. Kuhn and D. A. Case, Proteins: Struct., Funct., Bioinf., 2004, 56, 322–337 CrossRef CAS PubMed.
- P. C. Rathi, S. Radestock and H. Gohlke, J. Biotechnol., 2012, 159, 135–144 CrossRef CAS PubMed.
- T. Mamonova, B. Hespenheide, R. Straub, M. F. Thorpe and M. Kurnikova, Phys. Biol., 2005, 2, S137–S147 CrossRef CAS PubMed.
- A. Sljoka and D. Wilson, Phys. Biol., 2013, 10, 056013 CrossRef CAS PubMed.
- D. de Juan, F. Pazos and A. Valencia, Nat. Rev. Genet., 2013, 14, 249–261 CrossRef CAS PubMed.
- W. S. J. Valdar, Proteins: Struct., Funct., Bioinf., 2002, 48, 227–241 CrossRef CAS PubMed.
- M. Novinec, M. Korenč, A. Caflisch, R. Ranganathan, B. Lenarčič and A. Baici, Nat. Commun., 2014, 5, 3287 CrossRef PubMed.
- G. M. Süel, S. W. Lockless, M. A. Wall and R. Ranganathan, Nat. Struct. Biol., 2003, 10, 59–69 CrossRef PubMed.
- N. Halabi, O. Rivoire, S. Leibler and R. Ranganathan, Cell, 2009, 138, 774–786 CrossRef CAS PubMed.
- K. A. Reynolds, R. N. McLaughlin and R. Ranganathan, Cell, 2011, 147, 1564–1575 CrossRef CAS PubMed.
- H. Tian, X. Jiang and P. Tao, Mach. Learn. Sci. Technol., 2021, 2, 035015 CrossRef PubMed.
- W. Huang, S. Lu, Z. Huang, X. Liu, L. Mou, Y. Luo, Y. Zhao, Y. Liu, Z. Chen, T. Hou and J. Zhang, Bioinformatics, 2013, 29, 2357–2359 CrossRef CAS PubMed.
- K. Song, X. Liu, W. Huang, S. Lu, Q. Shen, L. Zhang and J. Zhang, J. Chem. Inf. Model., 2017, 57, 2358–2363 CrossRef CAS PubMed.
- A. Panjkovich and X. Daura, Bioinformatics, 2014, 30, 1314–1315 CrossRef CAS PubMed.
- D. Stauffer and A. Aharony, Introduction To Percolation Theory, Taylor & Francis, 2018 Search PubMed.
- T. A. Springer and M. L. Dustin, Curr. Opin. Cell Biol., 2012, 24, 107–115 CrossRef CAS PubMed.
- J. J. P. Perry, R. M. Harris, D. Moiani, A. J. Olson and J. A. Tainer, J. Mol. Biol., 2009, 391, 1–11 CrossRef CAS PubMed.
- P. Schmidtke and X. Barril, J. Med. Chem., 2010, 53, 5858–5867 CrossRef CAS PubMed.
- S. C. Tso, X. Qi, W. J. Gui, J. L. Chuang, L. K. Morlock, A. L. Wallace, K. Ahmed, S. Laxman, P. M. Campeau, B. H. Lee, S. M. Hutson, B. P. Tu, N. S. Williams, U. K. Tambar, R. M. Wynn and D. T. Chuang, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9728–9733 CrossRef CAS PubMed.
- C. Köhler, G. Carlström, A. Gunnarsson, U. Weininger, S. Tångefjord, V. Ullah, M. Lepistö, U. Karlsson, T. Papavoine, K. Edman and M. Akke, Sci. Adv., 2020, 6, eabb5277 CrossRef PubMed.
- G. La Sala, A. Gunnarsson, K. Edman, C. Tyrchan, A. Hogner and A. I. Frolov, J. Chem. Inf. Model., 2021, 61, 3667–3680 CrossRef CAS PubMed.
- M. Getlik, J. R. Simard, M. Termathe, C. Grütter, M. Rabiller, W. A. L. van Otterlo and D. Rauh, PLoS One, 2012, 7, e39713 CrossRef CAS PubMed.
- G. F. De Nicola, E. D. Martin, A. Chaikuad, R. Bassi, J. Clark, L. Martino, S. Verma, P. Sicard, R. Tata, R. A. Atkinson, S. Knapp, M. R. Conte and M. S. Marber, Nat. Struct. Mol. Biol., 2013, 20, 1182–1190 CrossRef CAS PubMed.
- M. N. Preising, B. Görg, C. Friedburg, N. Qvartskhava, B. S. Budde, M. Bonus, M. R. Toliat, C. Pfleger, J. Altmüller, D. Herebian, M. Beyer, H. J. Zöllner, H.-J. Wittsack, J. Schaper, D. Klee, U. Zechner, P. Nürnberg, J. Schipper, A. Schnitzler, H. Gohlke, B. Lorenz, D. Häussinger and H. J. Bolz, FASEB J., 2019, 33, 11507–11527 CrossRef CAS PubMed.
- D. Milić, M. Dick, D. Mulnaes, C. Pfleger, A. Kinnen, H. Gohlke and G. Groth, Sci. Rep., 2018, 8, 3890 CrossRef PubMed.
- C. Pfleger, J. Kusch, M. Kondapuram, T. Schwabe, C. Sattler, K. Benndorf and H. Gohlke, Biophys. J., 2021, 120, 950–963 CrossRef CAS PubMed.
- A. Cuadrado and A. R. Nebreda, Biochem. J., 2010, 429, 403–417 CrossRef CAS PubMed.
- M. Machius, J. L. Chuang, R. M. Wynn, D. R. Tomchick and D. T. Chuang, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 11218–11223 CrossRef CAS PubMed.
- C. J. Tsai, A. del Sol and R. Nussinov, J. Mol. Biol., 2008, 378, 1–11 CrossRef CAS PubMed.
- S. Liu, B. L. Kormos, J. D. Knafels, P. V. Sahasrabudhe, A. Rosado, R. F. Sommese, A. R. Reyes, J. Ward, R. J. Roth Flach, X. Wang, L. M. Buzon, M. R. Reese, S. K. Bhattacharya, K. Omoto and K. J. Filipski, J. Biol. Chem., 2023, 299, 102959 CrossRef CAS PubMed.
- L. Laraia, G. McKenzie, D. R. Spring, A. R. Venkitaraman and D. J. Huggins, Chem. Biol., 2015, 22, 689–703 CrossRef CAS PubMed.
- S. M. Bertrand, N. Ancellin, B. Beaufils, R. P. Bingham, J. A. Borthwick, A.-B. Boullay, E. Boursier, P. S. Carter, C. Chung, I. Churcher, N. Dodic, M.-H. Fouchet, C. Fournier, P. L. Francis, L. A. Gummer, K. Herry, A. Hobbs, C. I. Hobbs, P. Homes, C. Jamieson, E. Nicodeme, S. D. Pickett, I. H. Reid, G. L. Simpson, L. A. Sloan, S. E. Smith, D. O. Somers, C. Spitzfaden, C. J. Suckling, K. Valko, Y. Washio and R. J. Young, J. Med. Chem., 2015, 58, 7140–7163 CrossRef CAS PubMed.
- A. Kuzmanic, G. R. Bowman, J. Juarez-Jimenez, J. Michel and F. L. Gervasio, Acc. Chem. Res., 2020, 53, 654–661 CrossRef CAS PubMed.
- V. Oleinikovas, G. Saladino, B. P. Cossins and F. L. Gervasio, J. Am. Chem. Soc., 2016, 138, 14257–14263 CrossRef CAS PubMed.
- R. D. Smith and H. A. Carlson, J. Chem. Inf. Model., 2021, 61, 1287–1299 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc06272k |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2023 |