Open Access Article
Open Access ArticleA quantum spin liquid candidate isolated in a two-dimensional CoIIRhIII bimetallic oxalate network†
Enrique
Burzurí
 *abc,
María José
Martínez-Pérez
*abc,
María José
Martínez-Pérez
 d,
Carlos
Martí-Gastaldo
d,
Carlos
Martí-Gastaldo
 e,
Marco
Evangelisti
e,
Marco
Evangelisti
 d,
Samuel
Mañas-Valero
d,
Samuel
Mañas-Valero
 e,
Eugenio
Coronado
e,
Eugenio
Coronado
 e,
Jesús I.
Martínez
e,
Jesús I.
Martínez
 d,
Jose Ramon
Galan-Mascaros
d,
Jose Ramon
Galan-Mascaros
 fg and
Fernando
Luis
fg and
Fernando
Luis
 *d
*d
aDepartamento de Física de la Materia Condensada, Universidad Autónoma de Madrid, E-28049 Madrid, Spain. E-mail: enrique.burzuri@uam.es
bCondensed Matter Physics Center (IFIMAC) and Instituto Universitario de Ciencia de Materiales “Nicolás Cabrera” (INC), Universidad Autónoma de Madrid, E-28049 Madrid, Spain
cIMDEA Nanociencia, C\Faraday 9, Ciudad Universitaria de Cantoblanco, Madrid, Spain
dInstituto de Nanociencia y Materiales de Aragón (INMA), CSIC-Universidad de Zaragoza, Zaragoza 50009, Spain. E-mail: fluis@unizar.es
eInstituto de Ciencia Molecular (ICMol), Universidad de Valencia, Calle Catedrático José Beltrán 2, Paterna, 46980, Spain
fInstitute of Chemical Research of Catalonia (ICIQ), The Barcelona Institute of Science and Technology (BIST), Av. Paisos Catalans 16, Tarragona 43007, Spain
gICREA, Passeig Lluís Companys 23, Barcelona 08010, Spain
First published on 22nd March 2023
Abstract
A quantum spin liquid (QSL) is an elusive state of matter characterized by the absence of long-range magnetic order, even at zero temperature, and by the presence of exotic quasiparticle excitations. In spite of their relevance for quantum communication, topological quantum computation and the understanding of strongly correlated systems, like high-temperature superconductors, the unequivocal experimental identification of materials behaving as QSLs remains challenging. Here, we present a novel 2D heterometallic oxalate complex formed by high-spin Co(II) ions alternating with diamagnetic Rh(III) in a honeycomb lattice. This complex meets the key requirements to become a QSL: a spin ½ ground state for Co(II), determined by spin–orbit coupling and crystal field, a magnetically-frustrated triangular lattice due to the presence of antiferromagnetic correlations, strongly suppressed direct exchange interactions and the presence of equivalent interfering superexchange paths between Co centres. A combination of electronic paramagnetic resonance, specific heat and ac magnetic susceptibility measurements in a wide range of frequencies and temperatures shows the presence of strong antiferromagnetic correlations concomitant with no signs of magnetic ordering down to 15 mK. These results show that bimetallic oxalates are appealing QSL candidates as well as versatile systems to chemically fine tune key aspects of a QSL, like magnetic frustration and superexchange path geometries.
In a quantum spin liquid (QSL), strong quantum fluctuations prevent long-range magnetic order and spontaneous symmetry breaking in a system of interacting spins, even at zero temperature.1–3 The spins in this phase are strongly correlated in the short-range but remain fluctuating in the long-range in analogy to a conventional liquid. The growing interest in QSLs is both fundamental and applied. QSLs are predicted to show long-range entanglement4,5 between spins, which could be exploited for quantum communication. They are also characterized by the existence of quasiparticle excitations, like anyons6 and charge neutral fractional spin excitations like spinons7 and Majorana fermions,8 which are key actors for topological quantum computing.9,10 Very recently, they have been proposed as superior refrigerants for cascade demagnetization cooling.11 Besides, the understanding of electron–electron correlations in QSLs may help to unveil the physics behind other strongly correlated systems like high-temperature superconductors.12
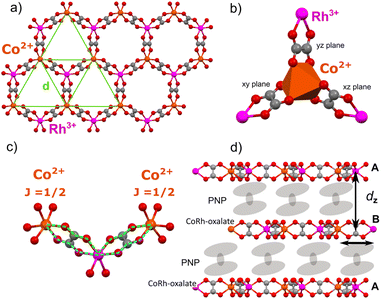
Quantum spin liquids were first theorized by Anderson for spin networks with magnetic frustration.13 In this framework, two-dimensional (2D) triangular and kagomé lattices showing strong antiferromagnetic interactions are natural physical systems to host frustration and strong quantum fluctuations that may lead to a QSL (see Fig. 1a). In a QSL, any two antiparallel spins in the lattice pair up into a spin singlet. The resulting wave function is a liquid-like quantum superposition of all possible configurations of singlets that can be accessed via quantum fluctuations. This quantum superposition gives rise to the so-called spinons.14
The lack of a defined magnetic order parameter and the presence of spin frustration hindered the development of a theoretical framework describing QSLs. For the same reason, identifying materials that provide physical realizations of this state also remains challenging. Some examples of QSL candidates in magnetically frustrated systems are: 1-TaS2,15 κ-(BEDT-TTF)2Cu2 (CN)3 (triangular),16 ZnxCu4−x(OH)6Cl2 (Kagome),17 and the recent NdTa7O19 (triangular),18 among others.1,19
In 2006, the search for QSLs took a big leap forward when Kitaev proposed an exact solution for a S = 1/2 honeycomb lattice6 that can be extended to any tri-coordinated spin lattice.20,21 In this model, magnetic frustration is replaced as ingredient by directional spin–spin exchange interactions through the bonds connecting the spins, i.e.: the bond-dependent Kitaev interaction. Kitaev's solution expands QSLs beyond frustrated magnetic lattices and thus the availability of experimental candidates grows. In real materials, such anisotropic Kitaev interaction can arise in transition metals showing strong spin–orbit coupling (SOC) with a J = 1/2 ground state resulting from the entanglement of spin and orbital moments.20–22 Inequivalent bond-dependent Kitaev interactions appear through otherwise equivalent tridentate ligands. Some recent examples include inorganic materials like α-RuCl3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8,23,24 and iridates25,26 in which direct evidence of dominant bond–directional interactions has been obtained.27
8,23,24 and iridates25,26 in which direct evidence of dominant bond–directional interactions has been obtained.27
However, the main obstacle for inorganic materials to be good Kitaev QSLs is the presence of strong direct exchange interactions that may compete with Kitaev interactions and even lead, in many of them, to a classical long-range antiferromagnetic order.8,26 A possible alternative may be found in coordination materials, where the metal centres carrying the spin are spaced by non-magnetic organic ligands.20,21 Direct exchange interactions can be largely suppressed leaving only the weak through-bond superexchange interactions. Interestingly, Jackeli and Khaliullin showed theoretically that Kitaev interactions can be dominant in these compounds for specific geometries.22 Two main requirements need to be met by the transition metal centre: (i) a spin–orbit entangled, low effective spin ground state (J = 1/2) and (ii) an octahedral coordination site with oxygens (see Fig. 1b) leading to multiple superexchange paths (see Fig. 1c). In this geometry, two equivalent parallel paths can interfere destructively exactly suppressing isotropic superexchange22 whereas any remnant direct exchange contribution is suppressed exponentially with distance.
In coordination chemistry, 2D honeycomb frameworks as well as 3D hyper-honeycomb ones, such as those provided by the metal-oxalate coordination polymers,28 seem to present an optimal geometry to host the Jackeli–Khaliullin mechanism (Fig. 1a). In these compounds, the metal coordination is octahedral with each oxalate being contained in orthogonal xy, yz and xz planes (see Fig. 1b). Moreover, the coupling between metal centres is mediated via two equivalent parallel paths (see Fig. 1c). Kitaev interactions are therefore expected to become dominant, as recently proposed theoretically.20,21 A first experimental result suggesting an oxalate-based QSL was reported for the homometallic Cu2+ oxalate hyper-honeycomb framework. Note, however, that the main QSL indication was the absence of magnetic order in susceptibility measurements limited to temperatures above 2 K,29,30 whereas similar homometallic31 and bimetallic32,33 oxalates have shown antiferromagnetic phases not far from that temperature region. These fingerprints could still be associated with a spin glass1,34 or with magnetic order below the experimentally accessible temperatures. Besides, Cu2+ does not present significant spin–orbit coupling, which is a necessary ingredient for the predominance of Kitaev interactions.
Here we report a novel bimetallic oxalate complex in which magnetic Co2+ centres are coordinated through oxalate bridges to non-magnetic Rh3+ centres, and vice versa, leading to a 2D honeycomb lattice, as shown in Fig. 1a. The resulting spin network is a triangular planar lattice in which exchange and superexchange interactions between Co2+ ions are further suppressed by very long –(ox)–Rh3+–(ox)– bridges (Fig. 1c), as compared with the links present in conventional homometallic counterparts. Besides, a double equivalent super-exchange path is maintained throughout the bridge (Fig. 1c). Exploiting a combination of different and complementary experimental techniques (magnetic resonance, heat capacity and micro-SQUID ac susceptometry), we characterize the effective magnetic properties of each Co2+ ion, determine the average energy scale associated with their mutual spin correlations in the 2D metal-oxalate lattice and explore the magnetic response down to very low temperatures to look for the existence (rather absence) of long range magnetic order in the vicinity of absolute zero. On basis of these results, we discuss the possibility that this molecular system provides a realization of a QSL.
Results and discussion
Synthesis and structure
The bimetallic CoRh-oxalate compound is synthesized by following the procedure reported for analogous bimetallic oxalates,33 by adding a salt of the bis(triphenylphosphine)iminium cation [(C6H5)3PNP(C6H5)3]+ (PNP), to an aqueous solution containing Co2+ and [Rh(C2O4)3]3−. The product precipitates out of solution, given the typical insolubility of these materials. The compound is isostructural to the series of 2D bimetallic oxalate materials, and contains alternating anionic and cationic layers as described for the analogous PNP[FeIIFeIII(ox)3].35 The X-ray powder diffraction (XRPD) pattern is shown in Fig. S1 in the ESI.† Besides, Fig. S2† shows a direct comparison with the isostructural PNP[FeFe(ox)3] and PNP[MnFe(ox)3] reported previously.35 The analogous diffraction pattern confirms all three are isostructural (Fig. 1). Chemical analysis by Inductively Coupled Plasma Mass Spectrometry (ICP-MS) show a close to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Co/Rh ratio, as expected for the bimetallic complex. See Section S2 in the ESI† for details.
1 Co/Rh ratio, as expected for the bimetallic complex. See Section S2 in the ESI† for details.
In this compound, the [CoRh(ox)3]− layers are spaced and held together in the crystal by non-magnetic molecular cations PNP, as seen in Fig. 1d. The average distance between adjacent bimetallic layers is dz = 14.5 Å,35 thus larger than the average separation (d = 9 Å) between magnetic ions within these layers and considerably larger than in previously reported compounds (3.5 Å),29 due to the larger size of the cation. In addition, the layer packing is AB-hexagonal. Therefore, the Co2+ atoms are not aligned along the out-of-plane crystal axis (see Fig. 1d), thus reducing even further the magnetic interactions between different 2D layers.
Electronic paramagnetic resonance
Electron paramagnetic resonance (EPR) measurements (see the experimental section for details) give information on the spin level structure of the Co2+ ions in [PNP][CoRh(ox)3]. The EPR spectrum, shown in Fig. 2, displays a single, broad and slightly asymmetric feature, compatible with an effective J = 1/2 system. Its peak-to-peak width is very large, of the order of 80 mT at 40 K, and it is centered at 140 mT (g ≈ 4.8). No evidence for hyperfine splitting associated with the I = 7/2 nuclear spin of 59Co is seen in this spectrum. In oxalates, the close environment of Co(II) shows slight distortions over the pure octahedral coordination. As shown for an analogous system in Section S3 of the ESI,† this would induce g matrix anisotropy, with the three principal values of g deviating from the isotropic value geff = 4.33. The results of Fig. 2 suggest that this anisotropy is averaged out in [PNP][CoRh(ox)3], likely by spin–spin interactions that would also introduce a shift of the effective g and some asymmetry of the EPR feature. Such behavior has been identified for the analogous CoRh 2D structure (see ESI†). All these features provide a first indication of sizeable magnetic interactions between Co2+ centres.36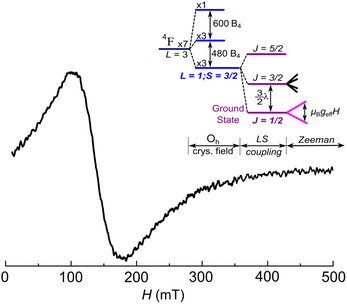 | ||
| Fig. 2 EPR spectrum of a [PNP][CoRh(ox)3] powder sample, at 40 K. A broad asymmetric signal is observed centred at g ≈ 4.8. The inset shows the energy level diagram of a Co2+ in an octahedral crystal field and under spin–orbit coupling with strength λ. B4 is related to the strength of the crystal field. The ground state can be described with an effective angular momentum J = 1/2 and geff = 4.33. Distortion of the octahedral symmetry would cause some anisotropy of the actual g values around the effective one (see text and Fig. S3 in the ESI†), which is here averaged out by the effect of spin–spin interactions between Co(II) centres in the oxalate layer. | ||
Specific heat: energy scales of spin–spin interactions
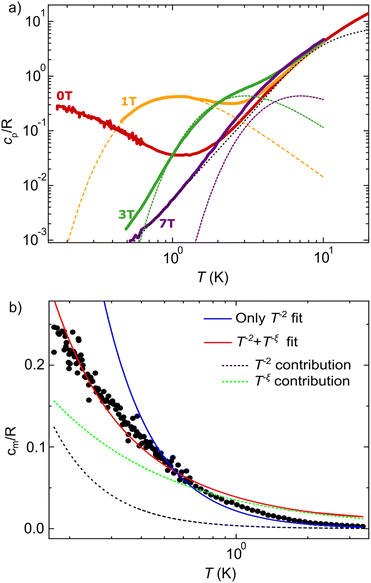
The specific heat cp complements the information on magnetic levels gained from EPR and allows exploring spin correlations at much lower temperatures. Fig. 3a shows cp measured on a powder sample as a function of temperature and for different magnetic fields B. A commercial measuring system, equipped with an 3He refrigerator (T > 400 mK) and a 3He–4He dilution refrigerator (170 mK < T < 640 mK) were combined to access a wide temperature range. See the experimental section for additional details. The high temperature regime (T ≥ 6 K) is dominated by the contributions from lattice phonons and molecular vibrations. The dotted line is a fit to a Debye model with a Debye constant θD = 35.2 K. Below 2–3 K, the specific heat is dominated by the contribution cm arising from magnetic excitations. We first consider data measured for B ≠ 0. As the magnetic field tends to supress spin–spin correlations, these data admit a simpler interpretation on basis of the properties of individual Co2+ ions. A broad peak is observed for B ≥ 1 T that shifts towards higher temperatures for increasing B. The shape and magnetic field dependence are consistent with a Schottky anomaly due to the Zeeman splitting of the Co2+ spins. The dashed lines in Fig. 3a are calculated by using the fluctuation–dissipation theorem with g = 3.8 and J = 1/2 (see ESI†). As it is shown in the accompanying ESI,† the magnetic entropy estimated by integrating cm/T measured at B = 1 T agrees well with R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. These results support therefore the presence of an effective J = 1/2 ground state determined by the crystal field and spin–orbit couplings, as already shown by the EPR measurements and by previous examples for other Co2+ systems.37
2. These results support therefore the presence of an effective J = 1/2 ground state determined by the crystal field and spin–orbit couplings, as already shown by the EPR measurements and by previous examples for other Co2+ systems.37
No such broad peak anomaly is observed in specific heat data measured for B = 0. Instead, they show a monotonic increment of cp below T = 1.75 K that continues down to the lowest temperatures attained in these experiments (172 mK). Fig. 3b shows the zero-field magnetic specific heat cm after subtraction of the lattice component. Above roughly 0.5 K, this low temperature tail can be fitted to cm = αT−2 with α = 0.025 K2 (blue solid line). Note that in this temperature region we can safely discard the contribution of excited levels above the ground spin doublet of each Co2+ ion (see Fig. S5 in the ESI†). Hyperfine interactions are also too weak to give any sizeable contribution at these temperatures. Therefore, this dependence can be ascribed to growing correlations between spins.37 The fit of this T−2 “tail” to the high-temperature prediction for a J = 1/2 Heisenberg model allows estimating the spin–spin exchange interaction constant J ≃ 0.2 K.37 See ESI† for details. This analysis therefore shows the presence of relatively strong couplings between the spins located within each oxalate layer.
In spite of this, and quite remarkably, no indication of magnetic order is observed in the specific heat measured at lower temperatures. Even though no clear peaks, the fingerprints of Majorana fermions and a Kitaev QSL, may be observed in the experimental temperature range,39,40 the deviation from a T−2 dependence may be indicative of the saturation to a broad maximum that has been associated to quasiparticle excitations in QSLs.8 Interestingly, a better fit (red solid line) can be obtained over the whole temperature range by introducing an additional T−ξ contribution (green dotted line) that accounts for the contribution of the QSL state, such that cm = αT−2 + βT−ξ. The fit gives an exponent ξ = 0.65, which is consistent with values reported for other QSL candidates.41,42 As expected from the monotonic increase of cm with decreasing temperature, there remains a residual entropy for B = 0 T at the lowest temperature. This is shown in Fig. S6 and S7 in the ESI.† Although the observed behaviour is compatible with a QSL, it does not allow to completely discard a magnetic transition at temperatures lower than the experimental range.38
AC magnetic susceptibility: absence of long-range magnetic order
The complex ac magnetic susceptibility χ* (ω,T) = χ′(ω,T) + iχ′′(ω,T) where ω is the ac frequency, provides a tool to study spin–spin interactions and explore the onset (or lack) of long-range magnetic order. As with the specific heat measurements, we have combined two different experimental set-ups that allow us to access a very broad temperature region and, in particular, measure the magnetic response very close to absolute zero. The high temperature χ* was measured with a commercial SQUID magnetometer from Quantum Design whereas the low temperature χ* was measured with a μ-SQUID susceptometer43,44 immersed inside the mixing chamber of a 3He–4He dilution refrigerator, to maximize the thermal exchange between sample and helium bath. The Experimental section provides details about the sample preparation and measurement protocols employed in these experiments.Fig. 4a shows the in-phase component χ′T measured in [PNP][CoRh(ox)3] at ω/2π = 1379 Hz down to T = 40 mK. [PNP][CoRh(ox)3] behaves as a paramagnet down to the lowest temperatures. The two consecutive drops observed in χ′T can be well reproduced by a susceptibility model45 that includes the contributions from the ground and an excited spin doublets and spin–spin antiferromagnetic interactions between neighbours (green curve). The mathematical description of this model and the fitting parameters are given in the ESI.† The high-temperature drop in χ′T marks the depopulation of the excited spin doublet, and allows determining the energy distance Δ = 366 K from the ground state. At T = 10 K, χ′T is close to 1.7 emu K mol−1, to which a system of non-interacting J = 1/2 spins with g = 4.3, close to those inferred from EPR and heat capacity measurements, would be expected to saturate (red dashed curve in Fig. 4a). However, the low-temperature drop shows a deviation from this picture, which can be associated with antiferromagnetic spin–spin interactions. This behaviour can be fitted by introducing an equivalent of the Weiss temperature T0 = −0.38 K (green solid line in Fig. 4a). The blue curve is the Curie–Weiss prediction for a J = 1/2, g = 4.3 system with Weiss constant θCW = −0.38 K. A plot of the reciprocal susceptibility (χ′)−1, shown in Fig. 4b, confirms this and shows below 10 K a close to linear behaviour compatible with a Curie–Weiss law with θCW = −0.39 K, similar to what has been found for other oxalates.33 These results show that, below ∼15 K, [PNP][CoRh(ox)3] can be safely described by a pure J = ½ system with quite sizeable short-range spin correlations between cobalt centres. This scenario is supported by the nearly negligible value of the high-order expansion parameters in the susceptibility model.45 See ESI† for additional details.
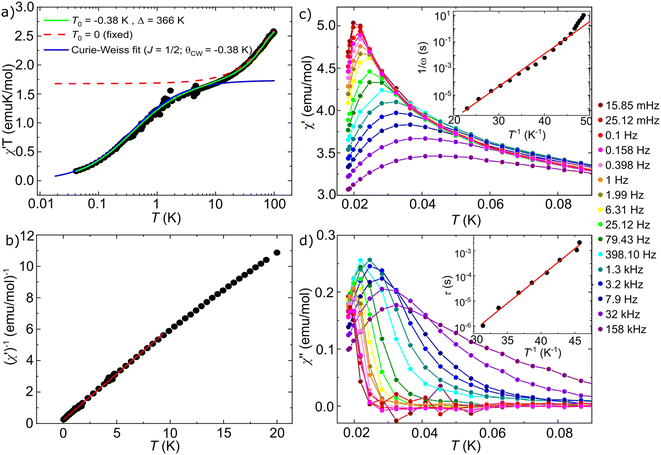 | ||
| Fig. 4 (a) χ′T product as a function of temperature (from 40 mK to 100 K) measured at a fixed frequency 1379 Hz. The two drops observed in χ′T can be well reproduced by a susceptibility model43 that includes the ground and an excited spin doublets and spin–spin antiferromagnetic interactions between neighbour spins (green curve). The high-temperature drop in χ′T is mainly determined by the depopulation of an excited doublet separated Δ = 366 K from the ground state (green curve). The low-temperature drop can only be fitted by introducing antiferromagnetic spin–spin interactions with characteristic energy scales given by T0 = −0.38 K. Contrarily, by fixing T0 = 0 (red dashed curve) the theoretical prediction saturates to 1.7 emu K mol−1 corresponding to a system of non-interacting J = 1/2 spins with g = 4.3. The blue curve is the Curie–Weiss prediction for a J = 1/2, g = 4.3 system with a Weiss temperature θCW = −0.38 K. This result shows that, below ∼15 K, [PNP][CoRh(ox)3] can be safely described by a pure J = 1/2 system with antiferromagnetic interactions. (b) (χ′)−1 as a function of temperature. The Curie–Weiss fit and its extrapolation to (χ′)−1 = 0 (red solid line) provide a Curie–Weiss temperature θCW = −0.39 K. This negative value is a signature of significant antiferromagnetic interactions. (c) χ′ and (d) χ′′ measured in a wide range of frequencies from 15.85 mHz (dark red) to 158 kHz (dark purple) and down to T = 15 mK. The insets show the temperature dependence of the respective maxima. | ||
These findings agree with the results of specific heat measurements and, incidentally, also help understanding the EPR spectrum (Fig. 2). For a 2D exchange interaction with a Curie–Weiss temperature around 0.4 K (or 8 GHz) the resonance line broadens and the mean g factor shifts with respect to that expected for isolated Co2+ centres (see Fig. S3†).
Below T ≈ 70 mK, both χ′ and χ′′ develop a maximum that shifts to lower temperatures as frequency decreases, as shown in Fig. 4c and d. The frequency dependence signals a deviation of the spin response from equilibrium. Such slow magnetic relaxation has been observed in other compounds based on Co2+ in octahedral coordination.46–48 For isolated Co(II) centres, it has been explained in terms of temperature dependent direct spin–phonon processes.49 The maxima in χ′′ can be identified with the condition 1/ω = τ, where τ is the characteristic spin relaxation time. The inset in Fig. 4d shows that τ increases exponentially with decreasing temperature, with activation energy U ≈ 0.2 K, a behaviour that contrast sharply with the linear dependence expected for a direct process. Besides, the peaks in χ′ also approximately follow an Arrhenius dependence (see inset in Fig. 4c). This shows that the spin dynamics in this 2D oxalate layer slows down with decreasing temperature much more sharply than what would be expected for the isolated ions. Another characteristic trait is the low value of χ′′, that would be expected to reach a maximum of χ′′ = χ′/2 for a paramagnet with uncorrelated spins. This behaviour and the fact that U is close to the scale of spin–spin interactions point to an additional slowing down due to the growth of spin correlations.
The spin dynamics can be investigated more in depth by inspecting the frequency spectra of χ* at different temperatures, as shown in Fig. 5. Fig. 5b shows that χ′′ develops a low frequency tail that grows with decreasing temperature. This is a signature of the onset of multiple slow spin-relaxation mechanisms that, in turn, would explain the low intensity of the χ′′ peaks in Fig. 4d. The multiplicity of relaxation times in a spin system could again be originated by growing correlations between spins or by a certain degree of magnetic frustration in the triangular magnetic layers.
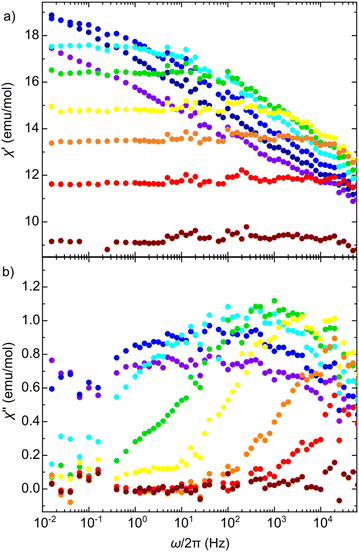 | ||
| Fig. 5 Frequency spectra of (a) χ′ and (b) χ′′ measured at different temperatures from 18 mK (blue) up to 91 mK (dark red). The out-of-phase component develops a low-frequency tail indicting the emergence of multiple slow spin relaxation processes. These dynamics, together with the reduced χ′′ value in Fig. 4 has been typically associated to the growing presence of spin correlations or a certain degree of magnetic frustration. | ||
In spite of the onset of correlations and their effect on the spin dynamics, the magnetic susceptibility shows no signs of magnetic order nor of a spin glass-like transition down to 15 mK. This temperature is orders of magnitude lower than what has been found in some paradigmatic QSL candidates.8,29,50 Besides, it is also remarkably low when compared with θCW, setting a lower limit for the frustration factor of at least f > 45. Note also that the absence of magnetic order in this temperature range is significant when compared with the ferromagnetic transition at T = 13 K observed in analogous oxalates, like the [NBu4][CoMn], where both metallic species are magnetic.33
Conclusions
In conclusion, a bimetallic CoIIRhIII oxalate honeycomb framework, which stabilizes and isolates a 2D triangular magnetic lattice of Co2+ centres, has been investigated. Each high-spin Co2+ centre has an effective J = 1/2 ground state mediated by spin–orbit coupling and crystal field interactions. Nearest neighbour spins are coupled via two equivalent superexchange paths provided by a long oxalate–Rh–oxalate diamagnetic bridge. These ingredients are key to promote Kitaev interactions and thus to enable a QSL. Experiments performed on this material down to temperatures close to absolute zero are compatible with this picture. In particular, specific heat and magnetic susceptibility measurements reveal comparatively strong antiferromagnetic spin correlations, with energy scales given by the effective T0 ≃ 0.4 K, while no sign of magnetic order is observed down to 15 mK. The magnetic contribution to the heat capacity also hints at the existence of spin excitations that are compatible with those expected for a QSL phase.Bimetallic oxalate compounds containing magnetic centres (here Co2+) bridged by non-magnetic metal ions (such as Rh3+) are therefore promising candidates to realize QSLs. In addition, they provide versatile platforms to modulate key aspects of a QSL, like magnetic frustration, lattice dimensionality, superexchange paths geometry or even the relative influence of long-range dipolar interactions as compared to short range exchange couplings.51 Further measurements, as muon spin relaxation, will be performed to better characterize these QSL candidates in order to determine the spinon diffusion and critical parameters, allowing a more direct comparison with currently available theoretical models.
Experimental
Synthesis
All chemicals and solvents were commercially available and used without further purification. K3[Rh(ox)3]·3H2O was obtained by previously reported methods.52 CoRh-oxalate: An aqueous solution (20 mL) of K3[Rh(ox)3]·3H2O (2.4 mmol) and CoCl2·4H2O (12.6 mmol) was added dropwise to [PNP]Cl (2.4 mmol) dissolved in warm distilled water (150 mL). Immediately, a precipitate appeared. After the solution was left to stand at room temperature for 30 min, it was filtered to vacuum, washed with water (3 × 100 mL), and dried at room temperature.Electron paramagnetic resonance
EPR data were measured with a Bruker Elexys 580 spectrometer working in X-band. Microwave frequency was 9.477 GHz (X-band). Microwave power was selected in order to avoid saturation effects. The magnetic field was determined with a Bruker ER035 gaussmeter. An Oxford CF900 continuous flow cryostat refrigerated with liquid Helium was used for cooling the samples.Specific heat
High-temperature cp measurements (T > 400 mK) were performed in a commercial calorimeter (model 721) that uses the thermal relaxation method, installed in a Physical Properties Measuring System by Quantum Design equipped with 3He refrigerator. Lower temperature (172 mK < T < 640 mK) cp measurements were performed with the same calorimeter inserted in a Kelvinox 25 dilution refrigerator thanks to a home-made holder. Heat pulse and thermometer were driven with a Keithley 220 programmable current source and the output thermometer voltage was recorded with a high precision digital voltmeter and a high speed Analog to Digital card.Ac magnetic susceptibility
Ac susceptibility data were measured above 2 K with a commercial superconducting quantum interference device magnetometer from Quantum Design (MPMS-XL). The low temperature ac susceptibility was measured with a μ-SQUID susceptometer43,44 immersed inside the mixing chamber of a 3He–4He dilution refrigerator to maximize the thermal exchange between sample and helium bath. A small amount of powder sample was mixed with Apiezon N grease to enhance thermal contact and to prevent sample from moving.Data availability
All data are available at the FATMOLS Zenodo repository https://zenodo.org/communities/fatmols-fet-open-862893/?page=1&size=20. Additional data including EPR, XRPD, inductively coupled plasma mass spectroscopy and details on the entropy, specific heat and magnetic susceptibility models can also be found in the ESI.†Author contributions
FL conceived the idea and supervised magnetic susceptibility experiments. CMG and JRGM, EC and SMV designed, synthesized and characterized the compounds. JIM performed the EPR measurements and analysis. MJMP and EB performed the low temperature magnetic characterization. ME and EB performed the specific heat measurements. EB wrote the manuscript. All the authors contributed to the discussion of the results and the revision of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
EPR spectrum of the sample TBA[Co0.05Zn0.95Rh(ox)3] at 20 K prepared by José Troya under the supervision of Miguel Clemente. Simulation by Ziqi Hu. This work has received support from grants RTI2018-096075-A-C22 (FL), PID2021-124796OB-I00 (JRGM), CEX2019-000919-M (CMG, SMV, EC), RTI2018-096075-B-C21 (EB), PID2020-118117RB-I00 (CMG), PID2021-124734OB-C21 (ME), RYC2019-028429-I (EB), and the María de Maeztu Excellence Seal CEX2018-000805-M (EB) funded by MCIN/AEI/10.13039/501100011033, ERDF A way of making Europe and ESF Investing in your future. We also acknowledge funding from the European Union Horizon 2020 research and innovation program through FET-OPEN grant FATMOLS-No 862893 and ERC Advanced grant Mol-2D-No788222, the Gobierno de Aragón grant E09-17R-Q-MAD and CSIC Research Platform PTI-001. ICIQ acknowledges the Ministerio de Ciencia e Innovación for support through Severo Ochoa Excellence Accreditation 2020–2023 (CEX2019-000925-S, MIC/AEI).Notes and references
- J. Wen, S.-L. Yu, S. Li, W. Yu and J.-X. Li, Quantum Mater., 2015, 4, 1–9 CrossRef.
- J. Knolle, D. L. Kovrizhin, J. T. Chalker and R. Moessner, Phys. Rev. Lett., 2014, 112, 207203 CrossRef.
- C. Broholm, R. J. Cava, S. A. Kivelson, D. G. Nocera, M. R. Norman and T. Senthil, Science, 2020, 367, eaay0668 CrossRef CAS PubMed.
- A. Kitaev and J. Preskill, Phys. Rev. Lett., 2006, 96, 110404 CrossRef PubMed.
- H.-C. Jiang, Z. Wang and L. Balents, Nat. Phys., 2012, 8, 902–905 Search PubMed.
- A. Kitaev, Ann. Phys., 2006, 321, 2–111 CAS.
- Y. Shen, Y.-D. Li, H. Wo, Y. Li, S. Shen, B. Pan, Q. Wang, H. Walker, P. Steffens, Y. Hao, D. L. Quintero-castro, L. W. Harriger, D. Frontzek, L. Hao, S. meng, Q. Zhang, G. chen and J. Zhao, Nature, 2016, 540, 559 CrossRef CAS PubMed.
- S.-H. Do, S.-Y. Park, J. Yoshitake, J. Nasu, Y. Motome, Y. S. Kwon, D. T. Adroja, D. J. Voneshen, K. Kim, T.-H. Jang, J.-H. Park, K.-Y. Choi and S. Ji, Nat. Phys., 2017, 13, 1079–1084 Search PubMed.
- C. Nayak, S. H. Simon, A. Stern, M. Freedman and S. Das Sarma, Rev. Mod. Phys., 2008, 80, 1083–1159 CrossRef CAS.
- A. Y. Kitaev, Ann. Phys., 2003, 303, 2–30 CAS.
- X. Y. Liu, Y. Gao, H. Li, W. Jin, J. Xiang, H. Jin, Z. Chen, W. Li and G. Su, Commun. Phys., 2022, 5, 1–10 CrossRef CAS.
- P. A. Lee, N. Nagaosa and X.-G. Wen, Rev. Mod. Phys., 2006, 78, 17–85 CrossRef CAS.
- P. W. Anderson, Mater. Res. Bull., 1973, 8, 153–160 CrossRef CAS.
- L. Balents, Nature, 2010, 464, 199–208 CrossRef CAS PubMed.
- S. Mañas-Valero, B. M. Huddart, T. Lancaster, E. Coronado and F. L. Pratt, npj Quantum Mater., 2021, 6, 69 CrossRef.
- Y. Shimizu, K. Miyagawa, K. Kanoda, M. Maesato and G. Saito, Phys. Rev. Lett., 2003, 91, 107001 CrossRef CAS PubMed.
- M. P. Shores, E. A. Nytko, B. M. Bartlett and D. G. Nocera, J. Am. Chem. Soc., 2005, 2, 13462–13463 CrossRef PubMed.
- T. Arh, B. Sana, M. Pregelj, P. Khuntia, Z. Jagličić, M. D. Le, P. K. Biswas, P. Manuel, L. Mangin-Thro, A. Ozarowski and A. Zorko, Nat. Mater., 2021, 21, 416–422 CrossRef PubMed.
- T. Itou, A. Oyamada, S. Maegawa, M. Tamura and R. Kato, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 104413 CrossRef.
- M. G. Yamada, V. Dwivedi and M. Hermanns, Phys. Rev. B, 2017, 96, 155107 CrossRef.
- M. G. Yamada, H. Fujita and M. Oshikawa, Phys. Rev. Lett., 2017, 119, 057202 CrossRef PubMed.
- G. Jackeli and G. Khaliullin, Phys. Rev. Lett., 2009, 102, 017205 CrossRef CAS PubMed.
- K. W. Plumb, J. P. Clancy, L. J. Sandilands, V. V. Shankar, Y. F. Hu, K. S. Burch, H. Y. Kee and Y. J. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 041112 CrossRef CAS.
- H. Li, H. K. Zhang, J. Wang, H. Q. Wu, Y. Gao, D. W. Qu, Z. X. Liu, S. S. Gong and W. Li, Nat. Commun., 2021, 12, 1–11 CrossRef PubMed.
- Y. Singh, S. Manni, J. Reuther, T. Berlijn, R. Thomale, W. Ku, S. Trebst and P. Gegenwart, Phys. Rev. Lett., 2012, 108, 127203 CrossRef PubMed.
- Y. Singh and P. Gegenwart, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 064412 CrossRef.
- S. Hwan Chun, J. W. Kim, J. Kim, H. Zheng, C. C. Stoumpos, C. D. Malliakas, J. F. Mitchell, K. Mehlawat, Y. Singh, Y. Choi, T. Gog, A. Al-Zein, M. M. Sala, M. Krisch, J. Chaloupka, G. Jackeli, G. Khaliullin and B. J. Kim, Nat. Phys., 2015, 11, 462–466 Search PubMed.
- E. Coronado and G. M. Espallargas, Chem. Soc. Rev., 2013, 42, 1525–1539 RSC.
- B. Zhang, Y. Zhang, Z. Wang, D. Wang, P. J. Baker, F. L. Pratt and D. Zhu, Sci. Rep., 2015, 4, 6451 CrossRef PubMed.
- B. Zhang, P. J. Baker, Y. Zhang, D. Wang, Z. Wang, S. Su, D. Zhu and F. L. Pratt, J. Am. Chem. Soc., 2018, 140, 122–125 CrossRef CAS PubMed.
- Z. Duan, Y. Zhang, B. Zhang and F. L. Pratt, Inorg. Chem., 2009, 48, 2140–2146 CrossRef CAS PubMed.
- M. Clemente-León, E. Coronado, C. Martí-Gastaldo and F. M. Romero, Chem. Soc. Rev., 2011, 40, 473 RSC.
- E. Coronado, J. Ramón Galán-Mascarós and C. Martí-Gastaldo, J. Mater. Chem., 2006, 16, 2685–2689 RSC.
- J. A. Mydosh, Spin Glasses: An Experimental Introduction, CRC Press, London, 1993 Search PubMed.
- C. J. Nuttall, Bimetallic tris-oxalate magnets: Synthesis, structure and properties. ProQuest U642291, PhD Thesis, University of London, 1998 Search PubMed.
- A. Bencini and D. Gatteschi, Electron Paramagnetic Resonance of Exchange Coupled Systems, Springer Berlin Heidelberg, 1990 Search PubMed.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions (Oxford Classic Texts in the Physical Sciences), Oxford University Press, USA, 2012 Search PubMed.
- Y. Li, H. Liao, Z. Zhang, S. Li, F. Jin, L. Ling, L. Zhang, Y. Zou, L. Pi, Z. Yang, J. Wang, Z. Wu and Q. Zhang, Sci. Rep., 2015, 5, 1–8 Search PubMed.
- K. Mehlawat, A. Thamizhavel and Y. Singh, Phys. Rev. B, 2017, 95, 144406 CrossRef.
- J. Nasu, M. Udagawa and Y. Motome, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 115122 CrossRef.
- A. Mizuno, Y. Shuku, M. M. Matsushita, M. Tsuchiizu, Y. Hara, N. Wada, Y. Shimizu and K. Awaga, Phys. Rev. Lett., 2017, 119, 057201 CrossRef PubMed.
- Y. Misumi, A. Yamaguchi, Z. Zhang, T. Matsushita, N. Wada, M. Tsuchiizu and K. Awaga, J. Am. Chem. Soc., 2020, 142, 16513–16517 CrossRef CAS PubMed.
- M. J. Martínez-Pérez, J. Sesé, F. Luis, D. Drung and T. Schurig, Rev. Sci. Instrum., 2010, 81, 016108 CrossRef PubMed.
- M. J. Martinez-Perez, J. Sese, F. Luis, R. Cordoba, D. Drung, T. Schurig, E. Bellido, R. de Miguel, C. Gomez-Moreno, A. Lostao and D. Ruiz-Molina, IEEE Trans. Appl. Supercond., 2011, 21, 345–348 CAS.
- E. Bartolomé, P. J. Alonso, A. Arauzo, J. Luzón, J. Bartolomé, C. Racles and C. Turta, Dalton Trans., 2012, 41, 10382–10389 RSC.
- E. Burzurí, J. Campo, L. R. Falvello, E. Forcén-Vázquez, F. Luis, I. Mayoral, F. Palacio, C. Sáenz De Pipaón and M. Tomás, Chem.–Eur. J., 2011, 17, 2818–2822 CrossRef PubMed.
- J. M. Zadrozny, J. Liu, N. A. Piro, C. J. Chang, S. Hill and J. R. Long, Chem. Commun., 2012, 48, 3927–3929 RSC.
- J. Vallejo, I. Castro, R. Ruiz-García, J. Cano, M. Julve, F. Lloret, G. De Munno, W. Wernsdorfer and E. Pardo, J. Am. Chem. Soc., 2012, 134, 15704–15707 CrossRef CAS PubMed.
- S. Gómez-Coca, A. Urtizberea, E. Cremades, P. J. Alonso, A. Camón, E. Ruiz and F. Luis, Nat. Commun., 2014, 5, 4300 CrossRef PubMed.
- Y. Okamoto, M. Nohara, H. Aruga-Katori and H. Takagi, Phys. Rev. Lett., 2007, 99, 137207 CrossRef PubMed.
- N. Y. Yao, M. P. Zaletel, D. M. Stamper-Kurn and A. Vishwanath, Nat. Phys., 2018, 14, 405–410 Search PubMed.
- E. Coronado, J. R. Galán-Mascarós, C. J. Gómez-García, E. Martínez-Ferrero and S. Van Smaalen, Inorg. Chem., 2004, 43, 4808–4810 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc06407c |
| This journal is © The Royal Society of Chemistry 2023 |