Open Access Article
Open Access ArticleReconciling experimental catalytic data stemming from structure sensitivity†
Xue
Zong
ab and
Dionisios G.
Vlachos
 *ab
*ab
aDepartment of Chemical and Biomolecular Engineering, University of Delaware, 150 Academy St., Newark, Delaware 19716, USA. E-mail: vlachos@udel.edu
bCatalysis Center for Energy Innovation, RAPID Manufacturing Institute, Delaware Energy Institute (DEI), University of Delaware, 221 Academy St., Newark, Delaware 19716, USA
First published on 27th March 2023
Abstract
Experimental data have long served as a valuable resource for model validation and identification of the active site. Yet, literature kinetics data often exhibit significant differences among laboratories for the same catalyst and reaction, but the reasons have remained elusive. Here, we exploit if we can rationalize (most of) this variation through catalyst structure sensitivity. We introduce a methodology to build a structure-descriptor-based microkinetic model and investigate the relations between nanoparticle structure and reaction kinetics using the complete methane oxidation on Pt as a model reaction and literature data mining. A volcano-like rate is observed with an optimum coordination number. Unlike common expectations, smaller particles have very low reactivity because of carbon poisoning. Interestingly, most of the data variation can be successfully traced to structure sensitivity. This methodology also enables rapid prediction of kinetic performance and active site determination for designing optimal catalyst structures. It can also serve as a data quality tool to assess experimental outliers. Additional reasons for data variability are discussed.
Introduction
The turnover frequency (TOF) of catalytic reactions is of immense interest as it dictates the activity and selectivity of a reaction. It is also a fundamental metric for comparing catalysts and the structure sensitivity of a reaction. Yet, its value is (very) sensitive to the experimental determination of the surface area, the assumption of the active site, whose density is used to normalize the reaction rate, and the amount of the catalyst. For example, the TOF would not reflect the actual catalyst activity if the wrong active site is picked. Kinetic signatures, such as apparent activation energies and reaction orders, contain implicit information about the active site and do not depend on surface area measurements. As a result, they are more robust for learning about the catalyst's active site. Such experimental data often exhibits considerable variation among laboratories for the same reaction under similar operating conditions. Such variation can stem from poor quality, non-reproducible data, or other fundamental reasons. Understanding the factors affecting the experimental data and the degree of reconciliation can enable the interrogation of outliers, better quality science, and identification of the actual active site.Metal nanoparticles on high surface area supports are ubiquitous in heterogeneous catalysis.1,2 Experimental studies often reveal size- and shape-dependent activity.3–5 However, practical catalysts comprise nanoparticles with poorly defined facets and broad distributions of sizes and shapes6 and can also be dynamic and responsive to the reaction conditions.7 Different synthesis and pretreatment conditions can lead to different particle size and shape distributions. We hypothesize that some data variation can arise from the catalyst heterogeneity. Since a systematic understanding of the size- and shape-dependent activity based solely on experiments remains a significant challenge, computational methods can unravel mechanistic details and fill in this gap.8,9 It is often assumed that a nanoparticle consists of a few well-defined facets with properties being an average.10,11 Yang et al.12 investigated the effect of Cu surface termination on the water gas–shift reaction via density functional theory (DFT) calculations. Similar works have been reported for other reactions.13–15 Only certain facets were typically considered due to the intensity of DFT calculations. Scaling relations of a structure descriptor, such as the generalized coordination number (GCN), with the adsorption energies,16,17 have also been pursued when the rate can be described with an a priori chosen binding energy.18–20 The success is currently limited to simple reactions.
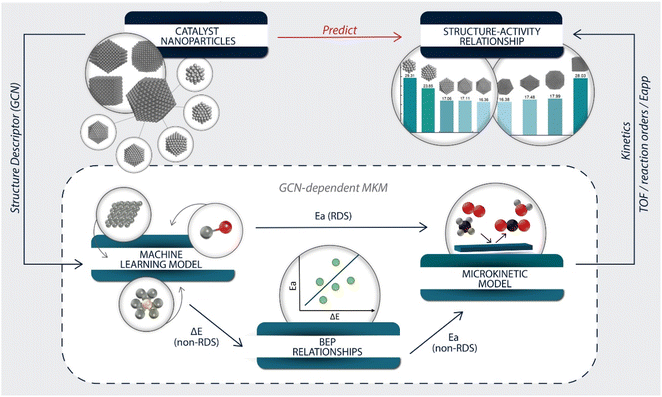
In this work, we developed a structure-descriptor-based microkinetic modeling (MKM) for predicting catalyst activity and selectivity. The parameters in the model were estimated using a machine-learning model and scaling relations. The complete methane oxidation was chosen as a model reaction due to its significance in emissions control and the wide availability of experimental and theoretical data.21–27 Debate still exists among diverse experimental data28–31 on whether this reaction is structure sensitive. Herein, an ensemble of Pt nanoparticles with various morphologies and diameters was constructed to establish structure–reactivity relations. The model identifies kinetic regimes and the most active site. It rationalizes the effect of catalyst heterogeneity in published experimental data discrepancies. It can be extended to other reaction systems and serve as a data quality tool.
Computational methods
DFT settings
DFT calculations were conducted using the Vienna ab initio Simulation Package32,33 (VASP) and the Atomic Simulation Environment (ASE).34 The projector augmented-wave (PAW) method35 was used to describe the electron–ion interactions, and the electronic exchange-correlation functions were adopted for the generalized gradient approximation with the Revised Perdew–Burke–Erzerhof (RPBE).36 The Kohn–Sham one-electron valence states were expanded in plane-wave basis sets with cutoff energy up to 400 eV. Gaussian smearing of 0.1 eV was used. The convergence criterion for the self-consistent electronic minimization was set to 10−6 eV and the k-point sampling was 3 × 3 × 1. At least 20 Å of vacuum was added vertically between repeated images and dipole moment corrections were applied to avoid unphysical periodic interactions. All metal atoms in the two top-most layers of the slabs and the adsorbates were allowed to relax in all directions until the maximum force on any atom was below 0.02 eV Å−1. The gas-phase species energies were calculated in cubic boxes of 20 Å × 20 Å × 20 Å and spin-polarization was considered when calculating gas-phase energies. The transition state energy was calculated by subtracting the empty slab energy from the total energy.The nudged elastic band (NEB) method combined with the climbing-image/dimer37,38 were selected to search for the transition states (TS) of the elementary reactions, and TSs were verified by vibrational frequency analysis. Constant frequencies were assumed over all facets for each adsorbate.
Microkinetic modeling (MKM)
MKM was performed using the CHEMKIN kinetic libraries.39,40 The reactor was assumed to be an ideal plug flow reactor and simulated using a series of continuous stirred-tank reactors. The input energetics were obtained from the ML model, GCN scaling relations, and Brønsted–Evans–Polanyi (BEP) relationships. The thermal corrections to adsorption energies and transition states were calculated using the harmonic oscillator approximation with the Python Multiscale Thermochemistry Toolbox (pMuTT).41 To ensure thermodynamic consistency, we referenced the energies and thermochemistry of the intermediates to NIST experimental values as discussed in the literature.42,43The elementary reactions in the MKM were taken from our previous work44,45 and consisted of thermal and oxidative dehydrogenation reactions via O* and OH*. Overall, the model included 22 species (16 adsorbed and 6 gaseous species) and 40 elementary reactions. The elementary steps and their pre-exponential factors (sticking coefficients for adsorption reactions) and activation energies on Pt(111) are presented in Table S1.† The site occupancy of surface species is given in Table S2.† Lateral interactions of important reaction intermediates were included with coefficients taken from the literature45 (see Table S3†). Reaction conditions were those of the experiments,46 and the conversion was differential by varying the surface area to volume ratio.
Atomic structures and generalized coordination numbers
The generalized coordination number (GCN)17 was selected to represent the catalyst surface structures. GCN is a generalization of the conventional coordination number, which also takes account of the second nearest neighbors (see details in Note S1†). The extended surfaces and corresponding GCNs for developing GCN scaling relations were adopted from our previous work.47 Pt nanoparticles were constructed using the Atomic Simulation Environment (ASE).34 Each Pt atom in the outermost layer constituted a site, and its associated GCN was calculated.Results and discussion
Variance in experimental data
We mined experimental data for complete methane oxidation from ten published papers under similar reaction conditions. The experiments were conducted under 553–823 K and 1 atm over Pt/Al2O3. Only fuel-rich conditions were considered to avoid catalyst oxides,48,49 so the Pt's active phase is metallic.27,31 The results are shown in Fig. 1 (see detailed data in Table S4†).28–30,46,50–55 Due to many influential factors affecting the reaction rate that prevent direct comparison among experimental literature, e.g., knowledge of the exact surface area and active site, here we focus on reaction orders and apparent activation energies, which are essential kinetic signatures of catalyst reactivity. Fig. 1a shows that the apparent activation energy mainly falls between 20 and 30 kcal mol−1, with the lowest value at 4 kcal mol−1 and the highest at 47 kcal mol−1. The lowest activation energy may result from mass transfer effects, but the rest indicate some kinetic control. The reaction order of methane is mostly around 1.0, with one exception (a value of 0). The oxygen reaction order ranges from −0.6 to 1.3, indicating different reaction mechanisms. The variance of the experimental data is vast and beyond typical experimental errors.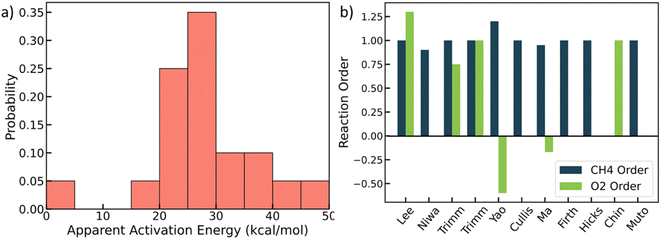 | ||
| Fig. 1 Experimental literature data. (a) Probability distribution of apparent activation energies (kcal mol−1); (b) reactions orders of methane and oxygen. See data in Table S4.† | ||
It is unclear where all this scatter arises from. This could be due to (poor) data quality in some of the works, such as lack of reproducibility, proper analytical calibrations and chromatographic columns, inappropriate analysis, or results from impurities and/or small water fractions in the feed, etc. Beyond data quality, other factors that may contribute to the observed scatter include different catalyst preparation methods and Pt salt precursors,56 different pretreatments, and differences in the support that result in different metal particle size and shape distributions. The latter group of factors underlines the structure sensitivity of a catalytic reaction. Here, we developed a structure-sensitive MKM to exploit the degree of explainability of the scatter of the data stemming from structure sensitivity.
Modeling overview
The overall modeling framework is depicted in Fig. 2. The development of the structure–activity relationship started with constructing catalyst particles of various sizes and shapes. The GCN was selected as the structure descriptor representing a nanoparticle's surface sites. The GCN values of selected extended surfaces were calculated to derive energetic parameters (Fig. S2†).Our previously developed machine learning (ML) model47 and GCN scaling relations were employed, with the most accurate of the two methods selected for estimating the adsorption energies of each species (Note S2†). Nearly all errors were within ±0.1 eV (Fig. S3 and Table S5†). Based on the error, GCN scaling relations were applied to estimate the adsorption energies of C* and H2O* and the ML model for all other species.
The rate-determining steps (RDS) of the overall reaction could be the first dehydrogenation of methane57 or the oxygen dissociation.53 Since the literature BEPs do not account for structure sensitivity, we developed scaling relations of the transition state (TS) energies of these two RDS vs. GCN, as shown in Fig. S4 and Table S6.† The R-squared value was chosen as an evaluation metric; the results showed that GCN correlates with both transition state energies very well. The slope of the scaling relation is indicative of the reaction structure sensitivity. The O2 dissociation is much more structure sensitive than the CH4 dehydrogenation reaction – the corresponding slopes are 0.40 and 0.08. For the remaining elementary steps, BEP relationships from the literature58,59 were adopted to estimate the activation barriers (see Table S7†).
With the necessary energetic parameters, a MKM for each site of a given structure was established. The accuracy of the GCN-dependent MKM was tested by comparing its performance to a DFT-based MKM and a BEP-based model (with DFT-calculated TS energies for the RDS), all on Pt(111), whose GCN is 7.5. We refer to these models as GCN-7.5, 111-DFT, and 111-BEP. The important kinetic signatures are compared in Table S8.† Except for the TOF, all other kinetic signatures calculated from the GCN-7.5 model are in good agreement with the 111-DFT model. The error in apparent activation energy is only 3 kcal mol−1, within the acceptable range. The TOF of GCN-7.5 model is one order of magnitude larger, and similar to the 111-BEP model, which indicates that the errors in the BEP-estimated activation barriers cause the difference. Considering the errors involved in estimating energetics, this deviation in the reaction rate is satisfactory for approximate models. Overall, our methodology can approximate first principles-based MKM results well.
Lastly, the total reaction rate for each nanoparticle was calculated by summing over all its site-specific rates weighed by their fractions. The particle-averaged kinetic signatures were calculated from the total reaction rate, similar to conducting experimental data analysis (Fig. 2).
GCN-dependent kinetic analysis
Kinetic analysis includes the estimation of TOF, surface coverages, reaction orders, apparent activation energies, and reaction paths. The results vs. GCN are summarized in Fig. 3. The model exhibits multiple kinetic regimes, demarcated by the surface coverages. For GCN < ∼5, the TOF increases sharply with increasing size (Fig. 3a). The TOF is extremely small due to poisoning of the surface by C* (Fig. 3b). The over-binding of C* blocks the active sites and leads to a high activation energy. Identified from sensitivity analysis by perturbing the pre-exponential factors,45 the RDS is O2 adsorption, leading to a positive reaction order in O2 and a negative in CH4 (Fig. 3c). All dehydrogenation reactions from to C* are equilibrated. The overall reaction is retarded by the sluggish removal of C* from the surface. The formation of C* from CH* proceeds by oxidative dehydrogenation (CH* + O* → C* + OH*) and is followed by the recombination with OH* to form CHO*.
to C* are equilibrated. The overall reaction is retarded by the sluggish removal of C* from the surface. The formation of C* from CH* proceeds by oxidative dehydrogenation (CH* + O* → C* + OH*) and is followed by the recombination with OH* to form CHO*.
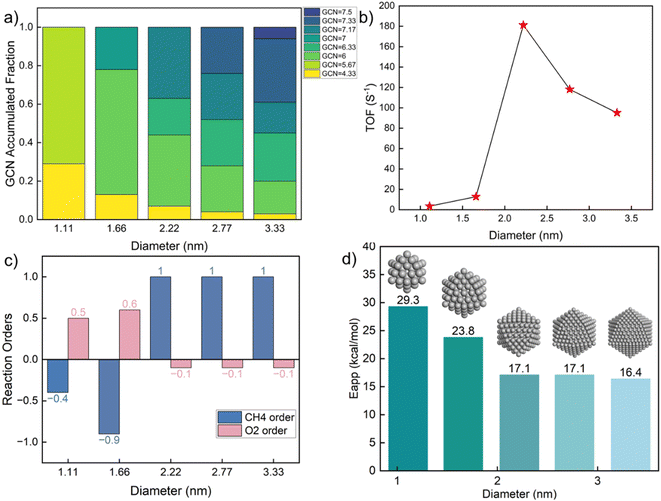
As the GCN increases above ∼5 and below ∼6.3, the C* binding is sufficiently weak, and the surface is gradually covered by CO* and C*. The TOF is high despite Eapp being large. For GCN between ∼6.3 and 7.2, CH* and CO* become the dominant surface species. The TOF reaches a maximum at a GCN of 7.17, above which, O* and vacancies form. The regime of the highest TOF coincides with the onset of significant free Pt sites. Above this GCN, the reaction product is purely CO2 without any trace of CO. This change in kinetics is manifested by the coordination-dependent reaction path bifurcation shown in Fig. 3e. For small GCNs, CH* dehydrogenates to form C* first, then CO* is produced from C* or COH*. In contrast, for large GCNs, CH* forms directly from CHO* without dehydrogenating to C*, as reported in the literature.24 The RDS is the CH4 first dehydrogenation reaction; thus, the reaction order of CH4 is 1 and of O2 is close to 0. The apparent activation energy in this regime decreases with increasing GCN. The smallest activation energy is about 10 kcal mol−1, and the largest is 32 kcal mol−1. Most values are between 20–30 kcal mol−1, similar to the experimental data (Fig. 1). Interestingly, the highest TOF doesn't correspond to the lowest Eapp, as the latter is a complex combination of kinetic and thermodynamic parameters and depends on the dominant surface species.
This dramatic change in model behavior with GCN is caused by the interplay of kinetics and thermodynamics. The adsorption energies of surface species and the activation barriers of elementary reactions depend on GCN. Surprisingly, our results reveal that, unlike the common expectation where the optimal activity occurs on low-coordinated sites, the prohibitively high C* coverage on the surface causes low activity and facilitates different reaction pathways. No detailed experimental data has been reported to our knowledge that exposes this behavior for this reaction. Coke formation induced by strong carbon binding has been predicted for complete methane oxidation under high reaction temperature.24 CO* inhibition of small Rh particles has also been reported experimentally,60 implying that this behavior probably also applies to other chemistries and is worth investigating further.
Structure effects on kinetics
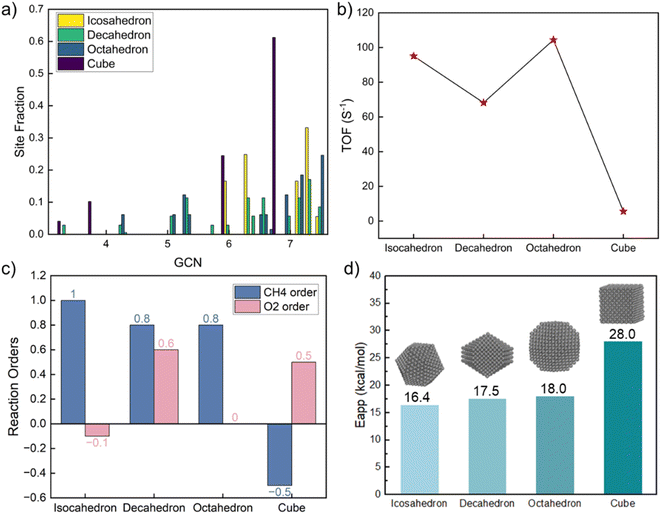
The above model explores the effect of GCN on activity and identifies the most active site but does not consider specific structures seen in the laboratory. One way to build structures is the Wulff construction. While doable, nanoparticle structures are not necessarily in equilibrium. Given that, we explored the reaction structure sensitivity as a function of size and shape to deduce the magnitude of data variation and the most desirable structures to make synthetically.To investigate shape effects, four morphologies were constructed, including icosahedron, decahedron, truncated octahedron, and cube (structures shown in Fig. S5†), which have been observed experimentally.61 Their sizes, chosen around 3 nm to minimize size effects, are consistent with experimental values.62 For each nanoparticle, GCNs of all atoms in the outermost layer, including facets, edges, and corners, were calculated. For studying size effects, icosahedron nanoparticles of five diameters were constructed (structures shown in Fig. S6†). To calculate the kinetics for each nanoparticle, firstly, the total reaction rate on each nanoparticle was calculated by simply summing over the TOF on every adsorption site multiplied by the fraction of each site (a similar spatial average approach was applied before to dehydrogenation).19,63 Then, the particle-averaged TOF was regressed to obtain the reaction orders and apparent activation energies, similarly to how experimental data is analyzed.
The GCN distribution varies with shape (Table S9† and Fig. 4a). The decahedron has the most diverse GCN numbers and a relatively uniform distribution. The icosahedron's GCN varies between 4.33 and 7.5; 7.33 is the most abundant. The octahedron's GCN varies between 4.25 and 7.5, with a considerable fraction of 7.5. Unlike other shapes, a cube shows only four distinct GCNs; the most abundant one is 6.67. Congruent with the GCN distributions, the three shapes share similar kinetics except for the cube, as shown in Fig. 4. The CH4 reaction order is close to one for the three shapes but negative for the cube. The O2 reaction order ranges from negative to positive, reminiscent of the experimental data in Fig. 1. As the dominant GCN on cubes is 6.67, which is below the optimum 7.17, the surface is mainly covered by CH* and CO*, leading to a significantly lower reaction rate, different reaction orders, and a much higher apparent activation energy. The highest TOF on the octahedron is 20 times larger than on the cube, indicating the significance of shape effects. Our findings underscore that cubic nanoparticles should be avoided for complete methane oxidation but may be useful for syngas production. The average TOF varies by up to 30% among the icosahedron, decahedron, and octahedron shapes.
To explore the effect of nanoparticle size on kinetics, we constructed icosahedral particles with a diameter ranging from 1 to 3 nm and calculated the GCN distributions of surface atoms (Table S10† and Fig. 5a). Small nanoparticles (∼1 nm) expose a few, distinct, highly undercoordinated sites. In contrast, larger nanoparticles exhibit a broader distribution, including larger GCNs (more highly coordinated sites), as expected. The kinetics (Fig. 5b) shows a remarkable variation with changing diameter at ∼2 nm, where the TOF reaches a maximum. Similar observations have also been reported in experiments.64–67 Consistent with Fig. 3, smaller Pt particles are richer in undercoordinated sites of lower activity due to prohibitively high coverage of C*. As a result, the oxygen reaction order becomes positive (Fig. 5c), and the apparent activation energy is high (Fig. 5d). The surface of large nanoparticles consists of high coordination sites, leading to a decrease in the apparent activation energy and a change in reaction orders. The fraction of sites with near optimum GCN of 7.17 drops with increasing size from 2.22 to 2.77 to 3.33 nm due to forming more extended (111) facets.
The above results indicate a significant structure sensitivity of complete methane oxidation with varying GCN through size and shape over a wide range. This structure sensitivity is only modest over a narrower GCN range. The most abundant GCN on the surface dominates the nanoparticle kinetic behavior. When the abundant sites are low coordinated, the CH4 reaction order is negative and the O2 reaction order is positive, with a high apparent activation energy. In contrast, for larger nanoparticles with highly coordinated surface sites, the CH4 order is close to one and the O2 reaction order is zero. The surfaces of small, well-faceted nanoparticles only possess limited types of GCNs. Yet, a small fraction of different GCNs can profoundly alter the kinetic performance. As shown in Fig. 5c, a slight change in the particle diameter from 1.66 to 2.22 nm qualitatively alters the reaction pathways. To demonstrate the application of our methodology for realistic catalysts, we took the particle size distribution reported by Lee et al.46 as an example. Assuming the particles followed a log normal distribution, the estimated probability density function (pdf) is plotted in Fig. S7.† Combining the calculated probability (see Table S11†) with the size-dependent reactivity results in Fig. 5b, we estimated the averaged reaction rate to be 21.9 s−1 with significant variation across the particle size distribution. The results suggest an optimal reactivity for a particle size of around 2 nm.
Connections to experimental data and future applications
By combining the GCN distributions with GCN-dependent kinetic analysis, we can rationalize most of the observed experimental data variance shown in Fig. 1. Such differences could emerge from differences in Pt particle structures. Most of the apparent activation energies collected from experimental literature fall between 15–30 kcal mol−1, consistent with our simulation results in Fig. 4d and 5d. The experimental outliers outside the range generated by the MKM (see Fig. 3d) could be caused by other factors discussed above that seem to also be at play but their effect is secondary. The observed experimental variance in O2 reaction order can be caused by both particle shapes (cube) and sizes (smaller particles), indicating more rigorous catalyst characterization should be reported along with kinetic performance. The long-standing structure sensitivity or insensitivity debate for complete methane oxidation can also be explained by particle size effects. Only when the synthesized nanoparticles are small, the reaction shows structure sensitivity. As the diameter becomes large, the reaction becomes structure insensitive.To identify the active sites in future experiments, we propose performing size and shape analysis as done here to explore structure sensitivity and demarcate the boundaries of kinetic regimes of each chemistry. Subsequently, one can fit a distribution of sites to the kinetic data and interrogate it with microscopy and infrared spectroscopy. Detailed characterization analysis, such as high-resolution transmission electron microscopy (HRTEM) and extended X-ray absorption fine structure (EXAFS), could provide more detailed information about particle structures to refine our approach. The developed methodology here can serve to explore structure–activity relations of catalytic reactions. It could be used to assess experimental data quality; data unexplained by the model structure sensitivity implicate a unique catalyst or data quality issues arising from dopants, impurities, etc.
Conclusions
Many catalytic reactions depict a significant variation in kinetic parameters, but the reasons have remained elusive. A GCN-dependent microkinetic modeling methodology was introduced to exploit the degree of experimental data scatter stemming from structure sensitivity. The approach was applied to the complete methane oxidation on Pt. The results show that Pt site coordination can profoundly impact the kinetic performance and reaction paths. Both particle morphology and diameter can significantly influence reaction kinetics. An optimum site with GCN of 7.17 was identified for this chemistry. Undercoordinated sites overbind carbon, leading to catalyst poisoning and a very low reaction rate. A broad site distribution could reconcile most of the data scatter in the published literature; additional factors rationalizing data outside the predicted distribution of kinetics were discussed. The method introduced here enables studying the geometric and size effects for other complex reactions and predicting optimal catalyst structures. Importantly, it also provides a data quality metric for experimental data falling outside the predicted kinetics range.Data availability
All the data supporting this work have been included in the main text and the ESI.†Author contributions
X. Z. performed all DFT calculations and microkinetic modeling. D. G. V. contributed to the idea, funding acquisition, and supervision. Both authors contributed to analyzing the results and writing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the RAPID manufacturing institute, supported by the Department of Energy (D.O.E.) Advanced Manufacturing Office (A.M.O.), award number DE-EE0007888-9.5, is gratefully acknowledged. RAPID projects at the University of Delaware are also made possible in part by funding provided by the State of Delaware. The Delaware Energy Institute gratefully acknowledges the support and partnership of the State of Delaware in furthering the essential scientific research being conducted through the RAPID projects. The authors acknowledge Kelly Walker for the graph design.References
- L. Liu and A. Corma, Chem. Rev., 2018, 118, 4981–5079 CrossRef CAS PubMed.
- Z. Li, S. Ji, Y. Liu, X. Cao, S. Tian, Y. Chen, Z. Niu and Y. Li, Chem. Rev., 2020, 120, 623–682 CrossRef CAS PubMed.
- S. Cao, F. Tao, Y. Tang, Y. Li and J. Yu, Chem. Soc. Rev., 2016, 45, 4747–4765 RSC.
- R. Narayanan and M. A. El-Sayed, Nano Lett., 2004, 4, 1343–1348 CrossRef CAS.
- M. Laskar and S. E. Skrabalak, ACS Catal., 2014, 4, 1120–1128 CrossRef CAS.
- A. Ruditskiy, H.-C. Peng and Y. Xia, Annu. Rev. Chem. Biomol. Eng., 2016, 7, 327–348 CrossRef CAS PubMed.
- R. Cheula, A. Soon and M. Maestri, Catal. Sci. Technol., 2018, 8, 3493–3503 RSC.
- R. Cheula, M. Maestri and G. Mpourmpakis, ACS Catal., 2020, 10, 6149–6158 CrossRef CAS.
- Z. W. Ulissi, A. J. Medford, T. Bligaard and J. K. Nørskov, Nat. Commun., 2017, 8, 14621 CrossRef PubMed.
- Y. Shi, Z. Lyu, M. Zhao, R. Chen, Q. N. Nguyen and Y. Xia, Chem. Rev., 2021, 121, 649–735 CrossRef CAS PubMed.
- B. W. J. Chen, L. Xu and M. Mavrikakis, Chem. Rev., 2021, 121, 1007–1048 CrossRef CAS PubMed.
- Z. Li, N. Li, N. Wang, B. Zhou, P. Yin, B. Song, J. Yu and Y. Yang, ACS Omega, 2022, 7, 3514–3521 CrossRef CAS PubMed.
- W. Zhao, L. Ma, B. Wang, L. Ling and R. Zhang, J. Phys. Chem. C, 2021, 125, 23085–23097 CrossRef CAS.
- K. Kaźmierczak, P. Clabaut, R. Staub, N. Perret, S. N. Steinmann and C. Michel, J. Phys. Chem. C, 2021, 125, 10370–10377 CrossRef.
- Y. Wang, L. Xiao, Y. Qi, J. Yang, Y.-A. Zhu and D. Chen, J. Phys. Chem. C, 2020, 124, 2501–2512 CrossRef CAS.
- F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, P. Sautet and D. Loffreda, Angew. Chem., Int. Ed., 2014, 53, 8316–8319 CrossRef CAS PubMed.
- F. Calle-Vallejo, J. Tymoczko, V. Colic, Q. H. Vu, M. D. Pohl, K. Morgenstern, D. Loffreda, P. Sautet, W. Schuhmann and A. S. Bandarenka, Science, 2015, 350, 185–189 CrossRef CAS PubMed.
- M. Jørgensen and H. Grönbeck, Angew. Chem., Int. Ed., 2018, 57, 5086–5089 CrossRef PubMed.
- T. Shen, Y. Yang and X. Xu, Angew. Chem., Int. Ed., 2021, 60, 26342–26345 CrossRef CAS PubMed.
- M. Jørgensen and H. Grönbeck, ACS Catal., 2017, 7, 5054–5061 CrossRef.
- J. A. Labinger and J. E. Bercaw, Nature, 2002, 417, 507–514 CrossRef CAS PubMed.
- C. Hammond, S. Conrad and I. Hermans, ChemSusChem, 2012, 5, 1668–1686 CrossRef CAS PubMed.
- J. Nilsson, P.-A. Carlsson, S. Fouladvand, N. M. Martin, J. Gustafson, M. A. Newton, E. Lundgren, H. Grönbeck and M. Skoglundh, ACS Catal., 2015, 5, 2481–2489 CrossRef CAS.
- J. S. Yoo, J. Schumann, F. Studt, F. Abild-Pedersen and J. K. Nørskov, J. Phys. Chem. C, 2018, 122, 16023–16032 CrossRef CAS.
- J. Nilsson, P.-A. Carlsson, N. M. Martin, E. C. Adams, G. Agostini, H. Grönbeck and M. Skoglundh, J. Catal., 2017, 356, 237–245 CrossRef CAS.
- J. S. Yoo, T. S. Khan, F. Abild-Pedersen, J. K. Nørskov and F. Studt, Chem. Commun., 2015, 51, 2621–2624 RSC.
- A. Trinchero, A. Hellman and H. Grönbeck, Surf. Sci., 2013, 616, 206–213 CrossRef CAS.
- K. Otto, Langmuir, 1989, 5, 1364–1369 CrossRef CAS.
- C. F. Cullis and B. M. Willatt, J. Catal., 1983, 83, 267–285 CrossRef CAS.
- R. F. Hicks, H. Qi, M. L. Young and R. G. Lee, J. Catal., 1990, 122, 280–294 CrossRef CAS.
- R. Burch and P. K. Loader, Appl. Catal., B, 1994, 5, 149–164 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dulak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- G. Henkelman and H. Jonsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901 CrossRef CAS.
- G. Henkelman and H. Jonsson, A dimer method for finding saddle points on high dimensional potential surfaces using only first derivatives, J. Chem. Phys., 1999, 111, 7010 CrossRef CAS.
- R. J. Kee, F. M. Rupley and J. A. Miller, The Chemkin Thermodynamic Data Base, Sandia National Lab, No. SAND87-8215B, 1990 Search PubMed.
- R. J. Kee, F. M. Rupley and J. A. Miller, Chemkin-II: A Fortran chemical kinetics package for the analysis of gas-phase chemical kinetics, Sandia National Lab, No. SAND89-8009, 1989 Search PubMed.
- J. Lym, G. R. Wittreich and D. G. Vlachos, Comput. Phys. Commun., 2020, 247, 106864 CrossRef CAS.
- M. Salciccioli, M. Stamatakis, S. Caratzoulas and D. G. Vlachos, Chem. Eng. Sci., 2011, 66, 4319–4355 CrossRef CAS.
- D. W. Blaylock, T. Ogura, W. H. Green and G. J. O. Beran, J. Phys. Chem. C, 2009, 113, 4898–4908 CrossRef CAS.
- T. Xie, G. R. Wittreich and D. G. Vlachos, Appl. Catal., B, 2022, 316, 121597 CrossRef CAS.
- N. R. Peela, J. E. Sutton, I. C. Lee and D. G. Vlachos, Ind. Eng. Chem. Res., 2014, 53, 10051–10058 CrossRef CAS.
- G. Lee, W. Zheng, K. A. Goulas, I. C. Lee and D. G. Vlachos, Ind. Eng. Chem. Res., 2019, 58, 17718–17726 CrossRef CAS.
- X. Zong and D. G. Vlachos, J. Chem. Inf. Model., 2022, 62, 4361–4368 CrossRef CAS PubMed.
- C. P. O'Brien, G. R. Jenness, H. Dong, D. G. Vlachos and I. C. Lee, J. Catal., 2016, 337, 122–132 CrossRef.
- A. A. Saraev, S. A. Yashnik, E. Y. Gerasimov, A. M. Kremneva, Z. S. Vinokurov and V. V. Kaichev, Catalysts, 2021, 11, 1446 CrossRef CAS.
- M. Niwa, K. Awano and Y. Murakami, Appl. Catal., 1983, 7, 317–325 CrossRef CAS.
- J. G. Firth and H. B. Holland, Trans. Faraday Soc., 1969, 65, 1121 RSC.
- I. Yu. Pakharukov, A. Yu. Stakheev, I. E. Beck, Y. V. Zubavichus, V. Yu. Murzin, V. N. Parmon and V. I. Bukhtiyarov, ACS Catal., 2015, 5, 2795–2804 CrossRef CAS.
- Y.-H. Chin, C. Buda, M. Neurock and E. Iglesia, J. Am. Chem. Soc., 2011, 133, 15958–15978 CrossRef CAS PubMed.
- D. L. Trimm and C.-W. Lam, Chem. Eng. Sci., 1980, 35, 1405–1413 CrossRef CAS.
- L. Ma, D. L. Trimm and C. Jiang, Appl. Catal., A, 1996, 138, 275–283 CrossRef CAS.
- V. A. Drozdov, P. G. Tsyrulnikov, V. V. Popovskii, N. N. Bulgakov, E. M. Moroz and T. G. Galeev, React. Kinet. Catal. Lett., 1985, 27, 425–427 CrossRef CAS.
- W. Qi, J. Ran, R. Wang, X. Du, J. Shi and M. Ran, Comput. Mater. Sci., 2016, 111, 430–442 CrossRef CAS.
- J. E. Sutton, P. Panagiotopoulou, X. E. Verykios and D. G. Vlachos, J. Phys. Chem. C, 2013, 117, 4691–4706 CrossRef CAS.
- J. E. Sutton and D. G. Vlachos, ACS Catal., 2012, 2, 1624–1634 CrossRef CAS.
- M. Schumann, M. R. Nielsen, T. E. L. Smitshuysen, T. W. Hansen, C. D. Damsgaard, A.-C. A. Yang, M. Cargnello, J.-D. Grunwaldt, A. D. Jensen and J. M. Christensen, ACS Catal., 2021, 11, 5189–5201 CrossRef CAS.
- F. H. Kaatz and A. Bultheel, Nanoscale Res. Lett., 2019, 14, 150 CrossRef PubMed.
- G. Corro, J. Cruz-Mérida, D. Montalvo and U. Pal, Ind. Eng. Chem. Res., 2021, 60, 18841–18852 CrossRef CAS.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef PubMed.
- I. E. Beck, V. I. Bukhtiyarov, I. Yu. Pakharukov, V. I. Zaikovsky, V. V. Kriventsov and V. N. Parmon, J. Catal., 2009, 268, 60–67 CrossRef CAS.
- A. M. Gololobov, I. E. Bekk, G. O. Bragina, V. I. Zaikovskii, A. B. Ayupov, N. S. Telegina, V. I. Bukhtiyarov and A. Yu. Stakheev, Kinet. Catal., 2009, 50, 830 CrossRef CAS.
- A. Yu. Stakheev, A. M. Gololobov, I. E. Beck, G. O. Bragina, V. I. Zaikovsky, A. B. Ayupov, N. S. Telegina and V. I. Bukhtiyarov, Russ. Chem. Bull., 2010, 59, 1713–1719 CrossRef CAS.
- A. Yu. Stakheev, A. M. Batkin, N. S. Teleguina, G. O. Bragina, V. I. Zaikovsky, I. P. Prosvirin, A. K. Khudorozhkov and V. I. Bukhtiyarov, Top. Catal., 2013, 56, 306–310 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc06819b |
| This journal is © The Royal Society of Chemistry 2023 |

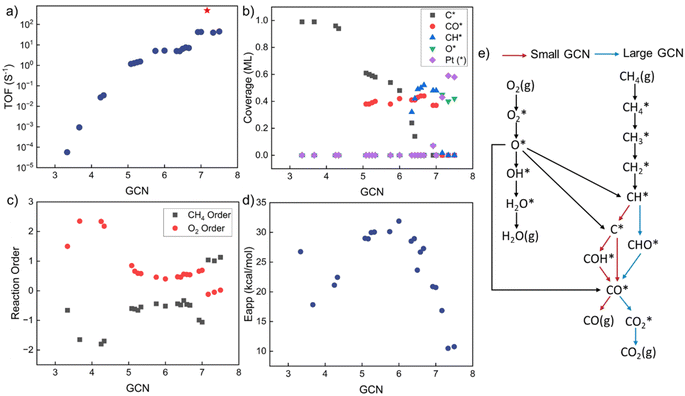
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O2 = 1% balanced by He and a temperature of 613 K; (c) reaction orders of CH4 and O2; (d) apparent activation energies (kcal mol−1).
O2 = 1% balanced by He and a temperature of 613 K; (c) reaction orders of CH4 and O2; (d) apparent activation energies (kcal mol−1).