Can anions possess bound doubly-excited electronic states?

Abstract

Anions play an important role in many fields of chemistry. Many molecules possess stable anions, but these anions often do not have stable electronic excited states and the anion loses its excess electron once excited. All the known stable valence excited states of anions are singly-excited states, i.e., valence doubly-excited states have not been reported. As excited states are relevant for numerous applications, and constitute basic properties, we searched for valence doubly-excited states which are stable, i.e., exhibit energies below that of the ground state of the respective neutral molecule. We concentrated on two promising prototype candidates, the anions of the smallest endocircular carbon ring Li@C₁₂ and of the smallest endohedral fullerene Li@C₂₀. By employing accurate state-of-the-art many-electron quantum chemistry methods, we investigated the low-lying excited states of these anions and found that they possess several low-lying stable singly-excited states and, in particular, a stable doubly-excited state each. It is noteworthy that the found doubly-excited state of Li@C₁₂⁻ possesses a cumulenic carbon ring in sharp contrast to the ground and singly-excited states. The findings shed light on how to design anions with stable valence singly- and doubly-excited states. Possible applications are mentioned.

---

1 Introduction

Anions are fascinating subjects in modern chemistry. Although they are abundant even in space,¹ not every molecule can accommodate an extra electron and form a bound anion.² Prominent examples are the molecules N₂ and CO.³ The main reason for the instability of anions is the spontaneous emission of electrons due to the electron–electron repulsion.^3,4 Theoretical investigations of anions and their excited states are necessary since their properties are often difficult to study experimentally. Excited states of anions have promising application potential in many fields, such as organic transformations,⁵ multi-photon redox catalysis,⁶ and electron acceptors in polar cells.⁷ The fundamental property of these applications is the ability of accepting extra electrons playing the role of electron acceptors.⁷ However, most of the excited states cannot fulfill this purpose because of their short life-time and unstable nature. Typically, the excited states of stable closed-shell anions are metastable resonance states and not bound states.⁸ The question of how to design anions with stable excited states is still unanswered.

Doubly-excited states of neutral systems are quite common in nature and one can find them even in the smallest molecules like H₂.⁹ Doubly-excited states of molecules and cations have been widely applied in several fields.^10,11 Usually, the interesting doubly-excited states are the ones with two electrons excited from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO). Such states are “dark” as they cannot be reached from the ground state by the absorption of a single photon, but they are known to play an important role in photochemistry.¹⁰ After excitation of cyclopentadiene, for instance, the excited bright state relaxes extremely fast to the dark state within 37 femto-seconds.¹² It is generally necessary to study dark states to understand the relaxation process. Excited states localized on one chromophore can decay into doubly-excited states of different chromophore dimers,¹³ and doubly-excited states commonly play an important role in singlet fission generating charge carriers in solar cells,¹⁴ astrophysical plasmas¹⁵ and ionic plasmas.¹⁶

In view of the relative scarcity of stable singly-excited states of anions, one may wonder whether anions can exhibit low-lying and stable doubly-excited states. Until now, we have only found reports on double-Rydberg anions, such as N₂H₇⁻,^17–19 where a closed-shell cationic core supports the binding of two electrons in diffuse Rydberg-like orbitals. To the best of our knowledge, there is no report on stable doubly-excited valence states of anions.

How to start the search for suitable anions supporting stable doubly-excited states? One may anticipate that molecules that possess several bound singly-excited states are suitable candidates. We first envisage an endocircular carbon ring. Carbon rings have attracted much attention over many years. Two decades ago, it was found that carbon ring anions possess considerable electron affinities (EAs) and can be observed in experiments.²⁰ Indeed, we found that the carbon ring anion C₂₀⁻ which has a considerable EA, possesses three stable low-lying singly-excited states.²¹ Recently, researchers successfully synthesized and characterized properties of the C₁₈ ring,²² and this led to a further increase of the interest in carbon rings. More recently, interest has arisen in endocircular carbon rings,^23–27 in which the carbon ring encircles a metal atom. These studies are, however, not on the anionic system. Our present work is the first attempt to study the ground and excited states of an endocircular carbon ring anion. Our main emphasis is to find a stable low-lying doubly-excited state.

Fullerenes,²⁸ constitute another class of promising candidates as they form strongly bound anions and even long-lived multiply-charged anions.^3,4 As an example, several stable valence and non-valence singly-excited states have been found in the C₆₀⁻ anion.^28–34 By introducing alkali guest atoms into the fullerene cage, the daughter endohedral fullerenes have been seen to possess more stable low-lying states than the parent fullerene anions.^35–37 We would like to answer the question whether endohedral fullerene anions can support stable doubly-excited excited states.

Since doubly-excited states are difficult to calculate and highly accurate computational methods are required, it is necessary to choose systems of the size which can be attacked by such methods. In this work, we focus on the anions of the smallest endocircular carbon ring Li@C₁₂ and the smallest endohedral fullerene Li@C₂₀. We employed the state-of-the-art coupled cluster methods to study the ground state, the low-lying singly-excited states and most of all the doubly-excited states. We found each of these systems to possess several low-lying stable singly-excited states and at least one doubly-excited state. Such doubly-excited states are hitherto unknown. In all these states, the extra electron of the anion and the valence electron of Li are delocalized on the carbon ring. The energy of the doubly-excited states is much lower than that of the respective neutral system. It is noteworthy that at its optimized geometry, the doubly-excited state of the endocircular Li@C₁₂⁻ is found to be cumulenic. There is a long ongoing search in the literature for cumulenic systems also due to their potential applications.^22,38–41

Before addressing the results, we discuss the methods of calculation. We have optimized the equilibrium geometries of the ground states of Li@C₁₂⁻ and Li@C₂₀⁻ employing the coupled-cluster singles and doubles (CCSD)⁴² method with the CFOUR code.⁴³ To study the singly-excited electronic states, the equation-of-motion coupled cluster method for electron excitations (EE-EOM-CCSD)⁴⁴ has been used based on the Hartree–Fock wavefunctions of the closed-shell Li@C₁₂⁻ and Li@C₂₀⁻ as reference functions. To find the equilibrium geometries of the closed-shell doubly-excited states, we employed the so-called delta-SCF procedure within the CCSD method.⁴⁵ To ensure that the found geometries provide minima on the energy surfaces, we have computed the respective harmonic vibrational frequencies. The basis set used is Dunning's correlation-consistent triple-zeta (cc-pVTZ)^46,47 set which is considered to be a solid and reliable basis set.⁴⁸ Due to limitations in resources, we did not add diffuse functions and the computed electron affinities are likely to be too low, implying that the anion is expected to be even more stable than reported here. The validity of CCSD and EOM-CCSD has been confirmed in many cases and it has been explicitly reported that CCSD correctly predicts the structure of carbon rings.^22,49,50 The triple excitations which are missing in these methods and are much too expensive to be included, can only be expected to have a minor impact on the ground state,⁴⁸ but to further energetically lower and hence stabilize the doubly-excited states investigated here. In all calculations, the core orbitals of carbon and lithium were kept active in all the studies. Many useful results not shown in the main text, like the vibrational frequencies, are collected in the ESI.†

2 Results and discussion

An endocircular system consists of a guest atom and a ring of identical atoms around it. Since the smallest carbon ring found in experiment is C₁₀,^51,52 one may naturally assume that the smallest endocircular carbon ring system is formed by C₁₀ or may be C₁₁ carbon rings. However, our results show that the C₁₀ and C₁₁ rings cannot accommodate a Li guest atom and form an endocircular carbon ring system. The details of the calculations can be found in Section S1 of the ESI.† The smallest endocircular system we found is Li@C₁₂ and its anion Li@C₁₂⁻ is the endocircular carbon ring we investigate.

The optimized equilibrium geometries of the ground state and of the doubly-excited state of the anion are shown in Fig. 1. The coordinates and harmonic vibrational frequencies of these structures are collected in Sections S2 and S3 of the ESI,† respectively. All the frequencies are real proving that the structures shown in Fig. 1 correspond to minima on the respective energy surfaces. The ground state is the charge-separated state with a cationic Li⁺ guest atom and a strongly distorted dianionic carbon ring. The strong distortion is the result of accommodating two extra electrons repelling each other but being electrostatically attracted by the metal cation. The geometry reminds of that of the ground state of the neutral endocircular Mg@C₁₂ ring,²⁷ and looks like a slightly drawn bow. This similarity may be attributed to the C₁₂²⁻ dianionic ring surrounding a positive ion in both systems. Correspondingly, both systems, neutral Mg@C₁₂ and the Li@C₁₂⁻ anion, possess a similar HOMO and LUMO pair as they are located on the carbon ring. The doubly-excited state of the Li@C₁₂⁻ will be addressed later on.

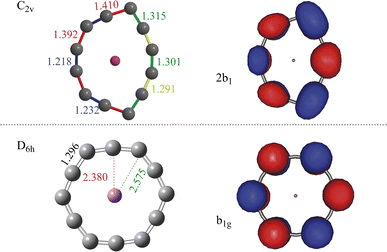Fig. 1 Equilibrium geometries and natural orbitals of Li@C₁₂⁻. The natural orbitals shown resemble the Hartree–Fock HOMOs of the respective states and are referred to here and throughout the paper as the highest occupied natural orbitals. Upper panel: The equilibrium geometry of the ground state (closed shell, C_2v symmetry) and its highest occupied natural orbital. Lower panel: The equilibrium geometry of the doubly-excited state (closed shell, cumulenic D_6h symmetry) and its highest occupied natural orbital. The occupation numbers of the natural orbitals shown are 1.890 (ground state) and 1.900 (doubly-excited state). For the contributing Hartree–Fock orbitals see Tables S3 and S5 and Section S8 of the ESI.† Note that both states are charge-separated with two excess electrons being on the carbon ring which surrounds the positive lithium ion and the natural orbitals shown accommodate these electrons. The results were obtained on the CCSD level with the correlation-consistent triple-zeta basis set. The bond lengths are in Å.

To have the full picture of the excited states of Li@C₁₂⁻, we studied the triplet and singlet singly-excited states of Li@C₁₂⁻ in its ground state equilibrium geometry. The low-lying singlet and triplet states are shown in Fig. 2 and a more complete account of the states is provided in Section S4 of the ESI.† One finds that there are three low-lying singly-excited triplet states and three singlet singly-excited states of Li@C₁₂⁻, which are lower in energy than the ground state of neutral Li@C₁₂ in its equilibrium geometry. These low-lying excited states are bound states, i.e., they are stable against spontaneous loss of an electron. It is noteworthy that all three low-lying triplet states (1³B₂, 1³B₁, and 1³A₂) as well as their singlet counterparts are formed by a single-electron excitation from occupied orbitals to the LUMO. This is probably due to the large energy gap between the LUMO and the other virtual orbitals. All the low-lying singly-excited states shown in Fig. 2 are valence to valence singly-excited states and all the stable states of Li@C₁₂⁻ are valence states. The non-charge-separated states are not energy favored and they are higher in energy than the neutral Li@C₁₂ and thus not bound. Electrons in the non-charge-separated orbitals reduce the stabilizing effect of the guest metal cation.

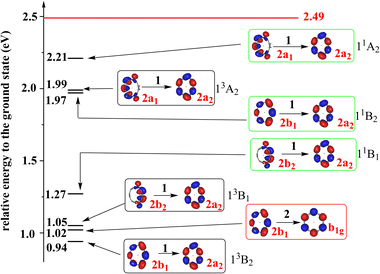Fig. 2 The energies of the low-lying excited states of Li@C₁₂⁻ relative to that of its global ground state. The states in black, green and red blocks are singly-excited triplet states, singly-excited singlet states and the doubly-excited singlet state, respectively. The doubly-occupied HOMO of the doubly-excited state and the singly-occupied orbitals of the singly-excited states are shown. The irreducible representations of the orbitals and states are indicated. The 2b₁ and 2a₂ orbitals are the HOMO and LUMO of the ground state, respectively. The energies of the singly-excited states are vertical excitation energies based on the equilibrium geometry of the anion in its ground state. The energy of doubly-excited is calculated using its own optimized equilibrium geometry. To each triplet state there is a corresponding open-shell singlet state at higher energy with a similar electronic structure. All states are charge-separated (CS) states where Li has donated its valence electron to the ring. The red horizontal line indicates the relative energy of the ground state of the neutral Li@C₁₂ system in its equilibrium geometry. The electron affinity of Li@C₁₂ is 2.49 eV. All the states below the horizontal red line are thus bound states. Additional states at higher energies and a list of the frontier orbitals are given in the ESI (Fig. S2 and S3, Table S5†).

As mentioned above, a low-lying and bound doubly-excited valence state is found and also depicted in Fig. 2. Surprisingly, this singlet anionic state is as much as about 1.5 eV lower in energy than the ground state of the neutral Li@C₁₂ at its equilibrium geometry. And, may be even more surprising, it seems to be lower in energy than all singly-excited singlet states, see also Fig. S3 in the ESI.† Care must be taken here as the doubly-excited state is at its own equilibrium geometry and the singly-excited states at the equilibrium geometry of the anion in its ground state. It could thus be that the doubly-excited state and the lowest singlet singly-excited state (1¹B₁) will be closer in energy at some geometries and exhibit a conical intersection as closely lying states are likely to have conical intersections.⁵³ A conical intersection between two states of such different electronic character is of general interest and may lead to unusual dynamics.

The geometry of the Li@C₁₂⁻ anion in its doubly-excited state is shown in the lower panel of Fig. 1. To assure that the optimized geometry is related to a minimum of the energy, all the harmonic vibrational frequencies at this equilibrium geometry have been computed and found to be real (see Section S3 of the ESI†). As seen in Fig. 1, the doubly-excited state is also a charge-separated state with two extra electrons on the ring. Interestingly, unlike the distorted ring structure of the ground state, the ring of the doubly-excited state in the lower panel is of a highly-symmetric shape (D_6h). Noteworthy is that, at the equilibrium geometry of the doubly-excited state, all the C–C bonds of the carbon ring are of equal length (1.296 Å). In this state, with the aid of the two extra excited electrons a cumulenic structure of the carbon ring is obtained. In the literature, cumulenic chains constitute an interesting topic of research, as they play roles in applications, such as controlling the electronic properties and nanostructure of the material,⁵⁴ and building blocks of supramolecular systems.⁵⁵ Cumulenic chains are known to mediate charge transfer^41,56–59 and we assume that cumulenic rings may also be utilized in charge transfer processes.

To better understand the doubly-excited states of the Li@C₁₂⁻ anion, we scanned the potential energy surfaces of its low-lying three closed-shell states along two minimum energy pathways. The results are shown in Fig. 3. The computational details and the orbital compositions of the curves are shown in Section S8 of the ESI.† The states are numbered 1¹A₁, 2¹A₁ and 3¹A₁ according to their lowest possible energies. At the equilibrium geometry of the anion's ground state 1¹A₁ (C_2v symmetry, left side of the figure), there are two doubly-excited states, the lower one (3¹A₁, blue curve) is below the energy of the neutral (dashed curve) at the same geometry, while the upper one (2¹A₁, green curve) is above this energy. Both doubly-excited states drop strongly in energy along the minimum energy pathway (q₁) maintaining their electronic composition to arrive at a polyynic D_6h structure where the 2¹A₁ state is a transition state. The ground state 1¹A₁ grows in energy (red curve) along this pathway maintaining its electronic composition. From the polyynic D_6h structure, the 2¹A₁ state relaxes along the minimum energy pathway q₂ maintaining its electronic composition to arrive at its absolute minimum which is the cumulenic D_6h structure discussed above (Fig. 1 and 2), while the 3¹A₁ state grows in energy. Thus, the 2¹A₁ state is a bound and stable doubly-excited state of the anion which can be reached by a vertical excitation from the anion's ground state either directly, if it lives long enough at C_2v as it is energetically above the energy of the neutral, or indirectly via the vertical excitation to the bound 3¹A₁ doubly-excited state, as seen in Fig. 3.

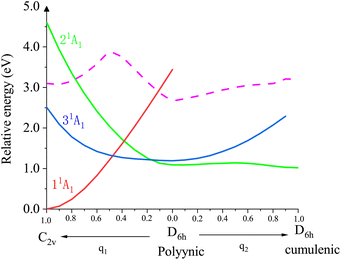Fig. 3 Cuts through the potential energy surfaces of the three low-lying closed-shell states (solid lines) of the Li@C₁₂⁻ anion along the q₁ and q₂ modes. The equilibrium geometry of the ground state 1¹A₁ is C_2v (left corner). At this geometry, there are two doubly-excited states (3¹A₁ and 2¹A₁). q₁ and q₂ are two minimum energy pathways. Along the q₁ mode, the system keeps C_2v symmetry and along q₂, the system keeps C_2h symmetry. Along these pathways the states maintain their electronic structure. Starting at C_2v, the doubly-excited states drop in energy and arrive at a D_6h polyynic geometric structure, where the 2¹A₁ state is a transition state continuing along q₂ to the D_6h cumulenic structure discussed in Fig. 1 and 2. This structure is a bound and stable state with all frequencies real. For completeness, the energy curve of the neutral Li@C₁₂ along q₁ and q₂ is also shown (dashed curve). The dashed line is the energy for vertical ionization and everything vertically below the dashed line is bound. More details are given in the text and in the ESI, Sections S8 and S9,† including a calculation in C_2v demonstrating the single-reference character of all states shown.

Are anions with rings unique, or do other kinds of anions also possess low-lying doubly-excited states? As mentioned in the Introduction, potential candidates are anions with several bound singly-excited states as Li@C₁₂⁻ and endohedral fullerene anions. Now, we turn to the endohedral fullerene anion Li@C₂₀⁻. C₂₀ is the smallest fullerene. Unlike C₆₀, due to the Jahn–Teller effect,^60,61 its neutral geometry is not in I_h symmetry. The resulting distorted geometries can be in three possible symmetries: D_2h, D_3d and D_5d. We have optimized the geometries of Li@C₂₀⁻ in these three symmetries and found that the geometry in D_5d is the one with the lowest energy (see Section S5 of the ESI†). Its all real vibrational frequencies ensured this geometry to be at a minimum of the energy surface (see Section S6 of the ESI†). Thus, the global energy minimum of Li@C₂₀⁻ is in D_5d symmetry.

The singly-excited electronic states of the Li@C₂₀⁻ anion have been computed and the low-lying ones are shown together with their energies relative to the anion's ground state energy in Fig. 4, all computed at the geometry of the latter. The other states are collected in the ESI, Section S7.† All low-lying states computed are found to be valence states. This anion possesses more bound singly-excited states than the endocircular anion discussed above. Whether this is due to the cage or just due to the larger number of carbon atoms which accommodate the two excess electrons remains an open question. Clearly, as for the endocircular anion, all low-lying electronic states are charge-separated states where the carbon cage carries the two excess electrons and the metal atom is positively charged.

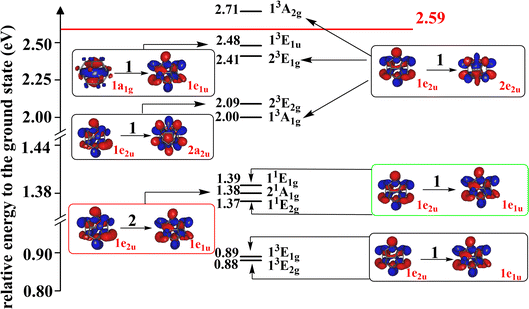Fig. 4 The energies of the low-lying excited states of Li@C₂₀⁻ relative to that of its global ground state. The states in black, green and red blocks are singly-excited triplet states, singly-excited singlet states and the doubly-excited singlet state, respectively. The doubly-occupied HOMO of the doubly-excited state and the singly-occupied orbitals of the singly-excited states are shown. The irreducible representations of the orbitals and states are indicated. The 1e_2u and 1e_1u orbitals are the HOMO and LUMO of the ground state, respectively. The energies of the singly-excited states are vertical excitation energies based on the equilibrium geometry of the anion in its ground state. The energy of the doubly-excited state is calculated using its own optimized geometry (for simplicity the orbitals of the ground state are shown in all boxes). To each triplet state there is a corresponding open-shell singlet state at higher energy with a similar electronic structure. All states are charge-separated (CS) states where Li has donated its valence electron to the ring. The red horizontal line indicates the relative energy of the ground state of the neutral Li@C₂₀ system in its equilibrium geometry. The electron affinity of Li@C₂₀ is 2.59 eV. All the states below the horizontal red line are thus bound states. Additional states at higher energies and a list of the frontier orbitals are given in the ESI (Fig. S5 and S6, Table S10†).

In addition to the pronounced spectrum of singly-excited states, we have found a low-lying valence doubly-excited state. We also optimized the equilibrium geometries of this doubly-excited state in D_5d symmetry (Section S5 of the ESI†). The highest natural orbitals of the ground 1¹A_1g and the doubly-excited 2¹A_1g states in their respective equilibrium geometries are shown in Fig. 5. Both the ground state and the doubly-excited state of the anion are valence states with the electrons of their respective highest occupied natural orbitals distributed on the carbon cage. Additionally, both natural orbitals exhibit clear p(π) character, which is similar to that found for the neutral Li@C₂₀.⁶²

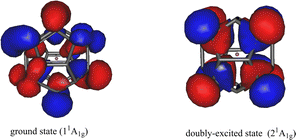Fig. 5 Li@C₂₀⁻ endohedral fullerene anion. Left: The highest occupied natural orbital of the ground state 1¹A_1g. The ground state is closed-shell. The geometry is optimized (D_5d symmetry). Right: The highest occupied natural orbital of the doubly-excited state 2¹A_1g of the anion in its respective equilibrium geometry in D_5d symmetry. The occupation numbers of the natural orbitals shown are 1.890 (ground state) and 1.882 (doubly-excited state). The contributing Hartree–Fock orbitals are listed in Tables S6 and S10 of the ESI.† The shown natural orbitals resemble the Hartree–Fock HOMOs of the respective states. In the doubly-excited state electrons are transferred from the left natural orbital to that in the right. The total energy of the doubly-excited state is 1.38 eV above that of the ground state. The results were obtained on the CCSD level with the correlation-consistent triple-zeta basis set.

It is noteworthy that the doubly-excited anionic state is a low-lying state with only 1.38 eV energy higher than that of the ground state. The EA of the neutral Li@C₂₀ is 2.59 eV (see Section S5 of the ESI†) implying that the doubly-excited state is bound and lies by more than 1.2 eV below that of the energy of the neutral Li@C₂₀. In contrast to the anionic ground state where we could compute the vibrational frequencies, a technical difficulty hindered us to compute these quantities for the doubly-excited state of the endohedral anion. If this state would possess one or more imaginary frequencies, this will imply that its minimum energy is even lower than the energy given in Fig. 4 making the state even more bound. Thus, we can safely draw the conclusion that a very stable doubly-excited state of the anion of the smallest endohedral fullerene Li@C₂₀ exists.

3 Conclusions

In spite of the immense work on anions in the literature and the relevance of their excited electronic states, bound valence doubly-excited states have not been reported. Since not all molecules can bind an electron and, in contrast to neutral molecules, the abundance of even singly-excited states is low, our main goal is to find bound valence doubly-excited states of anions and to analyze their nature and properties looking thereby for possible applications. Of course, one may anticipate that very large anions can have such states. Imagine a very long chain with a negative charge at one end and a chromophore at the other end. The excitations localized on the chromophore are far from the negative charge and will only be moderately influenced by it. But such a system is not a typical anion where the excess negative charge has a decisive influence on the structure and properties of the anion.

The starting point to accomplish our goal was systems with sizeable electron affinities and, in particular, anions which possess several bound singly-excited states. There are molecules which have substantial electron affinities,^63–65 but the anions do not necessarily possess several bound singly-excited states. We present two explicit examples: the anions of the smallest endocircular carbon ring Li@C₁₂ and the smallest endohedral fullerene Li@C₂₀. The calculations show that both have a sizeable electron affinity and the anions have several bound singly-excited states. Interestingly, the ground state and all the bound singly-excited states of both anions are charge-separated states where the Li guest atom has donated an electron to the carbon moiety and the extra electron of the anion is also on the carbon moiety.

Doubly-excited states of anions are not straightforward to calculate and since they are new land, accurate and reliable methods are needed. The fact that the size of our examples is moderate is helpful and allows us to apply such computational methods. Indeed, we have found that both systems possess a bound valence doubly-excited state where its energy is below that of the respective neutral molecule. The ground state of the anion is singlet and the doubly-excited state is singlet too. Following the literature,⁴⁸ the doubly-excited states found here can be classified as closed shell (D_CS). These possess different characteristics compared to the partially doubly-excited states in polyenes, for example, and are not easy to find in general.⁴⁸ The closed-shell doubly-excited state of cyclobutane provides an interesting example. It is, however, 18 eV above the ground state, i.e., more than 8 eV above the ionization potential of cyclobutane, and relaxes by breaking apart into two ethylene molecules⁴⁸ and thus differs even qualitatively from the present examples which are electronically stable and, as shown explicitly for Li@C₁₂⁻, relax into a final product which corresponds to a true minimum on the potential energy surface.

The doubly-excited states of the anions show interesting properties and possibilities. A particularly interesting finding is that in the anion of endocircular Li@C₁₂ the carbon ring is of a cumulenic structure where all carbon–carbon distances are identical. This is in strong contrast to the anion in its ground state where the ring is substantially distorted and shows a drawn bow structure. We attribute the cumulenic structure to the repulsion of the two excess electrons on the ring which is smallest when the electrons are rather homogeneously delocalized over the ring still maintaining a substantial attraction with the central Li⁺ cation. Depending on the nuclear coordinates, the doubly-excited states are likely to have conical intersections with the lowest singly-excited singlet states. This is of particular interest as it provides a unique opportunity to investigate a conical intersection and its dynamical fingerprints between two very different kinds of states concerning their electronic and geometrical structures. We have also investigated the singly-excited triplet states which lie energetically slightly lower than their respective singlet states. Here, one may expect unusual intersystem crossing phenomena between them and the doubly-excited states.

We hope that the work will stimulate further search for doubly-excited states of anions and, in particular, the investigation of the properties and utility of such states.

Data availability

The data that support the findings of this study are openly available in https://doi.org/10.1039/D3SC00370A. The authors confirm that the data supporting the findings of this study are available within the article and its ESI.†

Author contributions

S.-J. Hou and Dr Y.-F. Yang carried out the numerical calculations. Dr Y.-F. Yang, Prof. Z.-H. Cui and Prof. L. S. Cederbaum contributed equally to the analysis of the results. All the authors contributed equally to the writing of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Prof. Z.-H. Cui acknowledges the support by National Natural Science Foundation of China (Grants 91961204, 11922405, and 11874178). Dr Y.-F. Yang acknowledges Prof. John Stanton and Dr Peter Franke for valuable discussions.

Notes and references

1. M. Larsson, W. D. Geppert and G. Nyman, Rep. Prog. Phys., 2012, 75, 066901.
2. J. Simons, Annu. Rev. Phys. Chem., 2011, 62, 107.
3. A. Dreuw and L. S. Cederbaum, Chem. Rev., 2002, 102, 1810.
4. M. K. Scheller, R. N. Compton and L. S. Cederbaum, Science, 1995, 270, 1160.
5. M. Schmalzbauer, M. Marcon and B. Koenig, Angew. Chem., Int. Ed., 2021, 60, 6270.
6. J. S. Beckwith, A. Aster and E. Vauthey, Phys. Chem. Chem. Phys., 2022, 24, 568.
7. T. Liu and A. Troisi, Adv. Mater., 2013, 25, 1038–1041.
8. T.-C. Jagau, Chem. Commun., 2022, 58, 5205.
9. I. Sánchez and F. Martín, J. Chem. Phys., 1997, 106, 7720.
10. M. E. Sandoval-Salinas and D. Casanova, ChemPhotoChem, 2021, 5, 282.
11. J. Zhao, K. Xu, W. Yang, Z. Wang and F. Zhong, Chem. Soc. Rev., 2015, 44, 8904.
12. W. Fuß, W. E. Schmid and S. A. Trushin, Chem. Phys., 2005, 316, 225.
13. P. E. Teichen and J. D. Eaves, J. Phys. Chem. B, 2012, 116, 11473.
14. H. Kim and P. M. Zimmerman, Phys. Chem. Chem. Phys., 2018, 20, 30083.
15. P. Jiang, S. Kar and Y. Zhou, J. Plasma Phys., 2013, 20, 012126.
16. J. K. Saha, T. K. Mukherjee, P. K. Mukherjee and B. Fricke, Eur. Phys. J. D, 2012, 66, 1.
17. J. V. Ortiz, J. Chem. Phys., 2002, 117, 5748.
18. S.-J. Xu, J. M. Nilles, J. H. Hendricks, S. A. Lyapustina and K. H. Bowen Jr, J. Chem. Phys., 2002, 117, 5742.
19. E. Opoku, F. Pawłowski and J. V. Ortiz, Phys. Chem. Chem. Phys., 2022, 24, 18347.
20. H. Prinzbach, A. Weiler, P. Landenberger, F. Wahl, J. Wörth, L. T. Scott, M. Gelmont, D. Olevano and B. v. Issendorff, Nature, 2000, 407, 60.
21. Y.-F. Yang and L. S. Cederbaum, J. Chem. Phys., 2020, 152, 244307.
22. K. Kaiser, L. M. Scriven, F. Schulz, P. Gawel, L. Gross and H. L. Anderson, Science, 2019, 365, 1299.
23. Z. Liu, X. Wang, T. Lu, A. Yuan and X. Yan, Carbon, 2022, 187, 78.
24. Y. Jiang, Y. Wu, J. Deng and Z. Wang, Phys. Chem. Chem. Phys., 2021, 23, 8817.
25. Q. L. Lu, Y. Ling and Q. Q. Luo, Chem. Phys. Lett., 2022, 787, 139221.
26. Y.-F. Yang and L. S. Cederbaum, Angew. Chem., Int. Ed., 2021, 60, 16649.
27. Y.-F. Yang and L. S. Cederbaum, Chem. Phys. Lett., 2022, 799, 139554.
28. M. Feng, J. Zhao and H. Petek, Science, 2008, 320, 359.
29. V. G. Zakrzewski, O. Dolgounitcheva and J. V. Ortiz, J. Phys. Chem. A, 2014, 118, 7424.
30. V. K. Voora and K. D. Jordan, Nano Lett., 2014, 14, 4602.
31. V. K. Voora, L. S. Cederbaum and K. D. Jordan, J. Phys. Chem. Lett., 2013, 4, 849.
32. S. Klaiman, E. V. Gromov and L. S. Cederbaum, J. Phys. Chem. Lett., 2013, 4, 3319.
33. S. Klaiman, E. V. Gromov and L. S. Cederbaum, Phys. Chem. Chem. Phys., 2014, 16, 13287.
34. E. V. Gromov, S. Klaiman and L. S. Cederbaum, Phys. Chem. Chem. Phys., 2016, 18, 10840.
35. M. Stefanou, H. J. Chandler, B. Mignolet, E. Williams, S. A. Nanoh, J. O. F. Thompson, F. Remacle, R. Schaub and E. E. B. Campbell, Nanoscale, 2019, 11, 2668.
36. Y.-F. Yang, E. V. Gromov and L. S. Cederbaum, J. Phys. Chem. Lett., 2019, 10, 7617.
37. Y.-F. Yang and L. S. Cederbaum, Phys. Chem. Chem. Phys., 2021, 23, 11837.
38. V. Parasuk, J. Almlof and M. W. Feyereisen, J. Am. Chem. Soc., 1991, 113, 1049.
39. B. Bildstein, Coord. Chem. Rev., 2000, 206, 369.
40. M. Tommasini, A. Milani, D. Fazzi, A. Lucotti, C. Castiglioni, J. A. Januszewski, D. Wendinger and R. R. Tykwinski, J. Phys. Chem. C, 2014, 118, 26415.
41. Y. Zang, T. Fu, Q. Zou, F. Ng, H. Li, M. L. Steigerwald, C. Nuckolls and L. Venkataraman, Nano Lett., 2020, 20, 8415.
42. G. D. Purvis III and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910.
43. D. A. Matthews, L. Cheng, M. E. Harding, F. Lipparini, S. Stopkowicz, T.-C. Jagau, P. G. Szalay, J. Gauss and J. F. Stanton, J. Chem. Phys., 2020, 152, 214108.
44. J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029.
45. X. Zheng and L. Cheng, J. Chem. Theory Comput., 2019, 15, 4945.
46. T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007.
47. B. P. Prascher, D. E. Woon, K. A. Peterson, T. H. Dunning and A. K. Wilson, Theor. Chem. Acc., 2011, 128, 69.
48. M. T. do Casal, J. M. Toldo, M. Barbatti and F. Plasser, Chem. Sci., 2023, 14, 4012–4026.
49. S. Arulmozhiraja and T. Ohno, J. Chem. Phys., 2008, 128, 114301.
50. Y. Jin, A. Perera, V. F. Lotrich and R. J. Bartlett, Chem. Phys. Lett., 2015, 629, 76.
51. G. von Helden, P. R. Kemper, N. G. Gotts and M. T. Bowers, Science, 1993, 259, 1300.
52. H. L. Anderson, C. W. Patrick, L. M. Scriven and S. L. Woltering, Bull. Chem. Soc. Jpn., 2021, 94, 798.
53. D. G. Truhlar and C. A. Mead, Phys. Rev. A, 2003, 68, 032501.
54. L. Ravagnan, P. Piseri, M. Bruzzi, S. Miglio, G. Bongiorno, A. Baserga, C. S. Casari, A. L. Bassi, C. Lenardi, Y. Yamaguchi, T. Wakabayashi, C. E. Bottani and P. Milani, Phys. Rev. Lett., 2007, 98, 216103.
55. B. Hong, Comments Inorg. Chem., 1999, 20, 177.
56. A. Milani, A. Lucotti, V. Russo, M. Tommasini, F. Cataldo, A. Li Bassi and C. S. Casari, J. Phys. Chem. C, 2011, 115, 12836.
57. K. Lambropoulos and C. Simserides, Phys. Chem. Chem. Phys., 2017, 19, 26890.
58. T. Bartik, W. Weng, J. A. Ramsden, S. Szafert, S. B. Falloon, A. M. Arif and J. A. Gladysz, J. Am. Chem. Soc., 1998, 120, 11071.
59. S. Pecorario, A. D. Scaccabarozzi, D. Fazzi, E. Gutiérrez-Fernández, V. Vurro, L. Maserati, M. Jiang, T. Losi, B. Sun, R. R. Tykwinski, C. S. Casari and M. Caironi, Adv. Mater., 2022, 34, 2110468.
60. Z. Wang, K. Lian, S. Pan and X. Fan, J. Comput. Chem., 2005, 26, 1279.
61. F. A. Gianturco, G. Y. Kashenock, R. R. Lucchese and N. Sanna, J. Chem. Phys., 2002, 116, 2811.
62. Y.-F. Yang, E. V. Gromov and L. S. Cederbaum, J. Chem. Phys., 2019, 151, 114306.
63. M. K. Scheller and L. S. Cederbaum, J. Chem. Phys., 1993, 99, 441.
64. A. V. Kulsha and D. I. Sharapa, J. Comput. Chem., 2019, 40, 2293.
65. M. Willis, M. Götz, A. K. Kandalam, G. F. Ganteför and P. Jena, Angew. Chem., Int. Ed., 2010, 49, 8966.

---

Footnote

† Electronic supplementary information (ESI) available: Li@C₁₀ and Li@C₁₁ systems, Cartesian coordinates and vibrational frequencies of Li@C₁₂⁻ and Li@C₂₀⁻, the full pictures of excited states of Li@C₁₂⁻ and Li@C₂₀⁻, the computational details of potential energy surface scan, and the CASSCF calculation. See DOI: https://doi.org/10.1039/d3sc00370a

---