Open Access Article
Open Access ArticleLong-range hydrogen-bond relay catalyses the excited-state proton transfer reaction†
Kai-Hsin
Chang‡
a,
Yu-Chiang
Peng‡
a,
Kuan-Hsuan
Su‡
 b,
Yi-Hsien
Lin
b,
Yi-Hsien
Lin
 b,
Jiun-Chi
Liu
a,
Ying-Hsuan
Liu
a,
Chao-Hsien
Hsu
a,
Hsiao-Ching
Yang
b,
Jiun-Chi
Liu
a,
Ying-Hsuan
Liu
a,
Chao-Hsien
Hsu
a,
Hsiao-Ching
Yang
 *b and
Pi-Tai
Chou
*b and
Pi-Tai
Chou
 *a
*a
aDepartment of Chemistry, National Taiwan University, Taipei, 10617 Taiwan, ROC. E-mail: chop@ntu.edu.tw
bDepartment of Chemistry, Fu Jen Catholic University, New Taipei City, 24205, Taiwan, ROC. E-mail: hcyang_chem@mail.fju.edu.tw
First published on 30th May 2023
Abstract
Solvent (e.g., water)-catalyzed proton transfer (SCPT) via the relay of hydrogen (H)-bonds plays a key role in proton migration. In this study, a new class of 1H-pyrrolo[3,2-g]quinolines (PyrQs) and their derivatives were synthesized, with sufficient separation of the pyrrolic proton donating and pyridinic proton accepting sites to probe excited-state SCPT. There was dual fluorescence for all PyrQs in methanol, i.e., normal (PyrQ) and tautomer 8H-pyrrolo[3,2-g]quinoline (8H-PyrQ) emissions. The fluorescence dynamics unveiled a precursor (PyrQ) and successor (8H-PyrQ) relationship and the correlation of an increasing overall excited-state SCPT rate (kSCPT) upon increasing the N(8)-site basicity. kSCPT can be expressed by the coupling reaction kSCPT = Keq × kPT, where kPT denotes the intrinsic proton tunneling rate in the relay and Keq denotes the pre-equilibrium between randomly and cyclically H-bonded solvated PyrQs. Molecular dynamics (MD) simulation defined the cyclic PyrQs and analyzed the H-bond and molecular arrangement over time, which showed the cyclic PyrQs incorporating ≧3 methanol molecules. These cyclic H-bonded PyrQs are endowed with a relay-like proton transfer rate, kPT. MD simulation estimated an upper-limited Keq value of 0.02–0.03 for all studied PyrQs. When there was little change in Keq, the distinct kSCPT values for PyrQs were at different kPT values, which increased as the N(8) basicity increased, which was induced by the C(3)-substituent. kSCPT was subject to a deuterium isotope effect, where the kSCPT of 1.35 × 1010 s−1 for PyrQ-D in CH3OD was 1.68 times slower than that (2.27 × 1010 s−1) of PyrQ in CH3OH. MD simulation provided a similar Keq for PyrQ and PyrQ-D, leading to different proton tunneling rates (kPT) between PyrQ and PyrQ-D.
Introduction
The transfer of protons via a relay of solvent molecules has long been proposed as a Grotthuss mechanism,1–3 where the excess protons diffuse through the hydrogen bond (H-bond) network of water molecules or other hydrogen-bonded liquids through the formation and rupture of the covalent bonds around neighbouring solvent molecules. This mechanism, also known as proton-hopping or a proton-jump, may ubiquitously exist in bio-systems,4 although the proof is somewhat elusive. Chemically, this can be probed by the solvent-catalyzed proton transfer (SCPT) reaction5 of the designated chromophore in the excited state triggered by light excitation, where the proton-transferred isomer exhibits a distinct emission from that of the normal species prior to proton transfer. The ratiometric emission and the corresponding relaxation dynamics serve as a signal transduction for the mechanism study.6Pertinent systems require core chromophores with proton donor and acceptor sites that possess sufficient distance between them such that intramolecular H-bond formation does not exist. As a result, if the designated molecule undergoes excited-state proton transfer in solution, in theory, either aggregate-catalyzed proton transfer or SCPT must be operative. In this regard, one of the prototypical systems is ascribed to 1H-pyrrolo[2,3-b]pyridine, or the more common name of 7-azaindole (7AI, see Scheme 1), which can be simply viewed as an analogous structure of the nucleobase adenine or the amino acid tryptophan.7–10
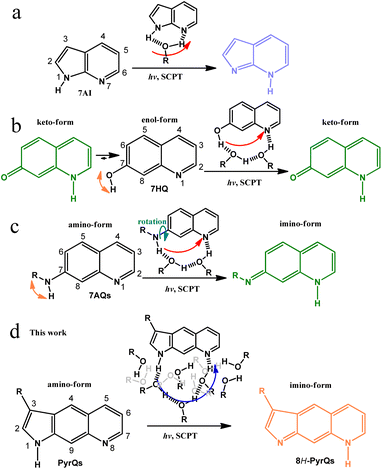 | ||
| Scheme 1 (a) The well-known excited-state SCPT molecule 7AI and the role of protic solvents in the SCPT reaction. (b) 7HQ and its corresponding excited-state SCPT in alcohols. Note the existence of ground-state equilibrium between the enol and keto forms in alcohols.21 (c) 7AQs and its associated excited-state SCPT in alcohols. Note the rotation of NRH along the C(7)-N bond.22 (d) The present work on the excited-state SCPT in PyrQs. In (d), both H-bonded relay alcohols required for proton transfer and bulk alcohols are presented according to the molecular dynamics (MD) simulation (see text). | ||
In the self-catalyzed proton transfer reaction, excited-state double-proton transfer takes place via the formation of 7AI hydrogen-bonded (H-bonded) dimer in nonpolar solvents, resulting in the 7H-pyrrolo[2,3-b]pyridine tautomeric dimer. The associated reaction dynamics have provided valuable information regarding the role of proton-transfer tautomerization in the possible mutation of the adenine-thymine base pair.11–13
As for the excited-state SCPT, 7AI has also been applied to mimic tryptophan, where excited state SCPT occurs via the formation of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 7AI
1 7AI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) methanol cyclic H-bonded complex, resulting in the tautomer 7H-pyrrolo[2,3-b]pyridine (Scheme 1a).8 Many studies have been performed on a number of 7AI derivatives in protic solvents,14,15 and the results support the mechanism of excited-state SCPT. Waluk and co-workers have studied SCPT in a number of pyrrole–pyridine systems.16–19 Further SCPT study has been extended to another class of molecules where the 7-hydroxyquinoline enol form (7HQ, Scheme 1b) serves as a prototype.20
methanol cyclic H-bonded complex, resulting in the tautomer 7H-pyrrolo[2,3-b]pyridine (Scheme 1a).8 Many studies have been performed on a number of 7AI derivatives in protic solvents,14,15 and the results support the mechanism of excited-state SCPT. Waluk and co-workers have studied SCPT in a number of pyrrole–pyridine systems.16–19 Further SCPT study has been extended to another class of molecules where the 7-hydroxyquinoline enol form (7HQ, Scheme 1b) serves as a prototype.20
There is considerable distance between the proton-donating and -accepting sites of 7HQ (cf.7AI), and the occurrence of excited-state SCPT in, e.g., methanol, requires the formation of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 7HQ
2 7HQ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) methanol cyclic H-bonded complex, resulting in a keto-tautomer (Scheme 1b). However, the –OH group in 7HQ is much more acidic than that of the pyrrolic-H group in 7AI. Therefore, proton-transfer tautomerism also takes place for 7HQ in the ground state, resulting in a non-negligible amount of keto-tautomer in methanol. In stronger H-bonded solvents such as water, the ground-state equilibrium between enol and keto forms is nearly 1
methanol cyclic H-bonded complex, resulting in a keto-tautomer (Scheme 1b). However, the –OH group in 7HQ is much more acidic than that of the pyrrolic-H group in 7AI. Therefore, proton-transfer tautomerism also takes place for 7HQ in the ground state, resulting in a non-negligible amount of keto-tautomer in methanol. In stronger H-bonded solvents such as water, the ground-state equilibrium between enol and keto forms is nearly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for 7HQ. The co-existence of enol and keto tautomer complicates the study of excited-state SCPT.21
1 for 7HQ. The co-existence of enol and keto tautomer complicates the study of excited-state SCPT.21
Recently, the replacement of –OH in 7HQ by less acidic amino protons has been reported, forming 7-aminoquinoline (7AQ, see Scheme 1c) and its derivatives, where one amino proton of –NH2 can be substituted by –R, with various degrees of electron donating/withdrawing strength to fine-tune the –NRH acidity.22 Such a configuration prevents the formation of the ground-state tautomer imino-form in methanol (Scheme 1c). However, the –NRH single bond rotation is unavoidable and results in unsymmetrical distribution of the amino proton along the C(7)-N bond (see Scheme 1c), which complicates the excited-state SCPT study. To advance in the study of long-range SCPT, it is necessary to explore a rigid system with only a single, well-defined structure in the ground state, where its proton-donating and -accepting sites are far separated at a designated distance suitable for probing fundamental insights into excited-state SCPT.
Herein, we report the strategic design and synthesis of a new class of the SCPT system by fusing the amino proton of 7AQ, which results in the formation of pyrroloquinoline (PyrQ, see Scheme 1). PyrQ can be regarded as an extension of 7AI by adding a fusing benzene ring between pyrrole and pyridine moieties, so that the proton donor and acceptor are far more separated than that of 7AI. Importantly, the rigid pyrrolic ring prevents N–H rotation, and the protruding C(9)–H site (Scheme 1d) imposes steric hindrance to prevent the dimeric formation that was reported in 7AIs under high concentration.8 These designed strategies eliminate the aforementioned complications, which simplifies experimental and theoretical approaches (vide infra).
We also derivatized PyrQ such that the aldehyde or cyanide group can be tailored at the C(3)-position in an aim to probe the structure-SCPT relationship. The synthetic route of these PyrQs involves multiple steps and is non-trivial (see Scheme 2). Comprehensive spectroscopy and dynamics, together with computation in quantum mechanics and molecular dynamics (MD) approaches, were carried out to elucidate the mechanism of long-range H-bonded relay SCPT. Details are elaborated in the following sections.
Results and discussion
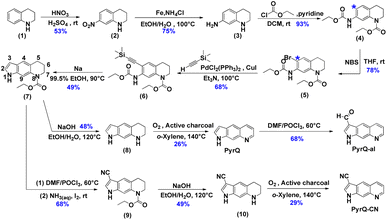
The details for the synthetic routes for 1H-pyrrolo[3,2-g]quinolone (PyrQ), 1H-pyrrolo[3,2-g]quinoline-3-carbaldehyde (PyrQ-al), and 1H-pyrrolo[3,2-g]quinoline-3-carbonitrile (PyrQ-CN) are depicted in Scheme 2. The details for synthesis, purification, identification, and characterization are provided in the experimental section of the ESI.† In brief, nitration of 1,2,3,4-tetrahydroquinoline (1) followed by reduction of –NO2 yielded compound 3.23,24 The N–H site was then protected as carbamate by the –COOCH2CH3 group and transferred into compound 4. The C(*)-position (see Scheme 2) of compound 4 was brominated, followed by reaction with ethynyltrimethylsilane under a palladium and copper co-catalyst, i.e., the Sonogashira coupling, to obtain compound 6.25 A subsequent cyclization reaction transformed 6 into compound 7, which then underwent oxidization with O2/active charcoal to yield PyrQ in satisfactory yield (48%).26For further derivatization, PyrQ was converted to PyrQ-alvia the Vilsmeier–Haack reaction.27 Also, the C(3)–H hydrogen of compound 7 was substituted with a cyano group, yielding nitrile 9via one-pot transformation of electron-rich aromatics into the aromatic nitriles using the Vilsmeier–Haack reaction. Then, 9 was deprotected into 10, but was unstable and required immediate oxidization with O2/active charcoal to yield PyrQ-CN. The details regarding PyrQ, PyrQ-al, and PyrQ-CN characterization are elaborated in the ESI.†
The X-ray diffraction pattern of PyrQ is depicted in Fig. 1, and shows a fully planar configuration. Different from 7AQs (see Scheme 1c), which have been found to have cis- and trans-forms relative to the NR-H orientation along the C–N bond,22 there is only one configuration for PyrQ because of the fused pyrrolic nitrogen. The distance between the proton donor site N(1) and proton acceptor site N(8) is as far as 5.14 Å, which is significantly longer than that of 4.84 Å for 7AQ.22 Because of this long distance, the intrinsic intramolecular proton transfer is not feasible. Instead, in solution, if excited-state SCPT occurs, PyrQ requires a long-range, multiple solvent H-bond relay to bridge the proton donor and acceptor sites, which virtually act as a conduit to assist the proton transfer reaction. We also made great efforts to grow the crystal of other PyrQs but unfortunately failed, possibly because of hindrance by the C(3)-substitution.
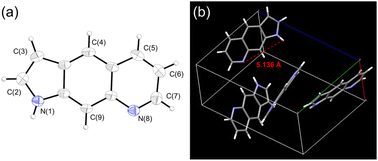 | ||
| Fig. 1 (a) The molecular structure of PyrQ drawn with a 50% probability for a thermal ellipsoid. (b) The distance between the N(1) and N(8) atoms was calculated to be 5.136 Å. | ||
Photophysical properties
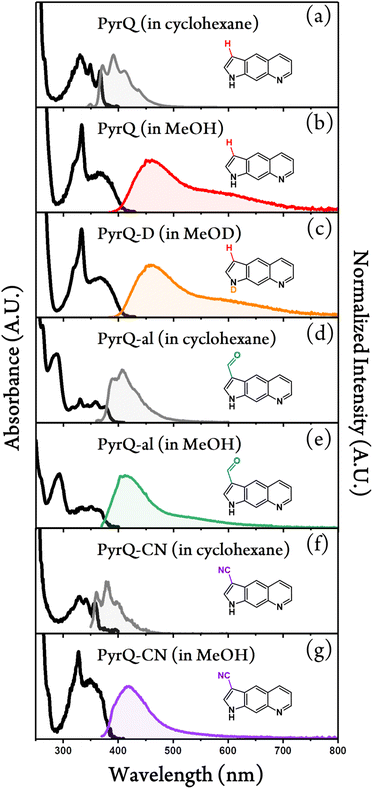
Fig. 2 shows the absorption and emission spectra of PyrQ, PyrQ-al, and PyrQ-CN. In a non-polar aprotic solvent such as cyclohexane, PyrQ reveals the vibronic structured absorption spectrum with the lowest-lying absorption peak (0–0) at 370 nm. In a protic solvent such as methanol, however, the absorption of PyrQ significantly changes such that the lowest-lying band becomes structureless, broad, and slightly redshifted to 380 nm versus that in an aprotic solvent such as cyclohexane (cf.Fig. 2a and b). Similarly, a significant difference in absorption spectra was observed for PyrQ-al and PyrQ-CN in cyclohexane and methanol (Fig. 2). The results clearly imply that all studied PyrQs undergo H-bond formation with methanol solvents in the ground state, most plausibly using the pyridinyl N(8) site and the pyrrolic N(1)–H proton of PyrQs as the proton acceptor and donor, respectively.22 This viewpoint is further supported by the following emission spectra and MD approaches.Upon excitation, PyrQ, PyrQ-al, and PyrQ-CN in cyclohexane exhibit a deep violet emission maximized at 392 nm, 406 nm, and 380 nm, respectively, and possess a vibronic feature that is mirror imaged with their corresponding absorption spectra. The photoluminescence quantum yield (PLQY) was measured to be 25.7%, 5.5%, and 4.2% for PyrQ, PyrQ-al, and PyrQ-CN, respectively (see Table 1), where a high PLQY of PyrQ indicates the structural rigidity of the core, and hence, low internal reorganization energy. In other polar aprotic solvents such as CH2Cl2, similarly, all studied PyrQs exhibited solely normal Stokes-shifted emission, and no anomalous emission phenomenon was observed (see Fig. S25†).
| Name | Solvent | λ ab | λ em | ϕ | pKa | |
|---|---|---|---|---|---|---|
| nm | nm | % | N(1)-H | N(8)-H+ | ||
| a The absorption peak wavelength in cyclohexane or methanol. b The fluorescence peak wavelength in cyclohexane or methanol. The excitation wavelength was selected at the S0 → S1 absorption peak wavelength for all studied compounds. c The photoluminescence quantum yield of all titled compounds in cyclohexane or methanol, which was calculated by comparing with the quantum yield of 87% for Coumarin 480 (in methanol).28 d The appearance of a shoulder. | ||||||
| PyrQ | C6H12 | 330 | 391 | 26 | ∼14 | 6.3 |
| CH3OH | 367 | 461 (F1) | 0.2 | |||
| 600 (F2)d | ||||||
| PyrQ-D | CH3OD | 367 | 461 (F1) | 0.4 | — | — |
| 600 (F2)d | ||||||
| PyrQ-al | C6H12 | 331 | 406 | 5.5 | 11.8 | 5.3 |
| CH3OH | 351 | 413 | 1.0 | |||
| ∼527d | ||||||
| PyrQ-CN | C6H12 | 327 | 382 | 4.2 | 11.6 | 5.1 |
| CH3OH | 349 | 416 (F1)d | 1.1 | |||
| ∼524 (F2)d | ||||||
In methanol, by sharp contrast, the electronic excitation of all PyrQs revealed dual emission, consisting of a blue emission band maximized at 461 nm, 413 nm, and 416 nm, denoted as the F1 band, and an obvious shoulder (the F2 band) located at approximately 600 nm, 527 nm, and 524 nm for PyrQ, PyrQ-al, and PyrQ-CN, respectively. The excitation spectra monitored at the F1 and F2 bands are identical, and also resemble the absorption spectrum (see Fig. S23†). Therefore, the dual emission originating from the same ground state is unambiguous, and two emissions correlated with two excited states are expected to possess a precursor-successor kinetic relationship (vide infra).
Knowing that the dual emission properties are only observed in protic solvents when the H-bonding formation with PyrQs in the ground state has been verified (vide supra), it is reasonable to propose the occurrence of excited-state SCPT in methanol, where protons migrate from the N(1)–H site to the N(8) site of the amino-form (Scheme 1d) via a solvent H-bonded relay, yielding the proton-transferred imino-form. The amino-conformer and the imino-conformer thus exhibit F1 and F2 bands, respectively (Scheme 1d).
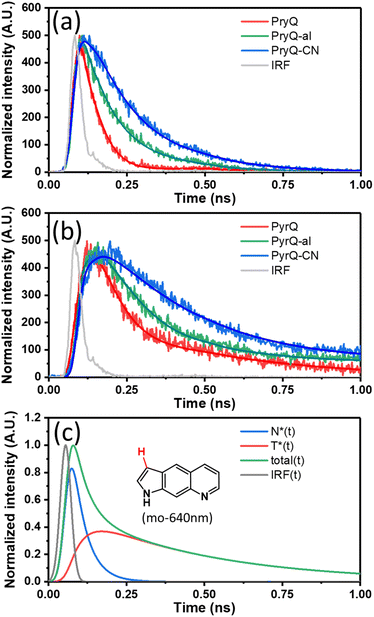
To gain in-depth insight into the SCPT dynamics, we then probed the fluorescence relaxation dynamics by carrying out time-resolved fluorescence spectroscopy. Because the F1 and F2 bands can be resolved in a steady-state manner, we predicted the kinetics of SCPT for PyrQs to be relatively slow in the range of tens to hundred picoseconds. We therefore exploited the time-correlated single-photon counting (TCSPC) technique, coupled with a femtosecond Ti:sapphire laser as an excitation source (120 fs) and a fast MCP-PMT detector as the acquisition system. This overall system response time gives approximately 13 ps resolution after deconvolution.
In our experience, if the associated kinetic time constant is >15 ps, the current TCSPC system with its low excitation photon flux and rapid counting speed is more reliable than that of the femtosecond emission up-conversion technique currently used in our laboratory. Fig. 3a and b depicts the emission relaxation profiles of PyrQs monitored at the F1 and F2 bands, and their pertinent data are displayed in Table 2. For PyrQ, upon monitoring at the F1 band emission of, e.g., 450 nm, the relaxation of emission reveals a single exponential decay component (Fig. 3a), and the lifetime was fitted to be 44 ps.
| Compound | F1 band | F2 band | ||||
|---|---|---|---|---|---|---|
| λ em (nm) | τ decay (ps) | λ em (nm) | τ decay1 (ps) | τ rise (ps) | τ decay2 (ps) | |
| a The excitation wavelength was selected at the S0 to S1 absorption peak for all studied compounds. | ||||||
| PyrQ | 450 | 44 | 640 | 45 | 42 | 427 |
| PyrQ-D | 450 | 74 | 640 | 76 | 78 | 834 |
| PyrQ-al | 395 | 100 | 550 | 105 | 104 | 3262 |
| PyrQ-CN | 420 | 155 | 600 | 157 | 155 | 2922 |
When monitoring at the F2 band region of, e.g., 640 nm, the most optimal fit for the kinetic profile is an increasing component of 42 ps and two exponential decay time constants of 45 ps and 427 ps (Fig. 3b). The 42 ps risetime component, within experimental uncertainty, is consistent with the 44 ps decay time constant for normal emission (the F1 band). Firm support for this viewpoint is given by the deconvolution of the F2 band (640 nm), which is composed of a rise (44 ps) and two decay (44 ps and 427 ps) components under the consideration of the system response function (see Fig. 3c).
In cyclohexane, where no SCPT takes place, the lifetime of PyrQ's normal emission (the F1 band) was measured to be as long as 3.7 ns (see Fig. S27†). Therefore, it is reasonable for us to assume that the decay of the F1 band in methanol is dominated by the rate of SCPT. We thus concluded that the rate of SCPT (PyrQ) was equal to the inverse of 44 ps, which is 2.27 × 1010 s−1. Next, the approximately 45 ps decay component monitored at 640 nm was more plausibly attributed to the residue of the F1 emission. This viewpoint can be rationalized by minimal separation between the proximal F1 and F2 bands. In addition, the radiative decay rate constant for the F1 band was significantly larger than that of the F2 band (vide infra). Therefore, despite the fact that the F1 emission intensity was rather low at 640 nm, its contribution to TCSPC is non-negligible. Finally, the 427 ps decay component of the F2 band can reasonably be ascribed to the population decay of the imino-tautomer.
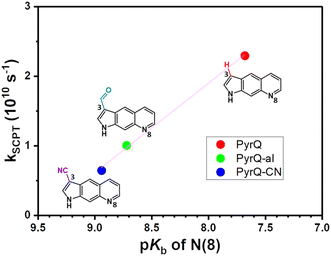
The TCSPC data for PyrQ-al and PyrQ-CN emissions are also depicted in Fig. 3a and b. The decay lifetimes of F1 for PyrQ-al and PyrQ-CN were fitted at 100 ps and 155 ps, respectively, which correlate well with the risetime of the corresponding F2 bands of 104 ps and 155 ps, respectively (see Table 2). The rate of SCPT (kSCPT), taking the inverse of the F1 decay time (vide supra), is in the order of PyrQ (2.27 × 1010 s−1) > PyrQ-al (1.00 × 1010 s−1) > PyrQ-CN (0.65 × 1010 s−1). These results imply that an increase in the electron-withdrawing ability at the C(3)-position decreases the rate of SCPT, which seems to be contradictory to the expected increase in kSCPT due to the increase in the N(1)–H acidity by the C(3) electron-withdrawing strength via a resonance effect. This puzzle is reminiscent of previously reported SCPT molecules where the chemical substitution not only influenced the proton-donating site but also the proton-accepting site.14–22
To probe the interplay between the proton-donating and -accepting sites of PyrQs, pKa values for the pyrrolic proton N(1)–H and the protonated pyridium N(8)+–H in PyrQs were measured by pH-titration absorption spectrometry in water. The titration spectra are shown in Fig. S29,† and the pertinent data are listed in Table 1. As a result, the pKa value of the N(1)–H proton was measured to be PyrQ (approximately 14), PyrQ-al (11.8), and PyrQ-CN (11.6) at room temperature, and decreased upon increase in the electron-withdrawing ability from H in the aldehyde to the cyano group. In yet another approach, the pKa of the N(8)+–H proton at 25 °C was also measured by absorption pH titration and determined to be 6.3, 5.3, and 5.1 for PyrQ, PyrQ-al, and PyrQ-CN, respectively. Accordingly, the pKb of the N(8) site, based on pKa + pKb = 14, was calculated to be 7.7, 8.7, and 8.9 for PyrQ, PyrQ-al, and PyrQ-CN, respectively. Therefore, the basicity is in the order of PyrQ > PyrQ-al > PyrQ-CN. In other words, the N(1)–H donor and N(8) proton acceptor are influenced by the C(3) substitution via a resonance effect.
It should be noted that we are aware that excited-state phenomena would be based on excited-state 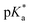 values (* denotes the electronically excited state), which are conventionally measured by fluorescence pH titration experiments. However, the validity of this approach is based on the establishment of excited-state equilibrium between the protonated and deprotonated species, which is not the case due to the fast SCPT of tens to hundred ps for the studied PyrQs. Therefore, we only acquired the pKa for each site and assumed a similar trend for
values (* denotes the electronically excited state), which are conventionally measured by fluorescence pH titration experiments. However, the validity of this approach is based on the establishment of excited-state equilibrium between the protonated and deprotonated species, which is not the case due to the fast SCPT of tens to hundred ps for the studied PyrQs. Therefore, we only acquired the pKa for each site and assumed a similar trend for 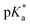 in the excited state.
in the excited state.
Fig. 4 depicts a plot of the rate constant for excited-state SCPT (kSCPT) as a function of the pKb of the N(8) site. The trend of increasing kSCPT upon increase in the N(8) basicity infers that the rate-determining step is prone to the proton-accepting property of the N(8) site rather than the proton donation of the N(1)–H site. Further in-depth discussion will be elaborated in the section on MD simulation.29
We also performed time-resolved fluorescence measurement of N(1)–H-deuterated PyrQ, namely PyrQ-D in methanol-d1 (CH3OD). The observed kSCPT rate and the tautomer population decay lifetime were 1.35 × 1010 s−1 (74 ps) and 834 ps, respectively. The kSCPT of PyrQ-D was smaller than that (2.27 × 1010 s−1) of PyrQ-D by 1.68 times. Because kSCPT is the dominant decay process for the F1 band (vide supra), the F2/F1 ratio for PyrQ-D is expected to be smaller than that for PyrQ by approximately 1.68 fold. However, as shown in Fig. 2, the 1.11 ratio of steady-state emission intensity for F2/F1 between PyrQ and PyrQ-D seems to conflict with the kinetic measurement (Tables 2 and S4†).
This controversy is not unusual, and can be rationalized by the different nonradiative decay rate of the F2 band between PyrQ (in CH3OH) and PyrQ-D (in CH3OD). The overall PLQY was measured to be 0.2% and 0.4% for PyrQ and PyrQ-D, respectively, in CH3OH and CH3OD (see Table 1). The PLQY of F2 can be further deduced by convolution of the dual fluorescence spectra, assuming a dominant SCPT in the excited state, which gives 0.042% and 0.062% for PyrQ and PyrQ-D, respectively. For the F2 band of PyrQ-D in CH3OD, the population decay time (1/kobs) was measured to be 834 ps, which is twice as long as 427 ps for PyrQ in CH3OH (Table 2).
We applied PLQY = kr/kobs = kr/(kr + knr), where kr and knr denote the radiative decay rate and nonradiative decay rate constants for the F2 band, respectively. kr and knr were then deduced and are listed in Table S4.† Clearly, while kr of the F2 band is approximately the same between PyrQ and PyrQ-D, the knr of 1.20 × 109 s−1 for PyrQ-D in CH3OD is nearly twice as slow as that (2.34 × 109 s−1) for PyrQ in CH3OH. Because the O-D stretching frequency is lower than that of O–H, it is thus reasonable to expect that the emission quenching associated with vibronic coupling in the PyrQ-D/CH3OD H-bonded complex is weaker than that in the PyrQ/CH3OH H-bonded complex.
Previous reports have established a mechanism for SCRT that requires a series of H-bonded solvent molecules to bridge proton donor and acceptor parts, forming a conduit for the occurrence of a relay type of proton transfer.14–22 Due to the great separation distance of 5.136 Å between N(1) and N(8) atoms, intuitively, there will be insufficient length with two methanol molecules to construct an H-bonded relay for the SCPT reaction in PyrQs.
For a solvent relay consisting of a distance greater than that of two methanol molecules, the structure of the H-bonded relay to bridge the N(1)–H and N(8) sites may have multiple configurations. To extract the population of these configurations among all randomized solvated methanol molecules, we then performed MD simulation,29 the results of which would be able to differentiate the relay states from those of the bulk states (excluding the relay states). The details of the corresponding results and discussion are elaborated below.
Computational approach
The calculations were carried out in methanol using a polarizable continuum model (PCM).38 We also performed the calculation using the CAM-B3LYP/6-31+G(d,p)33 level (see Table S6†). In comparison, the results of B3LYP/6-31+G(d,p) were closer to the experimental values from the energy point of view, such as absorption and emission. Alternatively, the structural parameters based on B3LYP/6-31+G(d,p) seemed to be more convenient for the MD approach and will be used later.
The pertinent data for DFT calculations for PyrQs (in methanol) are listed in Table S5.† Clearly, the calculated absorption and emission energy gaps were consistent with the experimentally observed peak wavelengths for the amino-(normal) and imino-(tautomer) forms. For the normal form, the calculated emission gap was in the order of PyrQ < PyrQ-al < PyrQ-CN, which can be rationalized by the electron-withdrawing strength of the substituent at the C(3) position, which was in the order of H (PyrQ) < HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (PyrQ-al) < CN (PyrQ-CN).
O (PyrQ-al) < CN (PyrQ-CN).
As shown in Fig. 5a (also in Fig. S31 and S32†) the electron density distribution for the highest occupied molecular orbital (HOMO) for PyrQs covered the C(3) substituents, while it was negligible for the lowest unoccupied molecular orbital (LUMO). Therefore, the increase in electron-withdrawing strength of the C(3)-substituent decreases the energy of HOMO, whereas there is little change in LUMO (see Fig. 5a and S30–S32†), resulting in an increase in the energy gap. There is a similar argument for the tautomer form (see Fig. 5a and S30–S32†), and the calculated results were consistent with the experimental observations (Fig. 2). Fig. 5b depicts the relative energies between the normal and tautomer forms in the S0 and S1 states, where SCPT in the excited state is energetically favorable by >15 kcal mole−1 for all PyrQs, while clearly the proton transfer is thermally unfavorable by more than 8 kcal mol−1 in the ground state.
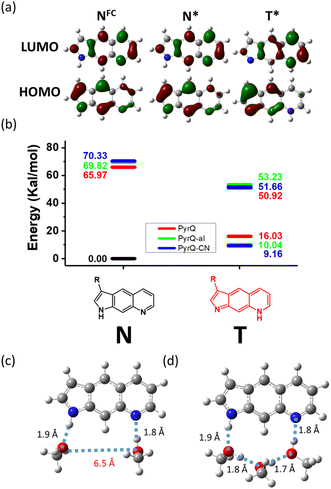 | ||
| Fig. 5 (a) The electron density distribution of HOMO and LUMO for PyrQ monitored at Franck–Condon excitation (NFC), with structural optimization at the normal S1 (N*) and tautomer S1 (T*) state. The molecular orbital isovalue was set at 0.05. See also Fig. S31 and S32† for PyrQ-al and PyrQ-CN, respectively. (b) The relative energies between the normal and tautomer forms in the S0 and S1 states for PyrQs, calculated under the methanol continuum model. (c) Upon optimization via the B3LYP/6–31+G(d,p) level, two methanol molecules are insufficient to form a relay to link proton-donating and -accepting sites (S0 state). (d) Three methanol molecules linked via hydrogen bonds offer a reasonable relay for proton transfer from the N(1)–H to the N(8) site (S0 state). | ||
We next performed preliminary DFT calculations to examine the methanol molecules required for forming the H-bonded relay suitable for SCPT of PyrQs. We started from two methanol molecules placed around the N(1)–H and N(8) sites of PyrQs, and then completed the structural optimization (Fig. 5c, d, and S33†) under a continuum model (methanol). As a result, the two methanol molecules in the methanol-PyrQs (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) hydrogen-bonded complex, where each methanol attaches to either the N(1)–H or N(8) site, are separated far away by >5 Å (see Fig. 5c). When three methanol molecules were used, the associated methanol-PyrQs complex will not be able to form a hydrogen-bonded relay configuration (Fig. 5d). After obtaining these results, we next performed the MD calculation elaborated in the following section.
1) hydrogen-bonded complex, where each methanol attaches to either the N(1)–H or N(8) site, are separated far away by >5 Å (see Fig. 5c). When three methanol molecules were used, the associated methanol-PyrQs complex will not be able to form a hydrogen-bonded relay configuration (Fig. 5d). After obtaining these results, we next performed the MD calculation elaborated in the following section.
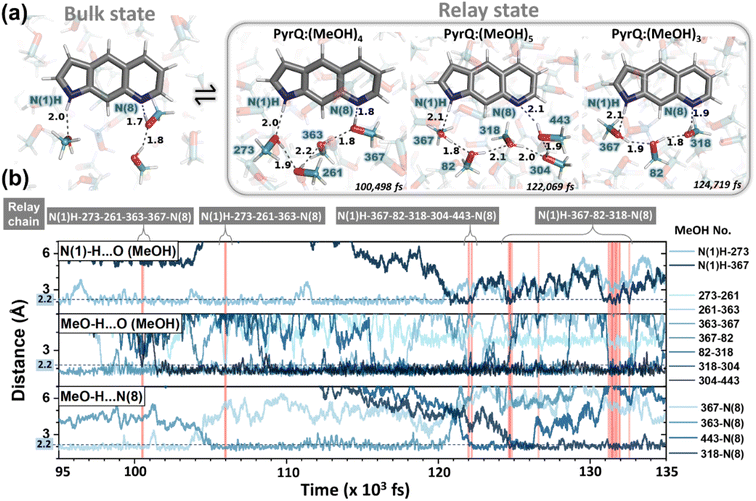
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 39 were performed on a series of PyrQ-derived molecules (PyrQ, PyrQ-D, PyrQ-al, and PyrQ-CN) in methanol to investigate their dynamics and equilibrium between the bulk and relay state (see Fig. 6a) in methanol. The results indicate that the PyrQs are dynamically coupled to the methanol relay configuration in a hydrogen-bonding network (Fig. 6).
39 were performed on a series of PyrQ-derived molecules (PyrQ, PyrQ-D, PyrQ-al, and PyrQ-CN) in methanol to investigate their dynamics and equilibrium between the bulk and relay state (see Fig. 6a) in methanol. The results indicate that the PyrQs are dynamically coupled to the methanol relay configuration in a hydrogen-bonding network (Fig. 6).
These results, together with the close-up inspections of the H-bonding configurations for each PyrQs in methanol, elicit two important remarks. First, methanol micro-solvation with hydrogen-bonding does exist for the N(1)–H and N(8) site in PyrQs (Fig. 6a). Second, there are clearly time-dependent configuration changes in the methanol relay state and bulk state (Fig. 6b). When compared with explicit methanol MD simulations, a locally fluctuating density profile is revealed, and therefore, it seems apparent that fewer trapped methanol molecules associate with the sites. Both results are consistent with the experimental observations. With MD simulation, we are able to define how many methanol molecules are feasibly required to conduct the proton transfer (Fig. 7a) and estimate the fraction of both states from the output trajectory.40 In the current study, we used femtosecond (fs) time resolution to analyse the MD trajectory data of PyrQs (see the Experimental Section).
All the PyrQ MD trajectories were collected up to 10 ns, with every 1 fs as a snapshot resolution. The 10 ns simulated period is reasonably longer than τdecay of SCPT in the current time-resolved experiment, and therefore, a total of 107 fs snapshot structures were used to obtain the statistics for the H-bond relay configurations. To precisely measure the time-dependent evolution of methanol relay structures in the PyrQ:(MeOH)n complex, it is necessary for the relevant methanol orientations between N(1)–H and N(8) to strictly obey these two rules: (1) the distance between the H atom and the acceptor O or N atom (r(N–H⋯O) or r(O–H⋯O) or r(O–H⋯N)) must be shorter and within 2.5 Å; (2) the angle of ∠ O⋯H–N, ∠H–O⋯O, and ∠N⋯H–O must be 150° to 180°.
Such criteria are substantial for the complex of chains of MeOH molecules engaged in the Grotthuss-type transport1 of a proton, i.e., the proton-jump,2via an H-bond relay located between the SCPT-triggered proton donor and the proton acceptor. The relay is a group bearing an H atom able to accept an H-bond from the methanol relay group, and at the same time, form an H-bond with the proton-accepting chain. Note that because the computation time and capacity are limited, the MD simulation in the current study is based on ground-state-optimized PyrQs. Also, the ground-state MD simulation to probe fractions between bulk and relay configurations takes advantage of the thermally unfavorable ground-state SCPT in the relay PyrQ states, which eliminates the complication of simulation in the excited state due to SCPT.
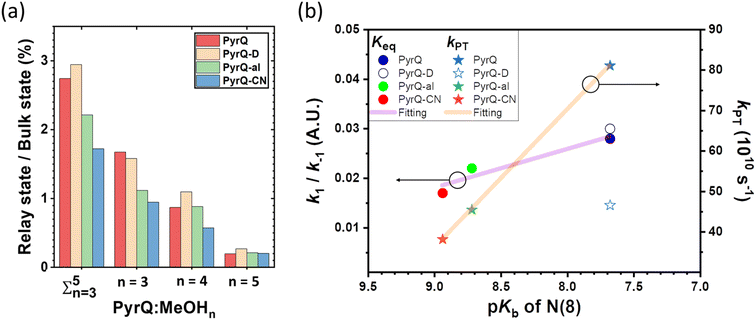
The MD simulation results shown in Fig. 6 confirm the above viewpoint through observation of the transformation between the bulk state and relay state of PyrQ. Additionally, it was noted that the cyclic methanol train(s) is not an isolated H-bond system. There is a huge methanol source that can immediately participate in the H-bonding in the PyrQ:(MeOH)n complex when one hydrogen bond is broken. For the observed duration up to 10 ns, the PyrQ:(MeOH)n complexes of n ≥ 6 were too few in fraction and can thus be ignored (Fig. 6a and 7a). These results imply that the contribution to SCPT is mainly from the configurations of PyrQ:(MeOH)3, PyrQ:(MeOH)4, and PyrQ:(MeOH)5.
These results are also consistent with at least three (n ≥ 3) methanol molecules being required to form a PyrQ:(MeOH)n relay state in the above DFT calculation. Fig. 7a illustrates this point by showing the distributions of different cyclic relay configurations, with an equilibrium fraction less than 3%. Also, we found that the formation of ‘reactive’ complexing geometry requires additional nearly linear hydrogen bonds to the N(1)–H and N(8) sites, as illustrated by showing the MD snapshot of PyrQ:(MeOH)3 (Fig. S34†). Such a complex is severely inhibited in methanol solvents, whereby the fraction of PyrQ molecules in ‘reactive’ states is observed to be less than 1%. Thus, it can be rationalized that the small proportion of reactive solvation states is due to geometry.40
From the view of MD fs dynamics (see Fig. 6 and Movie S1†), the hydrogen-bonding network is switched to different relay states by the rapid rotation of the methanol OH group, which thus facilitates the reorganization of the intermolecular H-bond network as well as the exchange of the surrounding MeOH molecules, and therefore converts PyrQs to the bulk state.
As shown in Fig. 7a, we can easily and clearly determine the continuum relay state and the bulk state and consider the fluctuation in the femtosecond scale. To consider n = 3, 4, and 5 for PyrQs:(MeOH)n, the bulk state existence time (τ1) and the relay state existence time (τ−1) were counted within an observed duration of 10 ns (see Fig. 7a). In concept, this existence time (τ1 and τ−1) was analyzed by the MD trajectory statistics, and τ−1/τ1 thus is equivalent to a pre-equilibrium constant Keq between the bulk and relay type of solvation. If one assumes 1/τ−1, denoted as k−1, is >proton-transfer (tunneling) rate kPT (see Scheme 3), the overall excited-state SCPT rate kSCPT can be expressed by eqn (1) below.40–42
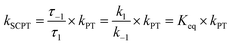 | (1) |
The Keq value calculated by MD simulation (see Table 3) was used in eqn (1), as well as the experimentally obtained kSCPT (Table 2), and thus, the proton tunnelling rate kPT was calculated to be 8.11 × 1011 s−1, 4.55 × 1011 s−1, and 3.82 × 1011 s−1 for PyrQ, PyrQ-al, and PyrQ-CN, respectively (Fig. 7b and Table 3). Clearly, the tunnelling rate kPT is influenced by the N(3)-substituent and leads to a decrease in the basicity, i.e., the ability to accept protons is in the order of PyrQ > PyrQ-al > PyrQ-CN. Therefore, it is reasonable for us to conclude that the N(8) proton-accepting process plays a role in the rate-determining step.
| Name | Solvent | K eq | k PT |
|---|---|---|---|
| — | (s−1) | ||
| a Equilibrium constant between the bulk and relay states in methanol solvents calculated by MD. b Rate constant of proton transfer, which was calculated by eqn (1) (kSCPT was measured by time-resolved fluorescence spectroscope) (see Tables S9 and S10). | |||
| PyrQ | CH3OH | 2.8% | 8.11 × 1011 |
| PyrQ-D | CH3OD | 2.9% | 4.66 × 1011 |
| PyrQ-al | CH3OH | 2.2% | 4.55 × 1011 |
| PyrQ-CN | CH3OH | 1.7% | 3.82 × 1011 |
Experimentally, the ratio for the measured kSCPT (2.27 × 1010 s−1) of PyrQversus that (1.35 × 1010 s−1) of PyrQ-D is 1.68. Although Keq is virtually the same between PyrQ (0.028 in CH3OH) and PyrQ-D (0.029 in CH3OD, see Table 3) from MD simulation, the major difference lies in the deduced tunnelling rate kPT of 8.11 × 1011 s−1 for PyrQversus 4.66 × 1011 s−1 for PyrQ-D, i.e., the deuterium isotope effect for SCPT (see Fig. 7b). Finally, it should be noted that the above Keq is based on the sum of the fraction of the n = 3 to 5 methanol relay, assuming they all undergo a similar kPT. Considering that the increasing number of solvents involved in the geometrical relay leads to a decrease in the SCPT rate,40n = 3 should be considered as the major contributor to execute excited-state SCPT. Therefore, the Keq deduced here is considered as an upper limit. For example, KKeq ≈ 1.6% (see Fig. 7a) for PyrQ if we only take n = 3 into account for the occurrence of excited-state SCPT.
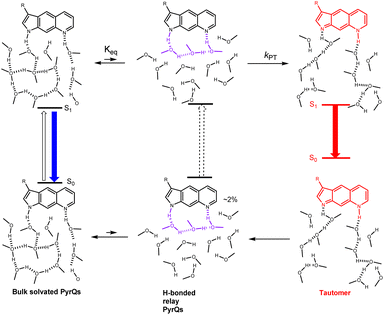
Summarizing all of the above results and discussion, the overall excited-state SCPT for PyrQs is depicted in Scheme 3, where an equilibrium is established between bulk solvated, i.e., non-H-bonded relay PyrQs and H-bonded relay PyrQs. The contribution of the H-bonded relay PyrQs was small (<3%), and their direct excitation and the associated fast proton transfer was not pursued in this study. The major bulk solvated PyrQs, upon excitation, undergo equilibration with the H-bonded relay PyrQs state, from which proton transfer takes place. The overall kinetic expression is depicted by eqn (1), where the tunnelling rate kPT is N(3)-substituent- as well as N(1)–H deuterium isotope-dependent.
Conclusions
PyrQ and its derivatives, PyrQ-al, PyrQ-CN, were synthesized, and their physical and photophysical properties were comprehensively examined. All studied PyrQs underwent excited-state SCPT, in which a slower SCPT rate (kSCPT) was resolved upon increasing the electron-withdrawing ability of the C(3)-substituent. MD simulation was applied to probe and analyze the solute/solvent H-bonding configuration and the solvent molecule arrangement over time for SCPT.The statistical results confirmed that long-distance SCPT of PyrQs required 3–5 methanol molecules in a relay configuration to accomplish the relay-type proton transfer reaction. Further pH titration hence –N(8) basicity measurement led us to conclude that the –N(8) proton-accepting strength is the rate-determining step, which is well correlated with the intrinsic proton transfer rate kPT. The overall reaction is depicted in Scheme 3, with the associated kinetics expressed in eqn (1), where the tunnelling rate was N(3)-substituent- as well as N(1)–H deuterium isotope-dependent. The structurally rigid PyrQs and their sufficiently separated proton-donating and -accepting sites thus provide valuable fundamental insights into the excited-state long-range SCPT reaction.
Experimental section
General method of synthesis
All reactions were performed under nitrogen saturated. Commercially available reagents were used without drying. Chromatographic separation was carried out using silica gel from Merck (230–400 mesh). 1H and 13C NMR spectra were measured with a Varian Unity 400 spectrometer at 400 and 100 MHz, respectively. The chemical shifts (δ) and the coupling constants (J) were recorded in parts per million (ppm) and in Hertz (Hz), respectively.Photophysics measurements
The absorption and emission spectra were measured by a Hitachi U-3310 spectrophotometer and Edinburgh FS980 fluorometer. Merck spectrum grade methanol used in the photophysics experiment. The pH meter (PH500 pH/mV/Temp Meter; Clean Corp.) employed an electrode of Polilyte HT (Hamilton). The sodium hydroxide was First Grade (Shimakyu).An OB-900 lifetime spectrometer (Edinburgh) TCSPC system with an MCP-PMT was used for picosecond time-resolved measurement in these studies. The light source was femtosecond laser pulses at 740 nm (Tsunami, Spectra-Physics), and second-harmonic generation (SHG, 370 nm) of pulses was selected. The polarization of excitation was set at a magic angle (54.7°) to eliminate the anisotropy.
MD simulations on solvated PyrQ systems
To observe the balance between the bulk state and the relay state of the PyrQs:(MeOH)n complex, we performed MD simulations with the AMBER program.39 The partial charges of PyrQs and methanol molecules were calculated by DFT B3LYP/6-31G+(p,d) optimization. The Mulliken charges of atoms were added to the force field. The quantum calculations were performed in the Gaussian 16 package.30 The initial configurations of the systems consisted of one PyrQ molecule and 710 methanol molecules, which were generated using the PACKMOL package43 in a simulation box of 603 Å3 with a density of approximately 0.4 g cm−3.All simulations began from a random configuration, energy minimization was carried out by a combination of the steepest descent and conjugated gradient method for 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps. Then, the simulation box was slowly compressed to a target density of approximately 0.8 g cm−3. This simulation occurred at 300 K over 10 ns with the NVT ensemble. A constant pressure and constant temperature (NPT ensemble) simulation was performed at 300 K and 1 atm for 1 ns to allow the molecules overcome the local traped well undergoing the thermal relaxation process. Energies and densities were monitored to ensure adequate convergence within the equilibration period. After equilibration, the 10 ns NVT ensemble was implemented at 300 K to collect 107 fs snapshots per system for the time-resolved structural analyses.
000 steps. Then, the simulation box was slowly compressed to a target density of approximately 0.8 g cm−3. This simulation occurred at 300 K over 10 ns with the NVT ensemble. A constant pressure and constant temperature (NPT ensemble) simulation was performed at 300 K and 1 atm for 1 ns to allow the molecules overcome the local traped well undergoing the thermal relaxation process. Energies and densities were monitored to ensure adequate convergence within the equilibration period. After equilibration, the 10 ns NVT ensemble was implemented at 300 K to collect 107 fs snapshots per system for the time-resolved structural analyses.
Data availability
The photophysics spectrum, dynamic data, and MD trajectory results in this paper are available from the authors.Author contributions
Prof. Pi-Tai Chou designed and guided all the investigations. Prof. Hsiao-Ching Yang led the theoretical study and MD simulation. Yu-Chiang Peng, Jiun-Chi Liu, Ying-Hsuan Liu, and Kai-Hsin Chang carried out the synthesis of all titled compounds. Kai-Hsin Chang and Chao-Hsien Hsu performed all the spectroscopic and dynamic measurements. Kai-Hsin Chang performed the DFT computation using the Gaussian program. Kuan-Hsuan Su and Yi-Hsien Lin performed the MD simulation using the Amber program.Conflicts of interest
The authors declare no competing interests.Acknowledgements
P.-T. C. and H.-C. Y. thank the National Science and Technology Council, Taiwan and Ministry of Science and Technology, Taiwan, for financial support (NSTC 111-2639-M-002-005-ASP and NSTC 111-2113-M-030-003). P.-T. C. gratefully thanks Ms Shou-Ling Huang for the assistance in NMR experiments at the Instrumentation Center at NTU, which is supported by the Ministry of Science and Technology, Taiwan. We acknowledge MOST for research support (MOST 110-2731-M-002-001, XRD000200) in performing the single-crystal X-ray diffraction measurements at the Instrumentation Center, National Taiwan University. This work was financially supported by the Ministry of Science and Technology of Taiwan (MOST 109-2113-M-143-004 and 108-2113-M-143-002). The authors thank Ms Hsiu-Ni Huang (Instrumentation Centre of National Taiwan Normal University; MS005900) for technical support.Notes and references
- C. J. T. de Grotthuss, Ann. Chim., 1806, 58, 54–73 Search PubMed.
- N. Agmon, Chem. Phys. Lett., 1995, 244, 456–462 CrossRef CAS.
- K.-D. Kreuer, Chem. Mater., 1996, 8, 610–641 CrossRef CAS.
- P. Ball, Chem. Rev., 2008, 108, 74–108 CrossRef CAS PubMed.
- S. Sharif, G. S. Denisov, M. D. Toney and H.-H. Limbach, J. Am. Chem. Soc., 2006, 128, 3375–3387 CrossRef CAS PubMed.
- M. Mohapatra and A. K. Mishra, Photochem. Photobiol. Sci., 2019, 18, 2830–2848 CrossRef CAS PubMed.
- P. K. Sengupta and M. Kasha, Chem. Phys. Lett., 1979, 68, 382–385 CrossRef CAS.
- P. T. Chou, C. Y. Wei, C. P. Chang and M. S. Kuo, J. Phys. Chem., 1995, 99, 11994–12000 CrossRef CAS.
- J. Guharay and P. K. Sengupta, Biochem. Biophys. Res. Commun., 1996, 219, 388–392 CrossRef CAS PubMed.
- V. De Filippis, S. DeBoni, E. De Dea, D. Dalzoppo, C. Grandi and A. Fontana, Protein Sci., 2004, 13, 1489–1502 CrossRef CAS PubMed.
- K. C. Ingham and M. A. El-Bayoumi, J. Am. Chem. Soc., 1971, 93, 5023 CrossRef CAS.
- C. A. Taylor, A. M. El-Bayoumi and M. Kasha, Proc. Natl. Acad. Sci. U. S. A., 1969, 65, 253 CrossRef PubMed.
- K. C. Ingham and M. A. El-Bayoumi, J. Am. Chem. Soc., 1974, 96, 1674 CrossRef CAS.
- Y. Chen, R. L. Rich, F. Gai and J. W. Petrich, J. Phys. Chem., 1993, 97, 1770–1780 CrossRef CAS.
- P. T. Chou, W. S. Yu, C. Y. Wei, Y. M. Cheng and C. Y. Yang, J. Am. Chem. Soc., 2001, 123, 3599–3600 CrossRef CAS PubMed.
- J. Waluk, Acc. Chem. Res., 2003, 36, 832–838 CrossRef CAS PubMed.
- J. Waluk, S. J. Komorowski and J. Herbich, J. Phys. Chem., 1986, 90, 3868–3871 CrossRef CAS.
- J. Herbich, J. Dobkowski, R. P. Thummel, V. Hegde and J. Waluk, J. Phys. Chem. A, 1997, 101, 5839–5845 CrossRef CAS.
- A. Kyrychenko, J. Herbich, M. Izydorzak, M. Gil, J. Dobkowski, F. Y. Wu, R. P. Thummel and J. Waluk, Isr. J. Chem., 1999, 39, 309–318 CrossRef CAS.
- J. Konijnenberg, G. B. Ekelmans, A. H. Huizer and C. A. G. O. Varma, J. Chem. Soc., Faraday Trans. 2, 1989, 85, 39–51 RSC.
- S. F. Mason, J. Philp and B. E. Smith, J. Chem. Soc. A, 1968, 3051 RSC.
- K. H. Chang, Y. H. Liu, J. C. Liu, Y. C. Peng, Y. H. Yang, Z. B. Li, R. H. Jheng, C. M. Chao, K. M. Liu and P. T. Chou, Chem. – Eur. J., 2019, 25, 14972–14982 CrossRef CAS PubMed.
- S. M. Westaway, Y. K. Chung, J. B. Davis, V. Holland, J. C. Jerman, S. J. Medhurst, H. K. Rami, G. Stemp, A. J. Stevens, M. Thompson, K. Y. Winbornb and J. Wright, Bioorg. Med. Chem. Lett., 2006, 16, 4533–4536 CrossRef CAS PubMed.
- R. D Patil and Y. Sassona, Org. Chem.: Curr. Res., 2015, 4, 1000154 Search PubMed.
- K. Sonogashira, J. Organomet. Chem., 2002, 653, 46–49 CrossRef CAS.
- M. Hayashi, Chem. Rec., 2008, 8, 252–267 CrossRef CAS PubMed.
- A. Vilsmeier and A. Haack, Ber. Dtsch. Chem. Ges. B, 1927, 60, 119–122 CrossRef.
- A. N. Fletcher and D. E. Bliss, Laser Dye Stability. Part 5, Effect of Chemical Substituents of Bicyclic Dyes Upon Photodegradation Parameters, Appl. Phys., 1978, 16, 289–295 CAS.
- W. F. v. Gunsteren and H. J. C. Berendsen, Angew. Chem., Int. Ed. Engl., 1990, 29, 992–1023 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- A. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. Parr, Phys. Rev. B, 1988, 37, 785–789 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. v. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- S. Miertuš, E. Scrocco and J. Tomasi, J. Chem. Phys., 1981, 55, 117–129 Search PubMed.
- D. A. Case, K. Belfon, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham, III, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, G. Giambasu, M. K. Gilson, H. Gohlke, A. W. Goetz,R. Harris, S. Izadi, S. A. Izmailov, K. Kasavajhala, A. Kovalenko, R. Krasny, T. Kurtzman, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, V. Man, K. M. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, A. Onufriev, F. Pan, S. Pantano, R. Qi, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. L. Simmerling, N. R. Skrynnikov, J. Smith, J. Swails, R. C. Walker, J. Wang, L. Wilson, R. M. Wolf, X. Wu, Y. Xiong, Y. Xue, D. M. York and P. A. Kollman, AMBER 2020, University of California, San Francisco. 2020 Search PubMed.
- S. Mente and M. Maroncelli, J. Phys. Chem. A, 1998, 102, 3860–3876 CrossRef CAS.
- R. S. Moog, J. Phys. Chem., 1991, 95, 10359–10369 CrossRef CAS.
- C.-C. Hsieh, K.-Y. Chen, W.-T. Hsieh, C.-H. Lai, J.-Y. Shen, C.-M. Jiang, H.-S. Duan and P.-T. Chou, Chemphyschem, 2008, 9, 2221–2229 CrossRef CAS PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 2249836. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc01441j |
| ‡ Kai-Hsin Chang, Yu-Chiang Peng, Kuan-Hsuan Su with equal contribution. |
| This journal is © The Royal Society of Chemistry 2023 |