Structures of LaH₁₀, EuH₉, and UH₈ superhydrides rationalized by electron counting and Jahn–Teller distortions in a covalent cluster model

Abstract

The superconducting hydrides LaH₁₀, EuH₉ and UH₈ are studied using chemically intuitive bonding analysis of periodic and molecular models. We find trends in the crystallographic and electronic structures of the materials by focusing on chemically meaningful building blocks in the predicted H sublattices. Atomic charge calculations, using two complementary techniques, allow us to assign oxidation states to the metals and divide the H sublattice into neutral and anionic components. Cubic [H₈]^q− clusters are an important structural motif, and molecular orbital analysis of this cluster in isolation shows the crystal structures to be consistent with our oxidation state assignments. Crystal orbital Hamilton population analysis confirms the applicability of the cluster model to the periodic electronic structure. A Jahn–Teller distortion predicted by MO analysis rationalises the distortion observed in a prior study of EuH₉. The impact of this distortion on superconductivity is determined, and implications for crystal structure prediction in other metal-hydrogen systems are discussed. Additionally, the performance of electronic structure analysis methods at high pressures are tested and recommendations for future studies are given. These results demonstrate the value of simple bonding models in rationalizing chemical structures under extreme conditions.

---

1 Introduction

Activity surrounds high-pressure hydrides due to reports of superconductivity near room temperature.¹ In an effort to realise the prediction that hydrogen would become a room-temperature superconductor under sufficient pressure,² a variety of hydrogen-rich binary materials AH_x have been predicted and synthesized. Among non-metal elements the sulfur-hydride system has been fruitful, with H₃S predicted and confirmed to be a superconductor with a critical temperature T_c of 203 K,^3,4 and controversy surrounds reports of room-temperature superconductivity in an indeterminate compound of carbon, sulfur, and hydrogen.^5–7 Metal-hydride systems have produced a number of superhydrides – compounds of hydrogen and one or more metals which contain covalently bonded H–H sublattices – particularly involving metals near the s/d border of the periodic table. LaH₁₀, a high-temperature superconductor, is an important example of this class, predicted and analysed theoretically⁸ before experiments confirmed the structure⁹ and then superconductivity at 250 K.^10,11 Other examples include CaH₆,^12,13, zirconium hydrides including ZrH₃, Zr₄H₁₅, and ZrH₆,^14–17 and various hydrides of yttrium.^8,18–20 Some predictions of new hydride superconductors are yet to be realised,²¹ which has been attributed to shortcomings in DFT methods or the possibility that the superhydrides are not conventional phonon-mediated superconductors described by BCS theory.^22,23

The “workhorse” of this field is crystal structure prediction (CSP), an umbrella term for computational methods for determining the crystal structure of a material without any prior information.^24–29 Studies utilizing this method generally identify the most thermodynamically stable phases for a chosen AH_x system as a function of pressure by running CSP calculations at various pressures and A : H ratios.⁸ Superconducting critical temperatures can then be estimated for all candidate structures.

Some researchers have worked to understand these materials from a chemical perspective. “Chemical precompression” describes the strategy of ‘alloying’ hydrogen with another metal, so the compound should require a lower pressure to induce superconductivity than pure hydrogen would.²⁵ A growing focus of material design is ternary hydrides ABH_x, where it is hoped that the combination of two metals will stabilize the phase at more accessible pressures due to additional chemical precompression.³⁰ The combinatorial space of ternary phases is much larger than the binary phases, so chemical intuition must be combined with proper computational methods to search efficiently for candidate materials. Ion size effects have also been explored, as the reduction in enthalpy arising from dense packing of atoms is a major contributor to thermodynamic stability at high pressures. Some of the highly symmetrical structures predicted for binary hydrides, such as CaH₆ and LaH₁₀, are the densest binary sphere packings for the appropriate stoichiometry and radius ratio.^31,32 However, this model does not account for covalency in the anion sublattice, and hard-sphere radii are poorly defined under pressure, particularly for hydrides. Geometrical strain arising from size-cavity mismatch has been studied in a quantum chemical framework by chemical pressure density functional theory, showing that distortions of symmetrical hydrides can indeed be caused by metal ion size (e.g. hexagonal channel widening in SrH₆ compared to CaH₆).^33,34 Electron density and electron localization function calculations of compressed metal lattices have shown that the metals act as templates for the hydrogen networks, even though metal-hydrogen covalency is weak.^35,36 Chemical intuition also led to the discovery of Eu₈H₄₆, a high-pressure hydride isostructural to the “Zintl clathrates” (e.g. Ba₈Si₄₆), because such large unit cells are too expensive to be included in routine CSP studies.³⁷ Electron counting is widely used in solid state chemistry to assign formal oxidation states,³⁸ and can be used to rationalise structural trends through models like the Zintl–Klemm concept or the 18-n rule.^39,40 Solids containing cluster anions are particularly amenable to electron counting analysis – for example, the conductivities of metal hexaborides, MB₆, can be predicted from the metal valence state by application of the Wade–Mingos rules.^41–44

In this study we focus on covalently bonded hydrogen clusters in LaH₁₀,¹¹ EuH₉,³⁷ and UH₈,^45,46 all shown in Fig. 1, in order to explain structural trends. LaH₁₀ is well-studied by theory and experiments, as described above.^8–11 EuH₉ was predicted to exist in two forms, F4̄3m and P6₃/mmm, of which we study the pseudo-cubic F4̄3m form, and XRD data collected at 86–130 GPa were consistent with this material. The strong spin polarization of Eu²⁺ is expected to preclude superconductivity, though a calculation neglecting magnetism predicted a superconducting T_c of 27 K.³⁷ UH₈ was first predicted in a CSP survey of uranium hydrides and a T_c of 23–33 K was calculated, but XRD data were ambiguous over whether a produced phase was UH₈ or UH₉.⁴⁶ A subsequent synthetic study confirmed that the phase was indeed UH₈.⁴⁵

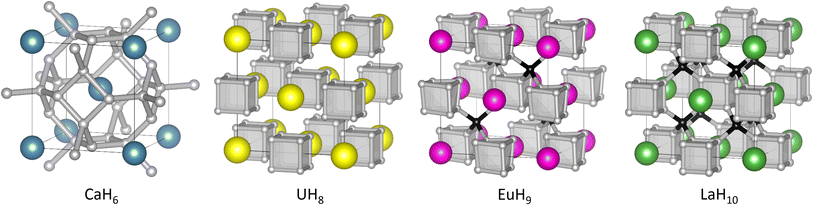Fig. 1 Structures of high-pressure hydrides CaH₆,UH₈, EuH₉, and LaH₁₀. In EuH₉ and LaH₁₀, grey and black spheres represent H atoms in cube and tetrahedral sites respectively.

All three contain cubic H₈ clusters in their anion sublattices, as shown in Fig. 1, but the cubes are distorted in EuH₉, so we wish to explain the stability of this motif and the distortion in an electron counting framework, and find whether it is related to superconductivity. It is important to note that the positions of hydrogen atoms in superhydrides are determined principally by theoretical methods because high-pressure X-ray diffraction cannot accurately locate light atoms when heavier metal atoms are present. Experimentally determined lattice parameters and metal atom positions must then be compared to theoretical predictions to determine the most likely crystal structure. We analyse charge and bonding patterns in periodic structures, including benchmarking of analytical methods on CaH₆, and use these insights to devise cluster models which capture the balance of covalent and ionic behaviour of hydrogen. Crystal orbital Hamilton population (COHP)^47,48 calculations, an established tool for studying hydride-rich materials,⁸ validate the cluster models and reveal striking differences between inequivalent hydrogen atoms. Electron counting and molecular orbital theory provide intuitive explanations of structural trends in the superhydrides.

2 Methodology

Periodic density functional theory calculations were performed with VASP,⁴⁹ version 5.4.4, using the PAW⁵⁰-PBE⁵¹ method with plane-wave cutoff of 600 eV. k-point grids of 15-15-15 were used for optimizations of CaH₆, UH₈, and LaH₁₀, and a 12-12-12 grid was used for EuH₉. All geometries were optimized until the components of the forces on all atoms were less than 0.03 eV Å⁻¹. The effect of pressure was included by the ‘PSTRESS’ method of VASP, which adds an energy correction of V*PSTRESS and modifies the diagonal elements of the stress tensor to simulate fixed external pressure during geometry optimization. To investigate the effect of changing the hydrogen pseudopotential, calculations on CaH₆ were performed using a hard H pseudopotential (“H_h”) and a 700 eV plane-wave cutoff, though subsequent tests found that this did not cause a significant change to the structural optimizations compared to the ordinary method (see Fig. S1† for details).

Electron densities were analysed with the quantum theory of Atoms in Molecules (AIM) method.⁵² Calculations were performed with the Bader program.⁵³ To ensure accurate results for compressed structures, we tested the effect of the number of fine grid points (NG(X,Y,Z)F in VASP) on the computed AIM charges for CaH₆. At 210 GPa, 200 points along each vector were required to ensure convergence of the Ca charges to within 0.05 |e|, while at ambient pressure this threshold is reached with the default value of 80. The H charges converged at 80 points at 0 GPa and 140 points at 210 GPa. Full results are available in Fig. S2.† In summary, in CaH₆ the metal charges converge with respect to grid points more slowly than the H charges, and pressure significantly increases the required number of points. All AIM results were collected with 250 grid points.

Local orbital bonding analysis was performed with LOBSTER.⁵⁴ Single-point calculations for LOBSTER analysis used 12-12-12 grids due to memory constraints. LOBSTER analysis requires projection of the plane-wave wavefunction into a local (Slater) orbital basis, and the quality of the results depends on the basis functions chosen for each element. Projection quality is measured by “charge spilling”, which is the percentage of electron density lost by the projection. The dependence of charge spilling on basis set were determined for CaH₆, UH₈ and LaH₁₀ by performing LOBSTER projections at various pressures with and without high-lying p orbitals (4p for Ca, 6p for La, 7p for U). For all three compounds, the two bases give similar results at 0 GPa but inclusion of the extra p orbital causes the charge spilling to rise rapidly as pressure increases. In particular, for CaH₆ the larger projection basis gives a superior projection at 0 GPa (1.90% vs. 2.34%) but much worse results at 210 GPa (10.4% vs. 3.7%). Full results are available in Fig. S3.† Important conclusions from these tests:

1. Inclusion of diffuse, high-energy atomic orbitals worsens projection quality for compressed structures.

2. Basis sets must be tested on high-pressure structures.

Full basis functions used in this study were Ca 3s3p4s, La and Eu 4f5s5p5d6s, U 5f6s6p6d7s, H 1s, with the PBEVaspFit basis set.⁵⁴ All projections for UH₈, EuH₉ and LaH₁₀ have charge spillings of less than 3% except for UH₈ at 210 GPa (3.09%). 3% was recommended as a threshold for a good projection in a recent study on high-throughput analysis with LOBSTER.⁵⁵ COHP analysis of LaH₁₀ and UH₈ was done with structures optimized at 0 GPa to maximise the quality of the projection. Phonon calculations were performed with VASP in the density functional perturbation theory framework, and the results were analysed using phonopy.⁵⁶

Gas-phase DFT calculations were performed with ORCA,⁵⁷ version 5.0.3, using the PBE functional,⁵¹ def2-SVP basis functions,⁵⁸ and a CPCM solvent model⁵⁹ with the dielectric constant of water to aid convergence of anions. The cubic H₈ structure was taken from the 150 GPa optimized structure of UH₈, and molecular orbitals were calculated by a single-point with a 6-charge. The distorted H₈ structure was taken from the 150 GPa optimized structure of EuH₉, and molecular orbitals were calculated by a single-point with a 2-charge.

3 Results and discussion

To establish a chemically intuitive picture of the metal hydrides, we optimized the structures of CaH₆, UH₈, EuH₉ and LaH₁₀ at 0–210 GPa, in 30 GPa steps, and then calculated atomic charges with the aim of determining oxidation states for the metals. Results for EuH₉ could not be collected at 0–30 GPa because the H network formed H₂ molecules. UH₈ and LaH₁₀ retain cubic symmetry at all pressures, but EuH₉ undergoes a small compressive tetragonal distortion (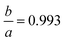 at 150 GPa) because the distorted cube contains four parallel edges which are fractionally shorter than the other eight. We will describe this structural distortion in detail later.

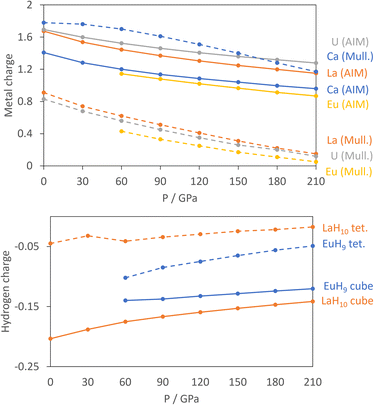
For the atomic charge calculations we use AIM,⁵² based solely on electron density, and Mulliken analysis,⁶⁰ based on atomic orbitals, as the fundamentally different methods of apportioning electrons to individual atoms provide complementary pictures of the materials. Fig. 2 shows the calculated charges of the metals from both methods.

Fig. 2 Upper: computed charges of metal atoms in CaH₆ (blue), LaH₁₀ (orange), UH₈ (grey) and EuH₉ (yellow) vs. pressure. AIM charges are shown by solid lines, and Mulliken charges by dashed lines. Lower: AIM atomic H charges in EuH₉ (blue) and LaH₁₀ (orange) resolved into cube (solid line) and tetrahedral (dashed line) atoms.

All curves show that the magnitude of the metal charge decreases as pressure increases, because compression increases overlap and reduces charge separation. The AIM charges show small differences between the metals, with charges ranging from 1.4 to 1.8 at 0 GPa and increasing in the order Eu, Ca, La, U.

The Mulliken charges have one qualitative difference in that Ca has a far larger charge – almost 2 – than the other three metals. This reflects the strongly ionic nature of Ca, while Eu, La and U all have valence d orbitals which are low enough in energy to bond with the H network covalently. The computed charges are as expected in that Ca and Eu typically form +2 cations, La is typically 3+, and U can have oxidation states ranging from +3 to +6. Support for the assignment of Eu²⁺ comes from the computed numbers of unpaired electrons of 6.81–6.82 per Eu, indicative of a 4f⁷ configuration, and the projected density of states in Fig. S9,† which shows that the 4f orbitals are filled in the spin-up channel and empty in the spin-down channel. The similarity between La and U in both methods suggests an assignment of U³⁺, which would match UH₃, the ambient-pressure uranium hydride.

In the hydrogen charge calculations, the charges become less negative as pressure increases. For LaH₁₀ and EuH₉ we can divide the hydrogens into those which form H₈ cubes, H^cube, and those which occupy the tetrahedral interstitial sites, H^tet. In LaH₁₀ each H^tet atom is connected to four H^cube atoms in a tetrahedral arrangement, while each H^cube is connected to three other H^cube atoms and one H^tet (in EuH₉ only half the H^cube atoms have an H^tet neighbour due to stoichiometry). The two types are shown as grey and black atoms respectively in Fig. 1. The AIM hydrogen charges for EuH₉ and LaH₁₀ are shown in Fig. 2, separated into the cube and tetrahedral sites. The H^tet atoms have smaller negative charges than the H^cube atoms, according to QTAIM and Mulliken analysis, and resemble neutral atoms, while the H₈ cubes are anionic. Mulliken charges were excluded from the figure for clarity and can be found in Fig. S8.† This result agrees qualitatively with the chemical template theory,³⁶ which found that the La sublattice of LaH₁₀ has a higher electron localization function value on the octahedral interstital sites (where the H₈ cubes are) than on the tetrahedral sites (where the H^tet atoms are). For our electron-counting analysis of the H₈ cubes, we will therefore assume that the interstitial atoms are neutral and consider only electron transfer from the metal to H₈. This assumption allows us to treat UH₈, EuH₉ and LaH₁₀ on an equal basis when rationalizing the symmetric and distorted cube geometries.

The left-hand side of Fig. 3 shows a molecular orbital (MO) diagram for a free H₈ cube, with O_h point symmetry, which is our starting point for studying the structures of UH₈, EuH₉ and LaH₁₀. The shapes and energetic ordering of the orbitals have been computed by DFT (Fig. S10†), but are shown here in a simplified representation and have not been orthogonalized to maximise the similarity between the cartoon and computed orbitals. Stable formal oxidation states arise from any configuration which gives completely filled valence shells. The simplest is neutral H₈, where the a_1g and t_1u sets are completely filled and the t_2g and a_2u sets are vacant, as described in a previous study.³⁶ Completely filling the t_2g set gives a closed-shell H⁶⁻₈ ion, which fits into an extreme ionic counting picture of UH₈ since +6 is the highest accessible oxidation state for U. The final option is to singly fill each of the t_2g orbitals, forming H³⁻₈ which matches with La³⁺ in LaH₁₀, supporting the model of neutral tetrahedral H atoms. The H–H bond lengths in the cubes offer another perspective on the oxidation state of U; the optimized cube edge length at 150 GPa in LaH₁₀ is 1.231 Å, while in UH₈ it is elongated to 1.293 Å, consistent with additional electron donation into the antibonding t_2g orbitals. This may be interpreted ionically, in which case U would have a formal oxidation state higher than 3+, or as a sign of greater covalency between U and H₈, or the difference may arise from the absence of H^tet atoms in UH₈.

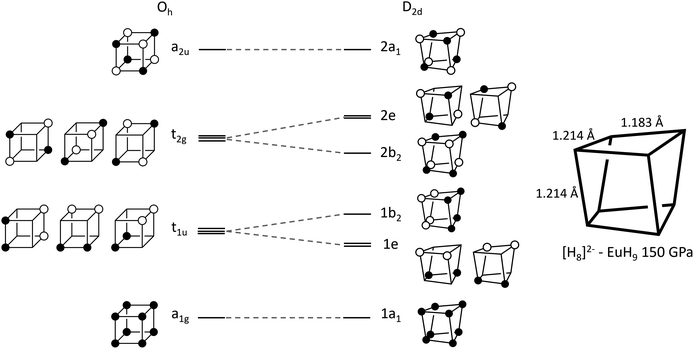Fig. 3 Walsh diagram showing orbital correlations between the cubic (O_h) and distorted (D_2d) geometries of an H₈ cluster.

A free H³⁻₈ ion would have a quartet ground state, having three unpaired electrons, but in a solid the local spin polarization will be lost when the t_2g MOs form bands by overlapping with other atoms. To investigate the possibility of a net spin moment on H₈ in LaH₁₀ we performed a calculation which was initialized with a spin polarization equivalent to 0.5 unpaired electrons per H^cube atom, adding up to a total of 4 unpaired electrons on H₈ in a ferromagnetic arrangement, slightly larger than the proposed formal value. The calculation converged rapidly to a diamagnetic state, suggesting that the H₈ t_2g orbitals do indeed form delocalized electronic bands (this is supported by the COHP calculations in Fig. 4 below). Such delocalization could be interpreted as contrary to the formal oxidation state picture that we have outlined here, but we believe that the behaviour of LaH₁₀ is comparable to other phases containing open-shell molecular anions such as K₃C₆₀, which is also a superconductor.⁶¹ The [C₆₀]³⁻ anions can be described as having three electrons a triply degenerate t_1u HOMO (which is the LUMO of C₆₀), but K₃C₆₀ is metallic due to orbital overlap between adjacent [C₆₀]³⁻ ions and displays only Pauli paramagnetism, having no unpaired spins localized on the anions.^62,63 Formal oxidation states remain a useful tool for understanding these complex materials.

Fig. 4 Crystal orbital Hamilton population (COHP) analysis of LaH₁₀. H^cube atoms are shown in grey and H^tet in black. Upper left: H^cube–H^cube with annotations showing the assignment of [H₈] molecular orbitals to COHP peaks. Lower left: H^cube–H^tet. Upper right: La–H^cube. Lower right: La–H^tet. Energies are given relative to the Fermi level (E_f).

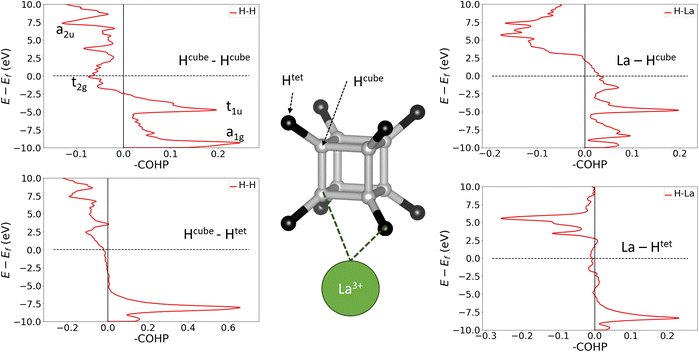
To confirm the applicability of the molecular bonding model to the crystalline materials, we must show that hydrogen-metal interactions and H–H bonds between cube and tetrahedral atoms do not fundamentally change the bonding within the cube. We have therefore calculated crystal orbital Hamilton populations (COHPs) for neighbouring pairs of atoms in LaH₁₀, which are shown in Fig. 4. COHP is a measure of the bonding or antibonding character of electronic states, obtained by weighting the density of states by the corresponding Hamiltonian matrix element. By convention, COHP graphs plot the negative value of the COHP on the x axis so that positive values denote stabilizing bonding interactions. This analysis was done for the 0 GPa structure because it has the highest projection quality (lowest charge spilling). To confirm that the 0 GPa optimized structure contains the same essential bonding features as the compressed unit cells, in Fig. S14† we plot the PDOS for La and both inequivalent H sites at 0 and 150 GPa, which show that the distinguishing features of each atom are preserved across the pressure range, and the PDOS for all atoms broadens quite uniformly under pressure. Furthermore, Fig. S15† compares the H^cube–H^cube and H^cube–H^tet COHPs at 0 and 150 GPa. The structures of the curves for the two pairwise interactions are unchanged by compression, suggesting that the dominant bonding interactions are the same across the studied pressure range. The 150 GPa COHP curves show the same peak broadening seen in the PDOS, making them more difficult to interpret without having first looked at the 0 GPa plots, so we will use the 0 GPa plots to explain the bonding nature of LaH₁₀.

The plots on the left side of Fig. 4 show COHPs for a H^cube–H^cube bond and a H^cube–H^tet bond. The principal peaks in the H^cube–H^cube and Hcube–H^tet do not appear at the same energies (they are “non-coincident”), showing that the two types of H–H bond are composed of distinct electronic states. Importantly, this tells us that the dominant H^cube–H^cube interactions are the same in the LaH₁₀ crystal as in the free H₈ cluster. The H^cube–H^tet COHP shows a single large peak, indicative of a strong bonding interaction, so these interactions are important in determining structure. The peaks in the cube edge COHP can be matched to the H₈ MOs in Fig. 3 by comparing the relative energies and bonding characters, since –COHP is positive for bonding and negative for antibonding interactions. The a_1g and t_1u peaks are bonding and fully occupied, while the t_2g antibonding peak crosses the Fermi level, supporting our molecular model of [H₈]³⁻ with a half-filled t_2g manifold. The a_2u peak is difficult to assign on the basis of this COHP alone, but the ambiguity can be resolved with other COHPs (see below). Corresponding plots for UH₈, in Fig. S12,† show very similar behaviour for the H–H and U–H COHPs; since UH₈ has no tetrahedral interstital H atoms, the similarity between H–H COHPs in LaH₁₀ and UH₈ validates the H₈ molecule as a structural model for the periodic hydrides. One noticable difference is that the H–H t_2g antibonding peak is largely below E_F in UH₈, indicating greater electron transfer to the cube, as suggested above on the basis of H–H bond lengths. The right side of Fig. 4 shows La–H COHPs for the cube and tetrahedral H sites. The largest bonding peak in the La–H^cube COHP coincides with the t_1u H–H band, and the H–H t_2g band also coincides energetically with an La–H bonding band that crosses the Fermi level. The interaction between H₈ t_2g and La 5d orbitals may therefore control the transport properties of LaH₁₀, possibly including superconductivity. The La–H^tet COHP has a single bonding peak coincident with the cube-interstitial H–H bonding peak, and an antibonding peak well above the Fermi level.

Finally, we plotted H–H COHPs for the face and body diagonals of the cube (Fig. S13†), which allow us to assign the high-energy peak corresponding to the fully antibonding a_2u orbital. The peaks appear at the same energies as in the H^cube–H^cube COHP (Fig. 4) but differ in their sign, i.e. whether they are bonding or antibonding, and the absolute values are much smaller because these are not nearest–neighbour interactions. The face diagonal behaves as expected from the MOs – the a_1g and a_2u peaks are bonding, while the t_1u and t_2g peaks are antibonding. However, the body diagonal peaks all have the opposite signs to those expected from the MOs, with a_1g and t_2g paradoxically antibonding while t_1u and a_2u are bonding. We believe that this anomaly is due to the H atoms at opposite corners of the cube interacting with their periodic images through a metal atom, which could be comparable in strength to the intra-cube covalency along the body diagonal. This theory is supported by the fact that the t_1u peak, which overlaps strongly with the metal, is larger than the a_1g peak, and that the same behaviour is observed in LaH₁₀ and UH₈. In conclusion, the COHP results clearly demonstrate that the H networks of the periodic materials are well represented by a molecular H₈ model.

In EuH₉ the cubes distort to a D_2d geometry in which four parallel edges shorten relative to the other eight (1.183 Å vs. 1.214 Å at 150 GPa), as shown in the diagram on the right of Fig. 3, and the angles distort so the faces go from square to rhombic.³⁷ The Walsh diagram in Fig. 3 shows that this is consistent with the assignment of a 2-charge to H₈.⁶⁴ As before, the orbital energies and shapes are computed by DFT but shown in a simplified representation here, and the computed results are shown in Fig. S11.† Placing two electrons in the t_2g orbitals renders the structure unstable with respect to a Jahn–Teller distortion which lowers the symmetry to stabilize that pair of electrons. The reduction in symmetry causes the triply degenerate t_2g to separate into a b₂ orbital and a doubly degenerate e pair. The occupied 2b₂ orbital is bonding along the four shorter edges of the cluster and antibonding along the other eight, consistent with the observed distortion.

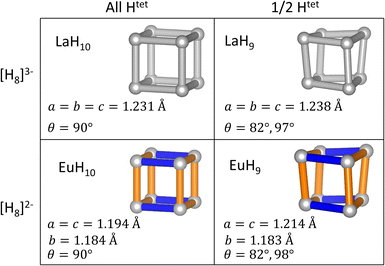
To test the relationships between structural distortions, H^tet occupancy, and electron count, we have exchanged metals to form LaH₉ and EuH₁₀ and optimized their structures at 150 GPa. The results, shown in Fig. 5, are enlightening. EuH₁₀ has a cuboidal H₈ cluster with an axial compression, as expected from the Jahn–Teller effect, but all bond angles 90°, unlike in EuH₉. LaH₉ has a rhombic H₈ cluster with all side lengths equal, but angle distortions of equal magnitude to those in EuH₉. The angle distortion is therefore driven by the partial occupancy of the tetrahedral sites, shown along the rows of Fig. 5, while the length distortion is driven by the formal charge of H₈, shown in the columns of Fig. 5. This theory is corroborated by the predicted structures of PrH₉ and PaH₉,^36,65,66 which have the same structure as LaH₉. Pr typically adopts the +3 oxidation state, so the fact that PrH₉ and LaH₉ have the same structure is consistent with our model. The behaviour of PaH₉ is ambiguous because Pa may adopt oxidation states from +2 to +5, and the greater covalent overlap of the 5f orbitals may also have structural consequences. The rhombic cluster has been shown to have triply degenerate HOMO and LUMO,³⁶ so the distortion, which changes angles but leaves all bonds at equal length, is not a Jahn–Teller distortion. In contrast, the cuboidal distortion in EuH₁₀ is consistent with the orbital mechanism shown in Fig. 3 so it is a Jahn–Teller distortion. We also tried to test the limits of the distortion theory by optimizing the structures of [EuH₉]⁻ and [LaH₁₀]⁺, but the results were inconclusive. [LaH₁₀]⁺ distorts in the same way as EuH₁₀, but [EuH₉]⁻ retains the EuH₉ structure. Details of these calculations can be found in the ESI.†

Fig. 5 Geometries of H₈ clusters in MH₉ and MH₁₀ (M = La, Eu) arranged by the formal charge on H₈ and the occupancy (full or half) of the H^tet sites. Bond lengths and angles are calculated at 150 GPa. H is shown in grey, La in green, and Eu in pink. Orange and blue bonds denote elongated and compressed H–H bonds respectively.

Predictions for stable structures of superhydrides can be made on the basis of our analysis. For a ternary hydride, the average oxidation state of the cations must be +3 for a cubic LaH₁₀-type structure to be stable. A H₈ cube in a superhydride of a 4+ cation, e.g. Zr, would also have a Jahn–Teller instability, but it would differ from EuH₉ in that the distortion would need to stabilize two pairs of electrons. The cube should therefore shorten eight bonds and elongate four, reversing the ordering of the 2e and 2b₂ orbitals in Fig. 3. To our knowledge, the structures of high-pressure Zr hydrides have only been investigated for compositions up to ZrH₆,^14–17 and determining the positions ZrH₉ and ZrH₁₀ relative to the convex hull for the Zr–H system is outside the scope of this work.

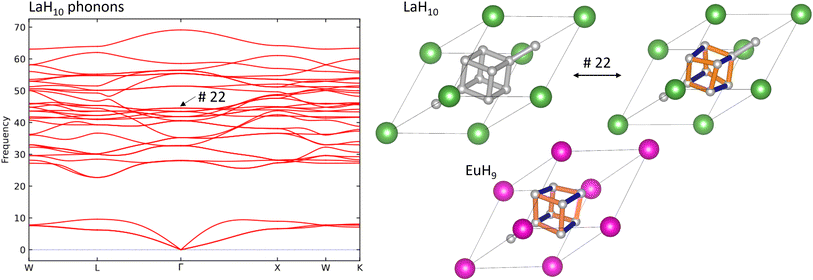
Finally, we investigate the connection between superconductivity and the Jahn–Teller distortion in EuH₉ by calculating the phonon band structure of LaH₁₀, identifying the mode which most closely resembles this distortion, and comparing to electron-phonon coupling (EPC) calculations in literature⁸ to see whether this mode contributes significantly to the EPC constant. Fig. 6 shows the phonon band structure of LaH₁₀, undistorted and distorted primitive cells of LaH₁₀, and the primitive cell of EuH₉ for comparison. These calculations were done at 300 GPa to eliminate imaginary frequencies and maximise comparability to literature. The Brillouin zone, annotated with high-symmetry k-points, is shown in Fig. S16.† By inspection of the computed vibrational modes we find that mode 22 (44.54 THz at Γ) distorts the H₈ cube in LaH₁₀ to resemble EuH₉ most strongly. This comparison is shown on in Fig. 6, and an important structural detail is that this distorted structure has one short and two long H–H bonds in the cube, just like EuH₉. The distorted structures in Fig. 6 show longer bonds in orange and shorter bonds in blue. The phonon band structure is very similar to one previously computed⁸ which shows the contribution of each phonon mode to EPC. Comparing the two graphs shows that the Jahn–Teller distortion mode makes no contribution to EPC, so the distortion does not directly explain the difference in predicted critical temperatures between LaH₁₀ and EuH₉. The difference must therefore be due to other factors such as stoichiometry or metal-hydrogen interactions, the latter of which has been proposed to be an important difference between LaH₁₀ and YH₁₀.⁸ Conversely, if this vibrational mode is not a vital ingredient for superconductivity in LaH₁₀ then distorted derivatives featuring 2+ or 4+ cations may yet be viable candidates for high-temperature superconductors.

Fig. 6 L: phonon band structure of LaH₁₀ at 300 GPa. R: undistorted and distorted primitive unit cells of LaH₁₀, where the distortion is over mode 22, and the optimized structure of EuH₉. La atoms are shown in green, Eu in pink, and H in grey. Orange and blue bonds denote elongated and compressed H–H bonds respectively.

4 Conclusions

Structural trends in the high-pressure hydrides UH₈, EuH₉, and LaH₁₀ have been rationalised by the intuitive chemical tools of oxidation states and molecular orbital theory. Viewing the predicted hydrogen networks as an assemblage of atoms and clusters, rather than a metal-centered clathrate, allows us to divide the H atoms into chemically meaningful groups and study their electronic structures. Ab initio atomic charge calculations, using the AIM and Mulliken formalisms, show that some H atoms are effectively neutral in the lattice, while the H₈ cubes are anionic. Formal oxidation states for the metals were assigned on the basis of charge calculations, so the electronic structures of the hydrides could be discussed in terms of electron transfer from metal atoms to hydrogen clusters. Molecular orbital descriptions of the H₈ clusters, validated by COHP analysis, rationalize the previously predicted crystal structures, including a Jahn–Teller distortion in EuH₉. The distortion is found not to be directly relevant to superconductivity, so these results inform the scope of the search for new high-temperature superconductors. These methods can be easily applied to predictions of composition and structure in the growing family of compressed metal hydrides.

Data availability

The optimized structures supporting this article have been uploaded as part of the ESI.†

Author contributions

Harry W. T. Morgan: conceptualization, investigation, visualization, writing – original draft, writing – review and editing. Anastassia N. Alexandrova: conceptualization, supervision, writing – review and editing, resources.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge computational resources from the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility located at Lawrence Berkeley National Laboratory, and DOE-BES grant DE-SC0019152. The authors thank Robert H. Lavroff for valuable discussions of vibrational properties.

Notes and references

1. B. Lilia, R. Hennig, P. Hirschfeld, G. Profeta, A. Sanna, E. Zurek, W. E. Pickett, M. Amsler, R. Dias, M. I. Eremets, C. Heil, R. J. Hemley, H. Y. Liu, Y. M. Ma, C. Pierleoni, A. N. Kolmogorov, N. Rybin, D. Novoselov, V. Anisimov, A. R. Oganov, C. J. Pickard, T. G. Bi, R. Arita, I. Errea, C. Pellegrini, R. Requist, E. K. U. Gross, E. R. Margine, S. R. Xie, Y. D. Quan, A. Hire, L. Fanfarillo, G. R. Stewart, J. J. Hamlin, V. Stanev, R. S. Gonnelli, E. Piatti, D. Romanin, D. Daghero and R. Valenti, J. Phys.: Condens. Matter, 2022, 34, 183002.
2. N. W. Ashcroft, Phys. Rev. Lett., 1968, 21, 1748.
3. D. F. Duan, Y. X. Liu, F. B. Tian, D. Li, X. L. Huang, Z. L. Zhao, H. Y. Yu, B. B. Liu, W. J. Tian and T. Cui, Sci. Rep., 2014, 4, 6968.
4. A. P. Drozdov, M. I. Eremets, I. A. Troyan, V. Ksenofontov and S. I. Shylin, Nature, 2015, 525, 73.
5. E. Snider, N. Dasenbrock-Gammon, R. McBride, M. Debessai, H. Vindana, K. Vencatasamy, K. V. Lawler, A. Salamat and R. P. Dias, Nature, 2020, 586, 373.
6. D. van der Marel and J. E. Hirsch, Int. J. Mod. Phys. B, 2023, 37(04), 2375001.
7. G. A. Smith, I. E. Collings, E. Snider, D. Smith, S. Petitgirard, J. S. Smith, M. White, E. Jones, P. Ellison, K. V. Lawler, R. P. Dias and A. Salamat, Chem. Commun., 2022, 58, 9064–9067.
8. H. Y. Liu, I. Naumov, R. Hoffmann, N. W. Ashcroft and R. J. Hemley, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 6990–6995.
9. Z. M. Geballe, H. Y. Liu, A. K. Mishra, M. Ahart, M. Somayazulu, Y. Meng, M. Baldini and R. J. Hemley, Angew. Chem., Int. Ed., 2018, 57, 688–692.
10. M. Somayazulu, M. Ahart, A. K. Mishra, Z. M. Geballe, M. Baldini, Y. Meng, V. V. Struzhkin and R. J. Hemley, Phys. Rev. Lett., 2019, 122, 027001.
11. A. P. Drozdov, P. P. Kong, V. S. Minkov, S. P. Besedin, M. A. Kuzovnikov, S. Mozaffari, L. Balicas, F. F. Balakirev, D. E. Graf, V. B. Prakapenka, E. Greenberg, D. A. Knyazev, M. Tkacz and M. I. Eremets, Nature, 2019, 569, 528.
12. H. Wang, J. S. Tse, K. Tanaka, T. Iitaka and Y. M. Ma, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 6463–6466.
13. L. Ma, K. Wang, Y. Xie, X. Yang, Y. Y. Wang, M. Zhou, H. Y. Liu, X. H. Yu, Y. S. Zhao, H. B. Wang, G. T. Liu and Y. M. Ma, Phys. Rev. Lett., 2022, 128, 167001.
14. C. L. Zhang, X. He, Z. W. Li, S. J. Zhang, S. M. Feng, X. C. Wang, R. C. Yu and C. Q. Jin, Sci. Bull., 2022, 67, 907–909.
15. H. Xie, W. T. Zhang, D. F. Duan, X. L. Huang, Y. P. Huang, H. Song, X. L. Feng, Y. S. Yao, C. J. Pickard and T. Cui, J. Phys. Chem. Lett., 2020, 11, 646–651.
16. K. Abe, Phys. Rev. B, 2018, 98, 134103.
17. X. F. Li, Z. Y. Hu and B. Huang, Phys. Chem. Chem. Phys., 2017, 19, 3538–3543.
18. E. Snider, N. Dasenbrock-Gammon, R. McBride, X. Y. Wang, N. Meyers, K. V. Lawler, E. Zurek, A. Salamat and R. P. Dias, Phys. Rev. Lett., 2021, 126, 117003.
19. P. P. Kong, V. S. Minkov, M. A. Kuzovnikov, A. P. Drozdov, S. P. Besedin, S. Mozaffari, L. Balicas, F. F. Balakirev, V. B. Prakapenka, S. Chariton, D. A. Knyazev, E. Greenberg and M. I. Eremets, Nat. Commun., 2021, 12, 5075.
20. C. Heil, S. di Cataldo, G. B. Bachelet and L. Boeri, Phys. Rev. B, 2019, 99, 220502.
21. J. E. Hirsch, Appl. Phys. Lett., 2022, 121, 080501.
22. J. E. Hirsch, J. Appl. Phys., 2021, 130, 181102.
23. L. Novakovic, D. Sayre, D. Schacher, R. P. Dias, A. Salamat and K. V. Lawler, Phys. Rev. B, 2022, 105, 024512.
24. S. M. Woodley and R. Catlow, Nat. Mater., 2008, 7, 937–946.
25. K. P. Hilleke and E. Zurek, J. Appl. Phys., 2022, 131, 070901.
26. M. S. Miao, Y. H. Sun, E. Zurek and H. Q. Lin, Nat. Rev. Chem., 2020, 4, 508–527.
27. Z. Falls, P. Avery, X. Y. Wang, K. P. Hilleke and E. Zurek, J. Phys. Chem. C, 2021, 125, 1601–1620.
28. A. R. Oganov, C. J. Pickard, Q. Zhu and R. J. Needs, Nat. Rev. Mater., 2019, 4, 331–348.
29. Y. C. Wang, J. Lv, P. Y. Gao and Y. M. Ma, Acc. Chem. Res., 2022, 55, 2068–2076.
30. Z. H. Zhang, T. Cui, M. J. Hutcheon, A. M. Shipley, H. Song, M. Y. Du, V. Z. Kresin, D. F. Duan, C. J. Pickard and Y. S. Yao, Phys. Rev. Lett., 2022, 128, 047001.
31. R. Koshoji, M. Kawamura, M. Fukuda and T. Ozaki, Phys. Rev. E, 2021, 103, 023307.
32. A. B. Hopkins, F. H. Stillinger and S. Torquato, Phys. Rev. E, 2012, 85, 021130.
33. K. P. Hilleke and E. Zurek, Angew. Chem., Int. Ed., 2022, 61, e202207589.
34. D. C. Fredrickson, J. Am. Chem. Soc., 2012, 134, 5991–5999.
35. S. Yi, C. Z. Wang, H. Jeon and J. H. Cho, Phys. Rev. Mater., 2021, 5, 024801.
36. Y. Sun and M. Miao, Chem, 2022, 2, 443–459.
37. D. V. Semenok, D. Zhou, A. G. Kvashnin, X. L. Huang, M. Galasso, I. A. Kruglov, A. G. Ivanova, A. G. Gavriliuk, W. H. Chen, N. V. Tkachenko, A. I. Boldyrev, I. Troyan, A. R. Oganov and T. Cui, J. Phys. Chem. Lett., 2021, 12, 32–40.
38. A. Walsh, A. A. Sokol, J. Buckeridge, D. O. Scanlon and C. R. A. Catlow, J. Phys. Chem. Lett., 2017, 8, 2074–2075.
39. R. Nesper, Z. fur Anorg. Allg. Chem., 2014, 640, 2639–2648.
40. V. J. Yannello and D. C. Fredrickson, Inorg. Chem., 2015, 54, 11385–11398.
41. R. W. Johnson and A. H. Daane, J. Chem. Phys., 1963, 38, 425.
42. K. Wade, J. Chem. Soc. D, 1971, 792.
43. D. M. P. Mingos, Nature, Phys. Sci., 1972, 236, 99.
44. H. W. T. Morgan and A. N. Alexandrova, Inorg. Chem., 2022, 61, 18701–18709.
45. B. Guigue, A. Marizy and P. Loubeyre, Phys. Rev. B, 2020, 102, 014107.
46. I. A. Kruglov, A. G. Kvashnin, A. F. Goncharov, A. R. Oganov, S. S. Lobanov, N. Holtgrewe, S. Jiang, V. B. Prakapenka, E. Greenberg and A. V. Yanilkin, Sci. Adv., 2018, 4, eaat9776.
47. R. Dronskowski and P. E. Blochl, J. Phys. Chem., 1993, 97, 8617–8624.
48. V. L. Deringer, A. L. Tchougreeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466.
49. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
50. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
51. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
52. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
53. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
54. S. Maintz, V. L. Deringer, A. L. Tchougreeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035.
55. J. George, G. Petretto, A. Naik, M. Esters, A. J. Jackson, R. Nelson, R. Dronskowski, G. M. Rignanese and G. Hautier, Chempluschem, 2022, 87, e202200123.
56. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
57. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
58. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
59. M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681.
60. R. S. Mulliken, J. Chem. Phys., 1955, 23, 2338–2342.
61. A. F. Hebard, M. J. Rosseinsky, R. C. Haddon, D. W. Murphy, S. H. Glarum, T. T. M. Palstra, A. P. Ramirez and A. R. Kortan, Nature, 1991, 350, 600–601.
62. K. Holczer and R. L. Whetten, Carbon, 1992, 30, 1261–1276.
63. W. H. Wong, M. E. Hanson, W. G. Clark, G. Gruner, J. D. Thompson, R. L. Whetten, S. M. Huang, R. B. Kaner, F. Diederich, P. Petit, J. J. Andre and K. Holczer, Europhys. Lett., 1992, 18, 79–84.
64. A. D. Walsh, J. Chem. Soc., 1953, 2260–2266.
65. D. Zhou, D. Semenok, D. F. Duan, H. Xie, X. L. Huang, W. H. Chen, X. Li, B. B. Liu, A. R. Oganov and T. Cui, Sci. Adv., 2020, 6, eaax6849.
66. X. H. Xiao, D. F. Duan, H. Xie, Z. J. Shao, D. Li, F. B. Tian, H. Song, H. Y. Yu, K. Bao and T. Cui, J. Phys.: Condens. Matter, 2019, 31, 315403.

---

Footnote

† Electronic supplementary information (ESI) available: additional figures as described in the text, and optimized geometries in VASP POSCAR format. See DOI: https://doi.org/10.1039/d3sc00900a

---