Open Access Article
Open Access ArticleObservation of parallel intersystem crossing and charge transfer-state dynamics in [Fe(bpy)3]2+ from ultrafast 2D electronic spectroscopy†
Angela
Lee
 a,
Minjung
Son‡
a,
Minjung
Son‡
 a,
Mawuli
Deegbey
a,
Mawuli
Deegbey
 b,
Matthew D.
Woodhouse
c,
Stephanie M.
Hart§
b,
Matthew D.
Woodhouse
c,
Stephanie M.
Hart§
 a,
Hayden F.
Beissel
c,
Paul T.
Cesana
a,
Elena
Jakubikova
a,
Hayden F.
Beissel
c,
Paul T.
Cesana
a,
Elena
Jakubikova
 b,
James K.
McCusker
b,
James K.
McCusker
 *c and
Gabriela S.
Schlau-Cohen
*c and
Gabriela S.
Schlau-Cohen
 *a
*a
aDepartment of Chemistry, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: gssc@mit.edu
bDepartment of Chemistry, North Carolina State University, Raleigh, NC 27695, USA
cDepartment of Chemistry, Michigan State University, East Lansing, MI 48824, USA. E-mail: jkm@chemistry.msu.edu
First published on 30th October 2023
Abstract
Transition metal-based charge-transfer complexes represent a broad class of inorganic compounds with diverse photochemical applications. Charge-transfer complexes based on earth-abundant elements have been of increasing interest, particularly the canonical [Fe(bpy)3]2+. Photoexcitation into the singlet metal–ligand charge transfer (1MLCT) state is followed by relaxation first to the ligand-field manifold and then to the ground state. While these dynamics have been well-studied, processes within the MLCT manifold that facilitate and/or compete with relaxation have been more elusive. We applied ultrafast two-dimensional electronic spectroscopy (2DES) to disentangle the dynamics immediately following MLCT excitation of this compound. First, dynamics ascribed to relaxation out of the initially formed 1MLCT state was found to correlate with the inertial response time of the solvent. Second, the additional dimension of the 2D spectra revealed a peak consistent with a ∼20 fs 1MLCT → 3MLCT intersystem crossing process. These two observations indicate that the complex simultaneously undergoes intersystem crossing and direct conversion to ligand-field state(s). Resolution of these parallel pathways in this prototypical earth-abundant complex highlights the ability of 2DES to deconvolve the otherwise obscured excited-state dynamics of charge-transfer complexes.
1. Introduction
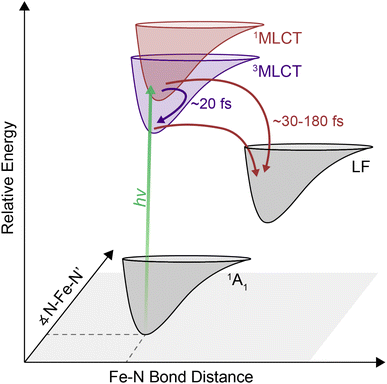
Transition metal-based polypyridyl complexes represent an important class of inorganic chromophores with photophysical properties amenable for applications ranging from solar energy conversion1–5 to organic transformations.6–8 Amongst this class of complexes, the prototypical chromophore is tris(2,2′-bipyridine)ruthenium(II), i.e., [Ru(bpy)3]2+. The photophysical properties of [Ru(bpy)3]2+ – specifically the existence of a metal-to-ligand charge-transfer (MLCT) excited state that stores ∼2 V of energy9 and persists for ∼1 μs in deoxygenated solution10 – lie at the heart of its utility in such a wide range of settings. Despite its advantages, the elemental scarcity of ruthenium (as well as related chromophores containing iridium, rhenium, osmium, etc.) raises important questions about the cost and scalability of processes built on these materials.11 This realization has spurred recent efforts to develop alternatives that replicate the photochemical properties of compounds such as [Ru(bpy)3]2+ while using components for which material availability ceases to be an issue.12–17 Accordingly, there has been a rapid expansion of research into the synthesis and photophysical properties of chromophores based on elements of the first transition series (e.g., iron, cobalt, nickel, chromium).Many of these efforts have focused on ions possessing a d6 configuration due to their valence isoelectronic relationship with Ru(II). The canonical example of this class of compounds, [Fe(bpy)3]2+, exhibits similar steady-state optical properties to its second- and third-row transition metal analogs, namely a strong MLCT absorption in the mid-visible region, yet its excited-state properties bear little resemblance to its heavier group 8 congeners.18 Specifically, the absence of a spectroscopic signature associated with the bipyridyl radical anion (i.e., bpy˙−) within 10 ps following MLCT excitation was an early indication of an excited-state lifetime that was many orders of magnitude shorter than its Ru(II) counterpart.4 The sub-100 fs lifetime of the MLCT manifold for an Fe(II) polypyridyl complex was first quantified in 2000 using ultrafast time-resolved absorption spectroscopy in conjunction with spectrochemical identification of an optical signature for the MLCT excited state.19 This was later observed specifically in [Fe(bpy)3]2+ using XANES20 and ultraviolet transient absorption spectroscopy.21 Similar timescales have also been seen for a range of related compounds.12,22–24 The dramatic attenuation in MLCT-state lifetime observed for the Fe(II) complexes results from an inversion in the relative energies of the charge-transfer and ligand-field excited states compared to what exists in the second- and third transition series due to the so-called primogenic effect.25–27 These ligand-field states are characterized by large geometric distortions relative to both the ground- and MLCT excited states, thereby facilitating rapid non-radiative decay out of the charge transfer-state manifold and the eventual formation of the high-spin 5T2 excited state on a timescale of ∼200 fs.
Following conversion from the MLCT excited state manifold to the lowest-energy ligand-field excited state, specifically the 5T2 state, ground state recovery (i.e., 5T2 → 1A1 relaxation) occurs on a timescale of ∼1 ns. Recently, Miller and McCusker identified solvent dependent kinetics for this ground-state recovery.28 The dependence was attributed to solvent reorganization in response to the large decrease in molecular volume associated with the conversion from a high-spin to a low-spin configuration. Although subtle, the solvent dependence associated with electronic state evolution localized on the metal center and relatively insulated from the solvent environment raises questions about the solvent dependence of dynamics in the charge-transfer manifold. Here, the transfer of an electron from the metal to the ligand places negative charge density on the periphery of the molecule and therefore in direct contact with the surrounding solvent. Despite there being ample evidence from studies on complexes possessing long-lived charge-transfer states that ultrafast solvent-coupled processes can influence their initial evolution,22,28–30 the effect of solvent at early timescales and its coupling to intersystem crossing processes in [Fe(bpy)3]2+ have not been investigated.
Although relaxation from the MLCT manifold into the ligand-field 5T2 state has been established for [Fe(bpy)3]2+, the pathway involved in this relaxation is still under debate. Direct relaxation from the MLCT band into the 5T2 state is formally a two-electron process, thus making a direct transition highly improbable.31 It has therefore been proposed that the 1MLCT → 5T2 conversion likely occurs via intermediate metal-centered states. While progress has clearly been made with regard to bringing processes localized on the metal center into better focus, details are sparse when it comes to dynamics occurring within the initially formed charge-transfer state(s). Transient absorption spectroscopy conducted by Auböck and Chergui was interpreted in terms of a 1MLCT → 3MLCT intersystem crossing event followed by a 3MLCT → 5T2 direct relaxation mechanism with an overall timescale of <50 fs,32 whereas X-ray fluorescence spectroscopy data were modeled without invoking an intersystem crossing event within the charge-transfer manifold.33 Because the photoexcited MLCT state relaxes into the high-spin 5T2 state within a few hundred femtoseconds, fast time resolution33–36 is required to properly resolve the early-time dynamics within the MLCT manifold. A range of time-resolved methodologies are available to access this regime, but the issue is compounded by the broad and overlapping spectroscopic features associated with relevant processes in [Fe(bpy)3]2+. These temporal and spectral requirements present significant challenges for determining what mediates the excited-state dynamics. Two-dimensional electronic absorption spectroscopy (2DES) is an advanced spectroscopic technique that combines the ability of transient absorption spectroscopy to probe ultrafast dynamics with direct excitation and detection frequency correlation. The additional dimension attained through this correlation allows for energetic deconvolution of different contributions to the excited-state dynamics of systems, providing information about the energy landscape that would be difficult, if not impossible, to divine from transient absorption spectroscopy alone. Although 2DES has been commonly used to study light harvesting systems,34,37–39 inorganic nanomaterials,40–43 and organic molecular chromophores,35,44,45 amongst other systems, it has been underutilized as a tool to understand ultrafast dynamics in molecular, transition-metal based chromophores.
In this report, we show that challenges associated with characterizing early-time dynamics within the MLCT manifold of [Fe(bpy)3]2+ can be overcome using 2DES. Here, the additional spectral separation afforded by this technique uncovered a previously hidden 1MLCT → 3MLCT cross peak while simultaneously resolving sub-100 fs dynamics of intersystem crossing and transfer out of the MLCT manifold. Collectively, these observations revealed parallel pathways of triplet-mediated and direct relaxation to the metal centered states. These results demonstrate the ability of 2DES to be a particularly effective tool for elucidating the early-timescale excited-state dynamics in the class of transition metal-based chromophores (like [Fe(bpy)3]2+) to provide new insights into the ultrafast processes underlying their functionality.46
2. Results
2.1. Steady-state absorption features
Fig. 1A shows the steady-state absorption spectrum of [Fe(bpy)3]2+ in methanol. In this frequency range, the dominant peak at ∼19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1 is the 1A1 → 1MLCT transition with a tail on the red edge associated with the formally spin forbidden 1A1 → 3MLCT transition.47 Consistent with this assignment, TD-DFT calculations (Fig. 1B) showed that the 3MLCT states primarily contribute to the lower-energy range of the absorption spectrum while the higher-energy range of the spectrum is dominated by a 1MLCT transition with a large oscillator strength. The dominant calculated excitation at 21
200 cm−1 is the 1A1 → 1MLCT transition with a tail on the red edge associated with the formally spin forbidden 1A1 → 3MLCT transition.47 Consistent with this assignment, TD-DFT calculations (Fig. 1B) showed that the 3MLCT states primarily contribute to the lower-energy range of the absorption spectrum while the higher-energy range of the spectrum is dominated by a 1MLCT transition with a large oscillator strength. The dominant calculated excitation at 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 832 cm−1 seen in Fig. 1B corresponds to a doubly-degenerate 1MLCT state (Table S9†). Only minor solvatochromic effects were observed in the absorption spectra of [Fe(bpy)3]2+ (Fig. S1A and S17†).
832 cm−1 seen in Fig. 1B corresponds to a doubly-degenerate 1MLCT state (Table S9†). Only minor solvatochromic effects were observed in the absorption spectra of [Fe(bpy)3]2+ (Fig. S1A and S17†).
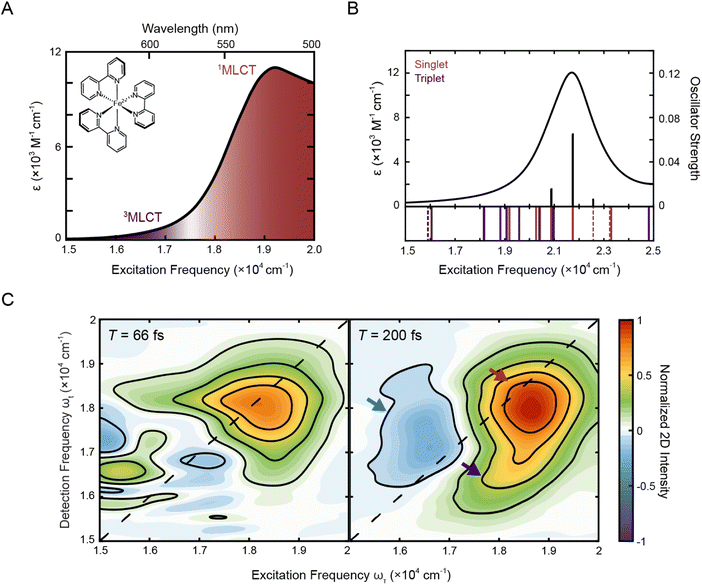 | ||
| Fig. 1 (A) Absorption spectrum of [Fe(bpy)3]2+ in methanol with singlet and triplet metal-to-ligand charge transfer bands (1A1 → 1MLCT, red; 1A1 → 3MLCT, purple). The molecular structure of [Fe(bpy)3]2+ is shown in the inset. (B) Calculated stick spectrum (top, black sticks) and broadened line spectrum (top, black line) obtained from TD-DFT calculations of [Fe(bpy)3]2+ in acetonitrile. Energy spectrum of the singlet metal-centered (dashed red lines) and 1MLCT (solid red lines) and triplet metal-centered (dashed purple lines) and 3MLCT (solid purple lines) transitions, including those with zero oscillator strength, are shown below the plotted spectrum (see Tables S9 and S10† for full information of the calculated singlet and triplet states, respectively). (C) Phased 2D spectra of [Fe(bpy)3]2+ in methanol at T = 66 fs (left) and T = 200 fs (right). Positive intensity corresponds to ground state bleach or stimulated emission signals and negative intensity corresponds to excited state absorption signal. Plots are normalized to the maximum and minimum intensities of the T = 200 fs spectrum. Contour lines are drawn at 20% intervals. Arrows denote predominant peaks. | ||
2.2. 2DES spectra features
To investigate the dynamics of the charge-transfer transitions, 2DES was used to measure a series of spectra that map out the excited-state evolution. Correlation plots of excitation (ωτ) and detection (ωt) energies were created as a function of the delay time between excitation and detection events, known as the waiting time (T).34,39 The spectra were measured with ∼10 fs temporal resolution. The nonresonant response (coherent artifact) of the pulse was also characterized spectrally (Fig. S2†). To minimize contributions from the nonresonant response, the 2D data were analyzed only for T > 47 fs. Representative 2D spectra of [Fe(bpy)3]2+ in methanol are shown in Fig. 1C. For 2DES experiments performed in the BOXCARS geometry, positive intensity corresponds to ground state bleach/stimulated emission and negative intensity corresponds to excited state absorption.The 2D spectra contain three primary features. First, the spectra are dominated by a positive peak on the diagonal at ωτ = 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1, ωt = 18
500 cm−1, ωt = 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (Fig. 1C, red arrow). Second, a positive peak grows in below the dominant peak at approximately ωτ = 18
000 cm−1 (Fig. 1C, red arrow). Second, a positive peak grows in below the dominant peak at approximately ωτ = 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 cm−1 and ωt = 16
250 cm−1 and ωt = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 at T = 200 fs (Fig. 1C, right, blue arrow, Fig. S13†). Third, a negative peak is also present, particularly at later waiting times, at approximately ωτ = 16
500 cm−1 at T = 200 fs (Fig. 1C, right, blue arrow, Fig. S13†). Third, a negative peak is also present, particularly at later waiting times, at approximately ωτ = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 and ωt = 17
500 cm−1 and ωt = 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (Fig. 1C, right, purple arrow).
000 cm−1 (Fig. 1C, right, purple arrow).
Previous studies of [Fe(bpy)3]2+ using more traditional spectroscopic methods allow us to orient our understanding of these three features. First, the initially-formed (<200 fs) excited state is a 1MLCT state that can be described in terms of oxidation of the metal center (i.e., Fe(II) to Fe(III)) and the creation of a radical anion associated with the bipyridyl ligand (bpy˙−). This formulation allows for the use of spectroelectrochemistry to approximate the optical signatures that will characterize this initial state (Fig. S4†).18 These data indicate that the 1MLCT excited state will consist of two overlapping contributions: first, a loss of absorption (and stimulated emission at early times <100 fs) due to ground-state depletion and the concomitant change in oxidation state of the metal,52 which contributes positively to the 2D signal; and second, a new absorption feature associated with the bpy radical anion (bpy˙−), which contributes negatively to the 2D signal. The former appears at the steady-state absorption of the MLCT states (Fig. 1A) whereas the latter manifests as a broad feature starting at 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and extending into the UV regime. Owing to the large oscillator strength associated with the charge-transfer band, the overall spectrum will be dominated by the former. Consistent with this picture, the dominant positive feature on the diagonal is approximately at the 1MLCT absorption in the steady-state spectrum, although the maximum is slightly red-shifted due to the spectral profile of the ultrafast laser pulse (Fig. S1B†). Therefore, the dominant positive diagonal feature is denoted as the 1MLCT ground-state bleach/stimulated emission (1MLCT GSB/SE) peak. Any ESA contribution from the bpy radical anion at T < 200 fs at lower energies (ωτ < 17
000 cm−1 and extending into the UV regime. Owing to the large oscillator strength associated with the charge-transfer band, the overall spectrum will be dominated by the former. Consistent with this picture, the dominant positive feature on the diagonal is approximately at the 1MLCT absorption in the steady-state spectrum, although the maximum is slightly red-shifted due to the spectral profile of the ultrafast laser pulse (Fig. S1B†). Therefore, the dominant positive diagonal feature is denoted as the 1MLCT ground-state bleach/stimulated emission (1MLCT GSB/SE) peak. Any ESA contribution from the bpy radical anion at T < 200 fs at lower energies (ωτ < 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) is obscured due to contribution from the nonresonant response signal (Fig. 1C, left). Second, the positive cross peak below the diagonal corresponds energetically to excitation into the 1MLCT state and detection of population in the 3MLCT state at early waiting times (T < 200 fs). It is important to note that the contribution of stimulated emission to these features is tied to the persistence of the 1MLCT state. Further details about this assignment will be discussed in Section 2.3.4.
000 cm−1) is obscured due to contribution from the nonresonant response signal (Fig. 1C, left). Second, the positive cross peak below the diagonal corresponds energetically to excitation into the 1MLCT state and detection of population in the 3MLCT state at early waiting times (T < 200 fs). It is important to note that the contribution of stimulated emission to these features is tied to the persistence of the 1MLCT state. Further details about this assignment will be discussed in Section 2.3.4.
After initial photoexcitation into the MLCT manifold, the molecule relaxes into the ligand-field excited state manifold within 200 fs.20,21 This relaxation corresponds to the electron in the ligand-based π* orbital transferring back to the metal. Formation of these ligand-field excited state(s) has two consequences for the absorptive properties of the complex: loss of absorption associated with the bpy radical anion; and the eventual creation of an MLCT excited-state absorption feature associated with the lowest-energy ligand-field excited state of the molecule. These new net absorptive contributions to the spectrum can be expected to arise from MLCT transitions associated with the excited ligand-field states, in particular a 5T2 → 5MLCT transition that will persist until ground-state recovery (∼1 ns). The intensity of this band is expected to be roughly an order of magnitude less than that associated with the ground state.53 Its contribution to the overall signal depends on the nature of its overlap with the ground-state bleach. Thus, the ESA feature observed is assigned to the 5T2 → 5MLCT transition, supported by TD-DFT calculations (discussed in more detail in Section 2.3.3) and a nanosecond decay consistent with ground-state recovery (Fig. S5D and Table S3†). Although previous studies of similar complexes have shown an ESA signature in this region as a result of multi-photon excitation,54 the intensity of the laser pulse used in this study, is ten-fold below the advent of these multi-photon features. By T = 200 fs, the 1MLCT peak, which by this time is comprised solely of the ground-state bleach, also shifts slightly below the diagonal. Given the broad peak structure of the 5T2 ESA peak, the redshift in detection frequency of the 1MLCT GSB/SE peak is therefore most likely from partial cancellation from the rise of the 5T2 ESA.
2.3. Kinetic analysis of 2DES spectra
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500–20
500–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and ωt = 18
000 cm−1 and ωt = 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–20
000–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (i.e., the region indicated by the red arrow in Fig. 2A, B, S6, and S18†) and normalized to the time point with maximum intensity. The asymmetric ranges were selected to minimize the contribution from the nonresonant response at early waiting times, and thus should best capture the dynamics associated with [Fe(bpy)3]2+ (Fig. S2†). The waiting time trace was fit to a biexponential function (Fig. 2B, solid line) where the where the first term (which has negative amplitude) tracks the rapid rise (with its time constant called the “rise time”) and second term tracks the slow ground-state recovery (Eqn S1, Table S1†). A biexponential function was used because additional terms did not lead to a significant improvement in fit quality, consistent with previous experiments that reported a monoexponential decay28 and a monoexponential rise.32 The initial rise in peak intensity occurred on a ∼30 fs timescale. The lower intensity at early times is consistent with spectrally overlapped 1MLCT GSB/SE and bpy˙− ESA signatures generated upon photoexcitation into the MLCT manifold.18 Excited-state evolution from the MLCT manifold to the lower-lying ligand-field manifold results in the disappearance of the bpy˙− (and therefore loss of the bpy˙− ESA signature), leaving only the contribution from the underlying ground-state bleach signal. The increase in magnitude of the ground-state bleach can only be rationalized through the removal of a partial cancellation from an overlapping negative signal. For this reason, the intensity rise in the bleach signal can be assigned to conversion from the charge-transfer to ligand-field manifold of the compound due to loss of the partial cancellation from the ESA as opposed to relaxation within the charge-transfer band where no such change in partial cancellation would occur.
000 cm−1 (i.e., the region indicated by the red arrow in Fig. 2A, B, S6, and S18†) and normalized to the time point with maximum intensity. The asymmetric ranges were selected to minimize the contribution from the nonresonant response at early waiting times, and thus should best capture the dynamics associated with [Fe(bpy)3]2+ (Fig. S2†). The waiting time trace was fit to a biexponential function (Fig. 2B, solid line) where the where the first term (which has negative amplitude) tracks the rapid rise (with its time constant called the “rise time”) and second term tracks the slow ground-state recovery (Eqn S1, Table S1†). A biexponential function was used because additional terms did not lead to a significant improvement in fit quality, consistent with previous experiments that reported a monoexponential decay28 and a monoexponential rise.32 The initial rise in peak intensity occurred on a ∼30 fs timescale. The lower intensity at early times is consistent with spectrally overlapped 1MLCT GSB/SE and bpy˙− ESA signatures generated upon photoexcitation into the MLCT manifold.18 Excited-state evolution from the MLCT manifold to the lower-lying ligand-field manifold results in the disappearance of the bpy˙− (and therefore loss of the bpy˙− ESA signature), leaving only the contribution from the underlying ground-state bleach signal. The increase in magnitude of the ground-state bleach can only be rationalized through the removal of a partial cancellation from an overlapping negative signal. For this reason, the intensity rise in the bleach signal can be assigned to conversion from the charge-transfer to ligand-field manifold of the compound due to loss of the partial cancellation from the ESA as opposed to relaxation within the charge-transfer band where no such change in partial cancellation would occur.
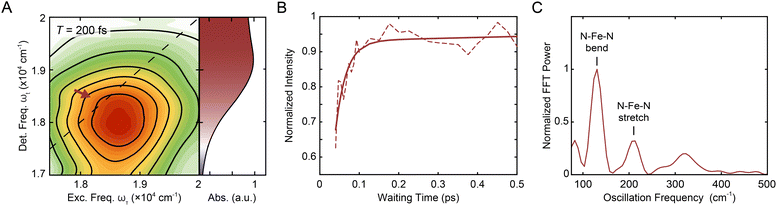 | ||
| Fig. 2 (A) Reproduction of the positive, on-diagonal region of the T = 200 fs 2DES spectrum in Fig. 1C with the corresponding linear absorption spectrum on the right. The red arrow indicates the GSB signal of the 1MLCT (and, at early times, the SE signal). (B) Intensity trace (dashed line) of the 1MLCT diagonal peak over waiting time T with its respective biexponential fit (solid lines) in methanol. See text for details. (C) Fourier transform of the residuals from the exponential fit depicted in (B) see also Fig. S12.† The peaks denoted correspond to the N–Fe–N bending (lower frequency) and N–Fe–N stretching (higher frequency) from a hot ground state during the waiting time.48–51 | ||
The waiting time traces also exhibit rapid oscillations.
Fourier analysis of the residuals from the biexponential fitrevealed two primary frequencies at 129.4 ± 0.4 cm−1 and 209 ± 1 cm−1 (Fig. 2C) corresponding to a N–Fe–N bending mode (∼114–157 cm−1) and a Fe–N stretching mode (∼185–280 cm−1) (see also Fig. S12 and Table S4†).49–51 Fourier filtering and subsequent biexponential fitting revealed similar rise timescales as reflected in the biexponential fit of the unfiltered data (Fig. S11†); in order to minimize assumptions made in the kinetic analysis, the unfiltered data were used. In addition, global kinetic analysis was performed on the region of the MLCT peaks using the method illustrated in Volpato et al.55 The ESA peak was not included in the analysis as the region is dominated by the nonresonant response signal at early timescales. Consistent with the results from the analysis described above, growth of both the 1MLCT GSB/SE peak and the 1MLCT → 3MLCT cross peak was observed with a sub-100 fs timescale (Section 2.3.4).
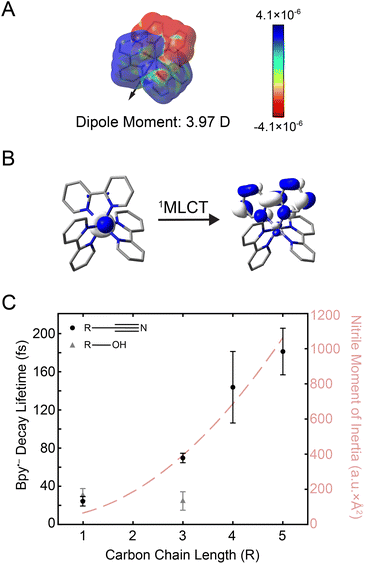 | ||
Fig. 3 (A) Electron density difference surface between the ground and the initially-excited 1MLCT state densities (isovalue = 0.0004 electrons per a.u.3). The 1MLCT state depicted here corresponds to one of the double degenerate transitions at 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 832 cm−1 shown in Fig. 1B (see Fig. S24† for both states). Red values indicate an increase in the excited-state electron density relative to the ground state (particle), while blue values indicate a decrease (hole). The excited-state dipole moment (3.97 Debye) is depicted by an arrow pointing in the positive direction. (B) Molecular orbitals associated with excitation of the 1MLCT state (see Fig. S25† for depictions of both the singlet and triplet MLCT transitions). (C) Plot of the bpy˙− decay lifetime in nitriles (black circles) and alcohols (gray triangles) as a function of carbon chain length (R). Error bars reflect standard error from three replicates. The moment of inertia (I) of the nitrile solvents is also plotted (light red dashed line). 832 cm−1 shown in Fig. 1B (see Fig. S24† for both states). Red values indicate an increase in the excited-state electron density relative to the ground state (particle), while blue values indicate a decrease (hole). The excited-state dipole moment (3.97 Debye) is depicted by an arrow pointing in the positive direction. (B) Molecular orbitals associated with excitation of the 1MLCT state (see Fig. S25† for depictions of both the singlet and triplet MLCT transitions). (C) Plot of the bpy˙− decay lifetime in nitriles (black circles) and alcohols (gray triangles) as a function of carbon chain length (R). Error bars reflect standard error from three replicates. The moment of inertia (I) of the nitrile solvents is also plotted (light red dashed line). | ||
The electron placed in the π* orbital of the bpy ligand dramatically alters the nature of the charge density with which the solvent interacts. In the ground state, the solvent organizes around an overall dicationic state wherein the charge is buried on the metal ion whereas, in the excited 1MLCT state, the charge is localized on the periphery of the complex. Alcohols can respond by simply rotating about the C–O single bond, whereas the rigid-rod nature of nitriles requires at least a partial rotation of the entire solvent molecule. The timing of this molecular rotation is therefore dependent on the moment of inertia of the molecule,22 which can be as fast as 25 fs.58,59 2D spectra were measured in these two classes of solvents, alcohols and nitriles, to examine the effect of these different mechanisms of reorganization in response to the creation of the MLCT excited state.
The kinetics from 2D spectra of [Fe(bpy)3]2+ in methanol, 1-propanol, acetonitrile, butyronitrile, are compared in Fig. 3C, with values from the biexponential fit reported in Table 1. The rise times, shown as gray triangles in Fig. 3C, were ∼30 fs for both methanol (carbon chain length R = 1) and 1-propanol (R = 3). The similarity observed can be attributed to the fact that an extension of the aliphatic chain from methanol to 1-propanol should have little effect on the dynamics of rotation about the C–O bond.28 On the other hand, the time constant for the same signal in the nitrile solvents was observed to increase from ∼30 fs acetonitrile (R = 1) to ∼70 fs for butyronitrile (R = 3). This solvent-dependent evolution observed in the nitrile solvents likely originates from the nature of the anticipated solvent response, a rotation of the entire molecule.
| Solvent | bpy˙− decay lifetime (fs) |
|---|---|
| Methanol | 32 ± 6 |
| 1-Propanol | 24 ± 10 |
| Acetonitrile | 25 ± 5 |
| Butyronitrile | 70 ± 5 |
| Pentanenitrile | 140 ± 40 |
| Hexanenitrile | 180 ± 20 |
To further investigate the nature of this solvent response, 2DES studies were performed in commercially-available nitriles with longer carbon chains, namely pentanenitrile (R = 5) and hexanenitrile (R = 6). The dynamics in propionitrile were not measured because [Fe(bpy)3]2+ was observed to interact with impurities in the solvent and degrade too fast for 2DES experiments (ESI Section 6.1†). The bpy˙− ESA decay lifetime in all nitrile solvents is as a function of carbon chain length (R) is plotted as black circles in Fig. 3C (black circles).
The reported lifetimes of the bpy˙− decay increased to ∼140 fs and ∼180 fs for pentanenitrile and hexanenitrile, respectively. The overall trend follows closely with the trends of the moment of inertia (I) of the solvent, plotted as a light-red dashed curve in Fig. 3C (see also ESI Section 4†). This clear scaling reflects the ability of the surrounding solvent to stabilize the change in charge density upon photoexcitation.
These data represent the first observation of solvent dynamics coupled to MLCT-state evolution in an Fe(II) polypyridyl complex and moreover suggest that the conversion from the charge-transfer to ligand-field manifolds may indeed be gated by solvent response.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–17
000–17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and ωt = 16
000 cm−1 and ωt = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800–17
800–17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 cm−1 and the intensity of the positive peak was integrated over ωτ = 17
800 cm−1 and the intensity of the positive peak was integrated over ωτ = 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500–19
500–19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 and ωt = 17
500 cm−1 and ωt = 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–19
000–19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. These limits were selected to span the contour lines that denote this feature (Fig. 1C) as no other overlapping contributions are present in this spectral region. The magnitude of the negative peak was ∼10% of the positive peak (Fig. 4D and S16†), consistent with the order-of-magnitude reduction in intensity expected for a 5T2 → 5MLCT absorption relative to the corresponding transition in the low-spin ground state. To further investigate the relevant states, TD-DFT calculations were performed on the 5T2 states (Fig. S23†). Analysis of the transitions showed 5T2 → 5MLCT transition with a similar energy gap (Fig. 4C), supporting the assignment. Along the waiting times sampled, the system undergoes nuclear equilibration within the 5T2 state primarily assigned to be an expansion of the Fe–N bond distance.28 Therefore, the differences in intensity of the ESA peak between the solvents studied (Fig. 4D) are likely reflective of differences in the nature of the nuclear equilibration due to each type of solvent interactions.
000 cm−1. These limits were selected to span the contour lines that denote this feature (Fig. 1C) as no other overlapping contributions are present in this spectral region. The magnitude of the negative peak was ∼10% of the positive peak (Fig. 4D and S16†), consistent with the order-of-magnitude reduction in intensity expected for a 5T2 → 5MLCT absorption relative to the corresponding transition in the low-spin ground state. To further investigate the relevant states, TD-DFT calculations were performed on the 5T2 states (Fig. S23†). Analysis of the transitions showed 5T2 → 5MLCT transition with a similar energy gap (Fig. 4C), supporting the assignment. Along the waiting times sampled, the system undergoes nuclear equilibration within the 5T2 state primarily assigned to be an expansion of the Fe–N bond distance.28 Therefore, the differences in intensity of the ESA peak between the solvents studied (Fig. 4D) are likely reflective of differences in the nature of the nuclear equilibration due to each type of solvent interactions.
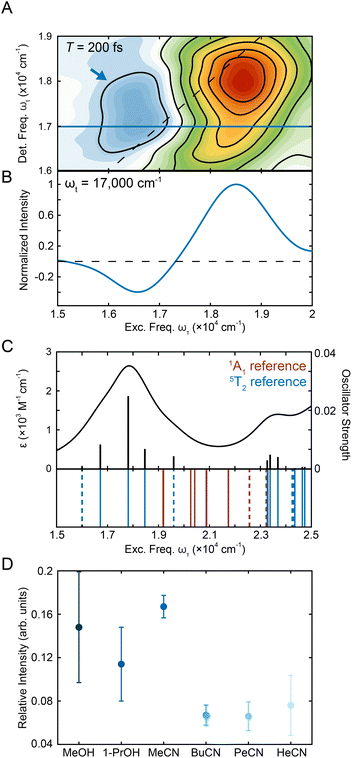 | ||
Fig. 4 (A) Region of representative [Fe(bpy)3]2+ 2DES spectrum in methanol centering the ESA peak (blue arrow) at T = 200 fs. (B) Horizontal slice in detection frequency at ωt = 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (shown as a blue line in Fig. 4A) that shows the presence of the negative ESA peak. (C) Absorption spectrum obtained from TD-DFT calculations in acetonitrile utilizing the fully-optimized lowest-energy quintet state (5T2) of [Fe(bpy)3]2+ as a reference. Calculated stick spectrum (black sticks) along the broadened line spectrum (half-width at half-maximum, HWHM = 968 cm−1 (0.12 eV), black line) is shown at the top. Energy spectrum of all calculated transitions (even those with zero oscillator strength) is displayed on the bottom. Blue lines represent transitions from the 5T2 state, while the red lines represent singlet transitions from the 1A1 state. MLCT transitions are represented by the solid lines while ligand-field transitions are represented by the dashed lines. See Tables S11 and S9† for full information about the transitions for the 5T2 and 1A1 states, respectively. (D) Relative intensity of the negative peak compared to the positive peak in methanol, 1-propanol, acetonitrile, butyronitrile, pentanenitrile, and hexanenitrile. The error bars are standard errors from three replicates. 000 cm−1 (shown as a blue line in Fig. 4A) that shows the presence of the negative ESA peak. (C) Absorption spectrum obtained from TD-DFT calculations in acetonitrile utilizing the fully-optimized lowest-energy quintet state (5T2) of [Fe(bpy)3]2+ as a reference. Calculated stick spectrum (black sticks) along the broadened line spectrum (half-width at half-maximum, HWHM = 968 cm−1 (0.12 eV), black line) is shown at the top. Energy spectrum of all calculated transitions (even those with zero oscillator strength) is displayed on the bottom. Blue lines represent transitions from the 5T2 state, while the red lines represent singlet transitions from the 1A1 state. MLCT transitions are represented by the solid lines while ligand-field transitions are represented by the dashed lines. See Tables S11 and S9† for full information about the transitions for the 5T2 and 1A1 states, respectively. (D) Relative intensity of the negative peak compared to the positive peak in methanol, 1-propanol, acetonitrile, butyronitrile, pentanenitrile, and hexanenitrile. The error bars are standard errors from three replicates. | ||
The relative intensities in the solvents were within error of each other for the alcohols whereas the relative intensity in acetonitrile was over double that in the longer nitriles. This observation is consistent with previous studies where solvent-dependent, outer-sphere effects influenced the dynamics of the ligand-field 5T2 state.28 Specifically, the solvent reorganization energy is coupled to the change in the volume of the complex as the system moves between high-spin and low-spin configurations, which in turn affects the oscillator strength of the transition. The effect of solvent on the relative oscillator strength of the ligand-field excited state can be difficult to quantify using traditional transient absorption spectroscopy experiments as the magnitude of the effect often falls below the noise threshold. In this experiment, the 2D apparatus utilizes a fully non-collinear, BOXCARS configuration for background-free detection, which vastly improves the signal-to-noise ratio40,60–62 by almost two orders of magnitude.63 The improved sensitivity was required to resolve the small changes in oscillator strength due to solvent effects. This result both establishes solvent-coupled behavior of [Fe(bpy)3]2+ in the lower-lying ligand-field states and highlights the power of 2DES as a tool for understanding excited-state dynamics in transition metal complexes.
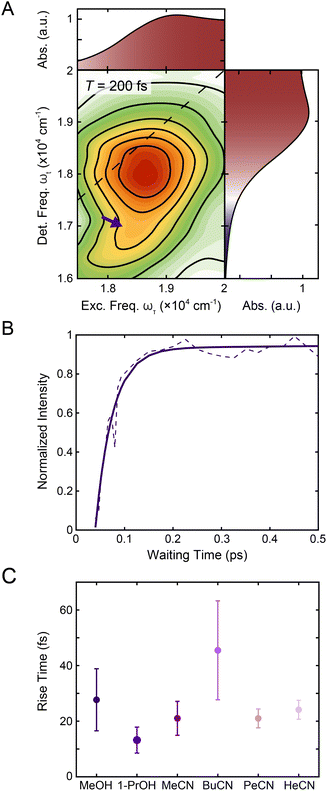 | ||
| Fig. 5 (A) Reproduction of the positive region of the T = 200 fs 2DES spectrum in Fig. 1C. The purple arrow indicates the contribution from 1MLCT → 3MLCT intersystem crossing. The corresponding linear absorption spectrum is reproduced on the top and right of the 2DES spectrum for clarity. (B) Intensity trace of the 1MLCT → 3MLCT cross peak (dashed lines) over waiting time T along with a biexponential fit (solid lines) in methanol. See text for details. (C) Rise times of the 1MLCT → 3MLCT cross peak (purple) in methanol, 1-propanol, acetonitrile, butyronitrile, pentanenitrile, and hexanenitrile extracted from the fits of the intensity traces (Fig. S9 and S20†). Error bars are the standard error from three replicates. | ||
To characterize the evolution of the 1MLCT/3MLCT cross peak, waiting time traces were constructed by integrating the peak intensity within ωτ = 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500–20
500–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and ωt = 15
000 cm−1 and ωt = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600–16
600–16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1 (Fig. 5A, purple arrow, Fig. 5B). The waiting time traces exhibited an intensity increase, which was fit to an exponential rise function (Fig. 5B, solid line, Eqn S1 and Table S2†). A rise was also observed for the diagonal peak, as discussed above, but the associated intensities were different. While the diagonal peak had ∼75% of the final intensity upon photoexcitation, the cross peak initially had a near-zero intensity, which increased to ∼40% of the diagonal peak intensity at later times (T > 200 fs, Fig. S16†). The timescales extracted from the fits captured the initial rise and were on the 20–40 fs timescale for all solvents. These values are both faster than the timescales extracted from the diagonal peak (Table 1) and lack the solvent dependence observed for that feature.
600 cm−1 (Fig. 5A, purple arrow, Fig. 5B). The waiting time traces exhibited an intensity increase, which was fit to an exponential rise function (Fig. 5B, solid line, Eqn S1 and Table S2†). A rise was also observed for the diagonal peak, as discussed above, but the associated intensities were different. While the diagonal peak had ∼75% of the final intensity upon photoexcitation, the cross peak initially had a near-zero intensity, which increased to ∼40% of the diagonal peak intensity at later times (T > 200 fs, Fig. S16†). The timescales extracted from the fits captured the initial rise and were on the 20–40 fs timescale for all solvents. These values are both faster than the timescales extracted from the diagonal peak (Table 1) and lack the solvent dependence observed for that feature.
The cross peak rise time is expected to contain some contribution from intersystem crossing as well as a rise of the overlapping 3MLCT GSB signal. The 3MLCT GSB signal, which is on the diagonal, rises with the loss of the bpy˙− absorption, similar to that of the 1MLCT GSB signal. The fast (<50 fs) relaxation from the 3MLCT to the ligand field states likely limits the population accumulated in the 3MLCT states,33 which may be the reason this feature does not become dominant in the 2D spectra. The extremely fast timescales and overlapping spectral signatures, however, mean that the intersystem crossing and relaxation to the ligand-field states cannot be fully isolated. As a result, the global kinetic analysis of the region extracted a timescale that is a mixture of the appearance of both the 1MLCT GSB/SE peak and the cross peak (Fig. S22†). The timescale of the cross peak rise alone gives a better approximation of the intersystem crossing rate. The rise timescales extracted through the biexponential fit were predominantly ∼20 fs (Fig. 5C), particularly in the solvents with slower relaxation to the ligand field manifold, where the intersystem crossing is expected to be better isolated. These values are consistent with expectations for an intersystem crossing event in this complex.65 Previous work proposed a sub-30 fs (ref. 32) intersystem crossing timescale based on fluorescence up-conversion measurements with an instrument response of ∼120 fs.47 The ∼10 fs temporal response of our 2D apparatus enabled quantification of this extremely fast process, revealing that intersystem crossing occurs on a timescale similar to that reported for the same process in [Ru(bpy)3]2+. This suggests that spin–orbit coupling is a necessary but not sufficient condition for describing intersystem crossing dynamics in transition metal complexes. Moreover, our data clearly reveal that intersystem crossing within the charge-transfer manifold occurs in competition with direct conversion from the initially formed 1MLCT state to ligand-field excited states localized on the metal center as illustrated in Fig. 6.
3. Concluding remarks
There is great interest in developing earth abundant photocatalysts using first-row transition metals.66–69 Their smaller ligand field splitting, however, leads to distinct photodynamics that cannot be interpreted within the framework of their second- and third-row transition metal counterparts.70 [Fe(bpy)3]2+ is the prototypical example of a d6 photocatalyst with an earth abundant metal center. Similar to others in its class, it has rapid and complex dynamics within the MLCT manifold. Disentangling this complexity to understand why they differ from their second- and third-row counterparts is a key step in the development of these complexes for photochemical applications. For [Fe(bpy)3]2+, uncovering the relaxation mechanisms at the early timescales can shed light into how the complex can undergo a formally two-electron relaxation process into the high-spin 5T2 state within 200 fs, which is not typically observed in other complexes.In this study, we observed a 1MLCT → 3MLCT intersystem crossing process nearly contemporaneous with direct relaxation from the 1MLCT state into lower-lying ligand-field states indicate parallel relaxation mechanisms. These parallel mechanisms indicate that in [Fe(bpy)3]2+, electrons both undergo 1MLCT → LF and 1MLCT → 3MLCT → LF relaxation out of the MLCT manifold. Therefore, the previously competing models of energy relaxation may not be mutually exclusive, and in fact may be occurring simultaneously. Furthermore, the correlation between solvent response and relaxation from the MLCT manifold indicates that the solvent interacts with the relative charge associated with these states and may even control the pathway of relaxation. On the timescales of relaxation from the MLCT manifold, solvent dynamics are largely governed by the inertial response,58,59 which can be as fast as 25 fs and so allows the solvent to mediate these ultrafast processes.
The high spectral and temporal resolution of 2DES revealed dynamics previously obscured in data measured with more traditional techniques. In particular, the GSB/SE and intersystem crossing peaks in [Fe(bpy)3]2+ became spectrally separated by simply resolving the excitation dimension, allowing for greater insight into the crowded excited-state landscape of first-row transition-metal photocatalysts.
In conclusion, the early-time excited-state dynamics of [Fe(bpy)3]2+ were measured using 2DES in a series of nitrile and alcohol solvents. The ultrafast pulse used in this experiment allowed for the resolution of early-time dynamics, making it possible to observe the effect of solvent dependence on the relaxation of the bipyridyl radical anion. Simultaneously, resolution along the excitation frequency axis allows for direct observation of the intersystem crossing dynamics. The timescale of this event was determined to be on the scale of ∼20 fs. The direct resolution of previously unobserved features in [Fe(bpy)3]2+ shows the power of 2DES to provide new information on the excited-state dynamics in this class of photocatalysts.
4. Methods
4.1. Sample preparation
To ensure sufficient sample solubility in all four solvents, [Fe(bpy)3]2+ was synthesized using reported literature methods28,71,72 with different counteranions: tetrafluoroborate (BF4−, for dissolving in acetonitrile, butyronitrile, pentanenitrile, and hexanenitrile) and bromide (Br−, for dissolving in methanol and 1-propanol).For the 2DES experiments, the sample solutions were prepared by dissolving [Fe(bpy)3]2+ powder in spectroscopic grade solvents purchased from Millipore Sigma.
4.2. Two-dimensional electronic spectroscopy
The 2D measurements were performed in a fully non-collinear, BOXCARS phase-matching geometry. Full details on the setup used can be found in Son et al.62 The laser spectrum (Fig. S1A†) has a spectral bandwidth (FWHM) of 106 nm (3300 cm−1) centered at 540 nm (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 510 cm−1). The pulse was compressed with two pairs of chirped mirrors (Ultrafast Innovations) and characterized by transient grating frequency-resolved optical gating (TG-FROG) at the sample position using a 0.1 mm thick quartz cuvette (Starna) filled with acetone.73 The FROG trace revealed a pulse duration of 12 fs (Fig. S1B†). The samples were measured in a 0.1 mm path length quartz cuvette. The optical density of the sample in each solvent was measured to be 0.21 (acetonitrile), 0.27 (butyronitrile), 0.28 (pentanenitrile), 0.25 (hexanenitrile), 0.27 (methanol) and 0.21 (1-propanol) per 0.1 mm at 535 nm. An excitation pulse energy of 68 nJ was utilized, which corresponds to 1.9 × 1014 photons per cm2 per pulse. Coherence time (τ), the time delay between the first two pulses, was sampled from −80 to 80 fs in 0.4 fs steps. Waiting time (T), the time delay between the second and third pulses, was sampled every 6.67 fs for T = 0–100 fs, every 25 fs for T = 100–2500 fs, every 500 fs for T = 2500–10
510 cm−1). The pulse was compressed with two pairs of chirped mirrors (Ultrafast Innovations) and characterized by transient grating frequency-resolved optical gating (TG-FROG) at the sample position using a 0.1 mm thick quartz cuvette (Starna) filled with acetone.73 The FROG trace revealed a pulse duration of 12 fs (Fig. S1B†). The samples were measured in a 0.1 mm path length quartz cuvette. The optical density of the sample in each solvent was measured to be 0.21 (acetonitrile), 0.27 (butyronitrile), 0.28 (pentanenitrile), 0.25 (hexanenitrile), 0.27 (methanol) and 0.21 (1-propanol) per 0.1 mm at 535 nm. An excitation pulse energy of 68 nJ was utilized, which corresponds to 1.9 × 1014 photons per cm2 per pulse. Coherence time (τ), the time delay between the first two pulses, was sampled from −80 to 80 fs in 0.4 fs steps. Waiting time (T), the time delay between the second and third pulses, was sampled every 6.67 fs for T = 0–100 fs, every 25 fs for T = 100–2500 fs, every 500 fs for T = 2500–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fs, every 5000 fs for T = 10
000 fs, every 5000 fs for T = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–100
000–100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fs, and every 50
000 fs, and every 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fs for T = 100
000 fs for T = 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–700
000–700![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fs. The absolute-value 2D spectra were phased using the projection slice theorem.64 After collection of each dataset, the linear absorption spectrum of the sample was measured and compared with the one measured before the 2D experiment to confirm the absence of photodegradation. Each sample was then measured an additional three (for the nitrile series) to four (for the alcohol series) times from T = 0–3000 fs to ensure reproducibility of the data.
000 fs. The absolute-value 2D spectra were phased using the projection slice theorem.64 After collection of each dataset, the linear absorption spectrum of the sample was measured and compared with the one measured before the 2D experiment to confirm the absence of photodegradation. Each sample was then measured an additional three (for the nitrile series) to four (for the alcohol series) times from T = 0–3000 fs to ensure reproducibility of the data.
For pentanenitrile and hexanenitrile experiments, an ND filter (0.2–0.5 OD) was added to the beam path after the sample to avoid detector saturation.
4.3. DFT calculations
Theoretical calculations on [Fe(bpy)3]2+ complex were carried out with the Gaussian 16, Revision A.03 software package.74 Geometry optimizations for the singlet and quintet states were performed with the TPSSH functional.75 The 6-311G* basis set was employed for all atoms (C, H, N)76,77 except for Fe, where the SDD basis sets and its accompanying pseudopotential78 were used. Solvent effects (acetonitrile) were included in the calculations via the polarizable continuum model (PCM).79 Vibrational frequency analysis was performed to ensure that all optimized structures are true minima with no imaginary frequencies. Natural orbital (NO) analysis was carried out to confirm the metal-centered character of the optimized quintet state.80 The absorption spectra were calculated with linear-response time-dependent DFT (TD-DFT)81–83 at the same level of theory as described for optimization. The UV-vis spectra were computed at the optimized singlet ground state structure utilizing the singlet reference state (30 lowest-energy singlet and 30 triplet excited states were calculated), as well as at the optimized quintet geometry utilizing the quintet reference state (30 lowest-energy excited states). The stick spectra were broadened using the Lorentzian functions with a half-width-at-half-maximum (HWHM) of 0.12 eV for the singlet and quintet states.Data availability
All the data files used to generate the plots in this manuscript are available from the authors upon request.Author contributions
A. L. performed ultrafast spectroscopy experiments and subsequent replicate experiments, analyzed the results, and wrote the manuscript with input from all authors. M. S. performed ultrafast spectroscopy experiments and assisted in the analysis of the results. M. D. performed the TD-DFT calculations on the complex studied. M. D. W. synthesized the complexes and precipitated the complex studied in various salts for spectroscopy experiments. S. M. H. assisted in conducting replicate experiments. H. F. B. curated the spectroelectrochemical data of the complex studied. P. T. C. curated the solvation information for the salts prepared. E. J. supervised the TD-DFT calculations. J. K. M. and G. S. S. C. supervised the project.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported as part of BioLEC, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under award no. DE-SC0019370. A. L. and S. M. H. acknowledge support from the National Science Foundation Graduate Research Fellowship Program. The authors would also like to thank and acknowledge Jonathan T. Yarranton for his help in identifying the cause of sample degradation in propionitrile.References
- E. R. Welin, C. Le, D. M. Arias-Rotondo, J. K. McCusker and D. W. C. MacMillan, Science, 2017, 355, 380–385 CrossRef CAS PubMed.
- K. Singh, S. J. Staig and J. D. Weaver, J. Am. Chem. Soc., 2014, 136, 5275–5278 CrossRef CAS PubMed.
- Z. Lu and T. P. Yoon, Angew. Chem., Int. Ed., 2012, 51, 10329–10332 CrossRef CAS PubMed.
- C. Creutz, M. Chou, T. L. Netzel, M. Okumura and N. Sutin, J. Am. Chem. Soc., 1980, 102, 1309–1319 CrossRef CAS.
- A. de Palo, G. La Ganga, F. Nastasi, M. Guelfi, M. Bortoluzzi, G. Pampaloni, F. Puntoriero, S. Campagna and F. Marchetti, Eur. J. Inorg. Chem., 2021, 2021, 861–869 CrossRef CAS.
- J. Oh, W. Ghann, H. Kang, F. Nesbitt, S. Providence and J. Uddin, Inorg. Chim. Acta, 2018, 482, 943–950 CrossRef CAS.
- J. C. Freys, J. M. Gardner, L. D'Amario, A. M. Brown and L. Hammarström, Dalton Trans., 2012, 41, 13105–13111 RSC.
- A. Reynal, A. Forneli and E. Palomares, Energy Environ. Sci., 2010, 3, 805–812 RSC.
- K. Kalyanasundaram, Coord. Chem. Rev., 1982, 46, 159–244 CrossRef CAS.
- A. Juris, V. Balzani, P. Belser and A. von Zelewsky, Helv. Chim. Acta, 1981, 64, 2175–2182 CrossRef CAS.
- O. S. Wenger, Chem.–Eur. J., 2019, 25, 6043–6052 CrossRef CAS PubMed.
- M. C. Carey, S. L. Adelman and J. K. McCusker, Chem. Sci., 2019, 10, 134–144 RSC.
- M. D. Woodhouse and J. K. McCusker, J. Am. Chem. Soc., 2020, 142, 16229–16233 CrossRef CAS PubMed.
- M. Guttentag, A. Rodenberg, C. Bachmann, A. Senn, P. Hamm and R. Alberto, Dalton Trans., 2013, 42, 334–337 RSC.
- Z. Zuo, D. T. Ahneman, L. Chu, J. A. Terrett, A. G. Doyle and D. W. C. MacMillan, Science, 2014, 345, 437–440 CrossRef CAS PubMed.
- S. K. Kariofillis, B. J. Shields, M. A. Tekle-Smith, M. J. Zacuto and A. G. Doyle, J. Am. Chem. Soc., 2020, 142, 7683–7689 CrossRef CAS PubMed.
- B. M. Hockin, C. Li, N. Robertson and E. Zysman-Colman, Catal. Sci. Technol., 2019, 9, 889–915 RSC.
- A. M. Brown, C. E. McCusker and J. K. McCusker, Dalton Trans., 2014, 43, 17635–17646 RSC.
- J. E. Monat and J. K. McCusker, J. Am. Chem. Soc., 2000, 122, 4092–4097 CrossRef CAS.
- C. Bressler, C. Milne, V.-T. Pham, A. ElNahhas, R. M. van der Veen, W. Gawelda, S. Johnson, P. Beaud, D. Grolimund, M. Kaiser, C. N. Borca, G. Ingold, R. Abela and M. Chergui, Science, 2009, 323, 489–492 CrossRef CAS PubMed.
- C. Consani, M. Prèmont-Schwarz, A. El Nahhas, C. Bressler, F. van Mourik, A. Cannizzo and M. Chergui, Angew. Chem., Int. Ed., 2009, 48, 7184–7187 CrossRef CAS PubMed.
- A. T. Yeh, C. V. Shank and J. K. McCusker, Science, 2000, 289, 935–938 CrossRef CAS PubMed.
- A. Cannizzo, C. Milne, C. Consani, W. Gawelda, C. Bressler, F. van Mourik and M. Chergui, Coord. Chem. Rev., 2010, 254, 2677–2686 CrossRef CAS.
- W. Zhang and K. J. Gaffney, Acc. Chem. Res., 2015, 48, 1140–1148 CrossRef CAS PubMed.
- J. K. McCusker, Science, 2019, 363, 484–488 CrossRef CAS PubMed.
- P. Pyykko, Chem. Rev., 1988, 88, 563–594 CrossRef CAS.
- M. Kaupp, J. Comput. Chem., 2007, 28, 320–325 CrossRef CAS PubMed.
- J. N. Miller and J. K. McCusker, Chem. Sci., 2020, 11, 5191–5204 RSC.
- P. Chen and T. J. Meyer, Chem. Rev., 1998, 98, 1439–1478 CrossRef CAS PubMed.
- A. Rondi, Y. Rodriguez, T. Feurer and A. Cannizzo, Acc. Chem. Res., 2015, 48, 1432–1440 CrossRef CAS PubMed.
- C. Sousa, C. de Graaf, A. Rudavskyi, R. Broer, J. Tatchen, M. Etinski and C. M. Marian, Chem.–Eur. J., 2013, 19, 17541–17551 CrossRef CAS PubMed.
- G. Auböck and M. Chergui, Nat. Chem., 2015, 7, 629–633 CrossRef PubMed.
- W. Zhang, R. Alonso-Mori, U. Bergmann, C. Bressler, M. Chollet, A. Galler, W. Gawelda, R. G. Hadt, R. W. Hartsock, T. Kroll, K. S. Kjær, K. Kubiček, H. T. Lemke, H. W. Liang, D. A. Meyer, M. M. Nielsen, C. Purser, J. S. Robinson, E. I. Solomon, Z. Sun, D. Sokaras, T. B. van Driel, G. Vankó, T.-C. Weng, D. Zhu and K. J. Gaffney, Nature, 2014, 509, 345–348 CrossRef CAS PubMed.
- S. Biswas, J. Kim, X. Zhang and G. D. Scholes, Chem. Rev., 2022, 122, 4257–4321 CrossRef CAS PubMed.
- J. Lu, Y. Lee and J. M. Anna, J. Phys. Chem. B, 2020, 124, 8857–8867 CrossRef CAS PubMed.
- S. Mukamel, Annu. Rev. Phys. Chem., 2000, 51, 691–729 CrossRef CAS PubMed.
- M. Son, A. Pinnola, R. Bassi and G. S. Schlau-Cohen, Chem, 2019, 5, 575–584 CAS.
- V. R. Policht, A. Niedringhaus, R. Willow, P. D. Laible, D. F. Bocian, C. Kirmaier, D. Holten, T. Mančal and J. P. Ogilvie, Sci. Adv., 2022, 8, eabk0953 CrossRef CAS PubMed.
- M. Son, S. M. Hart and G. S. Schlau-Cohen, Trends Chem., 2021, 3, 733–746 CrossRef CAS.
- E. Collini, J. Phys. Chem. C, 2021, 125, 13096–13108 CrossRef CAS PubMed.
- H. Seiler, S. Palato, C. Sonnichsen, H. Baker, E. Socie, D. P. Strandell and P. Kambhampati, Nat. Commun., 2019, 10, 4962 CrossRef PubMed.
- A. Liu, G. Nagamine, L. G. Bonato, D. B. Almeida, L. F. Zagonel, A. F. Nogueira, L. A. Padilha and S. T. Cundiff, ACS Nano, 2021, 15, 6499–6506 CrossRef CAS PubMed.
- A. Liu, D. B. Almeida, L. A. Padilha and S. T. Cundiff, J. Phys. Mater., 2022, 5, 021002 CrossRef.
- S. M. Hart, W. J. Chen, J. L. Banal, W. P. Bricker, A. Dodin, L. Markova, Y. Vyborna, A. P. Willard, R. Häner, M. Bathe and G. S. Schlau-Cohen, Chem, 2021, 7, 752–773 CAS.
- J. Brazard, L. A. Bizimana, T. Gellen, W. P. Carbery and D. B. Turner, J. Phys. Chem. Lett., 2016, 7, 14–19 CrossRef CAS PubMed.
- J. D. Gaynor, A. Petrone, X. Li and M. Khalil, J. Phys. Chem. Lett., 2018, 9, 6289–6295 CrossRef CAS PubMed.
- W. Gawelda, A. Cannizzo, V.-T. Pham, F. van Mourik, C. Bressler and M. Chergui, J. Am. Chem. Soc., 2007, 129, 8199–8206 CrossRef CAS PubMed.
- S. Dhamija, G. Bhutani, A. Jayachandran and A. K. De, J. Phys. Chem. A, 2022, 126, 1019–1032 CrossRef CAS PubMed.
- B. D. Alexander, T. J. Dines and R. W. Longhurst, Chem. Phys., 2008, 352, 19–27 CrossRef CAS.
- L. M. Lawson Daku, Phys. Chem. Chem. Phys., 2018, 20, 6236–6253 RSC.
- H. T. Lemke, K. S. Kjær, R. Hartsock, T. B. van Driel, M. Chollet, J. M. Glownia, S. Song, D. Zhu, E. Pace, S. F. Matar, M. M. Nielsen, M. Benfatto, K. J. Gaffney, E. Collet and M. Cammarata, Nat. Commun., 2017, 8, 15342 CrossRef CAS PubMed.
- O. Bräm, F. Messina, A. M. El-Zohry, A. Cannizzo and M. Chergui, Chem. Phys., 2012, 393, 51–57 CrossRef.
- A. L. Smeigh, M. Creelman, R. A. Mathies and J. K. McCusker, J. Am. Chem. Soc., 2008, 130, 14105–14107 CrossRef CAS PubMed.
- A. N. Tarnovsky, W. Gawelda, M. Johnson, C. Bressler and M. Chergui, J. Phys. Chem. B, 2006, 110, 26497–26505 CrossRef CAS PubMed.
- A. Volpato, L. Bolzonello, E. Meneghin and E. Collini, Opt. Express, 2016, 24, 24773–24785 CrossRef PubMed.
- A. B. Maurer and G. J. Meyer, J. Am. Chem. Soc., 2020, 142, 6847–6851 CrossRef CAS PubMed.
- D. A. Hoff, R. Silva and L. G. C. Rego, J. Phys. Chem. C, 2011, 115, 15617–15626 CrossRef CAS.
- S. J. Rosenthal, X. Xie, M. Du and G. R. Fleming, J. Chem. Phys., 1991, 95, 4715–4718 CrossRef CAS.
- M. Maroncelli, P. V. Kumar, A. Papazyan, M. L. Horng, S. J. Rosenthal and G. R. Fleming, AIP Conf. Proc., 1994, 298, 310–333 CrossRef CAS.
- J. O. Tollerud and J. A. Davis, Prog. Quantum Electron., 2017, 55, 1–34 CrossRef.
- J. D. Hybl, A. Albrecht Ferro and D. M. Jonas, J. Chem. Phys., 2001, 115, 6606–6622 CrossRef CAS.
- M. Son, S. Mosquera-Vázquez and G. S. Schlau-Cohen, Opt. Express, 2017, 25, 18950–18962 CrossRef CAS PubMed.
- F. Milota, C. N. Lincoln and J. Hauer, Opt. Express, 2013, 21, 15904–15911 CrossRef PubMed.
- D. M. Jonas, Annu. Rev. Phys. Chem., 2003, 54, 425–463 CrossRef CAS PubMed.
- L. S. Forster, Coord. Chem. Rev., 2006, 250, 2023–2033 CrossRef CAS.
- O. S. Wenger, J. Am. Chem. Soc., 2018, 140, 13522–13533 CrossRef CAS PubMed.
- A. Hossain, A. Bhattacharyya and O. Reiser, Science, 2019, 364, eaav9713 CrossRef PubMed.
- M. Kojima and S. Matsunaga, Trends Chem., 2020, 2, 410–426 CrossRef CAS.
- J. Liu, L.-Q. Lu, Y. Luo, W. Zhao, P.-C. Sun, W. Jin, X. Qi, Y. Cheng and W.-J. Xiao, ACS Catal., 2022, 12, 1879–1885 CrossRef CAS.
- M. Iwamura, S. Takeuchi and T. Tahara, Acc. Chem. Res., 2015, 48, 782–791 CrossRef CAS PubMed.
- J. K. McCusker, A. L. Rheingold and D. N. Hendrickson, Inorg. Chem., 1996, 35, 2100–2112 CrossRef CAS.
- Y. Yamamoto, E. Sumimura, K. Miyoshi and T. Tominaga, Anal. Chim. Acta, 1973, 64, 225–233 CrossRef CAS.
- R. Trebino, K. W. DeLong, D. N. Fittinghoff, J. N. Sweetser, M. A. Krumbügel, B. A. Richman and D. J. Kane, Rev. Sci. Instrum., 1997, 68, 3277–3295 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian Inc, Wallingford CT, 2016 Search PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872 CrossRef CAS.
- G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110 CrossRef PubMed.
- P.-O. Löwdin, Phys. Rev., 1955, 97, 1474–1489 CrossRef.
- R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464 CrossRef CAS.
- M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, J. Chem. Phys., 1998, 108, 4439–4449 CrossRef CAS.
- R. E. Stratmann, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 1998, 109, 8218–8224 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Data for Fig. 1–5, and further detailed analysis and calculations. Extended studies on nitriles. See DOI: https://doi.org/10.1039/d3sc02613b |
| ‡ Current address: Department of Chemistry, Boston University, 590 Commonwealth Ave, Boston, MA 02215, USA. |
| § Current address: Department of Chemistry, University of California, Berkeley, California 94720, USA. |
| This journal is © The Royal Society of Chemistry 2023 |