Early warning technology for common characteristic resistances of lithium-ion batteries with thermal runaway

Abstract

A technology for early warning (of over 25 minutes) of thermal runaway in lithium-ion batteries based on common characteristic resistances supported by thermodynamic calculations was derived. With great potential in practical application for avoiding property losses and human casualties, this technology was proven to be efficient and accurate.

---

Accidents associated with lithium-ion batteries (LIBs) mainly result from thermal runaway (TR). Commonly, TR is caused by mechanical abuse, electrical abuse or thermal abuse, and can be divided into three stages including the “evolution process”, “trigger point” and “spreading process”. In accordance with the three stages, three common characteristic temperatures have been discussed by researchers worldwide,^1–3 including the initial temperature of the self-exothermic process (T₁), the onset temperature of TR (T₂), and the highest temperature throughout the TR procedure (T₃). With the three common characteristic temperatures, the features of TR can be revealed quantitatively (in the form of time and temperature) and segmentally, providing references for approaches for preventing TR.^4–8 The common characteristic temperatures are currently obtained using an accelerating rate calorimeter (ARC). And the tendency of the alternating current (AC) internal resistance (“resistance” for short in the following text) can be tracked and recorded by combining an ARC with a resistance tester.

Current research on TR of LIBs depends mainly on the temperature systems (T₁, T₂, T₃).^9–11 As the safety issues are of great importance, prevention techniques relying on multiple sources of signals have been reported¹² but are still in urgent need of further development.

In the current research, a tracking and monitoring technology for TR derived from the resistance and its change rate (CRR) was developed. Abnormal resistance (R₁), reminding resistance (R₂), warning resistance (R₃), decision resistance (R₄) and maximum resistance (R_max) were defined as the common characteristic resistances to build the resistance system. Verified by the temperature system, which is widely employed in the discussion of TR,¹³ the resistance system proved to be efficient and precise for the prediction and warning of TR. Furthermore, the common characteristic resistances discovered through experiments were consistent with the results of thermodynamic calculations. The difference between the calculated values and the experimental values was found to be within 4.5%. Compared to the method solely relying on temperatures, the warning signal sent by R₃ was provided over 25 minutes in advance, for an earlier prediction of TR. Under the circumstance of an unavoidable TR, alarms rung by R₄ still reserved over 3 minutes for the preparation of fighting the TR. In a word, with great potential in practical applications for avoiding large property losses and human casualties caused by TR, this technology was proven to be efficient and accurate.

The nominal capacity of the soft-pack batteries with aluminium plastic film used for testing was 5 A h, and the nominal voltage was 3.2 V. The positive electrodes of the batteries were LiFePO₄ with an aluminium current collector, the negative electrodes were graphite with a copper current collector, and the electrolyte was a solution of 1 M LiPF₆ in ethylene and dimethyl carbonate (1 : 1 in volume). The test batteries (identified as S1, S2, S3, respectively), were employed for the TR experiment with THT ARC-EV. The TR experiment is called “the ARC experiment” in the following test.

Before the ARC experiment was performed, all test batteries were charged to a 100% state of charge (SOC) with an Arbin BT2000 multifunctional battery testing system. In detail, the test batteries were discharged to 2.0 V at 1 A and then allowed to rest for 30 minutes. After being charged to 3.6 V at 1 A, the test batteries were kept charged at 3.6 V until the current decreased to 0.25 A. All test batteries were ready for the ARC experiment after repeating the discharge–charge process as described above once more.

The ARC experiments were conducted by the THT ARC-EV with the HWS mode. In detail, first the test batteries were heated to 50 °C in a heating chamber. The change of temperature was recorded after 30 minutes. If the self-exothermic rate (SER) was below 0.02 °C min⁻¹, the test batteries were heated to 55 °C and held at this temperature for 10 minutes before the SER was recorded. Namely, the step-heating processes were carried out with temperature steps of 5 °C and a holding time of 10 minutes until the SER exceeded 0.02 °C min⁻¹, at which point the self-exothermic reactions were believed to be triggered.¹⁴ Thus, T₁ was recorded. From this time point, the external step-heating process was switched to a temperature tracking process. The temperature inside the chamber was adjusted concomitantly to track the temperature of the test batteries in order to maintain the thermally isolated environment. The temperature tracking process was continued until T₂ was recorded when the SER reached 1 °C min⁻¹, a state at which TR was believed to take place.⁹ As the TR proceeded, the temperature continuously increased until its highest value occurred, which was recorded as T₃. With the starting point of the ARC experiment defined as 0 minutes, T₁, T₂, T₃ and their times t₁, t₂, t₃ were recorded at the same time.

The resistances were monitored with an HIOKI BT3562 tester. In detail, the tester was connected to the tabs of the batteries. Then, the alternating root mean square (RMS) voltage (U) was measured while applying an alternating RMS current (I, which was set to 5 mA in this research) at a frequency of 0.9–1.1 kHz to the test batteries for 5 s. The internal AC resistance was calculated using the equation R_n = U/I.

To better understand here the relationship between resistance and time, the rate of change of the resistance (CRR) was introduced, with CRR_n = (R_n − R_n−1)/(t_n − t_n−1), where n is a natural number starting from 1, t₀ = 0 minutes, and R₀ is the initial resistance of the test battery. Relative rate of change in the resistance (RCRR, RCRR_n = CRR_n/CRR₁) was defined as well for excluding the individual differences between the test batteries.

Results of the ARC experiments are shown in Fig. 1. The temperature and resistance of each test battery were all recorded throughout the TR process. In the temperature curves, the most apparent feature was observed to be the sharp peak corresponding to T₃. The common characteristic temperatures (T₁, T₂, T₃) and their times (t₁, t₂, t₃) were collected from the ARC experiments and are listed in Table S1 (ESI†). Note that it only took about 10 minutes for the temperatures to increase from T₂ to T₃. This is a much quicker process in real working conditions (such as a battery in a running car), leaving almost no time for escaping (or even noticing) the fire. Thus, multiple sources of signals should be developed to forecast the TR process.

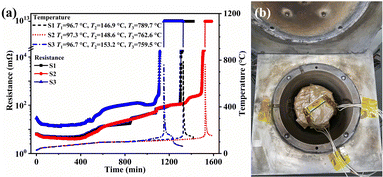Fig. 1 (a) Results of the ARC experiments (resistance and temperature) and (b) photograph of the set-up for the ARC experiments.

As for the resistance, a quite obvious and similar tendency occurred, as displayed in Fig. 1. That is, for each of the test batteries, the resistance changed dramatically at the same time when the temperature reached T₃. Before this change, it remained under 10 mΩ, but increased about a trillion fold after the change. Apart from the huge change near t₃, many smaller marks and trails for the resistance by the TR were left. First, in the range of 450–600 minutes, the resistance changed nearly linearly with time for all the test batteries. Secondly, before the dramatic changes near t₃, smaller but still obvious variations of resistances were also spotted.

In order to make use of the smaller changes that nevertheless should not be ignored, RCRR was defined and calculated. Fig. 2 displays the RCRR curves of the test batteries. Special tendencies were found before t₁, marked with the green square in Fig. 2a. For a clearer spotting of the unusual changes of RCRR, RCRR curves in the range of 450–600 minutes were enlarged as shown in Fig. 2b. The absolute values of RCRR gradually increased from 2 to 3, then to 4 and 5, and finally to out-of-control levels. In other words, the common features before T₁ can be reflected quantitatively with the absolute values of RCRR. Therefore, R₁, R₂ and R₃ were defined and employed to forecast the TR. In detail, R₁ (abnormal resistance) was defined to represent the resistance at the point the absolute value of RCRR reached 3, with the appearance of R₁ indicative of an abnormal situation (maybe occasional cases) requiring attention to the operating state. R₂ (reminding resistance) was defined to represent the resistance at the point the absolute value of RCRR reached 4, with the appearance of R₂ indicative of a confirmation of the abnormal operating state having been reached. Thus, in this case, special attention should be paid to the operating state. R₃ (warning resistance) was defined to represent the resistance at the point when the absolute value of RCRR reached 5, with the appearance of R₃ indicative of a worsening of the abnormal operating state, and suggesting that the operation should be shut down and that a comprehensive check procedure should be conducted.

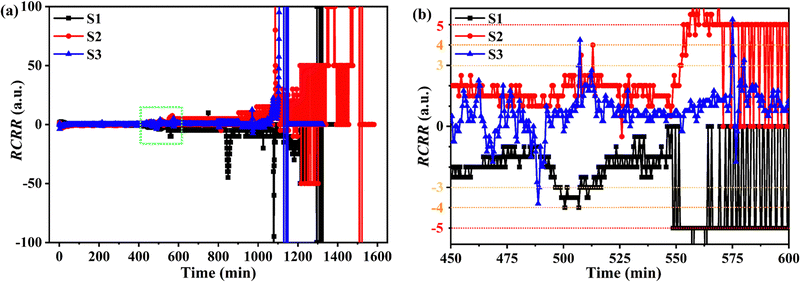Fig. 2 (a) RCRR curves of the test batteries and (b) magnified view of these RCRR curves between 450 and 600 minutes.

The times at which R₁, R₂, R₃ appeared in the ARC experiment of the test batteries, defined as t_R1, t_R2, and t_R3, are listed in Table S2 (ESI†). With comparison of the time, Δt₁(t₁ − t_R3) of S1, S2 and S3 are 44.5, 38.0 and 25.9 minutes, separately. In other words, by combining the T₁ in the temperature system and R₃ in the resistance system, an earlier prediction and warning of TR (of over 25 minutes) was realized, with these results consistent with the discussion about the chemical reactions inside the battery. That is, the LiPF₆ solute in the electrolyte for industrial batteries has been shown to start to decompose at temperatures of 60–70 °C without an obvious release of heat but quite a strong promotion of other side reactions.¹⁵ In the temperature system, these reactions would have no influence on temperature due to the lack of any obvious release of heat. Fortunately, R₁, R₂, and R₃ from the resistance system could be used to track decomposition reaction due to the changes of resistance not mainly resulting from the heat released but from the chemical reactions. This feature was the essential advantage of the resistance system in allowing for an earlier warning of TR.

In addition to the special tendency found for RCRR before 600 minutes as discussed above, a special tendency was found for times after 600 minutes as well. As shown in Fig. S1 (ESI†), the absolute values of RCRR increased obviously near t₂. The resistance at the maximum absolute value of RCRR was defined as R₄. Upon the resistance approaching close to R₄, TR would become unavoidable. However, as shown in Table S3 (ESI†), there would still be time for conducting cooling actions and preparing fire-fighting equipment. In detail, after introducing R₄ into the temperature system, there would be 3.8 minutes for preparing to deal with TR for S1. For the times of S2 and S3, there would be 7.7 and 17.5 minutes, respectively.

With R₃ appearing earlier than T₁ by over 25 minutes and R₄ showing up in advance of T₂ by over 3 minutes, combining the resistance system with the temperature system was proved to be sufficient, and that was more useful for an earlier warning for TR. Finally, R_max was defined to verify the accuracy and rationality of the resistance system, with specifically the resistance at the peak of RCRR defined as R_max (as shown in Fig. S2 and Table S4, ESI†).

For each of the test batteries, Δt₃(t₃ − t_Rmax) < 1 minute, indicative of the peak RCRR and the peak temperature (T₃) showing up at almost the same time, and hence confirming the reasonableness and precision of the whole resistance system (R₁, R₂, R₃, R₄, R₅, R_max). In other words, the temperature system may be considered “a widely accepted path on the map” to get to the “destination” of making the TR mechanism and regulation fairly clear—with the whole resistance system constituting “a better path”, and developed and modified from the temperature system to reach the same “destination”. Both the resistance system and the temperature system were shown to reveal the characteristics of TR, and an earlier prediction of TR can be realized by combining these two systems.

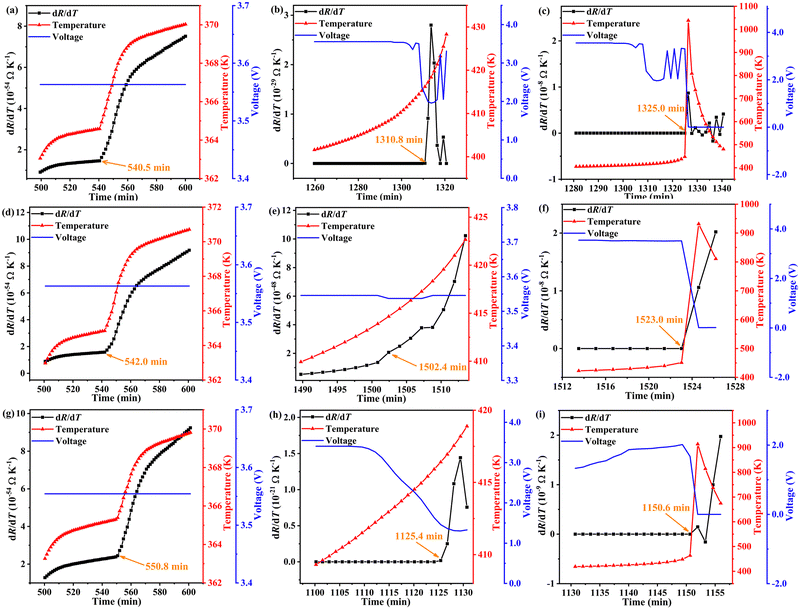
Considering that in general all the reactions during a TR process proceed in an adiabatic environment without an electric field, thermodynamics calculations were carried out in the current work based on the Arrhenius formula and Nernst equation to further verify the technology proposed through the experiments mentioned above. The detailed calculation and equations used are shown in ESI.†

Calculated variations of R with T (dR/dT) are exhibited as the curves in Fig. 3, as well as the relationships of E and T with t. For all the test batteries, some phenomena were found in the dR/dT curves around each common characteristic resistance. That is, the resistances were indicated from the thermodynamic analysis to make obvious changes at certain states. And the time for the occurrence of theoretical inflection points of resistances was indicated, from the comparison of data collected in Table S5 (ESI†), to be quite near the common characteristic resistances determined from the experiments. The deviation between the calculated and experimental values was within 4.5%. Note the very similar theoretical and experimental values for t_Rmax, this result which just like the situation for t₃ mentioned above, further confirmed the high reasonableness and precision of both the resistance system (R₁, R₂, R₃, R₄, R₅, R_max) and temperature system (T₁, T₂, T₃).

Fig. 3 Plots of calculated dR/dT versus t, E versus t, and T versus t for t values (a) around t_R3 for S1, (b) around t_R4 for S1, (c) around t_Rmax for S1, (d) around t_R3 for S2, (e) around t_R4 for S2, (f) around t_Rmax for S2, (g) around t_R3 for S3, (h) around t_R4 for S3, and (i) around t_Rmax for S3.

In conclusion, R₁, R₂, R₃, R₄, R₅, R_max were defined as common characteristic resistances to build a resistance system for predicting TR of LIBs. Before the early stage of TR, R₁, R₂ and R₃ tracked the side reactions without obvious heat release, which were quite useful clues for achieving an earlier prediction of TR that cannot be achieved by considering T₁ alone. The warning signal sent by R₃ provided over 25 minutes of advance warning for the earlier prediction of TR. For unavoidable TR, alarms rung by R₄ still reserved over 3 minutes for the preparation of fighting the TR. Actions such as conducting a cooling treatment and preparing fire-fighting equipment could still be taken in advance. Verified by the temperature system, which has previously been widely used to research TR, the resistance system built in the current research turned out to be accurate and reasonable. Furthermore, the deviation between the values from thermodynamic calculations and the values from experiments of the inflection points of resistances was within 4.5%. Thus, the technology for early warning of TR for LIBs based on the combination of the resistance system and the temperature system was concluded to be efficient, accurate and reasonable.

The present work was funded by the State Administration for Market Regulation of China (2021MK041, 2022MK037), Natural Science Foundation of Jiangsu Province, China (BK20201426), and National Natural Science Foundation of China (22279123).

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. X. Feng, X. He, M. Ouyang, L. Wang, L. Lu, D. Ren and S. Santhanagopalan, J. Electrochem. Soc., 2018, 165, A3748–A3765.
2. X. Feng, J. Sun, M. Ouyang, X. He, L. Lu, X. Han, M. Fang and H. Peng, J. Power Sources, 2014, 272, 457–467.
3. X. Feng, D. Ren, X. He and M. Ouyang, Joule, 2020, 4, 743–770.
4. S. Vashisht, D. Rakshit, S. Panchal, M. Fowler and R. Fraser, J. Energy Storage, 2023, 70, 107797.
5. K. Kausthubharam, P. K. Koorata and S. Panchal, Appl. Therm. Eng., 2023, 234, 121286.
6. R. Baveja, J. Bhattacharya, S. Panchal, R. A. Fraser and M. W. Fowler, J. Energy Storage, 2023, 70, 107967.
7. V. Talele, U. Moralı, M. S. Patil, S. Panchal, R. Fraser, M. Fowler, P. Thorat and Y. P. Gokhale, Int. Commun. Heat Mass Transfer, 2023, 146, 106907.
8. D. Subhedar, K. V. Chauhan, S. Panchal and A. Bais, Mater. Today Proc., 2023 DOI:10.1016/j.matpr.2023.08.055.
9. X. Feng, S. Zheng, D. Ren, X. He, L. Wang, H. Cui, X. Liu, C. Jin, F. Zhang, C. Xu, H. Hsu, S. Gao, T. Chen, Y. Li, T. Wang, H. Wang, M. Li and M. Ouyang, Appl. Energy, 2019, 246, 53–64.
10. D. Ren, H. Hsu, R. Li, X. Feng, D. Guo, X. Han, L. Lu, X. He, S. Gao, J. Hou, Y. Li, Y. Wang and M. Ouyang, eTransportation, 2019, 2, 100034.
11. J. Hou, M. Yang, D. Wang and J. Zhang, Adv. Energy Mater., 2020, 10, 1904152.
12. Z. Jia, S. Wang, P. Qin, C. Li, L. Song, Z. Cheng, K. Jin, J. Sun and Q. Wang, J. Energy Storage, 2023, 61, 106791.
13. B. Mao, P. Huang, H. Chen, Q. Wang and J. Sun, Int. J. Heat Mass Transfer, 2020, 149, 119178.
14. X. Liu, D. Ren, H. Hsu, X. Feng, G.-L. Xu, M. Zhuang, H. Gao, L. Lu, X. Han, Z. Chu, J. Li, X. He, K. Amine and M. Ouyang, Joule, 2018, 2, 2047–2064.
15. H. F. Xiang, H. Wang, C. H. Chen, X. W. Ge, S. Guo, J. H. Sun and W. Q. Hu, J. Power Sources, 2009, 191, 575–581.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cc05086f

---