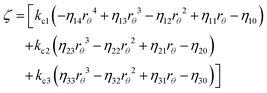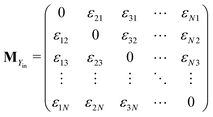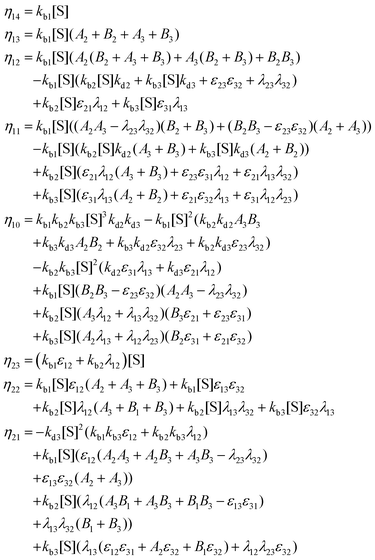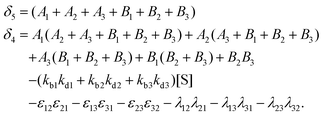A minimal kinetic model for the interpretation of complex catalysis in single enzyme molecules
Prasanta
Kundu
 a,
Soma
Saha
a,
Soma
Saha
 *b and
Gautam
Gangopadhyay
*b and
Gautam
Gangopadhyay
 a
a
aS. N. Bose National Centre for Basic Sciences, Block JD, Sector III, Salt Lake, Kolkata 700106, India
bDepartment of Chemistry, Presidency University, 86/1 College Street, Kolkata 700073, India. E-mail: soma.chem@presiuniv.ac.in
First published on 21st November 2023
Abstract
Multi-exponential waiting-time distribution and randomness parameter greater than unity ascribe dynamic disorder in single-enzyme catalysis corroborated to the interplay of transforming conformers [English et al., Nat. Chem. Biol., 2006, 2, 87]. The associated multi-state model of enzymatic turnovers with statically heterogeneous catalytic rates misdescribes the non-linear uprising of the randomness parameter from unity in relation to the attributes of the fall-offs of the waiting-time distribution at different substrate concentrations. To resolve this crucial issue, we first employ a comprehensive stochastic reaction scenario and further rationalize and work out the minimal indispensable dynamic-disorder model that ensures the foregoing relationship upon comparison with the data. We elucidate that specific disregard for the transition rate coefficients in the multi-state model on account of the especially slow conformational transitions is the underlying reason for not achieving interrelation between the observables.
1 Introduction
The advent of single-molecule spectroscopy since the last decades has unveiled the role of incessant structural variations of the enzyme molecules in real-time experiments and thereby illustrated the dynamic behaviour of the catalytic rate constant beyond the conventional Michaelis–Menten (MM) kinetics.1–6 Here, we are acquainted with one such renowned single-molecule fluorescence assay that exposed noteworthy outcomes while the fluorogenic product resorufin is formed from the hydrolysis of resorufin-β-D-galactopyranoside, catalysed by single β-galactosidase enzymes.7 The lengths of the time that elapsed for each enzymatic turnover, the waiting times, were monitored. Importantly, the prevalence of molecular memory at high substrate concentrations was quite evident and its longevity over the decades featured the interplay between the transforming conformers.The overview of the experimental outcomes is comprised of the following. Statistical distribution of the waiting times, f(t), executed apparent non-exponentiality at higher substrate concentrations. This fact is indeed inscrutable by the classical kinetics. However, the same attribute of ensemble-level mono-exponentiality in the regime of lower substrate concentration was conserved. Regardless, the kinetics at the ensemble level and the single-molecule level became compatible which was evident from the similar hyperbolic variations of the mean waiting times, 〈t〉, with the inverse of substrate concentration, represented in accordance with the Lineweaver–Burke fashion.8 Finally, the randomness parameter, R, the dimensionless variance of the turnover time fluctuations, exhibited a non-linear growth from its initial magnitude of unity with the rising substrate concentration.
The single-β-galactosidase experiment tangibly validated dynamic disorder in the reaction pathway when the substrate concentrations are large. This point along with the hyperbolic variation of 〈t〉 and the change of R from unity at low [S] to R > 1 at high [S] were qualitatively demonstrated by prior analysis of the Michaelis–Menten kinetics at the single-molecule level. The proposed model considered multiple conformational substates of the enzyme and the enzyme–substrate complex and was governed by the condition of quasi-static limit associated with much slower conformational transitions as compared to the catalytic rate.9 The authors estimated the overall waiting-time distribution by obtaining the steady-state weighted averages of the distribution corresponding to the reaction channel of every conformer. Simplification of the calculated results was achieved by assigning certain assumptions and retaining dynamic disorder exclusively in the catalytic step. Later, the same approximate model was employed unaltered to recover the outcomes of the time-dependent decay of f(t) and the linear increment of 〈t〉 with growing 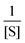 quantitatively.7 In contrast, no comparison was made with the observed data for the randomness parameter.
quantitatively.7 In contrast, no comparison was made with the observed data for the randomness parameter.
In successive studies it was discerned that the multi-state tool remained unable to show the differences between the magnitudes of R at altered substrate concentrations.10,11 A constant quantity of R contradicts straightaway the observed variations of the waiting-time distribution towards higher substrate concentration. Hence, the formulation of the multi-state reaction model led to the incompatible qualitative and quantitative predictions of the dependence of R on the substrate concentration and stayed away from a foolproof explanation of the experimental set of data.
It is known that simpler models12 of dynamic disorder are usable to explain the histograms of the reaction times and the corresponding mean values acceptably well.11 More instances are discussed in recent works where heterogeneous kinetics from the distinct single-molecule studies13–20 were rationalized with the aid of two-state21–23 and the multi-state24 frameworks. The better suitability of a proposed single-molecule kinetic model can be realized with reference to the higher moments of the statistical distribution. In the kinetic measurements of single β-galactosidase catalysis, the randomness parameter is the sole quantity described using the second moment of the waiting-time distribution.9 As a result, it is desirable that further regard to a kinetic framework for the given single-enzyme reaction will regenerate the observed time-distributions and the quantified randomness, described by the magnitudes of R, besides satisfying the mean values of the distribution function.
An earlier work10 considered the non-Poisson renewal reaction processes for single catalytic turnover in which the basic idea was to represent the turnover time distribution in terms of the three reaction time distributions of the elementary reversible and irreversible reaction processes.25 Subsequently, an excellent quantitative illustration of the behaviour of the parameter R was provided. Specifically, to the best of our knowledge, no emphatic model of stochastic chemical kinetics is available to date that rendered unified quantitative interpretation of the waiting-time distribution data and the randomness parameter data over the full range of chosen substrate concentration. It is indeed quite profound to possess this idea since it would direct a way out of the conflict caused by the exploitation of the same multi-state theory from the qualitative and quantitative perspectives.
To resolve the issue, a dynamic probe11 was proposed meanwhile that was shaped by the aspects of dynamical disorder in the line of Zwanzig's conception26 and the dynamics of a flexible polymer.27,28 This very model appeared successful to provide satisfactory explanations for the entire set of experimental data. The model however was unrelated with the conventional stepwise chemical conversions and structural dynamics of the active species was the principal trait of prolonged calculations. Nevertheless, remarkably, a worthy justification of dimensional analysis for a key model parameter accomplished immediate comparison with the data. To this end, we note that, in ref. 9, no use of the primary two-state model of dynamic disorder was made to check the qualitative tendencies of the measurable stochastic kinetic parameters. On the other hand, ref. 11 demonstrated that an application of the two-state kinetic scheme, involving product formation through either the single or parallel catalytic paths, best matched the numerals of R at the regime of low substrate concentration, in addition to satisfying the measured histograms and mean times for product formation. A concern for the whole scenario therefore motivated us to recognise the minimal kinetic model around the central theme of affirming the surpass of R from unity in consonance with the changing exponentiality of the waiting-time distribution.
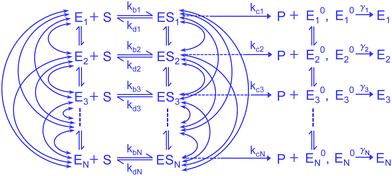
In the present work, we consider a comprehensive kinetic framework of single-enzyme catalysis in which the duplex states of the enzyme, E and ES, interconvert among finite number (N) of conformational substates. We show the mesh of transition paths such that any active isomer Xi (X stands for E, ES and E0) is allowed to make transitions to the N − 1 numbers of Xj across vertically (Fig. 1). It is alike with the multi-state model suggested by Kou et al.9 who acknowledged the multitude of transition possibilities while extending the methodology applied to the two-conformer case. The notable outlook of their analysis involved insertion of limiting conditions to depict the relevance of the ensemble Michaelis–Menten kinetics in the presence of structural dynamics of the enzyme molecule. Several convenient assumptions finally resulted in a fairly simple expression for the waiting-time distribution. The latter was defined by the integration of the product of the waiting-time distribution for the single reaction channel (in the absence of dynamic disorder) and the specific distribution complied with by the catalytic rate constant. Since this average distribution apposite to statically heterogeneous enzymatic description led to significant discrepancy with the available randomness data, the importance of the explicit subsistence of the transition coefficients within the calculated results needs to be assessed. Thereupon, it may be attempted to revisit the analysis making it free from the previous suppositions. Furthermore, despite the fact that the multiplicity of states for a real enzyme is soundly factual, a straightforward analytical evaluation of the reaction time distribution and other parameters of interest, retaining large finite number of substates and waiving the working approximations, would become utterly complex. Consequently, it seems quite methodic to abridge the multi-channel kinetic framework to one having a lower finite integer of conformers. This minimal model, in turn, ought to be enlarged compared with the two-state layout for which a worthy comparison of the theoretical results with the data would finally substantiate the effectiveness of the given model description.
The arrangement of the paper includes a description of the state-based model in Section 2. A comparison of the predicted results with the measured data is presented in Section 3. Finally, we present our conclusions in Section 4.
2 Kinetic model
Enzyme-catalyzed reactions when considered at the single-molecule level represent stochastic events.29–31 A kinetic reinvestigation is made here to fulfill our aim to interpret fully the characteristic relationship between the waiting-time distribution and the randomness parameter.Fig. 1 represents a comprehensive stochastic kinetic scheme of catalysis by a fluctuating single enzyme molecule. We take into consideration all possible transitions among the pairs of conformers and the parallel paths of product formation from every substate of the enzyme–substrate complex. To start with, the time evolution of the probability of the various possible states can be expressed as follows (we use the symbol P for probability throughout the calculations).32
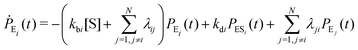 | (1) |
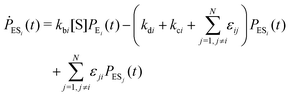 | (2) |
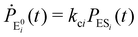 | (3) |
The indexes i and j vary from 1 to N. kbi, kdi and kci represent the rate constants for the binding of the substrate with the i-th conformer of the enzyme to form the ESi complex, unbinding rate constants and the catalytic rate constants, respectively. The structural transitions between the i-th and j-th conformers of the enzyme and enzyme–substrate complex are governed by λij, λji and εij, εji. E0i → Ei transitions are assumed instantaneous and hence ζij, ζji and γi are not involved in the rate equations.
It is to be noted that Fig. 1 depicts a generalized kinetic scheme and it may be desirable to opt for suitable assumption and approximation that would simplify the mathematical treatment. However, any such assumption or approximation should leave the portray of the reaction network unmodified. Referring to the parent work of Kou et al., it is assumed that the energy barrier between the two minima on the free-energy surface associated with E0i and Ei is negligible and hence the approximation γi → ∞ is rational. Moreover, for the case of E0i ↔ E0j conversions, the same assumption is followed and ζij, ζji → ∞ (E0i → Ei and E0i ↔ E0j transitions occur after the product formation). Consequently, these rate constants do not appear in the governing kinetic equations. Eqn (1)–(3) must fulfill the constraint 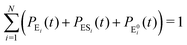 at any time t with the specified initial conditions of PE1(0) = 1, PEi≠1(0) = 0, PESi(0) = 0, and
at any time t with the specified initial conditions of PE1(0) = 1, PEi≠1(0) = 0, PESi(0) = 0, and 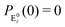 .
.
The formation of the fluorogenic product resorufin traced the completion of a single catalytic turnover complemented by the regeneration of the enzyme molecule via E0i. The time on which the product is formed is familiar as the turnover time or waiting time. Repeated measurements of the enzymatic turnovers yield different waiting times and hence a distribution due to the structural heterogeneity of the enzyme molecule during the course of the reaction. For the single enzymatic reaction, the primary attention is drawn to the waiting-time distribution, f(t). Since in the time interval t and t + Δt, the probability of an enzymatic turnover occurring, f(t)Δt, becomes equal to the probability that the enzyme exits in the E0i state, 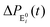 , then in the limit of Δt → 0, and f(t) is expressed by9
, then in the limit of Δt → 0, and f(t) is expressed by9
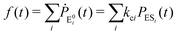 | (4) |
Next, it is crucial to evaluate f(t) from the solutions of the coupled differential equations containing both PEi(t) and PESi(t). Prior to that, eqn (1) and (2) are expressed as a set of 2N linear differential equations, noted as
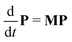 | (5) |
 | (6) |
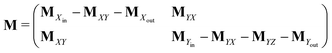 | (7) |
The initial conditions rational to eqn (5) are given by P0 = [1, 0, …, 0, …, 0]T. Eqn (5), upon Laplace transform, an integral transformation defined by33
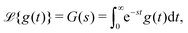 | (8) |
| P(s) = [sI − M]−1P0 | (9) |
To evaluate f(t), one needs to invert the Laplace-transformed solutions P(s), given in the preceding equation. Once known, f(t) leads to the generation of the various moments, formulated as34
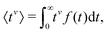 | (10) |
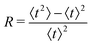 | (11) |
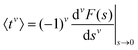 | (12) |
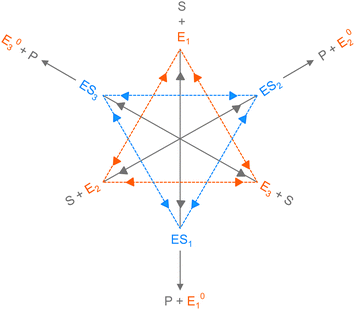
We have introduced all the prerequisites to proceed further in our analysis. At this point, however, we ponder the following fact. The essence of structural variations of the active species, enzyme and enzyme–substrate complex, that was earlier depicted with the two-state model came out efficient to elucidate the randomness parameter data at substrate concentrations not exceeding 20 μM. Beyond the latter, the steady growth of predicted R continued with the lower estimates than the data, as opposed to the constancy of results achieved by the multi-state model.11 Hence, a kinetic design is required which should be more extensive than the two-conformer description and unfollowed by the particularities of the conditions and assumptions of the multi-state model9 as well. Apparently, a set of kinetic schemes can be thought of that become distinct with regard to the number of reaction paths. It is customary to derive expressions for the observables related to every kinetic scheme, i.e. one needs to assign specific numbers of conformers of the active species in the comprehensive sketch (Fig. 1). Larger than a two-state model, any given scheme accounts for a greater number of mutual transitions among the conformational isomers that better befit the dynamic disorder scenario. However, switching to a higher state description imparts intensive complexity in analytical calculations, unaccompanied with working approximations, and gives rise to a significant increase in the number of adjustable parameters that need to be fixed suitably. Therefore, we reason that our primary choice concerns the three-conformer parallel pathway model to continue the illustration.
Consider the threefold coupled reaction description of the single-enzyme kinetics, shown in Fig. 2. It is characterized by nine reaction rate constants and twelve transition coefficients. In contrast to the two-conformer analogue,11,12 it offers the simplest model in which multitudes of conformational transitions for a given isomer is realized. Setting N = 3 in eqn (1) and (2), we arrive at the following revised forms of the involved matrices.
| P(s) = [PE1(s), PE2(s), PE3(s), PES1(s), PES2(s), PES3(s)]T | (13) |
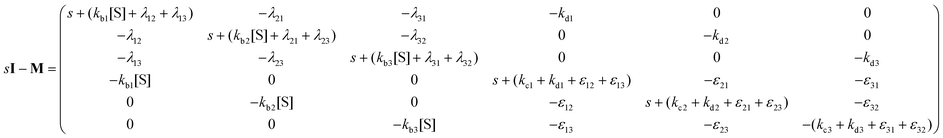 | (14) |
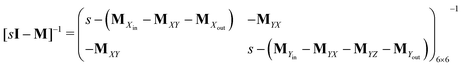 | (15) |
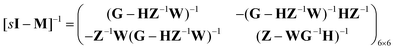 | (16) |
One important aspect of the solution is to be noticed during matrix multiplication. Every element of P0 is zero except the first one. Since the vector P0 multiplies [sI − M]−1, therefore, the first column of [sI − M]−1 will contribute exclusively to the multiplication output.35 The first three rows of the latter correspond to the probabilities of three conformers of the specie E, while its last three rows yield the probabilities of ES conformers in the Laplace domain. Because the definition of waiting-time distribution, eqn (3), involves the PESi(t) terms, it is evident that the first column of the block matrix, −Z−1W(G − HZ−1W)−1 in eqn (16) will be our only concern. Subsequently, the abbreviated expressions for PES1(s), PES2(s) and PES3(s) are obtained which show that
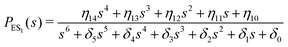 | (17) |
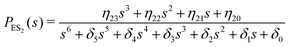 | (18) |
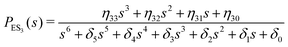 | (19) |
The inverse Laplace transforms of eqn (17) is given by
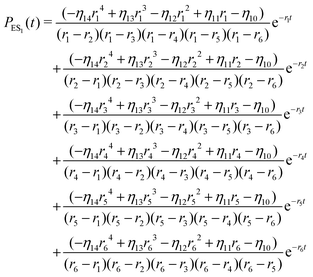 | (20) |
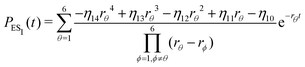 | (21) |
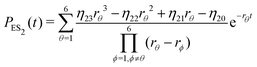 | (22) |
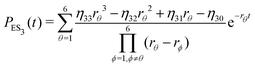 | (23) |
Substituting eqn (21)–(23) into eqn (4), the waiting-time distribution of the three-state stochastic kinetic model is attained, written below.
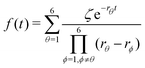 | (24) |
Afterwards, evaluations of the first and second moments of f(t) are carried out by making use of eqn (12) and found to be as shown below.
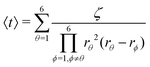 | (25) |
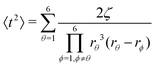 | (26) |
3 Results and discussions
In this section, we explore whether the exploitation of the key expressions, eqn (24)–(26), would lead to the productive comparison with the data. To execute it, in Fig. 3, we first show the temporal decay profiles of the waiting-time distribution obtained by using eqn (24) (solid lines) with the experimental estimates (symbols) at four substrate concentrations.7 We observe that our calculated results are in excellent agreement with the measured yields. The variation of the mean waiting times with the progress of inverse of substrate concentration is depicted in Fig. 4a. The theoretical output is the solid line, eqn (25), that efficiently recovers the mean times for product formation (circles). Finally, in Fig. 4b, we turn to look for the resemblance between our predicted randomness (curve) and the reported magnitudes of R (symbols) which is the key concern of our work. The variation of the estimated result upon increasing substrate concentration and the respective similarity with the data are quite remarkable. The adjustable parameters used for fitting in Fig. 3 and 4 are listed in the caption of the former. Therefore, the three-state model successfully restores the characteristic relationship uniting the nature of the decay profiles of the waiting-time distribution to the non-linear variation of the randomness parameter across the experimental range of substrate concentration. If otherwise stated, the present kinetic framework is able to overcome the limitations of the previous kinetic paradigms7,11,12 and serves as the minimum indispensable model to interpret the outcomes of the single β-galactosidase catalysis altogether.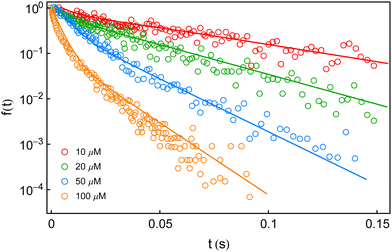 | ||
Fig. 3 Fall-offs of the waiting-time distributions of single β-galactosidase molecules measured at substrate concentrations of 10, 20, 50 and 100 μM (concentration increases downwards) in a log-linear scale (symbols).7 The solid lines are the theoretical results (eqn (24)) deduced from the three-conformer dynamic-disorder model of single β-galactosidase catalysis (Fig. 2). The parameter values extracted from the fits are as follows: kb1 = 4.8 × 107 M−1 s−1, kb2 = 9 × 107 M−1 s−1, kb3 = 3 × 107 M−1 s−1, kd1 = 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 s−1, kd2 = 20 300 s−1, kd2 = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 s−1, kd3 = 12 800 s−1, kd3 = 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 s−1, kc1 = 1050 s−1, kc2 = 800 s−1, and kc3 = 100 s−1. λij, λji, εij and εji values were adjusted between 10 and 50 s−1 for best results. The choice of the fit parameters suggests the prevalence of dynamic disorder in the reaction pathway. The coefficient of determination for each plot was calculated as 0.99. 300 s−1, kc1 = 1050 s−1, kc2 = 800 s−1, and kc3 = 100 s−1. λij, λji, εij and εji values were adjusted between 10 and 50 s−1 for best results. The choice of the fit parameters suggests the prevalence of dynamic disorder in the reaction pathway. The coefficient of determination for each plot was calculated as 0.99. | ||
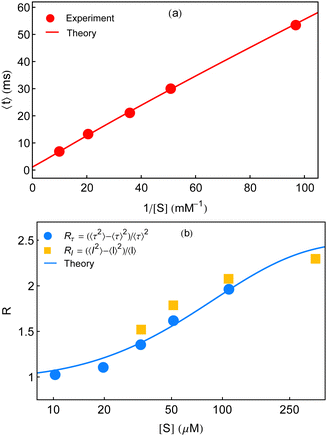 | ||
| Fig. 4 Concentration dependence of the mean waiting time data (circles) and randomness parameter data (circles and squares) adopted from ref. 7. (a) The solid line is given by eqn (25). (b) The non-linear variation of R is explained from its definition using eqn (25) and (26). In both the plots, the magnitudes of the adjustable parameters, opted in Fig. 3, are kept the same. | ||
The particulars of the two-state parallel and off-pathway models of single-enzyme catalytic turnover were assessed thoroughly in relation to the yields of the real time data.11 The off-pathway mechanism designated a single route of product formation. However, fluctuations between the paired conformational isomers of E and ES were explicit in both the cases. The respective outputs were very close among which the lower magnitudes of the randomness parameter towards higher [S] were quite obvious. The partial quantitative agreement looked more similar to the exponential type of growth than the expected sigmoidal type increment. It was then opined that to elevate the mere qualitative estimates more counts of the conformational substates over the duplet are required. Noting the insensitivity of the multi-state kinetic formalism9 towards the randomness data, we proposed a distinct model of dynamic disorder furnished with dynamic probes.11 This model appeared superior to the two-state kinetic narration in delineating the multi-state structural heterogeneity supported by the reproducibility of the entire kinetic outputs. A mere adjustment of a single parameter, after some dimensional analysis, looked effective to describe the effect of substrate concentration besides utilizing a fairly smaller number of fit parameters. Although, as a substantial model it is valued, the reappraisal of the state-based kinetic treatment in this regard was wanting and in the present study, we, therefore, focused on this aspect. In Fig. 5, we summarize the comparisons of the randomness parameter data against the estimates of R calculated based on the two-state parallel model,11 the present work and the multi-state model.9
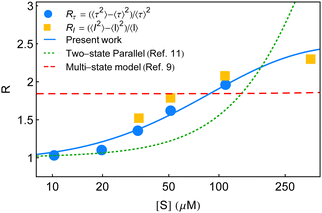 | ||
| Fig. 5 Estimates of the randomness parameter calculated based on the two-state parallel model11 (green dotted line) and the multi-state model9 (red dashed line) are compared with the present result (blue solid line). Symbols represent the experimental data adopted from ref. 7. | ||
A qualitative exploration to quantitative comparison of the single-enzyme kinetics were formalized by the conditions under which the suitability of MM equation holds good even in the circumstance of dynamic disorder.7,9 An initial two-state model was generalized to accompany the rather realistic multi-state persuation of the fluctuating enzyme. Keen emphasis on the slower rates of conformational transition compared to the catalytic rate eventually resulted in a statically heterogeneous kinetic model. The waiting-time distribution was expressed in terms of the sum of the distributions of the individual waiting times related to every reaction channel multiplied by the allied steady-state weights. The latter are the ratios of the catalytic efficiencies of the distinct conformers to the sum of the catalytic efficiencies of all the individual conformers. To make the theoretical result competent in order to find comparison with the data, further assumptions like identical forward and backward rate constants and a continuum approximation were implemented. Consequently, the steady-state weights of each reaction channel appeared to vary with the catalytic rate constant. Ultimately, to reveal the different catalytic activities of the large number of ES species, the final assumption that the weight function suits a γ-distribution was invoked. As previously mentioned, the multi-state kinetic model remained ineffectual to respond to the variation of R as a function of [S] and thus cannot be recognised as foolproof. Hence, it seemed all-important to afresh the kinetic treatment fortified with a revised framework larger than the two-conformer model. This representation will envisage an explicit subsistence of the transition coefficients within the calculated results.
To elaborate the last point further, we employ the expression for f(t) from eqn (24) of ref. 9 that is applicable for a three-state model, given by
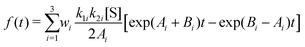 | (27) |
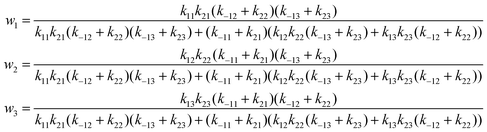 | (28) |
In deriving eqn (28), the following relationship between wi and the catalytic rate constants k2i and the Michaelis constants KMi from ref. 9 are used
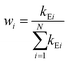 | (29) |
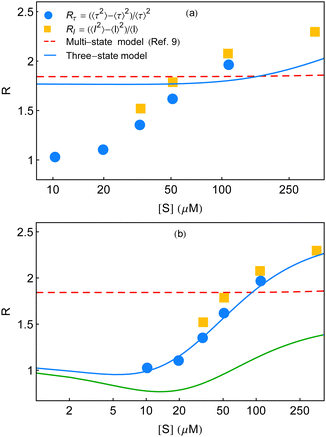 | ||
Fig. 6 Randomness parameter data (symbols) at different substrate concentrations7 are compared with the theoretical expressions. (a) Multi-state model used in ref. 7 to compare the experimental results yields a constant estimate throughout (red dashed line) employing eqn (31) of ref. 9. The corresponding three-state model shows little growth at a much higher substrate concentration regime (blue line). The fit parameters, we used for the latter case, are as follows. k11 = 5 × 107 M−1 s−1, k12 = 3 × 107 M−1 s−1, k13 = 6 × 107 M−1 s−1, k−11 = 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 s−1, k−12 = 21 300 s−1, k−12 = 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s−1, k−13 = 11 000 s−1, k−13 = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 s−1, k21 = 1150 s−1, k22 = 800 s−1, and k23 = 190 s−1. (b) Qualitative and quantitative explanations of the randomness parameter data adopted from English et al.7 The red dashed line is identical with that in (a). The solid line that appears below the data (green line) is the qualitative plot of R (k2 fluctuations) shown in Fig. 6 of ref. 9. We construct the quantitative comparison with the data (symbols), blue curve, with the aid of the multi-state formalism by Kou et al.9 using the following set of fit parameters. k1 = 3.5 × 107 M−1 s−1, k−1 = 150 s−1, a = 3.4, and b = 220. The data set of waiting-time distributions and the mean waiting times cannot be regenerated utilizing these parameter values. 300 s−1, k21 = 1150 s−1, k22 = 800 s−1, and k23 = 190 s−1. (b) Qualitative and quantitative explanations of the randomness parameter data adopted from English et al.7 The red dashed line is identical with that in (a). The solid line that appears below the data (green line) is the qualitative plot of R (k2 fluctuations) shown in Fig. 6 of ref. 9. We construct the quantitative comparison with the data (symbols), blue curve, with the aid of the multi-state formalism by Kou et al.9 using the following set of fit parameters. k1 = 3.5 × 107 M−1 s−1, k−1 = 150 s−1, a = 3.4, and b = 220. The data set of waiting-time distributions and the mean waiting times cannot be regenerated utilizing these parameter values. | ||
In view of the above result, the limiting conditions that restrained the form of the Michaelis–Menten equation9 such as much greater catalytic rates relative to the interconversion rates of ESi complexes, extremely slow structural transitions between the different ES conformers and extremely slow passage of one E conformer to another become incompetent in analysing the measurements of R presented in ref. 7. Moreover, the qualitative track of the randomness parameter shown in Fig. 6 of ref. 9 is quite different within the experimental range of substrate concentration to bring out the histograms of the waiting times. Note that, in producing Fig. 3 and 6a of the present work, the extracted values of the catalytic rate constants are similar. Importantly, the useful quantities of the parameters (λ and ε terms in Fig. 3) that are particularly relevant to the structural transitions are not limitingly small numbers and hence cannot be neglected. Our selection of the parameters thus aptly articulates the essence of dynamic disorder that involves changes in the conformations with rates comparable to or slower than the rates of chemical conversions.
As discussed in ref. 10, the expression for the multi-state waiting-time distribution, eqn (31) in Kou et al.'s work,9 is characteristic for an ensemble of enzymes which possess the same rate constants of k1 and k−1, whereas the catalytic rate constants are all different. In turn, the same equation verily represents the average of the waiting-time distribution of the individual enzymes with a given probability density of the k2 values. The inefficacy of the averaged distribution to expound the randomness quantified by R utterly reinforces the merit of the dynamic heterogeneity over the statically heterogeneous framework.
Jung et al. inquired that the randomness parameter (symbolized as Q and related to our notation of R by Q = R − 1) on account of a renewal reaction process disappears in the limit of low-substrate concentration. This is relevant to an ergodic and homogeneous reaction system and the reported enzymatic catalysis falls under the same grouping.25 Again, it was verified in Yang et al.'s work10 that the expression for the randomness parameter QGC, based on the generalized conventional chemical kinetics, does not meet the criteria for expected vanishing in the low substrate concentration limit onto any selection of the probability density function with a finite variance. Hence, the given definition of f(t) in Kou et al.'s work was reviewed as inept to narrate the correct turnover-time distribution of the β-galactosidase enzyme. Nonetheless, we surveyed a distinct set of fit parameters for the multi-state model that recovered the randomness parameter data in a quantitative manner. The corresponding result is displayed by the blue curve in Fig. 6b. The red line denotes the same estimate of R by the multi-state theory shown in Fig. 6a. The green curve represents the qualitative plot with k2 fluctuations considered in ref. 9.
The unforeseen agreement observed here does not refute our inference based on the analysis made for Fig. 6a, discussed as follows. It is basic to match the histograms with the theory before checking conformity of the randomness parameter. Albeit, because of the isolated restoration of the randomness parameter data, we aspired to obtain a comparison with the remaining experimental outputs and acquired highly non-exponential decay profiles of the waiting-time distributions at 10 and 20 μM (figures not shown). The extent of non-exponentiality increased at the other concentrations too, following substantive disagreement between the predicted results and the data for the histograms and the mean waiting times. Therefore, starting from either satisfying the waiting-time distribution data or the randomness parameter data, the other one, in consequence, cannot be elucidated. The fact of limited applicability of the multi-state depiction towards the single-enzyme trial clearly reveals its inadequate proficiency.
Looking back at the present model, some points need be highlighted regarding the appropriateness of the three-state kinetic representation. First, ordinarily, one may behold there occurs little difference when the two-conformer scheme is raised to the three-conformer one. Nevertheless, it initiates an important prospect that conformational isomers are entitled to make additional transitions other than Ez−1 ↔ Ez ↔ Ez+1 sequential interconversions. Accordingly, for the threefold reaction scenario, the primary (two-conformer) E1 ↔ E2 shifts are supplemented by E2 ↔ E3 and E1 ↔ E3 transformations. The same is valid for the ES species. More transitions appear naturally in the enlarged kinetic frameworks. The choicest feature of the three-conformer model is thus insightful owing to, in one side, the incapacity of the two-conformer scheme, governed by exclusive paired fluctuations, to explain the higher estimates of R and, on the other side, the fact of exceeding difficulty in dealing with an enlarged scheme accompanied by quite a large number of fit parameters. Since the three-state model provides worth agreement with the data, in practice, one needs not to employ any higher-state kinetic model beyond it to illustrate the experimental observations.
Second, in Fig. 7, we compare the calculated result of R with that obtained from the dynamic analysis.11 It is seen that both the dynamic approach and the present kinetic approach recovered similar yields, although, the former is unrelated to the conventional stepwise chemical conversions. Here, it is to be noted that different realizations of the fluctuating bottleneck and the instantaneous distance between the two locations across the polymer chain may not result in a few conformational states. The ingenious way of evaluating the waiting-time distribution stemmed from the mutual integral-differential relationship with the survival probability. The latter was a dimensionless quantity and concerned only for the probability of the unreacted species (substrate) at a given time unconditioned to the detailed mechanism of product formation. Therefore, a dimensionally conditioned parameter was distinguished so as to exhibit the effect of substrate concentration. On the other hand, the state-based kinetic interpretation is subjected to the interest of individual active species undergoing transformation. The seeming difference between the two approaches, therefore, does not suggest to procure a one-to-one correspondence with regard to the number of conformational states. As a result, it is not surprising to conclude the closeness of the estimates of R produced by the three-conformer layout with that of the dynamic model. Nevertheless, we note that the kinetic model is preferred over the dynamic model to address the observables of single β-galactosidase catalysis because of its identity with the reaction mechanism, straightforward evaluation of the time-distribution function and the simplicity of direct variation of the substrate concentration.
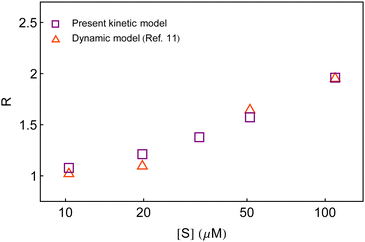 | ||
| Fig. 7 Comparison of the estimates of the randomness parameter from the present kinetic model and the previous dynamic model.11 | ||
The primary difference between the multi-state model of fluctuating enzyme by Kou et al.9 and our threefold description is that the former has a large extent of conformational fluctuations which, in turn, were made generalized by the involved assumptions. The other one, however, possesses the opposite characteristics. In between these outlooks, there exist various kinetic frameworks with a different number of conformational states. Although, we justified for evading a finite-state model beyond the three-conformer case, it might be interesting to analyse whether a generalization can be made across the varying number of interconverting conformers (N = 2,3,4,….). In making progress from a lower kinetic scheme of N1 conformers to higher N2 conformers, the numbers of reaction paths and reaction rate constants increase by N2 − N1 and 3(N2 − N1), respectively, whereas the count of the conformational transitions increases by 2(N2 − N1)(N2 + N1 − 1). Once N is definite, the order of the matrix becomes fixed. This clearly means that the requisite calculations must be performed each time when any change is made in the count of N. The distinct expressions for f(t) originated from the different schemes (different N) will be left unruled by a general structure owing to the forms of the denominators in the equations describing PESi(s) [degrees of the equations differ] and the coefficients η and δ terms. Nevertheless, after scrutinizing the schemes with two, three and four parallel catalytic routes (N = 2, 3, 4), the following common appearances are realized which are valid for any finite N.
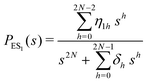 | (30) |
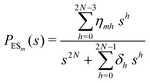 | (31) |
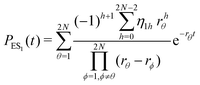 | (32) |
 | (33) |
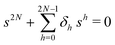 . The histogram of the waiting times takes the form
. The histogram of the waiting times takes the form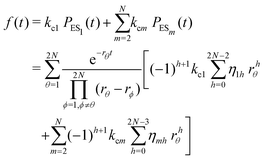 | (34) |
4 Conclusion
Fluctuations in β-galactosidase catalysis were probed using the single-enzyme turnover experiments that analyzed the turnover time traces and restored the dynamic information by the observable waiting time distribution. In this work, we investigated using an analytical model the influence of dynamic disorder in the catalytic pathway, especially focusing on the distinctive relationship between the waiting time distribution data and the randomness parameter data. We established that a three-conformer model provided a minimal kinetic illustration of the single-enzymatic reaction that quantitatively reproduced the observed time variations of the waiting time distribution and the allied non-linear uprise of the randomness parameter from unity over the experimental range of substrate concentrations.The added complexity of the current model in comparison to the elemental two-conformer dynamic disorder description became essential to minimally account for the flexibility in conformational transitions. This, however, appeared indispensable to elevate the calculated randomness at higher substrate concentrations. The direct application of our theoretical results to the single-β-galactosidase catalysis did not involve working assumptions as were associated with the previous multi-state analysis. The determination of the distribution function of the waiting times and its various moments must be accompanied by all the rate constants considered in the model. We showed that the view of retaining the transition coefficients is paramount since the expression for the waiting-time distribution unfurnished with those coefficients made the outcomes of the three-conformer layout indifferent to the randomness data. Besides satisfying the particularity of the connection between the waiting-time distribution data and the randomness parameter data, our results also led to successful recovery of the observed mean times for product formation. Our work thus suggests an effective stochastic kinetic theory where parallel transitions for the active conformers are acknowledged and the counts of the adjustable parameters are also least. The choice of the fit parameters remained worthy to discern the dynamic disorder scenario unlike the static heterogeneity prevailed in the multi-state formulation.
The interconnectivity of the kinetic schemes with the different numbers of conformational isomers is observed. Nevertheless, the structures of the waiting-time distribution for the case of N1, N2, N3, … conformational states cannot be made to obtain a generalized expression. Therefore, exercising with a higher-state kinetic framework beyond the three-state model to get back the similar agreement by means of more extensive calculations can be evaded.
Finally, we note that the conception of discrete state stochastic model and the mathematical strategy based on the Laplace transform employed here are also well applicable to other areas, such as DNA–protein binding kinetics37 besides DNA escape kinetics,21 force extension kinetics22 and electron transfer kinetics.24 The search of DNA-binding proteins for their specific target sites on DNA inside the living cell is an important biological phenomenon in regulating the cellular processes.37,38 A target search on a straight DNA fragment38 and the role of DNA loop formation and DNA conformational fluctuations37 received rich theoretical investigations.
Conflicts of interest
There are no conflicts of interest to declare.Appendices
Appendix A: structures of matrices in eqn (7)
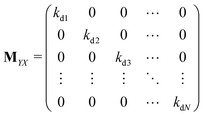
The matrix MXin denotes the rates of the transitions from all Xjs to any Xi. On the other hand, the matrix MXout denotes the rates of the transitions from any Xi to all Xjs. These can be written asSimilarly, matrices MYin and MYout representing the transition rates from all Yjs to any Yi and vice versa, respectively are found to be
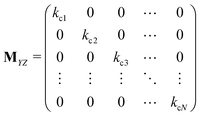
Matrices MXY and MYX correspond to the transition rates from Xi's to Yi's and the opposite way from Yi's to Xi's. Finally, the matrix MYZ indicates the conversion from Yi's to the product. These are detailed as follows.
Appendix B: exact expressions for the coefficients in eqn (17)–(19)
I. Coefficients in the numerators
with A1 = kb1[S] + λ12 + λ13, A2 = kb2[S] + λ21 + λ23, A3 = kb3[S] + λ31 + λ32 and B1 = kd1 + kc1 + ε12 + ε13, B2 = kd2 + kc2 + ε21 + ε23, B3 = kd3 + kc3 + ε31 + ε32.
II. Coefficients in the denominators

 with A1, A2, A3 and B1, B2, B3 as defined before.
with A1, A2, A3 and B1, B2, B3 as defined before.
Acknowledgements
P. K. acknowledges the financial support from S. N. Bose National Centre for Basic Sciences, Government of India.Notes and references
- M. Michaelis and M. L. Menten, Die kinetik der invertinwirkung, Biochem. Z., 1913, 49, 333–369 Search PubMed.
- H. P. Lu, L. Xun and X. S. Xie, Single-Molecule enzymatic dynamics, Science, 1998, 282, 1877–1882 CrossRef CAS.
- X. Zhuang, H. Kim, M. J. B. Pereira, H. P. Babcock, N. G. Walter and S. Chu, Correlating structural dynamics and function in single ribozyme molecules, Science, 2002, 296, 1473–1476 CrossRef CAS.
- A. M. van Oijen, P. C. Blainey, D. J. Crampton, C. C. Richardson, T. Ellenberger and X. S. Xie, Single-molecule kinetics of λ-exonuclease reveal base dependence and dynamic disorder, Science, 2003, 301, 1235–1238 CrossRef CAS.
- O. Flomenbom and K. Velonia, et al., Stretched exponential decay and correlations in the catalytic activity of fluctuating single lipase molecules, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 2368–2372 CrossRef CAS.
- K. Velonia and O. Flomenbom, et al., Single-enzyme kinetics of CALB-catalyzed hydrolysis, Angew. Chem., Int. Ed., 2005, 44, 560–564 CrossRef CAS.
- B. P. English, W. Min, A. M. van Oijen, K. T. Lee, G. Luo, H. Sun, B. J. Cherayil, S. C. Kou and X. S. Xie, Ever-fluctuating single enzyme molecules: Michaelis-Menten equation revisited, Nat. Chem. Biol., 2006, 2, 87–94 CrossRef CAS PubMed.
- P. Atkins and J. de Paula, Physical Chemistry, Oxford University Press, U. K., 2006 Search PubMed.
- S. C. Kou, B. J. Cherayil, W. Min, B. P. English and X. S. Xie, Single-molecule Michaelis-Menten equations, J. Phys. Chem. B, 2005, 109, 19068–19081 CrossRef CAS.
- S. Yang, J. Cao, R. J. Silbey and J. Sung, Quantitative interpretation of the randomness in single enzyme turnover times, Biophys. J., 2011, 101, 519–524 CrossRef CAS.
- P. Kundu, S. Saha and G. Gangopadhyay, A revisit to turnover kinetics of individual Escherichia coli β-galactosidase molecules, J. Phys. Chem. B, 2021, 125, 8010–8020 CrossRef CAS.
- A. Kumar, H. Maity and A. Dua, Parallel versus off-pathway Michaelis-Menten mechanism for single-enzyme kinetics of a fluctuating enzyme, J. Phys. Chem. B, 2015, 119, 8490–8500 CrossRef CAS PubMed.
- M. Wanunu, B. Chakrabarti, J. Mathe, D. R. Nelson and A. Meller, Orientation-dependent interactions of DNA with an α -hemolysin channel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 031904 CrossRef.
- T. L. Kuo and S. Garcia-Manyes, et al., Probing static disorder in Arrhenius kinetics by single-molecule force spectroscopy, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 11336–11340 CrossRef CAS PubMed.
- M. Schlierf, H. Li and J. M. Fernandez, The unfolding kinetics of ubiquitin captured with single-molecule force-clamp techniques, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 7299–7304 CrossRef CAS.
- A. F. Oberhauser, P. K. Hansma, M. Carrion-Vazquez and J. M. Fernandez, Stepwise unfolding of titin under force-clamp atomic force microscopy, Proc. Natl. Acad. Sci. U. S. A., 2000, 98, 468–472 CrossRef.
- M. Schlierf and M. Rief, Single-molecule unfolding force distributions reveal a funnel-shaped energy landscape, Biophys. J., 2006, 90, L33–L35 CrossRef CAS PubMed.
- T. Strunz, K. Oroszlan, R. Schafer and H. J. Güntherodt, Dynamic force spectroscopy of single DNA molecules, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 11277–11282 CrossRef CAS.
- H. M. Piwonski, M. Goomanovsky, D. Bensimon, A. Horovitz and G. Haran, Allosteric inhibition of individual enzyme molecules trapped in lipid vesicles, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, E1437–E1443 CrossRef CAS.
- H. Wang, S. Lin, J. P. Allen, J. C. Williams, S. Blankert, C. Laser and N. W. Woodbury, Protein dynamics control the kinetics of initial electron transfer in photosynthesis, Science, 2007, 316, 747–750 CrossRef CAS.
- P. Kundu, S. Saha and G. Gangopadhyay, Stochastic kinetic approach to the escape of DNA hairpins from an α -hemolysin channel, J. Phys. Chem. B, 2020, 124, 6575–6584 CrossRef CAS.
- P. Kundu, S. Saha and G. Gangopadhyay, An exactly solvable stochastic kinetic theory of single-molecule force experiments, J. Phys. Chem. B, 2020, 124, 7735–7744 CrossRef CAS PubMed.
- P. Kundu, S. Saha and G. Gangopadhyay, Kinetics of allosteric inhibition of single enzyme by product molecules, J. Phys. Chem. B, 2020, 124, 11793–11801 CrossRef CAS.
- P. Kundu, Kinetics of initial charge separation in the photosynthetic reaction centers of Rhodobacter sphaeroides, J. Phys. Chem. B, 2022, 126, 3470–3476 CrossRef CAS.
- W. Jung, S. Yang and J. Sung, Novel chemical kinetics for a single enzyme reaction: relationship between substrate concentration and the second moment of enzyme reaction time, J. Phys. Chem. B, 2010, 114, 9840–9847 CrossRef CAS.
- R. Zwanzig, Dynamical disorder: passage through a fluctuating bottleneck, J. Chem. Phys., 1992, 97, 3587–3589 CrossRef CAS.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Clarendon, Oxford, 1986 Search PubMed.
- A. Y. Grosberg and A. R. Khokhlov, Statistical Physics of Macromolecules, American Institute of Physics, New York, 1994 Search PubMed.
- C. W. Gardiner, Handbook of Stochastic Methods for Physics, Chemistry and Natural Sciences, Springer-Verlag, Berlin, Germany, 2004 Search PubMed.
- N. G. Van Kampen, Stochastic Processes in Physics and Chemistry, Elsevier, New York, 2007 Search PubMed.
- D. A. McQuarrie, Stochastic approach to chemical kinetics, J. Appl. Probab., 1967, 4, 413–478 CrossRef.
- S. Saha, A. Sinha and A. Dua, Single-molecule enzyme kinetics in the presence of inhibitors, J. Chem. Phys., 2012, 137, 045102 CrossRef.
- J. L. Schiff, The Laplace Transform: Theory and Applications, Springer-Verlag, New York, 1999 Search PubMed.
- S. Render, A Guide to First-passage Processes, Cambridge University Press, New York, 2001 Search PubMed.
- P. Lecca, I. Laurenzi and F. Jordan, Deterministic versus Stochastic Modelling in Biochemistry and Systems Biology, Woodhead Publishing, U.S.A., 2013 Search PubMed.
- J. R. Moffitt and C. Bustamante, Extracting signal from noise: kinetic mechanisms from a Michaelis-Menten-like expression for enzymatic fluctuations, FEBS J., 2014, 281, 498–517 CrossRef CAS PubMed.
- C. Felipe, J. Shin and A. B. Kolomeisky, DNA looping and DNA conformational fluctuations can accelerate protein target search, J. Phys. Chem. B, 2021, 125, 1727–1734 CrossRef CAS.
- P. Kar, A. G. Cherstvy and R. Metzler, Acceleration of bursty multiprotein target search kinetics on DNA by colocalisation, Phys. Chem. Chem. Phys., 2018, 20, 7931–7946 RSC.
| This journal is © the Owner Societies 2024 |