Group 13 five- and six-membered rings with rare 2π aromaticity

Abstract

According to Hückel's rule, cyclic species are aromatic if they have 4n + 2 (n = 0, 1, 2, etc.) π electrons. However, large aromatic rings (atom number > 4) with minimum 2π electrons (i.e., n = 0) are rather rare because of the structural instability stemming from the deficient π electrons compared to the ring size. To date, the largest 2π-aromatic ring is a five-membered Ga₅ core reported in a recent experiment. Herein, density functional theory calculations predicted seven inverse-sandwich Na₂(MH)₅ and half-sandwich Ca(MH)₅ or Ca(MH)₆ (M = Al, Ga or In) structures. They all have planar central five- or six-membered Al/Ga/In rings, rather negative binding energies and large HOMO–LUMO gaps. Their dianionic metal rings exhibit obvious aromatic characters and appreciable diatropic ring currents due to the good delocalization of 2π electrons donated by the Na/Ca metals. Interestingly, they also have novel collective bonding with the Na/Ca atoms interacting with both the metal ring and surrounding H atoms. These metalloaromatic rings not only greatly enrich the precious family of 2π aromatics, but also increase the maximum ring atom number from five to six, thus paving the way for Hückel-type 2π-aromatic large rings.

---

1. Introduction

Aromaticity is a fundamental concept in chemistry and has been widely applied to both organic and inorganic compounds.^1–7 For a planar cyclic molecule, its potential aromaticity in the singlet state can be predicted by using the famous Hückel's 4n + 2 π-electron counting rule (n = 0, 1, 2, etc.).⁸ For example, the prototypical benzene is aromatic due to the presence of 6π (n = 1) electrons on its six-membered conjugated ring plane. Its strong aromaticity causes special chemical and structural stability, where an important reason is that it has the same number of π electrons as ring atoms and the resultant good electron delocalization effectively stabilizes the whole ring structure.

The bottom line of Hückel's rule is n = 0, corresponding to the aromaticity stemming from the minimally required 2π electrons on the ring. However, such 2π-aromatic rings are rather rare and mainly limited to the simplest three-membered rings and slightly larger four-membered rings. Typical species include the group 14-based cyclopropenyl cation,⁹ the cyclobutadiene dication¹⁰ and its silicon analogue,¹¹ and group 13-based M₃ (M = B,^12,13 Al,¹⁴ and Ga^15,16) and M₄ (M = B,¹⁷ Al,¹⁸ Ga, and In^19,20) dianions in various derivatives or gas-phase clusters. Among them, the experimentally synthesized stable cyclogallanes of Na₂[(Mes₂C₆H₃)Ga]₃¹⁵ and K₂[(Mes₂C₆H₃)Ga]₃¹⁶ contain the first metalloaromatic rings (i.e., aromatic rings only composed of metal atoms). Thus, the group 13 compounds not only form the lightest possible Hückel 2π aromatics (i.e., B₃ ring),¹³ but also expand the traditional metalloaromaticity concept to all-metal rings.^21,22 In general, the four-membered rings exhibit lower stability (low temperature, additional ligands or gas phase condition are usually needed) than the three-membered ones (derivatives are stable at room temperature) because of the more insufficient π electrons compared to the ring size and resultant smaller aromatic stabilization.²³ Thus, it is even harder to obtain larger rings containing five or more atoms with 2π aromaticity.

Significantly, Kysliak et al. recently synthesized a stable dipotassium cyclopentagallene, and its structure was unambiguously determined by single-crystal X-ray diffraction to have a planar central Ga₅ ring (obtained as Ga₅R₅, R = CH(SiMe₃)₂) with nearly equal Ga–Ga bond lengths (ca. 2.4 Å) and Ga–Ga–Ga bond angles (ca. 108°).²⁴ Density functional theory (DFT) calculations reveal that the Ga₅ core is unprecedently stabilized by only 2π electrons donated by the two K atoms above and beneath the ring center in the Ga₅K₂ metallic pentagonal bipyramid. Their pioneering work not only proves that the aromatic stabilization effect can be much stronger than what we have thought, but also shows the great potential to obtain 2π-aromatic large rings by solely using the group 13 elements.

A fundamental question then arises: besides the above Ga₅ ring synthesized in an experiment, can we find/design more five-membered and even larger six-membered rings with the rare 2π aromaticity? If yes, it will greatly enrich the family and also expand the possible ring size range of 2π aromatics. Herein, by screening a series of inverse-sandwich and half-sandwich structures composed of central group 13 five/six-membered rings and two alkali/one alkaline-earth metal atoms, we predict seven new molecules to have the largest planar Al₅, Ga₅, In₅, Al₆ and In₆ rings with the unusual 2π aromaticity for the first time.

2. Computational methods

Full geometry optimizations were carried out by using the M06-2X functional²⁵ and def2-TZVP basis set for all the elements.²⁶ Harmonic vibrational frequencies were calculated at the same theoretical level after the optimization to characterize the nature of all the obtained stationary points on the potential energy surface. Recently, we predicted a series of inorganic five-membered heterocycles containing group 15 elements or group 15/16 elements to have π aromaticity and novel adaptive σ + π dual aromaticity, respectively, by using the same theoretical method.^27,28

To evaluate the feasibility of forming an inverse-sandwich structure from the isolated ring and two Na atoms, its binding energy was calculated as E_b = E_total – E_ring – 2E_Na, where E_total, E_ring and E_Na are the total energies of the whole molecule, central ring and an isolated Na atom, respectively. Similarly, for the half-sandwich structures, E_b = E_total – E_ring – E_Ca was calculated, where E_Ca is the energy of an isolated Ca atom. Therefore, a negative E_b value suggests that the sandwich formation is thermodynamically favorable.

The molecular orbitals were analyzed by using the Multiwfn program.²⁹ The quantum theory of atoms in molecules (QTAIM)³⁰ method was used for the topology analysis of electron density. As one most popular aromaticity criterion, nucleus-independent chemical shifts (NICS_iso; iso = isotropic, in ppm) and their perpendicular tensors, NICS_zz were computed at selected points in space by using the gauge-independent atomic orbital (GIAO) method.³¹ High aromaticity, antiaromaticity and nonaromaticity are indicated by more negative, more positive and zero NICS values, respectively. The orbital contribution to the NICS was calculated by using the continuous set of gauge transformation (CSGT) method,³² which generally obtains a very similar total contribution for the same type of orbital (σ or π) as the GIAO method. The magnetically induced ring current density was calculated using the AICD³³ and GIMIC^34,35 programs. All the DFT calculations were carried out by employing the Gaussian 16 software package.³⁶ The results were visualized using the Mercury,³⁷ VMD³⁸ and ParaView³⁹ softwares.

3. Results and discussion

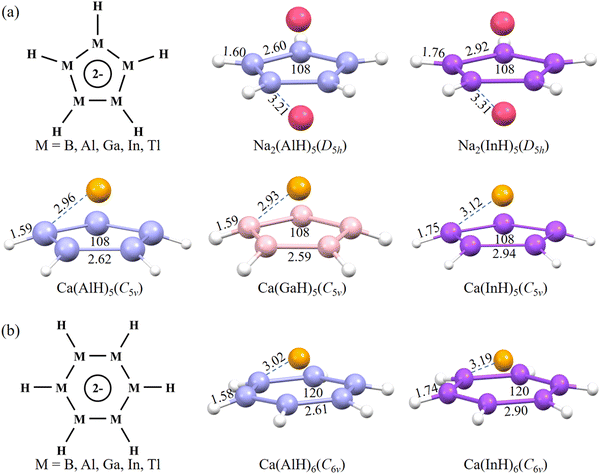
To search for planar five-membered rings with potential 2π aromaticity, ten inverse-sandwich structures in the neutral form of AM₂(MH)₅ (M = B, Al, Ga, In, and Tl; AM = Na, K) similar to the coordination environment of the experimentally reported Ga₅ ring²⁴ were first considered (Fig. 1a). They are designed also because similar isolated or ligand-protected inverse-sandwich systems but containing small three-membered M₃ (M = B, Al, and Ga) rings unambiguously exhibit 2π aromaticity.^{14–16,40,41} As a monovalent ligand, H atoms are added here to cause s–p hybridization of the central ring atoms. Each group 13 atom is then expected to assume the sp² hybridization state and all its three valence electrons (ns²np¹), respectively, occupy the three sp² orbitals, which overlap with the H-s orbital or the sp² orbitals of adjacent M atoms to form one M–H and two M–M bonds constituting the σ ring backbone. Its p_z orbital perpendicular to the ring plane is empty, meaning that the central (MH)₅ ring does not have any π electrons. The two alkali metal atoms sandwiching the central ring are then expected to donate two s valence electrons (one from each) to populate the latter's π orbitals formed from the p_z overlap to generate an (MH)₅²⁻ ring anion with possible 2π aromaticity.

Fig. 1 Schematic structures of the central (a) (MH)₅²⁻ and (b) (MH)₆²⁻ rings as well as optimized structures (with point-group symmetry) of the corresponding inverse- or half-sandwich molecules. Bond distances and interior angles are given in Å and degree, respectively. Al: blue, Ga: pink, In: purple, Na: red, Ca: orange, and H: white.

After the geometry optimization at the M06-2X/def2-TZVP level of theory, Na₂(AlH)₅ and Na₂(InH)₅ among them well maintain their planar central ring structures (Fig. 1a). It is noteworthy that K₂(AlH)₅ and K₂(InH)₅ both have seriously distorted five-membered rings, indicating the key role of Na atoms in maintaining the ring planarity. In previous gas-phase experiments, a Na⁺ cation can effectively interact with the metastable/unstable square planar M₄²⁻ (M = Al, Ga, and In) rings with 2π electrons to form stable NaM₄⁻ ionic clusters.^18,19

Besides the above inverse-sandwich structures, we further considered five half-sandwich structures containing the above (MH)₅ rings coordinated with a divalent Ca atom above the ring plane, which could also donate the expected two electrons to the central ring. Such half-sandwich structures are inspired by the pyramidal structures of the aforementioned 2π-aromatic NaM₄⁻ clusters achieved in gas-phase experiments.^18,19 This leads to the successful optimization of three Ca(AlH)₅, Ca(GaH)₅ and Ca(InH)₅ structures all featuring planar central rings (Fig. 1a). More importantly, we also obtained two half-sandwich structures with even larger planar six-membered (MH)₆ rings, Ca(AlH)₆ and Ca(InH)₆, using the same design strategy (Fig. 1b). It is worth noting that they would be the largest 2π-aromatic rings once the aromaticity is confirmed. Encouragingly, all of the above seven molecules (i.e., five five-membered Na₂(AlH)₅, Na₂(InH)₅, Ca(AlH)₅, Ca(GaH)₅ and Ca(InH)₅; two six-membered Ca (AlH)₆ and Ca(InH)₆) have no imaginary frequency at the current level of theory (optimized Cartesian coordinates and the lowest frequencies are provided in the ESI†), confirming that they are all energy minima on the corresponding potential energy surfaces. They can maintain perfect planar ring structures, which are also different from the four-membered boracycles with a puckered framework.¹⁷ They all have a singlet ground state with other spin states much higher in energy (Table S1, ESI†). The calculations using the larger def2-QZVP and def2-TZVPPD basis sets give very similar optimized geometries and relative energies, confirming that the current level of theory is reasonable and accurate enough (Fig. S1 and S2, ESI†).

The two inverse-sandwich Na₂(AlH)₅ and Na₂(InH)₅ have D_5h symmetry, whereas the five half-sandwich structures exhibit C_5v or C_6v symmetry. Regardless of the ring size, the calculated Al–Al (Ga–Ga) and In–In bond lengths are ca. 2.60 and 2.90 Å, respectively, whereas the peripheral Al–H (Ga–H) and In–H bonds are around 1.60 and 1.75 Å, respectively. All these distances are close to the sum of corresponding element covalent radii, indicating the formation of ring backbones via strong covalent bonds. Their M–Na (M–Ca) distances are all larger than 2.90 Å, which may favor ionic bonding at long distances.⁴⁰ The central M₅ and M₆ rings all have the same interior angles of 108° and 120°, respectively, which are consistent with a regular pentagon and hexagon. Their ring planarity was further quantitatively confirmed by the calculated zero values for both the molecular planarity parameter (MPP) and span of deviation from the plane (SDP) by using the Multiwfn program (Fig. S3, ESI†).²⁹ Thus, the perfect planar ring structures with equivalent M–M bond lengths (these characteristics should originate from the π electron delocalization, vide infra) promise their aromaticity. In addition, the calculated binding energies (E_b) of Na₂(AlH)₅, Na₂(InH)₅, Ca(AlH)₅, Ca(GaH)₅, Ca(InH)₅, Ca(AlH)₆, and Ca(InH)₆ are as negative as −86.8, −79.3, −50.6, −56.2, −41.9, −43.9 and −32.7 kcal mol⁻¹, respectively, indicating their good structural stabilities against dissociation.

Natural bond orbital (NBO) analyses were further conducted to investigate the electronic structures of all the above seven compounds (Table 1). All the group 13 atoms in the central ring have slightly positive charges (≤ +0.11), whereas each surrounding H atom has a negative charge of about −0.3. Compared to the free state (Na: [Ne]3s¹, Ca: [Ar]4s²), the obviously reduced populations on the Na-3s and Ca-4s orbitals confirm the transfer of about one and two electrons from each Na and Ca atom, respectively, to the central ring. The charges are indeed transferred from Na/Ca to the metal atoms as confirmed by the calculated charge density difference, in which large electron accumulations are found on the metallic rings (Fig. S4, ESI†). Accordingly, their electronic structures can be formally assigned as (Na₂)²⁺(AlH)₅²⁻, (Na₂)²⁺(InH)₅²⁻, Ca²⁺(AlH)₅²⁻, Ca²⁺(GaH)₅²⁻, Ca²⁺(InH)₅²⁻, Ca²⁺(AlH)₆²⁻ and Ca²⁺(InH)₆²⁻.

Table 1 Natural population analysis (NPA) charges, natural electron configuration populations, electron occupancies (Occ., e) and hybrid composition

Species	Atom	NPA	Population	Bond	Occ.	Hybrid composition
Na2(AlH)5	Al	+0.07	3s^1.113p^1.79	Al–Al	1.92	Al s(32%)p(68%)
	H	−0.36	1s^1.36	Al–H	1.99	Al s(37%)p(63%)
	Na	+0.74	3s^0.26			H s(100%)
Na2(InH)5	In	+0.07	5s^1.235p^1.69	In–In	1.87	In s(30%)p(70%)
	H	−0.34	1s^1.34	In–H	1.98	In s(40%)p(60%)
	Na	+0.68	3s^0.32			H s(100%)
Ca(AlH)5	Al	+0.10	3s^1.123p^1.74	Al–Al	1.86	Al s(31%)p(69%)
	H	−0.35	1s^1.35	Al–H	1.98	Al s(38%)p(62%)
	Ca	+1.27	4s^0.573d^0.18			H s(100%)
Ca(GaH)5	Ga	+0.04	4s^1.184p^1.76	Ga–Ga	1.84	Ga s(31%)p(69%)
	H	−0.30	1s^1.30	Ga–H	1.98	Ga s(39%)p(61%)
	Ca	+1.33	4s^0.513d^0.18			H s(100%)
Ca(InH)5	In	+0.08	5s^1.265p^1.65	In–In	1.79	In s(30%)p(70%)
	H	−0.33	1s^1.33	In–H	1.98	In s(40%)p(60%)
	Ca	+1.26	4s^0.583d^0.17			H s(100%)
Ca(AlH)6	Al	+0.11	3s^1.113p^1.75	Al–Al	1.89	Al s(31%)p(69%)
	H	−0.34	1s^1.34	Al–H	1.98	Al s(38%)p(62%)
	Ca	+1.39	4s^0.443d^0.19			H s(100%)
Ca(InH)6	In	+0.07	5s^1.235p^1.69	In–In	1.85	In s(30%)p(70%)
	H	−0.31	1s^1.31	In–H	1.97	In s(40%)p(60%)
	Ca	+1.42	4s^0.433d^0.15			H s(100%)

---

Fig. 2 and 3 depict the frontier molecular orbitals of the five- and six-membered ring systems, respectively. They all have large energy gaps (≥ 2.8 eV) between the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO), suggesting their good kinetic stabilities. Each of the five sandwiched Al/Ga/In atoms assumes the sp² hybrid state, as indicated by the calculated hybrid composition in Table 1, with its empty p_z orbital perpendicular to the ring plane. The in-phase overlap of the five/six p_z orbitals of the ring atoms forms a completely delocalized and doubly occupied π bonding orbital (HOMO or HOMO−1) after accepting two electrons from the two Na atoms or one Ca atom. Such good π electron delocalization should account for their perfect pentagonal/hexagonal structures with all equal M–M bonds. Their LUMOs are all the typical π* antibonding orbitals in aromatic compounds. These central rings thus obey the 4n + 2 π-electron rule (n = 0) and assure the 2π aromaticity, as confirmed by further analyses (vide infra).

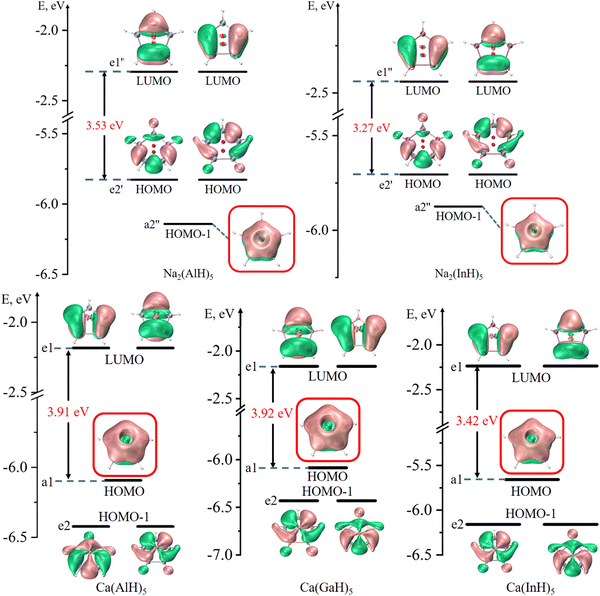Fig. 2 Frontier molecular orbitals of five-membered Na₂(AlH)₅, Na₂(InH)₅, Ca(AlH)₅, Ca(GaH)₅ and Ca(InH)₅ (isovalue: ±0.03 a.u.). The π bonding orbitals are highlighted in red boxes.

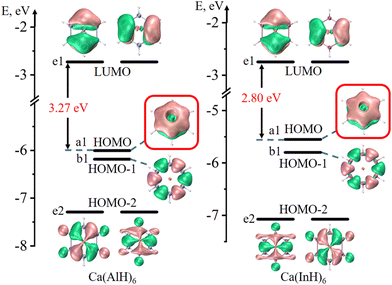Fig. 3 Frontier molecular orbitals of six-membered Ca(AlH)₆ and Ca(InH)₆ (isovalue: ± 0.03 a.u.). The π bonding orbitals are highlighted in red boxes.

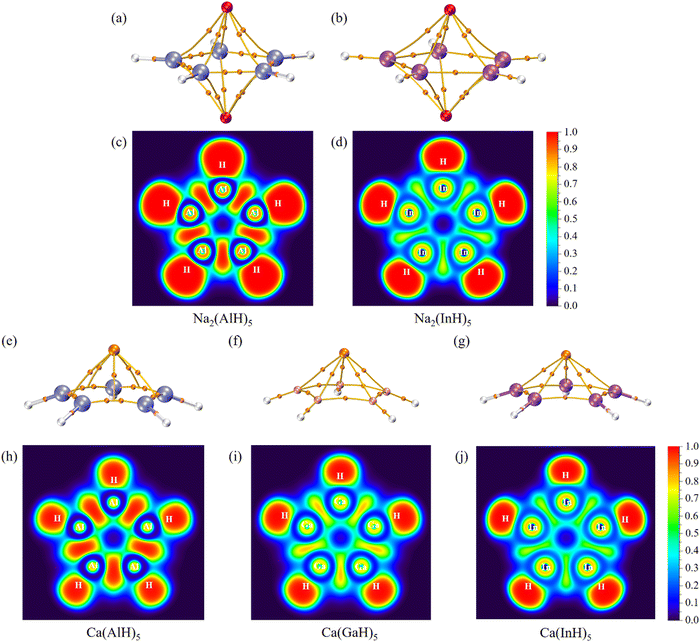
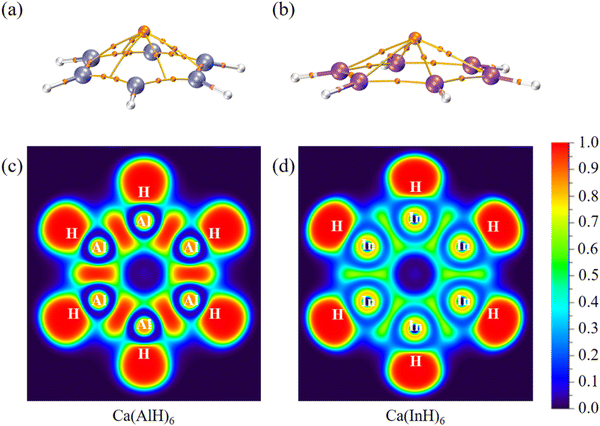
We further carried out QTAIM analyses to reveal their bonding nature. There is one bond critical point (BCP) for each homonuclear Ga–Ga or In–In bond (Fig. 4 and 5). However, two BCPs are located for each Al–Al bond due to the presence of a non-nuclear attractor (NNA, i.e., the maximum of the electron density, also named as pseudoatom) at the bond midpoint. A similar phenomenon can be found for Li₂ dimer, and the bonding analysis based on BCP is thus unsuitable for Al–Al bonds (but its covalent nature can be revealed by the following electron localization function results). As summarized in Table 2, these BCPs exhibit relatively large electron density (ρ: 0.04/0.05 a.u.), small Laplacian of electron density (∇²ρ: −0.05 to 0.01 a.u.), negative total energy density (H: −0.02/−0.01 a.u.), a ratio of potential energy density to kinetic energy density (|V|/G: 1.86 to 3.22) larger than 1 and a G/ρ ratio (0.19 to 0.30) smaller than 1. These are covalent bond characteristics and agree with the corresponding large Wiberg bond order (WBO) values (0.84 to 0.91), indicating the presence of M–M single bonds. Similarly, the covalent nature of M–H single bonds can be concluded as well. These results are also consistent with the calculated electron occupancies of ca. 2 for each bond (Table 1). The electron localization function (ELF)⁴² plots for their central ring planes further confirm the strong covalent M–M and M–H bonds with large local electron accumulation (Fig. 4c, d, h–j and 5c and d), ensuring the good stability of the whole ring plane and promising possible aromaticity.

Fig. 4 Molecular graphs (a, b, e–g) for all five-membered ring systems, where the BCPs are denoted by small orange balls with other critical points omitted for clarity as well as ELF plots (c, d, h–j) for their ring planes.

Fig. 5 Molecular graphs (a, b) for all six-membered ring systems, where the BCPs are denoted by small orange balls with other critical points omitted for clarity as well as ELF plots (c, d) for their ring planes.

Table 2 Interatomic distances (d, Å), WBOs and QTAIM parameters (a.u.) of seven molecules

Species		d	WBO	ρ	∇^2ρ	H	|V|/G	G/ρ
Na2(AlH)5	Al–Al	2.60	0.91	0.05	−0.04	−0.02	2.95	0.23
	Al–H	1.60	0.90	0.08	0.21	−0.02	1.31	0.96
	Al–Na	3.21	0.32	0.01	0.02	0.00	1.00	0.47
Na2(InH)5	In–In	2.92	0.91	0.04	0.01	−0.01	1.88	0.30
	In–H	1.76	0.92	0.10	0.12	−0.04	1.60	0.70
	In–Na	3.31	0.34	0.01	0.02	0.00	0.99	0.45
Ca(AlH)5	Al–Al	2.62	0.84	0.05	−0.05	−0.02	3.22	0.19
	Al–H	1.59	0.90	0.08	0.22	−0.02	1.32	0.99
	Al–Ca	2.96	0.79	0.02	0.04	0.00	1.12	0.56
Ca(GaH)5	Ga–Ga	2.59	0.84	0.05	−0.03	−0.02	2.61	0.23
	Ga–H	1.59	0.90	0.11	0.16	−0.05	1.51	0.78
	Ga–Ca	2.93	0.80	0.02	0.05	0.00	1.11	0.65
Ca(InH)5	In–In	2.94	0.85	0.04	0.01	−0.01	1.86	0.28
	In–H	1.75	0.92	0.10	0.12	−0.04	1.58	0.72
	In–Ca	3.12	0.79	0.02	0.04	0.00	1.12	0.59
Ca(AlH)6	Al–Al	2.61	0.86	0.05	−0.04	−0.02	3.09	0.21
	Al–H	1.58	0.89	0.08	0.22	−0.03	1.31	1.00
	Al–Ca	3.02	0.71	0.02	0.04	0.00	1.10	0.55
Ca(InH)6	In–In	2.90	0.89	0.04	0.01	−0.01	1.92	0.27
	In–H	1.74	0.91	0.10	0.12	−0.04	1.57	0.73
	In–Ca	3.19	0.68	0.02	0.03	0.00	1.00	0.55

---

For comparison, the corresponding density topology parameters and smaller WBOs for the M–Na bonds suggest that they are mainly ionic with some covalent characteristics, and the covalent component becomes more obvious for the M–Ca bonds, which are consistent with their large binding energies (vide supra). Thus, the Na/Ca atoms should play an important role in stabilizing the whole molecule structure, and they are not separated cations only providing the required two valence electrons. Similar strong Na–Al ring interactions can also be found in the experimentally achieved cyclotrialuminene, which was thus considered as a Na/Al cluster.¹⁴

Interestingly, our systems may also have novel collective bonding,⁴³ namely each Na/Ca atom (denoted here as M1) interacts with both the metal ring and the surrounding H atoms via the combination of electrostatic interactions and covalency. Table S2 (ESI†) summarizes the interacting quantum atoms (IQA) analysis results obtained by using the AIMAll software.⁴⁴ For all the complexes, the V_C(M1,M) and V_XC(M1,M) values are positive and negative, respectively, indicating that there is obvious coulombic repulsion and covalent interactions between Na/Ca atoms and the M₅/M₆ rings. For Na₂(InH)₅, Ca(GaH)₅, Ca(InH)₅ and Ca(InH)₆, the resultant V_Int(M1,M) values are negative and obvious attractions are thus present between their Na/Ca and metal rings. By comparison, all the M1–H interactions have both negative V_XC(M1,H) and V_C(M1,H) values, resulting in more negative V_Int(M1,H) values and strong attractions between Na/Ca and the surrounding H atoms.

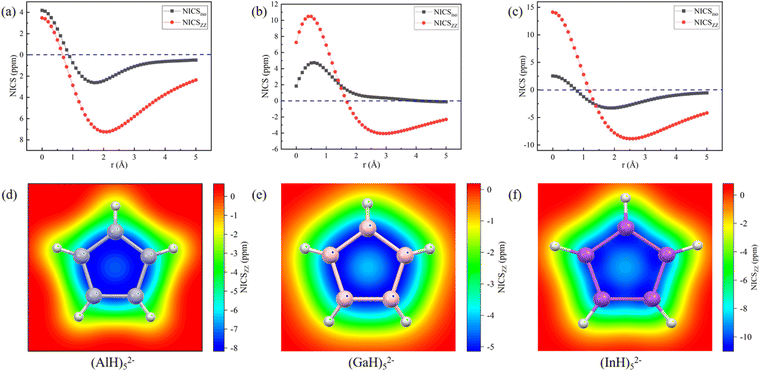
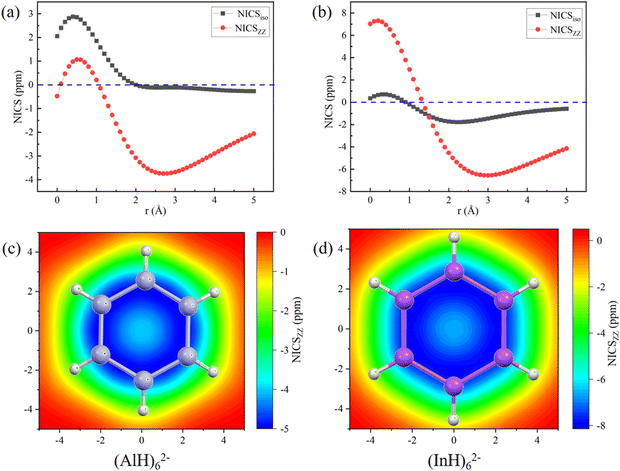
The aromatic characters of their central five- and six-membered rings were then quantitatively probed by scanning the NICS values, which were more suitable than those calculated at the single point.^45,46 To avoid the interference, both the NICS_iso and NICS_zz values were scanned for the central (MH)₅²⁻ and (MH)₆²⁻ ring anions without the Na/Ca atoms. The scan covers the distances of 0.0 to 5.0 Å (step: 0.1 Å) above each ring in the direction perpendicular to the ring plane. Fig. 6 and 7 show that all the NICS values along the curves change from positive (σ-electron dominated region) to negative (π-electron dominated region) with increased distance from the ring plane, thus showing an obvious π-aromatic behavior.⁴⁶ The smallest NICS_zz values for the (AlH)₅²⁻, (GaH)₅²⁻, (InH)₅²⁻, (AlH)₆²⁻ and (InH)₆²⁻ rings are −7.25, −4.07, −8.87, −3.75, and −6.56 ppm, respectively. For a direct comparison, the experimentally reported Ga₅[CH(SiMe₃)₂]₅²⁻ ring without two K atoms has the smallest NICS_zz value of −6.04 ppm at the current level of theory (Fig. S5, ESI†).²⁴ Thus, their central ring backbones all have comparable aromaticity. The aromaticity indeed mainly stems from their π orbitals highlighted in Fig. 2 and 3, as indicated by the calculated NICS_zz contributions of −6.04, −4.04, −5.64, −4.45 and −4.61 ppm from the π orbitals of (AlH)₅²⁻, (GaH)₅²⁻, (InH)₅²⁻, (AlH)₆²⁻ and (InH)₆²⁻, respectively, by using the Multiwfn program. For comparison, the π contribution to the smallest NICS_zz value is −8.58 ppm for the Al₄²⁻ cluster with the same 2π aromaticity, which also features a strong diatropic σ system (Fig. S6, ESI†).⁴⁷ For the two (InH)₅²⁻ and (InH)₆²⁻ rings, negative NICS_zz values also have minor contributions from several σ orbitals along the ring framework, probably due to the large atomic size of the element In. In addition, we further calculated the two-dimensional NICS_zz grids at 2.1, 2.9, 2.5, 2.7 or 3.0 Å (i.e., the height corresponding to the above smallest NICS_zz value for each ring) above the ring planes. As shown in Fig. 6d–f and 7c and d, all the rings exhibit obvious aromatic character with negative NICS_zz values (in blue) within the whole ring regions.

Fig. 6 NICS profiles along the direction perpendicular to the ring planes and two-dimensional NICS_zz grids above the ring planes (height: 2.1, 2.9 or 2.5 Å; area: 5 Å × 5 Å; and resolution: 0.2 Å) of (a) and (d) (AlH)₅²⁻, (b) and (e)(GaH)₅²⁻ and (c) and (f) (InH)₅²⁻.

Fig. 7 NICS profiles along the direction perpendicular to the ring planes and two-dimensional NICS_zz grids above the ring planes (height: 2.7 or 3.0 Å; area: 5 Å × 5 Å; and resolution: 0.2 Å) of (a) and (c) (AlH)₆²⁻ and (b) and (d) (InH)₆²⁻.

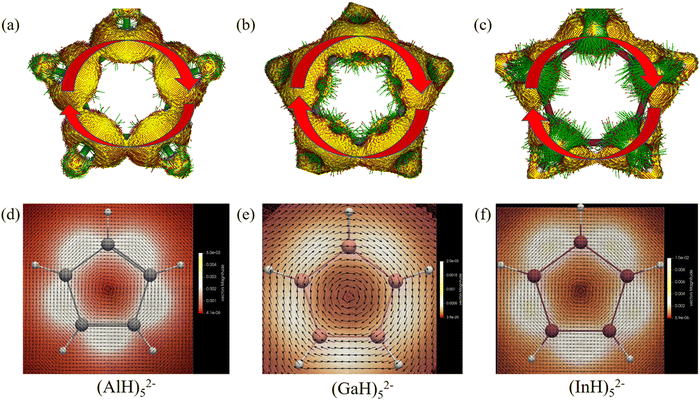
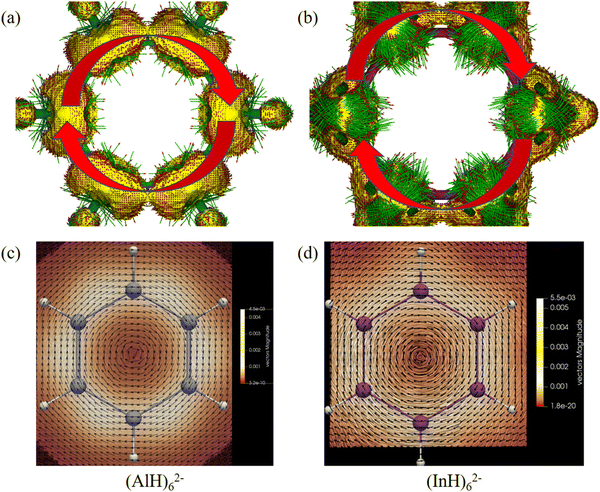
We then further investigated the anisotropy of the induced current density (ACID) in the central ring anions. Similar to the electron movement in a wire loop, they should sustain diatropic ring current when an external magnetic field is applied perpendicular to the ring plane due to the cyclical 2π-electron delocalization. Indeed, Fig. 8 and 9 reveal that they all have diamagnetic (clockwise) ring currents over the whole ring plane. The induced ring currents at the above heights were also visualized by using the GIMIC program to be purely diatropic (Fig. 8d–f and 9c and d), confirming again their obvious π aromaticity. The presence of the NICS maximum near the ring planes and the minimum far away from the rings in Fig. 6 and 7 can also be understood by the strong local diatropic electronic currents around the metal nuclei in the ring planes, which induces a magnetic deshielding around the ring centers as found for the Cu₃⁺ and Cu₄²⁻ clusters (Fig. S7, ESI†).⁴⁸ The magnitudes of magnetically induced ring-current strength obtained by integrating the current density flux along the M–M bonds are 3.87, 4.66, 4.68, 5.89 and 6.01 nA T⁻¹ for (AlH)₅²⁻, (GaH)₅²⁻, (InH)₅²⁻, (AlH)₆²⁻ and (InH)₆²⁻, respectively, all larger than that for the Ga–Ga bond in Ga₅[CH(SiMe₃)₂]₅²⁻ (3.77 nA T⁻¹ at the current level of theory). Evidently, their currents are all weaker than and about one third of that of benzene (13.02 nA T⁻¹), which is consistent with the number difference of their delocalized π electrons (2π vs. 6π).

Fig. 8 ACID isosurfaces (isovalue: 0.025 a.u.; green arrows denote current density vectors) and induced ring currents (height: 2.1, 2.9 or 2.5 Å; black arrows denote current density vectors) of (a) and (d) (AlH)₅²⁻, (b) and (e) (GaH)₅²⁻ and (c) and (f) (InH)₅²⁻. The external magnetic field is perpendicular to the ring plane and points towards the reader, and clockwise currents thus mean diatropic.

Fig. 9 ACID isosurfaces (isovalue: 0.025 a.u.; green arrows denote current density vectors) and induced ring currents (height: 2.7 or 3.0 Å; black arrows denote current density vectors) of (a) and (c) (AlH)₆²⁻ and (b) and (d) (InH)₆²⁻. The external magnetic field is perpendicular to the ring plane and points towards the reader, and clockwise currents thus mean diatropic.

Finally, their aromatic characters in three-dimensional space were further confirmed by the isosurface maps of the zz component of iso-chemical shielding surfaces (ICSS_zz).⁴⁹ As shown in Fig. S8 (ESI†), all our inverse- and half-sandwiches exhibit obvious aromaticity around the central rings, as indicated by the positive ICSS_zz values. For comparison, the more conventional sandwich such as [Al–Cp–Al]⁺ and its central Cp⁻ ring have stronger aromaticity due to the presence of 6π electrons.⁵⁰

4. Conclusions

In summary, by rationally designing and screening inverse-sandwich structures of AM₂(MH)₅ (M = B-Tl; AM = Na/K) and half-sandwich structures of Ca(MH)₅ or Ca(MH)₆, we found that seven among them have high symmetry and perfect planar central five- or six-membered rings as well as equal M–M bond lengths. After accepting two electrons from Na or Ca atoms to populate empty p_z orbitals, their central dianionic Al₅/Al₆, Ga₅, and In₅/In₆ rings each have a well-defined occupied π orbital and thus exhibit obvious 2π aromaticity and an induced ring current, which may be even stronger than those of the recently achieved Ga₅ analogue. Thus, these molecules represent the largest 2π-aromatic rings reported thus far. In addition, they also feature interesting collective interactions besides the rare ring aromaticity.

Our work not only adds five five-membered and two six-membered large rings to the family of precious 2π aromatics, but also demonstrates the great potential of group 13 elements in constructing 2π-aromatic rings of larger sizes. It enriches the concept of metalloaromaticity by extending to more heavy main group all-metal rings. The disclosed aromatic characteristics of such systems are also useful for designing, synthesizing and understanding related organometallic compounds containing the same/similar rings as building blocks although they may need to be stabilized via additional coordination and organic ligands.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors gratefully acknowledge financial support from the National Natural Science Foundation of China (No. 22171068) and Natural Science Foundation of Hebei Province (B2022202036).

Notes and references

1. V. I. Minkin, Pure Appl. Chem., 1999, 71, 1919–1981.
2. M. Solà, Nat. Chem., 2022, 14, 585–590.
3. J. Zhu, Commun. Chem., 2020, 3, 161.
4. G. Merino, M. Solà, I. Fernández, C. Foroutan-Nejad, P. Lazzeretti, G. Frenking, H. L. Anderson, D. Sundholm, F. P. Cossío, M. A. Petrukhina, J. Wu, J. I. Wu and A. Restrepo, Chem. Sci., 2023, 14, 5569–5576.
5. H. Ottosson, Chem. Sci., 2023, 14, 5542–5544.
6. A. I. Boldyrev and L. S. Wang, Chem. Rev., 2005, 105, 3716–3757.
7. J. M. Mercero, A. I. Boldyrev, G. Merino and J. M. Ugalde, Chem. Soc. Rev., 2015, 44, 6519–6534.
8. E. Hückel, Z. Phys., 1932, 76, 628–648.
9. R. Breslow, J. Am. Chem. Soc., 1957, 79, 5318.
10. G. A. Olah, J. M. Bollinger and A. M. White, J. Am. Chem. Soc., 1969, 91, 3667–3669.
11. X. Sun, T. Simler, R. Yadav, R. Köppe and P. W. Roesky, J. Am. Chem. Soc., 2019, 141, 14987–14990.
12. C. Präsang, A. Mlodzianowska, Y. Sahin, M. Hofmann, G. Geiseler, W. Massa and A. Berndt, Angew. Chem., Int. Ed., 2002, 41, 3380–3382.
13. T. Kupfer, H. Braunschweig and K. Radacki, Angew. Chem., Int. Ed., 2015, 54, 15084–15088.
14. R. J. Wright, M. Brynda and P. P. Power, Angew. Chem., Int. Ed., 2006, 45, 5953–5956.
15. X.-W. Li, W. T. Pennington and G. H. Robinson, J. Am. Chem. Soc., 1995, 117, 7578–7579.
16. X.-W. Li, Y. Xie, P. R. Schreiner, K. D. Gripper, R. C. Crittendon, C. F. Campana, H. F. Schaefer and G. H. Robinson, Organometallics, 1996, 15, 3798–3803.
17. W. Mesbah, C. Präsang, M. Hofmann, G. Geiseler, W. Massa and A. Berndt, Angew. Chem., Int. Ed., 2003, 42, 1717–1719.
18. X. L. Li, A. E. Kuznetsov, H. F. Zhang, A. I. Boldyrev and L. S. Wang, Science, 2001, 291, 859–861.
19. A. E. Kuznetsov, A. I. Boldyrev, X. Li and L. S. Wang, J. Am. Chem. Soc., 2001, 123, 8825–8831.
20. A. V. Protchenko, J. Urbano, J. A. B. Abdalla, J. Campos, D. Vidovic, A. D. Schwarz, M. P. Blake, P. Mountford, C. Jones and S. Aldridge, Angew. Chem., Int. Ed., 2017, 56, 15098–15102.
21. H. Masui, Coord. Chem. Rev., 2001, 219–221, 957–992.
22. Y. Wang and G. H. Robinson, Organometallics, 2007, 26, 2–11.
23. R. Breslow and E. Mohacsi, J. Am. Chem. Soc., 1963, 85, 431–434.
24. O. Kysliak, S. H. F. Schreiner, N. Grabicki, P. Liebing, F. Weigend, O. Dumele and R. Kretschmer, Angew. Chem., Int. Ed., 2022, 61, e202206963.
25. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
26. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
27. X. Gu, L. Yang and P. Jin, Phys. Chem. Chem. Phys., 2022, 24, 22091–22101.
28. J. Chen, L. Yang, Y. Li, Q. Hou, L. Li and P. Jin, Int. J. Quantum Chem., 2019, 119, e25961.
29. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
30. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990.
31. K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260.
32. T. A. Keith and R. F. W. Bader, Chem. Phys. Lett., 1993, 210, 223–231.
33. D. Geuenich, K. Hess, F. Kohler and R. Herges, Chem. Rev., 2005, 105, 3758–3772.
34. J. Jusélius and D. Sundholm, J. Chem. Phys., 2004, 121, 3952–3963.
35. H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518.
36. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2019.
37. C. F. Macrae, P. R. Edgington, P. McCabe, E. Pidcock, G. P. Shields, R. Taylor, M. Towler and J. van de Streek, J. Appl. Crystallogr., 2006, 39, 453–457.
38. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
39. J. Ahrens, B. Geveci and C. C. Law, ParaView: An End-User Tool for Large Data Visualization, Visualization Handbook, Elsevier, 2005, ISBN-13: 9780123875822.
40. Y. Xie, P. R. Schreiner, H. F. Schaefer III, X.-W. Li and G. H. Robinson, J. Am. Chem. Soc., 1996, 118, 10635–10639.
41. X. Li, J. Sun, Y. Zeng, Z. Sun, S. Zheng and L. Meng, J. Phys. Chem. A, 2012, 116, 5491–5496.
42. A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403.
43. S. Sowlati-Hashjin, V. Šadek, S. Sadjadi, M. Karttunen, A. Martín-Pendás and C. Foroutan-Nejad, Nat. Commun., 2022, 13, 2069.
44. T. A. Keith, AIMAll (Version 19.10.12), TK Gristmill Software, Overland Park KS, USA, 2019 (https://aim.tkgristmill.com).
45. A. Stanger, J. Org. Chem., 2006, 71, 883–893.
46. J. O. C. Jiménez-Halla, E. Matito, J. Robles and M. Solà, J. Organomet. Chem., 2006, 691, 4359–4366.
47. R. Islas, T. Heine and G. Merino, J. Chem. Theory Comput., 2007, 3, 775–781.
48. Z. Badri, S. Pathak, H. Fliegl, P. Rashidi-Ranjbar, R. Bast, R. Marek, C. Foroutan-Nejad and K. Ruud, J. Chem. Theory Comput., 2013, 9, 4789–4796.
49. S. Klod and E. Kleinpeter, J. Chem. Soc., Perkin Trans. 2, 2001, 1893–1898.
50. I. Fernández, E. Cerpa, G. Merino and G. Frenking, Organometallics, 2008, 27, 1106–1111.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04159j

---